钦定古今图书集成.历象汇编.历法典.算法部
钦定古今图书集成历象汇编历法典
第一百二十二卷目录
算法部汇考十四
算法统宗十〈方程章第八 句股章第九〉
算法统宗十〈方程章第八 句股章第九〉
历法典第一百二十二卷
算法部汇考十四
《算法统宗十》方程章第八
方,正也;程,数也。以诸物总并为问,去繁就简为主。乃诸物繁亢,诸价错杂,必须布置行列,或损益加减,同异正负,递互遍乘,求其有等。以少减多,馀物为法,馀价为实。性实相除,得一价以推其馀。若繁杂甚者,次第求之。正者,正数。负者,欠数。
二色方程歌
世人欲要识方程,物价俱将左右陈。右上法乘左中下,次将左上右行乘。中间相减馀为法,下位相减馀实情。法除实为右中价,得价须将右中乘。右下价内减去积,馀为实数甚分明。右上为法除下实,便为上价细推寻。
今有马三匹,牛二头,共价银一百一十四两。又马四匹,牛五头,共价一百六十二两五钱。问:马牛价各若干。
答曰:马每匹价三十五两,牛每匹价四两五钱。法曰:列所问数
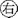 上马〈三匹〉为法〈先乘左〉中牛二〈乘得八〉 下价〈一百一十四两〉 得〈四百五十六两〉
上马〈三匹〉为法〈先乘左〉中牛二〈乘得八〉 下价〈一百一十四两〉 得〈四百五十六两〉 上马〈四匹〉为法〈次乘右〉中牛五〈乘得一十五〉 下价〈一百六十二两五钱〉 得〈四百八十七两五钱〉先以右行马三为法,遍乘左行中牛五,得一十五。又以法乘左行下价一百六十二两五钱,得四百八十七两五钱。却以左行马四为法,复遍乘右行中牛二,得八。减左行乘得牛十五,馀七为法。又以左上马四乘右下价一百一十四两,得四百五十六两。减左行乘价四百八十七两五钱,馀三十一两五钱为实。以法七除之,得牛匹价四两五钱。却以右行中牛二乘之,得九两。以减右行下价一百一十四两,馀一百零五两为实。以右行马三为法除之,得马一匹价三十五两。合问。
上马〈四匹〉为法〈次乘右〉中牛五〈乘得一十五〉 下价〈一百六十二两五钱〉 得〈四百八十七两五钱〉先以右行马三为法,遍乘左行中牛五,得一十五。又以法乘左行下价一百六十二两五钱,得四百八十七两五钱。却以左行马四为法,复遍乘右行中牛二,得八。减左行乘得牛十五,馀七为法。又以左上马四乘右下价一百一十四两,得四百五十六两。减左行乘价四百八十七两五钱,馀三十一两五钱为实。以法七除之,得牛匹价四两五钱。却以右行中牛二乘之,得九两。以减右行下价一百一十四两,馀一百零五两为实。以右行马三为法除之,得马一匹价三十五两。合问。今有绫三尺,绢四尺,共价四钱八分。又绫七尺,绢二尺,共价六钱八分。问:绫绢各价若干。
答曰:绫每尺价八分,绢每尺价六分。
法曰:列所问数
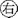 绫〈三尺〉为法〈先乘左〉 绢〈四尺〉得〈二十八〉 价〈四钱八分〉 得三两三钱六分
绫〈三尺〉为法〈先乘左〉 绢〈四尺〉得〈二十八〉 价〈四钱八分〉 得三两三钱六分 绫〈七尺〉为法〈次乘右〉 绢〈二尺〉乘得〈六〉 价〈六钱八分〉 乘得二两零四分先以右行绫三为法遍乘左中下,得数。却以左行绫七为法复遍乘右行中绢四,得二十八。减左行中得绢六馀二十二为法。又以左绫七乘右价四钱八分,得三两三钱六分。减左行乘得价二两零四分,馀一两三钱二分为实。以法二十二除之,得绢每尺价六分。就以右行绢四尺乘之,共得绢价二钱四分。以减右行价四钱八分,馀二钱四分。以绫三尺为法除之,得绫每尺价八分。合问。
绫〈七尺〉为法〈次乘右〉 绢〈二尺〉乘得〈六〉 价〈六钱八分〉 乘得二两零四分先以右行绫三为法遍乘左中下,得数。却以左行绫七为法复遍乘右行中绢四,得二十八。减左行中得绢六馀二十二为法。又以左绫七乘右价四钱八分,得三两三钱六分。减左行乘得价二两零四分,馀一两三钱二分为实。以法二十二除之,得绢每尺价六分。就以右行绢四尺乘之,共得绢价二钱四分。以减右行价四钱八分,馀二钱四分。以绫三尺为法除之,得绫每尺价八分。合问。三色方程歌
三色方程法更奇,物价三行左作基。左右互乘须减尽,中下价馀左位宜。又列二行仍乘减,中中左中减无馀。下馀为法价馀实,法实相除下价知。
此三色方程已后,内中或有正负、同异加减者。
今有砚三个,墨五匣,笔九枝,共价八钱一分。又砚四个,墨六匣,笔七枝,共价八钱九分。又砚五个,墨七匣,笔八枝,共价一两零六分。问:砚墨笔各价若干。答曰:砚每个八分,墨每匣六分,笔每枝三分。
法曰:列所问数
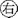 砚〈三〉为法〈先乘左右〉墨〈五〉得〈二十〉 笔〈九〉得〈三十六〉价〈八钱一分〉 得三两二钱四分
砚〈三〉为法〈先乘左右〉墨〈五〉得〈二十〉 笔〈九〉得〈三十六〉价〈八钱一分〉 得三两二钱四分 砚〈四〉得〈一十二〉 墨〈六〉得〈一十八〉笔〈七〉得〈二十一〉价〈八钱九分〉 得二两六钱七分
砚〈四〉得〈一十二〉 墨〈六〉得〈一十八〉笔〈七〉得〈二十一〉价〈八钱九分〉 得二两六钱七分 砚〈五〉得〈一十五〉 墨〈七〉得〈二十一〉笔〈八〉得〈二十四〉价〈一两零六分〉得三两一钱八分先以右行砚三为法,遍乘左中二行得数。却以中行砚四遍乘右行墨笔得数。墨得二十,笔得三十六,价得三两二钱四分。与中行对减,馀墨二,笔十五,价五钱七分。另列右位,又以左行砚五为法,遍乘右行墨笔得数,墨二十五,笔四十五,价四两零五分。与左行对减,馀墨四,笔二十一,价八钱七分。另列左位,再列减馀,以分左右位数。以右行墨二为法,遍乘左行笔价,得数列左位。
砚〈五〉得〈一十五〉 墨〈七〉得〈二十一〉笔〈八〉得〈二十四〉价〈一两零六分〉得三两一钱八分先以右行砚三为法,遍乘左中二行得数。却以中行砚四遍乘右行墨笔得数。墨得二十,笔得三十六,价得三两二钱四分。与中行对减,馀墨二,笔十五,价五钱七分。另列右位,又以左行砚五为法,遍乘右行墨笔得数,墨二十五,笔四十五,价四两零五分。与左行对减,馀墨四,笔二十一,价八钱七分。另列左位,再列减馀,以分左右位数。以右行墨二为法,遍乘左行笔价,得数列左位。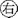 墨〈二〉 笔〈十五〉 得〈六十〉 价〈五钱七分〉 得二两二钱八分
墨〈二〉 笔〈十五〉 得〈六十〉 价〈五钱七分〉 得二两二钱八分 墨〈四〉 笔〈二十一〉 得〈四十〉价〈八钱七分〉 得一两七钱四分复以左行墨四为法,遍乘右行笔价,得数列右位。却以左右对减,墨尽,馀得笔一十八枝为法。又以馀价得数相减,馀五钱四分为实。以法除实,得笔价每枝三分。就以笔价乘后右馀笔十五,得四钱五分。以减右行馀价五钱七分,馀一钱二分。以右行馀墨二为法除之,得墨价每匣六分。于前右行原价八钱一分内,减原笔九价二钱七分,原墨五价三钱,馀二钱四分为实。以前右原砚三为法除之,得砚价每个八分。今有马一匹,骡二匹,驴三匹。皆载四石二斗,至坡皆不能上。马借骡一匹,骡借驴一匹,驴借马一匹,方过其坡。问:三等力各若干。
墨〈四〉 笔〈二十一〉 得〈四十〉价〈八钱七分〉 得一两七钱四分复以左行墨四为法,遍乘右行笔价,得数列右位。却以左右对减,墨尽,馀得笔一十八枝为法。又以馀价得数相减,馀五钱四分为实。以法除实,得笔价每枝三分。就以笔价乘后右馀笔十五,得四钱五分。以减右行馀价五钱七分,馀一钱二分。以右行馀墨二为法除之,得墨价每匣六分。于前右行原价八钱一分内,减原笔九价二钱七分,原墨五价三钱,馀二钱四分为实。以前右原砚三为法除之,得砚价每个八分。今有马一匹,骡二匹,驴三匹。皆载四石二斗,至坡皆不能上。马借骡一匹,骡借驴一匹,驴借马一匹,方过其坡。问:三等力各若干。答曰:马二石四斗,骡一石八斗,驴六斗。
法曰:列所问数
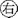 正马〈一〉为法〈先乘左中〉 〈借〉骡〈一〉 下空 四石二斗
正马〈一〉为法〈先乘左中〉 〈借〉骡〈一〉 下空 四石二斗 空 正骡〈二〉 〈借〉驴〈一〉 四石二斗
空 正骡〈二〉 〈借〉驴〈一〉 四石二斗 〈借〉马〈一〉 空〈负一〉 正驴〈三〉得〈三〉 四石二斗 得四石二斗先以右行正马一为法,遍乘左行中下得数。却以左行借马一为法,遍乘右行中下,得数。中得一因左行中空无减,加入负骡一。下空无数,转乘本行下正驴三,得三四石二斗。得四石二斗,与左行减尽。又以中行正骡二遍乘左行中下得数。中加一得二,下三得六。四石二得八石四斗。再以左行中一为法,遍乘中行中下得数。中中正二得二,与左中二减尽。下一得一,加左行下六,得七。为法四石二斗。得四石二斗与左行八石四斗对减,馀四石二斗为实。以法除之,得驴匹力六斗。中行四石二斗内减借驴一匹,除六斗仍三石六斗。作骡二匹除之,得骡力一石八斗。右行四石二斗内减借中行骡一匹,除一石八斗,馀二石四斗,为马一匹力。合问。
〈借〉马〈一〉 空〈负一〉 正驴〈三〉得〈三〉 四石二斗 得四石二斗先以右行正马一为法,遍乘左行中下得数。却以左行借马一为法,遍乘右行中下,得数。中得一因左行中空无减,加入负骡一。下空无数,转乘本行下正驴三,得三四石二斗。得四石二斗,与左行减尽。又以中行正骡二遍乘左行中下得数。中加一得二,下三得六。四石二得八石四斗。再以左行中一为法,遍乘中行中下得数。中中正二得二,与左中二减尽。下一得一,加左行下六,得七。为法四石二斗。得四石二斗与左行八石四斗对减,馀四石二斗为实。以法除之,得驴匹力六斗。中行四石二斗内减借驴一匹,除六斗仍三石六斗。作骡二匹除之,得骡力一石八斗。右行四石二斗内减借中行骡一匹,除一石八斗,馀二石四斗,为马一匹力。合问。今有朱二斤,粉三斤,价二两零四分。又粉五斤,丹六斤,价六钱四分。又朱三斤,丹七斤,价二两九钱八分。问:三色各价若干。
答曰:朱每斤九钱,粉每斤八分,丹每斤四分。
法曰:列所问数
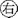 朱〈二〉为法〈先乘左行〉 粉〈三〉 得〈一〉 空 价〈二两零四分〉
朱〈二〉为法〈先乘左行〉 粉〈三〉 得〈一〉 空 价〈二两零四分〉 空 粉〈五〉 丹〈六〉 价〈六钱四分〉
空 粉〈五〉 丹〈六〉 价〈六钱四分〉 朱〈三〉 空〈负九〉 丹〈七〉得〈一十四〉价〈二两九钱八分〉 得五两九钱六分先以右行朱二为法,遍乘左行。得数列于左位。却以左行朱三为法,遍乘右行粉三,得九。左空亦立负九价二两零四,得六两一钱三分。与左行得数五两九钱六分对减馀,一钱六分。又以中行粉五为法,遍乘左行粉负九,得负四十五,丹十四,得七十馀价一钱六分,得八钱。再以左行负粉九为法,遍乘中行粉五,得四十五。与左行负粉对减,尽丹六,得五十四异。加左丹七十,共一百二十四为法。以中原价六钱四分,亦以负粉九乘,得五两七钱六分。减左馀价八钱。馀四两九钱六分为实。以法除之,得丹每斤价四分于中行。价六钱四分内减原丹六共价二钱四分,馀价四钱为实。以粉五为法除之,得粉每斤价八分。又于右行价二两零四内除粉三斤,共减价二钱四分,馀价一两八钱为实。以朱二斤为法除之,得朱每斤价九钱。合问。
朱〈三〉 空〈负九〉 丹〈七〉得〈一十四〉价〈二两九钱八分〉 得五两九钱六分先以右行朱二为法,遍乘左行。得数列于左位。却以左行朱三为法,遍乘右行粉三,得九。左空亦立负九价二两零四,得六两一钱三分。与左行得数五两九钱六分对减馀,一钱六分。又以中行粉五为法,遍乘左行粉负九,得负四十五,丹十四,得七十馀价一钱六分,得八钱。再以左行负粉九为法,遍乘中行粉五,得四十五。与左行负粉对减,尽丹六,得五十四异。加左丹七十,共一百二十四为法。以中原价六钱四分,亦以负粉九乘,得五两七钱六分。减左馀价八钱。馀四两九钱六分为实。以法除之,得丹每斤价四分于中行。价六钱四分内减原丹六共价二钱四分,馀价四钱为实。以粉五为法除之,得粉每斤价八分。又于右行价二两零四内除粉三斤,共减价二钱四分,馀价一两八钱为实。以朱二斤为法除之,得朱每斤价九钱。合问。今有鹅四只,鸭三只,共价七钱五分。又鹅三只,鸡四只,共价六钱。又鸭五只,鸡六只,共价八钱一分。问:三色价各若干。
答曰:鹅每只价一钱二分,鸭每只价九分,鸡每只价六分。
法曰:列所问数。
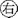 鹅〈四〉为法〈先乘中行〉 鸭〈三〉中法〈乘得九〉 空 七钱五分〈中法乘得二两二钱五分〉
鹅〈四〉为法〈先乘中行〉 鸭〈三〉中法〈乘得九〉 空 七钱五分〈中法乘得二两二钱五分〉 鹅〈三〉为法〈次乘右行〉 空〈照左负九〉 鸡〈四右法乘得十六左法乘得八十〉 六钱〈右法乘得二两四钱咸右馀一钱五分左法乘得七钱五分〉
鹅〈三〉为法〈次乘右行〉 空〈照左负九〉 鸡〈四右法乘得十六左法乘得八十〉 六钱〈右法乘得二两四钱咸右馀一钱五分左法乘得七钱五分〉 空 鸭〈五〉中法〈负九乘得四十五〉 鸡〈六〉中法〈负九乘得五十四〉 八钱一分〈中法负九乘得七两二钱九分〉先以右行鹅四为法,遍乘中行,得数鸡一十六、价二两四钱,列中位。又以中行鹅三为法,遍乘右行,得数鸭九、价二两二钱五分,列右位。以中右对减,馀鸡一十六,价一钱五分,又列中位为用。再以左行鸭五为法,复遍乘中行得数。鸭照右设立,负九得四十五。鸡十六得八十,价一钱五得七钱五分,列中位。又以中行负九为法,遍乘左行,得数鸭四十五,鸡五十四,价七两二钱九分,列左位。以中左对减,鸭尽。鸡中行八十加左行五十四,共一百三十四为法。以价中七钱五分加左七两二钱九分,共八两零四分为实。以法除之,得六分为鸡一只之价。另以左行原价八钱一分减鸡六只,共价三钱六分,馀四钱五分。以鸭五只为法除之,得鸭价每只九分,再以右行原价七钱五分减鸭三只,共价二钱七分,馀四钱八分。以鹅四为法除之得鹅每只价一钱二分。合问。
空 鸭〈五〉中法〈负九乘得四十五〉 鸡〈六〉中法〈负九乘得五十四〉 八钱一分〈中法负九乘得七两二钱九分〉先以右行鹅四为法,遍乘中行,得数鸡一十六、价二两四钱,列中位。又以中行鹅三为法,遍乘右行,得数鸭九、价二两二钱五分,列右位。以中右对减,馀鸡一十六,价一钱五分,又列中位为用。再以左行鸭五为法,复遍乘中行得数。鸭照右设立,负九得四十五。鸡十六得八十,价一钱五得七钱五分,列中位。又以中行负九为法,遍乘左行,得数鸭四十五,鸡五十四,价七两二钱九分,列左位。以中左对减,鸭尽。鸡中行八十加左行五十四,共一百三十四为法。以价中七钱五分加左七两二钱九分,共八两零四分为实。以法除之,得六分为鸡一只之价。另以左行原价八钱一分减鸡六只,共价三钱六分,馀四钱五分。以鸭五只为法除之,得鸭价每只九分,再以右行原价七钱五分减鸭三只,共价二钱七分,馀四钱八分。以鹅四为法除之得鹅每只价一钱二分。合问。今有卖二牛、五羊,买十三猪,剩银五两。卖一牛、一猪,买三羊适足。卖六羊、八猪,买五牛,少银三两。问:牛、羊、猪,各价若干。
答曰:牛价银六两,羊价银二两五钱,猪价银一两五钱。
法曰:以卖牛为正,以买猪为负。以多为正,以少为负。列所问数
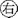 牛〈正〉二为法 羊〈正〉五 猪〈负〉十三 〈正〉五两
牛〈正〉二为法 羊〈正〉五 猪〈负〉十三 〈正〉五两 牛〈正〉一 羊〈负〉三〈得负六〉 猪〈正〉一〈得正二〉 空适足
牛〈正〉一 羊〈负〉三〈得负六〉 猪〈正〉一〈得正二〉 空适足 牛〈负〉五 羊〈正〉六〈得正十二〉 猪〈正〉八〈得正十六〉 〈负〉三两〈得六两〉先以右行牛正二为法,遍乘中左二行得数。却以中行牛正一为法,复遍乘右行羊正五得正五。异加中行羊负六,共得羊负十一。猪负十三得负十三。异加中行猪正二,共得猪正十五,价正五两得正五两。因中行价空,无减得正五两。再以左行牛负五为法复遍乘右行羊正五,得羊正二十五。同名加左羊正十二,共得三十七。猪负十三得猪负六十五。异减左行猪正十六,馀得猪负四十九。价正五两得正二十五两。异减左行负六两,馀得负一十九两。再以中行羊负十一为法遍乘左行羊正三十七,得羊正四百零七。猪负四十九得猪负五百三十九。价负一十九两得价负二十两零九钱。却以左行羊正三十七为法复遍乘中行羊负十一,得羊负四百零七。与左行羊正四百零七异名对减尽。猪正十五得猪正五百五十五。异减左行猪负五百三十九,馀得猪正一十六为法。价正五两得正一十八两五钱。异减左行价二十两零九钱,馀得正二两四钱为实。以法除之得猪价一两五钱。中行猪正十五。以价一两五钱乘得二十二两五钱。加正五两共二十七两五钱。以羊十一除之,得羊价二两五钱。右行猪负十三。以价一两五钱乘,得一十九两五钱。加入正五两,共得二十四两五钱。减五羊价共一十二两五钱,馀得一十二两。以牛二除之得牛价六两。合问。
牛〈负〉五 羊〈正〉六〈得正十二〉 猪〈正〉八〈得正十六〉 〈负〉三两〈得六两〉先以右行牛正二为法,遍乘中左二行得数。却以中行牛正一为法,复遍乘右行羊正五得正五。异加中行羊负六,共得羊负十一。猪负十三得负十三。异加中行猪正二,共得猪正十五,价正五两得正五两。因中行价空,无减得正五两。再以左行牛负五为法复遍乘右行羊正五,得羊正二十五。同名加左羊正十二,共得三十七。猪负十三得猪负六十五。异减左行猪正十六,馀得猪负四十九。价正五两得正二十五两。异减左行负六两,馀得负一十九两。再以中行羊负十一为法遍乘左行羊正三十七,得羊正四百零七。猪负四十九得猪负五百三十九。价负一十九两得价负二十两零九钱。却以左行羊正三十七为法复遍乘中行羊负十一,得羊负四百零七。与左行羊正四百零七异名对减尽。猪正十五得猪正五百五十五。异减左行猪负五百三十九,馀得猪正一十六为法。价正五两得正一十八两五钱。异减左行价二十两零九钱,馀得正二两四钱为实。以法除之得猪价一两五钱。中行猪正十五。以价一两五钱乘得二十二两五钱。加正五两共二十七两五钱。以羊十一除之,得羊价二两五钱。右行猪负十三。以价一两五钱乘,得一十九两五钱。加入正五两,共得二十四两五钱。减五羊价共一十二两五钱,馀得一十二两。以牛二除之得牛价六两。合问。四色方程歌〈附五六色仿数〉
四色方程法可誇,须存末位作根芽。诸行乘减同前例,偶与奇行认莫差。若遇奇行须减价,偶行之价要相加。加减作实须加法,减法亦须减法佳。随问几多繁杂色,凭斯推广更无他。
今有瓜二个,梨四个,共价四分。梨二个,桃七个,共价四分。桃四个,榴七个,共价三分。瓜一个,榴八个,共价二分四釐。问:各该价若干。
答曰:瓜八釐,梨六釐,桃四釐,榴二釐。
法曰:列所问数。以一行、三行为奇,二行、四行为偶。
 瓜〈二〉 梨〈四〉 空 空 价四分
瓜〈二〉 梨〈四〉 空 空 价四分 空 梨〈二〉
空 梨〈二〉 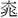 〈七〉 空 价四分
〈七〉 空 价四分 空 空
空 空 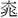 〈四〉 榴〈七〉 价三分
〈四〉 榴〈七〉 价三分 瓜〈一〉 空〈负四〉 空 榴〈八〉得〈一十六〉 价二分四釐 得四分八釐先以一行瓜二为法,遍乘四行梨空。负四桃,空榴八得一十六。价二分四釐,得四分八釐。却以四行瓜一遍乘一行梨四,得四。第四行梨空无,减桃空。价四分得四分。与四行四分八釐对减,馀八釐。次以二行梨二遍乘四行梨负四,得八桃。空榴十六得三十二。价八釐得一分六釐。却以四行梨负四遍乘二行梨二得八。与二行梨八对减尽桃七,得二十八榴空。价四分得一钱六分。加四行一分六釐共一钱七分六釐。又以三行桃四遍乘四行桃负二十八,得一百一十二。榴三十二得一百二十八。价一钱七分六釐得七钱零四釐。却以四行桃负二十八遍乘三行桃四,得一百一十二。与四行桃减尽榴七,得一百九十六。减四行榴一百二十八,馀六十八为法。价三分得八钱四分。减四行价七钱零四釐,馀一钱三分六釐为实。以法除之得二釐为榴价。于三行价三分内减榴七共价一分四釐,馀一分六釐。以桃四除之得四釐为桃价。于二行价四分内减七桃价,共二分八釐,馀一分二釐。以二梨除之得六釐为梨价。于一行价四分内减四梨,共价二分四釐,馀一分六釐。以二瓜除之,得八釐为瓜价。合问。
瓜〈一〉 空〈负四〉 空 榴〈八〉得〈一十六〉 价二分四釐 得四分八釐先以一行瓜二为法,遍乘四行梨空。负四桃,空榴八得一十六。价二分四釐,得四分八釐。却以四行瓜一遍乘一行梨四,得四。第四行梨空无,减桃空。价四分得四分。与四行四分八釐对减,馀八釐。次以二行梨二遍乘四行梨负四,得八桃。空榴十六得三十二。价八釐得一分六釐。却以四行梨负四遍乘二行梨二得八。与二行梨八对减尽桃七,得二十八榴空。价四分得一钱六分。加四行一分六釐共一钱七分六釐。又以三行桃四遍乘四行桃负二十八,得一百一十二。榴三十二得一百二十八。价一钱七分六釐得七钱零四釐。却以四行桃负二十八遍乘三行桃四,得一百一十二。与四行桃减尽榴七,得一百九十六。减四行榴一百二十八,馀六十八为法。价三分得八钱四分。减四行价七钱零四釐,馀一钱三分六釐为实。以法除之得二釐为榴价。于三行价三分内减榴七共价一分四釐,馀一分六釐。以桃四除之得四釐为桃价。于二行价四分内减七桃价,共二分八釐,馀一分二釐。以二梨除之得六釐为梨价。于一行价四分内减四梨,共价二分四釐,馀一分六釐。以二瓜除之,得八釐为瓜价。合问。今有绢三疋,添价六钱,买布十疋。又布五疋,添价一钱,买绢二疋。问:绢布价各若干。
答曰:绢疋价八钱,布疋价三钱。
法曰:如前正负术之法。〈此问可作盈不足算〉
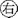 绢三〈正〉为法 布十疋〈负〉 价六钱〈正〉
绢三〈正〉为法 布十疋〈负〉 价六钱〈正〉 绢二〈负〉 布五疋〈得正十五〉 价一钱〈正〉得三钱先以右行绢正三为法,遍乘左行布正五,得正一十五。价正一钱得正三钱。却以左行绢负二为法,遍乘右行布。负十疋得正二十疋。减左行布正十五,馀五为法。价正六钱得一两二钱。加左行三钱共一两五钱为实。以法除实得三钱为布疋价。却以左行布五疋,以每疋三钱乘之,得一两五钱。加添价一钱共一两六钱,以绢二疋除之,得绢疋价八钱。合问。
绢二〈负〉 布五疋〈得正十五〉 价一钱〈正〉得三钱先以右行绢正三为法,遍乘左行布正五,得正一十五。价正一钱得正三钱。却以左行绢负二为法,遍乘右行布。负十疋得正二十疋。减左行布正十五,馀五为法。价正六钱得一两二钱。加左行三钱共一两五钱为实。以法除实得三钱为布疋价。却以左行布五疋,以每疋三钱乘之,得一两五钱。加添价一钱共一两六钱,以绢二疋除之,得绢疋价八钱。合问。句股章第九
横阔谓之句,直长谓之股,两隅斜去谓之弦。此章以句股求弦之斜;句弦求股之长;以股弦求句之阔;求句股形图

句股中容方、容圆;求山之高、水之深、城之广、路之远,皆可知也。
句股之形,即今木匠曲尺之
形也。句是尺,股是尺稍,自尺头至稍尾斜去,是弦也。
设如句三尺,股四尺,弦即五尺也。句股名义〈生变有一十三〉
句〈横曰句〉 句股较〈句股相减〉
句弦较〈句弦相减〉 句股和〈句与股并〉
句弦和〈句与弦并〉
股〈直曰股〉 股弦较〈股弦相减〉
股弦和〈股与弦并〉
弦〈斜曰弦〉 弦较和〈弦与句股较并〉弦和和〈弦与句股和并〉 弦和较〈弦与句股和相减〉弦较较〈弦与句股较相减〉
句股论说释义
假如句二十七步,股三十六步,弦四十五步。
其求句,求股,求弦。容方、容圆另具图于后。
句股之法:横曰句,直曰股,斜之为弦。句二
十七、股三十六相减,其差九曰较。句股相并得六十三曰和。股三十六减弦四十五之差九曰股弦较。句二十七弦四十五之差十八曰句弦较。并句股共六十三,减弦四十五之差十八则曰弦和较。
弦四十五减句股之差九,其差三十六曰弦较较。股弦相并得八十一,则曰股弦和。句弦相并得
七十二,曰句弦和。句股之差九并弦共五十四,则曰弦较和。句股弦并得一百零八,曰弦和和。倍弦实〈即弦自乘倍之〉得四千零五十,减句股和,自乘得三千九百六十九,馀八十一为实,平方开之,得九为句股较。前倍弦实减句股较九,自乘得八十一,馀三千九百六十九,平方开之,得六十三为句股和。并句弦共七十二,除股自乘得一千二百九十六,得十八为句股较。即句弦之差十八,除股自乘得一千二百九十六,得七十二为句弦,和并得股弦共八十一,以除句自乘得七百二十九得九为股弦较。即股弦之差九,除句自乘得七百二十九得八十一为股弦和。句股和六十三自乘得三千九百六十九,减弦自乘得二千零二十五,馀一千九百四十四为实,以弦较较三十六除之,得五十四为弦较和。弦较和除前实,得弦较较。句股之差九自乘得八十一,以减弦自乘得二千零二十五,馀一千九百四十四为实,以弦和和一百零八除之,得十八为弦和较。弦和较除前实得弦和和。句二十七加股弦较九,共三十六即弦较较。句二十七减股弦较九,馀十八即弦和较。句加弦较和五十四共八十一即股弦和。股三十六加句弦较十八共五十四即弦较和。股三十六减句弦较十八馀十八即弦和较。股加弦较较三十六共七十二即句弦和。句股较九加股弦较九共十八即句弦较。句股较九减股弦和八十一馀七十二即句弦和。句股和六十三加股弦较九共七十二为句弦和。股弦和八十一减句股和六十三馀十八即句弦较。句股较九加句股和六十三共七十二半之为股。句股和六十三减句股较九馀五十四折半为句。股弦较九加股弦和八十一共九十,半之为弦。股弦和八十一减股弦较九馀七十二,半之为股。句弦较十八加句弦和七十二共九十,半之为弦。句弦和七十二减句弦较十八馀五十四,半之为句。弦和较十八加弦和和一百零八共一百二十六,半之为和。弦和和一百零八减弦和较十八馀九十,半之为弦。弦较较三十六加弦较和五十四共九十,半之为弦。
弦较和五十四减弦较较三十六馀十八,半之为
较。变而通之,神而明之,存乎其人焉。
句股求弦句弦求股股弦求句共歌
句股求弦各自乘,乘来相并要分明。开方便见弦之数,法术从来有见成。句弦求股要推详,各自乘来各一张。以少减多馀作实,实求股数要开方。弦股求句皆一例,算师熟记莫相忘。
句股求弦法,曰:置句自乘,股自乘,并二数以开平方法除之,得弦数。
其句自乘,股自乘,二数并之。合弦自乘。数故用开平方法除之,即得弦斜数也。
句弦求股法,曰:置弦自乘内减句,自乘,馀以开平方除之,得股长数。
其弦自乘数内有一句,自乘一股。自乘数今减去句,自乘数馀是股自乘数。故用开平方除之,得股长数。
股弦求句法,曰:置弦自乘内减股自乘,馀以开平方除之,得句阔数。
其弦自乘有一句、一股。自乘数今减去股,自乘数馀是句。自乘数故用开平方除之,得句阔数。
今有句二十七尺、股三十六尺。问:弦斜若干。
答曰:弦斜四十五尺。
法曰:置句二十七尺自乘,得七百二十九尺。另以股三十六尺自乘,得一千二百九十六尺。二数并之得二千零二十五尺为实,乃合弦。自乘数以开平方法除之,初商四十于左,亦置四十于右。为方法左四对右四呼四,四除实一千六百尺,馀实四百二十五尺。却以下位初商方法四十,倍作八十。为廉法次商五尺于左位,初商四十之次,亦置五于右位。廉法八十之次。为隅法左五对右八呼五,八除实四百。又左五对右五呼五,五除实二十五尺恰尽,得弦斜四十五尺。
今有句二十七尺、弦四十五尺。问:股长若干。
答曰:股长三十六尺。
法曰:置弦四十五尺自乘,得二千零二十五尺。内有一句、一股。自乘之数另以句自乘,得七百二十九尺。二数相减,馀一千二百九十六尺为实。是股自乘数以开平方法除之。初商三十于左位,亦置三十于右位。为方法左三对右三呼三,三除实九百馀实三百九十六尺。另以下位初商三十倍作六十。为廉法次商六尺于左三十之次。亦置六于右,廉法六十之次。为隅法左六对右六呼六,六除实三百六十。又左六对右六呼六,六除实三十六尺恰尽。得股长三十六尺。合问。
今有股三十六尺、弦四十五尺。问:句阔若干。
答曰:句阔二十七尺。
法曰:置弦四十五尺自乘,得二千零二十五尺。内有一句、一股。自乘之数另以股自乘,得一千二百九十六尺。二数相减,馀七百二十九尺为实。〈是句自乘数〉以开平方法除之,初商二十于左。亦置二十于右。为方法左二对右二呼二,二除实四百,馀实三百二十九尺。却以下位初商二十倍作四十。为廉法次商七尺于左,初商二十之次亦置七尺于右廉法四十之次。为隅法左七对右四呼四,七除实二百八十。又左七对右七呼七,七除实四十九恰尽。得句阔二十七尺。合问。
句股容方容圆共歌
句股容方法最良,以句乘股实相当。并之句股数为法,以法除实便知方。句股容圆法可知,句弦股数并为奇。三数并来为法则,句股相乘倍实宜。法除倍实为圆数,算者详之不用疑。
今有句股内容方,句二十七尺、股三十六尺。问:中容方面径若干。
勾股容方图

答曰:中容方面一十五尺有畸。法曰:置句二十七尺乘股三十六尺,得九百七十二尺为实。以句股并得六十三尺。为法除之
得中容方面径一十五尺有畸。
今有句股容圆,句二十七尺、股三十六尺、弦四十五尺。问:中容圆径若干。
句股容圆图缺答曰:中容圆径一十八尺。法曰:置句二十七尺、股三十六尺相乘,得九百七十二尺。倍之得一千九百四十四尺为实。并
句、股、弦三数共一百零八。为法除实得容圆径一十八尺。合问。
今有句股玉一块。长一尺二寸、阔六寸。今欲截角为方取印一颗。问:方面若干。
答曰:方面四寸。
勾股容方图缺法曰:置句股相乘得七十二寸为实。以句股相并得十八,为法除之即得。
若以圆径十八尺,用一尺二寸归除,得方径十五尺。若
以方径十五尺,用一尺二寸乘之,得圆径十八尺。
较求句股弦共歌〈较差也是股弦相差及句弦相差也〉
股较求股句自乘,股较自乘减句盈。减除句馀为实数,股较倍之为法行。法实相除为股数,句较求句一样成。弦较求弦句自乘,弦较除之为实情。仍加弦较须折半,就得弦长数即成。
今有句阔二十七步,只云弦多股九步。问:股弦各若干。
答曰:股三十六步,弦四十五步。
法曰:置句二十七步自乘得七百二十九步。另以弦多股九步为股较,即以此自乘得八十一步。二位相减,馀六百四十八步为实。倍较九步得一十八步。为法除之,得股长三十六步。加较九步,得弦长四十五步。合问。
此是股较求股即股弦相差也。
一法名弦较求弦。置句自乘得七百二十九步为实。以弦较九步为法除之,得股弦和八十一步。仍加弦较九步得九十步。折半是弦长四十五步。内减较九步是股长三十六步。亦可得也。
今有葭二茎生池中。并根杪齐出水三尺,即葭一茎斜去至岸九尺,与水适平。问:水深若干。
答曰:水深一丈二尺。
股较求股图

法曰:置去岸九尺为句,自乘得八十一尺。以出水三尺为股较,自乘得九尺。以减八十一尺,馀七十二尺为实。以较三尺倍作六尺。
为法除之,得水深一丈二尺。合问。〈水深如股葭至岸如弦〉今有句九尺,却将弦比股有馀三尺。问:弦股各若干。答曰:弦一十五尺,股一十二尺。
法曰:以句九尺自乘,得八十一尺为实。以多三尺为法除之,得二十七尺。减去多三尺馀得二十四尺,折半得股长一十二尺。加入弦多三尺,得弦一十五尺。合问。
今有立木不知其高,索不知其长。垂索委地二尺,引
股较求股弦

索去木八尺,其索斜柱地适尽。问:木高、索长各若干。答曰:木高一丈五尺,索长一丈七尺。
法曰:置去木八尺为句,自
乘得六十四尺。以委地二尺为股较,自乘得四尺。以减六十四尺馀六十尺为实。以较二尺倍作四尺。为法除之,得木高一丈五尺。如股加较二尺,得索长一丈七尺,如弦。合问。若以弦较求弦法。置去木八尺为句,自乘得六十四尺为实。以委地二尺如弦较,为法除之得三十二尺。加弦较二尺共得三十四尺,折半,得索长一丈七尺。将弦内减去较二尺,得木高一丈五尺,即股。
今有厅门外悬帘下垂,离地五寸,引帘离阈六尺,离
弦较求弦图

地二尺五寸。问:帘高若干。答曰:帘高一丈。
法曰:置去阈六尺为句,自乘得三十六尺。以离地二尺五寸减去原离地五寸,馀二尺为弦较。
除之得一十八尺。加弦较二尺共得二十尺,折半得帘高一丈。合问。
今有开门,去阈一尺,不合二寸。问:门广若干。
答曰:门二扇广九尺九寸。
股较求股图

法曰:置去阈十寸为句,自乘得一百寸。以不合二寸折半,得一寸为股较,自乘得一寸。以减一百寸馀九十九寸为实。以较一
寸倍作二寸,为法除之得一扇门广四尺九寸五分。如股倍之得二扇门广九尺九寸。合问。
今有墙高一丈,斜倚二木于上。木杪与墙头齐,其木根抵地。却将木一根平卧于地,其木杪抵墙脚,此木根则过斜木根一尺。问:木长并去墙若干。
弦较求弦股图

答曰:木长五丈零五寸,去墙四丈九尺五寸。
法曰:依弦较求弦。以墙高十尺为句,自乘得一百尺。以过斜木根一尺为弦较,除之如故。一百尺加较一尺,共得一百零一尺,折半,得木长五丈零五寸。如弦减过斜木一尺,馀如股至墙四丈九尺五寸。合问。
今有圆木泥在壁中,不知径。以锯锯之,深一寸,锯道
弦较求弦图

长一尺。问:木径若干。答曰:木径一尺六寸。法曰:置锯道一尺折半,得五寸为句。自乘得二尺五寸为实。以深一寸为股较,除之如故,得二尺五寸为
股。加深一寸,共得木径二尺六寸。合问。此如圆田中截去一张矢田问原径,同法。置锯道一尺如弧矢之弦,折半得五寸。自乘得二尺五寸为实。以深一寸如矢,为法除之得二尺五寸。并入矢深一寸,共二尺六寸为圆木原径,亦得。
今有圆木径二尺六寸,锯深入木八寸。问:锯道长若干。
答曰:锯道长二尺四寸。
此问与右图式相同,今以数并注于图内径左,以便共览。
法曰:以径二尺六寸减深八寸,馀一十八寸。复以锯深八寸乘之,得一百四十四寸为实。以开平方法除之,得一十二寸。倍之得二尺四寸。合问。
今有股长三十六步,只云弦多句十八步。问:句弦各若干。
答曰:句二十七步,弦四十五步。
法曰:置股三十六步自乘,得一千二百九十六步。另以弦多句一十八步为句较,自乘得三百二十四步。二位相减馀九百七十二步为实。倍较十八得三十六步,为法除之得句一十七步。加较一十八步得弦长四十五步。合问。〈此即句弦相差〉一法名弦较求弦。置股自乘得一千二百九十六步为实。以弦较十八步为法除之,得句弦和七十二步。仍加较一十八步,共九十步,折半得弦四十五步。内减较一十八步,馀二十七步即句之数也。
今有弦长四十五步,只云股多句九步。问:句股各若干。
答曰:句二十七步,股三十六步。
法曰:置弦四十五步自乘,得二千零二十五步。另以股多句九步为句股,较自乘得八十一步。二位相减馀一千九百四十四步。加入弦自乘得二千零二十五步。共三千九百六十九步为实,以开平方法除之,得句股相和六十三步。加入差九步,共得七十二步,折半得股三十六步。内减差九步,馀得句二十七步。合问。
今有户高多广六尺八寸,两隅斜去十尺。问:高广各若干。
答曰:高九尺六寸,广二尺八寸。
法曰:置两隅斜十尺如弦自乘,得一百尺。另以高多广六尺八寸为句股较,自乘得四十六尺二寸四分。二位相减,馀五十三尺七寸六分。加入斜自乘得一百尺共一百五十三尺七寸六分为实。以开平方法除之,得句股相和一丈二尺四寸。加入差六尺八寸,共得一丈九尺二寸,折半得高九尺六寸。内减差六尺八寸,馀得广二尺八寸。合问。〈此二条即句股相差〉
股别句弦歌〈附句别股弦即句弦和亦即股弦和〉
股别句弦股自乘,句弦自乘减股零。折半留为句实积,句弦为法最公平。法除句积为句数,句别股弦依此行。
今有竹高一丈,为风所折仆地。稍尖去根三尺。问:折
股别勾弦图

处高若干。
答曰:高四尺五寸五分。法曰:置去根三尺如句,自乘得九尺。是以竹高一丈如股弦和,为法除之得九
寸。以减股弦和一丈,馀九尺一寸。折半,得四尺五寸五分即是折处高股也。
今有股长三十六步,只云句弦相和七十二步。问:句弦各若干。
答曰:句二十七步,弦四十五步。
法曰:置股三十六步自乘得一千二百九十六步。另以句弦和七十二步自乘得五千一百八十四步。二位相减,馀三千八百八十八步,折半得一千九百四十四步为实。以句弦七十二步为法除之,得句二十七步。以减句弦和,馀得弦四十五步。合问。
一法以股自乘得一千二百九十六步为实。以句弦和七十二步为法除之,得句弦相差一十八步。仍加和七十二步共九十步,折半,得弦四十五步。内减差一十八步,馀二十七步是句。亦得。〈此乃句弦和〉今有句阔二十七步,只云股弦相和八十一步。问:股弦各若干。
答曰:股三十六步,弦四十五步。
法曰:置句二十七步自乘得七百二十九步。另以股弦和八十一步自乘得六千五百六十一步。二位相减,馀五千八百三十二步,折半,得二千九百一十六步为实。以股弦和八十一步为法除之得三十六步为股长。以减股弦和八十一步,馀四十五步为弦。合问。
今有弦长四十五步,只云句股相和六十三步。问:句股各若干。
答曰:句二十七步,股三十六步。
法曰:置弦四十五步自乘得二千零二十五步。另以句股和六十三步自乘得三千九百六十九步。二位相减,馀一千九百四十四步。再减弦自乘得二千零二十五步,馀八十一步。以开平方法除之,得句股相差九步,加入相和六十三步,共七十二步,折半,得股三十六步。内减去差九步,馀得句二十七步。合问。〈此是句股相和〉
句弦较股弦较歌〈此是句弦差又股弦差〉
句弦股较法尤精,句乘股较二来因。平方开见弦和数,和加句较股分明。股较加和句可见,算师熟记看灵扃。
今将弦比句馀四尺,复将弦比股馀二尺。问:句弦股
勾弦股较图

各若干。
答曰:句六尺,股八尺,弦一丈。
法曰:以句较四尺乘股较二尺,
得八尺。倍之得一十六尺为实。以开平方法除之,得四尺。加入股较二尺,得六尺为句。另以四尺加入句较四尺,得八尺为股。又加入股较二尺,得一丈为弦。合问。
今有直田不知长阔,只云隅斜比长多二步,又云斜比阔多九步。问:长阔及斜各若干。
答曰:长一十五步,阔八步,斜一十七步。
法曰:置句弦较九步,以股弦较二步乘之,得一十八步。以二因之,得三十六步为实。以开平方法除之,得弦和六步。加句较九步,得股长一十五步。另以弦和六步加股较二步,得阔八步。再加句较九步,得斜弦一十七步。合问。
今有句弦和七十二步,股弦和八十一步。问:句股弦各若干。
答曰:句二十七步,股三十六步,弦四十五步。
法曰:置句弦和七十二步,以股弦和八十一步相乘,得五千八百三十二步。倍之得一万一千六百六十四步为实。以开平方法除之,得句股弦和一百零八步。以减股弦和八十一步,馀得句二十七步。又置一百零八步内减句弦和七十二步,馀得股三十六步。又置一百零八步以减句二十七步,减股三十六步,馀得弦四十五步。〈此是句弦和又股弦和〉
今有直田积一百二十步,广不及纵七步。问:广若干。答曰:广八步。
法曰:置田积一百二十步,以四因之得四百八十。以较七步自乘,得四十九步。相并得五百二十九步。以开平方法除之,得句股和二十三步。加较七步,共得三十步,折半,得股长一十五步。内减较七步,馀广八步。
今有井不知其深。井径五尺,直立木五尺于井上,从木末望井底,人目入径四寸。问:井深若干。
答曰:井深五丈七尺五寸。
法曰:以井径五尺除目入四寸,馀四十六寸。与木高五十寸相乘,得二千三百寸为容方积。以馀句四寸为法除之。
今有邑不知大小,四面居中开门。西门外三十步有
馀勾馀股求容方

木一根,出南门外七百五十步,见木。问:邑方若干。答曰:邑方三百步。
法曰:出西门三十步为馀句,出南门为馀股。相乘得
二万二千五百步。以平方开之,得一百五十步,为半邑之方。倍之,为全邑方也。〈即句股容方〉
今有邑方二百步,四面居中开门。东门外一十五步
容方馀勾求馀股

有木一根。问:出南门若干。答曰:六百六十六步六分步之一。
法曰:半邑方为容方一百步,自乘得一万步为实。以
东门外十五步为馀句,为法除之。合问。〈此是容方与馀句求馀股〉
求高求远法
海岛题解
魏刘徽注九章,重立差著于句股之下,以阐世术。夫度高测深,非句股之法,则无可知矣。故以重表累矩,旁求审察。其窥望海岛、隔水望木,是重表也。其岸望谷深,山望津广,是累矩也。以海岛去表为之篇首。因以名之实九章之遗法也。后至唐李淳风,而续算草。宋杨辉释名图解,以伸前贤之美。本经题目广远,难于引證学者。今将孙子度影量竿,题问于前,引用详解以验海岛之法,亦循循诱入之意。姑以一问,其馀好学者,自能触类而考知矣。
假有立木不知高,日影在地长五丈。随立一竿长一丈,在边影长一丈二尺五寸。问:立木高若干。
答曰:木高四丈。
法曰:置立木影长五丈为实。以竿影长一丈二尺五寸为法除之。合问。
今有立木不知高,日影在地长四丈。随立一竿长一丈,在边影长八尺。问:木高若干。
答曰:木高五丈。
法曰:置木影长四丈为实,以竿影八尺为法除之。合问。
右二问,乃孙子度影量竿之法。
遥望木竿歌
望木须知立表竿,表离木处几多宽。退行表后参眸望,望表斜平末与竿。表数减除人目数,馀表乘远实相看。退行之数为法则,法实相除加一竿。
假有木不知高,从木脚量远二十五尺立一丈表竿。表后退行五尺,用窥穴望表与木,斜平。其人窥穴高四尺。问:木高若干。
答曰:木高四丈。
法曰:以表高十足减去人目穴四尺,馀六尺。以乘表竿去木远二十五尺,得一百五十尺为实。以退行五尺为法除之,得三十尺。加表高十尺,得木高四十尺。合问。
解曰:木高如股,〈是上节三十尺表高十尺 减人目四尺馀六尺是馀股〉末如句二十五尺,表后退行五尺是馀句,木顶斜至
股较求高之图
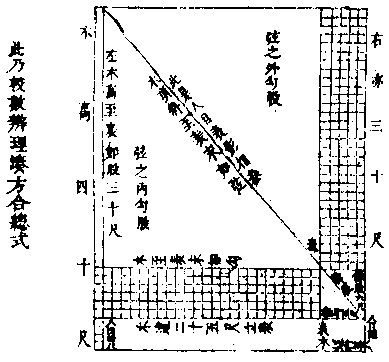
表末如弦,表末斜至人目是馀弦。弦之内外分二段句股,其句中容横股,中容直二积皆同,各一百五十尺。以馀句五尺除横积一百五十尺,得积外之股,即木上三十尺。加表高十尺即木高四十尺,以馀股六尺。除直积一百五十尺,得
积外之句,即木至表二十五尺。〈古人以题易名若非释名则无以知其源〉今较还原法曰:置弦内外二句股,木高四丈内除人目四尺,馀股各三丈六尺为长。以远二十五尺加退后五尺,共三十尺为阔相乘得方积一千零八十尺。今复将弦内外二股各长三十尺,二句各阔二十五尺相乘,得方积七百五十尺。另以下句直长二十五尺、阔六尺乘之,得直积一百五十。又以右边股直三十尺,以阔五尺乘之,得直积亦一百五十。再以馀句五尺乘馀股六尺,得积三十尺。四共亦得一千零八十尺,较之以合前数而不差也。
已上遥望木竿是一表望木也。
今立表三尺六寸,退行二尺又立表三尺。人目望其高处,二表俱与参合,自前表相去二丈五尺。问:高若干。
答曰:高一丈一尺一寸。
法曰:置远二十五尺,加入退行二尺,共二十七尺。以二表相减馀六寸。乘之得一十六尺二寸为实。却以退行二尺为法除之,得八尺一寸。加入后表三尺,得高一丈一尺一寸。合问。
若依前法置前表三尺六寸,减去后表三尺,即是人目数,馀六寸以。乘远去二丈五尺,得一丈五尺为实。以退行二尺为法除之,得七尺五寸。加入前表三尺六寸,共高一丈一尺一寸。
今立表三尺,退行一尺八寸。又立表三尺六寸,人目望其二表俱对远处参合。问:远若干。
答曰:十尺零八寸。
法曰:置后表三尺六寸,以退行一尺八寸乘之,得六
句较求远之图
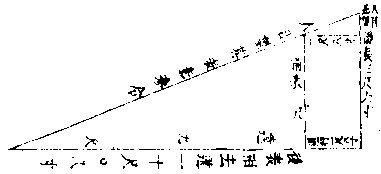
十四寸八分为实。却以二表相减,馀六寸。为法除之,得一十尺零八寸,为后表相去之远。若以前表三尺,以退行一尺八寸乘之,得五尺四寸为实。却以二表相减,馀六寸。为法除之,得九尺为前表相去之远也。
窥望海岛歌
望岛知高法术奇,立来二表并高低。表间尺数乘高数,以作实情更不疑。二表退行相减较,减馀为法以除之。更将一表相加并,海岛巅高尽可知。另置表间之尺数,以乘前表退行宜。前法除之知隔水,水程远近不差池。
假如隔水望木有竿,不知其高。立二表各长一丈,前后参直相去一十五尺。从前表退行五尺,人目四尺窥望,表与竿齐平。复从从表退行八尺窥望,亦与竿齐平。问:竿高隔水各若干。
答曰:竿高四丈,隔水广二丈五尺。
法曰:置表高十尺减人目四尺,馀六尺。以相去一十五尺乘之,得九十为实。另以前表退行五尺减去后表退行八尺,馀三尺。为法除实得三十尺。加表高十尺,得竿高四十尺。另置相去一十五尺,以前表退行五尺乘之,得七十五尺。仍以前法三尺除之,得隔水广二十五尺。合问。
解曰:前表是第一图,以表望木后表是第二图。以表望木,盖总设人不知所以分作两图。其以隔水望木为问,设窥望海岛为题,以重差为术。好事者引而伸
股较隔水望木之图
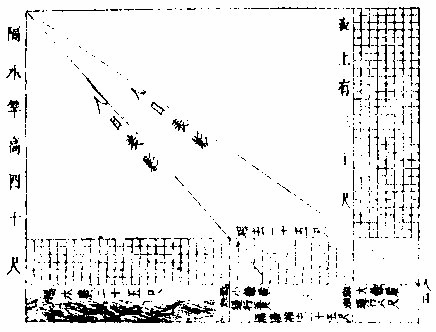
〈此乃二表〉
较数,辨理
凑方式以
合,总而不
差故也。
之,以发其馀也。其前表去木远乃小,股中容积一段。后表去木远乃大,股中容积一段。以小容积减大容积,其馀不尽者,乃前后表两界之中各表间积。所以古人以表高减人目四尺,馀六尺,乘为实。以前图小馀股五尺减后图大馀股八尺,馀三尺,为法除实得弦外之高,即木上节三十尺。加表高十尺,得木高四十尺。本是大小容积相减馀为实。以大小馀股相减,馀为法除实得弦外之高。加表高十尺为木高也。今有海岛不知其高,远立表竿三丈,退行六十丈。又
窥望海岛之图窥望海岛之图

立短表三尺。人目望其二表,俱与岛峰参合。复却退行五百丈,又立表三丈。退行六十二丈,又立表三尺。人目望其二表,俱与岛峰参合。问:海岛高远各该若干。
答曰:岛高三里一百三十八丈,岛远八十三里六丈。
法曰:置表高三丈减去短表三尺,即是人目数也。馀二丈七尺,以表间相去五百丈乘之,得一千三百五十丈为实。另置后表退行六十二丈减去前表退行六十丈,馀二丈。为法除之,得六百七十五丈。加入表高三丈,共六百七十八丈。以里法一百八十丈为法除之,得岛高三里一百三十八丈。又置表间相去五百丈,以前表退行六十丈乘之,得三万丈为实。亦以所馀二丈为法除之,得一万五千丈。以里法一百八十丈为法除之,得岛远八十三里六丈。合问。