声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
钦定古今图书集成经济汇编乐律典
第六十一卷目录
律吕部汇考十五
明朱载堉律吕精义一〈总论造律得失 不宗黄钟九寸 不用三分损益 不拘隔八相生〉
明朱载堉律吕精义一〈总论造律得失 不宗黄钟九寸 不用三分损益 不拘隔八相生〉
乐律典第六十一卷
律吕部汇考十五
明·朱载堉《律吕精义一》总论造律得失第一律非难造之物,而造之难成,何也。推详其弊,盖有三失:王莽伪作,原非至善,而历代善之以为定制。根本不正,其失一也。刘歆伪辞,全无可取,而历代取之以为定说。考据不明,其失二也。三分损益,旧率疏舛,而历代守之,以为定法。算术不精,其失三也。欲矫其失,则有三要:不宗王莽律度量衡之制,一也。不从《汉志》刘歆、班固之说,二也。不用三分损益疏舛之法,三也。以此三要矫彼三失,《律吕精义》所由作也。或曰:大泉之寸,秬黍之分,非莽歆遗法乎。今乃取之,何也。答曰:大泉之径,汉尺以为寸。秬黍之长,古尺以为分。而莽、歆之尺,则不然,所以与新法不同也。
《汉书·王莽传》曰:天凤四年,初献新乐于明堂太庙。或闻其乐声,曰:清丽而哀,非兴国之声也。根本不正,此之谓也。《宋书·律志》曰:班氏所志,未能通律吕本源,徒训角为触,徵为祉,阳气施种于黄钟,如斯之属,空烦其文而为辞费。又推九六,欲符刘歆三统之数,假托非类,以饰其说,皆孟坚之妄矣。考据不明,此之谓也。《宋书·律志》又曰:三分益一为上生,三分损一为下生,此其大略,犹周天斗分四分之一耳。京房不思此意,引而伸之,仲吕上生执始,执始下生去灭,至于南事,为六十律,竟复不合,弥益其疏。算术不精,此之谓也。大泉之寸,秬黍之分,详见审度篇中。
不宗黄钟九寸第二
律由声制,非由度出。制律之初,未有度也。度尚未有,则何以知黄钟乃九寸哉。以黄钟为九寸,不过汉尺之九寸耳。周尺则不然也。商尺又不然也。虞夏之尺皆不然也。黄帝之尺亦不然也。
先儒谓:夏禹十寸为尺,成汤十二寸为尺,武王八寸为尺。三代之尺不同,尺虽不同,而黄钟则无不同也。解释黄钟之义,迁就九寸之说,自汉儒为始耳。汉儒已前,《周礼》、《左传》、《国语》、《管子》、《吕览》之类,皆未尝以黄钟之长为九寸也。此说闻诸臣父云。
盖黄帝之尺,以黄钟之长为八十一分者,法雒书阳数也。
黄帝时,雒出书,见沈约《符瑞志》,犹禹时《雒书》也。《雒书》数九,自乘得八十一,是为阳数。盖十二者,天地之大数也。百二十者,律吕之全数也。除去三十九,则八十一耳。故《吕氏春秋》曰:断两节间三寸九分。后学未达,遂指三寸九分为黄钟之长者,误矣。八寸一分,三寸九分,合而为十二寸,即律吕之全数。全数之内,断去三寸九分,馀为八寸一分,即黄钟之长也。《管子》曰:凡将起五音,先主一而三之四开,以合九九,以是生黄钟。盖谓算术,先置一寸为实,三之为三寸,又四之为十二寸也。开以合九九者,八十一分,开方得九分,九分自乘得,八十一分,为黄钟之长也。
虞夏之尺,皆以黄钟之长为十寸者,法河图中数也。
《书》称:舜同律度量衡。尧、舜、禹相禅,未尝改制度。然则禹以十寸为尺,即舜所同之度尺也。旧谓度本起于黄钟之长,又谓黄钟之长九寸外加一寸为尺。何瑭尝辨之曰:《汉志》谓黄钟之律九寸加一寸以为尺,夫度量权衡所以取法于黄钟者,盖贵其与天地之气相应也。若加一寸以为尺,则又何取于黄钟。殊不知黄钟之长,固非人所能为。至于九其寸而为律,十其寸而为尺,则人之所为也。《汉志》不知出此,乃欲加黄钟一寸为尺,谬矣。臣按黄钟之律长九寸,纵黍为分之九寸也,寸皆九分,凡八十一分。《雒书》之奇,自相乘之数也。是谓律本黄钟之度,长十寸,横黍为分之十寸也。寸皆十分,凡百分,河图之偶,自相乘之数也。是为度母纵黍之律,横黍之度,名数虽异,分剂实同,孰使之然哉。天地自然之理耳。
成汤以夏尺之十二寸有半寸为尺,则黄钟之长,乃商尺之八寸。武王以夏尺之八寸为尺,则黄钟之长,乃周尺之十二寸有半寸。黄钟无所改,而尺有不同,彼执著九寸为黄钟之律,然则商之黄钟太长,周之黄钟太短,岂不谬哉。
起度之法,十寸为尺,八寸为咫,商之咫,夏之尺也。夏之咫,周之尺也。十寸自乘为实,八寸为法除之,得十二寸有半寸也。
不用三分损益第三
律家三分损其一,三分益其一,历家四分度之一,四分日之一,与夫方则直五斜七圆,则周三径一等率,皆举大略而言之耳,非精义也。新法算律,与方圆皆用句股术,其法本诸《周礼》栗氏为量,内方尺而圆其外,内方尺而圆其外,则圆径与方斜同,知方之斜则知圆之径矣。度本起于黄钟之长,则黄钟之长,即度法一尺,命平方一尺,为黄钟之率,东西十寸为句,自乘得百寸为句,羃南北十寸为股,自乘得百寸为股,羃相并共得二百寸为弦,羃乃置弦羃为实,开平方法除之得弦。一尺四寸一分四釐二毫一丝三忽五微六纤二三七三○九五○四八八○一六八九,为方之斜,即圆之径,亦即蕤宾倍律之率,以句十寸乘之,得平方积一百四十一寸四十二分一十三釐五十六毫二十三丝七十三忽○九五○四八八○一六八九,为实。开平方法除之,得一尺一寸八分九釐二毫○七忽一微一纤五○○二七二一○六六七一七五,即南吕倍律之率。仍以句十寸乘之,又以股十寸乘之,得立方积一千一百八十九寸二百○七分一百一十五釐○○二毫七百二十一丝○六十六忽七一七五,为实。开立方法除之,得一尺○五分九釐四毫六丝三忽○九纤四三五九二九五二六四五六一八二五,即应钟倍律之率。盖十二律,黄钟为始,应钟为终。终而复始,循环无端。此自然真理,犹贞后元生坤尽复来也。是故各律皆以黄钟正数十寸乘之为实,皆以应钟倍数十寸○五分九釐四毫六丝三忽○九纤四三五九二九五二六四五六一八二五为法。除之,即得其次律也。安有往而不返之理哉。旧法往而不返者,盖由三分损益,算术不精之所致也。是故新法,不用三分损益,别造密率,其详如左。
积算旁通图〈此条命尺为京后条,或命寸为兆,或命寸为亿,盖欲多列位数,见开方之妙也〉
二〈本是二尺,进作二百寸为实,以上文所载应钟倍律之数,十寸五分有奇,为法,除之。馀条仿此〉
右乃黄钟倍律积算,〈置黄钟倍律,积算,进一位为实,以应钟倍律积算为法,除之,得大吕〉
一八八七七四八六二五三六三三八六九九三二八三八二六,
右乃大吕倍律积算。〈置大吕倍律积算,进一位为实。以应钟倍律积算,为法,除之,得太簇〉
一七八一七九七四三六二八○六七八六○九四八○四五二。
右乃太簇倍律积算。〈置太簇倍律积算进一位为实,以应钟倍律积算为法,除之,得夹钟〉
一六八一七九二八三○五○七四二九○八六○六二二五一。
右乃夹钟倍律积算。〈置夹钟倍律积算进一位为实,以应钟倍律积算为法,除〉
之,得姑洗
一五八七四○一○五一九六八一九九四七四七五一七○六。
右乃姑洗倍律积算。〈置姑洗倍律积算进一位为实,以应钟倍律积算为法,除之,得仲吕〉
一四九八三○七○七六八七六六八一四九八七九九二八一。
右乃仲吕倍律积算。〈置仲吕倍律积算进一位为实,以应钟倍律积算为法,除之,得蕤宾〉
一四一四二一三五六二三七三○九五○四八八○一六八九。
右乃蕤宾倍律积算。〈置蕤宾倍律积算进一位为实,以应钟倍律积算为法,除之,得林钟〉
一三三四八三九八五四一七○○三四三六四八三○八三二。
右乃林钟倍律积算。〈置林钟倍律积算进一位为实,以应钟倍律积算为法,除之,得夷则〉
一二五九九二一○四九八九四八七三一六四七六七二一一。
右乃夷则倍律积算。〈置夷则倍律积算进一位为实,以应钟倍律积算为法,除之,得南吕〉
一一八九二○七一一五○○二七二一○六六七一七五○○。
右乃南吕倍律积算,〈置南吕倍律积算进一位为实,以应钟倍律积算为法,除之,得无射〉
一一二二四六二○四八三○九三七二九八一四三三五三三。
右乃无射倍律积算。〈置无射倍律积算进一位为实,以应钟倍律积算为法,除之,得应钟〉
一○五九四六三○九四三五九二九五二六四五六一八二五。
右乃应钟倍律积算。〈置应钟倍律积算进一位为实,以应钟倍律积算为法,除之,得黄钟〉
密率源流图密率源流图
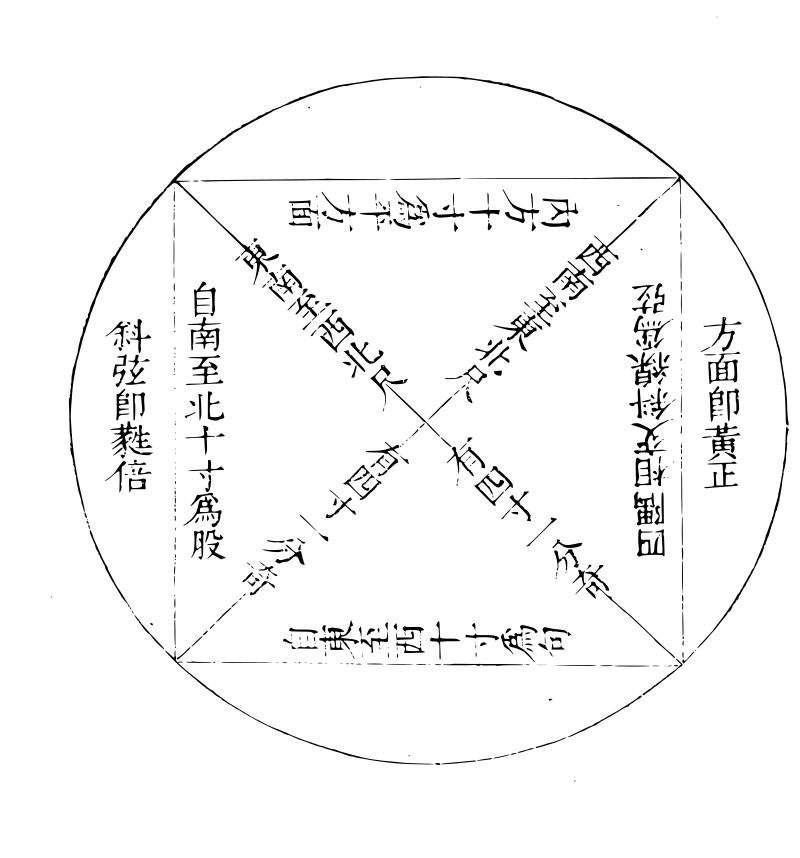
密率源
流出于
《周礼·考
工记》:栗
氏为量
内方尺,
而圆其
外。
新造密率二种。〈倍律命寸为兆,正律命寸为亿,欲初学者知命法之变通云耳〉黄钟之率二十兆。〈本是二十寸命作二十兆〉
大吕之率十八兆八千七百七十四万八千六百二十五亿三千六百三十三万八千六百九十九。太簇之率十七兆八千一百七十九万七千四百三十六亿二千八百○六万七千八百六十○。
夹钟之率十六兆八千一百七十九万二千八百三十亿○五千○七十四万二千九百○八。
姑洗之率十五兆八千七百四十万○一千○五十一亿九千六百八十一万九千九百四十七。
仲吕之率十四兆九千八百三十万○七千○七十六亿八千七百六十六万八千一百四十九。
蕤宾之率十四兆一千四百二十一万三千五百六十二亿三千七百三十万○九千五百○四。
林钟之率十三兆三千四百八十三万九千八百五十四亿一千七百万○○三千四百三十六。
夷则之率十二兆五千九百九十二万一千○四十九亿八千九百四十八万七千三百一十六。
南吕之率十一兆八千九百二十万○七千一百一十五亿○○二十七万二千一百○六。
无射之率十一兆二千二百四十六万二千○四十八亿三千○九十三万七千二百九十八。
应钟之率十兆 五千九百四十六万三千○九十四亿三千五百九十二万九千五百二十六。
黄钟之率十亿〈本是十寸命作十亿〉。
大吕之率九亿四千三百八十七万四千三百一十二。
太簇之率八亿九千○八十九万八千七百一十八。夹钟之率八亿四千○八十九万六千四百一十五。姑洗之率七亿九千三百七十万○○五百二十五。仲吕之率七亿四千九百一十五万三千五百三十八。
蕤宾之率七亿○七百一十万○六千七百八十一。林钟之率六亿六千七百四十一万九千九百二十七。
夷则之率六亿二千九百九十六万○五百二十四。南吕之率五亿九千四百六十万○三千五百五十七。
无射之率五亿六千一百二十三万一千○二十四。应钟之率五亿二千九百七十三万一千五百四十七。
论曰:造率始于黄钟,必先求蕤宾者,犹冬夏二至也。次求夹钟及南吕者,犹春秋二分也。太极生两仪,两仪生四象,此之谓也。始于黄钟者,履端于始也。中于蕤宾者,举正于中也。终于应钟者,归馀于终也。律与历,一道也。黄钟为宫,蕤宾为中,应钟为和,此三律者,律吕之纲纪也。尤见变宫、变徵,有益于乐,而不可妄废也。
不拘隔八相生第四
新法不拘隔八相生,而相生有四法,或左旋,或右旋,皆循环无端也。以證三分损益,往而不返之误。所谓四法者,开列于后。
其一,黄钟生林钟,林钟生太蔟,太蔟生南吕,南吕生姑洗,姑洗生应钟,应钟生蕤宾,蕤宾生大吕,大吕生夷则,夷则生夹钟,夹钟生无射,无射生仲吕,仲吕生黄钟。长生短,五亿乘之。短生长,十亿乘之。皆以七亿四千九百一十五万三千五百三十八除之。
其二,黄钟生仲吕,仲吕生无射,无射生夹钟,夹钟生夷则,夷则生大吕,大吕生蕤宾,蕤宾生应钟,应钟生姑洗,姑洗生南吕,南吕生太蔟,太蔟生林钟,林钟生黄钟。长生短,五亿乘之。短生长,十亿乘之。皆以六亿六千七百四十一万九千九百二十七除之。
其三,黄钟生大吕,大吕生太蔟,太蔟生夹钟,夹钟生姑洗,姑洗生仲吕,仲吕生蕤宾,蕤宾生林钟,林钟生夷则,夷则生南吕,南吕生无射,无射生应钟,应钟生黄钟半律。此系长生短,皆以五亿乘之,皆以五亿二千九百七十三万一千五百四十七除之。
其四,黄钟半律生应钟,应钟生无射,无射生南吕,南吕生夷则,夷则生林钟,林钟生蕤宾,蕤宾生仲吕,仲吕生姑洗,姑洗生夹钟,夹钟生太蔟,太蔟生大吕,大吕生黄钟。此系短生长,皆以十亿乘之,皆以九亿四千三百八十七万四千三百一十二除之。
横黍百分律,依新法算。
黄钟长十寸。
新法置黄钟之率,十亿为实,五亿乘之,七亿四千九百一十五万三千五百三十八除之。所得亿约为寸,得林钟。
林钟长六寸六分七釐四毫一丝九忽九微二纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七为实,十亿乘之,七亿四千九百一十五万三千五百三十八除之。所得亿约为寸,得太蔟。
太蔟长八寸九分○八毫九丝八忽七微一纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八为实,五亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得南吕。
南吕长五寸九分四釐六毫○三忽五微五纤。
新法置南吕之率,五亿九千四百六十万○三千五百五十七为实,十亿乘之七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得姑洗。
姑洗长七寸九分三釐七毫○○五微二纤。
新法置姑洗之率,七亿九千三百七十万○○五百二十五为实,五亿乘之七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得应钟。
应钟长五寸二分九釐七毫三丝一忽五微四纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七为实,十亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得蕤宾。
蕤宾长七寸○七釐一毫○六忽七微八纤。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一为实,十亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得大吕。
大吕长九寸四分三釐八毫七丝四忽三微一纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二为实,五亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得夷则。
夷则长六寸二分九釐九毫六丝○五微二纤。
新法置夷则之率,六亿二千九百九十六万○五百二十四为实,十亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得夹钟。
夹钟长八寸四分○八毫九丝六忽四微一纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五为实,五亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得无射。
无射长五寸六分一釐二毫三丝一忽○二纤。
新法置无射之率,五亿六千一百二十三万一千○二十四为实,十亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得仲吕。
仲吕长七寸四分九釐一毫五丝三忽五微三纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八为实,十亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得黄钟。
黄钟长十寸〈还元〉。
新法置黄钟之率,十亿为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得仲吕。
仲吕长七寸四分九釐一毫五丝三忽五微三纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得无射。
无射长五寸六分一釐二毫三丝一忽○二纤。
新法置无射之率,五亿六千一百二十三万一千○二十四为实,十亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得夹钟。
夹钟长八寸四分○八毫九丝六忽四微一纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得夷则。
夷则长六寸二分九釐九毫六丝○五微二纤。
新法置夷则之率,六亿二千九百九十六万○五百二十四为实,十亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得大吕。
大吕长九寸四分三釐八毫七丝四忽三微一纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得蕤宾。
蕤宾长七寸○七釐一毫○六忽七微八纤。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得应钟。
应钟长五寸二分九釐七毫三丝一忽五微四纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七为实,十亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得姑洗。
姑洗长七寸九分三釐七毫○○五微二纤。
新法置姑洗之率,七亿九千三百七十万○○五百二十五为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得南吕。
南吕长五寸九分四釐六毫○三忽五微五纤。
新法置南吕之率,五亿九千四百六十万○三千五百五十七为实,十亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得太蔟。
太蔟长八寸九分○八毫九丝八忽七微一纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八为实,五亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得林钟。
林钟长六寸六分七釐四毫一丝九忽九微二纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七为实,十亿乘之,六亿六千七百四十一万九千九百二十七除之,所得亿约为寸,得黄钟。
黄钟长十寸〈还元〉。
新法置黄钟之率,十亿为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得大吕。
大吕长九寸四分三釐八毫七丝四忽三微一纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得太蔟。
太蔟长八寸九分○八毫九丝八忽七微一纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得夹钟。
夹钟长八寸四分○八毫九丝六忽四微一纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得姑洗。
姑洗长七寸九分三釐七毫○○五微二纤。
新法置姑洗之率,七亿九千三百七十万○○五百二十五为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得仲吕。
仲吕长七寸四分九釐一毫五丝三忽五微三纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得蕤宾。
蕤宾长七寸○七釐一毫○六忽七微八纤。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得林钟。
林钟长六寸六分七釐四毫一丝九忽九微二纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得夷则。
夷则长六寸二分九釐九毫六丝○五微二纤。
新法置夷则之率,六亿二千九百九十六万○五百二十四为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得南吕。
南吕长五寸九分四釐六毫○三忽五微五纤。
新法置南吕之率,五亿九千四百六十万○三千五百五十七为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得无射。
无射长五寸六分一釐二毫三丝一忽○二纤。
新法置无射之率,五亿六千一百二十三万一千
○二十四为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得应钟。
应钟长五寸二分九釐七毫三丝一忽五微四纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七为实,五亿乘之,五亿二千九百七十三万一千五百四十七除之,所得亿约为寸,得黄钟半律。
黄钟半律长五寸。
新法置黄钟半率,五亿为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得应钟。
应钟长五寸二分九釐七毫三丝一忽五微四纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得无射。
无射长五寸六分一釐二毫三丝一忽○二纤。
新法置无射之率,五亿六千一百二十三万一千○二十四为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得南吕。
南吕长五寸九分四釐六毫○三忽五微五纤。
新法置南吕之率,五亿九千四百六十万○三千五百五十七为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得夷则。
夷则长六寸二分九釐九毫六丝○五微二纤。
新法置夷则之率,六亿二千九百九十六万○五百二十四为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得林钟。
林钟长六寸六分七釐四毫一丝九忽九微二纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得蕤宾。
蕤宾长七寸○七釐一毫○六忽七微八纤。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得仲吕。
仲吕长七寸四分九釐一毫五丝三忽五微三纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得姑洗。
姑洗长七寸九分三釐七毫○○五微二纤。
新法置姑洗之率,七亿九千三百七十万○○五百二十五为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得夹钟。
夹钟长八寸四分○八毫九丝六忽四微一纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得太蔟。
太蔟长八寸九分○八毫九丝八忽七微一纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得大吕。
大吕长九寸四分三釐八毫七丝四忽三微一纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二为实,十亿乘之,九亿四千三百八十七万四千三百一十二除之,所得亿约为寸,得黄钟。
黄钟长十寸〈还元〉。
已上横黍百分之律,依新密率四法,算竟。
斜黍九十分律依新法算。
黄钟长九寸〈每寸十分馀律仿此〉。
新法置黄钟之率,十亿折半为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得林钟。
林钟长六寸○○六毫七丝七忽九微三纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得太蔟。
太蔟长八寸○一釐八毫○八忽八微四纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八折半为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得南吕。
南吕长五寸三分五釐一毫四丝三忽二微○。
新法置南吕之率,五亿九千四百六十万○三千五百五十七为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得姑
洗。
姑洗长七寸一分四釐三毫三丝○四微七纤。
新法置姑洗之率,七亿九千三百七十万○○五百二十五折半为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得应钟。
应钟长四寸七分六釐七毫五丝八忽三微九纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得蕤宾。
蕤宾长六寸三分六釐三毫九丝六忽一微○。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得大吕。
大吕长八寸四分九釐四毫八丝六忽八微八纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二折半为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得夷则。
夷则长五寸六分六釐九毫六丝四忽四微七纤。
新法置夷则之率,六亿二千九百九十六万○五百二十四为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得夹钟。
夹钟长七寸五分六釐八毫○六忽七微七纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五折半为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得无射。
无射长五寸○五釐一毫○七忽九微二纤。
新法置无射之率,五亿六千一百二十三万一千○二十四为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得仲吕。
仲吕长六寸七分四釐二毫三丝八忽一微八纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八为实,九亿乘之,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得黄钟。
黄钟长九寸〈还元〉。
纵黍八十一分律,依新法算。
黄钟长八寸一分。
新法置黄钟之率,十亿,以八十一亿乘之,折半退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得林钟。
林钟长五寸四分○六毫一丝○一微四纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得太蔟。
太蔟长七寸二分一釐六毫二丝七忽九微六纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八,以八十一亿乘之,折半退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得南吕。
南吕长四寸八分一釐六毫二丝八忽八微八纤。
新法置南吕之率,五亿九千四百六十万○三千五百五十七,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得姑洗。
姑洗长六寸四分二釐八毫九丝七忽四微二纤。
新法置姑洗之率,七亿九千三百七十万○○五百二十五,以八十一亿乘之,折半退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得应钟。
应钟长四寸二分九釐○八丝二忽五微五纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得蕤宾。
蕤宾长五寸七分二釐七毫五丝六忽四微九纤。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得大吕。
大吕长七寸六分四釐五毫三丝八忽一微九纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二,以八十一亿乘之,折半退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得夷则。
夷则长五寸一分○二毫六丝八忽○二纤。
新法置夷则之率,六亿二千九百九十六万○五
百二十四,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得夹钟。
夹钟长六寸八分一釐一毫二丝六忽○九纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五,以八十一亿乘之,折半退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得无射。
无射长四寸五分四釐五毫九丝七忽一微二纤。
新法置无射之率,五亿六千一百二十三万一千○二十四,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得仲吕。
仲吕长六寸○六釐八毫一丝四忽三微六纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八,以八十一亿乘之,退位为实,七亿四千九百一十五万三千五百三十八除之,所得亿约为寸,得黄钟。
黄钟长八寸一分〈还元〉。
已上斜黍九十分律,及纵黍八十一分律,各具四法。今载其一,馀三法皆仿此,故不悉载。
纵黍八十一分,作九寸律,依新法算。
例曰:此法每寸九分,每分九釐,每釐九毫,每毫九丝,每丝九忽,每忽九微,每微九纤,皆以九为法。故与十不同。
算盘首位为寸位 第二位为分位
第三位为釐位 第四位为毫位
第五位为丝位 第六位为忽位
第七位为微位 第八位为纤位初九因至寸位住 又九因至分位住
又九因至釐位住 又九因至毫位住
又九因至丝位住 又九因至忽位住
又九因至微位住 又九因至纤位住云至分位者,不许至寸位。云至釐位者,不许至分位。馀仿此。
黄钟长九寸。
新法置黄钟之率,十亿为实,九因至寸位住,得九寸,为黄钟。
大吕长八寸四分四釐○六丝七忽四微五纤。
新法置大吕之率,九亿四千三百八十七万四千三百一十二为实,初九因至寸位住,得八寸。又九因至分位住,得四分。又九因至釐位住,得四釐。又九因至毫位住,得○毫。又九因至丝位住,得六丝。又九因至忽位住,得七忽。又九因至微位住,得四微。又九因至纤位住,得五纤。凡九因八遍,共得八寸四分四釐○毫六丝七忽四微五纤,为大吕。
太蔟长八寸○一釐四毫一丝六忽○八纤。
新法置太蔟之率,八亿九千○八十九万八千七百一十八为实,初九因至寸位住,得八寸。又九因至分位住,得○分。又九因至釐位住,得一釐。又九因至毫位住,得四毫。又九因至丝位住,得一丝。又九因至忽位住,得六忽。又九因至微位住,得○微。又九因至纤位住,得八纤。凡九因八遍,共得八寸○分一釐四毫一丝六忽○微八纤,为太蔟。
夹钟长七寸五分一釐○一丝○七微四纤。
新法置夹钟之率,八亿四千○八十九万六千四百一十五为实,初九因至寸位住,得七寸。又九因至分位住,得五分。又九因至釐位住,得一釐。又九因至毫位住,得○毫。又九因至丝位住,得一丝。又九因至忽位住,得○忽。又九因至微位住,得七微。又九因至纤位住,得四纤。凡九因八遍,共得七寸五分一釐○毫一丝○忽七微四纤,为夹钟。
姑洗长七寸一分二釐五毫四丝二忽○○。
新法置姑洗之率,七亿九千三百七十万○○五百二十五为实。初九因至寸位住,得七寸。又九因至分位住,得一分。又九因至釐位住,得二釐。又九因至毫位住,得五毫。又九因至丝位住,得四丝。又九因至忽位住,得二忽。又九因至微位住,得○微。又九因至纤位住,得○纤。凡九因八遍,共得七寸一分二釐五毫四丝二忽○微○纤,为姑洗。
仲吕长六寸六分六釐一毫一丝六忽八微一纤。
新法置仲吕之率,七亿四千九百一十五万三千五百三十八为实,初九因至寸位住,得六寸。又九因至分位住,得六分。又九因至釐位住,得六釐。又九因至毫位住,得一毫。又九因至丝位住,得一丝。又九因至忽位住,得六忽。又九因至微位住,得八微。又九因至纤位住,得一纤。凡九因八遍,共得六寸六分六釐一毫一丝六忽八微一纤,为仲吕。
蕤宾长六寸三分二釐四毫二丝八忽四微七纤。
新法置蕤宾之率,七亿○七百一十万○六千七百八十一为实,初九因至寸位住,得六寸。又九因
至分位住,得三分。又九因至釐位住,得二釐。又九因至毫位住,得四毫。又九因至丝位住,得二丝。又九因至忽位住,得八忽。又九因至微位住,得四微。又九因至纤位住,得七纤。凡九因八遍,共得六寸三分二釐四毫二丝八忽四微七纤,为蕤宾。
林钟长六寸○○四毫八丝四忽二微七纤。
新法置林钟之率,六亿六千七百四十一万九千九百二十七为实,初九因至寸位住,得六寸。又九因至分位住,得○分。又九因至釐位住,得○釐。又九因至毫位住,得四毫。又九因至丝位住,得八丝。又九因至忽位住,得四忽。又九因至微位住,得二微。又九因至纤位住,得七纤。凡九因八遍,共得六寸○分○釐四毫八丝四忽二微七纤,为林钟。
夷则长五寸六分○二毫一丝四忽七微五纤。
新法置夷则之率,六亿二千九百九十六万○五百二十四为实,初九因至寸位住,得五寸。又九因至分位住,得六分。又九因至釐位住,得○釐。又九因至毫位住,得二毫。又九因至丝位住,得一丝。又九因至忽位住,得四忽。又九因至微位住,得七微。又九因至纤位住,得五纤。凡九因八遍,共得五寸六分○釐二毫一丝四忽七微五纤,为夷则。
南吕长五寸三分一釐四毫一丝六忽六微三纤。
新法置南吕之率,五亿九千四百六十万○三千五百五十七为实,初九因至寸位住,得五寸。又九因至分位住,得三分。又九因至釐位住,得一釐。又九因至毫位住,得四毫。又九因至丝位住,得一丝。又九因至忽位住,得六忽。又九因至微位住,得六微。又九因至纤位住,得三纤。凡九因八遍,共得五寸三分一釐四毫一丝六忽六微三纤,为南吕。
无射长五寸○四釐一毫二丝一忽一微五纤。
新法置无射之率,五亿六千一百二十三万一千○二十四为实,初九因至寸位住,得五寸。又九因至分位住,得○分。又九因至釐位住,得四釐。又九因至毫位住,得一毫。又九因至丝位住,得二丝。又九因至忽位住,得一忽。又九因至微位住,得一微。又九因至纤位住,得五纤。凡九因八遍,共得五寸○分四釐一毫二丝一忽一微五纤,为无射。
应钟长四寸六分八釐一毫五丝一忽○五纤。
新法置应钟之率,五亿二千九百七十三万一千五百四十七为实,初九因至寸位住,得四寸。又九因至分位住,得六分。又九因至釐位住,得八釐。又九因至毫位住,得一毫。又九因至丝位住,得五丝。又九因至忽位住,得一忽。又九因至微位住,得○微。又九因至纤位住,得五纤。凡九因八遍,共得四寸六分八釐一毫五丝一忽○微五纤,为应钟。
黄钟半律长四寸四分四釐四毫四丝四忽四微四纤。
新法置黄钟半率,五亿为实,八因九归,亿约为寸,得四寸四分四釐四毫四丝四忽四微四纤,为黄钟半律。
谨按约十为九,主意盖为三分损益,而设使归除,无不尽数耳。夫律吕之理,循环无端,而秒忽之数,归除不尽,此自然之理也。因其天生自然,不须人力穿凿,以此算律,何善如之。历代算律,祇欲秒忽除之有尽,遂致律吕往而不返,此乃颠倒之见,非自然之理也。是以新法不用三分损益,不拘隔八相生,然而相生有序,循环无端。十二律吕,一以贯之。此盖二千馀年之所未有,自我朝始也。学者宜尽心焉。