钦定古今图书集成历象汇编历法典

　第一百二十六卷目录

历法典第一百二十六卷

算法部汇考十八

《新法历书》比例规解〈远西罗雅谷著〉序目

天文历法等学，舍度与数，则授受不能措其辞。故量法、算法、恒相发焉。其法种种，不袭而器。因之各国之法与器，大同小异。如算法之或以书、或以盘珠，吾西国犹以为未尽其妙也。近世设立筹法，似更超越千古。至几何家用法，则筹有所不尽者，而量该之不能不藉以为用。今繇《几何》六卷六题，推显比例规尺一器，其用至广，其法至妙，前诸法器，不能及之。因度用数开阖。其尺以规支度得算最捷，或加减，或乘除，或三率，或开方之面与体，此尺悉能括之。又函表度、倒景、直景、日晷、句股、弦算、五金轻重、诸法及百种技艺，无不赖之。功倍用捷，为造玛得玛，第嘉最近之津梁也。昔在上海，曾为徐宗伯造其尺，而未暇译书。今奉旨修历，兼用敝庠之法。思此小器，为用既广，曷敢秘而不传。第中西文字，绝不相同，倘因艰涩而辍译，是坐令此器不得其用，不甚可惜哉。因草创成书，请教宗伯。此器之倘为用于世也，则润色之，增补之，定有其时而谷之不文，或见亮于天下后世也矣。
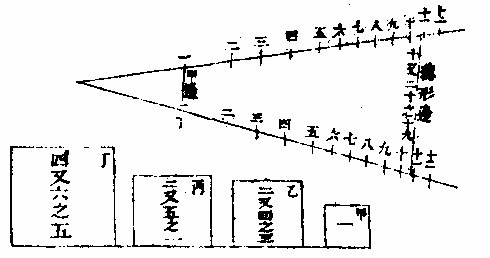
论度数者其纲领，有二：一曰量法，一曰算法。所量所算者，其节目有四焉。曰点，曰线，曰面，曰体。总命之曰：《几何之学》。而其法不出于比例，盖比例法又不出于句股。第句股为正方角，而别有等角、斜角。句股不足尽其理。故总名之曰：三角形，此规名比例者，用比例法也。器不越咫尺，而量法、算法，若线、若面、若体、若弧、矢方圆诸法。凡度数所须，该括欲尽，斯亦奇矣。所分诸线，篇中称引之说，特其指要，各有本法。本论未及详焉。若所从出，与其致用，则三角形之比例而已。按《几何原本》六卷四题云：凡等角三角形，其在等角旁之各两腰线，相与为比例必等。而对等角之边，为相似之边。六题云：两三角形之一角等，而对等角旁之各两边比例等，即两形为等角形。而对各相似边之角各等。作者因此二题创为此器。今依左图解之，如
图

甲乙丙与丁乙戊大小两三角形，同用乙角即为等角，则甲乙与乙丙之比例。若丁乙与乙戊而对等角之边，如甲丙与丁戊为相似之边也，又显两形为等角形，而对各相似边之角各等也。今此规之枢心，即乙角两股、即乙甲乙丙两腰，甲丙为底，即与乙丁戊为等角形，而各相当之各角各边其比例悉等矣。任张翕之，但取大
图

小两腰，其两底必相似也，或取两底，其两腰必相似也，或取此腰，此底其与彼腰彼底必相似也，以数明之，如甲乙大腰一百，乙丁小腰六十，而设甲丙大底八十，以求小底丁戊，即定尺用规器量取丁戊，为度向平分线。取数必四十八，不烦乘除矣。又如平方积一万，其根一百，求作别方为大方四之三，即以一百为腰，分面线之，

四点为大，底次以三点为小，腰取小底为度向平分线，得八十六半强为小方根。自之约得七千五百为小方，积不烦开平方矣。又如立方积八千，其根二十，求作大方倍元方，即以二十为小底，分体线之一点为小腰，次以二点为大腰，取大底为度于平分线。得二十五半自之，再自之约得一万六千为大方积，不烦开立方矣。篇中所言某为腰，某为底，设某数得某数者，皆此类也。规凡二面，面有五线，共十线，其目如左。
第一平分线；
第二分面线；
第三更面线；
第四分体线；
第五更体线；
第六分弦线；
第七节气线；
第八时刻线；
第九表心线；第十五金线。
右比例十类之外，依几何原本其法甚多，因一器难容多线，故止设十线，其不为恒用者。姑置之稍广焉。更具四法如左，
一、平面形之边与其积；
二、有形五体之边与其积与其面；
三、有法五体与球或内或外两相容；
四、随地造日晷求其节气。
比例规造法〈一名度数尺，其式有二。〉
第一式第一式

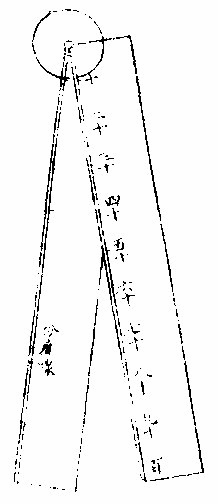
一以簿铜板或厚纸，作两长股，如图，任长一尺，上下广如长八之一，两股等长、等广、股首上角为枢，以枢心为心，从心出各直线，以尺大小定线数，今折中作五线，两股之面共十线，可用十种比例之法。线行相距之地取足书字而止。尺首半规馀地以固枢也，用时张翕游移。
第二式第二式

一以铜或坚木作两股，如图：厚一分以上，长任意，股上两用之际以为心。规馀地以安枢，其一规面与尺面平，而空其中，其一剡规而入于彼尺之空，令密无罅也，枢欲其无偏也，两尺并欲其无罅也，枢心为心，与两尺之合线，欲其中绳也。用则张翕游移之，张尽令两首相就成一直线。可作长尺，或以两半直角相就成一直角，可作矩尺。
比例矩之类别有二种。一为四锐定心规；一为四锐百游规，不解之其造法，颇难为用未广，姑置之。
比例各线总图四

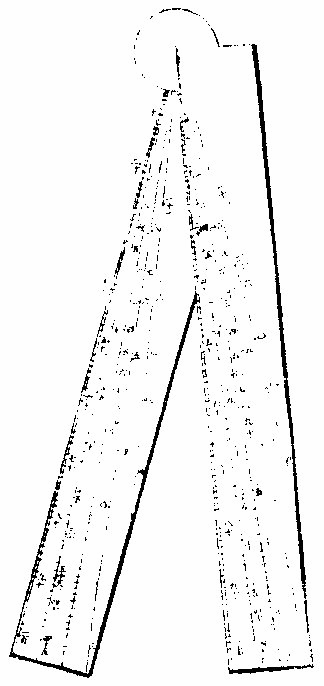
比例各线总图二比例各线总图二

比例各线总图三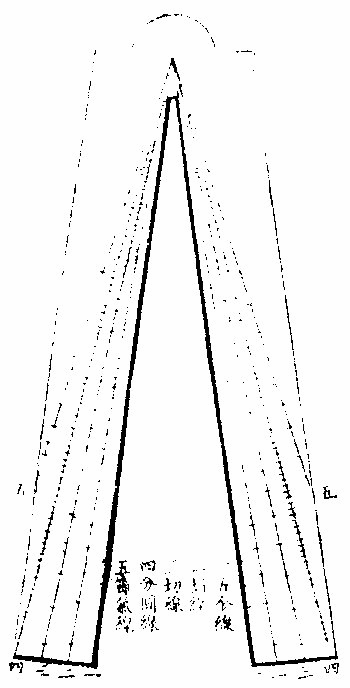第一平分线比例各线总图三比例各线总图二比例各线总图三

第一平分线比例各线总图二比例各线总图三

第一平分线第一平分线
分法

此线平分为一百或二百，乃至一千量尺之大小也。分法如取一百先平分之为二，又平分为四，又各五分之为二十，自此以上不容分矣，则用更分法，以元分四复五分之，或以元分六复五分之，如左图：甲乙线分丙丁戊为元分之四，今更五分之，得己庚辛壬。元分与次分之较为壬丙为戊己，皆甲乙二十分之一，为元分五之一。
图

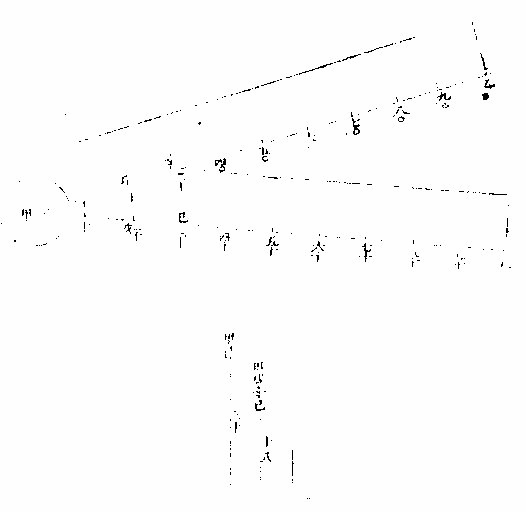
每数至十、至百，各书字识之。
论曰：甲乙四与甲丙一，若甲己四与甲壬一更之甲乙四与甲己四，若甲丙一与甲壬一，甲己为甲乙五之四，即甲壬为甲丙五之四，壬丙为甲丙五之一，又甲丁为十，甲辛为八，辛丁为甲丁十之二，或丙丁五之二，戊庚为丁戊五之三，又壬丙为甲丙五之一，必为甲壬四之一。〈几何五卷〉
用法一：

凡设一直线任欲作几分，假如四分。即以设线为度数，两尺之各一百以为腰，张尺以就度，令设线度为两腰之底。置尺数两尺之各二十五以为腰。敛规取二十五，两点间之度以为底。向线上简得若干数，即所求分数。　凡言线者皆直线，依几何原本，大小两三角形之比例，则二十五与得线。若一百与设线也，更之二十五与一百，得线与设线皆若一与四也。若求极微分，如一百之一，如上以一百为腰，设线为底，置尺次以九十九为腰，取底比设线，其较为百之一。　若欲设线内取零数，如七之三，即以七十为腰。设线为底，置尺次以三十为腰，敛规取底，即设线七之三。〈置尺者置不复动下仿此〉
用法二：

凡有线求几倍之，以十为腰，设线为底置尺。如求七倍以七十为腰，取底即元线之七倍。若求十四倍，则倍得线，或先取十倍，更取四倍并之。
用法三：

有两直线欲定其比例，以大线为尺末之数〈尺百即百千即千〉置尺，敛规取小线度于尺上，进退就其等数，如大线为一百，小线为三十七，即两线之比例。若一百与三十七可约者约之。
约法以两大数约为两小数，其比例不异如一百与三十约为十与三。
用法四：

乘法与倍法相通。〈乘者求设数之几倍也〉如以七乘十三，于腰线取十三为度，七倍之。即所求数也。
用法五：

设两线或两数。
凡言数者，腰上取其分，或以数变为线，或以线变为数。

欲求一直线而与元设两线为连比例。　若设大求小，则以大设为两腰，中设为底，次以中设为两腰，得小底，即所求。如甲乙、甲丙尺之两腰，所设两数为三十，为十八，欲求其小，比例从心向两腰取三十。如甲辛、甲己识之，敛规取十八为度，以为底，如辛己次从
图图

心取十八，如甲丁、甲戊。即丁戊为连比例之小率，得十一有奇。　若设小求大，则反之，以中设为两腰，小设为底，置尺以中设为度，进求其等数以为底。从底向心得数，即所求。如甲丁、甲戊为两腰，丁戊为底，次以甲丁为度。引之至辛、至己而等，从辛从己向心得三十。即大率论。见几何六卷十一题
凡言等数者皆两腰，上纵心取两数等。下同
用法六：

凡有四率连比例，既有三率而求第四，或以前求后，则丁戊为第一率，辛巳、甲丁、甲戊为第二。又为第三而得辛甲，为第四。若以后求前，则甲辛、甲己为第一，辛巳、甲戊、甲丁为第二。又为第三而得丁戊为第四。
甲辛与辛己若甲丁与丁戊，故也。
图

用法七：
有断比例之三率求第四，如一星行九日得一十一度，今行二十五度，日几何。即用三率法以元得一十一度为两腰，元行九日为底，置尺以二十
五度为两腰，取大底腰上数之得二十日〈十一之五〉为所
求日。
此正三率法九章中名异乘同除也。
图

用法八：
句股形有二边，而求第三法于一尺。取三十为内，句一尺，取四十为内股，更取五十为底，以为内弦，即腰间角为直角置尺，若求弦，则以各相当之句股进退取数，各作识于所得点。两

点相望，得外弦线。以弦向尺，上取数为外弦数。
言内外者以先定之，句股成式为内，甲乙丙是以所设所得之。他句股形为外，甲戊己是。

若求句于内股，上取外股作识，以设弦为度，从识向句尺。取外弦得点，作识，从次识向心数之。得句求股亦如之。
下有开方术为句股本法可用。
用法九：

若杂角形有一角及各傍两腰，求馀边。先以弦线法
图

依设角，作尺之腰，间角次用前法取之。〈见下二十一用四法〉
用法十：
有小图欲更画大几倍之图，则尺上取元图之各线加几倍，如前作之。
用法十一：

此线上宜定两数其比例，若径与周为七、与二十二、或七十一与二百二十三，即二十八数上书径八十六上书周。　有圈求周径法，以元周为腰，设周为底，
图

次于元两径。取小底得所求径。　反之以径求周径为腰如前。
用法十二：
此线上定两数，求为理分中末线之比例。则七十二与四十二又三之一，不尽为大分其小，分为二十四又三之二弱。　有一直线

欲分中末分，则以设线为度，依前数取之。〈几何六卷三十题〉
第二分面线，

今为一百不平分，分法有二：一以算，一以量。
图

以算分：
算法者以枢心为心，任定一度为甲乙十平分之，自之得积一百。　今求加倍，则倍元积一百为二百。其方根为十四又十四之九。即于甲乙十分线加四分半强，而得甲丙为倍面之
图

边。求三倍，则开三百之根，得十七有半为甲丁，求五六七倍以上者，边法同。〈用方根表甚简易〉
以量分：
任取甲乙度为直角方形之一边，求倍，则于甲乙引至丁，截乙丁倍于甲乙，次平分，甲丁于戊戊心。甲界作半圈，从乙作乙己垂线，截圈于己。即己乙线为二百容形之一边。〈六卷二十六增〉求

三倍则乙丁三倍于甲乙，四倍以上法同于尺上，从心取甲乙，又从心取乙己。等线成分面线。
试法：

元线为一正方〈直角方形省曰正方〉之边，倍之。得四倍容方之边。否则不合。三倍之得九倍容方之边，四倍得十六，五倍二十五，又取三倍之边，倍之，得十二，再加倍，得二十七倍之边。再加倍，得四十八倍之边。再加倍，得七十五倍之边。若五倍容形之边，倍之得二十倍容形之边。再加倍，得四十五倍容形之边。再加倍，得八
图

十倍容形之边。〈本边之论见几何六卷十三〉
用法一：
有同类之几形。
方圆三边，多边等形容与容之比例。若边与边其理具几何诸题。
欲并而成一同类之形，其容与元几形并之容等。如
图

正方大小四形，求作一大方其容与四形并等。第一形之容为二，二形之容为三，三形之容为四有半，四形之容为六又四之三。其法从心至第二点为两腰，以第一小形之边为底置尺，次并四形之容得十六又四之一。以为两腰，取其
图

底为大形边，其容与四形之容并等。　若无容积之比例，但设边如甲乙丙丁，四方形其法从心至尺之第一点为两腰，小形甲边为底置尺，次以乙形边为度，进退取等数得第二点，外又四分之三，即书二又四之三，次丙形边为度得

三又五之一，丁形边得四又六之五，并诸数及甲形一得十又二十之十九，向元定尺上进退，取等数为底，即所设四形同类等容之一大形边。〈此加形之法〉
图

用法二：
设一形，求作他形大于元形几倍法。曰元形边为底，从心至第一点为腰，引至所求倍数点为大腰。取大底即大形之边。〈此乘形之法〉
用法三：

若于元形求几分之几，以元形边为底，命分数为腰，退至所求数为腰，取小底即得。　如正方一形求别。作一正方，其容为元形四之三，以大形边为底，第四点为腰。〈即命分数〉次以第三点为腰。〈即得分数〉得小底即小形边。
此除形之法。若设一形之积大，而求其若干倍小，而求其若干分，则以原积当单数，用第一线求之。
用法四：

有同类两形，求其较，或求其多寡，或求其比例若干。法曰：小形边为底，第一点为腰置尺，以大形之边为度。进退就两等数以为腰，得两形比例之数。次于得数减一所馀为同类，他形之一边，此他形为两元形之较。　如前图，小形边为一，大形边为六，其比例为一与六，则从一至六为较形边。〈此减形之法〉
用法五：

有一形，求作同类之他形。但云两形之容积，若所设之比例。法曰：设形边为底，比例之相当率为腰，次他率为腰，取其底为他形之边。
用法六：

有两数，求其中比例之数。法曰：先以大数变为线，变线者于分度线上。取其分与数等为度也，以为底。以
图

本线上之本数为腰。置尺次于小数上，取其底线变为数，变数者于分度线上查，得若干分也，此数为两元数中比例之数。　如前图，二与八为两元数，先变八为线以为底，以本线之第八点为腰，置尺次于第二点上，取

其底线变为四数，则二与四若四与八也。　若设两线不知其分，先于分度数线上查几分法，如前。
用法七
图

有长方，求作正方，其积与元形等法。曰：长方两边变两数，求其中比例之数变作线。即正方之一边与元形等积。
用法八：

有数求其方根，设数或大或小。若大如一千三百二十五。先于度线上取十分为度以为底，以本线一点为腰。即一正方之边其积一百次，求一百与设数之比例。得十三倍又四之一。以本线十三点强为腰，取其底于度线上，查分得三十五强为设数之根。
第三更面线。
分法，

如有正方形，欲作圆形与元形之积等。置公类之容积四三二九六四以开方，得六五八正方边也。以开三边形之根，得一千为三边等形之一边。开五边之
图

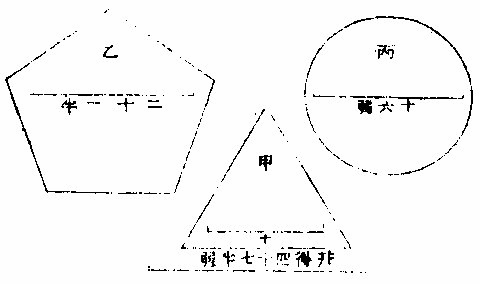
根，得五○二，六边形之根为四○八，七边形之根为三四五，八边形之根为二九九，九边形之根为二六○，十边形之根为二三七，十一边形之根为二一四，十二边形之根为一九七。圆形之径为七四二。以本线为千平分而取各类之

数。从心至末取各数加本类之号。
言平形者，有法之形，各边各角俱等。
用法一：

有异类之形欲相并，先以本线各形之边为度，以为底。以本类之号为腰，置尺取正方号之底线别书之末。以各正方之边于分面线上，取数合之而得总边也。
假如甲乙丙三异类形欲相并。先以三边号为腰，甲一边为底，置尺取正方号，四点内之底向分面线上
图

用十数为腰。正方底为底，于甲形内作方底线书十次，五边号为腰，乙一边为底，如前。取正方底向分面线得二十一半。即于乙形内作方底线，书之次圆号为腰径，为底，如前。得十六弱并，得四十七半弱。　若欲相减，则先通类。如前法

次于分面线上相减。〈同上图〉
用法二：

有一类之形，求变为他类之形。同积以元形边为度以为底，从心至本号点为腰，置尺次以所求变形之号为腰得底，即变形边。
用法三：

凡设数求开各类之根，先于分面线求正方之根次，以方根度为底，本线正方号为腰，置尺，则所求形之号之底线，即元数某类之根。
有法之平形，其边可名为根，与方根相似。
用法四：

若异类形，欲得其比例与其较。则先变成正方，依分面线求之。
第四分体线。

线不平分，分法有二：一以算，一以量。
以算分：

从尺心任定一度为甲乙，十平分自之，又自之得积一千。即定其线为一千，即体之根。今求加一倍积体
图

之根。倍元积得二千，开立方根得十二又三之一。即于甲乙加二又三之一为甲丙。乃倍体之边，求三倍开三千数之立方根，以上同。
又捷法取甲乙元体之边，四分之一加于甲乙元边，得甲丙，即倍体边又取甲

丙七分之一，加于甲丙得甲丁。乃三倍体之边，取甲丁十分之一加于甲丁，得甲戊，乃三倍体之边。再分再加如图。
图图

试置元体之边二十八四之一，得七，以加之，得三十。五法曰：两根之实数，即用再自之数为一，与二不远。盖二十八之立实为二一九五二，倍之为四三九○四。比于三十五倍体边之实四二八七五，其差才○一○二九，约之为一千四百五十二分之一，不足为差。若用三十六之四六六五六，其差为远。　又加倍体七之一，得再倍体之边三十五又七之一，七之一者五也。以加之得四十。其实为六四○○○。元积再倍之，数为六五八五六。较差才○一八五六，或三十五之一可不入算也，若用四十一根之实六八九二一，其差为远。
又试倍边上之体为体之八倍。即依图计零数至第八位，为五之四，八之七，十一之十，十四之十三，十七之十六，二十之十九，二十三之二十二。用合分法合之得一二○四二八○之六○八六○八。约之为一○七五○之五四三四，与二之一不远。则法亦不远，右两则皆用开立方之法，不尽数难为定法。
以量分：

先如图，求四率连比例线之第二，盖元体之边与倍体之边为三，加之比例也。今求第二。几何法曰：第二线上之体与第一线上之体，若四率连比例线之第四与第一。假如丙乙元体之边，求倍体之边。则倍丙
图缺乙，得甲丁。以甲丁乙丙作壬巳辛庚矩形，于壬角之两腰引长之。以形心为心，如戊作圈，分截引长线于子、于午渐试之。必令子午直线切矩形之辛角乃止。即乙丙〈即辛庚〉午庚子己甲丁〈即壬庚〉为四率连比例线。用第二率午庚为次体之

一边，其体倍大于元体。〈详双中率论〉　若甲丁为乙丙之三倍、四倍。即午庚边上之体大于元体，亦三、四倍以上仿此。　用前法则元体之边倍之，得八倍体之边。若三之得二十七倍体之边，四之得六十四倍体之边，五之得一百二十五倍体之边。
又取二倍体边倍之，得十六，再倍得一二八。倍体之边，本线上量体任用其边，其根、其面、其对角线、其轴皆可。
用法一
设一体，求作同类体大于元体几倍法，以元体边为
底，从心至第一点为腰，置尺次以所求倍数。　为腰得大底，即所求大体边。　若设零数如元体，设三求作七，以三点为初腰，七点为次腰，如上法。〈此乘体之法〉
用法二：

有体求作小体，得元体之几分。如四分之一，四分之三等。法以元体之边为底，命分数之点为腰，置尺，退至得分数为小腰，得小底是所求分体边。〈此分体之法〉
用法三：

有两体求其比例。以小体边为底，第一点为腰，置尺次以大体边为底。就等数得比例之数也，不尽则引小体边于二点以下。以大边就等数两，得数乃上可，得比例之全数而省零数。
用法四：

有几同类之体，求并作一总体。　若有各体之比例，则以比例之数合为总数。以小体边为底，一点以上为腰，置尺于总数点内，得大底，即总体边。　若不知其比例，先求之次，用前法。〈此加体之法〉
图图

如图：甲乙丙三立方体，求并作一大立方体。其甲根一，乙三又四之三，丙六并。得十又四之三，以甲边为底，本线一点以上为腰，置尺向外，求十又四之三为腰，取底为度，即所求总体之根。
用法五：

大内减小所存，求成一同类之体。　先求其比例，次以小体边为底，比例之小率点以上为腰。置尺次以比例。两率较数点上为腰。得较底，即较体之边。〈此减体之法〉
用法六：

有同质同类之两体，得一体之重知他体之重。盖重与重若容与容。先求两体之比例，次用三率法。某容得某重若干。求某容得某重若干。
同质者、金铅银铜等同体者，方圆长立等。
用法七：

有积数欲开立方之根。　　置积与一千数，求其比例。次于平分线上取十分为底，本线一点以上为腰，置尺次比例之大率以上为腰，得大底于平分线上，取其分为所设数之立方根。如设四万则四万与一千之比例为四十与一，如法于四十点内，得大底线变为分得三十四强。　若所设积小不及千，则以一分为底，一点或半点或四之一等数为腰，置尺设数内。求底而定其分，若用半点，用所设数之一半，用四之一，亦用设数四之一。盖算法通变或倍、或分、不变比例之理。
用法八：

有两线，求其双中率。〈线数同理〉如三为第一率，二十四为第四率，求其比例之中两率。　法求两率之约数，得一与八以小线为底，一点以上为腰，置尺次八点以上为腰，取大底即第二率有第二，第四依平分线求第三。
第五变体线

变体者如有一球体，求别作立方其容与之等。
分法

置公积百万，依算法开各类之根，则立方之根为一百四，等面体之根为二○四八，等面体之根为一二
图

八半十二，等面体之根为五十二十，等面体之根为七六。　圆球之径为一二六。　因诸体中独四等面体之边最大，故本线用二百○四分平分之，从心数各类之根至本数加字。
开根法见测量全义六卷
用法一：

有异类之体，求相加以各体之边为度以为底。本线本类之点以上为腰，置尺次从立方点内，取底别书之各书讫，依分体线法合之。
用法二：

有异类之几体，求其容之比例。先以各体变而求同容之立方边、次于分体线，求其比例。乃所设体之比例。若知一体之容数，因三率法求他体之容数。
第六分弦线〈亦曰分圈线〉
图

分法有二：
一法、
别作象限圈分，令半径与本线等长，分弧为九十度。各作识从一角向各识，取度移入尺线，从尺心起度各依所取度作识加字。若尺身大加半，度之点可作一百八十○度，若身小
图

可六十度、或九十度止。
又法
用正弦数表取度分数，半之。求其正弦倍之，本线上从心数之识之。
如求三十度弦，即其半十五度之正弦为二五九，倍之得千分之五一九。为三十度之弦从心
识之。
用法一：

有圈径，设若干之弧，求其弦以半径为底，六十度为腰，置尺次以设度为腰，取底，即其弦移试元圈上合其弧。　反之有定度之弦，求元圈径，以设弧之弦为底，设度为腰，置尺次取六十度为腰，取底。即圈之半径。
用法二：

有全圈，求作若干分法。以半径为底，六十度〈其弦即半径也〉为腰，置尺命分数为法，全圈为实，而一得数为腰，取底试元圈上合所求分。〈此分圈之法〉　约法本线上先定各分之点。如百二十为三之一，九十为四之一，七十二为五之一，六十为六之一，五十一又七之三为七之一，四十五为八之一，四十为九之一，三十六为十之一，三十二又十一之八为十一之一，三十为十二之一各加字。
用法三：

凡作有法之平形，先作圈以半径为底，六十度为腰，置尺次本形之号为腰，取底，移圈上得分。
用法四：

有直线角，求其度，以角为心任作圈，两腰间之弧度即其对角之度。〈有半径有弧求度如左〉
用法五：

有半径，设弧不知其度数，法以半径为底，六十度为腰，置尺次以弧为度，就等数作底，其等数即弧度。反之设角度不知，其径及弧求作图。其法先作直线，一界为心任作圈。分以截线为底，六十度之弦线为腰，
图

置尺次于本线，取设度之弦线为腰，得底以为度，从截圈点取圈分。即设度之弧，再作线到心，即半径成直线角如所求。

因此有两法可解。三角形省布数详测量全义首卷
第七节气线。〈一名正弦线〉
分法：

全数为一百平分，尺大可作一千用，正弦表从心数
图

各度之数。每十度加字。如三十度之正弦五十，则五十数傍书三十二度之正弦五，则五数傍书三。
简法

第一平分线可当此线为各有百平分，则一线两傍，一书分数字，一书度数字。
用法一：

半径内有设弧求其正弦。以半径为底，百为腰，置尺次以设度为腰，取底即其正弦。
用法二：

凡造简平仪、平浑日晷等器。用此线甚简易，如简平仪之下盘，周天圈其赤道线左右，求作各节气线。先定赤道线为春秋分，次于弧上取赤道左右各二十三度半之弧，两弧相向作弦。以其半弦为底，本线百数为腰，置尺次数各节气离春秋分两节之数。寻本线之相等数为腰，取底为度，移赤道线，左右两旁作直线与相对之节气相连，为各节气线。
或于赤道线上及二至线上定时刻线之相距若干亦可。

如欲定立春、立冬、立夏、立秋、
因四节离赤道之度等。故为公度。

法曰：立春至春分四十五度，则取本线四十五度内之底线，移于仪上春分线左右。　若欲定小暑、小寒之线离秋分、春分各七十五度，则取七十五度内之底线为度，移二分线左右得小暑、小寒之线。
第八时刻线。〈一名切线线〉
图

分法、
切线之数无限，为九十度之切割两线，皆平行无界。故今止用八十度，于本线

立成表。上查八十度得五六七，即本线作五六七平分，次因各度数加字。
一度至十五切线正弦，微差尺上不显可，即用正弦。
第九表心线、〈一名割线线〉
分法、

此线亦止八十度，依表查得五七五平分之，其初点与四十五度之切线等。〈初点即全数故等〉次依本表加之。
用法一：

有正弧或角，欲求其切线、或割线，法以元圈之半径为底切线，线四十五度之本数为腰割线，线则以○度○分为腰，置尺次以设度为腰，取底为某度之切线割线。　反之有直线又有本弧之径，欲求。设线之弧若干，度以半径为度以为底，设弧之度数为腰，置尺又设线为底，求本线上等数即设线之弧。
用法二：

表度说：以表景长短求日轨高度分。今作简法，用切
图

线，线凡地平上立物皆可当表，以表长为底，本线四十五度上数为腰，置尺次取景长为底，求两腰之等数。即日轨高度分。　若用横表法，如前，但所得度分乃日离天顶之度分也。安表法见本说。
用法三：

地平面上作日晷法，先作子午直线，卯酉横线。令直角相交，从交至横线端为底，就切线，线上之八十二
图

度半为腰，置尺次于本线七度半点内。取底为度，向卯酉线交处左右各作识。为第一时分次递加七度半取底为度。如前递作识为各时分。
每七度半者，如七度半、十五度，二十二度半，三十度，三十七度半，四十五度，五十二度半，六十度六，十七度半，七十五度，八十二度半。

若求刻线，则递隔三度四十五分，而取底为度也。次于元切线上取四十五度线〈四十五度之切线即全数〉为底割线。初点为腰，置尺次以本地北极高度数为腰，于本线上取底为表，长于子午卯酉两线之交，正立之又取北极高之馀度线为度。于子午线上从交点起，向南得日晷。心从心向卯酉线上各时分点作线，为时线在子午线西者，加午前字。如巳辰卯在子午线东者加午后字，如未申酉。
日晷图说。
图

子午卯酉两线相交于甲，甲酉为度以为底，以切线之八十二度半为腰，置尺递取七度半之底，向甲左右作识。如甲乙、甲丙次取十五度线之底作第二识。

如甲丁、甲戊每识递加七度半，每识得二刻，则丁点为午初，戊为未初，馀点如图。　次取甲己线上四十五度之切线为底，割线之。初点为腰，置尺取北极高馀度〈顺天府约五十〉之割线为度。从甲向南取辛辛为心，从心过乙丁等点作线为时刻，线又割线，上取北极高度之线〈顺天府约四十〉为表，长即甲庚也，表与面为垂线。
立表法，以表位甲为心，任作一圈次立表，表末为心，又作圈，若两圈相合或平行则表直矣。
用法四：

先有表度，求作日晷。则以表长为底，割线上之北极高度为腰。置尺次以极高馀度为腰，取底为度，定日晷之心。次用元尺于切线上，取每七度半之线如前。
凡言表长以垂表为主，或垂线。
用法五：

有立面向正南，作日晷。法如前，但以北极高度求晷心，以北极高之馀度为表长。
又平晷之子午线为此之垂线，书时刻以平晷之卯为此之酉各反之。
图

用法六：
若立面向正东、正西。先用权线作垂线定表处。即晷心从心作横线与垂线为直角。　若面正东于横线下，向北作象限弧，若面正西于横线下，向南作弧。弧上从下数北极高之馀度为界。从心过界作线为赤
道线。又以表长为底切线，线上之四十五度为腰，置
尺递，取七度半之线，从心向外于赤道上，各作识，从各识作线与赤道为直角。则时刻线也。其过心之线向东晷为卯，正线向西晷为酉正线。　若欲加入节气线，法以表长为度，从表位甲上取乙点为表心。从心取赤道上各时刻点为度以为底。以切线，线之四十五度为腰，置尺，又以二十三度半为小腰，取小底为度于各时刻线上。从赤道向左、向右各作识为冬夏至日景所至之界。　如左图：甲乙为卯酉正线，以
图

表长为度，从甲取乙为表心，以切线上之四十五度为腰，甲乙为底，置尺，又以二十三度半为小腰。取小底于本线上从赤道甲向左向右各作识。即卯酉正时冬夏至之景界。　次从表心向卯酉初刻线，取赤道之交丙点为底，切线之

四十五度为腰，置尺，以二十三度半为小腰，取小底于丙左右，各作识为本时冬夏至之景界。次于各时线如上法，各作二至景界，讫联之为本晷。上冬夏二至之景线。　次作二至前后各节气线，以节气线之两至点为腰。〈即鹑首之次西历为巨蟹宫〉以各时线上赤道至两至界为底。置尺，次以各节气为小腰，取小底为度，从各线之赤道左右作识，如前法。
第十五金线

分法用下文各分率及分体线。
置金一度、
下方所列者，先造诸色体，大小同度，权之得其轻重，之差以为比例。

置水银一度又七十五分度之三十八；
置铅一度又二十三分度之一十五；
置银一度又三十一分度之二十六；
置铜二度又九分度之一；
置铁二度又八分度之三；
置锡二度又三十七分度之一。
先定金之方立体，其重一斤为一度，本线上从心向外任取一点为一度，即是金度。次以分体线第十点为腰，此度为底。置尺，依各色之本率。于分体线上取若干度分之线为底，从心取两等腰，合于次底作点。即某色之度点。
又法

取各率之分子，用通分法乘之。
得金四五九五九二五；
得水银六九二四五二七；
得铅八六二七四○○；
得银八四三一二一二一七；
得铜九○○一四○○；
得铁一○九一四○七五；
得钖一一七九九○○○；
次以各率开立方求各色之根；
得金一六六弱；
得水银一九一弱；
得铅二○二；
得银二○四；
得铜二一三；
得铁二二二；
得锡二二八。
若金立方重一斤，其根一百六十六弱，用各色之根率为边，成立方。即与金为同类、〈皆为立方〉同重〈皆为一斤〉之体也。
今本线用此以二二八为末点。如各率分、各色之根数加号。
石体轻重不等，故不记其比例。
用法一

有某色某体之重。欲以他色作同类之体，而等重。求其大小。法以所设某色某体之一边为度以为底，以本线本色点为腰。置尺，次以他色号点为腰，取底即所求他体之边。
用法二

若等体等大求其重。法以所设体之相似一边为度以为底，置尺于他色号点，取其底，两底并识之。次于分体线上，先以设体之重数为腰。以先设体之底为底。置尺，以次得他体之底为底，进退求相等数为腰，即他体之重。
用法三

有异类之体，求其比例。先依更体线通为同类次，如前法。