钦定古今图书集成历象汇编历法典

　第一百二十卷目录

历法典第一百二十卷

算法部汇考十二

《算法统宗八》少广章第四下

分田截积法下

原有直田一丘。今从东北角截句股形，积三十八步七分二釐，其股数与句数相同。问：该田若干。
答曰：东北角各八步八分。
法曰：置截积三十八步七分二釐，倍得七十七步四分四釐为实。以开平方法除之，得截东北角各八步八分，合问。若还原，以句股自乘，折半即得。
梯田截积歌

梯田截积细端详，倍积阔差乘最良。却用原长为法则，归除乘数实之行。若截大头田积步，大阔自乘减实当。若截小头田积步，小阔自乘并实傍。俱用开方为截阔，两广并来折半强。折半数来为法则，法除截积便知长。
今有梯田长九十步，西广二十步，北广三十八步，今
梯截小头图

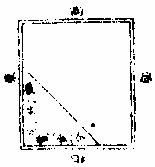
自南边小头截积八百二十二步五分。问：截长阔各若干。答曰：截上长三十五步，截中阔二十七步。

法曰：置截积八百二十二步五分，倍之得一千六百四十五步，以二广相减，馀一十八步为阔差。以乘倍积得二万九千六百一十步。以原长九十步除之，得三百二十九步。另以小头自乘，得四百步。并入三百二十九步，共七百二十九步为实。以开平方法除之，得截阔二十七步。就以截阔二十七步并小头原阔二十步，共四十七步，折半得二十三步五分为法，以除截积八百二十二步五分，得截长三十五步。合问。今有梯田长九十步，小头阔二十步，大头阔三十八
梯截大头图

步。今自大头截积一千七百八十七步五分。问：截长阔各若干。答曰：截下长五十五步，截中阔二十七步。

法曰：置截积倍之，得三千五百七十五步。以大小二阔相减，馀一十八步为阔差。以乘倍积得六万四千三百五十步。以原长九十步除之，得七百一十五步。另以大阔三十八步自乘，得一千四百四十四步。减去七百一十五步，馀七百二十九步为实。以开平方法除之，得二十七步为截中阔。就以此阔二十七步并大头原阔三十八步，共得六十五步。折半得三十二步五分为法。以除截积一千七百八十七步五分，得截长五十五步。合问。若作三段分者，先截大小二头，长并中阔，馀长即是中段数也。或又作四五段分者，亦先截去大小二头长阔。再将原长内减截去二头长数，馀长步数，并截二段中广。复作梯法截之是也。其斜形截法与梯形同理。如截东西两旁积，具载难题少广章中。
环田截积歌

环田要截外周积，倍积二周差步乘。原径为法除见数，另以外周周自乘。以少减多馀作实，开方便得内周成。二周相减馀零数，六而取一径分明。
今有环田外周七十二步，内周二十四步，径八步。今
环截外圆图

自外周截积二百八十五步。问：截中周并径若干。
答曰：中周四十二步，截径五步。法曰：置截积二百八十五步，倍之得

五百七十步。却以外周减内周二十四步，馀四十八步为差步。以乘倍积五百七十步，得二万七千三百六十步。以原径八步除之，得三千四百二十步。又置外周七十二步，自乘得五千一百八十四步。以少减多，馀一千七百六十四步为实。以开平方法除之，得中周四十二步。以减外周七十二步，馀三十步。以六除之，得径五步。合问。
今有环田外周七十二步，内周二十四步，径八步。欲
环截内周图

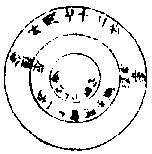
从内周截积九十九步。问：截中周并径若干。
答曰：中周四十二步，径三步。法曰：先将内外二周并之、折半，以径

乘之，得总积三百八十四步。内减今截内积九十九步，馀二百八十五步，即是前截外周积也。
圆田截积

今有圆田中径一十三步，今从边截积三十二步。问：
圆田截积图

所截弦矢各若干。
答曰：弦一十二步，矢四步。
法曰：倍积得六十四步，自乘得四千零九十六步为实。另以四因积三十

二步，得一百二十八步为上廉。又以四因径一十三步，得五十二步为下廉。以五为负隅，用开三乘方法除之，商四步于左上为法。以乘上廉得五百一十二步。就以商四乘隅五，得二十。以减下廉五十二步，馀三十二。另以商四自乘，得一十六。以乘下廉三十二，得五百一十二。并上廉五百一十二，共一千零二十四。为下法除实，得矢四步。另置积倍之，得六十四步。以矢除之，得一十六步。减矢四步，馀得弦一十二步。合问。
今有圆田径二十六步。今从旁截一弧矢，积一百二十八步。问：截弦矢各若干。
答曰：矢八步，弦二十四步。
法曰：倍积自乘，得六万五千五百三十六步为实。另以四因积，得五百一十二步为上廉。又以四因径，得一百零四步为下廉。又以五为负隅法商，得八于左上为法。以乘上廉，得四千零九十六步。又以商八乘隅五，得四十。以减下廉，馀六十四步。另以商八步自乘，得六十四步。以乘馀下廉，得四千零九十六步。并上廉共八千一百九十二步为下法。除实得矢八步也。若问求弦法，曰：置积倍之，得二百五十六步。以矢八除之，得三十二。于内减矢八步，馀得弦二十四步。合问。
弧矢法
圆径与截矢求截弦歌

圆径与矢求弧弦，半径自乘立一边。另以半径减去矢，馀亦自乘减却前。又馀平方开见数，倍之名即是弧弦。
假如有圆径十寸，弧矢阔一寸。问：截弦若干。
答曰：弦六寸。
弧矢内股弦求句图

法曰：置半径五寸为弦，自乘得二十五寸。另以半径五寸，减矢一寸，馀四寸为股。自乘得一十六寸。相减，馀九寸。平方开之，得三寸为句。倍之得六寸为截弧弦，即是二句相并为弦。馀皆仿此。
又法：以圆径自乘，得一百

寸为弦幂。另以圆径减倍矢二寸，馀八寸。自乘得六十四寸为股幂。相减馀三十六寸为句幂。平方开之，得全弦六寸。
圆径与截弦求截矢歌

圆径与弦求截矢，半径为弦自乘是。弧弦折半名为句，亦自乘之相减矣。馀用开方得股数，半径减股馀者矢。
假如有圆径十寸，弧弦长八寸。问截矢若干。
答曰：矢二寸。
弧矢内句弦求股图

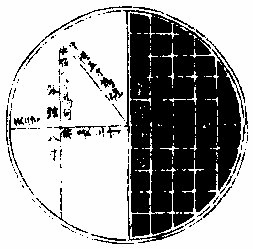
法曰：以半俓五寸为句股之弦。另以弧弦八寸折半，得四为句。各自乘、相减，馀九寸。平方开之，得股三寸。以减半径五寸，馀二寸即矢。圆径与截矢求截弧、背其截弦求弧背，同。术曰：先求出弦径，除矢幂，得半弦背差。
解曰：圆之大小本于弧背之长短，系于圆之大小与矢之多寡。假如平圆十寸，平分一半，则矢长五寸。自乘得二十五寸。以径除之，得二寸五分为半弦背。差倍之，得五寸。加入圆径，得一十五寸为半圆周。故不论圆之大小、矢之多寡，皆准也。
弧矢求积、积求弦矢〈调寄西江月〉

一段田禾之外东边近有荒丘，离边五步系头牛。只为绳长游走，践迹五分八步，如同弧矢弦。畴索长多少。是根由演立天源穷究。
原在难题少广章中，无图。今共图之于此，以便检阅并具法于后。

假如今有弧矢田积一百二十八步，离径五步。问：矢阔、弦长各若干。
答曰：索长一十三步，弧周二十八步有零，矢阔八步，离径五步，弧弦二十四步，圆径二十六
步。
法曰：置积一百二十八步为实。另以此数倍之，得二百五十六步。以开平方法除之，得一十六步为法。除
弧矢求积积求弦矢图

实得矢八步。加法十六共二十四步是弦长。折半得一十二步。自乘，得一百四十四步为实。以矢八步为法，除之，得一十八步。加矢八步，共得圆径二十六步。若问索长，以矢八步，加离边五步，乃是索长一十三步。合问。
弧矢求积歌

弧矢求积弧矢形，丈量之法注分明。弧矢弦长并矢步，半之又用矢相乘。
法曰：置弦二十四步，并矢八步，共三十二步。折半得一十六步。以矢八步乘之，得积一百二十八步。
积求弧弦歌

弧矢之积求弧弦，倍积以矢除为先。除来之数减去矢，馀存此即是弧弦。
法曰：置积一百二十八步，倍之，得二百五十六步为实。以矢八步为法，除之，得三十二步。减矢八步，馀得弧弦二十四步。
积求矢阔歌

积求矢阔倍为实，弦为纵方莫教迟。商于左位右并纵，前后呼除矢得宜。
法曰：置积一百二十八步，倍得二百五十六步为实。以弦二十四步于右为纵方。约初商八步于左。亦置商八步于右。纵方二十之下共三十二步，皆与上商八相呼。三八除实二百四十二，八除实一十六步，恰尽得矢八步。
弦矢求圆径并离径歌

弦矢求圆径可推，半弦自乘矢除之。再加矢阔为圆径，半之减矢离无疑。
法曰：置弦二十四步，折半，得一十二步。自乘，得一百四十四步为实。以矢八步为法除之，得一十八步。再加矢阔八步，得圆径二十六步。复折半，得一十三步。减矢八步，馀为离径五步。
圆径及弧径求离径并矢阔歌

径弦求离径矢阔，圆径弧弦各折半。各自乘减馀开方，离径圆径弧矢辨。
法曰：置圆径二十六步，折半，得一十三步。自乘，得一百六十九步。另以弧弦二十四步，折半，得一十二步。自乘，得一百四十四步。二数相减，馀二十五步。以开平方法除之，得离径五步。另以圆径二十六步折半，得一十三步。减离径五步，馀为矢八步。
圆径及矢阔求弧弦歌

圆径矢阔求弧弦，圆径矢阔减馀存。复以矢阔乘为实，开方倍之得弧弦。
法曰：置圆二十六步，减矢八步，馀一十八步。以矢八步乘之，得一百四十四步。以开平方法除之，得一十二步。倍之得弧弦二十四步。
弧弦及离径求圆径歌

弧弦离径求圆径，弧弦折半自相乘。离径自乘并为实，开方倍数为圆径。
法曰：置弦二十四步，折半，得一十二步。自乘，得一百四十四步。以离径五步，自乘，得二十五步。相并，得一百六十九步为实。以开平方法除之，得一十三步。倍之，得二十六步为圆径。
圆径及离径求弧弦歌

圆径离径求弧弦，圆径折半自相乘。离径自乘减馀实，开方倍得弧弦成。
法曰：置圆径二十六步，折半，得一十三步。自乘，得一百六十九步。以离径五步自乘，得二十五步。相减，馀一百四十四步为实。以开平方法除之，得一十二步。倍之，得弧弦二十四步。
解曰：弧矢状类句股。句股得直方之半。故倍其积以股除之，即得句弧背。曲倍积则长一弦而又一矢。以矢乘积、倍之，恰得一弦。一矢之数因未知矢，故以积自乘为实。约矢一度乘积，以为上廉；两度乘径以为下廉。并之为法，而后可以得矢。用三乘者，何也。积本平方。以积乘积是两度平方矣。故用三乘方法开之。上廉下廉俱用四因者，何也。倍积则乘出之数为积者四，故上下廉俱四以就之。减径者，何也。径乃圆之全径，矢乃截处之句。矢本减径而得，故亦减径以求矢。五为负隅者，何也。凡平圆之积得平方，四分之三在内者，七五在外者。二五不拘圆之大小，每方一尺。该虚隅二寸五分，其矢得四，其虚隅得一，合而为五，亦升实就法之意也。如不倍积，廉不用四，因以一二五为隅法，亦通。或不减径作添，积三乘方法，亦通。

商功章第五

商度也，商量用力之法也。此章以坚壤之率，求穿地之实。以广、阔、高、深，求城堑沟渠之积。以车担往来，求程途负载之功。
商功歌〈即修筑〉

商功须要问工程，长阔相乘深又乘。乘此数来以为实，每日工程为法行。惟以筑城别一样，上下将来折半平。高以乘之长又续〈又以长乘之也〉，以为城积甚分明。五因其积三而一，此是坚求壤法行。穿地四因为壤积，法中仍用五归成。
穿地四尺，为壤五尺。为坚三尺〈壤是虚土也。坚是实土也〉。穿地　求壤〈五因〉　求坚〈三因〉　皆四归之。
壤地　求穿〈四因〉　求坚〈三因〉　皆五归之。
坚地　求穿〈四因〉　求壤〈五因〉　皆三归之。
城垣堤沟求积。并上下广折半。以高深乘之。又以长乘之，得积。
方台求积。上方自乘，下方自乘。另以上下方相乘并之。又以高乘。再以三归之。如方窖刍童者，倍上长，加下长，以上广乘之。又倍下长，加上长，以下广乘之。并二数以高乘又，以六归之。
圆台求积。上周自乘，下周自乘。上下周相乘，并之。又以高乘。再用三十六除之。如圆窖圆锥者，下周自乘。又以高乘。再用三十六除之，如尖堆。
方锥求积。下方自乘，以高乘之，又三归之，如圭形〈下方上尖〉。
方堡壔求积。以方自乘，又以高乘之，如方仓方柱也。圆堡壔求积。以周自乘，又以高乘之，再用十二除之，如圆仓圆柱也。
刍荛倍下长，加上长。以广乘之。又以高乘。用六归之，一如屋脊上斜下平。
羡除并三广，以深乘之，用六归之〈上平下尖，或倍上长加下长〉。假如今有坚地，积七千五百尺。问：穿地壤土各该若干。
答曰：穿地一万尺，壤土一万二千五百尺。
法曰：置坚地积，以五因三归之。为壤土积，另置壤积以四因五归之，得穿地积。合问。
今有开河长七千五百五十尺，上广五十四尺，下广四十尺，深一十二尺。每日一工开三百尺。问：用工若干。
答曰：一万四千一百九十四工。
法曰：并上下二广、折半，得四十七尺。以深一十二尺乘之，得五百六十四尺。又以长乘之，得积四百二十五万八千二百尺为实。以每工三百尺为法除之，即得。
今有穿渠上广二丈四尺，下广二丈一尺，深九尺，长三百八十四尺。每用人夫一十二名，日开积六百尺。问：该人夫几何。
答曰：一万五千五百五十二名。
法曰：并两广共得四十五尺。折半得二十二尺五寸。以深九尺乘之，得二百零二尺五寸。又以长乘之，得七万七千七百六十尺为积。又以人夫一十二名乘之，得九十三万三千一百二十尺为实。却以六百尺为法除之。
今有开濠上广七尺，下广九尺，深四尺，长一千八百尺。每人日穿一百四十四尺，今用人夫二百名。问：几日开毕。
答曰：二日开毕。
法曰：并上下广，折半，得八尺。以深四尺乘之，得三十二尺。又以长乘之，得五万七千六百尺为实。另置二百人，以每人一百四十四尺乘之，得二万八千八百尺，为法除之。合问。
筑台歌

筑台丈尺要推详，上长倍之加下长。上广乘之别列位，另倍下长加上长。仍以下广乘见数，二数共并积相当。原高乘并积为实，六归实数积如常。
今有筑直台一所。上广八尺，长二丈，下广一丈八尺，长三丈，高一丈八尺。问：积若干。
答曰：六千尺。
法曰：倍上长，得四十尺。加下长共七十尺。以上广八尺乘之，得五百六十尺。另倍下长，得六十尺。加上长二十尺，共八十尺。以下广一十八尺乘之，得一千四百四十尺。并二数，共二千尺。以高一十八尺乘之，得三万六千尺。以六归之。合问。
今有筑方台，上方六尺，下方八尺，高一十二尺。问：积若干。
答曰：五千九百二十尺。
法曰：依方窖法，以上方六尺自乘，得三十六尺。下方八尺自乘，得六十四尺。又以上方乘下方，得四十八尺。并三数共一百四十八尺。以高一十二尺乘之，得一千七百七十六尺。以三归之。合问。
一法依筑台歌，倍上方，加下方，共二十尺。以上方乘之，得一百二十尺。另倍下方，加上方，共二十二尺。以下方乘之，得一百七十六尺。并二数共二百九十六尺。以高一十二尺乘之，得三千五百五十二尺。以六归之，亦得。
今有圆台，上周一十八尺，下周二十四尺，高一十二尺。问：积若干。
答曰：四百四十四尺。
法曰：置上周自乘，得三百二十四尺。以下周自乘，得五百七十六尺。又以上下二周相乘，得四百三十二尺。并三数共一千三百三十二尺。以高一十二尺乘之，得一万五千九百八十四尺为实。以圆率三十六除之。合问。此如圆窖。
今有立锥，高三十二尺，下方二十四尺。问：积若干。答曰：六千一百四十四尺。
法曰：置下方自乘，得五百七十六尺。以高乘之，得一万八千四百三十二尺为实。以三归之。合问。
今有圆锥，高三十二尺，下周七十二尺。问：积若干。答曰：四千六百零八尺。
法曰：置下周自乘，得五千一百八十四尺。再以高三十二尺乘之，得一十六万五千八百八十八尺为实。以圆率三十六尺除之，得积。合问。
筑墙截高问今上广歌

上下原广数相减，馀用今高数相乘。原高为法除为积，积减下广上广存。
假如原筑墙上广一尺，下广三尺，高一十二尺，今已筑高九尺。问：上广若干。
答曰：一尺五寸。
法曰：将原下广三尺减原上广一尺，馀二尺。以今筑高九尺乘之，得一十八尺为实。以原高一十二尺为法除之，得一尺五十。却于原下广三尺减去一尺五寸，馀得今筑上广。合问。
一法将原下广三尺减原上广一尺，馀二尺。另以原高一十二尺内减今高九尺，馀三尺。以乘二尺，得六尺为实。以原高一十二尺为法除之，得五寸。加原上广一尺，共一尺五寸。亦得。
原筑墙上广一尺，下广三尺，高一丈二尺。今欲筑高一丈五尺。问：上广若干。
答曰：上广五寸。
法曰：置原下广三尺减原上广一尺，馀二尺。另以原高一丈二尺减今高一丈五尺，馀三尺。以乘二六尺为实。以原高一丈二尺为法除之，得五寸。以减原上广一尺，馀五寸为今上广。合问。
筑墙截下广问今高歌〈即是截今下节〉

原今下广数相减，馀以原高乘为实。原下广减原上广，馀为法除高数是。
原筑墙上广一尺，下广四尺，高一十二尺。今只筑下广二尺一寸。问：今高若干。
答曰：七尺六寸。
法曰：置原下广四尺减今筑下广二尺一寸，馀一尺九寸。以原高一十二尺乘之，得二十二尺八寸为实。另以原下广四尺减原上广一尺，馀三尺。为法除之。合问。
原筑墙上广二尺，下广六尺，高二丈。今已筑上广三尺六寸。问：今筑高若干。
答曰：一丈二尺。
法曰：置原下广六尺内减去今筑上广三尺六寸，馀二尺四寸。以原高二十尺乘之，得四十八尺为实。另以原下广六尺减原上广二尺，馀四尺。为法除之，得今高。合问。
原筑墙上广十尺，下广三十尺，高四十尺。今欲筑上广九尺。问：接高若干。
答曰：二尺。
法曰：置原高四十尺为实。另以原上广十尺减原下广三十尺。馀二十尺。除之，得二尺，又为实。以今欲筑上广九尺，减原上广十尺，馀一尺。为法除之，得接高二尺。合问。
筑方锥丈尺今改作方台歌

今上方与原高乘，便为实积数分明。原下方数宜为法，法除实积截高成。
原筑方锥下方二十四尺，高三十二尺，今改作方台只用上方六尺。问：截去高若干。
答曰：截去高八尺。
法曰：置原高三十二尺，以今只用上方六尺乘之，得一百九十二尺为实。以下方二十四尺为法除之，得截去高八尺。合问。
原有方锥下方二十四尺，高三十二尺。今改作方台。已筑高二十四尺。问：今上方若干。
答曰：六尺。
法曰：置原高内减今高二十四尺，馀截去八尺。以乘下方二十四尺，得一百九十二尺为实。以原高为法除之，得上方。合问。
原有方锥下方二十四尺，高三十二尺，今改作方台。只用上方六尺。问：今高若干。
答曰：二丈四尺。法曰：置原下方二十四尺内减今上方六尺，馀一十八尺。以原高三十二尺乘之，得五百七十六尺为实。以原下方二十四尺为法除之，得今高二十四尺。合问。
筑方台丈尺今改作方锥问接高歌

上方与高乘为实，下方内减上方积。馀积为法除实数，便见接高今丈尺。
原方台上方六尺，下方二十四尺，高二十四尺。今改作方锥。问：接高若干。
答曰：接高八尺。
法曰：置原高二十四尺乘原上方六尺，得一百四十四尺为实。另以原下方二十四尺内减原上方六尺，馀一十八尺。为法除之，得接高八尺。合问。
原有圆锥下周七十二尺，高三十二尺。今改作圆台，只用上周一十八尺。问：今筑高若干。
答曰：二十四尺。
法曰：置原下周七十二尺，内减今用上周一十八尺，馀五十四尺。以原高三十二尺乘之，得一千七百二十八尺为实。以原下周七十二尺为法除之，得今高二十四尺。合问。
原有圆锥下周七十二尺，高三十二尺。今改作圆台。已筑高二十四尺。问：今上周若干。
答曰：一十八尺。
法曰：置原高三十二尺减今高二十四尺，馀八尺。以乘原下周七十二尺，得五百七十六尺。以原高为法除之。合问。
筑堤歌

筑堤之法最蹊跷，东高倍之加西高。上下广并乘折半，西高另倍加东高。上下广并仍乘折，一折数并共相交。却用原长乘为实，五归其实积无饶。
今筑堤一所。东头上广八尺，下广一十四尺，高九尺。西头上广二十尺，下广二十二尺，高二十一尺。东至西长九十六尺。问：积若干。
答曰：二万八千八百尺。
法曰：倍东高九尺为一十八尺。加西高二十一尺共三十九尺。却以东头上下广相并，为二十二尺。乘之得八百五十八尺。折半得四百二十九尺。另倍西高加东高共五十一尺。却以西头上下广相并，为四十二尺。乘之得二千一百四十二。折半得一千零七十一。二数相并共一千五百尺。再以长九十六尺乘之，得一十四万四千尺为实。以五归之，得积。合问。今有甲乙二人开渠。甲日开积四百尺，乙日开积三百五十尺。先甲开七十日后令乙开。问：几日与甲同。答曰：八十日。
法曰：置甲开七十日。以每日四百尺乘，得二万八千尺为实。却以乙日开三百五十尺为法除之，得八十日，才与甲同数。
今有人快行者，日行九十五里。慢行者，日行七十五里。今令慢行者先行八日。问：快行者几日赶至追及之。行路程各若干。
答曰：快行者三十日，慢行者多八日，路程二千八百五十里。
法曰：置慢行者日行七十五里，以八日乘之，得六百里为实。以慢行减快行，馀二十里。为法除之即得。今有慢行者已去七日，后令快行者赶去。六日追至中途。及之其路程已行一千一百七十里。问：快慢每日各行若干。
答曰：快者日行一百九十五里，慢者日行九十里。法曰：置已行路程一千一百七十里为实，以六日为法除之，得快者日行一百九十五里。另将先行七日并后赶六日共一十三日，为法除总一千一百七十里，得慢行里数。合问。
今有甲乙二人行步不等。甲日行八十里，乙日行四十八里。令乙先行二百四十里，甲才发步追之。问：几里可及。
答曰：六百里。甲七日半，乙十二日半。
法曰：置先行二百四十里以甲日行八十里乘之，得一万九千二百里为实。却以甲乙日行里数相减，馀三十二里，为法除之。合问。
今有人盗马乘去，已去三十七里，马主方觉。追去一百四十五里不及二十三里，仍复追之。问：几里可及。答曰：二百三十八里又一十四分里之三。
法曰：置不及二十三里以马主追去一百四十五里乘之，得三千三百三十五里为实。另置已行三十七里减去不及二十三里，馀一十四里，为法除实二百三十八里不尽三，以法约之。
今有大都路至杭州四千二百七十五里。马从大都往南日行一百二十里。船从杭州往北日行七十里。问：船马几日相会，各行若干。
答曰：二十二日半。马行二千七百里，船行一千五百七十五里。法曰：置四千二百七十五里为实。却并船马日行共一百九十里，为法除之，得二十二日半又为实。各以原行里数乘之，得各行里数。
原有一夫日耘田七亩，一夫日耕三亩，一夫日种五亩。今令一夫自耘自耕自种。问：治田若干。
答曰：一亩四分七釐又七十一分之六十三。
法曰：以田为分母，夫为分子。以母互乘之，列分母分子之位〈七亩一夫　三亩一夫　五亩一夫〉。先以七亩乘三亩得二十一亩又以五亩，乘之得一百零五亩为实又以七亩，乘三亩得二十一亩。又以三亩乘五亩得一十五亩。又以五亩乘七亩得三十五亩。并之得七十一亩。为法除实得一亩四分七釐不尽六十三，以法命之。原有三女各纳锦一方。长女五日完，中女七日完，小女九日完。今令三女共纳锦一方。何日可毕。
答曰：二日又一百四十三分日之二十九。
法曰：以日为分母，方为分子。以三母相乘。先以五日乘七日得三十五日，又以九日乘之得三百一十五日为实。以母互乘子法〈五日长女　七日中女　九日小女〉。先以五日乘七日得三十五日，又以七日乘九日得六十三次，以九日乘五日得四十五。并之得一百四十三日。为法除实得二日不尽二十九，以法命之。
堆垛歌

缶瓶堆垛要推详，底脚先将阔减长。馀数折来添半个，并入长内阔乘良。再将阔搭一乘实，以三除之数相当。一面尖堆只添一，乘来折半积如常。三角果垛亦堪知，脚底先求个数齐。一二添来乘两遍，六而取一不差池。要知四角盘中果，添半仍添一个随。乘此数来以为实，如三而一法求之。
今有酒瓶一垛。底脚阔八个，长一十三个。问：该积若干。
答曰：三百八十四个。
法曰：置长内减阔，馀五个。折半得二个半。添半个作三个，并入长，共一十六个。以底脚八个因之，得一百二十八个。另以阔八个添一个作九个，乘之，得一千一百五十二个，以三除之。合问。
今有物靠壁，一面尖堆，底脚阔一十八个。问：积若干。答曰：一百七十一个。
法曰：置阔一十八个为实。另以一十八个加顶一个，共一十九个。为法乘之得三百四十二个。折半即得。今有物一面平堆，底脚阔七个，上阔三个。问：积若干。答曰：二十五个。
法曰：置底脚七个减去上阔三个，馀四个。加一个，共五个。为法乃是五层也。另并上下阔，共得十个为实。以法五乘之，得五十个。折半得二十五个。合问。堆垛图式具左。
一面尖堆图


右二图用法权变，便人易晓。故立此以仿其馀。右二图用法权变，便人易晓。故立此以仿其馀。

今有三角果一垛。底阔，每面七个。问：该若干。
答曰：八十四个。
法曰：置底阔七个，另以七个添一个，共八个，相乘得五十六个。又以七个添二个共九个，乘五十六个，得五百零四个为实。以六归之。合问。
今有三角半堆果一垛。每面上阔五，个底阔一十二个。问：该若干。
答曰：三百四十四个。
法曰：亦用三角法。先以底阔一十二个求出全积三百六十四。另以上尖虚底阔四个，求出虚积二十。以减全积，馀半堆，积三百四十四个。
一法上阔五个自乘得二十五。下法十二自乘得一百四十四。上阔五乘下阔十二，得六十。又倍下阔，得二十四。加上阔五得二十九。并四数共二百五十八为实。另以下阔十二减上阔五，馀七加一得高八。为法乘实得二千零六十四。以六除之。合问。
今有物，四面尖堆。底阔一十二个。问：该若干。
答曰：六百五十个。
法曰：置底阔一十二个，另以十二加一个共一十三个，乘之得一百五十六个。又以十二加半个共一十二个半，乘一百五十六个，得一千九百五十个。以三归之。即得。
今有物一堆。横面下阔十个，上阔一个，正面下阔一十二个，上阔三个。问：该若干。
答曰：四百九十五个。
法曰：置正面下阔一十二个，倍之得二十四，加上广三，共二十七。以横面下广一十乘之，得二百七十。另置二百七十以横下广一十乘之，得二千七百。并入二百七十，共得二千九百七十。以六除之，即得。
半堆歌

半堆瓶法另推详，上长倍之加下长。却用上阔乘见数，下长仍倍加上长。别以下阔乘见积，下长另减上头长。馀存三位同相并，再以高乘为实良。要知其积从何见，六而取一积该当。
今有半堆酒瓶一栈。上长二十五个，阔一十二个，下长三十个，阔一十七个，高六个。问：积若干。
答曰：积二千四百一十个。
法曰：倍上长加下长，以上阔乘之，得九百六十。又倍下长加上长，以下阔乘之，得一千四百四十五。并之得二千四百零五。又以下长减去上长，馀五。并入共得二千四百一十。以高乘之，得一万四千四百六十为实。以六为法除之，即得。
今有砖一堆。长三丈，高九尺，入深四尺。每块长一尺，阔五寸，厚二寸。问：共该若干。
答曰：一万零八百块。
法曰：置长三丈为实。以每块二寸为法归之，得一百五十块。另以高九尺，以每块阔五寸归之，得一十八块。乘之，得二千七百块。又以入深四尺乘之。合问。
挑土计方歌〈每一方长阔各一丈，高一尺，开塘法同〉。

东西并折半，南北亦如斯。互乘为实位，深数再乘之。今有田内开土、挑泥、填基。东六丈五尺，西七丈五尺，南八丈，北九丈，深二尺。问：取泥该方数若干。
答曰：一百一十九方。
法曰：置东六丈五尺并西七丈五尺，共一十四丈。折半得七丈。又以南八丈并北九丈，共一十七丈。折半得八丈五尺。相乘得五十九丈五尺。又以深二尺乘之，得一百一十九方。合问。
量木梱〈调寄西江月〉

梱有封书模样，
梱法不一。一名一封书，一名方梱。

深阔各倍相乘。
如阔若干，深若干，俱各加倍，以五寸为一根，即是为倍法也。

丈五除长再乘行，
如长若干，以每根长一丈五尺除之，馀数再乘。

书梱加深为定。
如一封书梱，深阔长俱乘讫。又照原深若干加之是也。

方梱须知加阔，
如方梱深阔长俱乘讫，又照原阔若干加之是也。

荒深三折倍成。
又名荒排者，异前二形，即以深三归而一方可倍之，即一尺二根也。

阔长皆是照前因，
虽荒排阔，亦倍之。与三归深者相乘，长亦照前丈五除者相乘。

三折一加有准。
但荒排阔深长俱乘讫。亦照深三归而一加之。

今有一封书梱。深七尺五寸，阔四丈七尺，长九丈。问：木若干。
答曰：一万四千八百零五根。
法曰：置深七尺五寸，以每尺二根计之，得一十五根，即倍法也。又以阔四丈七尺倍作九十四根，相乘得一千四百一十根为实。另置长九丈以每根长一丈五尺除之，得六根。为法乘实得八百四十六根。又以深七尺五寸加之，或用一七五乘亦可。合问。
今有方梱深七尺，阔五丈，长六丈。问：木若干。
答曰：八千四百根。
法曰：置深七尺倍作一十四根。又以阔五丈亦倍作一百根。相乘得一千四百根为实。另置长六丈以一丈五尺除之，得四根。为法乘实得五千六百根。又以阔五丈加之。合问。
今有荒排深二丈一尺，阔四丈四尺，长六丈。问：木若干。
答曰：八千三百七十七根六分。
法曰：置深二丈一尺，以三归，得七尺。倍作一十四根。又以阔四丈四尺倍作八十八根。相乘得一千二百三十二根为实。另以长六丈以一丈五尺除之，得四根。为法乘之，得四千九百二十八根。又以深二丈一尺用三归，得七尺，加之。合问。若量方圆束木法，已见前少广章中。
右梱法虽设则，厂弊客弊或差免。但一封书并荒排法无异。其方梱所加，或阔深长不一，法难必矣。
均输章第六
均，平也。输，送也。此章以户数多寡、道里远近，而求车数粟数。以粟数高下而求僦直。以钱数多少而求佣钱。
歌曰

均输只要一般般，不许亏民及损官。劳费程途知远近，分毫依法要详端。行道驾船皆一体，负挑车载重轻看。
今有银二十二两八钱，买黄白蜡。各要均平，其黄蜡每三斤价银四钱，白蜡每斤价银五钱。问：黄白蜡各若干。
答曰：各三十六斤。黄该银四两八钱，白该银一十八两。
法曰：置总银以黄蜡三斤乘之，得六百八十四斤为实。另置黄蜡三斤以白蜡价五钱乘之，并黄蜡价四钱，共得一两九钱。为法除之，得黄白各三十六斤。就以白蜡三十六斤以每斤五钱乘之，得价一十八两。再置黄蜡三十六斤以价四钱乘之，得一十四两四钱。又以蜡三斤为法除之，得价四两八钱。合问。今有银三十七两八钱，籴米、麦、豆，三色各要均平。每石米价八钱，麦价六钱，豆价四钱。问：各若干。
答曰：米、麦、豆，各二十一石。
法曰：置总银为实并米、麦、豆价共一两八钱，为法除之，得每色二十一石之数。各以价乘之。合问。
右法不拘四色五色者，仿此推之。

今有甲、乙、丙三人以田多寡应当一年差役。甲田三十五亩，乙田二十五亩，丙田二十亩。问：各该值月若干。
答曰：甲该五个月零七日半，乙该三个月二十二日半，丙该三个月。
法曰：置甲、乙、丙三人田共并得八十亩为法。另置甲田以十二月乘之，得四百二十为实。以法八除之，得五个月零二五。却以三十日乘二五，得七日半。又置乙田以十二月乘之，得三百为实。以法八除之，得三个月零七五。却以三十日乘七五，得二十二日半。又置丙田以十二月乘之，得二百四十为实。以法八除之，得三个月。合问。
又法：置一年计三百六十日为实，并甲、乙、丙三人田共八十亩，为法除之每亩得值月四十五日。以乘各人田数，亦得。
今有甲、乙二人往县应役。甲该十二日一往，乙该十五日一往。问：一人何日同会。
答曰：六十日会。
法曰：置甲十二日以乙十五日乘之，得一百八十日为实。却以乙十五日减甲十二日，馀三日，为法除之。合问。
今有官派粮八百四十石。令四县照依田地多寡纳之。甲县田五十六亩，乙县四十四亩，丙县三十二亩，丁县二十八亩。问：各该纳若干。
答曰：甲三百九十四石，乙二百三十一石，丙一百六十八石，丁一百四十七石。
法曰：置列甲、乙、丙、丁四县田数，各以官派粮八百四十乘之，各列为实。另以四县田并之，得一百六十亩。为法以除各县乘数即得各县该纳之数。合问。又法：置总粮为实，并四县田为法除之，以乘各田数。亦得。
今有五县输粟二万石。照人户多少、道里远近、价值上下而均输之。每车载二十五石，行道一里与僦里钞一钱。甲县二万零五百二十户，粟石价二两。乙县一万二千三百一十二户，粟石价一两，远输所二百里。丙县七千一百八十二户，粟石价一两二钱，远输所一百五十里。丁县一万三千三百三十八户，粟石价一两七钱，远输所一百五十里。戊县五千一百三十户，粟价一两三钱，远输所一百五十里。问：各输粟若干。
答曰：甲七千一百四十二石三斗五升九合九勺。乙四千七百六十一石五斗七升三合二勺，该僦里钞二十两。丙二千七百七十七石五斗八升四合，该僦里钞一十五两。丁三千四百三十八石九斗一升四合，该僦里钞二十五两。戊一千八百七十九石五斗六升八合三勺，该僦里钞一十五两。
解曰：甲县乃自输本县而无僦里，惟乙、丙、丁、戊四邑有之。各昭里数远近以僦钞一钱，因之各得僦里钞也。

法曰：置甲县户数为实，以粟价二两为法除之，得一千零二十六衰。乙县行道二百里以每车载二十五石除之，得八钱，并粟价一两共一两八钱，除户数得六百八十四衰。丙县行道一百五十里以每载二十五石除之，得六钱并粟价共一两八钱，除户得三百九十九衰。丁县行道二百五十里亦以二十五石除之，得一两并粟价共二两七钱，除户得四百九十四衰。戊县行道一百五十里亦以二十五石除之，得六钱并粟价共一两九钱，除户得二百七十衰。就以五衰列置五县，再并五衰共二千八百七十三衰为法。另以赋粟二万石以乘五县各衰为实，以法除之。合问。
原有绫每疋价四两一钱，绢每疋价二两一钱。今欲将绫换绢。问：多少可均。
答曰：绫二疋一，绢四疋一。
法曰：以绫绢价相乘，得八两六钱一分为实。以绢疋价除之，得绢数。以绫价除之，得绫数。合问。
其疋下有零者，照疋长若干加之，是也。

今有麻每石价九钱，米每石价八钱，豆每石价七钱。今三主只以价均扣算麻、米、豆数及价。问：各若干。答曰：各该价五钱零四釐，麻五斗六升，米六斗三升，豆七斗二升。
法曰：先置麻、豆价相乘，得六斗三升，退位为米数。又以米、豆价相乘，得五斗六升，退位为麻数。再以麻、米价乘之，得七斗二升，退位为豆数。各以价乘之。合问。
但相乘数多者，为贱；少者，为贵。可以辨之。

原有人挑茶九十斤行道，五百里脚银九钱。今挑一百二十斤，行道三百里。问：该银若干。
答曰：七钱二分。
法曰：以今挑茶一百二十斤乘今行三百里，得三百六十。又以脚银九钱乘之，得三两二钱四分为实。另以九十斤乘原行五百里，得四百五十里，为法除之。合问。
原雇车一辆议行道一千里，载重一千二百斤与银七两五钱。今重一千五百斤，行一千三百里。问：该银若干。
各曰：一十二两一钱八分七釐五毫。
法曰：置今重一千五百斤以，今行一千三百里乘之，得一千九百五十里。又以银七两五钱乘之，得一十四两六钱二分五釐为实。以原重一千二百斤乘原行一千里为法除之。合问。
今有货重一千六百斤，先付车主银六两，照前议行道一千里载重一千二百斤，价七两五钱。问：该行道若干。
答曰：六百里。
法曰：置今付车主银六两以原行道一千里乘之，得六千里。又以原重一千二百斤乘之，得七千二百里为实。另以今重一千六百斤以原价七两五钱乘之，得一十二两，为法除之。合问。
今有道一千七百里，车主已支去银七两六钱五分，照前议每一千里载重一千二百斤，价七两五钱。问：该载重若干。
答曰：七百二十斤。
法曰：置原重以原行道乘之，仍得一千二百里。又以今去银七两六钱五分乘之，得九两一钱八分为实。另置今行道以原与银七两五钱乘之，得一十二两七钱五分。为法除之，即得。
原有人担物一百五十斤行道，一百三十里与脚银二钱。今担一百八十斤行道九十里。问：该银若干。答曰：一钱六分六釐一毫五丝。
法曰：置今重一百八十斤乘今行道九十里，得一百六十二里。又以原脚银二钱乘之，得三钱二分四釐为实。另以原担重一百五十斤乘原行道一百三十里，得一百九十五斤。为法除之，即得。
今有空车日行七十里，重车日行五十里。今载谷至仓五日三返。问：路远若干。
答曰：四十八里又三十六分之二十二。
法曰：置空车、重车日行里数相乘，得三百五十里。又以五日乘之，得一千七百五十里为实。另并空车、重车日行里数。以三返乘之，得三百六十，为法除之不尽二十二，以法命之。
原有人负米一石一斗二升，行三十步，日五十返。今负米一石二斗，行四十步。问：日几返。
答曰：三十五返。
法曰：置负米一石一斗二升以行三十步乘之，得三百三十六。又以五十返乘之，得一千六百八十为实。另以今负米一石二斗以行四十步乘，得四百八十，为法除之。合问。
今有众兄弟辈出钱买物。长兄出钱八文，次兄以下各加一文，顺至小弟出钱六十文。问：兄弟辈及共钱各若干。
答曰：五十三人，共钱一千八百零二文。
法曰：以八文并入六十文共得六十八文。另置六十文于内，减去八文，馀五十二文，再加长兄一人共得五十三人。另以六十八文乘五十三人，得三千六百零四文。折半，即得。
今有中式举人一百名。第一名官给银一百两。自第二名以下挨次各减五钱。问：该银若干。
答曰：七千五百二十五两。
法曰：置一百名减去第一名，馀九十九名。以五钱乘之，得四十九两五钱。以减一百两馀，五十两零五钱，为第一百未名之数。并入第一名给一百两，共一百五十两零五钱。以乘一百名，得一万五千零五十两，折半。合问。
今有钱一文，日增一倍，倍至三十日。问：该若干。答曰：十亿零七千三百七十四万一千八百二十四文。
法曰：置钱一文以十度八因即得〈一度八因乃三日倍数，十度八因乃三十日数〉。
一法：以五度六十四乘亦得〈一度六十四乘，乃六日倍数。五度六十四乘，是三十日数〉。
一法：以三度三十二乘得数，自乘亦得〈三度三十二乘乃，十五日数，自乘即三十日也〉。
解曰：十度者，以八因十次也。五度者，以六十四乘五次也。馀仿此。

今有天干十位，地支十二位。问：干支相配若干。答曰：六十甲子。
法曰：置天干十位，以地支十二乘之，得一百二十为实。却以天干十位减地支十二，馀二。为法除之即得。今有车一轮。轮高六尺，推行二十里。问：输转若干。答曰：输转二千次。
法曰：置二十里以里率一千八百尺乘之，得三万六千尺为实。另以轮高六尺三，因得周一十八尺为法除之。合问。
今有人车，不知其数。凡三人共车，二车空；二人共车，九人步行。问：人车各若干。
答曰：一十五车，三十九人。
法曰：置二人以三人乘之，得六。加九人得车一十五。又以：二人乘车十五，得三十。加九人得人数。
今斋僧不知人数。初日每五人米八斗，次日每九人米七斗。凡二日共米三十二石一斗。问：僧并米各该若干。
答曰：一百三十五人，初日米二十一石六斗，次日米一十石零五斗。
法曰：置列〈五人　九人〉互〈八斗　七斗〉，另以九人乘八斗，得七十二。又以五人乘七斗，得三十五。并之得一百零七为法。另以九人五人相乘，得四十五。复乘共米三十二石一斗，得一千四百四十四石五斗为实。以法除之。合问。
今有围兵二万三千四百人，以布围之，各相去五步。今围内缩除一十六里九十步而止。问：围兵各相去若干。
答曰：四步七分五釐。
法曰：置兵数以五步乘之，得一十一万七千步。另以一十六里以三百六十步通之，得五千七百六十步。加零九十步，共五千八百五十步。以减上数馀一十一万一千一百五十步，以围兵二万三千四百，为法除之，即得。
今有粮三千六百石。只云每石则例令三处仓上纳。东仓二斗三升四合，西仓三斗四升五合，南仓四斗二升一合，依则均开。问：各仓该米若干。
答曰：东仓八百四十二石四斗，西仓一千二百四十二石，南仓一千五百一十五石六斗。
法曰：置总粮为实，以各仓则例数乘之，合问。
今有夏税麦二百七十四石。三限催徵。初限五分六月完，中限三分半七月完，末限一分半八月完。问：各限该徵若干。
答曰：初限一百三十七石，中限九十五百九斗，末限四十一石一斗。
法曰：列置麦数三位。一位以五分乘为初限数。二位以三分半乘为中限数。三位以一分半乘为末限数。合问。
今有鸡兔同笼。上有三十五头，下有九十四足。问：鸡兔各若干。
答曰：鸡二十三只，兔一十二只。
法曰：置总头倍之，得七十。于总足内减七十馀二十。四折半得一十二，是兔。以四足乘之，得四十八足，于总足减之，馀四十六足，为鸡足。折半得二十三只。合问。
一法：以四因总头，减去总足，馀折半得鸡。另以二因四归总足，减总头，馀得兔。
倍头减足折半是兔。
不分鸡兔，以鸡二足乘头数，于共足内减之，所馀者是一兔。剩二足，故折半为兔也。

四头减足折半是鸡。
不分鸡兔，以兔四足乘头数，以共足减之，所馀者，鸡足也。故折半为鸡。
此法名二率分身，即贵贱差分也。

今有狐狸一头，九尾、鹏鸟一尾，九头。只云前有七十二头，后有八十八尾。问：二禽兽各若干。
答曰：狐狸九个，鹏鸟七只。
法曰：置总头七十二以减总尾八十八，馀一十六，是二禽兽共数。以尾九因之，得一百四十四，内减总尾八十八，馀五十六，为实。另以尾九内减一头，馀八，为法除实，得鹏鸟七只。以减共数，馀得狐九个。合问。