钦定古今图书集成历象汇编历法典

　第一百十五卷目录

历法典第一百十五卷

算法部汇考七

《算法统宗三》方田章第一

此章以田畴界域之形状，求亩步之积实。以广纵而求方、直、圭、梭、梯、斜等形。以周径而求圆田、碗田、环田等形。按田之形状甚多，具载难尽，学者不必执泥，在于临时机变。必须截盈、补虚、俾小、减大，以合规式。但田中央先取出方、直、勾、股、圭、梭等形，另积旁馀并而于一，然后用法乘、除之，用少广章开平等法还原，始为精密之术焉。
丈量田地总歌

古者，量田较阔长，全凭绳尺以牵量。一形虽有一般法，惟有方田法易详。若见喎斜并凹曲，直须俾补取其方。却将乘实为田积，二四除之亩数明。
又歌

方自乘之积步明，直田长阔互相乘。勾股圭梭乘折半，圆田周径折半乘。周自乘之十二约，径自乘之七五乘。周径相乘四归是，碗田丘田同上乘。环田内外周相并，折半须将径步乘。梯斜两头相并折，长乘便见积分明。三广倍中加二阔，四归得步以长乘。弧矢弦长并矢步，半之又用矢相乘。牛角眉田长步并，折半还将半径乘。二不等并东西步，折半仍将阔步乘。蛇船三阔同相并，三归得步以长乘。四不等田分两段，一为勾股一斜形。田形不一须推类，二四除之亩数明。
新制丈量步车图新制丈量步车图

前图下段作车三式，总合于一以完成车样。于上外套似无。盖底墨匣两旁木比十字。木空长存作两头。横木插角合栒。内空仅容十字转动。下横木凿一匾眼，后高前低，出篾。上可钉环，下钉钻脚。十字中心如墨斗搅转之心。作曲尺，样三折装在十字中心。内者方而不动，外者俱圆活动。以便收放，即似纺车之形。套匣上头，横木之下，凿一眼。其十字四头各开一口。但遇一头凑著，匣眼用拴拴之，置锁其篾，择嫩竹竹节平直者。接头处用铜丝扎住。篾上逐寸写字。每寸为二釐。二寸为四，三寸为六，四寸为八，不必釐字。五寸为一分。自一分至九分俱用分字。五寸为一步，依次而增至三十步。以上或四十步，以下可止。篾上用明油油之，虽污泥可洗。
又后制一式，只用十字内中开槽留头，不通中。用木圆饼转篾。篾虽不散，但转其篾尽，皆挨擦损坏甚速，总不如前制车式。篾在十字，十字转动，其篾安静，故难坏也。
丈量之法以五尺为一步。每步自方五尺计积二十五尺也。以五尺计之，步下五寸为一分。一寸为二釐积步。问亩，用二四归除亩。问积步，用二四乘法。〈今惟休邑新立亩法。〉
方圆定则九图

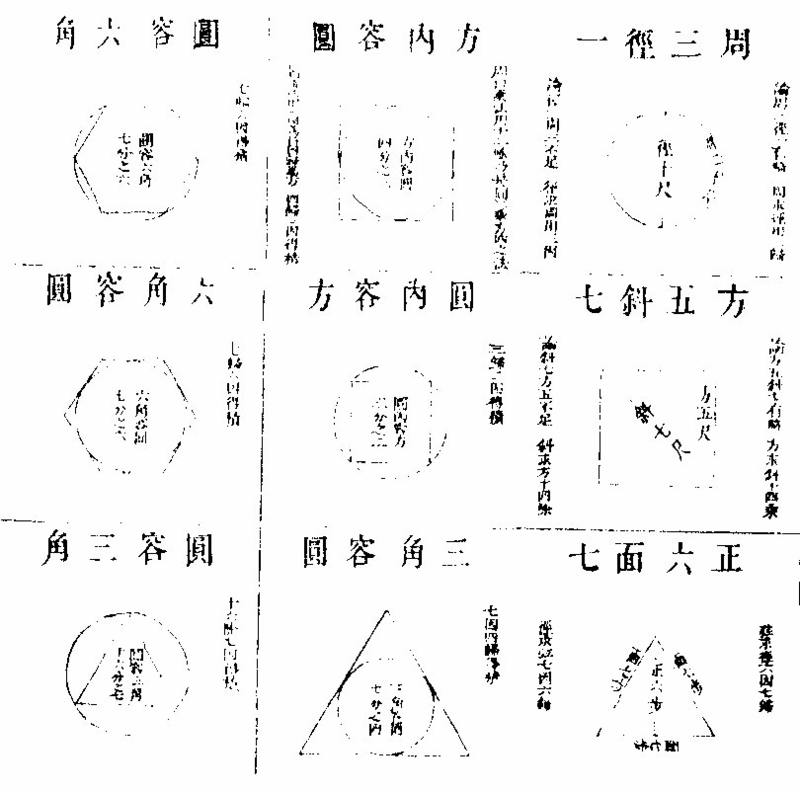
假如今有方田一丘，长阔各五十步。问：积、税各若干。
答曰：积二千五百步，税十亩零四分一釐六毫六丝。
方田

法曰：置长五十步，以阔亦五十步乘之，得积二千五百步为实。以亩法二四除之。定位法先从原实首位数几十起，顺下至几步止。下一位定法，首十数逆数升上至实首位，合得二千顺下，即是五百也。馀皆仿此。

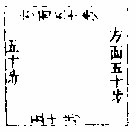
假如方田斜量东南角至西北角，西南角至东北角，
方形斜量

各斜七十步。问：积、税各若干。答曰：积二千四百五十步，税十亩零二分零八毫。
法曰：置斜弦七十步自乘，得四千九百步。折半，得二千四百五十步为实。

以亩法二四除之，合问。定位同前。
假如直田南北各长六十步，东西各阔三十二步。问：积、税各若干。
直田

答曰：积一千九百二十步，税八亩。法曰：置长六十步，以阔三十二步乘之，得积一千九百二十步为实。以亩法二四除之，合问。

假如今有圆田径五十六步，周一百六十八步。问：积
圆田

步若干。
答曰：二千三百五十二步。法曰：以径问积，置径五十六步自乘，得三千一百三十六步。又以七五乘

之，得积二千三百五十二步。若周径问积步，置周一百六十八步，以径五十六步乘之。再以四归之，亦得。若周问积步，以周自乘，用十二除之，亦得。
假如覆月田弦长五十六步，矢阔二十八步。问：积步
覆月形

若干。
答曰：一千一百七十六步。法曰：置弦五十六步并矢二十八步共八十四步，折半，得四十二步。又以矢二十八步乘之，得积。

一法以弦矢相乘，另以矢自乘，并之，折半，亦得。假如弧矢田弦长四十步，矢阔八步。问：积步共该若
弧矢形

干。
答曰：一百九十二步。
法曰：置弦矢相并得四十八步，折半得二十四步。又以矢八步乘之，得积合问。

又考如前圆田内除方田一丘。方四十步，占积一千六百步，四边四弧矢占积七百六十八步，共合圆田
考矢量圆图

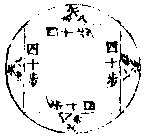
积，却多一十六步。其多者，何也。是弦自乘得一千六百步。每百步中多一步，该十六步也。或每弧矢内减去四步，只该一百八十八步。又考弧矢田居直田四分之三。

假如孤矢田弦长四十步，矢阔八步。问：圆中径该若干。〈又设此问以辨前大小二弧矢虚实之数。〉
答曰：今改正得径五十六步。
法曰：置弦长折半得二十步。自乘得四百步。以矢八步除之得五十步。加矢八步共得五十八步。却比前图径多二步。今减去是也。
今改其数乃是细半个。圆田因弦长而矢短，故虚数差，不准。
今减二步者，何也。是弦长折半得二十步，是十步中多一步，故减二步也。或云弦长四十步，矢二十步。问圆径者。置弦四十步折半得二十步。自乘得四百步。以矢二十步除之，得二十步。加矢二十步，即得。此乃是平半圆田，则数再无差矣。
假如圭田中正长六十步，下阔三十二步。问：该积若干。
答曰：九百六十步。
圭田　即半梭

法曰：置中长六十步，以下阔三十二步乘之，得一千九百二十步。折半得积九百六十步。合问。圭形乃直田之半，故用折半之法。梭形则是二圭合一也。

假如三角田每面一十四步。问：该积若干。
答曰：八十四步。
法曰：置十四步以六因之，得八十四步。以七归之，得
三角形

中长十二步。另以每面十四步折半，得七步。因之，合问。三角即圭也，以半阔乘中长十二步亦得。〈按三角田用六因七归得中长十二步。其数有差。今以句弦求股法校之，得十二步一分〉
有零之数。


假如梭田中长五十二步，中广一十二步。问：积若干。答曰：三百一十二步。
梭形

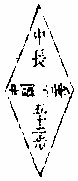
法曰：置长五十二步，以广十二步乘之，得六百二十四步。折半得积三百一十二步。合问。勾、股、圭、梭、乘，折半。田形虽异，理一同。

假如斜圭田长三十步，阔一十六步。问：该积若干。
斜圭形

答曰：二百四十步。〈计税一亩。〉法曰：置长三十步，以阔十六步乘之，得四百八十步。折半得积二百四十步。合问。

假如梯田上广二十步，下广三十步，中长四十五步。问：该积若干。
答曰：一千一百二十五步。
梯田

法曰：置上下二广并之得五十步。折半得二十五步。以中长四十五步乘之，得积。合问。
一法并二广以乘长，折半亦得。

假如斜田南广三十步，北广四十二步，纵六十四步。问：该积若干。
斜形田

答曰：二千三百零四步。法曰：置南北二广并得七十二步。折半得三十六步。以纵六十四步乘之，得积。合问。

假如眉田上周四十步，下周三十步，径八步。问：积若
眉形田

干。
答曰：一百四十步。法曰：置上下二周相并得七十步。折半得三十五步。另以径八步折半得

四步。乘之得积。合问。
假如牛角田中依湾长十七步五分，阔八步。问：该积若干。
牛角形如眉之半

答曰：七十步。
法曰：置中长一十七步五分，以广八步折半，得四步乘之，得积。合问。或量内外湾并之，折半。另以半径乘之亦得。

假如榄形中长四十步，阔一十六步。问：该积若干。
榄形如圆弧矢合一

答曰：三百八十四步。法曰：置长四十步如弧弦，以半阔八步如矢并得四十八步。折半得二十四步。又以矢八步乘之，得一百九十二步，即一弧矢之积。倍得榄积。合问。

假如三广田南广二十六步，北广五十四步，中广一十八步，正长八十六步。问：积若干。
答曰：二千四百九十四步。
法曰：并南北二广折半，得四十步。加中广共五十八
三广形即倒顺二梯

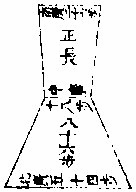
步。以长乘之，得四千九百八十八步。折半得积。合问。
一法倍中广，并南北二广，共一百一十六步。以四归之得二十九步。以长乘之亦得。按三广田乃是二段梯

田之并，必其三广相去，俱停乃可。以三广法算，或上段长，下段短；或上段短，下段长。并不可用。三广法当以二梯算而并之，乃为无弊。又按鼓田杖鼓田，又有箭箬、箭翎田亦要三广相去俱停，可用三广法。若不停者，亦可以二梯或以二斜算而并之是也。
假如勾股田股长六十步，勾阔三十二步。问：积若干。
勾股形

答曰：九百六十步。法曰：置股长六十步，以勾阔三十二步乘之，得一千九百二十步。折半得九百六十步。合问。

假如直田广纵相和九十二步，两隅斜去六十八步。问：积若干。
答曰：一千九百二十步。〈若折半如句股积。〉
直如句股和

法曰：置斜六十八步自乘得四千六百二十四步。另以相和九十二步自乘得八千四百六十四步。以少减多馀三千八百四十步。折半得积一千九百二十步。合问。

假如直田纵长六十步，广斜相和一百步。问：积步若干。
答曰：一千九百二十步。〈若折半如句股积。〉
法曰：置广斜百步自乘得一万步。另以纵六十步
直如句弦和股弦和同

自乘得三千六百步。以少减多馀六千四百步。折半得三千二百步为实。以广斜一百步为法除之，得广三十二步。以纵六十步乘之，得积一千九百二十步。合问。〈按句弦和以股〉自乘。以句弦和除之得较较。加和折半得弦。弦减较即得句。再以股乘之见积。

假如直田两隅斜去六十八步，只云纵多广二十八步。问：积若干。
答曰：一千九百二十步。〈若折半如句股积。〉
直如句股相差

法曰：置斜六十八步自乘，得四千六百二十四步。另以纵多广二十八步自乘，得七百八十四步。以少减多馀三千八百四十步，折半得积。合问。

假如直田广三十二步，只云斜多纵八步。问：积若干。
直如股弦差

答曰：一千九百二十步。〈若折半如句股积。〉法曰：置广三十二步自乘得一千零二十四步。另以多八步自乘得六十四步。以少减多馀九百六十步为实。

倍多八步作一十六步。为法除之得纵长六十步。以广三十二步乘之得积。合问。
假如直田纵六十步，只云斜多广三十六步。问：积若干。
答曰：一千九百二十步。〈若折半如句股积。〉
直如句弦差

法曰：置纵六十步自乘得三千六百步。另以多广三十六步自乘得一千二百九十六步。以少减多馀二千三百零四步为实。倍多三十六步作

七十二步。为法除实得广三十二步。以纵六十步乘之得积。合问。
假如四不等田一丘截作三段。量之，一段直田长四十步，阔二十八步。南边句股一段股长三十二步，句
四不等形斜形正量

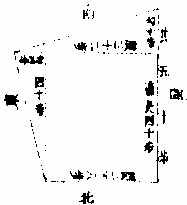
阔十步。东边句股一段股长四十步，句阔四步。问：共积若干。答曰：三段共积一千三百六十步。法曰：先置所截直田长四十步，以阔二十八步乘之，得直积一千一

百二十步。又置南句股一段股三十二步，以句十步乘之，折半得积一百六十步。再置东向股一段股四十步，以句阔四步乘之，折半得积八十步。三共并积一千三百六十步。〈此乃准数毫忽无差。〉若依古法南边依斜弦量比股多一步五分二釐，东边依斜弦量比股多二分。总合积多地二十七步二分七釐。今考较当以截法皆得其当，以见前古法。有差使学者易晓此理也。但遇歪斜不等，必有斜步。岂可作正步相乘。若截之，庶无误矣。
假如五不等田一丘，截作二段量之，四角斜长三十六步，上径十五步，二分下径十二步八分，三角长二十二步，径一十二步。问：积若干。
五不等形

答曰：共积六百三十六步。法曰：先置四角二径并得二十八步，折半得一十四步。以乘长三十六步，得积五百零四步。又置三角长二十二步，以径十二步乘之，折半得积一百三十二步。二共并得积六百三

十六步。合问。
倒顺二圭

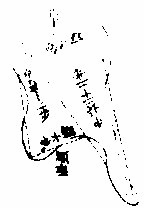
其形截作二圭量之，倒下圭中长二十二步，阔八步。向上顺圭中长一十二步，阔六步。问：共积若干。答曰：二共积一百二十四步。法曰：置倒圭中长数，以半阔四步乘

之得积八十八步。又以顺圭中长数，以半阔三步乘之得积三十六步。二数相并，共得积一百二十四步。合问。
三圭形

其形截作三圭形量之，东西二圭形同。中弦长二十六步，东径八步，西径十二步。又北半梭之弦十四步，径五步。问：共积若干。答曰：二百九十五步。法曰：置东西所共中弦长数，以二

径并之。折半、乘得二百六十步。又以北弦十四步，以径五步乘之。折半得三十五步。二共并得积二百九十五步。合问。
假如中段四角，中弦十六步，以东西二径共一十四
六角形

步折半乘之，得积一百一十二步。南尖三角，弦十步。以半径二步乘之，得积二十步。西弧矢弦十三步，以半径二步乘之，得积二十六步。东北三角弦十二步，以半

径二步乘之得积二十四步。四共计积一百八十二步。合问。
假如东北弦八步，以半径三步乘之，得积二十四步。
八角形

又正东三角弦六步，以半径二步乘之得积一十二步。又弦十八步，以半径四步乘之得积七十二步。又南弧矢弦八步加矢折半，以矢乘得积十步。
又西三角弦二十四步，以半径六步乘之得积一

百四十四步。又西北弧矢弦十四步加矢折半，以矢乘得十六步。六共计积二百七十八步。
凡图形内用点断节，以为绳索。耕形定式之辨。
图图

右。量田地之法举此数条，已见大意。若截作几段凑形以例，其馀如蛇、碗、丘、扇、辋、盆、瓜、罄、欹侧者，形状极多，难以一一尽述。考究校之数，无准积，恐误学者。故尽删去不录。今纂集直指图形，具之于前，以为通变之术。若平地而无碍者，或作几段定形立法，只以句股、圭、梭、梯、斜弧矢、牛角之类，截而量之。或并或减以求实积。倘遇基地有房屋者，难用此法，必须取其方直。或借别地以凑方直。算积内减除，还则形可穷而数。可尽学者详玩，形势理何异焉。
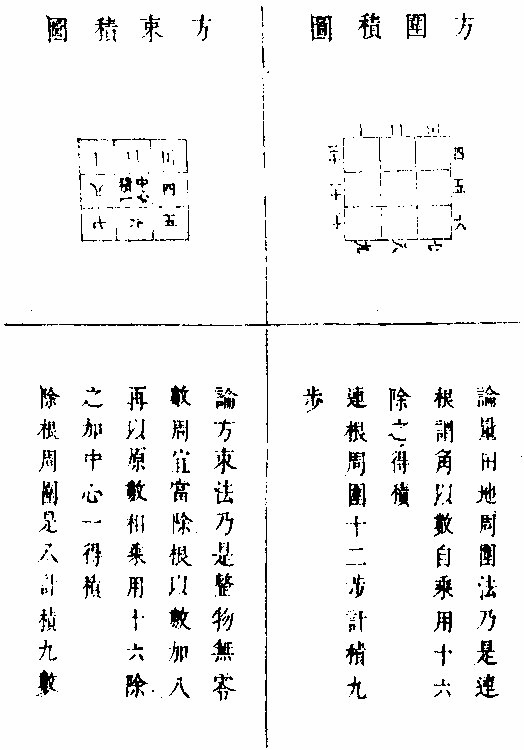
方图实

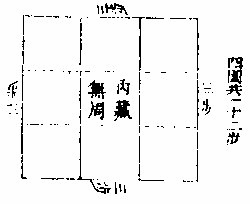
凡量田地切不可以周围步数算，而计积。其谬已甚。今举方直二形较之，其方
直图虚

田每面三步，计积九步。其直田长四步，阔二步，计积八步。论周围俱各一十二步。二者小数较之，而差一步，何况于大者乎。
解曰：方者内中藏一步，
而无周直者，外周而无藏隐也。

假如钱田外周二十七步，径三步，内钱眼方周一十二步。问：该积若干。
答曰：五十一步四分步之三。〈步之三即是七分五釐也。〉原法曰：置外周二十七步自乘得七百二十九步。以圆法十二除之，得六十步零七分五釐。以减内方周十二步，自乘得一百四十四步。以方周法十六除之，得内方积九步，馀积五十一步七分五釐。
孤峰马杰断曰：钱塘算师吴信民编集比类，世罕闻。孤峰裁改鹤坡校钱田之法，有差争。
又论：此钱眼方周一十二步，中间明有迹一十六步，何云九步。已知圆三、径一，得径九步。除方四步、外径一面，岂有三步哉。
又增比意驻云飞，比意钱田题法难明不足观。非俺自誇羡，改正珍宝鉴〈嗏〉二十七步圆眼中，间十二方周改法精制，算图样明名天下传。答曰：改正得四十四步七分五釐。
又改正法置钱周二十七步自乘，得七百二十九步。以圆法十二除之，得六十步零七分五釐为实。另以钱眼方周一十二加八，得二十步。与一十二步相乘得二百四十步为实。以方周法一十六除之，得一十五步。加一步共一十六步。以减前实六十步零七分五釐，馀四十四步七分五釐。合问。大位因杰辨吴氏之非，故立图考校前法。每一步自方五尺横直相乘，得积二十五尺。乃是本身连根，其理甚明。
假如钱内方周每面三步，四围共合为十二。得积九步无差。
据杰用方束之法反正为邪，不免有差殊。不知束积皆是论个、论只之物。而无零者宜当除根不辩，自明矣。求束法具载少广章。
大位歌曰：孤峰改正吴氏法，未得真传奇妙诀。丈量之法要分明，方自乘之为何说。方周摺角数连根，岂可除根用束法。今立图形考校明，例依吴氏为定决。
图

缺田亩演段根源图解

方求积法：置方十步自乘，得积一百步。合问。
方演段图

张丘建方求斜法：置方十步，用五归，得二是两个。方五却用七因得斜十四步。故曰方五斜七。若依方五求斜，则斜有馀。若依斜七求方，则方不足。

假如方田隅斜一十四步。问：积步并方面各若干。答曰：积一百步，〈实只有九十八步。〉方面十步。〈实只有九步九分。〉
斜演段图

张丘建法：置斜十四步，用七归得二，乃是二个。斜七却用五，因得方面十步，是两个。方五就以方十步自乘，得积一百步。有斜必有方，只以方求积，无差。

杨辉方求斜法：置方步自乘，得一百步，是一个小方积。倍之，得二百步，是两小方积。用开平方法除之，得斜十四步。却有不尽，馀实四步。斜求积法：置斜步如大方面自乘，得积一百九十六步，如两个斜方积。折半，得九十八步，如一个斜方积。却比前方积步中少二步。斜求方面，斜自乘折半得积九十八步，如
个斜方积。以开平方法除之，得方面九步九分。
方斜演段图

此论大方一个，方面一十四步，内容斜方一个。〈即小方也。〉斜亦一十四步，自乘得一百九十六步。是两个斜方积。内小方斜积一个，九十八步。外四角用句股求弦法得弦九步九分，即如小方面自乘，亦得九十

八步。将四角总合，亦为一小方。每角正方二十一步。斜方七步，折半得三步五分。并得二十四步五分。以四角因之，得九十八步，亦为一斜方积也。此合大方
方斜黑白演段图

求积，毫忽无差。〈杨辉用开平求方，求斜理明以合方积。张建丘用方五斜七，难以合数。〉　又论大方面十四步。内容小方斜十四，自乘得一百九十六步，是两个斜方积。乃黑白四段，以上下斜白配合为一方。又以左右斜黑配合，为一方。故
周三径一图

用折半得一个斜方积九十八步。古法：周围三尺，圆径一尺。假如圆径三十二尺，以周三因之，得九十六尺，而四尺闲矣。

徽术：周百尺、径三十一尺四寸。
密术：周二十二尺、径七尺。
智术：圆径三十二尺、周有百尺。
术曰：圆径即方径。若求圆积四分之三，不必立法。惟以圆求方，其法不一，姑录于此。盖圆径一则，周不止于三。所谓周三径一者，举其大概耳。
方五斜七者，言其大略耳。内方五尺，外方七尺有奇。
方五斜七图

方面求弦法曰：以方面自乘，倍之为实。以开平方法除之，得七步。○七一故曰斜七有奇。以此自乘折半得积二十五步。若以七步自乘折半得积二十四步。半校之得积，不全矣。

假如圆田径六步，周十八步。问：积若干。
答曰：二十七步。
圆演段图

径六步是一个六，周十八步是三个六。故曰周三径一也。其方积三十六步是四个九，其圆积二十七步是三个九。其圆外剩九，是一个九。故曰圆居方四分之三也。〈圆三象天，方四象地。〉

径求积法：置径六步如方面自乘，得方积三十六步。用三因得一百零八步，是三个方积，合四个圆积。故用四归之，得一个圆积二十七步。
周求积法：置周十八步如大方面自乘得三百二十四步，是九个小方积。每积三十六步，正合十二个圆田积。故用十二除之，得一个圆积二十七步。
周径求积法：置径六步是一个六，与周十八是三个六，相乘得数，即如前径自乘，以三因数同。故仍用四归得积二十七步。
半周求积法：置半周九步自乘，得八十一步，如三个圆田积。故用三归之，得圆积亦二十七步。
半径求积法：置半径三步自乘，得九步如方田积四分之一，即圆三分之一，故用三因之得圆积。
半周半径求积法：置半周九步，以半径三步相乘，得圆积二十七步，如方积四分之三，正合圆田之积。若问圆田外四角剩积法：置一角长阔各三步，折半得一步半。自乘得一角，剩二步二分五釐。以四因得四角，剩积共九步也。〈已上求积六法皆合周三径一。已后二术惧有不尽非良法也。〉徽术周求径：以五十因周，再以一百五十七除之，得径。径求周：以一百五十七乘径，用五十归之，得周。密术周求径：以七因周，再以二十一除之，得径。径求周：以二十二乘径，用七归之，得周。
虚隅图说


方圆论说方圆论说

世之习算者咸以方五、斜七、围三、径一为准，殊不知方五则斜七有奇，径一则围三有奇。故古人立法有句三、股四、弦五之论，而不能使方斜为一定之法。有割圆矢弦之论，而不能使方圆为一定之法。试以句股法求之，句股各自乘，并为弦实。平方开之，此施之于长，直方则可若一整方。句五股五各自乘，并得五十。平方开之，得七而又多一算矣。割圆之法求矢、求弦，固是至于求弧背，则恐未尽也。何以知之。试以平圆径十寸者例之。中心割开矢阔五寸，自乘得二十五寸。以径除之，得二寸五分为半背弦差。倍之得五寸。以加弦得一十五寸。与围三径一之论正合。然径一则围三有奇，奇数则不能尽矣。以是知弧背之说犹未尽也，不特是也。凡平圆一十二，立圆三十六，皆不过取其大较耳。或曰密率径七，则围二十二。徽率径五十则围一百五十七。何不取二术酌之，以立一定之法。曰：二术以圆为方，以方为圆，非不可。但其还原与原数不合，数多则散漫难收。故算历者止用径一、围三，亦势之不得已也。曰历家以径一、围三、立法，则其数似犹未精然。郭守敬之历至今行之无弊，何也。曰历家以万分为度，秒以下皆不录。纵有小差不出于一度之中，况所谓黄赤道、弧背度乃测验而得止，以径一、围三定其平差，立差耳。虽然，行之日久，安保其不差也。窃尝思之，天地之道阴阳而已。方圆，天地也。方象法，地静而有质，故可以象数求之。圆象法，天动而无形，故不可以象数求之。方体本静，而中斜者乃动而生阳者也。圆体本动，而中心之径乃静而根阴者也。天外阳而内阴，地外阴而内阳。阴阳交错而万物化生。其机正合于畸零不齐之处，上智不能测巧历，不能尽者也。向使天地之道，俱可以限量求之，则化机有尽而不能生万物矣。余因论方圆之法而并著其理如此。
又述直圭、梯斜、句股、弧矢等形图于左。
今有直田长一十二步，阔九步。问：田积并斜弦各若干。
答曰：积一百零八步，该斜弦一十五步。
直演段图

求积法曰：置长阔相乘得一百零八步。若问斜者，如句股求弦。以长自乘，又以阔自乘，并二数得二百二十五步为实。以开平方法除之，得弦十五步。若以斜问积置斜十五步自

乘，折半，得一百一十二步。半却比直积多四步。半其多者何也。是长多阔三步。自乘折半得四步半也。假如斜若干，只云广纵相和若干。问积。以斜自乘，另以相和自乘，二数相减，馀折半得积。
假如有广若干，只云纵斜相差若干。问积。以广自乘，另以相差自乘，二数相减，馀折半为实。以相差为法除之，得纵。以广乘之，得积。
纵斜相和者，仿此。广斜相和、相差，及广纵相差，与前广纵相和者俱同。

假如今有圭形田广八步，纵一十二步。问：该田积若干。
答曰：积四十八步。
法曰：置广纵相乘折半得积四十八步。合问。
句股相乘折半图

半纵乘广图半纵乘广图

句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图句股演段图半纵乘广图句股演段图

半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图半句乘股图半纵乘广图句股演段图半句乘股图

长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图长阔相乘折半图半纵乘广图句股演段图半句乘股图长阔相乘折半图

半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图半广乘纵图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图

斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图

斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图斜形折广图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图

梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图梯形演段图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图

并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图并上下广乘半长图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图

梯形折广图并上下广折半乘长图并上下广乘长折半图梯形折广图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图

并上下广折半乘长图并上下广乘长折半图并上下广折半乘长图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图

并上下广乘长折半图并上下广乘长折半图半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图

半纵乘广图句股演段图半句乘股图长阔相乘折半图半广乘纵图斜形折广图梯形演段图并上下广乘半长图梯形折广图并上下广折半乘长图并上下广乘长折半图

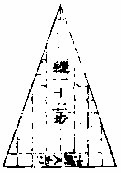
今有直田长一十四步，阔七步，计积九十八步。问：内容弧矢田一段，占积并二角。馀积各若干。
答曰：弧矢积七十三步半，二角积二十四步半。法曰：置长一十四步为弧弦，以阔七步为矢，相并得
直内容弧矢图

二十一步。折半得十步零五分。又以矢七步乘之，得弧矢占积七十三步五分。以减直积九十八步，馀二十四步五分，是二角馀积。

今有直田长二十步，阔十八步，计积三百六十步。内容六角田一段，每角面十步。问：六角占田积并馀积各若干。
答曰：六角积二百七十步，角外馀积九十步。
法曰：置中长二十步减去半面阔五步，馀长一十五步。以通阔一十八步乘之，得六角占积二百七十步。
直容六角图

另以角外之馀长九步，以馀阔五步折半得二步五分。乘之得一角。馀二十二步五分以四因之，得四角馀积九十步。并入六角，占积二百七十步。共合直田之总积也。

假如方田一段面方十七步，计积二百八十九步，内容八角田一段。每角面阔七步，问：八角占积并外馀
方容八角图

若干。
答曰：八角占积二百三十九步，角外馀积五十步。
法曰：方七步是上下斜角面。如斜求方，以五因七归得五。倍之得十步，是上下二段长。加中一段面七步，

共十七步。自乘得方面总积二百八十九步。另以一角长五步自乘，得二十五步。倍之得外馀积五十步。以减上积馀得八角。占积二百三十九步。合问。假如圆田径十四，计积一百四十七步，内容锭田占积并两腰，外馀积如榄形田。二段长十步，阔四步。问：各该积若干。
答曰：锭占积一百步，两腰外馀积四十八步。
法曰：圆径即锭长十四步，又如圆内方之斜也。以方五斜七之法置十四步，以七归五因得方十步。自乘
方内容锭图

得锭占积一百步。另置两腰外如榄田，长十步加半阔二步，共十二步。以阔四步乘得馀积四十八步。加入锭占积共合圆田。总多一步者是榄。长十步自乘得百步，内多一步。
旧法以锭长自乘、折半得九十八步。却少二步。其锭

长如方田斜求积，则百步中少二步，可用九八归除，即一百步。
一法：截上下有馀补两腰不足，作方十步自乘，得一百步。锭田还原以积，用开平方法除得十步。却以五归七因得斜长十四步也。
方圆环总图说

平方求积法曰：以方面十六步自乘得二百五十六步。平圆求积法曰：以外周四十八步自乘得二千三百零四步，再以十二除之，得全积一百九十二步。
方内容圆圆内减图为环图

四旁馀积六十四步，另以内周二十四步自乘得五百七十六步。再以十二除之，得内圆积四十八步。圆环求积法曰：以大圆积内减小圆积，馀一百四十四步，即是环积也。
又法以环径四步，以三因之，得一十二步。以减外周，

馀得三十六步为长。以径四步乘之，得环积一百四十四步。环田者如圆田中间有圆池也。若圆池不在中而偏者，只以圆田算之，得全积。却减去圆田积，馀为本田实积也。
法以外周自乘，又以内周自乘，二数相减馀数以十二除之，得环积。若以内周外周问径者，置外周减内周，馀数以六除之，得径。若以内周并径问外周者，置径以六因之，得数并入内周数，即是外周。若以外周并径问内周者，置径以六因之，得数减外周
方内容圆圆内容方图

数，馀为内周。
先论方内容圆。外方十四步自乘，计积一百九十六步。问：容圆并四旁庇积若干。
答曰：圆积一百四十七步，
四旁庇积四十九步。
法曰：置方径十四〈即圆径。〉自乘，再以七五乘之，得圆积

也。若问四庇积，以二五乘方积〈四庇居方四分之一〉是也。方积四分取三为圆积。故法用七五乘之，或用三因四归亦得圆积。
后论圆内容方。圆径〈即方斜。〉十四步计积一百四十七步。问：容方并四旁幂积若干。
答曰：圆内容方每面十步计积一百步，四旁幂积四十七步。
右明方圆之理

方环者，谓如方田中央有方池。方环求积法曰：以外
平方环积之图

方自乘，得全积。另以内方自乘，得内积。以减全积馀得方环积。又法以外方并入内方，倍之为长。以径阔乘之，得方环积。
解曰：非言田也，皆言托物比兴，算家穷理尽性致知格物，以明方圆句股之理，至于天地高广乎。
带分母用约分法

今有直田，广二步二十分，步之九纵。九十七步四十九分，步之四十七。问：该积若干。
答曰：一亩。
法曰：置广二步，以分母二十乘之，得四十。加分子九共四十九。另以纵九十七步，以分母四十九乘之。加分子四十七，共四千八百。以乘纵四十九得二十三万五千二百为实。又以分母二十乘四十九得九百八十。为法除之，得二百四十步。以亩法除之，合问。今有圭田，广五步二分，步之一纵。八步三分，步之二。问：该积若干。
答曰：二十三步六分步之五。
法曰：置广五步，以分母二通之，加分子一共十一。另置纵八步，以分母三通之，加分子二，共二十六。与广十一相乘，得二百八十六，折半得一百四十三为实。以分母二分、三分相乘，得六分。为法除之得二十三步。馀实五以法命之，得六分之五。
今有圆田，径六步十三分，步之十二。周围二十步四十一分，步之三十二。问：该积若干。
答曰：三十六步。
法曰：径求积。置径六步，以分母十三通之，加分子十二共九十，自乘得八千一百。又以分母十三减分子十二馀一，以乘分子十二，并前共得八千一百一十二。以三因四归之，得六千零八十四为实。以分母十三自乘，得一百六十九，为法除之合问。若以周求积。置周二十步，以分母四十一通之，加分子三十二共八百五十二。自乘得七十二万五千九百零四。又以分母四十一减分子三十二馀九，以乘分子三十二得二百八十八。并入前数共七十二万六千一百九十二。以圆法十二除之，得六万零五百一十六为实。以分母四十一自乘，得一千六百八十一为法除之。合问。
今有环田，内周六十二步四分，步之三。外周一百一十三步二分，步之一。径十二步三分，步之二。问：该积若干。
答曰：四亩六分五釐四分步之一。法曰：并内外周共一百七十五步。以内周之三乘外周二分，得六分。另以外周之一乘内周四分，得四。并之得十。却以分母二分四分相乘，得八。为法除十得一步二分五釐。并前共得一百七十六步二分五釐。折半得八十八步一分二釐五毫为实。却以径十二步，分母三通之，加分子二共三十八，为法乘之得三千三百四十八步七分五釐。又以分母三除之，得一千一百一十六步二分五釐。以亩法除之得四亩六分五釐，不尽步下二分五釐，以法约之，得四分步之一。合问。
今有方田一丘，面方十二步四分，步之二。问：该积若干。
答曰：一百五十六步五分。
法曰：置十二步，以分母四通之得四十八步。加分子二共得五十步。自乘得二千五百步。另以分母四减分子二，馀二。以乘分子二得四。并前积共得二千五百零四步为实。另以分母四自乘，得一十六。为法除之。〈此合开方不尽之法。已上皆双分母子法。〉
今有直田长一十五步，阔三步五分，步之四。问：该积若干。
答曰：五十七步。
法曰：置阔三步，以分母五通之，得十五。加分子四共十九。另置长十五步，以分母五通之，得七十五。将此二数相乘，得一千四百二十五为实。另以分母五自乘得二十五为法除之。合问。〈此是单分母子法。〉
休宁县科则〈附辨亩法论〉

休宁县于万历九年清丈有粮里，编号二百一十一里。带管无粮里三十四里半。〈以千字文编号，自在城东北隅天字一号。起至三十三都八图建字号止。〉
田亩起科等则〈每斗加耗七合，地山同。〉

田每一亩，古科米带耗共五升三合五勺。麦带耗共二升一合四勺。
地每一亩古科米带耗共三升二合一勺。麦带耗共二升一合四勺。新制米带耗共三升八合七勺。一抄三撮麦带耗共一升九合八勺七抄。
比古米增而麦减，何也。盖谓古有官庄产土租米重而租麦轻。又紫阳书院田府县学田有米无麦。今变总归于一，则丈出亩步摊派租米租麦各亩步不同等，而田山塘等起科不废。古法惟地扣合米麦总数之故云。
山按原额计亩，〈新丈不计步数。〉每亩米带耗共一升零七勺，麦数同。
塘池潭堨〈同田则〉　园圃洲堤〈同地则〉
坟茔境迹〈多作上地〉开垦陇野〈以作荒地三百为亩入山境〉
亩法论

愚按前贤亩法，率二百四十步为一亩。万历九年遵诏清之休邑总书，擅变亩法。田分四等。上则一百九十步，中则二百二十步，下则二百六十步，下下则三百步。地亦四等。上则二百步，中则二百五十步，下则三百五十步，下下则五百步。在城基地有等，正之名一等正三十步，二等正四十步，三等正五十步，四等正六十步。与前贤二百四十步一亩大相缪戾，借曰土地有肥硗，徵役有轻重，亦宜就土田高下别米麦之多寡。不得轻变亩法第。总书开其弊窦，举邑业已遵行，何容置喙。姑记于此以见作聪明乱旧章之自云。
古今折步

原用古弓每步五尺，今以钞弓校之，只有四尺八寸。问：古弓百步该钞弓若干。
答曰：九十二步一分六釐。
法曰：置四尺八寸倍之，得九分六釐。自乘得九分二釐一毫六丝，乃古弓一步今折得钞弓数也。自此升上合问。若钞弓步数每百步用八十五步，加之以合原古弓步之数。
其方直田形截积具载少广章中。