声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
钦定古今图书集成历象汇编历法典
第一百七卷目录
测量部汇考八
新法历书五〈测食〉
皇清
新法历引〈测太阳 测恒星 测太阴 测五纬 时晷〉
新法表异〈测算异古 测算皆依黄道 表测二分 五星测法〉
新法历书五〈测食〉
皇清
新法历引〈测太阳 测恒星 测太阴 测五纬 时晷〉
新法表异〈测算异古 测算皆依黄道 表测二分 五星测法〉
历法典第一百七卷
测量部汇考八
《新法历书五》测食似食实食说第一人恒言:日食月食矣,辄概混焉。不知月实食日,则似食而实非食也。何者。日为诸光之宗,永无亏损。月星皆借光焉。朔则月与日为一线,月正会于线上,而在地与日之间。月本厚体,厚体能隔日光于下。于是日
月食图
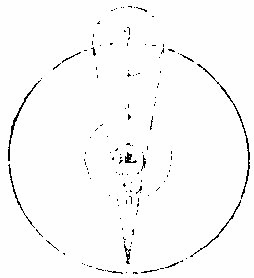
若无光,而光实未尝失也。恶得而谓之食。望则日月相对,而日光正照之,月体正受之。人目正视之月光满矣。此时若日月正相对,如一线,而地体适当线上,则在日与月之间。而地亦厚体,厚体隔日光于此面,而射影于彼面。月在影中,
日食图
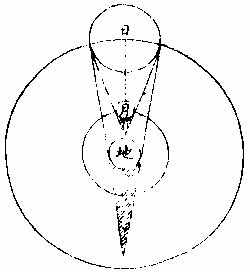
实失其所借之光,是为食也。然其食特地与月之失日光耳。而其光之失,因光在地面与月体之上,地与月互相遮掩耳。日固自若也,总之日也,月也,地也,使三体并不居一直线,则更无食矣。若食,则日体恒居一直线之界末,而彼界则
月体地体叠居焉。月体居界末,则月面之日光食于地影矣。地体居界末,则地之日光食于月影矣。
实会中会似会说第二
夫日月星宿之会,总名也。第有实会,有中会,有似会。实会者,以地心所出直线上至黄道者,为主而日月五星政当此线,则是实相会也。
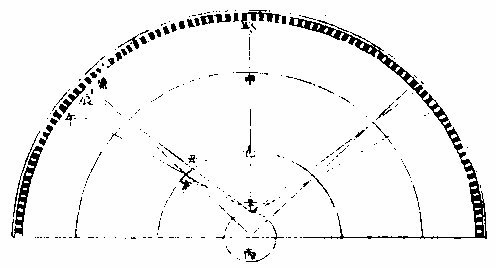
黄道圜黄道圜
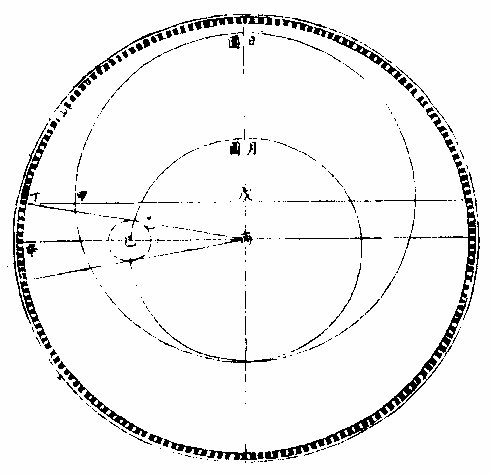
如右图日在甲,月在乙,地心在丙。甲乙丙线直至黄道圜之丁是也,即南北相距不同在一点,而总在此线。正对之过枢圜亦为实会。盖过枢圜者,过黄道之两极而交会于黄道,分黄道为四直角也。从北视南,虽不在地心,所出之一线却与地心所出之一线正相对,犹一线矣,故为实会也。然月与五星居小轮之边,地心所出线上至黄道,而小轮之心正当此线者,则为月与五星之中会也。但日无小轮,而日天本圜与地不同心。两心所出,必有两线,此两线若为平行。而月轮之心正当居地心线者,则是日月中会也。夫实会既以地心线,射七政之体为主。今此地心线过于小轮之心,则谓之中会矣。如地心为丙,日天之圜心为戊,月小轮之心为己,日在甲。甲日与戊心之戊甲径线而从,地心丙出线至黄道,辛平行乃是中会矣。然实会中,会俱准于地心。而吾人所居,乃在地面而从心所对一线,从面所对又一线。惟正当天顶之圜,则两线同在一线,与实会无异。过此而偏左偏右,即分两线矣。今人所见日食,皆地面上人目所对之
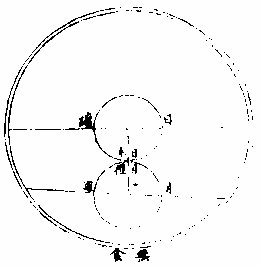
天顶
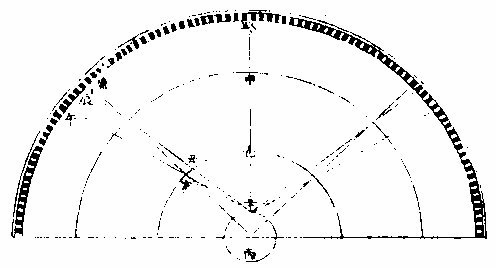
线也。日月在地心所对之线为实会,则在人目所对之线,不得为实会而特为似会矣。如上第二图地心为丙,地面为壬,天顶为癸,癸壬丙定为一直线也。若甲日乙月即在癸丙线上,则实会并是似会矣。若日在子,月在丑,与地面壬为
一线则似会也。必月至寅与地心丙为一线,方为实
会耳。则是实会在午前,必先于似会实。会在午后,必后于似会也。惟日食全以似会,故地面有不同。而食之分数时候,因之所以随地所见,亦不同也。第合朔论实会,交食论似会。实会、似会之线在日月,本天无度分而全依宗动天上。黄道圜十二宫之度分,则必当极论。会线至黄道之处,实会线所至,谓之实处。似会线所至,谓之似处矣。以实会线上之日月为据,而目视日至黄道,有日似处。目视月至黄道,有月似处。
天顶
得其似处,可以较实处之距度矣。如第二图子寅丙为实会线至黄道卯,则卯为实处。若壬目视子日至黄道辰视寅月至黄道午,则辰为日似处,午为月似处也。然所用既皆实会似会,而并论中会者,凡地与日圜不同心,而与列宿天
则同心。心同则径同,而日圜之心在列宿。天心与地心之上,则日圜之径亦在列宿。天径与地径之上列宿天之径,割日圜为大小两分。两分虽有大小,而各应黄道之一百八十度。此空度、隔度之所出,故不得不辩。夫必用地中会线者,求准对日与黄道,迟速不均不平之本动,又因而求实会之准则焉。
食之徵第三
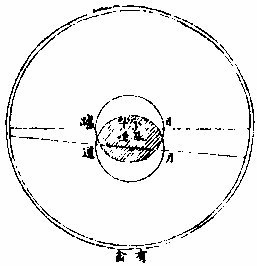
凡日月相会,未必皆食。惟因会之有,似有实而悉其差之远近几何。此必须测验而后得。凡人居赤道北
图
者,月之似处比实处恒若偏南。若偏低者,然夫月在日与目之一直线上,不偏斜不低,昂乃能掩日而为食。若精察之较,月食更难焉。第观日月似会之时,其距度比日月之半径或大或等者,必无食也。小则必食矣,愈小则食愈大矣。考
图
之在龙头、龙尾。若正当龙尾,或与龙尾不甚远,则当测其食否。若与龙头、龙尾相远,而月似会之距度过三十四分,则无食矣,可不必测矣。月食则于望日求之,月之距度若小于月半径与地半影者,必食也。其食之处定在龙头、龙尾之
图
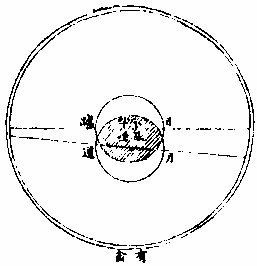
两傍十三度三分度之一。过此则月之行道不相涉而不相掩矣。如甲子年八月望日,月经龙尾不远,则应测其食而考其所经之躔度,乃在黄道。白羊宫三度五十六分四十一秒,其躔道距度则五分三十六秒矣。夫月半径得十六分
四十三秒。而地影之半径则四十五分十三秒。二数并之即为六十一分五十六秒,距度止五分三十六秒,是最小于月径及地影之半,而全体必尽食地影,必且有馀矣。若乙丑年八月望日,其月在龙尾双鱼宫二十三度半。夫月半径十七分十五秒,而地影之半径则四十六分三十七秒,二数并之得六十三分五十二秒。月距躔道四十八分二秒,则小过于地影之半径,而月体必半入地影而不得全食也。
食之处第四
黄道
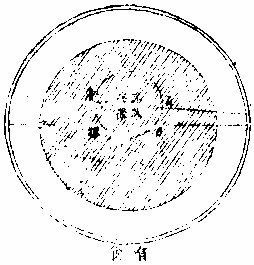
龙头、龙尾者,何是日躔之两界,月食所经之处也。昔人测日月之食必在所躔之二处,而月之距此益远则距度益广。广者,象腹也。则其所起、所止者,象头尾矣。十二宫右旋从头至尾,则左旋而此头尾二处非定于二宫,但设为多圜。嫌
于繁混,故止取龙之头尾,以略徵之也。如右图甲丁乙为日躔圜,甲丙乙为月行圜,两圜交于甲于乙。而从甲上升左旋至丙至乙,故甲为头,乙为尾,丙丁相距最广为腹也。但甲在白羊宫,则乙在天称宫,而腹在磨羯宫。若甲在双鱼宫,则乙在室女宫,而腹在人马宫。凡十九年乃复原处。故日月之食,不十九年不能在本躔同宫同度也。
日月地影之径说第五
日月之径,原自平分。今因日在本圜,月在小轮,有远有近。近则见其径大,远则见其径小。又地影者,是日与地所生,故日之远。近亦能为影之大小也。然无有食,而月不居本圜之高处第就。月居小轮,日居本圜,则每食自不同。而其径之大小,与小轮与日本圜无一定之规则。惟用日月之本动方可考定。今考月体本动之法:每四刻若行半度,则知其径亦半度矣。日体每四刻若行二分三十秒,须以十三乘之,则知其径十三倍于二分三十秒矣。此系一定之常法。但日月之行时刻不均,故以是法测其体之大小未免少差。盖日愈高其体愈觉小,其动亦愈觉迟。日愈下其体愈觉大,其行亦愈觉速。月在小轮,其高下迟速亦然。其考地影之法:须先定日之最远处,月径假有三十三分,即以三率法求月体于影,如五与十三之比例,即等于三十三与八十五零五分之四之比例也。若日不在最远,先当考日之居。所离最远处几何度,次考日行比最远处几何疾。以疾行之度减去地影,则得所求矣。
食大小迟速辨第六
夫距度广狭,实为月食大小迟速之分。故望日之月,视其进地影厚处,则其食迟。进地影浅处,则其食速。朔日之月,视其似会少偏日躔,或似会大偏日躔,而其故总由日月远乎。龙之头尾也。望日之月在头尾,正躔则月食至大至深。若少偏而躔影之半径与月体之半径等,则虽全食而即复。若距躔影又远,则食不全也。若日虽全食,亦不能久。因月径之似处小,仅能遮日体,而须臾便过,故但能全掩,不能久掩也。今欲知食分大几何,必须定其分数几何。盖西洋取日
量月食
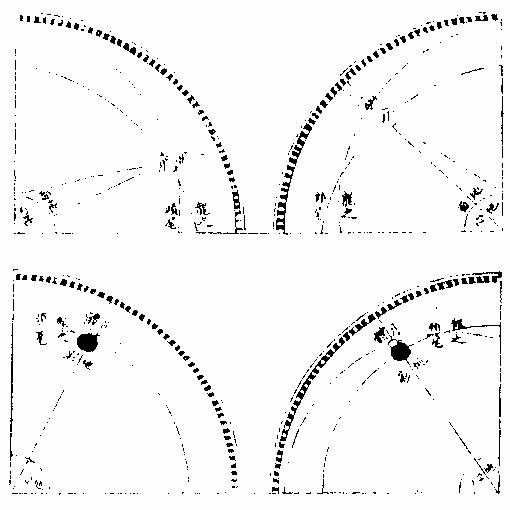
量日食量日食
 月本体为十二平分,移此分寸量月所经之处。若日月食十二分有馀者,是谓至全至大之食也。但欲精察不谬,月食则究食甚时月道距躔道几何。日食则究食甚时月似处距实会几何。量日食
月本体为十二平分,移此分寸量月所经之处。若日月食十二分有馀者,是谓至全至大之食也。但欲精察不谬,月食则究食甚时月道距躔道几何。日食则究食甚时月似处距实会几何。量日食

月本体为十二平分,移此分寸量月所经之处。若日月食十二分有馀者,是谓至全至大之食也。但欲精察不谬,月食则究食甚时月道距躔道几何。日食则究食甚时月似处距实会几何。月本体为十二平分,移此分寸量月所经之处。若日月食十二分有馀者,是谓至全至大之食也。但欲精察不谬,月食则究食甚时月道距躔道几何。日食则究食甚时月似处距实会几何。
经候几何第七
欲知食之经候几何,须知日月之本动。设若日月本动相同,则月必不能进影。进亦必不复出矣。今月行黄道比日甚速,能逐及于日而又过日前,故但较月过速日过迟之两候,即知日月食经候得几何也。此有算就立成。凡某时刻日月当食其本动之度几何,则以日过迟之少数减去月过速之多数。次取立成,视月多行之度几何则得。盖以过速之多数除初食至食甚之度数,即系初食至食甚经候之度分也。食甚至复圆,亦如之。顾日食之中,前中后与月食有异。盖日食惟在躔道九十度,正天中者,中前中后均平无异。若其食偏在东西,即有异矣。偏东则初食,至食甚短于食甚至复圆。偏西则食甚至复圆短于初食至食甚。故求日食毫釐不差,必须较看日月行动先后两时刻度分。其一在未食前,其一挨复圆后。而初食至食甚度分用以除食前一时刻度分,食甚至复圆度分用以除复圆后一时刻度分,即是日食中前中后之经候度分也。
日食月食辨第八
夫日食与月食,固自有异。盖月食天下皆同,而日食则否。日食此地速,彼地迟,此地见多,彼地见少。此地见偏南,彼地见偏北,无有相同者也。而月食则凡地面见之者,大小同焉,迟速同焉,经候同焉,唯所居不同。子午线者,则时刻不同矣。盖月一入影,失其借光,更无处可见其光也。
右所举不过略言食之固然与夫所以然耳。若精求合朔之时刻,日月之真方位及月离躔道之距度,考南北东西差。每处之异同,日月每时行几何度分与夫月进地影食甚时以较,太阳行度几何迟速及他种种议论,种种见解是书皆未及言,俱各有本论及立成井井胪列。俟翻译后开卷一目便已了然。〈以上原本卷上〉
月食为地影所隔第一
问月食必在于望,因日月相对之,故其说明矣。至谓地影隔之而食窃有疑焉。曰月对日而受其光,苟日月之间非有不通光之实体,为之障蔽则必不能阻。日光之照月体,无论空中之火、空中之气与夫天体,不能掩月。即金水二星虽居日月之间,其影俱不及地,况能过地而及月乎。则知能掩日者,惟有地体一面受光,一面射影,而月体为借光之物入此影中,安得不食。而半进则半食,全进则全食矣。
月体当食尚有光色第二
问无光之月一入地影,遂全失其借光也。然食时尚有依稀可见之光。天文家每视食月之色,预言食之徵验。若人以目切墙屋,掩其未食之光体,而独视其既食之乌体,其光尚明于星也。盖物之可见必借外光,不独能见物体,且更能发越物色也。月既在地影,即失借光,安得尚有色乎。曰月体虽食,尚有微光。今直以影为明者,误也。以影为暗者,亦误也。称影为明暗之中者,庶为近之。盖日所正照为最光明,有物隔之而四傍之气映射。或对面之光反照,虽无最光明,亦有次光明也。如一室之外为最光明,一室之内为次光明也。云之上为最光明,云之下为次光明也。直至所隔愈深,去光愈远。并次光明亦渐微,微而又微以至丝毫无光,乃为暗耳。夫人与地近日与地远,人居地此面,日在地彼面。至夜子初人在地影,至浓之中近物尚能别识,何况月在地影至锐之处。次光明正盛,其有光色又何疑乎。且人在极暗,则月光虽微,视之反觉明也。
日食在朔月体掩之第三
问前言月在日前,能掩日光,是已金水二星亦皆在日前,又皆实体,且水星虽小,而金星则大于月也。何独以食属月乎。曰:二星于人甚远,不能掩日百分之一二。而日光甚盛,即亏百分之一二人亦不觉。且二星去日甚近,去地甚远,所出锐角之影亦甚短,决不能及地面也。若夫月体,虽不及太白之大,然去地近去日远一指足蔽泰山,又何疑乎。由此言之,求一实体之能全掩日,又从西而东过之甚疾,唯月为能。盖月之右旋比诸天更速,且必至合朔方有食,则日食于月决然之理也。
因食知月体不通光第四
问月体受光而反照之,必不通光如铜铁镜。盖通光,则不能受日光,而反照他物亦不能掩日而生影也。曰镜之设,譬似矣而尚未尽。夫镜之照物而反生之象,其大小远近心与物体相当,然后可以镜喻月。今观镜之面有突如球,有平如案,有洼如釜。惟平者所生之象乃与物体相当。若如釜者,所生物象必倍于物体。如球者,所生物象必小于物体矣。试以球镜照远物,而人又从远视之,则物象必倍小。尝持球镜照太阳之体,其小如星。倘月体如球,镜欲其反生,太阳之象乌可得乎。又问合朔后月之下半未受日光,而月体微光比诸星更显。若不通明则此光又从何生。且观其掩日而日全食时,月之边际觉稍明于月之中心,似中间厚处难通,而薄处稍可通透乎。曰前既言月在地影最中处,乃天光映照之明若合朔时,则有光之天与月体最为切近。而日光上照月体,约有大半,四边岂得无光。或言月既非极通光如玻璃,或半通光如玉石,特因在后之物,其体质不明,故不能映见在后之物乎。曰试观日食甚之时,天光尽黑,星体亦现尔。时太阳在后,体质最为明显,何以不能映见丝毫。可知月体绝不通光也。或言在月后之物,必更坚密于月者,然后能照见。若较月更通彻即不能见乎。曰:若。然日体在月后,坚密不亚于月而亦不能见可,言日体为通彻乎。又凡目所注必须有色,及所照之光。此二者必不通彻之体,乃能受之,则月体从可推矣。
月食时人目不及见月受光之面第五
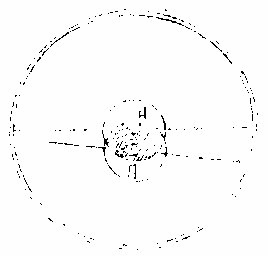
上言日光照月体大半,则知日比月体至大。然日食甚之时人目所见之面,何故绝无丝毫之光。曰:凡人
图
视圆球,止见小半。盖球有大圜,有小圜。若以两线切大圜,其线必为平行。今目所注视之线,既不能平行则不切至大圜,可知而目亦仅能及小圜矣。
详见几何一卷二十八题
又望后三日,虽月每日行十三度有奇,而月边尚似
图
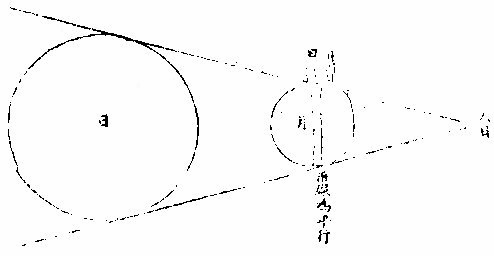
圆环。可见人目正及,其小圜也。或曰:望日所见月体之面,即月所受光之面,其光为大半。则二三日其光尚在大半之内,则晦后月轮稍移,便宜见光。而光今竟不即见,何也。曰:月掩日之时,一则人所注之圜与
图缺日光照月之圜为平行,一则日食时不过一两刻,则两线亦不能相切至望,则不同矣。又望时日光照月少于他时,盖晦日日与月止隔金水二星,天而甚近,故所照亦多。于望日望日与月隔金水,二天及月本天之体而甚远,故所照亦
少于他日。然晦日所照虽多于望日,而人目所及止见小圜,而月光不即见,职由此矣。
日月每月不食第六
夫月不恒食之故有二:一则日体常丽躔道,则地影亦常对躔道。一则月行常出入躔道,故地影不及。盖凡光照物必直射而作直线,今日在躔道,其光自平面而直通至地,则反影亦反射至天,如日光之射地。其日光绕地一周,则影亦绕天一周。其地影至月天,阔不过一度半。躔道平分地影,每边有四分之三。又望日月轮不在龙头、龙尾近处,故月体与地影不得相遇,故不食。此前篇言每月食,三体必在一直线也。或曰:日食应有多次,为其不论月之实所,但论月之似所。若论似所,则南北所差甚多。如此则人住两极近处者,视月远于躔道,亦能食日矣。曰:人居在北极下,而似所与实所相距不过一度。譬如月在地平东西,差亦不过一度。可见日欲食时,月不能离躔道一度强,故日食亦少也。但论一处,则日月之食不等。概论天下,日食应多于月食也。
因月食徵地圆如球第七
格物家悉言,地圆如球,验之洵不得不然也。盖凡物之性重者,势必就下。若一无所阻,必径就天心。天心者,最下处也。故大地四旁皆欲就下,其势不得不结为圆。然则虽山岳之高,湖海之深,亦无损于地体之圆也。今以地面论之,日月星之出入东西异,则时刻亦异。试观同此月食。欧逻巴见于丑正,亚细亚见于寅正,是可见日之没也。先没于亚细亚之东,后没于欧逻巴之西也。非圆如球者,必不然矣。大率从西而东七千五百里,则应天三十度,而先八刻见食。设地体如案,则天下见食共在一时,无有彼此后先矣。若地体如碗,则远于月之处先得见食,近于月之处反后得见食矣。至若地体如觚,而四方或八棱,则凡在一面者,见食皆同矣,何故。有时刻先后之异乎。非圆而何也。又问地固圆矣,但日月初出,半露地上,圜体切之宜若弧状,今但如弦,何也。曰地球掩日月之半,实自如弧。今见如弦者,因地形掩日月处较全圜甚短,人目视之如直,而实圆也。今设一圜线,其长寻丈
图缺若。截取分寸之长,则不见其曲矣。问地既为圆球,吾措足之地在球面,则所见四旁之地宜皆低也。今见近处觉低,远处反觉高,何也。曰:凡人视物之远近,皆从一直线来入吾目,而人之内司从外司亿之,故视远物出线,似过高于近物
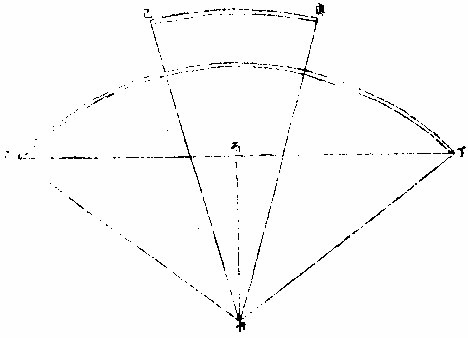
图
出线。
如图甲为人目,乙为远处,丙丁为近处,俱属一平线。乙远出线来甲目似高于丙丁近出者也。如人立长廊中,或长瓮道廊,道两头平正如一,而自此视彼只见其高矣。夫视近尚尔,况地面之远乎。惟据实理察
得之,则知外司之似误矣。
因食徵地海并为圆球第八
航海者,远望他舟之来,未见其舟,先见桅端,须臾渐两相近,则帆樯、头尾、全舟毕见矣。设海面为平,则此舟全体可见,何乃有先后、见不见之殊乎。
几何家正之云:从一点出线至一界,若其线长短若一,则所至界必为圜界之形。今从地心出线至海面,如此则海面果成肖圜界明矣。若弗允其说而谓线有长短,长者,其界更远。而远于心点。短者,其界更近
图
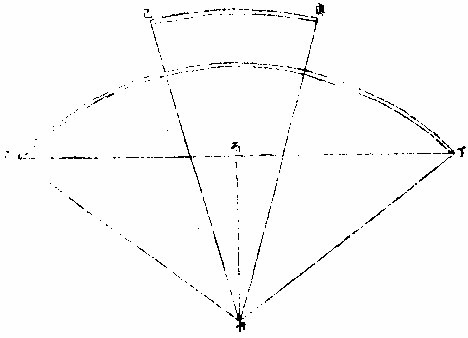
而近于心点。如此则地心出线有长有短,长处之水,独能居高而不下也,岂不逆水之性乎。如上图甲为地心,乙丙丁为水平面。丙近地心而为水低面,丁乙远地心而为水高面。则乙丁之水逆其性而居高,若居己庚处,则更高乎乙丁
水边也。观此可知地与海为圆之證,而其明白显现
者,无过于月食。敝国有人自依西巴尼亚国至墨,是谷国验月食之时刻,则先于依西巴尼亚国两地时刻俱一一较准,故知食有后先。而地与海为圆球,又食时,月内乌影不拘何地,其影必作圆形。而光体未受食处若半规。然以接其乌影,若影为方为扁,则月之乌影安得如圆形哉。若言影圆,而其生影之体为四方八角。种种异形,此犹不通之甚矣。说更详于视法诸书。其言乌影悉随其生影之体而肖之也。问谓影之圆应地体之圆,是已若夫水乃通明之物,不能并地而生影,亦不能并地而为圆形。如何曰:水离地之重浊能有几何,即不同体,宁非连体乎。既水与地为连体,则重浊搅混,岂得通明。而况加以深厚,孰谓水之通明全体而不能生影乎。盖月之食影惟系地影,则海中有岛如瓜哇老冷苏门之等星罗棋布在在有之有,则皆能生种种之影,则射于月体何处分别是水乎。是地乎。
因食知大山不损地圆第九
问客从欧逻巴航海,来于西海,首见分子午之福,岛其邻地有山。说者云:从千五十里之远以见其山脊,或言天下高山,此其首矣。又利未亚中一山名亚兰得其高视之若际天,故名天柱。又额勒济亚中一山名百峦,说者云:其高出于云表此数处有山之高,如此则天下各国岂无有类是者,然大地有此种种。高山则未免有凹凸之状,今言其形若球,不易信也。曰地海并为圆体,其形如球者,非实圆如天球,通光滑泽不洼不突者也。特谓其类天球而少异焉。尔额罗斯德逆尝云:地形如球者,大都肖球之圆,非如工匠车旋器物之浑圆,而毫无凹凸处也。否则山之高谷之深将安所置顿哉。然山谷在地面圆球之上,不过为球面之一点尘埃耳。今视山谷在地面,虽不齐而视月食乌影未尝不圆。若谓山谷与月相望之,一面不能生影,则地球与月相切之一边,岂不能生山谷之影而灭地球圆尖之影哉。今俱不见其圆可知矣。几何家用通光测量等器测亚兰,得百峦二山垂线之高只得千二百五十步,况雨雪时。天下诸高山顶处处皆有积雪,则较之彼所称天柱者,所差又多矣。曾何足损地之圆乎。
今测大地之围九万里矣,则其径应三万里也。以二山之高步化为里数,而以较地之全径,仅为五千七百二十七之一耳。今三倍其高,亦仅为一千七百零八之一。是山谷之高深较地全体之大,直九牛一毛耳。球上些须之点乌,能损大地之圆乎。
因食徵地球在天心第十
前论地球居天中心者,理势不得不然也。盖四行之重浊下坠者,惟地重浊。之反而轻清上凝者,惟天性之两相反而两相去。去之至远者,其惟天心乎。故地之上下四傍,面面皆生民所居,首俱戴天,足俱履地。其首上足下攒,聚皆不离斯是。知地面上之屋宇楼台,地面中之江河湖海,千古安于就下之性。初未尝见其起离地面,而超越于天也。
问天之四傍,恐未必皆是。九十度之高人视四傍之天似下垂而近乎地,又似相接而比乎地矣。且朝暮日月之出没,若出没于地平之近处,则近地平之天。
图缺未必九十度如天顶也。曰欲释此疑,盍验诸月食。夫日月不相望于一直长线之末,则终古不能食也。设地不居天中,而偏近于黄道之上下东西,则食不居半圜黄道之一百八十度矣。如上图甲乙丙丁为黄道,若地不居中心戊而居
图缺己,则日居甲而月至庚即食。然此日月非正居直长线之末相对相望处,其甲丁庚之长未足半圜。与古来测验之准的不易之常法大相背戾矣。若言地居黄道极,但去极不必相等,是又迂阔之甚,盖地影近黄道极,则地影不能与月
相对而掩其光。而月体亦终古不能离黄道而受地影,其能服天下高明之耳目乎。
夫人视地之四边若与天近,与天相接者,尚自有说。盖人从此处以目视,彼远物之界悉凭乎。中间有实体与否,如于地面视天,所见只有天、有地,以中间浑无实体以问之也。则地面之四边与天若近若比此其故矣。今试观林中竹木,或城上旗竿,鱼贯而列,若侧而视之在远者,若相近在近者。反似相远而远近恍惚之不定也。又河之两岸,各有人立。倘在远处视此二人,似觉并立而无远近,亦不能料二人中间尚有河隔。足徵从远视物易于淆乱,而视天何独不然。
因食而知黄道六宫恒在上六宫恒在下第十一
凡习浑仪之说者,即当知黄道之居仪上。随宗动天以运,旋第就黄道之随动。而言固有正斜迟速之不等,所以然者,因其随宗动天之极。而极与黄道之十二宫远近不同故也。又当知黄道之在仪,不拘何度次、何节气,其黄道宫从地面而升,则其所相对之宫由地面而没焉。夫地平与黄道两圜在仪为大圜,凡圜交错分为十字者,实为半圜而举黄道全圜。则半在地面上,半在地面下也。右所言不必胶执一定。即据浑仪审验,亦可窥见月食之大凡。而其故瞭如指掌矣。但食居东西两面方为相当,又见地海全球半居地平上,半居地平下。盖食在东则日居西,食在西则日居东。而日月实相对望于至长、至平线之末,则见日月出线,正当穿过地心,又见日月至地平上,则地球之面居地平之上矣。又见日居东,月居西,正当半乌影。设当此时以通光耳。测器平对日月,则日光正射月体,如此岂不昭然。见日月实居地平线之末,而贯地球于平线之中乎。又见日月及地心并贯于一平直线,如此则自通光耳。窍测影处以去地心,非如一小点乎。且凡有月食,无拘冬夏。天文家正测以日月相去黄道六宫,则明见六宫居上,六宫居下。是又不待食,而然四时恒若此也。第其宫当从地平游移上下,而至于原处地平也。
据月食即知其实本位所第十二
据子午高处,欲求星宿之偏居。原不属地心距度者,即因其偏居处求之,而知其居于黄道之处所,甚易易也。故天文家欲求其准的,详制若干仪象以测验焉。然仪象之巧妙,全在通光之窍。使其射光处有准的,不移动不更改,则是器之用不惟能测地面,足迹所不能至之处,即山岳楼台之高,江湖之阔,地里之远,井谷之深。凡诸种种,悉能测之,极而能测量天之星宿与天之彗孛也。第今用是器以求月之高度,因而知其在黄道之实,本位所惟除地方二十三度内。如广东广西等处不特难,之难且无准的可据,更难于推算也。盖月之始出其高度少则差度多,高度多则差度少。由是则时刻之所在,其差度恒不一。〈阙二字〉以仪象测月要,当取地心之所,方为不谬。今势不能得,不为虚器乎。但器虽有短,心灵无尽,故多罗某及。诸天文各家言细测月食,在于月行。本道进影时不居似处而居实处。则在食甚时,不得不准对乎。日既知其的确处所,则知其本动之行、本行之异。知其顺往则知其逆来,而食之时刻、食之大小、食之方所毕知之矣。
因食而知月有小轮第十三
问月有小轮,何所据乎。抑因其食而證其有乎。曰:天文家究心殚思屡经测验,月食悉见。夫食屡居本圜之极,远其日屡。居本圜一处,则生影不得不尽一也。然食时之分数有多有寡,多则月居影厚处,寡则月居影薄处,必有小轮焉。月体居之因其极,而动时居轮上则去地面,远时居轮下则去地面。近如后图所载。云:问月既有小轮如五星者,则其停居顺行退行
图缺亦宜,若五星然。今独未见,何也。曰夫月行随其本圜之疾,故不言其停居退行。只言其行速行迟也。速者,因其居小轮下,随本圜之动自西而东。迟者因其居小轮上,随其自动自东而西,逆本圜之自西而东故也。
问月体既居小轮,随轮而动,则无本动。若论其体之圆,则宜自能动,何如。曰:有谓月中影象,是地体厚处所映者,谓月体通光处。日光射而达之不得返照者,又谓月体中。自有高卑如山谷者,种种异说。然此影象恒俯对地面,而人恒仰见之不侧不移,则月体有本动明矣。其动因乎本极而逆乎小轮,行之迅速与小轮并速也。影象之明恒下垂之,安得谓月轮无本动乎。
因食而知日有不同心圜第十四
图缺问日食有或全食,经候多而见食多处者;或全食而经候不多而食不在多方者,其故何也。曰:天文家正㨿此以验日,有不同心圜,不然何其食同而经候不同。掩地面之广狭不同也。可见日月俱有不同心圜,而居不同心圜之上下,则
为去地之远近,生影之大小也。今有一光明之体照
一不通光之小物,两体相近则明体照。物体之大分而生影小,两体相远则明体照。实体之小分而生影大,此见日食全而大者,则日体必远乎。月体日食全而小者,日体必近乎。月体明矣,倘日月无不同心,圜之极而以地心为心。则其东西行动,必规随夫地心,何有远近之殊耶。丁先生者,大西高明之士,尤长于天学。亲见两日食之异,其一于耶稣降生一千五百六十年,在哥应巴府见月掩日,白昼如夜,星宿照然。其一于一千五百六十七年,居罗玛都。时见月居日前,当中掩之而未全,蔽月边四围,皆有日光,即此二食知日月去地面有远近,而日必有不同心圜也。
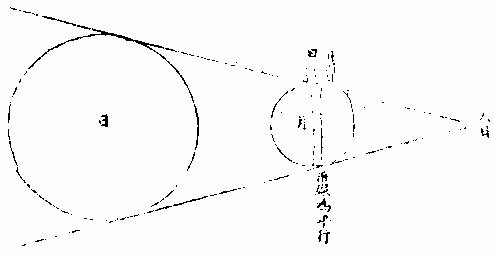
因食而知日月地大小之别第十五
问日体甚大于月与地,何徵。曰:昔有人叹世人止凭肉眼,不求物理。尝设喻曰:日出地时,设有骏马疾驰从日始,露至全现。亦可驰四里,纵令日行与马等速,则四里而仅见其全,则全体之径亦必四里矣。今骏马一昼夜所驰于地几何。最速不过全围百分之一也。而太阳日一周焉,则其行之疾莫拟也。是则马之四里日之行,几千万里矣。日体之大即此微可知也。且日月体之大小,即食可辨。盖凡物之有形象者,若空中无所障碍,则其体之全体之分,无不出其本象。于一直线而至乎界之一点,此凡物皆然。不拘方圆棱角等形,如有物体,于此其基址,即物体也。其界点则线之,锐角所至,而入人目者也。凡实体出锐角影者,照体必大乎。实体否,则其光不能照实体之全面。而使对面锐影之尽处,仍聚合而有光也。今欲验日大乎月,可视日食。月居日前,而掩其光,是时日边尚有光,是日体在外。而其象之入人目,非近来自月体,乃远来自日体也。其线既为角形,则从月体至日体更为广大,是其角形之锐从日来。目为一点,而中间能包月体有馀,则日体之大于月体,复奚疑哉。今欲知日体大乎地者,观诸月食可知月之食地居日前。而生角影掩月体也。当月食时,月体近乎地,则入阔影远乎地,则入锐影愈远愈锐。以聚于一点,若此者孰不信日体之大于地体也。设谓日体与地体均,则地影大小均,为无穷尽之等影。若言地体大乎日体,则地影必益远益大,为无穷尽之大影。其影既远,不独食诸天之星,必且食诸星之天矣。则每遇望时,月体讵能逸于大影之外乎。由此益信月体之小乎地球也。盖地影益远益锐,而月食居此影或有全而久者,则月径更小于影。而影小于地,故月体地球之大小从可知矣。
因食而知各地之子午第十六
多罗某者,天文家之宗匠也。其所定子午法,诸子皆宗之当时。欲定各国各府之子午以便测验,乃先定福岛以为西极。而此外因海弗论也。职方氏谓心亿不如足至多,罗某生平足履虽未遍地,而垂法之妙足踰百家矣。厥后,诸天文家自涉多方,目测多食,益精其遗法之妙而职方图志,益广其传焉。今欲求经度之准的,东西之远近,法莫善乎。考两地之月食,以此方之时刻与彼方之时刻相较,视所差几何即知两地相去几何度矣。假如癸亥年九月望应月食京师及邻近地,初食在酉初二十七分,食甚在戌,初五分,复圆在戌正四十三分,此中国之食,候也。若在西洋,则初食在巳正四十二分,食甚在午正十五分,复圆在未初四十八分,其差得三时零二刻半。则知中国去西洋之度,东西相距一百一度十五分。可见凡两处月食之先后,即能测两处道里之远近矣。然既确识东西之经度,即以西洋所定测算立成。举而按之,用力省而获便多矣。前癸亥九月望月食,若望承命以西洋法测算,是岁若望初来都中未尝测本地之食,莫得其经度,不敢轻任嗣。后复蒙严督因以先寓广东时,所测一次月食之经度。又用诸仪器较量知京师更东,凡三度强,于时刻应先十二分。离西洋中心勿尼济亚国,东西一百一度十五分。据法推算分秒时刻幸不少爽,甲子二月望,及本年八月望两度月食,承命推算,幸亦无爽。今乙丑岁又当月食,复蒙命推算,敢不祇承。谨据西法测验,一一条列于左,倘有讹谬,则拙算之未至,非成法之有讹也。诸食图具后
癸亥九月月食图缺
初食,月距躔道四十分强。
食甚距躔道三十六分,复
圆距躔道三十一分半,初
食酉初二十七分食,甚戌
初五分复圆戌正四十三
分,初食至复圆共一时五
刻,食甚入影四十分八秒
甲子三月月食图缺
初食月,距躔道六分强,食
甚距躔道十二分弱。复圆
距躔道十七分半,初食子
初三刻六分食尽子正三
刻十三分食,甚丑初三刻
三分,初复丑正二刻九分,
复圆寅初三刻,食全不见
月光共六刻十分。初食至
复圆共一时七刻九分食
甚入影十八分。
初食月距躔北十六秒,食甚距
躔道南五分二十六秒。复圆距
躔道九分二十八秒,初食丑初
二刻六分二十七秒,食尽丑正
甲子八月月食图缺
二刻十分二十七秒。食甚寅初
二刻四分三十九秒,初复寅正
一刻十三分五十一秒,复圆卯
初二刻二分五十一秒,初食至
复圆共一时七刻十一分二十
四秒,食甚入影二十分二十秒
乙丑八月月食图缺
初食月距躔道四十五分
五十五秒,食甚距躔道四
十八分二十二秒,复圆距
躔道五十三分三十一秒。
初食酉初四分三十六秒,
食甚酉正二十分二十秒,
复圆戌初三十六分四秒。
初食至复圆共十刻一分
二十八秒,食甚入影五分
二十二秒。
此图黑圜面,是地影圜面。东西过心一直线,是躔道甲乙线,是月行道甲圜,是月初食丙圜,是月食甚乙圜,是月复圆。然当知天体浑圆,而图为平面画图终不能得天之似,故玩图必须仰观,而以南北字面一一对如其方向,则甲月自西来,入地影肖厥天象矣。
食不言徵应第十七
前数则不过粗言其要而已。每有叩,若望以徵应者,因喻之曰星宿各有情好也。若性情之乾热者,相聚地必暑寒,湿者相聚地必冷。彗星,彩霞火属也。而相值荧惑之星,则地之乾燥也亦必矣。若此之类,理势必然。推验不谬者,岂有日月之食,宫次不一而毫无所徵应乎。第人过信其必然之理,遂泥其己然之迹。不事探求其所谓自然者,又不精求其所以使之自然者,其道未易言也。故先师多罗,某精于斯业尝曰:斯业之言,非一定之法。可永守而不变者,若望晚学也。法师以不言为言,而妄言徵应能无骇乎。〈以上原本卷下〉
皇清
《新法历引》测太阳
诸曜森罗太阳,其宗主也。或推或测,必首太阳。顾其应测之行,不外三种:一曰盈缩之限,一曰盈缩细行。一曰盈初,缩末之所,中历之测,太阳未尝及此三行,即所测止冬夏二至,犹未尽善也。其法立八尺表,用景符器于冬至前后三四日,测定三景。因以三景之较数,求太阳到冬至时刻,其法未尝不是。所以为未尽善者,盖表景短长乃太阳行南行北所生。论其近二至之候、南北之行极微,计一日所行,天度有分半者,有一分者,有半分者,乃于冬至近期建表寻丈,而其所得二景差为一分二釐。〈量度则云分秒量景则云丈尺分釐〉釐为八刻,而此一二釐间相差甚微。彼景符曷能定之,况景符。光线恒占数釐,或更稍为进退,其失弥甚是,恒差数十刻也。若测夏至,则倍难矣。今新法用八线表法查古所遗之数,以用于推步,庶称密近耳。然又不但用表,亦时用别法以相济也。比如春秋二分,太阳之南北行较大。日行天度二十四分,乃于其前后数日先测极出地度,得赤道高。次用象限仪测日轨高,不免相差一分。而其于本算,日轨入交点时刻则约差四刻耳。较之以寻丈,表测冬至差釐数而乖违。数十刻者,岂不大相远哉。且新法于太阳实躔宫度分秒,逐日可测。而旧法于二至外推步,遂穷何也。又新法本测曰:太阳从春分底立夏行黄道四十五度,历四十六日十刻十分。又从立秋底秋分亦四十五度,而所历则四十六日三十八刻十分。是逐日刻数不等,所谓春行盈、秋行缩也。故定此盈缩,初末之界非在二至点也,乃在二至之后六度,〈古今不同〉若如旧法谓:恒在二至,则是前后行度等也。何为所历之期日刻数不等乎。此率古称盈末缩初,新法称为最高因有此最高,遂晰太阳之行为一不同心规也。其行迟者,在最高行疾者,在最高之冲。此最高本行亦犹太阴之有月孛云。
测恒星
测星之法不一,大要以太阳为主,而以太阴或太白或岁星为中次。任取某星为界,互相测度即得其度法。于太阳将入之时,测月或太白、或岁星,其距太阳度分若干。日既没,再测月或太白、或岁星,其与某星相距度分若干。合两测即得太阳与此星之距。然后查太阳本日躔某宫度,则知此星所在宫度矣。测一星之经度如此,他星可以类推于是。又测此星出地平之最高,即其距极,距赤道之纬度,并可得也。然而恒星之经纬度分有二:其一以黄极为枢,每岁东行五十一秒有奇,而其距本极之纬度,则亘古无变。其一则因赤道以算,其经纬南北星位古今大异。如尧时,外屏星全座在赤道南,今则在北角宿古在北者,今亦在南星纬变易类多。如此至以赤道论,各宿距度亦有异者,如觜宿距星上古为三度。历代递减今,且侵入参宿二十四分。他宿互有损益,距度各各不同。因知赤极非恒星之极,而其经纬之度,亦非赤道之经纬度分也。由是观之,象数精微,弥测弥明。彼自画者,流辄谓循古已足,岂其然哉。测太阴
太阴行度所当测定者五:一迟疾之限,一迟疾初末一月孛行,一每日细行,一交行,五测有一不详。月离之违合难齐矣。又月有气差、时差。〈即地半径所生〉所测之经纬度分,于正度分复有相较。以此测月于七政,中为最难。旧历用表于午正,测定三景以求之。越四载而得一次,测验之时九载而复推定,疑太拙矣。新法用三会食,推算其法:以食甚正对太阳得月经度,以食甚分秒得距交若干,以各食中积,时日刻数不等,并得天上所行不等,度分于是用本法以求。月天之孛或最高。〈即极迟之行〉亦遂得平视二行相较之度,以简御繁,法莫善于此矣。其测上下二弦经度亦有本法。盖弦乃太阴,实距太阳或东或西九十度,即周天四分之一也。先以本仪测定某限次,用法算其平行,因其加分恒于所测差二度馀,赖有二三均数测算乃合。又弦时去离南北所测与算亦较天度差四分之一。缘白道斜交黄道,相距度分各广狭不同故也。至太阴之掩恒星测其出入,亦可以知月离度分,但须先以地半径差均之。测五纬
上三星为土木火,与太阳相冲会。然于冲会之二时各无岁,行加减分缘其会,太阳即在岁行圈之最高,而冲之即在其最卑,于实行为合故也。须知实行与平行不同,平行百千万年维均,各星本天各有迟疾。〈即最高最卑〉然而星合太阳无从可测每于其冲测之。〈测其对太阳用恒星各经度或太阳跨度推算〉得此冲经度,即有中积天度日数。及本星随日数之平行,而后用此三率以求各星,本天最高之所于是。又得其盈缩大差,因并得冲时各星以平行距冬至之界若干矣。下二星为金水,以其不能冲太阳也,测之较难。法先于或晨、或昏,求其与太阳距度者数次,然后依法测算,即可得其本天诸情也。凡岁行之测以二留,为本二留之限各星不同,即所躔天度亦不同。然而星在二留非冲太阳,乃折中之度。故本之以测岁行也,下三星亦然。又二留之际,因无岁圈纬度,故可得其本天之纬。其或在日之冲,距纬极远,又可得岁圈之本纬矣。五星之天皆斜交黄道,与白道同。但其相距之纬各多寡不等。又白道交行右旋,而五星左旋,此其异也。时晷凡日月交食,会合五星凌历,犯守其时刻。所由取准者,赖有时晷也。然而大地之广时,非合一古法不分。方土第用时,牌揆景以定者,非也。新法制晷,但须预定。本方北极出地之度,随在随处。虽垣墙正侧,皆可制造能于一晷之面,视太阳所躔节气宫次,度分及定日之高度。并黄道各时,出没其称最者,则地平晷立。晷百游晷通光晷数种他,若柱晷瓦、晷碗、晷十字、晷等不下。数十馀种,而此外又有星晷与测月之器以为夜中测时之需云:若遇阴雨,则又有自鸣钟沙水等漏之,制水漏与古壶漏异。古或以〈阙四字〉时箭浮新制,以水出壶而时牌转壶,体并不开孔似为胜之。
《新法表异》测算异古
天气浑圆,其面与诸道相割,所生三弧形不一而足。乃古法测天,惟以句股为本,用平立定三差,总是平形,岂能测圆又句与股交为直角。一遇斜角,其法立穷。新法测以天弧,三角形算以割圆八线表,是为以圆齐圆,遇直遇斜,无往不合。且其用甚大,其法甚简,弧矢诸线乘除一次即得。非若句股,必须展转商求,累时方成一率也。