声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
钦定古今图书集成历象汇编历法典
第八十六卷目录
仪象部汇考四
新法历书二〈浑天仪说二〉
新法历书二〈浑天仪说二〉
历法典第八十六卷
仪象部汇考四
《新法历书二》浑天仪说二
前以天行之效显仪之理,此复依天行之法晰仪之用。大端以求三曜,〈日、月、星〉为要领矣。至分论之,或依本行与黄赤二道相较,彼此得经纬度。或依宗动之行与地平天顶及子午等圈相较,求诸曜出没之时。又或依方位、地平、高度彼此相较求星距太阳远近,与出没之先后伏见之期限。总于本仪得全用焉。但恒星距黄道内外甚远,不能尽载圈上,又或光色微渺,未足测景,〈以景定度测时〉则自有天球之实仪在,借之以资本用,虽虚实两仪,大意相同。而推之亦略有异。此所以并论天球也。即本卷诸用尚多缺略,然欲求其难当自其易者,始欲求其烦当自其简者。始则从兹而详,及之姑以俟之他篇。安仪
凡测天诸仪有黄、赤道等圈,必以本圈正合天上所有之圈为准。如在天有过顶者,仪中相当圈宜竖立以应之,有距顶向南、北、东、西者,仪中相当之圈亦宜向南、北、或东西地平,皆与天上之圈合。则日月诸星行度为仪圈所得者,即天上诸曜实行之度分也。今浑仪虽未尽乎测天,然能以日景考查时刻,并求各方北极出地之度,及太阳高弧距地平等,用则必一切方位与天吻合。先以两极依出地度安定,徐以罗针所得,正其南北,又以垂线取准地平,任置台几之上,以听次第用焉。
求北极出地度
北极高、庳随地东、西,同南、北不一。此乃昼夜长短、寒暑异同。日月诸曜距天顶远近之所繇也。法先将本仪取准地平,考正南、北,随以游表于黄道上,定住太阳本日躔度,转仪切子午圈正面,候太阳当正午之时视表,周无景即本北极高度已定,而极高之度必为子午圈自地平至极中之弧也。若表尚射景,渐运子午圈于架内,或上、或下,展转那移,至表无景乃止。而因以得北极出地之度。
或先设象限等器于正午时,测定太阳出地平高度,次于本仪黄道上查取本日太阳躔度。置子午圈正面下随运仪,令自地平至躔度间子午圈之弧与前所测之度等。则自北极至地平度分即本北极出地度分,或不候午正即将游表,置太阳本躔度与时盘午正初刻正对子午圈,后用日晷等器测定时刻,以所得时转仪,令居子午圈下,后视表无景,〈如射景将子午圈上下那移无景乃止〉则子午圈自地平至极中之弧亦准,可得本北极高度。
或以星求之。即近极诸星中,〈因恒不没〉任测一星。先于最庳处识所测高度,待旋至最高处复测之,所得高度加前测之度,总而半之,为本北极高度。此常法也。今不拘出没,或距极远近之星,一测其至天中之高,〈另用一器〉即转球,〈天球〉令本星居子午圈下,较仪上地平与前所测等,则本仪北极亦自距地平为弧,因得本方北极高度,或依所测天中星高度,即球上查其本星之赤道纬,以加〈距南用加〉减〈距北用减〉于至中之高度,得本赤道高。因得本北极高度。如测大角高七十一度,球上查纬得距北二十一度,宜高度内减之,〈因距北故〉存五十度为赤道高。应四十度为顺天府北极出地高度。
求太阳躔度
太阳依黄道右旋,每日约行一度谓之躔度。法先依本北极出地高,令地平与子午圈如法安置,候午正初刻,将游表以直角切子午圈,上下试之,遇表无射景,乃止转仪。视黄道正居表下之度,即太阳本日所躔度。
又一法。用象限等仪测太阳距赤道度,因得其距南、或北随于本仪子午圈上点定作识。乃令全仪运转,视黄道度正交其点,即本日太阳躔度。但距赤道等度,与子午圈相交之点,黄道可有二处。必依昼渐长、或短,求之,即得其度在冬夏至之前、或后也。假如崇祯七年七月初八日壬申,历局午正,测得太阳高六十八度一十五分,因得距赤道北一十八度一十分,
北极高三十九度五十五分,即赤道高五十度○五分。
依之作识得大梁宫二十一度,或鹑火宫九度,俱与所识点相交,第此时夏至已过,昼渐短,即知所得必为鹑火宫度。
求恒星黄道经纬度
恒星较黄道有经、有纬,而共以黄极为主,必依黄道右行,任从冬至、或春分起算为之经,本道南北为纬法。以高弧切球上,使从黄极过星所至经度即本星之黄经度。所居黄道上及星间之弧即黄纬度。但星距北必高弧安之黄北极星,距南高弧亦安黄南极。如贯索大星。距黄道北以高弧从黄北极过本星,视至大火宫六度有奇,即贯索大星之黄经度。又自黄道北至本星处约得四十四度三十分,即其黄纬度也。若先得星黄经纬度,欲查球上星所当在之处。亦用高弧。依球上本星黄经度,因之安高弧初度,令末度至黄极中,〈黄极南北依星距南或北〉任黄道内外顺高弧数星纬度所止之点,即星居球上之处。假如崇祯元年测定心宿中星在黄道析木宫四度三十六分,距南四度二十七分,依此度分安高弧至南黄极,从球上黄道数起,得本距度之限即心宿中星所居之处。
求太阳赤经纬
太阳依黄道行近,考定冬、夏二至距赤道南北最远之处为二十三度三十一分三十秒。迨二至前后每日相距不等,而二道又以斜交惟分至之点,彼此得同经馀,俱不得合一也。今求纬度法。令本仪转,任取黄道若干度,正合子午圈下,即于本子午圈视两道间所容之弧得数即黄赤相距之纬也。求经度。亦任取春分或冬至起算,视黄道度在子午圈为限顺数,其赤道圈之度即黄道上之赤经度。若依地平求之,必先安仪使两极与本地平齐。即用地平当子午圈,则赤经弧必过赤极与赤道以直角相交,而东西所限赤纬弧亦为本圈南北所量。虽子午圈本当过极诸圈与赤道正球相交,而地平与正球亦不异。是故所指度分即得赤道经纬度分。
求恒星赤经纬
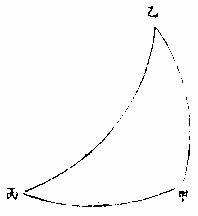
法以赤极为准,必顺十二宫为经,赤道南北为纬。先转其球以所求星切子午圈下,后视赤道是何度分,此即本星赤经度。又视赤道与星在子午圈上,所开之弧容何度分,乃其星之赤纬度。如设狼星居子午圈,得本圈下赤道度自夏至起,算约七度三十分即狼星赤经度分又赤道南距狼星一十六度乃即本星之赤纬度。求五星赤经纬法与同。但先以黄经纬点星于球上如法,使高弧自黄极中至黄道本经度过星处,即依高弧之黄纬点球作识,后转球,令其点合子午圈亦可得赤经纬也。若先算定恒星赤经纬于球上,考其处,即从春分依赤道顺查星经度,移至子午圈下,乃本圈上南、或北,〈依星距〉查其纬度用点作识,即其星所居之处也。如崇祯元年心宿中星,得赤经二百四十一度四十三分,以本度分转球至子午圈,因星纬度距南二十五度三十分,随以此度正对子午圈下作
 ,必指其本星之实处。
,必指其本星之实处。求黄道每度赤道纬
法任取黄道何度,移置子午圈正面,即从黄道中线至赤道上视本圈,所得若干度为黄道度之赤道纬。〈南或北依所求点得所距〉若从北极起算,亦于子午圈从极数至所求之点亦是。如求清明初度纬,得其距赤道北约五度,距北极八十五度,寒露初度距赤道南约五度,距北极九十五度馀,俱仿此。
求黄道各弧出没之时
黄道上出没较赤道圈之出没恒异。盖赤道等弧,或正球、斜球。
南、北两极并在地平为正球,一极出地平上,一极入地平下为斜球。
所应出入之时恒如一。黄道不然,遇正出或迟斜出反速,每日早晚先后不等,随地有变。试以最长之昼其见出止六宫,最短之昼亦为六宫。如太阳在鹑首初度,〈昼长时〉任北极高若干,使本度切仪,东地平渐转至正午,必见寿星初度东出矣。复转至西地平,即星纪初度东出总得黄道半圈为其所出没也。又如太阳躔星纪初度,〈昼短时〉本仪东地平转至正午为降娄初度,东出至本躔度,西入则东出者必鹑首初度本等。自早至晚亦得半圈,是黄道与地平皆大圈,相交必各平分故耳。法用赤道圈之度,或十五三十四,十五多寡,等弧以限定时刻,为黄道所同出入,则黄道不拘大小弧,总在其时内行者为是。假如北极高四十度,依本地求降娄全宫之升度应时若干。先以其初度在东地平,因并得赤道初升度。〈二道相交为春分,即各升度之初界。〉转仪使出至本宫末度,即见东地平,指赤道上一十八度强化为时,约得四刻一十二分,即降娄宫全升之时也。又求其入地平时,亦以本初度切西地平。试令本宫之度尽入,得赤道同入之弧为三十七度四十馀分,化为时得十刻有奇。即本宫全入之时,与先所升之时大相悬远。欲用时盘求之,即其初度之或出、或入,视子午圈所指何时。转仪至全宫之出入已尽,复视时盘与子午圈正切者,得时刻前后差若干。即黄道出入之总时矣。
因以度数变为时,而即以时变度数法。总度分秒各数以四相乘,所得为次行时之小数。如乘度得时之分,乘分得时之秒。试以一十六度二十分化为时,以度乘四得六十四分,以二十分乘四得八十秒,总为一时○五分二十秒。又总时分秒各数以四相除,所存为次行度之大数。故以时之微得度之秒,以秒得分,以分得度,以时得六十度之弧。因之推表,或度在初行可当分,亦可当秒。则时分秒在次行,以度数变为时数,或时在初行度,次之则以分秒微在初行度分秒,俱在后行,以时数反变为度数,若查表总数,初行不尽,即取其近小者,以馀数再查之,故列表如左:
<h3 id="度数变为时表〈此下以时反复查度数〉" style="text-align: center">度数变为时表〈此下以时反复查度数〉缺求两星出没之距时
凡两星在赤经度上同出没者,此正球也。斜球不然。盖距赤道北,其较赤道同度之星必先出后没,距南者反是。故求星出没之距时,惟以定其斜升度为先,法依本北极高安球,任取一星居东地平,并识赤道同居之度即本星斜升度,〈或从春分、或从冬至起算其法一〉复取一星亦如前,查其斜升度,乃以后得数受减前得之数,若不足减,则借全周减之馀赤道弧为二星东出其间相距之弧,化为时,即二星前后之距时也。求星之西入亦然。假如北极高四十度,移毕宿大星于东地平,得赤道同出为四十九度三十分,即本星依本地斜升度与井宿距星相较,亦令其居东地平得赤道同出为七十度,以减前度馀二十度三十分,为二星相较之弧,化时得五刻半,为二星东出之距时。若星入时,求法同,所得距时异。如毕宿大星至西地平得赤道同入为七十八度三十分,其井宿距星同入之赤道度为一百一十一度三十分,相减馀三十三度,乃得八刻一十二分,为二星西入之距时。
求星出没与在地平上之时
论恒星之出没难以定时者,繇太阳与之远近逐日不一,而在地平上之总时则百馀年后其本行渐变,其赤纬而时亦与之不同矣。若五星出没随太阳本行亦无定,而在地平上之时则因本行恒出赤道内外亦因之有异。法依本北极高安球,将太阳本躔度与时盘午正初刻正切子午圈,下次转球,任取一星居东地平,即于时盘得其星出之时刻,复转球,令其星至西地平,亦如前得其星入之时刻,通计前后,因得其在地平之总时,或欲密求应依赤道度法。以本日躔度,切子午圈下并识同居圈下之赤道度,次转球,令星至各地平,〈东或西〉复视此时赤道交子午圈之度为何度,两赤道度以后得数受减前数,不足借全周,减之馀为星出没之度,变之,即得若干时刻。假如北极高四十度,夏至日,求毕宿大星出没之时。依法鹑首初度在子午圈,并得赤道度为九十度,移本星至东地平,即赤道三百二十度,居子午圈以减前九十度馀二百三十度,化得一十五时〈小时〉二十分,即寅初一刻○五分。〈午正起算〉为夏至日毕宿大星之东出也,又移本星于西地平,得赤道在子午圈为一百六十九度,减前九十度,馀七十九度,化得五时一十六分,即酉初一刻○一分,为本日毕宿大星之西入。第此法亦就恒星近日之本行为然也。若执此以求前后数十年或数百年,则因其本行有变与,太阳相较必不能合其出没亦必自异,大率百年中依黄道行约差一度三十五分,每年差五十一秒,恒依此数前减后加,则得其正矣。论五星其在地平上之时,必先依本经纬度识之球上,而后可以如法查取与前同。
求黄道升降度
黄道每度分出入所得赤道在地平度分同出入者,谓之升降度。法转仪,任黄道某度在东地平,得同居东地平之赤道度,即其升度。又本黄道度在西地平得同居西地平之赤道度,即其降度。然惟正球不异于赤经度,而斜球则异,愈斜则二道之度其差愈远。如实沈初度距春分六十度,试令正球在东地平,得赤道同居约五十八度,如以斜球使北极高三十度,得赤道同居约四十七度,北极高四十度,赤道止居地平四十一度,此皆斜球中实沈初度之升度也。是赤道较黄道恒少,如北极高三十度,得赤道与实沈初度之同入约七十度,北极高四十度,则赤道同入约七十五度,此其斜球之降度,是赤道较黄道反多也。至欲以赤道升降度反查黄道同出入之度,法同此。
求黄道见与不见之弧
依北极出地异同,故黄道随处有先后全见或恒见与恒不见之弧。因太阳左行,遂以出入分昼夜,此常法也。然亦有出而不入,入而不出之时,何也。北极高度较二道相距最远之馀弧,〈二道相距二十三度半,馀弧为六十六度有奇〉或小或大、或等不同。小则黄道诸度每日尽为出入,无恒见与恒不见之弧。而昼夜并得满二十四小时。若极高与二道相距之馀弧等,即天顶距极与二道相距亦等。必其天旋行能令冬夏二至与地平齐。故太阳在夏至之日常不入得昼长二十四小时而无夜,太阳在冬至之日常不出必夜长二十四小时而无昼。设北极高弧大于二道相距之馀弧,即极与天顶近,夏至左右之弧,黄道常随天旋不入,冬至左右之弧黄道常随天旋不出,则得恒见与恒不见之弧。而本地昼夜长短,每至数月。试令本仪北极高七十五度,则见黄道自大梁宫一十度至鹑火宫二十度为恒见不入之弧。太阳此间依宗动行,虽数十次,周天恒昼无夜,又自大火宫一十度至元枵宫二十度为恒不见之弧,太阳此间行数十次,周天长夜无昼。但太阳近地平时每为蒙气中映之,使起入得地迟出反得速,宜以加减均之乃可。〈见日躔历指〉
求星当见之时
依北极出地高,各方有恒见恒不见之星。盖近北极星常在地平上,而近南极星则又在地平下,此定理也。惟往往出没诸星,每较太阳远近以为隐见之限。今欲求其见在何时,并其时刻若干,则如法。安球〈依本极高〉任取一星至东地平,并识其黄道同居地平度,复查太阳本躔度,因其距之远近定本星之出见。假如毕宿大星在东地平,因得黄道之实沈十度,同出其西没必为析木十度矣。设使日躔在实沈十度,即本星晓出昏入,通不可见。设析木十度为躔度,则本星反昏出晓入,终夜恒见矣。故求其当见之时,必先以躔度与时盘午正相对,随查星之大小等第。〈凡六等〉以定其距日光若干为见不见之限乃准。如毕宿大星为第一等,距日光〈距日光与距日不同〉十度,其见限也。设太阳躔鹑首初度北极高四十度,令本度正对时盘午正得本星出地平为寅初初刻,渐转球,至太阳将近地平,其未出约差十度,〈以正对星纪初度未入前尚高十度可考〉得寅初一刻,此后不复见星矣。则本日得见毕宿大星者仅一刻。又设日躔在鹑首十五度,距本星更远,依法转球,得本星东出为丑正初刻。至太阳近地平,其不见星之时为寅初二刻。总计见时约六刻,或太阳去之愈远,其见时愈多,渐可一夜恒见也。
求日月诸曜出没之广
赤道交地平之处为正东、正西,而从此左右之地平则限诸曜出没之广者也。法依极高安仪以太阳诸曜至地平相交之处为号限弧,即在东或西,可得出没之广。假如太阳躔实沈十五度,北极高四十度,转仪令十五度至地平,得偏北二十九度,强东西皆同此。即本度依本地太阳出没之广也。盖广弧大小不一,其缘有二:一缘黄道斜交赤道。因相交之点前后愈远,必得本弧愈大;一缘地平所得有正球、斜球,〈正斜球解见前〉因正即广弧小,因斜即广弧大,而愈斜愈大。如北极高二十度,得鹑首初度出没广二十四度,极高四十度,得鹑首初度出没广三十一度,使极高五十度,即本度广三十七度,此皆斜球也。若正球则本度出没之广大概不外二道相距之弧。
以出没之广,求本黄道度及北极高度
夫出没之广,或以测得,或任设若干度,而以之求本黄道度。法先定度于地平圈,依其在正东、西之距南或北,令本仪以黄道之中线正交其度,乃识黄道何度。即本黄道出没之广之度也。欲求北极高度,亦先于地平圈,查本出没之广所得度。用点作识,遂令仪转,使本太阳躔度正交本地平度。盖必相交,然后仪上之极高正合天上之极高,否则将子午圈低昂试之,必躔度与地平所识度吻合乃止。
求太阳地平经度
凡圈有经纬者,必以纵距为经,横距为纬。若诸曜不正行于圈下,即随其距等之圈可当经行。今诸曜较地平以高度相距得纬,而最距之极即天顶以南北距得经。而初界在正东、正西,末界在正南、正北。虽诸曜出离地平,而经度仍归之法。如黄道上太阳本躔度未有高度,必令之至地平,因求地平经度与求出没之广同。设太阳距地平有高度,则依前法,求高度若干。以高弧过其度,下至地平,即限其地平经度或在东西之南,若北,如北极高四十度,日躔在实沈初度,设本度在西,地平高五十度,以高弧过之,得其至地平距正西南约二十三度,即实沈初度。依本高度及极高之西,地平经度也。若依时刻考之,先以本躔度正对午正,随转仪,令所得时切子午圈下,乃以高弧过其躔度,如前,查地平经度,假令前得二十三度,今以申初初刻,求之所得复同。
求太阳出地平高度
日月诸曜东升渐至天中,所得高度不独前后时有异。即前后等,逐日相较亦皆异者,乃其依黄道行,去赤道内外远近恒不一故也。法以本仪黄道上,本躔度正切子午圈下,其正切之处至地平圈即得太阳午正初刻之高。因视赤道此时交东地平度,依所得度东入十五度,随将高弧过本躔度下至地平圈,而高弧所载度分,即太阳午初初刻之高度。若以前度出十五度,必高弧过本躔度至西地平,显太阳未初初刻之高馀时俱仿此。欲逐刻求之,即以三度四十五分出入赤道为准。盖躔度之交地平距午前后等,得高度亦等。假如北极高四十度,日躔为鹑首初度,移居子午圈得其距地平约高七十三度半,此时则秋分。初度交东地平使依赤道入三十度,即巳正,而高弧过躔度至地平为五十七度三十馀分,乃太阳在巳正之高度,或出三十度,即未正。而躔度西距地平所得高度亦五十七度三十馀分。设太阳躔星纪初度以本度居子午圈,得其地平高二十六度三十分,乃春分。初度在东地平,使入三十度为巳正,测得高度二十三度四十分,转仪往西,如前出三十度,得未正高度相等。若用时盘求之免,查赤道度,必先以盘上午正及躔度,如法居子午圈,任仪左右转,至本时交子午圈亦如前,得高度矣。或更以日景求高度与求时刻无异。〈见后段〉但遇表无景处,即过高弧以定日高焉。
用浑仪成高弧表
凡制长圆地平象限等,日晷界时刻及节气线,必依高弧得所以然。法依本北极高正仪,随将黄道上本节气躔度,使之从子午圈或左或右任取一刻或四刻为限,而每限必与高弧相交,因得太阳在某节气某日某时刻,高度若干,其时刻在午正前后等者,得高度亦等。故求其左不必复求其右。试以夏至初度北极高四十度,得其午正高七十三度三十分,未初高六十九度一十二分,未正五十九度五十一分,戌初高四度一十五分,午前及他节气俱仿此。但距两至等,得同时高度亦等。如芒种与小暑、小满与大暑、甚至大雪与小寒之类是也。因极高四十度列表如左:
图缺求恒星地平经纬度
恒星较地平经纬与太阳地平经纬不异。俱以南北得经,高度得纬。法先依极高安球,随以太阳躔度移居子午圈,并与时盘午正吻合。任取某时刻于盘上,以之正对子午圈,后令高弧与所求星相交,即得球上本星本时所向方位,及所距地平远近之度。如北极高四十度,太阳躔星纪初度,如法正对时盘,设寅初,求角。宿南星之地平经纬,乃以盘上寅初初刻对子午圈,以高弧过其星得交度一十七度,为本星当时之高度。即本地平纬也。因而高弧偏东南二十七度为本星方位。即本地平经也。复依此视球上方位得氐宿东出五车,偏西轩辕距午略东,俱一、一与天上相应。即更以象限等器测星之高,用高弧试于球上,鲜有不合者,则虽大象、森罗,而此器殆最为彰著者矣。
求星前后合伏之时
诸星会合太阳前后,伏见必依其体之大小,而本行迟速则又须时多寡不一。盖体大易显,虽近太阳,亦得见体小,必距太阳远。始见稍近,即伏矣。远近约有定限,如土星,限一十一度,木星十度,火与水十一度有半,金星五度,至恒星则依六等定限,约为十度。十二度、十四、十五、十六、及十七度。此外最小者惟暗乃见,而最大者即更近亦得见矣。论迟疾,因五纬右旋各有顺行、退行之异,伏见难以时限,而恒星则共一本行,独以形体分别其见伏之时耳。若依黄道以星与太阳相距定合伏,则误也。盖黄道升降有斜、正,能变其星见之时,虽设距度同,其见时必异。故正球出没之星自不等于斜球出没之星也。法先于球上任取一星,使之交西地平,后以高弧为定则,必在东地平上量星距日之限,令本限交黄道度所得之数,即星在西夕伏之度也。如使星交东地平,安高弧于西,量星距日限至黄道上所得交度,即星在东晨见度也。总以太阳日行分,依前后度为限,遂得各星合伏不见之期。如设毕宿大星距太阳十度应伏,试令北极高四十度,以黄道度相距,因本星黄经约在实沈五度,宜太阳躔大梁二十五度,即星夕伏,而今不然也。必太阳在大梁十四度,星即不见,何也。使本星交西地平高弧在东以十度,交黄道得正对大梁者,为大火宫十四度,是大梁十四度,星伏黄道上,毕宿大星已距太阳二十馀度,盖斜入故也。复依黄道距论晨见,宜太阳躔实沈十五度,其星即见,而今又不然也。直至太阳在本宫二十七度星乃见,盖移星于东地平,安高弧于西,则高弧十度已交析木二十七度,乃与实沈二十七度为正相对之处。是本星已距太阳二十二度,亦繇斜出故也。大都躔度前后相距约四十三度,因得毕宿大星前后合伏不见应四十三日有半矣。若五纬,则宜先定其经纬度于球面,馀法同前。如崇祯七年十二月二十日,大统载金星夕伏,至次年正月初三日晨见,临期实测不伏。试以天球考之,〈北极高四十度〉此时因金星退行,大统所载夕伏之时距太阳甚远,测时尚高十八度,固不足论。惟次年正月初二日,太阳躔元寺枵二十九度,金星在娵訾一度○二分,纬距北约九度,乃移星至西地平,而日躔对度〈在东〉尚高出五度馀,故夕可见。〈依前定限〉其正月初一日太阳躔元枵二十八度,金星在娵訾一度三十九分,纬距北约八度半,复转星至东地平,其西对度较太阳亦高五度馀,故次日夕见者前一日反晨见,又水星大统载崇祯八年三月十八日晨见,至四月二十四日晨伏不见。依新法推本星自三月初二日夕伏不见,直至六月初六日始夕见,前此俱伏,何也。三月十八日,太阳躔大梁一十三度,水星在本宫初度,距南三十六分,依黄道虽出距限之外,〈十一度半〉然使之交东地平,而与太阳相对之处止高五度,尚在距限内,其不得见也宜矣。至四月初三日距太阳最远,乃太阳躔大梁二十六度半,星仍在本宫初度,但距南二度半,较日躔之对度亦止高九度,故亦不得见。凡此皆繇于黄道斜升、斜降也。
求昼夜长短
太阳左旋因之以分昼夜,必依赤道上取同出弧为昼长,同入弧为夜长,法仪上查太阳本日躔度,移至东地平,因识赤道同在地平之度,后转仪,令本躔度至西地平,仍视赤道在东为何度,则总前后相距之弧。如法化时,即得昼长若干,因得夜长亦若干。假如顺天府北极高四十度,求最长之昼。设夏至太阳躔鹑首初度,即令本躔度交东地平,并得赤道对黄道之度约七十度。〈自春分起算〉随转仪,令本躔度至西地平,即得赤道东出为二百九十三度,与前七十度相减,馀二百二十三度,化时得一十四小时三刻半。即顺天府最长之昼。馀日长短法俱同。求夜长。本法以前夏至本躔度,安西地平得赤道同居为一百一十一度,复令本躔度东出,则西地平得赤道为二百四十八度,相减馀一百三十七度,变得九小时○七分馀,为当日昼所馀也。欲用时盘,则以午正与本躔度准对,即昼夜各时俱为子午圈所限,而并得太阳出没之时,如前夏至日出子午圈切寅正二刻,馀日入切戌初二刻是也。
以昼长时复求北极出地高
法取最长之昼查,黄道上太阳本躔度。令居子午圈下,并与时盘午正吻合,后转仪,以本太阳出地平之时正对子午圈为度,架内起仪、或稍下,游移试之,务使本躔度得交东地平,即得本方北极高度。假如顺天府最长昼〈夏至日〉约十五小时,半之为七时○二刻。算得寅正二刻,乃太阳自东出至午正之时刻也。先以鹑首初度〈夏至日〉与时盘午正,并居子午圈随将寅正二刻代居其下,惟游移本圈,令鹑首初度至东地平,即得仪上极高四十度,为顺天府北极出地度也。
求昼时刻
太阳西行每三度四十五分为一刻十五度,为一小时。〈四刻〉冬夏朝夕皆如此法。先依本北极安仪随置,游表于本躔度,移居子午圈与时盘午正相对,后令仪转,〈东或西〉至表无射景,则子午圈所切盘上时刻即其时刻。或不用游表,止取本躔度,与时盘午正居子午圈下,随用他器测日轮高度,以所得度识之高弧上,如法安弧,令高弧与躔度合为一处,则视子午圈所指即其时刻。
求朦胧时刻
太阳在地平下体虽不见,而光实射于空中,则此昏明之际,政所谓朦胧时刻是也。定限为一十八度,如距太阳在限外者,固宜地面周暗全无照光,然即在限之内因所行不同,为时亦各有多寡,或躔度在黄道为正出入,则太阳径离地平,其行速,为朦胧短或躔度在黄道为斜出入,则太阳略绕地平,其行较迟,得朦胧长。试令如法安仪,将高弧上十八度与日躔正对之度,〈在东用西互易之〉从地平数起,依限于赤道圈作识,随去高弧,视本躔度之对度在赤道上交地平为何度,则依赤道相距之弧变时,即得朦胧长短时刻。欲用时盘,则以午正与本躔度正对子午圈,馀法同前。如北极高四十度,太阳在星纪初度,若查晨刻,必安高弧于西地平,令弧上十八度与鹑首初度等,即时盘约得卯正,〈躔度东入十八度故〉则是本日朦胧之初刻,计至太阳出,约差六刻,或安高弧于东地平,令本仪以鹑首初度与弧上十八度等,得酉正为昏刻之末界,此时太阳已西入六刻。又如太阳在鹑首初度,宜以星纪初度与高弧十八度等,东西俱同前法,得本日晨初在丑正二刻,昏末在亥初二刻,总朦胧各得八刻,因知朝夕所得同,而冬夏所得异也。
求距太阳出入前后时刻
以太阳出没之时较,所得时即于昼夜长短,中推取此亦一法也。然又有从升入之度求得者,如法安仪,竖表于本躔度,转仪,令表无射景,因识赤道交东地平度,〈赤道升度是〉复转仪,使东至躔度交本地平,亦并识其赤道同居之度,〈日升度是〉两升度相较,必前减后馀为日出距本时之弧,化时,即所求前距时刻。或于表无射景时识,赤道交西地平度,〈赤道入度是〉又复定赤道与本躔度在西同居之度,〈日入度是〉两入度相较,必后减前,得赤道弧为后距时刻。如北极高四十度,日躔鹑首初度设巳正初刻,表无射景,必东地平得赤道一百四十九度,西地平三百二十九度,令躔度至东复得赤道六十九度,与前度相减馀八十度,化为五小时○二刻。即本日巳正之前距时刻。若令躔度至西复得赤道一百一十一度,借全周减前三百二十九度,馀一百四十二度,化得九小时○二刻。乃本日巳正之后距时刻也。欲用时盘,必先以午正与本躔度,上之游表居子午圈,至表无景处,得本时刻,随将躔度交东西地平,则本圈两次所指时刻,即距本时之前后时刻。
求七曜时分
七曜轮转各主一时,名为不等时,盖昼夜虽共分二十四时,然此则昼自昼,夜自夜,各平分必得十二时,而昼夜之长短所不论也。所以赤道上弧亦不得定以十五度为一小时。
七曜轮转之时,一太阳,二金,三水,四太阴,五土,六木,七火。因推每曜,当得一时,必自日出起算,所得第一时之曜即为本日之主。如遇昴日,其第一时应太阳本日,遂属太阳。依次轮转,次日第一时属太阴,太阴亦为次日之主,馀仿此。
法先查昼长总时,〈依前法〉化为分,以十二除之,所得数为本昼不等之一时。次于黄道圈查本昼躔度,令与时盘午正,依法相对,复移躔度至东地平以定日出时。〈依常法〉从此依先得七政不等时,平分盘周,自日出至日没之处,后用表依常法测日,依新分盘得时。如北极高四十度,最长昼为一十五小时,化得九百分,以十二除之,得七十五分为本日一不等时。〈正五刻〉或依前,设巳正表对太阳无景时,盘得新分四时三十分,为自日出至巳正之不等时也。与十二相减,馀七时四十五分为巳正至日没之不等时也。
求夜时刻
太阳依左行分昼夜,故此独为时刻之原。乃欲以星曜定时者,必先求其赤道上经度距太阳若干,随以相应之距弧加于午正变为时,即所当测之时刻。法依极安球,令本躔度及时盘午正相对,后用象限等器测星出地高度,并识其方位,〈东或西〉依之安高弧。转球,以星对高弧于前所测度,视子午圈所切时刻即本时刻。或不测星高度,〈先以本躔度合时盘午正〉止将本仪取正南北,视至天中之星,〈或出没之星亦可〉即于球上移居子午圈,而圈下所指时刻是其时刻。假如太阳躔降娄初度,即将本度正合盘上午正。设角宿南星至天中,乃移球上本星居子午圈下,得时为丑初初刻○六分,凡星及各节气躔度俱准此。若依赤道度求时,如前法,以本躔度及时盘午正居子午圈,并识圈下同居之赤道度,转球,以星所测得度正对高弧,复识其居子午圈之赤道度,将前后相距之赤道弧化为时,乃星居午正之时刻,必加于午正时,得所求时刻。如前角宿南星至天之中,得赤道同居为一百九十六度,
从春分起算顺数,因躔度在降娄初度,故止用星赤度化时。
查表应十三小时○四分,加于午正为丑初初刻○四分。
日躔不正在春分,后得度减去前度,不足借全周
减之。
求太阳等曜距午正之弧
法先以本曜所行度与时盘午正居子午圈,因识其同居之赤道度,后转仪,任所设时居子午圈,复识其同居之赤经度两经度相减所馀必本曜距午正之弧。如太阳躔寿星十五度,赤经为一百九十四度,转仪,令辰正初刻居子午圈,则同居赤经为一百三十三度,前后度相减,馀六十一度,即太阳距午正之弧也。他曜仿此。
求日月食之原
日、月、地三体必并居一直线上始有食,盖日体恒居一直线之初界,而彼界则月体、地体叠居焉。如月体居界末,则月面之日光食于地景;地体居界末,则地上之日光食于月景。〈月体厚不能透光故〉但太阳本行恒依黄道中线,而地居天之中心,一为日光所照,则此面受光,彼面必生景。虽所射景与日正对,亦不能越黄道之中线以为规也。乃太阴本行多在黄道内,外大端距日与地所居之直线远,则朔望无食,惟出入黄道之处与日与地相参直在一线上,则朔望必食。试于本仪考之。设太阴在阴,〈黄道北〉阳历,〈黄道南〉距两交甚远,任太阳在何宫度,使转太阴本圈与日体会为朔,或正对为望,从而视之,必日、月不能与地并居一直线,无缘得食。若移太阴至正交或中交,不拘得何宫度,与日相会或相望,必日、月地之体并居一直线,本朔望时虽欲不食,不可得也。
求交食方位
日月相食之轮,或从失光之处求之,或从存光之处求之,其起复方位恒自不同。此中繇于多缘。如黄道斜月在南北二曜居午正前后,俱能变易方位,一一细推其故甚难。惟于仪上视之,瞭如指掌法。论日食,依先所算黄道上二曜视度,中心图一小圈当日轮,并依太阴视距,或南或北,复图一圈与前约等,即当月轮。
求初亏,俱依二曜初亏各视度;求食甚复圆,必依食甚复圆时之视度。
随令时盘午正与躔度相对,转仪,令子午圈切初亏等时,后以高弧正居二曜之心,所至地平即其所食方位也。若月食法同,惟与太阳正对之处,图地景圈径约一度半,其左右或前后依月距及各宫度绘圈略小,即得月食之象。假如崇祯九年正月,月食三分馀,因太阳躔娵訾约二度,以本度对时盘午正,乃于太阳正对处。〈实沈约二度〉图景并月体圈,转仪,令卯初〈初亏时〉正居子午圈,即因月轮距南约五十分,〈以本行未至景心论〉以高弧试之,尚距正东十馀度。得其向东北至食甚时,月轮又低东行,又多约与景心南北相对,故此时得其向正北也。若欲查二曜初亏等时距地平高,即依时转仪,令高弧从天顶过二曜之中心至地平,数之即得二曜高度。如前月食初亏,依卯初定仪,而以高弧过太阴圈心,则地平上约得十九度,即月初亏高度也。
求彗星游星经纬度
先任测一恒星之高度,如法安球,必使高弧依所测星高度与球上本星吻合。随测彗星或五纬地平经纬度,而以本经度查于球之地平,随将高弧过所测之星,高于球上,用点作识。因较黄、赤道所距度,皆依前法,即得其星之经纬度。又一法,先测彗星高度,并测一恒星与本星相距之度,随依彗星方向,将高度于高弧上用点作识,乃复用规器于赤道上量其二星相距度,而以一锐指恒星,一锐指高弧所识点,〈高弧进或退必以规锐至其点为定〉即得彗星经纬度。或不必测彗星高度,而惟测与一恒星相距之度,复以界尺量之,更求一恒星与此二星同在一直线,而球上任将高弧纵横安之,必依二恒星引对。则高弧所得恒星距彗星度点之球上又可得彗星实度。游星俱仿此。若彗星有尾,欲图全容,即依前法先测得其首,后测其浑体之长短,并量一恒星同居直线上,随于球上使高弧从首至本恒星,依先所测之长识之球面,即得星尾之所止。或正引高弧向太阳躔度,以数其长短于球上,为号亦得。盖因彗尾多向太阳对度故也。〈以上原本卷二〉
立象
立象者何。任所得时刻应何宫度,依之以推定十二舍也。而各舍所当居之度分,并经、纬、诸曜,皆从本度起算,则此因时之变,得天之容,乃占验所繇以生。第此中紧要在定每舍之初界。〈即初度〉举所应得分数,绘以方图或圆形,随点入星曜,即浑天之象成矣。法依本北极高安球,以本日躔度与时盘午正较对,始转球与盘,将先所得时刻居子午圈下,而本球宛然一当时之天象。次于西地平识同居之赤道度,并得相应之黄道度,即第七舍初界。次起半圈至赤道上,距三十度之限,所得黄道度乃第八舍初界。递起递加,尽得地平上各舍初界。而地平下诸舍,则以黄道相对处可定。如一与七,二与八,三与九,四与十,五与十一,六与十二之类是也。假如崇祯九年正月十五日辛酉晓望月食,顺天府食甚在卯正一刻○二分,日躔在娵訾宫一度五十三分。因此时,求各舍躔度。先以日躔对时盘午正,依法转仪,得西地平交赤道一百五十○度,交黄道鹑火宫一十三度,此即七舍初界。正对东地平,得元枵宫一十三度,为第一舍初界。〈即命宫是〉上居天中,得析木宫○二度,为第十舍初界。正下得实沈宫○二度,为第四舍初界。半圈交赤道一百八十度,〈距前数三十度〉得黄道寿星宫初度,为第八舍初界。正对之降娄初度起第二舍,又以半圈交赤道二百一十度,得大火宫九度,为第九舍正对之大梁九度,即第三舍。后移半圈至子午圈之东,得析木宫二十度,为第十一舍,星纪一十度为第十二舍,而正对处即实沈鹑首相等之处,为第五及第六舍。因而上、下、左、右四角〈四角占验最得力处〉定矣。复求纬星所居之舍,或依表预算,或径用推定。七政细行,则以本北极高及本时刻,取各曜相应度分,入其舍,若星近舍初界有距度,或可入前舍中,必先以黄经纬安球上,随以本曜所居之处,求于本舍。而以前所立象定球渐移,半圈,如法起舍,乃星入前后界内者,即得本舍是也。若地平下各舍之星,法起南极于架上,与北极等高,移前第一舍之初界至西地平,而天容在地平下者,反居地平上。即得诸曜本舍之界。如以鹑火十三度,交西地平至寿星初度总弧内,得前月食。惟木星与太阴略近,查丙子年七政细行食甚时,木星躔鹑火二十九度五十七分,而火星则躔大火三度三十分,应入八舍,土星躔星纪一十一度三十分,纬北三十四分,必在十二舍之初界。太阳、金、水二星皆在娵訾宫,因同入命舍其土星。依本经度,惟纬北三十四分,故得在十二舍之初界,若距黄道北或一度半、或二度,试以舍圈限之,必其已入十一舍,因近顶纬多故也。求恒星法同此。盖此象一立,则凡各曜性情势力强弱可考,而知穷理之家,借以观变于未然,鲜有不验者。〈其法详天文卷中〉
求两星于立象圈上相合之时
凡两星本各无力,一合即增力,此实足为所立象损益之原也。故以初得某星、某宫度,主人生命等事者安东地平,〈依本地北极高〉即应查其与某星相合否。盖转立象圈于球面上下,得二星在通径上,即命星在地平时,其星必合,否则令球与立象圈各自那转,复求其当合时,法必得二星能如此合,遂识赤道交子午圈度,次移本日躔度合子午圈,并识其同居赤道度,乃以前赤道交度减后赤道交度,馀度化为时刻,即得二星应合之时。如极高四十度,一星在鹑尾宫二度,距纬南三度,又一星在本宫四度,距纬北一度,本日躔鹑首宫七度,试转仪,并半圈见子午圈西,未合必过东近地平方可得合。而合时赤道则以七十五度交子午圈,便移日躔至子午圈下,得同居赤道九十七度为前度,所减〈先借全周后减〉馀三百三十八度,化为时得二十二时二刻○四分,即二星去午时后合圈下之限。
求经纬星相照度
凡两星相照,增力或阻力多以向黄道为准,大约有五等。如会合,即同度同分为密,而同度不同分者则谓之疏。六照以六十度为界,四照止于一象限,三照以四宫相距,而云然望照则以正相对而得半圈之距,乃此数照。又各有亲或远者。盖星体居正照之界即亲而力强,若体未正居其界,而第以光居之即远而力弱,至若光之前后虽同,而各星所定之限有异。如土得十度,〈前十后十〉木十二度,火八度,太阳十七度,金、水皆七度,太阴复十二度,经星凡第一等有七度三十分,二等五度三十分,三等三度三十分,四等一度三十分,五、六等最微力弱,不入其数。总之,除会望二照,馀皆以顺十二宫为左照,逆十二宫为右照。试于仪上考之,法用规器量黄道上任取一照之界,〈六十九十等度〉以星为心,于黄道左右分顺与逆照之限。假如求大角,四照以九十度为限,将规一锐居本星体一锐,指左界九十度,必至星纪十七度为顺照,指右界九十度必至鹑首十七度为逆照。若七政,必先依各经纬度安其本位,馀法同前。又一法,用立象半圈,先依北极出地安球,任取本时升度居地平,乃移半圈,径过其星,依之于赤道上作识,后转球,从前所识赤道度,相距三四等照界,仍移半圈,其上所指黄道度即星照所至界也。假如升度在寿星十六度,求轩辕大星六照限。必移升度于东地平,立象圈过星,指赤道一百三十八度,复加六十度,应一百九十八度,居立象圈即并得寿星宫十六度,居本圈为轩辕大星六照之左限,其右限则以反减六十度为法。
求岁旋
凡从前所取时刻至太阳复躔元度分,其中相去总数谓之岁旋。盖依后时所立象,较前象所得七政等星居舍内,应增或阻前星之力,即效验所繇变也。法令球依前立象之时定住视,赤道交子午圈若干度,为前象天中升度。今越若干年,复求后象天中之升度,必每去一岁加八十八度四十九分,满全周则去之馀数,即后象赤道交子午圈度,使之于本圈正合,可得天容依岁旋之时。因以定各舍宫度,而各星安舍法亦同前。假如崇祯元年正月酉正时,立前象因太阳躔元枵一十六度一十九分,依法转球,令时盘酉正交子午圈,得赤道交本圈之升度为五十度,设相去八年,复立象,为崇祯八年十二月二十九日,〈太阳躔元度是〉则以八乘八十八度四十九分,去全周馀四十度三十三分,为后象之升度。移居子午圈,得本圈指酉初二刻,为岁旋之时。如用立成表,细求即后岁中。先查太阳躔元度分之日为岁旋终之日,次以后象升度减太阳是日之升度,〈不足减借全周减之〉馀数化为时刻分,即得当日立象之时刻焉。假如因十二月二十九日太阳躔元度为岁旋终之日,其升度三百一十八度四十八分,后象升度四十度三十三分,不足减,借全周共得四百○度三十三分,减去前数,馀八十一度四十五分,化为五小时一刻一十二分。〈从午正起算〉
加升度表缺引照元,与增力元相合。
凡初得某星、某宫居某舍,因之以占所效,是谓照元。设更有一星或一宫所居舍,能增力或阻前效,即谓为增力元。二元必各依定时著力乃就中,求以前者至后之位,或反以后者至前之位。俱依赤道弧相应二元之距为限,转球,查其弧之大小为引,则一度应一年度数,既定应在何时亦可限矣。故引后至前,以顺宗动为正,而引前至后,则因五纬逆行时用之,遂名曰反引。皆于球上可得正引者何。转球先依天象安定,令黄道应第一舍初界之度,正居东地平,次查照元移象圈径,过其上并识赤道合子午圈度,又转球右行,以增力元至半圈,复识赤道交子午圈度,则先后所识之间弧乃指正引限,而总数可推年时也。欲反引安球,令之转同前,惟立象圈宜先径过增力元,复识转球时赤道过子午圈弧,因以定其中相去之年。假如北极高四十度,设大梁十度在第一舍,初界太阴离黄道娵訾二十度,距北二度为照元,火星近东地平,躔大梁六度,距南三度为增力元,必先依各经纬度,带二曜于球上,然后令象圈过太阴处,所交赤道点约为三百五十二度,〈用本圈与用子午圈同〉次定住象圈,移火星与本圈正对,约得赤道交圈点为二十八度。以所得前后度相减馀中弧为三十六度,即正引之限。求反引法亦同。但引限在地平下必先起南极依,北极出地度,令黄道第一舍初界之度。正居西地平,馀法同前。〈见前第二卷〉
求引二元应止黄道何度
因照元渐离初得之象圈,乃更有黄道相应,故任至某年亦可求其相应度。法先安球,依本象,令象圈与照元合随,查赤道交子午圈度,因之顺或逆取本度与年数所止限,移至子午圈,必此时交象圈黄道度即其年所引照元止限也。如北极高四十度,设寿星十六度东出太阳躔元枵六度为照元,依去四十二年之数,复求躔度。因安寿星十六度于本地平,安象圈于鹑火六度,〈与元枵对度因后在地平下故〉得子午圈交赤道一百一十度,以加四十二度,依之应一百五十二度,交子午圈得象圈,交鹑尾一十六度,即娵訾一十六度,〈正对宫度是〉为照元去四十二年所至限。若照元自居四角,不必用象圈。依所取年数转球,复居本角黄道度即照元所止度,设寿星十六度为照元,而出地平者亦即此度,则得地平交赤道二百零一度。令球右转以赤道四十三度至地平,则所并居之大火十九度即为照元。任取之年后止限,又设增力元亦居地平等角,即以同居赤道度减年数之度所止限,复移至地平等角,亦即得黄道交地平等角为其当年所至之限。或增力元不正居角,仍用象圈与之交,并识其所过赤道度减总年数馀度,限移至本象圈复得并交黄道度为增力元当年之限也。
依浑仪解圆线三角形
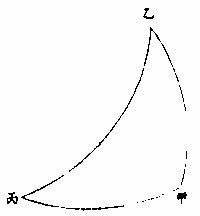
圆线三角形者何。乃过球心大圈相交三弧之形,而各弧不及圈之半周所成也。盖形内每两弧共抱一角在间者谓之腰弧。而与角相对之弧即底弧,或又谓直角三角形内以所抱直角弧为底弧,及垂弧即与勾股不异。而以所正对直角者为弦弧。论角,其大小以对弧之大小为则。盖用规器以本角为心,以九十度为界,则两腰间之弧〈腰先引长〉必量其角得本弧为一象限,即对角为直角。过象限为钝角,不及象限乃为锐角。凡弧或角不及满象限之度,名之为馀。又凡两腰引长至合一点则得抱角之对。三角形以底弧为公底,以对角为等角,而馀弧、馀角皆前三角形所不及满一百八十度之馀弧、馀角者也。因止一直角三角形得馀皆钝角者,则与直角正对之形内腰间角必直馀,反皆锐也。如止一直角三角形,得馀一钝一锐者,则与锐角正对之形内惟前形直角,相连之
图
角为直角,馀皆锐角也。如图:乙戊丙形内设戊为直角,乙、丙皆钝角,即其对形乙甲丙内,得甲为直角,乙丙皆锐角也。又丁丙戊形内设丙为锐角,戊直角,丁钝角,即其对形为丁己戊,而戊角独直,丁、己皆锐角。论斜角形,如三角总为锐
角,必对形独存一锐角,馀皆钝角也。设乙甲丙形内甲为锐角,即得对形乙戊丙内戊亦为锐角,乙丙皆钝角。如三角总为钝角,乃对形反存一钝角,馀皆锐角也。设乙戊丙形内、戊为钝角,即乙甲丙内甲亦钝角。今解三角形法多论不及一象限之弧,即锐角之底是也。因以斜钝角形先变为锐角形,以直角形有一或二钝角者,亦先改为对形,则就中推求之法与解原形不异。即馀弧、馀角之理所繇出也。今用浑天仪解之亦仿此。但先解直角形,尽之于三比法,有以先得一锐角,并与各弧者,又馀、锐角复并与各弧者,又以其底同各腰,或并得二腰者,各列法如左:
任取一弧一锐角,求馀弧及馀角
设甲乙丙三角形内,甲为直角,其底乙丙馀弧即腰,则乙与丙皆锐角也。先设得乙丙直角之底弧及乙角,欲求馀。尽解本三角形法,架内北起子午圈,令赤道前高依本角之度,然后或东、或西,自赤道交地平处与本地平,查底多寡之度以为限,移过极圈至此限上即三角形仪上定矣。如乙角为二十三度半,以
图
前子午圈弧为则,使赤道依之,其左右交地平角即得对弧以定大小。今甲为直角,必于赤道交过极圈处,求之,则地平上得底。若设乙丙底弧为六十度,而移过极圈至本度,〈从乙角算起〉因大腰在赤道弧约为五十八度,小腰在过极圈弧
图

为二十度有半,自过极圈交地平,查各圈满一象限即以其限,安高弧得二圈间之弧为丙锐角之对弧约七十八度。又设以小腰及本角,求馀弧及馀角。即先定角等法同前。而以所先得甲丙弧〈如二十度半〉与过极圈上为点,移之至交地
平,必自得腰与底弧合前度,即丙角亦在高弧同矣。或以大腰查求其馀。亦先定乙角而转仪以渐进,赤道弧入地平,令自其二圈相交之处独馀五十八度。至过极圈交赤道之角必馀,法馀度亦合前也。今试以三弧各与丙角为先得,如底为六十度,求馀弧、馀角。法移过极圈至地平距子午东或西三十度,〈六十度馀是〉定住球,使高弧距二圈相交之处各满一象限,得间弧为七十八度。即所设之形准否,则宜前或后,起子午圈必令高弧对丙角,如其度为止,即子午圈自地平以上得对乙角之弧,而直角两腰皆明矣。或设先得大腰与丙角,必进或退赤道圈定其腰之大小。〈如五十八度〉即安高弧而起子午圈,依前法,求馀弧及馀角也。或以小腰及丙角,求馀。即先于过极圈查腰弧大小之度,使之交地平,以试高弧得全形。盖对角弧不及其度,即球宜北起过极圈,宜南下若对弧已过其度,则球反宜南起随移过极圈,东西得正。然后馀角、馀弧皆依前法准得矣。任取一腰、一底或二腰,求馀弧及诸角。先设得小腰与底弧皆依前度法。令球转东或西以过极圈,限底弧之度。〈如六十度〉视本过极圈自赤道至交地平弧若正合其度,〈如二十度半〉即三角形已定。否则前后起仪,求小腰务合于地平。乃所对大腰亦复得五十八度。而查乙角、丙角必同前。又设得大腰与底弧,亦先定底弧度。渐起球或下令之左右转,以并对大腰度,即小腰亦自合,而求角。必依前法也。或复设得二腰,求底与角。即先定大腰,令球下或起即得馀腰与底,而求角亦不异前也。
解斜角三角形总为六题;
图

其一曰:以二腰及间角,求底弧及馀角。如甲乙丙三角形内,丙为钝角,甲、乙皆锐角。设先知甲角,〈即间角〉则乙、丙为底馀弧皆腰也。如甲角为三十度,大腰六十度,小腰止五十度。法于子午圈查距极〈南北不拘〉六十度之弧,移其限于天顶,次用
过极圈令距子午圈左、或右,而以赤道三十度为限,末安高弧东、西,必依极圈所居方位,令之交极圈距极限五十度。即三角全形定矣。大都子午圈为大腰,极圈为小腰,高弧为底,因而如前图得乙丙底为二十六度有半。乙角以地平为对弧,在子午圈及高弧之间得五十九度有半,所馀丙钝角,欲求其对弧。未免再移球,故先依高弧于球面上界线,后转极圈令交高弧之点正居子午圈下,而并其子午圈起之以当天顶,乃复依先界之线安高弧,而以至地平为限,则此限及子午圈之中弧即丙馀角之对弧,为一百八十度所减,存得丙角一百零三度。若用浑仪求之,线宜界于黄道上,或高弧本位不与黄道遇,即于未转极圈之先,移高弧于正对地平度。所遇多寡度界线,其上馀法同前。而所得弧即正丙钝角之对弧也。其二曰:以二弧及先所得一弧之对角,求馀弧馀角。如前图:设先得甲、乙弧六十度,乙丙二十六度半,及丙角一百零三度,法起子午圈以二十六度半为距极之限,令之居天顶则自极至顶得乙丙弧,将秋分
图

经圈西距子午圈十三度,〈依赤道为则〉或将春分经圈东距十三度,则自二至经圈至子午圈其中得赤道弧为一百零三度,乃丙角之对弧也。又安高弧使之以六十度〈自顶下数〉交过至经圈,即以高弧得甲乙,以经圈得甲丙,而甲乙丙形全矣。
今查甲丙必为五十度,乙角则自高弧至子午圈在地平上必五十九度半,所馀甲角因依高弧于黄道上界线,然后移经圈交高弧之点,以正居天顶而依界线,复安高弧得交地平至子午圈之中弧为三十度。或不移球,止安高弧于地平正对之处,用规器于前交经圈及高弧一象限之界,量二圈所距,亦必得三十度为甲角之度也。
设反得甲丙五十度,乙丙二十六度半,及甲角三十度,以求馀弧、馀角。法起子午圈令距极五十度之限在天顶,次转仪使过极圈距子午圈之东、或西,依赤道上三十度为则,即于高弧自顶而下数至二十六度半,以之交经圈即得馀弧于本圈为六十度。而高弧在地平上,其距子午圈一百零三度,乃为丙角之对弧,仍依高弧在黄道上作线,令前交之经圈六十度居顶,用高弧顺线下至地平,必得五十九度半。即形内乙角也。
其三曰:以二角及先所得一角之对弧,求馀角、馀弧。设甲乙丙形先得乙角为十度半,丙角为一百五十
图
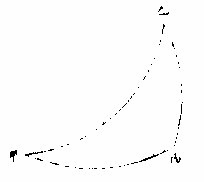
四度半,又得甲丙弧对乙角为二十三度半,宜求甲角与甲乙及乙丙弧,但既先得甲丙对乙角之弧。亦应知甲乙对丙角之弧过象限否。今使过象限法,查经圈左右赤道上之十度半,令之正居子午圈,随于地平上从北去南,查一百
五十四度半,以之安高弧。因而起或下子午圈,必视其所交经圈之点,距北极出象限外,乃并视经圈所交高弧之点,必距天顶二十三度半,一得距度准。即本形定矣。盖乙角在极中经圈及子午圈之间,与正对赤道得其若干,〈十度半〉丙角于地平,〈一百五十四度半〉甲乙弧于经圈上,约得一百零六度。乙丙于子午圈上得八十四度半,止馀甲角,必起高弧与经圈所交之点至顶,而求其角于地平。依前法得其为二十七度。其四曰:以二角及角间之弧,求馀角、馀弧。如前形,内设甲角为三十度,丙角一百零三度,甲丙弧为五十度。法自极中查子午圈上五十度,令之居天顶为甲丙弧,查地平去子午圈北一百零三度,以安高弧为丙角,末以赤道上距经圈三十度之限移居子午圈,乃得甲角而馀弧自明矣。因而高弧上得乙丙为三十六度半,经圈上得甲乙为六十度,若求馀角,必起高弧所交经圈之点至天顶,依前法查之乃得。其五曰:以三弧,求诸角。设甲乙弧为六十度,乙丙为五十度,甲丙为二十六度半,法使甲乙弧在子午圈
图
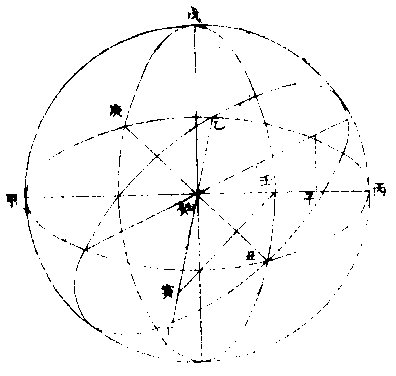
出极中至天顶,即以之安高弧,令以二十六度半〈从顶算〉交经圈,距极五十度之限,必得乙角于赤道圈,甲角于地平,而丙角则起经圈五十度至顶,依前法求也。或使乙丙五十度在子午圈,而以高弧安经圈之六十度,即乙角可在赤道
上得,丙角则反在地平,甲角则起球,求之法同前。其六曰:以三角,求诸弧。设甲角为五十九度半,乙角为三十度,丙角为一百零三度,法转经圈于子午圈之东、或西,任取相距三十度、或五十九度半、或一百零三度,皆以赤道弧为则,必得相应之角。在经圈过极之处安高弧亦同法。盖其交地平距北或三十、或五十九度半、或一百零三度,必皆在地平上算,而相应之角则在天顶,但安高弧必先于地平取准,乃于天顶未定之时渐起,或下仪,试二弧远近相交之处以对馀角,其法或识高弧交经圈之点于顶,而地平上试所求角正对之弧。或用规器从高弧与经圈相交之各点,距一象限量其二弧所距,〈必先转高弧于地平正对度〉得合馀角。即初起之球必准否,即更移之,总以试定三角后,而其弧自明矣。