钦定古今图书集成历象汇编历法典

　第七十二卷目录

历法典第七十二卷

历法总部汇考七十二

新法历书二十二

五纬历指八五纬后论

五纬之理，最奥且赜，故各有本指，以分解之；又复有总论，以合明之。然犹有所未备也。因著为后论，以补其遗，而于奥赜，终难穷尽。凡十二章。
五纬天各距地第一

月离历指第二十六章，求月距地之高，其法有五；又求太阳距地，其法有三，皆以地半径为度，又各法因高差〈亦名视差地半径差等〉或日月交食为本。恒星历指三卷中亦测恒星之远，借用五星之测，略定土星之高，并亦得恒星在上之高，今因五纬无视差。
土木二星甚远，其视差不过数秒。如无差难，测水星常在蒙气中，亦不能测火星。或有视差，然不足为测其高之本。说见下。

欲测其高，法有二。算或用古图或用新图，各有本论。如左。
左古图以地为日月五星恒星诸天之心，设诸曜各居一层天。其厚内函有小轮〈亦名岁轮〉，各层相切而无空。又各层上下有两面，下内为凹，上外为凸。
各天之厚因函小轮，其小轮于地有近有远，如两心差之理，则各天之厚为小轮全径及两心差之倍分数〈谓分数者盖各有均圈于最高减距高去岁心差之几会〉。图上各天小轮比本天许小以指外有两心差数
图图

本历测各星小轮及两心差定本天。半径皆为十万分，若加小轮半径及两心差数，必得其最高距地若干。若减之，则得最庳距地若干。如图。
系凡设一层天上面距地若干度〈以地半径为一度〉，必得次层下面距地之若干度，盖两面中无空隙。又设内面所距若干度及次层上下两面距本心比列，以三率法求之，并可得其厚距地之度。法曰：依内面距本心多寡分数，得度多寡，则上距分之某数，必知其度也。月离设三家之数，以测定其距地之度，今所为第谷。法曰：太阴大距地为六十，地半径有六十分之三十六或百分之六十。
水星天两心差为六八二二〈十万分为全本天半径下同〉，小轮半径为三八五○○，两数并之〈水星均圈法凡在最高不减其距地见本历指〉，又加半径〈全数〉，得一四五三二二，乃水星最大距之数。又前两数相并，于全数内减之，得五四六七八，乃极近之数也。置极近数为六十度，有六十分之三十六乃月天极高数也。以此度数或约为五分之三乘极高之数，以小距数除之得一六一，乃水星天上面距地之度也。
金星在水星上，则其下面距地为一六一〈奇零不算〉，设金星两心差为三二○八，用其半因有均圈用其半，他星仿此为一六○四，小轮半径为七二二四八，两数并，加于全数得大距数为一七三八五二，又两数相并，减于全数得二六一四八，为近距之数。法以内面距度之数乘大距数，以近距数除之，得一○七一，乃金星外面距地之度数也。
太阳有本法，求其中距地得一一四十二，地半径诸家小异以求大距，或用均圈〈见日躔历有表〉，或不用均圈，两法略差。今不用只因太阳两心差求之得近距为一一○一，远距为一一八二。
问：太阳天内面切金星外面是也，今因太阳本算其内面盈金星外面三十度，两算不合何也。曰：此测难求其密，其较虽盈三十度，以全数计之不及百分之三，数则小矣。又曰：所测定各天之数，皆以日月星诸体之心为测，其体之厚未尝入数，必月及水星金星各数略大而后算始无差。又曰：所用之数乃新图之数，不谓各曜各丽一天而相切，故其数于此论不合。或曰：星体到本天最高在此，其天或仍厚几许，要未可知所定之数，亦其大略而已。
火星两心差为一九六○，取五分之三〈均圈心距地心为三分不同心圈心距地心为五分〉为一一七六○，小轮极大半径〈有盈有缩故用大数〉为六五八○，○两数并之加于全数得远大距为一七七五六，○两数并之减于全数得近小距为二二四四，○用法以太阳大距数一一八二乘火星远大距数，以近距除之得九三五二，乃火星外面距地之度数或木星天内面距地之数也。
木星两心差为九一六○，用其半得四五八，○小轮半径为一九二九四，两数并加全数得一二三八七四，乃木星远大距数。两数并减于全数，得小距数为七六一二六，依前法以内面乘大距，以小距数除之得一五二一七，乃木星上面距地之数或土星下面距地之度数也。
土星两心差为一一六二八，用其半得五八一四，小轮心半径为一○四二六，两数并，加于全数得一一六二四○，乃土星大距数也。若以前两数并，减于全数得小距数为八三七六○，依前法乘除得二一一一七，乃土星上面距地之数或恒星天距地之数也。右算皆用古图以明今测之数，然亚耳罢德于唐僖宗广明中，算得水星本天中距地为一百一十五度，金星中距六百一十八度，火星中距四千五百八十四度，木星中距一万○千四百二十三度，土星中距一万五千八百度，恒星中距一万九千度也。
因各星距地及其体之视径亦并，可推其大小，下有本篇。
用新图算各星距地第二

新图以地为太阳太阴恒星所行之心，别五纬以太阳为本行之心。又土木火三星以太阳所行之圈，为古法所谓年岁圈，即上所用法，今非其真因用本法。又新图不言各星各有一天，而强星在本重之内，但各所行之轮或相切或相割耳。
土木火三星以太阳为本行之心，又因其心从太阳，即以太阳所行之轮为人目所见每年各星之行〈见本
土星行轮新图

历指
。欲知小轮于本天及两
心差各数比例，则设太阳距地若干，可得各星距地若干，如图。设甲乙〈日距地或小轮半径〉乙丙〈星本天半径为全数〉及丙丁，〈两心之差〉又设甲乙为若干度，依法可得乙丙丙丁各线之度，并之得甲丁乃星距地之度也，上三星之法无〉
图

二。今置土星各圈之数，如上用三率法，甲乙〈小轮半径〉为一○四二六，得距地为一千一百四十二度〈太阳中距度〉。今乙丙全数〈本天半径〉得若干，算得一○九五三有奇，又丙丁五八一四〈两心半差〉得六三六，以甲乙、乙丙、丙丁三线之数并之，得一二九三

二度，或地半径乃土星大距地之数也。若于乙丙全数或乙戊半径数内减去甲乙及戊己〈与丙丁等〉一七七八，得九一七五，乃土星近距数，若求其中距地〈引数为三宫九宫〉得一○五五○。
木星用法如上，求得大距度数为六一九○，中距为三九九○，近距为五九一九。
火星用法求得大距为二九九八，中距为一七四五，近距为二二二。
下金水二星因不围地球，其算法与上三星略不等。
图

如图甲乙为日距之线或小轮心距地之线，乙丙为小轮之半径，以乙甲加减得大小两距之数。
金星两心差半之得一六○四，并加小轮半径得一七三八五二，用法乙甲全数〈本天半径〉，得距地二四二度。今算乙丙分数得度为八
图

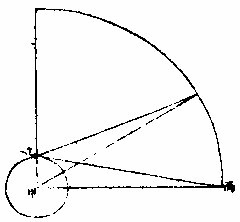
四三，以加于甲丙得一九八五，乃金星距地之度数也，若减之得三百度乃近距之度也。
水星以法求之得大距度为一六五九，小距为六二五度。
以上因其度数可推，各距地之里数盖以地半径为
度，有一度之里数，因可得各距之里数。置地半径为
二万八千六百六十二里，以各星距地之度乘之，先用古图数。
月距地小数为六十万七千六百四十六里有奇，大距数为八十六万七千里有奇，此古今小异。
水星小距数与太阴大距数等，其大距数为四百六十一万二千三百二十八里。
金星大距数为三千○六十七万二千○○八里。太阳中距为三千二百七十一万六千○一十六里。大距为三千三百八十六万一千九百三十六里。大星大距数为二万六千七百九十一万六千○九十六里。
木星大距数为四万三千五百八十五万六千六百一十六里。
土星大距数为六万○四百九十五万九千八百一十六里。恒星依法切土星上面，则得其距地之数也。若用新图推算亦可得各星之里数。
五星视差第三〈即地半径差〉
图

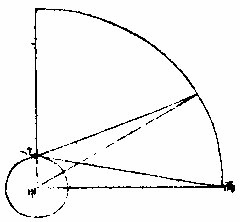
各星既有距地之度数，则可知视差之分数。借日躔视差图以明之，甲地心，乙人目，丙为某星，甲乙为一度，若知甲丙边之度，则可得乙丙甲角乃视差角也，
甲丙当全数，甲乙为切线。
依古图得各星视差如左。
设星在地平，求其视差。地平以上，若星更高，其差更小，在顶无。

月近地视差
水星距远视差为二十一分。
金星距远视差与太阳距近差数等为三分七秒。太阳中距为三分大距为二分五十四秒。
火木土三星其视差皆不满一分，故不算。
若用新图日月各视差无二
金水二星中距与太阳为近，金星距远，视差为二分。弱极近距为十一分，水星大距亦为二分，小距为六分。
以上火木土三星之差亦微，但火星在极近之距即太阳之冲，其差为十五分，盖其道切割太阳之道而于地更近。
以上视差之数，日月以外，难测难定，是以各家不合且不尝用，故不设表。
五星体视实两径第四

测日月视径实径见月离及交食诸书皆有本论，但日月体大可用仪器测定，五纬体小测之为难，惟以人目所见或于日月相比以定，其视径后以近远之，数求其实径大小相比等数。
亚耳巴得其学本多禄某有曰：水星中距地之时〈本算得一百一十五度〉，其视径比太阳视径如十五分之一，即天度〈周天三百六十度之度也〉之二分。金星中距时〈本算为六百一十八度〉，其视径为太阳视径十分之一，即天度之三分。火星中距〈本算为四千五百八十四度〉，其视径为太阳视径二十分之一，即天度之分半。木星中距〈本算为一万○四百二十三度〉，其视径为
图

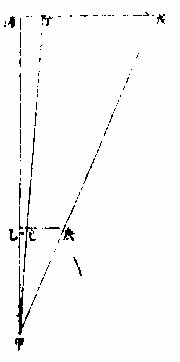
太阳视径十二分之一，即天度之二分半。土星中距〈本算为一万五千八百○○度〉，其视径为太阳视径十八分之一，即天度之一分四十三秒。又星高有视径，以法求实径。如图，甲人目〈地心无异〉，乙庚太阳半视径，乙己某星半视径，其比例如乙己于乙

庚。若星在太阳，如丙丁，则其比例为丙丁与丙戊〈丙戊当太阳视径〉，用法得丙丁天上度之几分，有丙丁分数则有本天周之分数，因周与径之比例〈见测量全义五卷中〉，甲丙半径得地半径若干，则其周得若干，以周之某分若干，得各星比例半径大小，又以各星同类之分数求其容〈见月离三大比例〉。
依法算得水星体比地球小，为一万一千分之一分。金星体小，于地球为三十六分之一分。
火星体大，为一地球又三分之一。
木星体比地球大，为八十一倍又曰九十五倍。土星体大，于地球为七十九倍又曰九十一倍。恒星六等之大小见本历指。
用新图求各星大小
新图以太阳为五星之心，金水二星或在日上或在日下，与古法大异。
第谷曰：水星视径中距时〈一一五○度〉，为二分○十秒，其实径与地径为三与八，则其体小于地球为十九分之一，于古法甚远。金星视径中距时〈一一五○度〉，为三十三分十五秒，其实径为地球径十一分之六，则其容为地球六分之一。火星中距〈一七四五度〉视径为二分弱，则其实径为地径六十分之二十五强，其体小于地球，为十三分之一弱。木星中距〈三九九○度〉视径为二分四十五秒，其实径于地为十二与五，则其体大于地球，为十四倍。土星中距〈一○五五○度〉视径为一分五十秒，其实径为二地球径又十分之一，则其体大于地球，为二十二倍。
若欲以里数求各星之大，则先求地球之容得里数，次依各比例数求之〈见月离三大比例〉。
问古今两数相悬何者为确。曰：各有本论。然以金星證之，见其绕太阳有弦，望之异觉，新法为准〈见五纬总论〉。
五星光色第五

月以光以魄，知其光非本体之光，乃所借于太阳之光，金星亦然。盖以远镜窥之，见其体亦如月有光有魄，故也他星觉无所倚然，以相似之理论之，亦可谓其光非自光，乃如月与金星并借光于太阳者也。问五纬之光既皆为日光之分，乃其色各不同者，何也。曰：如镜如水、如金诸能发光之物咸受太阳之光，而所发之光皆非一色，盖亦繇本体之色所染故也。然则五星之色亦各为本体之色从日光而发见耳，五星本体之色从其各类本质及其面之平与不平，或其体之虚实坚脆等势所发。
加利娄曰：凡大光照某体能发光之类，其所发之次光非全受本体之色而变为他色，如大光照黑体〈若鍊铁〉，其所发之光为红色，如火星〈以此西名火星亦谓之铁星〉；若照淡红体，其所发光色如木星〈红铜色为淡红故木星亦名为铜星〉；若白体，其发光色如土星；若黄体，其发光色如金星；若青体，其发光色如水星；试以黑铁等类炼之细阅，其光色必如上。
又曰：星色非纯从目审视可见，乃知各星亦非纯质也〈见格物诸书〉。
五星时有颤动，其理与恒星无异，或空中浮气之游移，或自体闪烁，如烛光之摇，又或人目之缺也。
五星中历考第六

按中历旧法，自古迄今修订诸家皆以测定太阳太阴之行为本，而五纬次之，今新法亦然。但求真切，不差之理，须辟从来舛谬之根，故著为日躔，考及古今交食，考以备参證而五纬行度之差，旧法之因循更甚尤宜讲求今订其谬于左。
一曰测晨夕二留日时折半得合伏之日时，非也。解曰所测之留乃视行之行也，星有视行有平行，及均数先于视行，以均数或加或减得平行，乃恒定之行也，星在留际有损分，益分其中积大小，原自不等，此根有二。
其一从本天行所谓盈缩法，此盈缩之数或繇小渐大，或繇大渐小，递有加减，其行非顺。如盈初十度与盈末十度损益差分非一，从留初到合伏又从合伏到次留若度数等，其均数必不等。
其二为二留中积时，太阳之行亦非一。如置首合伏在冬至，太阳行疾；次合伏在春分，太阳行平；第三合伏在夏至，太阳行迟；则星各合伏，太阳其行亦各有多寡之异。又如留初在盈历，次留在缩历，以视行得平行，或先留宜减均数，或次留宜加均数，或二留均
图

数皆宜加皆宜减，难胶于一，如图。
置太阳在中，其左右为二留际凡、二留损益，分为同类者，太阳非在其中界，若异类乃在其中界。
系二留之中积非一，又太阳不在二留平行之中间，则折半之说必不能得合
图

伏太阳之真时刻，故曰非也。
又按五星损益表，前后度同而盈缩差非一，如设星合伏前后五十度，前五十度得某差，后五十度又得某差，差数非一，则时刻亦非一。
又留际之日时刻最难测，

其真盖星繇渐而迟，如先一日行几度，次行几分以至几秒，此时星在进退二行之中，谁能别之。
若留际不测其日时刻而测天上别宿度分与之相比折半，则得合伏之度分。此因盈缩差段目非均非顺，则合伏前后视行果不如一，前行疾后行迟，欲得其真，难矣。
二曰用表晷或简仪以测五星非正当之法。
其一表晷非公法，如水星晨夕距太阳极多为二十三度，见时太阳下地平十五度〈或多或少兹取其中〉，水星在地平上不过十度。设表一尺，圭应长五尺五寸，若用表八尺，圭应设四丈四尺，如不便设，是法非公也。其二，若用简仪及赤道仪测五星亦不足盖五星所行，非赤道亦非黄道，其所测得五星在某宿度是赤道，宿度非真黄道及本道度，又星在南在北某宿与某宿相距之度非星之经度，测时欲得其真，有数度之差。
测五星正法第七

新法测定五星为本法，历元皆以恒星为本，设五星与某恒星相距若干，依法得其经纬度。
测星之仪为黄道浑仪及弧矢六合等仪〈见恒星历指〉。法曰：先定恒星二星与某纬星相近，用仪测其相距若干度，分以法求纬星之黄道经纬度〈见测量全义九卷及恒星历指〉。
首宜密测者乃纬星冲太阳之时刻，法曰：如本日测得其星经度，随推太阳经度，相距为天半周，即为相冲之时，若有多寡，则测之又测，务得其冲，岁岁如此，求之以两测中积日所行之度，相比则可得其盈缩差也〈见各星历指〉。
次测晨夕二留留时，推算太阳经度，必得前后二留距太阳之日度多寡非一，若太阳在某宫，宿次星在某宫，宿次相比得距太阳度数多寡，取其大距数而以本法推之可成加减表〈详见五纬历指〉。
测星纬行，古来无法。新法用黄道浑仪比测恒星，又求某星而变其纬，或从南往北，或从北往南，得各星黄道上有二相冲之处，定六宫为南，六宫为北，又测各星冲对合伏太阳及二留时之经度，多测亦可得其纬〈有本论〉。
五星盈缩历考第八

太阳有盈缩之限，或疾迟两行之界，古法定在冬夏二至，新法曰：不然。盖以今世最高庳在两至后六度为盈缩之限，太阳于限近远得均数大小，而视行有差，太阴最高，乃月孛也，太阳太阴二最高俱有本行，而非恒星之行。
五星亦有盈缩之行，有盈缩限及迟疾损益之界，古法未认其本行，而恒定于恒星某宿某度，则非也，此不合天之一根也。
又曰：所定于某宿之度分亦非真盈缩初末等界，如古法定木星在虚约四度或元枵宫二十二度，新法定木星二行之界在降娄宫十度，他星各有前后〈见本历指〉。
五星盈缩立成考第九

大统历分天周为二十二段，以十一段为盈，十一段为缩，各段十五度有奇，以三差法置各星盈缩大积度，求得各段之均数，今有可疑，盖各星大均数多寡各有真数，如云木星有六度半，实不过五度弱，土星有八度又四分度之一，实不过六度半弱，他星类此。若中段所立之均数，因三差法尤不足以得真数〈见日躔考〉，此又不合天之一根也。
历局新推土火金木四星之会合凌犯行度第十

一九月初四日丁巳昏初
新法推得火星与土星同度，南北相距差一度五十四分。
大统推在初七日同度。二法约差三日。
一九月初七日庚申卯正二刻，
新法推得金星与土星同度，南北相距差三度三十分。
大统推在初六日同度，二法约差一日。
一九月十一日甲子昏初，
新法推得金火二星同度，南北相距之差一度三十分。
大统推在初三日同度，二法约差八日。
一闰八月二十四日丁未。
新法推得木星犯鬼宿内积尸气。
一九月初一日甲寅，
新法推得木星在鬼宿二度有奇，先于闰八月十五日，已入鬼宿初度。
大统推在鬼宿初度，先于闰八月二十四日，始交鬼宿初度。二法约差九日。
新法四星经纬图式列后
崇祯七年九月初四日土火金三星经纬图缺崇祯七年九月十一日土火金三星经纬图缺崇祯七年闰八月二十四日及九月初一日木星经纬图缺崇祯七年九月初七日土火金三星经纬图缺缺
已上五测本年八月十八日疏奏奉旨临期登台公同测验，与本局所推悉合，覆奏，因命再测，又皆相符。今所绘木星犯积尸气图，算悉照曩日进呈者，其先后相犯时日及已经测验过各星行度与大统相去悬远者约录于后，以徵二法之孰疏孰密云。
崇祯七年十一月初三日，木星以赤道于积尸气为同度同分，依黄道则于初五日为同度同分，此日木星细行为百分度之十一，迨十月二十日木星自鬼，宿东南东北两星中而入于本宿座至十一月二十日，乃繇西南西北两星中线而出鬼宿，其木星体距积尸气体为百分度之五十四而为犯。
八年四月二十三日木星以赤道于积尸气为同度同分，依黄道则于二十四日为同度同分，此日木星细行为百分度之十九，自二十三日午时繇鬼宿西南西北二星之中而入本宿座至本月三十日酉时繇东南东北二星之中而出鬼座，其木星体距积尸气体为百分度之三十八而为犯〈云五十四三十八者即古书所谓五十四分及三十八分也〉。
图图

本年新法推水星三四五六等月俱晨不见，而大统载三月十八日晨见至四月二十一日晨伏，迨本月会同监局屡测，委无水星出见。
又新法推水星于七月二十五日晨见至八月二十三日晨不见，大统载八月初七日晨伏不见至九月二十一日夕见，及公同测验，果于八月二十三日以前皆晨见。
本年八月十二日己丑夜，新法推木星会合轩辕大星，依黄道算本月十二日夜即十三日子正初刻木星在鹑火宫二十四度三十九分纬北五十分，轩辕大星本年在鹑火宫二十四度四十七分纬北二十七分，本时木星在出极一直线上未及轩辕八分，而南北相距约二十三分，依赤道算本时，木星在张宿四度○分，是日与轩辕大星俱在出极，大统载在张一度，与新法约差三度，因于本日公同登台测验，果测得木星与轩辕大星同度同分。
本年八月二十七日测木火二星同度，以黄道算本日未时二星会同于鹑火宫二十七度二十六分，火在北三十分，依赤道算二星在张宿六度三十三分至子正时二星皆在出极，一直线下距夏至为五十九度五十分，大统推此日木星在张宿四度火星在张宿三度相会，合在二十九日，则木星差二度半，火星差三度半，会合差二日。又是日卯正初刻月与木同度，月在南三十六分，然因视差算得寅正二刻月木火约同度〈用直线过月之中心〉，至本日子丑时阴云监官未到迨，至寅时天已开霁，本局官生亲测得月木火皆为一直线。
本年新法推金星八九等月俱晨见，至十月初三日始晨不见，大统载九月初九日晨伏，则此后皆不见时矣，及九月十七等日会同，公测委见金星晓出。又新法推水星八月二十六日晨不见，至十月初六日始夕见，大统推九月二十一日夕见至十月二十四日夕伏不见，则前此皆见时矣，及九月二十八等日会同，公测委无水星出见。
九年二月十二十三十四等日，大统推木星在张宿二度，旧法谓轩辕大星在张宿三度又五分度之一，则此时木星该见于轩辕大星之西一度弱，新法推此日木星逆行将留在张六度又六分度之一，新法谓轩辕大星在张四度则木星在东，轩辕大星在西相距二度强，至测时木星果在轩辕大星之东。本年新法推木星自二月十二日至二十六日常见，大统推本日夕伏后此皆不见，共差十四日，迨部监同测，委见水星未伏。
本年大统推火星从三月二十七日起至五月初八日止，夕退夕留夕迟共三十九日，尝在轸宿十六十七度内，新法推此时火星尝在角宿一二三度内逆行不入，轸宿是旧法差四十日而宿度亦差三度矣，且据旧法推，在轸宿则火星当在角宿大星之西，新法推在角宿则火星当居角宿大星之东，及疏请亲览每至戌时，火星果在角宿大星之东，相距不过一度。
本年新法推木星七月十四日夕不见，大统推七月二十三日始夕不见，据旧法推则前九日皆为见期也，迨会同公测委无木星出见。
此上所录皆系会同部监公同测验过者其未经测者每年相差甚多，兹不备录。
古测五星相掩或掩他星摘推目第十一

新历列有日月五星永表者，或用以稽上古五星之凌历犯掩，或用以推未来千百年各星之行，故逆推而能上验往古，因知其亦必下合将来矣。
按史传所纪，某星之行每有仅录年月日而未有时刻，夫星有一日行度分者，今既无时刻，何能正合于表乎。故于不纪时者并不援以为證。又纪各星聚于某宿，不言相距度分及不言本宿某度者亦不借證。又如凌犯古纪甚多，迨考其时刻距度，仍皆挂漏，亦莫能用，即若言相掩者则惟土木可得其准缘其行迟耳。至于火金水则每日或行一度或行半度，盖行疾则第可仅得之而已，然其纬度数日但移数分又可以得其准也。
古史恒谓或金或水失行当见而不见不当见而见，此则新历备阐伏见正法，故亦援一二以徵之。表首横行为甲子数自，帝尧八十一年为第一甲子，至天启四年则统纪甲子者六十六，下为本甲子内之年。
〈按：此下有古测五星记十馀篇，年代先后讹谬已甚，悉去之〉
测五星经纬度第十二

一用黄赤全仪，此仪制有黄赤二道，上系移线二，一用测经，一用测纬，最为尽善之器，善用之者则各星所行宫度分秒靡不可得，其作法见浑仪说中。一凡见某纬星掩某恒星之一，即稽恒星表之经纬度分亦为某纬星所际之经纬度分也。
一凡某星近犯恒星，则经度可得其真，而纬度则仅可得之，盖经度乃从黄极过二星之心，必定于黄道一度分上。若纬度者不能用仪，惟以目测，其相距若干，故莫能得其真也。
一凡某星介于四恒星之或中或外在一直线之交，即取恒星图界二直线联而算之，亦能得其经纬。或不用图，但用算亦可。其法见测量全义九卷中。一凡某星在午线上或有恒星亦在午，则第测恒星高弧即可得其赤道经纬。
一凡某星在地平而得其出没点之地平经度，即可得其纬盖地经度乃正卯酉距南北之若干也。或此时有一恒星在午，亦略可得某星经纬〈用星球浑仪可算〉。一用弧矢仪测某星距二恒星若干，用法推算可得其经其纬，法见《测量全义》九卷。
以上概言其测法也，大抵测星得其赤道经纬度分，似易而最要者则在于以法变黄道之经纬云。
駮古测之舛

一以赤道仪测其行而莫能变黄道经纬，是其度分非从本枢所出也，安得无舛。
一测月掩某星者甚谬，盖月有气时二差，恒失其经纬之真度也。
一纪掩犯等会不详时刻，乃星恒有其行，时刻既略，胡可细算其经度乎。
一用移线人目迫近于线，则目瞳子较线为大焉，得视而不失。
测五星仪目

黄赤全仪
即浑仪之类也，其制不用他圈，惟具黄赤二道及子午规而已，测星系移线以用之。

简仪
以一盘当赤道，其移线则代活赤道云。

天环
亦浑仪之类也。

弧矢仪
以全规六分之一为弧，用半径为矢。

枢仪
以细绹系急用代天枢，然当定准北极出地及对正子午庶几不差，若二星以赤道在同度者，此可测之。

直线或界尺
用量二星成一直线。

经纬象限
测地平高及经度。

过极圈
用之可得赤道纬度〈以上原本历指卷二十四五纬之九〉。