钦定古今图书集成历象汇编历法典

　第六十卷目录

历法典第六十卷

历法总部汇考六十

新法历书十

交食历指二推会时简法第四〈凡四章〉

前依几何法，用日月行度推会时者，论其所以然也。若恒时推步，别用诸表。诸表虽从图出，其用之甚易不烦，故名简法。然以此便初学耳。明理之家，正须从难处入，不宜恃此为足也。
图

列表法
交会表从前图出者，止均度二表。〈即加减度表〉一为太阳均度，一为太阴均度。论太阳如图，甲丙、乙丙两直线至黄道之相距弧为均度，用三角形法求甲丙乙角，则与求丁戊弧不异。盖丁戊能代丁己，繇甲丙乙角
图

能代丁甲己角。〈见几何一卷二十九题〉但丁甲己非三角形，无从可得均度。故用甲乙丙，则恒有乙丙全数，有甲乙两心之相距，〈三五八四〉又有自行之正或馀角，如庚乙戊角，即周圈之上任所至，可以三角形推得均度也。论太阴如左图，独交会时其
图

本轮与地同心，则有本轮之加减度最大者，为次轮之最远，在最高最庳之间。因月体至此去本轮心最远，故其二轮之半径必合为乙丙直线，而指月体。其数八七○○，又有甲乙全数，有本轮上自行度丁戊，成甲乙丙三角形，依前法
图

可推乙〈阙〉丙角之均度外，此则月居次轮最近或最远之左右，从地心出直线指实行，即月体所居无两半径合并之数。故所求均度非一三角形可得，须用两形求之。如图，月居丙，因在次轮之，左必得乙丙直线，乃生乙丙丁及甲乙丙两三角形矣。求中会时历元后，推首朔至二百年，每年可当历元。法先定崇祯元年戊长天正冬至后第一日子正时为根，而恒减通闰一十日六十○刻一十一分一十二秒，遇闰年多减一日，不满数加朔策二十九日一十二时四十

四分三秒，减之得次首朔。若用加法则以太阴年〈十二朔策〉三百五十四日八时四十八分三十八秒，加所得之数，而减太阳年三百六十五日，遇闰年则三百六十六日，不满亦加朔策减之。
历元前总甲子亦于每甲子年定首朔，表自六十六甲子〈天启四年〉逆愬而上，每加六十太阴年，满朔策去之，馀为三日七时一十三分○六秒。依此递加共为若干甲子而得若干总数，满朔策去之，馀为本甲子年首朔也。更有每年零用表与历元后二百恒年同法，亦岁减通闰，每四年加闰一日，则先一年减之为一十一日一十五时一十一分一十二秒，得次上首朔也。
又有太阳引数、太阴引数二表，有交行度表，有太阳经度表。太阳引数者，是太阴年本行减最高行即一十一宫一十九度一十六分八秒，〈亦即三百五十四日八时四十八分三十八秒〉加朔策得一十八度二十二分三十九秒。太阳经度者，从最庳起算太阴年所行得一十一宫一十九度一十六分五十二秒，加朔策得一十八度二十三分一十六秒。太阴引数者，太阴之自行也。从本轮最高起算，太阴年所行除正周外得十宫九度四十八分○一秒，加朔策得十一宫五度三十七分○一秒。交行度者，太阴年所行除全周外，得八度○二分四十七秒，加朔策得一宫八度四十三分一秒。四表皆同一法，恒加太阴年行度。若首朔表加朔策，诸表亦加朔策。但首朔表论闰日，后四表不论闰日耳。其通闰在零年顺推则首朔用减，下四表用加。在甲子年逆推则首朔用加，下四表用减。
用表求中会

中会法若下推将来，用历元后五种行度表第一格，简得冬至后首朔，次用朔实十三月表加之即得。若上推既往，用历元前总甲子表得甲子年首朔，而所求交会即在本年，则于十三月表查朔策或望策，加之即得所求交会。不在本年，先查六十零年表，加相距之年，后加相距之朔策，或加望策即得。
假如壬申年九月庚戌夜望有食，用本年下首朔○日一十六时二十五分二十一秒，纪日三十七，从冬至至本月望相距十月又半，故朔实十三月表内对十月得二百九十五日七时二十○分三十一秒，加望策一十四日一十八时二十二分二秒，总得三百四十七日一十八时七分五十四秒，满旬周，〈六十日〉去之馀得中会。在庚戌，日时刻从子正起算，得在酉初七分五十四秒，又试用历元前总甲子表于六十六甲子下，得○日○三时四十四分○八秒，纪日五十五，至壬申积八年，查零年表八年下，得○日一十二时四十一分一十三秒，纪日四十二，朔策望策皆如前总，得四百有三日，满旬周，去之，馀亦得庚戌日时分秒，悉如前推，会朔则不加望策，馀法同。若尽求一年之中会则于首朔或首望加朔策于总数以后，累加之至十二次，然后从首会加太阴年三百五十四日八时四十八秒，得合于终会即所推十二会悉合矣。
用表求实会

两中会之间朔策也，定为二十九日十二时四十四分○三秒○九微，实会则二曜之自行，所至有时过朔策，有时不及朔策。过不及之大差，多禄某定为一十四时三十○分，第谷去减二十分，法用引数，依均度表加减求之。故推中会并列太阳、太阴两引数以求加减度。又列太阳平行经度，后来亦用太阳均度加减为实行度，而以两均度所推得之。近实时约略改为目见器测之视时，如下文表中太阳自行，从最庳起算，其经度从冬至起算，前图所说或从最高或从春分，其理不异。
假如求崇祯五年壬申三月癸丑夜望时，先定中时。
图

如图，总数一百七十○日，去二旬周，馀五十○，乃所用〈阙〉。癸丑日某时某分其引数经度必与本时相合，次以太阳引数对四宫六度查均度，得一度三十七分三十六秒，差度一分一十六秒，偕引数之小馀，用三率法，
六十分为一率，一分一十六秒为二率，小馀三十分四十八秒为三率。

求得本差三十九秒，又因向后之均度渐少，故以本差三十九秒减本均度，止一度三十六分五十七秒。次从表首行查号为加即书加，又以太阴引数对五宫八度，得一度五十五分○七秒，差度四分五十八秒。向后均度亦渐少，亦以差度偕引数小，馀所求本差分秒减本均度，止得一度五十一分二十○秒。其号为减即书减，依前法两均度一加一减，宜相加即
图缺得日月实相望差度，如上图。次用四行时表查月距日时，得其差时分秒，或加或减于中会，则不远于实会。若均度皆号为加，而太阴所得小于太阳所得，或均度皆号为减，而太阴所得反大于太阳所得，或太阴为减，太阳为加，则所化

时刻恒加于中会时刻，否则恒减于中会时刻，以得实时刻。今三度二分五十二秒，得六时，又度馀二十五分二十五秒，查得时馀五十分○二秒，加于前一十三时四十三分三十六秒，得实会在二十○时三十三分三十八秒，为戌正也。
密求实会

前以中会之引数求实会，今云密者，以前经加减，故得次引数，与实会相近。复如前，求得时刻复加或减于中会，乃得正实会。法依前所用四行时表，以时刻
图

反查度分，因太阳自行一日不异其平行，仍用其平行表。以六时五十分得一十六分五十秒，加于前引数得太阳总引数四宫六度四十七分三十七秒，此距间于本表查得太阴行三度四十三分一十一秒，以加于前引数总，为五宫

一十二度二十九分一十七秒。又以此两引数求得均度，如上图。亦以一加一减，故当相加，而两均度之差较前更少，变为时亦少，即依本表三度二分五十二秒，得六时，又度馀六分六秒，得时馀十二分，度馀二十八秒，得时馀五十五秒，总加于中会，复得十九时五十六分三十秒，为正实会，在成初三刻一十一分三十○秒，更欲密推则用次得之实时，又求第三引数，以复求均度以较，次得之太阳均度，其二曜相距之弧亦变为时刻，若同前，即前得无疑，若异者，用后得为正实会也。
图缺求视会实会第一

前所得实会时刻虽则合天，于人目所见仪器所测未尽合也。所以然者，太阳行度赤道交子午圈有升度差，随时变易，日日不均。〈详见日躔历指〉而今依历元推步，或用表查算，无能不均。须用加减时表以求本地可见可测之实时，又推步者，但依本地所定子午线，其在地方不同子午线者，难可通用。故又用里差加减，以求诸方所见所测之实时也。
实时改视时

如前求太阳实度得中实两会相距时刻，查太阳平行时表，得分数，依前加减；时刻亦加亦减于前得太阳经度，乃得实度。假如前推壬申三月望会太阳平经度为四宫〈冬至起算〉一十二度三十四分○一秒，中实两会之差得六时一十二分五十五秒，其距间又得太阳平行一十五分一十八秒，以加于中会时之太阳平经度，得其实会时平经度四宫一十二度四十九分一十九秒，更加其次均度一度三十六分三十六秒，则太阳实度四宫一十四度二十五分五十五秒，今查加减时表得○九分五十五秒，其号为加则以加于实会，共得二十时○五分四十四秒，算外得癸丑日戌正五分，为顺天府所见所测之食甚时。
见食随地异时

月食分数天下皆同，第见食时刻随地各异，何也。人各就所居之地，目力所及者，则见月食。而各所居地皆以子午正线为主，若其地同居一子午线者，〈南北地纬虽纬东西地经则同〉则所见月食之分数迟速皆同也。若地易，子午线易，则时刻并易矣。所以然者，时刻早晚因太阳行度随人所居，各以见日出入为东西为卯酉，即以日中为南，为子午，而平分时刻。故月食时必本地之日未东升，或已西沉，乃得见之。若在其昼时刻，不可得见也。天启三年九月十五夜望月食，顺天府及南北同经之地则初亏在酉初一刻一十二分，食甚在戌初初刻，复圆在戌正二刻一十三分，各算外高丽及其同经之地即初亏在酉末戌初，而西洋意大里亚诸国日尚在天顶，为午正，则不见月食。以里差推之，西洋之初亏在巳正三刻四分，食甚在午正一刻○七分，复圆在未初三刻一十分，各算外虽月入景七分五十六秒，所居宫度彼此远近皆同，而以里差，故彼地彼时太阳在午正二十二分，太阳反在子正二十二分，食甚正在日中，何从见之。今壬申年九月十五日夜望月食，初亏在卯初三刻，则陕西、四川等处得见，南京、山东等近海东境不可得见也。秦蜀之子午异于东方之子午故。
今以顺天府推算本食，因定各省直之食时。宜先定各省直视顺天子午线之里差几何，后以其所差度数化为所差时刻，每一度应得时四分，向东以加于顺天推定时刻，向西则减，乃可得各省直见食时刻也。若日食则其食分多寡，加时早晚，皆系视差东西南北悉无同者，必须随地考北极高下差，其距度随地测子午正线差，其经度乃可定。其目见器测之视时定子午术，见西测食略中，法于当身所居目见器测考，定一月食之时刻，与先所定他方之月食时刻较算，或两地两人同测一月食，彼此较算，乃以所差时刻得所差度分也。
前顺天府所推月食时刻，并具各省直先后差数，因未得诸方见食确数，无从遽定地之经度。但依广舆图计里画方之法，略率开载耳。既而咨报多相合者，然非甄明之辈躬至其地，测极高下，见食早晚，终未敢以耳闻臆断，勒为成书也。左方所记政所谓略率开载者，欲求决定，当俟异日。故称约加约减焉。南京应天府及福建福州府，约加四分。〈凡一十五分为一刻〉山东济南府，约加五分。
山西太原府，约减一刻○九分。
湖广武昌府、河南开封府，约减一刻。
陕西西安府、广西桂林府，约减二刻○四分。
浙江杭州府，约加十二分。
江西南昌府，约减一十分。
广东广州府，约减一刻○五分。
四川成都府，约减三刻○七分。
贵州贵阳府，约减二刻○八分。
云南云南府，约减四刻○八分。
證子午差变易见时

万历元年癸酉十一月望，依大统历推月食初亏丑正一刻，食甚寅初三刻。本夜第谷在西国测得食甚在戌正○三分，于时太阳近冬至，所测时即定望时，无加减。大统所推稍疏，大略东西差时三十馀刻，为顺天府所见，后于西国也。
万历五年丁丑三月十五日夜望，依大统历，月食甚寅正一刻。第谷测戌正三刻○五分，先后差七小时一刻一十分，为一彼一此，子午异线变易加时也。万历二十年壬辰十一月望，大统历记食甚寅初二，刻第谷测在戌初二刻○七分，加时差二分，总得差七小时三刻○二分，则西国之夜望为顺天府之晓望，西国半夜后所测在顺天为次昼，不可得见也。万历四十年壬子四月十五日夜望，历官报月食初亏寅正一刻，既实测得寅正四刻，当时西国把沕辣有测戌正三刻○八分者，更西多勒都测得戌正○，三方同测，不必加减时，得顺天府较极西差九小时，正较中西差八小时○七分。
万历四十四年丙辰正月十六日夜望，云阴不见，初亏至戌正一刻，见食一分，约食九分有奇。测复圆在亥正四刻。于时，小西洋之印度国，测月正出地平上食九分有奇，此地北极出地一十五度二十五分，因本食时，太阳在娵訾宫一十四度，其半昼弧得五小时三刻○八分，则太阳入地时，正太阴食甚时，为酉初三刻○八分。又复圆时，测毕宿大星高五十五度，次测轩辕大星高四十六度，以先测之毕宿大星得复圆在戌初二刻一十一分，以次测之轩辕大星得复圆在戌初三刻，则顺天府较后三小时一刻。万历四十五年丁巳正月十五日夜望，依大统历，推复圆亥正二刻，庶几密合广州府测得复圆亥正一十三分，南印度国测在戌初三刻，则广州府较顺天府偏西差一十七分。南印度更西较广东差二小时一刻一十三分。
天启三年癸亥九月十五日夜望，初亏月未出，顺天府测得复圆戌正二刻一十分，杭州府测戌正三刻○七分，上海县测亥初一刻三，方较得杭州视顺天偏东差一十二分，上海视杭州更东差一刻○八分，上海视顺天偏东，总差二刻○五分。
天启四年甲子八月十四日夜望，历官报月食一十三分六十五秒，初亏丑正初刻，既测得一十六分六十三秒，初亏丑初二刻○六分，小西洋北国测得子初三刻○八分，泰西教主京都测得酉正三刻一十三分，较得北印度视顺天府偏西差七刻一十三分，视泰西差六小时二刻○八分。
天启七年丁卯十二月望月食，历官报初亏寅正三刻，复圆长初三刻，既实测得初亏寅初初刻○一分，复圆卯正三刻○六分，与西法合。于时太阳在元枵宫一度，顺天府出地平上为辰初一十一分，依大统历推复圆在辰初三刻，则在日出后二刻，不可得见，而同时陕西西安府则见复圆，在天测得大角星高四十七度，其北极出地三十四度一十九分，得月食初亏丑正二刻○三分，将复圆，测角南星高四十一度五十分，得卯正一刻○二分，视京师偏西差二刻○四分，为八度半也。
崇祯四年辛未四月十五日戊午夜望，依大统历，月初亏丑初三刻，依新历初亏丑初○六分三十八秒，实测得丑初○五分，大角星高四十九度四十分，距午正三十九度，加其距太阳一百五十七度二十七分，得太阳过正午一十三小时○五分二十八秒，去半日刻，馀一时○五分，为丑初○五分，新历初报各省较顺天差数。在四川成都府初亏子正一十四分三十八秒，彼中实测正合，是成都府视京师偏西差三刻○六分，得一十二度四十五分，为两子午线之度差。较各处实测食之时，如此凡有两处，东西相距则所得时刻必差，若相距愈远，则所得食之时刻差必愈多。盖因子午不同證见食时故不同。
推步交食本论第二〈凡四章〉

步交食之术有二：一曰加时早晚，一曰食分浅深。加时者，日食于朔，月食于望。当豫定其食甚在某时刻分秒也。食分者，月所借之日光食于地景，地所受之日光食于月景，当豫定其失光几何分秒也。加时早晚非在日月正相会相望之实时，而在人目所见仪器所测之视时。乃视时无均度可推，故日月两食皆先求其实时，既得实时，然后从视处密求日食之定时。〈详见后篇〉惟月食则实时即近视时也，然日与月实相会之度分未定，即欲求其实时无从可得，故须先推中会时，计其平行及自行，而得均数。然后以均数加减求得其实会，因得其实时矣。古法所谓躔离朓朒，即自行均数之谓。兹特深求原委，以故倍加详密耳。若食甚之前为初亏，食甚之后为复圆，此两限间亦应推定时刻分秒，其法于前后数刻间推步日躔月离，求其实行视行。
月有迟疾，经时则生变易，故宜近取。

以得起复之间时刻久近也。食分多寡谓日食时月体掩日体若干，月食时月体入地景若干也。其法以日月两半径较太阴距黄道度分，得其大小，次求二曜距交远近，与古法不异。第日月各有最高庳，景径因之小大，黄白距度有广狭，食限为之多少。至于日食三差，尤多曲折，此为异矣。前论交食原及推交会时，太阳太阴皆同一理。次后论两食之徵亦然。更后即不复能为合论，故先论太阴入景浅深，奥其食时久近。次以三视差论太阳之食分加时，难易迥殊，详略亦异也。
推月食有无

欲徵月之有食，一论交之左右，一论交之前后。论左右者，视太阴距黄道之纬度，以方于月半径、地景半径，并而纬度为小，则食。若大者，过而不相涉，若等者，过而相切，皆不得食也。论前后则食之处必在正交中交之或前或后，而不甚远，甚远则距度广，月与景亦过而不相涉也。近则距度狭，狭则必小于两半径并而无能不食矣。是故徵食有两法：一略一详，略法者，未定月食之实时，先求中会时，亦聊可测其距度也。试用表查平望之宫度，并注其同格相当之交周度，若正得六宫或○宫初度，则太阴在正交中交之二点，〈即罗计即龙首龙尾〉无距度必食，若过交或不及交，而度分相近不出食限之外，亦食也。
假如考壬申年三月会望，用历元后表，查首朔相当之交周度得七宫一十八度四十二分一十一秒，为当时正合经朔之平交度，次用十三月交周度表，查第四月，又得四宫○二度四十○分五十六秒，加望策六宫一十五度二十分○七秒，得总数满平周，去之馀六宫○六度四十三分一十四秒，是太阴过中交六度有奇，入食限内已六七度，即月体必半入地景，而定为有食也。若用历元前总甲子表以推既往法，先考总甲子下首朔，及交周度，并列之。次查其零年亦如之，次加朔策或望策，亦如之，总之即得中望及其相当之交周度。万历五年丁丑三月壬寅夜望，大统历，纪月食一十二分五十秒，本年在六十五甲
图缺子第十三年，列数如上，得癸卯为本食日。
历纪壬寅者，是其夜望也。实过子正为癸卯日之卯初三刻，得食甚，故进一日。
再查交周度表，得太阴当时过交中止○五分三十三秒，深入食限之内，宜得
图缺全食，不止十二分五十秒也。
纲目纪唐肃宗乾元二年巳亥春二月月食，今上推其食分加时法，查本表五十一甲子，及零年朔策等依前，列数如上。
依总数得太阴过中交止一度四十五分有奇，宜全
食，食甚时在丁未日丑初三刻也。
其详法则更推太阴实望时之距黄纬度，以较二径折半，若距纬度小者，即月不能不入于地景，因而有食，如下文。
求太阴实望时距度

中望时表中已得相当之交周度，今更以加减之时，更求交周度。复加或复减于前所得，即实望时之平交度也。次又以均度或加或减，乃得实望时之实交度矣。
假如壬申年三月，中望时交周度过中交六度四十三分一十四秒，时差〈实会与中会相距〉得六时一十二分五十五秒，交周时表中查得三度二十五分三十四秒，因时加度数亦加，若减亦减，总得一十度○八分四十八秒，犹是平交度也。更减前均度一度三十二分五十秒，得实交度八度三十五分五十八秒，今以交周度求距度，用太阴距度表于六宫八度，得四十一分二十九秒，表中次度多五分○九秒，故以交周度之馀三十六分，得差三分五秒，相加得太阴距黄道南四十四分三十四秒。
因交周度为太阴之右旋度，相加于左旋之交行度，〈即两交行一名罗计行度〉故所用均度不异于自行之均度，其平行一年得四宫二十八度四十二分四十五秒，一日得一十三度一十三分四十六秒，一时得三十三分○五秒，以此求距度，用甲子年为纪首，于时太阴去正交八十三度二十九分二十四秒，依法算得总平行数六宫一十度○九分○五秒，次减前均度所得数六宫○八度三十六分一十五秒，为实交度也。次
图

依三角形之比例，则全数与全距度之正弦若交周度之正弦与距度之正弦，盖黄白道之全距算交食，无过五度交周度之弧，又从近交所始也。如图，甲丁为白道，甲戊为黄道，己丙乙为过黄极及交周度之弧各一象限，丁戊为黄白

之全距。〈相去最远〉太阴在丙近于中交甲，求其距度丙乙，则甲丁与丁戊若甲丙与丙乙，算得四十四分三十三秒，今依距度四十四分三十三秒，考壬申年三月会望有食与否，简半径表中用太阴引数○五宫一十二度，得月半径地半景并为一度四分三十五秒，而距度止四十四分三十四秒，距少径多，太阴之行无能不入景，即无能不食矣。
推日食有无

欲考会朔有食与否，须定会朔时太阴之视距度，以较于日月两半径并，若视距度大于二径折半，或等者，不食也，小则食矣。视距度者，生于视差而本于高度，故当先求高度。法于会朔时以太阳本日距赤道度加于本方之赤道高度，得本方之子午最高度，又于赤道高度去减距赤道度，得本方之子午最庳度。次求两数之正弦并而半之，为三率，以太阳距午正弧之正矢为二率，全数为一率，依法算得第四率，以减子午最高或最庳，馀者为二曜高弧之弦。大约太阳距赤道北则所得之数与子午最高相减，若太阳距赤道南，则与最庳相减。
假如崇祯七年甲戌二月朔日，顺天府定朔在巳正一十四分，日月距午正线七刻○一分，于赤道得二十六度半，用其馀弧求正矢得一○五○七，为二率。因太阳在降娄宫八度三十分四十秒，得其距度在赤道北三度二十二分，以加赤道高得五十三度二十七分，为子午最高，相减馀四十六度四十三分，为子午最庳。次求其二正弦并而半之，得七六五六五，为三率。算得四率为八○四四，以减五十三度二十七分之正弦，馀七二二九○，查得四十六度一十八分，太阳在地平上之正弦也。今查日月高庳差表，〈即地半径差在日食表中〉于转周度得太阴距地之远其下依高度取其相当之视差得四十三分，去减太阳之视差二分，〈高度左方取之〉馀四十一分，以减太阴之距北实度四十八分五十五秒，馀○七分五十五秒，为太阴视距度，以较二径折半，为甚小，知月之掩日分数为多矣。凡人目所见，太阴在天顶南，则月之视所较其实所恒偏南偏庳，故其距度多能变易太阳之食分，又月在黄道南，则当以视差加于距度，人所居愈向北，所得视差愈大，其视月愈偏南，而所见日食愈小。若月在黄道北，所得视差或小或等于距度，当以减于距度，则视处反近于黄道，而北方所见日食大于南方矣。第视差之大若过于距度之大，而去减距度，即北方视月又偏居黄道之南，比南方所见更远，而得日食又小。
试如祟祯二年己巳五月己酉朔日食，四年辛未十月辛丑朔日食，今以相较，己巳年太阴实所距南八分四十九秒，〈阳历〉顺天府本时之地平高得七十三度一十八分，其二曜高庳差一十七分四十秒，以加距度八分四十九秒，总得视距度二十六分二十九秒，以减于二径折半三十二分○四秒，馀止五分三十五秒，以推日食，所见宜少矣。若浙江杭州府高度八十三度一十四分，推二曜高庳差，得七分○九秒，以加距度八分四十九秒，得一十五分五十八秒，视二径折半为一倍小，即月掩日宜得大半也。辛未岁不然，太阴距度在黄道北一度一十五分二十二秒，顺天府合朔时得日月高止三十五度四十一分二十○秒，二曜高庳差四十八分，以减距度，馀二十七分二十二秒，视二径折半不及者五分一十六秒，即见日食若杭州府高度四十三度四十八分，得高庳差四十四分，以减距度，尚馀三十一分二十二秒，是其视距度略等于二径折半，则月不能掩日也。大约太阴实距度在黄道南，〈论中国相等同讳之地〉其六十度以下之高庳差必大，或等于二径折半，即使无距度，犹未得食也。若距在北，则太阴之视差能偏南一度强。
最大者六十三分，减日视差二分得六十一分，

必距度之大倍视差之大，乃不食，否则有食，详见后篇。
累推历元前后交食

交食之法上推往古，下验将来，百千万年当如指掌。若悉用古法推步，穷年累月不能得竟矣，此交食诸表所为作也。用表则远愬唐虞，下沿万祀，开卷暸然，不费功力，如读先秦古书，见春秋前后一切日食皆不记月日，今欲一一考定是何月日，又如目前推得
图

见食，而欲累求向后若干年应得若干食，是皆不用交食全法。依交周度表，便可得之。法先求某年第一中会，〈即首朔也〉周表取相当之交周度，若入食限即第一食也。求次食加五月或六月，亦必入食限矣。若初所求交周度未入食限，则查

交周度十三月表，求某数相加而入食限者用之。假如周考王六年乙巳，史记年表但云日月食，不言某朔望。今求其月日，则是年八月一日食，三月九月两月食也。依表，本年在三十一甲子，首朔为二十七日○二时一十○分二十九秒，其相当之交周在四宫二十六度四十四分一十八秒，纪日一十零年乙巳，在表为第四十二年首朔，得一十四日二十一时四十七分二十四秒，相当之交周度为三宫一十八度四十分三十八秒，纪日四十，并两交周度未入食限，更加四月，〈是春三月癸巳朔〉所得距正交不远，然定朔在二时五十四分，则是丑正三刻有奇，非此方所见古未有记夜食者，亦非也，更加五月，得其交平行列数如上。
以一十八时三十三分，知中会在酉正三刻，此时用太阳引数得均度一度四十一分，太阴引数得均度三度五十四分，并之得日月相距五度三十五分，化为时得一十一，以减平朔，得定朔在辰初三刻，是为周考王六年八月辛酉朔，本地所见地平上之日食矣。
甲戌乙亥丙子丁丑戊寅己卯
一二○一二○一二○一一二
宿四三四二一二二一二一九八

纪　二二一四四四三三三二五五
日四一八六三○八五二九七四

时　一一二一一二○○一一○一
时二七一三七二二七一五七一
五二四二五一四○二五三五
分九三七八二六一五九三四八

交　○○○○一○○○○○一○
宫○六○五一五○六○六一五

周　○一一一二二○○○一一二
度七一五八二六○四八三六○

度　二二三五五五五五○二二
分九九○二三四六七九○一二

求本年月食则于前总甲子及零年乙巳数外，总加望策，得第一平望，其交周度在两交之间，无食。更加三月，则丁丑夜望，月过交中，分数甚少，必全食。然定望在昼，但见其初亏，不见其食甚，更加六月，得交周度○宫○六度四十七分，太阴入食限，又时在九月乙亥日，用均度得定望为戌初三刻，但见其复圆，不见其初亏也。是两皆带食，故史官纪焉。又日一食，月再食，故统言之曰日月食也。
甲戌乙亥丙子丁丑戊寅己卯
二○一二○一二○一二○一
宿七八八七八七五六五四六五

纪　○○○○五五二二一一一○
日九六四一八五三○七四二九

时　一二○○一一○一一二○○
时八三三七二六八二七一一六
三○二五一三一四○三五二
分七一五○四八九三七二六○

交　○一○○○○○一○一○○
宫五一六○○○五一五一六○

周　二二○○○一一一二二○○
度二六○四八二五九三七一五

度　○一一一一一三三三四四四
分九○一三九五七八九一二四

欲下推累年之交食，先如前求第一食，自此以后或越五月而一食，或越六月而一食，日月皆然，此其大凡也。法查交周度十三月表，用片楮别书五月六月之数，向本表之各月下递并而试之，但合于食限以内者即有食之月也。如崇祯七年甲戌第一日食在三月朔，算本年及向后各年有食之朔，如前图。每两平朔皆入食限，惟乙亥之两朔间，戊寅后，己卯前之两朔间，各越五月，馀皆越六月，其食也，太阴有昼有夜，太阳有昼夜，又分南北，故非一方所见。惟用此考其可见者，推之求平望法同此。如后图，图中独丙子后越五月，馀皆越六月，凡交食得某月入食限，即次后一、二、三、四月皆无食，必至五至六，或十一、十二月则食。欲更求本方所见，则推实朔望以时刻定之。
食分多寡之原第三〈凡五章〉

推日食分数，则以太阴距黄道之视度，日月两视径之半，以及二视差。此并有其本论，后篇详之。此求月食分数，则用太阴之实距黄道度，及其视半径地景半径，即可得之。今先论日月景之各半径，次乃定食限及食分也。
视半径所繇变易

凡圆球之去人远，则目视之为平面。欲测其大小者，不依其形，依其径也。目之视径虽以平行线受其像，然相距有远近，即所测得之大小随而变易。近则见大，远则见小矣。暗球生景，其理准此。故受光之体小于施光之体，即其景亦随相距远近而有变易，距远者景钜而长，距近者景细而短也。
如左，日月食合作一图，甲为地球，太阳在最高，为丁，在最庳为戊，太阴日食时在其最高，为己，在其最庳
图图

为庚，月食时在其最高为壬，在其最庳为辛。若从最远之太阳周癸丑引直线切地周乙丙，必相遇于卯，从最近之太阳周子寅切地周者，必遇于辰子寅辰，在癸卯丑限内。在内者，细且短；在外者，钜且长。因太阳距地远近不同故也。论太阴其在最高己，目依甲未、甲午两线视之，若在最庳庚，又以甲申、甲酉两线视之，故两所之小大不同，若在壬在辛，其理准此。上言日月地景三视径能为变易，则日月最高、最庳相距之远近为其缘也。自此而外，更有二缘：一为地所出之蒙气随地不一，一为人所禀之目力随人不一。蒙气居日月与目之间，气厚能散日月之光，使易其本象。如玻璃水晶等体厚光彻，以照他物之象，能改易之。是以人所见日食时，太阴掩日之视径实大于太阳之视径，或相等，一遇厚蒙之气，
蒙之厚薄或本地固然，或因时增减。

即太阳之光体因而展拓，比于依法推步之视径每多不合，故全食时四周亦显有金环也。若蒙气微薄，则月之视径能掩日之视径，全食时昼晦星见矣。其在月也，遇蒙气亦饶有馀光，其初亏复圆，光曜展拓，亦能侵入地景，使食时先后稍损于推步之加时也。欲明其理，姑以数事徵之，试用一平边尺切目窥月体，则白月之光能侵入于尺，尺之暗体当月之处似有阙焉，此其一也。生明之月，其有光之半周大于无光之半周，光之两端芒角犀锐似欲包其魄体，至日食时，魄体入日，日之光体，不收光以让月，反舒光以拒月，故其两端不作锐角而作钝角也。此在晴明时，蒙气微薄，犹不免尔，况浓且厚乎。此又其一也。日轮西没将及地平，适遇云气，全轮若为停轨，累测不移，少选则忽焉而入，又其一也。况日食时月之魄体，月食时地景之角体，全居蒙气之中，蒙气所受日光尤盛，四周皆能消景，则日食时太阴居日月之间，其视径岂能大于日之视径而全掩日体。月食时，地景之角体岂不能稍杀于推步之实景，而损其初末之加时乎。若论目力亦能变日月景之各视径者，目力既衰，大光损之，每每易于见暗，难于见明。故月食时，较少壮之目，能先见月食侵周之景，若日食时，太阳见耀，初亏不能遽见其阙也。西史第谷测月每夕用五六人，皆利眼能手，悉用大仪，种种合法，所测月径趋求画一，乃经二十二测，得其径为三十一分者二，三十二分者六，三十二分者七，三十四分者六，三十六分者一，何故。太光射目，当之者利钝不齐，径之小大随异也。盖人目之难凭如此。
月无大光，不能入于窥表通光之窍，须人目测，有此不齐，若日光透表，其有不齐，繇器疏密矣。
定视径分秒之数
古多禄某限日月地景三径之数，定太阳为三十一
分二十○秒，不论最高最庳，恒如是。太阴最大者定为三十五分二十○秒，最小者亦三十一分二十○秒，地景小者四十○分四十○秒，大者不过四十六分也。然多禄某所当之时乃尔，迨其后，太阳本天之心与地心渐次相就，至于今，最高之去地近于多禄某时，其最庳乃去地稍远，而太阳视径遂不得过三十一分，太阳稍缩则地景稍赢，亦不若变时之细且短也。以故第谷所立新法定太阳之视径，在最高为三十○分，在最庳为三十二分，若太阴则虽距地同，所限朔望二时之视径犹不同也。盖合朔时，月会太阳，四周环受其光，则此时全魄小于望日之全光几及四分之一，是以月在最高即望时，得径三十二分，朔时止二十五分三十六秒，在最庳望时得三十六分，朔时二十八分四十八秒也。又第谷测候之地其北极出地五十六度，清蒙之气甚厚，故推步交食，必依此径乃可得合，何者。月望时明光甚盛，蒙以厚气，光乃加显，径即似大。月朔时，遇日之大光，自己失光，而受光之蒙气环围照映，若或消减，其魄径即似小也。然此第谷所当之地乃尔，用之他方，未必合，何者。此所限大小之径，以步日食，虽则食既，犹显金环，月不能全掩日体，若他方食既，则有昼晦星见，虫飞鸟栖者，故知一方所定未可概诸宇内，以为公法也。假如崇祯二年己巳五月朔日食，依新历先推食甚二分有奇，至日实测得二分，若以第谷所限径用之，此日即见食分数仅得一分一十○秒，谬于实测远矣。崇祯四年辛未十月朔日食，新历先推食甚二分一十二秒，至日实测不及二分，若用小月径推算，即所得更少，不及一分也。视径因乎蒙气而为小大，如此岂可强执一率以概诸方乎。故欲定本地之日食，分必先定本地之蒙气差，以限本地之视径，又宜累验本地之食分加时，然后酌量消息蒙差，视径可得而定也。今所考求酌定者，太阳最高得径三十○分，在最庳径三十一分，太阴不分朔望，〈蒙气稍薄故也〉在最高视径三十○分三十○秒，在最庳视径三十四分四十○秒，地景最小者四十三分，最大者四十七分，日月行最高最庳处之间，视径亦渐次不一，故列表左右，并纪太阳及太阴自行宫度，以考日月地景各相当之分数，是为视半径表。
太阴视径差

视半径表计太阴从其最高至最庳，渐次加大也。若论蒙气则南北二方亦有差别，西国之北地滨大海，其气更厚，故月朔应减，月望应加，以改表中之半径。如北极高三十度，其加减于半径一十○秒，高四十度，其加减三十○秒，过五十至七十极高度，即所加减更多，至六分以上也。
中国北极出地虽止四十二度半，亦近海，故用加减数如前所列，然亦须测验数食，审其果否，乃可执为恒法耳。
地景视差

地景半径之最小者，为四十三分。今本表中太阴自行○宫○度，与相当者是也。继此渐大，至太阴自行六宫初度，其相当四十七分，则为最大。其求之有二：法一以测候，一以推步。第两法所得却又不同，则气能变景故也。以推步者，用太阳在其最高时下照地球所生景长以为定率。若太阴过景之处，则依其远近随时算之。如第谷当太阳在最高时测其距地之远，得一千一百八十二地半径。此所推全景之长得二百五十二地半径又六十分之二十三，恒如是。若太阴在其最高距地之远得五十八地半径又八分，欲求其所当地景者，先于全景内减太阴距地之径数，馀者为过太阴以外之景角，〈景角者景为角体也〉得一百九十四地半径又一十五分，如左图，甲乙地半径定为
图

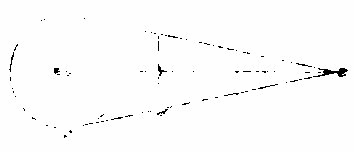
六十万，甲丙为全景，亦通为一五一四三分。〈临算末加五位〉丁丙为过月以外之景角一一六五五分，〈临算末加五位〉而求月食相当之处丁戊几何广，则甲丙与甲乙若丁丙与丁戊也，算得四五五一九三九，又甲丁戊直角三角形内求丁甲戊角，为

所限目窥丁戊之大，则甲丁为太阴距地远，通为分得三四八八分，甲丁戊为直角，丁戊依前算得四五五一九三九，而甲丁与丁戊若全数与丁甲戊角之切线，得一三○五，查表得四十四分五十○秒，为太阴在最高时所过地景之半径也。若太阴在最庳求其食时过景之半径，用全景长，如前，内减五十四地半径五十二分，馀一百九十七地半径又三十一分，为丁丙直线。依前法算得四六四二八○四，为丁戊线。求角以太阴距地之分三二九二，为一率。丁戊线为二率。直角为三率。算切线为一四一○，查得四十八分二十八秒，为太阴在最庳时所过地景之半径也。今表中列地景半径小者四十三，大者四十七，皆少于推得者，为月过地景，不论高庳皆受外光围迫侵销其景故也。论其实则推步所得为真，然不可得见耳。若太阴在高庳之间，求其过景者，依此法随时求丁丙线，推算也。
以测候者，用前后两月食，择食之法欲太阴去其最高最庳，距度同则其入于地景之小大亦同。但月距黄道不必同，又不必全食，因以两距度及两食分求得其所过之景径也。多禄某引周襄王三十一年庚子三月，其地距顺天府西八十一度，卯初时得见食，于是太阴交周得九度二十○分，距黄道北四十八分三十○秒，食全径一十二分之三，又引周景王二十二年戊寅六月里差同上，顺天府寅初时得见食，于时太阴交周得○七度四十二分，距黄道南四十○分四十○秒，食十二分之六，如图，己乙戊丙圈为地景，两食为太阴，所过乙甲丙线为黄道。
前图

如前图，第一食太阴在丁，次食在戊，各依食分入景，为己辛，为戊庚，其太阴之距度为甲丁四十八分三十○秒，甲戊四十○分四十○秒，而甲戊与甲己必相等，〈地景之两半径〉则甲丁减甲戊，馀己丁七分五十○秒，〈两距度之较〉又己丁为月径四
图

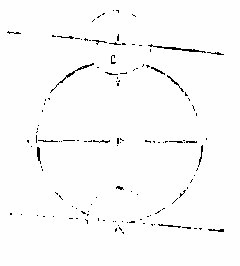
分之一，而先得月径三十一分二十○秒，四分之，为己丁。今去减己丁，所馀为甲己半景四十○分四十○秒，或以距度与食分相较，则食差三分，与距度之差七分五十○秒，若全食一十二分与全月径三十一分二十○秒，亦以距度
后图

之差推得其景也。若后图，两距度一大于半景，一小于半景，亦用此比例以求景。假如初食三分，得距度四十七分五十四秒，次食十分，距度二十九分三十七秒，食分之差七分，距度之差一十八分一十七秒，则七分与一十八分一十
图

七秒，若全食一十二分与全月径三十一分二十○秒，今既食三分，即全月径四分之一为七分五十○秒，以减距度，馀四十○分○四秒，为地半景。又次食得一十分，即月心至地景之周得四分，亦全食三分之一也。全以月全径三分

之，其一为一十分二十七秒，以加距度二十九分三十七秒，亦得半景四十○分○四秒。
地景实差

表中记地景差不及半分，恒减于地景。盖前所论之景实无差，或因蒙气有差耳。其有差者，太阴以其自行高庳，有距地之远近，入于最中时时不同也。又太阳居其最高，所生之景最大，过此渐向最庳，去地渐近，即从地出景渐小渐短也。故月食时先以太阴自行定地景之半径，又以太阳自行求此实景差，而减之乃正得太阴过景之处矣。推算之法设太阳先在景高推所生景，又设在最庳推所生景，得二景之最长最短，又设太阳先后距地同，而以先过景之径比于后过景之径，其二径差即表中之地景差。
假如丁己为太阳半径，第谷所测为甲庚地半径五又四十一分，依戊庚平行线，减丁戊地半径，馀戊己，得地半径四又四十一分，设戊庚为太阳在最高，距地之远一千一百八十二地半径，则戊己与戊庚若甲庚与甲辛，得甲辛地景于太阳在最高时，其长二
图

百五十二地半径又二十三分，太阴在其最高最庳
之间，距地之远得五十六地半径又四十三分，为甲乙以减甲辛，馀乙辛一百九十五地半径四十○分，以推月食之半景乙丙，则乙辛与乙丙若甲辛与甲庚，得乙丙四六五一六五四。
算法以原数通为分，又于每率后加五位乘除之，

又求乙甲丙角所限，目窥乙丙之大，以太阴距地之远，依前法算得切线一三六四，查八线表得四十六分五十二秒，又依此法以太阳在最庳距地之远一
图图

一四一地半径，推算地景为二百四十三地半径又三十八分，去减太阴在高庳之间距地之径，馀一百八十六地半径又四十五分，依前算得四五九九一二四，为乙丙线。次以太阴距地之远三四○三，推得切线一三五一，查得乙丙半景四十六分二十六秒，比前所得差二十六秒，为地景之最大实差。其馀者，以太阳自行距最高远近，依法次第求之。〈以上原本历指卷十一交食之三〉