钦定古今图书集成历象汇编历法典

　第五十九卷目录

历法典第五十九卷

历法总部汇考五十九

新法历书九

交食历指一
或问：日月薄蚀，是灾变乎﹖非灾变乎﹖若言是者，则躔度有常，上下百千万年如视掌耳，岂人世之吉凶亦可以筹算穷也。若言否者，则古圣贤戒惧修省，又复何说。曰：灾与变不同，灾与灾变与变又各不同。如水旱虫蝗之属，伤害民物者，灾也。日月薄蚀，无患害可指，然以理揆之，日为万光之原，是生暄燠。月为夜光之首，是生湿润。大圜之中，惟是二曜相资相济以生万有，若能施之体，受其蔽亏，即所施之物成其阙陷矣，况一朔一望，两光盛长受损之势将愈甚焉。是谓无形之灾，不可谓非灾也。夫晕珥彗孛之属，非凡所有者，异也。交食虽躔度有常，推步可致，然光明下济忽焉。掩抑如月食入景深者，乃至倍于月体，日食既者，乃至昼晦星见。嘻。其甚矣。是则常中之变，不可谓非变也。既属灾变，即宜视为谴告，侧身修省，是以有修德正事之训，有无敢驰驱之戒。兢业日慎犹惧不塈矣。曰：既称灾变，凡厥事应可豫占乎。可豫备乎。曰：从古历家不言事应，言事应者，天文也。天文之学，牵合傅会，傥过信其说，非惟无益，害乃滋大。欲辨真伪，总之能言其所以然者近是。如日月薄蚀，宜论其时，论其地，论时则正照者灾深。论地则食少者灾减。然月食天下皆同，宜专计时。日食九服各异，宜并记地矣。迨于五纬恒星，其与二曜各有顺逆乖违之性，亢害承制之理，方隅冲合之势，为其术者一一持之有故。然以为必然不爽，终不可得也。惟豫备一法，则所谓灾害者，不过水旱、虫蝗、疾疠、兵戎数事而已，诚以钦若昭事之衷，修勤恤顾畏之实，过求夙戒，时至而救之者裕如，则所谓天不能使之灾，又何必徵休咎于梓裨。问：祲祥于京翼乎﹖然则星历之家，概求精密，尤勤于交食者，何也。曰：太阴去人最近，饶有视差。凡人目所见，人器所测，则视度而已。其实行度分，非人可见，非器可测，必以食甚时知。为定望与日正相对，从是知其实度，从是知其本行，自馀行度，渐可推算也。又因月食知地景为角体之形，月体过之，其距地同而入景之浅深不同，可推日在其本天行与地为不同心也。又因日食，推月距地时时不等，知其有本轮有次轮也。又兼以日月食推日月体之大小，及日月距地之远近也。别有度地之学，因月食可推地在天之最中，其四周皆以天为上，人则环居地面也。又因月食知地景为圆体，而居东者渐远渐后见食，即非月食。以地为先后，特因各所见之时刻为先后也。因以推地为圆体，而水附于地，合为一球也。又以月食与子午线相距远近，知诸方之地经度也。若泯薄蚀于二曜，即造历者，虽神明默成，无所措其意矣。是则交食者，密术之所繇生，故作者述者咸于此尽心焉。今撰历指，有合论，有分论月食，术稍简以附合论之末，日食颇繁，釐为别卷，诸立成表，以类从焉。
界说

凡物体能隔他物之象，使不至目，则为暗体。若以体之一面受光，而光复透射出于彼面，则为彻体。〈如玻璃水晶是也〉
目所司存惟光惟色，而色又随光发见，故解彻体必以通光，解暗体必以其能隔他象。如月掩日，而日全食，昼为之晦，恒星皆见，尔时太阳在外，体质明显，又坚密无比，光力甚厚，乃为月体所隔，不能映见微光，可證月乃全非彻体，而全为暗体。其彻体有二：通明之极全无隔碍者，为甚彻。虽则透光而微杂昏蒙者，为次彻。
光在本体为原光，其出而显他物之象，为照光。日有原光，地与月皆借之为光者，照光也。谓显他物之象者，因他物之势随施随受，有原先后，无时先后也。非如寒热燥湿之类，渐及于物，力尽而止。
原光以直径发照为最光，因而旁及者，为次光。日光正照以直线至于物体，则为最光，有物隔之旁周，映射则生次光。如云之上，日体所照，最光也。云之下，不复见日，而犹有光，是次光也。
满光者，原光之全体所发。少光者，原光之半体所发也。日未全出地平上，所生光为少光，全升在上，则生满光。日未全食时，则存少光，既以复圆，即得满光。景之四周有最光绕之，即景为次光。以景为明者，误也。以影为暗者，亦误也。称景为明暗之中，庶几近之。盖全无光乃为暗，今至夜子初，人在地景至深之中，去最光极远，而近日之物尚能别识，即见景中犹存微光，不失为次光也。
最光所不及为初景，次光所不及则为次景，景与光并行，光渐微，景渐厚，故次景与最光相反，若初景即次光也。
最光全不及之处则为满景，若受正照之微光，即为
图

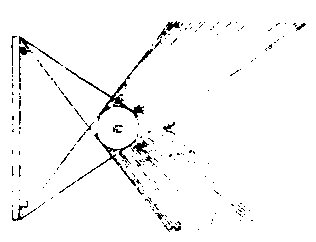
缺景。景与光正相反，无景之极则为满光，无光之极则为满景。假如甲乙为施光之物，丙为暗球，从甲出正照之光过丙球左右，其切丙之界者，得甲戊及甲己。从乙出光又得乙戊及乙丁。其庚戊辛为最光，全不及之处则满景也。若庚

戊、辛戊以外，则甲乙光体之多分渐照之至乙丁甲己，乃全光之界。即自戊至丁至己，丙球之景渐薄，以趋于尽矣。
太阳光照月及地第一〈凡五章〉

日、月、地三球体，大小不等，地为静体，日月则有诸种行度，则有高庳内外。其去地去人远近不等，法当以大小之比例，及其相远相近之比例，推其施光受光之体势，乃得景之体势，因而得交食之体势。盖交食者，生于景，景生于光。不寻其本而求其末，无法可得，其说五章。
一曰：有两球于此，一为暗体，一为明体，而小大等，即明者以半面施光，暗者以半面受光。

如左图，甲为明球，乙为暗球，小大等，即其径丙丁及戊己各与甲乙线为直角，而丙丁与戊己等，即甲丙甲丁乙戊乙己与甲庚乙辛皆以半径相等，而丙庚丁半球与戊辛己半球亦相等。今于明球之旁，从丙从丁出两切线至暗球之旁，戊巳、戊己与丙丁为平行线，即丙戊与丁己亦平行线也。〈见几何一卷三十三题〉又因
图

丙戊乙及丁己乙俱为直角，即戊丙甲及己丁甲亦俱直角，〈见几何一卷二十九题〉即丙戊丁己线不能割两球而止切两周于丙于戊于丁于己，其所抱为丙庚丁，为戊辛己，是甲乙两球之各半也。若日、月、地三球相等，而月与地皆以半面受太

阳之光，如上所说，则定朔日食，半地面宜皆见之，安得复有南北不等食分，望日太阴全食时，才食既，即生光，安得复有食甚时刻及既内分，今皆不然，可见三球无相等之球。
二曰：明体大，暗体小，则施光以小半，受光以大半。

如左图，甲为明球，乙为暗球，作两切线为丙己为戊庚，从四切点作横线为丙戊为己庚。甲既大球，即己丙戊为锐角，丙己庚角为钝角。如曰不然，或皆为直
图

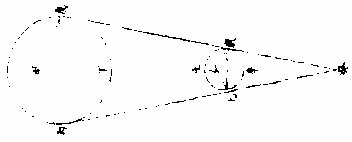
角，即庚戊丙戊庚己亦皆直角，两切线必平行，而乙球与甲球等，〈见几何一卷二十八题〉必不然也。或己丙戊反为钝角，而丙己庚反为锐角，即两切线不能相交于癸，又不然也。今以两切线相交于癸，明己丙戊为锐角，丙己庚为钝角，即于丙丁
图

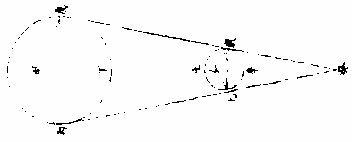
戊弧内作负圈角，必钝角矣。于己壬庚内作负圈角，必锐角矣。〈见几何三卷三十一三十二题〉故丙丁戊施光者，不及半圈；己壬庚受光者，又不止半圈也。因此推知太阳照地及太阴，必各照其大半，而暗体所隔之日光渐远，又渐敛渐进，以趋于一处，

即景居暗球之背，不得不为角体之形矣。又因此推求望日先后，人目所见太阴受日之光不长不消者，久之而后生魄，此为何故。盖亦因月体以大半受光，以小半入于人目，光不辄转，而魄未遽见。故未望时已见全光，已望后犹未失全光矣。
三曰：明体小，暗体大，则施光以大半，受光以小半。

如前图，反论之，可明太阴何以照地而地何反隔日之光也。
四曰：大施小受，愈相近，则施者之小半愈小，受者之大半愈大。

如左图，丙为小暗球，甲与乙皆大明球。作庚未直线过三球心以交于左右切线，其乙球之两切线交于午甲球之两切线交于未，即庚未长于乙午，而庚丁未与乙辛午两角，庚丁与乙辛两线，皆相等。则庚未线与庚丁线之比例大于乙午与乙辛，而丁庚未角大于辛乙午角也。〈见几何五卷八题〉又庚未线过三球之心，必截丁己、辛癸两线为两平分，而庚甲丁、乙子辛两
图

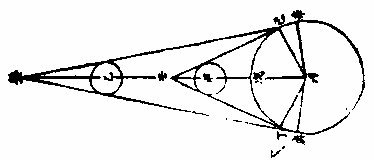
形内之甲与子皆为直角，则其馀庚丁两角并乙辛两角并皆等，一直角即两并率等。〈几何一卷三十二题〉两并率之甲庚丁角大于子乙辛角，各减之所存庚丁甲角，必小于乙辛子角矣。次以庚丁甲及乙辛子不等之两角各减庚丁未及乙辛

午相等之两直角，所存甲丁未角更大于子辛午角。又丁戊己弧内作负圈角，必等于甲丁未角。辛壬癸弧内作负圈角，必等于子辛午角。辛壬癸弧之负圈角，既小于丁戊己弧之负圈角，则辛壬癸弧必大于丁戊己弧。〈几何三卷三十一三十二题〉夫辰寅己与辛壬癸，相似之弧也。丑寅卯与丁戊己，亦相似之弧也。
大小圈左右各有切线，其切点过分圈之线，其所分大小圈分各相似，其大小两弧亦相似。

即辰寅己弧亦大于丑寅卯弧，可见明球在近比在远者，尤能照小暗球之多分也。因推知日全食而视为大者，日体去月体远故也。日全食而视为小者，日体去月体近故也。何以分远近。日与月俱有自行圈，与地不同心。其行于自行圈之上下，为最高最庳，则为距地之远近，因而生景之大小也。日既全食矣，又何以分大小。月掩日至既，有时昼晦，恒星皆见，虫飞鸟栖，此为全食。而大月在日内从中掩蔽，虽至食既而其四周日光皆见，历家谓之金环，此为全食而小矣。若然者，日与月与地相去，或远或近之所繇生也。
五曰：小施大受，愈相远则施者之大半加小，受者之小半渐大。

如左图，甲乙皆为小明球，丙为大暗球，乙去丙远于甲，作各切线过三球心之直线，皆如前。次从暗球心丙至各切点作丙丁、丙己、丙庚、丙辛各半径，得丙丁为丁壬之垂线，丙庚为庚癸之垂线，而丁与庚皆为直角，丙丁与丙庚两线又等，则丙癸线与丙庚半径之比例大于丙壬与丙丁，而丙庚癸角又大于丙丁壬角也。〈几何五卷八题〉依显丙辛癸角亦大于丙己壬角，以
图

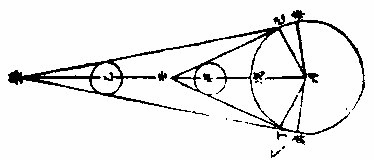
并前率，为庚丙辛合角，亦大于丁丙己合角，而其弧庚戊辛必大于丁戍己，可见小明球照大暗球，愈远愈照其多分也。今依本图，设丙为地外切线，〈癸辛也〉以内为地景，〈日光过丙大球所出景〉甲乙两小球为月体，其两小球之小大既等，则同以外

切线为外光之界，或为内景之界。惟因月体循本轮行，时居上周，如乙，则去地远。时居下周，如甲，则去地近。以是月食之分数有多有寡，月居影厚处，如甲，左右，则食多。月居影薄处，如乙，左右，则食寡。故曰：月食有多寡者，亦相距或远或近之所繇生也。
景之处所第二〈凡二章〉

凡光以直线照物体，其无光之处则有景之处也。欲于交食时求影所在，理不异此。盖月与地能出景者，不在其受光之面，或其左右必于受光反对之面，日
图

光不照之地，在日食则为月景之处，在月食则为地景之处矣，说二章。
一曰：景与光所居正相反。
暗体得光于此面，射景于彼面，是景之中心与原光之心、暗体之心，参相对如一直线。则暗体隔光于景，
图

使原光之心恒居一线之末界。其正相反之，彼界其景之心在焉。如曰：不然，设原光在甲，其照及乙，乙为暗体，隔光生景。据云景不射丙，〈丙者与甲正相对之处〉为甲乙丙直线而斜射丁，则乙甲丁者，角也。有角则有几何，凡几何皆分之无穷，能出
直线至于无数，而皆至乙丁边。夫甲既为原光之体，
其所照必以直线出之。〈试诸仪器足以为證〉即乙丁皆在受光之地，何自能为乙暗体之景乎。因此明景与光正在相反之两界。论暗体者，其受光之面必向光所出之原界，其生景之面必向景所射之彼界，亦正相反也。论日与月独至两交之处而有食，亦依此理。
二曰：明暗两体任一运动，景随之移。

试以暗体移动其所借之光，随处不一，即所生之景亦随处不一。盖景与光既如一直线，即暗体所居定
图

为景之末界。如直线之首，首移而线尚不移，则是曲线，非直线也。又试以明体移动，设甲为明体，乙为暗体，乙丙为影，则甲乙丙如一直线，如曰明体甲移至丁，丁仍照乙，而乙尚射景至丙，则丁乙丙犹直线也，有是理乎。

问：太阳照室，仅通隙光，光照墙壁，奕奕颤动。太阳既自顺行，墙隙仍无变迁，则此颤动为从何来。或者光与景未必定为直线，而能微作曲势乎。曰：西古博物者亚利斯多言空中尝有浮埃，轻而不坠，微而不显，庄周氏谓之野马，或亦称为白驹。幽室之内，原光既微，次光反厚，即显此物在于光中纷入沓出，能乱光景之界。使目视景絪缊浮动，而实非景动，乃景之界线为浮埃所乱，致使其然也。更以气为證，今观太阳出地，地面以上多生蒙气，气在日体与人目之间，即见日之光界亦如，颤动非独日也。日中晴朗，切视地面，光耀闪烁，如波浪然。炽炭在炉，炭之四周火光煜煜，亦如颤动。凡若此者，一皆繇气而生，在日在地在炭固无颤动之理，是以景必系于暗体，如轮必系于枢轴。光上景即下，光东景即西，必相对也，无相就也。故太阳照地，其光绕地一周，则景在其相冲之界，亦绕天一周。盖日光从其本天直射至于地面，而景在地之彼面，亦直射至于月天。第日体常依黄道中线，则地景亦常依黄道中线。而月行常出入黄道中线之内外，是以月体与地景不得恒相遇合，大都不合时多，合时少，故日月不食时多，食时少，以此。
景之形势第三〈凡二章〉

求食分之几何，必先求景之几何，景几何者，以日月地之大得景之形势，以日月地相距之远近分数，得景之变易大小分数也。此所论则景之形势，后考其变易之势，得景分以定食分焉。凡二章。
一曰：二体相等，其景平行而无穷，明小暗大，其景渐展而无穷。
图

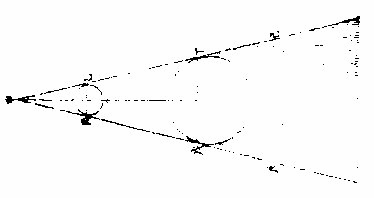
论相等者，證以平行之切线也。如图，甲乙两球等，丙己、丁戊为两球之切线，与两球之径丙丁、己戊遇于切点，皆为直角，则互为平行线。又球等，即径之长短亦等。以遇丙己及丁戊，无不为平行线也。〈几何一卷三十三题〉若两球之周遭切线无数，
图

皆同此论。则引之至庚辛以迨无穷，终平行，终不能相遇。而其形为长圆柱之无穷体。
论明球小于暗球，则推以三角形相似之比例也。如图，乙丙为小明球，丁戊为大暗球。两球之切线丁乙及戊丙引长之，过小球必
图

相遇于甲，成甲丁戊三角形，又从丁戊底作己庚平行线在大球之外，成庚甲己三角形，与甲丁戊相似，则甲己庚角与甲丁戊角相等，其各边各角皆相似，而甲丁与丁戊若甲己与己庚也。反而更之己庚与丁戊，若甲己与甲丁也。甲

己长与甲丁，则己庚亦长与丁戊，愈远愈长，可见大球之景渐远渐拓矣。〈几何六卷四题〉更论丁戊线之内外角，则在内者为锐角，在外者为钝角。故引切线向内过小球，必相遇，引之向外，愈远愈拓，终不相遇而其形为无限长，无限广之角体。又因两球所居远近不同，景之张翕随而变易，故两球相近即乙丙底线为小，其景愈狭，而乙甲丙角形愈短。两球相远即底线为大，其景愈拓，而角形愈长也。
今验诸日食，有食分同而所历时刻不同者，月景之在地面广狭不同也。月与日会，月在日与地之间，或月近地而日在远，则目之见界过月周至日体，其界广，日过迟，其见食时刻多。或月远地而日反近，则目之见界过月周至日体，其界狭，日过速，其见食时刻少也。姑以前图明之，目在甲，乙丙为月体，丁戊为日体，切线甲丁及甲戊为目所见之界，若日在近，为丁戊，即从丁过戊道，近行速，其食时寡。若在远，为己庚，从己过庚道，远行迟，其食时多。皆太阳有不同心圈，而太阴又有小轮所繇生也。
二曰：日、月、地三体大小不同。

凡暗体出角景者，施光之体必大于暗体，否者，其光不能照暗体之大半，而使其景渐小以趋于尽也。试观月食时，月体近地，则入大景，远地则入小景，愈远愈小，必至于尽，安得不信日体大于地体乎。设谓日体与地体或等，则景宜亦等。或小则宜渐大，又当皆为无穷之景，遇望时月体必不能出大景之外，不应有不食之望矣。有不食者，是地景之益远益锐也。月食于地景之中，又有全而且久者，是月径更小于景而，景小于地也。地景之远而益锐者，是日大于地也。此以景理推论三体之小大，略可明矣。若又以日体之大推月地之景，则更有法可考其大小之比例也。昔人因太阳照地所生之景及其远近，其视径时时不同，又以较于他体得其实体之大，说见月离历指中。此独用视径定食时刻分之数，其论实体为景与食之原，略举一二如左。
几何原本论三角形，于一边之两界，出两线复作一三角形在其内，则内形两腰并之，必小于相对两腰，
图

而后两线所作角必大于相对角，如图，甲乙为太阳之径，丙为目从远视之，丁亦为目从近视之。此所谓内外两三角形也。今先以线论，因内形之甲丁乙丁两腰小于相对之甲丙乙丙两腰，则所作丁角比相对之丙角亦近于共用之。

甲乙底近则见大，故丁目视甲乙日径必见大于丙目所视之甲乙径也。次以角论，因内两线所作丁角大于相对丙角，则此内角所对线亦似大于外角所对线，而丁目所见之甲乙大于丙目所见之甲乙也。此太阳视径不同之缘也。
求太阳实体之大，第谷设最高最庳之中处得其距地一千一百五十地半径，全数十万，其半径一十五分三十秒，得正弦四百五十一，以三率算法推其全径，得地之全径五又七十五之一十四，如三百八十九与七十五也。又以其径与其周之比例，得太阳体之立方五千八百八十六万三千八百六十九，地球之立方四十二万一千八百七十五，其终数得一百四十弱，为太阳大于地之倍数也。此其照月照地生角体锐景之原也。
景之作用第四〈凡三章〉

月与地若各以其景相酬报，然如月望，则地景隔日光，令月不受照，有时失满光，有时全失光也。至月朔则月体隔日光，令地不受照，有处射满景，有处留少光而已，说三章。
一曰：月食于地景。

月食在望，缘日月相对，其理明矣。独谓闇虚为地景者，或致疑焉。今解之，月对日受光，藉非日月之间有不通光之实体为其映蔽，则何繇阻日光之直照。若天体及空中之火、空中之气皆通明透彻，不能作障，使月失光也。即金、水二星亦是实体，有时居日月之间，然其景俱不及地，况能过地及月乎。则知能掩月者，惟有地体，一面受光，一面射景，而月体为借光之物，入此景中，无能不食，半进而半食矣，全进而全食矣。
二曰：日食者，月掩之。

恒言月在内，去人近。日在外，去人远。故定朔时月体能掩日光是已。第金、水二星，亦皆时在日内又皆不通光之实体，水星虽小，金星则大于月也。何独月能食日乎。曰：二星虽有时在日内，则去人甚远，远则视径见小，不能掩日百分之一二，而日光甚盛，所亏百之一二，非目力所及。且二星比月去日更近，所出锐角之景更短，不能及地面也。若月体之大，虽不及太白而去地甚近，去日甚远，一指足蔽泰山，又何疑乎。由此言之，求一实不通光之体全掩日体者，惟月为能，又自西而东，不及三十日而周，其行度较于诸天最为疾速，故每望定朔，皆同经度，皆能有食，其不食者繇距度不及交耳。
三曰：因景之径生多变易。

月以距度广狭为食分多寡，一因去交有远有近，去黄道中线有正有偏。一因入地景有浅有深故也。今论其全食者，而大小迟疾犹多变易，曾非一定。盖日在自行本天，月在小轮，相距远近往往不等。日距月近较距远时，更照月体之多分。从月体出景更短，其景至地更小，则日虽全食月体，见小历时亦速也。日与地亦然，以两体相距之远近为地景之大小，使月食时入于地景，在其近末之锐分，则闇虚之体见小，食分少，历时速，皆因三体之相距远近以生大小迟疾。地景月景皆无一定之径，致令随时变易如此。若月景、地景二径之小大又自不等，故日食尽于食既，而月则食既以后尚有既内馀分，盖地景大于月景，故两食皆全其亏复迟疾，无能不异矣。又月食天下皆同，日食则否，日食则此地速彼地迟，此地见多，彼地见少，此地见偏南，彼地见偏北，无不异也。月食则凡居地面者，目所共见。其食分大小同，亏复迟疾同，经历时刻同，唯所居不同子午线者，则见食之时刻先后不同耳。盖月一入景，失去借光，更无处可见其光也。又概论天下日食应多于月食，为二径折半，其近交时加以南北视差，易相逮及，故论一方则日食应少于月食，为月食共见日食，因地故。〈见后卷详之〉
月在景之光色第五〈凡三章〉

月既暗体，当全食时一入地景，遂应失其借光，非复人目可见也。盖可见之物悉无原光，必借外光以显其象，无外光即无从见有此物，安从更显物色乎。今月居厚景，尚有微光可见，更发色象，或赤色，或青黑色，或杂色，此何从生。今略解之凡三章。
一曰：月不独食于地景。

论通光者，有二体。一谓物象遇甚澈之体，易于通射，比于发象元处更加透明，则形若开而散焉。一谓物象遇次澈之体，难于通射，比于发象元处少杂昏暗，则形若敛而聚焉。其遇甚澈者，如舟用篙橹，半在水中发象，上出出于水面，所遇空明气之光，甚澈之体也，则其象散而斜射，视之若曲焉。其遇次澈者，如太阳入地平下，其光照地旁，本宜直上，乃所遇清蒙之气，次澈之体也，则其象合聚而射于地面，凡地平以上皆得其次光，为朦胧焉。〈即昧爽黄昏亦曰晨昏〉此两者，皆以一物经繇两体，其势曲折，皆谓之折照。
图

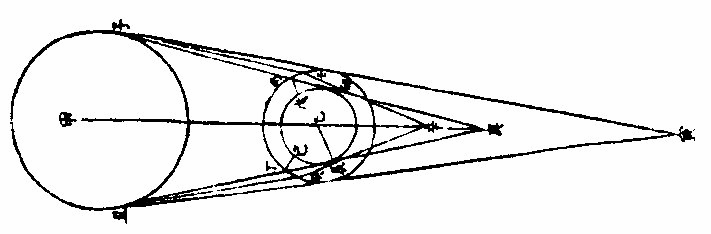
若一物在一体之中，以一直线入目，谓之直照。

夫同是，日光也。在地面之上能折入于地景之根际，则自地面而上，何独不能折入于景之中际，至月体经行之处乎。如图，甲为太阳，乙为地球，藉非清蒙气能迎太阳之光而成折照，则宜从子出光至丙，从丑出光至丁，切地面径，过而复合于庚，为地景锐角也。今不其然，因清蒙气周绕地球，日光至丙至丁，遇其次澈之体难于透射，则曲而内聚，止于戊己地面矣。而大圜中大气无不受日之照光，光在壬癸者，遇于
图图

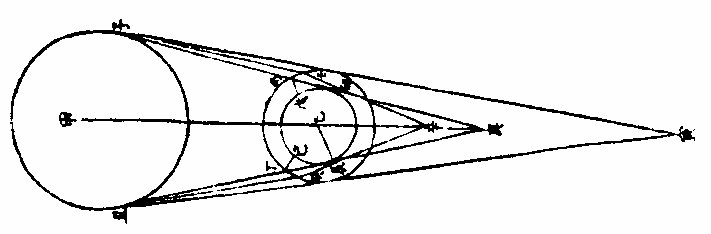
蒙气即内敛，至于卯辰，此为初折。从卯辰切地而过，若遂以直线引之，即复合于辛，成卯辰辛杂线三角形，为地之满景。自此以外，全景之中皆得太阳折照之光，与朦胧次光相类，而实为初景，能食望月之满光也。欲求满景之长，姑先依初折之光，引直线复出于蒙气之外。
姑先云者，不宜遽引直线也。盖初折之光至于卯辰，既抵地面，又复内敛，谓之次折，则两线之交尚在辛点之内，今云然者，姑先明初折之理，约定乙
图

辛之数。如太阴之言交，泛言平朔，言本轮也。其次折之理，次二章详言之，求辛点以内之定距率矣。

而借第谷所测清蒙差，与多禄某所定地景角之大，得辛辰庚角三十四分，〈近地平之气差大率如此〉得卯庚辰全角二十五分三十六秒，半之为辛庚辰角一十二分四十八秒。其相对之外角乙辛辰为四十六分四十八秒，〈辛庚辰辛辰庚相对之两内角并〉次乙辛辰三角形，其乙辛辰角既得四十六分四十八秒，乙辰辛为切线与垂线所作角，必直角，此直角与乙辛边如乙辛辰角与乙辰地半径，即得乙辛短线长于地半径七十三倍。若论地之全景，乙庚线尚长三四倍也。夫月食于地景，必依其景之体势，显其食之貌象。今全景之中既以地景兼蒙气之景，则并有初景，有满景。月入于中，随其所至变易光色，无足异矣。或曰：从古论食月者，全属地景。今云不止地景，而更加之气景，此为全景，方之地景不亦愈长愈广乎。则从上古以来，以地径度月体过景之数，以地径定日月之视径，以地径较日月之两高，以地径求日月之去地远近，悉皆乖舛，而当更定新率然乎。抑否乎。曰：不然。所论蒙气之景，谓太阳之光，因于此气，能令全景之中分别厚薄，变易景中之色象，非谓地之径因景而加大也。譬如眼镜，本无厚之体，徒以变易物象显其用耳。且气景之于地景，亦何能加长加大乎。计清蒙出地之高，不能过极高之山，极高之山测其垂线，不能过千四百步，大地之径则三万里，以高山之步数化为里数，而较地径则五千分之一耳。此气之厚，何能加于地径。而云设此论者，有妨于地径测量之法乎。
二曰：月体当食而成赤色，是气景所生。

月全食时，其光色往往更迭变易，其初食既与水生光，当此二际，则成赤色。夫月入地景，果必失光，宜为纯黑，不应复显他色。今赤色者，得无是其本光乎。曰：次光之物，惟无光之处能显其光。一遇大光之体，则次者之光泯矣。今以地景言之，月居其甚厚之际，即甚远于大光，果有自体之光于此，尤宜显著。乃今测之，则在浅见，盛在深见，微可證食时所见非月体自有之光也。故应论定月能食于气景，如上所说矣。然食时亦能变易诸色，何以独言赤色。试观太阳下照，地面受之，论其本然皓明无色，日地之间，或发昏蒙之气，即地面所见时转为黄，时转为赤，皆因所遇之气，如玻璃映目，色青见青，色绿见绿也。今日照地旁，照光所过清蒙之气，因于斜穿而成厚体，月体所显光色尤深，成为赤色矣。试论其所以。
视学家有公论，凡象斜射次澈之体，以垂线为主，曲折通之。初入则聚折而向于垂线，既出则散折而离于垂线也。何谓垂线，盖于澈体之面，过受形之点，作
图

线下垂，则是折照所向所离之线。如图，圆体甲戊乙，方体甲丁戊，皆次澈也。当其面有斜照之光在丙，至甲点而入至乙点，而出则甲丁与丁乙皆为垂线，照光至甲点，而入必聚而折向于甲丁垂线，至乙点而出必又散而折离于乙丁
图

或乙壬垂线。若言光至乙点出，或不照庚而更照己，则是反照之光，非折照之光也。依此申言上章所推地球满景之长。如图，太阳之光遇于蒙气，从壬癸折入作壬卯癸辰线，为初折。又从卯辰折出，作卯午辰未线，为次折。以复合于己，

别生午己未杂线角形，乃因乙己未角生己未辛，及己辛未为外，两角并之得，乙己未内角一度二十○分四十八秒，今设从满景之角己出切线至地球辰，得乙己辰直三角形，则因乙己辰角一度二十○分，
乙己辰角比乙己未角差数甚微，略得四十八秒，故以算景之长，不论为数。

如前比例，得地满景之心长于地半径四十三倍，比月最庳之入景处近地一十一地半径也。
月最庳入景五十四，最高入景五十八。

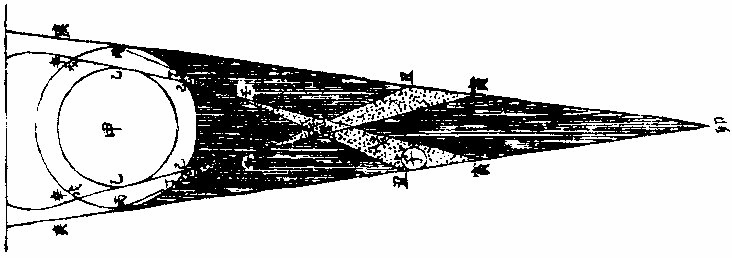
今图月在景之形势，地球为甲乙内圈，其四周有气，为丙乙圈，气外切边之光复合于卯，是为全景透气之光。自丙至戊，因戊以上所照必聚而止于地面，无从透达也。则光至丙为太阳之外边，所照光至戊，乃其近中体所照，以丙较戊更斜，从庚而来入气处，更曲从辛来之光，已透气而复出更直，故令丙丁线割戊己线于壬为丁己壬角形，是为次光。又为初景，其角形周遭为环体，抱满景而居全景之中也。丁己壬角形既尽于壬，而又展开至癸，左右相交至丑寅，愈
图图

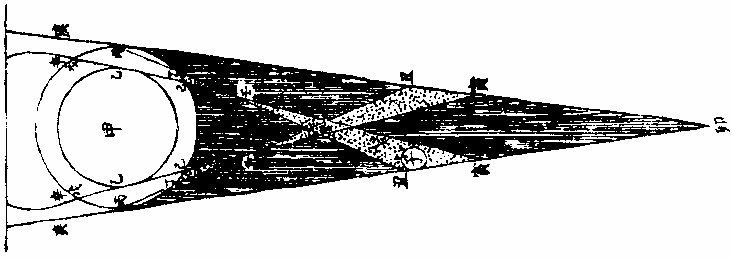
远愈拓，复出乎景矣。则丁己壬以内，壬丑寅以内，皆初景之所居也。因此设月体为子，入景正初景展拓之处，月食既正在其中，将复光，亦如之。是故两时皆显赤色，食甚离于次景入于满景，乃变青黑矣。
三曰：月体当食而成青黑色，是借光所生。

月居食甚之中时显杂色，时但青黑皆须因光而见，若并无光当纯黑色也。前已言既入此界，即无太阳入气折照之光，则所繇见色者，意或月体自有微光乎。曰：凡杂色之映见，皆不繇于纯光，纯光自当无色也。杂色所从著见者，必因湿气居其中间，如虹霓是已。若虹霓是湿云所映，无从可證。试以玻璃瓶满贮清水，别为密室止穿一隙以达日光，瓶水承隙，则光透墙壁，亦成虹霓，大气之体本是热湿，因于地气时重时轻，若太阳之光从地旁过而地景在湿气之中，则月体所至生种种色，亦此理矣。若青黑色，月在满景多见之。则因去光最远，所得希微之光，不足显其本体。故光色近于纯黑，果绝无光，又不能显此色矣。第所谓希微之光者，实非本光，如前言人在地景最厚处，天光尚映照之，近日之物略能别识。若月食时则受光之天去月体最为切近，而诸星环绕四周皆有借光可照月体，较人在地面尚为景之薄处，岂得无微光可借聊显色象乎。何必假此疑为自有之本光。问：合朔以后，月之下半未受日光，而月体微光亦显青黑之色，若无本光，此光又何从而生。曰：生明以后魄显微光，然能去离月体，足知其非本光。去离者，未至上弦，此光渐消渐不可见也。若实为本光，则上下弦前后深夜视之，比朔后之月尚近太阳者，尤为窈黑，其本光愈宜显著。今为不然，深夜即无，初昏即有，其为此时地面反照之光甚易明矣。
此论月为暗体，绝无本光，与月离历指四卷第二十六所论者不同，盖西土原有此二说，不妨互存之。
日月食有定时第六〈凡二章〉

日月交食皆有定时者，在月则因地景，在日则因月景，景之推移既随日躔所至，终古不爽。又月行本道，所距黄道度分亦有一定之法，是以一在定朔，一在定望，当食必食，多寡、先后、上下、千百世可知也。说二章。
一曰：地球在天心。

日食恒在定朔，月食恒在定望者，何也。地球在天心故也。验诸日食，必两曜同居一线，而月在地与日之间，正隔日光于地。又验诸月食，令日月不相望于一直线，两界之末则终古无食也。设地不居天中，或偏近于黄道之上下左右，则食不在半周，而月食之冲非太阳所在矣。〈古法以月食冲简知太阳所在〉如图，甲为地，从甲心
图

作乙丁丙戊圈，为宗动天之地平，则甲必为天之心也，何者。从乙出直线至丙丁至戊亦如之。乙为东，并为鹑首初度。丙为西，亦为星纪初度。丁为鹑火，戊为元枵，皆初度也。则有视学之公论三：其一曰：月所视物必从直线乃见之，使目
图

在甲能遍见乙丁丙戊，即甲乙、甲丁、甲丙、甲戊、皆直线也。其二曰：若光从一窥表出，能射黄道正相对之两点，必为径线。此乙丙及丁戊能过甲，亦如光过窥表，甲能至黄道鹑首、星纪等宫，正相对之初度，则乙丙及丁戊必为本圈之径。

更试测日月定望时，得并在地平，此出彼没，若距度同，即日月略居其一径之两末，则乙丙及丁戊为圈径无疑也。其三曰：凡圈中有多径线交而相分，其两分线必等。此两径乙丙及丁戊交而相分于甲，即甲乙、甲丙、甲丁、甲戊线皆相等。又几何一卷第十七，三卷第三界说，皆言圈中一点所出多直线，至其界皆相等，即此点定为圈之心。今甲点出甲乙甲丙等直线至乙丁丙戊各界诸线皆相等，即甲必为本圈之心。因此推之地球在天之心，甚易明矣。
二曰：食之大小疏密，因月距度。

昔人测日月食必在正中二交，月体去交渐远，则食分渐少，以至无食。何也。月以本体掩日，而日为之食，又以本体入于地景而自为食。故恒言日、月、地居一直线之上则食，偏则否。三球之所以偏者有二：一则日体恒行黄道中线，地景恒在其正冲度分。一则月行常出入黄道中线，是故有时不入地景，则食与不食，皆因月行本道与日与景之距度多寡而已。若其距度较日月景之二径折半，或大或等者，必不食也，小则必食也。愈小则食愈大也。但月与景之二径折半大不过一度，日与月之二径折半止三十馀分耳。故两交左右之距度或在阳历或在阴历，各有食限。不入食限者，虽遇朔望无缘相及，故一岁之中不能多有食矣。即入于食限而去两交有远有近，则其距度有广有狭，即食分有寡有多，相因致然，不能齐一也。
日月食合论第七〈凡一章〉

日食与月食不同势，食日谓之障食，食月谓之藏食。何谓障食。日为诸光之宗，月与星皆从受光焉。月之食日，非真食日也。定朔则地与月与日自下而上为一线，相参直，月本暗体，今在日与地之间，以暗体之上半受光于日，以下半射景于地，如屏蔽然。特能下掩人目，而不能上侵日体，日之原光自若也。虽人见为食，而实非食也。何谓藏食。定望则日月相对，日光正照之，月体正受之，人目正视之。若于此际经度相及，适及两交，日与地与月，亦为一线，相参直，而地在日与月之閒，地既暗体，以其半体受光于日，以其半体射景于月。若月体全入于景中，则纯为晦魄，必待出于景际，然后苏而生明，如没而复出者。然是则可谓真食也。总之，日月两曜若同行一道之上，则每朔每望无不食矣。日、月、地三体若并不居一直线，则永无食矣。惟各行于一道，时及于两交，故日与月皆隔五月而一食，或六月而一食，岁岁大率有之。不食者，半食于夜，日食则此方所见，他方所不见耳。其食也，日体恒居一直线之此界，其彼界则月体、地体叠居焉。月居末界，即月面之日光食于地景矣。地居末界，
图

即地面之日光食于月景矣。如上图，甲为地，己为日，卯辰圈为黄道，乙丙为白道，其大距〈两距之最远〉五度弱二分，丁戊为两交，〈即龙头龙尾亦名罗㬋计都〉论月食日照地球，其光自庚辛至地，切两旁过之，而复合于壬，自甲至壬，角体之形为地景。地景

之心恒随太阳而行黄道中线，若躔处去两交远，二径折半小于两道之距度分，月行本道，从旁相过不能逮及，则不食矣。若正遇于两交或交之左右，二径折半大于二道之距度分，则两相涉入，月为之食，其食分多寡在距度广狭，距度广狭在去交远近也。论日食则人目所见恒在地面，推得实会，仍须推其视会。若仅据实会，则是地心之见食，非地面之见食。凡有无多寡，加时先后，悉皆乖失矣。如图，丁为月，或正居于两交，或在交之左右，日月二径之各半，合之小于距度分，则月能掩日，日为之食，不然则不食也。所谓实会、视会兼推则合者，地面所见，推食于地平以上，至天顶之正中，则独推实会，便为视会，自此以外地面所见先后、大小、迟疾，渐次不同。如图，人在地面，癸依丁月之径适满太阳之庚辛径，则见为全食。若人在地面，子依丁月之径，乃见两切线所至为己寅，则月掩太阳，止于己庚半径，见为半食矣。大凡日欲食时，月不能离躔道一度强，自此以上无缘相涉，故定朔之日有食时少，无食时多也。〈以上原本历指卷九交食之一〉
日月本行图第一〈凡二章〉

日居本圈，月居本轮，行度参差，因而有交食，因而每食不同。此略图，二曜本行以明交食之原，月离图独言朔望者，交食时必在其本轮内圈之周也。
太阳本行图

甲为地球，在天心，其大小之比例难可计算，略言之，则地之与天若尺土之与大地也。如图，外大圈为黄道，与地同心，内圈为太阳本天，其心在乙，乙之离地心，依第谷算为全数十万分之三千五百八十四，约
图

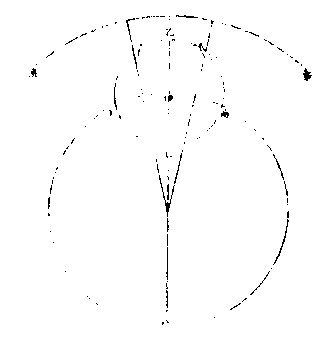
之为百分之三有半也。其最高今时在鹑首宫六度，为丙，太阳右行从辛过内，一周天而复于辛，为三百六十五日二十三刻三分四十八秒，是谓岁实。任躔某宫某度分皆以地心甲为主，而地心所出直线至戊黄道指，为太阳之实行。
其平行则又以本圜之乙心为主，故人在地所测之
实行，时速时迟，而太阳因最高在北任分本圈，则北为大半，故北六宫之日数多于南六宫几八日有奇也。
依此见求太阳之躔度，必用两法，一者定其平行，如随乙丁己直线窥之，从乙心见黄道上之己点。二者定其实行，如随甲丁戊窥之，乃从地心见黄道上之戊点。先得其平行，又以加减求实行，而平实之差为戊己弧，以甲丁乙三角形求之，即得也。其自丙过秋分至庚，两行之差必减平行而得实行。自庚过辛春分至丙，则加于平行而得实行。若用表则从丙最高起算，或从庚最庳起算，至日体之本度为引数，以求加减之度。
太阴朔望本行图

月离之术依歌白泥论有本圜，有本轮，有次轮，本轮之心依本圈之边满一转，即次轮之心依本轮之边得两转，故朔望时月体皆在次轮之最近。最近者，近于本轮之心也。因是不用次轮但以最近处为界，得
图

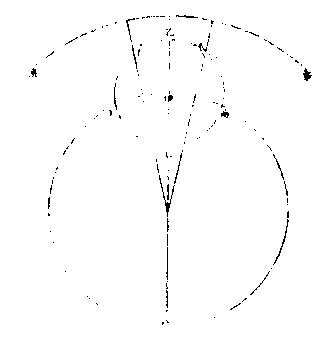
圆圈。月离历指谓为本轮之内圈，此可名朔望之小轮也。
假如丙丁戊为太阴朔望时之本圈，则与地同心。〈因无差故设为同心〉本轮为乙丙丁，其心在本圜之边，甲右距日得每日十二度一十一分，其最高在乙，最庳在己，月

体则又居次之边左行，自乙至丙而己而丁，谓之引数。最外有黄道为辛庚，若从地心出直线上至黄道，而次轮心正居此线之上，则所指者，为太阴之平行度分也。又从地心出直线上至黄道，而月体正居此线之上，则所指者为太阴实行度分也。凡月转或在高或在庳，正当一宫初度〈乙也〉或七宫初度，〈己也〉则平行即是实行过此必有两行之差则以差数加减于平行度分，得其实行度分。又月在乙丙己半转，则以减得之，若在己丁乙半转则以加得之。以在朔望，故平实行相距之极大差不过四度五十八分二十七秒，〈甲丙甲丁是也〉过此为两弦之差则更少与交食，无与月离，历详之。若用不同心圈论，则并不用此本轮其加减平行度分而得实行度分。理则一也，因日月以平实分本行，故平朔平望时两体未必正相合正相对，凡实会之或先或后，日月各以其平行直线相遇而合为一直线，则是中会。
实会中会视会第二〈凡三章〉

测天约说言日月之行有隅照，〈相距三之一〉有方照，〈相距四之一〉有六合照，〈相距六之一〉然悉无交食而独相会、〈朔也亦名合会〉对相，〈望也亦名照会〉则能有食。故本篇所论者，止于相会、相对也。抑会者，总名也。细言之有实会，有中会，有视会。三者皆为推步之原，故言交食之术，必先言相会、相对，言相会、相对之理，必从实会、中会始。
实会中会以地心为主

实会者，以地心所出直线上至黄道者为主，而日月五星两居此线之上，则实会也。即南北相距非同一点，而总在此线正对之过黄极圈，亦为实会。盖过黄极圈者，过黄道之两极而交会于黄道，分黄道为四直角者也。则从旁视之虽地心，各出一线南北异纬，从黄极视之即见地心，所出二线东西同经，是南北正对如一线也，是故谓之实会。若月与五星各居其本轮之周，地心所出线上至黄道而两本轮之心俱当此线之上，则为月与五星之中会。日无本轮、本行圈，与地为不同心。两心所出则有两线，此两线者，若为平行线，而月本轮之心正居地心线上，则是日与月之中会也。盖实会既以地心线射太阴之体为主，则此地心线过小轮之心，谓之中会矣。若以不同心圈之平行线论之，因日月各有本圈，即本圈心皆与地心〈即黄道心〉有相距之度分，即日月循各本圈之周右行，所过黄道经度必时时有差。〈与地不同心故也〉其从地心出直线过日月之体，上至黄道，此所指者为日月之实行度分也。设从地心更出一平行直线与木圈心所出直线偕平行而上至黄道，此所指者为日月之平行度分也。盖太阳心线与地心一线平行，太阴心线亦与地心一线平行，恒时多不相遇，至相遇时两地心线合为一线，则是日月之中相会。若太阳实行之直线与太阴实行之直线合为一线，则是日月之实相会。合会、望会皆有中有实，其理不异。
先依小轮法作图，甲为地心，亦为黄道心，亦为太阴本圈心。
太阴与地同心者，为用本轮故。盖本轮周即太阴圈心绕地心之周，其理一也。

乙为太阳本圈心，〈与地不同心〉太阳在丁，太阴在戊，甲戊丁线直至黄道圈，得辛，指日月实相会之度。如太阳
图

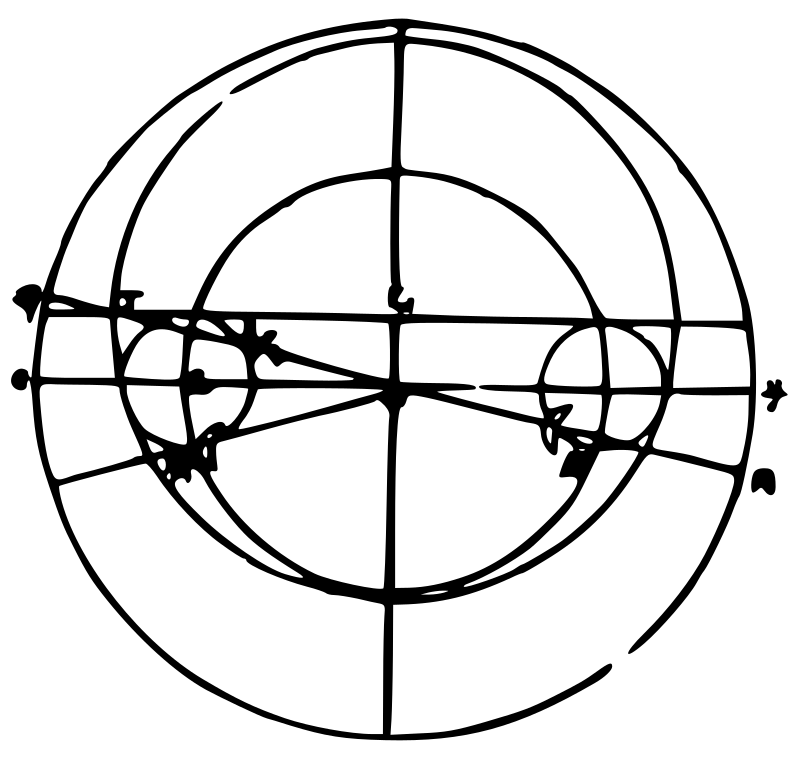
在丁，太阴亦在甲辛直线上，为庚，而此线至黄道圈得丙，即指日月实相望之度。若太阴在癸，与太阳不同一线之上，乃过月本轮之心已而至黄道壬，此直线之所指则日月中相会之度也。如月在庚，从地心出平行线甲子与甲壬，太
图

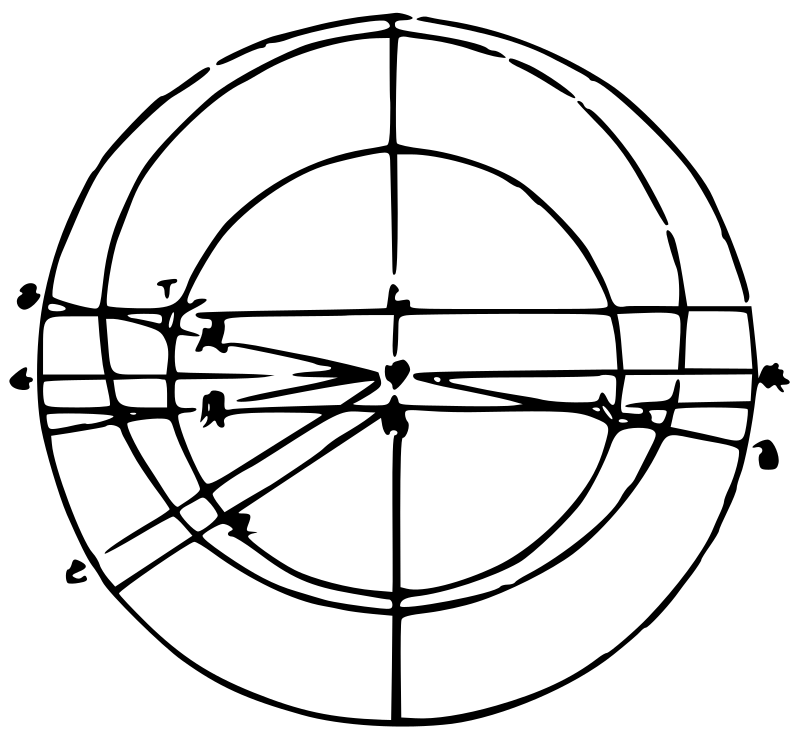
阳平行为一线而至黄道，子亦指日月中相望之度矣。
次依不同心圈法。如后图，黄道与太阳之本圈皆同前，独太阴无本轮而易为本圈，其心与地心不同在甲，乃在丙，此亦以日月并居一直线为实会。如太阳
图

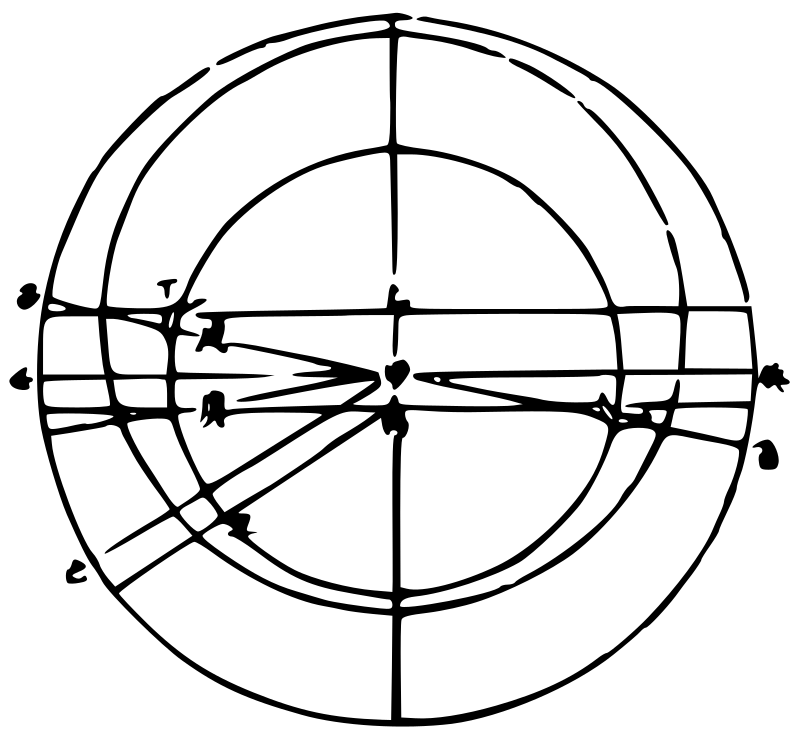
在丁，太阴在本圈之边戊，地心所出甲戊丁线至辛，则所指为实会。而正对月体，至黄道寅，则所指为实望。若中会、中望则以平行线为主，盖甲壬为地心所出直线，既偕太阳本圈心所出过日体之直线乙丁为平行线，又偕太阴本圈

心所出过月体之直线丙庚为平行线，则是两偕行之直线合为一甲壬而至黄道，故所指者为日月中相会之度也。其至相对之黄道上为癸，则所指者为日月中相望之度。设过此交会之时，太阴在丑，则月圈心出者为丙丑线，地心出者为甲己线，两线自偕为平行，而甲壬与乙丁自偕为平行，甲壬甲己不得合为一线矣。故地心所出之两偕行线能合为一甲壬者，必指中交之度为日月相会之共界也。
实会中会相距无定度

日月本圈各与地不同心，故两圈心所出直线各与地心所出直线虽恒为平行线，而又与地心所出直线，其相距广狭恒无定数。设日在本圈之最高，月在本圈之最庳，其实行所至即平行所至，则中会即实会矣。或太阳在最庳，太阴在最高，或两最高两最庳在黄道上同度，则中会、实会亦皆无距度也。惟日月去本圈之最高及最庳右行渐远，则地心所出平行直线渐相去，至半圈周则甚相远，而为实中两会之相距最大差。
图

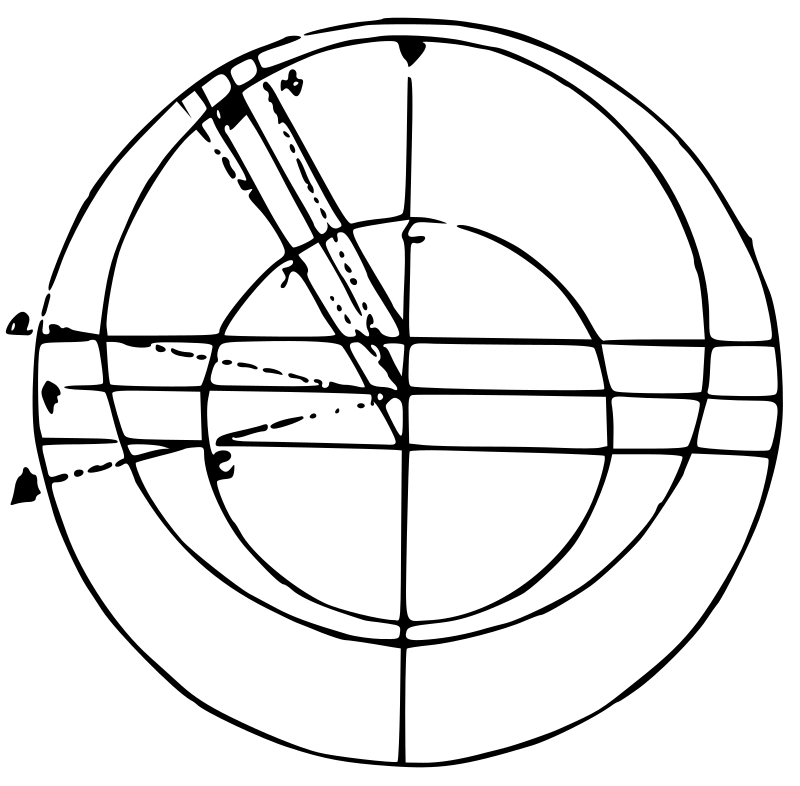
假如甲为太阳之最高，乙为太阴之最庳，若太阳在甲，太阴在乙，即两本圈心及地心所出直线上至黄道，皆合于甲乙线，则实会无分于中会也。若太阳至丙，太阴至丁，去最高各不甚远，则地心所出辛平行线，距本圈心所出直线亦
图

左右稍远，即中会亦稍远于实会矣。又使太阳在戊，太阴在己，则三直线相距更远，而实会、中会相距亦更远，此则以太阳之引数九宫二度得戊辛弧二度三分一十五秒，应减以太阴之引数八宫二十八度，得辛庚弧四度五十八分

二十七秒，应加依法合之，得戊庚弧七度○一分四十二秒，为太阳太阴实会相距数。
实会中会互相随因有变易

实会与中会多不同时，或中会在先，实会在后，或实会在先，中会在后。惟日月各居其本圈之最高或最庳，或一居最高，一居最庳，则中会不分于实会。〈因平行度乃正是实行度〉即不用加减度分，若彼此俱加于平行度，或俱减于平行度，而所加减之度分等，则中会亦不分于实会也。〈两均数相减若俱等无所试故〉又依黄道右行论之，使中会之时太阳之实行在前，太阴之实行在后，则实会在前，中会必随而在后。〈月行速过中而得实会〉若中会时太阴在前，太阳在后，则实会必后于中会也。〈实会之后月乃过中〉若太阳与太阴或皆在本轮中转之半周，〈从最高至最庳〉则两曜所得加减度，其一较狭者，必在前也。或皆在本轮正转之半周，〈从过庳至最高〉则两加减度，其一较广者，必在前也。若其不同在最高庳之间，而各居一半周，则过最高者在前，过最庳者反在后矣。
如图，太阳在本圈，太阴在次轮，外圈为黄道，从地心
图

出直线至黄道而过本轮心，所指者为日月两平行度之中会。盖地心所出日月两平行线合为一线也。若地心线从中会线之左右过日月两体而至黄道，所指者为日月之实行度，而两线相距之广，即日月相距之度。法应化为时、刻、
图

分，以加以减于中会，乃得实会也。又日月平行同在甲或在乙，加减度不同类，〈一实在前一实在后〉则两率并之得日月相距之度。若日月同在丙丁戊己，加减度同类，〈或都在前或都在后〉则两率相减之馀为日月相距之度也。依本图论，日月在甲则以太

阳之加减度加于平行而得实行，〈在前故也〉太阴则减之而得实行。〈在后故〉其所差时刻则以加于中会得实会也。〈月过中而逐及于日故〉日月在乙其加减度则太阳用减，〈在后〉太阴用加，〈在前〉其时刻则相减以得实会也。〈既会之后月乃过中〉若在丙，太阴之加减度大，太阳小，皆减之。其时刻则加之，以得实会。〈月欲及日故〉若在丁，太阳之加减度大，太阴小，亦皆减之，其时刻亦减之，而得实会。〈月已过日故〉若在戊，太阴之加减度大，太阳小，皆加之。〈皆过中故〉其时刻则减之得实会。〈月已过日故〉若在己，太阴之加减度小，太阳大，皆加之，其时刻亦加之得实会也。〈月欲及日故〉总论之，行度在中会前即当加，〈甲日乙月戊己之日月〉在中仑后即当减。〈甲月乙日丙丁之日月〉时刻月实行在日后则当加，〈甲丙己是〉月实行在日前则当减也。〈乙丁戊是〉
推中会实会元法第三〈凡五章〉

日月同居黄道经度，分秒不异，是为正相会。正相会者，实朔也。日月相距正得黄道半周，分秒不异，是为正相对。正相对者，实望也。其推步之法因二曜之实行度不同，其实行之变易又时时不同，故先以平行求得其中相会、中相对，而后渐得其实相会、实相对焉。第中会之法以纪首，〈甲子为纪首〉以每年每日每时之平行度分推步易得耳。实会法必用几何术中三角形弧弦切割诸线，非是则无从可得，故今交食历中所列诸表不过求中求实两法，而求实甚难，不得不繁曲，不得不详密也。
求中会

月行黄道视日行甚速，其在后也，能逐及于日，其既及也，又超于日前。其在朔也，有时隔日光于在下，其在望也；有时失光于地景。求朔望法先定太阳之平行度分，以求太阴距日之度分。若同居黄道经无距度分秒，则为朔。若相距正得半周则为望。外此则中会在先，必减其已过之时刻，而得中会。若中会在后，则加以不及之时刻而得中会。
假如壬申年三月十六日癸丑，日月相望，求太阳平行。其纪首为天启四年甲子天正冬至后第一日子正，时太阳在九宫○度五十一分四十五秒，至本日癸丑午正时，得中积时为八年一百三十五日六时，用太阳平行度，每年一十一宫二十九度四十五分四十一秒，每日五十九分八秒二十微，每小时二分二十七秒五十一微，并得中积度为三千○一十一度三十八分四十七秒，加纪首前宫度得总数满平周，〈三百六十度〉去之馀四十二度三十○分三十一秒，为本日午正时太阳躔大梁宫之平行度分。
次如前法，求同时太阴中积度分一百二十九度三十七分二十二秒四十微，每日一十二度一十一分二十六秒四十一微，为太阴自太阳平行度分。加纪首前十度一十七分三十六秒五十三微，并得二千六百九十九度七分二十四秒，满平周，去之馀五宫二十九度七分二十四秒，为本日午正时月距太阳之经度分。以减半平周，为不及者五十二分三十六秒，未得正望。求其时，用不及度三十分二十八秒三十七微为一小时，其馀得时四十三分三十三秒，为正中望，算外得未初二刻一十三分三十三秒。
求引数

凡日月在最高或最庳，其实行与平行者无异外。此则不同行而两行相距又无定数，故从最高右行，指其平行所至黄道之弧，为引数。因之以求太阳太阴两处所差加减度，若太阴则从其本轮之最高起算，左行为引数之弧也。第须先定日月在中会时之平行度，如前，太阳正午在大梁宫十二度三十分三十一秒，一小时又行二分二十七秒五十一微，尚未至中会，须行四分一十五秒〈并小时〉得中会时刻，以加前得数，其中会平行度在本宫一十二度三十四分四十六秒。其正相对为太阴平行度分，则在大火宫矣。若太阳平行度正合于最高，则无引数，亦无加减。过之即相减，不及则于平行度外加一平周〈三百六十度也〉而减最高，馀为引数。假如最高每年行四十五秒，从甲子至壬申年三月，得六分一十七秒，以加于纪首之最高得三宫○五度五十六分五十八秒，并得三宫○六度○三分一十五秒，为太阳最高行度。因太阳平行度在二宫，不及，加平周减之，得十宫○六度三十一分三十一秒，为太阳中会时引数。同时依太阴每年之本行二宫二十八度四十三分八秒，每日行一十三度三分五十四秒，其中积得二千四百八十度五十九分五十三秒，加入纪首前六宫一十七度四十六分二十三秒，满平周，去之得五宫八度四十六分一十六秒，为太阴壬申年三月中会时之引数也。
求实会

法先求太阳加减度，依前所得最高及平行作图外圈，为黄道，从春分向左计其平行度，从地心出直线指之，次从心又出一直线，至最高度。线上任取一点
图

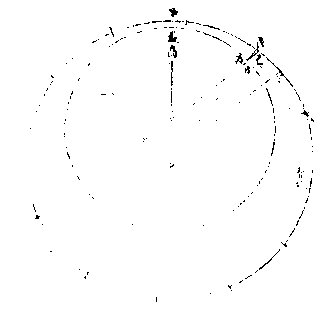
为太阳本圈心，从太阳圈心又出直线与平行度之指线为平行线，至黄道。更从黄道心〈即地心〉出直线，过太阳体之心，至黄道，指其实行度也。
如图，外圈为黄道，其心甲出直线至丁，即前所推太阳平行在大梁宫十二度，

又出直线至三宫六度，为当会时之最高行度。内圈为太阳本圈，其心乙出直线过太阳至己，更作甲丙直线引至戊，指太阳之实行度，即戊己弧为加减度，应推丙角，用甲乙丙三角形，如法求之。
如图，引数之馀弧为丁辛或己辛五十三度二十八分二十九秒，〈止论角故异弧同度〉即丙乙辛外角也。甲乙两心之差为全数十万分之三五八四，今以弦线求加减度，先依甲乙线作甲乙庚直角三边形，用句股开方，求弦线。其比例为甲丙线与甲庚丙角之正弦，若甲
图

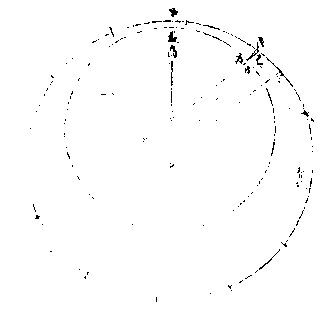
庚线与甲丙庚角之正弦，得一度三十六分五十五秒，为太阳加减度。若用切线则更省，以全数加两心之差数，得一○三五八四，恒为第一率，又相减得九六四一六，为第二率。引数之角随时不一，半之而求切线，为第三率。如法求得

第四率，为切线，查其本度分以减半引数，馀为加减度。若本图，则引数馀弧之角半之为二十六度四十四分一十四秒，其切线五○三九○，为三率。如法得第四率四六九○三，为二十五度九分四十一秒之切线，以减半，引数得一度三十六分三十三秒，为太阳加减度也。
次求太阴加减度，按西历近世名家，先有歌白泥，后有第谷，从前所论会法，两家之说略同，至论太阴则第谷之术更为精密，今先言旧法，次言密法。
图

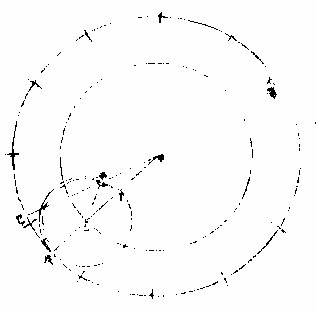
旧法曰：如图，黄道内作同心圈，从太阳平行度越半周而定太阴平行度之一点，从心出直线至此点，必为本圈之过心线，而指本轮之心。次从本轮最高左旋，查其引数，又从黄道心作一直线过太阴体，两线所至黄道间得一弧，此弧

为太阴之加减度也。〈加减度即名均数〉
假如太阴平行度在大火宫正对太阳，其引数自戊左行至丙未，及半周，月体在丙，两直线并出甲，甲乙戊指平行度，甲丙己指实行度，戊己弧为所求加减度。其求之者，甲乙丙三角形也。若用句股法，则自丙至丁下垂线开方，求得甲丙弦，则甲丙线与甲丁丙角若丙丁线与丁甲丙角也。如用切线，则甲乙全数十万，本轮之半径乙丙八六○○，相加得一○八六○○，相减得九一四○○，又半引数求其切线如恒法，即得均度之切线矣。以此推步交食，未免彻差，第谷新法更为详密，鲜不合者。今诸列表悉用此术，故应说其义指如下文。
密求实会〈第谷法〉

月离历指论太阴之本行，故备晦朔弦望。此说交会，故图说止于朔望也。太阴交会仅用三圈：一为本天，一为本轮，一为次轮。本天即本圈也，与地同心，负本轮之心，其半径当十万，则本轮之半径得五千八百，从最高左旋，负次轮之心。如次轮心从最高丁行至
图


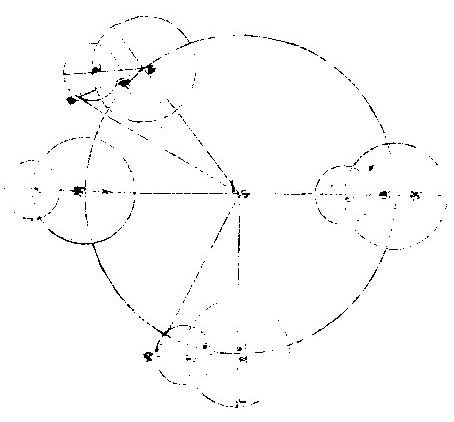
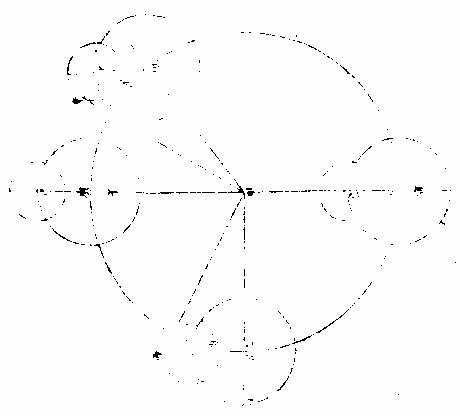
己，其自行度即表中所名引数。用以求加减度，加减度即均数也。若本轮在子或寅，则月体在庚自行在一宫初度或六宫末度，则无引数可计，亦无均度可求矣。若本轮在丑，则月体在丙自行，得三宫初度为交会时之极大差，欲得此数，用甲乙丙三角形求之，甲乙线为全数，乙己与巳丙相加，得乙丙为八千七百，甲乙丙角系自行之象限，必为直角。依前法，以切线求乙甲丙均度角，必得四度五十八分有奇。若自轮在卯，为十宫，月体在辛，必用两三角形乃得均度。
图图

其一为甲卯辛形，所求均度为卯甲辛角，形中特有全数，无从得角。宜先推卯己辛三角形，形有本轮之半径卯己，有次轮之半径己辛，有引数馀弧之倍角卯己辛，如法推得卯辛线及己卯辛角，以减于引数，得其馀弧之数，为甲卯辛角。因此可求卯甲辛角，为均度也。更论次轮之周月体循而右旋，其半径仅得本轮半径之半，以较全数得十万之二千九百，两半径并得八千七百，为会时所用之数。以推最大均度。太阴在次轮，从最近庚起算，恒倍本轮行。如丁己为
图

本轮之一象限，而太阴行小轮，从庚至丙得半周，是自行得半周，太阴行全周。故前言本轮在子在寅，月体至庚，悉无加减数也。今依图求太阴均度如前，设得其自行五宫八度四十六分一十六秒，距太阳半周。其经度在大火宫一十

二度，则本轮在乙，从地心引直线为甲乙全数，从乙出直线至自行之限丙，必与中最高线甲戊为平行线，而定引数为庚丙倍引数，从最近右旋，得太阴在次轮丁，从乙至丁引乙丁直线，则得乙丙丁三角形，其乙丙丙丁两线为两小轮之半径，乙丙丁角为倍引数〈辛壬丁是〉之馀角，〈丁辛弧是〉即可求丙乙丁角与乙丁直线也。又甲乙丁三角形，欲求乙甲丁均度之角，以切线算之，宜先得己乙丁角，以偕全数及乙丁线，乃得其所包角矣。法见下文。
如图，求丙乙丁角倍引数，〈辛壬丁也〉得三百一十七度三十二分三十二秒，馀〈丁辛〉四十二度二十七分二十八秒，为乙丙丁角其馀角。〈乙丁两角也〉总而半之，得六十八度四十六分一十六秒，其切线得二五七四三○，为三率。两轮之半径相加得八七○○，为一率。相减馀二九○○，为二率。算得第四率切线八五八一○，其弧四十度三十八分，以减前总馀角之半数，得二十八度○八分一十六秒，为丙乙丁角也。次求乙丁线，则丙乙丁角之正弦〈四七一六○〉与丙丁，〈二九○○〉若乙丙丁
图

角之正弦〈六七五○五〉与乙丁线，算得四一二九，次以甲乙丁大三角形求均度，先得己乙丙角，〈引数之馀未满半周〉以加丙乙丁角，得己乙丁角四十九度二十二分。其馀角〈甲丁两角〉总而半之，得六十五度一十九分，查切线二一七五八二，为三率。以乙
丁线加全数，共一○四一二九，为一率。相减得九五
八七一，为二率。算得第四率切线二○○三二○，其弧六十三度二十八分一十七秒，以减前六十五度一十九分，馀一度五十分四十三秒，为所求太阴均度，与列表合。
今以两所得均度，求实会时，查图视均度，或以加于平行度，或以减于平行度，即见太阴距对处若干，或过之，或不及，则以其相距之度分化为时刻，依前法或加或减于中会时刻，必近于实会时刻。
如前，推壬申三月月食，其会时，太阳之平行在实行后，则以均度加于平行，得实行。太阴之平行在实行前，则以均度减实行，又以二实行相较，见太阴视正相对，不及者三度二十七分三十八秒，化为二十七刻三分四十五秒，以加前中会，算外得实会在戌正二刻二分一十八秒。
复求实会时

日月之两实行变动不居，非一圆形能尽其理。几何家欲径测径推，无法可得。故须先用平行以渐推其实行，顾又非一推可遽合也。盖初用之引数，其所指者中会之引数，非实会之引数。则其加减度所推实时，特近于实时，非正实时也。法宜更求中实会之间日月自行度分，依加减时，法或加或减于前之平自行，乃得次引数。求其均度，复查二曜实相距度，化为时刻，或加或减于中会时刻，乃得正实时刻。若三推之终，所得时刻分秒不异于次得，即合天无疑矣。假如前得差二十七刻三分四十五秒，其间太阳复平行一十六分四十七秒，以加初平行得一宫一十二度五十一分三十三秒，减其最高〈最高不动即用前数〉得自行一十宫六度四十八分一十七秒，馀弧〈至满周〉五十三度一十一分四十二秒，半之而求切线得五○○七○，为三率。以全数加不同心差为一率，相减为二率，算得四率四六六○五，其弧一度三十六分三十四秒，为太阳次均度也。
太阴中实会之距时间〈即前二十七刻有奇〉复平行三度二十七分二十八秒，以加前经度，总得经度七宫一十六度二分二十四秒，为本轮居本圈之处。而本轮此时
图

间亦向右自行三度四十二分三十一秒，以加前自行，得次自行五宫一十一度二十八分四十七秒，即次引数也，为次轮心居本轮周之处。倍之，得太阴居次轮周之度也。借前图，则乙丙丁角今为三十五度二分二十六秒，馀角〈乙丁两角〉

总而半之，得七十二度二十八分四十七秒，其切线三一六七六八，为三率。一二率如前算得一○五五八八，其弧四十六度三十三分，以减前半弧七十二度二十八分四十七秒，得二十五度五十五分二十二秒，为丙乙丁角。次求乙丁线，则此角之正弦四三七一六，为一率，丙丁半径为二率，乙丙丁角之正弦五七四一六，为三率，算得三八○八，为乙丁直线也。今求均度以自行馀之甲乙丙角，并丙乙丁角，为己乙丁角四十三度二十六分三十五秒，馀者〈甲丁两角〉总
图

而半之，得六十八度一十六分四十二秒，为三率。第一及二为乙丁线，一加一减于全数，〈甲乙也〉算得二三二五九六，求应减之度，而得次均度一度三十二分三十三秒，又以太阴次均度加于太阳次均度，见太阴视正相对不及者三度

○九分○七秒，化为时刻，得二十四刻一十二分一十七秒，以加于中会，算外得实会在戌初三刻一十分五十秒。