钦定四库全书
御制数理精蕴下编卷三十
　　体部八
　　　各体权度比例
　　　堆垛

　　各体权度比例
数学至体而备以其综线面之全而尽度量衡之用
也盖线面存乎度体则存乎量求轻重则存乎衡是
以又有权度之比例其法槩以诸物制为正方其边
一寸其积千分较量豪釐俾有定率然后凡物知其
体积即知其重轻知其重轻即知其体积而权度无
遁情也且体之为质不一边积等者轻重不同轻重
等者边积不同皆有互相比例之法而各体无混淆

也
　　赤金十六两八钱
　　纹银九两
　　水银十二两二钱八分
　　红铜七两五钱
　　白铜六两九钱八分
　　黄铜六两八钱
　　纲六两七钱三分
　　生铁六两七钱

　　熟铁六两七钱三分

　　高锡六两三钱
　　六锡七两六钱
　　倭铅六两
　　黑铅九两九钱三分
　　白玉二两六钱
　　金珀八钱
　　白玛瑙二两三钱
　　红玛瑙二两二钱

　　砗磲一两五钱二分
　　青石二两八钱八分
　　白石二两五钱
　　红石二两五钱六分
　　象牙一两五钱四分
　　牛角一两九钱
　　沉香八钱二分
　　白檀八钱三分
　　紫檀一两零二分

　　花梨八钱七分

　　楠木四钱八分
　　黄杨七钱五分
　　乌木一两一钱
　　油八钱三分
　　水九钱三分
设如有金一方每边三寸问重几何
　　　　　法以一寸为一率金寸方重一十六两
　　　　　八钱为二率今所设之金方每边三寸

　　　　　自乘再乘得二十七寸为三率求得四
　　　　　率四百五十三两六钱即金之重数也
　　　　　此法盖因金方每边三寸则体积为二
　　　　　十七寸以一寸与一十六两八钱之比
　　　　　同于二十七寸与四百五十三两六钱
　　　　　之比也
设如有银一方每边二寸问重几何
　　　　　法以一寸为一率银寸方重九两为二
　　　　　率今所设之银方每边二寸自乘再乘

　　　　　得八寸为三率求得四率七十二两即

　　　　　银之重数也此法盖因银方每边二寸
　　　　　则体积为八寸以一寸与九两之比同
　　　　　于八寸与七十二两之比也
设如黄铜一条重三百七十四两问积几何
　　　　　法以黄铜寸方重六两八钱为一率一
　　　　　寸为二率今所设黄铜重三百七十四
　　　　　两为三率求得四率五十五寸即黄铜
　　　　　之积也

设如熟铁一块重十六两欲镕为正方体问每边几
　何
　　　　　法以熟铁寸方重六两七钱三分为一
　　　　　率一寸为二率今铁重十六两为三率
　　　　　求得四率二寸三百七十七分四百一
　　　　　十四釐有馀开立方得一寸三分三釐
　　　　　有馀即每边之数也
设如水银一匣但知匣阔四寸长六寸高三寸五分
　问内水银重数几何

　　　　　法以匣阔四寸与长六寸相乘得二十

　　　　　四寸又以高三寸五分再乘得八十四
　　　　　寸为水银一匣之积数爰以一寸为一
　　　　　率水银寸方重一十二两二钱八分为
　　　　　二率今所得之水银一匣之积数八十
　　　　　四寸为三率求得四率一千零三十一
　　　　　两五钱二分即水银之重数也
设如白玉一方重九十三两六钱但知阔比高多一
　寸长比阔多三寸问高阔长各几何

　　　　　法以玉寸方重二两六钱为一率一寸
　　　　　为二率今所设玉重九十三两六钱为
　　　　　三率求得四率三十六寸为长方体积
　　　　　乃以阔比高多一寸长比阔多三寸为
　　　　　带两纵之较用带两纵不同较数开立
　　　　　方法算之得高二寸加阔比高多一寸
　　　　　得三寸为阔再加长比阔多三寸得六
　　　　　寸为长也
设如金与银镕于一处共得正方体积二十七寸重

　二百七十四两二钱问金与银各几何

　　　　　法以共积二十七寸以银寸方重九两
　　　　　乘之得二百四十三两与共重二百七
　　　　　十四两二钱相减馀三十一两二钱乃
　　　　　以银寸方重九两与金寸方重十六两
　　　　　八钱相减馀七两八钱为一率金一寸
　　　　　为二率今相减所馀之三十一两二钱
　　　　　为三率求得四率四寸即金之寸数于
　　　　　共积二十七寸内减去四寸馀二十三

　　　　　寸即银之寸数也以金四寸与金寸方
　　　　　重十六两八钱相乘得六十七两二钱
　　　　　以银二十三寸与银寸方重九两相乘
　　　　　得二百零七两两数相并得二百七十
　　　　　四两二钱仍与原数相合也此即和较
　　　　　比例之法盖银二十七寸则其重数应
　　　　　得二百四十三两与共重二百七十四
　　　　　两二钱相减馀三十一两二钱即金重
　　　　　于银之数而金每寸比银每寸多七两

　　　　　八钱故多七两八钱则金有一寸今多

　　　　　三十一两二钱则知金有四寸也若欲
　　　　　先得银数则仍以七两八钱为一率一
　　　　　寸为二率将共积二十七寸以金寸方
　　　　　重十六两八钱乘之得四百五十三两
　　　　　六钱内减共重二百七十四两二钱馀
　　　　　一百七十九两四钱为三率求得四率
　　　　　二十三寸即银之寸数与共积二十七
　　　　　寸相减馀四寸即金之寸数盖少七两

　　　　　八钱则银有一寸今少一百七十九两
　　　　　四钱则知银有二十三寸也
设如金镶玉炉一座共重四十六两七钱问金玉各
　几何
　　　　　法用盛水器皿一件置炉其中实之以
　　　　　水取出炉看水浅几何设如盛水器皿
　　　　　系正方形每边五寸取出炉水浅五分
　　　　　即以每边五寸自乘得二十五寸以水
　　　　　浅五分为高再乘得一十二寸五百分

　　　　　为炉之体积即金玉之共积爰以共积

　　　　　一十二寸五百分以玉寸方重二两六
　　　　　钱乘之得三十二两五钱与共重四十
　　　　　六两七钱相减馀一十四两二钱乃以
　　　　　玉寸方重二两六钱与金重一十六两
　　　　　八钱相减馀一十四两二钱为一率金
　　　　　一寸为二率今相减所馀一十四两二
　　　　　钱为三率求得四率一寸为金之寸数
　　　　　于共积一十二寸五百分内减去一寸

　　　　　馀十一寸五百分为玉之寸数金一寸
　　　　　重得十六两八钱玉十一寸五百分与
　　　　　玉寸方重二两六钱相乘得二十九两
　　　　　九钱为玉之重数两数相并共得四十
　　　　　六两七钱仍与原数相合也如欲先得
　　　　　玉数则仍以一十四两二钱为一率一
　　　　　寸为二率将所得共积一十二寸五百
　　　　　分以金寸方重十六两八钱乘之得二
　　　　　百一十两内减共重四十六两七钱馀

　　　　　一百六十三两三钱为三率求得四率

　　　　　一十一寸五百分为玉之寸数与共积
　　　　　一十二寸五百分相减馀一寸即金之
　　　　　寸数也
设如空心金球一个外径一尺二寸厚三分问重几
　何
　　　　　法以金球外径一尺二寸自乘再乘得
　　　　　一尺七百二十八寸乃用方边球径相
　　　　　等方积球积不同之定率比例以方积

　　　　　一○○○○○○○○○为一率球积
　　　　　五二三五九八七七五为二率今球径
　　　　　自乘再乘之正方体积一尺七百二十
　　　　　八寸为三率求得四率九百零四寸七
　　　　　百七十八分六百八十三釐有馀为球
　　　　　之全体积又以厚三分倍之得六分与
　　　　　外径一尺二寸相减馀一尺一寸四分
　　　　　为空心径自乘再乘得一尺四百八十
　　　　　一寸五百四十四分仍以方积一○○

　　　　　○○○○○○○为一率球积五二三

　　　　　五九八七七五为二率今空心径自乘
　　　　　再乘之正方体积一尺四百八十一寸
　　　　　五百四十四分为三率求得四率七百
　　　　　七十五寸七百三十四分六百二十三
　　　　　釐有馀为球内空心虚积两积相减馀
　　　　　一百二十九寸零四十四分零六十釐
　　　　　有馀为空心球体积乃以一寸为一率
　　　　　金寸方重十六两八钱为二率空心球

　　　　　体积一百二十九寸零四十四分零六
　　　　　十釐有馀为三率求得四率二千一百
　　　　　六十七两九钱四分有馀即空心金球
　　　　　体之重数也
设如正方青石一块红石一块红石比青石每边多
　二寸体积多五十六寸问二石之边数及重数各
　几何
　　　　　法以红石比青石每边多二寸为边较
　　　　　体积多五十六寸为积较用大小二立

　　　　　方有边较积较求边法算之以边较二

　　　　　寸自乘再乘得八寸与积较五十六寸
　　　　　相减馀四十八寸三归之得一十六寸
　　　　　以边较二寸除之得八寸为长方面积
　　　　　以边较二寸为长阔之较用带纵较数
　　　　　开平方法算之得阔二寸即青石之边
　　　　　数加红石比青石每边多二寸得四寸
　　　　　即红石之边数乃以一寸为一率红石
　　　　　寸方重二两五钱六分为二率红石每

　　　　　边四寸自乘再乘得六十四寸为三率
　　　　　求得四率一百六十三两八钱四分即
　　　　　红石之重数也又以一寸为一率青石
　　　　　寸方重二两八钱八分为二率青石每
　　　　　边二寸自乘再乘得八寸为三率求得
　　　　　四率二十三两零四分即青石之重数
　　　　　也此法因二石皆为正方体故用大小
　　　　　二立方有边较积较求边之法求得二
　　　　　石之边自乘再乘即得二石之体积用

　　　　　寸方重数定率以比例之即得二石之

　　　　　重数也
设如有正方水桶三个第一桶每边一尺第三桶比
　第二桶每边多二寸第三桶体积与第一桶第二
　桶两桶之共积相等问三桶水之重数各几何
　　　　　法以一寸为一率水寸方重九钱三分
　　　　　为二率第一桶正方每边一尺自乘再
　　　　　乘得一千寸为三率求得四率九百三
　　　　　十两为第一桶水之重数又以第三桶

　　　　　比第二桶每边多二寸为边较以第一
　　　　　桶体积一千寸为第三桶比第二桶所
　　　　　多之积较用大小二立方有边较积较
　　　　　求边法算之以边较二寸自乘再乘得
　　　　　八寸与积较一千寸相减馀九百九十
　　　　　二寸三归之得三百三十寸六百六十
　　　　　六分六百六十六釐有馀以边较二寸
　　　　　除之得一尺六十五寸三十三分三十
　　　　　三釐有馀为长方面积以边较二寸为

　　　　　长阔之较用带纵较数开平方法算之

　　　　　得阔一尺一寸八分九釐有馀为第二
　　　　　桶之边数加较二寸得一尺三寸八分
　　　　　九釐有馀为第三桶之边数乃以一寸
　　　　　为一率水寸方重九钱三分为二率第
　　　　　二桶每边一尺一寸八分九釐有馀自
　　　　　乘再乘得一尺六百八十寸九百二十
　　　　　四分有馀为三率求得四率一千五百
　　　　　七十两九钱九分三釐有馀即第二桶

　　　　　水之重数又以一寸为一率水寸方重
　　　　　九钱三分为二率第三桶每边一尺三
　　　　　寸八分九釐有馀自乘再乘得二尺六
　　　　　百七十九寸八百二十六分有馀为三
　　　　　率求得四率二千四百九十二两二钱
　　　　　三分八釐有馀即第三桶水之重数也
　　　　　此法盖因第三桶之体积与第一第二
　　　　　两桶之共积相等则第一桶体积一千
　　　　　寸即第三桶体积比第二桶体积所多

　　　　　之较也而第三桶比第二桶每边多二

　　　　　寸故用大小二立方有边较积较求边
　　　　　法求得二桶之边数自乘再乘即得二
　　　　　桶之体积用寸方重数定率以比例之
　　　　　即得二桶水之重数也
设如金球一个径二寸二分六釐今欲作一银球其
　重与金球等问径几何
　　　　　法以金方边一寸为一率银方边一寸
　　　　　二分三釐为二率今所设之金球径二

　　　　　寸二分六釐为三率求得四率二寸七
　　　　　分七釐有馀即银球之径数也此法盖
　　　　　因各色俱为正方体其重数俱设为十
　　　　　六两八钱与金寸方等故金方边为一
　　　　　寸银方边为一寸二分三釐水银方边
　　　　　为一寸一分一釐铅方边为一寸一分
　　　　　九釐铜方边为一寸三分一釐铁方边
　　　　　为一寸三分六釐锡方边为一寸三分
　　　　　九釐石方边为一寸八分九釐水方边

　　　　　为二寸六分四釐油方边为二寸七分

　　　　　四釐皆系边与边之比例故球径与球
　　　　　径之比同于方边与方边之比而为相
　　　　　当比例四率也
设如青石一块正方一尺二寸重四千九百七十六
　两六钱四分今欲作与青石一样大熟铁一块问
　重几何
　　　　　法以青石寸方重二两八钱八分为一
　　　　　率熟铁寸方重六两七钱三分为二率

　　　　　今所设之青石重四千九百七十六两
　　　　　六钱四分为三率求得四率一万一千
　　　　　六百二十九两四钱四分即与青石一
　　　　　样大熟铁之重数也

　　堆垛
堆垛之法虽为体属而一面平堆与方圆束形实与
面同方者即平方法其馀则用梯形法以其每层皆
递加之数也束形亦与一面平堆同法盖圆者以六
包一方者以八包一三角者以九包一有边求积有
周求积其理皆相通也若夫以方面层累者则为四
角尖堆以三角面层累者则为三角尖堆此二者每
层之边皆同为递加一数每层之面积则三角为按

位相加之数四角为按位自乘相加之数其傍皆崚
嶒不平故与体亦微异也至于以长方面层累者则
为长方堆以全堆而减去上截者则为半堆总以尖
堆之法御之分之以立其法合之以明其理一一按
法解之于后
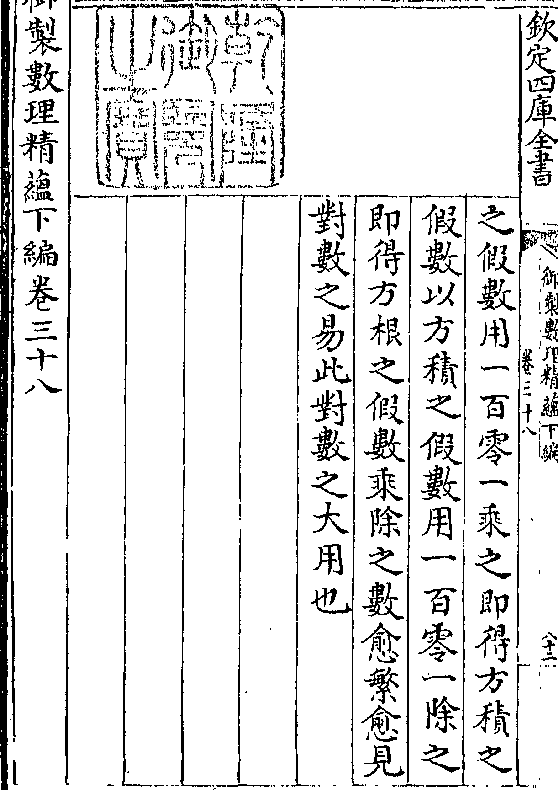
设如一面直角尖堆底十二求积几何
　　　　　法以底十二加尖上一得十三与层数
　　　　　十二相乘得一百五十六折半得七十
　　　　　八即一面直角尖堆之积也如图甲乙

　　　　　丙一面直角尖堆乙丙为底十二其甲

　　　　　乙高亦即为十二层其每层皆加一为
　　　　　挨次递加之数成直角三角形试另作
　　　　　一丁戊己直角三角形合于原形之侧
　　　　　则成甲乙丁戊长方形其高即层数其
　　　　　底即首数与末数相加之数其积即总
　　　　　数加一倍之数(见算法原本二/卷第三十二节)故以底
　　　　　十二与上尖一相加与层数十二相乘
　　　　　得长方积析半即得一面直角尖堆之

　　　　　积也此法与勾股求积之法异者盖勾
　　　　　股之上尖为一点无数可纪此上尖一
　　　　　即其上之阔成斜方形故用斜方求积
　　　　　之法以上阔与下阔相加以高数乘之
　　　　　折半而得积也
设如一面直角尖堆积二十八求底几何
　　　　　法以一面直角尖堆积二十八倍之得
　　　　　五十六为长方积以一为长阔之较用
　　　　　带纵较数开平方法算之得阔七即一

　　　　　面直角尖堆之底数也如图甲乙丙一

　　　　　面直角尖堆积倍之则成甲乙丁戊长
　　　　　方形积其乙丁长比甲乙阔多一故用
　　　　　带纵较数开平方法算之得甲乙与乙
　　　　　丙等为一面直角尖堆之底阔也
设如一面三角尖堆底七求积几何
　　　　　法以底七加上尖一得八与层数七相
　　　　　乘得五十六折半得二十八即一面三
　　　　　角尖堆之积也如图甲乙丙一面三角

　　　　　尖堆乙丙为底七其甲乙高亦即为七
　　　　　层其每层皆加一为挨次递加之数成
　　　　　等边三角形试另作一丁戊巳等边三
　　　　　角形合于原形之侧则成甲乙丁戊斜
　　　　　方形其高即层数其底即首数与末数
　　　　　相加之数其积即总数加一倍之数故
　　　　　以底七与上尖一相加与层数七相乘
　　　　　得斜方积折半得一面三角尖堆之积
　　　　　也

设如一面三角尖堆积三十六求每边几何

　　　　　法以一面三角尖堆积三十六倍之得
　　　　　七十二为长方积以一为长阔之较用
　　　　　带纵较数开平方法算之得阔八即一
　　　　　面三角尖堆每一边之数也如图甲乙
　　　　　丙一面三角尖堆积倍之则成甲乙丁
　　　　　戊斜长方积若直排之即与直角长方
　　　　　积等故其求边之法亦与前直角尖堆
　　　　　求边之法同也

设如一面梯形堆上五下九求积几何
　　　　　法以上五与下九相加得十四又视上
　　　　　五以上至一虚四位即以所虚之四与
　　　　　下九相减馀五为层数与上下相加之
　　　　　十四相乘得七十折半得三十五即一
　　　　　面梯形堆之积也如图甲乙丙丁一面
　　　　　梯形堆甲丁为上五乙丙为下九甲乙
　　　　　为层数五(凡自一递加之数其末数即/位数今首数为五计自一己)
　　　　　(截去四位故于末数内减去所少之位/即为今之所有之位见算法原本二卷)

　　　　　(第三十/二节)试另作一戊己庚辛梯形合于

　　　　　原形之侧则成甲乙己庚斜方形其底
　　　　　即上数与下数相加之数其高即层数
　　　　　其积即总数加一倍之数故以上数与
　　　　　下数相加与层数相乘折半即得一面
　　　　　梯形堆之积也
　　　　　又法以底九用一面三角尖堆求积法
　　　　　求得总积四十五又以上五内减一馀
　　　　　四为上虚小一面三角尖堆之底亦用

　　　　　三角尖堆求积法求得上虚小一面三
　　　　　角尖堆积十两积相减馀三十五即一
　　　　　面梯形堆之积也如图甲乙丙丁一面
　　　　　梯形堆先求得戊乙丙三角尖堆总积
　　　　　又求得戊己庚上虚小三角尖堆积相
　　　　　减即得甲乙丙丁梯形堆之积也如有
　　　　　上阔或下阔与层数求积者则于层数
　　　　　内减一馀为上下阔之较与上阔相加
　　　　　则得下阔与下阔相减则得上阔皆用

　　　　　有上下阔之法算之而得积也

设如一面梯形堆积三十五下九问上几何
　　　　　法以下九用一面三角尖堆求积法求
　　　　　得总积四十五内减梯形积三十五馀
　　　　　十为上虚小一面三角尖堆积用一面
　　　　　三角尖堆有积求边法求得每边四加
　　　　　一得五即一面梯形堆之上阔也如图
　　　　　甲乙丙丁一面梯形堆先以乙丙下九
　　　　　求得戊乙丙三角尖堆总积内减甲乙

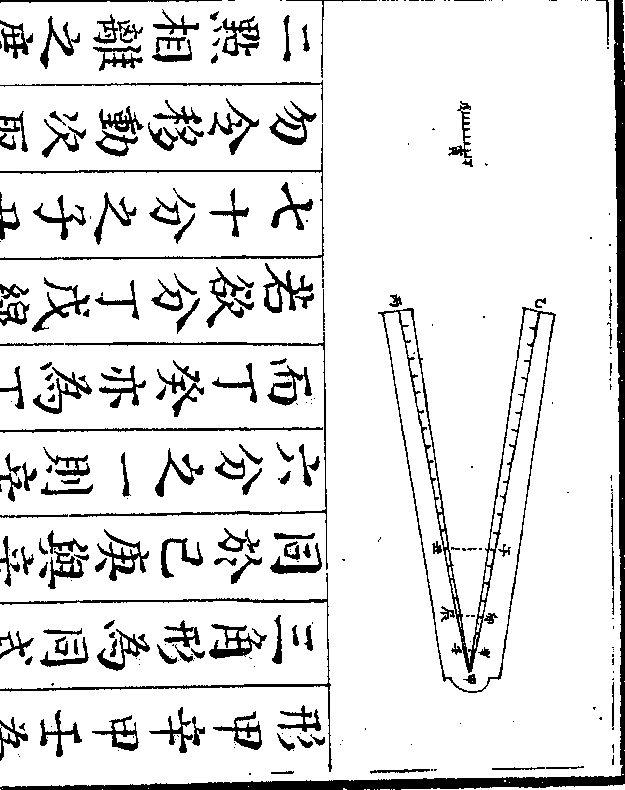　　　　　丙丁梯形堆积馀戊己庚上虚小一面
　　　　　三角尖堆积乃用有积求边法求得己
　　　　　庚四因每层埃次递加一故加一即得
　　　　　甲丁五为上阔也如有上阔求下阔者
　　　　　则以上阔内减一为上虚小三角尖堆
　　　　　之底求得上虚小三角尖堆积与梯形
　　　　　积相加为三角尖堆总积亦用有积求
　　　　　边法算之即得下阔也
设如一面梯形堆积三十五上阔比下阔少四问上

　下阔各几何

　　　　　法以梯形堆积三十五倍之得七十又
　　　　　以上下阔之较四加一得五为层数以
　　　　　除倍积七十得十四为上下阔之和加
　　　　　较四得十八折半得九为下阔内减较
　　　　　四馀五为上阔也如图甲乙丙丁一面
　　　　　梯形堆积每层挨次加一今甲丁上阔
　　　　　比乙丙下阔少四即知甲乙为五层矣
　　　　　故以甲乙丙丁梯形积倍之则成甲乙

　　　　　戊己斜方积以甲乙五层除之得乙戊
　　　　　为上下阔之和加上下阔之较折半即
　　　　　得下阔于下阔内减上下阔之较即得
　　　　　上阔也如有积与上下阔之和求上下
　　　　　阔者则将积数加一倍以上下阔之和
　　　　　除之即得层数内减一即得上下阔之
　　　　　较或有积与层数求上下阔者则于层
　　　　　数内减一即得上下阔之较以层数除
　　　　　倍积即得上下阔之和既有较有和即

　　　　　得上下阔矣

设如一面六角堆每边六求积几何
　　　　　法以一面六角堆分作六三角尖堆算
　　　　　之以每边六减一馀五为每一面三角
　　　　　尖堆之底与每边六(即底加/一也)相乘得三
　　　　　十折半得十五为每一面三角尖堆积
　　　　　六因之得九十加中心一得九十一即
　　　　　一面六角堆之积也如图甲乙丙丁戊
　　　　　己一面六角堆六分之则成甲庚辛类

　　　　　六三角尖堆而馀中心一其每一三角
　　　　　尖堆之甲庚一边比六角堆之甲己一
　　　　　边少一故以六角堆之每一边内减一
　　　　　即得三角尖堆之每一边而求得一面
　　　　　三角尖堆积六因之再加中心一即得
　　　　　一面六角堆之总积也
设如一面六角堆积九十一求每边几何
　　　　　法以一面六角堆积九十一减中心一
　　　　　馀九十六归之得十五为一面三角尖

　　　　　堆积用一面三角尖堆有积求边法算

　　　　　之得每边五加一得六即六角堆之每
　　　　　一边也如图甲乙丙丁戊己一面六角
　　　　　堆积先减去中心一以六归之则得甲
　　　　　庚辛一三角尖堆积其三角尖堆之甲
　　　　　庚一边比六角堆之甲己一边少一故
　　　　　用一面三角尖堆有积求边法求得一
　　　　　边再加一为一面六角堆之每一边也
　　　　　此即算书所谓圆束也本以六包一不

　　　　　能成圆凡云圆者皆六边也
　　　　　周四十求积几何
　　　　　法以外周四十加四得四十四四归之
　　　　　得十一为方束每一边之数自乘得一
　　　　　百二十一即方束之积也如图甲乙丙
　　　　　丁方束其四隅之四各为两边所同用
　　　　　故必以外周加四以四归之始得甲乙
　　　　　每一边之数以一边自乘即为方束之
　　　　　积数也

　　　　　又法以外周四十加八得四十八与外

　　　　　周四十相乘得一千九百二十十六除
　　　　　之得一百二十加中心一得一百二十
　　　　　一为方束之积也盖方束以八包一其
　　　　　外周所包之数亦必以八递加为超位
　　　　　平加之数如甲乙丙丁方束除却中心
　　　　　之一最内一层为八第二层为十六第
　　　　　三层为二十四第四层为三十二第五
　　　　　层为四十每层皆加八为超位平加之

　　　　　数引而长之成戊己庚辛梯形外周四
　　　　　十即梯形之底内周八即梯形之上阔
　　　　　如以首数八与末数四十相加得四十
　　　　　八用层数五乘之折半即得总数(见算/法原)
　　　　　(本二卷第/三十二节)然其层数之五乃系外周四
　　　　　十用八归所得之数今以内周八与外
　　　　　周四十相加即与外周四十栒乘是未
　　　　　用八归故将相乘所得之数必以八归
　　　　　又以二归(即折/半)始得总数夫先用八归

　　　　　后用二归即与用十六归除等(二与八/相因得)

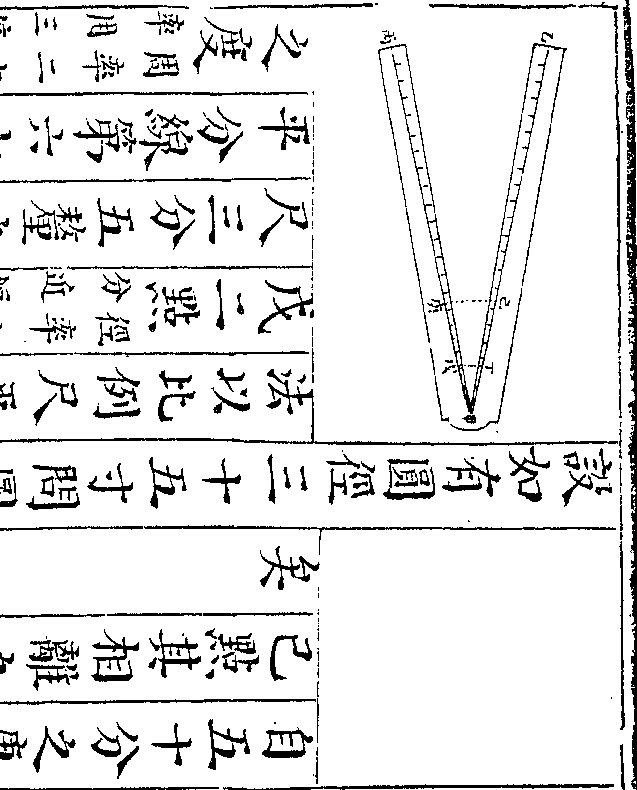　　　　　(一十六合两次/除为一次除)故以十六归除得总数
　　　　　再加中心一即得方束之积也又按第
　　　　　一法以外周四十加四以四归之得方
　　　　　束之每一边是外周加四则得每边之
　　　　　四倍若以外周加四自乘必得方束积
　　　　　之十六倍而以十六归除亦即得方束
　　　　　之积今以外周加八与外周相乘成长
　　　　　方形则其长比每边之四倍多四其阔

　　　　　比每边之四倍少四其积必为方束积
　　　　　之十六倍而少十六以十六归除则得
　　　　　方束积而少一故加一而得方束积也
　　　　　此方束每边十一系奇数故有中心之
　　　　　一若方束每边系偶数者则无中心之
　　　　　一详见下法
设如方束外周三十六求积几何
　　　　　法以外周三十六加四得四十四归之
　　　　　得一十为方束每一边之数自乘得一

　　　　　百即方束之积也

　　　　　又法以外周三十六加八得四十四与
　　　　　外周三十六相乘得一千五百八十四
　　　　　十六除之得九十九加一得一百为方
　　　　　束之积也此方束每边系偶数无中心
　　　　　一其最内一层为四其外周三十六用
　　　　　八归之则得四层半然其立法亦与前
　　　　　法同乘除得数仍加一者盖以外周加
　　　　　四则得每边之四倍若以外周加四自

　　　　　乘必得方束积之十六倍而以十六归
　　　　　除亦即得方束之积今以外周加八与
　　　　　外周相乘成长方形则其长比每边之
　　　　　四倍多四其阔比每边之四倍少四其
　　　　　积必为方束积之十六倍而少十六以
　　　　　十六归除则得方束积而少一故加一
　　　　　而得方束积也
设如方束积一百求外周几何
　　　　　法以方束积一百开平方得一十四因

　　　　　之得四十内减四馀三十六即方束外

　　　　　周之数也如图甲乙丙丁方束开方则
　　　　　得甲乙一边前法以外周加四四归之
　　　　　而得一边此法以一边四因之减四而
　　　　　即得外周也
　　　　　又法以方束积一百内减一馀九十九
　　　　　以十六乘之得一千五百八十四为长
　　　　　方积以八为长阔之较用带纵较数开
　　　　　平方法算之得阔三十六即方束之外

　　　　　周数也此即方束有外周求积之法而
　　　　　转用之前法以外周加八与外周相乘
　　　　　十六除之再加一而得积此法则以积
　　　　　数减一馀用十六乘之以八为长阔之
　　　　　较用带纵开方得阔而为外周也
设如三棱束外周二十七求积几何
　　　　　法以外周二十七加三得三十三归之
　　　　　得一十为三棱束每一边之数用一面
　　　　　三角尖堆有边求积法以每边一十加

　　　　　一得一十一与每边一十相乘得一百

　　　　　一十折半得五十五即三棱束之积也
　　　　　如图甲乙丙三棱束其三角之三各为
　　　　　两边所同用故必以外周加三以三归
　　　　　之始得甲乙每一边之数即如一面三
　　　　　角尖堆之每一边故用一面三角尖堆
　　　　　有边求积法算之即得三棱束之积也
　　　　　又法以外周二十七加九得三十六与
　　　　　外周二十七相乘得九百七十二以十

　　　　　八归除得五十四加中心一得五十五
　　　　　为三棱束之积也盖三棱束以九包一
　　　　　其外周所包之数亦必以九递加为超
　　　　　位平加之数如甲乙丙三棱束除却中
　　　　　心之一最内一层为九第二层为十八
　　　　　第三层为二十七每层皆加九为超位
　　　　　平加之数引而长之成丁戊己庚梯形
　　　　　外周二十七即梯形之底内周九即梯
　　　　　形之上阔如以首数九与末数二十七

　　　　　相加得三十六用层数三乘之折半即

　　　　　得总数(见算法原本二/卷第三十二节)然其层数之三
　　　　　乃系外周二十七用九归所得之数今
　　　　　以内周九与外周二十七相加即与外
　　　　　周二十七相乘是未用九归故将相乘
　　　　　所得之数必以九归又以二归(即折/半)始
　　　　　得总数夫先用九归后用二归即与十
　　　　　八归除等(二与九相乘得一十八/合两次除为一次除)故以
　　　　　十八归除得总数再加中心一即得三

　　　　　棱束之积也又按第一法以外周二十
　　　　　七加三以三归之得一面三角尖堆之
　　　　　每一边是外周加三则得每边之三倍
　　　　　若以每边之三倍再加三与每边之三
　　　　　倍相乘必得一面三角尖堆积之十八
　　　　　倍(盖以一面三角尖堆之每一边加一/与每边之数相乘则得一面三角尖)
　　　　　(堆积之二倍今以每边之三倍加三与/每边之三倍相乘是边加三倍则积加)
　　　　　(九倍彼既为一面三角尖堆积/之二倍故此即为十八倍也)而以十
　　　　　八归除亦即得三棱束之积今以外周

　　　　　加九与外周相乘成长方形则其长比

　　　　　每边之三倍加三者尚多三其阔比每
　　　　　边之三倍少三其积必为一面三角尖
　　　　　堆积之十八倍而少十八以十八归除
　　　　　则得一面三角尖堆积而少一故加一
　　　　　而得三棱束之积也此三棱束亦有无
　　　　　中心之一者盖缘三棱束包中心一为
　　　　　一层者周围九其底则四包中心一为
　　　　　二层者周围十八其底则七凡如此类

　　　　　周递加九边递加三者皆有中心之一
　　　　　其馀皆无中心之一详见下法
设如三棱束外周三十求积几何
　　　　　法以外周三十加三得三十三三归之
　　　　　得十一为三棱束每一边之数用一面
　　　　　三角尖堆有边求积法以每边十一加
　　　　　一得十二与每边十一相乘得一百三
　　　　　十二折半得六十六即三棱束之积也
　　　　　又法以外周三十加九得三十九与外

　　　　　周三十相乘得一千一百七十十八除

　　　　　之得六十五加一得六十六为三棱束
　　　　　之积也此三棱束无中心其最内一层
　　　　　为三其外周三十用九归之则得三层
　　　　　又三分之一然其立法亦与前法同乘
　　　　　除得数仍加一者盖以外周加三则得
　　　　　每边之三倍若以每边之三倍再加三
　　　　　与每边之三倍相乘必得一面三角尖
　　　　　堆积之十八倍而以十八归除亦即得

　　　　　三棱束之积今以外周加九与外周相
　　　　　乘成长方形则其长比每边之三倍加
　　　　　三者尚多三其阔比每边之三倍少三
　　　　　其积必为一面三角尖堆积之十八倍
　　　　　而少十八以十八归除则得一面三角
　　　　　尖堆积而少一故加一而得三棱束之
　　　　　积也
设如三棱束积六十六求外周几何
　　　　　法以三棱束积六十六倍之得一百三

　　　　　十二为长方积以一为长阔之较用带

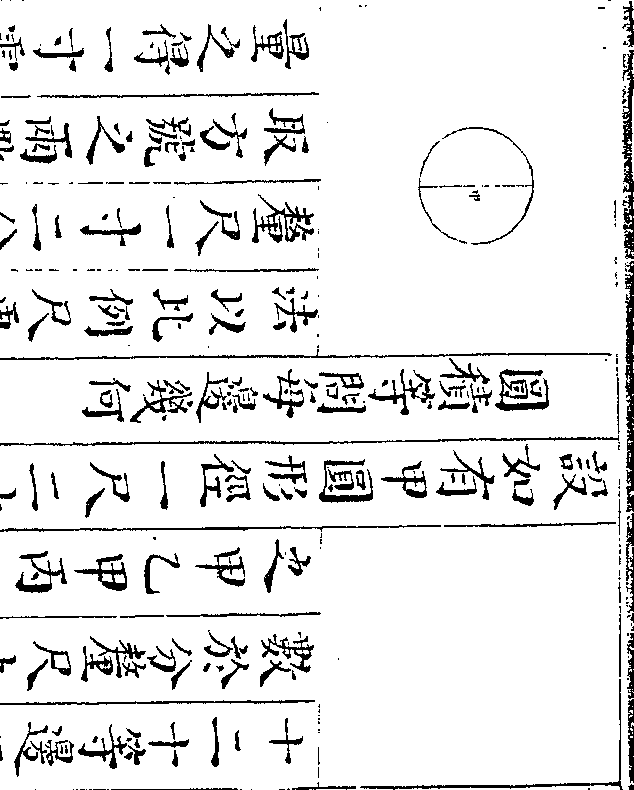　　　　　纵较数开平方法算之得阔十一为三
　　　　　棱束之每一边三因之得三十三内减
　　　　　三馀三十即三棱束之外周数也如图
　　　　　甲乙丙三棱束用一面三角尖堆有积
　　　　　求边法求得甲乙一边前法以外周加
　　　　　三三归之而得一边此法以一边三因
　　　　　之减三而即得外周也
　　　　　又法以三棱束积六十六内减一馀六

　　　　　十五以十八乘之得一千一百七十为
　　　　　长方积以九为长阔之较用带纵较数
　　　　　开平方法算之得阔三十即三棱束之
　　　　　外周数也此即三棱束有外周求积之
　　　　　法而转用之前法以外周加九与外周
　　　　　相乘十八除之再加一而得积此法则
　　　　　以积数减一馀用十八乘之以九为长
　　　　　阔之较用带纵开方得阔而为外周也
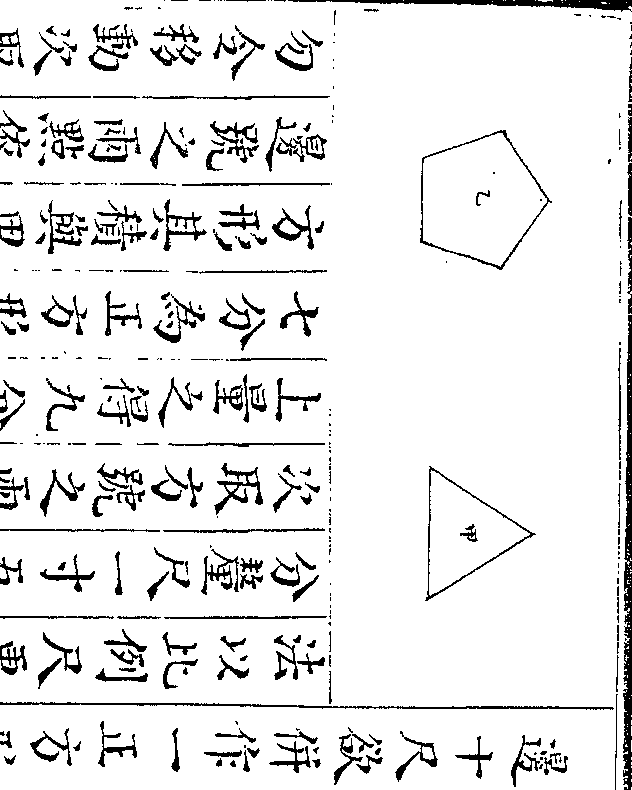
设如圆束外周三十求积几何

　　　　　法以外周三十六归之得五为一面三

　　　　　角尖堆之每一边用一面三角尖堆有
　　　　　边求积法以每边五加一得六与每边
　　　　　五相乘得三十折半得十五为每一三
　　　　　角尖堆积六因之得九十加中心一得
　　　　　九十一即圆束之积也如图甲乙丙丁
　　　　　戊己圆束六分之则成甲庚辛类六三
　　　　　角尖堆形而馀中心一故以外周六分
　　　　　之而得甲庚每一边之数即如一面三

　　　　　角尖堆之每一边而求得一三角尖堆
　　　　　积六因之得六三角尖堆积加中心一
　　　　　即为圆束之积数也
　　　　　又法以外周三十加六得三十六与外
　　　　　周三十相乘得一千零八十十二除之
　　　　　得九十加中心一得九十一为圆束之
　　　　　积也盖圆束以六包一其外周所包之
　　　　　数亦必以六递加为超位平加之数如
　　　　　甲乙丙丁戊己圆束除却中心之一最

　　　　　内一层为六第二层为十二第三层为

　　　　　十八第四层为二十四第五层为三十
　　　　　每层皆加六为超位平加之数引而长
　　　　　之成庚辛壬癸梯形外周三十即梯形
　　　　　之底内周六即梯形之上阔如以首数
　　　　　六与末数三十相加得三十六用层数
　　　　　五乘之折半即得总数(见算法厚本二/卷第三十二节)
　　　　　然其层数之五乃系外周三十用六归
　　　　　所得之数今以内周六与外周三十相

　　　　　加即与外周三十相乘是未用六归故
　　　　　将相乘所得之数必以六归又以二归
　　　　　(即析/半)始得总数夫先用六归后用二归
　　　　　即与十二归除等(二与六相因得一十/二合两次除为一次)
　　　　　(除/)故以十二归除得总数再加中心一
　　　　　即得圆束之积也又按第一法以外周
　　　　　三十六归之得一面三角尖堆之每一
　　　　　边是圆束之外周为一面三角尖堆每
　　　　　边之六倍若以外周加六与外周相乘

　　　　　则必得一面三角尖堆积之七十二倍

　　　　　(盖以一面三角尖堆之每一边加一与/每一边之数相乘则得一面三角尖堆)
　　　　　(积之二倍今以每边之六倍加六与每/边之六倍相乘是边加六倍则积加三)
　　　　　(十六倍彼既为一面三角尖堆积/之二倍故此即为七十二倍也)以一
　　　　　面三角尖堆积六倍之加中心一则得
　　　　　圆束积今将七十二倍积以十二除之
　　　　　亦得一面三角尖堆积之六倍故加中
　　　　　心一而得圆束之积也凡圆束皆有中
　　　　　心设此解与前法相通耳

设如圆束积九十一求外周几何
　　　　　法以圆束积九十一减中心一馀九十
　　　　　六归之得一十五倍之得三十(或即以/九十三)
　　　　　(归之所得亦同盖六归二/因与三归所得之数同也)为长方积以
　　　　　一为长阔之较用带纵较数开平方法
　　　　　算之得阔五又以六因之得三十即圆
　　　　　束之外周数也如图甲乙丙丁戊己圆
　　　　　束减去中心一以六归之则得甲庚辛
　　　　　一面三角尖堆形故用一面三角尖堆

　　　　　有积求边法求得甲庚一边以六因之

　　　　　而得外周也
　　　　　又法以圆束积九十一减一馀九十以
　　　　　十二乘之得一千零八十为长方积以
　　　　　六为长阔之较用带纵较数开平方法
　　　　　算之得阔三十即圆束之外周数也此
　　　　　即圆束有外周求积之法而转用之前
　　　　　法以外周加六与外周相乘十二除之
　　　　　再加一而得积此法则将积数减一馀

　　　　　用十二乘之以六为长阔之较用带纵
　　　　　开方得阔而为外周也
设如堑堵堆底五求积几何
　　　　　法以底五自乘得二十五为底面积又
　　　　　以位数五加一得六与底面积二十五
　　　　　相乘得一百五十折半得七十五即堑
　　　　　堵堆之积也如图甲乙丙丁戊堑堵堆
　　　　　即一面直角尖堆累积之体也两直角
　　　　　面相合成长方面形比原位数多一行

　　　　　而两堑堵体相合成长方体形比原位

　　　　　数亦必多一面故以位数加一与底面
　　　　　积相乘所以增其一面之数成长方体
　　　　　形为堑堵堆之二倍折半而得堑堵堆
　　　　　之积也
设如三角尖堆每边五求积几何
　　　　　法以每边五加一得六与每边五相乘
　　　　　得三十折半得十五为底面积再以每
　　　　　边五加二得七与底面积十五相乘得

　　　　　一百零五三归之得三十五即三角尖
　　　　　堆之积也如图甲乙丙丁三角尖堆每
　　　　　面皆一面三角尖堆累积成等边三角
　　　　　体形其每边之数即位数也试按位作
　　　　　点排之第一层为一第二层为三第三
　　　　　层为六第四层为十第五层为十五为
　　　　　每次按位相加之数如以位数加二与
　　　　　末数相乘取其三分之一即得总数(见/算)
　　　　　(法原本二卷/第三十四节)今以每边加一与每边之

　　　　　数相乘折半即得底面积再以位数加

　　　　　二为高与底面积相乘成平行面之三
　　　　　棱体是为三角尖体之三倍故以三除
　　　　　之而得也然必以位数加二为高者盖
　　　　　以三三角尖体相凑乃成上下相等之
　　　　　平行面体其高必比原有之位数多二
　　　　　层(两相角面相合比原位数多一行今/三三角体相合故必比原位数多二)
　　　　　(面/也)又以一平行面三棱体分为三三角
　　　　　尖体其二面为两体所同用今以位数

　　　　　加二为高与底数相乘所以增其二面
　　　　　之分也
　　　　　又法以每边五加一得六与每边五相
　　　　　乘得三十为倍底积再以位数加二得
　　　　　七与倍底积三十相乘得二百一十六
　　　　　归之亦得三十五为三角尖堆之积也
　　　　　此法与前法同盖以每边加一与每边
　　　　　之数相乘则得底面积之二倍前法以
　　　　　位数加二与底数相乘既为三角尖堆

　　　　　积之三倍此法以位数加二与倍底积

　　　　　相乘即为三角尖堆积之六倍矣故以
　　　　　六归之得积也
　　　　　又法以每边五自乘再乘得一百二十
　　　　　五为第一数再以每边五自乘得二十
　　　　　五为第二数又以每边五加一得六与
　　　　　每边五相乘得三十倍之得六十为第
　　　　　三数三数相加共得二百一十六归之
　　　　　得三十五即三角尖堆之积也此法与

　　　　　第二法同盖以每边自乘再乘为第一
　　　　　数是未以每边加一相乘亦未以位数
　　　　　加二再乘也因未以每边加一相乘则
　　　　　其所成之正方形必比前所得之长少
　　　　　一层之数故又以每边自乘为第二数
　　　　　也因未以位数加二再乘则其高必比
　　　　　前所得之高少二层之数故又以每边
　　　　　加一与每边相乘(即如前之/倍底积)又倍之为
　　　　　第三数也三数相加始为三角尖堆积

　　　　　之六倍故以六归之而得积也

设如三角尖堆积一百二十求每边几何
　　　　　法以三角尖堆积一百二十六因之得
　　　　　七百二十为长方体积以一为长与阔
　　　　　之较以二为高与阔之较用带两纵不
　　　　　同较数开立方法算之得阔八即三角
　　　　　尖堆之每一边也此法即三角尖堆有
　　　　　边求积之法而转用之盖有边求积则
　　　　　以每边加一与每边相乘又以每边加

　　　　　二再乘得长方体积为三角尖堆积之
　　　　　六倍是长比阔多一高比阔多二今以
　　　　　三角尖堆积六因之得长方体积故用
　　　　　带两纵不同较数开立方法算之得阔
　　　　　为每边之数也
设如四角尖堆每边五求积几何
　　　　　法以每边五加半得五个半与每边五
　　　　　相乘得二十七个半又以每边五加一
　　　　　得六与二十七个半相乘得一百六十

　　　　　五三归之得五十五即四角尖堆之积

　　　　　数也如图甲乙丙丁四角尖堆底面为
　　　　　正方傍四面皆一面三角尖堆累积成
　　　　　方底四角尖体形其每边之数即位数
　　　　　也试按位作点排之第一层为一第二
　　　　　层为四第三层为九第四层为十六第
　　　　　五层为二十五为每次按位自乘相加
　　　　　之数如以每边加半与每边相乘复以
　　　　　位数加一乘之取其三分之一即得总

　　　　　数(见算法原本二/卷第三十五节)今以每边加半与每
　　　　　边相乘是得长方面积复以位数加一
　　　　　为高乘之是得长方体积为四角尖体
　　　　　之三倍故以三除之即得也然以边数
　　　　　加半为长以位数加一为高者盖以三
　　　　　四角尖体相凑乃成上下相等之长方
　　　　　体其底必比正方面多半行其高必比
　　　　　原有之位数多一层(三角体以边数加/一与边数相乘四)
　　　　　(角体以边数加半与边数相乘三角体/以位数加二为高四角体以位数加一)

　　　　　(为高总以四角体比三角体底式大一/倍故三角体为长方体六分之一四角)

　　　　　(体为长方体三分之一三角体加/数几何而此四角体皆用其半也)又以
　　　　　一长方体分为三四角尖体其三面为
　　　　　两体所同用而少一行之数试以甲乙
　　　　　丙丁四角尖体作为戊己庚辛阳马尖
　　　　　体形为长方体三分之一所馀为三分
　　　　　之二其戊己庚戊庚辛两面为两体所
　　　　　同用而戊庚一行又为两面所同用是
　　　　　此两面为两体所同用而少一行之数

　　　　　也又以其所馀三分之二平分之必有
　　　　　一面为两体所同用是以长方体分为
　　　　　三四角尖体有三面为两体所同用而
　　　　　少一行之数也今以每边加半与每边
　　　　　之数相乘又以位数加一乘之所以增
　　　　　其三面少一行之分也(盖其高既比原/位数多一则其)
　　　　　(傍面一层宜为一面三角尖堆之倍数/而其傍面只比每边多半是傍面只为)
　　　　　(一面三角尖堆之数也又其高既比原/位多一则其上面一层为每边自乘之)
　　　　　(数即为一面三角尖堆之倍数而少/一行共之为三面少一行之数也)

　　　　　又法以每边五自乘再乘得一百二十

　　　　　五为第一数再以每边五自乘得二十
　　　　　五为第二数又以每边五加一得六与
　　　　　每边五相乘得三十折半得十五为第
　　　　　三数三数相加共得一百六十五三归
　　　　　之得五十五即四角尖堆之积也此法
　　　　　与第一法同盖以每边自乘再乘为第
　　　　　一数是未以每边加半与每边相乘亦
　　　　　未以位数加一再乘也因未以位数加

　　　　　一再乘则其上层即少一每边自乘之
　　　　　数故以每边自乘为第二数也因未以
　　　　　每边加半相乘则其傍面即少一面三
　　　　　角尖堆之数故以每边加一与每边相
　　　　　乘折半为第三数也三数相加始为四
　　　　　角尖堆积之三倍故以三归之而得积
　　　　　也
　　　　　又法以每边五加一得六与每边五相
　　　　　乘得三十又以每边五加二得七乘之

　　　　　得二百一十三归之得七十为三角尖

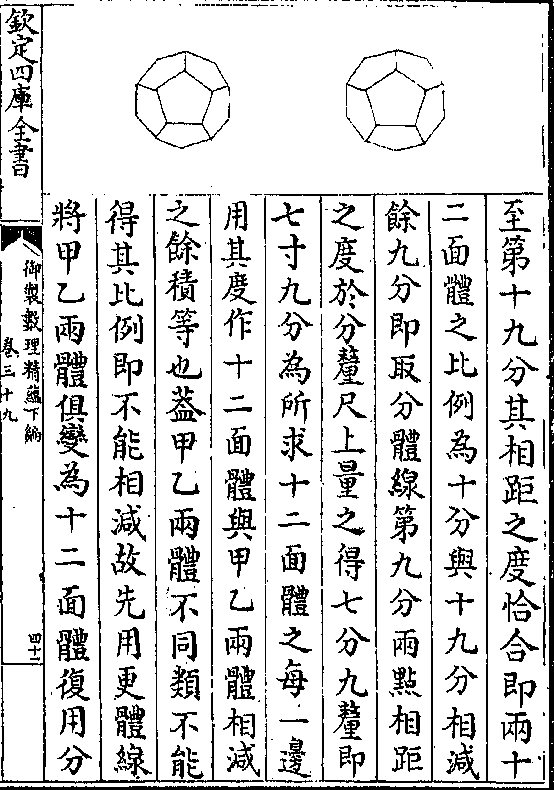　　　　　堆之倍积又以每边五求得一面三角
　　　　　尖堆积十五与倍三角尖堆积七十相
　　　　　减亦得五十五为四角尖堆之积也如
　　　　　图甲乙丙丁四角尖堆为戊己庚辛三
　　　　　角尖堆积之一倍而少一面之数盖四
　　　　　角尖堆底面积为三角尖堆底面积之
　　　　　一倍而少一行故四角尖堆体积为三
　　　　　角尖堆体积之一倍而少一面是以求

　　　　　得倍三角尖堆积内减一面三角尖堆
　　　　　积即得四角尖堆积也
　　　　　又法以每边五用堑堵堆求积法求得
　　　　　堑堵堆积七十五又以每边五用三角
　　　　　尖堆求积法求得三角尖堆积三十五
　　　　　两数相加得一百一十折半得五十五
　　　　　即四角尖堆之积也如图甲乙丙丁四
　　　　　角尖堆先以乙丙一边求得戊己庚辛
　　　　　壬堑堵堆积四角尖体为堑堵体三分

　　　　　之二三角尖体为堑堵体三分之一故

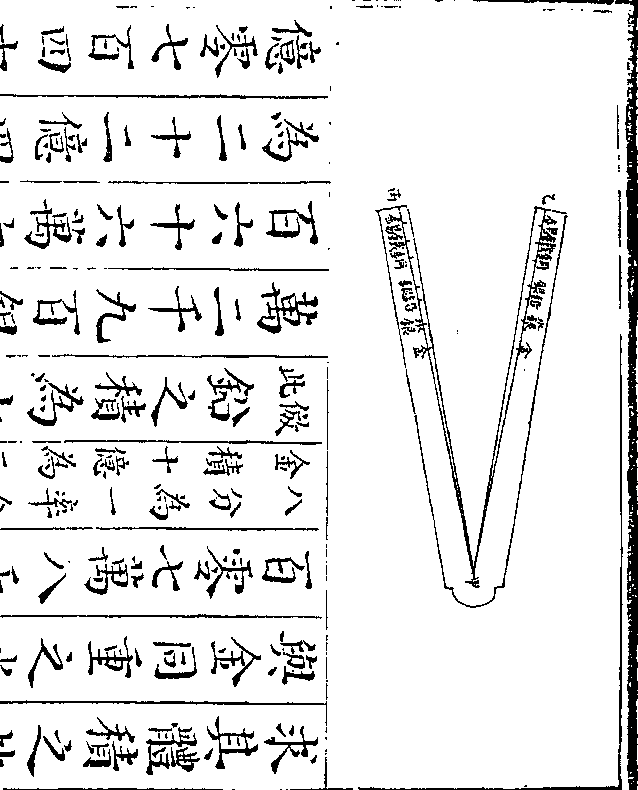　　　　　又求得癸子丑寅三角尖堆积与堑堵
　　　　　堆积相加即与二方底四角尖堆之积
　　　　　等故折半而得四角尖堆之积也
设如四角尖堆积二百零四求每边几何
　　　　　法以四角尖堆积二百零四三因之得
　　　　　六百一十二为长方体积以半为长与
　　　　　阔之较以一为高与阔之较用带两纵
　　　　　不同较数开立方法算之得阔八即四

　　　　　角尖堆之每一边也此法即四角尖堆
　　　　　有边求积之法而转用之盖四角尖堆
　　　　　有边求积则以每边加半与每边相乘
　　　　　又以每边加一再乘得长方体积为四
　　　　　角尖堆积之三倍是长比阔多半高比
　　　　　阔多一今以四角尖堆积三因之得长
　　　　　方体积故用带两纵不同较数开立方
　　　　　法算之得阔为每边之数也
设如长方堆底长九阔七上一行收顶求积几何

　　　　　法以底阔七为方堆之底用四角尖堆

　　　　　有边求积法求得四角尖堆积一百四
　　　　　十又以底阔七与长九相减馀二为两
　　　　　一面三角尖堆即以底阔七用一面三
　　　　　角尖堆有边求积法求得一面三角尖
　　　　　堆积二十八二因之得五十六为两一
　　　　　面三角尖堆积与前所得四角尖堆积
　　　　　一百四十相加得一百九十六即长方
　　　　　堆之积也如图甲乙丙丁戊长方堆丙

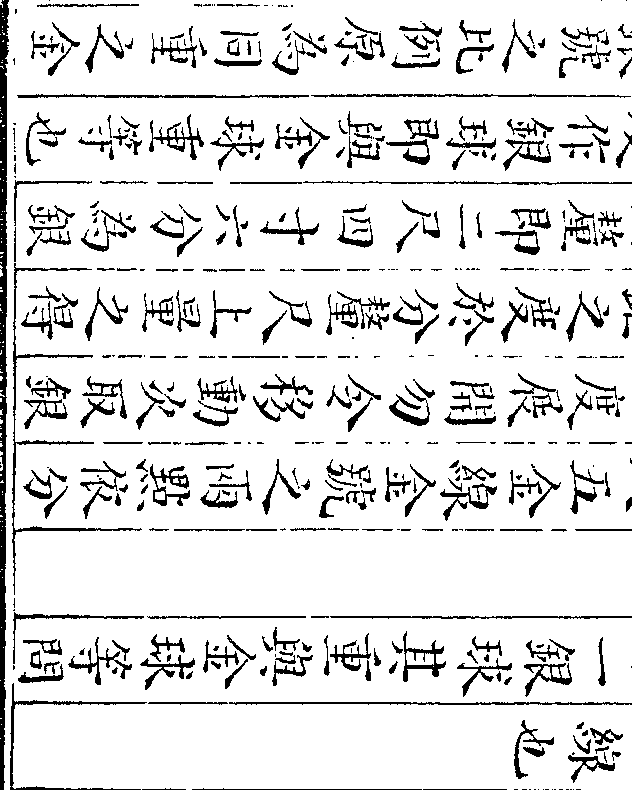
　　　　　丁长比乙丙阔多庚丁二试自己至庚
　　　　　截去二面则成甲乙丙庚一四角尖堆
　　　　　形己庚丁戊两一面三角尖堆形其乙
　　　　　丙阔与丙庚等即四角尖堆之每一边
　　　　　亦即一面三角尖堆之每一边故以一
　　　　　边求得四角尖堆积又求得两一面三
　　　　　角尖堆积相加即得长方堆之积也
　　　　　又法以阔七与长九相减馀二折半得
　　　　　一又加半得一个半与长九相加得十

　　　　　个半与底阔七相乘得七十三个半又

　　　　　以底阔七(即层/数)加一得八再乘得五百
　　　　　八十八三归之得一百九十六即长方
　　　　　堆之积也此法与前法之理同如甲乙
　　　　　丙丁戊长方堆既分为一四角尖堆两
　　　　　一面三角尖堆其甲乙丙庚四角尖堆
　　　　　固当以丙庚加半与乙丙相乘以甲乙
　　　　　加一再乘得一长方体形为一四角尖
　　　　　堆之三倍其己庚丁戊两一面三角尖

　　　　　堆当以庚丁与乙丙相乘以戊丁(同甲/乙)
　　　　　加一再乘得二长方面形为两一面三
　　　　　角尖堆之二倍因一为三倍一为二倍
　　　　　其倍数不同故又以庚丁折半与庚丁
　　　　　相加即增其一长方面之分得三长方
　　　　　面形亦为两一面三角尖堆之三倍故
　　　　　以三归之得一四角尖堆两一面三角
　　　　　尖堆合之与甲乙丙丁戊一长方堆之
　　　　　积相等也

　　　　　又法以底阔七与长九相减馀二再加

　　　　　一得三为顶上之长乃以底长九倍之
　　　　　得十八加顶长三得二十一与底阔七
　　　　　相乘得一百四十七再以高数七加一
　　　　　得八再乘(阔数即/高数也)得一千一百七十六
　　　　　六归之得一百九十六即长方堆之积
　　　　　也此法与第二法同盖前法以长阔相
　　　　　减折半加半与长相加此法以长阔相
　　　　　减不折半加一与倍长相加则其长比

　　　　　前法多一倍阔与高皆与前数同而体
　　　　　积亦必比前数大一倍故前法用三归
　　　　　此法用六归也
设如长方堆积二百七十六长比阔多二求每边几
　何
　　　　　法以长方堆积二百七十六三因之得
　　　　　八百二十八为长方体积以长比阔多
　　　　　二折半又加半得一个半与二相加得
　　　　　三个半为长与阔之较以一为高与阔

　　　　　之较用带两纵不同较数开立方法算

　　　　　之得阔八为底阔加长比阔多二得十
　　　　　为长也此法即长方堆有边求积之法
　　　　　而转用之盖长方堆有边求积则以原
　　　　　长阔之较折半又加半与原长相加乃
　　　　　与阔相乘又以阔加一再乘得长方体
　　　　　积为长方堆之三倍是长比阔多原长
　　　　　阔之较又多半较仍多半高比阔多一
　　　　　今以长方堆积三因之得长方体积故

　　　　　用带两纵不同较数开立方法算之得
　　　　　阔为底边之阔加长阔之较得数为长
　　　　　也
设如三角半堆底边八上边五求积几何
　　　　　法以底边八用三角尖堆有边求积法
　　　　　求得三角尖堆全积一百二十又以上
　　　　　边五减一得四为上虚三角尖堆之每
　　　　　边亦用三角尖堆有边求积法求得上
　　　　　虚三角尖堆积二十与先所得三角尖

　　　　　堆全积一百二十相减馀一百即三角

　　　　　半堆之积也如图甲乙丙丁戊己三角
　　　　　半堆若于其上加一小三角尖堆则成
　　　　　一大三角尖堆形其上所加之小三角
　　　　　尖堆之每边比三角半堆之上边少一
　　　　　故先求得大三角尖堆全积又求得上
　　　　　虚小三角尖堆积相减即得三角半堆
　　　　　之积也
　　　　　又法以底边八加一得九与底边八相

　　　　　乘得七十二为第一数又以上边五与
　　　　　底边八相并得十三以上边五加一得
　　　　　六乘之得七十八为第二数两数相并
　　　　　得一百五十又以上边五与下边八相
　　　　　减馀三加一得四为层数与两数相加
　　　　　之一百五十相乘得六百六归之得一
　　　　　百为三角半堆之积也此法与等边三
　　　　　角尖堆求积之法同盖等边三角尖堆
　　　　　其上尖一即上边其每边之数即底边

　　　　　亦即层数其法以每边加一与每边相

　　　　　乘又以每边加二再乘得长方体积为
　　　　　三角尖堆积之六倍分之则得长比高
　　　　　阔多一之一长方体形又得长比阔多
　　　　　一之二长方面形(即上多/二层)若依此法以
　　　　　底边加一与底边相乘即长比阔多一
　　　　　之长方体之一面数也以上边一与下
　　　　　边相加又以上边一加一得二乘之则
　　　　　得长比阔多一之二长方面之两行数

　　　　　也此两数相并以层数乘之则亦得长
　　　　　比高阔多一之一长方体形又得长比
　　　　　阔多一之二长方面形共成一长方体
　　　　　形为三角尖堆之六倍矣
设如三角半堆积一百上边五求底边几何
　　　　　法以上边五减一馀四为上虚小三角
　　　　　尖堆之底用三角尖堆有边求积法求
　　　　　得上虚三角尖堆积二十与半堆积一
　　　　　百相加得一百二十为等边三角尖堆

　　　　　全积用三角尖堆有积求边法求得每

　　　　　边八即三角半堆之底边也如有底边
　　　　　求上边者则以底边求得三角尖堆全
　　　　　积与半堆积相减馀为上虚三角尖堆
　　　　　积求得上虚小三角尖堆之每边加一
　　　　　即上边也
设如四角半堆底边十二上边五求积几何
　　　　　法以底边十二用四角尖堆有边求积
　　　　　法求得四角尖堆全积六百五十又以

　　　　　上边五减一得四为上虚四角尖堆之
　　　　　每边亦用四角尖堆有边求积法求得
　　　　　上虚四角尖堆积三十与先所得四角
　　　　　尖堆全积六百五十相减馀六百二十
　　　　　即四角半堆之积也如图甲乙丙丁戊
　　　　　己庚四角半堆若于其上加一小四角
　　　　　尖堆则成一大四角尖堆形其上所加
　　　　　之小四角尖堆之每边比四角半堆之
　　　　　上边少一故求得大四角尖堆全积又

　　　　　求得上虚小四角尖堆积相减即得四

　　　　　角半堆之积也
　　　　　又法以上边五自乘得二十五为第一
　　　　　数以底边十二自乘得一百四十四为
　　　　　第二数以上边五与底边十二相乘得
　　　　　六十为第三数又以上边五与底边十
　　　　　二相减馀七折半得三个半为第四数
　　　　　四数相并得二百三十二个半又以上
　　　　　下边相减所馀之七加一得八为层数

　　　　　与四数相并之二百三十二个半相乘
　　　　　得一千八百六十三归之得六百二十
　　　　　即四角半堆之积也此法与等边四角
　　　　　尖堆求积之法同盖等边四角尖堆其
　　　　　上尖一即上边其每边之数即底边亦
　　　　　即层数其法以每边加半与每边相乘
　　　　　又以每边加一再乘得长方体积为四
　　　　　角尖堆积之三倍分之则得每边自乘
　　　　　再乘之一正方体形每边自乘之一正

　　　　　方面形又得长比阔多一之半层长方

　　　　　面形若以底边自乘即正方体之一面
　　　　　数也以上边一与底边相乘则得每边
　　　　　自乘正方面之一行数也以上边一自
　　　　　乘又以上边一与底边相减折半此两
　　　　　数相并即得长比阔多一之半层长方
　　　　　面之一行数也四数相并再以层数乘
　　　　　之则亦得一正方体形一正方面形又
　　　　　得长比阔多一之半层长方面形共成

　　　　　一长方体形为四角尖堆之六倍矣又
　　　　　此法与上下不等正方体之法异者在
　　　　　多上下边相减折半之一数因堆垛之
　　　　　傍面有馀分故也
设如四角半堆积六百二十上边五求底边几何
　　　　　法以上边五减一馀四为上虚小四角
　　　　　尖堆之底用四角尖堆有边求积法求
　　　　　得上虚四角尖堆积三十与半堆积六
　　　　　百二十相加得六百五十为等边四角

　　　　　尖堆全积用四角尖堆有积求边法求

　　　　　得每边十二即四角半堆之底边也如
　　　　　有底边求上边者则以底边求得四角
　　　　　尖堆全积与半堆积相减馀为上虚四
　　　　　角尖堆积求得上虚小四角尖堆之每
　　　　　边加一即上边也
设如长方半堆底长十二阔十上长八阔六求积几
　何
　　　　　法以底长十二阔十用长方堆求积法

　　　　　求得长方堆全积四百九十五又以上
　　　　　长八阔六各减一得长七阔五为上虚
　　　　　长方堆之长阔亦用长方堆求积法求
　　　　　得上虚长方堆积八十五与先所得长
　　　　　方堆全积相减馀四百一十即长方半
　　　　　堆之积也如图甲乙丙丁戊己庚长方
　　　　　半堆若于其上加一小长方堆则成上
　　　　　一行收顶之长方堆形其上所加之小
　　　　　长方堆之每边比长方半堆之上边少

　　　　　一故先求得长方堆全积又求得上虚

　　　　　小长方堆积相减即得长方半堆之积
　　　　　也
　　　　　又法以上长八与上阔六相乘得四十
　　　　　八为第一数以底长十二与底阔十相
　　　　　乘得一百二十为第二数以上长八与
　　　　　底阔十相乘得八十以上阔六与底长
　　　　　十二相乘得七十二两数相并折半得
　　　　　七十六为第三数又以上下长相减馀

　　　　　四折半得二为第四数以此四数相加
　　　　　得二百四十六又以上长与底长相减
　　　　　所馀之四加一得五为层数与四数相
　　　　　加之二百四十六相乘得一千二百三
　　　　　十三归之得四百一十即长方半堆之
　　　　　积也此法与四角半堆求积之法同盖
　　　　　四角半堆长阔皆相等此则有长阔之
　　　　　不同故四角半堆以上边自乘为第一
　　　　　数者此则以上长阔相乘为第一数四

　　　　　角半堆以下边自乘为第二数者此则

　　　　　以下长阔相乘为第二数四角半堆以
　　　　　上下相乘为第三数者此则以上长与
　　　　　下阔相乘上阔与下长相乘相并折半
　　　　　为第三数四角半堆以上下相减折半
　　　　　为第四数者此则以上下长相减折半
　　　　　为第四数(如以上下阔相/减折半亦同)其理皆相通
　　　　　也
　　　　　又法以上长八倍之得十六加下长十

　　　　　二得二十八以上阔六乘之得一百六
　　　　　十八又以下长十二倍之得二十四加
　　　　　上长八得三十二以下阔十乘之得三
　　　　　百二十又以下长十二与上长八相减
　　　　　馀四三数相加得四百九十二又以上
　　　　　下长相减所馀之四加一得五为层数
　　　　　与三数相加之四百九十二相乘得二
　　　　　千四百六十六归之得四百一十即长
　　　　　方半堆之积也此法与第二法同盖此

　　　　　法用数比前法大一倍故前法用三归

　　　　　此法用六归也又此法与上下不等长
　　　　　方体之法异者在多上下长相减之一
　　　　　数因堆垛之傍面有馀分故也
　　　　　又法以底阔十与长十二相乘得一百
　　　　　二十又以长十二阔十各减一得长十
　　　　　一阔九相乘得九十九又以长十一阔
　　　　　九各减一得长十阔八相乘得八十又
　　　　　以长十阔八各减一得长九阔七相乘

　　　　　得六十三再以长九阔七各减一得长
　　　　　八阔六(即上/长阔)相乘得四十八以此五数
　　　　　相加共得四百一十即长方半堆之积
　　　　　也此法将每层长阔相乘得每层之积
　　　　　故总加之即五层之共积也法虽层累
　　　　　相加实为显而易见凡堆垛诸法皆可
　　　　　以此法御之若层数太多者用本法为
　　　　　简易也
设如长方半堆积四百一十上长八阔六求底长阔

　各几何

　　　　　　法以上长八阔六各减一得长七阔五
　　　　　　为上虚小长方堆之长阔用长方堆有
　　　　　　边求积法求得上虚小长方堆积八十
　　　　　　五与半堆积四百一十相加得四百九
　　　　　　十五为长方堆全积用长方堆有积求
　　　　　　边法求得阔十长十二即长方半堆之
　　　　　　底边数也如有底边长阔求上边长阔
　　　　　　者则以底边求得长方堆全积与半堆

　　　　　　积相减馀为上虚小长方堆积求得上
　　　　　　虚小长方堆之长阔两边各加一即长
　　　　　　方半堆上边长阔之数也
　
　
　
　
　
　

御制数理精蕴下编卷三十