声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
律历融通卷一 第 1a 页 WYG0786-0556a.png
 钦定四库全书
钦定四库全书律历融通卷一
明 朱载堉 撰
自落下闳造太初历取法黄钟律数而后知创历不
可无所本自僧一行造大衍历改从大易策数而后
知修历不可有所拘易大传曰河出图雒出书圣人
则之所谓则之者非止画卦叙畴二事而已至若律
历礼乐莫不皆然盖天地万物无非阴阳而图书二
律历融通卷一 第 1b 页 WYG0786-0556b.png
 者阴阳之妙尽矣夫六经之道同归礼乐之用为急
者阴阳之妙尽矣夫六经之道同归礼乐之用为急然而历者礼之本也律者乐之宗也何以言之夫历
之兴也测景于天景有消长因之以考分至以序四
时而五礼本之律之始也候气于地气有深浅因之
以辨清浊以正五音而六乐宗之圣人作乐以应天
制礼以配地故曰律居阴而治阳历居阳而治阴律
历迭相治也其间不容发而相错综也以河图雒书
言之则河图者礼也雒书者乐也乐记曰天尊地卑
律历融通卷一 第 2a 页 WYG0786-0557a.png
 君臣定矣卑高以陈贵贱位矣动静有常小大殊矣
君臣定矣卑高以陈贵贱位矣动静有常小大殊矣方以类聚物以群分则性命不同矣在天成象在地
成形如此则礼者天地之别也其河图之谓欤地气
上齐天气下降阴阳相摩天地相荡鼓之以雷霆奋
之以风雨动之以四时煖之以日月而百化兴焉如
此则乐者天地之和也其雒书之谓欤故河图圆而
左旋其数则偶所谓居阳而治阴也十二辰次以之
雒书方而右转其数则奇所谓居阴而治阳也七曜
律历融通卷一 第 2b 页 WYG0786-0557b.png
 以之阳道常饶阴道常乏故河图之数五十五视大
以之阳道常饶阴道常乏故河图之数五十五视大衍而有馀雒书之数四十五视大衍而不足合河图
与雒书共得百数若阴阳之交构牝牡之相衔均而
分之得大衍之数者二此天地自然之至理故律历
倚之而起数语其经则历有十二辰次律有十二宫
调语其纬则历有七曜律有七音河图历也故有四
时迭运之象雒书律也故有三分损益之象是以黄
钟之管九寸则雒书而为律元黄钟之尺百分则河
律历融通卷一 第 3a 页 WYG0786-0557c.png
 图而为度母从黍之律横黍之度长短分齐交相契
图而为度母从黍之律横黍之度长短分齐交相契合斯乃造化之妙故名之曰黄钟历法盖言倚数取
诸此也夫七八九六者天地之大数也七为少阳八
为少阴九为老阳六为老阴阳属于天阴属于地天
体圆其用方故七□为天之象而九□为天之数地
体方其用圆故八□为地之象而六□为地之数夫
数者混融乎太极之先昭晰乎有象之后方圆曲直
天下之真象围径积实天下之真数即象以求数则
律历融通卷一 第 3b 页 WYG0786-0557d.png
 数外无象因数以会象则象外无数二者相须而未
数外无象因数以会象则象外无数二者相须而未尝相离也图书者方圆之至方圆者动静之机动静
者阴阳之本阳奇而阴耦故天一而地二阳动而阴
静故天圆而地方刓方以为圆则静者不能无动引
圆以为方则动者不能无静静为之体则动为之用
动为之体则静为之用用以体为基体以用为本此
阴阳之所相根而造化之所不穷也河图者其天地
对待之数乎以天一处于北则地二自然处于南以
律历融通卷一 第 4a 页 WYG0786-0558a.png
 天三处于东则地四自然处于西四位既定则天五
天三处于东则地四自然处于西四位既定则天五自然居乎中中也者四方所取正也六与一合六即
一五也七与二合七即二五也为八为九者三五四
五也四方既正则五五相比十复居于中矣此皆自
然相合之数五行之所以生成也故孔子曰天数五
地数五五位相得而各有合此之谓也雒书者其参
天两地之数乎阳生于下而左旋阴生于上而右旋
阳数则参天参者三也自一三如三三三如九三九
律历融通卷一 第 4b 页 WYG0786-0558b.png
 二十七本文无十故去其二十而言七三其七为二
二十七本文无十故去其二十而言七三其七为二十一去二十则一复处于下阴数则两地两者二也
自二二如四二四如八二八十六本文无十故去其
十而言六二其六为十二去十则二复处于上过此
以往积数万亿皆不越乎此八位既定则五数自然
居乎中中也者是亦八位所取正也以一加五则六
在一后以六加五为十一去十则一在六先以三加
五则八在三后以八加五为十三去十则三在八先
律历融通卷一 第 5a 页 WYG0786-0558c.png
 以至四九二七亦莫不互相加益而为先后也此皆
以至四九二七亦莫不互相加益而为先后也此皆自然相比之数亦五行之所以生成也故孔子曰参
天两地而倚数此之谓也是知河图之数五十五者
天也合而用之者圣人也雒书之数四十五者天也
倚而用之者圣人也河图之五行则以相生而顺行
雒书之五行则以相制而逆运二者皆起于一推其
生则土居未中推其制则土居丑中是又自然有相
合之理刘歆谓河图雒书相为经纬岂微义哉邵雍
律历融通卷一 第 5b 页 WYG0786-0558d.png
 曰圆者河图之数方者雒书之文当知方以为体则
曰圆者河图之数方者雒书之文当知方以为体则圆以为用圆以为体则方以为用圆者径一而围三
方者径一而围四河图以十居中圆以推之三其十
为三十故图外成数六七八九总三十方以推之四
其十为四十故图内外生成之数总四十雒书以五
居中圆以推之三其五为十五故书从横皆十五方
以推之四其五为二十故书外阳数一三九七总二
十阴数二四八六亦总二十体用相因莫匪自然至
律历融通卷一 第 6a 页 WYG0786-0559a.png
 哉图书其象数之原乎夫物生而后有象象而后有
哉图书其象数之原乎夫物生而后有象象而后有滋滋而后有数象之与数若异用也而本则一若殊
途也而归则同不明乎数不足与语象不明乎象不
足与语数是故欲明律历之学必以象数为先天道
生于太一一变而为七七变而为九七与八乾坤之
体坎离之象也九与六乾坤之用坎离之数也七九
中实六八中虚奇偶阴阳之理也故天象多用七而
天数多用九用七者若日月五星而为七政四方各
律历融通卷一 第 6b 页 WYG0786-0559b.png
 七宿是也用九者三九二十七故二十七日有奇而
七宿是也用九者三九二十七故二十七日有奇而月离一周焉四九三十六故三百六旬有馀而日躔
一周焉河图一六属水而为北方七宿二七属火而
为南方七宿三八属木而为东方七宿四九属金而
为西方七宿五十属土而为大衍之数故唐志云大
衍为天之枢如环之无端盖律历之大纪也十乃全
数居中央而为宫九次之居西方而为商八次之居
东方而为角七次之居南方而为徵六次之居北方
律历融通卷一 第 7a 页 WYG0786-0559c.png
 而为羽此五声之位清浊之序也然五声之相生由
而为羽此五声之位清浊之序也然五声之相生由中而南故宫生徵由南而西故徵生商由西而北故
商生羽由北而东故羽生角始于宫终于角左旋一
周以象河图也六律之相生自子而亥故黄钟生仲
吕自亥而戌故仲吕生无射自戌而酉故无射生夹
钟自酉而申故夹钟生夷则乃至于丑而止故始于
黄钟而终于林钟右旋一周以象雒书也日为太阳
其数九居雒书之正南故蕤宾在午月为太阴其数
律历融通卷一 第 7b 页 WYG0786-0559d.png
 六居雒书之西北故应钟在亥黄钟为填星太蔟为
六居雒书之西北故应钟在亥黄钟为填星太蔟为太白姑洗为岁星林钟为荧惑南吕为辰星蕤宾为
日应钟为月历有五纬七政律有五声七始故律历
同一道天之阴阳五行一气而已有气必有数有声
历以纪数而声寓律以宣声而数行律与历同流行
相生黄钟者声气之元者乎蕤宾应钟是名中和所
以济五音和阴阳旋宫之律可定声气之元周流而
不穷矣故周髀曰冬至夏至观律之数听钟之音知
律历融通卷一 第 8a 页 WYG0786-0560a.png
 寒暑之极明代序之化是知律者历之本也历者律
寒暑之极明代序之化是知律者历之本也历者律之宗也其数可相倚而不可相违故曰律历融通此
之谓也
黄钟历法上(凡五篇)
步律吕第一
律元九
黄钟之管长九寸从黍为分之九寸也寸皆九分凡
八十一分雒书之奇自相乘之数也是为历本故以
律历融通卷一 第 8b 页 WYG0786-0560b.png
 万历九年为元义取诸此上考往古下推来今皆距
万历九年为元义取诸此上考往古下推来今皆距律元为算
律母百
黄钟之尺长十寸横黍为分之十寸也寸皆十分凡
百分河图之偶自相乘之数也是为母法秒满法从
分分满法从刻刻满法从日度下分秒放此不满秒
者为忽
律限三百
律历融通卷一 第 9a 页 WYG0786-0560c.png
 纪之以三是也律母三之得律限夫三十为世三百
纪之以三是也律母三之得律限夫三十为世三百为十世年远数盈渐差天度古人所谓斗历改宪之
期
律总六十
平之以六是也五声乘十二律得六十调是名律总
置律总为实三而一所得是名律差
律数十二
国语曰纪之以三平之以六成于十二天之道也天
律历融通卷一 第 9b 页 WYG0786-0560d.png
 之大数不过十二是故律历宗之
之大数不过十二是故律历宗之律率三十
古法日馀十六分之七今改日馀千六百分之六百
九十九大馀纪之以三小馀满法从日不满退除为
刻及分
黄钟 冬至益卦初九 小寒益卦六二
复卦 初九 六二 六三 六四 六五 上六
颐卦 初九 六二 六三 六四 六五 上九
律历融通卷一 第 10a 页 WYG0786-0561a.png
 屯卦 初九 六二 六三 六四 九五 上六
屯卦 初九 六二 六三 六四 九五 上六既济 初九 六二 九三 六四 九五 上六
家人 初九 六二 九三 六四 九五 上九
大吕 大寒益卦六二 立春益卦六四
临卦 初九 九二 六三 六四 六五 上六
明夷 初九 六二 九三 六四 六五 上六
贲卦 初九 六二 九三 六四 六五 上九
损卦 初九 九二 六三 六四 六五 上九
律历融通卷一 第 10b 页 WYG0786-0561b.png
 节卦 初九 九二 六三 六四 九五 上六
节卦 初九 九二 六三 六四 九五 上六太蔟 雨水益卦九五 惊蛰益卦上九
泰卦 初九 九二 九三 六四 六五 上六
大畜 初九 九二 九三 六四 六五 上九
需卦 初九 九二 九三 六四 九五 上六
小畜 初九 九二 九三 六四 九五 上九
中孚 初九 九二 六三 六四 九五 上九
夹钟 春分震卦初九 清明震卦六二
律历融通卷一 第 11a 页 WYG0786-0561c.png
 大壮 初九 九二 九三 九四 六五 上六
大壮 初九 九二 九三 九四 六五 上六归妹 初九 九二 六三 九四 六五 上六
丰卦 初九 六二 九三 九四 六五 上六
离卦 初九 六二 九三 九四 六五 上九
噬嗑 初九 六二 六三 九四 六五 上九
姑洗 谷雨震卦六三 立夏震卦九四
夬卦 初九 九二 九三 九四 九五 上六
大有 初九 九二 九三 九四 六五 上九
律历融通卷一 第 11b 页 WYG0786-0561d.png
 睽卦 初九 九二 六三 九四 六五 上九
睽卦 初九 九二 六三 九四 六五 上九兑卦 初九 九二 六三 九四 九五 上六
革卦 初九 六二 九三 九四 九五 上六
仲吕 小满震卦六五 芒种震卦上六
乾卦 初九 九二 九三 九四 九五 上九
履卦 初九 九二 六三 九四 九五 上九
同人 初九 六二 九三 九四 九五 上九
无妄 初九 六二 六三 九四 九五 上九
律历融通卷一 第 12a 页 WYG0786-0562a.png
 随卦 初九 六二 六三 九四 九五 上六
随卦 初九 六二 六三 九四 九五 上六蕤宾 夏至恒卦初六 小暑恒卦九二
姤卦 初六 九二 九三 九四 九五 上九
大过 初六 九二 九三 九四 九五 上六
鼎卦 初六 九二 九三 九四 六五 上九
未济 初六 九二 六三 九四 六五 上九
解卦 初六 九二 六三 九四 六五 上六
林钟 大暑恒卦九三 立秋恒卦九四
律历融通卷一 第 12b 页 WYG0786-0562b.png
 遁卦 初六 六二 九三 九四 九五 上九
遁卦 初六 六二 九三 九四 九五 上九讼卦 初六 九二 六三 九四 九五 上九
困卦 初六 九二 六三 九四 九五 上六
咸卦 初六 六二 九三 九四 九五 上六
旅卦 初六 六二 九三 九四 六五 上九
夷则 处暑恒卦六五 白露恒卦上六
否卦 初六 六二 六三 九四 九五 上九
萃卦 初六 六二 六三 九四 九五 上六
律历融通卷一 第 13a 页 WYG0786-0562c.png
 晋卦 初六 六二 六三 九四 六五 上九
晋卦 初六 六二 六三 九四 六五 上九豫卦 初六 六二 六三 九四 六五 上六
小过 初六 六二 九三 九四 六五 上六
南吕 秋分巽卦初六 寒露巽卦九二
观卦 初六 六二 六三 六四 九五 上九
渐卦 初六 六二 九三 六四 九五 上九
涣卦 初六 九二 六三 六四 九五 上九
坎卦 初六 九二 六三 六四 九五 上六
律历融通卷一 第 13b 页 WYG0786-0562d.png
 井卦 初六 九二 九三 六四 九五 上六
井卦 初六 九二 九三 六四 九五 上六无射 霜降巽卦九三 立冬巽卦六四
剥卦 初六 六二 六三 六四 六五 上九
比卦 初六 六二 六三 六四 九五 上六
蹇卦 初六 六二 九三 六四 九五 上六
艮卦 初六 六二 九三 六四 六五 上九
蒙卦 初六 九二 六三 六四 六五 上九
应钟 小雪巽卦九五 大雪巽卦上九
律历融通卷一 第 14a 页 WYG0786-0563a.png
 坤卦 初六 六二 六三 六四 六五 上六
坤卦 初六 六二 六三 六四 六五 上六谦卦 初六 六二 九三 六四 六五 上六
师卦 初六 九二 六三 六四 六五 上六
升卦 初六 九二 九三 六四 六五 上六
蛊卦 初六 九二 九三 六四 六五 上九
求汎距定距
置律元所距积年为汎距来加往减律限为定距若汎
距在律限已下不及减者反减律限为定距诸应加减
律历融通卷一 第 14b 页 WYG0786-0563b.png
 亦反之
亦反之求汎积定积
置所求定距以律数乘之为积月以积月乘日率为积
日以积月乘日馀为积馀积馀满法并入积日为岁汎
积
置定距自相乘为实七之八而一所得满律母为分不
满退除为秒忽是名所求岁差来减往加汎积为岁定
积
律历融通卷一 第 15a 页 WYG0786-0563c.png
 求正律策
求正律策置所求定积与次年定积相减馀如律数而一得正律
策
求半律策
置所求正律策二而一得半律策
求均策
置所求半律策三而一得均策
求声策
律历融通卷一 第 15b 页 WYG0786-0563d.png
 置所求均策五得一而声策
置所求均策五得一而声策求黄钟正律大小馀及时刻
置所求岁定积来加往减大馀五十五小馀六大馀满
律总去之不尽来即所求往反减律总得黄钟正律大
小馀其大馀命甲子算外小馀以律数乘之刻满律母
为时命子正算外若满半律母亦进作一时命子初算
外馀如律数而一为刻不满为初刻
求黄钟前段半律及次律
律历融通卷一 第 16a 页 WYG0786-0564a.png
 置所求黄钟正律大小馀减去半律策即得黄钟前段
置所求黄钟正律大小馀减去半律策即得黄钟前段半律之数如不及减则加律总减之若求次律者以半
律策累加之满律总去之各得次律正半之数命法如
前
求均及声
置本月正律或半律大小馀以均策累加之即得次均
之大小馀其正半律日即为初均加者为中均再加为
末均求五声之日者以声策累加之即得次声之大小
律历融通卷一 第 16b 页 WYG0786-0564b.png
 馀其正半律日即命为宫次第加者为商为角为徵为
馀其正半律日即命为宫次第加者为商为角为徵为羽馀同上
求爻象
置黄钟正律大小馀命为益卦初九爻象以半律策累
加之得益六二至巽上九而止是为二十四气爻象又
置黄钟正律大小馀即复卦初九爻象以声策累加之
得复六二至蛊上九而止是为三百六十当期之日惟
盈日无爻象馀同上
律历融通卷一 第 17a 页 WYG0786-0564c.png
 步发敛第二
步发敛第二建寅 立春正月节 雨水正月中
东风解冻 蛰虫始振 鱼陟负冰
獭祭鱼 候雁北 草木萌动
建卯 惊蛰二月节 春分二月中
桃始华 仓庚鸣 鹰化为鸠
玄鸟至 雷乃发声 始电
建辰 清明三月节 榖雨三月中
律历融通卷一 第 17b 页 WYG0786-0564d.png
 桐始华 田鼠化为鴽 虹始见
桐始华 田鼠化为鴽 虹始见萍始生 鸣鸠拂其羽 戴胜降于桑
建巳 立夏四月节 小满四月中
蝼蝈鸣 蚯蚓出 王瓜生
苦菜秀 靡草死 麦秋至
建午 芒种五月节 夏至五月中
螳螂生 鵙始鸣 反舌无声
鹿角解 蜩始鸣 半夏生
律历融通卷一 第 18a 页 WYG0786-0565a.png
 建未 小暑六月节 大暑六月中
建未 小暑六月节 大暑六月中温风至 蟋蟀居壁 鹰始挚
腐草为萤 土润溽暑 大雨时行
建申 立秋七月节 处暑七月中
凉风至 白露降 寒蝉鸣
鹰乃祭鸟 天地始肃 禾乃登
建酉 白露八月节 秋分八月中
鸿雁来 玄鸟归 群鸟养羞
律历融通卷一 第 18b 页 WYG0786-0565b.png
 雷始收声 蛰虫坏户 水始涸
雷始收声 蛰虫坏户 水始涸建戌 寒露九月节 霜降九月中
鸿雁来宾 雀入大水为蛤 菊有黄华
豺乃祭兽 草木黄落 蛰虫咸俯
建亥 立冬十月节 小雪十月中
水始冰 地始冻 雉入大水为蜃
虹藏不见 天气上升地气下降 闭塞而成冬
建子 大雪十一月节 冬至十一月中
律历融通卷一 第 19a 页 WYG0786-0565c.png
 鹖鴠不鸣 虎始交 荔挺出
鹖鴠不鸣 虎始交 荔挺出蚯蚓结 麈角解 水泉动
建丑 小寒十二月节 大寒十二月中
雁北乡 鹊始巢 雉雊
鸡乳 征鸟厉疾 水泽腹坚
求二十四气
并所求正律半律策及黄钟大小馀满律总去之即立
春正月节累加半律策得次气大小馀满律总去之命
律历融通卷一 第 19b 页 WYG0786-0565d.png
 如上
如上求七十二候
置立春大小馀即东风解冻之候累加均策得次候大
小馀满律总去之命如上
求五行用事
各以四立之节为春木夏火秋金冬水始用事日声策
三之以减四季中气各得其季土始用事日
求列宿当直
律历融通卷一 第 20a 页 WYG0786-0566a.png
 置岁定积并入正半律策来加往减九日六刻满宿周
置岁定积并入正半律策来加往减九日六刻满宿周二十八日去之不尽来即所求往反减宿周馀为立春
日当直宿命起角宿算外累加半律策满宿周去之各
得次气日当直宿
求建除
建除满平定执破危成收开闭终而复始交节之后各
以同月之日为建故交节之始与上日重名
求纳音
律历融通卷一 第 20b 页 WYG0786-0566b.png
 子午丑未甲乙起宫寅申卯酉甲乙起商辰戌巳亥甲
子午丑未甲乙起宫寅申卯酉甲乙起商辰戌巳亥甲乙起角丙丁而下例知凡宫为土商金角木徵火羽水
迭为次第终而复始各以所生者为纳音
步朔闰第三
朔策二十九日五十三刻五分九十三秒
望策十四日七十六刻五十二分九十六秒半
弦策七日三十八刻二十六分四十八秒少
寅月策五十九日六刻十一分八十六秒
律历融通卷一 第 21a 页 WYG0786-0566c.png
 卯月策八十八日五十九刻十七分七十九秒
卯月策八十八日五十九刻十七分七十九秒辰月策百一十八日十二刻二十三分七十二秒
巳月策百四十七日六十五刻二十九分六十五秒
午月策百七十七日十八刻三十五分五十八秒
未月策二百六日七十一刻四十一分五十一秒
申月策二百三十六日二十四刻四十七分四十四秒
酉月策二百六十五日七十七刻五十三分三十七秒
戌月策二百九十五日三十刻五十九分三十秒
律历融通卷一 第 21b 页 WYG0786-0566d.png
 亥月策三百二十四日八十三刻六十五分二十三秒
亥月策三百二十四日八十三刻六十五分二十三秒子月策三百五十四日三十六刻七十一分十六秒
丑月策三百八十三日八十九刻七十七分九秒
求闰馀
置岁定积来加往减二十日二十刻五十分朔策为法
除之不尽来即所求往反减朔策得闰馀
求汎闰
视闰馀在十八日已上者其年有闰置所求闰馀全分
律历融通卷一 第 22a 页 WYG0786-0567a.png
 加九十刻六十三分却与朔策相减视馀几日为闰几
加九十刻六十三分却与朔策相减视馀几日为闰几月起建寅月命之即汎闰月不满日者有闰在年前子
丑月
求朔积
置所求月策减去闰馀即其月朔积若求闰月及闰后
月者复加朔策方为其月朔积
求经朔弦望
置所求朔积加黄钟正律大小馀满律总去之各得其
律历融通卷一 第 22b 页 WYG0786-0567b.png
 月经朔加以望策即得经望以弦策加经朔得上弦加
月经朔加以望策即得经望以弦策加经朔得上弦加经望得下弦
又法置正月经朔大小馀累加弦策满律总去之亦得
弦望及次朔大小馀若径求次朔以朔策加之
凡考古系天正者以年前十一月为正月正月为三月
系地正者以年前十二月为正月正月为二月各照常
法推之
求盈虚
律历融通卷一 第 23a 页 WYG0786-0567c.png
 置十六日减所求半律策馀为没限恒气小馀在没限
置十六日减所求半律策馀为没限恒气小馀在没限已上为有没之气以十五乘之用减半律策馀如半律
策小馀而一为日并恒气大馀为没古历谓之没今历
谓之盈
置三十日减去朔策馀为朔虚经朔小馀在朔虚已下
为有灭之朔以三十乘之如朔虚而一为日并经朔大
馀为灭古历谓之灭今历谓之虚
步日躔第四
律历融通卷一 第 23b 页 WYG0786-0567d.png
 日平行一度
日平行一度躔周三百六十五度二十五分
躔中百八十二度六十二分半
象策九十一度三十一分二十五秒
半象策四十五度六十五分六十二秒半
辰策三十度四十三分七十五秒
半辰策十五度二十一分八十七秒半
赤道岁差一分五十秒
律历融通卷一 第 24a 页 WYG0786-0568a.png
 黄道岁差一分三十八秒
黄道岁差一分三十八秒盈初缩末限八十八日九十一刻
缩初盈末限九十三日七十一刻
求经朔弦望入历
置岁定积与次年岁定积相减馀为岁周半之为岁中
凡所求月朔积即经朔入历以弦望策加之得弦望入
历冬至后为盈夏至后为缩满岁中去之即盈缩相代
求盈缩初末限
律历融通卷一 第 24b 页 WYG0786-0568b.png
 视入历盈者在盈初缩末限已下缩者在缩初盈末限
视入历盈者在盈初缩末限已下缩者在缩初盈末限已下为初限已上反减岁中馀为末限
求盈缩差
盈初缩末者立差三十一忽平差二分四十六秒定差
五百一十三分三十二秒缩初盈末者立差二十七忽
平差二分二十一秒定差四百八十七分六秒各置立
差以所求限大馀乘之加平差又乘之用减定差再乘
之满万为度不满退除为分秒命为盈缩积与次限盈
律历融通卷一 第 25a 页 WYG0786-0568c.png
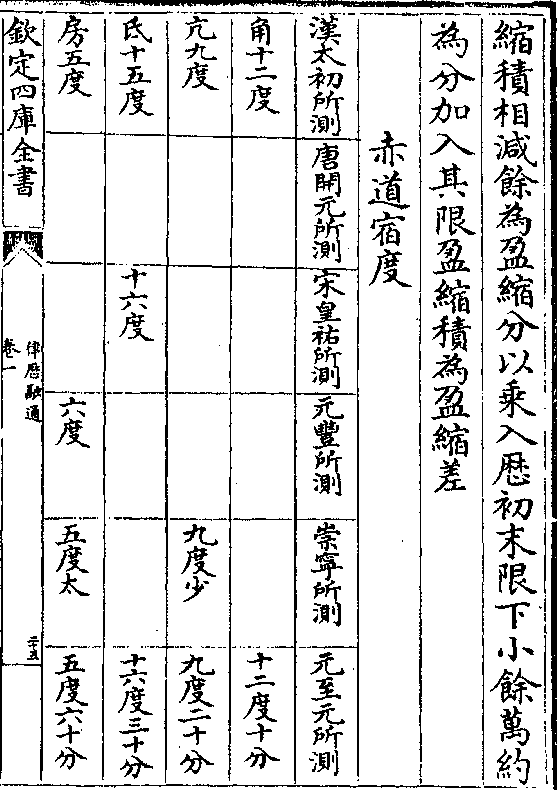 缩积相减馀为盈缩分以乘入历初末限下小馀万约
缩积相减馀为盈缩分以乘入历初末限下小馀万约为分加入其限盈缩积为盈缩差
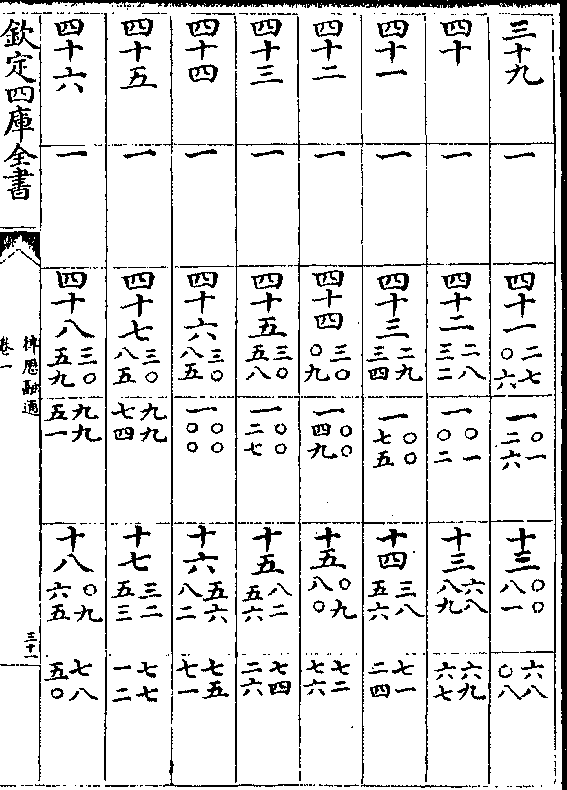
赤道宿度
律历融通卷一 第 25b 页 WYG0786-0568d.png

律历融通卷一 第 26a 页 WYG0786-0569a.png

律历融通卷一 第 26b 页 WYG0786-0569b.png

律历融通卷一 第 27a 页 WYG0786-0569c.png

列宿相距度数历代所测不同非微有动移则前人所
测或有未密汉唐宋用管窥止存大略元人始用二线
遂及分焉今历因之用为常数校天为密若考往古仍
依当时宿度命之其时无宿度者壹准前人宿度故并
律历融通卷一 第 27b 页 WYG0786-0569d.png
 载之以备考古所须惟推密率日躔无论古今并依今
载之以备考古所须惟推密率日躔无论古今并依今历有分赤道宿度为准
求冬至加时赤道日度
置岁定积命日为度来加往减七十八度八十分赤道
岁差折半加躔周为历率以除积度不尽来即所求往
反减历率命起角宿初度算外满今赤道宿度去之至
不满者即所求岁前冬至加时赤道日度及分秒
求四正加时赤道日度
律历融通卷一 第 28a 页 WYG0786-0570a.png
 置所求岁前冬至加时赤道日度及分秒以象策累加
置所求岁前冬至加时赤道日度及分秒以象策累加之满赤道宿度去之各得四正定气加时赤道日度及
分秒
求四正后赤道宿积度
置四正赤道宿全度以四正赤道日度及分秒减之馀
为距后度以赤道宿度累加之各得四正后赤道宿积度
及分秒
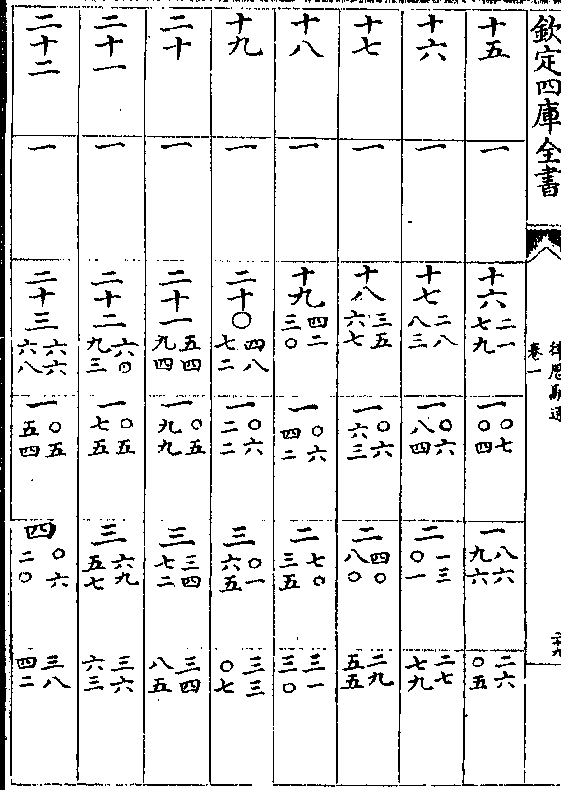
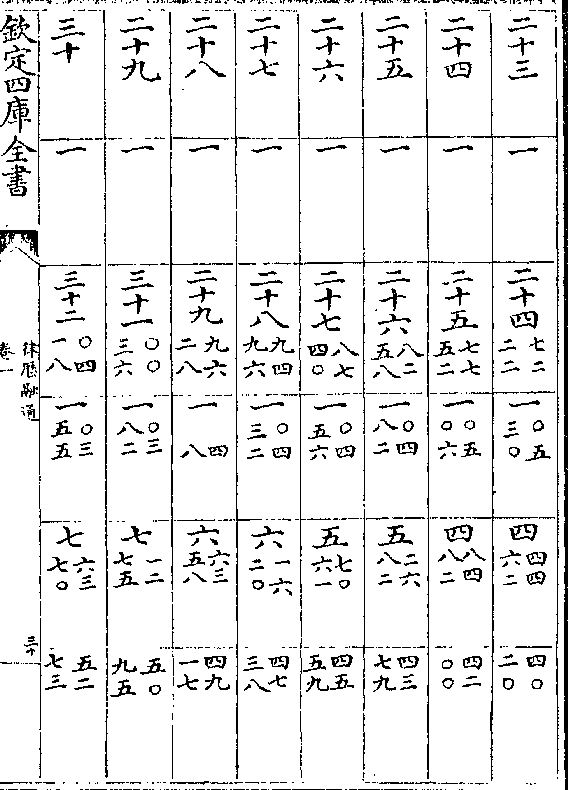
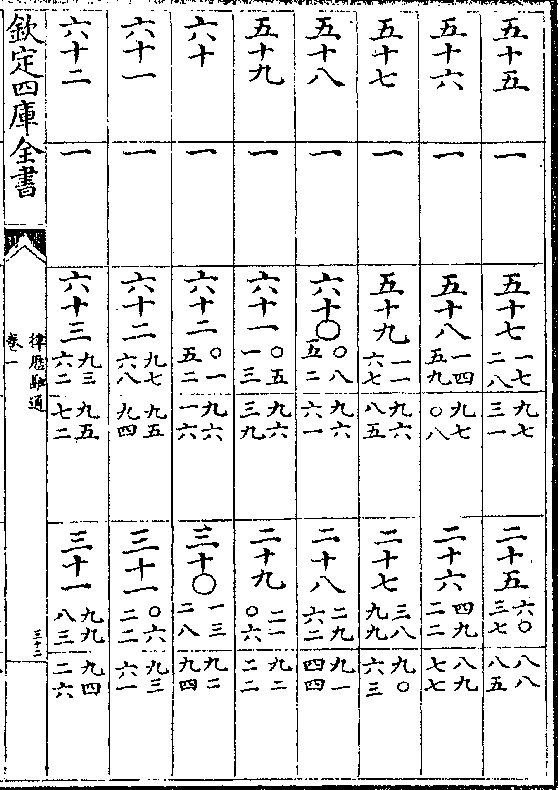
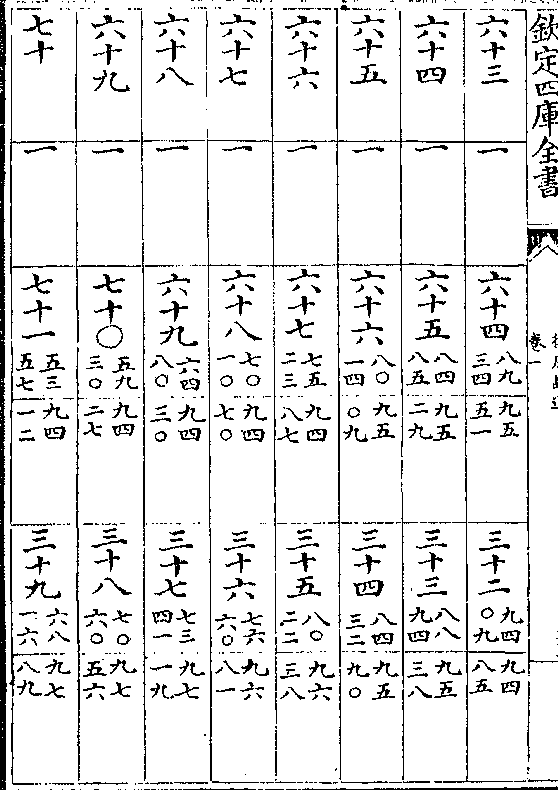
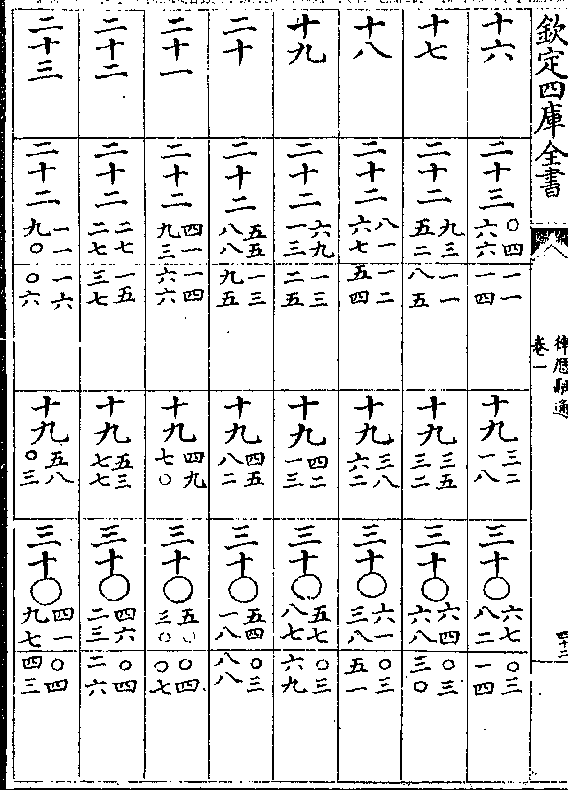
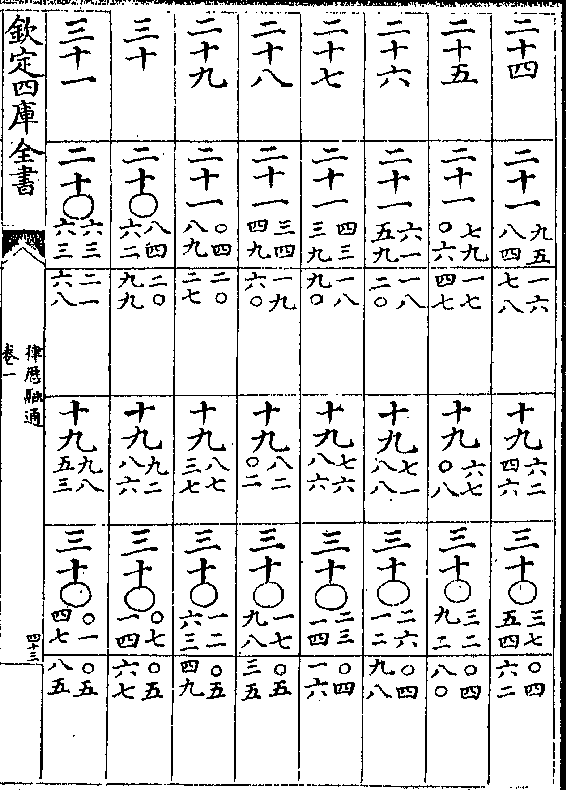
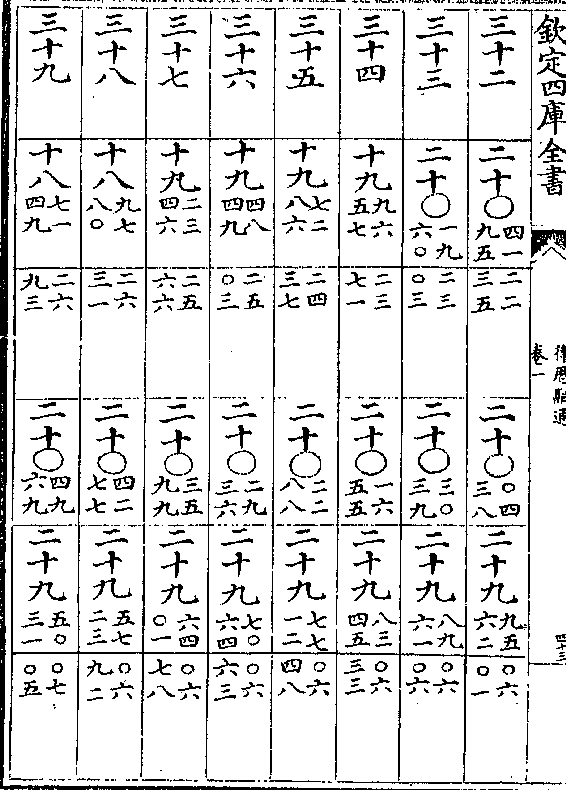
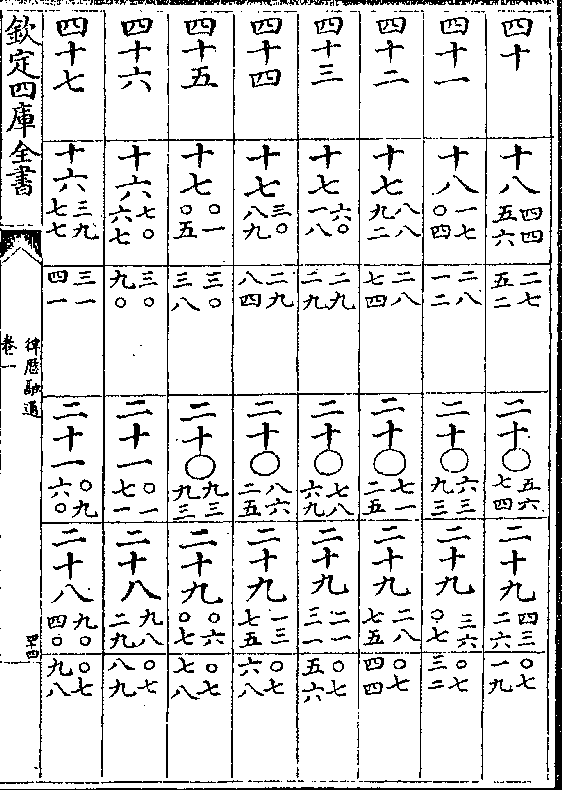
黄赤道率
律历融通卷一 第 28b 页 WYG0786-0570b.png
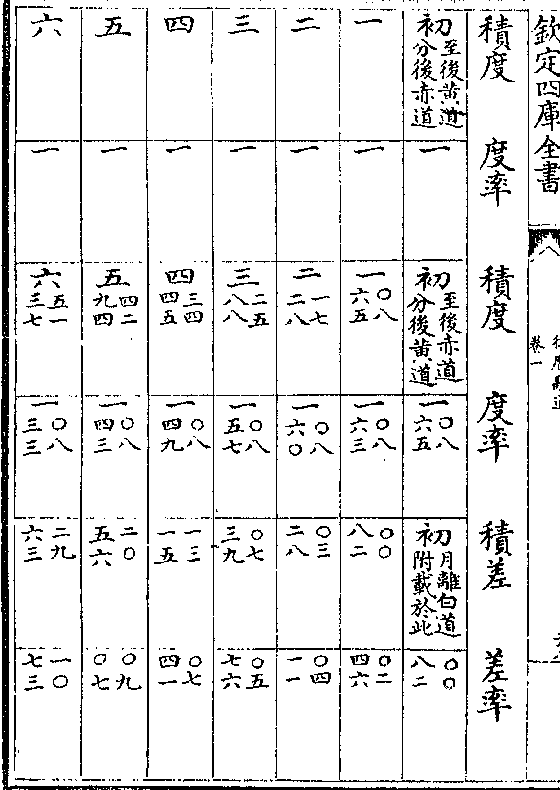 积度 度率 积度 度率 积差 差率
积度 度率 积度 度率 积差 差率律历融通卷一 第 29a 页 WYG0786-0570c.png

律历融通卷一 第 29b 页 WYG0786-0570d.png
律历融通卷一 第 30a 页 WYG0786-0571a.png
律历融通卷一 第 30b 页 WYG0786-0571b.png

律历融通卷一 第 31a 页 WYG0786-0571c.png
律历融通卷一 第 31b 页 WYG0786-0571d.png

律历融通卷一 第 32a 页 WYG0786-0572a.png
律历融通卷一 第 32b 页 WYG0786-0572b.png
律历融通卷一 第 33a 页 WYG0786-0572c.png

律历融通卷一 第 33b 页 WYG0786-0572d.png

律历融通卷一 第 34a 页 WYG0786-0573a.png
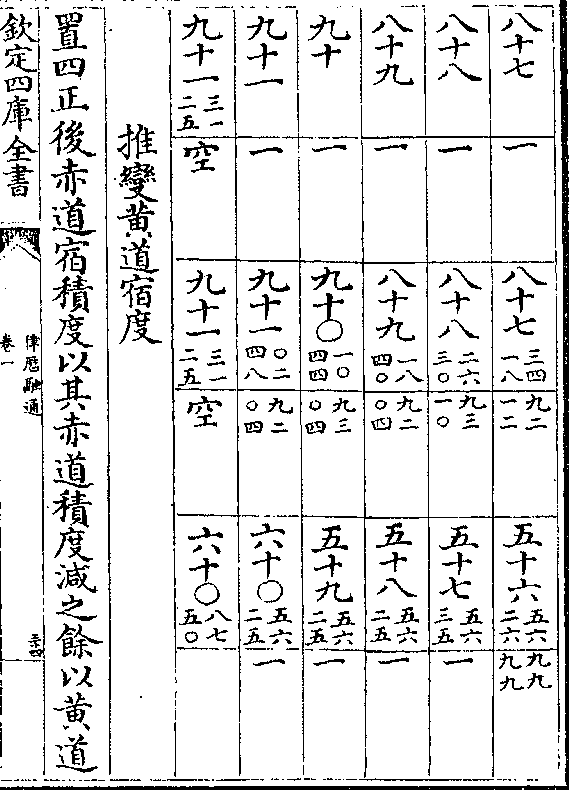
推变黄道宿度
置四正后赤道宿积度以其赤道积度减之馀以黄道
律历融通卷一 第 34b 页 WYG0786-0573b.png
 率乘之如赤道率而一所得以加黄道积度为二十八
率乘之如赤道率而一所得以加黄道积度为二十八宿黄道积度以前宿黄道积度减之为其宿黄道度及
分(其秒就近为分)
黄道宿度
右东方七宿七十七度四十一分
律历融通卷一 第 35a 页 WYG0786-0573c.png

右北方七宿九十四度八十六分
右西方七宿八十三度十九分
律历融通卷一 第 35b 页 WYG0786-0573d.png

右南方七宿百九度七十九分
右黄道宿度依万历甲午年岁前冬至日躔所在算定
以凭推步若上考已往下验方来即据岁差每移一度
依术推变黄道各得当时宿度
求冬至加时黄道日度
律历融通卷一 第 36a 页 WYG0786-0574a.png
 置所求岁前冬至加时赤道日度及分秒以其赤道积
置所求岁前冬至加时赤道日度及分秒以其赤道积度减之馀以黄道率乘之如赤道率而一所得以加黄
道积度即所求岁前冬至加时黄道日度及分秒
求四正加时黄道日度
置所求岁定积与次年岁定积相减馀命日为度及分
秒以赤道岁差折半加之以黄道岁差减之为定率四
约之为四正定象度置所求岁前冬至加时黄道日度
及分秒以四正定象度累加之满黄道宿度去之各得
律历融通卷一 第 36b 页 WYG0786-0574b.png
 四正定气加时黄道日度及分秒
四正定气加时黄道日度及分秒求四正晨前夜半黄道日度
冬夏二至盈缩之端以恒为定春秋二分置恒气日及
分秒以盈缩差命度为日盈减缩加之即四正定气日
及分秒置日平行度万通之以盈缩分盈初缩末加之缩
初盈末减之为其日行定度置四正小馀以其日行定
度乘之如平行度而一所得以减四正加时黄道日度
各得四正晨前夜半黄道日度及分秒
律历融通卷一 第 37a 页 WYG0786-0574c.png
 求每日晨前夜半黄道日度
求每日晨前夜半黄道日度以四正定气日距后正定气日为相距日以四正晨前
夜半日度距后正晨前夜半日度为相距度累计相距
日之行定度与相距度相减馀如相距日而一为日差
相距度多为加相距度少为减加减四正每日行度率
为每日行定度累加四正晨前夜半日度满黄道宿度
去之为每日晨前夜半黄道日度及分秒
求每日子午二正黄道日度
律历融通卷一 第 37b 页 WYG0786-0574d.png
 置所求月经朔入历以经朔小馀减之馀为经朔晨前
置所求月经朔入历以经朔小馀减之馀为经朔晨前子正入历累加一日为每日晨前子正入历又以五十
刻加之为午正入历命日为度各视其限求盈缩差盈
加缩减之为所求黄道定积度以岁前冬至加时黄道
日度加而命之满黄道宿度去之即每日子午黄道日
度及分秒(或以其日行定度折半加积前夜半黄道定积度亦得午中黄道定积度)
求每日子午二正赤道日度
视黄道定积度在象策已下为至后已上去之为分后
律历融通卷一 第 38a 页 WYG0786-0575a.png
 再去之为至后复去之为分后内减黄道积度以赤道
再去之为至后复去之为分后内减黄道积度以赤道率乘之如黄道率而一所得以加赤道积度及所去象
策以岁前冬至加时赤道日度加而命之满赤道宿度
去之即每日子午赤道日度及分秒
赤道黄道十二次宿度
赤道娵訾之次初起危十二度二十六分八十七秒半
降娄之次初起奎一度六十分六十二秒半
大梁之次初起胃三度六十四分三十七秒半
律历融通卷一 第 38b 页 WYG0786-0575b.png
 实沈之次初起毕七度十八分十二秒半
实沈之次初起毕七度十八分十二秒半鹑首之次初起井九度六分八十七秒半
鹑火之次初起柳四度空分六十二秒半
鹑尾之次初起张十四度八十四分三十七秒半
寿星之次初起轸九度二十八分十二秒半
大火之次初起氐一度十一分八十七秒半
析木之次初起尾三度十五分六十二秒半
星纪之次初起斗四度九分三十七秒半
律历融通卷一 第 39a 页 WYG0786-0575c.png
 玄枵之次初起女二度十三分十二秒半
玄枵之次初起女二度十三分十二秒半黄道娵訾之次初起危十二度八十分三十一秒
降娄之次初起奎一度七十三分六十七秒
大梁之次初起胃三度七十分四十五秒
实沈之次初起毕六度八十一分三十三秒
鹑首之次初起井八度三十六分十一秒
鹑火之次初起柳三度九十一分六十七秒
鹑尾之次初起张十五度四十四分二十三秒
律历融通卷一 第 39b 页 WYG0786-0575d.png
 寿星之次初起轸十度六分四十二秒
寿星之次初起轸十度六分四十二秒大火之次初起氐一度十三分三十九秒
析木之次初起尾二度九十八分十八秒
星纪之次初起斗三度七十七分九十六秒
玄枵之次初起女二度八分八十四秒
赤道有常黄道无定凡推辰次当以赤道为准随日度
岁差推变黄道右据万历甲午年岁差所推已后临时
推变
律历融通卷一 第 40a 页 WYG0786-0576a.png
 推变十二次宿度
推变十二次宿度置赤道入次宿度及分秒以前宿赤道距后积度加之
满象策去之为四正后赤道入次积度以其赤道积度
减之馀以黄道率乘之如赤道率而一所得以加黄道
积度为四正后黄道入次积度以前宿黄道距后积度
减之如不及减加象策以减之馀即所求黄道入赤道
十二次宿度及分秒
求入十二次时刻
律历融通卷一 第 40b 页 WYG0786-0576b.png
 各置黄道入次宿度及分秒以其日晨前夜半黄道日
各置黄道入次宿度及分秒以其日晨前夜半黄道日度及分秒减之馀以日平行度乘之为实以其日行定
度为法实如法而一所得依时刻法求之即入次时刻
步晷漏第五
京师北极出地四十度太
冬至中晷恒数丈五尺九寸六分
夏至中晷恒数二尺三寸四分
冬至昼夏至夜三十八刻
律历融通卷一 第 41a 页 WYG0786-0576c.png
 夏至昼冬至夜六十二刻(已上见元志)
夏至昼冬至夜六十二刻(已上见元志)岳台北极出地三十五度
冬至中晷恒数丈二尺八寸三分
夏至中晷恒数尺五寸七分
冬至昼夏至夜四十刻
夏至昼冬至夜六十刻(已上见宋志)
黄道出入赤道内外度及半昼夜分
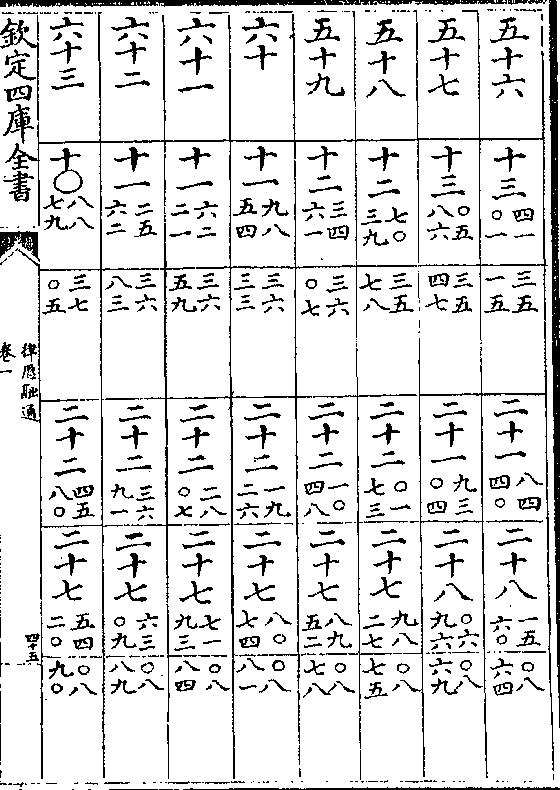
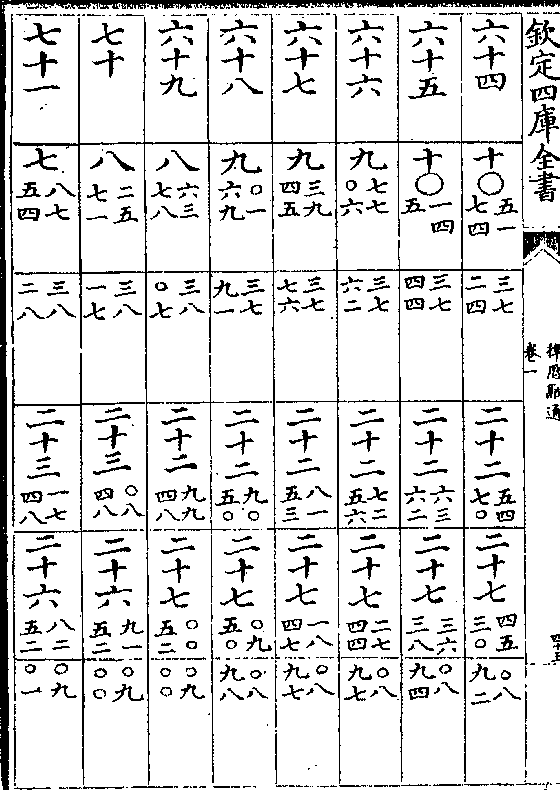
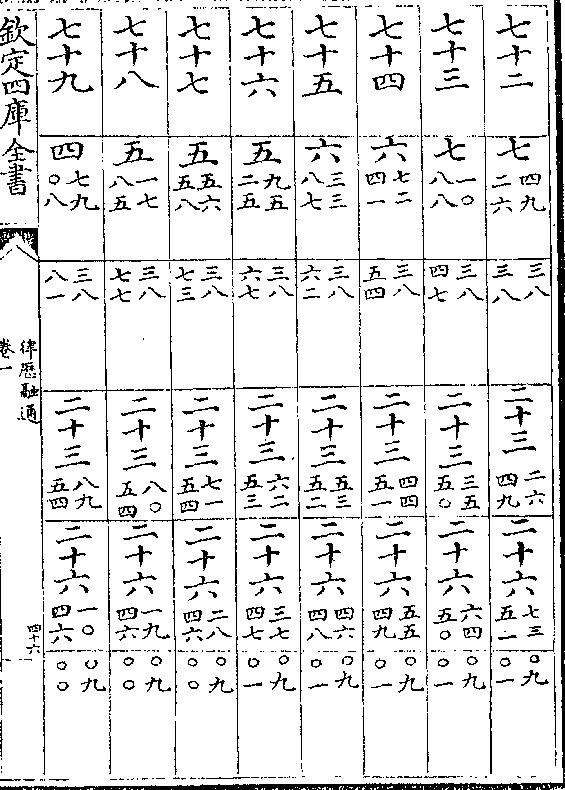
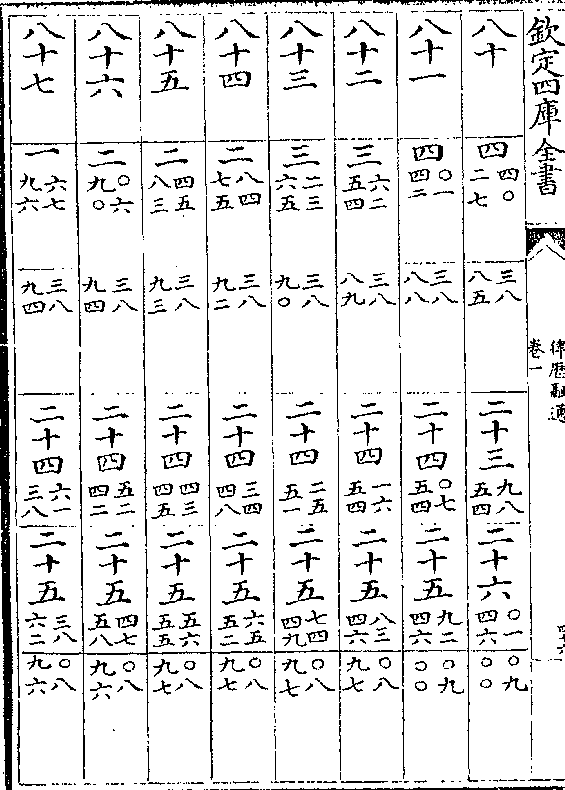
律历融通卷一 第 41b 页 WYG0786-0576d.png

律历融通卷一 第 42a 页 WYG0786-0577a.png

律历融通卷一 第 42b 页 WYG0786-0577b.png
律历融通卷一 第 43a 页 WYG0786-0577c.png
律历融通卷一 第 43b 页 WYG0786-0577d.png
律历融通卷一 第 44a 页 WYG0786-0578a.png
律历融通卷一 第 44b 页 WYG0786-0578b.png

律历融通卷一 第 45a 页 WYG0786-0578c.png
律历融通卷一 第 45b 页 WYG0786-0578d.png
律历融通卷一 第 46a 页 WYG0786-0579a.png
律历融通卷一 第 46b 页 WYG0786-0579b.png
律历融通卷一 第 47a 页 WYG0786-0579c.png
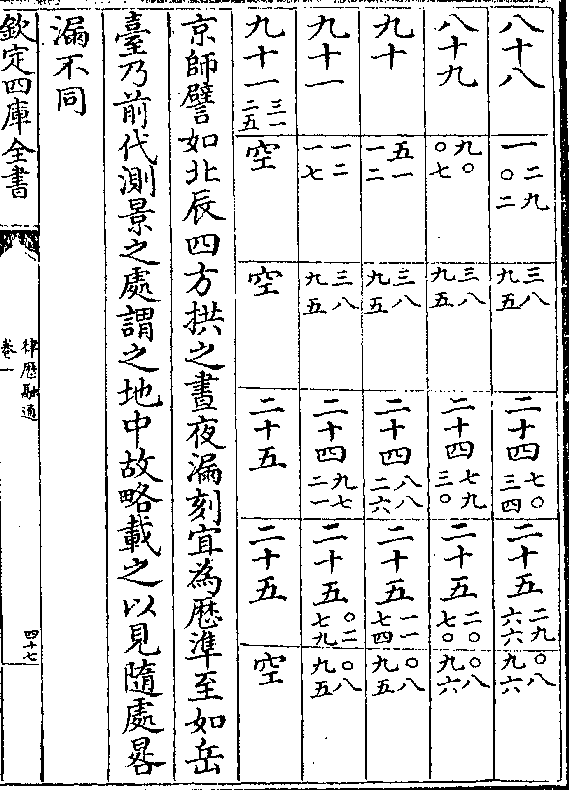
京师譬如北辰四方拱之昼夜漏刻宜为历准至如岳
台乃前代测景之处谓之地中故略载之以见随处晷
漏不同
律历融通卷一 第 47b 页 WYG0786-0579d.png
 求每日子正午正日躔黄道去极度
求每日子正午正日躔黄道去极度置所求日晨前夜半黄道积度满躔中去之在象策已
下为初限已上反减躔中馀为末限满积度去之馀以
其段内外差乘之如律母而一为分用减内外度为出入
赤道内外度内减外加象策即所求日子正去极度及分
秒求午正去极度放此
求每日午正随处日去地度
置所求日午正日躔黄道去极度及分并其处北极出
律历融通卷一 第 48a 页 WYG0786-0580a.png
 地度及分用减躔中馀即其处日去地度为弧半背(若弧
地度及分用减躔中馀即其处日去地度为弧半背(若弧半背在象策已上反减躔中馀为弧半背则知景在表南)约量矢数与限二十九度
五分五十秒相减馀以六十一分七十七秒乘之律母
除之为加减差矢在限已上加已下减加减百八十七
度九十分为定差以矢与五十八度十一分相减馀以
定差乘之度如律母而一为分不满退除为秒并入九
度为法复以矢与百一十六度二十二分相减相乘及
矢自乘相并为实开方所得进一位以法除之为弧半
律历融通卷一 第 48b 页 WYG0786-0580b.png
 背即其处日去地度及分秒如不同更增损矢数算之
背即其处日去地度及分秒如不同更增损矢数算之以同为矢定数
求每日随处中晷汎数
置五十八度十一分减去所求矢定数馀用八因为实
复以矢与百一十六度二十二分相减相乘平方开之
为法除实命度为尺即其日其处中晷汎数
求每日随处中晷定数
各于其处立八尺表每日实测午晷真数而与算术所
律历融通卷一 第 49a 页 WYG0786-0580c.png
 求晷数相减馀名为地形差所测晷数多则为加少则
求晷数相减馀名为地形差所测晷数多则为加少则为减加减所算晷数即其日其处中晷定数
求二至加时真数
取二至前后晷数近似者相减馀以律母乘之为实取
其次日晷数相减馀为法实如法而一为刻求冬至视
其前晷多则为减差少则为加差夏至反之总计距日
刻数以差加减折半加五十刻为前距定日以其日算
外命之即二至加时真数
律历融通卷一 第 49b 页 WYG0786-0580d.png
 求每日半昼夜及日出入晨昏分
求每日半昼夜及日出入晨昏分置所求初末限满积度去之馀以其段昼夜差乘之如
律母而一为分前多后少为减前少后多为加加减其
段半昼夜分为所求半昼夜分以半夜分便为日出分
用减百刻馀为日入分于日出分减二刻半馀为晨分
于日入分加二刻半则为昏分
求昼夜刻及日出入时刻
置其日半夜分二因之如律母而一所得为夜刻用减
律历融通卷一 第 50a 页 WYG0786-0581a.png
 百刻馀为昼刻以日出入分依时刻法求之即得所求
百刻馀为昼刻以日出入分依时刻法求之即得所求时刻
求更点所在时刻
置其日晨分二因五约之为更率又五约之为点率各
以其率乘所求更点数用加其日昏分内减更点率满
百刻去之不满依时刻法求之即得所求时刻
求昏后夜半中星
置躔中度及分以其次日晨前夜半赤道日度及分秒
律历融通卷一 第 50b 页 WYG0786-0581b.png
 加而命之即所求日昏后夜半中星积度及分秒
加而命之即所求日昏后夜半中星积度及分秒求逐日昏晓中星
置其次日晨分以躔周加一度乘之万约为度昏减晓
加所求日昏后夜半中星积度即昏晓中星积度及分
秒
求逐更逐点中星
置昏后晓中星积度(不及则加躔周)以晓前昏中星积度减之
馀二十五而一所得为点差置昏中星积度命为一更
律历融通卷一 第 51a 页 WYG0786-0581c.png
 一点以点差累加之满赤道宿度去之即逐更逐点中
一点以点差累加之满赤道宿度去之即逐更逐点中星宿度及分秒
求九服所在漏刻
各于所在以仪测验或下水漏以定其处冬至或夏至
夜刻与五十刻相减馀为至差刻以所求日黄道出入
赤道内外度及分秒乘之二十三度九十分除之所得
内减外加五十刻即所求夜刻以减百刻馀为昼刻
其九服所在逐段昼夜差半昼夜分及日出入晨昏分
律历融通卷一 第 51b 页 WYG0786-0581d.png
 更点中星等率并准随处晷漏脩短依术推之
更点中星等率并准随处晷漏脩短依术推之律历融通卷一