钦定四库全书
　句股引蒙卷二
　　　　　　　　　　　　海宁　陈吁　撰
开方
　　开方为句股积幂测量步算之源其法取积实归
　　除使均齐方正知每边得若干数其用筹除实视
　　某格为某商若干等类俱如前法有平方大筹立
　　方大筹置廉用散筹

　　平方开面立方开体皆开除所积之实平方则开
　　平面所积之方故大筹每格止一自乘立方则开
　　立体所积之方故大筹每格其右边直行先平列
　　一自乘数其中左两行虽有斜格而平行每格又
　　以自乘之数与每格之一二三四五六七八九相
　　乘盖如围棋子平方则四边十九而三百六十一
　　为十九个十九也立方则十九个三百六十一也
　　又平方立方俱以第一次大筹除实之格为方根

　　后各依法加廉其大筹所除之格其实即隅积其
　　平行之数即隅数且隅积即在平廉约法中并列
　　并除此天然之巧也凡测算虽极远极大其所测
　　中心止凭一点其远近多少相距亦止凭一点从
　　此点至彼点则有线线即有所积之面面即有所
　　积之体故平方开面立方开体皆因其所积之面
　　与体以求其所距之线与所测之点为句股三角
　　之用也(此所测之点非开/方点定开位之点)

开平方法
　先点定开位从末单位点起(如积实尾无单位者/于尾位置○点起)隔
　一位点以至实首一点一开二点二开开不尽者命
　分
　一点者根必单二点者根必十(俱以/次增)先从左大数视
　平方筹相近之格除之开数定则方根之十百千万
　亦定矣(立方同/)
　凡初商除至前第一点止次商除至前第二点止如

　次商点位前原止二位而筹格有三位不得除至第
　二点后便须置○于次商为次商○三商以下皆然
初商法
　平方筹取近少除实至前第一点止在第几格即为
　初商若干此第一次除之商数名为方根
　点前无馀者从筹上一二三格之单位除点前有馀
　者从筹上四五六七八九格之双位除如实少于筹
　者用退位法除

　
　
　
　
　
次商法
　以初商所得数倍之为廉以所倍之廉数列筹于平
　方筹左取某格近少除之为次商若干

三商法
　以次商所得数倍之为廉列筹于次商筹之右平方
　筹之左除实同前法(各商同此/)
　　每商置○定位三则(开方定位依点递加不/用顺寻逆寻法立方同)
三商式
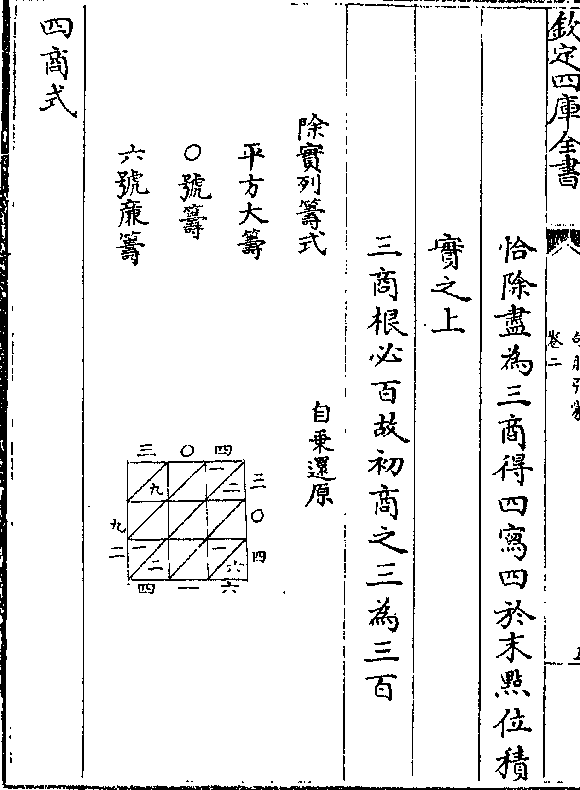
　　　　　　如列实三点为三开(从末零位点/起每开一位)点
　　　　　　前无馀该大筹单位除实三格内除
　　　　　　九为初商三写三字在首点积实之

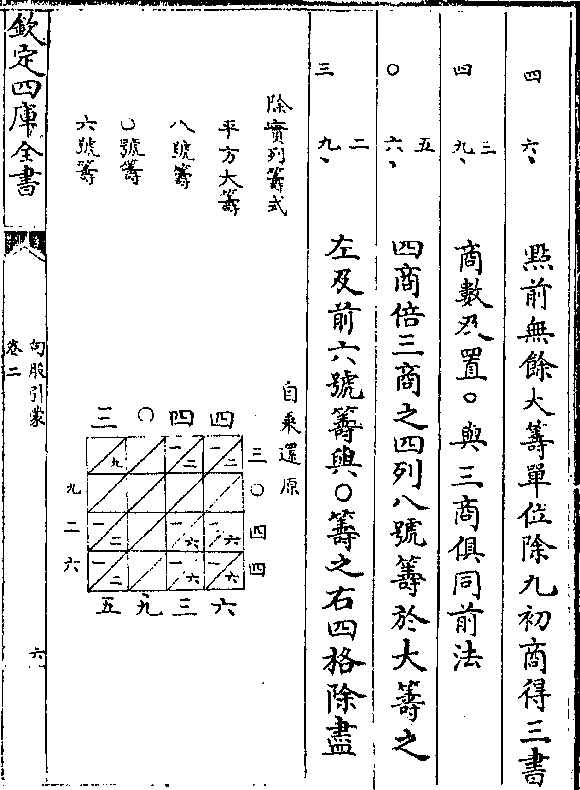　　　二　　上
　三　九　　次商应倍初商之三列六号筹为廉除
　　　○　　实若取近少莫如三格但次点位前实
　　　　　　止有二位而筹有三位不得除至次点
　　　　　　位后便须置○是为次商得○写○于
　　　　　　次点位积实上隔○筹于平方筹左
　　　　　　三商既列六号筹○筹于平方筹之左
　　　　　　便应统取近少除至末点位止今四格

　　　　　　恰除尽为三商得四写四于末点位积
　　　　　　实之上
　　　　　　三商根必百故初商之三为三百
　
　
　
　
四商式

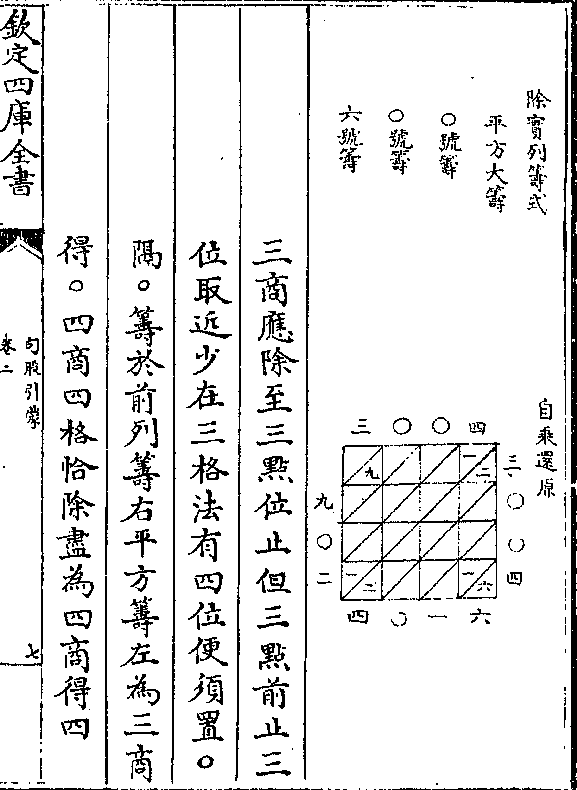　　　　　　点前无馀大筹单位除九初商得三书
　　　　　　商数及置○与三商俱同前法
　　　　　　四商倍三商之四列八号筹于大筹之
　　　　　　左及前六号筹与○筹之右四格除尽
　
　
　
　

　　　　　　为四商四
　　　　　　四商根必千故初商之三为三千
四商○○式
　　　　　　初商视平方筹取三格除九为初商得
　　　　　　三次商倍方根列六号筹于表左应除
　　　　　　至次点位止但次点前实止一位而法
　　　　　　之一格两位下俱三位便须置○隔○
　　　　　　筹于前列筹右平方筹左为次商得○

　
　
　
　
　　　　　　三商应除至三点位止但三点前止三
　　　　　　位取近少在三格法有四位便须置○
　　　　　　隔(○/)筹于前列筹右平方筹左为三商
　　　　　　得(○/)四商四格恰除尽为四商得四

　　　　　　四商根必千故初商之三为三千
加筹
　凡商除之后如两廉必倍前商之数如前商一加二
　号筹前商二加四号筹之类此易明惟前商五倍之
　加一十则加一号○号两筹盖五加一筹○筹方是
　一十若不𢃄○筹则一为单数矣若前商之廉是十
　数又当为升筹
升筹

　凡商除之后如有加两筹者当用升筹法盖同位则
　升也如平方三开其初商二是为二百次商倍之为
　廉是四百应列四号筹矣其次商六是为六十三商
　倍之为廉是一百二十似应再列一号二号筹于前
　商四号筹之右然从四号筹挨次而来似乎四百一
　十二而非倍六十之一百二十矣故应将一百与四
　百并之为五百连二十为五百二十升作五二筹列
　于平方筹左而前商之四号筹去之

隔筹
　每商必加倍数筹以为廉法故前商既置○矣亦须
　隔○筹于前列筹之右以为后商之廉法而取近少
　除实为后商其前列筹固倍数也而○不必倍者盖
　置一○只应隔一○筹耳(立方每隔○○/两筹与平方异)
命分
　见前筹算法视末商筹之第一格为若干分视所馀
　不尽之实命为若干分之若干分

　　如馀积五十七如末商两廉列八号四号筹(连前/商筹)
　　(在/内)视第一格八四一命为八百四十一分之五百
　　七十分盖第一格是两廉每加一分之全数故止
　　视第一格而命其全数与现在不尽之分也
求分杪
　凡有开不尽者或不命分欲知若干分杪于馀实下
　增两○位为○○则多开一位而分杪可得矣(平方/隔一)
　(位点是每开两/位故增○○)

　　　右皆开平方法其平方带纵者开方附左
平方𢃄纵
　列积实依开方商除法每商除实得商数以乘纵数
　除馀实其次商倍初商数除实以次商数乘纵数除
　馀实但倍商不倍纵馀商同法合每商之数为阔(即/正)
　(方/)加纵数即𢃄纵之长方
　如纵数有比例可求者先以比例分其积而馀积以
　平方开之得阔因以知其长

　　开方得阔加纵式
　　　假如长田六百二十四步　　阔不及长二步
　
　
　　　　初商得二除四百步　又以商数二乘纵二
　　　　步(二二/如四)除四十步　　馀一百八十四步
　　　　又倍初商列四号筹次商四格除一百七十
　　　　六步　又以商数四乘纵二步(二四/如八)　共一

　　　　百八十四步除尽为次商四
　　　开得阔二十四步　加纵二步为长二十六步
　　比例分积式
　　　假如直田积四百五十步　长多阔一倍
　　　　法平分其积得二百二十五步平方开之得
　　　　阔一十五步倍之得三十步即长
　　　假如长田积二百五十二步　长比阔多四分
　　　(分母/)之三(分子/)

　　　　法以分子三加分母四共七为法以分母四
　　　　乘积为实法除实得一百四十四步开方得
　　　　阔一十二步又以阔一十二步七因四除之
　　　　得二十一步为长(长比阔多九步较之/十二步为四分之三)

开立方法
　从末单位点起每点隔二位视列实位一点一开二
　点二开馀同
　凡一点者方根必单二点者方根必十以次而增先
　从列实左大位视立方筹取近少除之
　点前无馀除一二格之单位点前馀一除三四格之
　十位点前馀二除五六七八九之百位
　　立方根单其积实必从单至几百止如九之所积

　　其平面自乘得八十一而立体则九与八十一相
　　乘得七百二十九故根单必积实至百位而单位
　　点起隔两位至百也
　　立方根十其积实必从几千至几万几十万止如
　　九十之所积其平面自乘得八千一百而立体则
　　九十与八千一百相乘得七十二万九千故根十
　　其积实必从千位万位至十万位止而点亦隔两
　　位也馀以类推

　　立方积实必得三位故一点一开二点二开而开
　　数定于此矣一点者根必单二点者根必十方根
　　定于此矣初商除至左首点位止次商除至次点
　　位止置○肇于此矣若尾位列实止于十则实右
　　补一○列实止于百则实右补○○以便从单位
　　点起若列实不至单位止则点位一错而开数方
　　根置○俱因之以错矣故列至单位开方之异于
　　筹除者在此

初商
　法同平方视列实用立方大筹视单位十位百位依
　法取近少除之至前首点位止在第几格为初商若
　干为方根
次商
　以初商方根自之(即自乘/)又三倍自乘之实得若干
　列某号筹于立方筹之左为平廉法
　再以初商方根竟三倍之列某号筹于立方筹之右

　为长廉法
　
　
　
　
　视平廉筹及大筹某格近少列为平廉约数
　将平廉约数在某格之隅数(即大筹两行/平写之数)乘立方大
　筹右之长廉(如九格之八一为隅数即将长廉筹/八格一格所列之数依大小次并之)得

　若干数为长廉约法
　并平廉长廉两约数若干以减初商所馀之实至次
　点位止为次商若干
　如并两廉数浮于实须退位改商如位多于实应置
　○不得除至次点位后
　　　右立方有平廉三长廉三与平方异
三商
　去前商左右列筹

　以初商两商自之又三倍之为平廉列筹于立方筹
　左
　再以初次两商竟三倍之为长廉列筹于立方筹右
　如前商法除至三点位止
四商(以下皆同/)
　去前商筹依法列平廉长廉筹除至末点位止为四
　商若干如尚有馀实依命分法
　　右前法俱前商之后即将前各商数自之又三倍

　　之为平廉列筹视某格与馀实近少列为平廉约
　　数再以前各商竟三倍之为长廉列筹(俱依前法/分列大筹)
　　(左/右)视平廉约数在某格之隅数取以乘长廉得若
　　干数为长廉约数其万千百十各依位数附于平
　　廉之本位并之而除馀实其隅数即在大筹之除
　　格其廉积即在散筹之每格仍是于全数中除两
　　廉应除之馀实而隅数亦不烦再乘再除也梅定
　　九先生筹算仍依古法先以前商三倍之为廉法

　　以前商数自之又三倍之为方法以方法除馀积
　　得次商既得次商用其数以乘方法为三平廉积
　　又次商自乘以乘廉法为三长廉积再以次商为
　　隅法以隅法自乘再乘得小立方形为隅积三共
　　并之除馀积不知既列筹除则筹之每格即乘有
　　廉之全积何必多此一乘且大筹在初商为方根
　　在每商即为隅积今用筹并除何必又自乘再乘
　　耶

　　　立方筹右行隅数定位
　　二开　次商三格以上是单位　　四格以下是
　　　　　十位
　　三开　三商三格以上是单位　　四格以下是
　　　　　十位
　　　　　次商三格以上是百位　　四格以下是
　　　　　千位
　　四开　四商三格以上是单位　　四格以下是

　　　　　十位
　　　　　三商三格以上是百位　　四格以下是
　　　　　千位
　　　　　次商三格以上是万位　　四格以下是
　　　　　十万位
　　　　右隅数以末商三格以上是单四格以下是
　　　　十起层累递加
　　法式

二开商式
　　假如积实六千八百五十九
　　　　　　　　两点两开
　　　　　　　　两点根必十
　　　　　　　　点前无馀从单位
　　　　　　　　点俱隔二位(连本位共三位/)

　初商　列立方大筹视第四格之六四虽系近少然
　　点前无馀必从单位除宁可在第一格除一盖第
　　二格虽亦单位然八浮于六不可除实故除一格
　　之一为近少除去一千为初商一(两点根必十此/初商一为方根)
　　(一/十)
　次商　以方根一十自之又三倍自乘之实得三百
　　列三号筹于立方筹左为平廉筹又以方根竟三
　　倍之得三十列三号筹于立方筹右为长廉筹

　　前商馀实五八五九视平廉筹之九格三四二九
　　相近列为平廉约数其九格之隅数八一乘长廉
　　之三十得二千四百三十为长廉约数
　　并两廉约数共五千八百五十九除实尽在第九
　　格为次商九
　　　次商在九格除尽即次商隅数九亦在除内盖
　　　隅在长平两廉相凑之角故次商之隅即同次
　　　商之商数其在大筹之第几格者为隅之边数

　　　而在第几格之自乘者为隅之实数今与大筹
　　　并列同除故隅亦在其中也
　　　三平廉贴于前商方形之正面侧面及或上或
　　　下而后成四方平等之方故次商先以方根自
　　　乘者乘平廉一面之全数也三倍之则所贴方
　　　根三面之平廉全数也但全数与方根等方而
　　　全数之积多于现在之馀积故于此三平廉全
　　　数中视某格与馀实近少而为平廉约数然此

　　　三平廉者与方根阔狭厚薄相等今三面贴凑
　　　止能悉照方根之方而不能凑合成方根外加
　　　廉之方故又有长廉三一纵二横补于平廉不
　　　能合缝之际始得凑合成方法以方根又三倍
　　　之者成三个长廉之全数也再以平廉之隅数
　　　乘长廉则为现在平廉贴身应得之数为长廉
　　　约数并之除馀实而隅亦在所除之中而此四
　　　面之方凑合无缺矣盖平廉以方根为准长廉

　　　以平廉为准而隅数与平廉长廉又互相为准
　　　数藏大筹巧在与大筹并列同除法精密矣
初商次商退位除式
　　假如积实一万九千六百八十三
　
　
　
　

　初商二十　积实两点两开方根必十点前馀一位
　　应从立方筹之十位除实但筹之三格四格俱大
　　于积实应退在第二格之八除八千(筹格退位/)馀
　　一一六八三
　　　此退位不用三四格除实而退至二格者筹数
　　　浮于实数用退位除恰除至点位止故取二格
　　　之八为近少也此初商止退筹格不退商位
　次商七　先以方根二十自之得四百又三倍之得

　　一千二百取一号二号筹列立方筹左为平廉以
　　方根二十竟三倍之得六十取六号筹列立方筹
　　右为长廉　虽九格一万一千五百二十九相近
　　然再加长廉便浮于实故不取九格(凡平廉筹格/与除至点位)
　　(之实位数相当者则万千十百之数亦必相符今/点位前实系一万一千六百八十三平廉九格恰)
　　(五位便是一万一千五百二十九矣盖二开次商/得九以九乘平廉法得廉约数一万○八百加隅)
　　(约数七百二十九共数如前以此推算即得实数/然不如即视位数更为简捷故比点位少一位则)
　　(其数必小多一/位便须置○也)八格之一○五一二虽更相近然

　　若以八格之隅数六十四乘长廉之六十得三千
　　八百四十并平廉八格之一○五一二为一万四
　　千三百五十二亦浮于现在之馀实故又应退格
　　取七格之八千七百四十三单为平廉约数取七
　　格之四九隅数乘长廉之六十得二千九百四十
　　为长廉约数俱系千数可并进而除首位次位之
　　一　一矣于是并两廉约数共一万一千六百八十
　　三单除尽为次商七

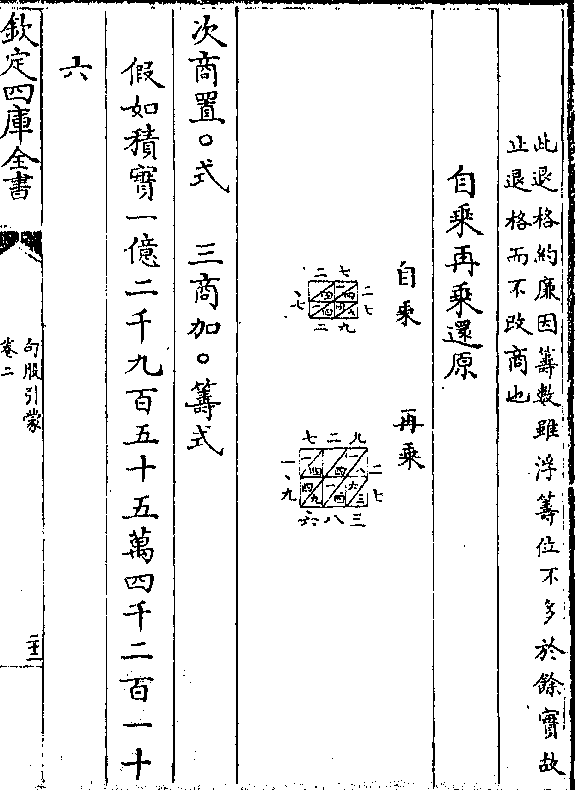
　　　(此退格约廉因筹数虽浮筹位不多于馀实故/止退格而不改商也)
　　　　自乘再乘还原
　
　
　
次商置○式　三商加○筹式
　假如积实一亿二千九百五十五万四千二百一十
　六

　　　　　　　　　三点三开
　　　　　　　　　点前馀二位
　
　
　
　初商点前馀二位视立方大筹百位除实第五格之
　一二五近少除之得初商五百
　次商以方根五百自之得二十五万又三倍之得

　　七十五万为平廉列七号五号筹于立方筹左以
　　方根竟三倍之得一千五百为长廉列一号五号
　　筹于立方筹右若取平廉筹相近莫如第六格之
　　四五二一六相近然次商应除至次点位止今筹
　　位多实位少若依筹位即平廉巳除至点位后何
　　况更有长廉是必变商之大位为小位则有后商
　　点前之实应除而不患除至点位之后故应商数
　　置○为次商○(前二商式是退格并廉此处次商/是退位再商故有置○不置○之)

　　(别/)
　三商　因前平廉筹巳备三廉实数尚未商除而前
　　商之○又无实数可三倍故不去前筹不将前商
　　自之又三倍之止于立方筹左前平廉筹右加○
　　○两筹盖立方每点隔二位今加○○筹则前商
　　变为后商变次商之十为三商之单矣故平廉筹
　　仍照前七十五万而七五列筹之第六格之四百
　　五十万相近又立方大筹六格之二百一十六单

　　共四五○○二十六列为平廉约数
　　再以隅数之三六在三开次商为三千六百者今
　　为三开三商之三十六(见前隅/数定位)以之乘三倍方根
　　之一千五百为五万四千列为长廉约数并之共
　　四百五十五万四千二百一十六除馀实尽为三
　　商六
　　　　右共开方得五百○六
　　　　　自乘再乘还原

　
　
　
　
五开
　　三商列筹不隔○　商数置○式
　　四商隔○筹式　　又商数置○式
　　五商又隔○筹式

　假如积实一万七千三百一十八亿(即万/万)九千○百
　九十一万六千七百二十九
　　　(按他书十万曰亿算学书万万曰亿后同/)
　　　　五开列实如左
　
　　　　　　　　　　五点五开
　　　　　　　　　　五点根必万
　　　　　　　　　　点前无馀从单位

　
　
　
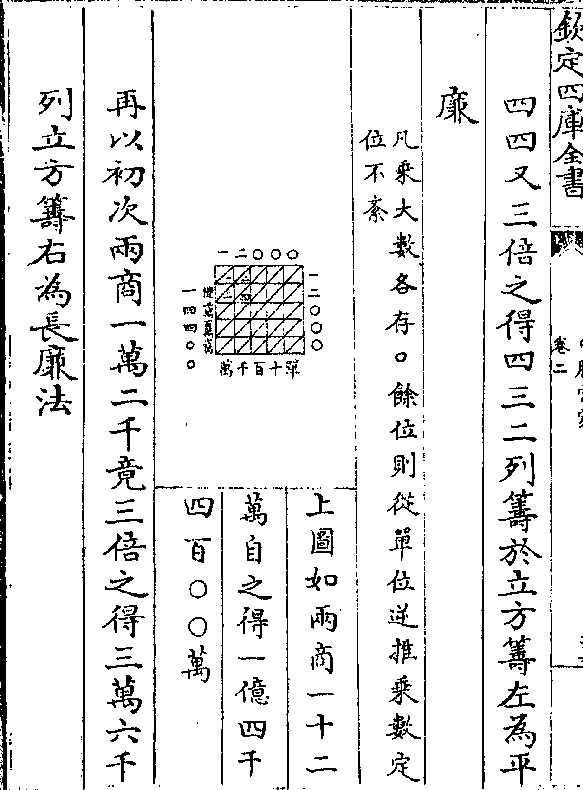
　初商　点前无馀从立方筹单位一格除实一万亿
　　为初商方根一万
　次商　以初商一万自之得一亿又三倍之得三亿
　　列三号筹于立方筹左为平廉
　　以方根一万竟三倍之得三万列三号筹于立方

　　筹右为长廉
　　视第二格之六○八近少为平廉约数
　　以此三号筹二格之隅数四乘长廉之四得一二
　　为长廉约数(按隅数五开次商三格以上是百万/位)
　　　　　并之除七千二百八十亿为次商二千
　三商　以前初商除一万亿次商除七千二百八十
　　亿馀实三八九○九一六七二九
　　去前所列筹以初次两商(共一万二千/)自之得一

　　四四又三倍之得四三二列筹于立方筹左为平
　　廉
　　　(凡乘大数各存○馀位则从单位逆推乘数定/位不紊)
　　　　　　　　　　　　　上图如两商一十二
　　　　　　　　　　　　　万自之得一亿四千
　　　　　　　　　　　　　四百○○万
　　再以初次两商一万二千竟三倍之得三万六千
　　列立方筹右为长廉法

　　如法列两廉约数取近少莫如九格(三八九五二/)
　　(九/)但三商应除至三点位止今筹格六位而第三
　　点前连点位亦止四位法实不符应商除退位不
　　但变大数商为小数商又有后商点前之实可合
　　筹格之多位应本商置○为三商○百
　四商　立方凡前商置○则后商应隔○○两筹以
　　当每点之隔二位列于平方筹左前商平廉四三
　　二号筹之右为平廉再如法列长廉筹取两廉约

　　数并除馀实又莫如九格(三八八○/七二九)但五开四商
　　应除至第四点止今第四点之前止七位而筹格
　　有八故又应置○为四商○十
　五商　依立方法后商应去前商之廉筹另依商法
　　置平长两廉筹约数除实今前三四两商俱未除
　　实俱退商数置有○○今五商仍存前商廉筹及
　　○○筹再加○○筹以当每点之隔二位列于立
　　方筹左廉筹及○○筹之右为五商之平廉仍用

　　九格之三八八八○○○七二九为平廉约数(此/)
　　(约数首位三系十亿位/)
　　再以九格之隅数八十一(五开五商次格以下是/)
　　(十位/)乘长廉之三万六千得二百九十一万六千
　　为长廉约数并之除馀实至五开尾点位止为五
　　商九
　　　　右五商共一万二千○○九
　　　　　(末商平廉/ 长廉)　(三八八八○○○七二九/ 二九一六)

　　　　　　　(并之/)　(三八九○九一六七二九/)
　　　右五开式末商九是单数凡立方积不过至十
　　　位百位止今何以能除至三十八亿九千○百
　　　万各位之多盖三商○四商○虽两商无除而
　　　○无定位列实未除之三八九○万即皆前商
　　　平廉之所应有之数改商而未尝改廉但因筹
　　　数位多实数位少故知三四商之皆应置○而
　　　前商未除之平廉其约数仍在至五商则但以

　　　五商之隅数乘前商原有之长廉以为长廉约
　　　数盖隅因廉为升降而廉依方限不因商为升降
　　　特借五商之九同格并除非单九能除至十亿位也
立方带纵
　方为阔加纵为长法与开方无异先视某格与方根
　近少为商数乘纵数再乘得纵积并入方积以减原
　实为初商
　次商以下更加纵积纵廉积除馀实为次商(馀商/同)并

　两商数得阔因阔以知长
　　　(用点定开位悉依立方/)　(纵积除至点后/)
　　如初商视立方大筹某格近少之格数取为方根
　　依定位列于原实之下又以方根之数因纵数若
　　干即以因得之数再乘方根数得若干为纵积依
　　定位列方根之下并减原实为初商若干
　　　(按方根悉如开方法但未即除实如并纵积多/于原实应退位或改商或退格在方根不可除)
　　　(至点后其并纵积则除至点位之后盖纵在立/方之外积非立方之积不可以每点之位为定)

　　　(也/)
　　如次商列平廉长廉法悉如立方先取平廉约数
　　依定位列馀实之下再取长廉约数列平廉约数
　　之下次以次商之商数(有两廉约数在某/格即某格是商数)因纵数
　　得若干再以商数乘之为次商纵积依定位列两
　　廉约数之下又以纵数倍之为纵廉法乘初商数
　　得若干以乘得之数与次商数乘之得若干为纵
　　廉积依位列于约数之下共并之减原实为次商

　　若干
　　　右𢃄纵方两开者次商之平廉必列至次点位
　　　止如有三开者则加纵积纵廉积除至次点位
　　　之后(与开方/不同)止两开者即并积亦必次点位止
　　　若并积之位浮于馀实应退格改商以除实若
　　　平廉各格多于点前之实或应退格或应置○
　　　同前开方置○法
　　三商以下列廉法悉如前其纵廉法应乘上初商

　　次商再以乘得之数乘末商为纵廉积并除实(四/)
　　(商以下同/)
　如积实九万七千二百○十○尺但云阔不及长三
　尺
　
　
　
　　初商近少在四格即方根四十阔不及长三尺即

　　三为纵法乘初商之四十得一百二十(此纵面/)再
　　以初商四十乘一百二十得纵积四千八百(此纵/)
　　(体/)先以方根积六万四千照位列实下又以纵积
　　四千八百列方根积之千位下并之得六万八千
　　八百减原实为初商四十馀实二万八千四百
　　　不先除方根者恐加纵积多于原实故先并后
　　　除
　　次商以方根四十自乘得一千六百尺又三倍之

　　得四千八百为平廉列大筹左再以方根四十竟
　　三倍之得一百二十为长廉列大筹右取平廉第
　　五格(二四一二五/)为近少为平廉约数以五格之
　　隅数(二五/)乘长廉之一百二十得三千(两开次商/四格以下)
　　(隅数/是十)为长廉约数列于平廉下之千位
　　以纵法三尺乘次商五得一十五再以五乘一十
　　五得七十五为次商纵积照定位列于两廉之下
　　又以纵法之三竟三倍之得六为纵廉法乘次商

　　四十得二百四十再以二百四十乘次商五得一
　　千二百为纵廉积照定位列于纵积之下
　　并之共除馀实二万八千四百尽为次商五
　　　　右共开方四十五尺加长三尺为长四十八
　　　　尺
　如积实二百万○○○○○○尺　但云阔不及长
　三尺
　　　　　　　　　　三点三开　初商是百

　　　　　　　　　　点前无馀
　
　初商一(在大筹单/位除实)以三为纵法乘商数一百得三百
　　(此纵面/)又以商数一百乘三百得三万(此纵体/)合
　　方根积共一百○三万减积实为初商阔之一百
　　　　按此初商除方根并除长三尺之纵但止除
　　　　方根等形之纵未除次商后加纵廉积之纵
　次商依立方法平廉三万长廉三百取近少(三格九/二七以)

　　(相近因𢃄纵有纵积/应加故退格约廉)二格之六○八相近为平廉
　　约数
　　以第二格隅数四(三开次商三格/以上是百位)乘长廉得一十
　　二万为长廉约数
　　以纵法三尺乘次商二十(取平廉长廉约数俱/在二格即是二十)得
　　纵面六十又以商数二十乘纵面六十得纵积一
　　千二百
　　以纵法三尺倍之得六为纵廉(次商方根加廉则/所𢃄之纵亦应加)

　　(廉但次商之纵是小于方根加廉之纵而非短于/方根之纵止纵旁两边有廉而纵顶无廉故法止)
　　(倍/之)乘初商一百得六百即以六百乘次商二十得
　　纵廉积一万二千
　　　并之
　　　　　平廉约数六十○万八千
　　　　　长廉约数一十二万
　　　　　纵积一千二百
　　　　　纵廉积一万二千

　　共七十四万一千二百减馀积仍馀二十二万八
　　千八百○十○单
　　为次商二十
　三商平廉三千二百长廉三百六十依开方法置筹
　　取第五格近少二十一万六千一百二十五为平
　　廉约数
　　以第五格隅数二十五乘长廉三百六十得九千
　　为长廉约数

　　以纵法三尺乘商数五得一十五又以商数五乘
　　一十五得七十五为纵积
　　以纵廉六(纵法三尺/倍之得六)乘初次两商之一百二十得
　　七百二十又以七百二十乘三商五得三千六百
　　为纵廉积
　　依法并之共二十二万八千八百○○除实尽为
　　三商五
　　　右共开方一百二十五尺加纵三尺为一百二

　　　十八尺
　　按立方𢃄纵初商未开之前其所开之方未有定
　　数而纵长三尺则有定数然虽有定数而如三开
　　者其方阔必等于每开立方之边或匾纵或长纵
　　故每商必先依开方法开本身立方之方再以纵
　　之三尺乘商数得纵之面更以商数乘纵之面而
　　得纵之积在初商无廉故止并方根积与纵积除
　　实为初商若干也至于次商则方根有廉而所立

　　之方其形更大于方根今𢃄纵方则其长虽定于
　　三尺而其方之大小应与次商之方相等但立方
　　之廉有三而此𢃄纵方则纵首无廉止应两旁有
　　廉故廉止于二但此两廉亦止如方根之方其合
　　缝之处亦如立方平廉之不能凑合必有一长廉
　　焉于是以纵法乘次商而得𢃄纵长廉之面又以
　　次商商数乘纵面而得𢃄纵长廉之积此所谓纵
　　积也其实乃𢃄纵之长廉积也于是𢃄纵之两平

　　廉以纵法倍之即以乘初商之数为𢃄纵平廉之
　　面以此𢃄纵平廉之面乘次商商数而得𢃄纵平
　　廉之积于是所𢃄之纵其纵则定于三尺而其方
　　之形与次商之方等矣盖其法与开立方同而立
　　方则先有平廉后有长廉今开所𢃄之纵乃先有
　　长廉后有平廉此为异耳至三商与次商同惟纵
　　廉积以纵法乘初商次商之商数而以乘得之数
　　再乘三商之商数盖必连初商次商再乘三商方

　　是三商𢃄纵之平廉其廉比初商次商较薄而其
　　方之形则初商次商后之三商其阔狭与三商有
　　廉之方相等其理一也
　附立方减纵法
　假如立方积五千七百七十六尺　但云长不及阔
　三尺
　　　　　　　　　点前无馀除单格
　

　　初商除一格之单位因二格之八浮于列实故止
　　除一格之一为商数以三尺为纵法乘商数一十
　　(两点根/必十)得三十再以三十乘商数一十得纵积三
　　百以初商方根积一千减去纵积三百馀七百以
　　减原实为初商一十
　　　馀实五千○七十六尺
　　次商依开立方法列平廉长廉筹近少取三号筹
　　(次商以初商自/之又三倍之)之九格三千四百二十九为平廉

　　约数以隅乘长廉得二千四百三十尺为长廉约
　　数合之为五千八百五十九(其数稍浮于实者立/方积也后以纵积等)
　　(减之乃成匾方形故凡减纵之/末商必约数浮于实以待后减)为立方两廉约数
　　次以纵法三尺乘次商九得二十七尺为纵面又
　　以次商九乘纵面之二十七得二百四十三尺为
　　立方减纵之长廉积今名纵积
　　次以纵法三尺倍之得六尺为纵廉以乘初商一
　　十得六十即以六十乘次商九得五百四十尺为

　　立方减纵之两平廉积今名纵廉积
　　合纵积纵廉积共七百八十三尺以减立方之两
　　廉约数馀廉积五千○七十六尺减馀实尽为次
　　商九(此馀廉积即前立方两廉不浮之约数盖既/先于前所稍浮之立方廉约中除纵廉等积)
　　(则所馀者乃方根应有各廉之真数/因本商未除故末后除之而合也)
　　　右共开得阔一十九尺减长不及阔三尺为十
　　　六尺长
　　　　　以上𢃄纵方开法初商方根积必至首点