钦定四库全书

　　同文算指通编卷八

　　明　李之藻　撰

　　带纵诸变开平方第十五

　　开方带纵其变无穷更绎其要有十一种馀可神而明
之若积与二阔较及长阔较求阔用带纵减积开平方
假如三广田积二千四百六十五步第云中广不及南
广八步亦不及北广三十六步又不及正长六十七步

　　问广并长各几何列积为实

　　并不及二广(共四十四)以四而一

　　得一十一为纵方以不及正

　　长(六十七)为减积初商一纪右

　　(即一十)以并带纵共二十一列

　　注首点下为方法以乘减积得一千四百七先以减积
所乘呼商一七除七尾位伍变八　进位陆变五　一
四除四　进位肆变○一一除一首位贰变一　次以

　　所注方法呼商一二除二

　　二上○变八进削一　一

　　一除一　一上五变四馀

　　实八四八乃倍方一作二

　　为廉法(即二十)并减积(六十七)

　　又并带纵(一十一)共九十八为方法注退位续商八纪右
以并方法得一百六呼除一八除八　一上削八　六
八四十八恰尽得中广一十八步各加不及得南广二

十六步北广五十四步正长八十五步

　　右凡梯田斜田箕田杖鼓田四不等田以积求长广
者俱以此法求之

　　凡大小二方和积求径者用减积带纵负隅并纵开平
方

　　假如大小方田二段共积七千五百九十二步大方面
较小方面多二十八步求大小方面各几何用较自乘
(得七百八十四)以减积馀六千八百零八为实倍较(二十八)得五

　　十六为带纵剐置二为负隅初

　　商四(即四十)乘负隅(二)得八十并

　　纵方共一百三十六为方法注

　　积下以呼所商一四除四　一

　　上陆变二　三四一十二　三

　　上捌变六进位二变一　四六二十四　六上○变六
进位六变三馀实一三六八次倍商得八并初方(一百三十
六)共二百一十六为廉法注退位续商六纪右亦乘负

隅得一十二为隅法并入廉法共二百二十八与次商
呼除尽得小方面四十六步加较得大方面七十四步
又假如大小方田三段共积四千七百八十八步大方
面多中方面十八步中方面多小方面十二步求各方
面几何以大方面较小面数(三十)自乘得(九百)以中方面较
小面数(十二)自乘得(一百四十四)相并共一千四十四以减共
积馀三千七百四十四为实并二较倍之得八十四为
纵方以三为负隅初商二纪右(即二十)以乘负隅(三)得六

　　十并纵方共一百四十四为

　　方法列首位以呼所商二四

　　除八　四上肆变六　二四

　　除八　四上㭍变八进位参

　　变二　一二除二　一上削

　　二馀实八百六十四倍方法(六十)作一百二十为廉法以
并纵方(八四)得二百四注退位为方法次商四纪右以乘
负隅(三)得一十二为隅法并方法共二百一十六与次

商呼除二四除八　二上削八　一四除四　一上六
变二　四六二十四恰尽得小方面二十四步以较加
之得中方面三十六步大方面五十四步

　　凡方田圆田径相似以其共积求相似之径几何者用
隅算开平方凡圆者之四可当方者之三并方圆之率
为七用七为隅算用四乘原积开方

　　假如方圆田共积二千二百六十八步只云方面圆径
相等求方面圆径者四乘原积得九千七十二步为实

剐列七为隅算初商三纪右(即三十)乘隅(七)共二百一十为
方法与商相呼二三除六　二上玖变三一三除三
一上○变七进位三变二馀实二七七二乃倍三十作

　　六十为廉法注退位次商六以乘

　　隅(七)得四十二为隅法又以乘廉

　　六十得三百六十并共四百○二

　　仍并入廉法共四六二与商相呼

　　恰尽得方面圆径俱三十六步

　　又法四乘原积得九千○七十二步并方四圜三得
七为法除之得一千二百九十六为实乃以开平方
法求得方面圜径三十六步更简易

　　凡匿其原积只云一长二阔三和四较更以长乘之共
数若干其长阔之较若干以求其长几何者用益积以
补阔则有带纵隅益积开平方

　　假如田不知积但以长乘一长二阔三和四较共得四
万四千九百二十八步其长阔之较二十四步求长者

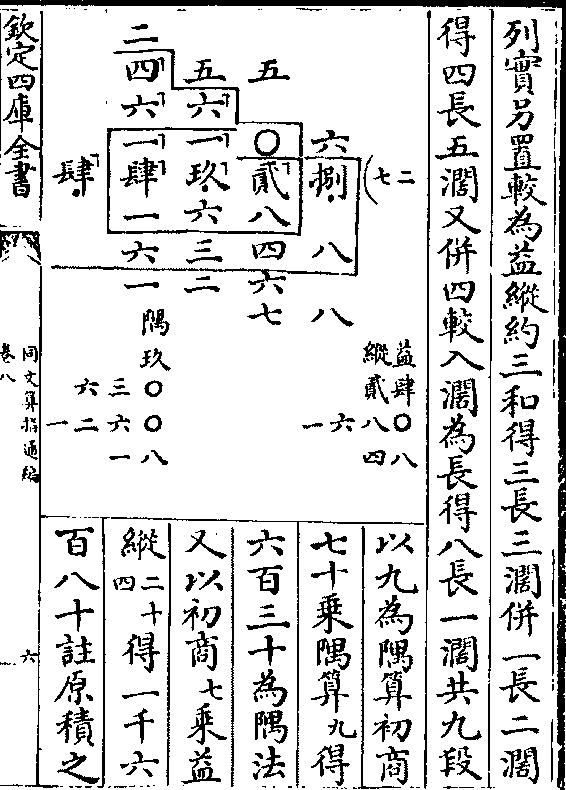列实剐置较为益纵约三和得三长三阔并一长二阔
得四长五阔又并四较入阔为长得八长一阔共九段

　　以九为隅算初商

　　七十乘隅算(九)得

　　六百三十为隅法

　　又以初商(七)乘益

　　纵(二十四)得一千六

　　百八十注原积之

　　下以益原积　八上贰变○进加一六上玖并一变六
进加一　一上肆并一变六共四万六千六百○八却
以隅法(六百三十)注退位与商相呼六七四十二六上六变
四进削四　三七二十一　三上六变五进位四变二
馀实二五○八乃倍隅法(六百三十)得一千二百六十为方
法注退位以商馀实得二纪右又乘隅算(九)得一十八
为隅法另以所商二乘益纵(二十四)得四十八并入馀实
　八上八变六　四上○变五共得二五五六却以方

隅二法并共一千二百七十八皆与所商(二)呼除恰尽
得长七十二步

　　又同前田不知实用长数乘一长二阔三和四较共若
干及其较若干以求长者或损长以就之用带纵负隅
减纵开平方

　　假如一长二阔三和四较以长乘之得四万七千二百
一十二其较二十八步而不知其积求其长列长乘之
积为实较为纵方仍前法推得(九)为负隅初商七十纪

　　右乘负隅得六百三十为

　　方法内减纵法(二十八)剩六

　　百二退位注实下以呼所

　　商六七四十二六上㭍变

　　五进削肆　二七一十四

　　二上壹变七进位贰变

　　○馀实五○七二次倍方法得(一千二百六十)内减纵法(二十八)
得一千二百三十二为廉法列馀实之下约实续商得

四纪右乘负隅得三十六为隅法并廉法共一二六八
改注尾位与续商相呼恰尽得长七十四步

　　又有同前不知积知较而以阔乘其一长二阔三和四
较得若干求长者用减积带纵隅益积开平方

　　假如设为一长二阔三和四较以阔数乘之得二万九
千九百五十二其较二十四问长几何置较自乘(五百七十
六)以减原积馀二万九千三百七十六为实(以较自乘减其原积
故曰减积)较为益纵六为隅算初商七十纪右乘隅(六)得四

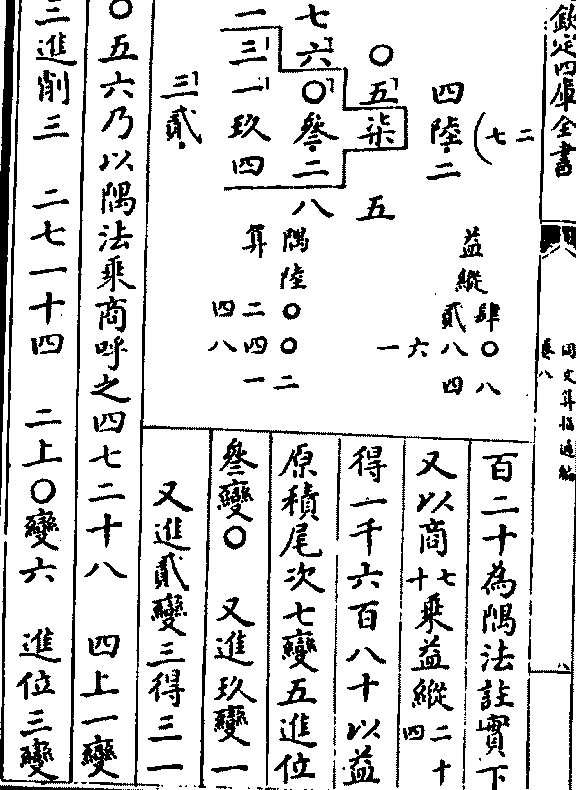　　百二十为隅法注实下

　　又以商(七十)乘益纵(二十四)得一千六百八十以益

　　原积尾次七变五进位

　　参变○　又进玖变一

　　又进贰变三得三一

　　○五六乃以隅法乘商呼之四七二十八　四上一变
三进削三　二七一十四　二上○变六　进位三变

一馀实一六五六乃倍隅法得八百四十为廉法续商
(二)以乘隅(六)得一十二为隅法另以所商(二)乘益纵得
四十八以益馀实尾位陆变四进位五变○进位六变
七共一千七百四却以方隅二法共八百五十二注尾
位以呼续商恰尽得长七十二步

　　亦有匿积只以阔乘一长二阔三和四较共若干及较
若干求长而用带纵负隅减纵益实开平方者

　　假如田不知积一长二阔三和四较以阔乘得二万九

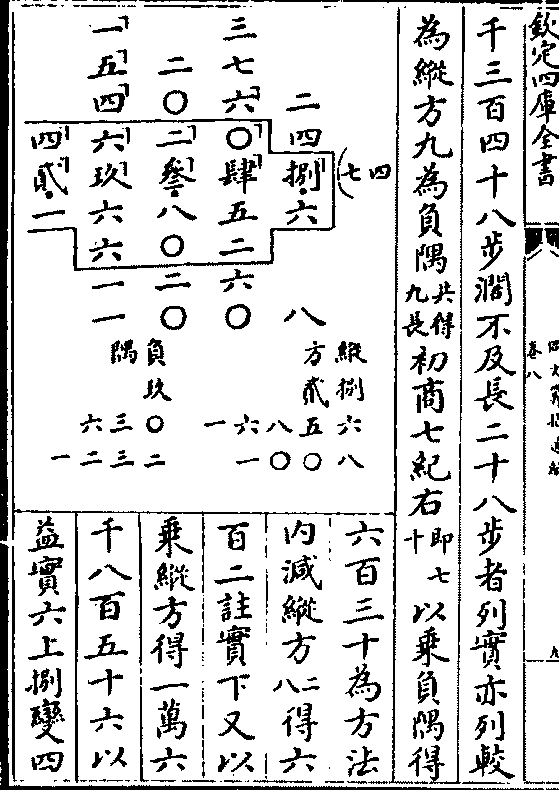千三百四十八步阔不及长二十八步者列实亦列较
为纵方九为负隅(共得九长)初商七纪右(即七十)以乘负隅得

　　六百三十为方法

　　内减纵方(二八)得六

　　百二注实下又以

　　乘纵方得一万六

　　千八百五十六以

　　益实六上捌变四

　　五上肆变○　八上参变二　六上玖变六　一上

　　贰变四乃以所商(七)呼除所注之下法(六百二)二上○变
六进位二变○　六上六变四进削四馀实四○六四
次倍方法(一千二百六十)减纵方得一千二百三十二为廉法
次商四纪右以乘负隅(九)得三十六为隅法以乘纵方
得一千零八为益实并入馀积八上四变二进位六变
七　一上四变五以廉(一千二百三十二)隅(三十六)相并(一千二百六十
八)呼商恰尽得长七十四步

　　右法以阔求长积欠一较故乘较为益实以补其缺

　　亦有同前不知积而以阔乘长阔和较共数及较求阔
者用带纵廉开平方

　　假如直田不云积步只云一长二阔三和四较以阔乘
得二万九千九百五十二步阔不及长二十四步求阔
者置乘积为实减较之半(一十二)为纵廉而以初商乘之
初商四(即四十)纪右为方法以乘纵廉得四十八即与商
相并共五十二注实下照式退位以呼初商(四)五四二

　　十进削贰　二四除八　二上玖变

　　一馀实九一五二次倍所乘纵廉得

　　(九十六)及方法(八)共一百四进位得一

　　千四十为方法再置纵方一十二为

　　廉以相并共一千五十二商实得八

　　纪右亦注尾位为隅以乘纵方得九

　　十六并方廉隅共一千一百四十四注实下以呼次商
恰尽得阔四十八步

　　又有同前匿积和较又以阔乘长阔和较共数求阔用
带纵廉负隅开平方者

　　假如田不知积只云一长二阔三和四较以阔乘之共
二万九千三百四十八其较二十八以求阔者置阔乘
数为实推得共八较九阔用九为负隅以较八乘得二
百二十四为纵廉以初商乘负隅为方法初商四(即四十)
纪右乘隅得三百六十并纵廉共五百八十四注实下
呼商五四除二十进削贰　四八三十二八上参变一

　　进位玖变六　四四一十

　　六　四上肆变八进位一

　　变九　进位六变五馀积

　　五九八八次倍方法得七

　　百二十为廉法并纵廉九

　　百四十四为实续商六纪

　　右以乘负隅(九)得五十四为隅法并廉法纵廉共九百
九十八注实下呼商恰尽得阔四十六步

　　若同前不知积步第置长阔和较以长乘得若干及较
求阔用带纵方廉开平方

　　假如一长二阔三和四较以长乘之得四万四千九百
二十八步较二十四步求其阔若干列实以较为纵方
推得八长一阔共九段倍之得一十八为纵廉以乘初
商而并计之又兼纵方乃以呼商除之初商四纪右(即四
十)为方法乘纵廉(一十八)得七百二十并入方法(四十)共七
百六十又并纵方(二十四)共七百八十四以呼商四七二

　　十八　七上肆变六进位

　　肆变一　四八三十二

　　八上玖变七进位六变三

　　四四一十六　四上贰

　　变六进位七变五馀实一

　　三五六八乃倍四得八为

　　方法倍纵廉得一千五百二十并入纵方(二十四)共一千
五百四十四为廉法以商馀实得八纪右以乘纵廉(一十

八)得一百四十四为隅法乃并方入廉(一千五百四十四)隅(一百
四十四)三法共一千六百九十六注实下呼商恰尽得阔
四十八步

　　又同前不知积及置长阔和较以长乘得若干及较求
阔用带纵廉负隅乘纵减实开平方者

　　假如一长二阔三和四较长乘得四万七千二百一十
二步阔不及长二十八步求阔几何列实推得八长用
八乘较得二百二十四为纵廉推得九段用九为负隅

又以较为减纵方初商四(即四十)纪右以乘负隅得三百
六十为方法并入纵廉共五百八十四为下法乘减纵

　　得一万六千三百五

　　十二为减实注实下

　　变为三○八六○乃

　　以初商四呼下法照

　　常注退位五四得二

　　十进位三变一　四

　　八三十二　八上八变六进位○变七进削一　四四
一十六　四上六变○进位六变五馀实七千五百乃
倍方法得(七百二十)并纵廉(二百二十四)共九百四十四为廉法
约商得六纪右以乘负隅得五十四为隅法即以隅法
乘减纵得一千五百一十二以减实馀五九八八以廉
隅二法相并得(九百九十八)与次商相乘开之恰尽得阔四
十六

　　开立方法第十六

　　凡数自乘平列一面为平方更以原数再乘则四面皆
方中积充实为立方矣凡立方点段俱隔二超三而首
段寻其原数以自乘再乘如适合见数者即为方法开
讫如少于见数则挨身减数寻原而以其再乘所得列
首段下除之以为方法(若再乘之数反浮见数即非其原)馀实三倍其
方为廉剐置而以方法进一十(如系一则作一十系二则作二十之类)与
相乘得数以较馀实约得几何分之几何假如已得二
之一者即以二为次商亦以乘廉法得数若干以并前

所乘数共若干而以次商数总乘之即得三面之廉复
以次商数自乘再乘为隅法并入开尽有不尽者以法
命之

　　依法分为四段先开首位之捌寻原系二乃以
二自乘再乘得八恰尽　抹捌右纪二　次开
参陆伍除点上之伍未用且作(六三)开之乃三倍
其二为六另置于方法之上试加一为(一二)以六
乘之得一百二十六以除原积参陆其数反浮

乃只作○纪格右为(○二)

　　次求第三位更三倍其(○二)为(○六)置于方法(○二)之
上随意加一位且如只加○为　以与(○六)相乘
得一万二千以视原积参陆伍肆贰约得三之
一乃商三纪格右为　以乘(○六)得一百八十并
前(一万二千)共得一万二千一百八十又以三乘之

　　得三万六千五百四十又以三自乘再乘得(二十七)为隅
法并入恰尽　凡隅法皆以尾位挨本位所点之下尚

馀尾段三个○再加一○于格右

　　假如列实一千七百二十八

　　首位一自乘再乘只得一以一为方法纪右
抹壹次倍一为三作廉法另置乃以方法加
○为(○一)以乘廉法三得(○三)约得原积(二十七)内
二之一矣乃改○作二为次商纪格右以乘
廉法三得六并(○三)共得三十六而以次商之
(二)乘之得七十二又以二自乘再乘得八为

隅法并入是为七百二十八开尽

　　假如列实三万二千七百六十八数

　　首位寻原系三以三为方法自乘再乘得(七二)二变
五抹参次倍三作九为廉法加○于方法之右为
(○三)以乘九得二百七十以视馀实(五千七百六十)为二之
一乃商二纪二于三右以二乘九得一十八并前
乘共得二百八十八以二总乘得五百七十六符
三廉之数又以二自乘再乘得八为隅法并入尽

　　若次商以方法进位乘廉法而乘得之数适符馀实或
于馀实相近不足二之一及三之一以上者只以一为
次商之数

　　假如列实九千二百六十一数

　　先开首位玖寻原用二自乘再乘得八即除
八于玖而抹玖变一以二为方法纪右次倍
二得六为廉法另置次以二为(○二)与相乘得
一百二十适近本积只以一为次商数以乘

所置六仍得六并前乘共得一百二十六又
以一自乘再乘为隅依法并入是为一千二
百六十一恰尽

　　广诸乘方法第十七

　　凡积数若干以平面开之适得自乘之数者为开平方
其立方乃开平再乘积也(四面皆方中积满布)三乘方长立方也
(如以二自乘起者得两立方以三自乘起者得三立方之类但以平面一边之数为准)四乘方平
面立方也(如长立方得两方数则进作四立方如长立方得三方数则进作九立方又如长立方系

九方数则进作八十一立方之类仿此以至无穷俱系平面)五乘方大立方也(如系二自
乘起者有四立方则进并十六方为大方如系五自乘起者有二十五立方则进并一百二十五方为大方之
类)自此推之六乘方视三乘形七乘方视四乘形八乘
方视五乘形馀乘仿此可至无穷旧法繁碎且仅止于
五乘此立捷法由平面至诸乘总一机轴先以诸乘原
委布为一图乘母为原乘出之子为开

　　凡开方列位以点分段者

　　平方每二位点作一段再

　　乘方每三位一段三乘方

　　每四位一段仿此推之至

　　九乘方则十位一段矣皆

　　自尾小数起而先以最大

　　数之首段检上图以寻其

　　原即以原数开之假如平

　　方开者检知首段数四十

　　九即知七是原数用七自

　　乘可开若首段数系六十

　　四者即知八是原数用八

　　自乘可开若系六十三者

　　不及六十四尚以七数开

　　之馀积另求再乘三乘以

　　上皆同此法假如再乘首

　　段系二十七检知其原系

　　三即以三开之若是六十

　　三以下亦以三开又假如

　　七乘方首段系二五六原

　　数是二以二开之若原数

　　是六五六不及三数之六

　　五六一仍以二开之也上

　　图系乘出之数已得乘出

　　之数开方之时第以此数

　　注首段下以除为开

　　右法已得首位方法馀实倍方为廉平方者一倍再乘
方者再倍三乘以上皆以本乘之数仿此倍之别立通
率凡平方只一率为(○二)再乘立方有二率为　(○三)三乘
方有三率为四十为六百为四千自此以上诸乘仿此
渐加而皆如后图所推乃以方法之数乘之以乘出之
数较馀实约得几何母之几何而即以其母为廉法

　　此图以首行所列

　　之二为平方三为

　　立方四为三乘至

　　十七则十六乘方

　　也馀乘仿此首行

　　顺列其第二行数

　　悉承首行上格二

　　数积之如(三三)为六

　　(四六)为(○一)之类数穷

　　则挨加一数如第

　　二行第五格为(○一)

　　其第三行第五格

　　亦为(○一)是也

　　右格内数以检各乘合用通率而各视其乘法多寡于本
位叠加虚○凡平方一乘者用一率为二以加○为(○二)以
与方法相乘其立方再乘者用两率为三三而左小数加
一○为(○三)右大数加两○为　而以　乘方法若三乘方
者则用三率为四六四于末位之四加一○为(○四)进位之
六加二○为　首位之四加三○为四千亦以大数乘方

法右图只具四六两位而乘法却宜三位则回用右方之
四以足三率若并位之数相重如四乘方之连用(○○一一)者
回转减其重数竟以首位之五用之末位为五(○○一一)五照
前依位增○其数则为五十为一千为一万为五万而以
五万乘方法也至六乘方八乘方以上皆然

　　一乘开平方

　　假如列实六百七十六万五千二百○一以平方开之
初商得二为方法以求廉法立(○二)为通率列
中位亦列方法于左位以相乘得(○四)以较馀
实(七二)约得六之一乃立六为廉法列于右位
以自乘得(六三)为隅法附列乃以廉数(六)乘四
十得二百四十以并自乘之三十六共二
百七十六尽第二段馀实五二○一另置通

　　率并廉入方为(六二)置左位以乘(○二)得数五
百二十以较馀实得一又以一为廉法置
右位自乘仍得一为隅法并入恰尽

　　若已得廉法而以乘通率反浮馀实或廉法相合而隅法
又浮馀实者皆减其廉法以乘之假如列实二百八十九
初商一除实一百馀实一百八十九次商以方法乘通率
只系(○二)以较馀积可用九除实一百八十而乘出隅法八
十一则浮原积又试用八除实一百六十而乘出隅法六

十四亦浮原积惟再减用七为廉法乘得
一十四以除馀积尚馀四十九而以廉法
自乘得四十九为馀法并入恰尽凡诸乘
所用廉法有浮原积者皆照递减求之

　　再乘开立方

　　假如列实二十三万八千三百二十八以立方开之寻原
以六为母以六自乘再乘得二一六除积　六上捌变
二一上参变二　进抹贰以六为方法以求廉法凡立

方皆用二数为通率为三十为三百自下而上叠位而
以方法(六)对(○三)以方法自乘得(六三)对□各列于左

　　初乘乃以(六三)乘□得一万八百以

　　视馀积约得二之一乃立二为廉

　　法以对□复以廉法(二)自乘得(四)

　　以对□各列于右又以(二)乘(四)得

　　(八)为隅法附列于下乃以廉二乘

　　一万八百得二万一千六百

　　再乘以六对(○三)乘之得一百八十

　　又以四乘得七百二十以上二次

　　乘出数并之得二万二千三百二

　　十加入隅法之八恰尽

　　凡方法之乘皆在通率位左以方法数对尾位其乘
数自下而上凡廉法之乘皆在通率位右以廉法
数对首位其乘数自上而下四乘五乘以上皆仿此

　　右再乘方法若以还原则以二十六自乘再乘

　　若初商方法只系一数者通率无乘须并诸率位除之
一而净即以一为廉法假如列实一千三百三十一以
再乘立方开之初商以一为方法除净首
位(一千)次并中位两通率一除可净以一为
廉法对通率三百次以自乘仍得一对次
通率三十又以再乘亦得一为隅法系其
下而以隅法之一并入三千三百恰尽

　　右式可例其馀凡以一为方法者不论几乘方皆以

诸位通率并求

　　三乘方

　　假如列实一千四百七十七万六千三百三十六以三乘
方开之寻原以六为母自乘再乘得一二九六除积　六
上㭍变一　九上㭍变捌　二上肆变一　一上削壹次
以六为初商方法以求廉法凡三乘皆叠用通率三位为

　　四十为六百为四千先列通率于中位

　　乃列方法于左尾位自乘(六三)再乘二一

　　六自下而上对列初乘以二百一十六
乘四千得数八十六万四千较原积约
二之一以二为廉法列右首位自乘(四)
再乘八三乘(六一)联列乃以(二)乘八十六
万四千得数一百七十二万八千
再乘以(六三)乘□得数二万一千六百又
以右(四)乘之得数八万六千四百
三乘以(六)乘(○四)得数二百四十以右八

乘之得数一千九百二十乃合三乘数
积之并入隅法(六一)共得一百八十一万
六千三百三十六恰尽

　　右三乘方法若以还原则以六十二之数自乘再乘三
乘　　一法以开平方法所得数更以平方开之

　　四乘方

　　假如列实九亿一千六百一十三万二千八百三十二
数以四乘方开之寻原六为初商除积七亿七千七百

六十万馀实一亿三千八百五十三万二千八百三十
二以求廉法凡四乘方通率叠用四位为五十为一千
为一万为五万中列自下而上而以方法(六)对尾位(○五)
列之又自乘再乘三乘四乘亦自下而上对列于左

　　初乘首位左乘得六千四百八十万

　　以较馀实约得二之一以二为廉法

　　对首位五万列之亦自乘再乘三乘

　　自上而下对列又四乘得(二三)为隅法

　　系于其下而以首位二数乘左乘所

　　得之数计得一亿二千九百六十万

　　次乘次位左乘得二百一十六万而

　　以右(四)乘之得八百六十四万

　　三乘第三位左乘得三万六千而以

　　右(八)乘之得二十八万八千

　　四乘尾位左乘得三百而以右(六一)乘

　　之得四千八百以上四乘之积并入

　　右廉四乘所得隅法三十二恰尽

　　右四乘方若以还原则以六十二数自乘再乘以至四乘

　　五乘方

　　假如列实五百六十八亿○○二十三万五千五百八十

　　四数以五乘方开之寻原六为

　　初商除积四百六十六亿五千

　　六百万馀积一百一亿四千四

　　百二十三万五千五百八十四

　　数以求廉法凡五乘方皆叠用

　　通率五位为六十为一千五百

　　为二万为一十五万为六十万

　　中列自下而上而以方法六对

　　尾位(○六)列之又自乘再乘三乘

　　四乘自下而上皆列于左位

　　初乘首位左乘得四十六亿六

　　千五百六十万以较馀实约得

　　二之一以二为廉法对首位六

　　十万列之亦自乘再乘三乘四

　　乘自上而下对列于右又(五)乘

　　得(四六)为隅法系下而以首位(二)

　　数乘左乘所得之数共得九十

　　三亿三千一百二十万

　　次乘次位左乘得数一亿九千

　　四百四十万而以右(四)乘之得

　　七亿七千七百六十万

　　三乘三位左乘得四百三十二

　　万而以右(八)乘之得三千四百

　　五十六万

　　四乘四位左乘得五万四千而

　　以右(六一)乘之得八十六万四千

　　五乘五位左乘得三百六十以

　　右(二三)乘之得一万一千五百二

　　十并上五乘积又并右廉所乘

　　隅法六十四恰尽

　　右五乘方若以还原则以六十二之数自乘再乘以
至五乘

　　六乘方

　　假如列实三万五千二百一十六亿一千四百六十万
六千二百○八以六乘方开之寻原六为初商除实二
万七千九百九十三亿六千万馀实七千二百二十二

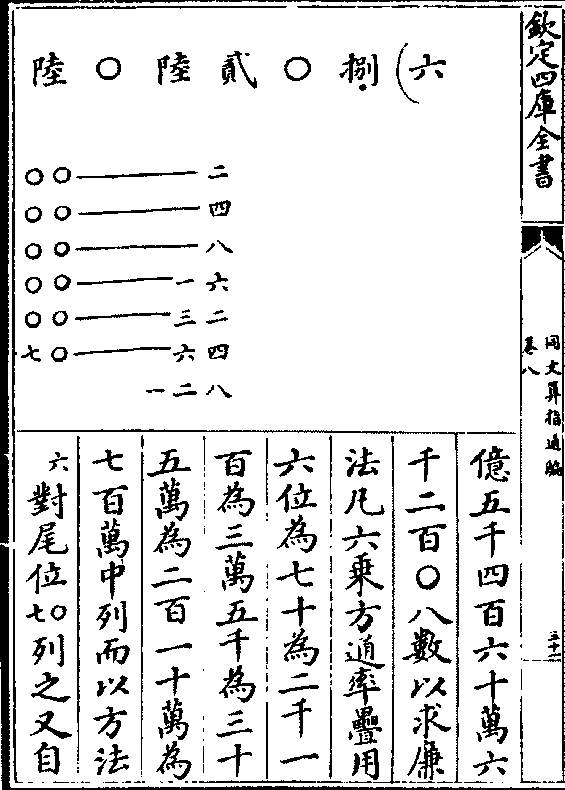　　亿五千四百六十万六

　　千二百○八数以求廉

　　法凡六乘方通率叠用

　　六位为七十为二千一

　　百为三万五千为三十

　　五万为二百一十万为

　　七百万中列而以方法

　　(六)对尾位(○七)列之又自

　　乘再乘三乘四乘五乘

　　自下而上皆列其左

　　初乘首位左位得数三

　　千二百六十五亿九千

　　二百万以较馀积约得

　　二之一以二为廉法对

　　首位七百万列之亦自

　　乘再乘三乘四乘五乘

　　对列于右又以六乘得

　　一二八为隅法系下而

　　以首位(二)数乘左乘所

　　得之数共得六千五百

　　三十一亿八千四百万

　　次乘次位左乘得一百

　　六十三亿二千九百六十

　　万以右(四)乘之得六百五

　　十三亿一千八百四十万

　　三乘三位左乘得四亿五

　　千三百六十万以右(八)乘

　　之得三十六亿二千八百

　　八十万

　　四乘四位左乘得七百五

　　十六万以右(六一)乘之得一

　　亿二千○九十六万

　　五乘五位左乘得七万五

　　千六百以右(二三)乘之得二

　　百四十一万九千二百

　　六乘六位左乘得四百二

　　十以右(四六)乘之得二十六

　　万八千八百并上六乘之

　　积又并隅法一百二十八

　　恰尽

　　右六乘方若以还原则以六十二之数自乘再乘以
至六乘

　　七乘方

　　假如列实四兆五千九百四十九万七千二百九十八
亿六千三百五十七万二千一百六十一数以七乘方
开之首位四其原一以一为方法馀实三兆五千九百
四十九万七千二百九十八亿共求一廉法因方法一
数无乘当并下位以较馀实而惟首次两数同位为大

　　数其馀小数不足为多寡

　　且从省只并首次两位开

　　之(若不相并者以首率八千万较馀实试用四为

　　廉法乘之似可除然次率八乘即浮原数矣试减用

　　三亦浮原数见后注)此二数并得一

　　亿○八百万以较馀实约

　　可用三数然缘次乘之六

　　以乘中列之第二位其数

　　反浮(初以三乘中首位固可除至次乘六以乘

　　次位得一亿六千八百万并初乘共四亿有奇反浮

　　馀实)当减用二为廉法自乘

　　再乘至七乘依式列右凡

　　乘数多于原数者减法仿

　　此

　　初乘以廉二乘八千万得

　　一亿六千万

　　再乘以廉再乘数(四)乘二

　　千八百万得一亿一千二

　　百万

　　三乘以廉三乘数(八)乘五

　　百六十万得四千四百八

　　十万

　　四乘以廉四乘数(六一)乘七

　　十万得一千一百二十万

　　五乘以廉五乘数(二三)乘五

　　万六千得一百七十九万

　　二千

　　六乘以廉六乘数(四六)乘二

　　千八百得一十七万九千

　　二百

　　七乘以廉七乘数　乘八

　　十得一万○三百六十八

　　右并前七乘之积共得三亿二千九百九十八万一
千四百四十并入隅法二百五十六以除馀积尚剩
二千九百五十一万五千六百二亿六千三百五十
七万二千一百六十一数再商自首至尾共以一段
开之

　　乃并廉法入方法共一十二为三商之数以对尾位(○八)列
于左以自乘再乘三乘四乘五乘六乘悉自下而上对列

　　一　　　　　　　　　　初乘首位左乘得二千八

　　百六十六万五千四百四

　　十六亿四千万以较馀积

　　只可一乃以一为廉法乘

　　无可乘故自乘至七乘皆

　　只一照式列右其对中末

　　位之下仍系一为隅法

　　再乘次位左乘得八十三

　　万六千○七十五亿五千

　　二百万

　　三乘三位左乘得一万三

　　千九百三十四亿五千九

　　百二十万

　　四乘四位左乘得一百四

　　十五亿一千五百二十万

　　五乘五位左乘得九千六

　　百七十六万八千

　　六乘六位左乘得四十万

　　三千二百

　　七乘尾位左乘得九百六

　　十并七乘之积增入隅法

　　之一恰尽

　　右七乘开方若欲还原则以一百二十一数自乘再乘
以至七乘

　　以上开方则例共七乘衍至十乘百乘亦复如是妙在

寻原变在通率熟玩自得难以备述

　　若夫寻原之法固与还原不同还原者依本乘之数以
还实积耳寻原者用前列乘图以寻下手方法凡寻原
惟平方最易以每段只二位也次则立方亦易以每段
只三位也三乘则四位为一段寻原难矣自是而上位
置愈多寻原愈难矣然而即平方可求立方之原兼平
方立方可以求多乘之原若三乘方者以平方法开之
得数又以平方法开之得数即原矣若五乘方者先以

平方开之得数乃以立方开之或先以立方开之得数
乃以平方开之即原矣若六乘方者作四乘方开二次
即得其原若七乘方者作开平方三次即得其原若八
乘方者作立方二次即得其原若九乘方者先以平方
开一次又以四乘方开之或先以四乘方开一次又以
平方开之即得其原若十乘方者作四乘开方三次亦
得其原错综变化总由自然进退开阖具有定法孰谓
开方诸乘迂远难冀者乎神而明之从积正负带减加

翻巧由心造妙以熟生智者于斯盖不啻思过半也
奇零诸乘开方法第十八

　　凡开方诸法不惟全数可开即奇零之数亦各有法大
都皆以寻原为第一义有母数子数俱有原数可用者
如平方九之四则以三之二为原以三自乘得九以二
自乘得四也如再乘立方(七二)之八亦以三之二为原以
三自乘得九再乘得(七二)以二自乘得四再乘得八也又
如三乘方(一八)之(六)以三之二为原谓三再乘得(七二)三乘

得(一八)谓二再乘得八三乘得(六一)也如五乘方者　之(四六)
以三之二为原谓三数以五乘则得　二数以五乘则
得(四六)也有二数并列于母不同而亦有原数可用者如
四之二与九之八并列依对乘法两母乘得三十六两
子乘得一十六是为(六三)之(六一)其平方之原为九之四以
四九三十六与夫四四一十六用四为钮数者也有以
全数带奇数而亦有原可寻者如有全数二又(七二)之(○一)
依化法乃为(七二)之(四六)寻其立方之原为三之四以三再

乘为(七二)四再乘为(四六)归其整数即一零三之一也凡有
原可寻则可开无原可寻则不可开必命分之母与得
分之子各有原则可开若一有原一无原则不可开寻
原之术数之多者约之以至于寡如(五四)之(○二)必约之为
九之四其开平方之原即三之二也如(一八)之(四二)必约之
为(七二)之八其立方之原亦三之二也他如九之六者九
有原六无原不可开矣又如(○二)之(一二)者命分数与得分
数俱无原不可开矣然则终不可开乎又非也数穷则

变变则通虽无原有数之最相近者可借之以为原吾
以本数析之又析而相近之原可得也析之之法多取
进位平方或析一为十为百立方或析一为百为千数
弥多者求弥密其原亦弥近也弥近之数或稍多干所
求或稍约于所求然而皆可以为原者也

　　假如以五数为开平方是为无原而任借(○一)为　之原
以自乘得一百以五乘得　虽(○一)不为　之原乃其原
之最近者有两数其一为　以(二二)为原(二十二自乘得四百八十四)

此近而朒者其一为　以(三二)为原(二十三自乘得五百二十九)此近
而盈者何也试以所借(○一)为命分之母以(二二)为得分之
子以(○一)之(二二)自乘(此　整二零　之二)得　之　内除四百为四
整数而(四八)为　之(四八)夫四零　之(四八)以视二零(○一)之二
犹五百与(二二)之比例也试以所借(○一)为母以(三二)为子以
(○一)之(三二)自乘(此系整二零二之三)得　之　内除五百为五整数
而(九二)为　之(九二)夫五零　之(九二)以视二零(三二)犹五百与
(三二)之比例也故(○一)可以为五借也

　　假如以九数为开立方亦为无原而任借(○一)为　之原
(以自乘再乘故)以九乘得　虽九千不以一十为原而其近原
者亦有两数一为　以(○二)为原(自乘再乘)此近而朒者一为
九二六一以(一二)为原(自乘再乘)此近而盈者则何也试以(○一)
为母(○一)之(○二)系整二数以自乘再乘即得(○一)之八试以
(○一)为母(○一)之(一二)系整二数零(○一)之一以自乘再乘即得
九零　之　也(母一十自乘得一百再乘得一千子整二化二十并入一仍二十一自乘得四
百四十一再乘得九千二百六十一以九千归元得整九馀为一千之二六一)故(○一)可以为九

借也

　　假如列实(○四)以四乘方开之为无原任借一数为(○一)以
自乘至四乘得一十万以(○一)乘之得四百万用前法推
衍其原之近者有两数其一为(○二)其一为(一二)何也以(○一)
为(○二)之母此(○一)之(○二)系整二数以二自乘再乘三乘四
乘为(○一)之(二三)以视(○四)其近而朒者以(○一)为(一二)之母此(○一)
之(一二)系整二数零(○一)之一以二零(○一)之一自乘再乘(化整
数并子法如前母四乘得一十万子自乘再乘得九千二百六十一)三乘四乘得整四十

数零一十万之八万四千二百○一(二十一以三乘得一十九万四千四
百八十一以四乘得四百○八万四千二百○一内以四百万还元得整四十数其零为八四二○一)以
视四十其近而盈者故(○一)可以为(○四)借也以上三论姑
借(○一)见例若进至百千万数其数弥多其析愈精则原
愈近矣

　　同文算指通编卷八