钦定四库全书

　　同文算指通编卷四

　　明　李之藻　撰

　　叠借互徵第七(附盈朒)

　　借虚徵实其术精矣又有子母杂互隐奥难知者则两
借虚数以徵之徵之于实尚远也或两浮而盈或两缩
而不足或一盈一不足俱以借数列上以较原数以多
寡之差列下而左右互乘焉其法有二凡俱盈俱不足

者以差数相减馀为法以乘数相减馀为实若一盈一
不足者以差数相并为实而以法除实则二法相同
旧有盈朒一章大都类此而此则于未有盈朒之先
借数推出盈朒以求隐数故曰借徵其显有盈不足
实数者但依旧法求之诸盈不足者两盈者两不足
者盈适足者不足适足者及叠互母子者各具数条
见例

　　问设一虚数以其半为用内除三之一又除四之一

尚馀三百其原总数几何其法先另借一通数以
分其半而通各分先借二十四为数列左上(其半为十
二其三之一为四其四之一为三尚馀五)以比三百则不足二百九十
五列左下另借九十六为数列右上(其半为四十八其三之一
为十六其四之一为十二尚馀二十)以比三百不足二百八十列右下
次以左上乘右下又以右上乘左下各得数附注其
下以少减多其馀为实而以左下右下相减其馀为法
除之

　　除得一千四百四十合原总以减半为七百二十其
三之一乃二百四十其四之一乃一百八十加三百
合一半七百二十之数

　　假如借四千八百为通数列左上(其半为二千四百其三之一为八百其四

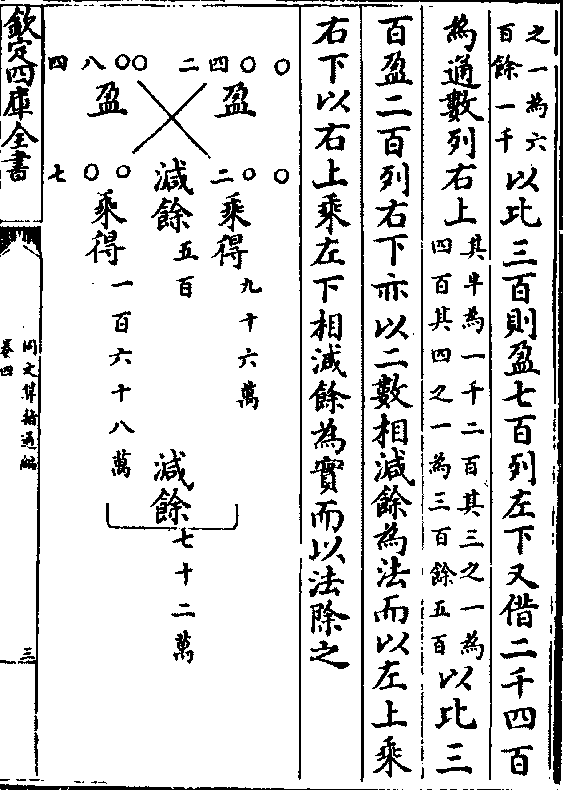之一为六百馀一千)以比三百则盈七百列左下又借二千四百
为通数列右上(其半为一千二百其三之一为四百其四之一为三百馀五百)以比三
百盈二百列右下亦以二数相减馀为法而以左上乘
右下以右上乘左下相减馀为实而以法除之

　　以法除实亦得一千四百四十合原总数

　　又假如借二千四百为通数列左上(即前第二式右上者尚馀五百)盈
二百列左下再借九十六列右上(即前第一右上者馀二十)不足二
百八十列右下此系一盈一不足者相并为法次以左上乘右
下以右上乘左下亦相并为实以法除实仍得一千四百四十

　　问三人共银四十四两乙多甲一倍外又多四两丙兼
甲乙之数外又多六两每人实数几何(此大约当以四分分之而算)
先借一十为通数列左上(甲一十乙倍得二十又加四共二十四丙兼二数又加六
得四十)共七十四以比四十四盈三十列左下又借六列
右上(甲六乙倍之加四得十六丙兼二数加六得二十八)共五十以比四十四盈
六列右下以相减馀为法乃以左上乘右下以右上乘
左下亦以相减馀为实以法除之得五为所求之甲数
倍之又加四得一十四为乙数兼之又加六得二十五

　　右图以甲之左数一十乘六及以右数六乘三十
者固除得甲五若以乙之二十四乘六及一十六
乘三十亦得乙数以丙之四十乘六及二十八乘

　　三十者亦得丙数以

　　共数七十四乘六及

　　五十乘三十者亦得

　　共数

　　问甲乙各不知数取乙九与甲则甲倍于乙取甲九与乙
则甲乙正等原数各若干借一百为等数乙既得甲九则
甲原一百九列左上而乙九十一列其次甲若取乙九则甲
一百十八而乙八十二以视甲之半盈二十三(因甲取乙九当倍乙数故)列

左下另借五十为等数乙既得甲九则甲原五十九列右上
而乙四十一列其次甲又取乙九则甲得六十八而乙三十
三以视甲之半不足二列右下盈不足相并二十五为法
左上乘右下右上乘左下相并为实以法除实系甲乘
者除得六十三为甲数系乙乘者除得四十五为乙数

　　问携酒游山到处沽增一倍俱饮六升至第四处饮讫
无馀原携若干借五升四合列左上倍之(一斗八合)减六(四升
八合)又倍之(九升六合)减六(三升六合)三次倍之(七升二合)减六(一升二合)四
次倍之(二升四合)以减六不足三升六合列左次另借六升
二合列右上倍之(一斗二升四合)减六(六升四合)又倍减至四次(倍得
一斗二升八合减存六升八合复倍得一斗三升六合减存七升六合又倍得一斗五升二合减存九升二合)
盈九升二合列右次盈不足相并为法以左上乘右下
右上乘左下并为实以法除实得五升六合二勺五抄

　　问贷榖不知数每年加息一倍一年还榖五斗至五年
本利俱完其原贷若干先借四十三石列左上倍之(八十
六)减所还(馀三十六)又倍之(七十二)又减(馀二十二)仍倍之(四十四)不
足六石列左下又借四十四石列右上倍之(八十八)减所
还(馀三十八)又倍之(七十六)又减(馀二十六)仍倍之(五十二)盈二石列

右下并盈不足为法左上乘石下右上乘左下得数并
为实以法除实得原榖四十三石七斗五升

　　或依三率置五十为实置

　　三年之倍(一二四)并得七乘

　　之加母(一)为法除之亦同

　　问逐兔百只每三人得四只该几人先借七十二人列左
上以四乘三除(九十六)盈四只列下另借九十人列右上
以四乘三除(一百二十)不足二十列下盈不足并为法左上乘

右下右上乘左下得数并为实以法除实得七十五人

　　此问依三率三

　　乘四除即得

　　借此见例云

　　问甲乙丙共数六十乙多甲一倍外加四丙兼甲乙数
外加六各该几何先借六为甲通乙丙数列左上(甲六乙十
六丙二十八)共得五十比正数不足一十列左下又借八为
甲通乙丙数列右上(甲八乙二十丙三十四)共六十二比正数盈

二列右下相并为法次以左上乘右下以右上乘左下
亦相并为实依法除得七零三之二为甲数倍之加四
得十九零三之一为乙数兼甲乙加六得三十三为丙
数总合六十数




　　问试以三十数随手剖为二以其一加六十以其一加

二十而加六十者为加二十者之三之二其剖分之数
各几何此取三十而随意剖之且借二十为甲数列左
上列乙一十于次而各如问加焉察其数(甲二十加六十得八十乙
一十加二十得三十)甲视乙固不足三之二(乙三十则甲之三分二者该九十今却八
十)以不足一十列左下又借二十四为甲数列右上亦
列乙六于其次各加如问而察其数(甲二十四加六十得八十四乙六外
加二十得二十六)甲又盈乙三之二(乙二十六则甲之三分二者该七十八今却八十四)
以盈六列右下盈不足积并为法次以左上乘右下以

右上乘左下并为实以法除实得二十二又二之一为
甲数然后求三之一则七零二之一为乙数也



　　问甲乙丙三数甲加七十三得为乙丙数者二乙加七
十三得为甲丙数者三丙加七十三得为甲乙数者四
其实数各几何此因有三之二及四之三当借奇数为

通数以求甲数而又因乙丙之加牵连难析则叠用前
法以徵之且如借一乃奇数也以当甲列左上(左图)加七
十三(共七十四)当兼乙丙而倍之(既以七十四为兼乙丙且倍之则乙丙当仅得其半
共得三十七)因以折半三十七为乙丙数而乙与丙又衰分
焉(乙加七十三又得甲丙三之二因寻乙所衰于丙者)依前法随意衰之为两如
借二为乙衰另列于左上(右图)则丙系三十五矣列左次
乃以二加七十三(得七十五)以较甲丙合数未足三之二(甲一
丙三十五共三十六则其三之二乃该一百零八今乙衰二加七十三只有七十五)尚缩三十三

列左下又借五当乙(三十七中之五)列右上则丙系三十二
矣列右次乃以五加七十三(得七十八)以较甲丙有三之
二否不足二十一(甲一丙三十二共三十三则其三之二该九十九今乙衰五加七十
三只七十八)列右下两不足相减馀为法而以左上乘右
下以右上乘左下相减馀为实法除实得一十零四
之一为乙实乃列乙实于左图初借立一之次既已
得乙实即得丙实(乙丙共三十七也乙得一十零四之一则丙得二十六零四之三)列
于又次

　　又另借三为甲衰列右上加七十三(共七十六)以其半为
乙丙衰(得三十八)而随意分之为两另作一法如前焉
如以二为乙衰列左上其馀三十六乃丙衰列左
次即以乙衰之二加其七十三(得七十五)与甲丙相较是三

之二否不足四

　　十二(甲三丙三十六共三)

　　(十九其三分之二乃一百十七)

　　(也今乙衰加之只七十五)即

　　以不足列左下

　　另借二十三为乙衰列右上其半十五为丙衰列右次
以乙衰二十三加七十三(得九十六)与甲丙相较是三之二
否又盈四十二(甲三丙十五共十八其三分之二当是五十四今乙衰之数与加数却有九十

六)以盈列右下盈与不足相并为法仍以左上乘右下
以右上乘左下而相并为实以法除实得一十二零二
分之一为乙实乃列乙实于前所借甲三之次因得丙
实(乙丙共三十八乙既得一十二又二分之一则丙得二十五零二分之一)亦列于又次俱照前式

　　乃依所问察之甲加七十三要兼乙丙数又多一倍乙加
七十三要得甲丙数者三丙加七十三要得甲乙数者四





　　如右图左上甲衰及所加(共七十四)已兼乙丙之数与其倍

数(乙丙共三十七兼而倍之则七十四也)左次乙衰所加(共八十三又四之一)亦兼
甲丙数之三(甲丙共二十七又四之三以加二倍合乙衰)俱合原问惟左又
次丙衰及所加(共九十九零四之三)以合甲乙(共十一零四之一)如原问但
欲得甲乙数者四只须四十五今却九十九零四之三乃
盈五十四零四之三到此不合矣仍依互乘之法求之
右上甲衰及所加(共七十六)亦合乙丙兼数与倍数(乙丙共三十八
兼倍之则七十六也)右次乙衰及所加(共八十五半)合甲丙亦具三因
(甲丙共二十八半三因之得八十五半)惟右又次之丙衰及所加(共九十八零半)

以合甲乙(共十五又二之一)以四因之当得六十二今却九十
八零二之一乃盈三十二零二之一也不合原问仍依
互乘之法求之　于是以左上甲衰乘右下以右上甲
衰乘左下相减馀为实以左下右下相减馀为法除之
得七为甲衰如欲得乙衰则以乙之左右上下互乘相
减以法除之得一十七为乙衰如欲得丙衰亦以丙之
左右上下互乘减除得二十三为丙衰

　　问设有一数以与三相乘外加一十又以此乘四外加

二十又乘五外加三十又乘六外加四十即共得六千
七百此其原设数几何其法先借二为主列左上以乘
三(得六)外加十(共十六)又与四相乘(六十四)加二十(共八十四)又与
五相乘(四百二十)加三十(共四百五十)又与六相乘(二千七百)加四十
(共二千七百四十)以此所问数(六千七百)不足三千九百六十列左
下次借三列右上以乘三(九)外加十(共十九)又乘四(七十六)
外加二十(共九十六)又乘五(四百八十)外加三十(五百一十)又乘六(三千
六十)外加四十(共三千一百)以比所问数(六千七百)不足三千六百

列右下两不足相减馀为法除之得一十三系原设





　　右法已除得十三者与三相乘(三十九)加一十(四十九)又与
四相乘(一百九十六)加二十(共二百一十六)以乘五(一千八十)加三十(共一

千一百一十)以乘六(六千六百六十)加四十实得六千七百合问

　　问二人共分银一百两不得其均若均分则每人当五十
两然须甲还所得银三之一乙又还所得银五之一方得
每人五十两其不均之分各得若干先借三十两为甲衰
列左上亦列乙衰七十于次乃减甲三之一(减一十存二十)亦减
乙五之一(一十四)而以乙减归甲(甲二十加乙十四共三十四)以比五十
不足一十六列左下另借六十为甲衰列右上亦列乙衰
四十于其次乃减甲三之一(减二十存四十)亦减乙五之一(八)而

以乙减归甲(甲四十加乙八共四十八)不足二列右下两不足相减
馀为法以左上乘右下以右上乘左下相减馀为实以
法除实得六十四两零七分两之二为甲衰就一百两
内减甲衰馀三十五两又七分两之五为乙衰合原分

　　不均

　　之数

　　问二人共分银一百两未得其均须甲损所得三之一

乙亦捐所得四之一和合平分乃各得五十两其未均
之数各若干先借六十为甲衰列左上亦列乙四十于
左次乃减甲三之一(减二十存四十)减乙四之一(减一十存三十)和所
减(甲二十乙一十共三十)而均分之(各得十五)以甲所得十五合减存
四十之数(甲原存四十加十五得五十五)以比五十盈五数列左下另
借二十四为甲衰列右上亦列乙衰七十六于右次乃
减甲三之一(减八存一十六)减乙四之一(减一十九)和所减(甲八乙一十九
共二十七)而均分之(各得十三零二之一)以甲所得一十三半之数合

减存一十六数(共二十九半)以比五十不足二十半列右下
盈不足相并为法右上乘左下左上乘右下相并为实
以法除实得五十二两零十七分两之一十六为甲衰

　　其馀四十七

　　两又十七分

　　两之一为乙衰

　　问以一千剖为二甲多于乙四十九作何剖之其法借六
百为甲衰列左上亦列乙四百于次相较差二百以比四

十九则盈一百五十一列左下另借五百五十为甲衰列
右上亦列乙四百五十于次相较差一百以比四十九则
盈五十一列右下两盈相减馀为法以左上乘右下右上
乘左下相减馀为实以法除实得五百二十四零二分两

　　之一为

　　甲衰馀

　　为乙衰

　　问香垆二座其盖重一百五十斤以盖加甲垆则多于
乙二倍以盖加乙垆则与甲垆正等此二垆各重若干
其法借三十为甲衰列左上盖一百五十列左次共一百
八十又列其次以三之一为乙衰得六十以乙加盖(得二
百一十)比甲衰三十盈一百八十列左下另借九十为甲
衰列右上盖一百五十列左次共二百四十又列其次
取其三之一为乙衰得八十以乙加盖(二百三十)比甲衰九
十盈一百四十列右下两盈相减馀为法左右上下互

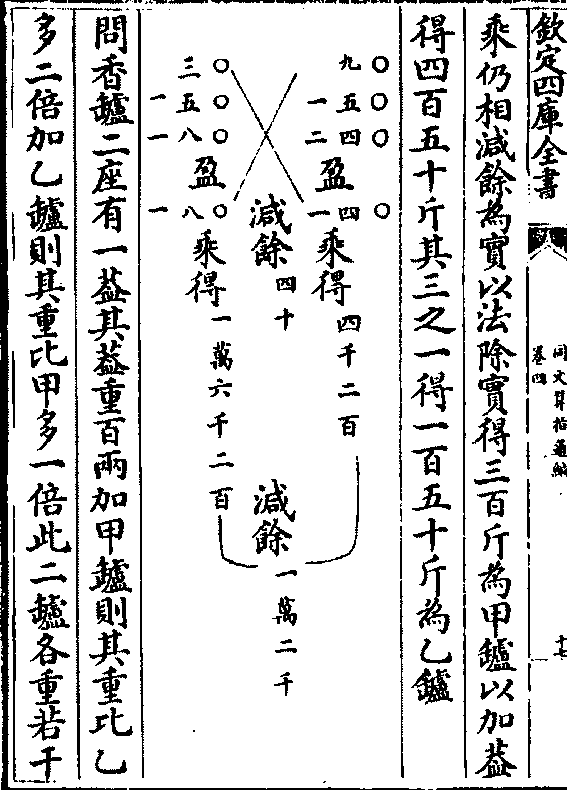乘仍相减馀为实以法除实得三百斤为甲垆以加盖
得四百五十斤其三之一得一百五十斤为乙垆




　　问香垆二座有一盖其盖重百两加甲垆则其重比乙
多二倍加乙垆则其重比甲多一倍此二垆各重若干

其法借五十为甲衰列左上盖数一百列左次共一百
五十又列其次而以其三之一五十为一衰(因甲加盖多乙二倍
故)加盖(得一百五十)比甲衰(五十)盈五十列左下(既倍甲五十只该一百今
却一百五十故盈五十)另借一百一十为甲衰列右上盖数一百
列右次共二百一十又列其次而以其三之一为乙衰
(七十)加盖(一百七十)比甲衰(一百一十)不足五十列右下(倍甲一百一十即该
二百二十今却一百七十故不足五十)盈不足相积为法左右互乘积为
实以法除实得八十两为甲垆其加盖三分之一得六

　　问有人买鹌鹑不知其数但云以其二之一加三之一
又加四之一再加二十二共得一百此是几何其法借
一通数可以二三四分之者为主先借十二列左上而
以二之一(六)三之一(四)四之一(三)并之得十三再加二

十二共得三十五以比一百不足六十五列所不足于
左下另借六十列右上而以二一(三十)三一(二十)四一(十五)并
之得六十五加二十二共得八十七以比一百不足一
十三列所不足于右下两不足相减为法左右互乘相
减为实以法除实得七十二为所问之数以其二之一

　　(三十六)三之一(二十四)

　　四之一(一十八)再加

　　二十二共一百只

　　问二商各携毋银未知其数但云取乙十二两与甲则
乙有甲六之一取甲十五两与乙则甲有乙十之一其实
数若干法从乙起算先借二十两为乙衰列左上内减
十二(馀八)以当甲六之一用六因求甲(六八四十八)内还乙所
加(十二)存数三十六又捐十五与乙(甲剩二十一其乙原馀八又取甲十二共
二十今又加得三十五)以甲剩数较乙加数甲是乙十之一否(甲二
十一则乙当二百一十今乙只三十五)不足一百七十五列左下另借一
百为乙衰列右上内减十二(得八十八)以六因求甲衰(五百二十

八)亦还所加(十二)存数五百一十六内除十五与乙(甲剩五百
一乙原馀八十八又取甲十二　共一百今加十五该一百一十五)以乙较甲甲是乙十之
一否(甲五百一则乙当五千一十今乙只一百一十五)不足四千八百九十五
列右下两不足相减为法左右上下互乘相减馀为实
以法除实得十七两零五十九之二为乙毋内捐十二
两与甲则实得五两又五十九之二以六因求甲得三
十两零五十九之十二内亦减十二实得十八两零五
十九之十二再捐十五两与乙加乙原数十七两又五

十九之二共得三十二两零五十九之二以十之一约





　　问二人所各携银不知其数但云减乙六两与甲则甲
多乙一倍减甲三两与乙则与乙正等各实数几何从
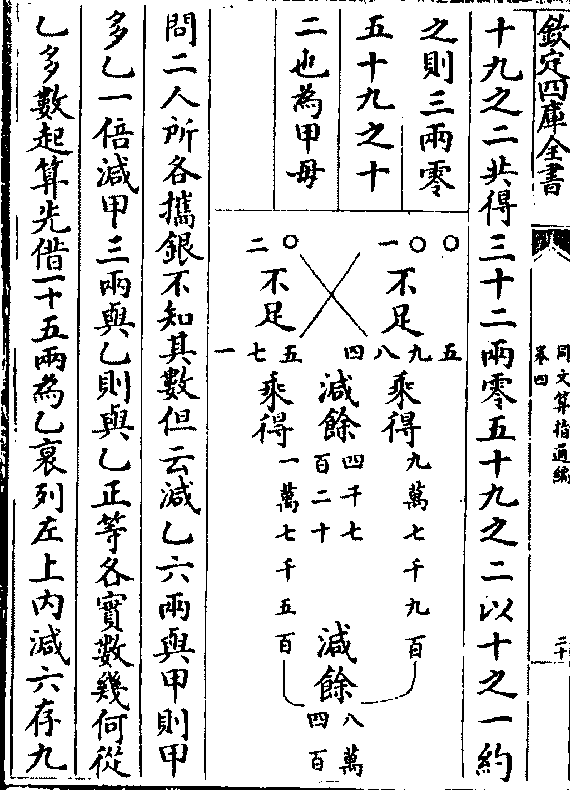
乙多数起算先借一十五两为乙衰列左上内减六存九

以当甲之半则甲该一十八内又除所加六得十二为
甲衰正数内减三与乙则甲剩者九以甲所剩九较乙
衰十五及所加之三乃盈九(甲九乙十八也)列所盈于左下另
借二十为乙衰列右上内减六存十四倍之为甲衰当
是二十八亦减所加六实得二十二为甲衰正数若取
三与乙则甲剩十九以甲之十九较乙之二十及所加
之三又盈四(甲十九乙二十三)列盈数于右下两盈相减为法
左右上下互乘相减馀为实以法除实得二十四为乙

衰内减六与甲馀倍之得三十六甲先借六与乙则甲
之本数只三十矣就三十之内减其三两并入乙二十
四两为二十七甲三十减三亦二十七故其数正等



　　问漏壶一座注水其中下有三孔其甲孔流水二时而
尽乙孔流水三时而尽丙孔流水六时方尽若三孔俱

开则几时水尽且借四时为用列左上而各据其孔之
大小流水之迟速测之(甲二时一壶则四时当尽二壶乙三时尽乙壶则四时当尽一
壶零三之一丙六时尽一壶则四时当尽三分壶之二)得数并计之共以四时尽
四壶而所问者一壶也为盈三列左下另借十时为用
列右上亦以时推其多寡(甲二时一壶则十时该五壶乙三时一壶则十时该三壶
零三之一丙六时一壶则十时该一壶零三之二)得数并计共以十时尽十壶
比原问一壶又盈九列右下两盈相减剩六为法上下
左右互乘相减亦得六为实以法除实得一是二孔俱

　　开则壶

　　水一时

　　泄尽也

　　问漏壶一具上有渴乌注水凡十二时而满下有窍通天池
泄水凡十八时而水尽若上注水下泄水当几时水可满且
借二十为满候列上以推注泄之时已知下泄十八时尽一
壶则二十时当尽一壶零九分壶之一而其上注二十时必
能满至二壶九之一方与此合乃且注且泄只有一壶三之

二不足九分壶之四列左下另借三十时为满候列右上而
各推其时已知下泄十八时尽一壶则三十时当尽一壶零三之
二而其上注三十时必须满至二壶三之二方与此合而又不
然只满二壶半亦不足六分壶之一列右下两不足相减馀
为法乃以右上乘左下以左上乘右下减馀为实以法除之

　　问甲匠做工三十日完加乙匠则十八日完若独用乙
匠须几日完先要知甲匠十八日所做之工乃三十日
内五分之三则知乙匠十八日之工乃其五分之二也
试借四十日为乙衰列左上以十八日完五之二推之
则四十日完九分工之八不足九之一列左下别借六
十日为乙衰列右上亦以十八日五之二推之则六十
日完全工外又溢九之三列右下两盈不足相并得九
之四为法次以左上乘右下右上乘左下相并得九之

一百八十为实以法除实得四十五日完工



　　右乙匠十八日完五分工之二所少五之三者算该
二十七日完以二十七加一十八是四十五也

　　问甲乙丙三人共博甲赢乙金二之一乙赢丙金三之
一丙又赢甲金四之一事毕各剩金七百两三人原携

母金若干法已知三人原共金二千一百两(三个七百)三分
之当于甲衰七百内与丙四之一又得乙二之一于乙
衰当加入丙三之一又与甲二之一于丙衰当得甲四
之一又与乙三之一乃先借一百两为甲衰列左上内
除四之一(二十五)该存七十五而总有七百两是所赢于
乙者为六百二十五两而乙衰当为一千二百五十两
矣列左次内输去二之一则所剩当亦为六百二十五
两又赢丙三之一而为七百两则亦得丙七十五两而丙

所携母为二百二十五两矣又列其次内输与乙三之
一尚存一百五十加入得甲四之一(二十五)共得一百
七十五两以较原问不足五百二十五列左下别借
二百为甲衰列右上内除四之一(五十)剩一百五十而
总有七百以乙二之一足之则知乙衰二之一该五
百五十两而乙总数为一千一百两矣列右次内输
与甲二之一当剩五百五十两又以丙三之一足之
而为七百两则亦得丙一百五十两而丙所携母为

四百五十两矣又列其次内输与乙三之一尚存三
百两加所得甲四之一(五十)仅得三百五十两比原问
不足三百五十列右下两不足相减剩为法左右上
下互乘相减剩为实以法除实得四百为甲母推
知乙母八百(以甲四百减四之一存三百加入乙二之一该增四百是知乙母八百)
丙母九百(以乙八百减二之一存四百加入丙三之一该增三百是知丙母九百也甲母四百
赢四百输一百乙母八百输四百赢三百丙母九百输三百赢一百俱剩七百而三人所携与所赢所输
皆得矣)

　　问甲乙丙三商共贩得子银四百两依母银分之乙比
甲多分十二两丙比乙多分十六两要知各分若干先
借一两为甲衰列左上推得乙该十三两丙该二十九

两共四十三两以视四百不足三百五十七两以次列
左下别借二两为甲衰列右上推得乙该十四两丙该
三十两共四十六两以视四百不足三百五十四两以
次列右下两不足相减剩为法左右上下互乘得数减

　　剩为实以法除实得

　　一百二十为甲衰以

　　推乙衰一百三十二丙

　　衰一百四十八合问

　　问调兵征倭内有南北西三处兵马南兵四万北兵为南
兵及西兵二分之一西兵为南兵北兵三分之一要知北
兵与西兵各若干并南兵共若干先借三万为北衰列左
上推得南西二兵共该六万而西兵仅该二万列左次若
为南北三之一则南北共只六万而实七万是盈一万也
列左下又借二万四千为北衰列右上推得南西二兵共
该四万八千而西兵仅该八千列右次若为南北三之一
则南北共只二万四千而实六万四千又盈四万也列右

下以盈相减剩数为法上下左右互乘得数亦相减剩为
实以法除实得三万二千为北衰推知西兵二万四千总

　　共九万六

　　千而北得

　　南西二之

　　一西得南

　　北三之一

　　问黄金百斤制垆一座既成虑匠人盗金和银销毁验
之恐伤工本欲知和银若干法以器贮水令满已知水
几斤乃以金垆百斤入器内溢水六十五斤加水令满
别以纯金百斤入之溢水六十斤另贮满水以银百斤
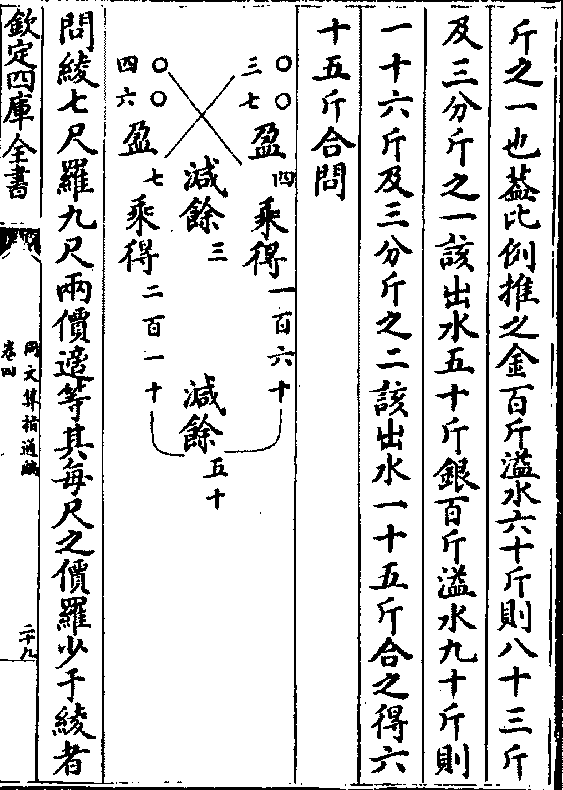
入之溢水九十斤今借银四十斤为匠所换数列左上
存金六十斤列左次其垆溢水六十五斤若以纯金只
溢六十斤推之实在垆内之金六十斤只该出水三十
六斤又以纯银溢水九十斤推之所和之银四十斤亦

该出水三十六斤共该溢七十二斤今视原数(六十五斤)盈
七斤列左下又借银三十斤为匠所换数列右上存金
七十斤列右次以纯金溢水六十斤推之则垆金七十
斤该出水四十二斤又以纯银溢水九十斤推之则和
银三十斤该出水二十七斤共该溢六十九斤今视原
数(六十五斤)又盈四斤列右下两盈相减剩为法左右上下
互乘得数减剩为实以法除实得一十六斤零三分斤
之二为匠人盗和银数其实在纯金乃八十三斤三分

斤之一也盖比例推之金百斤溢水六十斤则八十三斤
及三分斤之一该出水五十斤银百斤溢水九十斤则
一十六斤及三分斤之二该出水一十五斤合之得六
十五斤合问



　　问绫七尺罗九尺两价适等其每尺之价罗少于绫者

其较三十六文此绫罗各价若干是为匿价衰分法先
借七十二文为绫价列左上则罗价当三十六文列左
次各以尺数乘之(绫七尺得五百○四文罗九尺得三百二十四文)罗视绫不
足一百八十文不相等也又列其下别借一百文为绫
价列右上则罗价当六十四文列右次各以尺数乘之
(绫七尺得七百文罗九尺得五百七十六文)罗视绫不足一百二十四文亦
不相等也又列其下以两不足相减馀为法乃以左上
乘右下右上乘左下得数亦相减馀为绫实以法除之

得绫每尺价一百六十二文再以左次乘右下右次乘左下
各得数相减馀为罗实以法除得罗每尺价一百二十六
文又各以尺数乘之绫七尺共一千一百三十四文罗九尺亦一

　　千一百

　　三十四

　　文正等

　　问金九锭银十一锭其重适等互换一锭则金轻十
三两金银每锭重若干此因互换一锭而金轻十三
两因知金银之轻为六两五钱也乃先借一十三两
为金衰列右上则银该六两五钱列右次各以锭乘
(金九锭得一百一十七两银一十一锭得七十一两五钱)金视银盈四十五两五
钱列下另借二十四两为金衰列左上则银该一十
七两五钱列左次各以锭乘(金九锭得二百一十六两银十一锭得一百九
十二两五钱)金视银盈二十三两五钱又列其下两盈相减馀为法

　　而以左上乘右下右上乘左下得数相减馀为金实左
次乘右下右次乘左下得数相减馀为银实俱以法除
得金一锭重三十五两七钱五分银一锭重二十九两

二钱五分而各以锭乘金九锭共三百二十一两七钱
五分银十一锭亦三百二十一两七钱五分正等

　　问牛羊共一百牵总价一百六十八两每牛三头银十
二两羊四羫一两五钱欲知牛羊各数各价若干此于大总
内又立小总法先以三归十二得牛一头价四两以四归一两
五钱得羊一羫价三钱七分五釐而化两及钱分皆为釐算
之先借六十为牛衰列左上则羊该四十列左次而以各
价乘之(牛六十头乘四千釐得二十四万羊四羫乘三百七十五釐得一万五千并共得二百五十五两)以视

共价盈八十七两列左下又借三十为牛衰列右上则羊该
七十列右次而以各价乘之(牛得一十二万釐羊得二万六千二百五十釐并共得一百四十六
两二钱五分)以视共价不足二十一两七钱五分列右下并盈不

　　足为

　　法依

　　式互

　　乘

　　乃以左右上数互乘下并为牛实左右次数互乘下并为
羊实以法除得牛三十六羊六十四以各价乘得
总

　　问鸡兔同笼不言其数但云九十六头三百零八足
其鸡兔各几何法以九十六头为主先借到鸡四十
八只列右上兔亦四十八只列右次而以各足乘之
(鸡二足乘四十八得九十六足兔四足乘四十八得一百九十二足)并二百八十八足
以较三百○八足不足二十列右下又借作鸡六十

只列左上则兔该三十六只列左次而以各足乘之
(鸡二足乘六十得一百二十兔四足乘三十六得一百四十四)并二百六十四足
以较三百○八足不足四十四列左下两不足相
减馀二十四为法又以左上乘右下右上乘左下各
得数相减馀为鸡实以法除之得鸡三十八只
其左次右次亦如法乘减馀为兔实以法除得兔
五十八只各以两足四足乘之合三百○八足之
数

　　又法置九十六头倍之得一百九十二以减总足馀
一百一十六足以二归之得五十八为兔数却以四
足乘之得二百三十二又以减总足馀七十六以二

归之得三十八为鸡数盖以两物皆借作两足起算者
以上原二十二条补七条与旧法盈朒略似然本
无盈朒而借立一数以求盈朒乃以盈朒推之者
与前借衰互徵之法俱极超妙虽至隐至奥之数
用此推求未有不涣然冰释者学人熟此二法于
算义思过半矣其旧法盈朒章人所恒习亦附数
条于后相比拟

　　旧法未知借推之妙只立盈与不足或两盈两不

足为母两母相减为法以母子互乘之数求其物
实以两子或并或减之数求其人实大抵一盈一
不足者相并为实两盈两不足者减馀为实俱如
前法耳又有叠数盈朒(如几人分几许盈几数几人分几许不足几数之类)
列作上中下三位所求人实亦取下层盈不足并
减同前而取两上相乘以为通法更乘人实然后
乃以上中互乘减馀为法除之又以上中乘出之
数互乘下层仍前并减以为物实以法除之与人实同

　　问醵金买物每人出五两盈六两每人出三两不足四
两人数物价各若干左列五之六右列三之四互乘并
之为物实另并两子(六四)为人实两母相减馀二为法除
人实得人数五除物实得物价一十九两或先得人数
以乘出率五内减盈六及以乘三外加不足四皆同

　　右法若依借衰者且借立一数与五相乘内减六得若
干又与三相乘外加四得若干如相同即所求之数若
不同者则依盈朒推之假如借四人列左上以乘五减
盈六得一十四亦以乘三加不足之四得一十六两数
相较不足二列左下又借七人列右上以乘五减盈六
得二十九亦以乘三加不足之四得二十相较盈四列
右下以并左下共六为法左右上下互乘并得三十为
实以法除实得五人以乘出率五内减盈六得一十九

两若以乘三加不足亦同

　　(此并子数为法并乘数为实以求人数与

　　前两母减馀为法而除人实物实及以乘

　　出为物实而以母较除之者法稍异耳)

　　问众人分榖每人五石盈三十石每人六石不足四十
石其人榖各若干以五之三十列左六之四十列右互
乘并之为榖实并两子(三十四十)为人实两母(五六)相减馀一
为法除人实得人数七十除榖实得三百八十石或先

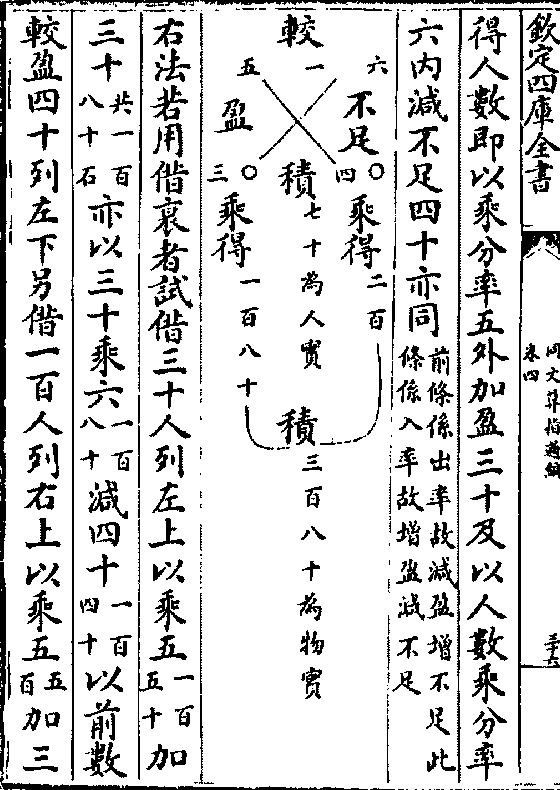得人数即以乘分率五外加盈三十及以人数乘分率
六内减不足四十亦同(前条系出率故减盈增不足此条系入率故增盈减不足)



　　右法若用借衰者试借三十人列左上以乘五(一百五十)加
三十(共一百八十石)亦以三十乘六(一百八十)减四十(一百四十)以前数
较盈四十列左下另借一百人列右上以乘五(五百)加三

十(五百三十)即以一百乘六(六百)减四十(五百六十)亦以前数较不
足三十列右下盈不足相并为法左右上下互乘并之
为实以法除实得七十为人数乃以人数乘五(得三百五十)
外加盈三十为三百八十石又以人数乘六(四百二十)内减

　　不足四十

　　亦三百八

　　十石

　　问以绢一匹作帐先摺成六幅比旧帐长六寸后摺成

七幅比旧帐短四寸新绢旧帐幅各长若干此先以幅
数乘盈不足数求之置六幅列左上以乘盈六寸得三
尺六寸列左下置七幅列右上以乘不足四寸得二尺
八寸列右下左右上下互乘并之为绢实另并盈不足
(三尺六寸二尺八寸)为旧帐幅实而以七幅六幅相减馀一为法

　　除之得绢长四

　　丈二尺旧帐幅

　　长六尺四寸

　　问直田一段欲截一半另佃第云截长六步不足七步
截长八步盈九步所截步及原阔步各若干列六之七
及八之九互乘并之为截积之实并子数为原阔之实
而以两母相较馀二为法除之得原阔之步八得截积
之步五十五

　　问每人出银三两五钱盈六两每人出银三两三钱盈
二两八钱人数物价各若干此以两出率左右列及以
两盈各置出率之下互乘得数相减馀为物实以两盈
相减馀为人实又以出率相减馀二为法除物实得价

　　五十两除

　　人实得一

　　十六人

　　问每人出银五两不足四两每人出五两四钱不足二

两人数物价各若干列两出率及两不足互乘得数亦
相减馀为物实以两不足相减馀为人实又以两出率
相减馀四为法除人实得五人除物实得价二十九两



　　问井不知深将绳摺作三股入井汲水馀绳四尺次将
绳摺作四股入井绳馀一尺井深绳长各若干置三股

四股为母各以所盈数乘之(以三乘四尺得一十二尺以四乘一尺得四尺)左
右列位互乘得数相减馀为绳实以前所乘出两盈数
相减馀为井深之实乃以二母相减馀一为法除绳实
得绳长三丈六尺除井实得井深八尺



　　问每人出银二两五钱盈六两每人出二两三钱适足

人数物价各若干置出率各以盈适足系之除适足无
乘只以左盈乘右出率为物实以盈数为人实仍以两
出率相减馀二为法除物实得物价六十九两除人实
得三十人或不乘盈数径求人数而以所得之人数乘
适足之出率者亦得物价同前

　　问每人出银七两不足一十四两每人出九两适足人
数物价各若干仍前列位以右九乘左不足为物实以
不足为人实两出率减馀二为法除人实得七人除物
实得价六十三两或不以乘法求物实径求人数而以
人数乘适足之出率亦得物价同前

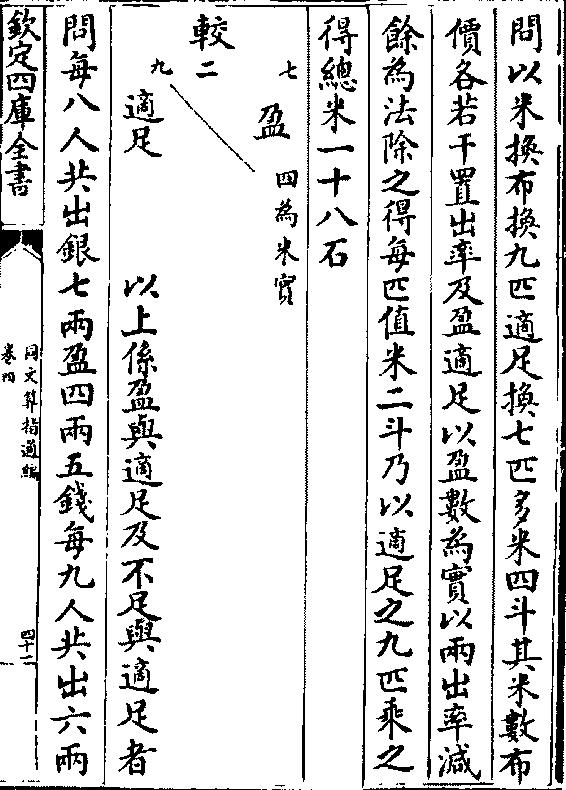　　问以米换布换九匹适足换七匹多米四斗其米数布
价各若干置出率及盈适足以盈数为实以两出率减
馀为法除之得每匹值米二斗乃以适足之九匹乘之
得总米一十八石



　　问每八人共出银七两盈四两五钱每九人共出六两

不足三两人数物价各若干此叠数盈朒也布位三层
先立通数以乘人率法取左上右上相乘为之(七十二)乃
以上中二位左右互乘得数(左六十三右四十八)相减以其馀数
(一十五)为后除人实物实之法而各以乘得之数与下位
左右互乘(左二百一十六右一百八十九)并之(四百零五)为物实以法除得
价二十七两仍并盈不足数为人实之率(七十五)而以前
求通法(七十二)乘之得数(五百四十)为人实亦以法除得三十
六人此法与前数条大略相同但物实则以上中乘出

之数乘其下位盈朒之数而人实则增二上相乘通数
以与再乘其所除人实物实之法则前条直以出率减
馀为之此以上中互乘得数相减馀数为之此其小异
耳

　　上　　中　　　　下

　　问每六人共出银九两盈三两每四人共出银七两盈
六两人数物价各若干法以左上右上乘得数为通法
(二十四)次以上中互乘(左得三十六右得四十二)相减馀(六)为除人实
物实之法(六)又以互乘所得之数与下两盈数互乘(左得
二百一十六右得一百二十六)相减馀为物实(九十两)以法除得价一十
五两以两盈相减馀(三)为人实之率而以通法(二十四)乘
之得人实(七十二)以法除得一十二人　　　其叠数两
不足仿此

　　上　　中　　　　下



　　问每三人共出银五两多一十两每五人共出银九两
适足人数物价各若干法以左上右上相乘得数为通
法(一十五)次以左上乘右中(二十七)右上乘左中(二十五)相减
馀(二)为除人实物实之法次以右中得数乘左下盈(得二

百七十两)为物实以法除得价一百三十五两就以左下盈
(一十)为人实率而以通法(一十五)乘之为人实(一百五十)以法除
得七十五人

　　上　　中　　　　下　　其叠数不足适足仿此



　　问银未知数以买物用三分之二盈三两用五分之三

不足一两银数物价各若干法取子母互乘以通盈朒
之数如子数二互乘母五得一十以通朒一两得一十
两列左子数三互乘母三得九以通盈三两得二十七两
列右乃以左中乘右下(二百七十)右下乘左下(九十)并之(三百六十)
而以两子相乘(六)为法除之(得六十)为银实而以左上右
上减馀(一)为法除之仍得总银六十两次并盈朒二数
(三十七)为物实而以法除得价三十七两

　　上　　　　　中　　下

　　问银未知数取六分之四买物盈二两取四分之三买
物盈三两五钱银数物价各若干以子数四互乘母四
得一十六以通盈三两五钱得五十六两列左以子数
三互乘母六得一十八以通盈二得三十六列右乃以
左中乘右下(五百七十六)以右中乘左下(一千零八)减馀(四百三十二)

亦以两子相乘(一十二)为法除之(得三十六)为银实以左中右
中减馀(二)为法除之得总银一十八两别以两盈相减
馀(二十)为物价之实仍以法除得物价一十两

　　上　　　中　下



　　问𣲖纳官银不言其数但知有甲乙二等户乙户所办

当甲户十之八先令甲等八户乙等五户纳之不足五
两后令甲等六户乙等八户纳之不足三两其𣲖银数
及各户则例若干法以甲乙二衰乘户数各并之列位
(甲衰一十以乘八得八十乙衰八以乘五得四十并得一百二十户列左又以甲衰十乘六得六十以乙衰八
乘八得六十四并得一百二十四户列右)以两不足数系之互乘相减馀为
银实(二百六十两)乃以上相减馀为法(四)得官𣲖银六十五
两别以两不足数相减馀(二两)为则例之实以法除之得
五钱而以各衰乘之甲衰一十乘得五两为甲等一户

办数乙衰八乘得四两为乙等一户办数




　　问钱未知数以买物取二分之一盈四文取七分之三
适足钱数物价各若干先取母子互乘一乘七得七列
右三乘二得六列左而以六互乘盈四得二十四列右

下即以为物价之实两母减馀为法(一)除得物价二十
四文又以适足之母(七)乘盈数(二十四)得数为钱实(一百六十八)
而以原子一三相乘得数为法(三)除之得钱五十六文



　　问粜麦不知数但云取三分之一粜银八两适足若取
八分之三粜银十两不足二石总麦石数若干每银一

两粜麦若干法取两子母互乘得数各通粜银(以母三互子三
得九通八两得七十二以母八互子一得八通十一两得八十)另以所通得数七十二
列左八十列右乃以适足银(八)乘不足之麦(二)得数(一十
六石)列右下如不足适足例而取适足所通出之银率(七十
二)以乘不足所乘出之麦率(一十六)得数(一千一百五十二)又以
两子相乘(三)为法除之以为麦实左中右中相减馀八
为法除得总麦四十八石另以不足乘出(一十六)为银实
亦以法除(八)得麦二石价银实一两

　　同文算指通编卷四