钦定四库全书
　张邱建算经卷上　　　周　甄　鸾　注经
　　　　　　　　　　　唐　李淳风　注释
　　　　　　　　　　　　　刘孝孙　撰细草
以九乘二十一五分之三　　问得几何
　　　　答曰一百九十四五分之二
　　草曰置二十一以分母五乘之内子三得一百八
　　然以九乘之得九百七十二却以分母五而一得

　　合所问
以二十一七分之三乘三十七九分之五　问得几何
　　　　答曰八百四二十一分之十六
　　草曰置二十一以分母七乘之内子三得一百五
　　十又置三十七以分母九乘之内子五得三百三
　　十八二位相乘得五万七百为实以二分母七九
　　相乘得六十三而一得八百四馀六十三分之四
　　十八各以三约之得二十一分之一十六合前问

以三十七三分之二乘四十九五分之三七分之四
问得几何
　　　　答曰一千八百八十九一百五分之八十三
　　草曰置三十七以分母三乘之内子二得一百一
　　十三又置四十九于下别置五分于下右之三在
　　左又于五分之下别置七分三分之下置四维乘
　　之以右上五乘下左四得二十以右下七乘左上
　　三得二十一并之得四十一以分母相乘得三十

　　五以三十五除四十一得一馀六以一加上四十
　　九得五十又以分母三十五乘之内子六得一千
　　七百五十六以乘上位一百一十三得一十九万
　　八千四百二十八为实又以分母三母相乘得一
　　百五为法除实得一千八百八十九馀一百五分
　　之八十三合所问
　　(臣淳风等谨按以前三条虽有设问而无成术可/凭宜云分母乘全内子令相乘为实分母相乘为)
　　(法若两有分母各乘其全内子令相/乘为实分母为法实如法而得一)

以十二除二百五十六九分之八　问得几何
　　　　答曰二十一二十七分之十一
　　草曰置二百五十六以分母九乘之内子八得二
　　千三百一十二为实又置除数十二以九乘之得
　　一百八为法除实得二十一法与馀俱半之得二
　　十七分之十一合所问
以二十七五分之三除一千七百六十八七分之四
问得几何

　　　　答曰六十四四百八十三分之三十八
　　草曰置一千七百六十八以分母七乘之内子四
　　得一万二千三百八十又以除分母五乘之得六
　　万一千九百为实又置除数二十七以分母五乘
　　之内子三得一百三十八又以分母七乘之得九
　　百六十六为法除之得六十四法与馀各折半得
　　四百八十三分之三十八得合所问
以五十八二分之一除六千五百八十七三分之二四

分之三　问得几何
　　　　答曰一百一十二七百二分之四百三十七
　　草曰置六千五百八十七于上又别置三分于下
　　右之二于左又置四分于三下之三于左维乘之
　　分母得十二子得一十七以分母除子得一馀五
　　加一上位得六千五百八十八以分母十二乘之
　　内子五得七万九千六十一又以除数分母二因
　　之得一十五万八千一百二十二又置除数五十

　　八于下以二因之内子一得一百一十七又以乘
　　数分母十二乘之得一千四百四为法以除实得
　　一百一十二法与馀俱半之得七百二分之四百
　　三十七
　　(臣淳风等谨按此术以前三条亦有问而无术宜/云置所有之数通分内子为实置所除之数以三)
　　(分乘之为法实如法得一若法实/俱有分及重有分者同而通之)
今有官猎得鹿赐围兵初围三人中赐鹿五头次围五
人中赐鹿七头次围七人中赐鹿九头并三围赐鹿一

十五万二千三百三十三头少半头　问围兵几何
　　　　答曰三万五千人
　　术曰以三赐人数互乘三赐鹿数并以为法三赐
　　人数相乘并赐鹿数为实实如法而得一
　　草曰置三人于右上五鹿于左上五人于右中七
　　鹿于左中七人于右下九鹿于左下以右中乘左
　　上五得二十五又以右下七乘左上二十五得一
　　百七十五又以右上三乘左中七得二十一又以

　　右下七乘左中二十一得一百四十七又以右上
　　三乘左下九得二十七又以右中五乘左下二十
　　七得一百三十五将左三位并之得四百五十七
　　为法以右三位相乘得一百五别置一十五万二
　　千三百三十三头少半头位于上先以三乘之内
　　子一得四十五万七千以一百五乘之得四千七
　　百九十八万五千置除法四百五十七以三因之
　　得一千三百七十一为法除之得三万五千人合

　　问
今有猎围周四百五十二里一百八十步布围兵十步
一人今欲缩令通身得地四尺　问围内缩几何
　　　　答曰三十里五十二步
　　术曰置围里步数一退以四因之为尺以步法除
　　之即得缩数
　　草曰置四百五十二里以里法三百步乘之内子
　　一百八十得一十三万五千七百八十步退一等

　　得一万三千五百七十八尺四因之得五万四千
　　三百一十二尺以六尺除之为步得九千五十二
　　步以里法三百除之得三十里五十二步合问
今有围兵二万三千四百人以布围周各相去五步今
围内缩除一十九里一百五十步而止　问兵相去几
何
　　　　答曰四步四分步之三
　　术曰置人数以五乘之又以十九里一百五十步

　　减之馀以人数除之不尽平约之
　　草曰置围兵二万三千四百人以五乘之得一十
　　一万七千步置一十九里以三百通之内子一百
　　五十步得五千八百五十步以减上位得一十一
　　万一千一百五十步以围兵二万三千四百除之
　　得四步馀以围兵数再折除馀得三除法得四
今有封山周栈三百二十五里甲乙丙三人同绕周栈
行甲日行一百五十里乙日行一百二十里丙日行九

十里　问周行几何日会
　　　　答曰十日六分日之五
　　术曰置甲乙丙行里数求等数为法以周栈里数
　　为实实如法而得一
　　草曰置甲乙丙行里数甲行一百五十乙行一百
　　二十丙行九十各求等数得三十为法除周栈数
　　得十日法馀二十五各以五除之法得六馀得五
　　各以三十约之甲乙丙行数乃甲得五周乙得四

　　周丙得三周合前问
今有内营周七百二十步中营周九百六十步外营周
一千二百步甲乙丙三人值夜甲行内营乙行中营丙
行外营俱发南门甲行九乙行七丙行五　问各行几
何周俱到南门
　　　　答曰
　　　　甲行十二周
　　　　乙行七周

　　　　丙行四周
　　术曰以内中外周步数互乘甲乙丙行率求等数
　　约之各得行周
　　草曰置内营七百二十步于左上中营九百六十
　　步于中外营一千二百步于下又各以二百四十
　　约之内营得三中营得四外营得五别置甲行九
　　于右上乙行七于右中丙行五于右下以求整数
　　以右位再倍上得三十六中得二十八下得二十

　　以左上三除右上三十六得十二周以左中四除
　　右中二十八得七周以左下五除右下二十得四
　　周是甲乙丙行数合前问
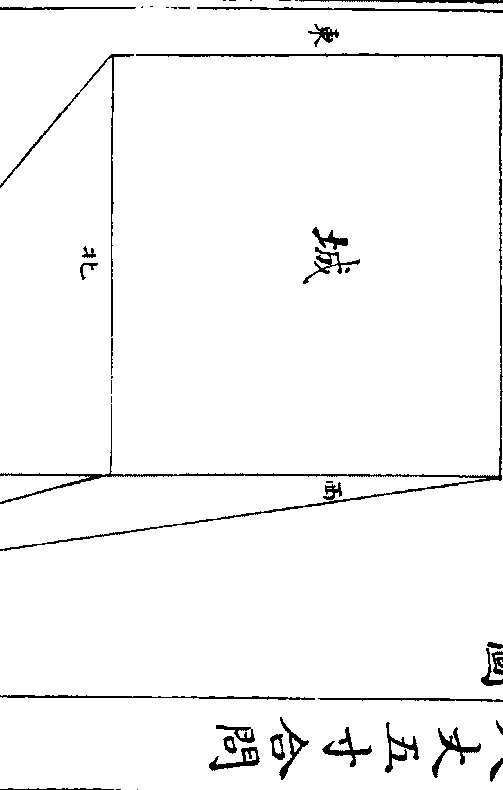
　　　案此下今有津今有椴今有木今有城四问俱
　　　各有形式高下进退俯仰线法视法毫不可紊
　　　非依问绘图无以阐其立意之妙将转疑其字
　　　句舛讹谨准测量法义为补四图各冠原问之
　　　右庶图问参观不至失其本义云

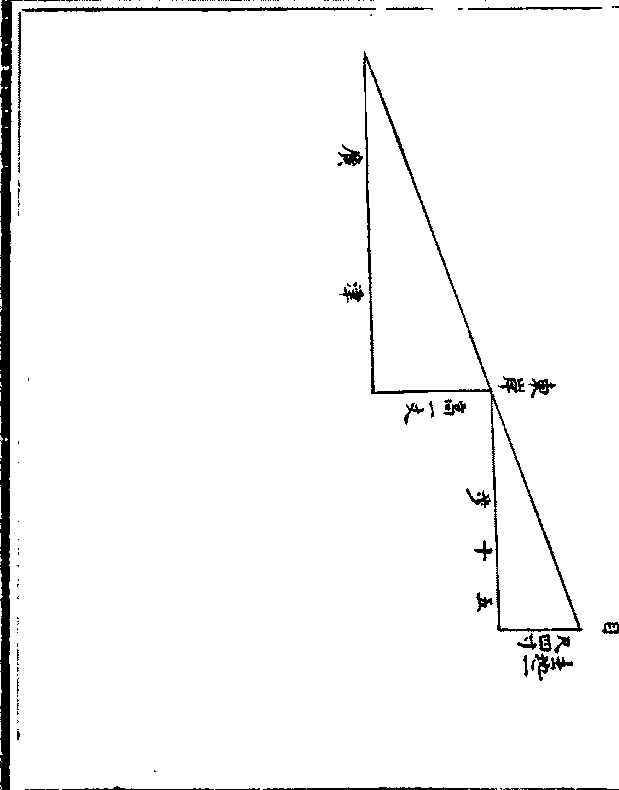
今有津不知其广东岸高一丈坐岸东去岸五十步遥
望岸上及津西畔适与人目参合人目去地二尺四寸
　问津广几何
　　　　答曰二百八步三分步之一
　　术曰以岸高乘人去岸为实以人目去地为法实
　　如法而一
　　草曰置岸高一丈又别置五十步于上以六乘之
　　得三百尺又以十尺乘之得三千尺为实以人眼

　　去地二尺四寸为法除三千尺得一千二百五十
　　尺又以六尺为步除之得二百八步法六馀二各
　　折半得三分之一合前问

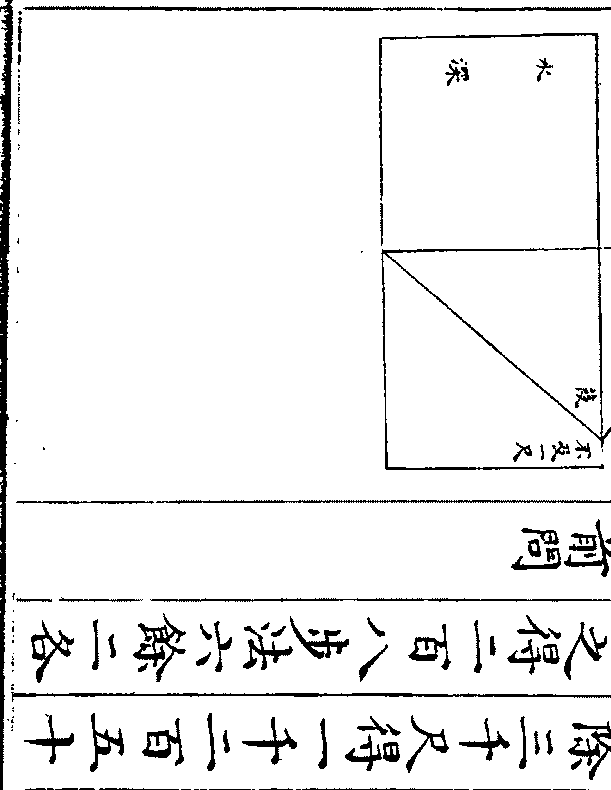
今有椴生于池中出水三尺去岸一丈引椴趋岸不及
一尺　问椴长及水深各几何
　　　　答曰
　　　　椴长一丈五尺
　　　　水深一丈二尺
　　术曰置椴去岸尺数以不及尺数减之馀自相乘
　　以出水尺数而一所得加出水而半之得椴长减
　　出水尺数即得水深

　　草曰置去岸一丈减不及一尺馀有九尺自乘之
　　得八十一尺以出水三尺除之得二丈七尺加出
　　水三尺共得三丈半之得椴长一丈五尺减出水
　　三尺馀水深一丈二尺合问

　
　
　
　
　
　
　
　

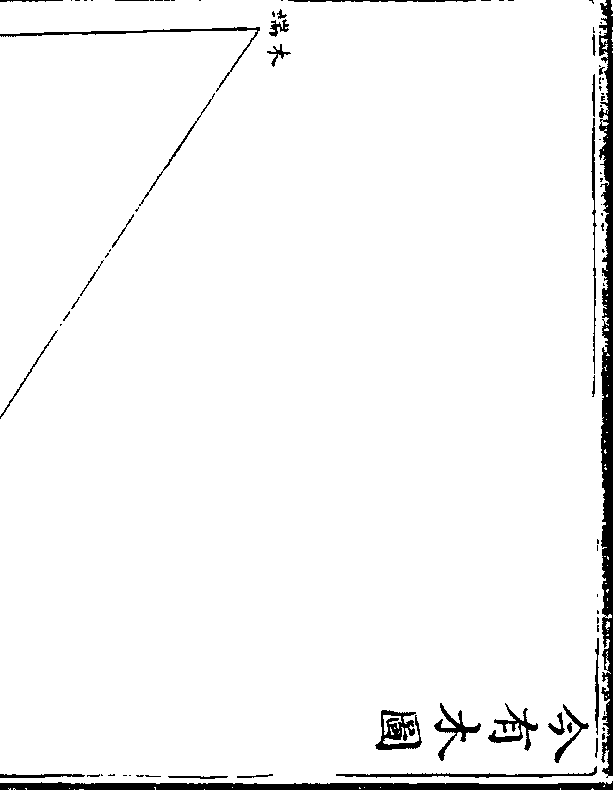
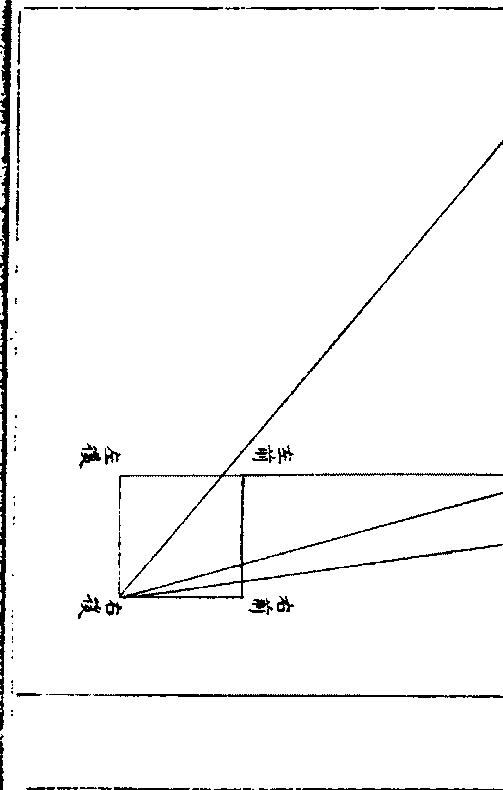
今有木不知远近高下立一表高七尺人去表九步立
望表头适与木端邪平人目去地七尺二寸又去表三十
步薄地遥望表头亦与木端邪平　问木去表及高几
何
　　　　答曰
　　　　去表三百一十五步
　　　　木高八丈五寸
　　术曰以表高乘人立去表为实以表高减人目去

　　地为法而一得木去表以表高乘木去表为实以
　　人目薄地去表为法实如法而一所得加表高即
　　木高
　　草曰置表高七尺以去表九步乘之得六十三为
　　实以表高七尺减人目去地七尺二寸馀有二寸
　　为法除实得去表三百一十五步又以表高七尺
　　乘去表三百一十五步得二千二百五以去表三
　　十步除之得七丈三尺五寸如入表高七尺得木

　　高八丈五寸合问

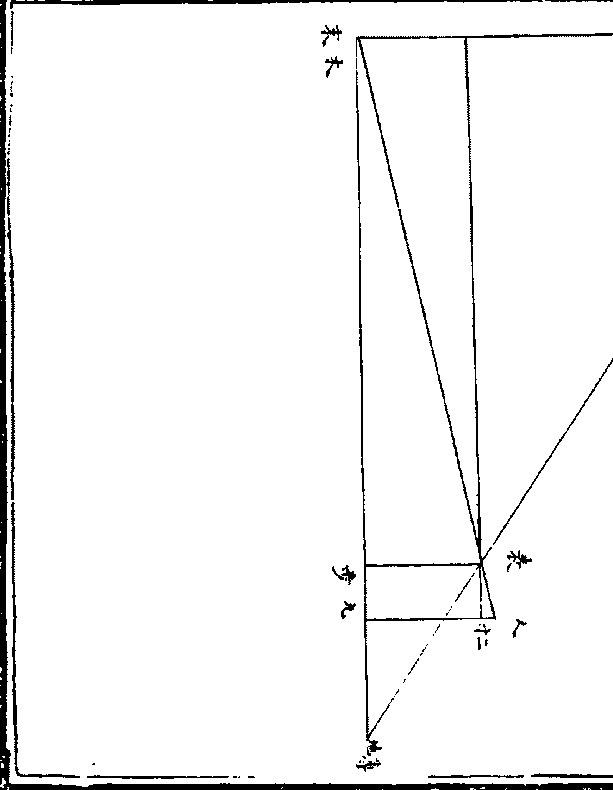
今有城不知大小去人远近于城西北隅而立四表相
去各六丈令左两表与城西北隅南北望参相直从右
后表望城西北隅入右前表一尺二寸又望西南隅亦
入右前表四寸又望东北隅亦入左后表二丈四尺
问城去左后表及大小各几何
　　　　答曰城去左后表一里二百步
　　　　东西四里四十步
　　　　南北三里一百步

　　术曰置表相去自乘以望城西北隅入数而一得
　　城去表又以望城西南隅入数而一所得减城去
　　表馀为城之南北以望城东北隅入左后表数减
　　城去表馀以乘表相去又以入左后表数而一即
　　得城之东西
　　草曰置表相去六丈自乘之得三千六百尺以西
　　北隅入表一尺二寸除之得三千尺以六尺除之
　　得五百步又以里法三百步除之得一里馀二百

　　步为城去表步数又别置三千六百尺以望城西
　　南隅入表四寸除之得九千尺以减城去表三千
　　尺馀有六千尺以六除之得一千步里法而一得
　　三里馀有一百步为城南北步数又置望城东北
　　隅入左后表二丈四尺以减城去表三千尺馀有
　　二千九百七十六尺以表相去六丈乘之得一十
　　七万八千五百六十尺以入左后表二丈四尺除
　　之得七千四百四十尺以六尺除之得一千二百

　　四十步里法而一得四里馀四十步为城东西步
　　合问
今有甲日行疾于乙日行二十五里而甲发洛阳七日
至邺乙发邺九日至洛阳　问邺洛阳相去几何
　　　　答曰七百八十七里半
　　术曰以甲乙所至日数相乘又以甲日行疾里数
　　乘之为实以甲至日减乙至日数馀为法实如法
　　而一

　　草曰置甲乙所至七日九日相乘得六十三又以
　　甲疾行二十五里乘之得一千五百七十五为实
　　以甲至七日减乙至九日馀有二日为法除实得
　　七百八十七里半合问
今有官出库金五十九斤一两赐王九人公十二人侯
十五人子十八人男二十一人王得金各多公五两公
得金各多侯四两侯得金各多子三两子得金各多男
二两　问王公侯子男各得金几何

　　　　答曰
　　　　王一斤六两
　　　　公一斤一两
　　　　侯十三两
　　　　子十两
　　　　男八两
　　术曰置王公侯子男数王位十四之公位九之侯
　　位五之子位二之并之以减出金两数馀以凡人

　　数而一所得各以本差之数加之得王公侯子男
　　各所得金之数不加即男之得金
　　草曰置王九人公十二人侯十五人子十八人以
　　王位十四之得一百二十六公位九之得一百八
　　侯位五之得七十五子位二之并之得三百四十
　　五以减出金五十九斤一两馀六百为实并五等
　　人数得七十五为法除实得八两乃加十四两为
　　王加九得十七两为公加五得十三两为侯加二

　　得十两为子男不加如数加满斤法而一不满者
　　命为两合问
今有十等人大官甲等十人官赐金依等次差降之上
三人先入得金四斤持出下四人后入得金三斤持出
中央三人未到者亦依等次更给　问各得金几何及
未到三人复应得金几何
　　　　答曰
　　　　甲一斤七十八分斤之三十三

　　　　乙一斤七十八分斤之二十六
　　　　丙一斤七十八分斤之十九
　　　　丁一斤七十八分斤之十二
　　　　戊一斤七十八分斤之五
　　　　己七十八分斤之七十六
　　　　庚七十八分斤之六十九
　　　　辛七十八分斤之六十二
　　　　壬七十八分斤之五十五

　　　　癸七十八分斤之四十八
　　　　未到三人共得三斤七十八分斤之十五
　　术曰以先入人数分所持金数为上率以后入人
　　数分所持金数为下率二率相减馀为差实并先
　　后入人数而半之以减凡人数馀为差法实如法
　　而一得差数并一二三以差数乘之以减后入人
　　所持金数馀以后入人数而一又置十人减一馀
　　乘差数并之即第一人所得金数以次每减差数

　　各得之矣并中央未到三人得应持金数
　　草曰先置入人数于左上置得金数于右上又置
　　后入人数于左下置后得金数于右下以后入人
　　数乘先得金数得十六以先入人数乘后得金数
　　得九以九直减十六得七为差实又并先后入人
　　数七半之得三半以减十人数馀六半又以先后
　　人数率分母三与分母四相乘得十二以乘六半
　　得七十八为差法(七十八是/一斤也)置后入所得金数三

　　以乘差法得二百三十四又置一二三得差以七
　　因之得四十二直减二百三十四馀有一百九十
　　二以后入四人数除之人得四十八乃是癸得之
　　数累加差七乃合前问
今有圆材径头二尺一寸欲以为方问各几何
　　　　答曰一尺五寸(淳风等谨按开方除之为一尺/四寸二十五分寸之二十一)
　　术曰置径尺寸数以五乘之为实以七为法实如
　　法而一

　　草曰置二尺一寸以五乘之得一百五寸以七除
　　之得一尺五寸合前问
今有泥方一尺欲为弹丸令径一寸　问得几何
　　　　答曰一千七百七十七枚九分枚之七
　　术曰置泥方寸数再自乘以十六乘之为实以九
　　为法实如法得一
　　草曰置一尺为十寸再自乘得一千以十六乘之
　　得一万六千为实以九为法除实得一千七百七

　　十七枚九分之七合前问(臣淳风等谨按密率为丸/一千九百九枚十一分枚)
　　(之/一)依密率术曰令泥方寸再自乘以二十一乘之
　　为实以十一为法实如法而一即得又依密率草
　　曰置泥方十寸再自乘得一千寸以二十一乘之
　　得二十一万为实以十一为法除之得一千九百
　　九枚十一分枚之一合问
今有客不知其数两人共盘少两盘三人共盘长三盘
　问客及盘几何

　　　　答曰
　　　　客三十人
　　　　十三盘
　　术曰以二乘少盘三乘长盘并之为盘数倍之又
　　以二乘少盘数增之得人数
　　草曰置二人于右上少两盘于右下置三人于左
　　上置剩三盘于左下各以人乘盘右下得四左下
　　得九并之得一十三盘数别置少盘二以剩盘三

　　乘之得六更并少剩盘乘之得三十人合前问
今有女善织日益功疾初日织五尺今一月日织九疋
三丈　问日益几何
　　　　答曰五寸二十九分寸之十五
　　术曰置今织尺数以一月日而一所得倍之又倍
　　初日尺数减之馀为实以一月日数初一日减之
　　馀为法实如法得一
　　草曰置九疋以疋法乘之内三丈得三百九十尺

　　以一月三十日除之每日得一丈三尺倍之得二
　　丈六尺又倍初日尺数得一丈减之馀一丈六尺
　　为实又置一月三十日减一日得二十九日为法
　　除之得五寸二十九分寸之十五合前问
今有女子不善织日减功迟初日织五尺末日织一尺
今三十日织讫　问织几何
　　　　答曰二疋一丈
　　术曰并初末日织尺数半之馀以乘织讫日数即

　　得
　　草曰置初日五尺讫日一尺并之得六半之得三
　　以三十日乘之得九十尺合前问
今有绢一疋买紫草三十斤染绢二丈五尺今有绢七
疋欲减买紫草还自染馀绢　问减绢买紫草各几何
　　　　答曰
　　　　减绢四疋一丈二尺十三分尺之四
　　　　买草一百二十九斤三两一十三分两之九

　　术曰置今有绢疋数以本绢一疋尺数乘之为减
　　绢实以紫草三十斤乘之为买紫草实以本绢尺
　　数并染尺为法实如法得一其一术盈不足术为
　　之亦得
　　草曰置绢七疋以疋法乘之得二百八十尺又以
　　买草绢一疋四十尺乘之得一万一千二百尺为
　　减绢实以本绢尺数六十五尺为法除实得一百
　　七十二尺法与馀皆倍之得一十三分尺之四又

　　置二百八十尺以紫草三十斤乘之得八千四百
　　斤为买草实亦以六十五尺为法除之得一百二
　　十九斤馀不尽者十六乘之得二百四十又以法
　　除之得三两馀与法皆倍之得一十三分两之九
　　合前问
今有生丝一斤练之折五两练丝一斤染之出三两今
有生丝五十六斤八两七分两之四　问染得几何
　　　　答曰四十六斤二两四百四十八分两之二

　　　　百二十三
　　术曰置一斤两数以折两数减之馀乘今有丝斤
　　两之数又以出两数并一斤两数乘之为实一斤
　　两数自乘为法实如法得一两数
　　草曰置五十六斤以两法十六乘之内子八两得
　　九百四两又以分母七乘之内子四得六千三百
　　三十二两为实又以练率十一染率十九相乘得
　　二百九以乘其实得一百三十二万三千三百八

　　十八为积以十六相乘得二百五十六又以分母
　　七乘之得一千七百九十二为法除积得七百三
　　十八两馀与法皆再折得四十八分两之二百二
　　十三若求练丝折法置积两以十六乘以十一除
　　得丝数
今有铁十斤一经入炉得七斤今有铁三经入炉得七
十九斤一十一两　问未入炉本铁几何
　　　　答曰二百三十二斤五两四铢三百四十三

　　　　分铢之二百八十四
　　术曰置铁三经入炉得斤两数以十斤再自乘乃
　　乘上为实以七斤再自乘为法实如法而得一
　　草曰置三经入炉得七十九斤以十六乘之内一
　　十一两得一千二百七十五两以十斤再自乘得
　　一千以乘之得一百二十七万五千为实以七斤
　　再自乘七两得三百四十三为法以除实得三千
　　七百一十七两馀六十九以二十四乘之得一千

　　六百五十六又以法除之得四铢三百四十三分
　　铢之二百八十四又以十六除所得两数得二百
　　三十二斤五两并前铢零合前问
今有丝一斤八两直绢一疋今持丝一斤裨钱五十得
绢三丈今有钱一千　问得绢几何
　　　　答曰一疋二丈六尺六寸大半寸
　　术曰置丝一斤两数以一疋尺数乘之以丝一斤
　　八两数而一所得以减得绢尺数馀以一千钱乘

　　之为实以五千钱为法实如法得一
　　草曰置丝一十六两以四十尺乘之得六百四十
　　以一斤八两通为二十四两为法除之得二丈六
　　尺六寸大半寸为丝所得之绢以减三丈馀三尺
　　三寸少半寸为钱之所直以三尺三寸三因之内
　　子一得十尺以乘一千钱得一万尺又以裨钱五
　　十以三因之得一百五十为法除实得六丈六尺
　　六寸大半寸合前问

今有甲贷乙绢三疋约限至不还疋日息三尺今过限
七日取绢二疋偿钱三百　问一疋直钱几何
　　　　答曰七百五钱十七分钱之十五
　　术曰以过限日息尺数减取绢疋尺数馀为法以
　　偿钱乘一疋尺数为实实如法而一
　　草曰置七日三疋绢日息三尺共九尺以乘七日
　　得六十三尺以减八十尺馀一十七尺为法又置
　　偿钱三百以四十尺乘之得一万二千钱以一十

　　七为法除之得七百五文馀十七分钱之十五合
　　前问
今有金方七银方九秤之适相当交易其一金轻七两
　问金银各重几何
　　　　答曰金方重十五两十八铢
　　　　银方重十二两六铢
　　术曰金银方数相乘各以半轻数乘之为实以超
　　方数乘金银方数各自为法实如法而一

　　草曰置金方七银方九相乘得六十三以半轻数
　　三两半乘得二百二十两半又以金银超方数二
　　以乘金方数得一十四为法除实得一十五两馀
　　不尽者以二十四乘之得二百五十二铢再以前
　　法除之得一十八铢若求银方又置前二百二十
　　两半以银方九二因得一十八为法除之得一十
　　二两馀二十四乘之得一百八以法除之得六铢
　　为银方合前问

今有器容九㪷中有米不知其数满中粟舂之得米五
㪷八升　问满粟几何
　　　　答曰八㪷
　　术曰置器容九㪷以米数减之馀以五之二而一
　　得满粟斗数
　　草曰置九㪷以米五㪷八升减之得三㪷二升以
　　粟数五因之得一石六㪷以糠率二㪷除之得八
　　㪷为粟合前问

今有七百人造浮桥九日成今增五百人　问日几何
　　　　答曰五日四分日之一
　　术曰置本人数以日数乘之为实以本人数今增
　　人数并之为法实如法而一
　　草曰置七百人以九百因之得六千三百又以增
　　五百人加七百人得一千二百人为法除之得五
　　日馀四分日之一合前问
今有与人钱初一人与三钱次一人与四钱次一人与

五钱以次与之转多一钱与讫还敛聚与均分之人得
一百钱　问人几何
　　　　答曰一百九十五人
　　术曰置人得钱数以减初人钱数馀倍之以转多
　　钱数加之得人数
　　草曰置人得钱一百减初人钱三文得九十七倍
　　之加初人得一百九十五合前问
　

　
　
　
　
　
　
　
　张邱建算经卷上