声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
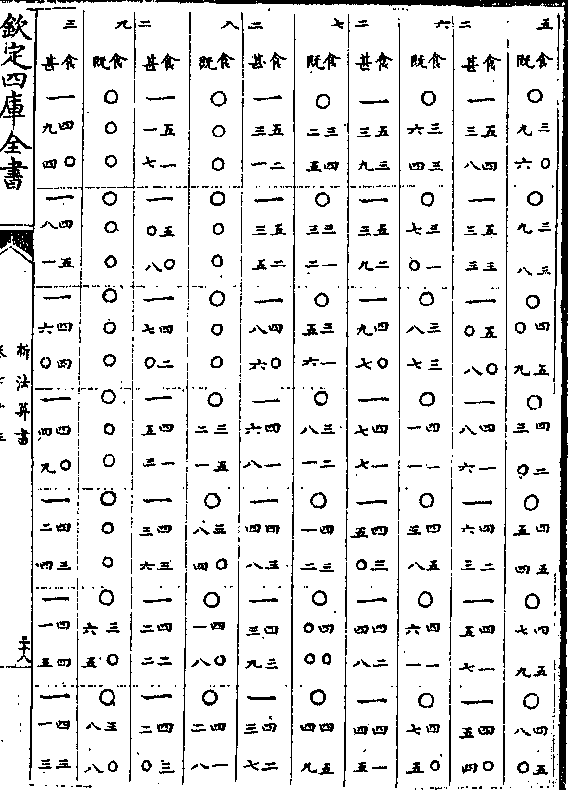
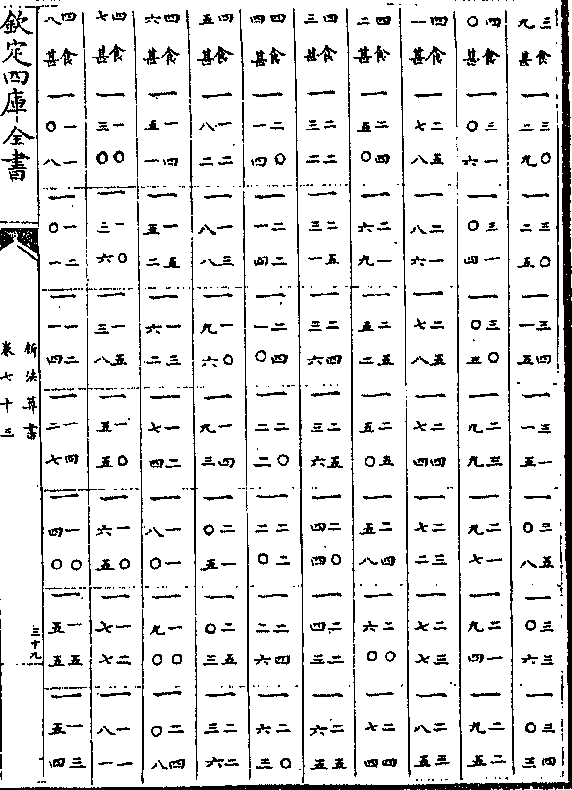
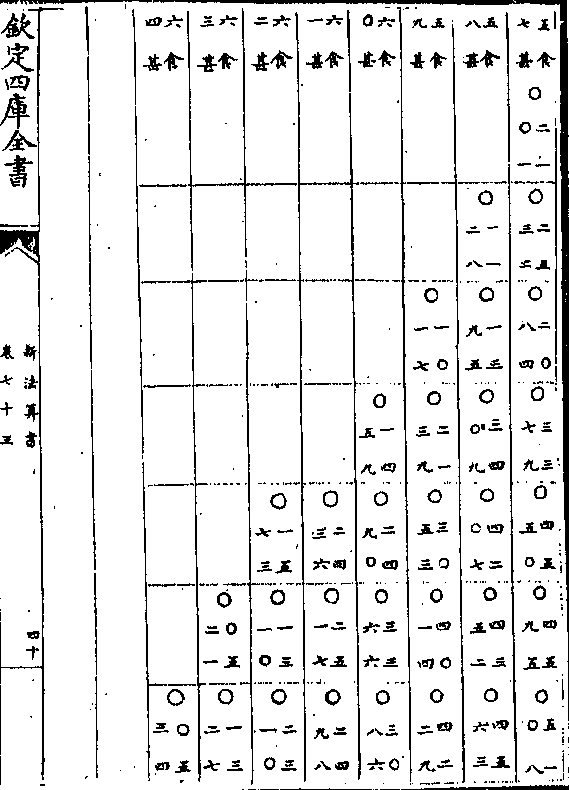
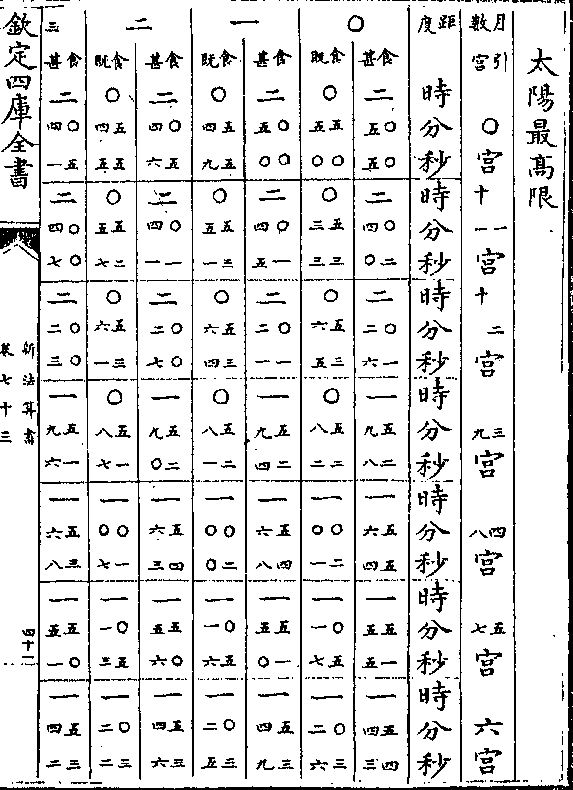
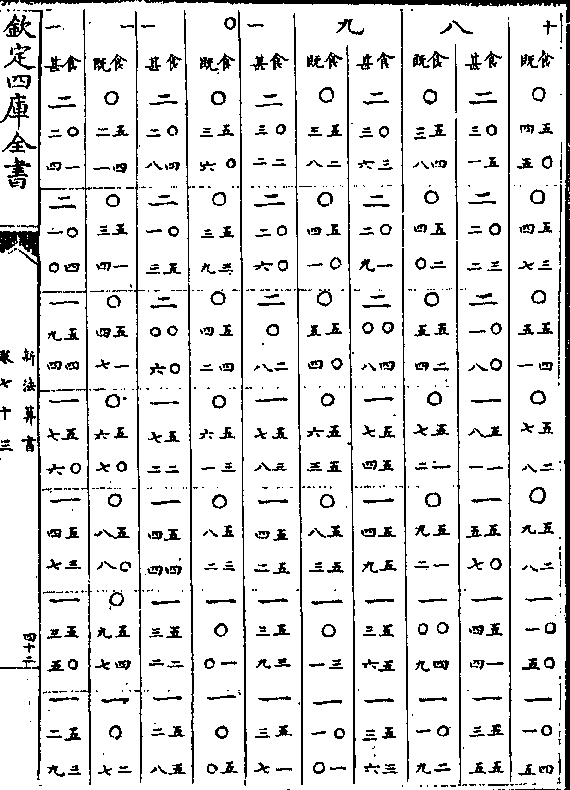
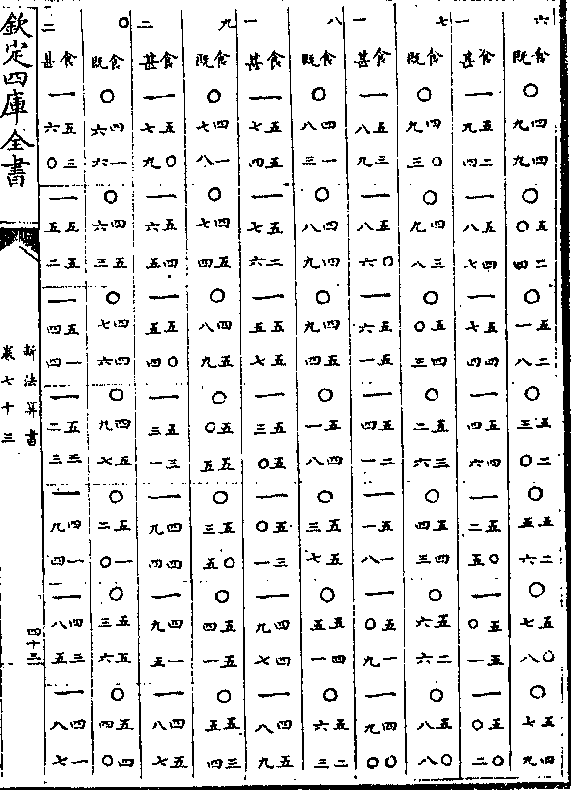
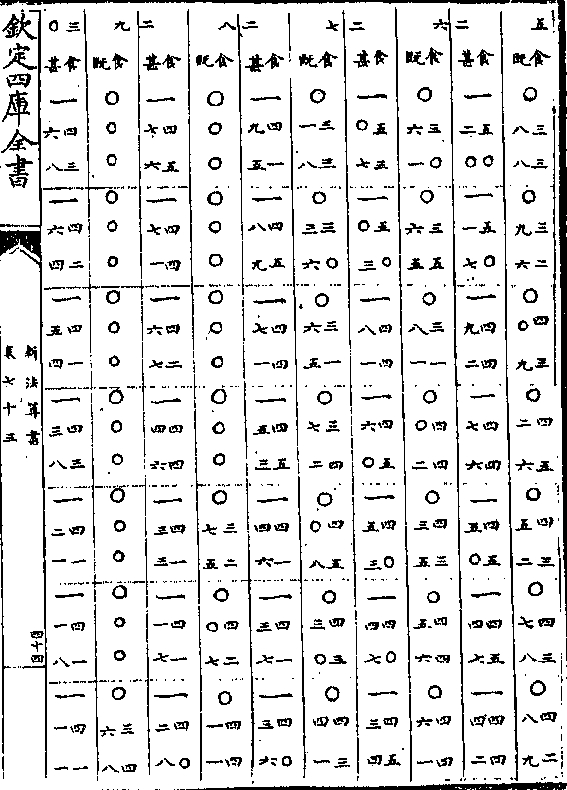
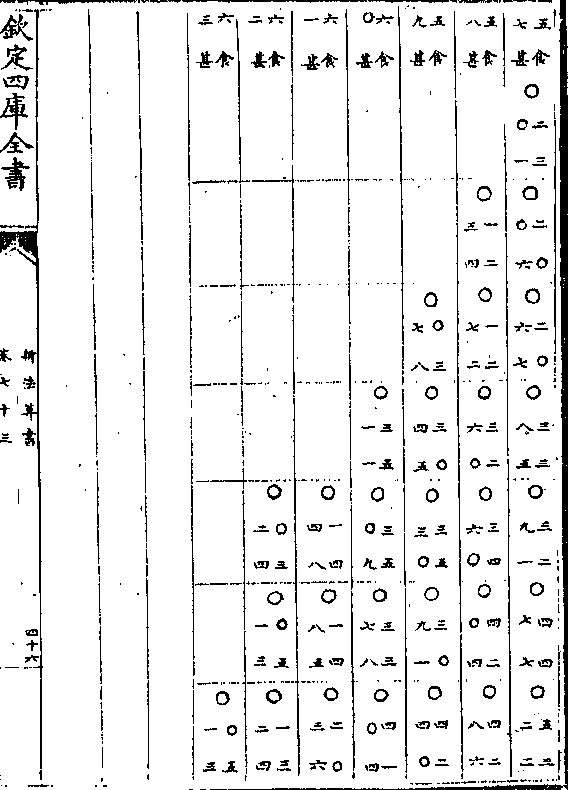
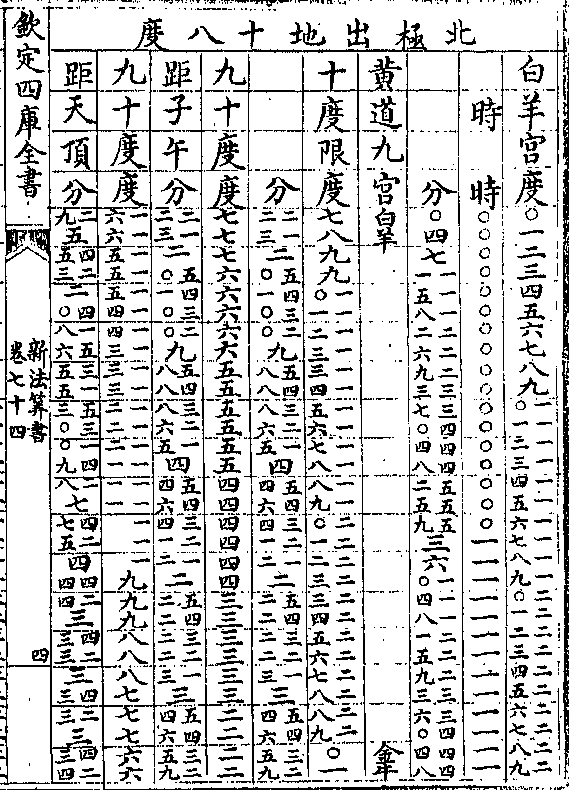
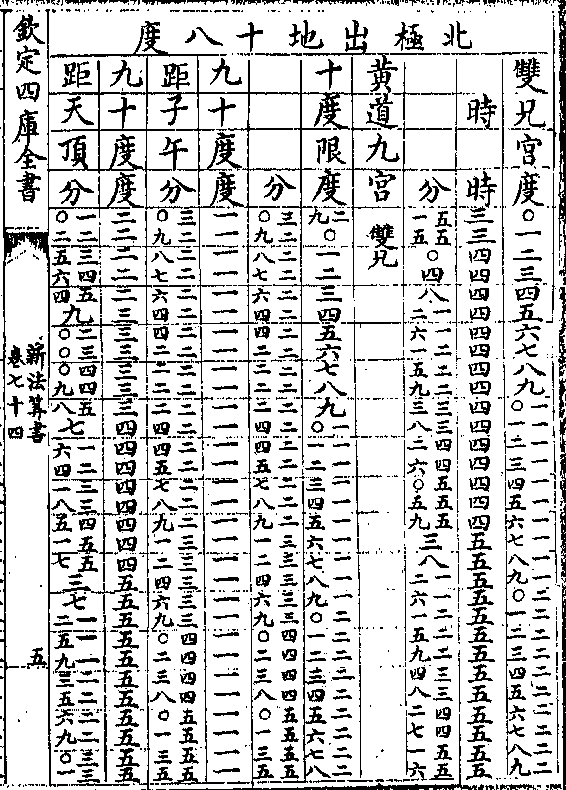
卷八十九 第 1a 页 WYG0789-0337b.png
 钦定四库全书
钦定四库全书新法算书卷八十九 明 徐光启等 撰
测量全义卷三
取地平线法 增题一
凡测高深广远必用直角者以小句股求大句股也地平为
句所测高为股股者垂线也垂线之末加权焉以
定地平有本器本论今用象限与矩度则于器
心施权线平直相切于象限之边其表边所向
之处别立他表则他表与器之心为平行线如
卷八十九 第 1b 页 WYG0789-0337c.png
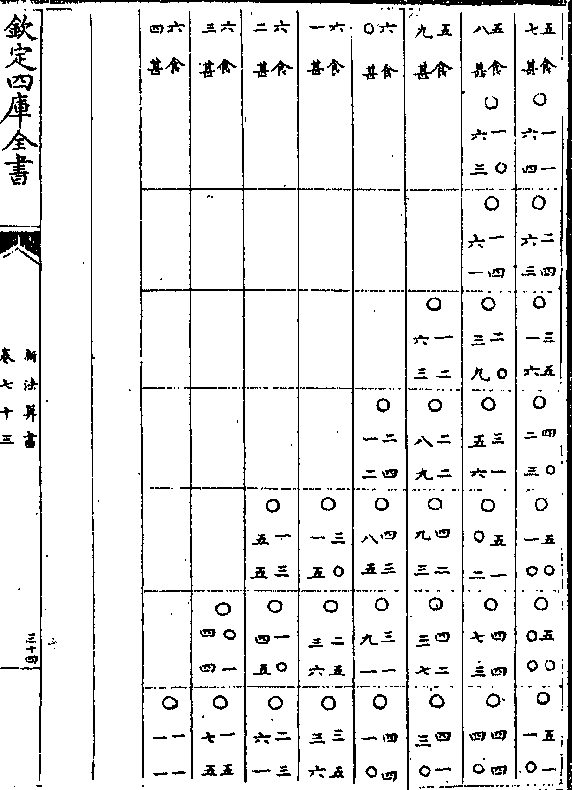 一图甲乙为物高丙上加器表边在上旁以
一图甲乙为物高丙上加器表边在上旁以权线准之从丙直视至甲定甲为他表则
甲丙线为地面上平行线何者垂线从天
顶向地心与地面上平线为直角故也
若道里相距太远难定其高下之较何
者地面为地球之一分弧分也远则目
与物为弧背所隔不相及矣法以相距
之远分为若干分每两分定其高下之
较末以各较加减之得总高下之较如
卷八十九 第 2a 页 WYG0789-0337d.png
 二图甲乙相距四里许乙上加器别
二图甲乙相距四里许乙上加器别立丙表令乙与丙等高丙上加器别
立丁表令丙与丁等高丁上加器望
甲令甲与丁等高次量各表距地各
几何加减之得甲乙之较
值两地之间为山城所隔如三图量
乙距丙几何令乙与丙平丙之表端
为丁距戊几何令丁与戊平戊下取
己与丙平戊己距庚辛表几何定己
卷八十九 第 2b 页 WYG0789-0338a.png
 与庚平戊与辛平庚辛距壬癸表几何
与庚平戊与辛平庚辛距壬癸表几何令辛庚与壬癸平从壬癸望甲令癸与
甲平次以丁丙己戊并庚辛壬癸并两
数相减馀为两地高下之较如近乙之
丁丙与己戊并多于近甲之庚辛与壬
癸并则乙下而甲高深浅反之
若山城中穷于用器则于山腰用之又
别有简法曰山顶戊用器求甲与乙之
深两数之较则高下之较(四/图)
卷八十九 第 3a 页 WYG0789-0338b.png
 如在乙欲测甲高乙上用器令乙与丁平则量丁乙之
如在乙欲测甲高乙上用器令乙与丁平则量丁乙之远而求甲丁之深(五/图)
矩尺测量法 增题二
法曰如一图欲于丁测甲乙之高丁上立表表端为山
口矩尺之直角加焉以己戊
尺向高际乙稍移就之令己
戊乙为直线次从戊己尺上
依直线向地平得丙成丁戊
丙甲乙丙相似两形则丙丁与丁戊若丙甲与乙甲以
卷八十九 第 3b 页 WYG0789-0338c.png
 高求远则戊丁与丁丙若乙甲与甲丙
高求远则戊丁与丁丙若乙甲与甲丙若据高求远如二图丁丙与戊丁若戊
丁与丁乙若因远求高则戊丁与丁丙
若乙丁与戊丁 论曰戊丁乙戊丁丙
两形有丁直角丁丙戊丙戊丁并为一
直角丙戊乙亦为直角两角内减丁戊
丙角馀戊丙丁丁戊乙两角等夫直角形有两角等即
形相似则丙角之对边戊丁也乙戊丁角之对边丁乙
也其比例必等
卷八十九 第 4a 页 WYG0789-0338d.png
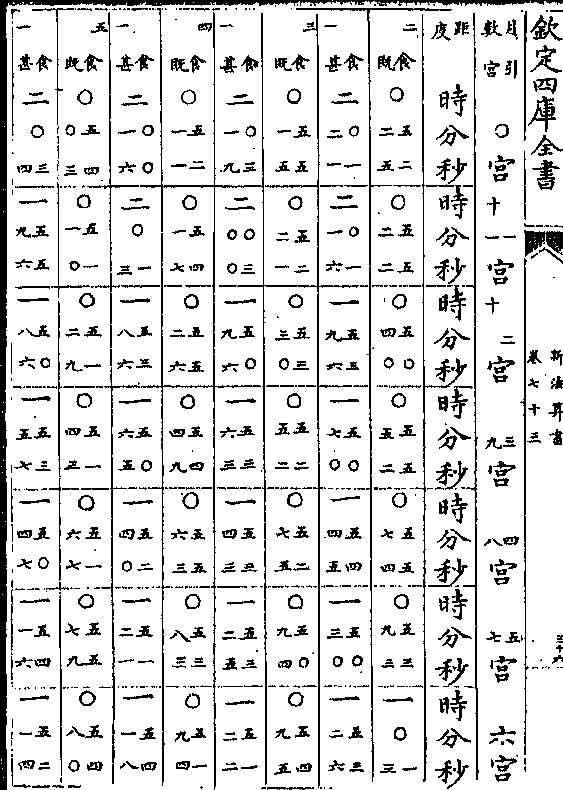 求井之深则于井口边甲上
求井之深则于井口边甲上立表向井底乙向地平之丁
成甲丁丙丙戊乙两形相似
是丙甲当广甲丁当深也
测极远别法 增题三
两郡邑相距太远以高求远表法为
穷则用四表遇地面不平四表法又
穷别法每邑取一高若山巅若楼台
若林木俱可或并为诸物又地平为
卷八十九 第 4b 页 WYG0789-0339a.png
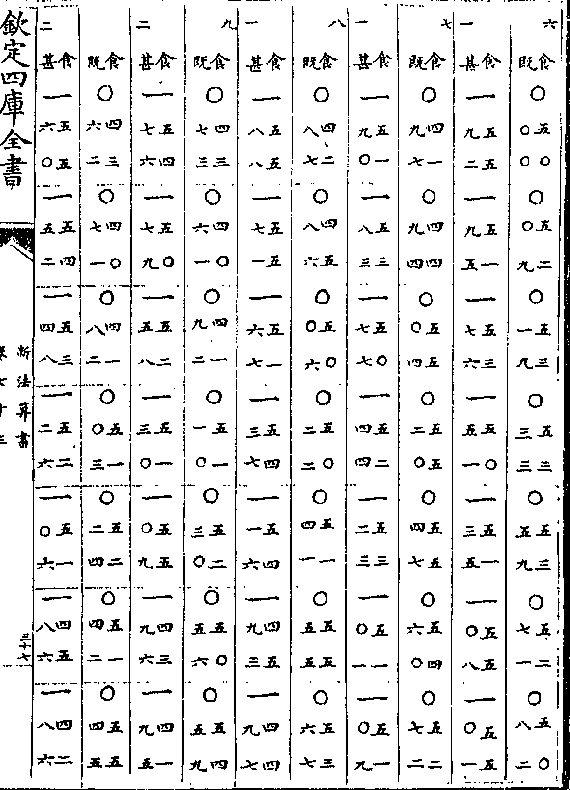 他物所碍则又穷当于气清日朗风恬时烧狼烟直上
他物所碍则又穷当于气清日朗风恬时烧狼烟直上作两处之表次于近山之顶取甲取乙甲山上加象限
向所测之丁与丙又向乙山定丙甲
丁乙甲丁两角乙山上加象限向甲
向丁向丙定丁乙丙甲乙丙两角夫
甲乙丙形有甲乙边乙甲两角可求
甲丙边甲乙丁形有甲乙边甲乙两
角可求甲丁边未甲丁丙形有甲丙
甲丁两边可求丁丙相距之远若一次不能测则分测
卷八十九 第 5a 页 WYG0789-0339b.png
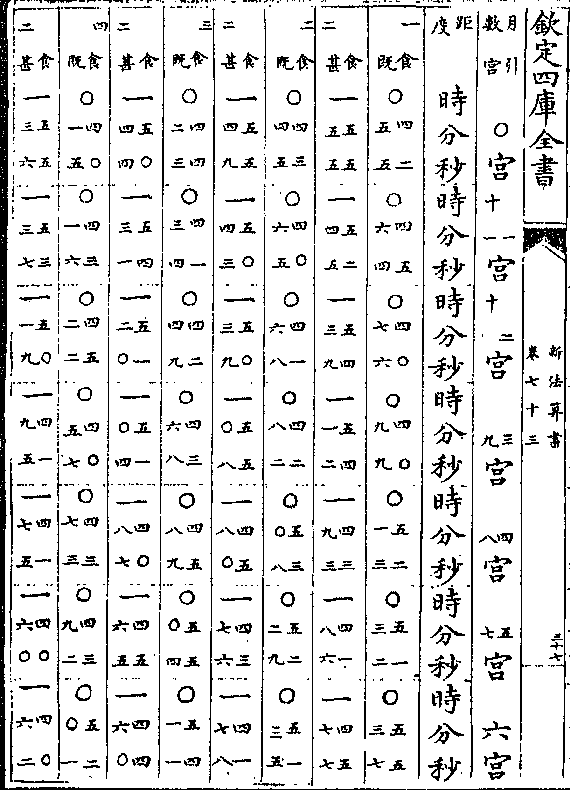 之如以甲乙测丁丙以乙辛测丙戊以辛庚测戊己
之如以甲乙测丁丙以乙辛测丙戊以辛庚测戊己量高远深 增题四
用方木表承以鼎足之跗垂权取直表端以下一尺或
五寸用一十或一百平分之下作方孔长寸许广三分
贯以横表游移无定亦以十或百平分之纵横作直角
解曰如一图欲测甲乙之高丙上立
表横表游移令丁戊乙为直线成丁
戊己丁乙庚两相似形即丁己若干
分与己戊一百分若丁庚与乙庚加甲庚得全高
卷八十九 第 5b 页 WYG0789-0339c.png
 以高求远则戊己一百分与丁己若
以高求远则戊己一百分与丁己若干分若乙庚与庚丁减丁己得甲丙
远物在下目在上如二图令戊丁丙
作直线则戊己与己丁若戊甲与甲
丙
若无高求远则用重表如三图以丑
壬两测之较当庚癸相距之远
高上测高用重表再测但须定表横
用游表直用在丙得己丙在丁得丁
卷八十九 第 6a 页 WYG0789-0339d.png
 戊其较庚己以当丙丁横表己辛
戊其较庚己以当丙丁横表己辛以当甲乙
在一高测两下在丁向乙向丙定
横表之两数则丁戊当丁甲戊辛
当甲丙己辛当乙丙己戊当甲乙
用五图以远求高其理亦同以远
求深或井口上立柱用四图以井
口之度求深用二图
造象限仪法(篇中或省曰/象限或曰仪)
卷八十九 第 6b 页 WYG0789-0340a.png
 用铜或木板作圈四分之一去板边三分作甲乙直线
用铜或木板作圈四分之一去板边三分作甲乙直线平面中任取丙为心甲为界作甲丁虚圈交甲乙线于
戊从戊过丙作直线交甲丁圈于丁从甲至丁作直线
成丁甲乙直角(几何/用法)次以甲为心去
版边一二分取乙为界作乙庚圈即
四分全圈之一象限也圈限外馀版
剡去之次离乙庚弧以内约二分作
相似弧两弧间平分各度分又同前作相似弧两弧间
识其十度或五度从庚从乙皆可起算互用之庚后作
卷八十九 第 7a 页 WYG0789-0340b.png
 小孔贯以权线至甲(若作两指尺/可不用权线)
小孔贯以权线至甲(若作两指尺/可不用权线)窥衡一名指尺铜为之首为小圜径
三四分从心出直线名指线以定度
分所至也广三分厚一分长与象限
之半径等上设二表一近心一近秒秒以钩钩象限边
令游移而不脱表形方高广约四三分中作直线铝通
之下为小孔表之下端为半枘入尺中令两表之前后
两缝两孔皆相对不爽毫发于指线为垂线象限边上
亦设二表如上法盖测量法每用两指线以定两测所
卷八十九 第 7b 页 WYG0789-0340c.png
 在也或作两指尺同心同线可定可
在也或作两指尺同心同线可定可移尤便
如图以木为架上为半圈两端开山
口深三四寸以受象限
用象限法
架口受象限之甲乙边以庚甲线取
平焉仪面正对所测物从窥衡觑物
与指线相参直得指线如弧所当度
分则从乙至指线者地平上之高也从指线至庚距天
卷八十九 第 8a 页 WYG0789-0340d.png
 顶之高也
顶之高也次法以架口受象限之弧
甲心上别用权线下垂过
弧甲庚边上立表游移觑
表与物参直审权线之度
定物之高从乙角起者地
平上之高也从庚角起者
距天顶之高也
三法若地或平或欹则别作圆转之架上端为球空大
卷八十九 第 8b 页 WYG0789-0341a.png
 半作实球与空球等入空中铁枘指外径二分长寸许
半作实球与空球等入空中铁枘指外径二分长寸许旋转回斡不出大球之口空球旁加螺
旋三具俟实球之体定而固之 仪后
面中心作孔受实球之枘用时以枘入
孔转仪得其面与所测物为直线以螺
旋固之
象限之用有二一定仪如首图其一边与地平为平行
线以窥衡定地平上之度一游仪如二图用权线其理
同也何者游表边与定衡同向一物作平行线定仪之
卷八十九 第 9a 页 WYG0789-0341b.png
 立边与游仪之权线作平行线则窥衡与立边所作角
立边与游仪之权线作平行线则窥衡与立边所作角表边与权线所作角等弧亦等
造矩度法
用铜木板作正方直角形如象限法任用一角为心两
旁作直角两线如甲乙甲丙次用元
度乙丙各为心各作小弧交于丁次
作丙丁乙丁两线成甲乙丙丁正方
形各边作一百分每对边分以直线
相联成网目形器小每五分十分作
卷八十九 第 9b 页 WYG0789-0341c.png
 直线器大更细分之
直线器大更细分之角止作心加窥衡加权线任用架具于前
定仪于立边书高深平边书远游仪于表旁边书远对
边书高深以便别识
约法象限弧之内空作矩度其窥衡
指线上分即矩度边之分是指线当
权线也为用殊大若欲取最小之分
则加两窥衡两指线相合为一线用时分指焉安衡法
管端之小圜心开圆孔象限心则方孔为螺柱当圆为
卷八十九 第 10a 页 WYG0789-0341d.png
 圆当方为方末圆而加螺旋焉仍以螺旋固之分象限
圆当方为方末圆而加螺旋焉仍以螺旋固之分象限法先三分之用元度庚乙两角各为心取庚辛乙寅得
庚寅寅辛辛乙为三分而等各又三分之为九分又各
半之为十八大分取四大分又五分之用元度每大分
之界为心左右参差定点每大分中各有五小分得九
十平分度也或取六大分作五分亦同(论见几/何用法)
分矩度法先平分之又平分之又各五分之为二十大
分取四大分五分之或取六大分五分之共得百平分
造小象限法
卷八十九 第 10b 页 WYG0789-0342a.png
 正方版一角为心作象限之弧弧外
正方版一角为心作象限之弧弧外两边二平分之又三平分之至四至
五六七八九十各平分用界尺从心
至各分为界弧上作疏密线线以内
书各分其弧外馀板去之加权线与矩度同用
用法 以表向物如前遇权线截弧表之旁则高多远少
截表之对边则高少远多如截表旁为二分则远一高
二截五分则远一高五反之则高一远二远一高五说
见二卷矩度法中
卷八十九 第 11a 页 WYG0789-0342b.png
 又法以甲乙边当一百依前法分乙戊弧为一百不平分
又法以甲乙边当一百依前法分乙戊弧为一百不平分若权线至己则股一百句五十也至辛则股一百句一
十也转用之权线至庚则甲丁股一百句五十也
卷八十九 第 11b 页 WYG0789-0342c.png
卷八十九 第 12a 页 WYG0789-0342d.png

卷八十九 第 12b 页 WYG0789-0343a.png

卷八十九 第 13a 页 WYG0789-0343b.png

卷八十九 第 13b 页 WYG0789-0343c.png
卷八十九 第 14a 页 WYG0789-0343d.png

卷八十九 第 14b 页 WYG0789-0344a.png

卷八十九 第 15a 页 WYG0789-0344b.png

卷八十九 第 15b 页 WYG0789-0345a.png

卷八十九 第 16a 页 WYG0789-0345b.png

卷八十九 第 16b 页 WYG0789-0345c.png

卷八十九 第 17a 页 WYG0789-0345d.png

卷八十九 第 17b 页 WYG0789-0346a.png
 法用平版如几案置仪其一端仪之心以当两测之初所
法用平版如几案置仪其一端仪之心以当两测之初所定仪用游表左右迁移令二表与次所相参直即于
两表间作一线名曰主线主线之左右视所绘之物令
与两表相参直即如前作线虚记本物之名号次用指
南针定其方向又各两线中间书其度分之数画讫至
次所置仪于版之他端以仪心加主线之上主线与初
所相参直令初测之仪心在两所之间也定仪如前用
两表视所绘之物各作线审方注度即每物各有两线
在图版之上必相遇相遇之点乃实注本物之名号末
卷八十九 第 18a 页 WYG0789-0346b.png
 去各线成所求作图
去各线成所求作图若欲知此物之距测所远近多寡先定两测之所相距
若干为主线之里数或步数或丈尺数依三角形法主
线为底向一物之两线为两腰是有底及底上之两角求
两腰为本物距两测处若干
又两物之两交作一线相联与一测处成三角形从测所
至两点之线为两腰联线为底如前先得腰再用其
角可得底为两物相距之数
如一图甲为两测之初所加仪向次所乙先作主线次向
卷八十九 第 18b 页 WYG0789-0346c.png
 午己戊癸等物作各线后至乙亦如之即得各两线
午己戊癸等物作各线后至乙亦如之即得各两线之交为午己戊癸各物之定所
若物在中不可得至欲绘其形即用仪几次周遭测之
如二图
卷八十九 第 19a 页 WYG0789-0346d.png

新法算书卷八十九