声明：本站书库内容主要引用自 archive.org，kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
卷二十六 第 1a 页 WYG0788-0430a.png
钦定四库全书新法算书卷二十六 明 徐光启等 撰
日躔表卷二
卷二十六 第 1b 页 WYG0788-0431a.png
卷二十六 第 2a 页 WYG0788-0431b.png
卷二十六 第 2b 页 WYG0788-0431c.png
卷二十六 第 3a 页 WYG0788-0431d.png
卷二十六 第 3b 页 WYG0788-0432a.png
卷二十六 第 4a 页 WYG0788-0432b.png WYG0788-0432c.png WYG0788-0432d.png WYG0788-0433a.png WYG0788-0433b.png WYG0788-0433c.png WYG0788-0433d.png WYG0788-0434a.png WYG0788-0434b.png WYG0788-0434c.png WYG0788-0434d.png WYG0788-0435a.png WYG0788-0435b.png WYG0788-0435c.png WYG0788-0435d.png WYG0788-0436a.png WYG0788-0436b.png WYG0788-0436c.png WYG0788-0436d.png
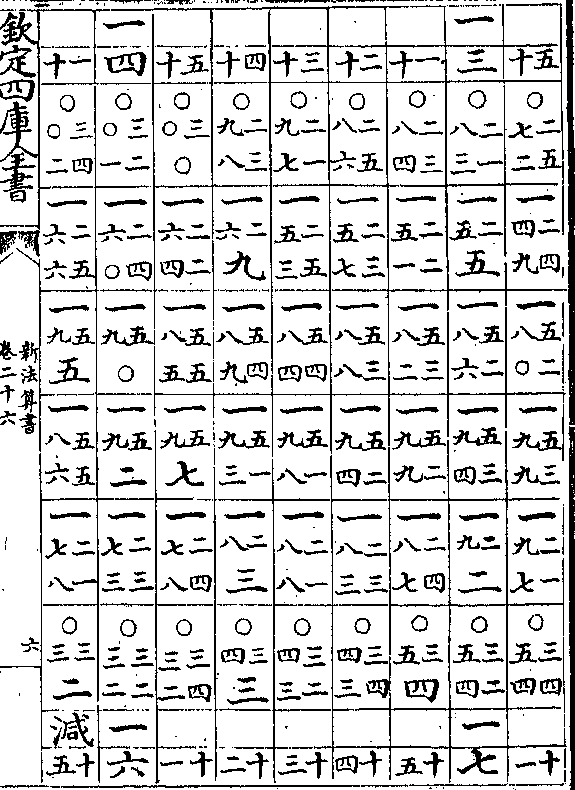
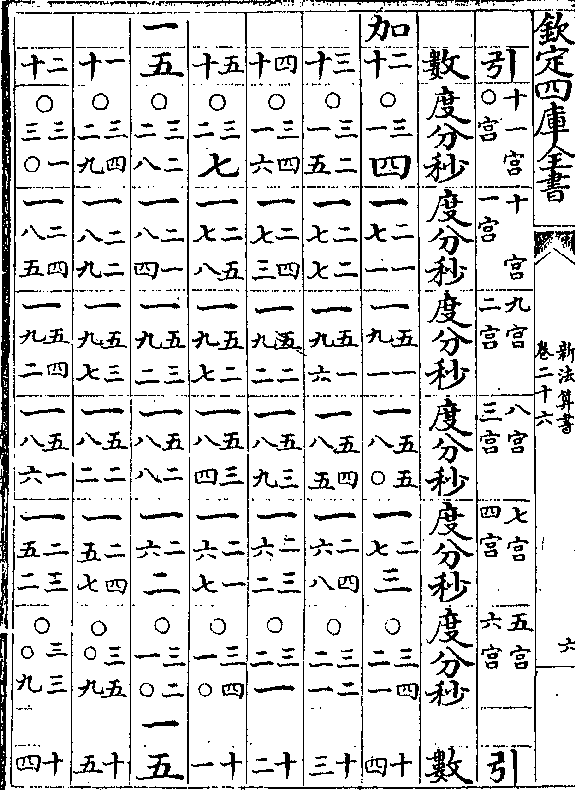
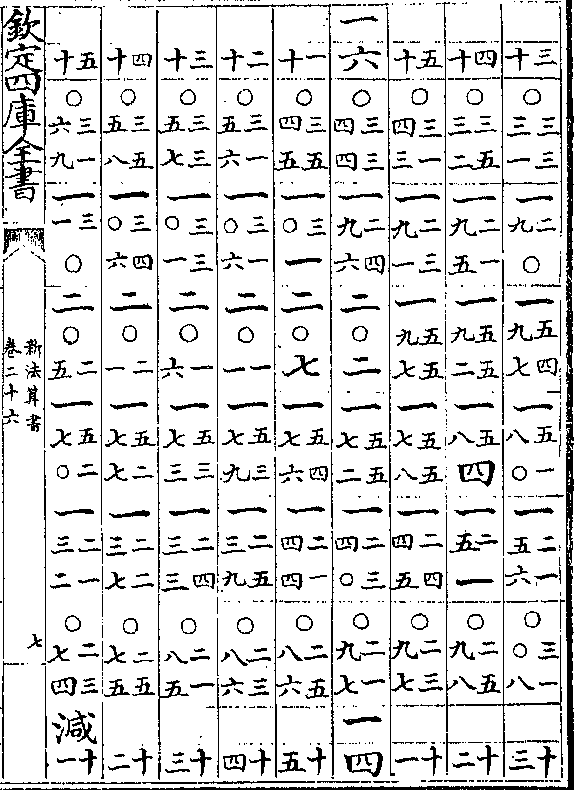
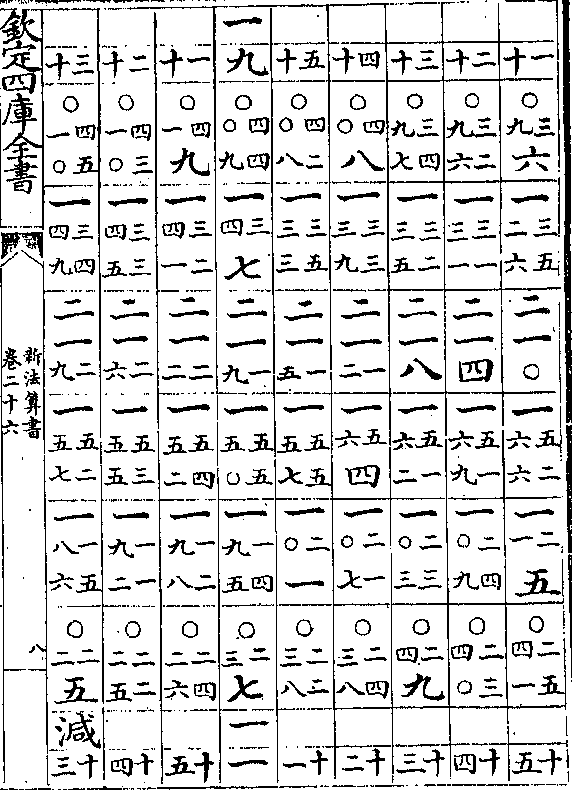
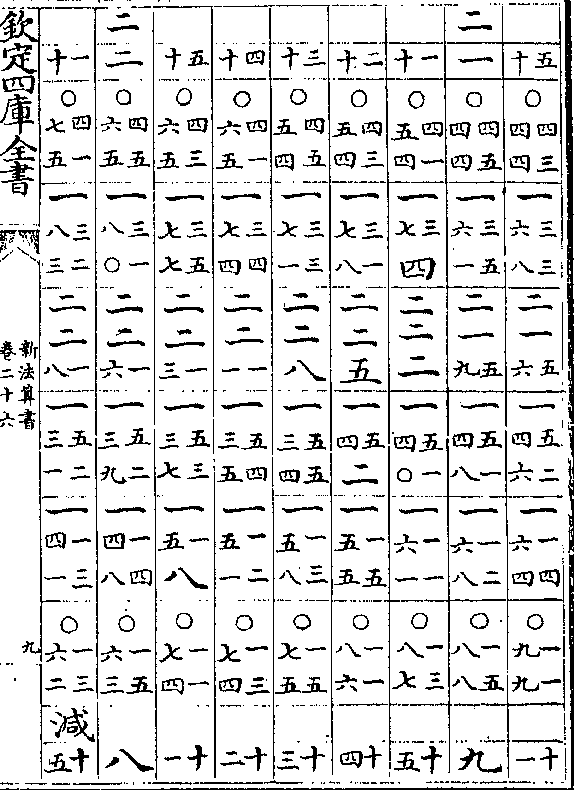
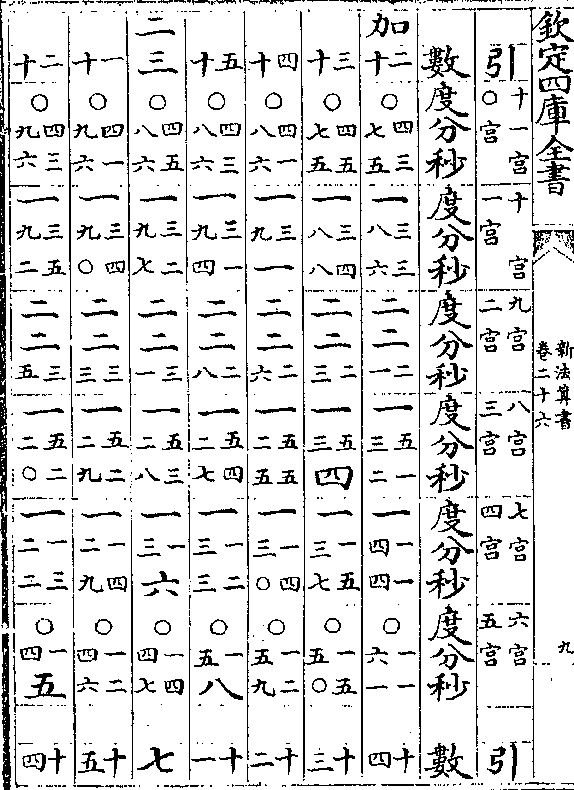
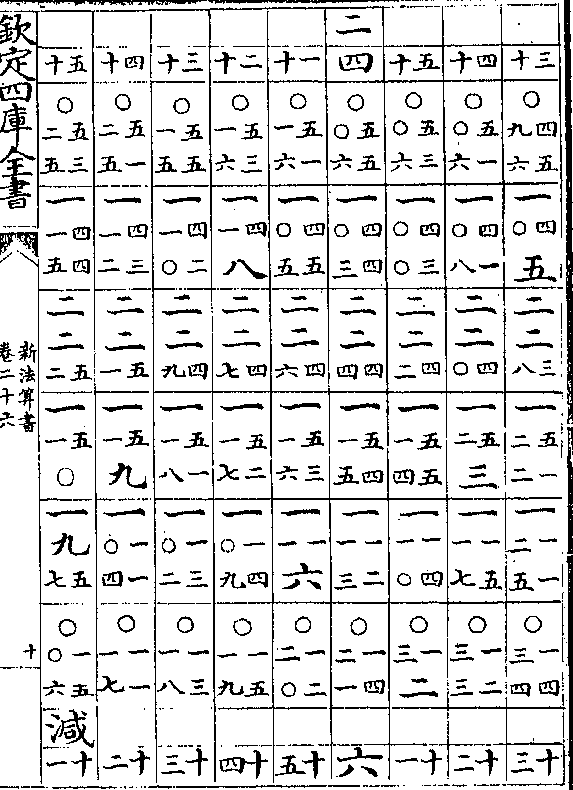
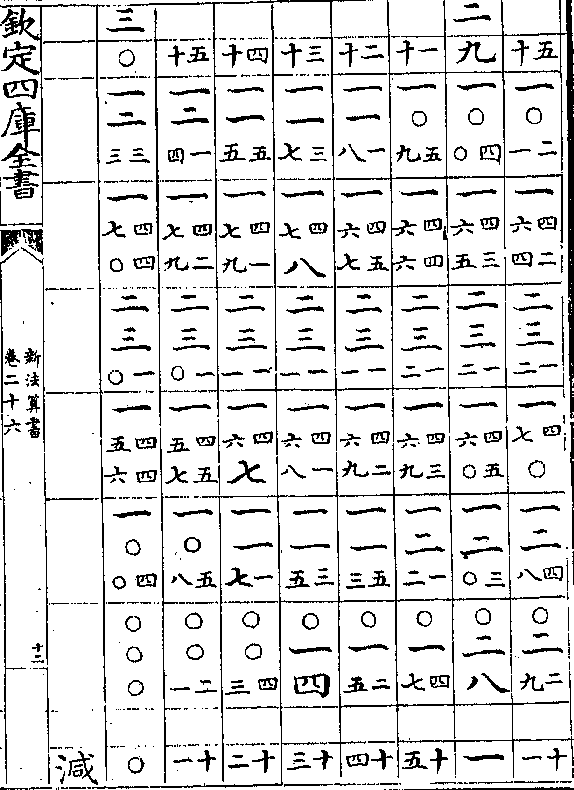
卷二十六 第 4b 页 WYG0788-0437a.png
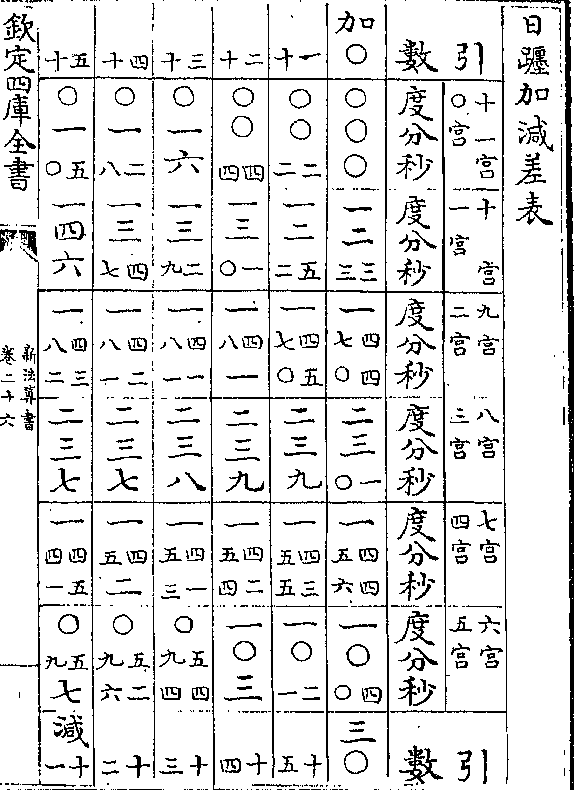
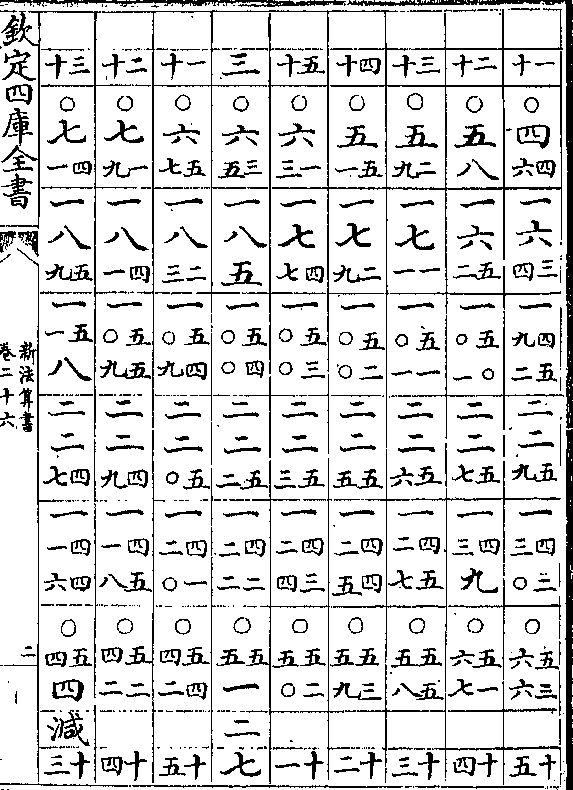
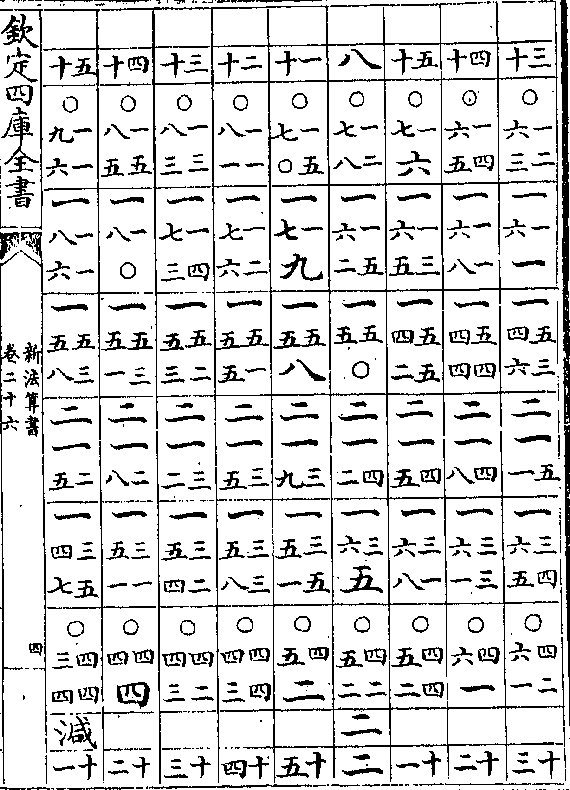
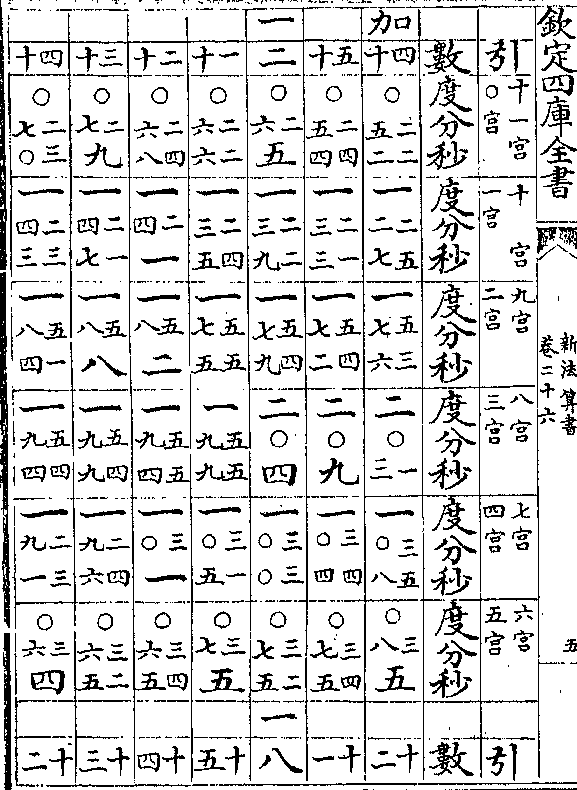
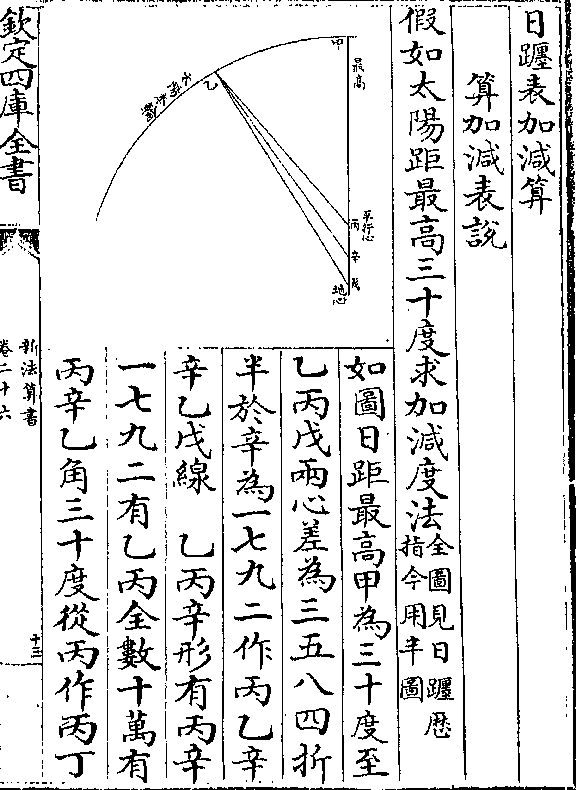日躔表加减算算加减表说
假如太阳距最高三十度求加减度法(全图见日躔历/指今用半图)
如图日距最高甲为三十度至
乙丙戊两心差为三五八四折
半于辛为一七九二作丙乙辛
辛乙戊线 乙丙辛形有丙辛
一七九二有乙丙全数十万有
丙辛乙角三十度从丙作丙丁
卷二十六 第 5a 页 WYG0788-0437b.png
垂线于辛乙分元形为二 一为丙丁辛 一为丙丁乙两三角形
丙丁辛直角形有丙辛边一七九二有辛角三十度辛为
心丙为界作弧以辛丙为全丙
丁为辛角之正弦辛丁为馀弦
法全数十万(内/)与丙辛一七
九二外若辛角正弦五○○○
○(内/)与丙丁八九六外全与丙
辛若辛角馀弦八六六○三与
卷二十六 第 5b 页 WYG0788-0437c.png
辛丁一五五一次以乙为心丙为界作弧乙丙为全丙丁为乙角之正
弦丁乙为乙角之馀弦查表得乙角三十分四十六秒
乙丁边九九九九六乙丁丁辛并之得一○一五四七
为乙辛边 乙辛戊形有辛戊一七九二有乙辛边一
○一五四七又有乙辛戊角三十度之馀为一百五十
度
乙辛引长作戊丁垂线成辛丁戊直角形
夫形有辛戊边一七九二有戊辛丁角为钝角之馀三
卷二十六 第 6a 页 WYG0788-0437d.png
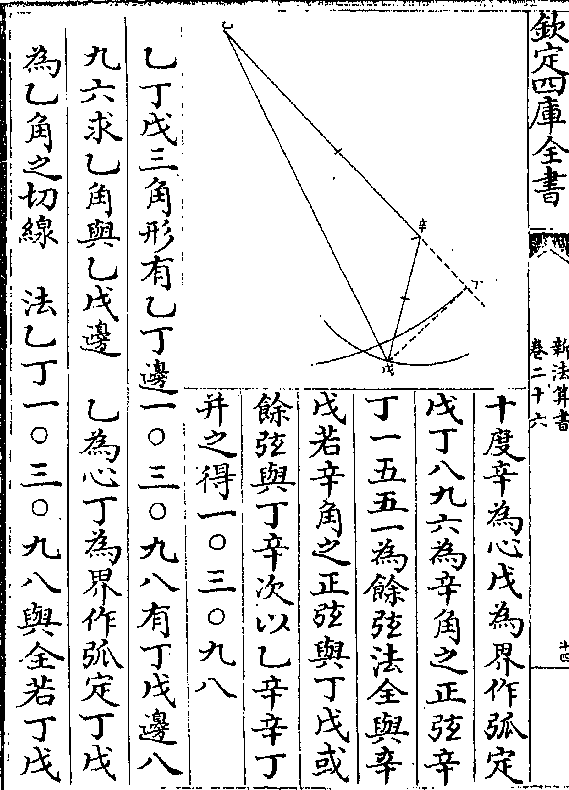十度辛为心戊为界作弧定戊丁八九六为辛角之正弦辛
丁一五五一为馀弦法全与辛
戊若辛角之正弦与丁戊或
馀弦与丁辛次以乙辛辛丁
并之得一○三○九八
乙丁戊三角形有乙丁边一○三○九八有丁戊边八
九六求乙角与乙戊边 乙为心丁为界作弧定丁戊
为乙角之切线 法乙丁一○三○九八与全若丁戊
卷二十六 第 6b 页 WYG0788-0438a.png
八九六与乙角之切线八六九查表得二十九分五十三秒两角并之共得一度○分三十九秒为甲乙距最
高三十度之加减均数如表
假如太阳距高冲三十度求加减度法
乙丙辛形有丙辛一七九二有乙
丙全数乙辛引长作丙丁垂线成
丙丁辛直角形
夫形有丁辛丙角三十度为丙辛
乙之馀有丙辛边求丙丁丁辛辛为
卷二十六 第 7a 页 WYG0788-0438b.png
心丙为界作弧定丙丁为辛角之正弦辛丁为其馀法全与丙辛若辛角之正弦与丙丁八
九六馀弦与丁辛一五五一
丙丁乙大形有丙乙为全数十万丙丁
八九六求丁乙边及乙角
乙为心丙为界作弧定丙丁为乙角之
正弦因丙乙为全数以丙丁查正弦表
得三十分四十六秒为辛乙丙角又取
其馀弦为九九九九六乙丁丁乙内减
卷二十六 第 7b 页 WYG0788-0438c.png
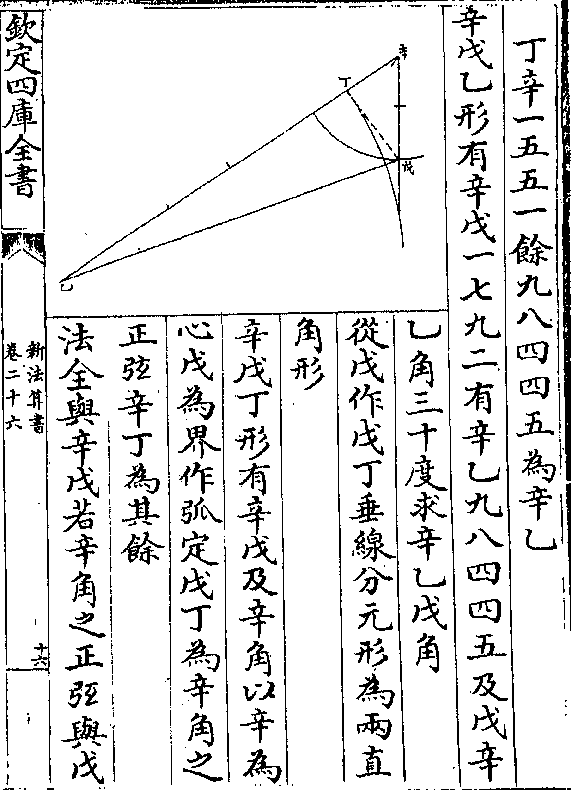丁辛一五五一馀九八四四五为辛乙辛戊乙形有辛戊一七九二有辛乙九八四四五及戊辛
乙角三十度求辛乙戊角
从戊作戊丁垂线分元形为两直
角形
辛戊丁形有辛戊及辛角以辛为
心戊为界作弧定戊丁为辛角之
正弦辛丁为其馀
卷二十六 第 8a 页 WYG0788-0438d.png
法全与辛戊若辛角之正弦与戊丁八九六馀弦与辛丁一五五一
辛乙内减丁辛得九六八九四为丁乙
丁戊乙形有戊丁八九六有丁乙九六八九四求乙角
乙为心丁为界作弧定戊丁为乙角之切线 法丁乙
与全若丁戊与乙角之切线算得九二五查切线表得
三十一分四十四秒为戊乙辛角戊乙辛辛乙丙两角
并之得一度二十分三十秒为太阳距高冲三十度之
加减均数如表
卷二十六 第 8b 页 WYG0788-0439a.png
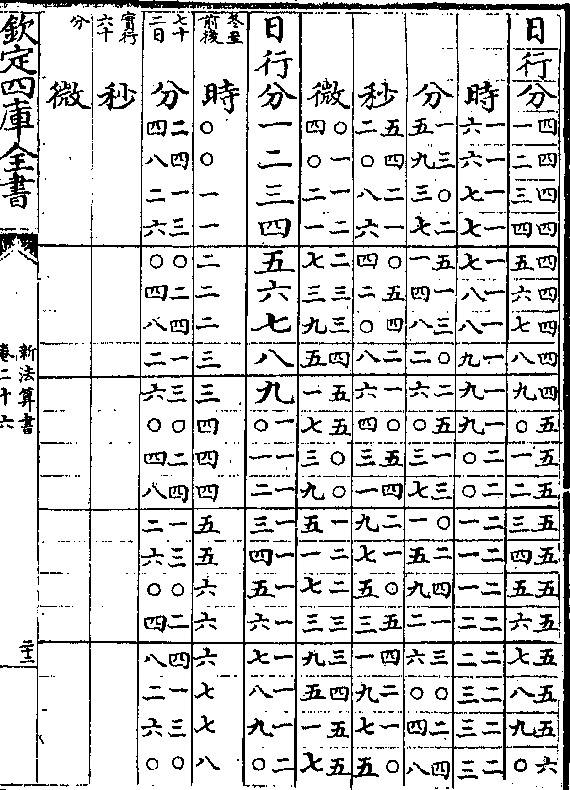
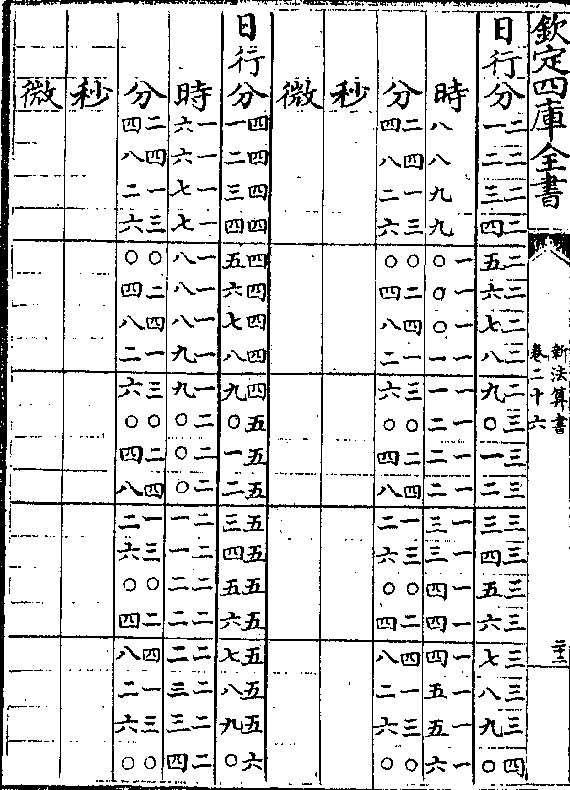
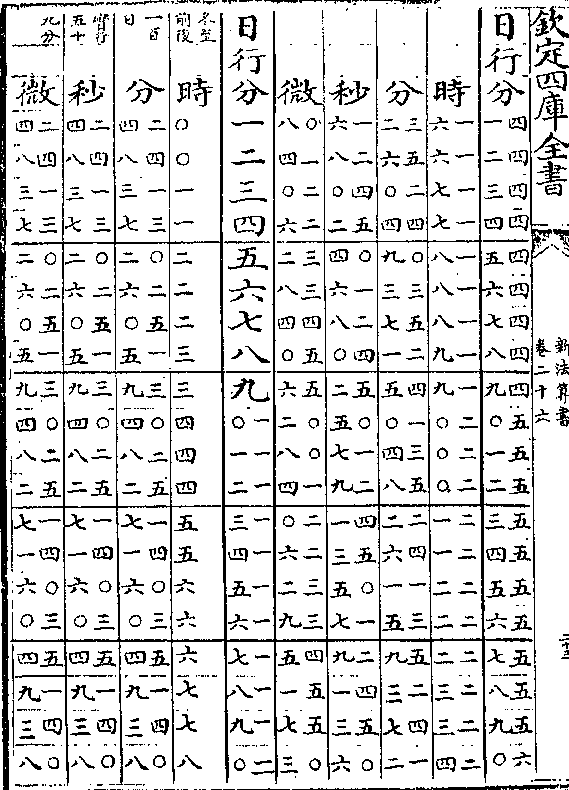
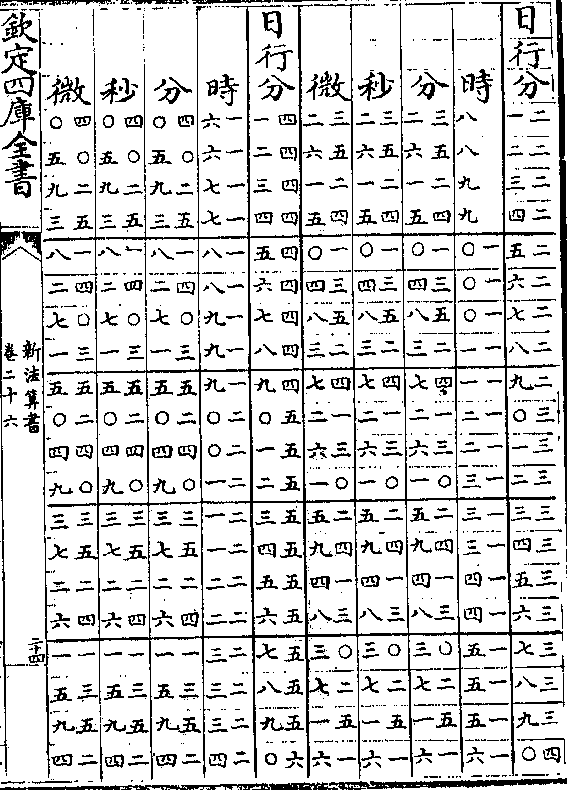
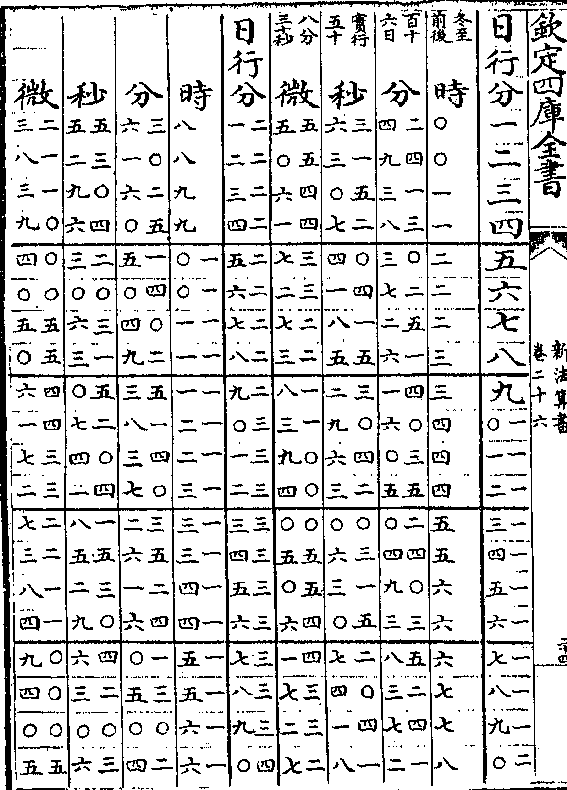
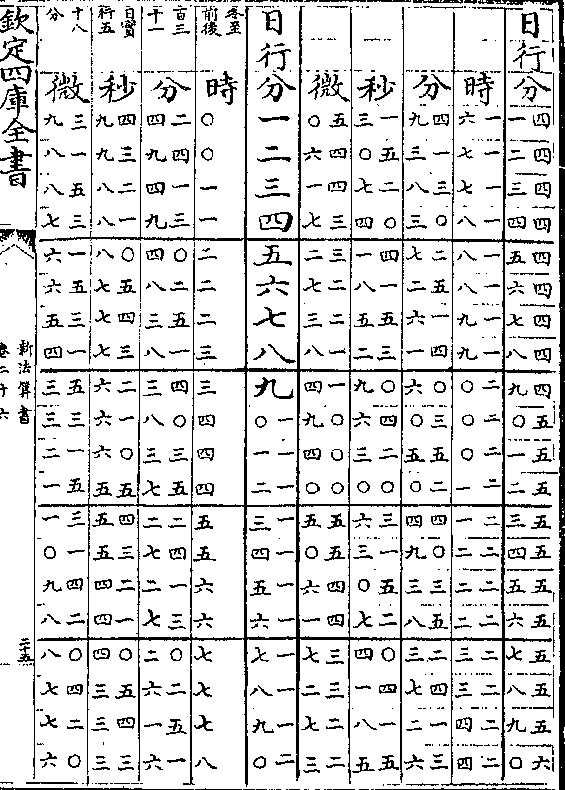
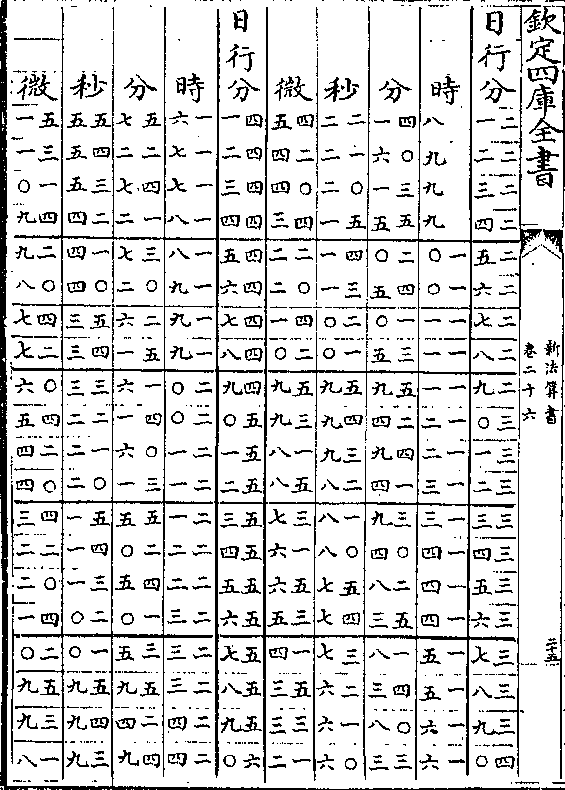
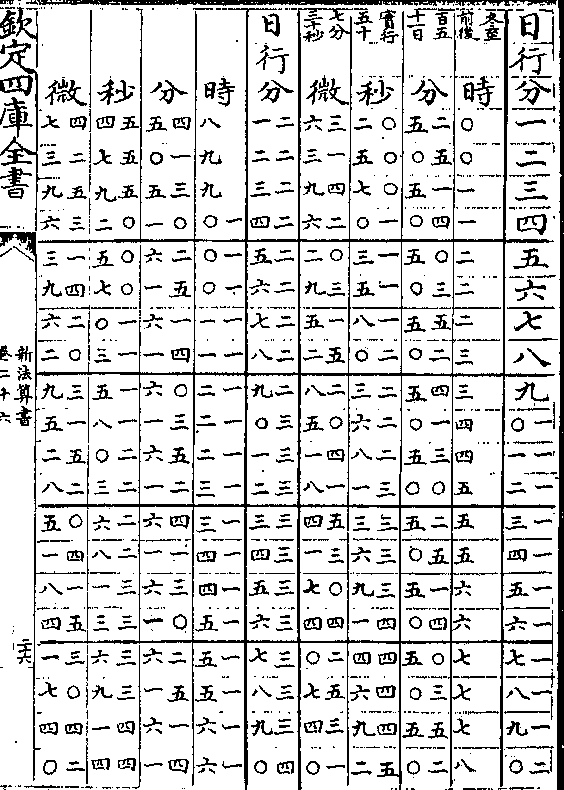
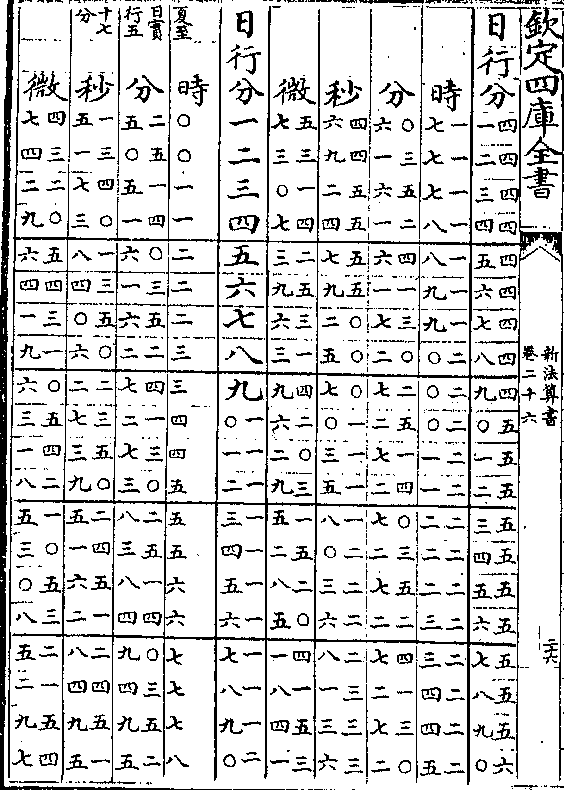
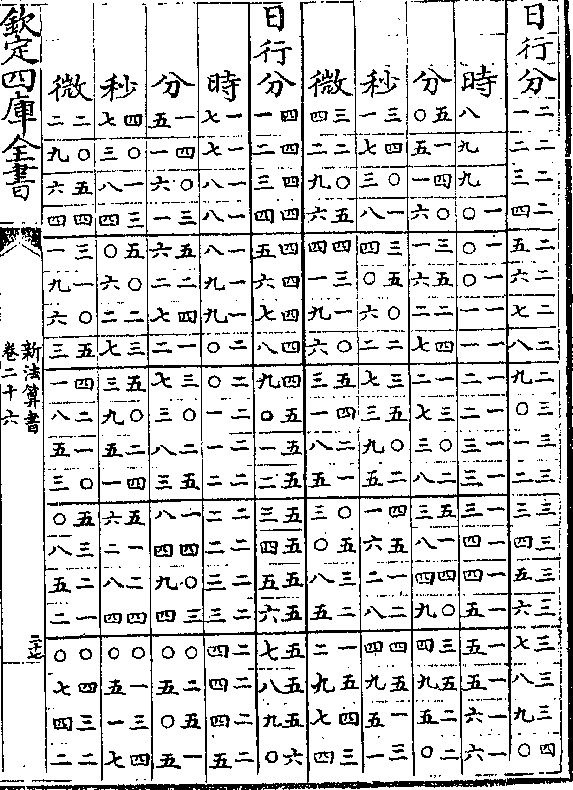
太阳周岁细行变时表说太阳之行度有二一曰平行即一日为五十九分○八秒
有奇一曰自行(自行亦名视行/又名实行细行)自行有大有小极大者
为六十一分二十秒极小者为五十七分六秒(见周日/细行表)
置太阳细行表法取自行之极大者六十一分二十秒递
减半分迄五十七分六秒而止共十类成表(如六十一/分六十分)
(三十/秒等)
算法以二十四时化微为实以细行分秒化微为法而一
得日行六十分对时之数各半之再半又以约法收之
卷二十六 第 9a 页 WYG0788-0439b.png
微收为秒秒收为分分收为时故设表有日行分其对又有时分秒微也
查表法凡有太阳所行之分数命变时则以本日细行分
数取本表又以所行之分数向右行日行分下求其相
当数之对即得其时分也若元数尚有秒则命右行分
为秒其所得亦为分秒微亦如之
假如崇祯戊辰年算冬至得距子正为三十三分四十四
秒二十微命变时查冬至表右行求三十三其时为十
二时五十四分四十六秒五十七微又查四十四秒得
卷二十六 第 9b 页 WYG0788-0439c.png
十七分一十三秒三微再查二十微得七秒四十九微并之共得十三时十二分○七秒四十九微
若所设日细行与表上方日行不合则用其相近数若欲
得细数则取其多寡两数用中比例法然所差不能过
秒其数极微故不细录
又如戊辰年算立夏得距子正三十八分五十六秒五十
七微命变时因立夏日距冬至为一百三十五日用一
百三十一日表向右行查三十八分得十五时四十三
分二十六秒五十三微又查五十六秒得二十三分十
卷二十六 第 10a 页 WYG0788-0439d.png
秒二十一微再查五十七微得二十三秒三十五微并之共得十六时○七分○秒四十九微
反之以时求分则于本日细行表中行求所设之时得右
行之相对数为分若中行无设时用近小数取其分又
以设时及近小两数较之再查中行数右行得秒又用
近小数再求之得微并之得行之分秒微
假如有时积一十四时二十九分○五秒一十二微而求
太阳之平行分则于本表(无本表则相近表/为五十九分可用)中行取近
小数即十四时十四分十四秒十四微其右行有三十
卷二十六 第 10b 页 WYG0788-0440a.png
五分又以设数与近小数较之为十四分五十秒五十八微以十四分查中行之相近数右行有三十六秒又
有时之十二秒查得三十微并之得三十五分三十六
秒三十微
卷二十六 第 11a 页 WYG0788-0440c.png
卷二十六 第 11b 页 WYG0788-0440d.png
卷二十六 第 12a 页 WYG0788-0441a.png WYG0788-0441b.png WYG0788-0441c.png WYG0788-0441d.png WYG0788-0442a.png WYG0788-0442b.png WYG0788-0442c.png WYG0788-0442d.png WYG0788-0443a.png WYG0788-0443b.png WYG0788-0443c.png WYG0788-0443d.png WYG0788-0444a.png
卷二十六 第 12b 页 WYG0788-0444c.png
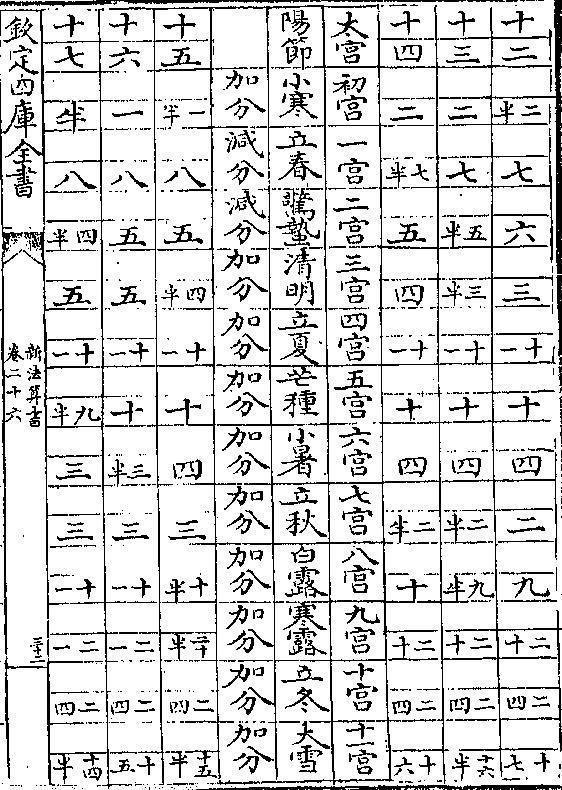
日差表说测太阳行度以春分为本因春分时无分平日用日(太阳/两行)
(略/同)故从春分起算立日差表
日差所以然者其故有二一太阳平视两行差一两道正
球升度差然求四正日差其故仅一盖四正时两道正
球升度无差故免日差之一根
夏至求日差则两行差为一度五十分(夏至在最高前约/六度则从春分至)
(夏至为八十四度除分秒不算求均数得十三分以二/度三分全均数或春分均数内减之馀一度五十分)
乃黄道上从春分至夏至两行之差因时刻用赤道度
卷二十六 第 13a 页 WYG0788-0444d.png
则求春分左右黄道一度五十分得赤道同升一度三十八分(均数大差在春分故/用春分左右升度)变时(赤道一度为时之四/分度之一分为时之)
(四/秒)得六分三十六秒约半分如表平行小视行大故表
用加号加于平时得视时
秋分则从春分起算两行差为四度六分变时得十六分
二十四秒(不及三十/秒故不算)如表平行小视行大故亦用加号
冬至未到最高冲(两行无/差之限)相距亦约六度均数为十三分
宜与二度三分全差加之得二度十六分查赤道升度
得二度○五分变时得八分二十秒(不满三十秒故不/算若欲微数秒亦)
卷二十六 第 13b 页 WYG0788-0445a.png
(可/用)号曰加立夏均数(从最高/起算)为三十六分赤道上为三十三分减去
春分两道升度差十三分馀二十○分(两行之日差第/一根也)
又黄道四十五度(立夏/点)得赤道同升为四十二度二十
九分其较为二度三十一秒(赤道升度小则用日为大/平日为小宜加又平行大)
(则用日小/亦宜加)以两故之两数并之得二度五十分变时为
十一分十六秒其号为加
立春均数其两行差为三十五分(从最低/起算)赤道上为三十
三分(平春分两道差为十三分今不算/盖春秋分两数相均)又立春赤道上
卷二十六 第 14a 页 WYG0788-0445b.png
得四十七度二十九分(从冬至/起算)其盈黄道数为二度二十九分而与升度日差两数相减(平行大视行小其差/宜加于平日赤道数)
(大黄道小宜减则两数为异类也/因均法相减当从实数之号)得一度五十六分变
时为七分四十四秒约算八分其号为减
各节气算表如上若用古世两行大差或黄赤两道各大
距度(从古各法/距度不同)或最高距夏至多寡直再算作立成
首直行为十二宫次行为节气首横行为宫度
用法
置所算太阳经宫度及节气(所算经度/皆平日度)视所置首直行宫
卷二十六 第 14b 页 WYG0788-0445c.png
节与首横行度数横直相遇得差数查本号与平时加减之得用日时
如癸酉年冬至算得十二时三十一分半查本表冬至得
八分号为加加之得三十九分为用时
若以某用日时刻求太阳经度先约得日躔宫度入表得
数反用其号加减之得平时可算太阳之平经度(其假/如见)
(日躔/历指)
卷二十六 第 15a 页 WYG0788-0446a.png WYG0788-0446b.png WYG0788-0446c.png WYG0788-0446d.png WYG0788-0447a.png
卷二十六 第 15b 页 WYG0788-0447c.png
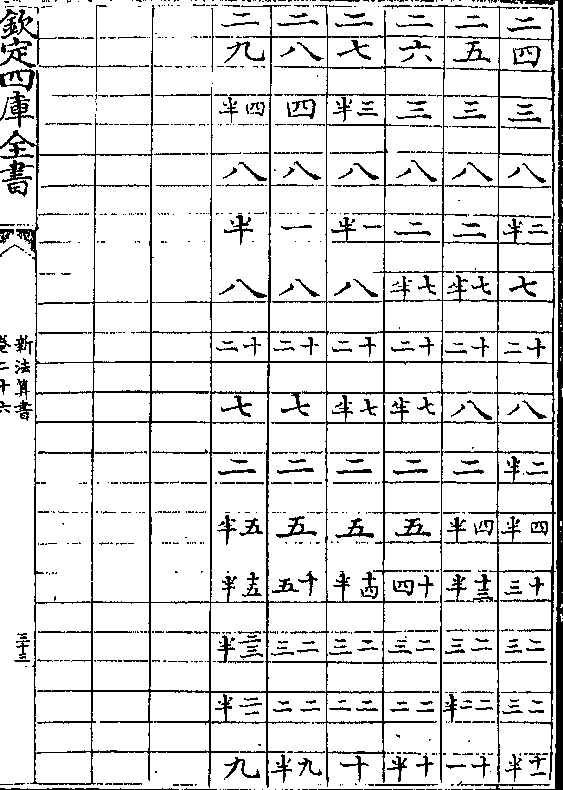
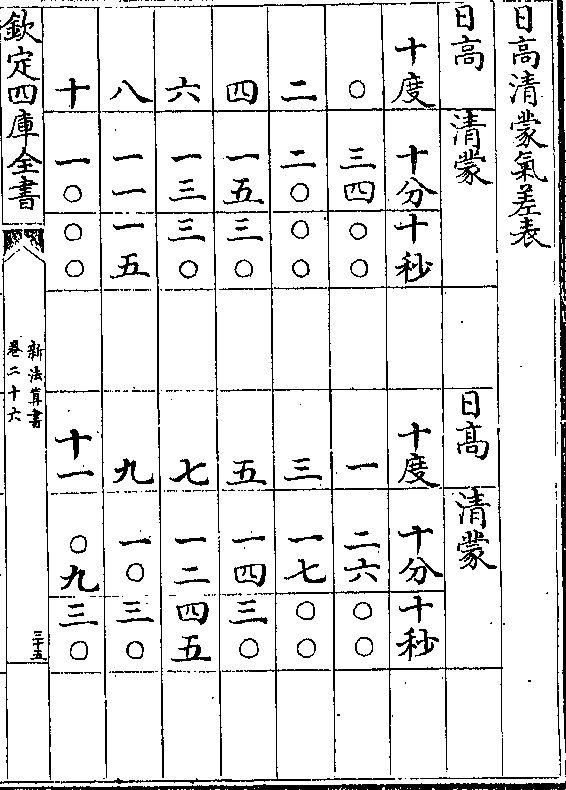
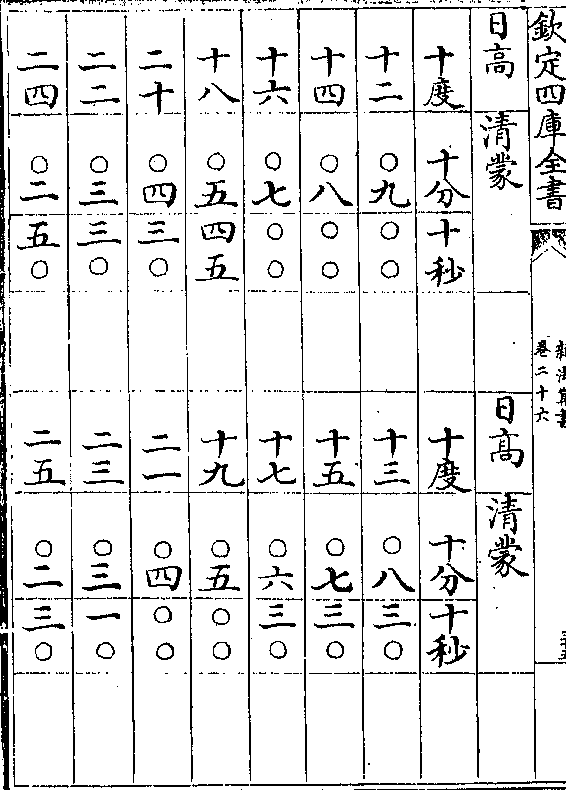
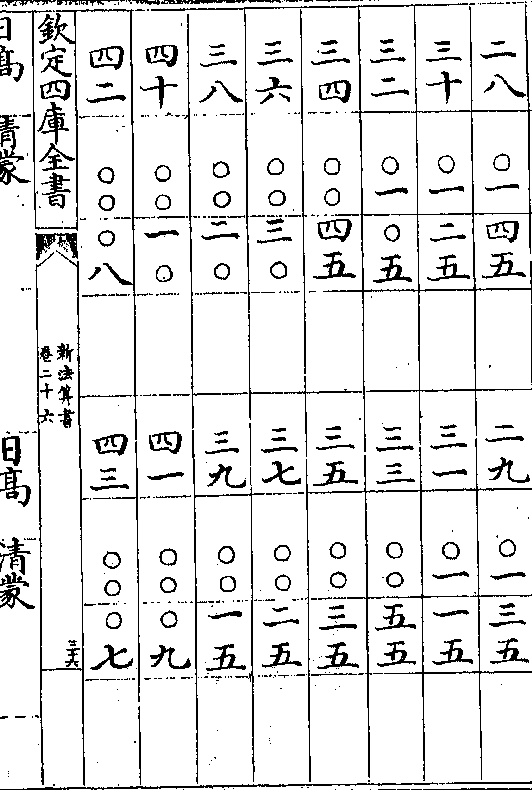
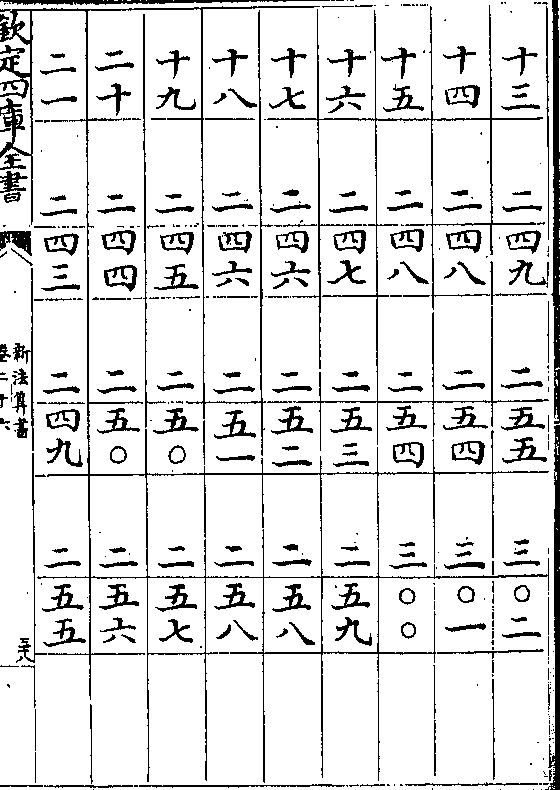
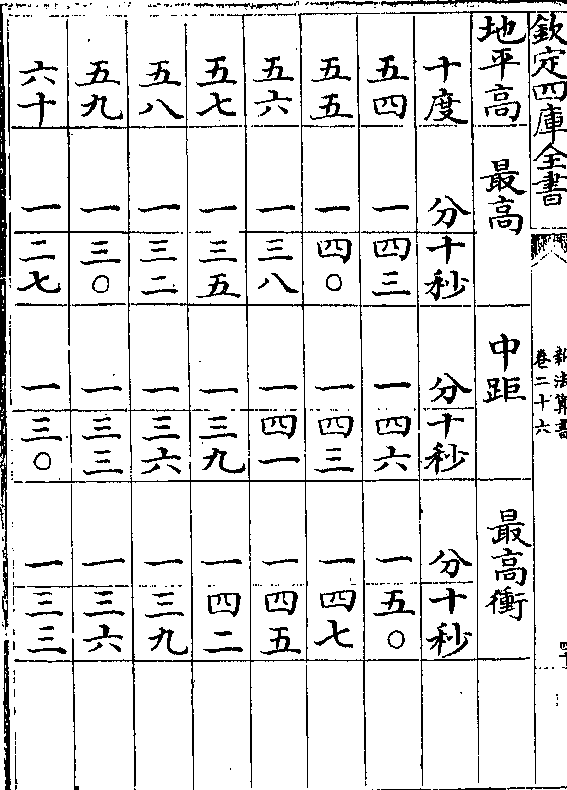
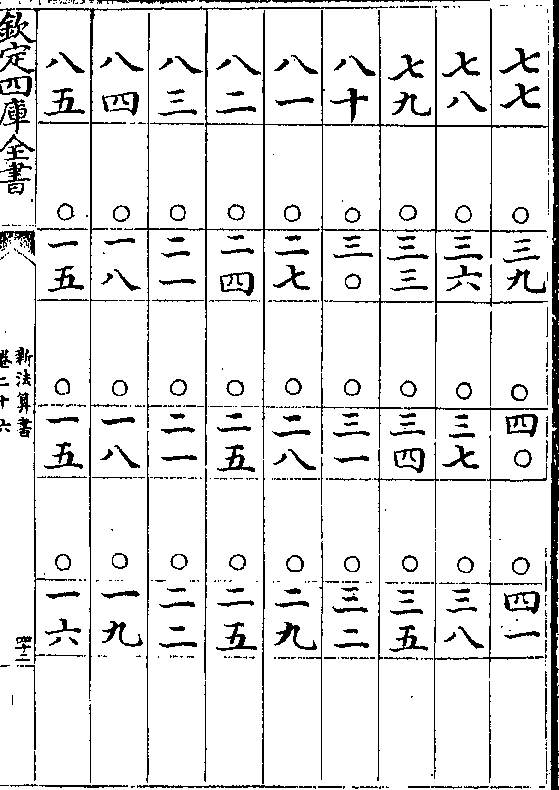
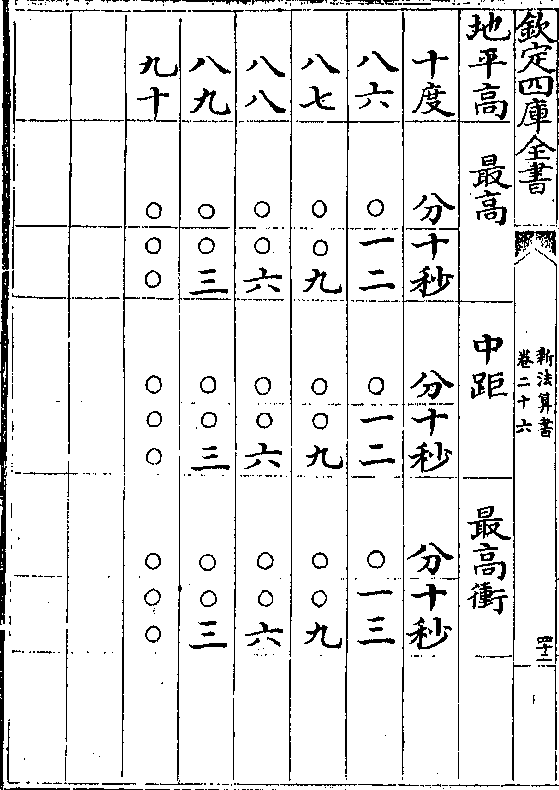
清蒙地半径表用法清蒙气说见日躔历指第三其用表法先测得日轨高
若干度查表得本度下之清蒙分秒以减日轨高得日
躔地平上之实高
如日轨高十六度查表十六度下得清蒙七分以减十
六度馀十五度五十三分为日躔地平上之实高
地半径说见日躔历指第八其用表法先测得日轨高
若干度次视本日最高三距如夏至左右三宫属最高
春秋分各左右三宫属中距冬至左右三宫属最高冲
卷二十六 第 16a 页 WYG0788-0447d.png
于日高度下查本距日之地半径分秒以加日轨高得日躔地平上之视高
如夏至测得日轨高十六度属最高查表十六度下得
地半径差二分四十七秒以加日轨高得十六度二分四
十七秒内减清蒙差七分馀十五度五十五分四十七
秒为日躔地平上之视高
卷二十六 第 16b 页 WYG0788-0448a.png WYG0788-0448b.png WYG0788-0448c.png
卷二十六 第 17a 页 WYG0788-0448d.png
其法以此差率减所测视高度分得实高度分
卷二十六 第 17b 页 WYG0788-0449a.png
卷二十六 第 18a 页 WYG0788-0449b.png
卷二十六 第 18b 页 WYG0788-0449c.png
卷二十六 第 19a 页 WYG0788-0449d.png
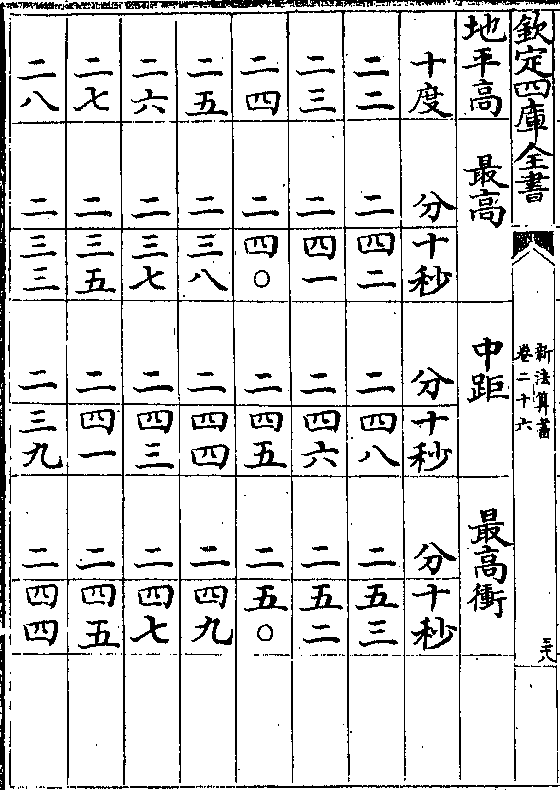
卷二十六 第 19b 页 WYG0788-0450a.png WYG0788-0450b.png WYG0788-0450c.png WYG0788-0450d.png WYG0788-0451a.png WYG0788-0451b.png WYG0788-0451c.png WYG0788-0451d.png WYG0788-0452a.png WYG0788-0452b.png WYG0788-0452c.png WYG0788-0452d.png WYG0788-0453a.png WYG0788-0453b.png WYG0788-0453c.png WYG0788-0453d.png WYG0788-0454a.png
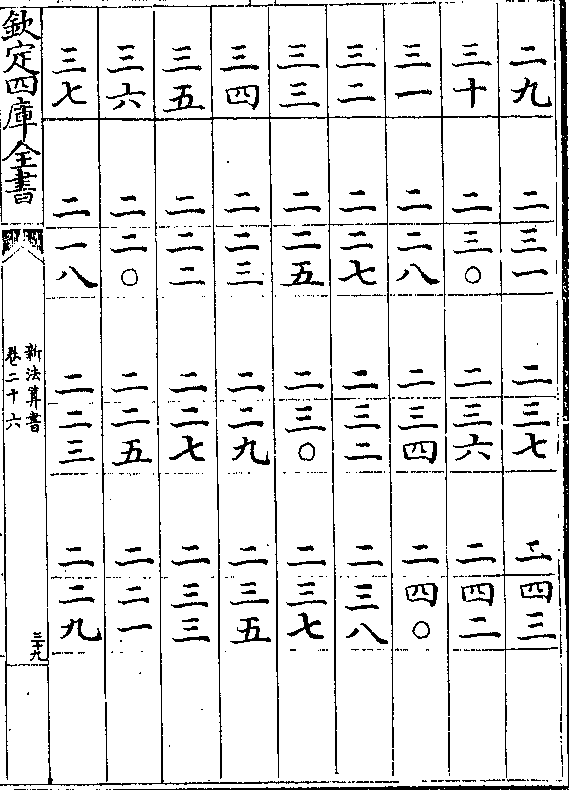
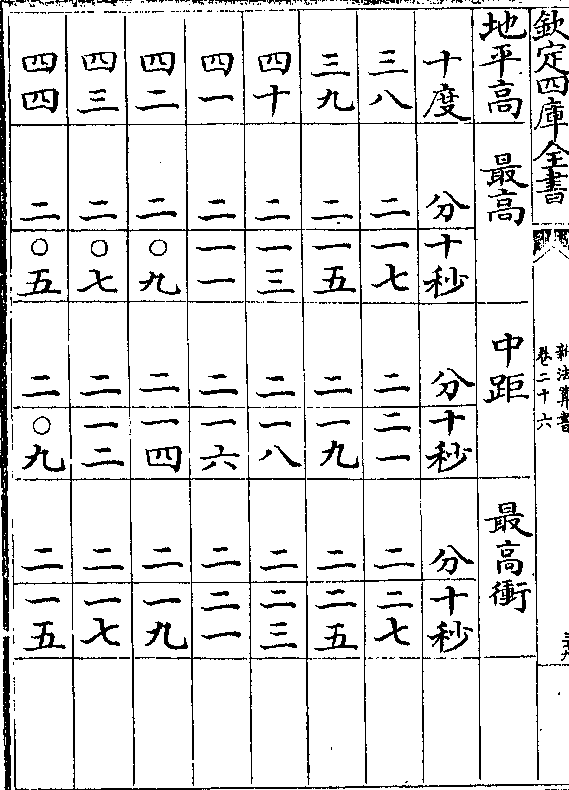
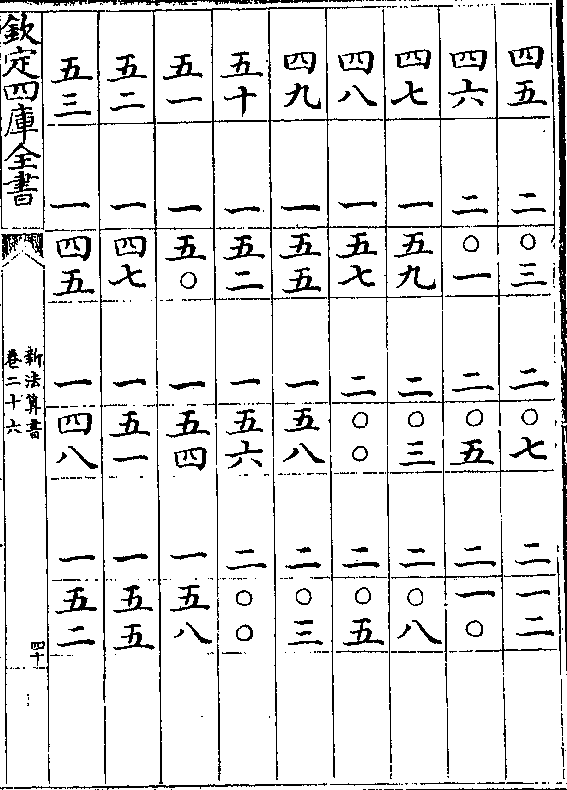
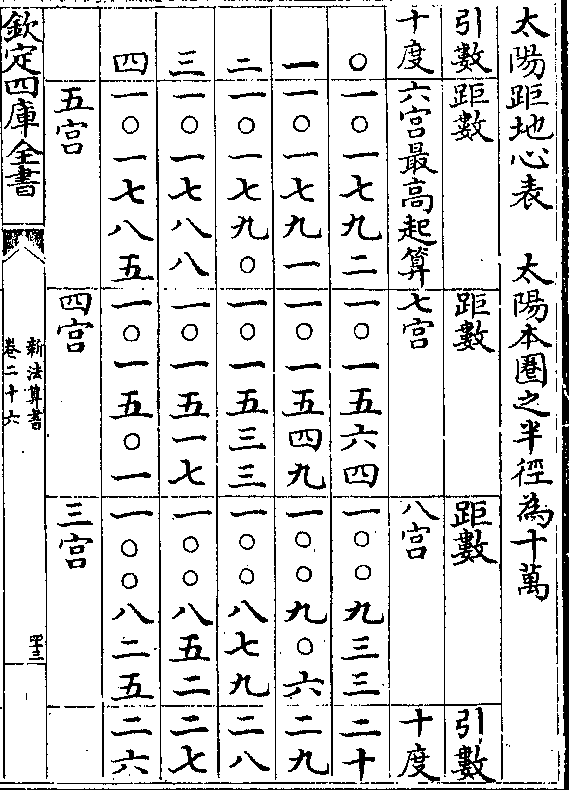
卷二十六 第 20a 页 WYG0788-0454b.png
新法算书卷二十六