钦定四库全书
　新法算书卷十二　　　　明　徐光启等　撰
　　测天约说卷下
　　　宗动篇第三
总论二条　论宗动有二端一言本天之点与线二言本
　天之运动
　三曜皆有两种运动宜以两物测之犹布帛之用尺度
　也七政恒星皆一日一周自东而西则以赤道为其尺
　度又各有迟速本行自西而东则以黄道为其尺度凡

　动天皆宗于宗动天故黄赤二道皆系焉(三曜者日/月星也)
论本天之点与线　凡三章
论赤道七条　赤道于诸大圈为最尊其义有三不知赤
　道则诸大圈无从可解一也赤道之理特为易明二也
　一日一周乃七政恒星之公运动赤道主之三也
　其两极即大圜之两极何者为本道与天元赤道相合
　为一线动静虽异终古不离也
　大圜之心中圈之心赤道之心地之心同是一点为赤
　道与大圈中圈同为大圈故也

　赤道既为大圈其分数亦有半圈有象限有三百六十
　度及分秒其算数则从一至三百六十与黄道地平异
　黄道分十二宫各以三十为限地平分四象各以九十
　为限故赤道亦有过极经圈一百八十为用甚大其左
　右旁各有距等侣圈(即纬/圈)每至极各九十不甚为用为
　与天元纬度一一同线故
　　　　　　其用则以赤道之经纬度测各点之所在
　　　　　　命为各点赤道经纬度
　　　　　　如上图赤道上任设甲点从赤道初点乙

　　　　　　数至甲为几度分即甲点之赤道经度分
　　　　　　也为在赤道上故无纬度
　　　　　　若所设甲点在赤道外则于过极大圈数
　甲点至赤道交即定赤道初点至设点之经度为六甲
　点至赤道即所容之纬度为五
　凡分南北大分独六合之内(即大/圜也)及日以赤道分之他
　则否
论黄道十条　黄道亦大圈也两交于赤道两交之间最
　远于赤道者二十三度有奇

　黄道之两极去赤道两极亦二十三度有奇与二道相
　离最远之数同也
　　　　　　如上图甲至丙为黄赤二道相离最远之
　　　　　　二十三度有奇则庚至戊亦黄赤二极相
　　　　　　离之二十三度有奇
　黄道分数其四象限三百六十度与赤道同又十二分
　之为宫二十四分之为节气七十二分之为候与赤道
　异十二宫曰玄枵娵訾降娄大梁实沈鹑首鹑火鹑尾
　寿星大火析木星纪后历家从便命之曰子亥戌酉申

　未午巳辰卯寅丑
　节气曰冬至小寒大寒立春雨水惊蛰春分清明谷雨
　立夏小满芒种夏至小暑大暑立秋处暑白露秋分寒
　露霜降立冬小雪大雪每一节分为三候节气中以二
　至二分为主
　黄赤道交处为春秋分相离最远为冬夏至
　黄道左右各八度以定月五星出入之道名为月五星
　道(又名六曜道/下文通用)诸曜出入于黄道度多寡不同最远者
　八度也又总名为黄道带(古法左右/各六度)

　　　　　　　　　　　　　　　如上图平分二十
　　　　　　　　　　　　　　　四气者为黄道带
　　　　　　　　　　　　　　　甲至乙广八度丁
　　　　　　　　　　　　　　　戊巳庚为赤道圈
　　　　　　　　　　　　　　　辛壬癸为夏至圈
　　　　　　　　　　　　　　　子丑寅为冬至圈
　　　　　　　　　　　　　　　丙则地心也
　
　

　周天分十二宫非独宗动天之面也凡六合之内(即大/圜)
　一切所有从宗动之面下至地心皆以十二分之故凡
　　　　　　言宫者有四义其一黄道带上有一长方
　　　　　　面为甲乙丙丁甲乙长三十度乙丙广十
　　　　　　六度凡七政彗孛等从地心作直线过本
　点至此面之某度分即命为本点在本宫之某度分也
　　　　　　其二以甲乙丙丁为面从地心戊出四线上
　　　　　　至方面之甲乙丙丁各角成锐角体凡六
　　　　　　合之内一切所有但入此锐体中即命为

　在本宫之某度分
　　　　　　其三为宗动天之内规面十二分之一以
　　　　　　黄道两大经圈各至极之巳庚为首尾中
　　　　　　相去三十度之辛壬为腰其中容即此分
　面也则凡诸点之在其面或在其下者皆命为在本宫
　之某度分
　　　　　　其四巳辛庚壬为面从面分至地心癸为
　　　　　　橘房体则入此体中者皆命为本宫之某
　　　　　　度分

　黄道有经度(一名/长度)有纬度(一名/广度)从黄道作过极圈以定
　其经度法与赤道同但本道本极异耳若起算从春分
　始其义有二一为是黄赤道二大圈之交也二为其为
　大圜之中中者二极之间也
　黄道之过极圈容其各纬度限各经度其左右侣圈限
　其各纬度容各经度
黄道比论八条　比论者一与赤道比一与地平圈比一
　与地平南北圈比
　与赤道比论　黄赤道之交为春秋分从此作过极大

　圈名为极分交圈从二道最远处作过极大圈为极至
　交圈此二大圈分黄赤道各为四分每分各为九十度
　　　　　　如上图甲乙为赤道极丙丁为赤道戊己
　　　　　　为黄道庚为二道之交则甲庚乙为极分
　　　　　　交圈甲丙己丁为极至交圈
　黄赤道相距不用黄道之纬度(经纬线交为直/角一名广度)而用赤
　道之纬度(从黄道出线与黄道为斜/角至赤道作直角名偏度)如降娄宫三十度
　若用广度则相距十三度今用偏度则十二度半所以
　然者为黄道斜迤若用广度则分及一象限无法可分

　矣不若用赤道之平直四象皆通也(本以黄道之三十/度立算而用赤道)
　(之侣圈且与赤道为直角与黄道为斜角故名为赤道/上之黄道偏度非从赤道目为偏度也其在赤道自名)
　(旁度/侣度)黄道一象限九十度各有其偏度最远者二十三度
　有奇不言三百六十者馀三象限与一同理故也
　　　　　　如上图甲丙为黄道弧若广度则值丙乙
　　　　　　偏度则值丙丁即作庚丙丁辛去离圈丙
　　　　　　丁在其上为距度
　测黄道弧之经度亦不用黄道之经度而用赤道之经
　度如降娄宫本三十度以赤道测之则二十七度为此

　宫之黄道斜而长赤道直而狭故不命降娄一次黄道
　上之长度曰三十而命赤道上之黄道升度曰二十七
　也(本以黄道之三十度立算而用赤道之经度二十七/其去离圈亦与赤道为直角名为赤道上之黄道升)
　(度非从赤道目为升度/也在赤道自名上度)
　　　　　　如上图甲乙为黄道弧若长度则值甲丁
　　　　　　升度则值甲丙于赤道上命甲丙曰黄道
　　　　　　之升度
　从黄赤交至北最远黄道圈上有九十度每度作一圈
　与赤道之距等圈平行其初圈则赤道也其第九十即

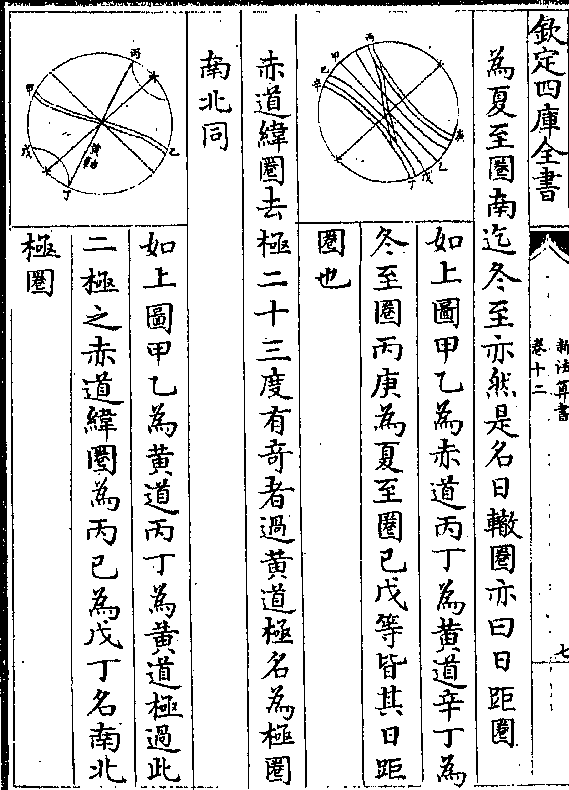　为夏至圈南迄冬至亦然是名日辙圈亦曰日距圈
　　　　　　如上图甲乙为赤道丙丁为黄道辛丁为
　　　　　　冬至圈丙庚为夏至圈己戊等皆其日距
　　　　　　圈也
　赤道纬圈去极二十三度有奇者过黄道极名为极圈
　南北同
　　　　　　如上图甲乙为黄道丙丁为黄道极过此
　　　　　　二极之赤道纬圈为丙己为戊丁名南北
　　　　　　极圈

　与地平圈比论　黄道与地平相遇作角其角随时随
　地大小不同正偏球皆然平球则否
　与地平南北圈比论　两圈交而作角自六十六度有
　奇而至九十九十为二至则直角六十六为二分则锐
　角
论本天之运动　凡四章
总论一条　宗动天常平行终古无迟疾赤道系焉故其
　行亦终古无迟疾
诸点与地平比论十八条　凡先在地平下不见后见在

　地平上为出反是为入
　凡平球各点见地平上者皆与地平平行无出入七政
　则否
　　　　　　如上图甲乙为地平与赤道同线丙丁等
　　　　　　为距等圈凡戊巳等点皆与地平平行独
　　　　　　七政循黄道行则否
　若黄道极在天顶则黄道每日一次与地平为一线一
　瞬则六宫在地平上六宫在地平下矣此非图像可明
　视浑球则得之离黄道极圈而外则出入皆有法一宫

　先出一宫继之入亦然若黄道极圈之内赤道极之外
　则反是
　欲测各点运行视其出入于地平测法必以赤道之升
　度为其尺度也何者赤道恒平行是名有法是为有准
　分之尺度故
　平球而外凡各宫出地平上在黄道俱三十度赤道则
　有长短测法俱不用黄道之长度而用赤道上之黄道
　升度
　如北极出地十度为丙乙其黄道初宫出地为丁戊三

　　　　　　十度则截取赤道先与黄道初度同出今
　　　　　　与黄道第三十度同在地平线上者为己
　　　　　　戊得二十四度弱是为黄道初宫之地升
　度凡论时刻及各点出入皆用之不用丁戊也
　凡测升度有二或连或断连者俱初宫初度起至本点
　依前法视赤道同出度即得若有别设二点在黄道上
　欲测二点之升度是为断也法以前点视初宫相距之
　升度几何是为前升度以后点距初宫之升度几何是
　为总升度于总升度中减去前升度即得后升度

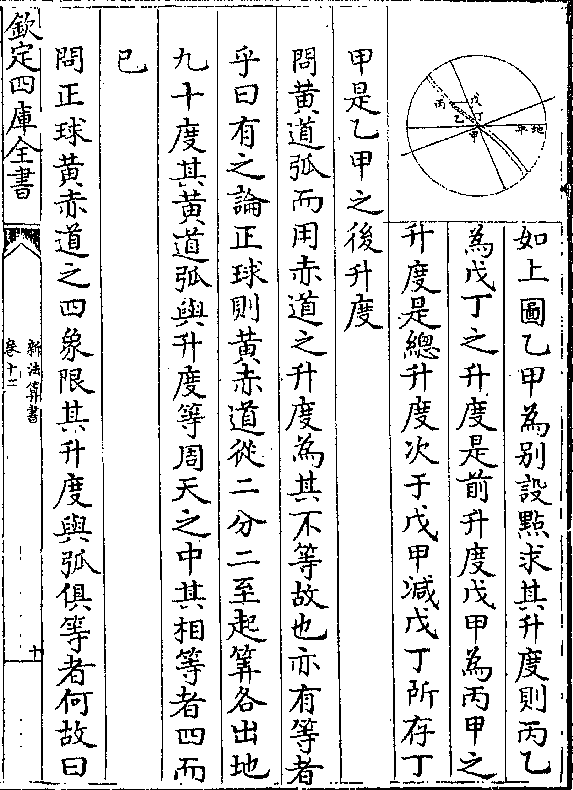　　　　　　如上图乙甲为别设点求其升度则丙乙
　　　　　　为戊丁之升度是前升度戊甲为丙甲之
　　　　　　升度是总升度次于戊甲减戊丁所存丁
　甲是乙甲之后升度
　问黄道弧而用赤道之升度为其不等故也亦有等者
　乎曰有之论正球则黄赤道从二分二至起算各出地
　九十度其黄道弧与升度等周天之中其相等者四而
　已
　问正球黄赤道之四象限其升度与弧俱等者何故曰

　黄赤道俱为二大圈相等则所分之相似圈分俱等一
　也又极至极分二大圈定黄赤道为四象限此二大圈
　出入地时即地平与四象限之交相合为一线故黄道
　之象限交必与赤道之象限交偕出偕入二也
　若欹球则黄道之半圈从分起从分止与赤道升降度
　等而周天之中其相等者二何者黄赤道二分之交同
　时至地平即二大半圈必相等故
　欹球二相等之外其他升度与黄道弧皆不等
　问二象限同升常自不等何以至九十度则等曰黄道

　弧与升度从初宫初度始每度之升度各有差初差渐
　多后差渐少渐近渐少至极远而平故也过二至则反
　是
　若正球则四象限之黄道弧与升度常相似其差甚少
　不过三度欹球则所差绝多
　　　　　　　　　　　如上正球甲乙赤道轴即地
　　　　　　　　　　　平故丁丙弧与丁戊升度相
　　　　　　　　　　　似欹球北极面则辛壬弧与
　辛癸升度所差多

　升降有二有正升降有斜升降各弧与升度同出入若
　赤道上升度大于黄道弧谓之正升降小者谓之斜升
　降愈大愈正为黄道与地平为角近于直角愈小愈斜
　为远于直角
　正球但有四宫为正升冬夏至前后各二宫是也冬至
　先后者析木星纪夏至前后者实沈鹑首馀八宫有斜
　者有半斜者
　若欹球则恒有六宫为正升正升谓之迟升
　斜升谓之疾升欹球有六宫焉正球有八宫焉

　问欹球之正升者六为何宫曰若北极出地一度至六
　十六度则鹑首鹑火鹑尾寿星大火析木是也此六宫
　则正升正升则斜降南极出地者反是
　球愈欹则黄道与地平为角亦愈斜
以升降比论四条　论正球黄道上两点去离二至二分
　(亦名为/四大点)各等则其升度亦等
　其相对之宫升度亦等如降娄寿星各二十七之类是
　也
　若欹球则相对宫之升度各不等

　有两点去春秋分大点等则其升度亦等
以正欹球比论二条　从降娄至鹑尾六宫欹球之升度小
　而正球大从寿星至娵訾六宫反是
　有两弧在黄道上相对相等其正球之两升度并为一
　率欹球之两升度并为一率此两率等
以黄道之出入比论(即升降度/之合也)五条　各宫各弧各点之
　出度必等于入度(不论正/偏球)
　各宫之出入度并与相对宫之出入度并等
　欹球各宫之出入度虽等而正斜不等此正升则彼斜

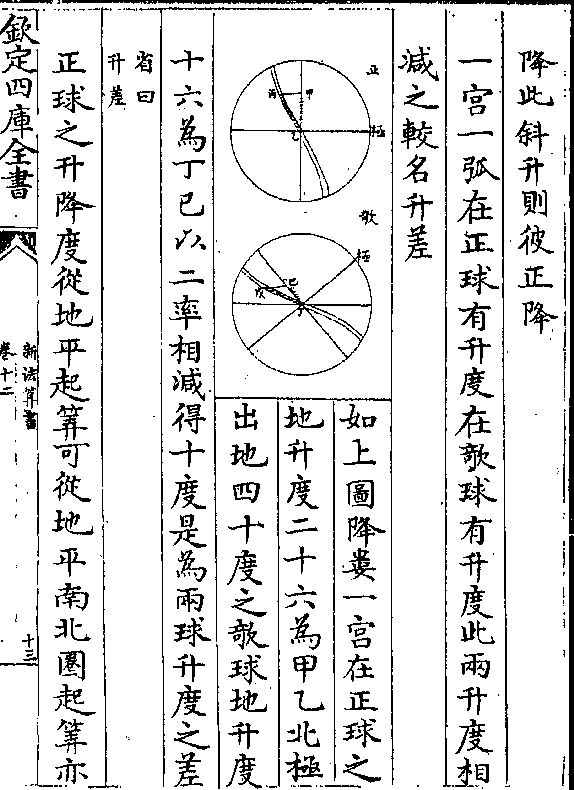　降此斜升则彼正降
　一宫一弧在正球有升度在欹球有升度此两升度相
　减之较名升差
　　　　　　　　　　　如上图降娄一宫在正球之
　　　　　　　　　　　地升度二十六为甲乙北极
　　　　　　　　　　　出地四十度之欹球地升度
　十六为丁己以二率相减得十度是为两球升度之差
　(省曰/升差)

　正球之升降度从地平起算可从地平南北圈起算亦
　可为赤道与地平圈与南北圈相遇俱为直角故等欹
　球则否必用地平也

太阳篇第四(不称日者篇中有时日之/日故别言之月称太阴同)
总论　宗动天之下则有列宿又下则填星则岁星则荧
　惑何以序先太阳其义有三一列宿与六曜之理皆系
　太阳不先论此不得论彼二理较易明先明其易难者
　并易三万光之原诸曜皆从受光焉月若其配星其从
　也
从本体论　凡三章
　论太阳之形象本是圆体　圆有面有体太阳之为圆
　面举目即是不待言矣其为圆体何从知之曰凡物未

　有有面无体者太阳之为物大矣知其必有体也凡自
　然生者初生者无物不圆太阳之生亦本自然曾无雕
　琢初生则然曾无迁变又诸体中圆为最尊以太阳较
　天下有形之物亦是最尊知其必为圆体也
　论太阳之大　欲知物大先知其径径有二一为视径
　视径者人目所视也旧云太阳之径一度近来测验实
　　　　　　止半度
　　　　　　如上图甲乙乙丁丁戊为宗动天内规面
　　　　　　之三度人从辛视太阳之己庚径于天度

　仅得乙丙不满乙丁之一度约如乙丙者七百二十则
　满黄道周故知视径为半度也
　一为本径欲知本径先论其去地之远太阳去地有时
　近有时远折取中数则以地全径为度(里数太多难计/故以地径之里)
　(数为其尺度也地之周约/九万里其全径约三万里)二十四其地径自之得五百
　七十六是太阳去地之中数也(其比例云地之径与太/阳去地之半径若一与)
　(五百七/十六也)既知其视径又得其去地之远因以割圆术求
　其本径得太阳之容大于地之容一百馀倍也(割圆术/有专书)
　(二径相比见几何原本第十二卷第十八题容者体之/容算术谓之立圆积非径线亦非面也其算法后篇详)

　
　论太阳之光　日为大光六合之内无微不照有不透
　明之物隔之则生影地在天中体小于日故影渐远渐
　　　　　　杀以至于尽其影之长不至太阳之冲
　　　　　　如上图甲乙为日丙丁为地其影至戊而
　　　　　　止不至己
　太阳面上有黑子或一或二或三四而止或大或小恒
　于太阳东西径上行其道止一线行十四日而尽前者
　尽则后者继之其大者能减太阳之光先时或疑为金

　水二星考其躔度则又不合近有望远镜乃知其体不
　与日体为一又不若云霞之去日极远特在其面而不
　审为何物
从运动论　凡五章
　太阳之动有二其一与黄道赤道比论其一与地平比论
　与黄赤道比论　如从冬至一点起算行天一日一周
　明日不在冬至即此一圈作螺旋一周次日复然迄夏
　至点行一百八十馀周而通作一螺旋线也第冬至线
　与次日一周线相离甚近以次渐远迄春分而甚远过

　此渐近迄夏至而甚近过此又渐远如是循环无穷耳
　详见后篇
　又冬至初日之线其螺圈甚小次日渐大至春分甚大
　过此渐小迄夏至而甚小如是小大循环者何也为纬
　圈中冬夏至皆小圈赤道为大圈故也从冬至迄夏至
　此为成岁之半矣若从夏至迄冬至亦作螺旋行每日
　一周百八十馀日通作一螺旋线但此线非复前线而
　别作一线每日与前线作一交耳此为成岁之全也
　如图作螺旋圈不能为三百六十作二十四以明其意

　
　
　
　
　
　
　
　

　已上所说螺旋线是太阳之体理实作如是运动无可
　疑者但螺旋则无法之线也以此测候亦复无法可立
　故天官家别用他术如下文
　测候之术　如用春分起算初日从初点循赤道行迄
　一周是为一日明日即不在赤道而在其第二圈又不
　直距于初点而东西相去为黄道之一长度其南北距
　度即不及一度也此一周即为赤道之一距等圈矣太
　阳恒在黄道下行故无黄道之广度至第三日复作第
　三距等圈与次日同凡九十日行黄道九十度即于赤

　道旁作九十距等圈其第九十则夏至圈夏至圈去春
　分圈止二十三度半故太阳之行亦如是而止此九十
　距等线以当全螺线之半也用此术则从夏至迄秋分
　亦有九十距等线其线即春夏距等之原线矣
　至秋分即复行赤道一日无距度距圈与前春分日所
　行同线相对其两对处则有极分交圈以为之限也自
　春迄秋二分之间行一百八十度黄道长度与赤道之
　距度其数皆等从秋分而后每日作一距等圈其第九
　十则冬至圈也凡诸距度圈皆交于黄道独二至之两

　圈切于黄道为其行至是尽矣其两尽处则极至交圈
　为之限也秋分迄冬至亦二十三度半与其迄夏至等
　故其间距等圈与其迄夏至之距等圈亦等从冬至以
　后亦依前所行距等原线以迄春分而岁成矣
　太阳之行恒在黄道下无广度亦恒在两至之内故两
　至之内皆为太阳所行之道而太阳每日行一度弱故
　两至间之距等圈凡一百八十二有奇每一圈岁两经
　焉如此术即分太阳所行为二路其一分计每日所行
　各行于赤道侣圈皆在两赤道极之间其二总计每岁

　所行皆行于黄道在两黄道极之间其一日一周于黄
　道为一长度于赤道上不及一上度此一上度弱者名
　为黄道一日之升度黄道之升度每宫与赤道不等故
　每日黄道之升度一一不等(见本/设表)
　螺旋合术与黄赤分术比论　论合术则自东而西每
　日不及一度故云日迟论分术则自西而东每日循黄
　道行一度故云日疾其实一也但螺旋于理甚合而无
　法可推分术则分数易明其间即有参差不能及一微
　一纤非仪象可测故历家专用分术(加减/法也)以便推步

　与地平比论　太阳至地平上为出为明从东而西没
　于地平下为入为晦
　论正球春分日太阳出于东方行赤道赤道即东西圈
　渐升至顶极即至南北圈为极高之弧此地平以上之
　半昼分也亦谓之东半昼弧午正后渐降至地平谓之
　西半昼弧东西合则为全弧行尽全弧为一昼
　其一日之中地平上凡有表即得影日出则为无穷之
　西影渐短至顶仅得一点(或云是为无影安得一点不/知无表即无影若令表离于)
　(地平即有与/表等大之影)午正后影渐长至地平复为无穷之东影

　日既入地平下则有朦胧分(一名昏度/一名黄昏)行地平之低度
　十八(低度者非黄道赤道之度乃地平之/纬度也在下故名低度在上名高度)后此为夜
　　　　　　如上图甲乙为赤道即东西圈丙甲丁为
　　　　　　南北圈甲高九十度满一象限己戊为表
　　　　　　日出辛表端影在庚至壬影在癸至庚则
　在辛也至甲止一点丙丁即地平低度十八至子丑而
　止
　日至于南北圈下为半夜迨近地平下十八低度复为
　朦胧分(一名晨度一名昧旦/一名黎明一名昧爽)凡黎明将尽日将出地平

　上有云则为朝霞黄昏之始日初入地平上有云则为
　晚霞所以赤色者为日光返照如火出烟本是黑色与
　火并见即黑见烟不见火即为红烟矣
　问日出入则大日中则小何故曰地居天中日周其外
　因于太阳如受燔炙恒出热气是名清蒙之气此气之
　厚去地不能甚远日出入时人目衡视积气甚多如物
　在水中其体大于本体故出入时日形似大非果大也
　至日中时以垂线照地人直视之积气甚少日不受蒙
　则似小矣若出入时或深紫或微红或似长圆亦皆是

　气之厚薄疏密所为也
　其春分次日太阳离赤道即不出于东西圈之初度而
　在其稍北之阔度(即地平之经度不言广/者以别于黄道纬度也)其相去也与
　其日之距度等(为正球则赤道与地平/为直角故也欹球则否)太阳既稍北则
　其表影亦稍南其昼分与初日等其南北圈下之极高
　弧则稍减于九十度又次日则阔度愈大极高弧愈小
　以迄夏至其阔为二十三度有奇其高弧为六十三度
　有奇从赤道南迄冬至亦如之其方之昼与夜恒等何
　者赤道与地平为直角即一切经纬圈其隐见恒相半

　故
　　　　　　如上图甲乙为赤道即东西圈春分日日
　　　　　　从此道行次日以后渐向丁戊行甲至丁
　　　　　　乙至戊各二十三度有奇庚至丁其高弧
　六十三度有奇
　论欹球一岁中独春秋分两日得昼夜平何者是其日
　太阳在赤道下赤道与地平皆大圈交而相分即所分
　之圈分相等若赤道距等圈大小不等以地平分之其
　圈分上下皆不等

　　　　　　如上图甲乙为南北极丙丁为赤道丑寅
　　　　　　为地平春秋分两日日在戊为黄赤道之
　　　　　　交则地平上下圈分等过春分日渐北如
　至辛壬距等圈则丑寅地平分昼夜于子过秋分日渐
　南如至己庚距等圈则地平分昼夜于癸上下皆不等
　又一岁之中凡两昼之距两至等则其昼分之长短亦
　等凡两昼之距两分等即一在赤道南一在赤道北其
　距度等而此日之昼与彼日之夜等
　凡球愈欹极愈高即高至(不曰冬夏至而曰/高至通南北言之)之日愈长

　凡正球之南北阔度等欹球则否
　凡正球之二至日中时其高下恒相等欹球则否日中
　时其二至一甚高一甚低
　论平球则以半年为一昼以半年为一夜何者北极与顶
　极合即赤道与地平亦合故九十距等圈从赤道迄一
　至皆在地平上其在下亦如之也其表恒作无穷及最
　长影不作短影每日为一周亦作十二时或二十四但
　百八十周恒在昼耳
　论䑃胧(早为晨分暮为昏分或并曰/晨昏或省曰朦曰朦影朦度)

　太阳在二点二点之距一至等其朦亦等何者去至等
　则同在一距等圈上故
　若二点之距一分等其朦不等孰大孰小近于上极者
　则大远则小
　北极出地处则北六宫之朦大于南六宫南极出地处
　反是
　北极出地处太阳在北六宫愈近夏至朦愈大迄夏至
　极大过夏至渐小南方近冬至愈大迄冬至则极大过
　冬至渐小北极出地处迄冬至不极小极小者在赤道

　冬至之间南方迄夏至不极小极小者在赤道夏至之
　间
　太阳在北六宫愈北朦愈大
　平球之处其太阳入地低度不过二十三去朦度之十
　八未远也故其晨昏最长一年之中明多于晦几乎不
　夜
　正球上两点在赤道南北其距赤道等其朦亦等其距
　赤道不等其朦亦不等孰大愈远赤道者愈大故二至
　之朦甚大二分之朦甚小

　问欹球北极出地处之朦夏至极大而冬至不极小极
　小者在赤道冬至之间然则安在曰此在秋分之后特
　随地不同皆在分后至前不在其日也如北极出地四
　十度春分则六刻三十三分夏至八刻六十分秋分六
　刻三十三分冬至则七刻最小者六刻二十六分有奇
　在寒露之中候五日也(有本/表)

太阴篇第五
五纬在二曜之上今先太阴者何故一凡论年月日时皆
　以二曜定之二其理较五纬特为易明三太阴体大昼时
　亦见四太阴之能力亚于太阳五纬无能及之
从本体论
　论太阴之形象　本是圆体与太阳同虽有晦朔弦望
　不害为圆详见后论
　论太阴之大　太阴去人时近时远折取中数八其地
　半径自之得六十四半径为三十二全径是太阴去地

　之中数也
　其视径去人愈近愈大愈远愈小折取中数亦得半度
　与太阳等
　其本径则小于地球地之容大于月约三十倍也
　论太阴之光　本自无光受光于太阳故本球之光恒
　得半以上因太阳之体大于其体故
　　　　　　　　　　如上图甲乙为日丙丁为月径
　　　　　　　　　　因日大故受光至于戊己
　太阴面上黑象有二种其一今人人所见黑白异色者

　是其二小者则日日不同非远镜不能见也详见后论
从运动论
　太阴之运动有二其一一日一周随宗动天行与六曜
　同公动也其二循白道(白道月之本道一/名月道下文通用)日行十三度
　有奇迄二十七日有奇而一周本动也因太阳同行二
　十七日有奇则过周二十七度有奇故又二日有奇乃
　及于日而与之会
　白道不与黄道同线而两交于黄道(两交名正交中交/亦名天首天尾亦)

　(名龙头龙尾/亦名罗计)两半交去黄道五度有奇故每行一周在
　黄道下者二交初交中是也他详后论

时篇第六　十三条
既明二曜之体又明二曜之运次因其运动以得时时者
　何物凡诸有形之物必有变革变革多端中有迁运一
　端因其迁运先后从而测量剖分之则为时也
　问草木鸟兽人事皆有变革迁运亦可用以为时何必
　二曜曰凡立术有三法一须公共一须分明一须永久
　惟二曜则然他无有足比者故也
　时之准分尺度一日是也一日者何太阳行一周而过
　赤道上之一升度弱(当黄道/一度)者是也日之起算有四法

　或以早或以晚或以昼之中或以夜之中
　日有大小分大者为昼夜小者为时辰时辰者十二分
　日之一也(西历为二十/四分之一)
　常静天之上有二大圈皆过两极而分赤道为四平分
　其一过顶即子午圈其一过东西点(东西点者赤道交/于地平是东西之)
　(最/中)即卯酉圈从卯至午其间又有二圈为辰为巳从午
　至酉其间又有二圈为未为申此六圈者终古不动凡
　三曜至某圈上即为某时也(十二时辰不止日也月所/至即为月之十二时星所)
　(至即为星/之十二时)其起算亦有四法或用子或用午或用卯或

　用酉
　时又有刻每时八刻一日则九十六刻东西所同用星
　官家用百刻取整数易算也
　刻又析为百分分析为百秒递为百以至微西法每刻
　为十五分分析为六十秒递分之皆以六十也
　其积日者以日加之初加为一旬一旬者甲至癸十日
　再加为一月一月者太阴行一周而与日会也(称一月/者有二)
　(义一为二十七日有奇而周于天一为二十九日有奇/而及于日因交会之理分明故不用月周而用朔实也)
　月之分也两分之为朔望四分之为晦朔弦望

　太阳行一周三百六十五日四分日之一弱为一岁谓
　之太阳年其起算亦有四法一从冬至一从春分(测天/用之)
　一从秋分(论二十八宿起于/角亢在秋分后)一从夏至(古时或/用之)用太阳
　年者四年而闰一日为四分之一也四百年而减一闰
　为弱也
　凡论岁以太阳为法太阴行十二周为一岁者为其近
　于太阳年也是谓之太阴年用太阴年者岁积气盈朔
　虚十日有奇三年一闰为十日故五年再闰十九年七
　闰为有奇故

　太阳年之分也二分之为半岁周四分之为四季八分
　之为分至启闭(立春立夏为启/立秋立冬为闭)十二分之为节二十四
　分之为节气中气七十二分之为候
　其积年者以年加之十二年为一纪三十年为一世六
　十年亦为一纪

恒星篇第七
向己说常静宗动二天二天之下则恒星天也略论其凡
　有四其一为几何其二为貌状其三为能力其四为迁
　变
几何　六条
　万物中形天为最大大有二义一在上所最远故最大
　二能力最大故其体亦大
　其形象为圆球何以知之天体最为精纯无杂最为单
　独无二圆之为象亦无杂亦无二体性如此故其形象

　亦当如此又运行最疾者莫如圆体他体则滞碍也
　其去地最远远之数以地之半径为度最近处得一万
　四千度自此以上非人思力所及知也此端似为难信
　證见后篇
　其所在万物之最上
　其质最细何以徵之常在上不霣坠知为轻虚细密也
　其质又极精纯为无他夹杂故
貌状　一条
　天下之物皆以颜色为其美饰颜色之外别有二美饰

　一为透彻一为光耀也颜色之美美之下分明光之美
　美之上分何者其形妙好异于他色一也人之见之无
　不喜悦二也他物不能自见其美惟光能自见三也他
　物有色惟光能发扬其美妙四也有此四者故为天下
　真宝天最尊于万物故一切颜色不足为其文饰惟光
　为其饰矣或云天望之苍苍然苍非色耶何谓无色曰
　苍苍非色也太空之中气盈其处气亦无色气积极厚
　则成苍苍之色譬之玻瓈本自透明略无他色积之数
　重则成苍色太空中色亦犹此耳

能力　四条
　天之下济其于下土有大能力何以徵之运行一周成
　为四季凉燠寒暑万物藉为生长收藏一也世间微物
　无不各有能力稍大则能力称之天如彼其大也知其
　能力与之等大二也
　天之能力下及每用二器其一光也其一施也光不独
　能照天下亦能作热如用洼镜对日而成返照则能生
　火又用玻瓈圆球对日而成折照亦能出火其故为何
　光于天下为最尊热于四大物情中(四大情者一热/二冷三燥四湿)亦

　为最尊以尊生尊是其理也其次亦能生冷亦能生燥
　亦能生湿为光本非热非冷非燥非湿而其中有精足
　当四情故能生热生冷生燥生湿也(如仁中无芽叶花/实而其精足当四)
　(物故能生/四物也)夫光之为体若其发而及物何为施之不尽
　若其不发则一切所受为从何来故其体其用总非人
　间意量所及
　光之外别有施者不属光也此有二證其一海潮大小
　不因于光亦不因于冷热燥湿譬如磁石吸铁别有相
　摄相受者则受者为所施摄者为能施也又如怀胎生

　子七月生则长八月生则夭无不验者此亦非因于光
　亦非因于四情亦如磁铁有别相摄受者故也
　从上二能知天于下土盖有四德一曰覆冒一曰包函
　一曰生育一曰保存也假令不动亦有此德而又加之
　运动于此若此于彼若彼变化无端真非思议所及矣
迁变　四条
　凡物迁变首运动
　天之运动皆环行何者天体单独无二故共运动亦应
　单独无二环行者单独无二之行也何谓单行曰凡动

　如人如鸟兽如风皆杂乱无法之行也单行有二一曰
　垂线一曰圆线石在空中下坠于地此为垂线一切循
　环无端者皆为圆线垂线之动势尽而止惟圆线独为
　无穷天以覆函生存下土者也故不能不为无穷不能
　不为环行矣
　天之运动恒不去其本所论其各分无一不动而其全
　体无一分动
　天之运动有四异其一甚疾一刻分中行几万里如鸟

　如矢如炮如霹历皆非所及其二恒平行(其中迟速别/有故实无一)
　(不平行者/详见后论)若非一一平行即测候之术无从可用其三
　恒久不已其四万物之动此为首何者天下之动于此
　焉系故也若无此动即无四季即无生物问运动而外
　更有迁变乎曰论其体则无变何者为在最上物无及
　其际者故不能受变于物论其情则有变如月星无光
　因于日光变而有光一也又如日月有光因于交食而
　若无光二也
　
　新法算书卷十二