声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
乾坤体义 卷下 第 1a 页 WYG0787-0779a.png
 钦定四库全书
钦定四库全书乾坤体义卷下
明 利玛窦 撰
容较图义
万形有全体目视惟一面即面可以推全体也面从界
显界从线结总曰边线边线之最少者为三边形多者
四边五边乃至千万亿边不可数尽也三边形等度者
其容积固大于三边形不等度者四边以上亦然而四
乾坤体义 卷下 第 1b 页 WYG0787-0779b.png
 边形容积恒大于三边形多边形容积恒大于少边形
边形容积恒大于三边形多边形容积恒大于少边形恒以周线相等者验之边之多者莫如浑圜之体浑圜
者多边等边试以周天度剖之则三百六十边等也又
剖度为分则二万一千六百边等也乃至秒忽毫釐不
可胜算万形愈多边则愈大故造物者天也造天者圜
也圜故无不容无不容故为天试论其槩
乾坤体义 卷下 第 2a 页 WYG0787-0780a.png
乾坤体义 卷下 第 2b 页 WYG0787-0780b.png
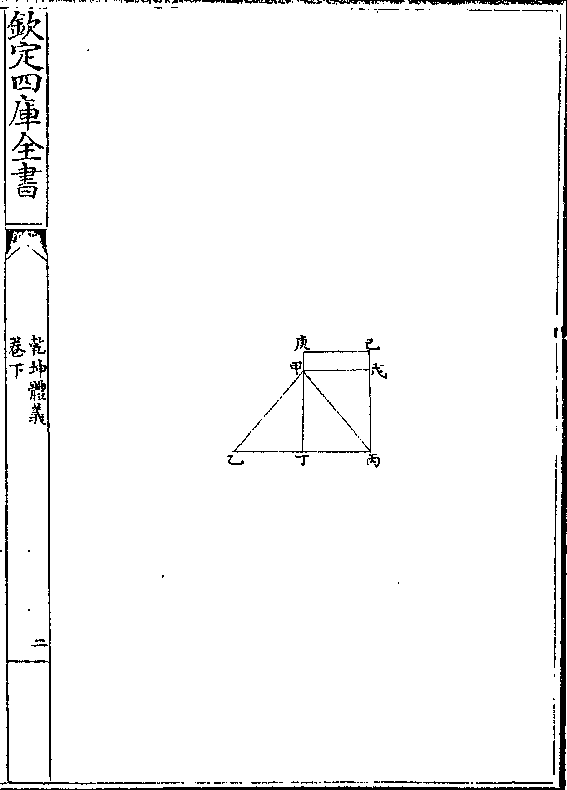
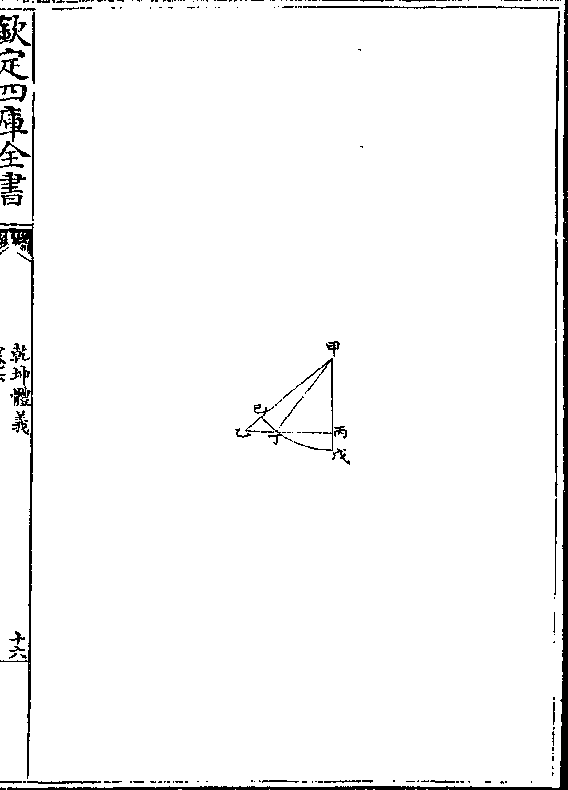
 凡两形外周等则多边形容积恒大于少边形容积
凡两形外周等则多边形容积恒大于少边形容积假如有甲乙丙三角形其边最少就底线乙丙两平
分于丁作甲丁线其甲乙甲丙两腰等丁乙丁丙又
等甲丁丙角甲丁乙角皆等则甲丁线为乙丙之垂
线(几何原本/一卷八)次作甲戊丙丁直角形而甲戊与丁丙
平行戊丙与甲丁平行视前形增一角者(一卷四又/三十六)
既甲丁丙甲丁乙两形等而甲丙戊与甲丁乙亦等
(一卷三/十四)则甲丁丙戊方形与甲乙丙三角形自相等
乾坤体义 卷下 第 3a 页 WYG0787-0780c.png
 矣以周论之其甲戊戊丙丙丁甲丁四边皆与乙丁
矣以周论之其甲戊戊丙丙丁甲丁四边皆与乙丁相等甲丙边为弦其线稍长试引丙戊至己引丁甲
至庚皆与甲丙甲乙线等而作庚丁己丙形与甲乙
丙三角形同周则赢一甲庚己戊形故知四边形与
三边形等周者四边形容积必大于三边形
乾坤体义 卷下 第 4a 页 WYG0787-0781a.png
 凡同周四直角形其等边者所容大于不等边者
凡同周四直角形其等边者所容大于不等边者假有直角形等边者每边六共二十四其中积三十
六另有直角形不等边者两边数十两边数二其周
亦二十四与前形等周而其边不等故中积只二十
又设直角形其两边各九其两边各三亦与前形同
周而中积二十七又设一形两边各八两边各四亦
与前同周而中积三十二或设以两边为七以两边
为五亦与前同周而中积三十五是知边度渐相等
乾坤体义 卷下 第 4b 页 WYG0787-0781b.png
 则容积固渐多也
则容积固渐多也乾坤体义 卷下 第 5a 页 WYG0787-0781c.png

乾坤体义 卷下 第 5b 页 WYG0787-0781d.png
 试作直角长方形令中积三十六同前形之积然周
试作直角长方形令中积三十六同前形之积然周得三十与前周二十四者迥异今以此周作四边等
形则中积必大于前形
乾坤体义 卷下 第 6a 页 WYG0787-0782a.png

乾坤体义 卷下 第 7a 页 WYG0787-0782c.png
 凡同周四角形其等边等角者所容大于不等边等角
凡同周四角形其等边等角者所容大于不等边等角者
设甲乙丙丁不等角形从丙丁各作垂线又设引甲
乙至己作戊丙己丁四角相等形(一卷三/十五)与不等角
形同底原相等(一卷十九/又三十四)甲乙亦同戊己而乙丁及
甲丙线则赢于己丁戊丙线是甲乙丙丁之周大于
戊丙己丁之周试引丁己至辛与乙丁等引丙戊至
庚与甲丙等而作庚丙辛丁形则多一庚戊辛己形
乾坤体义 卷下 第 7b 页 WYG0787-0782d.png
 因显四等角形大于不等角形
因显四等角形大于不等角形以上四则见方形大于长形而多边形更大于少
边形则圜形更大于多边形此其大略若详论之
则另立五界说及诸形十八论于左
第一界等周形
谓两形之周大小等
第二界有法形
谓不拘三边四边及多边但边边相等角角相等即
乾坤体义 卷下 第 8a 页 WYG0787-0783a.png
 为有法其攲邪不就规矩者为无法形
为有法其攲邪不就规矩者为无法形第三界求各形心
但从心作圜或形内切圜或形外切圜皆相等者即
系圜与形同心
第四界求形面
谓周线内所容人目所见乃形之一面
第五界求形体
如立方立圜三乘四乘诸形乃形之全体
乾坤体义 卷下 第 9a 页 WYG0787-0783c.png
 第一题
第一题凡诸三角形从底线中分作垂线与顶齐高以中分线
及高线作矩内直角方形必与三角形所容等
解曰有甲乙丙三角形平分乙丙于丁于庚作垂线
至甲至辛作甲丁己丙及辛庚己丙直角题言直角
与三角形等
先论曰甲乙丙三角形平分乙丙于丁作甲丁线次从
甲作戊己线与乙丙平行又作己丙戊乙二线成直
乾坤体义 卷下 第 9b 页 WYG0787-0783d.png
 角形此直角倍大于甲丁丙己形亦倍大于甲乙丙
角形此直角倍大于甲丁丙己形亦倍大于甲乙丙角形(一卷/四一)故甲乙丙三角形与甲丁丙己形等(一卷/二十)
(六/)
次论曰作甲丁垂线而第二图丁非甲乙之平分第
三图甲在方形之外皆从甲作戊己线引长之与乙
丙平行成戊己丙乙方形及甲己丙丁方形而各以
丙乙平分于庚作庚辛垂线视甲丁为平行亦相等
(一卷三/十四)其戊己丙乙倍大于辛庚丙己即倍大于三
乾坤体义 卷下 第 10a 页 WYG0787-0784a.png
 角形何者以辛庚丙己长方形分三角形底线半故
角形何者以辛庚丙己长方形分三角形底线半故(一卷三/十六)
乾坤体义 卷下 第 11a 页 WYG0787-0784c.png
 第二题
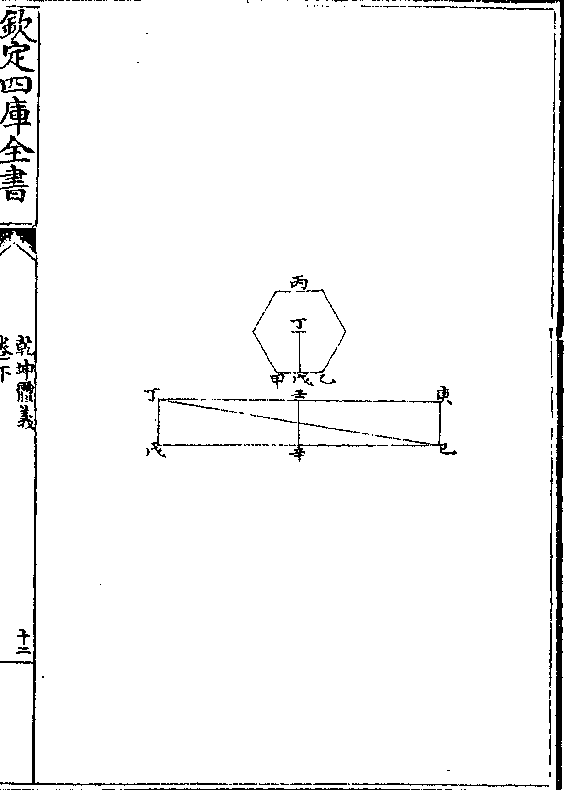
第二题凡有法六角等形自中心到其一边之半径线作直角
形线其半径线及以形之半周线舒作直线为矩内直
角长方形亦与有法形所容等
解曰有甲乙丙丁戊己法形其心庚自庚至甲乙作
直角线为庚辛另作壬癸线与庚辛等作癸子与甲
乙丙丁线等即半周线也题言壬癸子丑直角形与
甲乙丙丁戊己形之所容等
乾坤体义 卷下 第 11b 页 WYG0787-0784d.png
 论曰自庚到各角皆作直线皆分作三角形皆相等
论曰自庚到各角皆作直线皆分作三角形皆相等(一卷/八)其甲乙庚三角形与甲辛辛庚二线所作矩内
直角形等(以甲辛分甲乙之/半故见本篇一题)若以甲乙丙丁半形之
周线为癸子线以与壬癸线共作矩内直角形即与
有法全形等盖此半边三个三角形照甲乙庚形作
分中垂线其矩线内直角形俱倍本三角形故
乾坤体义 卷下 第 12a 页 WYG0787-0785a.png
乾坤体义 卷下 第 12b 页 WYG0787-0785b.png
 第三题
第三题凡有法直线形与直角三边形并设直角形傍二线一
长一短其短线与有法形半径线等其长线与有法形
周线等则有法形与三边形正等
解曰甲乙丙有法形其心丁从丁望甲乙作垂线又
有丁戊己直角形其边丁戊与法形丁戊等其戊己
线又与甲乙丙之周线等题言丁戊己三角之体与
甲乙丙全形等
乾坤体义 卷下 第 13a 页 WYG0787-0785c.png
 论曰试作丁戊己庚直角形两平分于壬辛作直线
论曰试作丁戊己庚直角形两平分于壬辛作直线与丁戊平行则丁戊辛壬直角形与甲乙丙形相等
(本篇/二题)何者戊辛线得甲乙丙之半周而又在丁戊矩
内即与有法形全体等故也其丁戊己三角形与丁
戊壬辛直角形等则丁戊己三角形与甲乙丙全
形亦等
乾坤体义 卷下 第 14a 页 WYG0787-0786a.png
乾坤体义 卷下 第 14b 页 WYG0787-0786b.png
 第四题
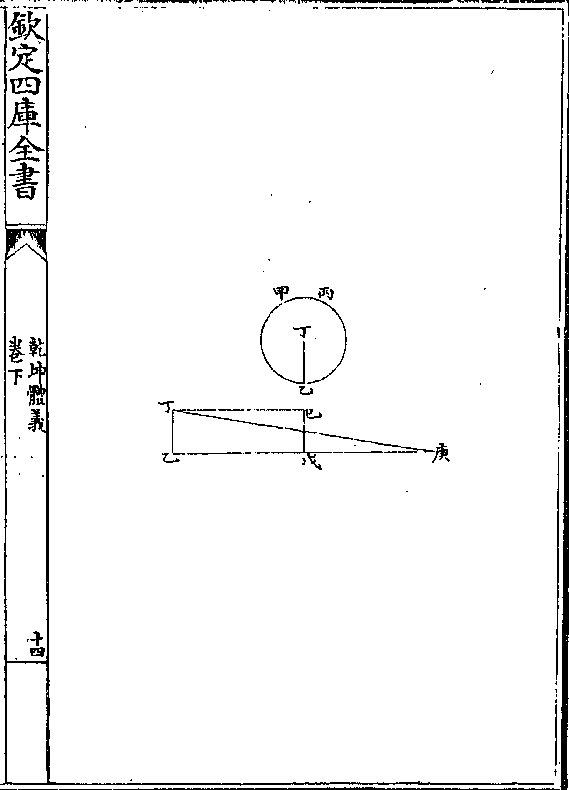
第四题凡圜取半径线及半周线作矩内直角形其体等
解曰有甲乙丙圜其半径为丁乙又有丁乙戊己直
角形两丁乙等半圜线与戊乙等题言甲乙丙所容与
丁乙戊己直角形所容等
论曰试以乙戊引长到庚令庚戊与乙戊等则乙庚
与圜周全等次从丁望庚作直线既丁乙庚三角形
之地与全圜地相等(在圜书/一题)而丁乙戊己又与丁乙
乾坤体义 卷下 第 15a 页 WYG0787-0786c.png
 庚三角形等(本篇四又一/卷四十注)则丁乙戊己自与全圜体
庚三角形等(本篇四又一/卷四十注)则丁乙戊己自与全圜体等
乾坤体义 卷下 第 16a 页 WYG0787-0787a.png
乾坤体义 卷下 第 16b 页 WYG0787-0787b.png
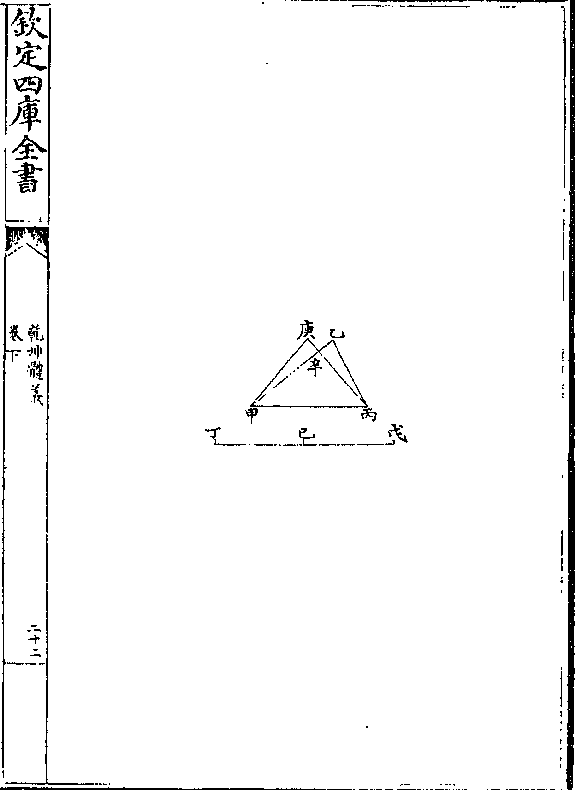
 第五题
第五题凡直角三边形任将一锐角于对边作一直线分之其
对边线之全与近直角之分之比例大于全锐角与所
分内锐角之比例
解曰有甲乙丙直角三边形丙为直角从甲锐角望
所对丙乙边任作甲丁线题言丙乙线与丙丁线之
比例大于乙甲丙角与丁甲丙角之比例
论曰甲丁线大于甲丙而小于甲乙(一卷/十九)若以甲为
乾坤体义 卷下 第 17a 页 WYG0787-0787c.png
 心以丁为界作半规必分甲己线于乙之内而透甲
心以丁为界作半规必分甲己线于乙之内而透甲戊线于丙之外其甲乙丁三角形与甲己丁三角形
之比例大于甲丁丙三角形与甲丁戊之比例何者
一为甲乙丁大形与甲己丁小形比一为甲丁丙小
形与甲丁戊大形比也则更之乙甲丁形与丁甲丙
形之比例大于己甲丁形与丁甲戊形之比例(五卷/二十)
(七/)合之则乙甲丙形与丁甲丙形即是乙丁线与丁
丙线之比例(形之比例与底线之/比例相等在六卷一)固大于甲己戊形
乾坤体义 卷下 第 17b 页 WYG0787-0787d.png
 与甲丁戊形之比例其甲己戊圜分与甲丁戊圜分
与甲丁戊形之比例其甲己戊圜分与甲丁戊圜分之比例原若己甲戊角与丁甲戊角之比例(六卷三/十三系)
则乙丙线与丁丙线之比例大于乙甲丙角与丁甲
丙角之比例也
乾坤体义 卷下 第 18a 页 WYG0787-0788a.png
乾坤体义 卷下 第 19a 页 WYG0787-0788c.png
乾坤体义 卷下 第 19b 页 WYG0787-0788d.png
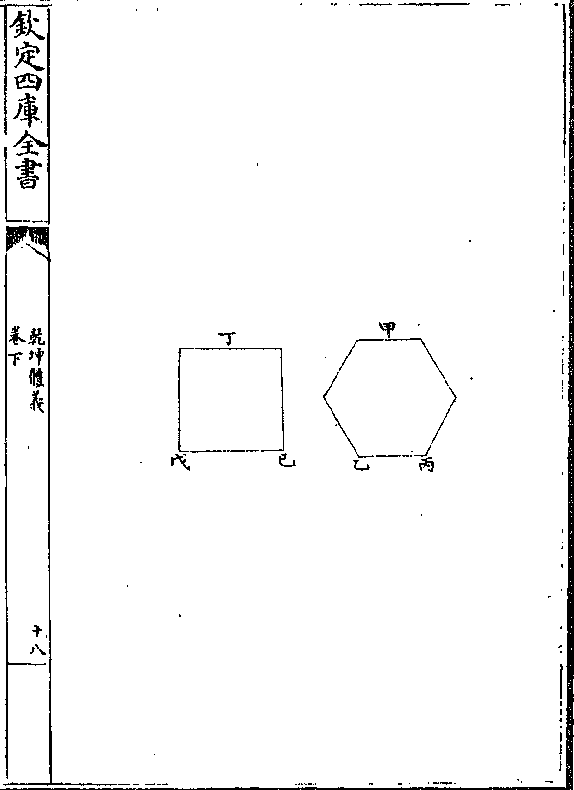
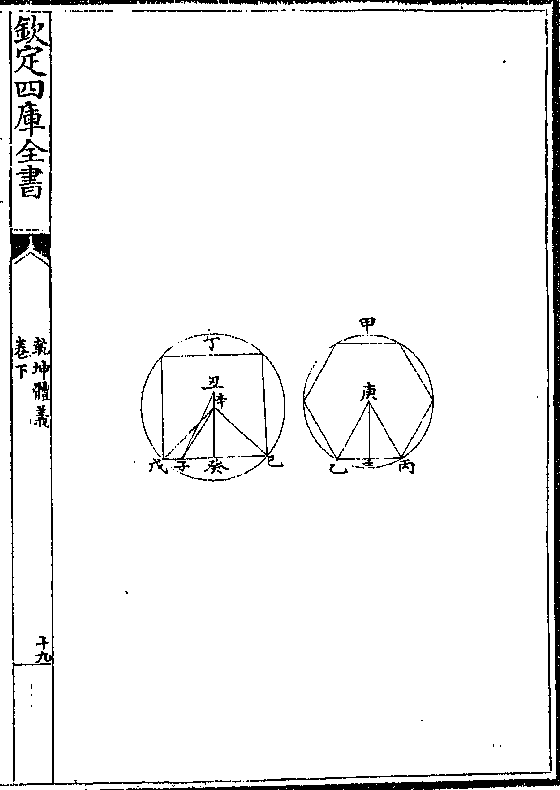
 第六题
第六题凡直线有法形数端但周相等者多边形必大于少边
形
解曰设直线有法形二为甲乙丙为丁戊己其圜周
等而甲乙丙形之边多于丁戊己(不拘四边六边虽/十边与十一二边)
(皆同/此论)题言甲乙丙之体大于丁戊己之体
论曰试于两形外各作一圜而从心望一边作庚壬
作辛癸两垂线平分乙丙于壬分戊己于癸(三卷/三)其
乾坤体义 卷下 第 20a 页 WYG0787-0789a.png
 甲乙丙形多边者与丁戊己形少边者外周既等而
甲乙丙形多边者与丁戊己形少边者外周既等而以乙丙求周六而遍以戊己求周四而遍则乙丙边
固小于戊己边而乙壬半线亦小于戊癸半线矣兹
截癸子与壬乙等而作辛子线又作辛戊辛己及庚
丙庚乙诸线次第论之其己丁戊圜内各切线等即
匀分各边俱等而全形边所倍于戊己一边数与全
圜切分所倍于戊己切分地亦等则甲乙丙内形全
边所倍于乙丙一边与其全圜切分所倍于乙丙切
乾坤体义 卷下 第 20b 页 WYG0787-0789b.png
 分不俱等乎其戊己圜切分与戊丁己全圜之切分
分不俱等乎其戊己圜切分与戊丁己全圜之切分若戊辛己角之与全形四直角(六卷三十/三题之系)则以平理
推之移戊己边于甲乙丙全边亦若戊辛己角之于
四直角也而甲乙丙内形周与乙丙一边犹甲乙丙
诸切圜与乙丙界之一切圜亦犹四直角之与庚乙
丙角也(六卷三十/三之二系)则又以平理推戊己与乙丙即戊
癸与乙壬而乙壬即是癸子又以平理推而戊辛己
角与乙庚丙角亦若戊辛癸之与乙庚壬也(五卷/六五)夫
乾坤体义 卷下 第 21a 页 WYG0787-0789c.png
 戊癸与癸子之比例原大于戊辛癸角与子辛癸角
戊癸与癸子之比例原大于戊辛癸角与子辛癸角之比例(本篇/五)则戊辛癸与乙庚壬之比例大于癸辛
戊与癸辛子之比例(五卷/十三)而癸辛子角大于壬庚乙
角(五卷/十)其辛癸子与庚壬乙皆系直角而辛子癸角
明小于庚乙壬角(一卷三/十二)令移壬乙庚角于癸子上
而作癸子丑角则其线必透癸辛到丑其庚壬乙三
角形之壬与乙两角等于丑癸子三角形之癸子两
角而乙壬边亦等于子癸边则丑癸线亦等于庚壬
乾坤体义 卷下 第 21b 页 WYG0787-0789d.png
 线而庚壬实赢于辛癸(一卷二/十六)今以庚壬
线而庚壬实赢于辛癸(一卷二/十六)今以庚壬线及甲乙丙半周线作矩内直角形必大于辛癸线
及丁戊己半周线所作矩内直角形也(本篇/二)然则多
边直线形之所容岂不大于等周少边直线形之所
容乎
乾坤体义 卷下 第 22a 页 WYG0787-0790a.png
乾坤体义 卷下 第 23a 页 WYG0787-0790c.png
 第七题
第七题有三角形其边不等于一边之上另作两边等三角形
与先形等周
解曰有甲乙丙三角形其甲乙大于丙乙两边不等
欲于甲丙上另作三角形与甲乙丙周等两边又等
其法作丁戊线与甲乙乙丙合线等两平分于己甲
乙乙丙两边并既大于甲丙边(一卷/十)则丁己己戊两
边并亦大于甲丙而丁己己戊甲丙可作三角形矣
乾坤体义 卷下 第 23b 页 WYG0787-0790d.png
 (一卷三/十二)以作甲庚丙得所求盖庚甲庚丙自相等而
(一卷三/十二)以作甲庚丙得所求盖庚甲庚丙自相等而甲丙同边则二形之周等而甲庚丙与甲乙丙为两
边等之三角形(此庚点必在甲乙线外若在甲乙边/上遇辛则辛丙线小于辛乙乙丙合)
(线即不/得同周)
乾坤体义 卷下 第 24a 页 WYG0787-0791a.png
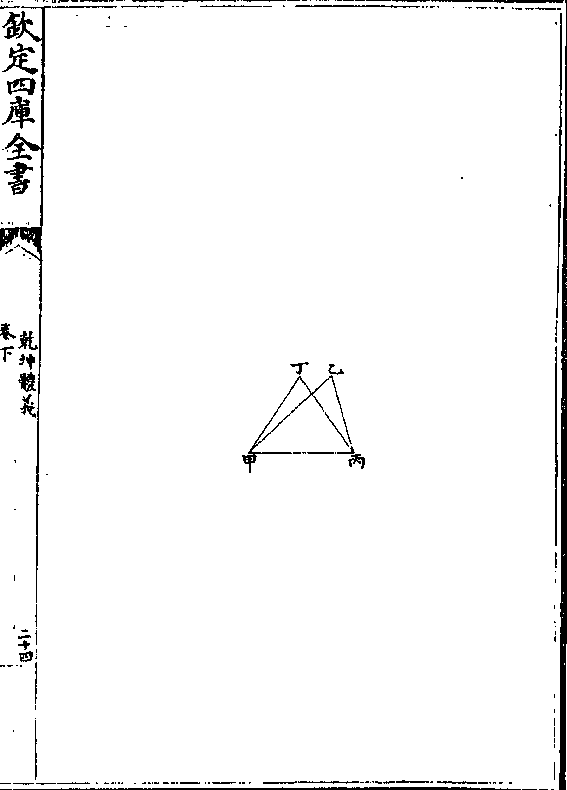
乾坤体义 卷下 第 25a 页 WYG0787-0791c.png
 第八题
第八题有三角形二等周等底其一两边等其一两边不等其
等边所容必多于不等边所容
解曰有甲乙丙形其甲乙边大于乙丙令于甲丙上
更作甲丁丙三角形与甲乙丙等周(本篇/七)而丁甲丁
丙两腰等亦与甲乙乙丙合线等题言甲丁丙角形
大于甲乙丙
论曰试引甲丁至戊令丁戊与丁甲等亦与丁丙等
乾坤体义 卷下 第 25b 页 WYG0787-0791d.png
 又作丁乙乙戊线夫甲乙乙戊合线既大于甲戊即
又作丁乙乙戊线夫甲乙乙戊合线既大于甲戊即大于甲丁丁丙合线亦大于甲乙乙丙合线此两率
者令减一甲乙则乙戊大于乙丙而丁戊乙三角形
之丁戊丁乙两边与丁丙乙三角形之丁丙丁乙两
边等其乙戊底大于乙丙底则戊丁乙角大于丙丁
乙角而戊丁乙角踰戊丁丙角之半(一卷三/十二)令别作
戊丁己角与丁甲丙角等则丁己线在丁乙之上而
与甲丙平行(一卷二/十八)又令引长丁己与甲乙相遇而
乾坤体义 卷下 第 26a 页 WYG0787-0792a.png
 作己丙线联之其甲丁丙甲己丙既在两平行之内又
作己丙线联之其甲丁丙甲己丙既在两平行之内又同底是三角形相等也(六卷/一)因显甲己丙大于甲乙
丙而甲丁丙两边等三角形必大于等周之甲乙
丙矣(问戊丁乙角何以踰戊丁丙角之半曰丁甲丙与丁丙甲两/角等而戊丁丙为其外角凡外角必兼两内角故也)
乾坤体义 卷下 第 27a 页 WYG0787-0792c.png
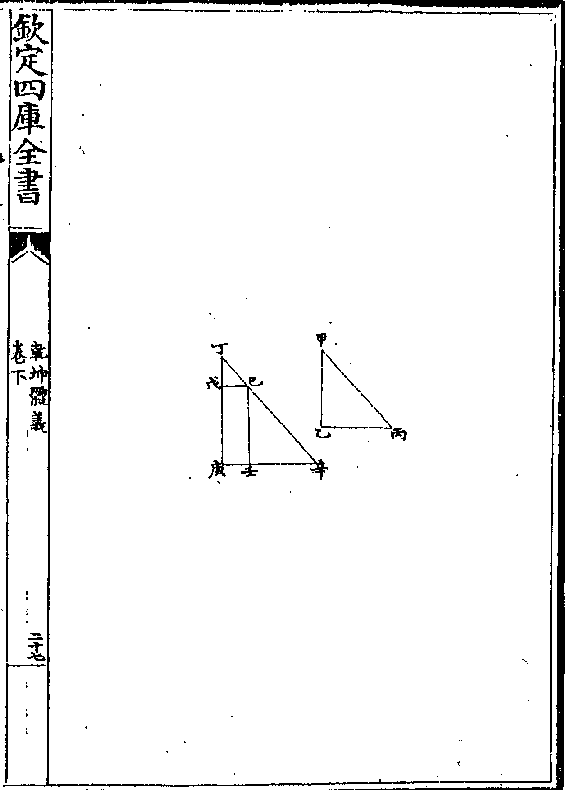
乾坤体义 卷下 第 27b 页 WYG0787-0792d.png
 第九题
第九题相似直角三边形并对直角之两弦线为一直线以作
直角方形又以两相当之直线四并二直线各作直角
方形其容等
解曰有甲乙丙及丁戊己三角形二相似其乙戊两
角为直角而甲与丁丙与己角各相等甲丙与丁己
相当甲乙与丁戊相当题言并甲丙丁己为一直线
于上作直角方形与并甲乙丁戊作直线及并乙丙
乾坤体义 卷下 第 28a 页 WYG0787-0793a.png
 戊己作直线各于其上作直形方形两并等
戊己作直线各于其上作直形方形两并等论曰引长丁戊至庚令戊庚与甲乙同度次从庚作
线与戊己平行又引丁己长之令相遇于辛从己作
己壬线与戊庚平行(一卷二/十九)则己壬辛之角形与丁戊
己相似而丁戊己与甲乙丙相似矣(一卷三/十二)何者己
壬辛角与庚角等庚角与丁戊己角等己角又与乙
角等而辛角与丁己戊角及丙角俱等壬己辛角与
甲角亦等(一卷三/十四)又己壬边与戊庚相等则亦与
乾坤体义 卷下 第 28b 页 WYG0787-0793b.png
 甲乙相等而壬辛与乙丙己辛与甲丙俱相等(一卷/二十)
甲乙相等而壬辛与乙丙己辛与甲丙俱相等(一卷/二十)(六/)故丁辛线兼丁己甲丙之度丁庚线兼丁戊甲乙
之度而庚辛亦兼戊己乙丙之度庚壬即戊己也(一/卷)
(三十/四)然则丁辛上直角方形与丁庚及庚辛上两直
角方形并自相等矣
乾坤体义 卷下 第 29a 页 WYG0787-0793c.png
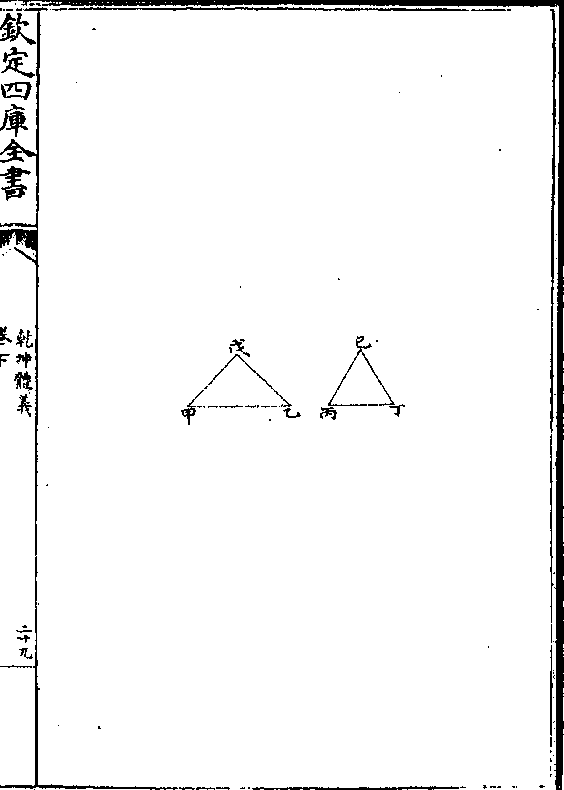
乾坤体义 卷下 第 30a 页 WYG0787-0794a.png
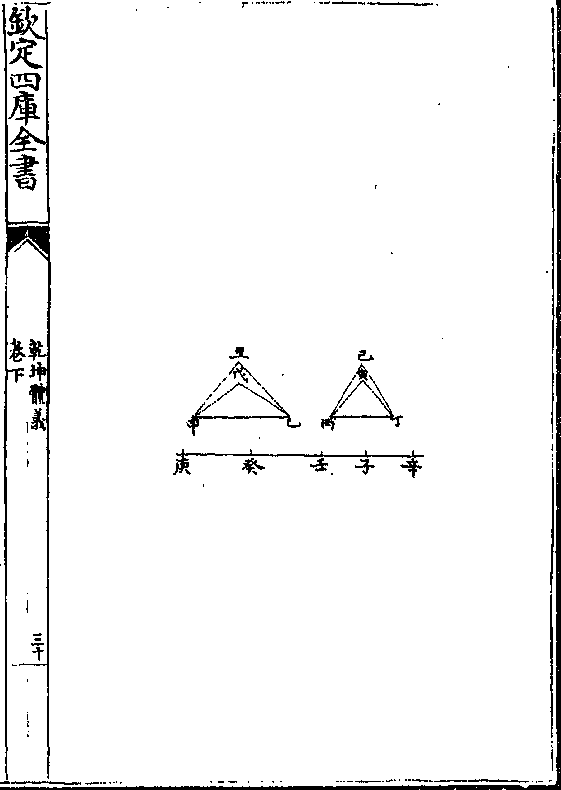
乾坤体义 卷下 第 30b 页 WYG0787-0794b.png
 第十题
第十题有三角形二其底不等而腰等求于两底上另作相似
三角形二而等周其两腰各自相等
解曰甲乙丙丁不等两底上有甲戊乙及丙己丁三
角形二其戊甲戊乙腰与己丙己丁腰俱相等若甲
乙大于丙丁者则戊角大于己角(一卷二/十五)而两三角
形不相似求于两底上各作三角形相似而两腰各
相等其周亦等
乾坤体义 卷下 第 31a 页 WYG0787-0794c.png
 法曰作庚辛线与甲戊戊乙丙己己丁四线等而分
法曰作庚辛线与甲戊戊乙丙己己丁四线等而分之于壬令庚壬与壬辛之比例若甲乙与丙丁(六卷/十)
甲乙既大于丙丁则庚壬亦大于壬辛而平分庚壬
于癸平分壬辛于子庚壬与壬辛既若甲乙与丙丁
则合之而庚辛之视壬辛若甲乙丙丁并之视丙丁
矣(五/卷)夫庚辛并既大于甲乙丙丁并(两边必大于一/边在一卷二十)
则壬辛大于丙丁而庚壬大于甲乙也(五卷/十四)甲乙庚
癸癸壬三线每二线必大于一线而丙丁壬子子辛
乾坤体义 卷下 第 31b 页 WYG0787-0794d.png
 亦然令于甲乙上用庚癸癸壬线作甲丑乙三角形
亦然令于甲乙上用庚癸癸壬线作甲丑乙三角形为两腰等而其周在甲戊乙形之外(以戊甲戊乙得/庚辛之半而庚)
(壬之度/过之故)于丙丁上用壬子子辛线作丙寅丁三角形
亦两腰等而其周在丙己丁之内(己丙己丁亦得庚/壬之半而壬辛之)
(度不及故俱/一卷二十二)
论曰并甲戊戊乙丙己己丁四线之度既与并甲丑
丑乙丙己己丁四线之度相等则甲丑乙丙寅丁两
形自与甲戊乙丙己丁两形同周而其两腰亦自相
乾坤体义 卷下 第 32a 页 WYG0787-0795a.png
 同至于两形相似何也甲乙与丙丁若庚壬与辛壬
同至于两形相似何也甲乙与丙丁若庚壬与辛壬而减半之庚壬与壬子(五卷/十五)又若丑甲与寅丙丑乙
与寅丁也则更之而甲乙与甲丑若丙丁与丙寅而
甲丑与丑乙若丙寅与寅丁是两形为同边之比
例自相似(六卷/五)
乾坤体义 卷下 第 33a 页 WYG0787-0795c.png
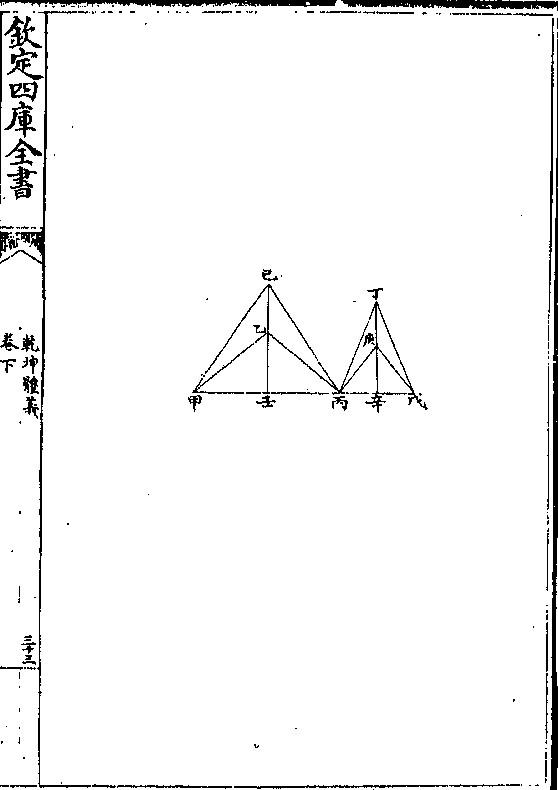
乾坤体义 卷下 第 34a 页 WYG0787-0796a.png
乾坤体义 卷下 第 34b 页 WYG0787-0796b.png
 第十一题
第十一题有大小两底令作相似平腰三角形相并其所容必大
于不相似之两三角形相并其底同其周同又四腰俱
同而不相似形并必小于相似形并
解曰甲丙丙戊两底上设有甲乙丙及丙丁戊两三
角形而甲乙乙丙丙丁丁戊四线俱等令于两底上
依前题别作甲己丙及丙庚戊两形相似而与前两
三角形相并者等周题言甲己丙丙庚戊并大于甲
乾坤体义 卷下 第 35a 页 WYG0787-0796c.png
 乙丙丙丁戊并
乙丙丙丁戊并论曰将甲丙丙戊作一直线而甲丙底大于丙戊底
乃从巳过乙作己壬线两分甲丙于壬又从丁过庚
作丁辛线两分丙戊于辛其甲己乙三角形之甲己
己乙两边与乙己丙三角形之己丙己乙两边等而
甲乙乙丙两底又等则甲己乙角与丙己乙角亦等
(一卷/八)又甲己壬三角形之甲己己壬两边与丙己壬
三角形之丙己己壬两边等则甲己壬角与丙己壬
乾坤体义 卷下 第 35b 页 WYG0787-0796d.png
 角等而甲壬壬丙之两底亦等(一卷/四)壬之左右皆直
角等而甲壬壬丙之两底亦等(一卷/四)壬之左右皆直角因显丙辛辛戊亦等而辛之左右角亦直角矣次
引丁辛至癸令辛癸与丁辛同度而从癸过丙作癸
丑直线则丁丙辛三角形之丁辛辛丙两边与辛癸
丙三角形之辛癸辛丙两边等而辛之上下角亦等
为直角丁丙丙癸两底等而丁丙辛角与癸丙辛角
俱等(一卷/四)丁丙辛角既大于庚丙辛角而庚丙辛角
相似与己丙壬角即相等(一卷/五)而丁丙辛即癸丙辛
乾坤体义 卷下 第 36a 页 WYG0787-0797a.png
 总大于己丙壬其癸丙辛角等于对角之丑丙壬(一/卷)
总大于己丙壬其癸丙辛角等于对角之丑丙壬(一/卷)(十/五)是丑丙壬亦大于己丙壬而引癸丑线当在于丙
己之外也若夫癸丙丙乙二线涵癸丙乙角向壬试
作癸乙线以分壬丙于子而并乙丙丙癸二线必大
于癸乙线(一卷/二十)则己丙丙庚并亦大于乙癸线何也
此四形者两两相并为等周则甲乙乙丙丙丁丁戊四
线并与甲己己丙丙庚庚戊四线并原相等而减半
之乙丙丙丁即乙丙丙癸与己丙丙庚亦相等故也
乾坤体义 卷下 第 36b 页 WYG0787-0797b.png
 并己丙丙庚二线为一直线就线上作直角方形必
并己丙丙庚二线为一直线就线上作直角方形必大于乙癸线上之直角方形夫己丙丙庚并之直角
方形与己壬庚辛并之直角方形及壬丙丙辛上之
直角方形并相等(九/题)而癸乙上之直角方形与乙壬
并辛丁(即辛/癸)上之直角方形及壬子子辛上直角方
形并又自相等(九题辛从子上分两对角其角等而/壬与 俱为直角相似之形令移置)
(辛癸与乙壬之下移置壬辛为癸垂线则/乙壬辛癸为股壬辛为勾乙癸为弦矣)此己壬庚
辛线并之直角方形及壬丙丙辛上之直角方形并
乾坤体义 卷下 第 37a 页 WYG0787-0797c.png
 明大于乙壬丁辛并之直角方形及壬子子辛上之
明大于乙壬丁辛并之直角方形及壬子子辛上之直角方形并也此两率者每减一壬辛上直角方形
则己壬庚辛共线上之直角方形大于乙壬丁辛共
线上直角方形矣而己壬庚辛两线并大于乙壬丁
辛两线并矣此两率者令一减乙壬一减庚辛则己
乙岂不大于丁庚乎壬丙原大于丙辛(以甲丙原大/于丙戊故)
则己乙与壬丙矩内直角形大于丁庚与辛丙矩内
直角形而乙己丙三角形为己乙壬丙矩内直角形
乾坤体义 卷下 第 37b 页 WYG0787-0797d.png
 之半何者令从壬丙作垂线与乙己平行而以乙己
之半何者令从壬丙作垂线与乙己平行而以乙己为底就作直角形此谓己乙壬丙矩内直角形其中
积倍于己乙丙三角形反之则己乙丙角形为己乙
壬丙矩形之半其丁庚丙三角形亦然乃丁庚及辛
丙矩内直角形之半也则己乙丙三角形大于丁庚
丙三角形而甲己丙乙甲形为丙乙己三角之倍者
亦大于丙庚戊丁形为丁庚丙三角之倍者矣此两
率者又每加甲乙丙与丙庚戊之三角形则甲己丙
乾坤体义 卷下 第 38a 页 WYG0787-0798a.png
 及丙庚戊之两三角形并岂不大于甲乙丙及丙丁
及丙庚戊之两三角形并岂不大于甲乙丙及丙丁戊之两三角形并哉
乾坤体义 卷下 第 39a 页 WYG0787-0798c.png
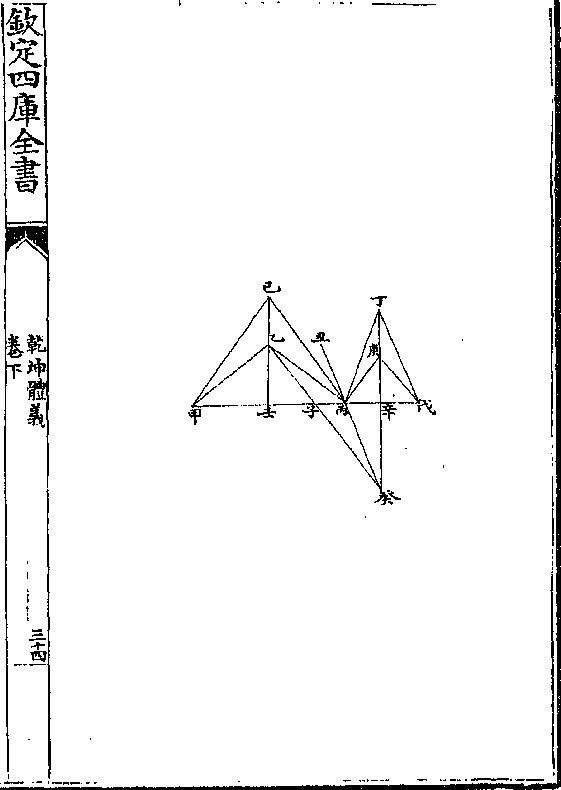
乾坤体义 卷下 第 39b 页 WYG0787-0798d.png
 第十二题
第十二题同周形其边数相等而等角等边者大于不等角等边
者
先解曰有甲乙丙丁戊己多边形与他形同周同角
者较必边边相等乃为最大之形
论曰若谓不然先设甲乙乙丙不等边如第一图又
作甲丙线于上作等边三角为甲庚丙形与甲乙丙
等周(本篇/七)则甲庚丙丁戊己形亦与甲乙丙丁戊己
乾坤体义 卷下 第 40a 页 WYG0787-0799a.png
 形等周而甲庚丙三角形必大于甲乙丙三角形(本/篇)
形等周而甲庚丙三角形必大于甲乙丙三角形(本/篇)(八/)令每加丙丁戊己角形则甲庚丙丁戊己形亦大
于甲乙丙丁戊己形故知不等边者不为最大其他
如丙丁边之类或不等者亦如此推
次解曰又设甲乙丙丁戊己等边形与他形同周同
边者较必角角相等乃为最大之形
论曰依上论各边俱等则甲乙丙丙丁戊为等边三
角形(边角/俱等)而甲乙乙丙与丙丁丁戊相等若谓不然
乾坤体义 卷下 第 40b 页 WYG0787-0799b.png
 而乙角可大于丁角则甲丙线必大于丙戊线(一卷四/二十)
而乙角可大于丁角则甲丙线必大于丙戊线(一卷四/二十)试于甲丙丙戊两底上别作三角形为甲庚丙为丙
辛戊如第十题相似形令与甲乙丙丙丁戊并者等
周则甲庚丙并丙辛戊者大于甲乙丙并丙丁戊(本/篇)
(十/一)而每加丙戊己角形则甲庚丙辛戊己必大于甲
乙丙丁戊己也何得以等周等边而不等角者为最
大乎
乾坤体义 卷下 第 41a 页 WYG0787-0799c.png
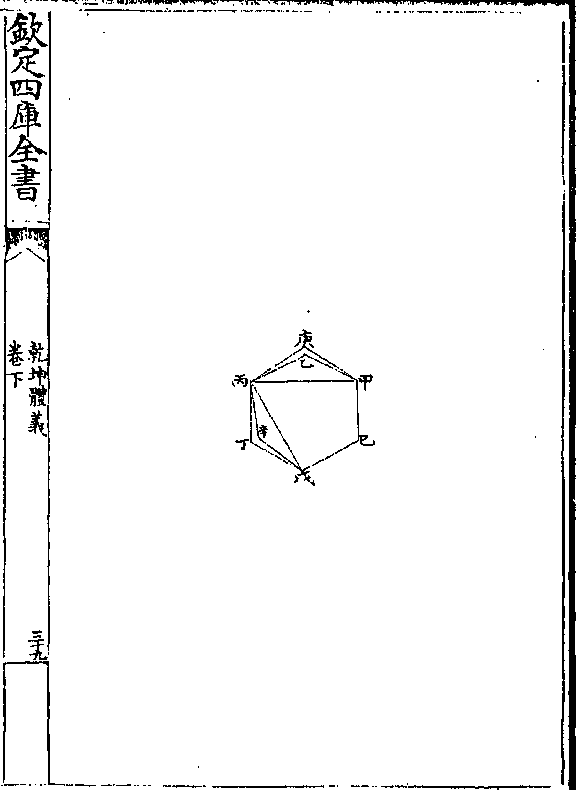
乾坤体义 卷下 第 42a 页 WYG0787-0800a.png
 第十三题
第十三题凡同周形惟圜形者大于众直线形有法者
解曰有甲乙丙圜形又有丁戊己多边有法形其周
等题言甲乙丙大于丁戊己
论曰庚为甲乙丙之心辛为丁戊己之心甲乙丙外
另作壬乙丙癸多边形与丁戊己相似(四卷十/六注)而从
壬癸切圜于甲者作半径线于庚则庚甲为壬癸垂
线而分壬癸之半(三卷/十八)又从辛作子丑垂线则辛丁
乾坤体义 卷下 第 42b 页 WYG0787-0800b.png
 亦分子丑之半(三卷三此设于两多边形外作切形/圜而以壬癸子丑为切圜线向心作)
亦分子丑之半(三卷三此设于两多边形外作切形/圜而以壬癸子丑为切圜线向心作)(垂线则垂线必分切线/之中故说在四卷十二)两形相似其壬全角与子全
角等则半之而甲壬庚角与丁子辛角亦等壬甲庚
直角与子丁辛直角亦等(一卷三/十二)然乙壬癸丙之周
大于圜周而圜周与丁戊己形相同则是乙壬癸丙
周原大于丁戊己周矣夫两形相似而壬癸边大于
子丑边则半之而壬甲亦大于子丁又壬甲与甲庚
若子丁与丁辛之比例(六卷/四)而壬甲大于子丁则甲
乾坤体义 卷下 第 43a 页 WYG0787-0800c.png
 庚亦大于丁辛(五卷/十四)是故取甲庚线与半圜周线以
庚亦大于丁辛(五卷/十四)是故取甲庚线与半圜周线以作矩内直角形其与圜地等也大于取丁辛线与丁
戊己半周线以作矩内直角形其与形地等也(本篇/四)
系曰推此见圜形大于各等周直线形(第五题证有/法形同周者)
(多边为大又十二题证等周及边数之等者有法为/大又本题证等周之有法形惟圜为大则圜为凡形)
(等周者/之最大)
乾坤体义 卷下 第 44a 页 WYG0787-0801a.png
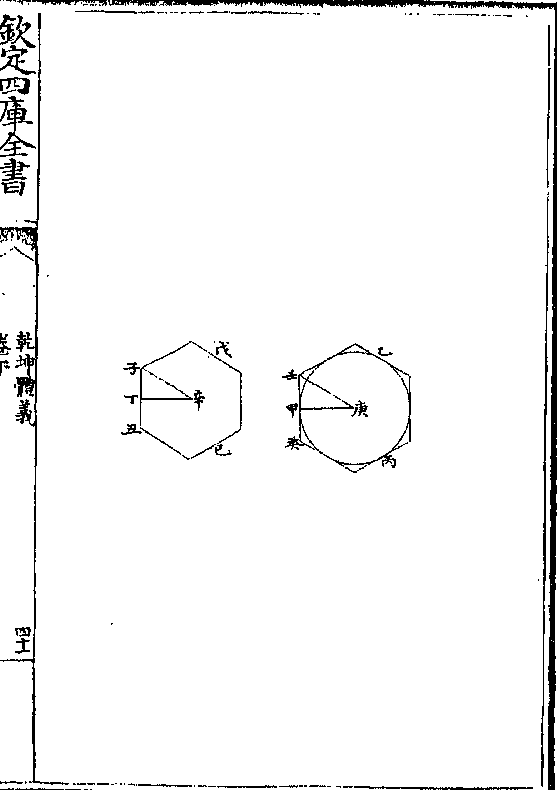
 第十四题
第十四题锐觚全形所容与锐顶至边垂线及三分底之一矩内
直角立形等
解曰有觚形不拘几面如甲乙丙丁戊底其顶巳又
有寅庚直角立方形者其底庚辛壬癸得甲乙丙丁
戊底三之一其高庚子与觚等高题言此寅庚形与
觚形所容等
论曰从立形底诸角与相对一角如子角者皆作线
乾坤体义 卷下 第 44b 页 WYG0787-0801b.png
 以成庚辛壬癸子觚形此形与寅庚形同底同高又
以成庚辛壬癸子觚形此形与寅庚形同底同高又同己甲锐觚之高既己甲形兼庚辛壬癸子觚之三
(十二卷六注言两觚形同高者其所容/之比例如其底底等亦等底倍亦倍)寅庚全形亦
兼庚辛壬癸子觚之三(以同底同高故/在十二卷七系)则寅庚全方
与己甲觚等
乾坤体义 卷下 第 45a 页 WYG0787-0801c.png
乾坤体义 卷下 第 45b 页 WYG0787-0801d.png
 第十五题
第十五题平面不拘几边其全体可容浑圜切形者设直角立形
其底得本形三之一其高得圜半径即相等(可容浑圜/切形者必)
(圜形与诸面相切若长广/不切诸面者不在此论)
解曰有甲乙丙丁形内含戊己庚辛圜其心壬而外
线甲乙切圜于戊(十一卷/三题)试从戊壬割圜之半作戊
己庚辛圜(圜形书一/卷一题)从壬心望各切圜之点作壬戊
为甲乙垂线(三卷/十八)壬己为乙丙垂线壬庚为丙丁垂
乾坤体义 卷下 第 46a 页 WYG0787-0802a.png
 线壬辛为甲丁垂线别一直角立方形午子其底子
线壬辛为甲丁垂线别一直角立方形午子其底子丑寅癸得甲乙丙丁体三之一而其高辰子与圜半
径等题言此直角立方形与甲乙丙丁全体等
论曰从壬心与甲乙丙丁各角作直线即分其体为
数觚形其面即为觚底而皆以壬心为觚锐顶此各
觚皆以其三分底之一及至锐高之数为直角立方
形皆与觚所容等(本篇/十四)又并为一形即与甲乙丙丁
体等亦与午子等以午子底正得甲乙全形三之一
乾坤体义 卷下 第 46b 页 WYG0787-0802b.png
 而其高分圜半径也
而其高分圜半径也乾坤体义 卷下 第 47a 页 WYG0787-0802c.png
乾坤体义 卷下 第 48a 页 WYG0787-0803a.png
 第十六题
第十六题圜半径及圜面三之一作直角立方形以较圜之所容
等
解曰有甲乙丙浑圜其心为丁又有直角立形之戊
在甲丁径及甲乙丁浑圜三之一矩内题言戊形所
容与甲乙丙浑圜等
论曰若言不等谓戊大于浑圜形其较有巳者合以
丁为心外作庚辛壬浑圜大于甲乙丙而勿令大于
乾坤体义 卷下 第 48b 页 WYG0787-0803b.png
 戊第令或等或小以验之而于庚辛壬内试作有法
戊第令或等或小以验之而于庚辛壬内试作有法形勿切甲乙丙圜(十二卷/十七)自丁心至形边各作垂线
则垂线必长于甲丁又自丁心至形各角作直线以
分此形为几觚其庚辛壬法形诸直线为觚底而垂
线至丁心为觚锐顶试取各觚底三之一及丁垂线
之高以作直角立形与觚等(本篇/十四)则并为大直角立
形亦与庚辛壬内之法形等(本篇/十五)如云以甲乙为高
而以各觚底三之一为直角立形并为大形则必小
乾坤体义 卷下 第 49a 页 WYG0787-0803c.png
 于前形因显庚辛壬三之一大于甲乙丙三之一而
于前形因显庚辛壬三之一大于甲乙丙三之一而戊形甲丁径及甲乙丙圜三之一内小于庚辛壬体
而谓庚辛壬不大于戊形则向庚辛壬之内形尚大
于戊形也
又论曰戊形小于甲乙丙浑圜体者其较为己试从
丁心再作癸子丑圜小于甲乙丙而勿令小于戊或
大或等者以验之于甲乙丙圜内作有法形不令切
癸子丑(十二卷/十七)而从丁至甲乙丙各面为垂线此垂
乾坤体义 卷下 第 49b 页 WYG0787-0803d.png
 线大于丁癸之半径又从丁向法形诸角作直线以
线大于丁癸之半径又从丁向法形诸角作直线以分此形为数觚以形之各面为觚底庚辛为觚锐顶
而取觚底三之一及底至丁之垂线以作直角立形
与觚等若使以甲丁为高而以各觚三之一为底以
作直角立形则其形必高于前形既甲乙丙圜之面
大于其内形之面则圜面三之一大于内形面三之
一而直角立方形在甲丁高及甲乙丁面三之一固
即戊体矣愈大于甲乙丁之内形矣而云癸子丑圜
乾坤体义 卷下 第 50a 页 WYG0787-0804a.png
 或等或大于戊岂癸子丑圜大于甲乙丙圜而分大
或等或大于戊岂癸子丑圜大于甲乙丙圜而分大于全欤则戊体不小于甲乙丙矣从后论不可为小
从前论不可为大故曰等也
乾坤体义 卷下 第 51a 页 WYG0787-0804c.png
 第十七题
第十七题圜形与平面他形之容圜者其周同其容积圜为大
解曰有甲圜其心甲其半径甲乙又丙形与甲等周
其周内可作诸切边圜形而从心至边为丙丁题言
甲圜大于丙形
论曰甲圜外试作与丙相似形(十二卷/)而从甲心至
各边切处作半径垂线皆等(本篇十/五有解)其一为甲乙甲
圜外形大于甲圜其周面亦大于丙面而甲乙垂线
乾坤体义 卷下 第 51b 页 WYG0787-0804d.png
 亦大于丁丙垂线以甲半径为高乃以三分圜体之
亦大于丁丙垂线以甲半径为高乃以三分圜体之一作直角立方形即与甲圜形等(本篇/十六)以丙丁线为高
而以三分丙形之一作直角立方形亦与丙形等而
甲之立方固大于丙之立方(本篇/十五)则甲圜与丙形虽
同周而甲圜所容为大矣
乾坤体义 卷下 第 52a 页 WYG0787-0805a.png
乾坤体义 卷下 第 53a 页 WYG0787-0805c.png
 第十八题
第十八题凡浑圜形与圜外圜角形等周者浑圜形必大于圜角
形
解曰有甲乙丙丁圜外作戊己庚辛等法形率以四
数相偶若八面十二面十六面二十面及二十四二
十八之类等边等角近于圜形者又作戊壬过心线
为枢以转甲乙丙圜及戊己庚辛法形使平面旋为
立圜之体则其形为圜外圜角之形而角与边周遭
乾坤体义 卷下 第 53b 页 WYG0787-0805d.png
 皆等(圜书一卷二十/二及二十七)又有浑圜形寅与圜角形等周
皆等(圜书一卷二十/二及二十七)又有浑圜形寅与圜角形等周题言寅圜大于圜角形
论曰圜角外形既大于内之甲乙丙圜形则寅圜亦
大于甲乙丙圜寅圜之半径亦大于甲乙丙圜之半
径也夫浑圜中剖是为过心最大之圜此过心大圜
之面恒得浑体四分之一(圜书一卷/三十一题)令倍寅径以作
卯辰径其圜面四倍大于寅之圜面(此专以圜面相/较也卯辰径既)
(倍寅径则卯辰圜固四倍于寅圜以圜与圜为/径与径再加之比例故也在六卷附一增题)则卯
乾坤体义 卷下 第 54a 页 WYG0787-0806a.png
 辰圜与寅浑圜等(此卯辰圜为欲见角故/画作扁圜实正圜也)次作未申圜
辰圜与寅浑圜等(此卯辰圜为欲见角故/画作扁圜实正圜也)次作未申圜与卯辰等作未酉申圜角形而取寅半径为酉戌之
高又于卯辰上亦作卯巳辰圜角形而取甲乙丙圜
半径为巳午之高两圜体等而未酉申圜角形高于
卯巳辰圜角形则亦大于卯巳辰圜角形(圜角形同/底之比例)
(若其高之比例在/十二卷十四题)夫割寅浑圜之中半以为底(即过/心大)
(圜/也)而以其半径之高为圜角形恒得寅浑圜四分之
一(此旋转所成尖顶半圜形非只论/其一面也在圜书一卷三十二十)则是一寅圜恒
乾坤体义 卷下 第 54b 页 WYG0787-0806b.png
 兼四圜角之形而未申圜原四倍大于寅圜则未酉
兼四圜角之形而未申圜原四倍大于寅圜则未酉申圜角形固与寅之浑圜形等矣(圜角形同高之比/例若其底之比例)
(故也在十二/卷十一题)其卯巳辰圜角形底原等戊己庚形之
面(戊己庚之面与/寅圜之面等故)而巳午之高亦等于甲圜半径即
戊己庚辛角形自与卯巳辰圜角形等(圜书一卷二/十九题论凡)
(圜外有圜角形如甲乙丙外有戊己庚形者以圜体/过心大圜为底而以圜半径为高旋作圜角形即与)
(圜外诸/圜各等)卯巳辰圜角形既小于未酉申圜角形而戊
己庚辛壬癸子丑形宁大于同周之寅乎
乾坤体义 卷下 第 55a 页 WYG0787-0806c.png

乾坤体义 卷下 第 55b 页 WYG0787-0806d.png

乾坤体义卷下