钦定四库全书

　　律吕成书卷一　　　　　　元　刘瑾　撰

　　候气求黄钟法第一(以律吕新书證辨第一第九第十章及彭氏律法第七章
参定)

　　后汉志曰候气之法为室三重户闭涂衅必周密(长乐陈氏
曰三室各有门为门之位外以子中以午内复以子杨子所谓九闭之中也)布缇缦(缯无文也)室
中以木为案每律各一案内庳外高从其方位加律其
上以葭莩灰抑其内端(长乐陈氏曰室中上圆下方依辰位埋律管使其端与地齐而
以薄纱覆之中秋白露降采葭莩为灰加管端　彭氏曰律管各当其辰斜埋地下入地处庳出地处高故云
内庳外高黄钟则埋于子位上头向南)按历而候之气至者灰去气所动
者灰散人及风所动者灰聚

　　蔡氏曰律吕散亡其器不可复见然古人所以制作

之意则犹可考也太史公曰细若气微若声圣人因
神而存之虽妙必效言黄钟始于声气之元也班固
所谓黄帝使伶伦取竹断两节间吹之以为黄钟又
曰天地之风气正而十二律定(汉前志曰黄帝使伶伦自大夏之西昆崙
之阴取竹之解谷生其窍厚均者断两节间而吹之以为黄钟之宫制十二筒以听凤之鸣其雄鸣为六
雌鸣亦六比黄钟之宫而皆可以生之是为律本至治之世天地之气合以生风天地之风气正十二律
定)刘昭所谓伏羲纪阳气之初以为律法又曰吹以
考声列以候气(汉后志曰伏羲作易纪阳气之初以为律法建日冬至之声以黄钟为宫

太簇为商姑洗为角林钟为徵南吕为羽应钟为变宫蕤宾为变徵此声气之元五音之正也又曰截管
为律吹以考声列以候气道之本也)皆以声之清浊气之先后求黄钟
者也是古人制作之意也夫律长则声浊而气先至
极长则不成声而气不应律短则声清而气后至极
短则不成声而气不应此其大凡也今欲求声气之
中而莫适为准则莫若且多截竹以拟黄钟之管或
极其短或极其长长短之内每差一分而为一管皆
即以其长权为九分而度其围径如黄钟之法焉如

是而更迭以吹则中声可得浅深以列则中气可验
苟声和气应则黄钟之为黄钟者信矣黄钟者信则
十一律与度量权衡者得矣后世不知出此而唯尺
之求(又曰隋志载十五等尺一周尺及王莽时刘歆铜斛尺后汉建武铜尺晋荀勖所造晋前尺祖
冲之所传铜尺长短近同按荀勖尺出于汲冢之律与刘歆之斛最为近古盖去古未远古之律度量衡
犹在也自董卓之乱而乐律散亡故魏杜夔之律围径差小而尺因以长荀勖虽改定新尺然其乐声高
急不知当时律之围径又果何如也后周以玉斗生律玉斗之容受则近古矣然当时以斗制律围径不
及三分其尺遂长于荀勖尺一寸五分八釐意者后世尺度之差皆由律围径之误也今司马公所传此

尺者出于王莽之法钱盖丁度所奏高若讷所定者也后之君子有能验声气之元以求古之律吕者于
此当有考而不可忽也二晋田父玉尺及梁法尺实比晋前尺一尺七釐三梁表尺实比晋前尺一尺二
分二釐一毫有奇按此即祖暅所算造铜圭影表者也四汉官尺及晋时始平掘地所得古铜尺实比晋
前尺一尺三分七毫五魏杜夔尺实比晋前尺一尺四分七釐六晋后尺江左所用实比晋前尺一尺六
分二釐七后魏前尺实比晋前尺一尺二寸七釐八后魏中尺实比晋前尺一尺二寸一分一釐九后魏
后尺实比晋前尺一尺二寸八分一釐十东魏尺实比晋前尺一尺五寸八毫十一蔡邕铜龠尺及后周
玉尺实比晋前尺一尺一寸五分八釐按铜龠玉斗二者当是古之嘉量后周㨿斗造尺但以容受乘除
求之耳然皆惑于三分之径故其尺律遂长唐之度量权衡与玉斗相符即此尺尔十二宋氏尺及钱乐

之浑天仪尺后周铁尺实比晋前尺一尺六分四釐按隋平陈以后即用此尺即本朝和岘所用影表尺
也范蜀公以为即今大府帛尺误矣十三万宝常所造律吕水尺实比晋前尺一尺一寸八分六釐十四
杂尺及刘晖浑天仪土圭尺实比晋前尺一尺五分十五梁朝俗间尺实比晋前尺一尺七分一釐按前
十五等尺其间多无所取证所以存而不削者要见诸代之不同多由于累黍及围径之误也)晋氏
而下则多求之金石梁隋以来又参之秬黍(隋志曰晋泰始
十年中书考古器揆校今杜夔尺长四分半所校古法有七器一曰姑洗玉律二曰小吕玉律三曰西京
铜望臬四曰金错望臬五曰铜斛六曰古钱七曰建武铜尺后魏律历志公孙崇永平中更造新尺以一
黍之长累为寸法刘芳受诏修乐以秬黍中者一黍之广即为一分而元匡以一黍之广度黍二缝以取

一分三家纷竞久不能决大和十九年遂用刘芳典修金石后周武帝保定中诏卢景宣等累黍造尺纵
横不定后因修仓掘地得古玉斗据斗造律度量衡)下至王朴刚果自用专恃
累黍而金石亦不复考矣(又曰唐张文收铸铜斛铭云大唐贞观十年岁次元
枵月旅应钟依新令累黍尺定律校龠成兹嘉量与古玉斗相符故唐乐器虽无法而声不失于古自王
朴以黍定尺以尺生律声与器始皆失之矣)夫金石真伪固难尽信若秬
黍则岁有凶丰地有肥瘠种有长短大小圆妥不同
尤不可恃况古人谓秬黍中者实其龠则是先得黄
钟而后度之以黍不足则易之以大有馀则易之以

小约九十黍之长中容千二百之实以见周径之广
以生度量权衡之数而已非律生于黍也百世之下
欲求百世之前之律者其亦求之于声气之元而毋
必之于秬黍则得之矣(又曰律者阳气之动阳气之始必声和气应然后可以见
天地之心今不此之先而乃区区于黍之纵横古钱之大小其亦难矣然非精于历数则气节亦未易正
也)

　　欧阳颖伯曰候冬至验诸管之中有气应灰飞之律
者即黄钟九寸之真数今岁得之则来年又从而验

之以两冬至相距三百六旬有六日内应者为可准
不必拘于当时太史算历所定冬至之时可也(彭氏曰欲
求黄钟的实者须依蔡元定说多截竹管以拟黄钟或短或长每差纤微各为一管悉以此诸管埋地中
俟冬至时验之若诸管之中有气应者即知此管合于造化自然也盖律之大要莫先候气故太史论律
谓气始于冬至周而复生神生于无形成于有形然后数形而成声)

　　求黄钟从长法第二(以新书本原第一章定)



　　古法黄钟长九寸今据此冬至气应之管分作九寸(蔡氏
曰天地之数始于一终于十其一三五七九为阳九者阳之成也其二四六八十为阴十者阴之成也黄钟者
阳声之始阳气之动也故其数九分寸之数具于声气之元不可得而见及断竹为管吹之声和候之气应而
后数始形焉故约其长得九寸)寸作十分分作十釐釐作十毫毫作十
丝丝作十忽此乃元气距地浅深长短自然之度是为
黄钟律管从长之数(欧阳颖伯曰一二三四五皆生数也六七八九十皆成数也天九与

地十则阴阳成数之极者也以九乘十以十乘九皆为九十此黄钟之长以九为寸数以十为分数也总而计
之为九十分者用阴阳之极也阳之极则阴生焉阴之极则阳生焉是以冬至一阳生于积阴之下而黄钟之
律应则理也气也数也出于一而不可以异观矣)既得从长之数如此于是准
此分釐毫丝之度用九章算经羃(音觅)积周径法互相推
算以求黄钟律管阔狭之的算法详具后章

　　求黄钟积实面羃法第三(以新书本原第一章及彭氏律法第六章参定)



　　(此圆内空者黄钟管内面羃也互算得九方分)

　　古法黄钟积实八百一十分今据前气应之管其长九
十分之分为准以度之凡一分管长知空围中当积九
立方分十分管长空围中当积九十立方分九十分管
长则空围中当积八百一十立方分是为黄钟之积实
也(凡论黄钟管内积分者宜取方分而汉志止言积实八百一十分者省文耳)既得积实之

数如此知管面深一分则空围中的容九方分无疑是
又黄钟之面羃也(羃者覆笾豆巾也有方目可纪故算管面平方忽丝毫釐分者皆取象于
羃)即蔡氏所谓审其围得九分(蔡氏又曰空围中广九分)积其实得
八百一十分者是也(面羃九方分者九数也积实八百一十分者九九数也皆阳数也)
既得面羃之数如此乃以平方羃法推之知一分有百
釐(从长一分该十釐故平方面有百釐馀仿此有图见后)釐有百毫毫有百丝丝
有百忽积而计之一平方分通有面羃一万万忽九平
方分通有面羃九万万忽由是可以起算黄钟之围径

矣第历代诸儒议论不一不可不先知也并附其说如
左

　　蔡氏曰按十二律围径自先汉以前传记并无明文
惟班志曰黄钟八百一十分繇此之义起十二律之
周径然其说乃是以律之长自乘而因之以十盖配
合为说尔未可以为据也(又曰汉志以黄钟长九寸九九八十一又以十因之
为八百一十应历一统八十一章之数此倚数配合为说而已其云起律之周径者盖空围九分长九寸
积八百一十分则其周径可以数起矣)惟审度章云一黍之广度之九

十分黄钟之长一为一分嘉量章则以千二百黍实
其龠谨权衡章则以千二百黍为十二铢则是累九
十黍以为长积千二百黍以为广可见也夫长九十
黍容千二百黍则空围当有九方分乃是围十分三
釐八毫径三分四釐六毫也每一分容十三黍又三
分黍之一以九十因之则一千二百也又汉斛铭文
云律嘉量方尺(斛面内平方一尺也)圆其外(循其方外四角而规圆之其径一尺
四寸有奇)庣(音条)旁九釐五毫(庣过也谓圆外四旁略加开广也)羃百六十

二寸(方尺羃百寸圆其外每旁约十五寸四旁共六十寸庣旁约二寸方圆皆在积羃之数)深
尺积一千六百二十寸(斛面平方平圆一寸面羃一百六十二寸斛深立方立圆
十寸故积一千六百二十寸)容十斗嘉量之法合龠为合十合为
升十升为斗十斗为石一石积一千六百二十寸为
分者一百六十二万(斛内立方立圆积分之数也下放此)一斗积一百
六十二寸为分者十六万二千一升积十六寸二分
为分者一万六千二百一合积一寸六分二釐为分
者一千六百二十则黄钟之龠为八百一十分明矣

空围八百一十分则长累九十黍广容一千二百黍
矣盖十其广之分以为长十一其长之分以为广自
然之数也自孟康以律之长十之一为围之谬其后
韦昭之徒遂皆有径三分之说而隋志始著以为定
论(又曰郑康成月令注云凡律空围九分蔡邕铜龠铭亦云空围九分盖空围中广九分也东都之乱
乐律散亡邕之时未乱当亲见之又晓解律书而于月令章句云径三分何也孟康韦昭之时汉斛虽在
而律不存矣康昭等不通律吕故康注汉志云黄钟径三分围九分林钟长六寸围六分太簇长八寸围
八分昭注周语云黄钟径三分围九分皆无足怪者隋氏之失制律管俱径三分岂康昭等有以启之欤

又曰汉魏而下造律竟不能成而度之长短量之容受权衡之轻重皆戾于古大率皆由径三分之说误
之也)然累九十黍径三分止容黍八百有奇终与一千
二百黍之法两不相通而律竟不成唐因声制乐虽
近于古而律亦非是本朝承袭皆不能觉独胡安定
以为九分者方分也以破径三分之法然所定之律
不本于声气之元一取之秬黍故其广量权衡皆与
古不合(胡瑗取羊头山黍用三等筛子筛之取中等者横累一百黍为尺)又不知变
律之法但见仲吕反生不及黄钟之数乃迁就林钟

以下诸律围径以就黄钟清声以夷则南吕为径三
分围九分无射为径二分八釐围八分四釐应钟为
径二分六釐五毫围七分九釐五毫夫律以空围之
同故其长短之异可以定声之高下而其所以为广
狭长短者莫不有自然之数非人之所能为也今其
律之空围不同如此则亦不成律矣遂使十二律之
声皆不当位反不如和岘旧乐之为条理亦可惜也
房庶以径三分周围九分累黍容受不能相通遂废

一黍为一分之法而增益班志八字以就其说范蜀
公乃从而信之过矣

　　彭氏曰予得蔡氏律吕新书又得九章算经载祖冲
之算圆径术极为精密乃若西山推求声气之元欲
多截竹管测候实为冠绝古今然布算又与祖氏未
合窃以为依蔡氏之候法加之以祖氏之算术何黄
钟不可定之有

　　又曰东汉蔡邕始创为径三分之说试依所言径三

分以祖冲之密率乘除止得面羃七分七釐奇乃少
一分九十二釐奇(平方羃法方一分计百釐也)积实止得六百三
十六分奇乃少一百七十三分奇如此则黄钟之管
无乃大狭谓曰不然请以图证之凡论黄钟空围内
羃积分者宜取方分今姑以九方分平置如此□则
是九方分纵横信有三分径矣若以九方分宛转为
圆则须得三分有馀径方可容之故必如此□使圆
径积阔则圆内始可容九方分不然则止从三分方

径取圆如此□则圆内所容方分少而方分之四角
犹有馀分者皆溢出圆外而无所容矣其面羃既差
则其积实愈差由此观之黄钟径止三分则面羃无
九方分积亦无八百一十分以之造律未为得也

　　晋孟康注汉律历志曰律孔径三分参天数也围九
分终天数也韦昭注国语唐魏徵作隋志及后周王
朴宋房庶和岘阮逸范镇等并从此说按此诸儒言
径三分与蔡邕同其说已差至于言围九分用径一

围三之法尤误盖径一围三虽是古率然古人大约
以此算圆田耳若以密率推之径一则围三有奇假
如径七则围当有二十二若依孟氏所言径三分则
围长当九分四釐二毫八丝强不但止于九分也若
依九分围长之数则径当止有二分八釐六毫三丝
六忽强又不及三分也谓曰不信请以图证之今且
以此○圆形取径取得圆内径长如此□又以此○
圆长分摺为三如此□三摺之中取一摺以比圆形

内径□或通以三摺比之圆内之径必短而三摺者
必长以此观之知围三径一乃大约之法长短自有
差殊圆田或可用此至于律管则空积忽微以之造
律未为得也

　　宋胡瑗不主诸儒径三围九之说驳之曰后世儒者
执守孤法但制尺求律便为坚证因谓围九分者取
空围长九分耳以是围九分之误遂有径三分之说
若从径三围九之说则黄钟之管止容九百黍积止

六百七分半如此则黄钟之声无从而正大要空围
中容九方分乃是围长十分三釐八毫径三分四釐
六毫也按胡氏此言围径数虽与诸儒异然亦用径
一围三之率殊不知此率未密故若依所言三分四
釐六毫径当得围长十分八釐七毫四丝二忽强不
但止于十分三釐八毫也若依十分三釐八毫围长
之数则径止得三分三釐奇又不及三分四釐六毫
也谓曰不信亦当以前图证之大槩胡氏知诸儒径

三分之短不知自说径三分四釐六毫者又失于长
兼又不知径七围二十有二密率止以径一围三约
率言故所言径围分数皆有参差不齐圆田或可用
此至于律管则空积忽微以之造律未为得也

　　宋蔡元定说径围分数与胡氏同辨己见前蔡氏又
曰算法置八百一十分分作九重每重得九分圆田
术三分益一得一十二以开方法除之得三分四釐
六毫强为实径之数不尽二毫八丝四忽今求圆积

之数以径三分四釐六毫自相乘得十一分九釐七
毫一丝六忽加以开方不尽之数二毫八丝四忽得
一十二分以管长九十分乘之得一千八十分为方
积之数四分取三为圆积得八百一十分今姑依其
说以九方分平置如此□又以三分益一以三方分
割置于九方分之外如此□共积十二方分其纵横
可得三分四釐六毫强不尽二毫八丝四忽的如蔡
氏说依古率十二方分通计十二亿忽开方亦得此

数但依此径以密率相乘则空围内面羃不但止得
九方分乃得九方分零四十釐六十毫五十七丝十
四忽奇空围内积实不但止得八百一十分乃得八
百四十六分五百四十五釐一百四十二丝六百忽
奇如此则黄钟之管无乃太大谓曰不信亦当以图
证之假如设此□为十二方分就此十二方分之中
取径则方内径如此□乃就方内之径圆之如此□
细考之则方内之圆所占者不止四分三圆外之方

所当退者又不及四分一以此知三分益一四分退
一乃虚加实退算家大约之法至于律管则空积忽
微以之造律未为得也盖律之大要莫先候气以求
从长又在善算以求周径今具算法于后

　　求黄钟围长法第四(以彭氏律法八章定)



　　(此圆者黄钟管之周围也又名围长互算得十分六釐三毫六丝八忽强)

　　算法从长平方立方图

　　一分从长十釐当万忽　平方百釐当万万忽约一
亿忽　立方千釐当万亿忽

　　一釐从长十毫当千忽　平方百毫当百万忽　立
方千毫当十万万忽约十亿忽

　　一毫从长十丝当百忽　平方百丝当万忽　立方
千丝当百万忽

　　一丝从长十忽　平方百忽　立方千忽

　　彭氏曰算经少广章开圆唐李氏注依密率八十八

乘之七而一开方除之即周此置积求周法也又方
田章圆田术李氏注密率以七乘周二十二而一即
径以二十二乘径七而一即周此置周求径置径求
周法也此密率本祖氏冲之所作比之古率极为精
密今以黄钟面羃开方求周径一依此术既得黄钟
面羃九方分该九万万忽约之为九亿忽依密律算
圆周法置九亿忽以八十八乘之得七百九十二亿
忽乃以七归之得一百一十三亿一千四百二十八

万五千七百一十四忽七分忽之二是为实数以此
实数开方求圆周置此实数在地借一算子步约至
亿下约得至万而止是名下法(谓亿之面万以此记方面从长数)乃
于实数之上商置一十万名上商(记方面从长就以此除地上实数)
乃于实数之下下法直上置一十亿名方法

　　□

　　□

　　忽

　　十

　　丌百

　　□千

　　万　　　　　　　下法丨

　　上商　□十

　　百

　　千

　　川亿

　　十　方法

　　实丨百

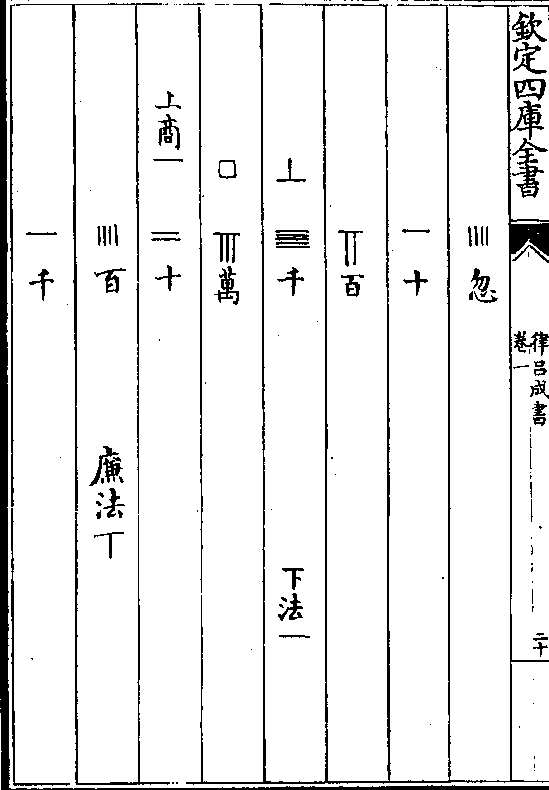
　　方法一十亿合商一(呼一一如一为一百亿)乃命上商除实数
一百亿犹存实数一十三亿一千四百二十八万五
千七百一十四忽七分忽之二第二重开之方法十
亿倍之得二十亿一退得二亿下法万一退得千乃
于上商十万位下续商置六千又于方法之下下法
直上置六百万名廉法

　　□

　　□

　　忽

　　十

　　丌百

　　上　□千　　　　　　　下法

　　□　万

　　上商　□十

　　百　　　　廉法下

　　千

　　川亿

　　实　十

　　方法二亿合商六得十二亿(呼二六一十二也)廉法六百万
亦从上商六得三千六百万(呼六六三十六也)乃命上商除
实数十二亿三千六百万犹存实数七千八百二十
八万五千七百一十四忽七分忽之二第三重开之
倍廉法六百万得一千二百万并入方法二亿内共
得二亿一千二百万一退得二千一百二十万下法
千再退百乃命上商六千位下续商置三百又于下
法直上置三万亦名廉法

　　□

　　□

　　□忽

　　一十

　　□　丌百　　　　　　　下法丨

　　上　□千

　　□　□万　　　廉法□

　　上商一　二十　　　二

　　□百　　　丨

　　实□千　方法□

　　方法二千一百二十万合商三得六千(呼二三得六也)三百
(又呼一三如三也)六十万(又呼二三如六也)廉法三万亦从上商三
得九万(呼三三如九也)乃命上商除实数六千三百六十九
万犹存实数一千四百五十九万五千七百一十四
忽七分忽之二第四重开之倍廉法得六万并入方
法二千一百二十万内共得二千一百二十六万一
退得二百一十二万六千下法再退得十乃于上商
三百位下续商置六十又于下法之上置六百亦名

廉法

　　

　　□

　　忽

　　上　一十　　　　　　　下法一

　　□　丌百　　　　廉法下

　　丨　□千　　　上

　　囗　万　　　

　　上商　□十　　　

　　百　方法

　　实千

　　方法二百一十二万六千合商六得一千二百七十
五万六千(呼二六一十二又呼一六如六又呼二六一十二又呼六六三十六共得此数)廉
法六百亦从上商六得三千六百(呼六六三十六也)乃命上
商除实数一千二百七十五万九千六百忽犹存实
数一百八十三万六千一百一十四忽七分忽之二
第五次开之又倍廉法六百得一千二百并入方法
二百一十二万六千中共得二百一十二万七千二
百一退得二十一万二千七百二十下法再退得一

乃于上商六十位下续商置八又于下法之上置八
亦名廉法

　　

　　□

　　忽忽　　　　廉法下法丨

　　上十十　　　□

　　□百丨百　　　丌

　　上千上千　　　□

　　囗　□万

　　上商一　□十　方法□

　　实丨百

　　方法二十一万二千七百二十合商八得一百七十
□万一千七百六十(以八呼上方法而得此数也)廉法八亦从上
商八得六十四(呼八八六十四也)乃命上商除实数一百七
十□万一千八百二十四忽犹存实数一十三万四
千二百九十□忽七分忽之二在地又须第六重开
之乃以一忽作万万分(每一忽从计一万分每一忽平方计一万万方)约之
为一亿分则在地不尽实数共积得一十三万四千
二百九十□亿二千八百五十七万一千四百二十

六分奇(以一忽作一亿分算故通前七分忽之二以七归之共得此数)前开方已得
每一面从计一十□万六千三百六十八忽乃倍前
廉法八得一十六忽并入前方法内共得二十一万
二千七百三十六忽以亿法通之(前所馀实数既以一忽作一亿分算
故此方法忽数亦以亿法通之)计得二十一万二千七百三十六亿
分一退得二万一千二百七十三亿六十万分前下
法一升为万再退得千前上商十□万六千三百六
十八升为十□亿六千三百六十八万乃于前上商

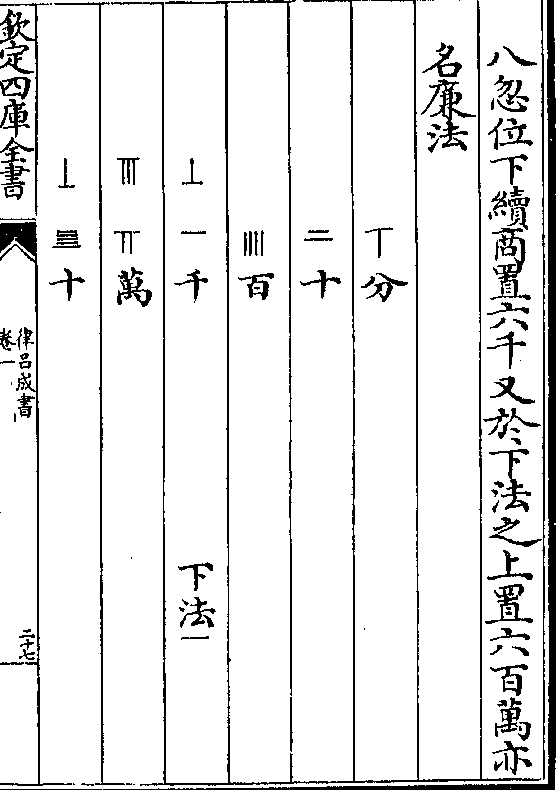八忽位下续商置六千又于下法之上置六百万亦
名廉法

　　下分

　　□十

　　百

　　上　　千　　　　　　下法

　　　丌万

　　上　□十

　　川　百　　　　廉法下

　　上　□千　　　上

　　□　　亿　　　川

　　上商　□十　　　□

　　百　　　

　　□千　　　

　　川万　方法

　　实十

　　方法二万一千二百七十三亿六千万分合商六得
一十二万七千六百四十一亿六千万分(以六呼上文方法而
得此数也)廉法六百万分亦从上商六得三千六百万分
(呼六六三十六也)乃命上商除实数一十二万七千六百四
十一亿九千六百万分犹存实数六千六百四十八
亿三千二百五十七万一千四百二十六分第七重
开之倍廉法六百万得一千二百万并入前方法内
共得二万一千二百七十三亿七千二百万一退得

二千一百二十七亿三千七百二十万下法再退得
百乃于上商六千位下续商置三百分又于下法之
上置三万亦名廉法

　　下分

　　□十

　　川　百　　　　　　　下法丨

　　上　一　千

　　　丌万　　　　廉法川

　　上　□十　　　

　　川　百　　　丌

　　上　☰千　　　☰

　　□　亿　　　丌

　　上商　□十　　　□

　　下百　　　丨

　　实上千　方法□

　　方法二千一百二十七亿三千七百二十万合商三
得六千三百八十二亿一千一百六十万分(以三呼上文方
法而得此数也)廉法三万亦从上商三得九万分(呼三三如九也)乃
命上商除实数六千三百八十二亿一千一百六十
九万分犹存实数二百六十六亿二千　　八十八
万一千四百二十六分第八重开之倍廉法三万得
六万并入前方法内共得二千一百二十七亿三千
七百二十六万一退得二百一十二亿七千三百七

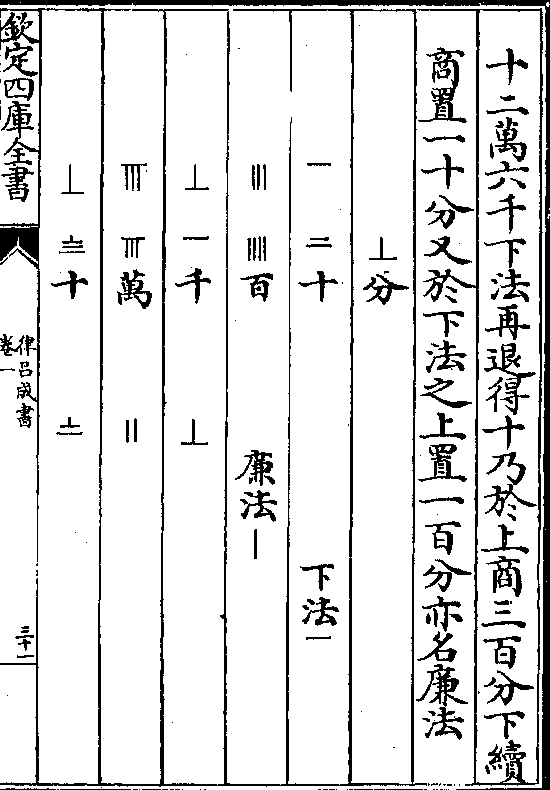十二万六千下法再退得十乃于上商三百分下续
商置一十分又于下法之上置一百分亦名廉法

　　上分

　　　□十　　　　　　　下法

　　川　百　　　　廉法丨

　　上　千　　　上

　　　万　　　

　　上　☰十　　　□

　　川　　百　　　川

　　上　□千　　　□

　　□　下亿　　　

　　上商一　上十　　　

　　实百　方法

　　方法二百一十二亿七千三百七十二万六千分廉
法一百分皆以上商一命之共计除实数二百一十
二亿七千三百七十二万六千一百分犹存实数五
十三亿四千七百一十五万五千三百二十六分第
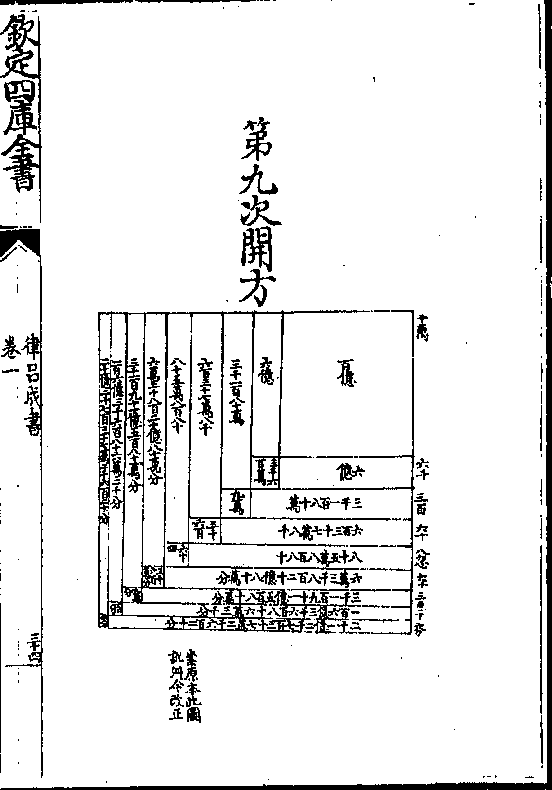
九重开之倍廉法一百得二百并入前方法内共得
二百一十二亿七千三百七十二万六千二百一退
得二十一亿二千七百三十七万二千六百二十下
法再退得一乃于上商一十位下续商置二又于下

　　法之上置二名隅法

　　　下分　　　　隅法下法丨

　　　□十　　□

　　川　川百　　下

　　上　□千　　□

　　　万　　丌

　　上　十　　☰

　　□　□百　　□

　　□　　□千　　　□

　　□　　□亿　　　丨

　　上商一　实□十　方法二十

　　方法二十一亿二千七百三十七万二千六百二十
分合商二得四十二亿五千四百七十四万五千二
百四十分(以二呼上文方法而得此数也)隅法二亦从上商二得四
分(呼二二如四也)乃命上商除实数四十二亿五千四百七
十四万五千二百四十四分犹存实数一十　亿九
千二百四十一万　　八十二分计一十忽奇开不
尽弃之

　　已上黄钟面幂九方分该九亿忽开方得一十万六

千三百六十八忽万分忽之六千三百一十二分即
圆周数以一万忽为从分法除之得一十分不尽六
千三百六十八忽万分忽之六千三百一十二分以
一千忽为从釐法除之得六釐不尽三百六十八忽
万分忽之六千三百一十二分以一百忽为从毫法
除之得三毫不尽六十八忽万分忽之六千三百一
十二分以一十忽为从丝法除之得六丝馀八忽万
分忽之六千三百一十二分黄钟律圆周的计一十

分六釐三毫六丝八忽万分忽之六千三百一十二
分

　　求黄钟径长法第五(以彭氏律法八章定)



　　(圆内直者黄钟管内径长也互算得三分三釐八毫四丝四忽强)

　　彭氏曰置前黄钟圆周数一十□万六千三百六十
八忽万分忽之六千三百一十二分在地今具数如
左

　　□分

　　□十

　　□百

　　上千

　　□忽

　　上十

　　□百

　　上千

　　□万

　　一十

　　据前在地之数依算经密率置周求径法以七乘之
(其以七相乘布算之法游移增减算位无常今不可以具图晓算法者当自知之后不具图者仿此)得
七十四万四千五百八十忽万分忽之四千一百八
十四分今具所得之数如左

　　□分

　　十

　　□百

　　□千

　　□忽

　　☰十

　　□百

　　□千

　　□万

　　□十

　　乃据上文以七乘之所得之数却以二十二而一除
之(即算法二归二除也盖于二十二分中取其一分以为径长之数)得三万三千八

百四十四忽不尽一十二忽万分忽之四千一百八
十四分今具所得之数及不尽之数如左

　　分　(此上一层三万三千八百四十四忽者即以二归二)□十　(除所得全忽之数也下一层一十二忽四千一百八)丨百　(十四分者乃不尽之馀数不可归除作全忽之数又)□千　(须别归除之作忽外零数详见下文)

　　忽　　忽

　　□十　　□十

　　百

　　☰千

　　□万

　　通分内子(即以前不尽之数通而计之也)得一十二万四千一百八
十四分以二十二而一除之得五千六百四十四分
馀二十二分分之一十六(馀分少六数于算法二十二分之数不足故不能满
一分止当得七釐有奇)今以馀分姑作一分通计五千六百四
十五分今具图说如左

　　下分　(此上一层五千六百四十四者即以二归二除已前)

　　十　(不尽之数而得此忽外全分之数也下一层一十六)

　　分　　　　　(分者又归除分外不尽之馀数不可归除作全分之)

　　□十　　　　　(数者也若归除之止得七釐强不满一分然此数所)

　　下百　　　　　(少者微尘耳算法不容不然今故举成数言姑作五)

　　□千　　　　　(千六百四十五分计之)

　　乃合前后归除所得全忽全分之数通计之共得三
万三千八百四十四忽万分忽之五千六百四十五

分乃黄钟管径长之数也其图如左

　　分

　　□十

　　下百

　　□千

　　忽

　　□十

　　百

　　☰千

　　川万

　　已上以七乘黄钟圆周之数以二十二除之得三万
三千八百四十四忽万分忽之五千六百四十五分
如上文所具即圆径数也乃以一万忽为从分法除
之得三分不尽三千八百四十四忽万分忽之五千
六百四十五分以一千忽为从釐法除之得三釐不
尽八百四十四忽万分忽之五千六百四十五分以

一百忽为从毫法除之得八毫不尽四十四忽万分
忽之五千六百四十五分以一十忽为从丝法除之
得四丝馀四忽万分忽之五千六百四十五分黄钟
律圆径的计三分三釐八毫四丝四忽万分忽之五
千六百四十五分

　　复以半周半径求黄钟羃积元数法第六(以彭氏律法八
章定)

　　彭氏曰既得黄钟周径数乃以半周半径求面羃九
方分其法置所得圆周数一十□万六千三百六十
八忽万分忽之六千三百一十二分半之得五万三
千一百八十四忽万分忽之三千一百五十六分通
分内子计五亿三千一百八十四万三千一百五十
六分各具图如左

　　圆周数　　半周数　　半周通分内子数

　　分　　　下分　　下分

　　十　　　□十　　□十

　　□百　　　丨百　　丨百

　　上千　　　☰千　　☰千

　　忽　　　忽　　　万

　　上十　　　☰十　　　☰十

　　川百　　　丨百　　　丨百

　　上千　　　☰千　　　☰千

　　万　　　万　　　□亿

　　十

　　另置所得圆径数三万三千八百四十四忽万分忽
之五千六百四十五分半之得一万六千九百二十
二忽万分忽之二千八百二十二分半通分内子计
一亿六千九百二十二万二千八百二十二分半各
具图如左

　　圆径数　　半径数　　半径通分内子数

　　半　　半

　　分　　　□分　　□分

　　□十　　　十　　□十

　　下百　　　□百　　□百

　　□千　　　□千　　□千

　　□忽　　　□忽　　　□万

　　□十　　　□十　　　□十

　　百　　　百　　　百

　　☰千　　　上千　　　上千

　　川万　　　丨万　　　丨亿

　　乃置所得半径内子分数列于上一位另置所得半
周内子分数列于下一位乘之得八亿九千九百九
十九万九千九百九十九亿八千五百六十二万七
千八百一十分各具图如左

　　半径(置半径内)　半周(置半周内)　乘所得此数(下一位与

子分数于　子分数于　上数此上一位　此下一位　相乘)

　　□分

　　□十

　　百

　　□千

　　□万

　　□十

　　□百

　　□半　　　　　　　　☰千

　　分　　　□分　　　亿

　　□十　　　□十　　　□十

　　百　　　丨百　　　百

　　□千　　　☰千　　　□千

　　万　　　万　　　万

　　□十　　　☰十　　　□十

　　百　　　丨百　　　百

　　上千　　　☰千　　　□千

　　丨亿　　　亿　　　亿

　　已上半周半径相乘所得数即面羃数乃以亿分当
一忽为法除之得八亿九千九百九十九万九千九
百九十九忽亿分忽之八千五百六十二万七千八
百一十分此介乎有形无形之间虽微尘不足以喻
之算法不容不然故云一忽弱(盖前以面羃九亿忽开方求圆周有不尽
之数故此面羃元数九亿忽内有此一弱忽)具图如左

　　□分

　　一十

　　□百

　　□千

　　万

　　上十

　　百

　　☰千

　　忽

　　□十

　　百

　　□千

　　万

　　□十

　　百

　　□千

　　亿

　　通前一忽弱姑以成数计之通作一忽算加入所少
之数一千四百三十七万二千一百九十分在前数
内凑得面羃元法九亿平方忽乃以百忽当一丝为
法除之得九百万平方丝既得九百万丝又以百丝
当一毫为法除之得九万平方毫既得九万毫又当
以百毫当一釐为法除之得九百平方釐既得九百
釐又以百釐为一分除之得九平方分是为黄钟面

羃元数既得面羃九平方分乃以九十分管长乘之
一分管长面羃容九平方分则十分管长当积九十
立方分九十分管长当积八百一十立方分是为黄
钟积实元数

　　复以羃积求黄钟从长元数法第七

　　彭氏曰既得黄钟元积八百一十立方分知空围内
积九立方分则其管当深长一分空围内积九十立
方分则其管当深长九分空围内积八百一十立方
分则其管当深长九十分是为黄钟从长元数则黄
钟算法至此而成矣合而论之的计从长九十分为
九寸积实八百一十分面羃九方分圆周十分六釐
三毫六丝八忽万分忽之六千三百一十二分圆径

三分三釐八毫四丝四忽万分忽之五千六百四十
五分盖以从长羃积周径五法参较推算而各得其
数如此皆出于自然无不符合则算法于此而成而
黄钟之所以为黄钟者信矣于是可以造律矣

　　造黄钟律管法第八(以彭氏律法六章及新书本原第二章参定)

　　如上章算法既成之后或以竹或以铜别为黄钟之
管依前冬至气应管长如前分作九十分乃取其分
为准计三分三釐八毫四丝四忽万分忽之五千六
百四十五以合孔径乃取子谷秬黍(汉书师古注曰子谷犹言谷子
秬即黑黍也)或大者或中者或小者各以一黍准一分累
九十黍以审其管之长而实千二百黍于中以审其
管之广必其所累之黍与其所实之黍大小一同而

所累之数与所实之数各无馀欠则与古人造律之
法无不合矣如此则围长面羃与夫空围内积实自
然无不谐会特径数自八毫以下非可细分而算法
不容不然故其制造之际非有上工如离娄之明公
输之巧师旷之聪弗能为已制造黄钟既成其从长
羃积周径皆如前法则黄钟之体由是立矣度量权
衡可于此而受法十一律可于此而相生又所以为
黄钟之妙用也今先具度量权衡之法于下又可以

交相审验黄钟律管之长阔焉

　　审度第九(以新书本原第十一章定)

　　度者分寸尺丈引所以度长短也生于黄钟之长以
前黄钟管长所累秬黍九十枚度之一黍为一分(凡黍
实于管中则十三黍三分黍之一而满一分积九十分长则容千有二百黍矣其长与广必相符也)十
分为寸十寸为尺十尺为丈十丈为引数始于一终
于十者天地之全数也律未成之前有是数而未见
律成而后数始得以形焉度之成在律之后度之数
在律之前故律之长短围径以度之寸分之数而定

焉

　　嘉量第十(以新书本原第十二章定)

　　量者龠合升斗斛所以量多少也生于黄钟之容以
其管内所容秬黍一千二百实其龠以井水准其槩
(孟康曰井水清清则平也)以度数审其容(一龠积八百一十分)合龠为合(两龠
也积一千六百二十分)十合为升(二十龠也积一万六千二百分)十升为斗(百合
二百龠也积十六万二千分)十斗为斛(二千龠千合百升也积一百六十二万分)

　　谨权衡第十一(以新书本原第十三章定)

　　权衡者铢两斤钧石所以权轻重也生于黄钟之重
以其管内所容秬黍一千二百实其龠百黍一铢一
龠十二铢二十四铢为一两(两龠也)十六两为斤(三十二龠
三百八十四铢也)三十斤为钧(九百六十龠一万一千五百二十铢四百八十两也)四
钧为石(三千八百四十龠四万六千八十铢一万九千二百两也)

　　胡安定曰黄钟管长九十黍之广积九寸度之所由
起也容千二百黍积八百一十分量之所由起也重

十有二铢权衡之所由起也既度量权衡皆出于黄
钟之龠则黄钟之龠围径容受可取四者之法交相
酬验使不失其实也(欧阳永叔曰声无形而乐有器古之作乐者知器之必有弊而
声不可以言传惧夫器失而声遂亡也乃多为法以识之故求声者以律而识律者以黍自一黍之广积
而为分寸一黍之多积而为龠合一黍之重积而为铢两使皆起于黄钟然后律度量权衡相用为表里
使得律者可以制度量衡而度量衡亦可以制律用其长短多少轻重以相参考四者既同而声必至声
至而乐可作　蔡九峰曰黄钟之长九寸以之审度而度长短则九十分黄钟之长一为一分以之审量
而量多少则其管容子榖秬黍中者一千二百以为龠而两龠为合以之平衡而权轻重则所容千二百

黍其重十二铢两龠则二十四铢为两此黄钟所以为万事根本也)

　　黄钟律寸九分十分法第十二(以新书本原第二章及彭氏律法第
八章参定)

　　律寸九分十分图







　　如上章度量权衡之法皆生于黄钟之管则黄钟之

管围径容受可以参校审验而无差矣乃取所造黄
钟之管分为九寸寸作九分分作九釐釐作九毫毫
作九丝丝作九忽以为十一律相生之法(凡律吕相生寸分釐
毫丝忽之法并以九为度)其分数以下虽别以九纪数然只是此
律也故蔡氏曰径围之分以十为法者天地之全数
也相生之分釐毫丝以九为法者因三分损益而立
也全数者即十而取九相生者约十而为九即十而
取九者体之所以立约十而为九者用之所以行(盖地

之数极于十十者阴数也造化之体所以立也天之数极于九九者阳数也造化之用所以行也)体
者所以定中声用者所以生十一律也

　　彭氏曰诸家言黄钟周径数各有差互而黄钟管又
有九分寸有十分寸九分寸则通一管为八十一分
十分寸则通一管为九十分管与寸虽无异而分则
有阔狭不同不知先儒论黄钟周径分数者指言何
分故今先以十分之分算出黄钟周径的数既如前
章所载矣因复用八十一分之分度之得圆周九分

五釐一毫五丝四忽强径长三分□□五毫一丝四
忽强亦不止如先儒所言径三分围九分也

　　黄钟律本三历十二辰法第十三(以新书本原第二章證辨第三
章参定)

　　子　一　黄钟之律

　　辰起于子数起于一子之一为黄钟之律者乃声气
之元而具十二辰之全体者也故置一而以三历十
二辰则各得黄钟之一体以为分寸釐毫丝之法与
数也至亥而得十七万七千一百四十七是为黄钟
之实凡分寸釐毫丝之法与数皆以此数乘除而得

之详具下文

　　丑　三(三其子之一也)　黄钟丝法

　　其法以三为一丝以此丝法三归黄钟十七万七千
一百四十七之数则得五万九千□□四十九为丝
数(其丝法与丝数自然相符馀仿此)

　　寅　九(三其丑之三也)　黄钟寸数

　　其寸数共九以黄钟十七万七千一百四十七之数
九归之则得一万九千六百八十三为寸法(其寸数又与寸

法自相符馀仿此)

　　卯　二十七(三其寅之九也)　黄钟毫法

　　其法以二十七为一毫以此毫法归除黄钟十七万
七千一百四十七之数则得六千五百六十一为毫
数

　　辰　八十一(三其卯之二十七也)　黄钟分数

　　其分数共八十一以黄钟十七万七千一百四十七
之数归除之则得二千一百八十七为分法

　　已　二百四十三(三其辰之八十一也)　黄钟釐法

　　其法以二百四十三为一釐以此釐法归除黄钟十
七万七千一百四十七之数则得七百二十九为釐
数

　　午　七百二十九(三其已之二百四十三也)　黄钟釐数

　　其釐数共七百二十九以黄钟十七万七千一百四
十七之数归除之则得二百四十三为釐法

　　未　二千一百八十七(三其午之七百二十九也)　黄钟分法

　　其法以二千一百八十七为一分以此分法归除黄
钟十七万七千一百四十七之数则得八十一为分
数

　　申　六千五百六十一(三其未之二千一百八十七也)　黄钟毫数

　　其毫数共六千五百六十一以黄钟十七万七千一
百四十七之数归除之则得二十七为毫法

　　酉　一万九千六百八十三(三其申之六千五百六十一也)黄钟寸法

　　其法以一万九千六百八十三为一寸以此寸法除

黄钟十七万七千一百四十七之数则得九为寸数

　　戌　五万九千□□四十九(三其酉之一万九千六百八十三也)黄钟丝数

　　其丝数共五万九千□□四十九以黄钟十七万七
千一百四十七之数归除之则得三为丝法

　　亥　十七万七千一百四十七(三其戌之五万九千四十九也)黄钟之实

　　置子之一而以三历十二辰至亥而得此数是为黄
钟之实所以统体十二辰之全数盖与子之一相为
首尾故凡黄钟寸分釐毫丝之法与数皆以此数乘

除而得之若由此数而三分损益之又所以递生十
一律也详见下章

　　蔡氏曰黄钟九寸以三分为损益故以三历十二辰
得一十七万七千一百四十七为黄钟之实其十二
辰所得之数在子寅辰午申戌六阳辰为黄钟寸分
釐毫丝之数在亥酉未己卯丑六阴辰为黄钟寸分
釐毫丝之法其寸分釐毫丝之法皆用九数故九丝
为毫九毫为釐九釐为分九分为寸九寸为黄钟由

是三分损益以生十一律焉

　　又曰按淮南子谓置一而十一三之积十七万七千
一百四十七为黄钟大数即律书所谓置一而九三
之以为寸法者其术一也(彭氏曰史记律书曰置一而九三之以为法实如法
得长一寸凡得九寸命曰黄钟之律按汉志太极元气函三为一三者天地人也一即天也二则兼天与
地三则参天地与人故元气之动始于子一而即巳具三三之于丑得三三之于寅得九三之于卯得二
十七三之于辰得八十一三之于巳得二百四十三三之于午得七百二十九三之于未得二千一百八
十七三之于中得六千五百六十一三之于酉得一万九千六百八十三三之于戌得五万九千四十九

三之于亥得十七万七千一百四十七此元气运行于十二辰用三施化其自然之数有如此也黄钟居
子位其忽数亦始于一凡十一次三之得十七万七千一百四十七忽与亥数合此即是黄钟一律从长
忽数所谓实也既得实数乃置一忽之数凡九次三之得万九千六百八十三忽与酉数合以此求黄钟
从长寸数此即所谓置一而九三之以为法也以法除实每万九千六百八十三得一寸凡九次除之而
实数尽适得九寸此即所谓实如法得长一寸凡得九寸命曰黄钟之律也)夫置一而九
三之既为寸法则七三之为分法五三之为釐法三
三之为毫法一三之为丝法从可知矣律书独举寸
法者盖已于生钟分内默具律寸分釐毫丝之法而

又于此律数之下指其大者以明凡例也一三之而
得三三三之而得二十七五三之而得二百四十三
七三之而得二千一百八十七九三之而得一万九
千六百八十三故一万九千六百八十三以九分之
则为二千一百八十七二千一百八十七以九分之
则为二百四十三二百四十三以九分之则为二十
七二十七以九分之则为三三者丝法也九其三得
二十七则毫法也九其二十七得二百四十三则釐

法也九其二百四十三得二千一百八十七则分法
也九其二千一百八十七得一万九千六百八十三
则寸法也一寸九分一分九釐一釐九毫一毫九丝
以之生十一律以之生五声二变上下乘除参同契
合无所不通盖数之自然也顾自淮南太史公之后
即无识其意者如京房之六十律虽亦用此十七万
七千一百四十七之数然乃谓不盈寸者十之所得
为分又不盈分者十之所得为小分以其馀为强弱

不知黄钟九寸以三损益数不出九苟不盈分者十
之则其奇零无时而能尽虽泛以强弱该之而卒无
以见强弱之为几何则其数之精微固有不可得而
纪者矣至于杜佑胡瑗范蜀公等则又不复知有此
数而以意强为之法故通典则自南吕而下各自为
法固不可以见分釐毫丝之实故范则止用八百一
十分乃是以积实生量之数为律之长而其因乘之
法亦用十数故其馀算亦皆弃而不录盖非有意于

弃之实其重分累析至于无数之可纪故有所不得
而录耳夫自丝以下虽非目力之所能分然既有其
数而或一算之差则法于此而遂变不以约十为九
之法分之则有终不可得而齐者故淮南太史公之
书其论此也已详特房等有不察耳(司马祯史记索隐注黄钟八寸
十分一云律九九八十一故云八寸十分一汉书云长九寸者九分之寸也此则古人论律以九分为寸
之明验也)