钦定四库全书
　益古演段卷中　　　　　　元　李冶　撰
　　第二十三问
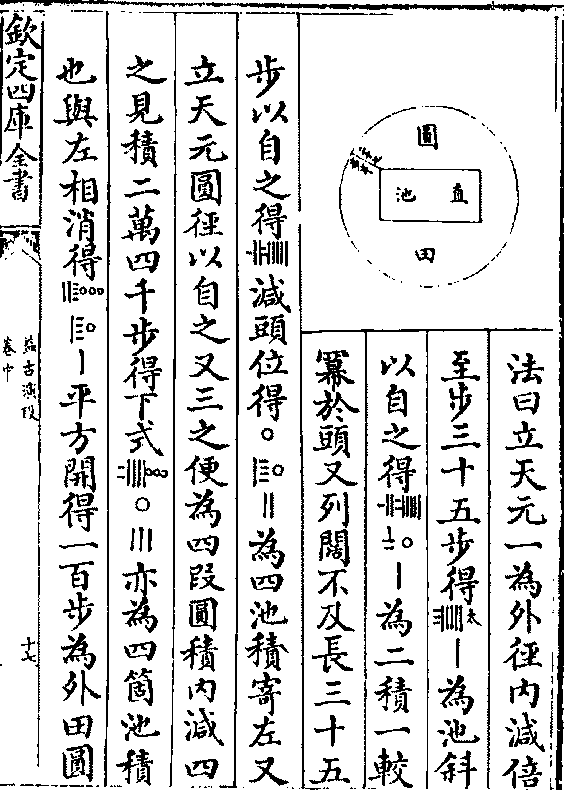
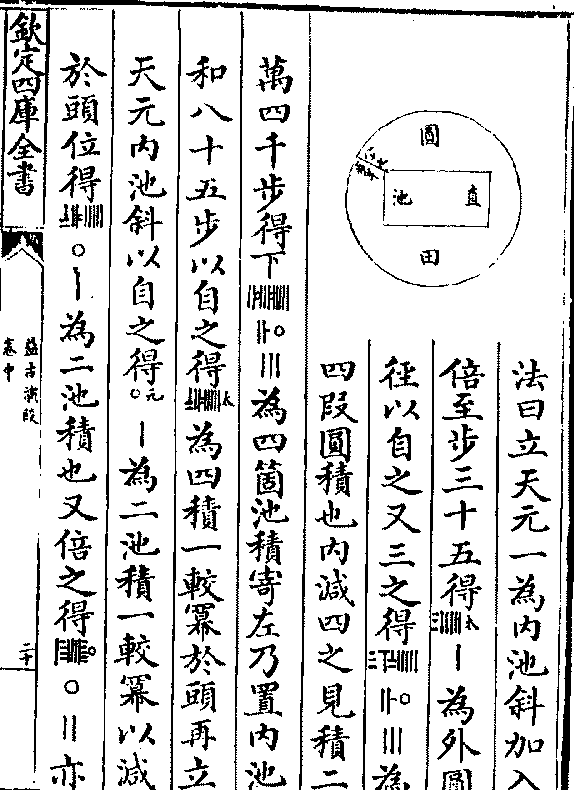
今有圆方田各为段共计积一千三百七步半只云方
　面大如圆径一十步圆依密率问面径各多少
　　答曰方面三十一步　圆径二十一步
　法曰立天元一为圆径加一十步得□丨为方面以
　自之得□(○/二)丨为方田积以十四之得下式□□□

　　　　　　　　为十四段方田积于头又立天元
　　　　　　　　圆径以自乘为幂又以十一之得
　　　　　　　　(太/○)□便为十四段圆田积(依密率/合以径)
　　　　　　　　(自乘又十一之如十四而一今以/十一乘不受除故就为十四分母)
　(也/)以并入头位得□□□为十四段如积寄左然后
　列真积一千三百七步半就分十四之得一万八千
　三百五步与左相消得□□□开平方除之得二十
　一步为密率径也加不及步为方田也

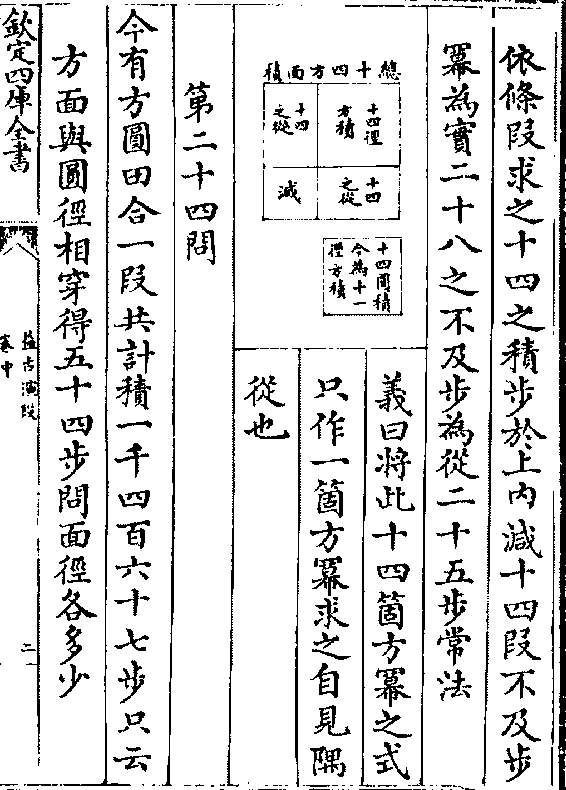　依条段求之十四之积步于上内减十四段不及步
　幂为实二十八之不及步为从二十五步常法
　　　　　　　　　义曰将此十四个方幂之式
　　　　　　　　　　只作一个方幂求之自见隅
　　　　　　　　　　从也
　　第二十四问
今有方圆田合一段共计积一千四百六十七步只云
　方面与圆径相穿得五十四步问面径各多少

　　答曰方面一十二步　圆径四十二步
　　　　　　　法曰立天元一为圆径减穿步五十
　　　　　　　四步得□丨为方田面以自增乘得
　　　　　　　下式□□丨为方田积于头位再立
　　　　　　　天元圆径以自之又三之四而一得
　(元/○)□为圆田积也并入头位得□□□为一段如积
　寄左然后列真积一千四百六十七步与左相消得
　□□□倒积倒从开平方得四十二步为圆田径也

　以减穿步即方面
　　按法内所言倒积倒从即翻积法也盖初商积常
　　减原积此独以原积减初商积倍廉常减从步此
　　独以从步减倍廉乃平方中之一变也古法多用
　　之今依数布算于后以存其式
　法列积一千四百四十九步为实以一百零八步为
　　　　　　　长与一阔又七分半之和即从数求
　　　　　　　阔初商四十步以一阔七分半乘之

　　　　　　　得七十步以减和数馀三十八步以
　　　　　　　初商乘之得一千五百二十步为初
　　　　　　　商积大于原积反减之馀实七十一
　　　　　　　步乃二因一阔七分半所乘初商之
　　　　　　　数得一百四十步大于和数反减之
　　　　　　　馀三十二步为次商廉次商二步以
　　　　　　　一阔七分半乘之得三步半为次商
　　　　　　　隅凡和数廉隅相减此反相加得三

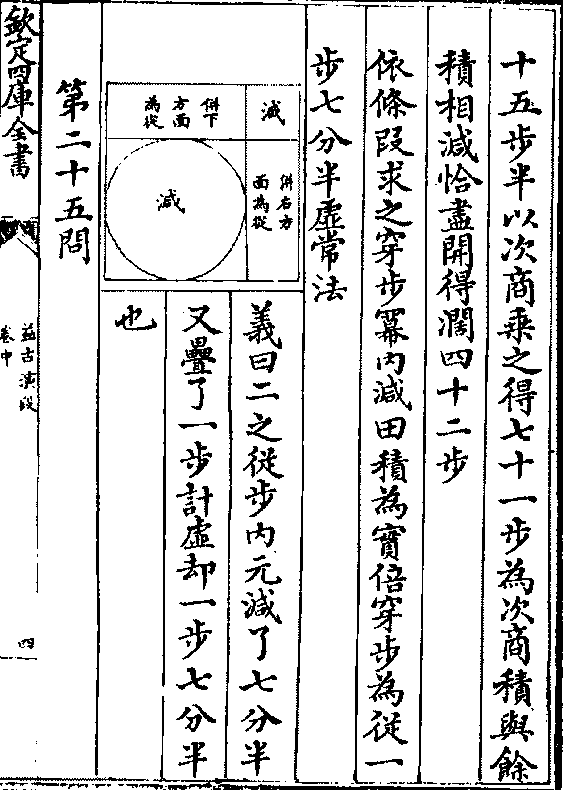　十五步半以次商乘之得七十一步为次商积与馀
　积相减恰尽开得阔四十二步
　依条段求之穿步幂内减田积为实倍穿步为从一
　步七分半虚常法
　　　　　　　　义曰二之从步内元减了七分半
　　　　　　　　又叠了一步计虚却一步七分半
　　　　　　　　也
　　第二十五问

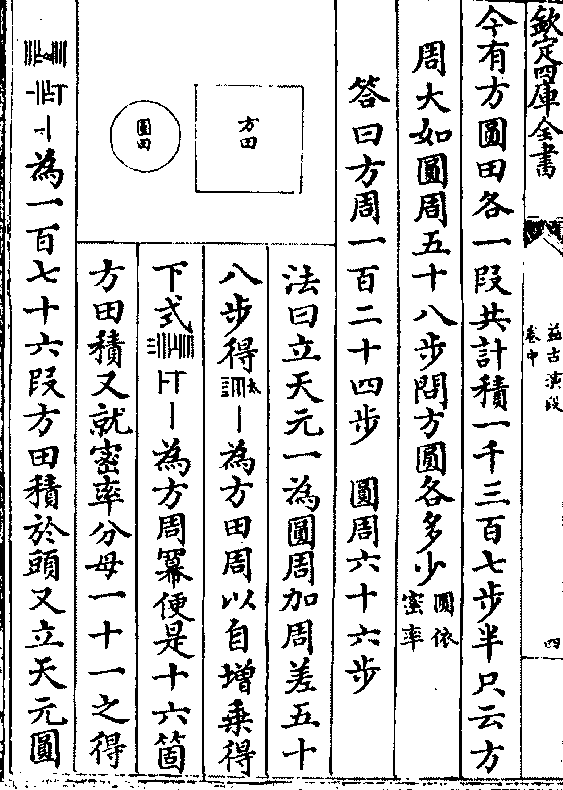今有方圆田各一段共计积一千三百七步半只云方
　周大如圆周五十八步问方圆各多少(圆依/密率)
　　答曰方周一百二十四步　圆周六十六步
　　　　　　　法曰立天元一为圆周加周差五十
　　　　　　　八步得□丨为方田周以自增乘得
　　　　　　　下式□□丨为方周幂便是十六个
　　　　　　　方田积又就密率分母一十一之得
　□□□为一百七十六段方田积于头又立天元圆

　周以自之为幂又就分一十四之得(元/○)□为一百七
　十六段圆田积(依密率周上求积合以周自乘又以/七乘之如八十八而一为一段田积)
　(也今又周密上更以十四乘之则合用/一百七十六而一故就分便为此数)以添入头位
　得□□□共为一百七十六段如积寄左然后列真
　积一千三百七步半就分以一百六十七乘之得二
　十三万一百二十步与左相消得□□□开平方得
　六十六步为圆田周也加多步见方周
　依条段求之一百七十六之积内减一十一段多步

　幂为实二十二之多步为从二十五步常法
　　　　　　　　　　义曰一百七十六之积步内
　　　　　　　　　　有一十一个方周方一十四
　　　　　　　　　　个圆周方也今画此式其一
　十四个圆周方与一十一个圆周方大小俱同者止
　为欲见差步权作此式其实合作一十二段圆式求
　之其实自见也(按十一方周幂十四圆周幂共积内/减去十一不及幂馀不及步乘圆周)
　(长方二十二圆周幂二十五故以二/十二不及步为从二十五为隅也)

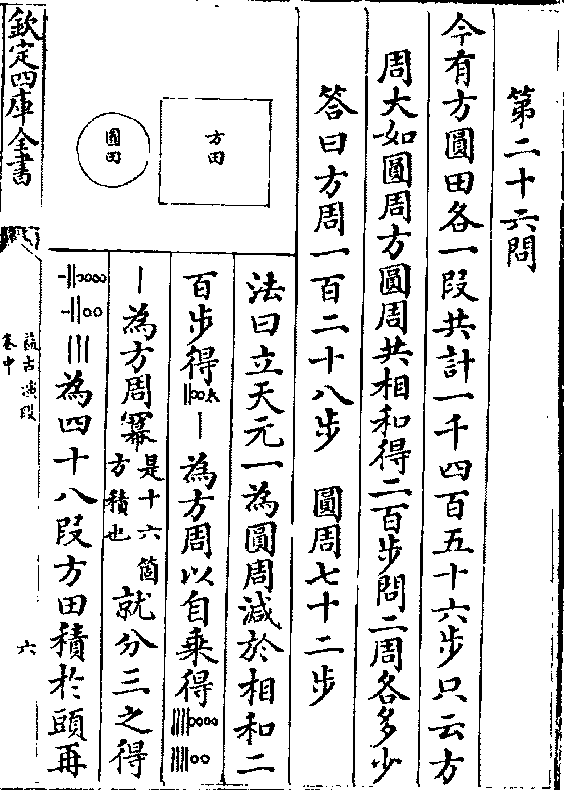　　第二十六问
今有方圆田各一段共计一千四百五十六步只云方
　周大如圆周方圆周共相和得二百步问二周各多少
　　答曰方周一百二十八步　圆周七十二步
　　　　　　　法曰立天元一为圆周减于相和二
　　　　　　　百步得□丨为方周以自乘得□□
　　　　　　　丨为方周幂(是十六个/方积也)就分三之得
　　　　　　　□□□为四十八段方田积于头再

　立天元圆周以自之又就分四之得(元/○)□亦为四十
　八段圆田积并入头位得□□□为四十八段如积
　数寄左然后列真积一千四百五十六步就分四十
　八之得六万九千八百八十八步与左相消得□
　□□开平方得七十二步为圆田径也减共步则方
　周
　依条段求之三段和步幂内减四十八之田积为实
　六之和步为从七益隅

　
　
　
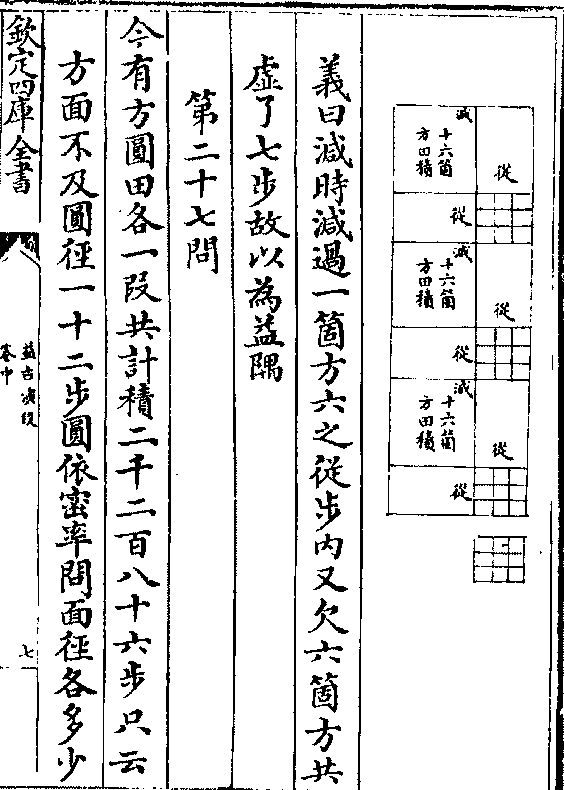
　义曰减时减过一个方六之从步内又欠六个方共
　虚了七步故以为益隅
　　第二十七问
今有方圆田各一段共计积二千二百八十六步只云
　方面不及圆径一十二步圆依密率问面径各多少

　　答曰方面三十步　圆径四十二步
　　　　　　　法曰立天元一为方面加不及一十
　　　　　　　二步得□丨为圆径以自之得□□
　　　　　　　丨为圆径幂以一十一之得下式□
　　　　　　　□□便为十四个圆积于头再立天
　元方面以自之又就分一十四之得(元/○)□为十四个
　方积也并又头位得□□□为十四段如积数寄左
　然后列真积二千二百八十六步就分一十四之得

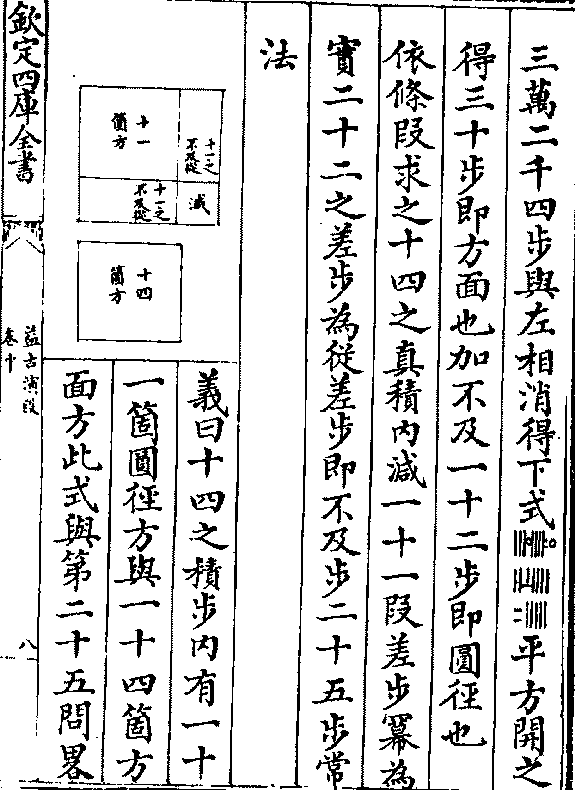　三万二千四步与左相消得下式□□□平方开之
　得三十步即方面也加不及一十二步即圆径也
　依条段求之十四之真积内减一十一段差步幂为
　实二十二之差步为从差步即不及步二十五步常
　法
　　　　　　　　　　义曰十四之积步内有一十
　　　　　　　　　　一个圆径方与一十四个方
　　　　　　　　　　面方此式与第二十五问略

　同其一十一个圆径幂有十一个方正当十一段之
　其数自见也
　　第二十八问
今有方圆田各一段共计积二千二百八十六步只云
　方周不及圆周一十二步问周各若干(圆依/密率)
　　答曰方周一百二十步　圆周一百三十二步
　法曰立天元一为方周加不及步一十二得(太/□)丨为
　圆周以自之得□□丨又以一十四乘之得□□□

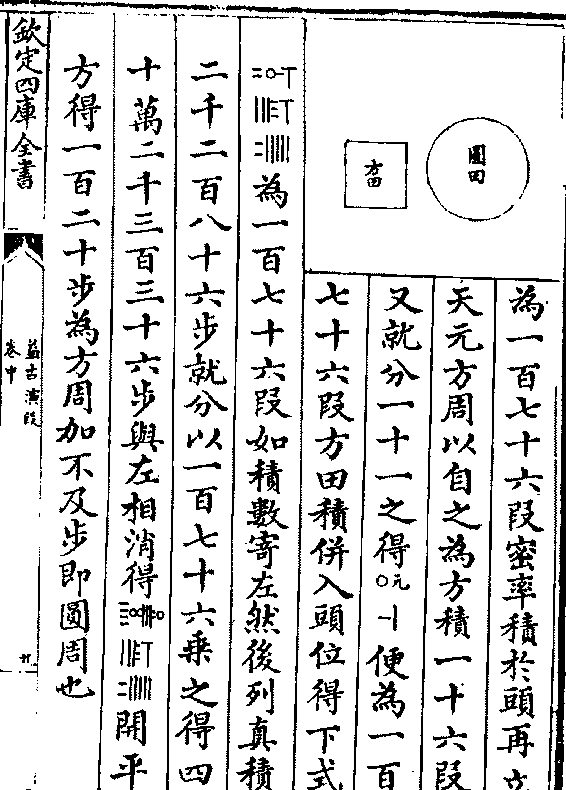　　　　　　　为一百七十六段密率积于头再立
　　　　　　　天元方周以自之为方积一十六段
　　　　　　　又就分一十一之得(元/○)□便为一百
　　　　　　　七十六段方田积并入头位得下式
　□□□为一百七十六段如积数寄左然后列真积
　二千二百八十六步就分以一百七十六乘之得四
　十万二千三百三十六步与左相消得□□□开平
　方得一百二十步为方周加不及步即圆周也

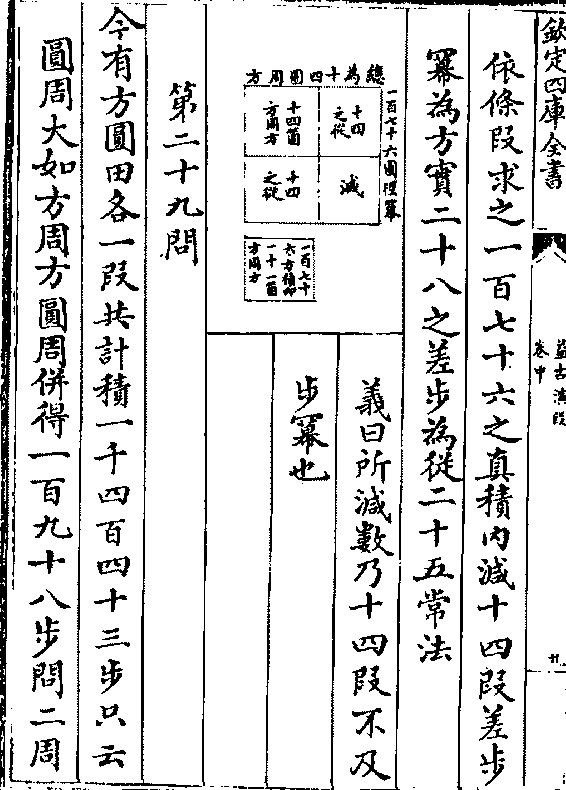　依条段求之一百七十六之真积内减十四段差步
　幂为方实二十八之差步为从二十五常法
　　　　　　　　　　义曰所减数乃十四段不及
　　　　　　　　　　步幂也
　
　　第二十九问
今有方圆田各一段共计积一千四百四十三步只云
　圆周大如方周方圆周并得一百九十八步问二周

　各多少
　　答曰方周九十六步　圆周一百二步
　　　　　　　　法曰立天元一为方周减共步一百
　　　　　　　　九十八得□丨为圆周以自增乘得
　　　　　　　　□□丨为十二段圆田积四之得下
　　　　　　　　□□□为四十八段圆田积于头再
　立天元方周以自之为十六段方田积又就分三之得(元/○)□
　便为四十八段方田积并入头位得□□□为四十八段如积

　寄左然后列真积一千四百四十三步就分母以四十
　八乘之得六万九千二百六十四与左相消得□□□
　开平方得九十六步为方周也减于并数见圆周也
　依条段求之四段共步幂内减四十八之积为实八
　之共步为从七益隅

　义曰八之从内合虚八个方今见有一个方外只虚
　了七步方也
　　第三十问
今有圆田二段(一段依圆三径一/率一段依密率)共积六百六十一步
　只云二径共相和得四十步问二径各数
　　答曰密径一十四步　古径二十六步
　法曰立天元一为密径以减相和四十步得□丨为
　古径以自之得下□□丨为古径幂以三因之得□

　　　　　　　□□合以四约之又就分母七之得
　　　　　　　□□□为二十八段古圆积于头再
　　　　　　　立天元密圆径以自之又二十二之
　　　　　　　得(元/○)□为二十八段密圆积也并入
　头位得□□□为二十八段如积寄左然后列真积
　六百六十一步就分二十八乘之得一万八千五百
　八步与左相消得□□□平方开之得一十四步为
　密圆径以减和步即古径也

　依条段求之二十一段和步幂内减二十八之田积
　为实四十二之和步为从四十三步虚常法
　　　　　　　　　义曰其二十八之田积内有古
　　　　　　　　　积二十一段密积二十二段元初
　　　　　　　　　减时减过一段又并从步内合
　　　　　　　　　除之数计虚却四十三个方也
　　第三十一问
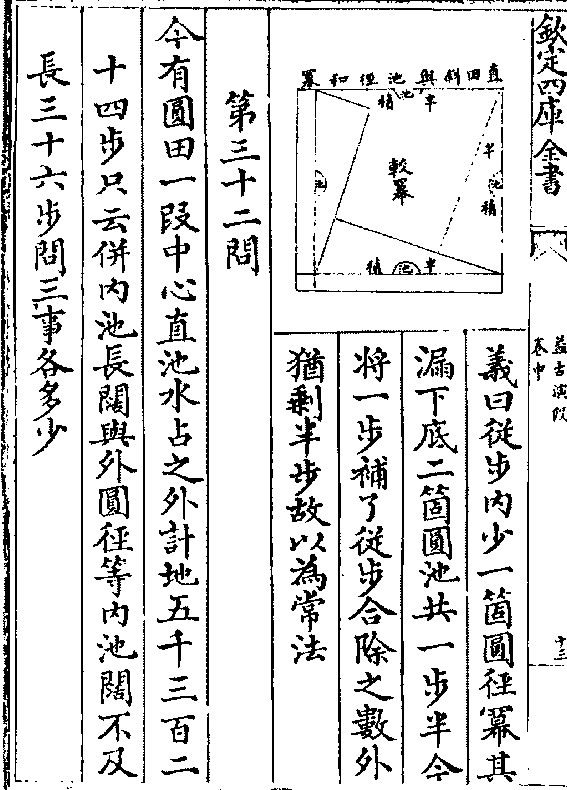
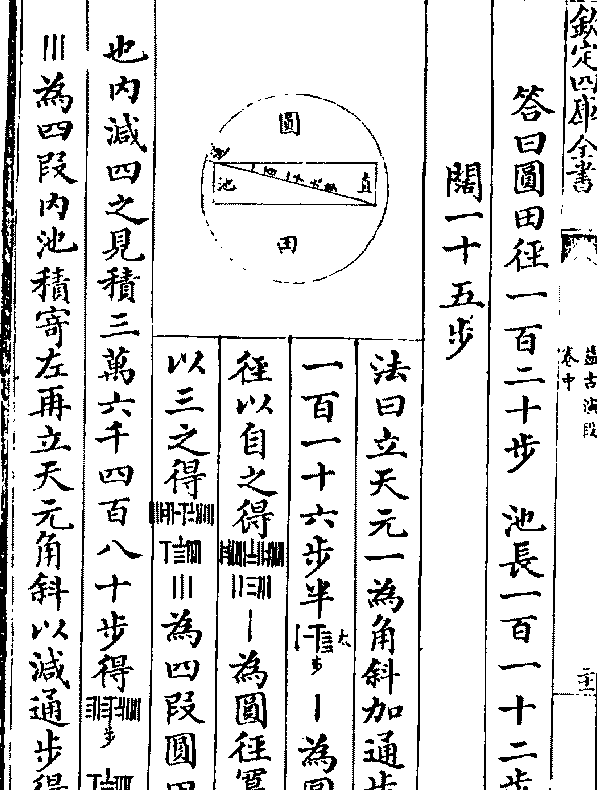
今有直田一段中心有圆池水占之外计地三千九百

　二十四步只云从外田角斜通内池径七十一步外
　田阔不及长九十四步问三事各多少
　　答曰圆池径一十二步　田长一百二十六步
　　　　阔三十二步
　　　　　　　法曰立天元一为内圆径以减倍通
　　　　　　　步一百四十二步得□丨为直田斜
　　　　　　　以自乘得□□丨为两段直田并一
　　　　　　　段较幂于头再置阔不及长九十四

　步自之得八千八百三十六步以减头位得□□丨
　为两段直积数寄左再立天元圆径以自之为圆径
　幂三之二而一得(元/○)□为两个池积数加入二之见
　积七千八百四十八步得□○□亦为二段真积与
　寄左相消得□□□平方开之得一十二步为圆径
　也
　依条段求之倍通步为幂内减二之见积一个较幂
　为实四之通步为从半步常法

　　　　　　　　　义曰从步内少一个圆径幂其
　　　　　　　　　漏下底二个圆池共一步半今
　　　　　　　　　将一步补了从步合除之数外
　　　　　　　　　犹剩半步故以为常法
　　第三十二问
今有圆田一段中心直池水占之外计地五千三百二
　十四步只云并内池长阔与外圆径等内池阔不及
　长三十六步问三事各多少

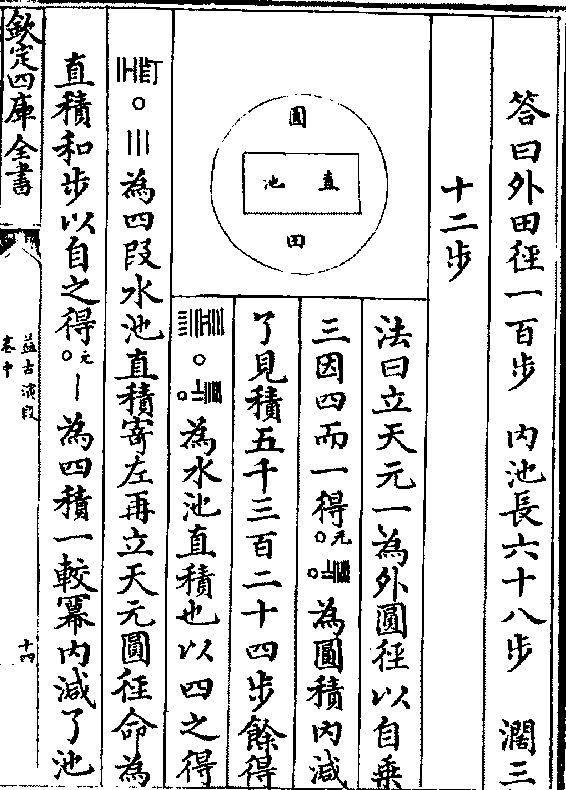　　答曰外田径一百步　内池长六十八步　阔三
　　　　十二步
　　　　　　　　法曰立天元一为外圆径以自乘
　　　　　　　　三因四而一得(元/○)□为圆积内减
　　　　　　　　了见积五千三百二十四步馀得
　　　　　　　　□○□为水池直积也以四之得
　□○□为四段水池直积寄左再立天元圆径命为
　直积和步以自之得(元/○)丨为四积一较幂内减了池

　较幂一千二百九十六步得□○丨亦为四段池积
　与左相消得□○□平方开之得一百步为外圆径
　也阔不及长减圆径馀折半见阔却以不及步加之
　即长也
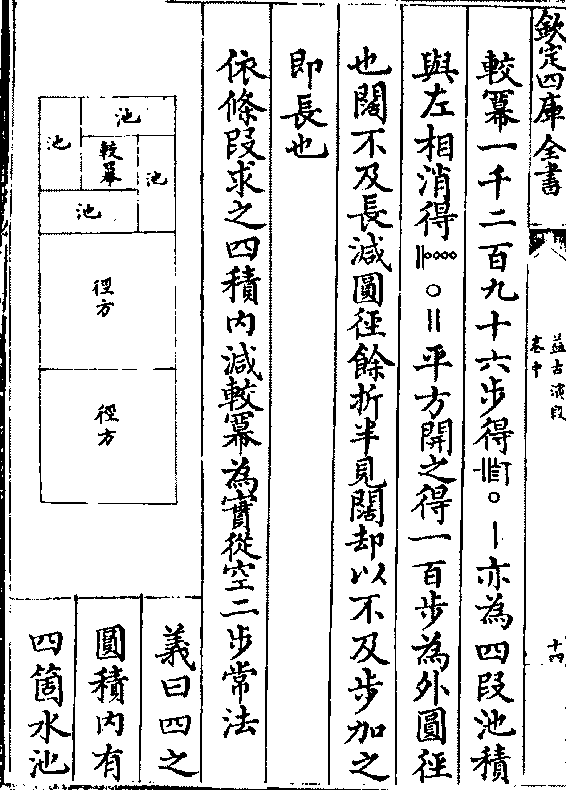
　依条段求之四积内减较幂为实从空二步常法
　　　　　　　　　　　　　　　　　义曰四之
　　　　　　　　　　　　　　　　　圆积内有
　　　　　　　　　　　　　　　　　四个水池

　又于见积内减了一个池较幂相并恰是一个和幂
　也今来池和与圆等共和幂恰是一个圆径幂也除
　外有两个方
　　第三十三问
今有圆田一段中心有直池水占之外计地七千三百
　步只云并内池长阔少田径五十五步阔不及长三
　十五步问三事各多少
　　答曰田径一百步　内池长四十步　阔五步

　　　　　　　　　法曰立天元一为外圆径自之
　　　　　　　　　得数又三之四而一得(元/○)□为
　　　　　　　　　外圆田积也减见积七千三百
　　　　　　　　　步得□○□为内池积也以四
　之得□○□为四段池积寄左再立天元圆径内减
　少径步五十五得□丨为池和也以自之得□□丨
　为四池一较幂内减池较幂一千二百二十五步得
　□□丨亦为四池积也与左相消得□□□平方开

　之得一百步为圆径也内减少径即水池和步内加
　一差即为二长若减一差即为二阔也
　依条段求之四之积步内减池较幂却加入少径幂
　为实二之少径为从二步常法
　　　　　　　　　　　　　　义曰四池并所减
　　　　　　　　　　　　　　底个较幂恰是一
　　　　　　　　　　　　　　个和自之
　旧术下积步四之于头位又以少径步自乘加头位

　内却减阔不及长幂馀折半为实用少径为从一步
　常法
　　第三十四问
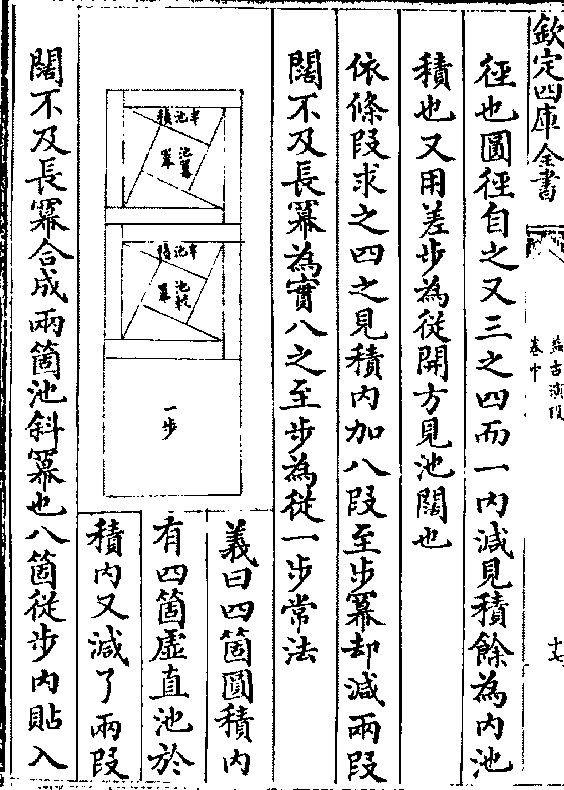
今有圆田一段内有直池水占之外计地六千步只云
　从内池四角斜至田楞各一十七步半其池阔不及
　长三十五步问三事各若干
　　答曰圆田径一百步　池长六十步　阔二十五
　　　　步

　　　　　　　　　法曰立天元一为外径内减倍
　　　　　　　　　至步三十五步得□丨为池斜
　　　　　　　　　以自之得□□丨为二积一较
　　　　　　　　　幂于头又列阔不及长三十五
　步以自之得□减头位得○□□为四池积寄左又
　立天元圆径以自之又三之便为四段圆积内减四
　之见积二万四千步得下式□○□亦为四个池积
　也与左相消得□□丨平方开得一百步为外田圆

　径也圆径自之又三之四而一内减见积馀为内池
　积也又用差步为从开方见池阔也
　依条段求之四之见积内加八段至步幂却减两段
　阔不及长幂为实八之至步为从一步常法
　　　　　　　　　　　　　　义曰四个圆积内
　　　　　　　　　　　　　　有四个虚直池于
　　　　　　　　　　　　　　积内又减了两段
　阔不及长幂合成两个池斜幂也八个从步内贴入

　八个斜至步幂其数与圆径正相应也外恰有一步
　方
　　第三十五问
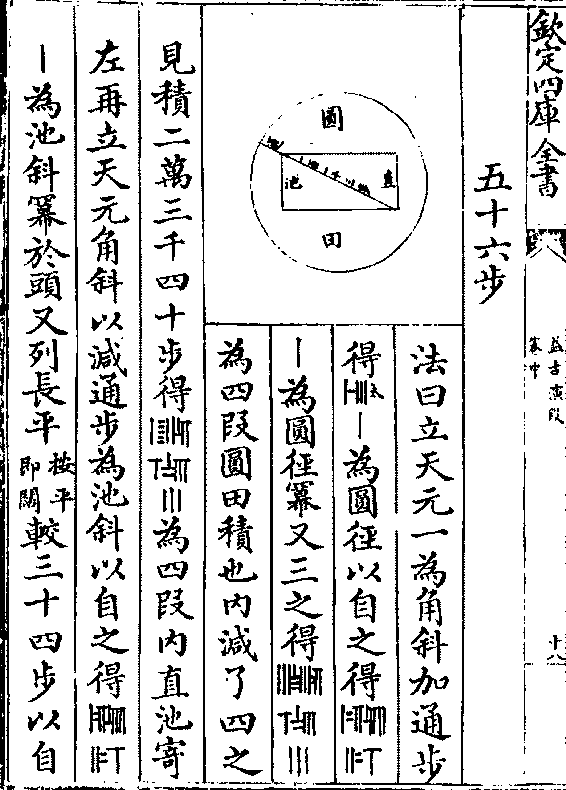
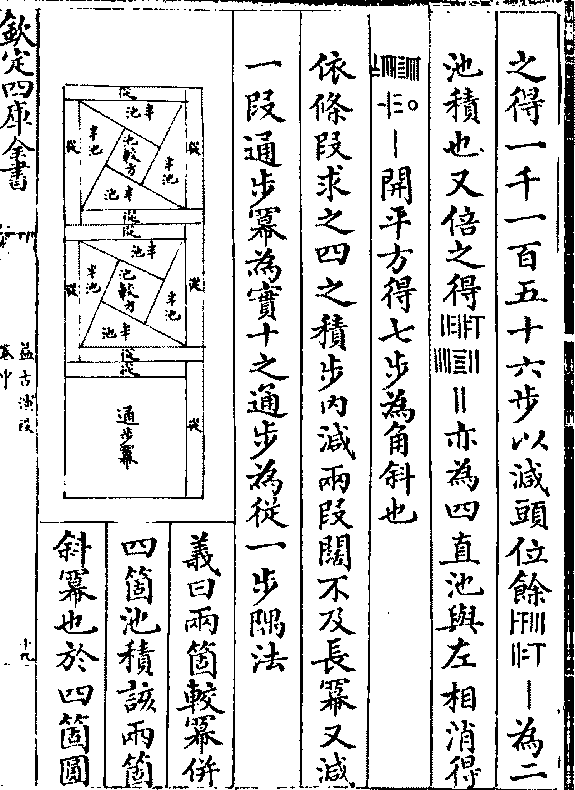
今有圆田一段中心有直池水占之外计地五千七百
　六十步只云从外田东南楞至内池西北角通斜一
　百一十三步其内池阔不及长三十四步问三事各
　多少
　　答曰外圆田径一百二十步　池长九十步　阔

　　　　五十六步
　　　　　　　　　法曰立天元一为角斜加通步
　　　　　　　　　得□丨为圆径以自之得□□
　　　　　　　　　丨为圆径幂又三之得□□□
　　　　　　　　　为四段圆田积也内减了四之
　见积二万三千四十步得□□□为四段内直池寄
　左再立天元角斜以减通步为池斜以自之得□□
　丨为池斜幂于头又列长平(按平/即阔)较三十四步以自

　之得一千一百五十六步以减头位馀□□丨为二
　池积也又倍之得□□□亦为四直池与左相消得
　□□丨开平方得七步为角斜也
　依条段求之四之积步内减两段阔不及长幂又减
　一段通步幂为实十之通步为从一步隅法
　　　　　　　　　　　　　　义曰两个较幂并
　　　　　　　　　　　　　　四个池积该两个
　　　　　　　　　　　　　　斜幂也于四个圆

　积内减此两个斜幂外更减了一个通步幂恰是十
　之从外有一步常法也
　　第三十六问
今有圆田一段中心有直池水占之外计地六千步只
　云从内池四角斜至田楞各一十七步半其内池长
　阔共相和得八十五步问三事各多少
　　答曰外田径一百步　池长六十步　阔二十五
　　　　步

　　　　　　　　　法曰立天元一为内池斜加入
　　　　　　　　　倍至步三十五得□丨为外圆
　　　　　　　　　径以自之又三之得□□□为
　　　　　　　　　四段圆积也内减四之见积二
　万四千步得下□□□为四个池积寄左乃置内池
　和八十五步以自之得□为四积一较幂于头再立
　天元内池斜以自之得(元/○)丨为二池积一较幂以减
　于头位得□○丨为二池积也又倍之得□○□亦

　为四池积与左相消得□□□平方开得六十五步
　为内池斜加倍至步即圆径也径自之又三之四而一
　内减去田积馀实以和步为从一虚隅开平方见阔也
　依条段求之四之积步内加两段和步幂却减十二
　段至步幂为实十二之至步为从五步常法
　　　　　　　　　　　　　　义曰所加两个和
　　　　　　　　　　　　　　幂该八积二较幂
　　　　　　　　　　　　　　数内元有四虚池

　外有四积二较幂其实只是添了两个池斜幂也于
　四圆积内除从步占外元有三个方今又加入两个
　池斜幂共得五步故五为常法
　　第三十七问
今有圆田一段中心有直池水占之外计地九千一百
　二十步只云从外田楞通内池斜一百一十六步半
　其内池长阔共相和得一百二十七步问三事各多
　少

　　答曰圆田径一百二十步池长一百一十二步
　　　　阔一十五步
　　　　　　　　　法曰立天元一为角斜加通步
　　　　　　　　　一百一十六步半□步丨为圆
　　　　　　　　　径以自之得□□丨为圆径幂
　　　　　　　　　以三之得□□□为四段圆田
　也内减四之见积三万六千四百八十步得□步□
　□为四段内池积寄左再立天元角斜以减通步得

　□步丨为内池斜以自乘得□步□丨为二积一较
　幂于头又列池和步以自乘得□内减头位馀得□
　(元/)□丨为二池积也倍之得下□步□□亦为四池
　积与左相消得□步□□平方开之得三步半为角
　斜也加通步为圆径
　依条段求之四之积步内加两段和步幂却减
　五个通步幂馀为实二之通步为从五步为常
　法

　
　
　
　义曰两个和幂内虚了四池只是两个池斜幂今将
　两个池斜幂减于两个通步幂止有二甲二乙所占
　之地今又将二甲二乙及三段通步幂并以减于四
　之见积外实在两个通步从五个方也
　　第三十八问

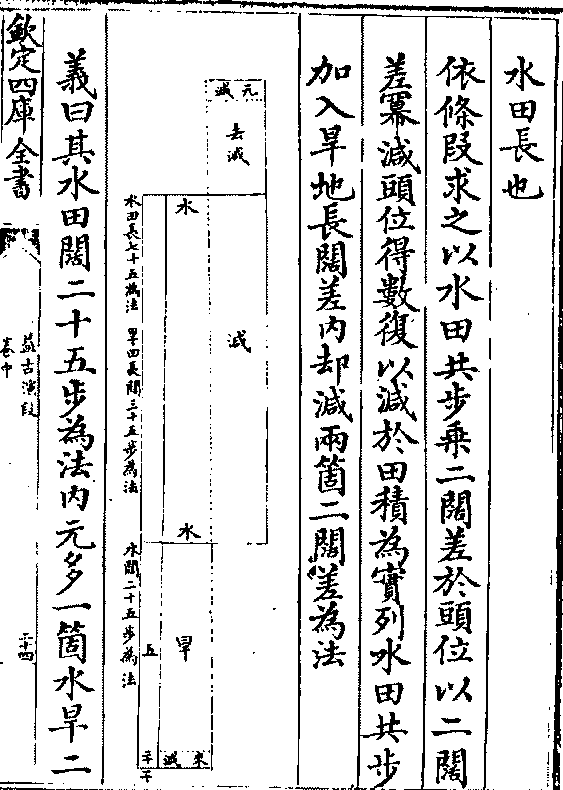
今有水旱田各一段共计积二千六百二十五步只云
　水田长阔共一百步其旱地阔不及长三十五步而
　不及水地阔十步问水旱地长阔各若干
　　答曰水地长七十五步　阔二十五步　旱地长
　　　　五十步　阔一十五步
　　　　　　　　　法曰立天元一为旱地阔加旱
　　　　　　　　　阔不及水阔一十步得□丨为
　　　　　　　　　水地阔以减水田长阔共一百

　步得□丨为水田长也以水田长阔相乘得□□丨
　为水田积于头再置天元旱地阔加不及三十五步
　得□(兀/丨)为旱田长也以天元乘之得(太/○)□丨为旱田
　积也加入头位得□□为一段如积寄左然后列真
　积二千六百二十五步与左相消得□□下法上实
　如法得一十五步为旱田阔也加阔不及长三十五
　步为旱田长也又于旱阔内加不及水地阔一十步
　为水地阔也以水地阔减于水田长阔一百步馀为

　水田长也
　依条段求之以水田共步乘二阔差于头位以二阔
　差幂减头位得数复以减于田积为实列水田共步
　加入旱地长阔差内却减两个二阔差为法
　
　
　
　义曰其水田阔二十五步为法内元多一个水旱二

　阔差数又积步内减了一段旱阔为长二阔差为平
　底直积是又虚了一个水旱二阔差数故于法内减
　去两个阔差也
　　按此条图与义不合盖傅写之误也今仍存旧式
　　另拟图义于后以明之
　　　　　　　　　义曰水田长阔共步乘二阔差
　　　　　　　　　内减差幂即附水田周一磬折
　　　　　　　　　积也以减共积馀同旱阔之两

　　长方共积为实其水田长阔比原数各减一阔差
　　于此长阔和内加旱田长阔较即两长方之共长
　　故为法即得旱田阔也
　　第三十九问
今有直田一段内有圆池水占之外计地三十九亩一
　分半只云从田两头至池各一百五步两畔至池各
　九步问三事各多少
　　答曰田长二百三十四步　阔四十二步　池径

　　　　二十四步
　　　　　　　法曰立天元一为内池径加二之边
　　　　　　　至一十八步得□丨为田阔又置天
　　　　　　　元池径加二之头至二百一十步得
　　　　　　　□丨为田长长阔相乘得下式□□
　丨为直田积于头再置天元径以自之又三之四而
　一得○□为内池积以减头位得□□□为一段如
　积数寄左然后列真积三十九亩一分半以亩法通

　之得九千三百九十六步与左相消得□□□开平
　方得二十四步为内池径也加二之边至步为田阔
　若加二之头至步即田长
　依条段求之倍头至步与倍边步相乘以减田积为
　实并一头一边步又倍之为从二分半常法
　　　　　　义曰此问与第一问条段颇同但所减
　　　　　　者为四个小池积(按池当/作隅)
　

　　第四十问
今有直田一段中心有圆池水占之外计地四亩五十
　三步只云外田长平和得七十六步太半步从田四
　角去池楞各一十八步问外田水池径各多少
　　答曰田长五十步　阔二十六步太　池径二十
　　　　步太
　法曰立天元一为内池径加倍角至步三十六得□
　丨为直田斜以自之得□□丨为田斜幂(便是二积/一较幂也)

　　　　　　　又九之得下式□□□为十八积九
　　　　　　　较幂也寄左列和步七十六步太(按/太)
　　　　　　　(即三分/步之二)通分内子得□以自之得五
　　　　　　　万二千九百步为九段和幂于头(为/九)
　(段和幂者元带三分母以自之得九也此/九段和幂该三十六直积九个较幂也)又置天元
　圆径以自之又三之四而一得(元/○)□为一段圆积也
　加入见积一千一十三步得□○□共为直积一段
　又十八之得□○□为十八段直积以减头位得□

　○□亦为九段田斜幂与左相消得□□□合以平
　方开之今不可开(按不可开者谓廉隅数/多而得数又不能尽也)先以隅法
　二十二步半乘实二万三千单二步得五十一万七
　千五百四十五步正为实元从六百四十八负依旧
　为从一益隅平方开之得四百六十五步以元隅二
　十二步半约之得二十步三分之二为内池径也加
　倍至步为田斜以自之为二积一较幂又二之于头
　位以和步幂减头位馀以平方开之即田较也加入

　和步折半为长若减于和步折半为阔也
　依条段求之列相和步自乘为幂内减倍积及四段
　至步幂为实四之至步为从二步半常法
　　　　　　　　　义曰和步幂内减了二直积只
　　　　　　　　　有一段斜幂也减二直积时漏
　　　　　　　　　下两个圆池该一步半又正有
　　　　　　　　　一步共计二步半常法也　求
　较者先置池径二十步太□带三分母便为三个径

　也加入六之至步一百八步得□便为三个田斜也
　以自之得□为九段斜幂(便是十八个直/积九个较幂)倍之得□
　为三十六段田积一十八段较幂于头再置和步七
　十六步太□亦带三分母便为三个和也以自之得
　□为九段和幂(便是三十六直/积九较幂也)以减头位馀□为九
　段较幂也平方开之得七十步以三约之得二十三
　步三分步之一为田较也欲见田长阔及斜者准此
　法求之　又法求圆池径者立天元一为三个内池

　径以自之得(元/○)丨为九段池径幂便是十二段圆积
　也加十二段见积得□○丨为十二段直积又身外
　加五得□○□为十八段直田积于头又列和步七
　十六步太通分内子得二百三十自之得□为和幂
　九段(便是直积三十六/段较幂九段也)内减头位得下式□○□为
　九段斜幂数寄左再置天元圆径加六之角至步一
　百八步得□丨为三个田斜以自之得□□丨亦为
　九段斜幂也与左相消得□□□开平方得六十二

　步为三个圆池径也以三约之得一个圆径二十步
　三分之二此名之分天元一术前法乃连枝同体术
　也(按分天元一术即天元一内带分求之得数而后/约之连枝同体术即通分开方得数而后约之皆)
　(兼通分/之法也)
　　第四十一问
今有直田一段中心有圆池水占之外计地三千九百
　二十四步只云从外田角斜通池径七十一步外田
　长阔相和得一百五十八步问三事各多少

　答曰圆径十二步　田长一百二十六步　阔三十二步
　　　　　　　法曰立天元一为内圆径以减倍通
　　　　　　　步一百四十二步得□丨为田斜以
　　　　　　　自之得□□丨为二积一较幂于头
　　　　　　　又立和步一百五十八步以自之得
　□为四积一较幂以减头位得□□丨为二直积寄
　左又立天元池径以自之又三之二而一得(元/○)□为
　两个池积也加入二之见积七千八百四十八步得

　□○□亦为一段直积与左相消得□□□平方开
　之得一十二步为内池径也
　依条段求之二之积步内加四段通步幂却减一段
　和步幂为实四之通步为从二步半虚常法
　　　　　　　　　义曰减一和步幂是减四积一
　　　　　　　　　较幂也四之通步幂内减了一
　　　　　　　　　个斜幂却又减过二个直积故
　　　　　　　　　二之积步加之从内欠一个方

　减二积时漏下二个圆池又该欠一个半方共欠二
　步半虚常法也
　　第四十二问
今有直田一段中心有圆池水占之外计地一万八百
　步只云从外田角至水池楞六十五步其外田阔不
　及长七十步问二事各多少
　　答曰田长一百五十步　阔八十步　圆池径四
　　　　十步

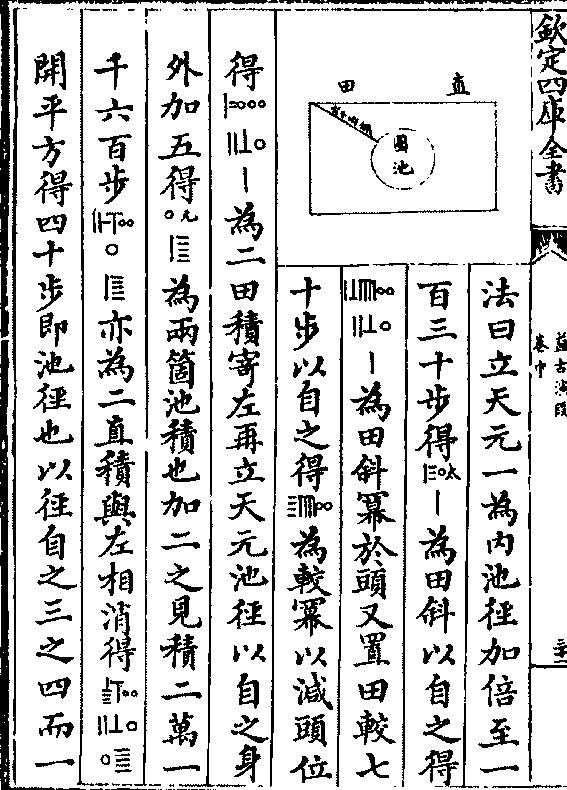　　　　　　　法曰立天元一为内池径加倍至一
　　　　　　　百三十步得□丨为田斜以自之得
　　　　　　　□□丨为田斜幂于头又置田较七
　　　　　　　十步以自之得□为较幂以减头位
　得□□丨为二田积寄左再立天元池径以自之身
　外加五得(元/○)□为两个池积也加二之见积二万一
　千六百步□○□亦为二直积与左相消得□□□
　开平方得四十步即池径也以径自之三之四而一

　加入见积为实以阔不及长为从开方得田阔
　依条段求之二之田积内加较幂却减四段至步幂
　为实四之至步为从半步虚常法
　　　　　　　　　义曰二积内加一个较幂恰补
　　　　　　　　　就一个斜幂也其二积内有两
　　　　　　　　　个圆池是元虚了一步半方也
　于积内却实有一步除外止虚了半步也
　

　
　
　
　
　
　
　
　益古演段卷中