钦定四库全书
御制数理精蕴下编卷三十八
　　末部八
　　　对数比例

　　对数比例
对数比例乃西士若往讷白尔所作以借数与真数
对列成表故名对数表又有恩利格巴理知斯者复
加增修行之数十年始至中国其法以加代乘以减
代除以加倍代自乘故折半即开平方以三因代再
乘故三归即开立方推之至于诸乘方莫不皆以假
数相求而得真数盖为乘除之数甚繁而以假数代
之甚易也其立数之原起于连比例盖比例四率二

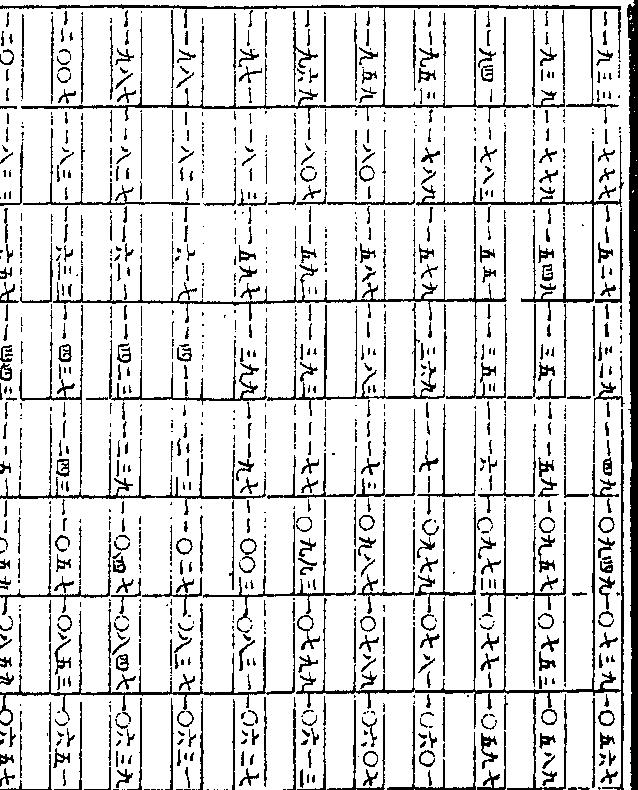率与三率相乘一率除之得四率而递加递减之四
数第二数第三数相加减第一数则得第四数作者
有见于此故设假数以加减代乘除之用此表之所
以立也然连比例之大者莫如十百千万盖一与十
十与百百与千千与万万与十万其数皆为一而递
进一位取其整齐而无奇零也一为数之始以之乘
除数皆不变故一之假数定为○而十之假数定为
一百之假数定为二千之假数定为三万之假数定
为四十万之假数定为五推之百千万亿皆递加一

数此对数之大纲也其间之零数则用中比例累求

而得以首率末率两真数相乘开方即得中率之真
数以首率末率两假数相加折半即得中率之假数
又法用递乘而得以真数递次相乘其乘得之位数
即所得之假数此二法者理虽易明而数则甚繁也
又有递次开方一法以真数递次开方假数递次折
半至于数十次使彼此皆可为比例而假数由之而
生又有相较之一法省开方之多次尤为甚捷至于
他数之可以乘除得者如二与三相乘而得六则以

二之假数与三之假数相加即为六之假数又以二
除十而得五则以二之假数与十之假数相减即为
五之假数之类其不由乘除而得者则又以累乘累
除之法求之此对数之细目也今为推其理考其数
先详作表之原次明用表之法使学者知作者之难
而用之甚易甚勿以易而忘其难也

　　明对数之原之一
凡真数连比例四率任对设递加递减之较相等之
　四假数其第二率相对之假数与第三率相对之
　假数相加内减第一率相对之假数即得第四率
　相对之假数若减第四率相对之假数即得第一
　率相对之假数
　　　　　如二四八十六连比例四率任对设二
　　　　　之假数为一四之假数为二八之假数

　　　　　为三十六之假数为四其递加递减之
　　　　　数皆为一以二率四相对之假数二与
　　　　　三率八相对之假数三相加得五内减
　　　　　一率二相对之假数一即得四率十六
　　　　　相对之假数四若减四率十六相对之
　　　　　假数四即得一率二相对之假数一或
　　　　　以二之假数为三四之假数为五八之
　　　　　假数为七十六之假数为九其递加递
　　　　　减之数皆为二以二率四相对之假数

　　　　　五与三率八相对之假数七相加内减

　　　　　一率二相对之假数三即得四率十六
　　　　　相对之假数九若减四率十六相对之
　　　　　假数九即得一率二相对之假数三
　　明对数之原之二
凡真数连比例三率任对设递加递减之较相等之
　三假数其中率相对之假数倍之内减首率相对
　之假数即得末率相对之假数若减末率相对之
　假数即得首率相对之假数

　　　　　如一三九连比例三率任对设一之假
　　　　　数为四三之假数为五九之假数为六
　　　　　其递加递减之数皆为一以中率三相
　　　　　对之假数五倍之得十内减首率一相
　　　　　对之假数四即得末率九相对之假数
　　　　　六若减末率九相对之假数六即得首
　　　　　率一相对之假数四或以一之假数为
　　　　　八三之假数为五九之假数为二其递
　　　　　加递减之数皆为三以中率三相对之

　　　　　假数五倍之内减首率一相对之假数

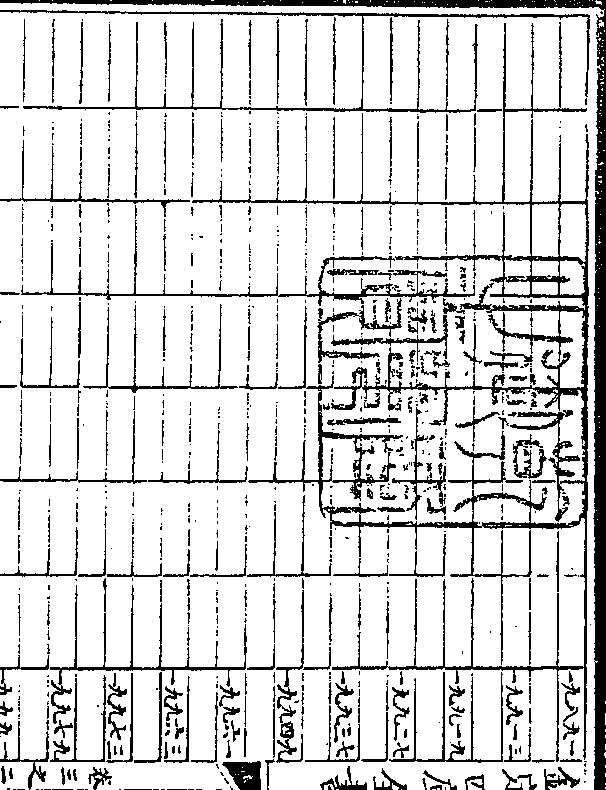　　　　　八即得末率九相对之假数二若减末
　　　　　率九相对之假数二即得首率一相对
　　　　　之假数八
　　明对数之原之三
凡真数连比例几率任对设递加递减之较相等之
　假数其中隔位取比例四率其第二率相对之假
　数与第三率相对之假数相加内减第一率相对
　之假数亦得第四率相对之假数若减第四率相

　对之假数亦得第一率相对之假数
　　　　　如二四八十六三十二六十四一百二
　　　　　十八二百五十六连比例几率任对设
　　　　　二之假数为一四之假数为二八之假
　　　　　数为三十六之假数为四三十二之假
　　　　　数为五六十四之假数为六一百二十
　　　　　八之假数为七二百五十六之假数为
　　　　　八其递加递减之数皆为一任取四八
　　　　　六十四一百二十八之四率以二率八

　　　　　相对之假数三与三率六十四相对之

　　　　　假数六相加得九内减一率四相对之
　　　　　假数二即得四率一百二十八相对之
　　　　　假数七若减四率一百二十八相对之
　　　　　假数七即得一率四相对之假数二

　　明对数之纲之一
凡假数皆可随意而定然一之假数必定为○方与
　真数相应而真数连比例率十百千万皆为一但
　递进一位则其假数亦皆递加一数
　　　　　盖乘除之数始于一故一不用乘亦不
　　　　　用除而加减之数始于○故○无可加
　　　　　亦无可减也假数既以加减代乘除故
　　　　　一之假数必定为○而一与十十与百

　　　　　百与千千与万万与十万皆为加十倍
　　　　　之相连比例率然其数皆为一但递进
　　　　　一位故一之假数定为○者十之假数
　　　　　即定为一百之假数即定为二千之假
　　　　　数即定为三万之假数即定为四十万
　　　　　之假数即定为五百万之假数即定为
　　　　　六千万之假数即定为七亿之假数即
　　　　　定为八亦皆递加一数而假数即与位
　　　　　数相同试以一百与一千相乘得十万

　　　　　为进二位以一百相对之假数二与一

　　　　　千相对之假数三相加即得十万相对
　　　　　之假数五亦为加二数也以一十除一
　　　　　千得一百为退一位以一十相对之假
　　　　　数一与一千相对之假数三相减即得
　　　　　一百相对之假数二亦为减一数也如
　　　　　或以十之假数定为二百之假数定为
　　　　　四千之假数定为六是为递加二数未
　　　　　尝不可然真数进一位者假数则加二

　　　　　数即不得与位数相同矣
　　明对数之纲之二
凡真数不同而位数同者其假数虽不同而首位必
　同真数相同而递进几位者其假数首位必递加
　几数而次位以后却相同
　　　　　如自一至九真数皆为单位则假数首
　　　　　位皆为○故二之假数为○三○一○
　　　　　二九九九五七三之假数为○四七七
　　　　　一二一二五四七四之假数为○六○

　　　　　二○五九九九一三五之假数为○六

　　　　　九八九七○○○四三六之假数为○
　　　　　七七八一五一二五○四首位以后零
　　　　　数递增至十则首位皆为一至百则首
　　　　　位皆为二至千则首位皆为三至万则
　　　　　首位皆为四至十万则首位皆为五如
　　　　　一十一一百一十一千一百一万一千
　　　　　一十一万虽递进一位而其数皆为一
　　　　　一故其假数首位虽递加一数而次位

　　　　　以后皆同为○四一三九二六八五二

　　明对数之目用中比例求假数法之一
凡连比例率以首率末率两真数相乘开方即得中
　率之真数以首率末率两假数相加折半即得中
　率之假数
　　　　　如一十为首率一百为中率一千为末
　　　　　率以首率一十与末率一千相乘开平
　　　　　方得一百为中率以首率一十之假数
　　　　　一○○○○○○○○○○与末率一

　　　　　千之假数三○○○○○○○○○○
　　　　　相加折半得二○○○○○○○○○
　　　　　○即中率一百之假数盖首率末率相
　　　　　乘与中率自乘之数等以首率末率两
　　　　　假数相加即与中率之假数加倍之数
　　　　　等故折半为中率之假数也
　　明对数之目用中比例求假数法之二
凡十百千万之假数既定而欲求其间零数之假数
　则以前后相近之两数一为首率一为末率求得

　中率之真数并求得中率之假数累次比例使中

　率恰得所求之真数其假数即为所求之假数
　　　　　如求九之假数因九在一与十之间则
　　　　　以一为首率十为末率相乘开方得三
　　　　　一六二二七七七为第一次之中率即
　　　　　以首率一之假数○○○○○○○○
　　　　　○○○与末率十之假数一○○○○
　　　　　○○○○○○相加折半得○五○○
　　　　　○○○○○○○为第一次中率之假

　　　　　数此所得之中率较之首率去九为近
　　　　　故以所得之中率复为首率十为末率
　　　　　相乘开方得五六二三四一三二为第
　　　　　二次之中率即以第二次之首率末率
　　　　　两假数相加折半得○七五○○○○
　　　　　○○○○为第二次中率之假数又以
　　　　　第二次所得之中率复为首率十为末
　　　　　率相乘开方得七四九八九四二一为
　　　　　第三次之中率即以第三次之首率末

　　　　　率两假数相加折半得○八七五○○

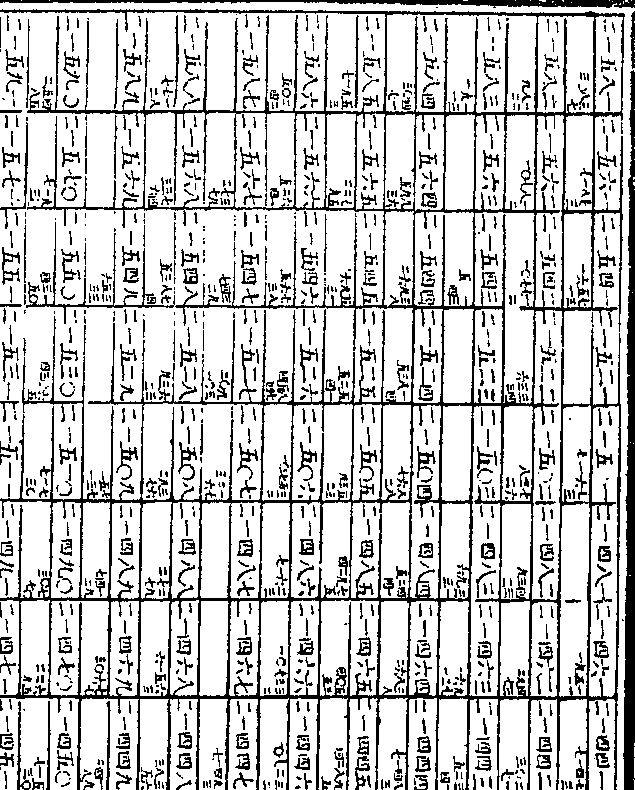　　　　　○○○○○为第三次中率之假数又
　　　　　以第三次所得之中率复为首率十为
　　　　　末率相乘开方得八六五九六四三二
　　　　　为第四次之中率即以第四次之首率
　　　　　末率两假数相加折半得○九三七五
　　　　　○○○○○○为第四次中率之假数
　　　　　又以第四次所得之中率复为首率十
　　　　　为末率相乘开方得九三○五七二○

　　　　　四为第五次之中率即以第五次之首
　　　　　率末率两假数相加折半得○九六八
　　　　　七五○○○○○为第五次中率之假
　　　　　数此所得之中率较之末率去九为近
　　　　　故以第五次所得之中率复为末率仍
　　　　　以第五次之首率为首率相乘开方得
　　　　　八九七六八七一三为第六次之中率
　　　　　即以第六次首率末率两假数相加折
　　　　　半得○九五三一二五○○○○为第

　　　　　六次中率之假数由此递推去九渐近

　　　　　而即以相近之两率比例相求得第七
　　　　　次之中率为九一三九八一七○其假
　　　　　数为○九六○九三七五○○○第八
　　　　　次之中率为九○一七九七七七其假
　　　　　数为○九五七○三一二五○○第九
　　　　　次之中率为九○一七三三三三其假
　　　　　数为○九五五○七八一二五○第十
　　　　　次之中率为八九九七○七九六其假

　　　　　数为○九五四一○一五六二五第十
　　　　　一次之中率为九○○七二○○八其
　　　　　假数为○九五四五八九八四三七第
　　　　　十二次之中率为九○○二一三八八
　　　　　其假数为○九五四三四五七○三一
　　　　　第十三次之中率为八九九九六○八
　　　　　八其假数为○九五四二二三六三二
　　　　　八第十四次之中率为九○○○八七
　　　　　三七其假数为○九五四二八四六六

　　　　　七九第十五次之中率为九○○○二

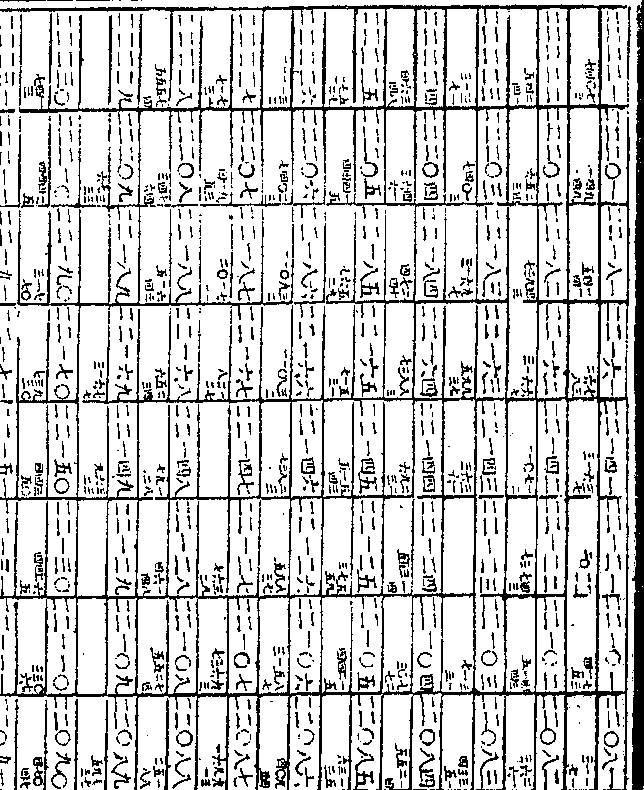　　　　　四一二其假数为○九五四二五四一
　　　　　五○三第十六次之中率为八九九九
　　　　　九二五○其假数为○九五四二三八
　　　　　八九一五第十六次之中率为九○○
　　　　　○○八二一其假数为○九五四二四
　　　　　六五二○九第十八次之中率为九○
　　　　　○○○○四一其假数为○九五四二
　　　　　四二七○六二第十九次之中率为八

　　　　　九九九九六五○其假数为○九五四
　　　　　二四○七九八九第二十次之中率为
　　　　　八九九九九八四五其假数为○九五
　　　　　四二四一七五二六第二十一次之中
　　　　　率为八九九九九九四三其假数为○
　　　　　九五四二四二二二九四第二十二次
　　　　　之中率为八九九九九九九二其假数
　　　　　为○九五四二四二四六七八第二十
　　　　　三次之中率为九○○○○○一六其

　　　　　假数为○九五四二四二五八七○第

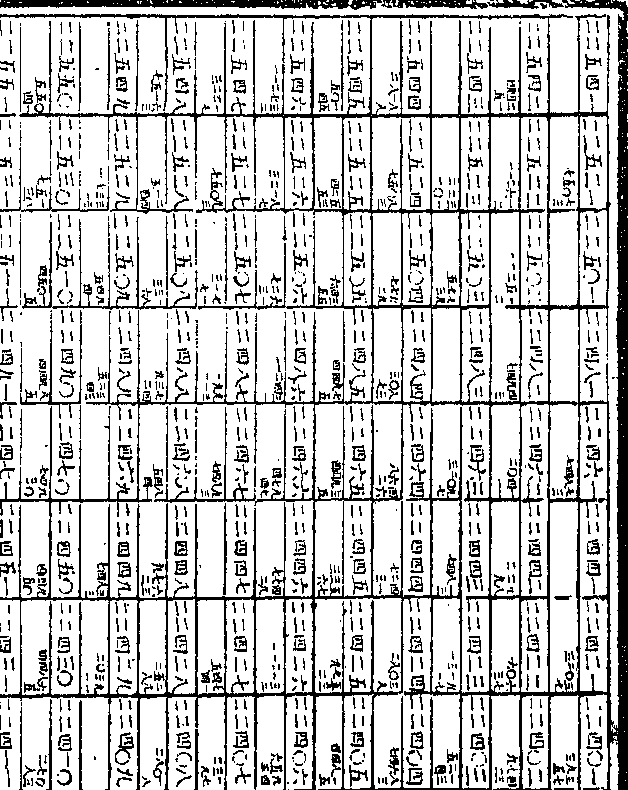　　　　　二十四次之中率为九○○○○○○
　　　　　四其假数为○九五四二四二五二七
　　　　　四第二十五次之中率为八九九九九
　　　　　九九八其假数为○九五四二四二四
　　　　　九七六至第二十六次之中率则恰得
　　　　　九○○○○○○○其假数为○九五
　　　　　四二四二五一二五即所求之假数也
　　　　　然所得中率虽为九而七空位之后尚

　　　　　有奇零故所得之假数犹为稍大故开
　　　　　方之位数愈多则所得之假数愈密也

　　明对数之目用递次自乘求假数法之一
凡连比例率之自小而大者以第一率之真数递次
　自乘即得加倍各率之真数以第一率之假数递
　次加倍即得加倍各率之假数而以各率之假数
　按率除之即得第一率之假数
　　　　　如以二为连比例第一率其假数为○
　　　　　三○一○二九九九五七以第一率之
　　　　　真数二自乘得四为第二率之真数以

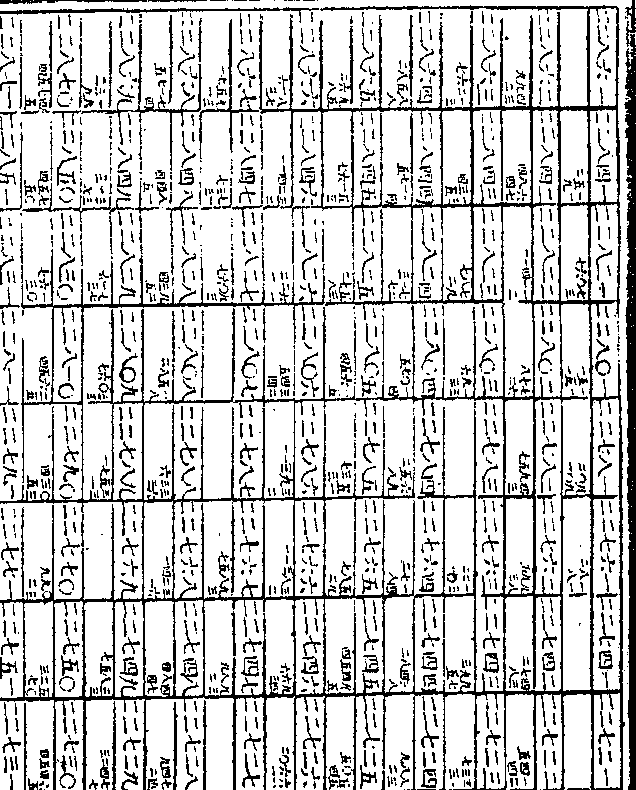　　　　　第一率之假数○三○一○二九九九
　　　　　五七加倍得○六○二○五九九九一
　　　　　三为第二率之假数而以第二率之假
　　　　　数用二除之即得第一率之假数又以
　　　　　第二率之真数四自乘得十六为第四
　　　　　率之真数以第二率之假数○六○二
　　　　　○五九九九一三加倍得一二○四一
　　　　　一九九八二六为第四率之假数而以
　　　　　第四率之假数用四除之即得第一率

　　　　　之假数也

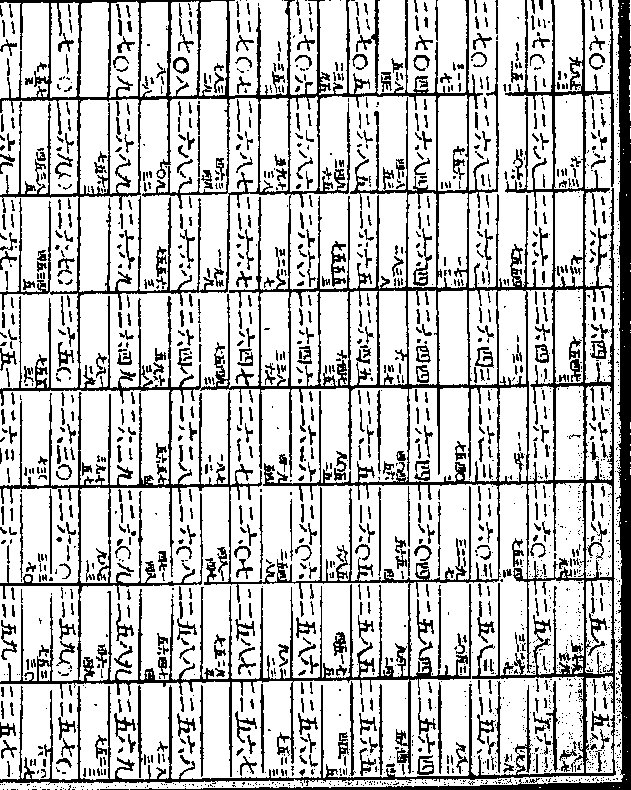　　明对数之目用递次自乘求假数法之二
凡连比例率自小而大者其假数之首位既因真数
　之位数而递加故求假数者以所求之真数为连
　比例第一率递次自乘即得加倍各率之真数以
　第一率假数之首位递次加倍即得加倍各率之
　假数而真数自乘又进一位者则假数加倍后又
　加一数而以各率之假数按次除之即得所求第
　一率之假数

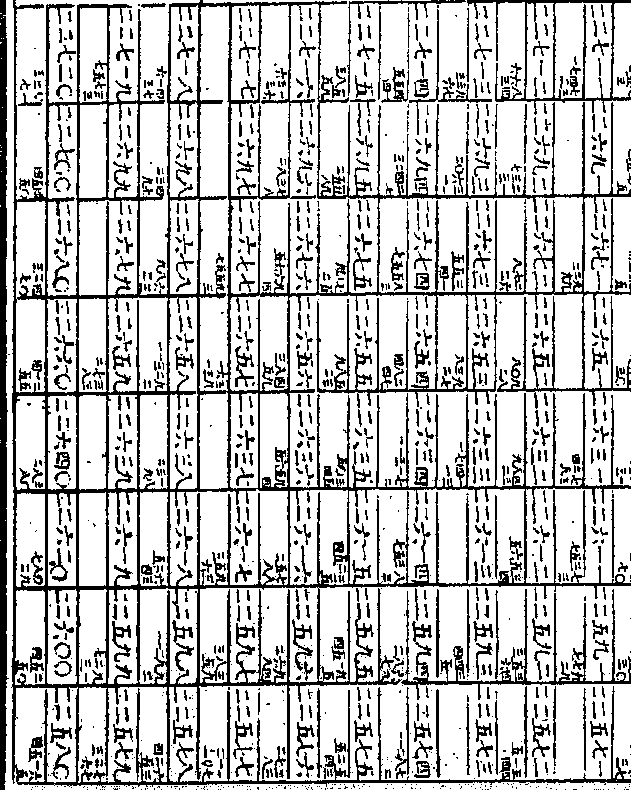
　　　　　如求二之假数则以二为连比例第一
　　　　　率是为单位故傍纪○即第二率之假
　　　　　数首位为○也又以第一率之真数二
　　　　　自乘得四为第二率之真数仍为单位
　　　　　故傍亦纪○即第二率之假数首位亦
　　　　　为○也又以第二率之真数四自乘得
　　　　　十六为第四率之真数是为进前一位
　　　　　故傍纪一即第四率之假数首位为一
　　　　　也又以第四率之真数十六自乘得二

　　　　　百五十六为第八率之真数以第四率

　　　　　之假数一倍之得二是为进前二位故
　　　　　傍纪二即第八率之假数首位为二也
　　　　　又以第八率之真数二百五十六自乘
　　　　　得六万五千五百三十六为第十六率
　　　　　之真数以第八率之假数二倍之得四
　　　　　是为进前四位故傍纪四即第十六率
　　　　　之假数首位为四也又以第十六率之
　　　　　真数六万五千五百三十六自乘得四

　　　　　十二亿九千四百九十六万七千二百
　　　　　九十六为第三十二率之真数以第十
　　　　　六率之假数四倍之得八又因第十六
　　　　　率真数自乘所得首位乃逢十又进一
　　　　　位之数故将假数加倍所得之八又加
　　　　　一得九是为进前九位故傍纪九即第
　　　　　三十二率之假数首位为九也由此递
　　　　　乘至第一万六千三百八十四率之真
　　　　　数则自单位以前共得四千九百三十

　　　　　二位故傍纪四九三二为第一万六千

　　　　　三百八十四率之假数以一万六千三
　　　　　百八十四除之得○三○一○即为第
　　　　　一率二之假数盖以一万除四千为实
　　　　　不足法一倍则其首位必为○也然其
　　　　　位数尚少故仅得五位若再递乘至第
　　　　　一千三百七十四亿四千六百九十五
　　　　　万三千四百七十二率之真数则自单
　　　　　位以前共得四百一十三亿七千五百

　　　　　六十五万五千三百零七位即其假数
　　　　　为四一三七五六五五三○七以率数
　　　　　除之得○三○一○二九九九五六六
　　　　　即为第一率二之假数也此法盖因真
　　　　　数进一位则假数首位加一数今递乘
　　　　　所得之真数既得若干位则其假数首
　　　　　位必加若干数乃以首位为单位递进
　　　　　向前者也而连比例各率之假数以率
　　　　　数除之即得第一率之假数故以率数

　　　　　除之所得第一率之假数为首位以后

　　　　　　之零数也

　　明对数之目用递次开方求假数法之一
凡连比例率之自大而小者以第一率之真数递次
　开方即得加倍各率之真数以第一率之假数递
　次折半即得加倍各率之假数而以各率之假数
　按率乘之即得第一率之假数
　　　　　如以二百五十六为连比例第一率其
　　　　　假数为二四○八二三九九六五三以
　　　　　第一率之真数二百五十六开方得十

　　　　　六为第二率之真数以第一率之假数
　　　　　二四○八二三九九六五三折半得一
　　　　　二○四一一九九八二六为第二率之
　　　　　假数而以第二率之假数用二乘之即
　　　　　得第一率之假数又以第二率之真数
　　　　　十六开方得四为第四率之真数以第
　　　　　二率之假数一二○四一一九九八二
　　　　　六折半得○六○二○五九九九一三
　　　　　为第四率之假数而以第四率之假数

　　　　　用四乘之即得第一率之假数

　　明对数之目用递次开方求假数法之二
凡递次开方率皆用二倍盖真数开方假数折半而
　折半即二归故递次折半之假数以递次加倍之
　率数乘之即得第一率之假数
　　　　　如原数为第一率加倍得二为第一次
　　　　　开方之率数(盖折半即二归以二归者/复用二乘必仍得原数也)
　　　　　又加倍得四为第二次开方之率数(盖/折)
　　　　　(半二次即四归以四归者/复用四乘必亦得原数也)递次加倍则

　　　　　第三次之率为八第四次之率为十六
　　　　　第五次之率为三十二第六次之率为
　　　　　六十四第七次之率为一百二十八第
　　　　　八次之率为二百五十六第九次之率
　　　　　为五百一十二第十次之率为一千零
　　　　　二十四第二十次之率为一百零四万
　　　　　八千五百七十六第三十次之率为十
　　　　　亿七千三百七十四万一千八百二十
　　　　　四第四十次之率为一兆零九百九十

　　　　　五亿一千一百六十二万七千七百七

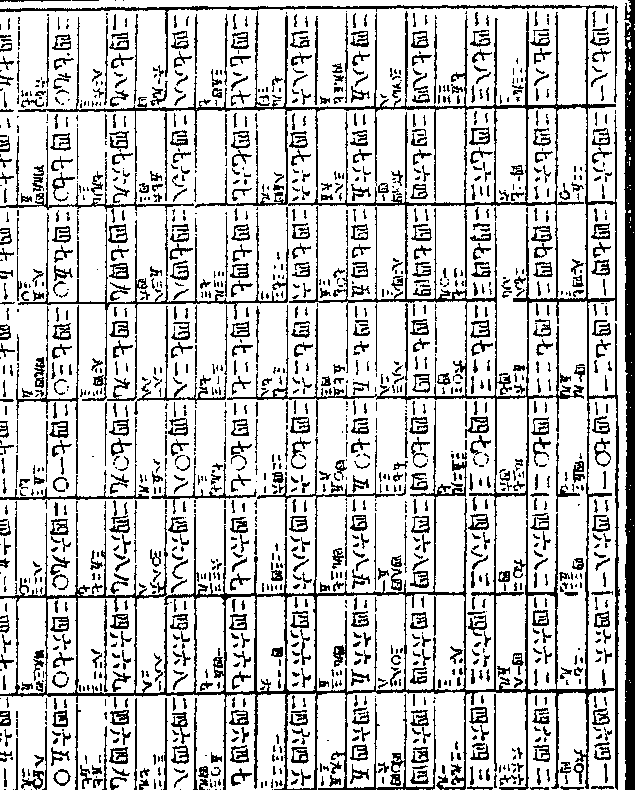　　　　　十六第五十次之率为一千一百二十
　　　　　五兆八千九百九十九亿零六百八十
　　　　　四万二千六百二十四凡有真数求假
　　　　　数皆以所求之数为第一率真数开方
　　　　　几次则假数必折半几次今虽无第一
　　　　　率之假数而苟得其折半第几次之假
　　　　　数则加倍几次必得第一率之假数故
　　　　　以加倍第几次之率数与折半第几次

　　　　　之假数相乘即得第一率之假数也
　　明对数之目用递次开方求假数法之三
凡真数不可与假数为比例者因真数开方假数折
　半其相比之分数不同若开方至于数十次则开
　方之数即与折半之数相同故假数即可用真数
　比例而得是以凡求假数者皆以其真数开方至
　几十次与此所得之假数相比即得其开方第几
　十次之假数按前率数乘之即得所求之假数
　　　　　如真数为一十假数为一○以真数一

　　　　　十开方得三一六二二七七六六○一

　　　　　六八三七九三三一九九八八九三五
　　　　　四第二次开方得一七七八二七九四
　　　　　一○○三八九二二八○一一九七三
　　　　　○四一三第三次开方得一三三三五
　　　　　二一四三二一六三三二四○二五六
　　　　　六五三八九三○八第四次开方得一
　　　　　一五四七八一九八四六八九四五八
　　　　　一七九六六一九一八二一三第五次

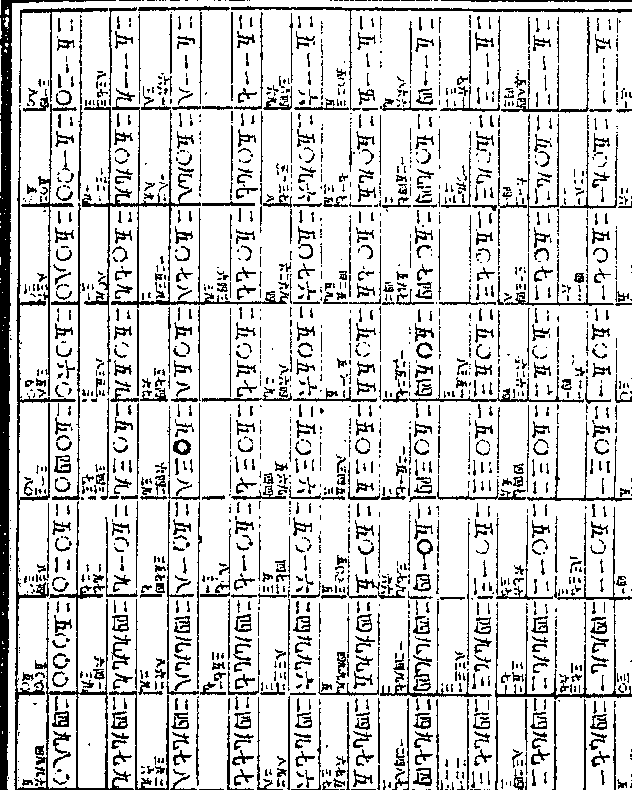
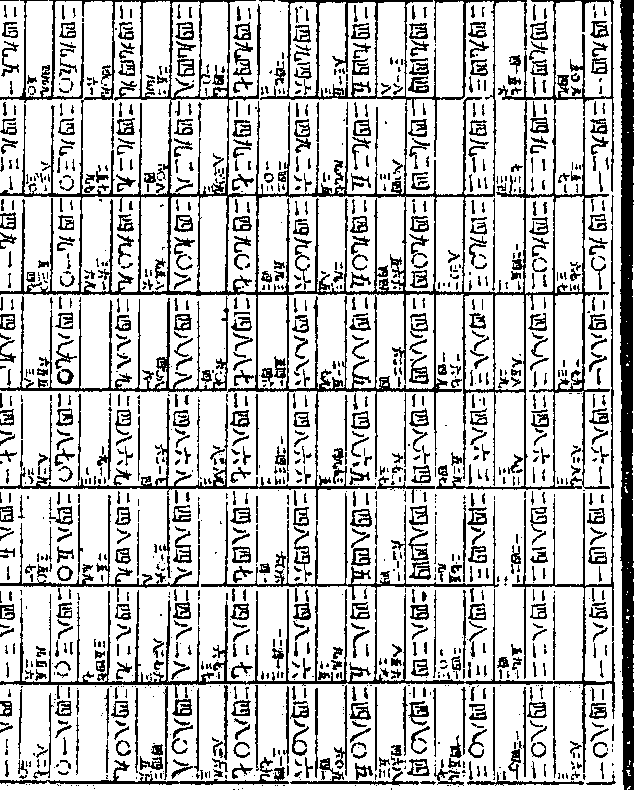　　　　　开方得一○七四六○七八二八三二
　　　　　一三一七四九七二一三八一七六五
　　　　　三八第六次开方得一○三六六三二
　　　　　九二八四三七六九七九九七二九○
　　　　　六二七三一三一第七次开方得一○
　　　　　一八一五一七二一七一八一八一八
　　　　　四一四七三七二三八一四四如此递
　　　　　次开方至第五十四次则得一○○○
　　　　　○○○○○○○○○○○○一二七

　　　　　八一九一四九三二○○三二三五而

　　　　　与第五十三次开方所得折半之数同
　　　　　是故真数即可与假数为比例矣乃以
　　　　　一十之假数一○折半得○五第二次
　　　　　折半得○二五第三次折半得○一二
　　　　　五第四次折半得○○六二五第五次
　　　　　折半得○○三一二五第六次折半得
　　　　　○○一五六二五第七次折半得○○
　　　　　○七八一二五如此递次折半亦至第

　　　　　五十四次则得十七空位五五五一一
　　　　　一五一二三一二五七八二七○即为
　　　　　第五十四次开方之假数于是以真数
　　　　　之零数一二七八一九一四九三二○
　　　　　○三二三五为一率假数之零数五五
　　　　　五一一一五一二三一二五七八二七
　　　　　○为二率真数之零数一为三率(一率/为十)
　　　　　(七位则三率亦加十/六空位以足其分)得四率四三四二
　　　　　九四四八一九○三二五一八○四即

　　　　　为一○○○○○○○○○○○○○

　　　　　　○○一之假数前亦仍得十七空位盖
　　　　　　真数为一则假数为○今真数之零数
　　　　　　即比一多之较假数之零数即比○多
　　　　　　之较故以真数之较与假数之较为比
　　　　　　例也凡求假数者皆以真数开方至几
　　　　　　十次首位得一又得十五空位则以其后
　　　　　　之零数与此所得之假数为比例即得
　　　　　　其开方第几十次之假数按前率数乘

　　　　　　之即得第一率之假数也

　
　
　
　
　
　
　
　

　　明对数之目用递次开方求假数法之四
凡真数首位为一者则开方首位必得一若首位非一
　者则以真数递乘几次使首位得一即以递乘所得
　之真数递次开方至得十五空位乃以其后之零数
　与前法所得一○○○○○○○○○○○○○○
　○一之假数相比例即得开方第几次之假数按
　前率数乘之即得递乘所得真数之假数再看递
　乘所得真数为连比例第几率则以第几率之数
　除之即得所求之假数

　　　　　如求二之假数则以二为连比例第一
　　　　　率递次乘之第二率得四第三率得八
　　　　　第四率得十六第五率得三十二第六
　　　　　率得六十四第七率得一百二十八第
　　　　　八率得二百五十六第九率得五百一
　　　　　十二第十率得一千零二十四是首位
　　　　　既得一又得一空位乃以此数命为第
　　　　　一率其首位之一千命为单位开方得

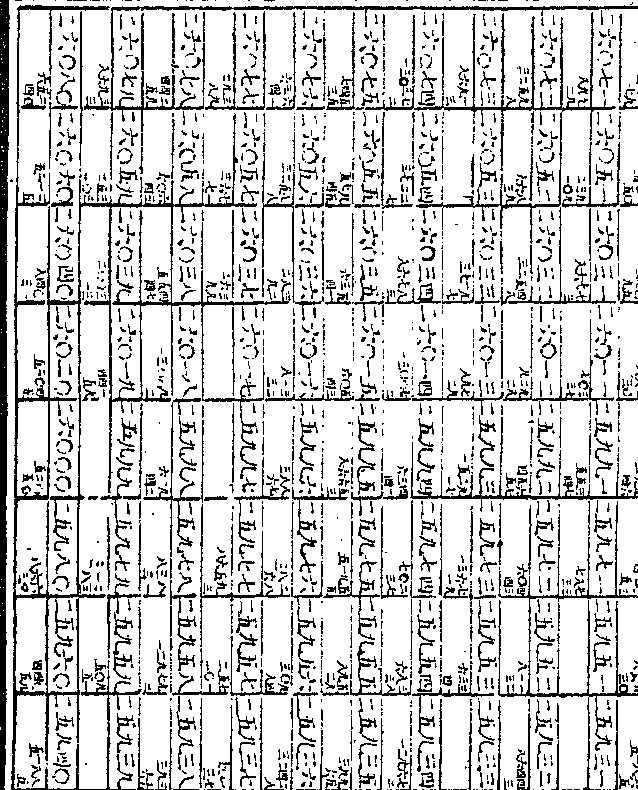
　　　　　一○一一九二八八五一二五三八八
　　　　　一三八六二三九七第二次开方得一
　　　　　○○五九四六七四三七四六三四八
　　　　　三二六六五四二四第三次开方得一
　　　　　○○二九六八九六四四九八○七八
　　　　　七三七三六二六八第四次开方得一
　　　　　○○一四八三三八二○三七九○四
　　　　　一八○三○一八三八第五次开方得
　　　　　一○○○七四一四一六一六九九八

　　　　　三五三三六二四九○六第六次开方

　　　　　得一○○○三七○六三六三九八二
　　　　　一○○一四○七一七六一五第七次
　　　　　开方得一○○○一八五三○二五三
　　　　　○五九一○八五三○五八二七七如
　　　　　此递次开方至第十七次则得一○○
　　　　　○○○○一八○九四二七五四八四
　　　　　四五三四三六三九五○一五四四第
　　　　　二十七次则得一○○○○○○○○

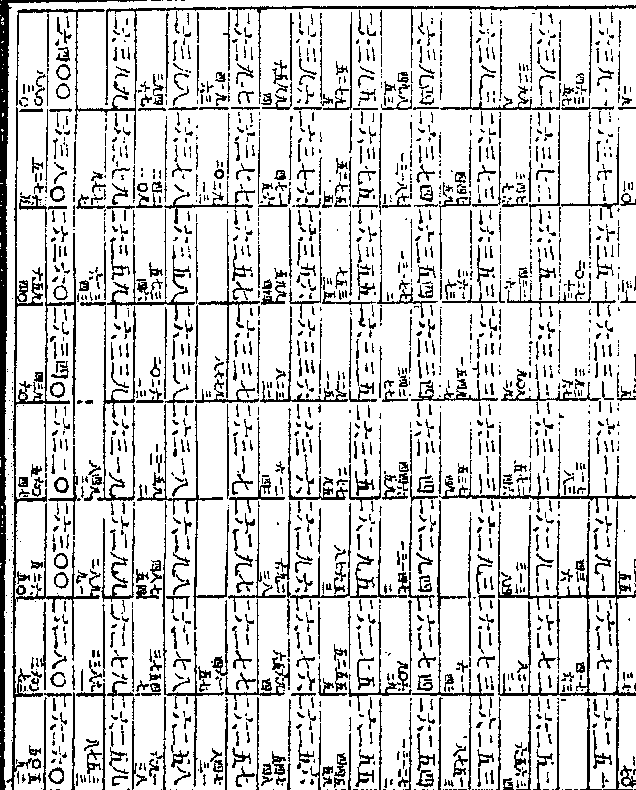
　　　　　○一七六七○一八九三○五七○一
　　　　　四一九四八二六二第三十七次则得
　　　　　一○○○○○○○○○○○○一七
　　　　　二五六○四四二四二三二五九四三
　　　　　四七七第四十七次则得一○○○○
　　　　　○○○○○○○○○○○一六八五
　　　　　一六○五七○五三九四九七七是已
　　　　　得十五空位矣乃以前法所得真数之
　　　　　零数一为一率(三率有十七位则一率/亦加十六空位以足其)

　　　　　(分/)其假数十七空位后之零数四三四

　　　　　二九四四八一九○三二五一八○四
　　　　　为二率今所得真数之零数一六八五
　　　　　一六○五七○五三九四九七七为三
　　　　　率得四率七三一八五五九三六九○
　　　　　六二三九二六八即为开方第四十七
　　　　　次之假数前亦仍为十七空位以加倍
　　　　　四十七次之率数一四○七三七四八
　　　　　八三五五三二八乘之得○○一○二

　　　　　九九九五六六三九八一一九五二六
　　　　　五即为第一率一○二四之假数(盖开/方第)
　　　　　(四十七次之假数为十八位前十七空/位共三十五位今相乘得三十三位故)
　　　　　(前止有二空位亦共三十/五位也此截用二十一位)然一○二四
　　　　　首位之一开方虽命为单位而其实则
　　　　　为千位千之假数首位应为三故首位
　　　　　加三得三○一○二九九九五六六三
　　　　　九八一一九五二六五是为一千零二
　　　　　十四之假数又因一千零二十四为二

　　　　　之连比例第十率故以十归之得○三

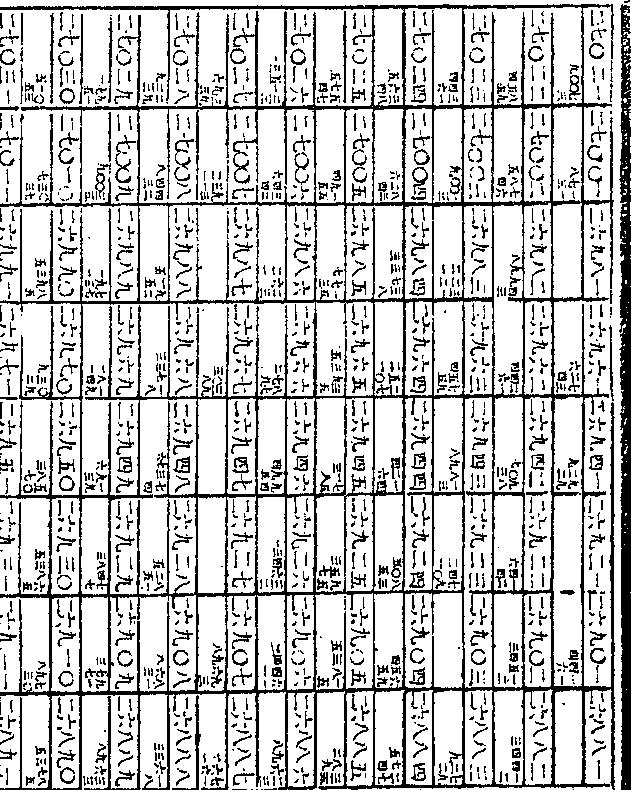　　　　　○一○二九九九五六六三九八一一
　　　　　九五二六五即为所求之连比例第一
　　　　　率二之假数也
　　明对数之目用递次开方求假数法之五
凡求假数真数开方之次数愈多则所得之假数愈
　密然用假数不过至十二位观前递次开方表内
　至九空位以后其开方之数与折半之数已同七
　位其零数所差甚微故真数开方至二十七次即

　可以立率
　　　　　如求二之假数按前法递次乘之至第
　　　　　十率得一○二四开方至二十七次得
　　　　　一○○○○○○○○○一七六七○
　　　　　一八九三○五七○一四一九四八二
　　　　　六二是已得九空位矣于是察前真数
　　　　　一○递次开方表内第三十四次数得
　　　　　一○○○○○○○○○一三四○二
　　　　　八○九二三二六三八三九九二七七

　　　　　七亦为九空位即以其真数之零数一

　　　　　三四○二八○九二三二六三八三九
　　　　　九二七七七为一率其假数十一空位
　　　　　后之零数五八二○七六六○九一三
　　　　　四六七四○七二二六五六二五为二
　　　　　率真数之零数一为三率(一率为二十/一位则三率)
　　　　　(亦加二十空/位以足其分)得四率四三四二九四四
　　　　　八一八七四一四七九九七二○六九
　　　　　五五即为一○○○○○○○○○一

　　　　　之假数前亦仍为十一空位乃即用此
　　　　　数为比例以真数之零数一为一率(三/率)
　　　　　(为二十二位则一率亦加/二十一空位以足其分)其假数十一
　　　　　空位后之零数四三四二九四四八一
　　　　　八七四一四七九九七二○六九五五
　　　　　为二率今以一○二四开方二十七次
　　　　　所得之零数一七六七○一八九三○
　　　　　五七○一四一九四八二六二为三率
　　　　　得四率七六七四○六五七○九一三

　　　　　七七○八九○七○一四三九即为一

　　　　　○二四开方第二十七次之假数前亦
　　　　　仍为十一空位以加倍二十七次之率
　　　　　数一三四二一七七二八乘之得○○
　　　　　一○二九九九五六六四○○即为第
　　　　　一率一○二四之假数与前法所得之
　　　　　数同(前法得三九八收之亦为四○○/以后奇零微有不合止截用十二)
　　　　　(位/)再按前法首位加三而以率数十归
　　　　　之即得○三○一○二九九九五六六

　　　　　四○为二之假数也此法较之前法开
　　　　　方省二十次而所得之数同故求假数
　　　　　者用此法亦便也
　　明对数之目用递次开方求假数法之六
凡开方之数与折半之数虽不同然而不同之较递
　次渐少故又有相较之法至开方第十次以后则
　以较数相减即得开方之数
　　　　　如求六之假数以六为连比例第一率
　　　　　递次乘之得连比例第九率为一千零

　　　　　七万七千六百九十六乃以此数命为

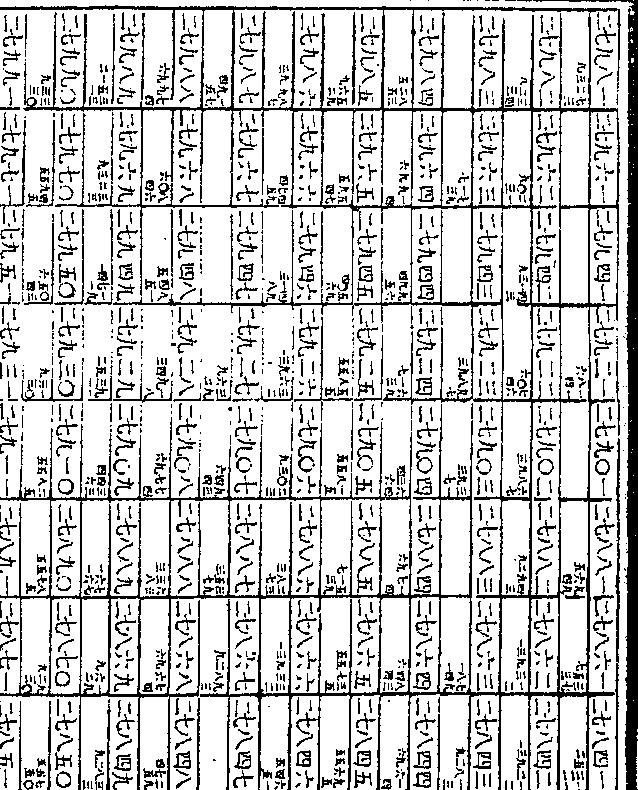　　　　　第一率其首位之一千万命为单位开
　　　　　方得一○○三八七七二八三三三六
　　　　　九六二四五六六三八四六五五一第
　　　　　二次开方得一○○一九三六七六六
　　　　　一三六九四六六一六七五八七○二
　　　　　二九第三次开方得一○○○九六七
　　　　　九一四六三九○九九○一七二八八
　　　　　九○七二○第四次开方得一○○○

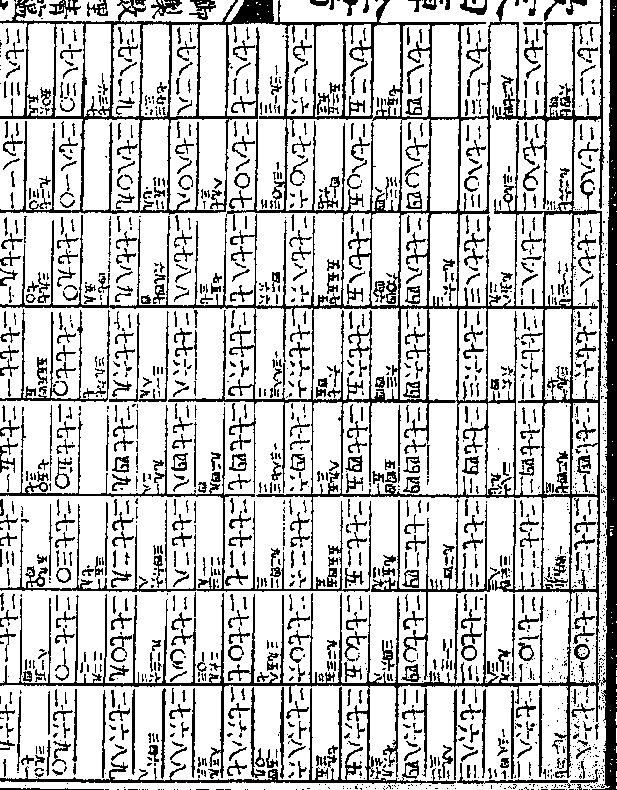　　　　　四八三八四○二六八八四六六二九
　　　　　八五四九二五三五第五次开方得一
　　　　　○○○二四一八九○八七八八二四
　　　　　六八五六三八○八七二七与第四次
　　　　　开方所得折半之数渐近乃以第四次
　　　　　开方所得数折半(首位之一不折半盖/首位之一诸次开方)
　　　　　(皆同其数/不变也)得二四一九二○一三四四
　　　　　二三三一四九二七四六二六七与第
　　　　　五次开方所得数相减馀二九二五五

　　　　　五九八六二九二八九三七五四○为

　　　　　第五次之较设使有第五次之较则将
　　　　　第四次开方所得数折半内减第五次
　　　　　之较即第五次开方所得数然第五次
　　　　　之较乃与第五次开方数相减而得故
　　　　　第五次犹必用开方也第六次开方得
　　　　　一○○○一二○九三八一二六三九
　　　　　七一三四五九四三九一九四又以第
　　　　　五次开方所得数折半得一二○九四

　　　　　五四三九四一二三四二八一九○四
　　　　　三六三与第六次开方所得数相减馀
　　　　　七三一三○一五二○八二二四六五
　　　　　一六九为第六次之第一较又将第五
　　　　　次之较四归之得七三一三八九九六
　　　　　五七三二二三四三八五与第六次之
　　　　　第一较相减馀八八四四四九○九七
　　　　　六九二一五为第六次之第二较设使
　　　　　有第二较则将第五次之较四归之内

　　　　　减第六次之第二较即为第六次之第

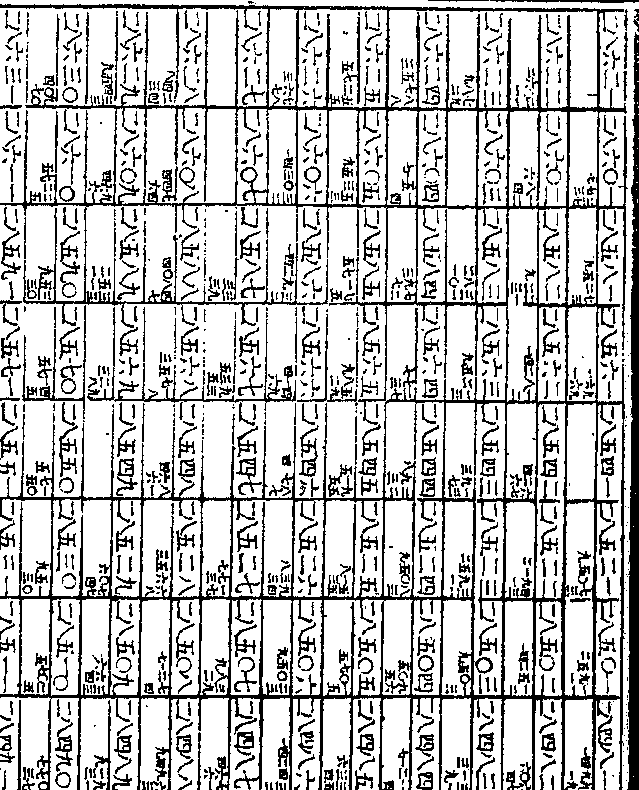　　　　　一较将第五次开方所得数折半内减
　　　　　第六次之第一较即第六次开方所得
　　　　　数然第二较乃与第一较相减而得而
　　　　　第一较乃与第六次开方数相减而得
　　　　　故第六次犹必用开方也第七次开方
　　　　　得一○○○○六○四六七二三五○
　　　　　五五三○九六八○一六○○五又以
　　　　　第六次开方所得数折半得六○四六

　　　　　九○六三一九八五六七二九七一九
　　　　　五九七与第七次开方所得数相减馀
　　　　　一八二八一四三二五七六一七○三
　　　　　五九二为第七次之第一较又将第六
　　　　　次之第一较四归之得一八二八二五
　　　　　三八○二○五六一六二九二与第七
　　　　　次之第一较相减馀一一○五四四四
　　　　　三九一二七○○为第七次之第二较
　　　　　又将第六次之第二较八归之得一一

　　　　　○五五六一三七二一一五二与第七

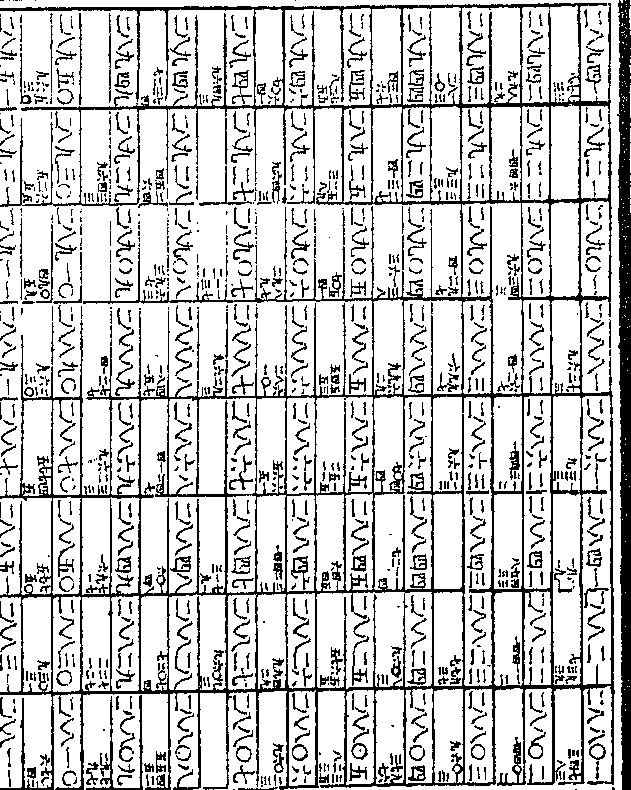　　　　　次之第二较相减馀一一六九八○八
　　　　　四五二为第七次之第三较设使有第
　　　　　三较则将第六次之第二较八归之内
　　　　　减第七次之第三较即为第七次之第
　　　　　二较将第六次之第一较四归之内减
　　　　　第七次之第二较即为第七次之第一
　　　　　较将第六次开方所得数折半内减第
　　　　　七次之第一较即第七次开方所得数

　　　　　然第三较乃与第二较相减而得第二
　　　　　较乃与第一较相减而得而第一较乃
　　　　　与第七次开方数相减而得故第七次
　　　　　犹必用开方也第八次开方得一○○
　　　　　○○三○二三三一六○五○五六五
　　　　　七七五九六四七九四又以第七次开
　　　　　方所得数折半得三○二三三六一七
　　　　　五二七六五四八四○○八○○二与
　　　　　第八次开方所得数相减馀四五七○

　　　　　二一九九七○八○四三二○八为第

　　　　　八次之第一较又将第七次之第一较
　　　　　四归之得四五七○三五八一四四○
　　　　　四二五八九八与第八次之第一较相
　　　　　减馀一三八一七三二三八二六九○
　　　　　为第八次之第二较又将第七次之第
　　　　　二较八归之得一三八一八○五四八
　　　　　九○八七与第八次之第二较相减馀
　　　　　七三一○六三九七为第八次之第三

　　　　　较又将第七次之第三较十六归之得
　　　　　七三一一三○二八与第八次之第三
　　　　　较相减馀六六三一为第八次之第四
　　　　　较设使有第四较则将第七次之第三
　　　　　较十六归之内减第八次之第四较即
　　　　　为第八次之第三较将第七次之第二
　　　　　较八归之内减第八次之第三较即为
　　　　　第八次之第二较将第七次之第一较
　　　　　四归之内减第八次之第二较即为第

　　　　　八次之第一较将第七次之开方数折

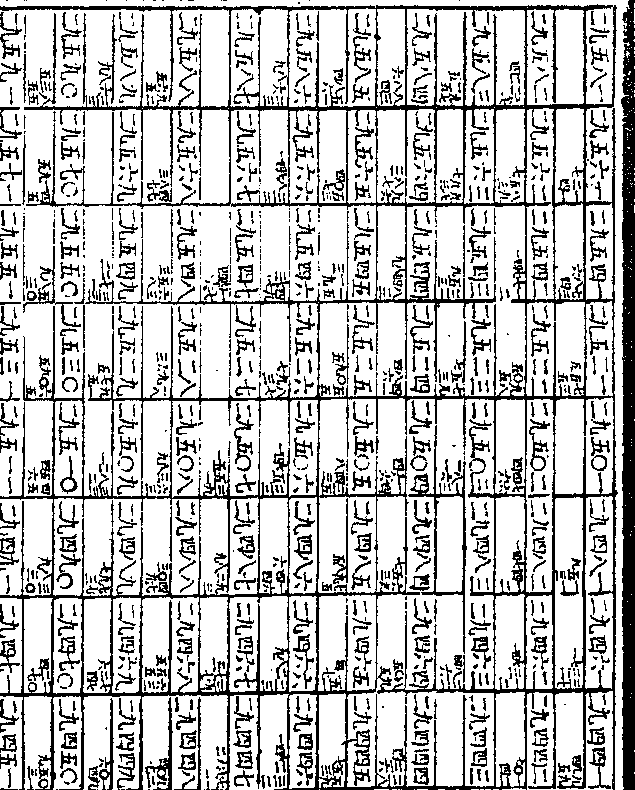　　　　　半内减第八次之第一较即第八次开
　　　　　方数然第四较乃与第三较相减而得
　　　　　第三较乃与第二较相减而得第二较
　　　　　乃与第一较相减而得而第一较乃与
　　　　　第八次开方数相减而得故第八次犹
　　　　　必用开方也至第九次开方得一○○
　　　　　○○一五一一六四六五九九九○五
　　　　　六七二九五○四八八又以第八次开

　　　　　方数折半得一五一一六五八○二五
　　　　　二八二八八七九八二三九七与第九
　　　　　次开方数相减馀一一四二五三七七
　　　　　二一五○三一九○九为第九次之第
　　　　　一较又将第八次之第一较四归之得
　　　　　一一四二五五四九九二七○一○八
　　　　　○二与第九次之第一较相减馀一七
　　　　　二七一一九七八八九三为第九次之
　　　　　第二较又将第八次之第二较八归之

　　　　　得一七二七一六五四七八三六与第

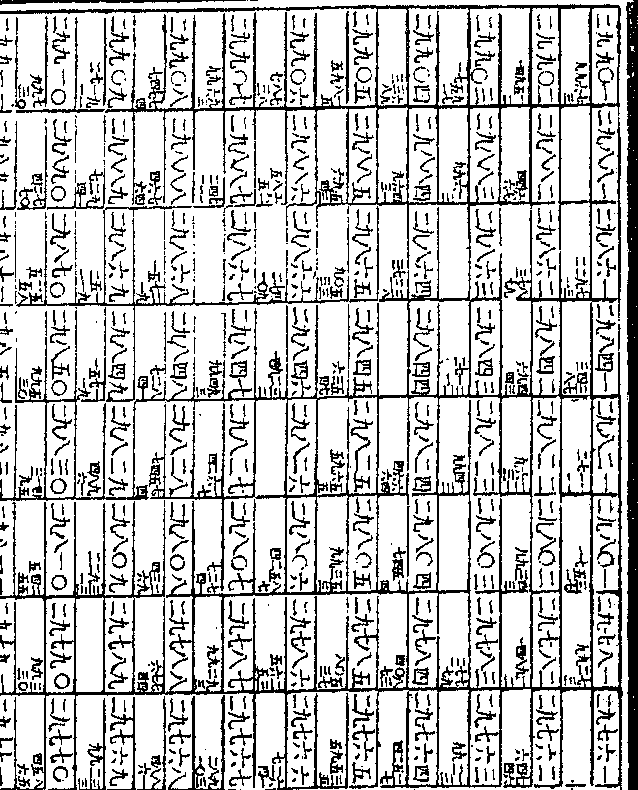　　　　　九次之第二较相减馀四五六八九四
　　　　　三为第九次之第三较又将第八次之
　　　　　第三较十六归之得四五六九一五○
　　　　　与第九次之第三较相减馀二○七为
　　　　　第九次之第四较又将第八次之第四
　　　　　较三十二除之亦得二○七与第九次
　　　　　之第四较同故自第十次以后则不用
　　　　　开方(若间方止用二十二位则第八次/之第三较已同至第九次即不用)

　　　　　(开方亦不/用第四较)即以第九次之第四较三十
　　　　　二除之得六为第十次之第四较将第
　　　　　九次之第三较十六除之得二八五五
　　　　　五八内减第十次之第四较馀二八五
　　　　　五五二即为第十次之第三较将第九
　　　　　次之第二较八归之得二一五八八九
　　　　　九七三六一内减第十次之第三较馀
　　　　　二一五八八七一一八○九即为第十
　　　　　次之第二较将第九次之第一较四归

　　　　　之得二八五六三四四三○三七五七

　　　　　九七七内减第十次之第二较馀二八
　　　　　五六三二二七一五○四六一六八即
　　　　　为第十次之第一较将第九次开方所
　　　　　得数折半得七五五八二三二九九九
　　　　　五二八三六四七五二四四内减第十
　　　　　次之第一较又加首位之一得一○○
　　　　　○○○七五五八二○四四三六三○
　　　　　一二一四二九○七六即为第十次开

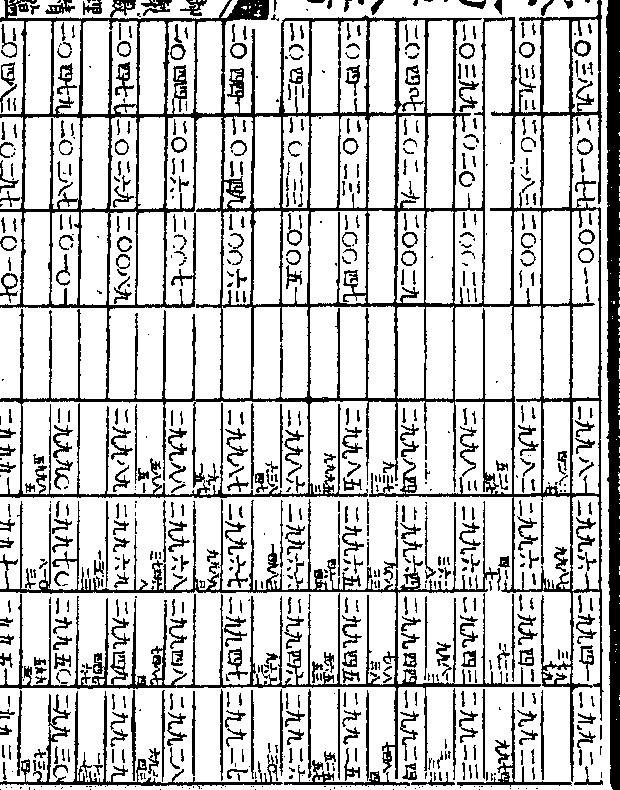　　　　　方所得数也至第十一次则将第十次
　　　　　之第四较三十二除之不足一倍故无
　　　　　第四较而以第十次之第三较十六除
　　　　　之得一七八四七即为第十一次之第
　　　　　三较将第十次之第三较八归之得二
　　　　　六九八五八八九七六内减第十一次
　　　　　之第三较馀二六九八五七一一二九
　　　　　即为第十一次之第二较将第十次之
　　　　　第一较四归之得七一四○八○六七

　　　　　八七六一五四二内减第十一次之第

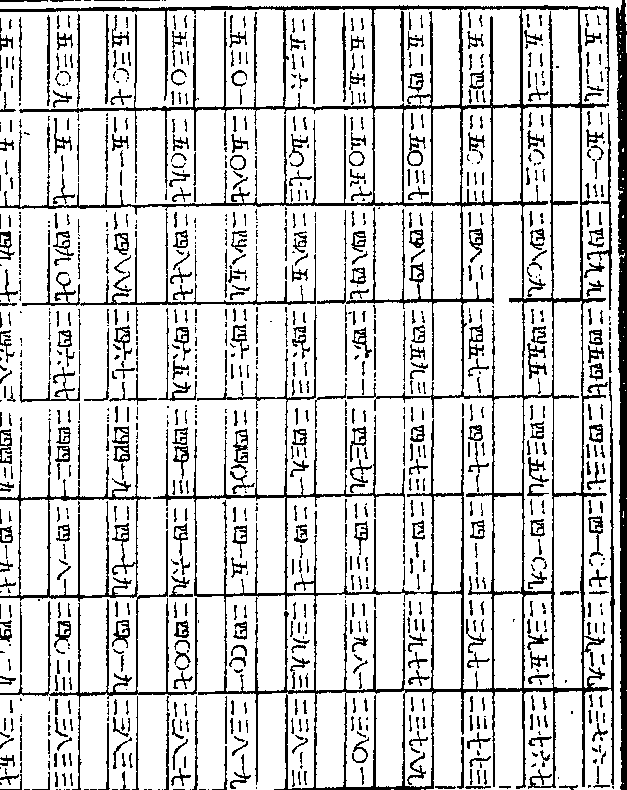　　　　　二较馀七一四○七七九八○一九○
　　　　　四一三即为第十一次之第一较将第
　　　　　十次开方所得数折半得三七七九一
　　　　　○二二一八一五○六○七一四五三
　　　　　八内减第十一次之第一较又加首位
　　　　　之一得一○○○○○三七九九○九
　　　　　五○七七三七○八○五二四一二五
　　　　　即为第十一次开方所得数也由此递

　　　　　推至第二十三次开方数得一○○○
　　　　　○○○○○○九二二六二八八九一
　　　　　○四三○七六六七是已得九空位矣
　　　　　乃以前法所得真数之零数一为一率
　　　　　(三率截用十四位则一率/亦加十三空位以足其分)其假数十一
　　　　　空位后之零数四三四二九四四八一
　　　　　八七四一四为二率(截用十四位/以从简易)今开
　　　　　方二十三次所得之零数九二二六二
　　　　　八八九一○四三○七为三率得四率

　　　　　四○○六九二六三六一九七六五二

　　　　　即为开方第二十三次之假数前则为
　　　　　十空位(二率有十四位而其前为十一/空位今四率得十五位故前为)
　　　　　(十空/位)以加倍二十三次之率数八三八
　　　　　八六○八乘之得○○○三三六一二
　　　　　五三四五(盖开方第二十三次之假数/为十五位并前十空位共二)
　　　　　(十五位今相乘得二十二位故前止有/三空位亦共为二十五位也此截用十)
　　　　　(二/位)即为第一率一○○七七六九六之
　　　　　假数然首位之一开方虽命为单位其

　　　　　实则为千万千万之假数首位应为七
　　　　　故首位为七得七○○三三六一二五
　　　　　三四五是为一千零七万七千六百九
　　　　　十六之假数又因其为连比例第九率
　　　　　故用九归之得○七七八一五一二五
　　　　　○三八即为连比例第一率六之假数
　　　　　也
　　明对数之目用递次开方求假数法之七
凡求假数先求得一至九一一至一九一○一至一

　○九一○○一至一○○九以及三○位零一至

　九四空位零一至九五空位零一至九六空位零
　一至九七空位零一至九八空位零一至九九空
　位零一至九之九十九数而他数皆由此生然此
　九十九数内有以两数相乘除而得者则以两假
　数相加减即为所求真数之假数至五空位以后
　则又可以比例而得不必逐一而求也
　　　　　如一至九之九数惟二三七之三数用
　　　　　前递次开方求假数法求之至于四则

　　　　　系二与二相乘所得之数故以二之假
　　　　　数○三○一○二九九九五六六倍之
　　　　　得○六○二○五九九九一三三即为
　　　　　四之假数至于五系以二除十所得之
　　　　　数故以二之假数与十之假数相减馀
　　　　　○六九八九七○○○四三四即为五
　　　　　之假数至于六系二与三相乘所得之
　　　　　数故以二之假数与三之假数相加得
　　　　　○七七八一五一二五○三八即为六

　　　　　之假数(或先得六之假数内减二/之假数即得三之假数)至于

　　　　　八系二与四相乘所得之数故以二之
　　　　　假数与四之假数相加得○九○三○
　　　　　八九九八六九九即为八之假数至于
　　　　　九系三与三相乘所得之数故以三之
　　　　　假数○四七七一二一二五四七二倍
　　　　　之得○九五四二四二五○九四四即
　　　　　为九之假数(或先得九之假数折/半即得三十假数)如一
　　　　　一至一九之九数惟一一一三一七一

　　　　　九之四数用前递次开方求假数法求
　　　　　之至于一二系二与六相乘所得之数
　　　　　故以二之假数与六之假数相加得一
　　　　　○七九一八一二四六○四为一十二
　　　　　之假数内减首位之一馀○○七九一
　　　　　八一二四六○四即为一二之假数(盖/自)
　　　　　(一一至九空位零九其首位之一皆为/单位首位以下为小馀试将一十二以)
　　　　　(十除之仍得一二则其首位之一即为/单位二为小馀故于十二之假数内减)
　　　　　(首位之一即减去十之假数/而所馀为一二之假数也)至于一四

　　　　　乃二与七相乘所得之数故以二之假

　　　　　数与七之假数相加得一一四六一二
　　　　　八○三五六七为一十四之假数内减
　　　　　首位之一馀○一四六一二八○三五
　　　　　六七即为一四之假数至于一五乃三
　　　　　与五相乘所得之数故以三之假数与
　　　　　五之假数相加得一一七六○九一二
　　　　　五九○六为一十五之假数内减首位
　　　　　之一馀○一七六○九一二五九○六

　　　　　即为一五之假数馀皆仿此(详见对/数阐微)至
　　　　　于一○○○○○一以后之假数则即
　　　　　可用前递次开方表内相近数比例而
　　　　　得之如求一○○○○○一之假数则
　　　　　以前表内开方第二十一次真数五空
　　　　　位后之零数一○九七九五八七三五
　　　　　为一率(截用十位/以从简便)其假数七空位后之
　　　　　零数四七六八三七一五八二为二率
　　　　　(亦截用/十位)今真数之零数一为一率(添九/空位)

　　　　　(以足/其分)得四率四三四二九四三有馀前

　　　　　亦仍为七空位(因假数止用十二位故/四率止求七位并七空)
　　　　　(位为十四位/已为足用)截前十二位得○○○○
　　　　　○○○四三四二九即为一○○○○
　　　　　○一之假数二因之得○○○○○○
　　　　　○八六八五九(第十三位满五则/进一数馀仿此)即为
　　　　　一○○○○○二之假数三因之得○
　　　　　○○○○○一三○二八八即为一○
　　　　　○○○○三之假数又以前表内开方

　　　　　第十九次真数五空位后之零数四三
　　　　　九一八四二一七三为一率其假数六
　　　　　空位后之零数一九○七三四八六三
　　　　　二为二率今真数之零数四为三率(添/九)
　　　　　(空位以/足其分)得四率一七三七一七四○前
　　　　　亦仍为六空位截前十二位得○○○
　　　　　○○○一七三七一七即为一○○○
　　　　　○○四之假数(不以前所得四率四因/之者因前所得一○○)
　　　　　(○○○一之假数四因之则微小且表/内第十九次开方数与此所求真数相)

　　　　　(近故又用比/例以求其准)将所得一○○○○○四

　　　　　之假数四归五因(将一○○○○○四/之假数四归五因者)
　　　　　(因欲得一○○○○○一/之假数而以五因之也)得○○○○
　　　　　○○二一七一四七即为一○○○○
　　　　　○五之假数将所得一○○○○○四
　　　　　之假数四归六因得○○○○○○二
　　　　　六○五七六即为一○○○○○六之
　　　　　假数又以前表内开方第十八次真数
　　　　　五空位后之零数八七八三七○三六

　　　　　三四为一率其假数六空位后之零数
　　　　　三八一四六九七二六五为二率今真
　　　　　数之零数七为三率得四率三○四○
　　　　　○四八○前亦仍为六空位截前十二
　　　　　位得○○○○○○三○四○○五即
　　　　　为一○○○○○七之假数(不以前所/得四率四)
　　　　　(归七因者因前所得一○○○○○四/之假数四归七因之则微小且表内第)
　　　　　(十八次开方数与此所求真数/相近故又用比例以求其准)将所得
　　　　　一○○○○○七之假数七归八因得

　　　　　一○○○○○三四七四三四即为一

　　　　　○○○○○八之假数又将所得一○
　　　　　○○○○七之假数七归九因得○○
　　　　　○○○○三九○八六三即为一○○
　　　　　○○○九之假数至于一○○○○○
　　　　　○一以后之假数则并不用比例盖五
　　　　　空位零一之假数为四三四二九而前
　　　　　所得十五空位零一之假数亦为四三
　　　　　四二九其假数皆相同但递退一位故

　　　　　以五空位零一至九之假数从未截去
　　　　　一位(末位满五以/上则进一数)前添一空位即得六
　　　　　空位零一至九之假数以六空位零一
　　　　　至九之假数从末截去一位前添一空
　　　　　位即得七空位零一至九之假数以七
　　　　　空位零一至九之假数从末截去一位
　　　　　前添一空位即得八空位零一至九之
　　　　　假数以八空位零一至九之假数从末
　　　　　截去一位前添一空位即得九空位零

　　　　　一至九之假数

　　明对数之目用前所得九十九数求他假数法
　　之一
凡求假数既得前九十九数而他数有由此乘除而
　得者则以假数相加减即得所求之假数其不由
　乘除而得者谓之数根(因无他数可以度尽即算/法原本所谓连比例之至)
　(小/数)则其假数亦不可以加减而得然有虽为数根
　而前九十九数中有为其根所生者则逆求之即
　得原根之假数

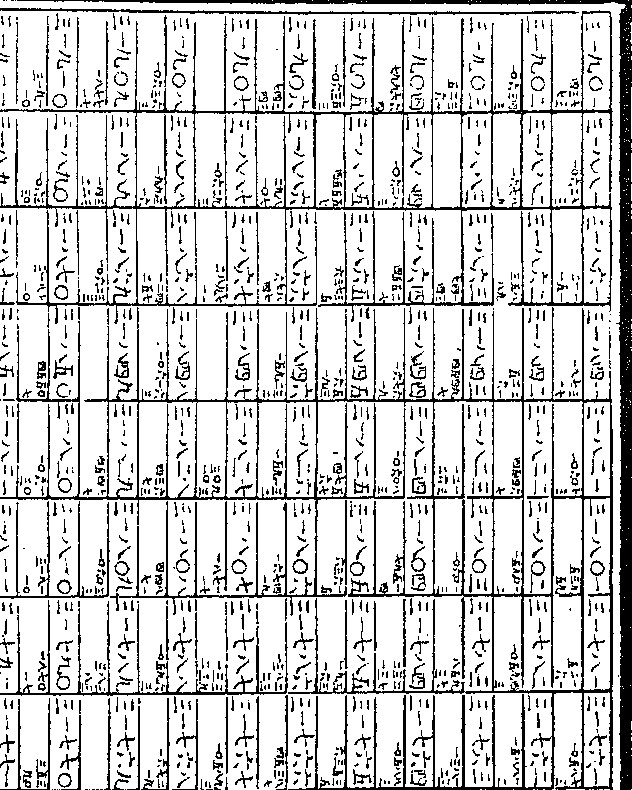　　　　　如前九十九数首位既皆为单位则以
　　　　　十乘之即为十以百乘之即为百以千
　　　　　乘之即为千以万乘之即为万故以二
　　　　　之假数与一十之假数相加即为二十
　　　　　之假数与一百之假数相加即为二百
　　　　　之假数与一千之假数相加即为二千
　　　　　之假数与一万之假数相加即为二万
　　　　　之假数又如十一之假数与一十之假
　　　　　数相加即为一百一十之假数以一○

　　　　　五之假数与一百之假数相加即为一

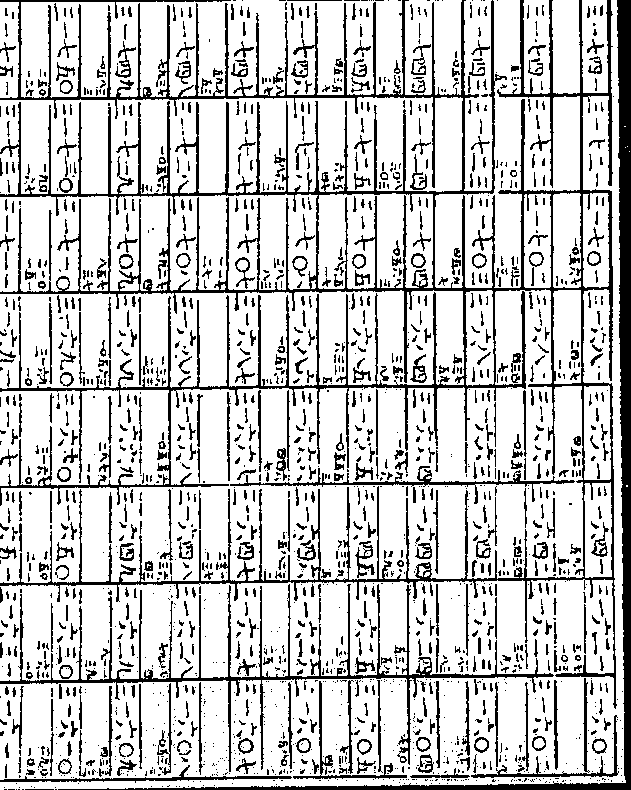　　　　　百零五之假数与一千之假数相加即
　　　　　为一千零五十之假数真数同则假数
　　　　　亦同但真数进一位则假数首位加一
　　　　　数耳又如三与七相乘得二十一则以
　　　　　三之假数与七之假数相加即为二十
　　　　　一之假数二与十一相乘得二十二则
　　　　　以二之假数与十一之假数相加即为
　　　　　二十二之假数至于二十三二十九之

　　　　　类则不以乘除而得是为数根若夫五
　　　　　十三虽亦为数根然以五十三与二相
　　　　　乘则得一百零六前既得一○六之假
　　　　　数则与一百之假数相加即为一百零
　　　　　六之假数内减二之假数即为五十三
　　　　　之假数由此类推数自繁衍而其不可
　　　　　以乘除而得者则又以累乘累除之法
　　　　　而得之(详见/后)要未有出于前九十九数
　　　　　之外者也

　　明对数之目用前所得九十九数求他假数法

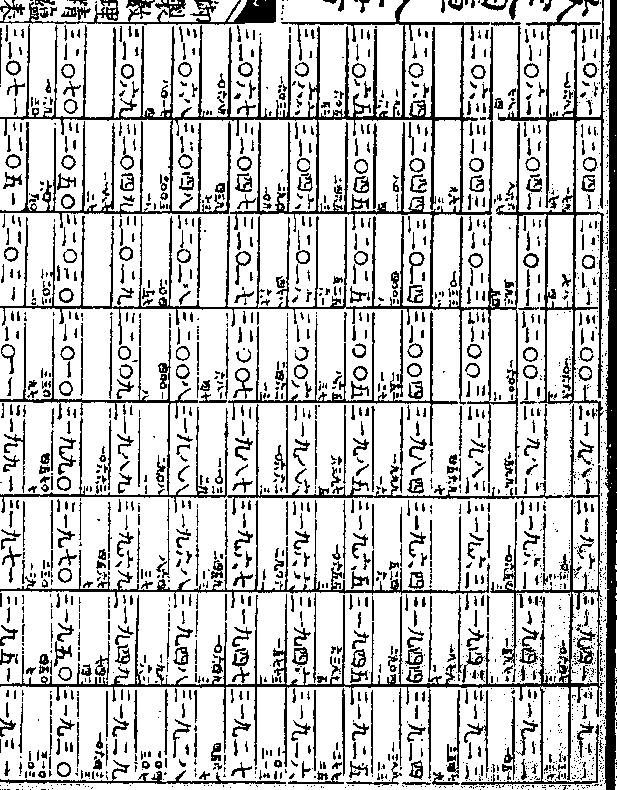　　之二
凡求假数其真数有以累乘而得者则以假数累加
　之即得所求之假数
　　　　　如二万零七百零三为二万与一○三
　　　　　及一○○五累乘所得之数则以二万
　　　　　之假数四三○一○二九九九五六六
　　　　　与一○三之假数○○一二八三七二
　　　　　二四七一及一○○五之假数○○○

　　　　　二一六六○六一七六相加得四三一
　　　　　六○三三二八二一三即为二万零七
　　　　　百零三之假数若先有假数四三一六
　　　　　○三三二八二一三求真数则视假数
　　　　　内足减二万之假数即以二万之假数
　　　　　书于原假数下相减馀○○一五○○
　　　　　三二八六四七足减一○三之假数即
　　　　　以一○三之假数书于减馀之下相减
　　　　　馀○○○二一六六○六一七六与一

　　　　　○○五之假数恰合是知其假数为二

　　　　　万与一○三及一○○五之三假数相
　　　　　加所得之数则其真数即知为三真数
　　　　　累乘所得之数矣乃以二万与一○三
　　　　　相乘得二万零六百再以一○○五乘
　　　　　之得二万零七百零三即为所求之真
　　　　　数也
　　明对数之目用前所得九十九数求他假数法
　　之三

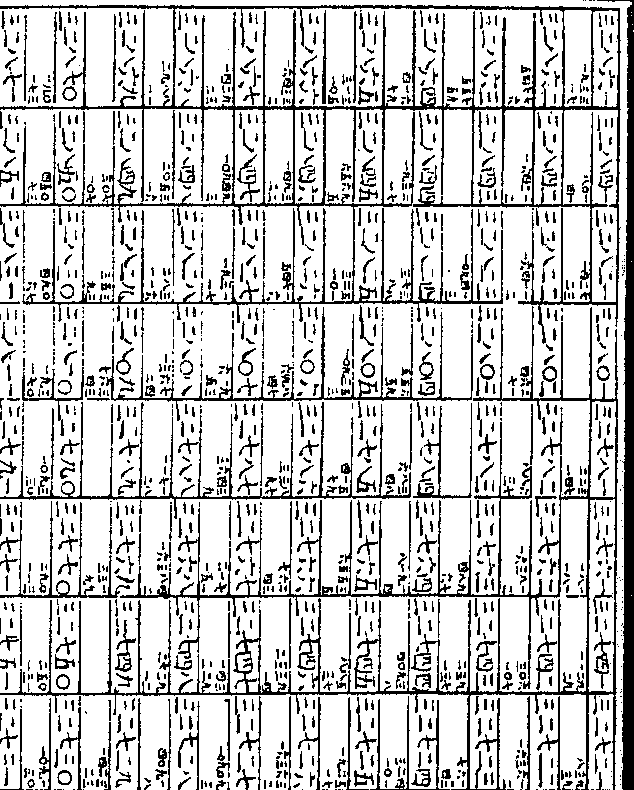凡求假数而不知其真数为何数累乘而得者则以
　所知前位之整数累除之除得累乘之真数则以
　其假数累加之即得所求之假数
　　　　　如求二十三之假数而不知其为何数
　　　　　累乘而得但知二十之假数为一三○
　　　　　一○二九九九五六六则以二十三为
　　　　　实以二十为法除之得一一又以两层
　　　　　所减数按位相加得二二即二十与一
　　　　　一相乘之数以之为法除原实二十三

　　　　　得一○四又以两层所减数按位相加

　　　　　得二二八八即二二与一○四相乘之
　　　　　数以之为法除原实二十三得一○○
　　　　　五又以两层所减数按位相加得二二
　　　　　九九四四即二二八八与一○○五相
　　　　　乘之数以之为法除原实二十三得一
　　　　　○○○二又以两层所减数按位相加
　　　　　得二二九九八九九八八八即二二九
　　　　　九四四与一○○○二相乘之数以之

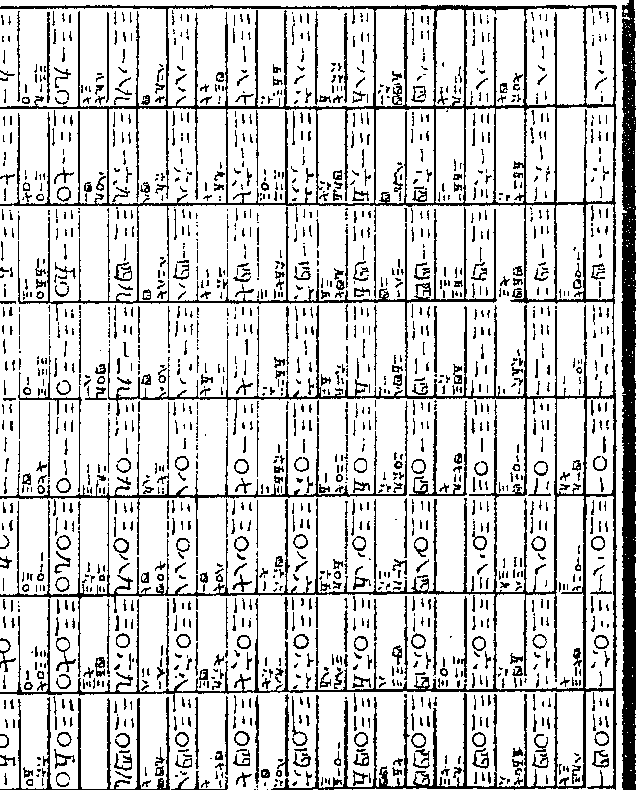　　　　　为法除原实二十三得一○○○○四
　　　　　又以两层所减数按位相加得二二九
　　　　　九九九一八八四(法止用十位故第十/一位满五以上者进)
　　　　　(一数用若不/满五则去之)即二二九九八九九八八
　　　　　八与一○○○○四相乘之数以之为
　　　　　法除原实二十三得一○○○○○三
　　　　　又以两层所减数相加得二二九九九
　　　　　九八七八四即二二九九九九一八八
　　　　　四与一○○○○○三相乘之数以之

　　　　　为法除原实二十三得一○○○○○

　　　　　○五又以两层所减数按位相加得二
　　　　　二九九九九九九三四即二二九九九
　　　　　九八七八四与一○○○○○○五相
　　　　　乘之数以之为法除原实二十三得一
　　　　　○○○○○○○二又以两层所减数
　　　　　按位相加得二二九九九九九九八○
　　　　　即二二九九九九九九三四与一○○
　　　　　○○○○○二相乘之数以之为法除

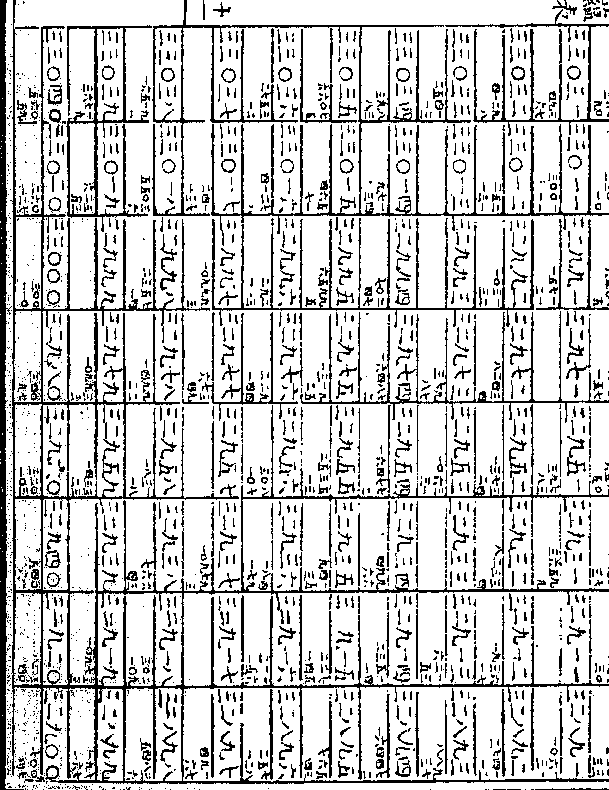
　　　　　原实二十三得一○○○○○○○○
　　　　　八又以两层所减数按位相加得二二
　　　　　九九九九九九九八即二二九九九九
　　　　　九九八○与一○○○○○○○○八
　　　　　相乘之数以之为法除原实二十三得
　　　　　一○○○○○○○○○八是知二十
　　　　　三系二十与一一及一○四一○○五
　　　　　一○○○二一○○○○四一○○○
　　　　　○○三一○○○○○○五一○○○

　　　　　○○○○二一○○○○○○○○八

　　　　　一○○○○○○○○○八累乘所得
　　　　　之数乃以其各假数累加之得一三六
　　　　　一七二七八三六○六即为二十三之
　　　　　假数也若先有假数一三六一七二七
　　　　　八三六○六求真数则视假数内足减
　　　　　二十之假数即以二十之假数书于原
　　　　　假数之下相减馀○○六○六九七八
　　　　　四○四○足减一一之假数即以一一

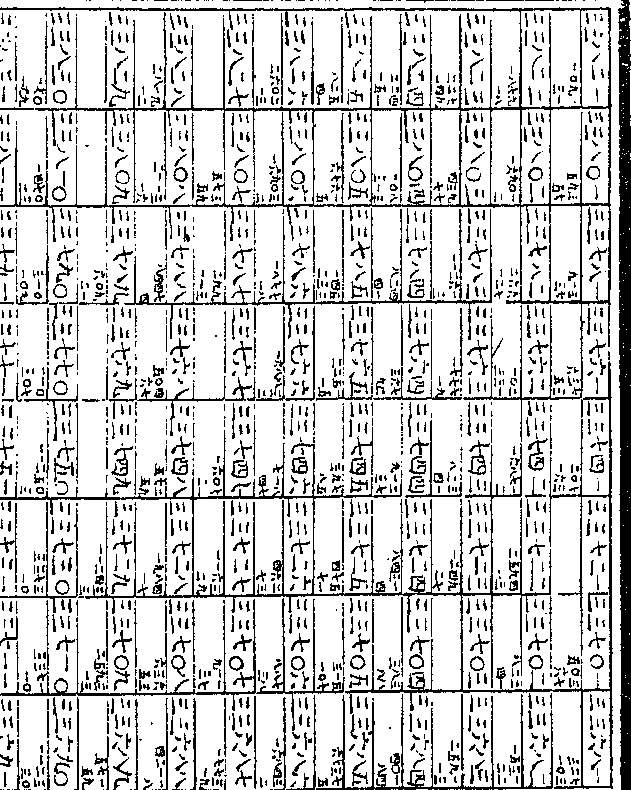　　　　　之假数书于减馀之下相减馀○○一
　　　　　九三○五一五五二四足减一○四之
　　　　　假数即以一○四之假数书于减馀之
　　　　　下相减馀○○○二二七一八一五九
　　　　　四足减一○○五之假数即以一○○
　　　　　五之假数书于减馀之下相减馀○○
　　　　　○○一○五七五四一八足减一○○
　　　　　○二之假数即以一○○○二之假数
　　　　　书于减馀之下相减馀○○○○○一

　　　　　八九○三九七足减一○○○○四之

　　　　　假数即以一○○○○四之假数书于
　　　　　减馀之下相减馀○○○○○○一五
　　　　　三二五四足减一○○○○○三之假
　　　　　数即以一○○○○○三之假数书于
　　　　　减馀之下相减馀○○○○○○○二
　　　　　二九六六足减一○○○○○○五之
　　　　　假数即以一○○○○○○五之假数
　　　　　书于减馀之下相减馀○○○○○○

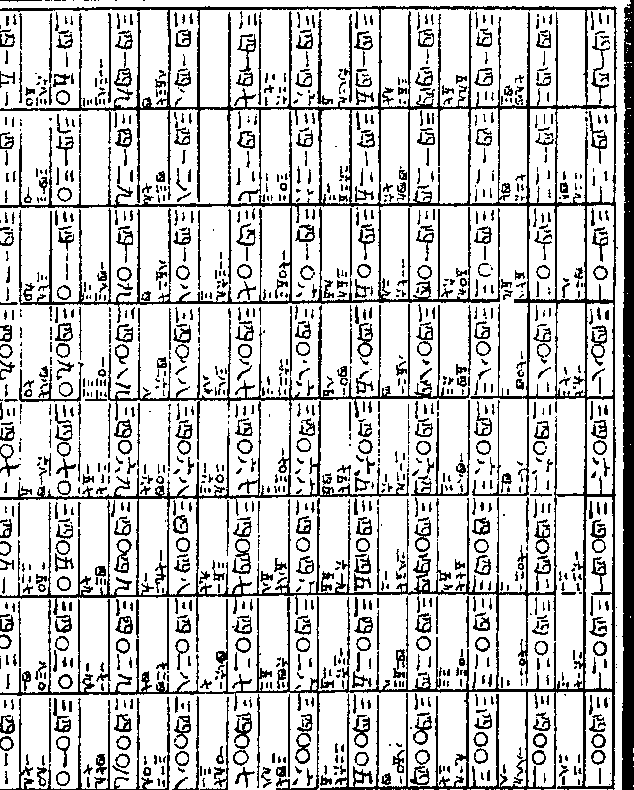　　　　　○○一二五一足减一○○○○○○
　　　　　○二之假数即以一○○○○○○○
　　　　　二之假数书于减馀之下相减馀○○
　　　　　○○○○○○○三八二足减一○○
　　　　　○○○○○○八之假数即以一○○
　　　　　○○○○○○八之假数书于减馀之
　　　　　下相减馀○○○○○○○○○○三
　　　　　五足减一○○○○○○○○○八之
　　　　　假数即以一○○○○○○○○○八

　　　　　之假数书于减馀之下相减恰尽是知

　　　　　其假数为此十一假数累加所得之数
　　　　　而真数即为此十一真数累乘所得之
　　　　　数乃以此十一真数累乘之得二十三
　　　　　即为所求之真数也
　　　　　又如求五千六百八十九之假数而不
　　　　　知其为何数累乘而得但知五千六百
　　　　　之假数为三七四八一八八○二七○
　　　　　○则以五千六百八十九为实以五千

　　　　　六百为法除之得一○一又以两层所
　　　　　减数按位相加得五六五六即五千六
　　　　　百与一○一相乘之数以之为法除原
　　　　　实五千六百八十九得一○○五又以
　　　　　两层所减数按位相加得五六八四二
　　　　　八即五六五六与一○○五相乘之数
　　　　　以之为法除原实五千六百八十九得
　　　　　一○○○八又以两层所减数按位相
　　　　　加得五六八八八二七四二四即五六

　　　　　八四二八与一○○○八相乘之数以

　　　　　之为法除原实五千六百八十九得一
　　　　　○○○○三又以两层所减数按位相
　　　　　加得五六八八九九八○八九即五六
　　　　　八八八二七四二四与一○○○○三
　　　　　相乘之数以之为法除原实五千六百
　　　　　八十九得一○○○○○○三又以两
　　　　　层所减数按位相加得五六八八九九
　　　　　九七九六即五六八八九九八○八九

　　　　　与一○○○○○○三相乘之数以之
　　　　　为法除原实五千六百八十九得一○
　　　　　○○○○○○三又以两层所减数按
　　　　　位相加得五六八八九九九九六七即
　　　　　五六八八九九九七九六与一○○○
　　　　　○○○○三相乘之数以之为法除原
　　　　　实五千六百八十九得一○○○○○
　　　　　○○○五又以两层所减数按位相加
　　　　　得五六八八九九九九九五即五六八

　　　　　八九九九九六七与一○○○○○○

　　　　　○○五相乘之数以之为法除原实五
　　　　　千六百八十九得一○○○○○○○
　　　　　○○八是知五千六百八十九系五千
　　　　　六百与一○一及一○○五一○○○
　　　　　八一○○○○三一○○○○○○三
　　　　　一○○○○○○○三一○○○○○
　　　　　○○○五一○○○○○○○○○八
　　　　　累乘所得之数乃以其各假数累加之

　　　　　得三七五五○三五九三三七一即为
　　　　　五千六百八十九之假数也若先有假
　　　　　数三七五五○三五九三三七一求真
　　　　　数则视假数内足减五千六百之假数
　　　　　即以五千六百之假数书于原假数之
　　　　　下相减馀○○○六八四七九○六七
　　　　　一足减一○一之假数即以一○一之
　　　　　假数书于减馀之下相减馀○○○二
　　　　　五二六五三二九三足减一○○五之

　　　　　假数即以一○○五之假数书于减馀

　　　　　之下相减馀○○○○三六○四七一
　　　　　一七足减一○○○八之假数即以一
　　　　　○○○八之假数书于减馀之下相减
　　　　　馀○○○○○一三一七四四八足减
　　　　　一○○○○三之假数即以一○○○
　　　　　○三之假数书于减馀之下相减馀○
　　　　　○○○○○○一四五八四足减一○
　　　　　○○○○○三之假数即以一○○○

　　　　　○○○三之假数书于减馀之下相减
　　　　　馀○○○○○○○○一五五五足减
　　　　　一○○○○○○○三之假数即以一
　　　　　○○○○○○○三之假数书于减馀
　　　　　之下相减馀○○○○○○○○○二
　　　　　五二足减一○○○○○○○○五之
　　　　　假数即以一○○○○○○○○五之
　　　　　假数书于减馀之下相减馀○○○○
　　　　　○○○○○○三五足减一○○○○

　　　　　○○○○○八之假数即以一○○○

　　　　　○○○○○○八之假数书于减馀之
　　　　　下相减恰尽是知其假数为此九假数
　　　　　累加所得之数而真数即为此九真数
　　　　　累乘所得之数乃以此九真数累乘之
　　　　　得五千六百八十九即为所求之真数
　　　　　也

　　求八线对数
凡求八线之假数定半径为一百亿位数既多为用
　愈密且真数十一位则假数首位为一○又取其
　便于用也先以正弦馀弦之真数求得假数复以
　正弦馀弦之假数加减之即得切线割线之假数
　　　　　如一分之正弦为二九○八八八二求
　　　　　其假数得六四六三七二六一一○九
　　　　　又如六十度之正弦为八六六○二五

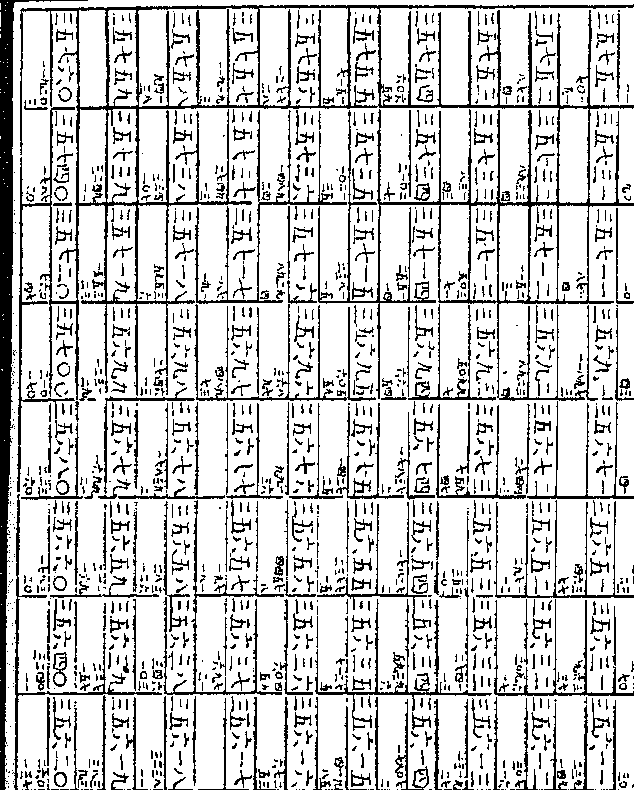
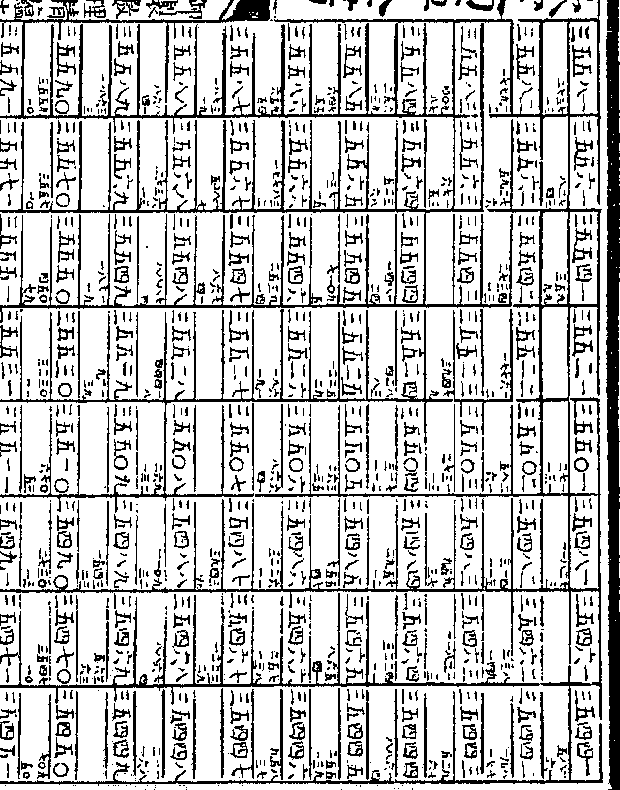　　　　　四○三八求其假数得九九三七五三
　　　　　○六三一七如求六十度切线之假数
　　　　　则以六十度正弦之假数九九三七五
　　　　　三○六三一七为二率半径之假数一
　　　　　○○○○○○○○○○○为三率六
　　　　　十度馀弦之假数九六九八九七○○
　　　　　○四三为一率二三率相加内减一率
　　　　　馀一○二三八五六○六二七四即六
　　　　　十度正切线之假数如求六十度割线

　　　　　之假数则以半径之假数一○○○○

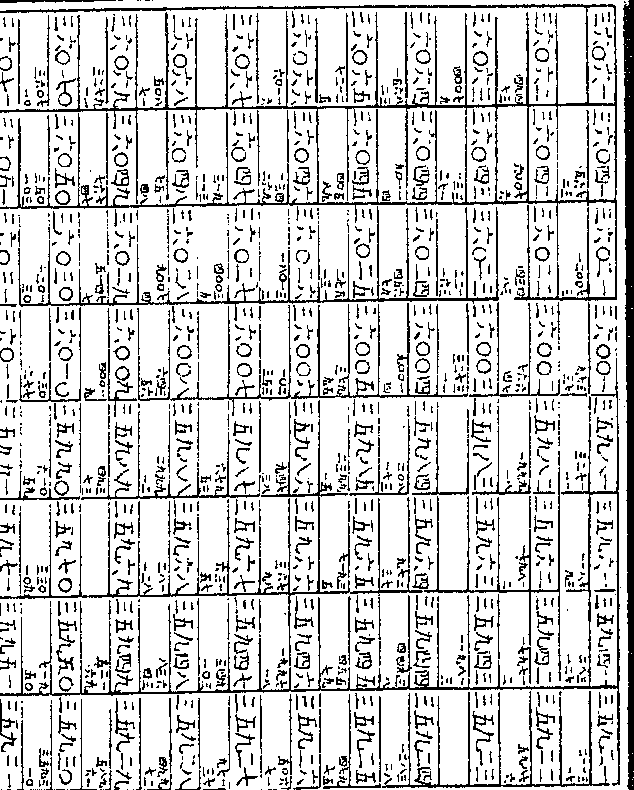　　　　　○○○○○○○为二率又为三率六
　　　　　十度馀弦之假数九六九八九七○○
　　　　　○四三为一率二率倍之内减一率馀
　　　　　一○三○一○二九九九五七即六十
　　　　　度正割线之假数也

　　对数用法
设如一百二十三与四百五十六相乘问得几何
　　　　　法以对数表之一二三之假数二○八
　　　　　九九○五一一一四与四五六之假数
　　　　　二六五八九六四八四二七相加得四
　　　　　七四八八六九九五四一乃查假数四
　　　　　七四八八六九九五四一所对之真数
　　　　　得五六○八八即五万六千零八十八

　　　　　为相乘所得之数也
设如三千四百五十六与二千六百七十九相乘问
　得几何
　　　　　法以对数表之三四五六之假数三五
　　　　　三八五七三七三三八与二六七九之
　　　　　假数三四二七九七二七一三六相加
　　　　　得六九六六五四六四四七四因对数
　　　　　表假数首位止于四真数止于五位故
　　　　　将相加所得假数首位之六暂当四查

　　　　　假数四九六六五四六四四七四相近

　　　　　略少者为四九六六五四五三二一六
　　　　　其相对之真数得九二五八六即为九
　　　　　二五八六○○(因假数首位多二数/则真数必多二位)又
　　　　　以九二五八六○○之假数与九二五
　　　　　八七○○之假数相减馀四六九○七
　　　　　为一率以九二五八六○○与九二五
　　　　　八七○○相减馀一○○为二率今相
　　　　　加所得之假数与九二五八六○○之

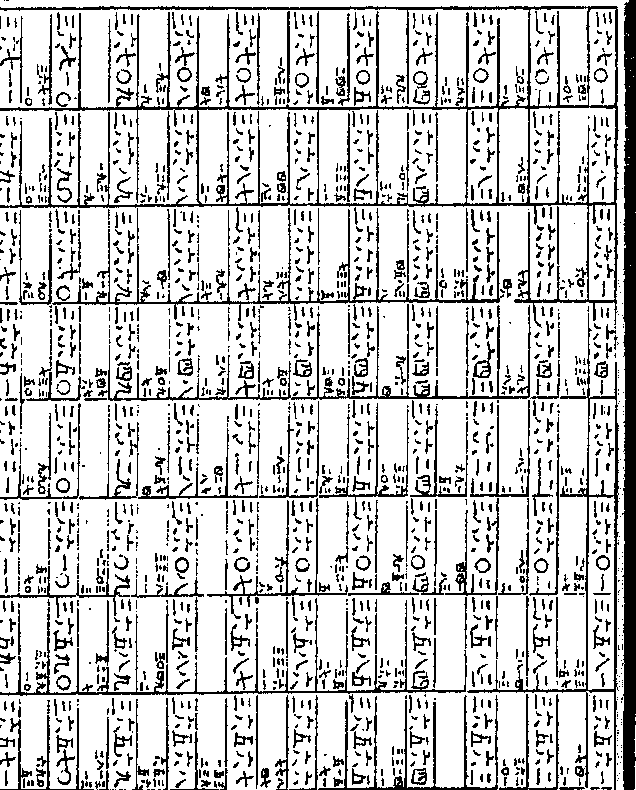　　　　　假数相减馀一一二五八为三率得四
　　　　　率二四即真数九二五八六之后二位
　　　　　之数盖假数多四六九○七则真数多
　　　　　一百今假数多一一二五八则真数应
　　　　　多二十四为比例四率也乃以所得二
　　　　　四与九二五八六○○相加得九二五
　　　　　八六二四即九百二十五万八千六百
　　　　　二十四为相乘所得之数也大凡真数
　　　　　二四位以后其假数之较相差无多故

　　　　　真数即可与假数为比例若用前累乘

　　　　　累除之法固为甚密然较之比例则难
　　　　　而得数则同此对数表所以止于五位
　　　　　也
设如三千七百四十四以十六除之问得几何
　　　　　法以对数表之三七四四之假数三五
　　　　　七三三三五八四○一内减一六之假
　　　　　数一二○四一一九九八二七馀二三
　　　　　六九二一五八五七四乃查假数二三

　　　　　六九二一五八五七四所对之真数得
　　　　　三三四即二百三十四为归除所得之
　　　　　数也
设有米三十二石令一千零二十四人分之问每一
　人应得几何
　　　　　法以对数表之三二之假数首位加二
　　　　　为三五○五一四九九七八三(因法之/假数大)
　　　　　(于实之假数故以实之假数加二/即如以实之真数加两空位也)内减
　　　　　一○二四之假数三○一○二九九九

　　　　　五六六馀○四九四八五○○二一七

　　　　　因假数首位为○即知真数应得单位
　　　　　其得数首位为升仍以假数首位加三
　　　　　查三四九四八五○○二一七所对之
　　　　　真数得三一七五(因真数得四位故将/假数首位作三查表)
　　　　　(若真数求五位则将假数首位作四查/表或五位后仍有馀数则用比例求之)
　　　　　即三升一合二勺五撮为每人所应得
　　　　　之数也
设如甲乙丙直角形甲角五十度丙角四十度甲乙

　边十二丈求丙乙边丙甲边各几何
　　　　　法以甲角五十度之正弦假数九八八
　　　　　四二五三九六六五与甲乙边十二丈
　　　　　(作一二/○○○)之假数四○七九一八一二四
　　　　　六○相加得一三九六三四三五二一
　　　　　二五内减丙角四十度之正弦假数九
　　　　　八○八○六七四九六七馀四一五五
　　　　　三六七七一五八为丙乙边之假数查
　　　　　假数相近所对之真数得一四三○一

　　　　　即一十四丈三尺零一分为丙乙边也

　　　　　求丙甲边则以乙角九十度之正弦假
　　　　　数一○○○○○○○○○○○(即半/径之)
　　　　　(数/)与甲乙边十二丈之假数四○七九
　　　　　一八一二四六○相加得一四○七九
　　　　　一八一二四六○内减丙角四十度之
　　　　　正弦假数九八○八○六七四九六七
　　　　　馀四二七一一一三七四九三为丙甲
　　　　　边之假数查假数相近所对之真数得

　　　　　一八六六九即一十八丈六尺六寸九
　　　　　分为丙甲边也
设如甲乙丙三角形甲角五十度甲乙边十六丈甲
　丙边十二丈问丙角乙角及乙丙边各若干
　　　　　法以甲乙边十六丈与甲丙边十二丈
　　　　　相加得二十八丈为边总甲乙边与甲
　　　　　丙边相减馀四丈为边较甲角五十度
　　　　　与一百八十度相减馀一百三十度折
　　　　　半为六十五度为半外角乃以边较四

　　　　　丈(作四○/○○)之假数三六○二○五九九

　　　　　九一三与半外角六十五度之正切假
　　　　　数一○三三一三二七四五二二相加
　　　　　得一三九三三三八七四四三五内减
　　　　　边总二十八丈(作二八/○○○)之假数四四四
　　　　　七一五八○三一三馀九四八六二二
　　　　　九四一二二为半较角正切之假数查
　　　　　正切假数相近所对之真数得十七度
　　　　　二分为半较角与半外角相加得八十

　　　　　二度二分为对甲乙大边之丙角与半
　　　　　外角六十五度相减馀四十七度五十
　　　　　八分为对甲丙小边之乙角也又求丙
　　　　　乙边则以五十度之正弦假数九八八
　　　　　四二五三九六六五与十六丈(作一六/○○○)
　　　　　之假数四二○四一一九九八二七相
　　　　　加得一四○八八三七三九四九二内
　　　　　减丙角八十二度二分之正弦假数九
　　　　　九九五七八八二○九八馀四○九二

　　　　　五八五七三九四为丙乙边之假数查

　　　　　假数相近所对之真数得一二三七六
　　　　　即一十二丈三尺七寸六分为丙乙边
　　　　　也凡真数用加减然后比例者须以真
　　　　　数加减得数再查假数依法算之馀皆
　　　　　仿此
设如六十四自乘问得几何
　　　　　法以对数表之六四之假数一八○六
　　　　　一七九九七四○用二因之得三六一

　　　　　二三五九九四八○仍查假数所对之
　　　　　真数得四○九六即四千零九十六为
　　　　　自乘所得之数也盖自乘两数相同则
　　　　　其两假数亦相同故二因之即如二假
　　　　　数相加也
设如正方面积三百六十一尺开平方问每一边数
　几何
　　　　　法以对数表之三六一之假数二五五
　　　　　七五○七二○一九折半得一二七八

　　　　　七五三六○○九仍查假数所对之真

　　　　　数得一九即一十九尺为开平方所得
　　　　　每边之数也盖正方面积之假数乃以
　　　　　每边之假数加倍所得之数故折半即
　　　　　得每边之假数对其真数即得每边之
　　　　　数也
设如正方面积一百五十二万二千七百五十六尺
　开平方问每一边数几何
　　　　　法先以方积前五位一五二二七查得

　　　　　假数为四一八二六一四三四七七因
　　　　　方积系七位今止查得五位仍馀二位
　　　　　故将假数首位之四加二得六一八二
　　　　　六一四三四七七即为一五二二七○
　　　　　○之假数又以一五二二七○○与一
　　　　　五二二八○○相减馀一○○为一率
　　　　　以一五二二七○○之假数与一五二
　　　　　二八○○之假数相减馀二八五二○
　　　　　四为二率方积之后二位数五六为三

　　　　　率得四率一五九七○四盖真数多一

　　　　　百则假数多二八五二○四今真数多
　　　　　五十六则假数应多一五九七一四为
　　　　　比例四率也乃以所得四率与一五二
　　　　　二七○○之假数相加得六一八二六
　　　　　三○三一九一即为一五二二七五六
　　　　　之假数折半得三○九一三一五一五
　　　　　九六仍查假数所对之真数得一二三
　　　　　四即一千二百三十四尺为开平方所

　　　　　得每边之数也
　　　　　又捷法以一五二二七之假数首位加
　　　　　二得六一八二六一四三四七七即为
　　　　　一五二二七○○之假数折半得三○
　　　　　九一三○七一七三八查假数相近略
　　　　　大者(盖一五二二七○○之假数略少/于一五二二七五六之假数则其)
　　　　　(折半之假数亦必略少于一二/三四之假数亦取略大者用之)对其真
　　　　　数得一二三四即为每边之数也此法
　　　　　因方根止四位查表即得不用比例故

　　　　　以方积前五位查表后有几位则假数

　　　　　首位加几数折半查假数相近者即可
　　　　　得之若方根过五位以上者须用比例
　　　　　则以方积查假数亦须用比例方得密
　　　　　合
设如正方面积一百五十二兆四千一百五十七亿
　六千五百二十七万九千三百八十四尺问每一
　边数几何
　　　　　法以方积前五位一五二四一查得假

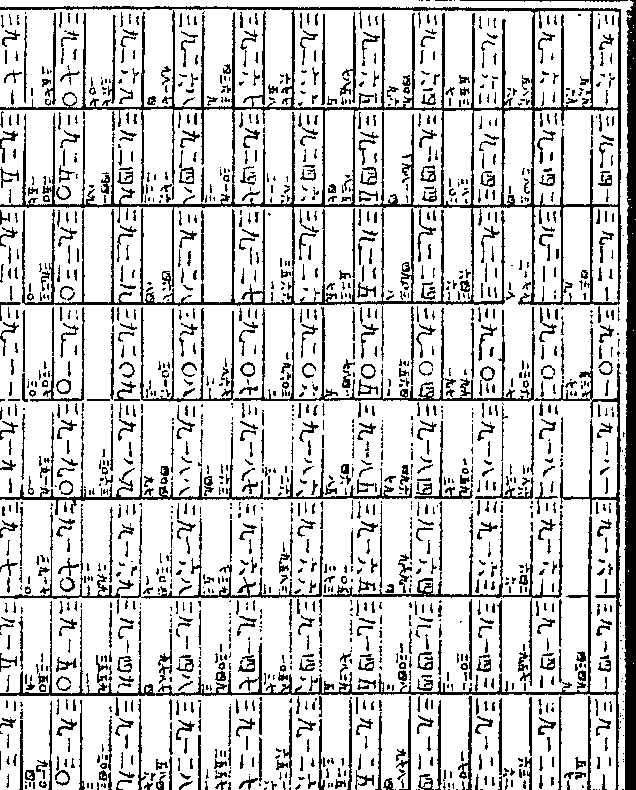　　　　　数为四一八三○一三四六三一因方
　　　　　积系十五位今止查得五位仍馀十位
　　　　　故将假数首位之四加十得一四一八
　　　　　三○一三四六三一即为一五二四一
　　　　　○○○○○○○○○○之假数又以
　　　　　一五二四一○○○○○○○○○○
　　　　　与一五二四二○○○○○○○○○
　　　　　○相减截用六空位得一○○○○○
　　　　　○为一率以一五二四一之假数与一

　　　　　五二四二之假数相减馀二八四九四

　　　　　二为二率方积后十位数截用前六位
　　　　　得五七六五二七为三率(因表中假数/止于十一位)
　　　　　(则真数亦止须用十一位虽真数后再/多几位其假数前十一位亦相同故查)
　　　　　(表用五位比例用/六位共为十一位)得四率一六四二七
　　　　　七与一五二四一○○○○○○○○
　　　　　○○之假数相加得一四一八三○二
　　　　　九八九○八即为一五二四一五七六
　　　　　五二七○○○○之假数亦即同于一

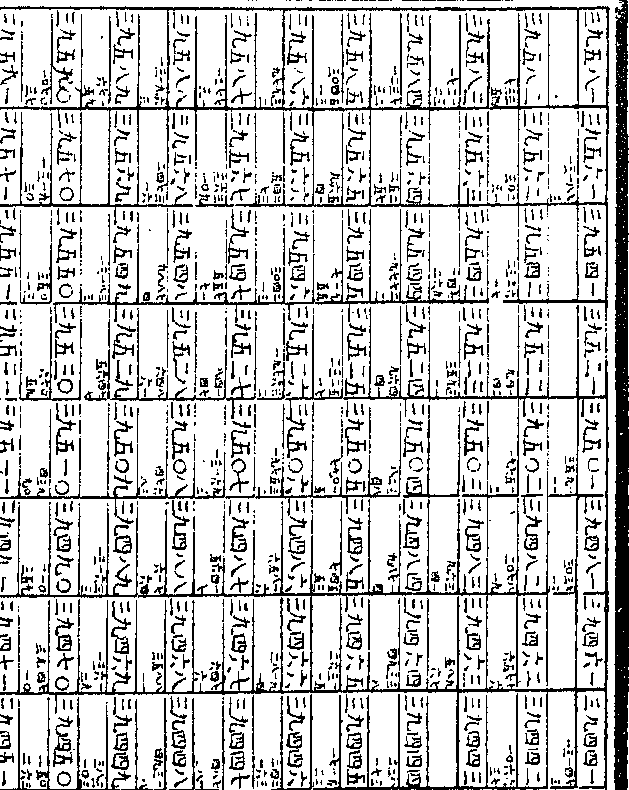　　　　　五二四一五七六五二七九三八四之
　　　　　假数折半得七○九一五一四九四五
　　　　　四因假数首位为七即知真数应得八
　　　　　位今对数表假数首位止于四真数
　　　　　止于五位故将折半所得假数首位之七
　　　　　减去三得四○九一五一四九四五四
　　　　　查假数相近略少者为四○九一四九
　　　　　一○九四三对其真数得一二三四五
　　　　　即为一二三四五○○○(因假数首位/多三数则真)

　　　　　(数进/三位)又以一二三四五○○○之假数

　　　　　与一二三四六○○○之假数相减馀
　　　　　三五一七八三为一率以一二三四五
　　　　　○○○与一二三四六○○○相减馀
　　　　　一○○○为二率今折半所馀之假数
　　　　　与一二三四五○○○之假数相减馀
　　　　　二三八五一一为三率得四率六七八
　　　　　与一二三四五○○○相加得一二三
　　　　　四五六七八即一千二百三十四万五

　　　　　千六百七十八尺为开平方所得每一
　　　　　边之数也
设如勾二十七尺股三十六尺求弦若干
　　　　　法以对数表之二七之假数一四三一
　　　　　三六三七六四二倍之得二八六二七
　　　　　二七五二八四为勾自乘之假数仍查
　　　　　假数所对之真数得七二九为勾自乘
　　　　　之真数又以三六之假数一五五六三
　　　　　○二五○○八倍之得三一一二六○

　　　　　五○○一六为股自乘之假数仍查假

　　　　　数所对之真数得一二九六为股自乘
　　　　　之真数两自乘之真数相加(不以两自/乘之假数)
　　　　　(相加者盖假数相加则是相乘/故必对其真数然后相加也)得二○
　　　　　二五为弦自乘之真数查其假数得三
　　　　　三○六四二五○二七六折半得一六
　　　　　五三二一二五一三八仍查假数所对
　　　　　之真数得四五即四十五尺为开方所
　　　　　得之弦数也

设如三十六自乘再乘问得几何
　　　　　法以对数表之三六之假数一五五六
　　　　　三○二五○○八用三因之得四六六
　　　　　八九○七五○二四仍查假数所对之
　　　　　真数得四六六五六即四万六千六百
　　　　　五十六为自乘再乘所得之数也盖自
　　　　　乘再乘系以方根乘二次则假数亦加
　　　　　二次故以方根之假数三因之即如以
　　　　　方根之假数加二次也其或位数多者

　　　　　依乘法之例推之

设如正方体积一万三千八百二十四尺开立方问
　每一边数几何
　　　　　法以对数表之一三八二四之假数四
　　　　　一四○六三三七二五一用三归之得
　　　　　一三八○二一一二四一七仍查假数
　　　　　所对之真数得二四即二十四尺为开
　　　　　立方所得每边之数也盖正方体积之
　　　　　假数乃以每边之假数三因所得之数

　　　　　故三归之即得每边之假数对其真数
　　　　　即得每边之数也其或位数多者依平
　　　　　方之例推之
设如方根一十六尺问三乘方积几何
　　　　　法以对数表之一六之假数一二○四
　　　　　一一九九八二七用四因之得四八一
　　　　　六四七九九三○八仍查假数所对之
　　　　　真数得六五五三六即六万五千五百
　　　　　三十六尺为三乘方之积数也盖三乘

　　　　　方系以方根乘三次则其假数亦加三

　　　　　次故以方根之假数四因之即如以方
　　　　　根之假数加三次也其或位数多者亦
　　　　　依乘法之例推之
设如三乘方积二万零七百三十六尺问方根几何
　　　　　法以对数表之二○七三六之假数四
　　　　　三一六七二四九八四二用四归之得
　　　　　一○七九一八一二四六○仍查假数
　　　　　所对之真数得一二即一十二尺为开

　　　　　三乘方所得方根之数也盖三乘方积
　　　　　之假数乃以方根之假数四因所得之
　　　　　数故四归之即得方根之假数对其真
　　　　　数即得方根之数也其或位数多者亦
　　　　　依平方之例推之大凡开诸乘方之理
　　　　　亦皆由于连比例盖方根为连比例第
　　　　　一率平方积为第二率立方积为第三
　　　　　率三乘方积为第四率四乘方积为第
　　　　　五率五乘方积为第六率六乘方积为

　　　　　第七率七乘方积为第八率八乘方积

　　　　　　为第九率九乘方积为第十率(与借根/方比例)
　　　　　　(定位/表同)以第一率方根之假数各以率数
　　　　　　乘之即得各乘方积之假数而以各乘
　　　　　　方积之假数各以率数除之亦即得第
　　　　　　一率方根之假数故由三乘方而进之
　　　　　　四乘方求积则用五因求根则用五归
　　　　　　五乘方求积则用六因求根则用六归
　　　　　　推之至于九乘方求积则用十因求根

　　　　　　则用十归即至于一百乘方则以方根
　　　　　　之假数用一百零一乘之即得方积之
　　　　　　假数以方积之假数用一百零一除之
　　　　　　即得方根之假数乘除之数愈繁愈见
　　　　　　对数之易此对数之大用也
　
　
　
　

御制数理精蕴下编卷三十八