钦定四库全书
御制数理精蕴下编卷十八
　　面部八
　　　测量(勾股测量/三角测量)

　　测量
周髀曰偃矩以窥高覆矩以测深卧矩以知远盖以矩
度或表杆相度窥测立者则取其直平者则取其方必
使成直角以大小勾股为比例以在器之勾股比所测
之勾股彼此相形而得之者也然勾股必为直角而三
角形则惟变所适而无定形要以角度为准而用割圜
八线以为比例凡求角求边皆以三角形之法为本总
以对所知为一率对所求为二率所知为三率得四率

即所求也或一测或屡测惟在随时而致用或用正或
用馀惟在比例之相当不特凡物之高深广远可得而
推即七政之躔度天地之形体俱可得而测也

　　勾股测量(凡用矩度或立表杆必用垂线取其/与地平成直角以为准则若地不平)
　　　　(须记取某处与人/目所看相平为记)
设如有一旗杆欲测其高但知距旗杆之远为三丈
　问得高几何
　　　　　　法用矩度(矩度之制必用正方每边定/一百分或二百分横𥪡俱界)
　　　　　　(线画成小方分自中心所出线俱平分/每边一半对中心所出线两边安定表)
　　　　　　(取中心安游表看分数必以其自中/心所出线为准见几何原本十二卷)定
　　　　　　准坠线以定表看地平游表看旗杆顶

　　　　　　得距地平分四十分(此矩度前边为百/分自中心平分半)
　　　　　　(边为五/十分)乃以中心平分距分五十分为
　　　　　　一率所得距分四十分为二率距旗杆
　　　　　　之远三丈为三率求得四率二丈四尺
　　　　　　即矩度中心定表所对地平至旗杆顶
　　　　　　之高加矩度中心距地之高四尺共得
　　　　　　二丈八尺即所求旗杆之高也如图甲
　　　　　　乙为旗杆之高丙乙为距旗杆之远丁
　　　　　　为矩度中心丁丙为矩度中心距地之

　　　　　　高己庚为定表所对地平为戊辛壬为

　　　　　　游表看旗杆顶甲其丁庚为矩度中心
　　　　　　平分距分五十分壬庚为游表距地平
　　　　　　分四十分其丁庚与壬庚之比同于丁
　　　　　　戊与甲戊之比故丁庚五十分为一率
　　　　　　壬庚四十分为二率丁戊距旗杆之远
　　　　　　三丈为三率得四率甲戊二丈四尺加
　　　　　　同丁丙高之戊乙四尺即得甲乙二丈
　　　　　　八尺为旗杆之高也

　　　　　　又用表杆测法于距旗杆三丈处立一
　　　　　　表高四尺向前又立一表高八尺看二
　　　　　　表端与旗杆顶齐量二表间相距得五
　　　　　　尺乃以五尺为一率前表八尺内减后
　　　　　　表四尺馀四尺为二率距旗杆之远三
　　　　　　丈为三率求得四率二丈四尺加入后
　　　　　　表高四尺得二丈八尺即旗杆之高也
　　　　　　如图甲乙为旗杆之高乙丙为距旗杆
　　　　　　之远三丈丁丙为后表之高四尺戊己

　　　　　　为前表之高八尺丙己为二表之距五

　　　　　　尺戊庚为二表之较四尺丁戊甲为人
　　　　　　目视线试与乙丙平行作辛丁线遂成
　　　　　　甲辛丁戊庚丁两勾股形为同式形故
　　　　　　丁庚与戊庚之比同于丁辛与甲辛之
　　　　　　比既得甲辛加与丁丙相等之辛乙即
　　　　　　得甲乙为旗杆之高也
设如一树欲测其远爰取一直角横量十五丈问得
　远几何

　　　　　　法以矩度定表与游表定准直角以定
　　　　　　表对树游表随直角立表杆二三处横
　　　　　　量十五丈于此处复安矩度以定表对
　　　　　　所立表杆取直看原处以游表看树得
　　　　　　距矩度中心平分线距分三十分乃以
　　　　　　所得距分三十分为一率矩度中心平
　　　　　　分距分五十分为二率横量十五丈为
　　　　　　三率求得四率二十五丈即离树之远
　　　　　　也如图甲为树甲乙为离树之远乙为

　　　　　　直角乙丙为横量十五丈丁戊为所立

　　　　　　二表杆丙为矩度中心丙己为矩度中
　　　　　　心平分距分五十分己庚为所得距分
　　　　　　三十分丙己庚勾股形与甲乙丙勾股
　　　　　　形为同式形故己庚与己丙之比即同
　　　　　　于丙乙与甲乙之比也
　　　　　　又用表杆测法先立一表于乙取直角
　　　　　　横量十五丈至丙次立一表于丙自丙
　　　　　　对甲相直复立一表于丁次依丁丙度

　　　　　　引至乙丙线上截乙丙于戊乃以丙戊
　　　　　　折半于己遂得丁己丙勾股形与甲乙
　　　　　　丙勾股形为同式形因量丙己得三丈
　　　　　　为一率丁己得五丈为二率丙乙十五
　　　　　　丈为三率求得四率二十五丈即甲乙
　　　　　　之远也
设如有山一座欲知其高用重矩之法测之问山之
　高得几何
　　　　　　法用矩度定准坠线以定表看地平游

　　　　　　表看山顶得距地平分四十分又向后

　　　　　　量九丈复安矩度定准坠线以定表仍
　　　　　　看前矩度定表所看地平原处游表看
　　　　　　山顶得距地平分三十二分乃以前矩
　　　　　　度距地平分四十分为一率中心平分
　　　　　　距分五十分为二率后矩度距地平分
　　　　　　三十二分为三率求得四率四十分为
　　　　　　前矩度游表与后矩度游表同距地平
　　　　　　分所得之中心距分乃以所得四十分

　　　　　　与后矩度中心平分距分五十分相减
　　　　　　馀十分为一率后矩度距地平分三十
　　　　　　二分为二率向后量九丈为三率求得
　　　　　　四率二十八丈八尺即矩度中心定表
　　　　　　所对地平至山顶之高加矩度中心距
　　　　　　地之高四尺共得二十九丈二尺即所
　　　　　　求之山之高也如图甲乙为山之高丙
　　　　　　为前矩度中心丙庚为定表所对地平
　　　　　　为戊丙己为游表看山顶甲其己庚为

　　　　　　游表距地平分四十分丙庚为中心平

　　　　　　分距分五十分丙丁为向后量九丈丁
　　　　　　为后矩度中心丁壬为定表所对地平
　　　　　　亦为戊丁辛为游表看山顶甲其辛壬
　　　　　　为游表距地平分三十二分丁壬为中
　　　　　　心平分距分五十分试依后矩度游表
　　　　　　距地平分辛壬度于前矩度作癸子线
　　　　　　则丙子中心距分必小于丙庚故己庚
　　　　　　与丙庚之比同于癸子与丙子之比而

　　　　　　得丙子之分既得丙子则以丙子与丁
　　　　　　壬相减馀丁丑(与前矩度/子庚等)即前后两矩
　　　　　　度游表同距地平分所得中心距分之
　　　　　　较乃自辛至丑作辛丑线遂成辛壬丑
　　　　　　勾股形与癸子丙同度俱与甲戊丙勾
　　　　　　股形为同式形而辛壬丁勾股形又与
　　　　　　甲戊丁勾股形为同式形且丁丙与丁
　　　　　　丑皆为两勾股形之各股之较故辛丑
　　　　　　丁三角形与甲丙丁三角形亦为同式

　　　　　　形是以丁丑与辛壬之比同于丁丙与

　　　　　　甲戊之比而为相当比例四率也
　　　　　　又法用矩度定准坠线以定表看地平
　　　　　　游表看山顶向后量九丈复安矩度定
　　　　　　准坠线以定表仍看前矩度定表所看
　　　　　　地平原处游表看山顶得距地平分三
　　　　　　十二分其中心平分距分为五十分爰
　　　　　　察前矩度距地平分三十二分处得距
　　　　　　中心距分为四十分乃以所得四十分

　　　　　　与后矩度中心平分距分五十分相减
　　　　　　馀十分为一率距地平分三十二分为
　　　　　　二率向后量九丈为三率求得四率二
　　　　　　十八丈八尺即矩度中心定表所对地
　　　　　　平至山顶之高加矩度中心距地之高
　　　　　　四尺共得二十九丈二尺即所求之山
　　　　　　之高也如图甲乙为山之高丙为前矩
　　　　　　度中心定表所对地平为戊游表看山
　　　　　　顶甲丙丁为向后量九丈丁为后矩度

　　　　　　中心其辛壬为游表距地平分三十二

　　　　　　分丁壬为中心平分距分五十分试依
　　　　　　后矩度距地平分三十二分辛壬度于
　　　　　　前矩度三十二分处作己庚线其丙庚
　　　　　　距中心距分得四十分乃以丙庚四十
　　　　　　分截后矩度丁壬中心平分距分于癸
　　　　　　则丁癸为减馀十分其丁癸与辛壬之
　　　　　　比即同于丁丙与甲戊之比也前法两
　　　　　　矩度游表距地平分不同故用比例四

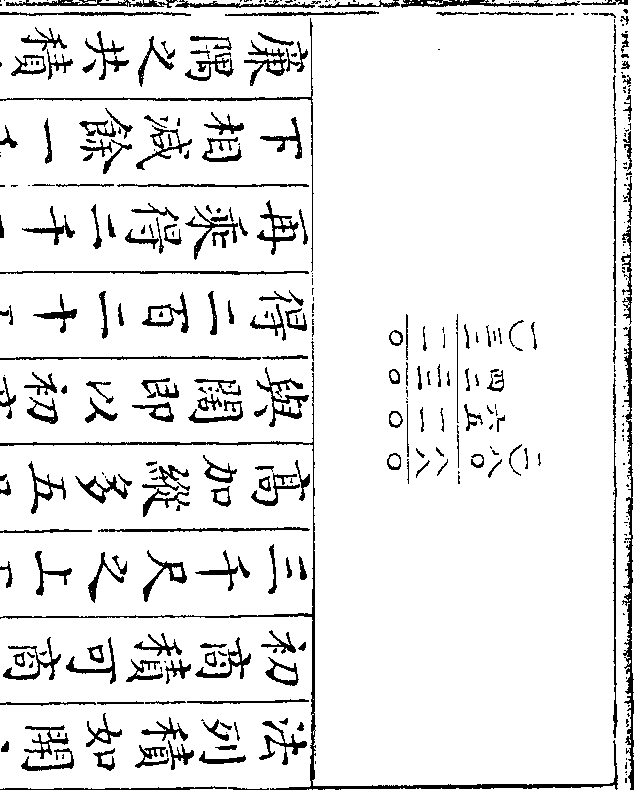　　　　　　率而得其距地平相等之中心距分以
　　　　　　取其两中心距分之较此法因取其距
　　　　　　地平相等之分故其两中心距分不同
　　　　　　相减即得其两中心距分之较也
设如一墙欲知其远用重矩之法测之问墙之远得
　几何
　　　　　　法用矩度定准坠线以定表看地平游
　　　　　　表看墙顶得距地平分四十分又向后
　　　　　　量一丈复安矩度定准坠线以定表仍

　　　　　　看前矩度定表所看地平原处游表看

　　　　　　墙顶得距地平分二十四分乃以前矩
　　　　　　度距地平分四十分为一率中心平分
　　　　　　距分五十分为二率后矩度距地平分
　　　　　　二十四分为三率求得四率三十分为
　　　　　　前矩度游表与后矩度游表同距地平
　　　　　　分所得之中心距分乃以所得三十分
　　　　　　与后矩度中心平分距分五十分相减
　　　　　　馀二十分为一率前矩度所得中心距

　　　　　　分三十分为二率向后量一丈为三率
　　　　　　求得四率一丈五尺即前矩度距墙之
　　　　　　远若求后矩度距墙之远则以后矩度
　　　　　　中心平分距分五十分为二率所得四
　　　　　　率二丈五尺即后矩度距墙之远也如
　　　　　　图甲乙为墙之高丙为前矩度中心丙
　　　　　　庚为定表所对地平为戊丙己为游表
　　　　　　看墙顶甲其己庚为游表距地平分四
　　　　　　十分丙庚为中心平分距分五十分丙

　　　　　　丁为向后量一丈丁为后矩度中心丁

　　　　　　壬为定表所对地平亦为戊丁辛为游
　　　　　　表看墙顶甲其辛壬为游表距地平分
　　　　　　二十四分丁壬为中心平分距分五十
　　　　　　分试依后矩度游表距地平分辛壬度
　　　　　　于前矩度作癸子线则丙子中心距分
　　　　　　必小于丙庚故己庚与丙庚之比同于
　　　　　　癸子与丙子之比而得丙子之分既得
　　　　　　丙子则以丙子与丁壬相减馀丁丑(与/前)

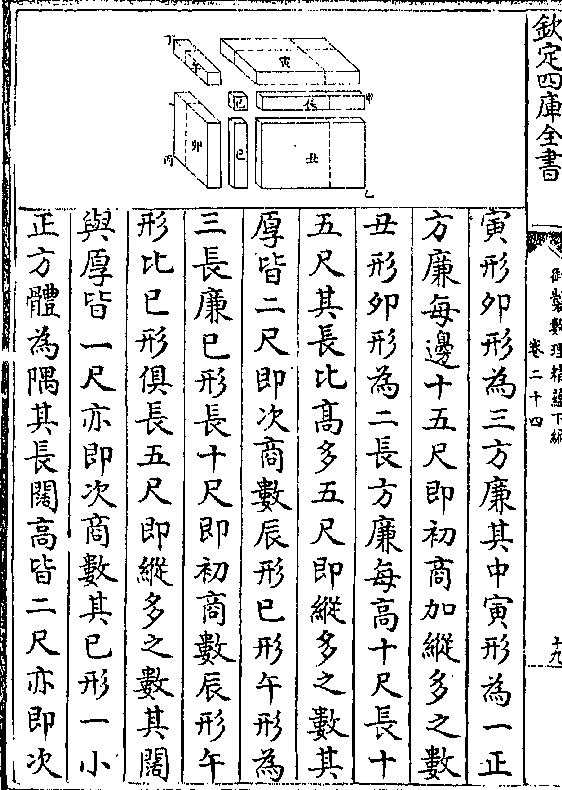
　　　　　　(矩度子/庚等)即前后两矩度游表同距地平
　　　　　　分所得中心距分之较乃自辛至丑作
　　　　　　辛丑线遂成辛壬丑勾股形与癸子丙
　　　　　　同度俱与甲戊丙勾股形为同式形而
　　　　　　辛壬丁勾股形又与甲戊丁勾股形为
　　　　　　同式形且丁丙与丁丑皆为两勾股形
　　　　　　之各股之较故辛丑丁三角形与甲丙
　　　　　　丁三角形亦为同式形是以丁丑与丑
　　　　　　壬之比同于丁丙与丙戊之比又丁丑

　　　　　　与丁壬之比亦同于丁丙与丁戊之比

　　　　　　也
　　　　　　又法用矩度定准坠线以定表看地平
　　　　　　游表看墙顶向后量一丈复安矩度定
　　　　　　准坠线以定表对前矩度中心游表看
　　　　　　墙顶得距地平分二十四分其中心平
　　　　　　分距分为五十分爰察前矩度距地平
　　　　　　分二十四分处得距中心距分为三十
　　　　　　分乃以所得三十分与后矩度中心平

　　　　　　分距分五十分相减馀二十分为一率
　　　　　　前矩度中心距分三十分为二率向后
　　　　　　量一丈为三率求得四率一丈五尺即
　　　　　　前矩度距墙之远若求后矩度距墙之
　　　　　　远则以后矩度中心平分距分五十分
　　　　　　为二率所得四率二丈五尺即后矩度
　　　　　　距墙之远也如图甲乙为墙之高丙为
　　　　　　前矩度中心定表所对地平为戊游表
　　　　　　看墙顶甲丙丁为向后量一丈丁为后

　　　　　　矩度中心其辛壬为游表距地平分二

　　　　　　十四分丁壬为中心平分距分五十分
　　　　　　试依后矩度距地平分二十四分辛壬
　　　　　　度于前矩度二十四分处作己庚线其
　　　　　　丙庚距中心距分得三十分乃以丙庚
　　　　　　三十分截后矩度丁壬中心平分距分
　　　　　　于癸则丁癸为减馀二十分其丁癸与
　　　　　　癸壬之比同于丁丙与丙戊之比又丁
　　　　　　癸与丁壬之比亦同于丁丙与丁戊之

　　　　　　比也
设如一石欲知其远不取直角于左右两处横量三
　十九丈测之问两处各距石几何
　　　　　　法先平安矩度于右以定表看左矩度
　　　　　　之中心游表看石得距矩度中心距分
　　　　　　三十七分五釐其游表之斜距分为六
　　　　　　十二分五釐次平安矩度于左以定表
　　　　　　看右矩度之中心游表看石得距矩度
　　　　　　中心距分十一分二釐五豪其游表之

　　　　　　斜距分为五十一分二釐五豪乃以所

　　　　　　得两距分相并得四十八分七釐五豪
　　　　　　为一率右矩度所得之游表斜距分六
　　　　　　十二分五釐为二率横量三十九丈为
　　　　　　三率求得四率五十丈为右矩度距石
　　　　　　之远若求左矩度距石之远则仍以两
　　　　　　距分相并为一率左矩度所得之游表
　　　　　　斜距分五十一分二釐五豪为二率横
　　　　　　量三十九丈为三率求得四率四十一

　　　　　　丈为左矩度距石之远也如图甲为石
　　　　　　乙为右矩度中心其丁戊为距分三十
　　　　　　七分五釐戊乙为游表斜距分六十二
　　　　　　分五釐乙丙为横量三十九丈丙为左
　　　　　　矩度中心其己庚为距分十一分二釐
　　　　　　五豪己丙为游表斜距分五十一分二
　　　　　　釐五豪试自甲角至乙丙线作甲辛垂
　　　　　　线分为两勾股形则丁戊乙勾股形与
　　　　　　甲辛乙勾股形为同式形已庚丙勾股

　　　　　　形与甲辛丙勾股形为同式形而乙丙

　　　　　　即为两勾之和故以丁戊与己庚两勾
　　　　　　相并与戊乙之比同于乙丙与甲乙之
　　　　　　比又丁戊与己庚两勾相并与己丙之
　　　　　　比同于乙丙与甲丙之比俱为相当比
　　　　　　例四率也
设如隔河一树欲测其远不能定直角爰取两处俱
　斜对树横量十七丈测之问离树之远得几何
　　　　　　法先平安矩度于一处随定表横量十

　　　　　　七丈复安一矩度(若止用一矩度则/记准一处亦可)以
　　　　　　先安矩度定表看后安矩度中心游表
　　　　　　看树得距矩度中心距分四十九分其
　　　　　　游表之斜距分为七十分次以后安矩
　　　　　　度定表看先安矩度中心游表看树得
　　　　　　距矩度中心距分十五分其游表之斜
　　　　　　距分为五十二分二釐乃以先安矩度
　　　　　　之中心距分四十九分与后安矩度之
　　　　　　中心距分十五分相减馀三十四分为

　　　　　　一率先安矩度游表斜距分七十分为

　　　　　　二率横量十七丈为三率求得四率三
　　　　　　十五丈为先安矩度距树之远若以后
　　　　　　安矩度游表斜距分五十二分二釐为
　　　　　　二率则得四率二十六丈一尺为后安
　　　　　　矩度距树之远也如图甲为树乙为先
　　　　　　安矩度中心其丁戊为距矩度中心距
　　　　　　分四十九分戊乙为游表斜距分七十
　　　　　　分乙丙为横量十七丈丙为后安矩度

　　　　　　中心其己庚为距矩度中心距分十五
　　　　　　分庚丙为游表斜距分五十二分二釐
　　　　　　按己庚十五分截丁戊四十九分于辛
　　　　　　则辛戊为减馀三十四分乃自辛至乙
　　　　　　作辛乙线与庚丙等又将乙丙线引长
　　　　　　于壬自甲作甲壬垂线遂成甲壬丙甲
　　　　　　壬乙两勾股形其乙丁辛勾股形与丙
　　　　　　己庚勾股形同度俱与甲壬丙勾股形
　　　　　　为同式形而乙丁戊勾股形又与甲壬

　　　　　　乙勾股形为同式形故乙戊辛三角形

　　　　　　与甲乙丙三角形亦为同式形是以辛
　　　　　　戊与乙戊之比同于乙丙与甲乙之比
　　　　　　而辛戊与乙辛(乙辛即与/丙庚度等)之比又同于
　　　　　　乙丙与甲丙之比也此法盖因游表视
　　　　　　线俱在对角以外故甲壬垂线所成甲
　　　　　　壬乙甲壬丙两勾股形同以甲壬为股
　　　　　　而矩度上所得之乙丁戊乙丁辛两勾
　　　　　　股形(乙丁辛即/丙己庚)亦同以乙丁为股故即

　　　　　　成两两同式形若游表视线在对角以
　　　　　　内或一在对角之内一在对角之外所
　　　　　　得距矩度中心距分不同者则须取其
　　　　　　同距矩度中心距分之度以为比例如
　　　　　　后法
设如隔河一亭欲测其远不能定直角爰取两处俱
　斜对亭横量三十丈测之问距亭之远得几何
　　　　　　法先平安矩度于一处随定表横量三
　　　　　　十丈复安一矩度以先安矩度定表看

　　　　　　后安矩度中心游表看亭得距矩度中

　　　　　　心距分二十七分其游表之斜距分为
　　　　　　五十六分八釐有馀次以后安矩度看
　　　　　　先安矩度中心游表看亭亦察距矩度
　　　　　　中心距分二十七分处得距中心距分
　　　　　　三十分其游表之斜距分为四十分三
　　　　　　釐有馀乃以所得距中心距分三十分
　　　　　　与先安矩度中心平分距分五十分相
　　　　　　减馀二十分为一率先安矩度游表斜

　　　　　　距分五十六分八釐有馀为二率横量
　　　　　　三十丈为三率求得四率八十五丈二
　　　　　　尺有馀为先安矩度距亭之远若以后
　　　　　　安矩度游表斜距分四十分三釐有馀
　　　　　　为二率则得四率六十丈四尺五寸有
　　　　　　馀为后安矩度距亭之远也如图甲为
　　　　　　亭乙为先安矩度中心其丁戊为距矩
　　　　　　度中心距分二十七分乙戊为中心平
　　　　　　分距分五十分丁乙为游表斜距分五

　　　　　　十六分八釐有馀乙丙为横量三十丈

　　　　　　丙为后安矩度中心其己庚亦为距矩
　　　　　　度中心距分二十七分丙庚为距中心
　　　　　　平分距分三十分己丙为游表斜距分
　　　　　　四十分三釐有馀按丙庚三十分截乙
　　　　　　戊中心平分距分五十分于辛则乙辛
　　　　　　为减馀二十分又自丁至辛作丁辛线
　　　　　　与己丙等又将乙丙线引长于壬自甲
　　　　　　作甲壬垂线遂成甲壬丙甲壬乙两勾

　　　　　　股形其丁戊辛勾股形与己庚丙勾股
　　　　　　形同度俱与甲壬丙勾股形为同式形
　　　　　　而丁戊乙勾股形又与甲壬乙勾股形
　　　　　　为同式形故丁乙辛三角形与甲乙丙
　　　　　　三角形亦为同式形是以乙辛与丁乙
　　　　　　之比同于乙丙与甲乙之比又乙辛与
　　　　　　丁辛(即己/丙)之比同于乙丙与甲丙之比
　　　　　　也此法盖因游表视线俱在对角以内
　　　　　　故甲壬垂线所成甲壬乙甲壬丙两勾

　　　　　　股形同以甲壬为勾而两矩度上亦取

　　　　　　与丁戊相等之己庚为勾使成两两同
　　　　　　式形然后可以为比例也
设如有塔一座欲知其高用相等两表测之问得高
　几何
　　　　　　法先立一表比人目高四尺看塔顶得
　　　　　　距分六尺又自前表向后量六丈复立
　　　　　　一表亦比人目高四尺看塔顶得距分
　　　　　　八尺乃以前距分六尺与后距分八尺

　　　　　　相减馀二尺为一率表比人目高四尺
　　　　　　为二率向后量六丈为三率求得四率
　　　　　　十二丈加表比人目之高四尺共得十
　　　　　　二丈四尺即人目以上之高也若求前
　　　　　　表距塔顶下地平之远则以两距分相
　　　　　　减之较为一率前表距分六尺为二率
　　　　　　向后量之数为三率得四率十八丈为
　　　　　　前表距塔顶下地平之远若求后表距
　　　　　　塔顶下地平之远则以后表距分八尺

　　　　　　为二率得四率二十四丈即后表距塔

　　　　　　顶下地平之远也如图甲乙为塔之高
　　　　　　丙丁与戊己为两表比人目之高四尺
　　　　　　丁目为前表距分六尺丁己为向后量
　　　　　　六丈己目为后表距分八尺试依前距
　　　　　　分丁目六尺度截后距分己目于庚则
　　　　　　庚目为减馀二尺乃自戊过丙至辛作
　　　　　　戊丙辛线又自戊至庚作戊庚线遂成
　　　　　　戊己庚勾股形与丙丁目勾股形同度

　　　　　　俱与甲辛丙勾股形为同式形而戊己
　　　　　　目勾股形又与甲辛戊勾股形为同式
　　　　　　形且丙戊与庚目皆为两勾股形之各
　　　　　　股之较故戊庚目三角形与甲丙戊三
　　　　　　角形又为同式形是以庚目与戊己之
　　　　　　比同于戊丙与甲辛之比又庚目与己
　　　　　　庚之比同于丙戊与辛丙之比庚目与
　　　　　　己目之比并同于丙戊与辛戊之比也
设如有楼一座欲知其高用不等两表测之问得高

　几何

　　　　　　法先立长表比人目高六尺看楼脊得
　　　　　　距分五尺四寸又自先立长表向后量
　　　　　　二丈立短表比人目高四尺看楼脊得
　　　　　　距分六尺四寸乃以前表比人目之高
　　　　　　六尺为一率前表距分五尺四寸为二
　　　　　　率后表比人目之高四尺为三率求得
　　　　　　四率三尺六寸为前表与后表同高所
　　　　　　得之距分爰以所得之三尺六寸与后

　　　　　　表距分六尺四寸相减馀二尺八寸为
　　　　　　一率后表比人目之高四尺为二率以
　　　　　　前表距分五尺四寸内减所得之三尺
　　　　　　六寸馀一尺八寸与两表相距二丈相
　　　　　　减馀一丈八尺二寸为三率求得四率
　　　　　　二丈六尺加后表比人目之高四尺得
　　　　　　三丈即人目以上之高也如图甲乙为
　　　　　　楼之高丙丁为前表比人目之高六尺
　　　　　　丁目为前表距分五尺四寸丁己为向

　　　　　　后量二丈戊己为后表比人目之高四

　　　　　　尺己目为后表距分六尺四寸试依后
　　　　　　表戊己度作庚辛垂线截丁目于辛则
　　　　　　辛目距分必小于丁目故丙丁与丁目
　　　　　　之比同于庚辛与辛目之比而得辛目
　　　　　　之分既得辛目则以辛目与己目相减
　　　　　　馀壬目即前后两表同高所得距分之
　　　　　　较又于两表相距丁己内减丁辛馀辛
　　　　　　己即同高两表相距之分故壬目与戊

　　　　　　己(即庚/辛)之比即同于戊庚(即辛/己)与甲癸
　　　　　　之比也

　　三角度数测量(度数测量必取资于仪器全圜/仪半圜仪象限仪虽为体不同)
　　　(其为用则一以九十度为准以定表游表/为二视线其相距之度即为所测之角)
设如一塔不知其高但知距塔之远为三十丈欲测
　其高几何
　　　　　　法以仪器定准坠线以定表看地平游
　　　　　　表看塔尖得两表相距二十四度乃以
　　　　　　二十四度与九十度相减馀六十六度
　　　　　　为对所知之角其正弦九万一千三百

　　　　　　五十五为一率仪器上二十四度为对
　　　　　　所求之角其正弦四万零六百七十四
　　　　　　为二率距塔之远三十丈为所知之边
　　　　　　为三率求得四率十三丈三尺五寸七
　　　　　　分加仪器之高即所求之塔之高也如
　　　　　　图甲乙为塔之高丙乙为距塔之远仪
　　　　　　器中心为丁丁丙为仪器中心距地之
　　　　　　高丁戊为定表所对地平为庚丁己为
　　　　　　游表看塔尖甲得两表距弧二十四度

　　　　　　为己戊其正弦为己辛其馀弦为壬己

　　　　　　与丁辛等象限九十度内减二十四度
　　　　　　馀六十六度为癸己即甲角之正弧其
　　　　　　正弦即壬己是以与壬己相等之丁辛
　　　　　　与己辛之比同于丁庚与甲庚之比为
　　　　　　相当比例四率既得甲庚加同丁丙高
　　　　　　之庚乙得甲乙即塔之高也
　　　　　　又法以半径十万为一率二十四度之
　　　　　　切线四万四千五百二十三为二率距

　　　　　　塔之远三十丈为三率求得四率十三
　　　　　　丈三尺五寸七分加仪器之高即塔之
　　　　　　高也如图己戊弧为二十四度丁戊为
　　　　　　半径壬戊为二十四度之正切故丁戊
　　　　　　与壬戊之比同于丁庚与甲庚之比为
　　　　　　相当比例四率也
设如一树欲知其远取一直角横量十五丈测之问
　得几何
　　　　　　法以仪器定游表于九十度定表看树

　　　　　　对游表立两表竿取直横量十五丈复

　　　　　　安仪器于此以定表看原处游表看树
　　　　　　得两表相距六十度乃以六十度与九
　　　　　　十度相减馀三十度为对所知之角其
　　　　　　正弦五万为一率仪器上六十度为对
　　　　　　所求之角其正弦八万六千六百零三
　　　　　　为二率横量十五丈为所知之边为三
　　　　　　率求得四率二十五丈九尺八寸即所
　　　　　　测之树之远也如图甲为树甲乙为距

　　　　　　树之远乙为所定直角丙乙为横量十
　　　　　　五丈丙为仪器中心丙丁为定表看原
　　　　　　处乙丙戊为游表看甲得两表距弧六
　　　　　　十度为戊丁其正弦为戊己馀弦为庚
　　　　　　戊与丙己等象限九十度内减六十度
　　　　　　馀三十度为辛戊即甲角之正弧其正
　　　　　　弦即庚戊是以与庚戊相等之丙己与
　　　　　　戊己之比同于丙乙与甲乙之比为相
　　　　　　当比例四率也

　　　　　　又法以半径十万为一率丙角六十度

　　　　　　之正切十七万三千二百零五为二率
　　　　　　横量十五丈为三率求得四率二十五
　　　　　　丈九尺八寸即所测之树之远也若求
　　　　　　甲丙斜距则以半径十万为一率丙角
　　　　　　六十度之正割二十万为二率横量十
　　　　　　五丈为三率求得四率三十丈即甲丙
　　　　　　斜距之远也如图戊丁弧为六十度丙
　　　　　　丁为半径己丁为六十度之正切己丙

　　　　　　为六十度之正割故丙丁与己丁之比
　　　　　　同于丙乙与甲乙之比又丙丁与己丙
　　　　　　之比同于丙乙与甲丙之比俱各为相
　　　　　　当比例四率也
设如一山欲知其高用重测之法测之退步十丈问
　山之高得几何
　　　　　　法先安仪器定准坠线以定表看地平
　　　　　　游表看山顶得两表相距五十度又退
　　　　　　行十丈复安仪器定准坠线以定表仍

　　　　　　看前仪器定表所看地平原处仍以游

　　　　　　表看山顶得两表相距四十度乃以前
　　　　　　仪器所得五十度内减后仪器所得四
　　　　　　十度馀十度为对所知之角其正弦一
　　　　　　万七千三百六十五为一率后仪器所
　　　　　　得四十度为对所求之角其正弦六万
　　　　　　四千二百七十九为二率退行十丈为
　　　　　　所知之边为三率求得四率三十七丈
　　　　　　零一寸为前仪器中心至山顶之斜距

　　　　　　次以山顶垂线与地平所成直角为对
　　　　　　所知之角其正弦即半径十万为一率
　　　　　　前仪器所得五十度为对所求之角其
　　　　　　正弦七万六千六百零四为二率前仪
　　　　　　器中心至山顶之斜距三十七丈零一
　　　　　　寸为所知之边为三率求得四率二十
　　　　　　八丈三尺五寸即所测之山之高也如
　　　　　　图甲乙为山之高丙丁为退行十丈前
　　　　　　测得丙角五十度后测得丁角四十度

　　　　　　而丙角为甲丙丁三角形之外角与丁

　　　　　　甲二内角相并之度等(解见三角形边/线角度相求卷)
　　　　　　(中/)故丙角五十度内减丁角四十度馀
　　　　　　十度即甲丙丁三角形之甲角故先用
　　　　　　甲丙丁钝角三角形求甲丙边既得甲
　　　　　　丙边然后用甲乙丙直角三角形求甲
　　　　　　乙边为山之高也
　　　　　　又法以前测所得五十度之馀切八万
　　　　　　三千九百一十与后测所得四十度之

　　　　　　馀切十一万九千一百七十五相减馀
　　　　　　三万五千二百六十五为一率半径十
　　　　　　万为二率退行十丈为三率求得四率
　　　　　　二十八丈三尺五寸即所求之山之高
　　　　　　也如图戊己为丙角之馀切即丙甲乙
　　　　　　角之正切与壬癸等庚辛为丁角之馀
　　　　　　切即丁甲乙角之正切与子癸等子壬
　　　　　　即两馀切之较甲癸与戊丙及庚丁俱
　　　　　　同为半径甲癸壬三角形与甲乙丙三

　　　　　　角形为同式形而甲癸子三角形与甲

　　　　　　乙丁三角形为同式形故甲壬子三角
　　　　　　形与甲丙丁三角形亦为同式形是以
　　　　　　子壬与甲癸之比同于丁丙与甲乙之
　　　　　　比而为相当比例四率也
设如人在山上欲测山之高但知山前有二树与山
　参直二树相距十八丈问山之高得几何
　　　　　　法于山顶安仪器定准坠线以定表向
　　　　　　空中取一平线先以游表看远树得游

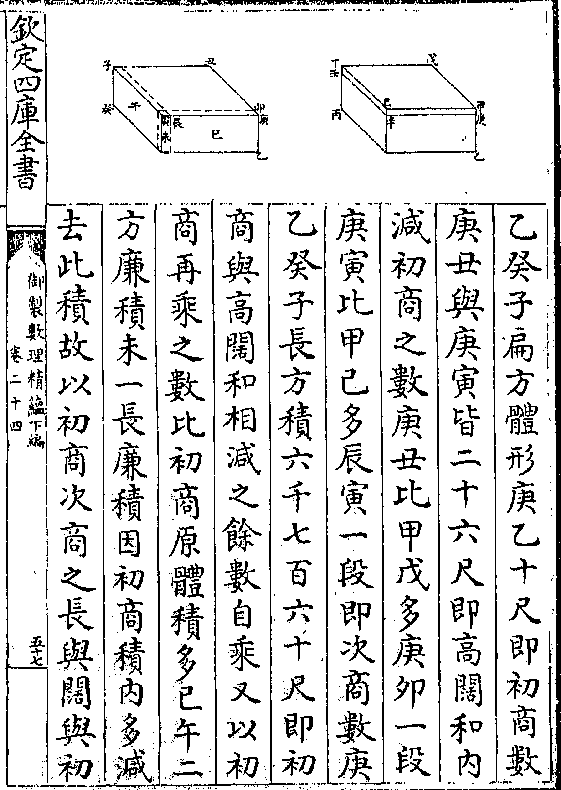　　　　　　表距垂线四十九度次以游表看近树
　　　　　　得游表距垂线三十八度乃以所得两
　　　　　　数相减馀十一度为对所知之角其正
　　　　　　弦一万九千零八十一为一率以看远
　　　　　　树所得之四十九度与九十度相减馀
　　　　　　四十一度为对所求之角其正弦六万
　　　　　　五千六百零六为二率二树相距十八
　　　　　　丈为三率求得四率六十一丈八尺九
　　　　　　寸为近树距山顶之斜距次以山顶垂

　　　　　　线与地平所成直角为对所知之角其

　　　　　　正弦即半径十万为一率以看近树所
　　　　　　得之三十八度与九十度相减馀五十
　　　　　　二度为对所求之角其正弦七万八千
　　　　　　八百零一为二率近树距山顶之斜距
　　　　　　六十一丈八尺九寸为所知之边为三
　　　　　　率求得四率四十八丈七尺七寸即所
　　　　　　测之山之高也如图甲乙为两树相距
　　　　　　十八丈丙丁为山之高甲丙丁角为看

　　　　　　远树所得之四十九度乙丙丁角为看
　　　　　　近树所得之三十八度两数相减馀十
　　　　　　一度为甲丙乙角甲丙丁角四十九度
　　　　　　与九十度相减所馀之四十一度为甲
　　　　　　角乙丙丁角三十八度与九十度相减
　　　　　　所馀之五十二度为乙角先用甲乙丙
　　　　　　钝角三角形求丙乙边既得丙乙边然
　　　　　　后用乙丙丁直角三角形求丙丁边为
　　　　　　山之高也

　　　　　　又法以先看远树所得四十九度之正

　　　　　　切十一万五千零三十七与后看近树
　　　　　　所得三十八度之正切七万八千一百
　　　　　　二十九相减馀三万六千九百零八为
　　　　　　一率半径十万为二率二树相距之十
　　　　　　八丈为三率求得四率四十八丈七尺
　　　　　　七寸即山之高也如图戊己为甲丙丁
　　　　　　角之正切庚己为乙丙丁角之正切戊
　　　　　　庚即两正切之较丙己为半径故戊庚

　　　　　　与丙己之比同于甲乙与丙丁之比而
　　　　　　为相当比例四率也
设如一石欲知其远不取直角于左右两处横量五
　十丈测之问两处各距石几何
　　　　　　法先平安仪器于左以定表看右仪器
　　　　　　之中心游表看石得两表相距七十度
　　　　　　次平安仪器于右以定表看左仪器之
　　　　　　中心游表看石得两表相距六十度乃
　　　　　　以两角度相并得一百三十度与一百

　　　　　　八十度相减馀五十度为对所知之角

　　　　　　其正弦七万六千六百零四为一率求
　　　　　　右边则以左边仪器所得七十度为对
　　　　　　所求之角其正弦九万三千九百六十
　　　　　　九为二率左右相距五十丈为所知之
　　　　　　边为三率求得四率六十一丈三尺三
　　　　　　寸为右边距石之远若求左边距石之
　　　　　　远则以右边仪器所得六十度为对所
　　　　　　求之角其正弦八万六千六百零三为

　　　　　　二率左右相距五十丈为所知之边为
　　　　　　三率求得四率五十六丈五尺三寸为
　　　　　　左边距石之远也如图甲为石乙丙为
　　　　　　左右相距五十丈乙角为左边所测七
　　　　　　十度丙角为右边所测六十度两角相
　　　　　　并与一百八十度相减得甲角五十度
　　　　　　共为甲乙丙锐角三角形盖知乙丙二
　　　　　　角及乙丙边而求甲乙边及甲丙边也
　　　　　　又法以左边仪器所得七十度之馀切

　　　　　　三万六千三百九十七与右边仪器所

　　　　　　得六十度之馀切五万七千七百三十
　　　　　　五相并得九万四千一百三十二为一
　　　　　　率右边仪器所得六十度之馀割十一
　　　　　　万五千四百三十为二率左右相距五
　　　　　　十丈为三率求得四率六十一丈三尺
　　　　　　三寸为右边距石之远若求左边距石
　　　　　　之远则以左边仪器所得七十度之馀
　　　　　　割十万六千四百一十八为二率左右

　　　　　　相距五十丈为三率求得四率五十六
　　　　　　丈五尺三寸为左边距石之远也如图
　　　　　　甲为石乙丙为左右相距五十丈乙角
　　　　　　为左边所测七十度丙角为右边所测
　　　　　　六十度试自甲至乙丙线上作甲丁垂
　　　　　　线分为甲丁乙甲丁丙两直角形戊己
　　　　　　为丙角之馀切即丁甲丙角之正切与
　　　　　　壬癸等己丙为丙角之馀割即丁甲丙
　　　　　　角之正割与甲癸等庚辛为乙角之馀

　　　　　　切即丁甲乙角之正切与壬子等庚乙

　　　　　　为乙角之馀割即丁甲乙角之正割与
　　　　　　甲子等而癸子即两馀切之和甲壬癸
　　　　　　与甲丁丙为同式形甲壬子与甲丁乙
　　　　　　为同式形故甲子癸与甲乙丙亦为同
　　　　　　式形是以癸子与甲癸之比同于丙乙
　　　　　　与甲丙之比又癸子与甲子之比同于
　　　　　　丙乙与甲乙之比皆为相当比例四率
　　　　　　也

设如隔河一树欲知其远不能定直角爰取两处俱
　斜对树横量十二丈测之问离树之远得几何
　　　　　　法平安仪器于一处随定表横量十二
　　　　　　丈复安一仪器(若止用一仪器则/记准一处亦可)以先
　　　　　　安仪器定表看后安仪器中心游表看
　　　　　　树得两表相距一百一十度次以后安
　　　　　　仪器定表看先安仪器中心游表看树
　　　　　　得两表相距四十度乃以两角度相并
　　　　　　得一百五十度与一百八十度相减馀

　　　　　　三十度为对所知之角其正弦五万为

　　　　　　一率后安仪器所得四十度为对所求
　　　　　　之角其正弦六万四千二百七十九为
　　　　　　二率横量十二丈为所知之边为三率
　　　　　　求得四率十五丈四尺二寸七分即所
　　　　　　测之树之远也如图甲为树甲乙为离
　　　　　　树之远乙丙为横量十二丈乙角为一
　　　　　　百一十度丙角为四十度两角相并与
　　　　　　一百八十度相减得甲角三十度共为

　　　　　　甲乙丙钝角三角形盖知乙丙二角及
　　　　　　乙丙边而求甲乙边也
　　　　　　又法以先安仪器所得之外角七十度
　　　　　　之馀切三万六千三百九十七与后安
　　　　　　仪器所得四十度之馀切十一万九千
　　　　　　一百七十五相减馀八万二千七百七
　　　　　　十八为一率先安仪器所得之外角七
　　　　　　十度之馀割十万六千四百一十八为
　　　　　　二率横量十二丈为三率求得四率十

　　　　　　五丈四尺二寸七分即所测之树之远

　　　　　　也如图甲为树甲乙为离树之远乙丙
　　　　　　为横量十二丈乙角为先安仪器所得
　　　　　　一百一十度丙角为后安仪器所得四
　　　　　　十度试将乙丙线引长自甲角作甲丁
　　　　　　垂线遂成甲丁乙直角三角形而甲乙
　　　　　　丁角即乙角之外角戊己为乙外角之
　　　　　　馀切即乙甲丁角之正切与壬癸等己
　　　　　　乙为乙外角之馀割即乙甲丁角之正

　　　　　　割与甲壬等庚辛为丙角之馀切即丙
　　　　　　甲丁角之正切与子癸等子壬即两馀
　　　　　　切之较甲癸壬三角形与甲丁乙三角
　　　　　　形为同式形甲癸子三角形与甲丁丙
　　　　　　三角形为同式形故甲壬子三角形与
　　　　　　甲乙丙三角形亦为同式形是以子壬
　　　　　　与甲壬之比同于丙乙与甲乙之比而
　　　　　　为相当比例四率也
设如远望一山欲知其高不得退步爰取左右两处

　横量一百丈先求斜距测之问山之高得几何

　　　　　　法以仪器斜对山顶随定表横量一百
　　　　　　丈任记一处游表看山顶得两表相距
　　　　　　八十六度五十三分又随定表横量一
　　　　　　百丈所记之处复安仪器斜对山顶以
　　　　　　定表看原处游表看山顶得两表相距
　　　　　　七十八度零七分乃以两角度相并得
　　　　　　一百六十五度与一百八十度相减馀
　　　　　　一十五度为对所知之角其正弦二万

　　　　　　五千八百八十二为一率后测所得七
　　　　　　十八度零七分为对所求之角其正弦
　　　　　　九万七千八百五十七为二率横量一
　　　　　　百丈为所知之边为三率求得四率三
　　　　　　百七十八丈零九寸为先安仪器至山
　　　　　　顶之斜距次以仪器安于原处定准坠
　　　　　　线定表看地平游表看山顶得两表相
　　　　　　距五十一度乃以山顶垂线与地平所
　　　　　　成直角为对所知之角其正弦即半径

　　　　　　十万为一率仪器所得五十一度为对

　　　　　　所求之角其正弦七万七千七百一十
　　　　　　五为二率仪器至山顶之斜距三百七
　　　　　　十八丈零九寸为所知之边为三率求
　　　　　　得四率二百九十三丈八尺三寸即所
　　　　　　测之山之高也如图甲为山顶甲乙为
　　　　　　先安仪器至山顶之斜距乙丙为横量
　　　　　　一百丈甲丙为后安仪器至山顶之斜
　　　　　　距乙角为八十六度五十三分丙角为

　　　　　　七十八度零七分两角相并与一百八
　　　　　　十度相减得甲角一十五度遂成甲乙
　　　　　　丙锐角三角形今有乙丙二角与乙丙
　　　　　　边求甲乙边即先安仪器至山顶之斜
　　　　　　距又甲丁为山之高甲乙为仪器至山
　　　　　　顶之斜距丁角即山顶垂线与地平所
　　　　　　成直角乙角为五十一度复成甲丁乙
　　　　　　直角三角形今有乙丁二角与甲乙边
　　　　　　求甲丁边即山之高也

设如人在山坡测山之高前后不得地平爰取斜坡

　前后两处相距一百丈测之问山之高得几何
　　　　　　法于山坡先安仪器定准坠线以定表
　　　　　　空取一地平以游表看山顶得两表相
　　　　　　距四十度于是向后就斜坡直量一百
　　　　　　丈复安仪器定准坠线以定表空取一
　　　　　　地平以游表看山顶得两表相距三十
　　　　　　五度又以游表看前仪器中心得两表
　　　　　　相距十三度乃以前仪器所得四十度

　　　　　　内减后仪器所得三十五度馀五度为
　　　　　　对所知之角其正弦八千七百一十六
　　　　　　为一率以前仪器所得四十度内减后
　　　　　　仪器看前仪器中心所得十三度馀二
　　　　　　十七度为对所求之外角其正弦四万
　　　　　　五千三百九十九为二率退量一百丈
　　　　　　为所知之边为三率求得四率五百二
　　　　　　十丈八尺七寸为山顶至后仪器之斜
　　　　　　距次以山顶垂线与地平所成直角为

　　　　　　对所知之角其正弦即半径十万为一

　　　　　　率后仪器所得三十五度为对所求之
　　　　　　角其正弦五万七千三百五十八为二
　　　　　　率山顶至后仪器之斜距五百二十丈
　　　　　　八尺七寸为所知之边为三率求得四
　　　　　　率二百九十八丈七尺六寸即所测之
　　　　　　山之高也如图甲乙为山之高丙丁为
　　　　　　山坡斜距一百丈甲丙戊角为前仪器
　　　　　　所得四十度甲丁乙角为后仪器所得

　　　　　　三十五度丙丁乙角为后仪器看前仪
　　　　　　器中心所得十三度若将戊丙线引长
　　　　　　至己则甲己戊角与甲丁乙角为二平
　　　　　　行线之内外角其度必等故于甲丙戊
　　　　　　角四十度内减甲丁乙角三十五度馀
　　　　　　五度为丁甲丙角(此即前题退/步两测之理)又试将
　　　　　　丁丙线引长至庚则庚丙戊角与丙丁
　　　　　　乙角亦为二平行线之内外角其度亦
　　　　　　等故于甲丙戊角四十度内减与庚丙

　　　　　　戊角相等之丙丁乙角十三度馀甲丙

　　　　　　庚角二十七度为甲丙丁钝角之外角
　　　　　　故先用甲丙丁钝角三角形求甲丁边
　　　　　　为后仪器至山顶之斜距次用甲乙丁
　　　　　　直角三角形求甲乙边为山之高也
设如东西二树欲知其相距之远测处距西树五十
　丈距东树七十丈问二树相距几何
　　　　　　法以仪器定表看东树游表看西树得
　　　　　　两表相距五十度乃以距西树五十丈

　　　　　　与距东树七十丈相加得一百二十丈
　　　　　　为一率又以五十丈与七十丈相减馀
　　　　　　二十丈为二率两表相距五十度与一
　　　　　　百八十度相减馀一百三十度为外角
　　　　　　折半得六十五度为半外角其正切二
　　　　　　十一万四千四百五十一为三率求得
　　　　　　四率三万五千七百四十二为半较角
　　　　　　之正切检表得十九度四十分与半外
　　　　　　角六十五度相减馀四十五度二十分

　　　　　　为小角与半外角六十五度相加得八

　　　　　　十四度四十分为大角既得二角则以
　　　　　　小角四十五度二十分为对所知之角
　　　　　　其正弦七万一千一百二十一为一率
　　　　　　两表相距五十度为对所求之角其正
　　　　　　弦七万六千六百零四为二率距西树
　　　　　　之远为所知之边其数五十丈为三率
　　　　　　求得四率五十三丈八尺五寸即东西
　　　　　　二树相距之远也如图甲为西树乙为

　　　　　　东树丙为仪器中心甲丙为距西树五
　　　　　　十丈乙丙为距东树七十丈丙角为两
　　　　　　表视线相距五十度今以丙角为心甲
　　　　　　丙小边为半径作一甲丁戊圜截乙丙
　　　　　　大边于戊将乙丙引长至圜界丁则丙
　　　　　　戊丙丁俱为半径与甲丙等自丁至乙
　　　　　　即两边之和自戊至乙即两边之较试
　　　　　　自甲至戊作甲戊线则成丙甲戊三角
　　　　　　形其丙甲戊与丙戊甲二角并之与甲

　　　　　　丙丁外角度等今折半用其正切即如

　　　　　　用丁戊甲角之正切故自甲至丁作甲
　　　　　　丁线即丁戊甲角之正切又戊甲乙角
　　　　　　即甲角大于丙甲戊角之较亦即乙角
　　　　　　小于丙戊甲角之较故自圜界戊至甲
　　　　　　乙边作己戊线与甲丁平行即戊甲乙
　　　　　　角之正切且乙甲丁与乙己戊为同式
　　　　　　形故两边之和乙丁与丁戊甲半外角
　　　　　　切线甲丁之比即同于两边之较乙戊

　　　　　　与半较角切线己戊之比为相当比例
　　　　　　四率也
　　　　　　又法以半径十万为一率两表相距五
　　　　　　十度之正弦七万六千六百零四为二
　　　　　　率距西树之远五十丈为三率求得四
　　　　　　率三十八丈三尺为西树至看东树视
　　　　　　线上之垂线又以半径十万为一率两
　　　　　　表相距五十度之馀弦六万四千二百
　　　　　　七十九为二率距西树之远五十丈为

　　　　　　三率求得四率三十二丈一尺四寸为

　　　　　　西树至看东树视线上垂线所分之小
　　　　　　段分边线将此数与距东树之远七十
　　　　　　丈相减馀三十七丈八尺六寸亦为西
　　　　　　树至看东树视线上垂线所分之大段
　　　　　　分边线爰以此线为勾所得垂线为股
　　　　　　求得弦五十三丈八尺五寸即东西二
　　　　　　树相距之远也如图甲乙丙三角形甲
　　　　　　为西树乙为东树丙为仪器中心甲丙

　　　　　　为距西树五十丈乙丙为距东树七十
　　　　　　丈试自甲角至乙丙视线上作甲丁垂
　　　　　　线遂分甲乙丙三角形为甲丁乙甲丁
　　　　　　丙两直角三角形先求得甲丁垂线为
　　　　　　股次求得丁丙小段分边线与乙丙相
　　　　　　减馀乙丁大段分边线为勾求得甲乙
　　　　　　弦即二树相距之远也
　　　　　　又法以距西树之远五十丈为一率距
　　　　　　东树之远七十丈为二率两表相距五

　　　　　　十度之馀割一十三万零五百四十一

　　　　　　为三率求得四率一十八万二千七百
　　　　　　五十七为西树至看东树视线上垂线
　　　　　　所分两分角之两正切之和内减两表
　　　　　　相距五十度之馀切八万三千九百一
　　　　　　十馀九万八千八百四十七为对西树
　　　　　　视线之对边角之馀切检表得四十五
　　　　　　度二十分即对西树视线之对边角乃
　　　　　　以此角度为对所知之角其正弦七万

　　　　　　一千一百二十一为一率两表相距五
　　　　　　十度为对所求之角其正弦七万六千
　　　　　　六百零四为二率距西树之远为所知
　　　　　　之边其数五十丈为三率求得四率五
　　　　　　十三丈八尺五寸即东西二树相距之
　　　　　　远也如图甲乙丙三角形甲为西树乙
　　　　　　为东树丙为仪器中心甲丙为距西树
　　　　　　五十丈乙丙为距东树七十丈丙角为
　　　　　　两表视线相距五十度试自甲角至乙

　　　　　　丙视线上作甲丁垂线遂分甲乙丙三

　　　　　　角形为甲丁乙甲丁丙两直角三角形
　　　　　　以甲角为心作一戊己庚半圜则甲丁
　　　　　　垂线平分于己两边各成一象限又与
　　　　　　乙丙平行作一辛壬线则辛己一段为
　　　　　　乙甲丁分角之正切即乙角之馀切己
　　　　　　壬一段为丙甲丁分角之正切即丙角
　　　　　　之馀切而甲壬为丙甲丁分角之正割
　　　　　　亦即丙角之馀割甲辛壬与甲乙丙两

　　　　　　三角形为同式形故甲丙边与乙丙边
　　　　　　之比同于丙角馀割甲壬(即丙甲丁分/角之正割)
　　　　　　与丙甲丁乙甲丁两分角之正切相合
　　　　　　之辛壬之比为相当比例四率既得辛
　　　　　　壬两分角之共切内减去丙甲丁分角
　　　　　　之正切己壬(即丙角/之馀切)所馀辛己为乙甲
　　　　　　丁分角之正切即为乙角之馀切检表
　　　　　　即得乙角既得乙角则用两角一边比
　　　　　　例求之而得甲乙边矣

设如南北二桥欲知其相距之远测处距南桥九十

　丈距北桥一百二十丈问二桥相距几何
　　　　　　法以仪器定表看北桥游表看南桥得
　　　　　　两表相距一百二十度乃以距南桥九
　　　　　　十丈与距北桥一百二十丈相加得二
　　　　　　百一十丈为一率又以九十丈与一百
　　　　　　二十丈相减馀三十丈为二率两表相
　　　　　　距一百二十度与一百八十度相减馀
　　　　　　六十度为外角折半得三十度为半外

　　　　　　角其正切五万七千七百三十五为三
　　　　　　率求得四率八千二百四十八为半较
　　　　　　角之正切检表得四度四十三分与半
　　　　　　外角三十度相减馀二十五度一十七
　　　　　　分为小角与半外角三十度相加得三
　　　　　　十四度四十三分为大角既得二角则
　　　　　　以小角二十五度十七分为对所知之
　　　　　　角其正弦四万二千七百零九为一率
　　　　　　两表相距一百二十度为对所求之角

　　　　　　其外角六十度之正弦八万六千六百

　　　　　　零三为二率距南桥之远为所知之边
　　　　　　其数九十丈为三率求得四率一百八
　　　　　　十二丈四尺九寸为南北二桥相距之
　　　　　　远也如图甲为南桥乙为北桥丙为仪
　　　　　　器中心甲丙为距南桥九十丈乙丙为
　　　　　　距北桥一百二十丈丙角为两表视线
　　　　　　相距一百二十度今以丙角为心甲丙
　　　　　　小边为半径作一甲丁戊圜截乙丙大

　　　　　　边于戊将乙丙引长至圜界丁则乙丁
　　　　　　为两边之和乙戊为两边之较试自甲
　　　　　　至戊作甲戊线成甲丙戊三角形其丙
　　　　　　甲戊与丙戊甲二角并之与甲丙丁外
　　　　　　角度等今折半用其正切即如用丁戊
　　　　　　甲角之正切故自甲至丁作甲丁线即
　　　　　　丁戊甲角之正切又戊甲乙角即甲角
　　　　　　大于丙甲戊角之较亦即乙角小于丙
　　　　　　戊甲角之较故自圜界戊至甲乙边作

　　　　　　己戊线与甲丁平行即戊甲乙角之正

　　　　　　切且乙甲丁与乙己戊为同式形故两
　　　　　　边之和乙丁与丁戊甲半外角切线甲
　　　　　　丁之比即同于两边之较乙戊与半较
　　　　　　角切线己戊之比为相当比例四率也
　　　　　　又法以半径十万为一率两表相距一
　　　　　　百二十度之外角六十度之正弦八万
　　　　　　六千六百零三为二率距南桥之远九
　　　　　　十丈为三率求得四率七十七丈九尺

　　　　　　四寸为南桥至看北桥视线引长虚边
　　　　　　线上之垂线又以半径十万为一率两
　　　　　　表相距一百二十度之外角六十度之
　　　　　　馀弦五万为二率距南桥之远五十丈
　　　　　　为三率求得四率四十五丈为南桥至
　　　　　　看北桥视线引长所成直角之虚边线
　　　　　　与距北桥一百二十丈相加得一百六
　　　　　　十五丈为南桥至看北桥视线引长之
　　　　　　总边线爰以此线为股所得南桥至虚

　　　　　　边之垂线为勾求得弦一百八十二丈

　　　　　　四尺八寸即南北二桥相距之远也如
　　　　　　图甲乙丙三角形甲为南桥乙为北桥
　　　　　　丙为仪器中心甲丙为距南桥九十丈
　　　　　　乙丙为距北桥一百二十丈试将乙丙
　　　　　　线引长自甲角作甲丁垂线遂成甲丁
　　　　　　丙甲丁乙两直角三角形先求得甲丁
　　　　　　垂线为勾次求得丙丁虚边线与乙丙
　　　　　　相加得乙丁总边线为股求得甲乙弦

　　　　　　即二桥相距之远也
　　　　　　又法以距南桥之远九十丈为一率距
　　　　　　北桥之远一百二十丈为二率两表相
　　　　　　距一百二十度之外角六十度之馀割
　　　　　　一十一万五千四百七十为三率求得
　　　　　　四率一十五万三千九百六十为南桥
　　　　　　至看北桥视线引长虚边线上之垂线
　　　　　　所成两分角之正切之较与两表相距
　　　　　　一百二十度之外角六十度之馀切五

　　　　　　万七十七百三十五相加得二十一万

　　　　　　一千六百九十五为对南桥视线之对
　　　　　　边角之馀切检表得二十五度十七分
　　　　　　即对南桥视线之对边角乃以此角度
　　　　　　为对所知之角其正弦四万二千七百
　　　　　　零九为一率两表相距一百二十度为
　　　　　　对所求之角其外角六十度之正弦八
　　　　　　万六千六百零三为二率距南桥之远
　　　　　　为所知之边其数九十丈为三率求得

　　　　　　四率一百八十二丈四尺九寸即南北
　　　　　　二桥相距之远也如图甲乙丙三角形
　　　　　　甲为南桥乙为北桥丙为仪器中心甲
　　　　　　丙为距南桥九十丈乙丙为距北桥一
　　　　　　百二十丈丙角为两表视线相距一百
　　　　　　二十度试将乙丙边引长自甲角作甲
　　　　　　丁垂线遂成甲丁丙甲丁乙两直角三
　　　　　　角形甲丁丙三角形之丙角即甲乙丙
　　　　　　三角形之丙角之外角其馀切戊己即

　　　　　　甲丁丙三(角/)形之甲角之正切如度辛

　　　　　　丙外角之馀割己丙即甲丁丙三角形
　　　　　　之甲角之正割如甲庚而甲乙丙三角
　　　　　　形之乙角之馀切壬癸即甲丁乙三角
　　　　　　形之甲角之正切如子辛若甲丁乙三
　　　　　　角形之乙角馀切与甲丁丙三角形之
　　　　　　丙角馀切相减即两甲角相差之较如
　　　　　　子庚甲辛庚三角形与甲丁丙三角形
　　　　　　为同式形甲辛子三角形与甲丁乙三

　　　　　　角形为同式形故甲子庚三角形与甲
　　　　　　乙丙三角形亦为同式形是以甲丙边
　　　　　　与乙丙边之比同于丙外角馀割甲庚
　　　　　　(即己/丙)与两馀切之较子庚之比为相当
　　　　　　比例四率既得子庚两馀切之较与丙
　　　　　　外角之馀切庚辛(即戊/己)相加得子辛即
　　　　　　乙角之馀切捡表得乙角既得乙角则
　　　　　　用两角一边比例求之而得甲乙边矣
设如隔河东西二树欲知其相距之远爰对一树取

　　一直角左右横量十三丈测之问二树相距几何

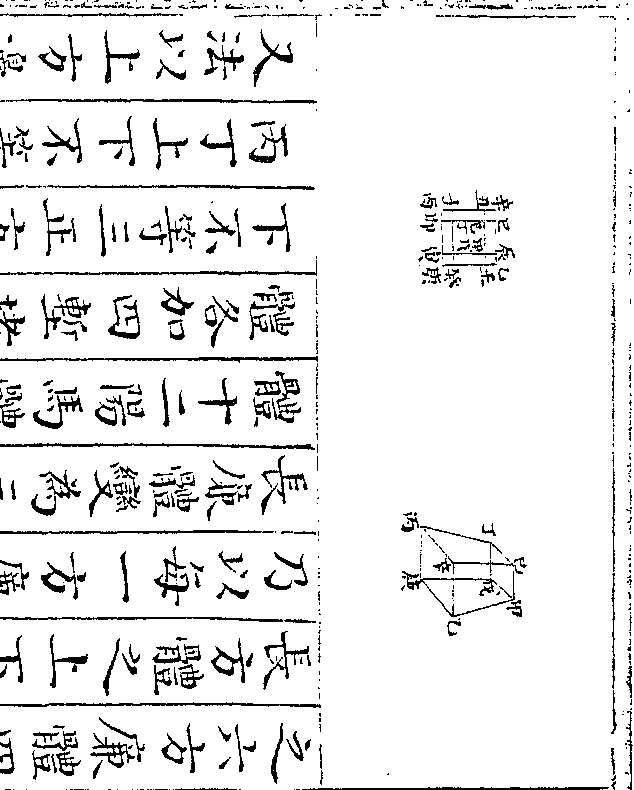　　　　　　法先对西树安仪器于右定游表于九
　　　　　　十度以定表看西树随游表横量十三
　　　　　　丈乃以游表看东树得西树视线距横
　　　　　　量边线九十度东树视线距横量边线
　　　　　　三十八度西树东树两视线相距为五
　　　　　　十二度次于直角横量十三丈处安仪
　　　　　　器于左以定表看右仪器中心游表看
　　　　　　东树得东树视线距横量边线一百一

　　　　　　十度复以游表看西树得西树视线距
　　　　　　横量边线四十五度乃先求右仪器距
　　　　　　西树之远以左仪器看西树距横量边
　　　　　　线之四十五度与九十度相减馀四十
　　　　　　五度为对所知之角其正弦七万零七
　　　　　　百一十一为一率以左仪器看西树距
　　　　　　横量边线之四十五度为对所求之角
　　　　　　其正弦七万零七百一十一为二率左
　　　　　　右横量十三丈为所知之边为三率求

　　　　　　得四率十三丈为右仪器距西树之远

　　　　　　次求右仪器距东树之远以右仪器看
　　　　　　东树距横量边线三十八度与左仪器
　　　　　　看东树距横量边线一百一十度相并
　　　　　　得一百四十八度与一百八十度相减
　　　　　　馀三十二度为对所知之角其正弦五
　　　　　　万二千九百九十二为一率以左仪器
　　　　　　看东树距横量边线一百一十度为对
　　　　　　所求之角其外角七十度之正弦九万