钦定四库全书
御制数理精蕴下编卷十
　　线部八
　　　方程(和数类变较数类法和较兼用类/和较交 类 附)

　　方程
方者比也程者式也因设数齐其分以比方之定为
已成之式凡法皆如之故曰方程盖用互乘者所以
齐其分使其首数皆同减尽而馀一法一实以得一
数也法虽有三色四色以至多色不过累乘累减亦
归于一法一实而已其二色者设二行三色者设三
行有几色者必设几行若三色设二行四色设三行
即不可算若二色设三行三色设四行则其一行又

可以不用是故解方程者又谓凡设数必成方而后
可算也然其要总在于分和较和数相比者则互乘
而相减较数相比者古人定为正负之名以辨加减
异同之号正负异号则相加正负同号则相减其理
与盈朒同盖正者为主之数负者虚比之数其始也
任以首色为正互乘众色与首色同类者皆正也与
首色异类者皆负也其继也以互乘所得之数视正
负之同异而加减之然加减之馀又有正变为负负
变为正者总之因彼此而分正负由多少而成虚实

互乘之后任以一层为主凡异号相加者悉依本层

其号皆不变也若同号相减者本层多其号亦不变
本层少反减者则正变为负负变为正盖此多则彼
少彼少则此多也至于首色减尽则第二色即为首
色故加减之后首色为负者悉变之以便互乘加减
始不淆也今定为例和数者不用正负之号较数者
则用正负之号和较兼用者和仍不用正负之号而
较则用之和较交变者则随其法而辨别之以定其
号焉或有非方程之本法而可以方程算者则又别

为设问以附其后古人所谓以御错糅正负者庶乎
尽于此矣
　　和数类
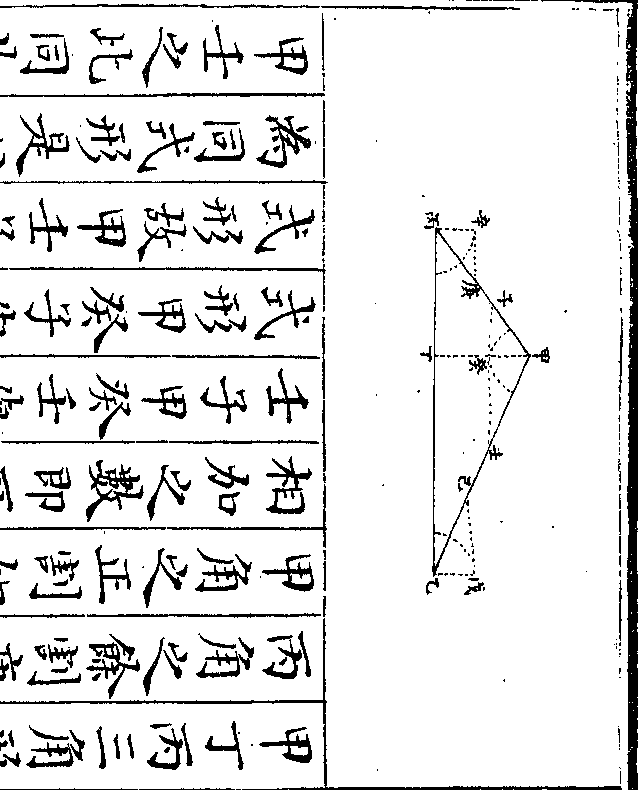
设如马四匹牛六头共价四十八两马三匹牛五头
　共价三十八两问马牛各价几何
　　　　　法以马四匹牛六头共价四十八两列
　　　　　于上马三匹牛五头共价三十八两列
　　　　　于下乃以上马四匹遍乘下马三匹牛
　　　　　五头价银三十八两得马十二匹牛二

　　　　　十头价银一百五十二两又以下马三

　　　　　匹遍乘上马四匹牛六头价银四十八
　　　　　两得马十二匹牛十八头价银一百四
　　　　　十四两两下相较则马各十二匹彼此
　　　　　减尽牛二十头内减十八头馀二头价
　　　　　银一百五十二两内减一百四十四两
　　　　　馀八两爰以馀牛二头除馀银八两得
　　　　　四两即牛每头之价以牛五头乘之得
　　　　　二十两为牛五头之共价于马牛共价

　　　　　三十八两内减去二十两馀十八两为
　　　　　马三匹之共价以马三匹除之得六两
　　　　　即马每匹之价也此法盖以首色二数
　　　　　遍乘各数使其分数齐等即互乘齐分
　　　　　之理故马四匹遍乘马三匹牛五头价
　　　　　银三十八两则为各增四倍马三匹遍
　　　　　乘马四匹牛六头价银四十八两则为
　　　　　各增三倍两下各色既俱各增倍分则
　　　　　其比例皆同是故马两下相平而减尽

　　　　　无馀牛两下相减馀二头价银两下相

　　　　　减馀八两是为相当之数盖一百五十
　　　　　二两内减去一百四十四两即减去马
　　　　　十二匹牛十八头之共价而所馀之八
　　　　　两为牛二头之价也
　　　　　又如以牛数列于前马数列于后则先
　　　　　得马价法以牛六头马四匹共价四十
　　　　　八两列于上牛五头马三匹共价三十
　　　　　八两列于下乃以下牛五头遍乘上牛

　　　　　六头马四匹价银四十八两得牛三十
　　　　　头马二十匹价银二百四十两又以上
　　　　　牛六头遍乘下牛五头马三匹价银三
　　　　　十八两得牛三十头马十八匹价银二
　　　　　百二十八两两下相较则牛各三十头
　　　　　彼此减尽马二十匹内减十八匹馀二
　　　　　匹价银二百四十两内减二百二十八
　　　　　两馀十二两爰以馀马二匹除馀银十
　　　　　二两得六两即马每匹之价以马三匹

　　　　　乘之得十八两为马三匹之共价于牛

　　　　　马共价三十八两内减去十八两馀二
　　　　　十两为牛五头之共价以牛五头除之
　　　　　得四两即牛每头之价也此法用互乘
　　　　　后则牛两下相平而减尽无馀马两下
　　　　　相减馀二匹价银两下相减馀十二两
　　　　　即为相当之数盖二百四十两内减去
　　　　　二百二十八两即减去牛三十头马十
　　　　　八匹之共价而所馀之十二两为马二

　　　　　匹之价也大凡方程之法各色俱可以
　　　　　更互相求者皆如此类也
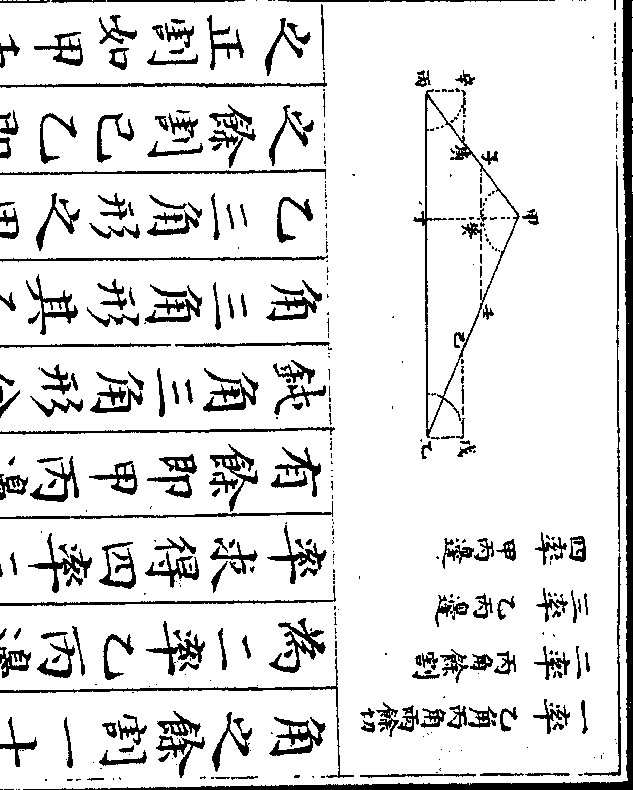
设如缎二疋纱六疋䌷八疋共价八十四两缎一疋
　纱四疋䌷七疋共价六十两缎三疋纱五疋䌷九
　疋共价九十两问缎纱䌷各价几何
　　　　　法先以缎二疋纱六疋䌷八疋共价八
　　　　　十四两列于上缎一疋纱四疋䌷七疋
　　　　　共价六十两列于下乃以上缎二疋遍
　　　　　乘下缎一疋纱四疋䌷七疋价银六十

　　　　　两得缎二疋纱八疋䌷十四疋价银一

　　　　　百二十两又以下缎一疋遍乘上缎二
　　　　　疋纱六疋䌷八疋价银八十四两仍得
　　　　　原数两下相较则缎各二疋彼此减尽
　　　　　纱八疋内减六疋馀二疋䌷十四疋内
　　　　　减八疋馀六疋价银一百二十两内减
　　　　　八十四两馀三十六两即为纱二疋䌷
　　　　　六疋价银三十六两也(缎既两下相平/而减尽无馀则)
　　　　　(所馀纱二疋䌷六疋价银三十六两即/为相当之数盖一百二十两内减去八)

　　　　　(十四两即减去缎二疋纱六疋䌷八疋/之共价而所馀三十六两为纱二疋䌷)
　　　　　(六疋之/共价也)次以缎一疋纱四疋䌷七疋价
　　　　　银六十两列于上缎三疋纱五疋䌷九
　　　　　疋价银九十两列于下乃以下缎三疋
　　　　　遍乘上缎一疋纱四疋䌷七疋价银六
　　　　　十两得缎三疋纱十二疋䌷二十一疋
　　　　　价银一百八十两又以上缎一疋遍乘
　　　　　下缎三疋纱五疋䌷九疋价银九十两
　　　　　仍得原数两下相较则缎各三疋彼此

　　　　　减尽纱十二疋内减五疋馀七疋䌷二

　　　　　十一疋内减九疋馀十二疋价银一百
　　　　　八十两内减九十两馀九十两即为纱
　　　　　七疋䌷十二疋价银九十两也(缎既两/下相平)
　　　　　(而减尽无馀则所馀纱七疋䌷十二疋/价银九十两即为相当之数盖一百八)
　　　　　(十两内减九十两即减缎三疋纱五疋/䌷九疋之共价而所馀九十两为纱七)
　　　　　(疋䌷十二疋/之共价也)于是将两次所得之馀作
　　　　　二色方程算之其纱二疋䌷六疋价银
　　　　　三十六两列于上纱七疋䌷十二疋价

　　　　　银九十两列于下以下纱七疋遍乘上
　　　　　纱二疋䌷六疋价银三十六两得纱十
　　　　　四疋䌷四十二疋价银二百五十二两
　　　　　以上纱二疋遍乘下纱七疋䌷十二疋
　　　　　价银九十两得纱十四疋䌷二十四疋
　　　　　价银一百八十两两下相较则纱各十
　　　　　四疋彼此减尽䌷四十二疋内减二十
　　　　　四疋馀十八疋价银二百五十二两内
　　　　　减一百八十两馀七十二两爰以馀䌷

　　　　　十八疋除馀银七十二两得四两即䌷

　　　　　每疋之价以䌷六疋乘之得二十四两
　　　　　为䌷六疋之共价于纱䌷共价三十六
　　　　　两内减二十四两馀十二两为纱二疋
　　　　　之共价以纱二疋除之得六两即纱每
　　　　　疋之价也以缎二疋纱六疋䌷八疋共
　　　　　价八十四两计之则纱六疋共价三十
　　　　　六两䌷八疋共价三十二两纱䌷共价
　　　　　为六十八两于共价八十四两内减六

　　　　　十八两馀十六两为缎二疋之共价以
　　　　　缎二疋除之得八两即缎每疋之价也
设如有上中下三等人户纳粮上等五户中等十二
　户下等三户共纳粮一石二斗六升又上等四户
　二等二户共纳粮五斗二升又中等二十户下等
　二十五户共纳粮一石五斗问上中下三等每户
　各纳粮几何
　　　　　法先以上等五户中等十二户下等三
　　　　　户纳粮一石二斗六升列于上上等四

　　　　　户(因无中等故作空位以/存其分馀仍对位列之)下等二户纳

　　　　　粮五斗二升列于下乃以下层上等四
　　　　　户遍乘上层上等五户中等十二户下
　　　　　等三户纳粮一石二斗六升得上等二
　　　　　十户中等四十八户下等十二户纳粮
　　　　　五石零四升又以上层上等五户遍乘
　　　　　下层上等四户下等二户纳粮五斗二
　　　　　升得上等二十户下等十户纳粮二石
　　　　　六斗两下相较则上等各二十户彼此

　　　　　减尽中等四十八户无可减仍得四十
　　　　　八户下等十二户内减十户馀二户纳
　　　　　粮五石零四升内减二石六斗馀二石
　　　　　四斗四升即为中等四十八户下等二
　　　　　户共纳粮二石四斗四升也(上等既两/下相平而)
　　　　　(减尽无馀则所馀中等四十八户下等/二户纳粮二石四斗四升即为相当之)
　　　　　(数盖五石零四升内减二石六斗即减/去上等二十户下等十户之共粮数而)
　　　　　(所馀二石四斗四升为中等四/十八户下等二户之共粮数也)既得中
　　　　　等四十八户下等二户之二色则中等

　　　　　二十户下等二十五户亦即为二色故

　　　　　即作二色方程算之其中等四十八户
　　　　　下等二户纳粮二石四斗四升列于上
　　　　　中等二十户下等二十五户纳粮一石
　　　　　五斗列于下乃以上层中等四十八户
　　　　　遍乘下层中等二十户下等二十五户
　　　　　纳粮一石五斗得中等九百六十户下
　　　　　等一千二百户纳粮七十二石又以下
　　　　　层中等二十户遍乘上层中等四十八

　　　　　户下等二户纳粮二石四斗四升得中
　　　　　等九百六十户下等四十户纳粮四十
　　　　　八石八斗两下相较则中等各九百六
　　　　　十户彼此减尽下等一千二百户内减
　　　　　四十户馀一千一百六十户纳粮七十
　　　　　二石内减四十八石八斗馀二十三石
　　　　　二斗爰以所馀下等一千一百六十户
　　　　　除馀粮二十三石二斗得二升即下等
　　　　　每户纳粮之数以下等二户乘之得四

　　　　　升为下等二户纳粮之共数于中等下

　　　　　等共纳粮二石四斗四升内减四升馀
　　　　　二石四斗为中等四十八户纳粮之共
　　　　　数以中等四十八户除之得五升即中
　　　　　等每户纳粮之数以上等四户下等二
　　　　　户共纳粮五斗二升计之(因无中户/故省一次)则
　　　　　下等二户共纳粮四升于五斗二升内
　　　　　减四升馀四斗八升为上等四户纳粮
　　　　　之共数以上等四户除之得一斗二升

　　　　　即上等每户纳粮之数也
设如有银赏四等人各不知数只云一等一人二等
　二人三等三人四等四人共赏银三十两又一等
　二人二等三人三等四人四等五人共赏银四十
　四两又一等四人二等五人三等七人四等八人
　共赏银七十七两又一等六人二等五人三等四
　人四等二人共赏银六十六两问每等人各赏银
　几何
　　　　　法先以一等一人二等二人三等三人

　　　　　四等四人共银三十两列于上一等二

　　　　　人二等三人三等四人四等五人共银
　　　　　四十四两列于下乃以下一等二人遍
　　　　　乘上一等一人二等二人三等三人四
　　　　　等四人共银三十两得一等二人二等
　　　　　四人三等六人四等八人共银六十两
　　　　　又以上一等一人遍乘下一等二人二
　　　　　等三人三等四人四等五人共银四十
　　　　　四两仍得原数两下相较则一等各二

　　　　　人彼此减尽二等两下相减馀一人三
　　　　　等两下相减馀二人四等两下相减馀
　　　　　三人共银两下相减馀一十六两即二
　　　　　等一人三等二人四等三人共银十六
　　　　　两也(盖六十两内减四十四两即减去/一等二人二等三人三等四人四)
　　　　　(等五人之共银数故所馀之十六两为/二等一人三等二人四等三人之共银)
　　　　　(数/也)次以一等二人二等三人三等四人
　　　　　四等五人共银四十四两列于上一等
　　　　　四人二等五人三等七人四等八人共

　　　　　银七十七两列于下乃以下一等四人

　　　　　遍乘上一等二人二等三人三等四人
　　　　　四等五人共银四十四两得一等八人
　　　　　二等十二人三等十六人四等二十人
　　　　　共银一百七十六两又以上一等二人
　　　　　遍乘下一等四人二等五人三等七人
　　　　　四等八人共银七十七两得一等八人
　　　　　二等十人三等十四人四等十六人共
　　　　　银一百五十四两两下相较则一等各

　　　　　八人彼此减尽二等两下相减馀二人
　　　　　三等两下相减馀二人四等两下相减
　　　　　馀四人共银两下相减馀二十二两即
　　　　　二等二人三等二人四等四人共银二
　　　　　十二两也(盖一百七十六两内减一百/五十四两即减去一等八人)
　　　　　(二等十人三等十四人四等十六人之/共银数故所馀之二十二两为二等二)
　　　　　(人三等二人四等/四人之共银数也)次以一等四人二等
　　　　　五人三等七人四等八人共银七十七
　　　　　两列于上一等六人二等五人三等四

　　　　　人四等二人共银六十六两列于下乃

　　　　　以下一等六人遍乘上一等四人二等
　　　　　五人三等七人四等八人共银七十七
　　　　　两得一等二十四人二等三十人三等
　　　　　四十二人四等四十八人共银四百六
　　　　　十二两又以上一等四人遍乘下一等
　　　　　六人二等五人三等四人四等二人共
　　　　　银六十六两得一等二十四人二等二
　　　　　十人三等十六人四等八人共银二百

　　　　　六十四两两下相较则一等各二十四
　　　　　人彼此减尽二等两下相减馀十人三
　　　　　等两下相减馀二十六人四等两下相
　　　　　减馀四十人共银两下相减馀一百九
　　　　　十八两即二等十人三等二十六人四
　　　　　等四十人共银一百九十八两也(盖四/百六)
　　　　　(十二两内减二百六十四两即减去一/等二十四人二等二十人三等十六人)
　　　　　(四等八人之共银数故所馀之一百九/十八两为二等十人三等二十六人四)
　　　　　(等四十人之/共银数也)于是将三次所得之馀作

　　　　　三色方程算之先以二等一人三等二

　　　　　人四等三人共银十六两列于上二等
　　　　　二人三等二人四等四人共银二十二
　　　　　两列于下乃以下二等二人遍乘上二
　　　　　等一人三等二人四等三人共银十六
　　　　　两得二等二人三等四人四等六人共
　　　　　银三十二两又以上二等一人遍乘下
　　　　　二等二人三等二人四等四人共银二
　　　　　十二两仍得原数两下相较则二等各

　　　　　二人彼此减尽三等两下相减馀二人
　　　　　四等两下相减馀二人共银两下相减
　　　　　馀十两即三等二人四等二人共银十
　　　　　两也(盖三十二两内减二十二两即减/去二等二人三等二人四等四人)
　　　　　(之共银数故所馀之十两为三/等二人四等二人之共银数也)次以二
　　　　　等二人三等二人四等四人共银二十
　　　　　二两列于上二等十人三等二十六人
　　　　　四等四十人共银一百九十八两列于
　　　　　下乃以下二等十人遍乘上二等二人

　　　　　三等二人四等四人共银二十二两得

　　　　　二等二十人三等二十人四等四十人
　　　　　共银二百二十两又以上二等二人遍
　　　　　乘下二等十人三等二十六人四等四
　　　　　十人共银一百九十八两得二等二十
　　　　　人三等五十二人四等八十人共银三
　　　　　百九十六两两下相较则二等各二十
　　　　　人彼此减尽三等两下相减馀三十二
　　　　　人四等两下相减馀四十人共银两下

　　　　　相减馀一百七十六两即三等三十二
　　　　　人四等四十人共银一百七十六两也
　　　　　(盖三百九十六两内减二百二十两即/减去二等二十人三等二十人四等四)
　　　　　(十人之共银数故所馀之一百七十六/两为三等三十二人四等四十人之共)
　　　　　(银数也此间两层相减虽下层数多/于上层然俱系反减故不用变号)于
　　　　　是又将两次所得之馀作二色方程算
　　　　　之其三等二人四等二人共银十两列
　　　　　于上三等三十二人四等四十人共银
　　　　　一百七十六两列于下乃以下三等三

　　　　　十二人遍乘上三等二人四等二人共

　　　　　银十两得三等六十四人四等六十四
　　　　　人共银三百二十两又以上三等二人
　　　　　遍乘下三等三十二人四等四十人共
　　　　　银一百七十六两得三等六十四人四
　　　　　等八十人共银三百五十二两两下相
　　　　　较则三等各六十四人彼此减尽四等
　　　　　两下相减馀十六人共银两下相减馀
　　　　　三十二两即四等十六人之共银数以

　　　　　四等十六人除之得二两即四等每一
　　　　　人所应得之数也以四等二人因之得
　　　　　四两为四等二人之共银数于三等二
　　　　　人四等二人共银十两内减之馀六两
　　　　　为三等二人之共银数以三等二人除
　　　　　之得三两即三等每一人所应得之数
　　　　　也以二等一人三等二人四等三人共
　　　　　银十六两计之则三等二人应得六两
　　　　　四等三人应得六两共十二两于共银

　　　　　十六两内减之馀四两即二等每一人

　　　　　所应得之数也再以一等一人二等二
　　　　　人三等三人四等四人共银三十两计
　　　　　之则二等二人应得八两三等三人应
　　　　　得九两四等四人应得八两共二十五
　　　　　两于共银三十两内减之馀五两即一
　　　　　等每一人所应得之数也
　　较数类
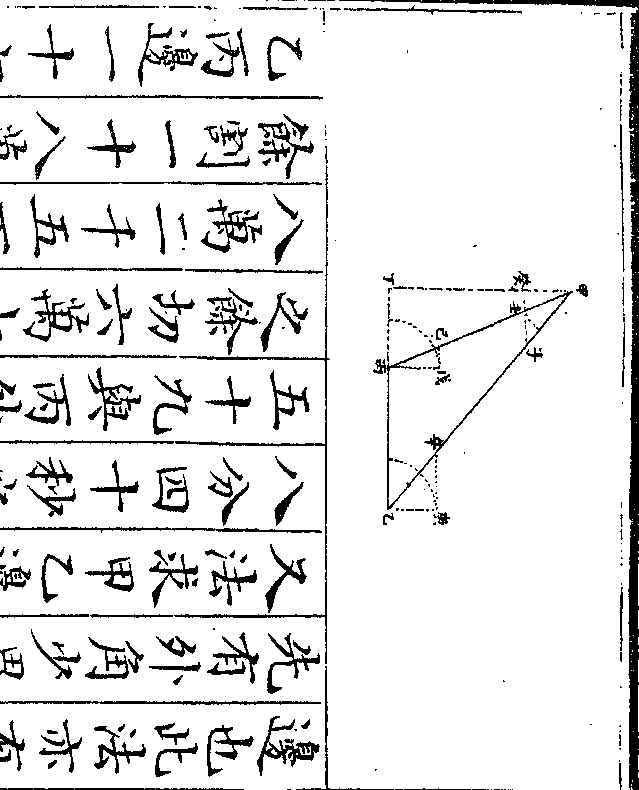
设如砚七方比笔三枝价多四百八十文又砚三方

　比笔九枝价少一百八十文问砚笔价各若干
　　　　　法以砚七为正笔三为负价多四百八
　　　　　十文为正(多为砚比笔之所多/与砚同类故亦为正)列于上
　　　　　又以砚三为正笔九为负价少一百八
　　　　　十文为负(少为砚比笔之所少即为笔/比砚之所多与笔同类故亦)
　　　　　(为/负)列于下乃以下砚三遍乘上砚七笔
　　　　　三价多四百八十文得砚二十一为正
　　　　　笔九为负价多一千四百四十文为正
　　　　　又以上砚七遍乘下砚三笔九价少一

　　　　　百八十文得砚二十一为正笔六十三

　　　　　为负价少一千二百六十文为负两下
　　　　　相较则砚各二十一彼此减尽笔九枝
　　　　　与六十三枝两层皆负故相减馀五十
　　　　　四枝价多一千四百四十文与少一千
　　　　　二百六十文一正一负故相加得二千
　　　　　七百文乃笔五十四枝之共价以减馀
　　　　　笔五十四除之得五十文即笔每一枝
　　　　　之价以三因之得一百五十文为笔三

　　　　　枝之共价与砚多四百八十文相加得
　　　　　六百三十文为砚七方之共价以砚七
　　　　　除之得九十文即砚每一方之价也此
　　　　　法用互乘则上层为砚二十一方比笔
　　　　　九枝价多一千四百四十文下层为砚
　　　　　二十一方比笔六十三枝价少一千二
　　　　　百六十文夫砚既皆二十一方则其共
　　　　　价必相等然比笔九枝之价则多比笔
　　　　　六十三枝之价则少是多与少相加之

　　　　　二千七百文即笔九枝与笔六十三枝

　　　　　相差之五十四枝之价也笔五十四枝
　　　　　共价为二千七百文则笔一枝价五十
　　　　　文而笔三枝价为一百五十文矣砚七
　　　　　方比笔三枝价既多四百八十文则于
　　　　　一百五十文加四百八十文共六百三
　　　　　十文即砚七方之共价故以砚七除之
　　　　　得九十文为砚每一方之价也
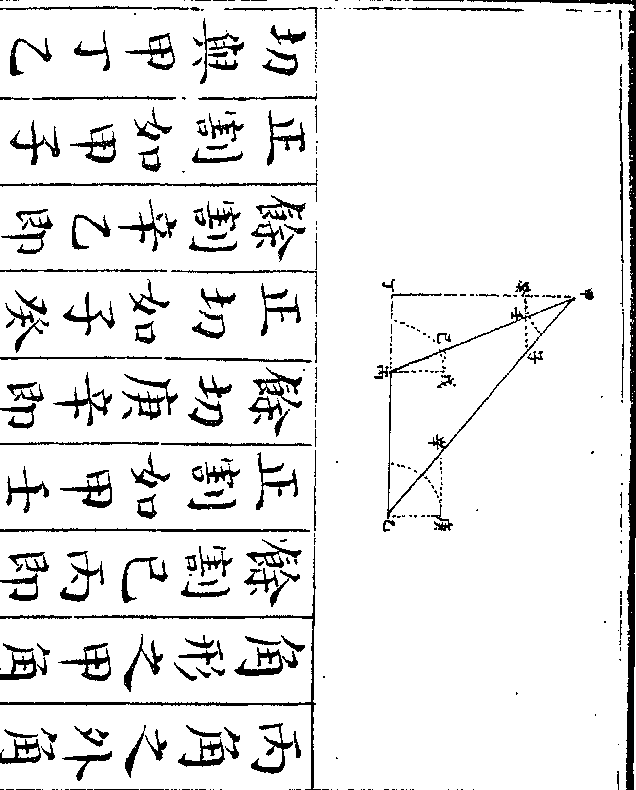
设如有甲丙二马群各不知数只云甲三群比丙二

　群多一千五百三十匹甲二群与丙七群相等问
　甲丙每群马数各几何
　　　　　法以甲三群为正丙二群为负多一千
　　　　　五百三十匹为正列于上又以甲二群
　　　　　为正丙七群为负相等作一空位(相等/无数)
　　　　　(可列故作一/○以存其位)列于下乃以下甲二群遍
　　　　　乘上甲三群丙二群多一千五百三十
　　　　　匹得甲六群仍为正丙四群仍为负多
　　　　　三千零六十匹亦仍为正又以上甲三

　　　　　群遍乘下甲二群丙七群得甲六群仍

　　　　　为正丙二十一群为负相等无可乘亦
　　　　　仍为空位两下相较则甲各六群彼此
　　　　　减尽丙四群与丙二十一群两层皆负
　　　　　故相减馀十七群多三千零六十匹与
　　　　　相等无可加减仍得三千零六十匹乃
　　　　　丙十七群之共数以减馀丙十七群除
　　　　　之得一百八十匹为丙每群之数七因
　　　　　之得一千二百六十匹为丙七群之共

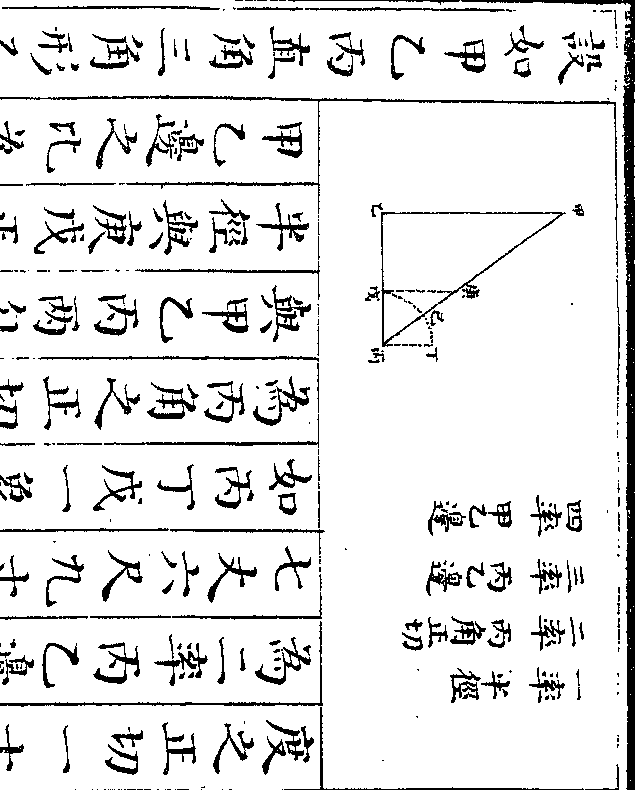　　　　　数甲二群既与丙七群相等则一千二
　　　　　百六十匹亦即为甲二群之共数以甲
　　　　　二群除之得六百三十匹即甲每群之
　　　　　数也此法用互乘则上层为甲六群比
　　　　　丙四群多三千零六十匹下层为甲六
　　　　　群与丙二十一群相等甲六群既与丙
　　　　　二十一群相等则丙二十一群比丙四
　　　　　群多三千零六十匹两下各减丙四群
　　　　　则为丙十七群共马三千零六十匹矣

　　　　　丙十七群既为共马三千零六十匹则

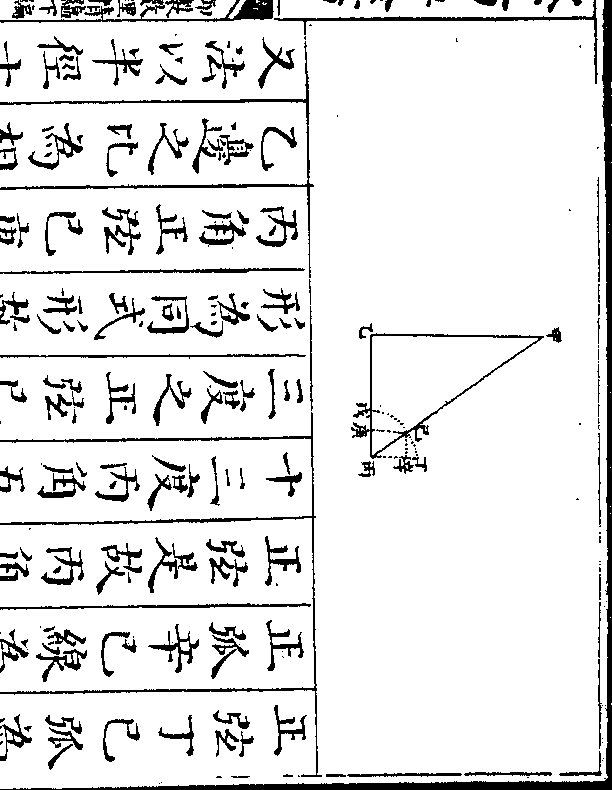　　　　　丙一群得马一百八十匹而丙七群为
　　　　　马一千二百六十匹甲二群既与丙七
　　　　　群相等则一千二百六十匹用甲二群
　　　　　除之得六百三十匹即甲每群之数也
设如有钱买桃蘋果梨三色各不知价只云桃三个
　比蘋果二个梨二个价多二十四文桃二个梨三
　个比蘋果五个价少十二文桃四个蘋果三个比
　梨八个价多一百零八文问桃蘋果梨各价几何

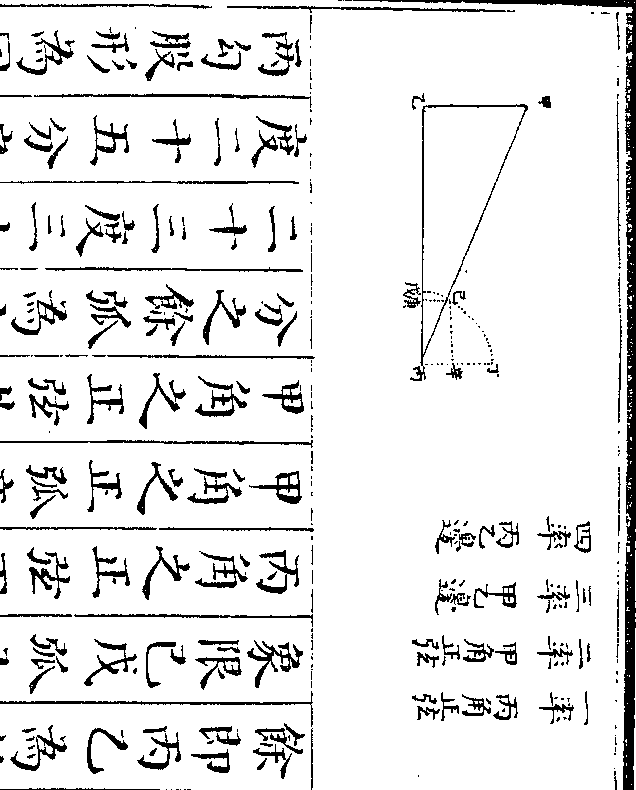　　　　　法先以桃三为正蘋果二梨二为负价
　　　　　多二十四文为正列于上又以桃二为
　　　　　正蘋果五为负梨三为正价少十二文
　　　　　为负列于下乃以下桃二遍乘上桃三
　　　　　蘋果二梨二价多工十四文得桃六仍
　　　　　为正蘋果四为负梨四为负价多四十
　　　　　八文为正(即桃六比蘋果四梨四价多/四十八文比原数加二倍)
　　　　　又以上桃三遍乘下桃二蘋果五梨三
　　　　　价少十二文得桃六仍为正蘋果十五

　　　　　为负梨九为正价少三十六文为负(即/桃)

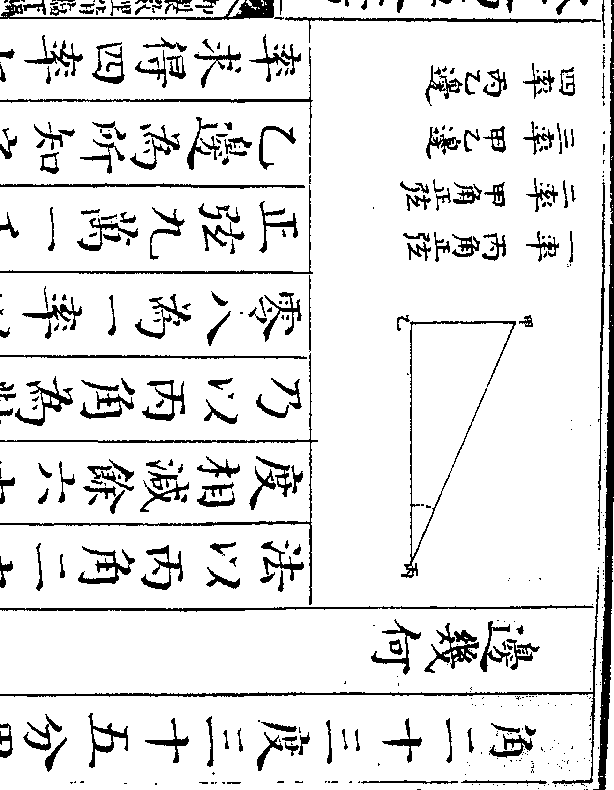　　　　　(六梨九比蘋果十五价少/三十六文比原数加三倍)于是任以上
　　　　　层为主两下相较则桃各六彼此减尽
　　　　　蘋果两层皆负故相减馀十一本层少
　　　　　反减故变负为正且为首一色减尽其
　　　　　次一色即转而为首故亦变负为正梨
　　　　　一正一负故相加得十三仍依本层为
　　　　　负多四十八文与少三十六文相加得
　　　　　八十四文仍依本层为正即为蘋果十

　　　　　一比梨十三价多三十四文也(盖桃彼/此减尽)
　　　　　(蘋果上层少四下层少十五是下层比/上层所少为十一即上层比下层多十)
　　　　　(一也梨上层少四下层多九下之所多/即上之所少是上层比下层少十三也)
　　　　　(钱上层多四十八文下层少三十六文/下之所少即上之所多是上层比下层)
　　　　　(多八十四文也蘋果多十一梨少十三/钱即多八十四文故为蘋果十一比梨)
　　　　　(十三价多八/十四文也)复以桃二为正蘋果五为
　　　　　负梨三为正价少十二文为负列于上
　　　　　又以桃四蘋果三为正梨八为负价多
　　　　　一百零八文为正列于下乃以上桃二

　　　　　遍乘下桃四蘋果三梨八价多一百零

　　　　　八文得桃八仍为正蘋果六亦仍为正
　　　　　梨十六为负价多二百一十六文为正
　　　　　(即桃八蘋果六比梨十六价多/二百一十六文比原数加二倍)又以下
　　　　　桃四遍乘上桃二蘋果五梨三价少十
　　　　　二文得桃八仍为正蘋果二十为负梨
　　　　　十二为正价少四十八文为负(即桃八/梨十二)
　　　　　(比蘋果二十价少四十/八文比原数加四倍)于是仍以上层
　　　　　为主两下相较则桃各八彼此减尽蘋

　　　　　果一正一负故相加得二十六仍依本
　　　　　层为正梨一正一负故相加得二十八
　　　　　仍依本层为负多二百一十六文与少
　　　　　四十八文相加得二百六十四文亦仍
　　　　　依本层为正即为蘋果二十六比梨二
　　　　　十八价多二百六十四文也(盖桃彼此/减尽蘋果)
　　　　　(上层多六下层少二十下之所少即上/之所多是上层比下层多二十六也梨)
　　　　　(上层少十六下层多十二下之所多即/上之所少是上层比下层少二十八也)
　　　　　(钱上层多二百一十六文下层少四十/八文下之所少即上之所多是上层比)

　　　　　(下层多二百六十四文也蘋果多二十/六梨少二十八钱即多二百六十四文)

　　　　　(故为蘋果二十六比梨二十/八价多二百六十四文也)爰将两次
　　　　　所得之馀作二色方程算之其蘋果十
　　　　　一为正梨十三为负价多八十四文为
　　　　　正列于上蘋果二十六为正梨二十八
　　　　　为负价多二百六十四文为正列于下
　　　　　乃以上蘋果十一遍乘下蘋果二十六
　　　　　梨二十八价多二百六十四文得蘋果
　　　　　二百八十六为正梨三百零八为负价

　　　　　多二千九百零四文为正(即蘋果二百/八十六比梨)
　　　　　(三百零八价多二千九百/零四文比原数加十一倍)又以下蘋果
　　　　　二十六遍乘上蘋果十一梨十三价多
　　　　　八十四文得蘋果二百八十六为正梨
　　　　　三百三十八为负价多二千一百八十
　　　　　四文为正(即蘋果二百八十六比梨三/百三十八价多二千一百八)
　　　　　(十四文比原数/加二十六倍)两下相较则蘋果各二
　　　　　百八十六彼此减尽梨两层皆负故相
　　　　　减馀三十两多数相同故亦相减馀七

　　　　　百二十文乃梨三十之共价(盖蘋果皆/二百八十)

　　　　　(六则其共价必相等然比梨三百三十/八之价则多二千一百八十四文比梨)
　　　　　(三百零八之价则多二千九百零四文/是两多相差之七百二十文即梨相差)
　　　　　(三十之/共价也)以梨三十除之得二十四文即
　　　　　梨每个之价以梨十三乘之得三百一
　　　　　十二文为梨十三之共价蘋果十一既
　　　　　比梨十三价多八十四文则于三百一
　　　　　十二文加八十四文得三百九十六文
　　　　　为蘋果十一之共价以十一除之得三

　　　　　十六文即蘋果每个之价以桃三比蘋
　　　　　果二梨二价多二十四文计之则梨二
　　　　　价四十八文蘋果二价七十二文共价
　　　　　一百二十文加桃三多二十四文共一
　　　　　百四十四文即为桃三之共价以三除
　　　　　之得四十八文即桃每个之价也
设如有银买铜锡铅铁各不知价只云铜三斤比锡
　二斤铅二斤铁四斤价多一钱又铜二斤铅一斤
　比锡二斤铁二斤价多二钱又铜一斤锡二斤与

　铅三斤铁八斤价相等又铜五斤铁三十斤比锡

　四斤铅二十四斤价少二钱问铜锡铅铁各价几
　何
　　　　　法先以铜三斤为正锡二斤铅二斤铁
　　　　　四斤俱为负价多一钱为正列于上又
　　　　　铜二斤为正锡二斤为负铅一斤为正
　　　　　铁二斤为负价多二钱为正列于下乃
　　　　　以下铜二斤遍乘上铜三斤锡二斤铅
　　　　　二斤铁四斤价多一钱得铜六斤为正

　　　　　锡四斤铅四斤铁八斤俱为负价多二
　　　　　钱为正又以上铜三斤遍乘下铜二斤
　　　　　锡二斤铅一斤铁二斤价多二钱得铜
　　　　　六斤为正锡六斤为负铅三斤为正铁
　　　　　六斤为负价多六钱为正于是以上层
　　　　　为主两下相较则铜各六斤彼此减尽
　　　　　锡两层皆负故相减馀二斤本层少乃
　　　　　变负为正铅一正一负故相加得七斤
　　　　　仍依本层为负铁两层皆负故亦相减

　　　　　馀二斤仍依本层为负价两层皆正故

　　　　　亦相减馀四钱本层少乃变正为负即
　　　　　锡二斤比铅七斤铁二斤价少四钱也
　　　　　(盖铜彼此减尽锡上层少四斤下层少/六斤是下层比上层所少为二斤即上)
　　　　　(层比下层多二斤也铅上层少四斤下/层多三斤下之所多即上之所少是上)
　　　　　(层比下层少七斤也铁上层少八斤下/层少六斤是上层比下层所少为二斤)
　　　　　(也价上层多二钱下层多六钱是下层/比上层所多为四钱即上层比下层少)
　　　　　(四钱也锡多二斤铅少七斤铁少二斤/价即少四钱故为锡二斤比铅七斤铁)
　　　　　(二斤价少/四钱也)次以铜二斤为正锡二斤为

　　　　　负铅一斤为正铁二斤为负价多二钱
　　　　　为正列于上又铜一斤锡二斤为正铅
　　　　　三斤铁八斤为负相等作一空位列于
　　　　　下乃以下铜一斤遍乘上铜二斤锡二
　　　　　斤铅一斤铁二斤价多二钱仍得原数
　　　　　又以上铜二斤遍乘下铜一斤锡二斤
　　　　　铅三斤铁八斤得铜二斤锡四斤仍为
　　　　　正铅六斤铁十六斤仍为负相等无可
　　　　　乘仍为空位于是以上层为主两下相

　　　　　较则铜各二斤彼此减尽锡一正一负

　　　　　故相加得六斤仍依本层为负铅一正
　　　　　一负故亦相加得七斤仍依本层为正
　　　　　铁两层皆负故相减馀十四斤本层少
　　　　　乃变负为正价多二钱与相等无可加
　　　　　减仍得二钱为正即铅七斤铁十四斤
　　　　　比锡六斤价多二钱也(盖铜彼此减尽/锡上层少二斤)
　　　　　(下层多四斤下之所多即上之所少是/上层比下层少六斤也铅上层多一斤)
　　　　　(下层少六斤下之所少即上之所多是/上层比下层多七斤也铁上层少二斤)

　　　　　(下层少十六斤是下层比上层所少为/十四斤即上层比下层多十四斤也铅)
　　　　　(多七斤铁多十四斤锡少六斤而价即/多二钱故为铅七斤铁十四斤比锡六)
　　　　　(斤价多/二钱也)因首色铜数减尽则锡即转而
　　　　　为首应为正今锡六斤为负则重列三
　　　　　色之际不能一体须俱变其号然后为
　　　　　顺故将锡六斤变负为正而以铅七斤
　　　　　铁十四斤价多二钱俱变正为负盖原
　　　　　铅七斤铁十四斤比锡六斤价多二钱
　　　　　今变为锡六斤比铅七斤铁十四斤价

　　　　　少二钱也(若以下层为主则相加应/依下层为正即不用变)次

　　　　　以铜一斤锡二斤为正铅三斤铁八斤
　　　　　为负相等作一空位列于上又铜五斤
　　　　　为正锡四斤铅二十四斤为负铁三十
　　　　　斤为正价少二钱为负列于下乃以下
　　　　　铜五斤遍乘上铜一斤锡二斤铅三斤
　　　　　铁八斤得铜五斤锡十斤为正铅十五
　　　　　斤铁四十斤为负相等无可乘仍为空
　　　　　位又以上铜一斤遍乘下铜五斤锡四

　　　　　斤铅二十四斤铁三十斤价少二钱仍
　　　　　得原数于是以上层为主两下相较则
　　　　　铜各五斤彼此减尽锡一正一负故相
　　　　　加得十四斤仍依本层为正铅两层皆
　　　　　负故相减馀九斤本层少乃变负为正
　　　　　铁一正一负故相加得七十斤仍依本
　　　　　层为负价少二钱与相等无可加减仍
　　　　　得二钱本层无数乃变负为正即锡十
　　　　　四斤铅九斤比铁七十斤价多二钱也

　　　　　(盖铜彼此减尽锡上层多十斤下层少/四斤下之所少即上之所多是上层比)

　　　　　(下层多十四斤也铅上层少十五斤下/层少二十四斤是下层比上层所少为)
　　　　　(九斤即上层比下层多九斤也铁上层/少四十斤下层多三十斤下之所多即)
　　　　　(上之所少是上层比下层少七十斤也/价下层少二钱即上层多二钱也锡多)
　　　　　(十四斤铅多九斤铁少七十斤价即多/二钱故为锡十四斤铅九斤比铁七十)
　　　　　(斤价多/二钱也)爰将三次所得之馀作三色方
　　　　　程算之先以锡二斤为正铅七斤铁二
　　　　　斤价少四钱俱为负列于上又锡六斤
　　　　　为正铅七斤铁十四斤价少二钱俱为

　　　　　负列于下乃以下锡六斤遍乘上锡二
　　　　　斤铅七斤铁二斤价少四钱得锡十二
　　　　　斤为正铅四十二斤铁十二斤价少二
　　　　　两四钱俱为负又以上锡二斤遍乘下
　　　　　锡六斤铅七斤铁十四斤价少二钱得
　　　　　锡十二斤为正铅十四斤铁二十八斤
　　　　　价少四钱俱为负于是以上层为主两
　　　　　下相较则锡各十二斤彼此减尽铅两
　　　　　层皆负故相减馀二十八斤仍依本层

　　　　　为负铁两层皆负故亦相减馀十六斤

　　　　　本层少乃变负为正价两层皆负故亦
　　　　　相减馀二两仍依本层为负即铁十六
　　　　　斤比铅二十八斤价少二两也(盖锡彼/此减尽)
　　　　　(铅上层少四十二斤下层少十四斤是/上层比下层所少为二十八斤也铁上)
　　　　　(层少十二斤下层少二十八斤是下层/比上层所少为十六斤即上层比下层)
　　　　　(多十六斤也价上层少二两四钱下层/少四钱是上层比下层所少为二两也)
　　　　　(铁多十六斤铅少二十八斤价即少二/两故为铁十六斤比铅二十八斤价少)
　　　　　(二两/也)次以锡六斤为正铅七斤铁十四

　　　　　斤价少二钱俱为负列于上又锡十四
　　　　　斤铅九斤为正铁七十斤为负价多二
　　　　　钱为正列于下乃以下锡十四斤遍乘
　　　　　上锡六斤铅七斤铁十四斤价少二钱
　　　　　得锡八十四斤为正铅九十八斤铁一
　　　　　百九十六斤价少二两八钱俱为负又
　　　　　以上锡六斤遍乘下锡十四斤铅九斤
　　　　　铁七十斤价多二钱得锡八十四斤铅
　　　　　五十四斤为正铁四百二十斤为负价

　　　　　多一两二钱为正于是以上层为主两

　　　　　下相较则锡各八十四斤彼此减尽铅
　　　　　一正一负故相加得一百五十二斤仍
　　　　　依本层为负铁两层皆负故相减馀二
　　　　　百二十四斤本层少乃变负为正价一
　　　　　正一负故相加得四两仍依本层为负
　　　　　即铁二百二十四斤比铅一百五十二
　　　　　斤价少四两也(盖锡彼此减尽铅上层/少九十八斤下层多五)
　　　　　(十四斤下之所多即上之所少是上层/比下层少一百五十二斤也铁上层少)

　　　　　(一百九十六斤下层少四百二十斤是/下层比上层所少为二百二十四斤即)
　　　　　(上层比下层多二百二十四斤也价上/层少二两八钱下层多一两二钱下之)
　　　　　(所多即上之所少是上层比下层少四/两也铁多二百二十四斤铅少一百五)
　　　　　(十二斤价即少四两故为铁二百二十/四斤比铅一百五十二斤价少四两也)
　　　　　爰将两次所得之馀作二色方程算之
　　　　　其所馀铅两首色俱为负是为同号可
　　　　　以互乘减尽故不变其号即将铅二十
　　　　　八斤为负铁十六斤为正价少二两为
　　　　　负列于上又铅一百五十二斤为负铁

　　　　　二百二十四斤为正价少四两为负列

　　　　　于下乃以下铅一百五十二斤遍乘上
　　　　　铅二十八斤铁十六斤价少二两得铅
　　　　　四千二百五十六斤为负铁二千四百
　　　　　三十二斤为正价少三百零四两为负
　　　　　又以上铅二十八斤遍乘下铅一百五
　　　　　十二斤铁二百二十四斤价少四两得
　　　　　铅四千二百五十六斤为负铁六千二
　　　　　百七十二斤为正价少一百一十二两

　　　　　为负两下相较则铅各四千二百五十
　　　　　六斤彼此减尽铁两层皆正故亦相减
　　　　　馀三千八百四十斤价两层皆负故亦
　　　　　相减馀一百九十二两即铁三千八百
　　　　　四十斤之共价以铁三千八百四十斤
　　　　　除之得五分即铁每一斤之价也以铁
　　　　　十六斤乘之得八钱为铁十六斤之共
　　　　　价铁十六斤既比铅二十八斤价少二
　　　　　两则加二两得二两八钱为铅二十八

　　　　　斤之共价以铅二十八斤除之得一钱

　　　　　即铅每一斤之价也以锡六斤比铅七
　　　　　斤铁十四斤价少二钱计之则铅七斤
　　　　　价七钱铁十四斤价亦七钱共一两四
　　　　　钱锡六斤既比铅七斤铁十四斤价少
　　　　　二钱则减二钱馀一两二钱为锡六斤
　　　　　之共价以锡六斤除之得二钱即锡每
　　　　　一斤之价也再以铜三斤比锡二斤铅
　　　　　二斤铁四斤价多一钱计之则锡二斤

　　　　　价四钱铅二斤价二钱铁四斤价二钱
　　　　　共八钱铜三斤既比锡二斤铅二斤铁
　　　　　四斤价多一钱则加一钱共九钱为铜
　　　　　三斤之共价以铜三斤除之得三钱即
　　　　　铜每一斤之价也
　　和较兼用类
设如有大小二石不知其重只云二大石比七小石
　少三十斤三大石二小石共三百三十斤问大小
　石各重几何

　　　　　法以大石二为正小石七为负少三十

　　　　　斤为负列于上大石三小石二共重三
　　　　　百三十斤列于下乃以上大石二遍乘
　　　　　下大石三小石二重三百三十斤得大
　　　　　石六小石四共重六百六十斤又以下
　　　　　大石三遍乘上大石二小石七少三十
　　　　　斤得大石六仍为正小石二十一仍为
　　　　　负少九十斤亦仍为负两下相较则大
　　　　　石各六彼此减尽小石四加小石二十

　　　　　一得小石二十五六百六十斤加九十
　　　　　斤得七百五十斤乃小石二十五之共
　　　　　数以小石二十五除之得三十斤即一
　　　　　小石之重数以二因之得六十斤为二
　　　　　小石之共数于大小石共重三百三十
　　　　　斤内减之馀二百七十斤为三大石之
　　　　　共数以三除之得九十斤即一大石之
　　　　　重数也此法盖因三大石二小石共重
　　　　　三百三十斤为和数皆一类为正故不

　　　　　用正负之号遇正则为同类相减遇负

　　　　　则为异类相加相加之后仍为和数者
　　　　　以其依本层之号故亦不用正号盖六
　　　　　大石四小石共重六百六十斤而六大
　　　　　石比二十一小石少九十斤则加九十
　　　　　斤即六大石与二十一小石等矣故小
　　　　　石二十五共重七百五十斤以二十五
　　　　　除之而得一小石之重数也既得小石
　　　　　之重数则于和数共重三百三十斤内

　　　　　减二小石重六十斤馀为三大石之共
　　　　　数若于较数七小石之共重二百一十
　　　　　斤内减少三十斤所馀即为二大石之
　　　　　共数既得三大石或二大石之共数乃
　　　　　以大石数除之即得一大石之重数矣
设如有米用牛马骡三色载之各不知数只云牛二
　马三骡四共载八石马三骡三与牛三所载相等
　牛四马一比骡八所载多三石问各载几何
　　　　　法先以牛二马三骡四共米八石列于

　　　　　上次以牛三为正马三骡三为负相等

　　　　　作一空位列于下(题言马三骡三比牛/三则马骡应为正牛)
　　　　　(应为负因列法以牛为首故以牛为正/马骡为负即牛三比马三骡三相等其)
　　　　　(理一/也)乃以上牛二遍乘下牛三马三骡
　　　　　三得牛六仍为正马六骡六仍为负又
　　　　　以下牛三遍乘上牛二马三骡四共载
　　　　　八石得牛六马九骡十二共载二十四
　　　　　石于是以下层为主两下相较(若以上/层为主)
　　　　　(则相加数皆为负况首色减尽二色即/转而为首即变负为正故不若以下层)

　　　　　(为主而皆/为正也)则牛各六彼此减尽马九加
　　　　　马六得马十五(因依本层为和/数故不用号)骡十二
　　　　　加骡六得骡十八二十四石无可加减
　　　　　仍为二十四石即马十五骡十八共载
　　　　　二十四石也(盖牛六马九骡十二共载/二十四石而牛六与马六)
　　　　　(骡六相等则将本层牛六变为马六骡/六矣故为马十五骡十八共载二十四)
　　　　　(石/也)次以牛三为正马三骡三为负相等
　　　　　作一空位列于上牛四马一为正骡八
　　　　　为负多三石为正列于下乃以上牛三

　　　　　遍乘下牛四马一骡八多三石得牛十

　　　　　二为正马三亦为正骡二十四为负多
　　　　　九石为正又以下牛四遍乘上牛三马
　　　　　三骡三得牛十二为正马十二为负骡
　　　　　十二为负于是以上层为主两下相较
　　　　　则牛各十二彼此减尽马一正一负故
　　　　　相加得十五仍依本层为正骡两层皆
　　　　　负故相减馀十二仍依本层为负九石
　　　　　无可加减仍为九石依本层为正即马

　　　　　十五比骡十二所载多九石也(盖牛彼/此减尽)
　　　　　(马上层多三下层少十二是上层比下/层多十五也骡上层少二十四下层少)
　　　　　(十二是上层比下层所少为十二也马/多十五骡少十二而米即多九石故为)
　　　　　(马十五比骡十二/所载多九石也)爰将两次所得之馀
　　　　　如和较兼用二色方程法算之其马十
　　　　　五骡十八共米二十四石列于上又马
　　　　　十五为正骡十二为负多米九石为正
　　　　　列于下因首色皆为十五两数齐同即
　　　　　不用互乘两下相较则马各十五彼此

　　　　　减尽骡十八加骡十二得三十米二十

　　　　　四石减九石馀十五石乃骡三十共载
　　　　　之数以三十除之得五斗即为每一骡
　　　　　所载之数以骡十二乘之得六石为骡
　　　　　十二共载之数加马十五之多九石得
　　　　　十五石即为马十五共载之数以马十
　　　　　五除之得一石为每一马所载之数以
　　　　　牛三与马三骡三相等计之则马三应
　　　　　载三石骡三应载一石五斗共四石五

　　　　　斗以牛三除之得一石五斗即为每一
　　　　　牛所载之数也
设如有银买绫罗绢三色各不知价只云绫一疋罗
　二疋绢四疋共价七两四钱又绫二疋绢八疋比
　罗四疋多六两八钱又绫三疋比罗六疋绢七疋
　少一两二钱问各价几何
　　　　　法先以绫一罗二绢四共银七两四钱
　　　　　列于上(和数皆为/正不用号)又绫二为正罗四为
　　　　　负绢八为正多六两八钱为正列于下

　　　　　乃以下绫二遍乘上绫一罗二绢四共

　　　　　银七两四钱得绫二罗四绢八共银十
　　　　　四两八钱又以上绫一遍乘下绫二罗
　　　　　四绢八多六两八钱仍得原数于是以
　　　　　上层为主两下相较则绫各二彼此减
　　　　　尽罗一正一负故相加得罗八依本层
　　　　　为正绢两层皆正故相减恰尽价两层
　　　　　皆正亦相减馀八两乃罗八疋之共价
　　　　　(盖绫彼此减尽绢亦减尽惟罗上层多/四疋下层少四疋是上层比下层多八)

　　　　　(疋而价即多八两故/为罗八疋之共价也)以罗八除之得一
　　　　　两即为罗每一疋之价也次以绫二为
　　　　　正罗四为负绢八为正多六两八钱为
　　　　　正列于上又绫三为正罗六为负绢七
　　　　　为负少一两二钱为负列于下乃以下
　　　　　绫三遍乘上绫二罗四绢八多六两八
　　　　　钱得绫六为正罗十二为负绢二十四
　　　　　为正多二十两四钱为正又以上绫二
　　　　　遍乘下绫三罗六绢七少一两二钱得

　　　　　绫六为正罗十二为负绢十四为负少

　　　　　二两四钱为负于是以上层为主两下
　　　　　相较则绫各六彼此减尽罗两层皆负
　　　　　亦减尽绢一正一负故相加得三十八
　　　　　银一正一负故相加得二十二两八钱
　　　　　乃绢三十八疋之共价(盖绫彼此减尽/罗亦减尽绢上)
　　　　　(层多二十四疋下层少十四疋是上层/比下层多三十八疋也银上层多二十)
　　　　　(两四钱下层少二两四钱是上层比下/层多二十二两八钱也绢多而银亦多)
　　　　　(故为绢之/共价也)以绢三十八除之得六钱即

　　　　　绢每一疋之价也以绫一罗二绢四共
　　　　　价七两四钱计之则罗二疋应价二两
　　　　　绢四疋应价二两四钱共四两四钱于
　　　　　共价七两四钱内减之馀三两即绫每
　　　　　一疋之价也此法互乘相减之后即得
　　　　　一法一实故省重列二色若物与价俱
　　　　　各减尽者则此层必为彼层之几倍与
　　　　　少一层者同是为少一行不可算也
　　和较交变类

设如有琴瑟筝三种乐器各不知价但知琴一张瑟

　三张筝三张共价九十两又琴一张瑟二张筝五
　张共价八十八两又琴三张瑟八张筝五张共价
　二百二十两问琴瑟筝每张各价几何
　　　　　法先以琴一瑟三筝三共银九十两列
　　　　　于上又琴一瑟二筝五共银八十八两
　　　　　列于下(因和数皆为/正故不用号)因首色皆为一故
　　　　　省互乘即以上层为主两下相较则琴
　　　　　各一彼此减尽瑟两下相减馀一本层

　　　　　多仍为正筝两下相减馀二本层少变
　　　　　正为负银九十两减八十八两馀二两
　　　　　本层多亦仍为正即瑟一比筝二价多
　　　　　二两也(盖两层琴各一张其价必相等/但上层多瑟一张下层多筝二)
　　　　　(张则上层多银二两即瑟/一比筝二所多之价也)次以琴一瑟
　　　　　二筝五共银八十八两列于上又琴三
　　　　　瑟八筝五共银二百二十两列于下乃
　　　　　以下琴三遍乘上琴一瑟二筝五共银
　　　　　八十八两得琴三瑟六筝十五共银二

　　　　　百六十四两又以上琴一遍乘下琴三

　　　　　瑟八筝五共银二百二十两仍得原数
　　　　　于是以上层为主两下相较则琴各三
　　　　　彼此减尽瑟两下相减馀二本层少变
　　　　　正为负筝两下相减馀十本层多仍为
　　　　　正银二百六十四两减二百二十两馀
　　　　　四十四两本层多亦仍为正即筝十比
　　　　　瑟二价多四十四两也(盖两层琴各三/张其价必相等)
　　　　　(但上层多筝十张下层多瑟二张则上/层多银四十四两即筝十张比瑟二张)

　　　　　(所多之/价也)因首色减尽则瑟转而为首应
　　　　　为正今瑟为负重列二色之际不能一
　　　　　体须俱变其号然后为顺故将瑟二变
　　　　　负为正而以筝十与价多四十四两俱
　　　　　变正为负盖原筝十比瑟二多四十四
　　　　　两今变为瑟二比筝十少四十四两也
　　　　　(若以下层为主则本层多/即得瑟二为正不用变号)爰将两次所
　　　　　得之馀如较数二色方程算之其瑟一
　　　　　为正筝二为负多二两为正列于上瑟

　　　　　二为正筝十为负少四十四两为负列

　　　　　于下乃以下瑟二遍乘上瑟一筝二多
　　　　　二两得瑟二仍为正筝四为负多四两
　　　　　为正又以上瑟一遍乘下瑟二筝十少
　　　　　四十四两仍得原数两下相较则瑟各
　　　　　二彼此减尽筝两层皆负故相减馀六
　　　　　多四两与少四十四两相加得四十八
　　　　　两即筝六张之共价也(盖瑟皆为二张/则其共价必相)
　　　　　(等然比筝四张之价则多比筝十张之/价则少是多少相加之四十八两即筝)

　　　　　(十与筝四相差/六张之价也)乃以筝六除银四十八
　　　　　两得八两为筝每张之价以筝十因之
　　　　　得八十两为筝十张之共价瑟二张既
　　　　　比筝十张少四十四两则于八十两内
　　　　　减四十四两馀三十六两即为瑟二张
　　　　　之共价以瑟二除之得十八两为瑟每
　　　　　张之价以琴一瑟三筝三共银九十两
　　　　　计之则瑟三价五十四两筝三价二十
　　　　　四两共七十八两于共银九十两内减

　　　　　之馀十二两即琴每一张之价也

设如有古量斛庾釜三种盛米各数不同只云三斛
　二釜比二庾多一石零八升又二斛比三庾五釜
　少六石又一斛一庾比二釜多一石三斗二升问
　斛庾釜各盛米若干
　　　　　法先以斛三为正庾二为负釜二为正
　　　　　多一石零八升为正列于上又斛二为
　　　　　正庾三釜五为负少六石亦为负列于
　　　　　下乃以下斛二遍乘上斛三庾二釜二

　　　　　多一石零八升得斛六仍为正庾四为
　　　　　负釜四为正多二石一斗六升亦为正
　　　　　又以上斛三遍乘下斛二庾三釜五少
　　　　　六石得斛六仍为正庾九釜十五俱为
　　　　　负少十八石亦为负于是以上层为主
　　　　　两下相较则斛各六彼此减尽庾两层
　　　　　皆负故相减馀五本层少乃变负为正
　　　　　釜一正一负故相加得十九仍依本层
　　　　　为正多二石一斗六升与少十八石相

　　　　　加得二十石一斗六升仍依本层为正

　　　　　即五庾十九釜共二十石一斗六升也
　　　　　(盖斛彼此减尽庾上层少四下层少九/是下层比上层所少为五即上层比下)
　　　　　(层多五也釜上层多四下层少十五是/上层比下层多十九也米上层多二石)
　　　　　(一斗六升下层少十八石是上层比下/层多二十石一斗六升也庾釜多则米)
　　　　　(亦多故为五庾十九釜/共二十石一斗六升也)次以斛二为正
　　　　　庾三釜五与少六石俱为负列于上又
　　　　　斛一庾一为正釜二为负多一石三斗
　　　　　二升为正列于下乃以上斛二遍乘下

　　　　　斛一庾一釜二多一石三斗二升得斛
　　　　　二庾二为正釜四为负多二石六斗四
　　　　　升为正又以下斛一遍乘上斛二庾三
　　　　　釜五少六石仍得原数于是以上层为
　　　　　主两下相较则斛各二彼此减尽庾一
　　　　　正一负故相加得五仍依本层为正釜
　　　　　两层皆负故相减馀一本层少乃变负
　　　　　为正多二石六斗四升与少六石相加
　　　　　得八石六斗四升仍依本层为正即五

　　　　　庾一釜共八石六斗四升也(盖斛彼此/减尽庾上)

　　　　　(层多二下层少三是上层比下层多五/也釜上层少四下层少五是下层比上)
　　　　　(层所少为一即上层比下层多一也米/上层多二石六斗四升下层少六石是)
　　　　　(上层比下层多八石六斗四升也庾釜/多而米亦多故为五庾一釜共八石六)
　　　　　(斗四/升也)爰以两次所得之馀如和数二色
　　　　　方程算之其庾五釜十九共二十石一
　　　　　斗六升列于上庾五釜一共八石六斗
　　　　　四升列于下(变为和数/故不用号)夫首数皆为五
　　　　　则省互乘两下相较庾各五彼此减尽

　　　　　釜十九减一馀十八米二十石一斗六
　　　　　升减八石六斗四升馀十一石五斗二
　　　　　升即为釜十八所盛之共数以十八除
　　　　　之得六斗四升为每一釜所盛之数于
　　　　　八石六斗四升内减之馀八石为庾五
　　　　　所盛之共数以五除之得一石六斗为
　　　　　每一庾所盛之数以斛三釜二比庾二
　　　　　多一石零八升计之则庾二应三石二
　　　　　斗加多一石零八升得四石二斗八升

　　　　　即为斛三釜二之共数减釜二之一石

　　　　　二斗八升馀三石为斛三所盛之共数
　　　　　以三除之得一石为每一斛所盛之数
　　　　　也
设如用船车驼运粮各不知数只云三船比七车一
　驼少三十三石六斗二车比一船十二驼少二十
　一石六斗八驼比一船三车少二十一石六斗问
　船车驼各载几何
　　　　　法先以船三为正车七驼一与少三十

　　　　　三石六斗俱为负列于上又船一改为
　　　　　正车二改为负驼十二亦改为正少二
　　　　　十一石六斗改为多二十一石六斗亦
　　　　　为正列于下(盖二车比一船十二驼少/二十一石六斗即一船十)
　　　　　(二驼比二车多二/十一石六斗也)乃以上船三遍乘下
　　　　　船一车二驼十二多二十一石六斗得
　　　　　船三为正车六为负驼三十六为正多
　　　　　六十四石八斗为正又以下船一遍乘
　　　　　上船三车七驼一少三十三石六斗仍

　　　　　得原数于是以上层为主两下相较则

　　　　　船各三彼此减尽车两层皆负故相减
　　　　　馀一本层少乃变负为正驼一正一负
　　　　　故相加得三十七仍依本层为正多六
　　　　　十四石八斗与少三十三石六斗相加
　　　　　得九十八石四斗亦依本层为正即车
　　　　　一驼三十七共载九十八石四斗也(盖/船)
　　　　　(彼此减尽车上层少六下层少七是下/层比上层所少为一即上层比下层多)
　　　　　(一也驼上层多三十六下层少一是上/层比下层多三十七也粮上层多六十)

　　　　　(四石八斗下层少三十三石六斗是上/层比下层多九十八石四斗也车多驼)
　　　　　(多则粮亦多故九十八石四斗/为车一驼三十七之共数也)次以船
　　　　　一为正车二为负驼十二为正多二十
　　　　　一石六斗为正列于上又船一车三俱
　　　　　改为正驼八改为负少二十一石六斗
　　　　　改为多二十一石六斗为正列于下(盖/八)
　　　　　(驼比一船三车少二十一石六斗即一/船三车比八驼多二十一石六斗也)
　　　　　首数皆一故省互乘即以上层为主两
　　　　　下相较则船各一彼此减尽车一正一

　　　　　负故相加得五仍依本层为负驼一正

　　　　　一负故亦相加得二十仍依本层为正
　　　　　粮两层皆正相减恰尽即为驼二十与
　　　　　车五相等今车应转为首色为正故重
　　　　　列之际须俱变其号以车变负为正驼
　　　　　变正为负即为车五与驼二十相等也
　　　　　(盖两下相较船数相等上层少车二下/层多车三上之所少即下之所多是下)
　　　　　(层多车五上层多驼十二下层少驼八/下之所少即上之所多是上层多驼二)
　　　　　(十今既两下粮数相等则/为车五与驼二十相等矣)爰以两次所

　　　　　得之馀如和较兼用二色方程算之其
　　　　　车一驼三十七共粮九十八石四斗列
　　　　　于上(因为和数/故不用号)又车五为正驼二十为
　　　　　负列于下(粮两下相等故无数可/列仍作空以存其位)乃以
　　　　　下车五遍乘上车一驼三十七共粮九
　　　　　十八石四斗得车五驼一百八十五共
　　　　　粮四百九十二石又以上车一遍乘下
　　　　　车五驼二十仍得原数两下相较则车
　　　　　各五彼此减尽驼一百八十五加驼二

　　　　　十得二百零五粮止一层无数可加减

　　　　　仍得四百九十二石即驼二百零五所
　　　　　载之共数也以驼二百零五除之得二
　　　　　石四斗为每一驼所载之数以二十乘
　　　　　之得四十八石为驼二十所载之共数
　　　　　车五既与之相等即以车五除之得九
　　　　　石六斗即为每一车所载之数以三船
　　　　　比七车一驼少三十三石六斗计之则
　　　　　一驼应二石四斗七车应六十七石二

　　　　　斗共六十九石六斗减三船少三十三
　　　　　石六斗馀三十六石为三船所载之共
　　　　　数以三除之得十二石为每一船所载
　　　　　之数也
设如有钱买瓜桃榴梨四色只云瓜二桃四共价一
　百五十六文瓜一梨八共价一百二十六文桃二
　榴七共价一百六十文榴四梨七共价一百四十
　八文问瓜桃榴梨各价几何
　　　　　法先以瓜二桃四共价一百五十六文

　　　　　列于上(因题有四色而此行无榴梨乃/各作空位以存其分馀俱照式)

　　　　　(对位/列之)又以瓜一梨八共价一百二十六
　　　　　文列于下(因为和数/故不用号)乃以上瓜二遍乘
　　　　　下瓜一梨八共价一百二十六文得瓜
　　　　　二梨十六共价二百五十二文又以下
　　　　　瓜一遍乘上瓜二桃四共价一百五十
　　　　　六文仍得原数于是以下层为主两下
　　　　　相较则瓜各二彼此减尽桃四无可减
　　　　　仍为四依本层为正榴仍为空位梨十

　　　　　六无可减仍为十六本层无数乃变正
　　　　　为负价二百五十二文内减一百五十
　　　　　六文馀九十六文本层少乃变正为负
　　　　　即为桃四比梨十六价少九十六文也
　　　　　(盖瓜皆为二则其共价必相等然上层/有梨十六则共价二百五十二文下层)
　　　　　(有桃四则共价一百五十六文其相差/之九十六文即桃四比梨十六所少之)
　　　　　(价/也)至是瓜既已减尽但馀三色即变四
　　　　　色为三色而以桃为首对位列之是以
　　　　　桃四为正(此行无榴数故仍作空位/以存其分馀俱对位列之)梨

　　　　　十六为负少九十六文为负列于上桃

　　　　　二榴七共价一百六十文列于下(因为/和数)
　　　　　(故不/用号)乃以上桃四遍乘下桃二榴七共
　　　　　价一百六十文得桃八榴二十八共价
　　　　　六百四十文又以下桃二遍乘上桃四
　　　　　梨十六少九十六文得桃八仍为正梨
　　　　　三十二仍为负少一百九十二文为负
　　　　　于是以上层为主两下相较则桃各八
　　　　　彼此减尽榴二十八无可减仍为二十

　　　　　八依本层为正梨三十二无可加仍为
　　　　　三十二本层无数乃变负为正六百四
　　　　　十文与少一百九十二文相加得八百
　　　　　三十二文仍依本层为正即榴二十八
　　　　　梨三十二共价八百三十二文也(盖桃/彼此)
　　　　　(减尽上层多榴二十八下层少梨三十/二即上层多梨三十二故多与少相差)
　　　　　(之八百三十二文即榴二/十八梨三十二之共价也)至是桃又减
　　　　　尽但馀二色即变三色为二色而以榴
　　　　　为首对位列之是以榴二十八梨三十

　　　　　二共价八百三十二文列于上榴四梨

　　　　　七共价一百四十八文列于下乃以上
　　　　　榴二十八遍乘下榴四梨七共价一百
　　　　　四十八文得榴一百一十二梨一百九
　　　　　十六共价四千一百四十四文又以下
　　　　　榴四遍乘上榴二十八梨三十二共价
　　　　　八百三十二文得榴一百一十二梨一
　　　　　百二十八共价三千三百二十八文两
　　　　　下相较则榴各一百一十二彼此减尽

　　　　　梨两下相减馀六十八价两下相减馀
　　　　　八百一十六文即梨六十八之共价也
　　　　　以梨六十八除之得十二文为梨每个
　　　　　之价以七因之得八十四文为梨七之
　　　　　共价于榴梨共价一百四十八文内减
　　　　　之馀六十四文为榴四之共价以四除
　　　　　之得十六文即榴每个之价以桃二榴
　　　　　七共价一百六十文计之则榴七应价
　　　　　一百一十二文于桃榴共价一百六十

　　　　　文内减之馀四十八文为桃二之共价

　　　　　以二除之得二十四文为桃每个之价
　　　　　再以瓜二桃四共价一百五十六文计
　　　　　之则桃四应价九十六文于桃瓜共价
　　　　　一百五十六文内减之馀六十文为瓜
　　　　　二之共价以二除之得三十文即瓜每
　　　　　个之价也
　　附法
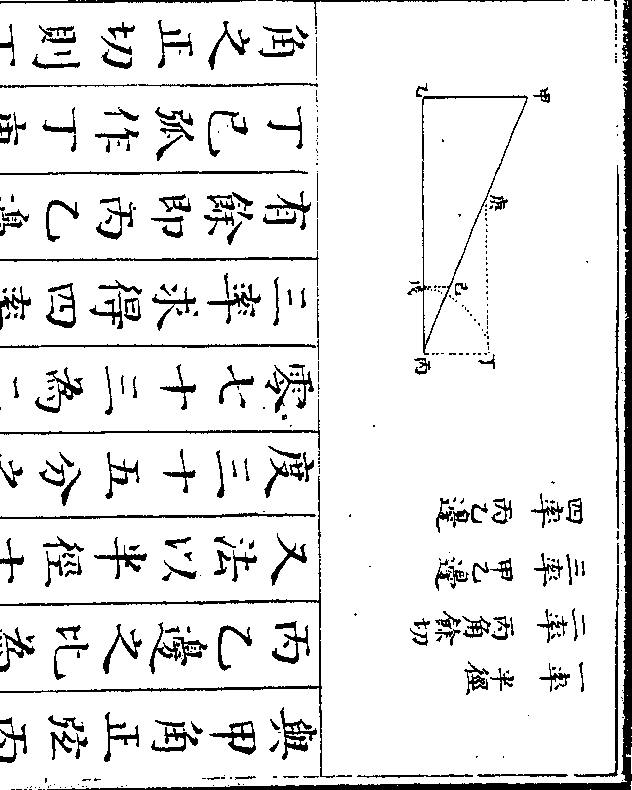
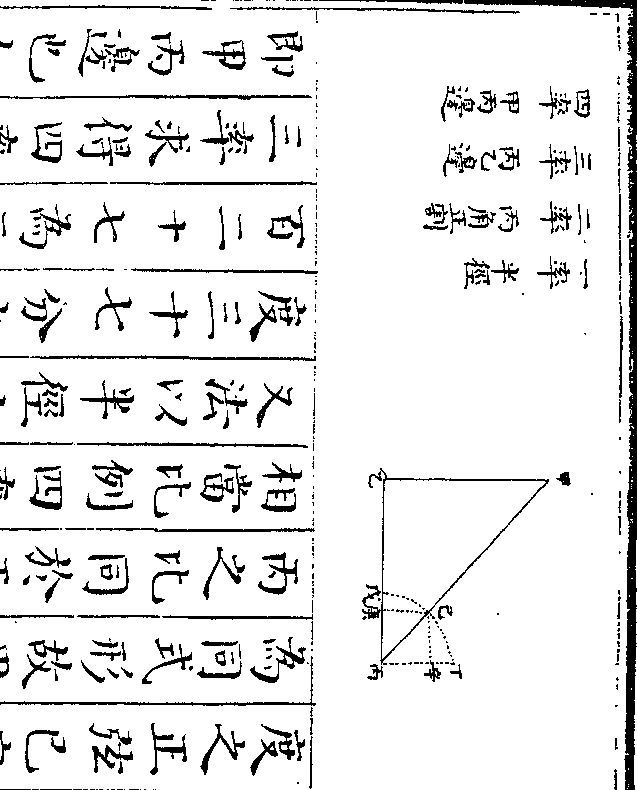
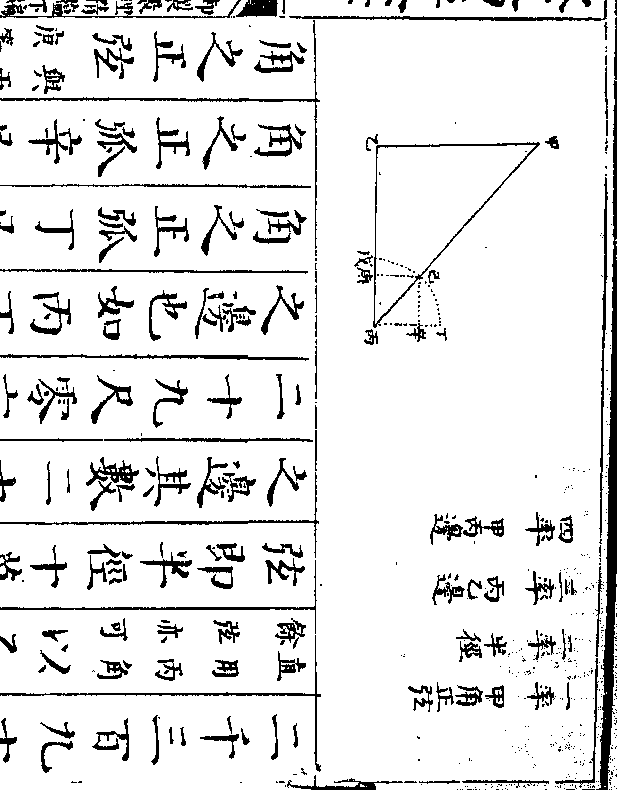
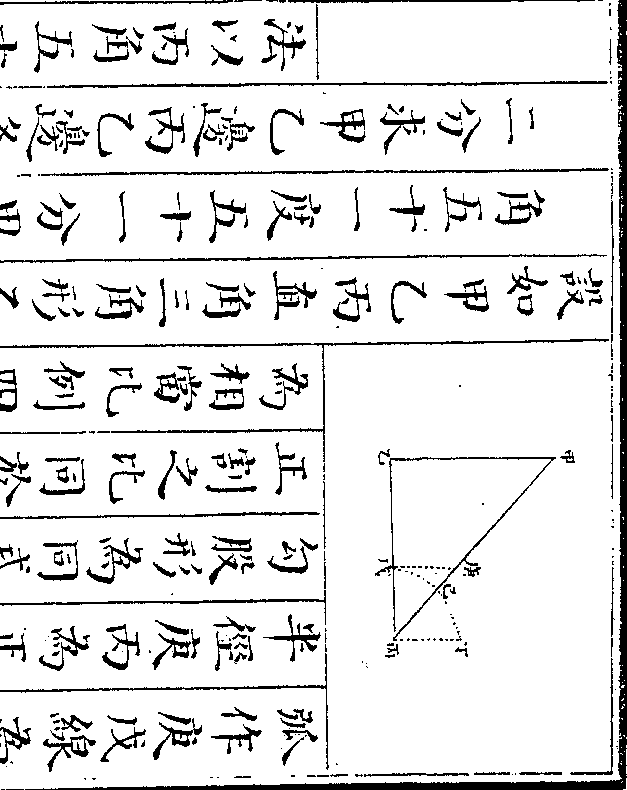
设如有石二块大小不等不知重数只有铜条一根

　重十二两均分十二分以绳系于第五分之上一
　头五分一头七分将大石挂于铜条一头离提系
　五分而以小石作砣称之离提系得六分始平又
　将小石挂在铜条一头离提系五分而以大石作
　砣称之离提系得四分始平问大小二石各重几
　何
　　　　　法先以五分加一倍与十二分相较馀
　　　　　二分折半得一分与五分相加为六分
　　　　　乃以五分为一率六分为二率馀二分

　　　　　作二两为三率得四率二两四钱即五

　　　　　分之端加二两四钱始与七分相平也
　　　　　爰将二两四钱以大石离提系五分因
　　　　　之得十二两为五大石比六小石所多
　　　　　之数(大石离提系五分小石离提系六/分而平是大石重六分小石重五)
　　　　　(分也若五大石六小石则各得三十分/其重始等然五分之一端应加二两四)
　　　　　(钱是大石重六分尚多二两四钱也若/五大石则多十二两矣故为五大石比)
　　　　　(六小石多/十二两也)又将二两四钱以小石离提
　　　　　系五分因之亦得十二两为四大石比

　　　　　五小石所少之数(小石离提系五分大/石离提系四分而平)
　　　　　(是小石重四分大石重五分也若五小/石四大石则各得二十分其重始等然)
　　　　　(五分之一端应加二两四钱是小石重/四分尚多二两四钱也若五小石则多)
　　　　　(十二两矣故为五小石比四大石多十/二两因以大石为首故变为四大石比)
　　　　　(五小石少/十二两也)因作较数方程法算之以大
　　　　　石五为正小石六为负重多十二两为
　　　　　正列于上又大石四为正小石五为负
　　　　　重少十二两为负列于下乃以上大石
　　　　　五遍乘下大石四小石五少十二两得

　　　　　大石二十小石二十五少六十两又以

　　　　　下大石四遍乘上大石五小石六多十
　　　　　二两得大石二十小石二十四多四十
　　　　　八两两下相较则大石各二十彼此减
　　　　　尽小石两层皆负故相减馀一重少六
　　　　　十两与多四十八两相加得一百零八
　　　　　两即为一小石之重数以小石六因之
　　　　　得六百四十八两为六小石之共重数
　　　　　加五大石所多十二两得六百六十两

　　　　　为五大石之共重数以五归之得一百
　　　　　三十二两即为一大石之重数也此本
　　　　　叠借互徵之法而以方程算之稍为简
　　　　　易焉
设如有银一千六百四十两兄弟二人分之各不知
　数只云兄之四分之一弟之六分之一共三百五
　十两问兄弟各分银几何
　　　　　法以一千六百四十两为兄四分弟六
　　　　　分之共银数以三百五十两为兄一分

　　　　　弟一分之共银数如和数方程法算之

　　　　　以兄四分弟六分共银一千六百四十
　　　　　两列于上兄一分弟一分共银三百五
　　　　　十两列于下乃以下兄一分遍乘上兄
　　　　　四分弟六分共银一千六百四十两仍
　　　　　得原数又以上兄四分遍乘下兄一分
　　　　　弟一分共银三百五十两得兄四分弟
　　　　　四分共银一千四百两两下相较则兄
　　　　　各四分彼此减尽弟两下相减馀二分

　　　　　银两下相减馀二百四十两即弟二分
　　　　　之共银数以弟二分除之得一百二十
　　　　　两为弟一分之银数以弟六分乘之得
　　　　　七百二十两即弟所分之共银数于共
　　　　　银一千六百四十两内减之馀九百二
　　　　　十两即兄所分之共银数也(此法用叠/借互徵算)
　　　　　(之亦/可)
设如甲乙二人分果不知其数只云甲予乙九枚则
　乙与甲等乙予甲九枚则一甲与二乙等问甲乙

　分果各几何

　　　　　法将甲予乙九枚以二因之得一十八
　　　　　枚为一甲比一乙所多之数(盖甲予乙/九枚则甲)
　　　　　(与乙等若甲不予乙则甲多九枚/乙少九枚是甲比乙多十八枚也)又将
　　　　　乙予甲九枚以三因之得二十七枚为
　　　　　一甲比二乙所少之数(盖乙予甲九枚/则一甲与二乙)
　　　　　(等若乙不予甲则乙多九枚二乙必多/十八枚甲少九枚是一甲比二乙少二)
　　　　　(十七/枚也)因作较数方程法算之以甲一为
　　　　　正乙一为负多十八枚为正列于上又

　　　　　甲一为正乙二为负少二十七枚为负
　　　　　列于下因甲首色皆为一故不用互乘
　　　　　两下相较则甲各一彼此减尽乙两层
　　　　　皆负故相减馀一果一正一负故相加
　　　　　得四十五枚即为乙之果数如甲多十
　　　　　八枚得六十三枚即为甲之果数也若
　　　　　甲与乙九枚则甲馀五十四乙亦得五
　　　　　十四是甲与乙相等若乙与甲九枚则
　　　　　乙馀三十六甲得七十二是一甲与二

　　　　　乙相等也(此法用叠借互/徵算之亦可)

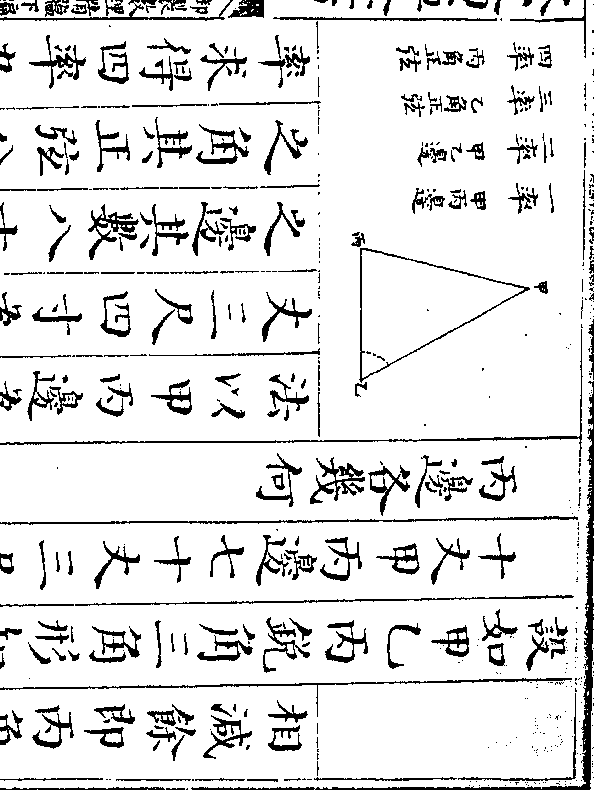设如有田二千六百五十亩令上中下三等农夫分
　耕上等四十人中等五十人下等七十人上等比
　中等每人多七亩中等比下等每人多五亩问上
　中下三等每人各耕几何
　　　　　法以二千六百五十亩为和以多七亩
　　　　　多五亩为较如和较兼用三色方程法
　　　　　算之先以上等四十人中等五十人下
　　　　　等七十人共田二千六百五十亩列于

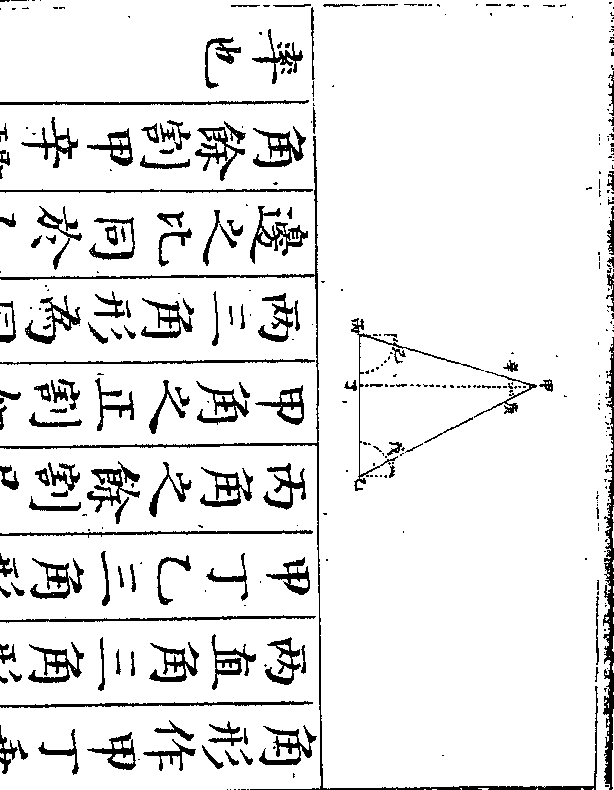　　　　　上(因为和数/故不用号)又上等一人为正中等一
　　　　　人为负多七亩为正列于下(无下等则/作空以存)
　　　　　(其/位)乃以下上等一人遍乘上上等四十
　　　　　人中等五十人下等七十人共田二千
　　　　　六百五十亩仍得原数又以上上等四
　　　　　十人遍乘下上等一人中等一人多七
　　　　　亩得上等四十人为正中等四十人为
　　　　　负多二百八十亩为正于是以上层为
　　　　　主两下相较则上等各四十人彼此减

　　　　　尽中等五十人加四十人得九十人下

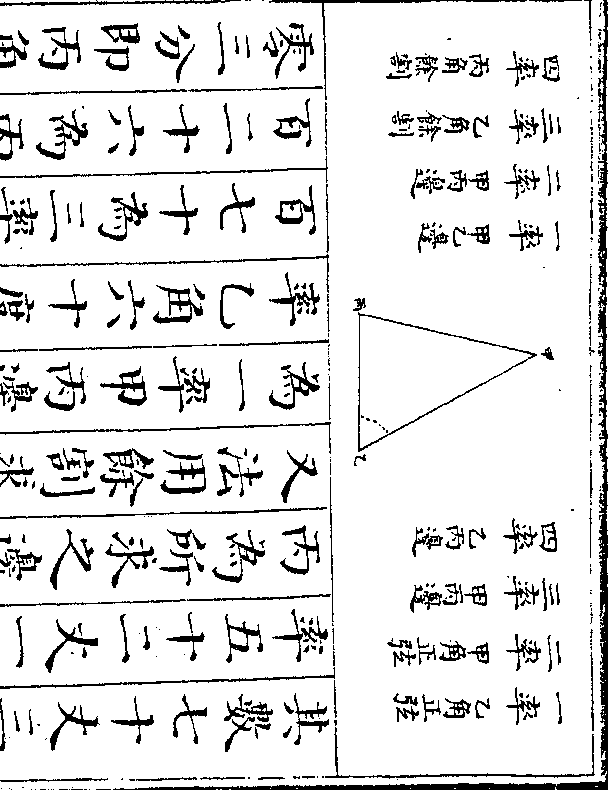　　　　　等无可加减仍得七十人田二千六百
　　　　　五十亩减二百八十亩馀二千三百七
　　　　　十亩即中等九十人下等七十人共田
　　　　　二千三百七十亩也(因依本层故/仍为和数)次以
　　　　　中等九十人下等七十人共田二千三
　　　　　百七十亩列于上(因为和数/故不用号)又中等一
　　　　　人为正下等一人为负多五亩为正列
　　　　　于下乃以下中等一人遍乘上中等九

　　　　　十人下等七十人共田二千三百七十
　　　　　亩仍得原数又以上中等九十人遍乘
　　　　　下中等一人下等一人多五亩得中等
　　　　　九十人为正下等九十人为负多四百
　　　　　五十亩为正两下相较则中等各九十
　　　　　人彼此减尽下等七十人加九十人得
　　　　　一百六十人田二千三百七十亩减四
　　　　　百五十亩馀一千九百二十亩即下等
　　　　　一百六十人之共数也以下等一百六

　　　　　十人除之得十二亩为下等每人所耕

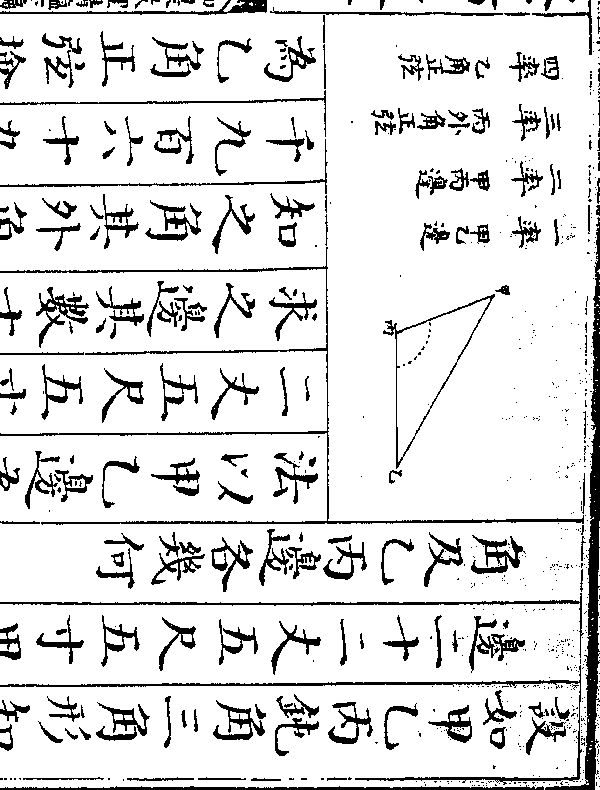　　　　　　之数加五亩得十七亩为中等每人所
　　　　　　耕之数又加七亩得二十四亩为上等
　　　　　　每人所耕之数也(此法本和数比例/以方程算之亦可)
　
　
　
　
　

　
　
　
　
　
　
　
御制数理精蕴下编卷十