声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
御制数理精蕴 下编卷七 第 1a 页 WYG0799-0491a.png
 钦定四库全书
钦定四库全书御制数理精蕴下编卷七
线部五
和较比例
御制数理精蕴 下编卷七 第 2a 页 WYG0799-0492a.png
 和较比例
和较比例比例之中有和数较数而复有和较者用和数相比
谓之和用较数相比谓之较至于设问中两物相和
两价相和或每色中几物相和乃于和数中推求较
数因较数而成比例是以和数为体而较数为用故
谓之和较比例在九章一名贵贱差分一名贵贱相
和其立法盖于总物中求其相差之较或于每物中
求其相差之较(此贵贱/差分法)或用互乘以齐其数然后于
御制数理精蕴 下编卷七 第 2b 页 WYG0799-0492b.png WYG0799-0492c.png

 互乘数中求其相差之较作为比例而得真数(此贵/贱相)
互乘数中求其相差之较作为比例而得真数(此贵/贱相)(和/法)按法立算虽各不同要之总以和数推出较数为
比此和较之所以名也
设如有银四百零五两七钱共买米麦五百石米每
石价银八钱六分麦每石价银七钱二分五釐问
米麦各该几何
法以米麦共五百石用米每石价银八
钱六分乘之得四百三十两与总银四
百零五两七钱相较则总银少二十四
御制数理精蕴 下编卷七 第 2b 页 WYG0799-0492b.png WYG0799-0492c.png

 两三钱又以米麦共五百石用麦每石
两三钱又以米麦共五百石用麦每石御制数理精蕴 下编卷七 第 3a 页 WYG0799-0493a.png
 价银七钱二分五釐乘之得三百六十
价银七钱二分五釐乘之得三百六十二两五钱与总银相较则总银多四十
三两二钱乃以多少两数相并得六十
七两五钱为一率米麦共五百石为二
率少二十四两三钱为三率得四率一
百八十石即麦数于共五百石内减之
馀三百二十石即米数如以多四十三
两二钱为三率得四率三百二十石亦
御制数理精蕴 下编卷七 第 3b 页 WYG0799-0493b.png WYG0799-0493c.png

 即米数也此法盖以五百石俱为米计
即米数也此法盖以五百石俱为米计之则价应四百三十两与今总银相较
则总银少二十四两三钱如以五百石
俱为麦计之则价应三百六十二两五
钱与今总银相较则总银多四十三两
二钱是米五百石比麦五百石价多六
十七两五钱即麦五百石比米五百石
价少六十七两五钱也是知麦价比米
价少六十七两五钱而麦为五百石今
御制数理精蕴 下编卷七 第 3b 页 WYG0799-0493b.png WYG0799-0493c.png

 总银比米价少二十四两三钱则麦必
总银比米价少二十四两三钱则麦必御制数理精蕴 下编卷七 第 4a 页 WYG0799-0494a.png
 为一百八十石也又米价比麦价多六
为一百八十石也又米价比麦价多六十七两五钱而米为五百石今总银比
麦价多四十三两二钱则米必为三百
二十石也
又法以米麦每石价银相减馀一钱三
分五釐为一率一石为二率以米麦共
五百石用米价乘之得四百三十两与
总银四百零五两七钱相减馀二十四
御制数理精蕴 下编卷七 第 4b 页 WYG0799-0494b.png WYG0799-0494c.png

 两三钱为三率得四率一百八十石即
两三钱为三率得四率一百八十石即麦数于共五百石内减之馀三百二十
石即米数如以米麦共五百石用麦价
乘之得三百六十二两五钱与总银四
百零五两七钱相减馀四十三两二钱
为三率得四率三百二十石亦即米数
也此法盖因米一石比麦一石其价相
差一钱三分五釐是知少一钱三分五
釐而麦为一石今少二十四两三钱则
御制数理精蕴 下编卷七 第 4b 页 WYG0799-0494b.png WYG0799-0494c.png

 麦少为一百八十石也又多一钱三分
麦少为一百八十石也又多一钱三分御制数理精蕴 下编卷七 第 5a 页 WYG0799-0495a.png
 五釐而米为一石今多四十三两二钱
五釐而米为一石今多四十三两二钱则米必为三百二十石也前法以五百
石总价之较与五百石为比此法以每
一石价之较与一石为比其理同也
设如有银一百两共买䌷绢一百疋䌷每疋价银一
两六钱绢每疋价银八钱问䌷绢各得几何
法以䌷绢共一百疋用䌷价一两六钱
乘之得一百六十两与共银一百两相
御制数理精蕴 下编卷七 第 5b 页 WYG0799-0495b.png WYG0799-0495c.png

 较则共银少六十两又以䌷绢共一百
较则共银少六十两又以䌷绢共一百疋用绢价八钱乘之得八十两与共银
一百两相较则共银多二十两乃以多
少两数相并得八十两为一率䌷绢共
一百疋为二率少六十两为三率得四
率七十五疋即绢数于共一百疋内减
之馀二十五疋即䌷数如以多二十两
为三率得四率二十五疋亦即䌷数也
此法盖以一百疋俱为䌷计之则价应
御制数理精蕴 下编卷七 第 5b 页 WYG0799-0495b.png WYG0799-0495c.png

 一百六十两与共银相较则共银少六
一百六十两与共银相较则共银少六御制数理精蕴 下编卷七 第 6a 页 WYG0799-0496a.png
 十两如以一百疋俱为绢计之则价应
十两如以一百疋俱为绢计之则价应八十两与共银相较则共银多二十两
是䌷一百疋比绢一百疋价多八十两
即绢一百疋比䌷一百疋价少八十两
也是知绢价比䌷价少八十两而绢为
一百疋今共价比䌷价少六十两则绢
必为七十五疋也又䌷价比绢价多八
十两而䌷为一百疋今共价比绢价多
御制数理精蕴 下编卷七 第 6b 页 WYG0799-0496b.png WYG0799-0496c.png

 二十两则䌷必为二十五疋也
二十两则䌷必为二十五疋也又法以䌷绢每疋价银相减馀八钱为
一率䌷一疋为二率以䌷绢共一百疋
用䌷价乘之得一百六十两与共银一
百两相减馀六十两为三率得四率七
十五疋即绢数于共一百疋内减之馀
二十五疋即䌷数如以䌷绢共一百疋
用绢价乘之得八十两与共银一百两
相减馀二十两为三率得四率二十五
御制数理精蕴 下编卷七 第 6b 页 WYG0799-0496b.png WYG0799-0496c.png

 疋亦即䌷数也此法盖因䌷一疋比绢
疋亦即䌷数也此法盖因䌷一疋比绢御制数理精蕴 下编卷七 第 7a 页 WYG0799-0497a.png
 一疋其价相差八钱是知少八钱而绢
一疋其价相差八钱是知少八钱而绢为一疋今少六十两则绢必为七十五
疋也又多八钱而䌷为一疋今多二十
两则䌷必为二十五疋也
设如鸡兔同笼但知头共三十六足共一百问鸡兔
各几何
法以鸡兔共三十六头用鸡二足乘之
得七十二足与共足一百相较则共足
御制数理精蕴 下编卷七 第 7b 页 WYG0799-0497b.png WYG0799-0497c.png

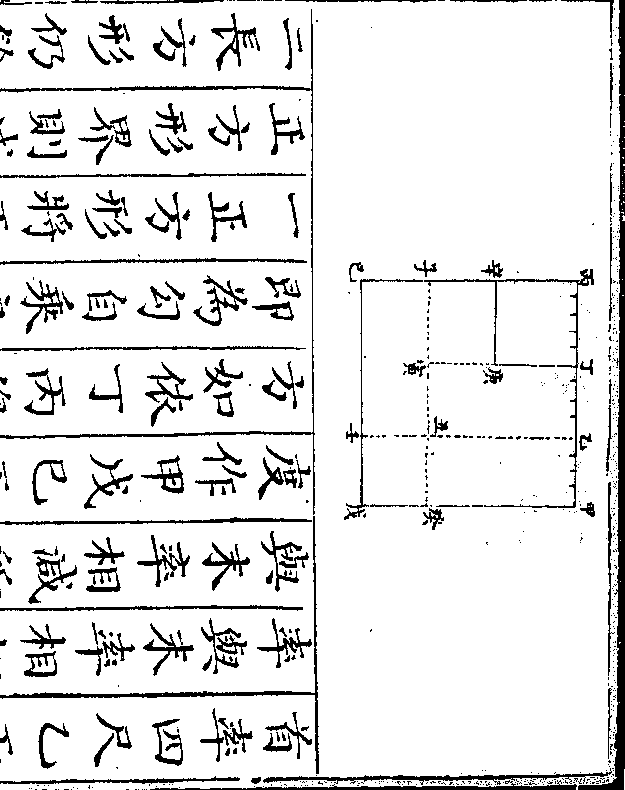 多二十八又以鸡兔共三十六头用兔
多二十八又以鸡兔共三十六头用兔四足乘之得一百四十四足与共足一
百相较则共足少四十四乃以多少两
数相并得七十二足为一率共三十六
头为二率少四十四足为三率得四率
二十二即鸡数于共三十六只内减之
馀十四即兔数如以多二十八足为三
率得四率十四亦即兔数也此法盖以
三十六俱为鸡计之则应七十二足与
御制数理精蕴 下编卷七 第 7b 页 WYG0799-0497b.png WYG0799-0497c.png

 今共足相较则共足多二十八若以三
今共足相较则共足多二十八若以三御制数理精蕴 下编卷七 第 8a 页 WYG0799-0498a.png
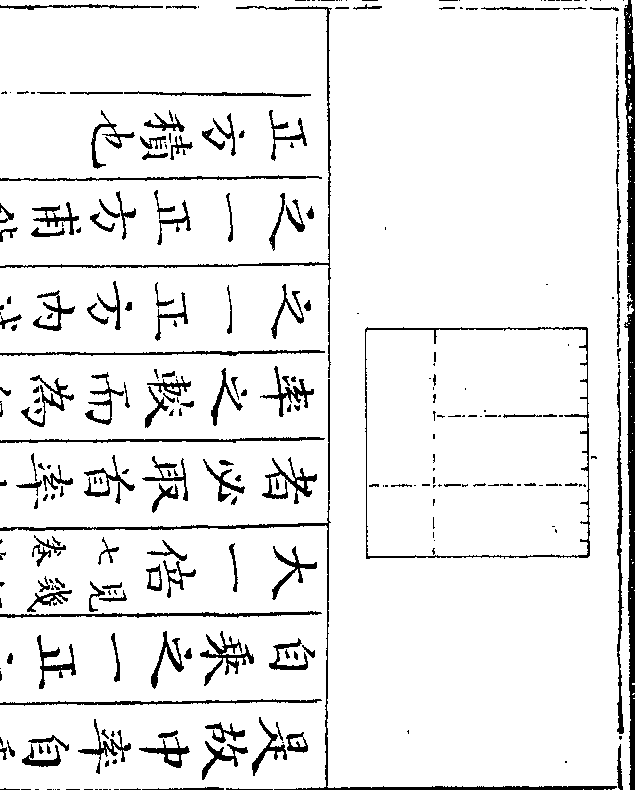 十六俱为兔计之则应一百四十四足
十六俱为兔计之则应一百四十四足与今共足相较则共足少四十四是兔
三十六比鸡三十六多七十二足即鸡
三十六比兔三十六少七十二足也是
知鸡少于兔七十二足而鸡为三十六
只今鸡少于兔四十四足则鸡必为二
十二只也又兔多于鸡七十二足而兔
为三十六只今兔多于鸡二十八足则
御制数理精蕴 下编卷七 第 8b 页 WYG0799-0498b.png WYG0799-0498c.png

 兔必为十四只也
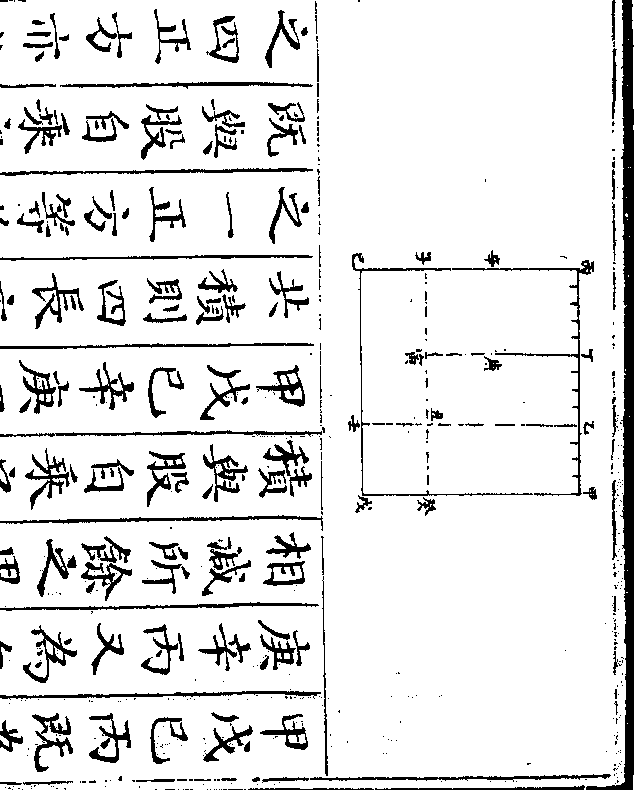
兔必为十四只也又法以鸡二足兔四足相减馀二足为
一率一只为二率又以共三十六只用
兔四足乘之得一百四十四足与共足
一百相减馀四十四为三率得四率二
十二即鸡数于共三十六只内减之馀
十四即兔数如以共三十六只用鸡二
足乘之得七十二足与共足一百相减
馀二十八为三率得四率十四亦即兔
御制数理精蕴 下编卷七 第 8b 页 WYG0799-0498b.png WYG0799-0498c.png

 数也此法盖因鸡一只比兔一只差二
数也此法盖因鸡一只比兔一只差二御制数理精蕴 下编卷七 第 9a 页 WYG0799-0499a.png
 足是知鸡少于兔二足而鸡为一只今
足是知鸡少于兔二足而鸡为一只今少于兔四十四足则鸡必为二十二只
也又兔多于鸡二足而兔为一只今多
于鸡二十八足则兔必为十四只也
设如有羊一百四十只大小不䓁共剪毛一百五十
斤大羊每只剪毛一斤二两小羊每只剪毛十二
两问大小羊各几何
法以共羊一百四十只用大羊剪毛十
御制数理精蕴 下编卷七 第 9b 页 WYG0799-0499b.png WYG0799-0499c.png

 八两乘之(一斤作十六两加/二两即十八两也)得二千五
八两乘之(一斤作十六两加/二两即十八两也)得二千五百二十两与共剪毛二千四百两相较
(一百五十斤变为/两得二千四百两)则共剪毛数少一百
二十两又以共羊一百四十只用小羊
剪毛十二两乘之得一千六百八十两
与共剪毛二千四百两相较则共剪毛
数多七百二十两乃以多少两数相并
得八百四十两为一率共羊一百四十
只为二率多七百二十两为三率得四
御制数理精蕴 下编卷七 第 9b 页 WYG0799-0499b.png WYG0799-0499c.png

 率一百二十只即大羊数于共一百四
率一百二十只即大羊数于共一百四御制数理精蕴 下编卷七 第 10a 页 WYG0799-0500a.png
 十只内减之馀二十只即小羊数如以
十只内减之馀二十只即小羊数如以少一百二十两为三率得四率二十只
亦即小羊数也此法盖以一百四十只
俱为大羊计之则应剪毛二千五百二
十两与共剪毛数相较则共剪毛数少
一百二十两若以一百四十只俱为小
羊计之则应剪毛一千六百八十两与
共剪毛数相较则共剪毛数多七百二
御制数理精蕴 下编卷七 第 10b 页 WYG0799-0500b.png WYG0799-0500c.png

 十两是大羊一百四十只比小羊一百
十两是大羊一百四十只比小羊一百四十只多八百四十两即小羊一百四
十只比大羊一百四十只少八百四十
两也是知多八百四十两而大羊为一
百四十只今少七百二十两则大羊必
为一百二十只也又少八百四十两而
小羊为一百四十只今少一百二十两
则小羊必为二十只也
又法以大羊剪毛十八两小羊剪毛十
御制数理精蕴 下编卷七 第 10b 页 WYG0799-0500b.png WYG0799-0500c.png

 二两相减馀六两为一率一只为二率
二两相减馀六两为一率一只为二率御制数理精蕴 下编卷七 第 11a 页 WYG0799-0501a.png
 以共羊一百四十只用小羊剪毛数乘
以共羊一百四十只用小羊剪毛数乘之得一千六百八十两与共剪毛二千
四百两相减馀七百二十两为三率得
四率一百二十只即大羊数于共一百
四十只内减之馀二十只即小羊数如
以共羊一百四十只用大羊剪毛数乘
之得二千五百二十两与共剪毛二千
四百两相减馀一百二十两为三率得
御制数理精蕴 下编卷七 第 11b 页 WYG0799-0501b.png WYG0799-0501c.png

 四率二十只亦即小羊数也此法盖以
四率二十只亦即小羊数也此法盖以大羊一只比小羊一只所剪毛差六两
是知多六两而大羊为一只今多七百
二十两则大羊必为一百二十只也又
少六两而小羊为一只今少一百二十
两则小羊必为二十只也
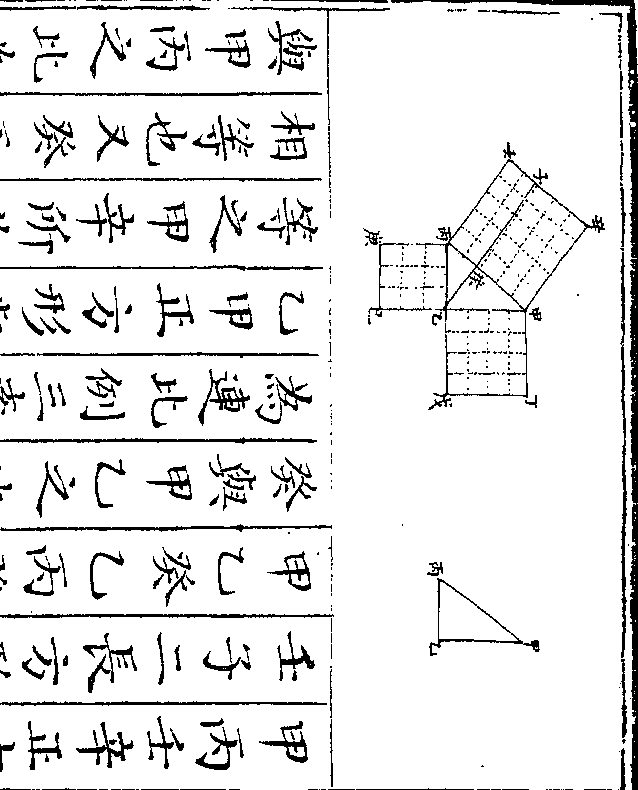
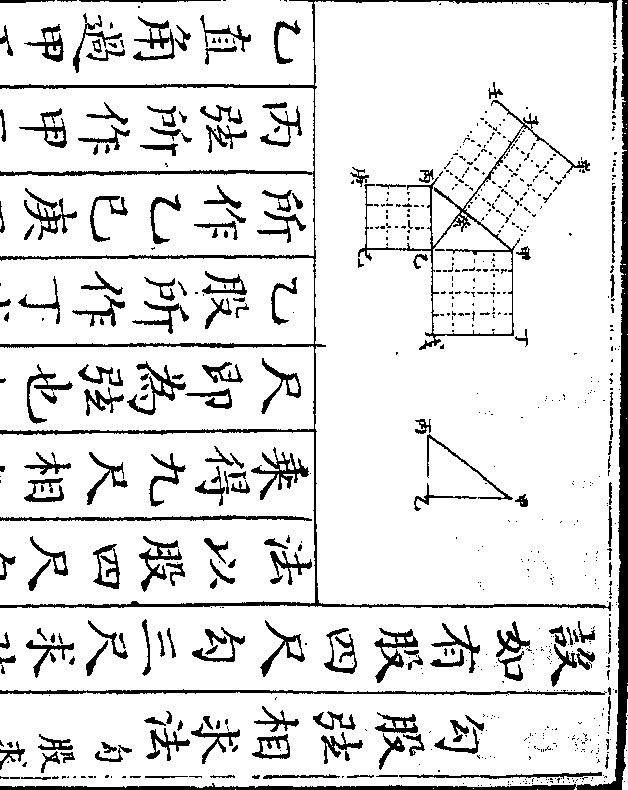
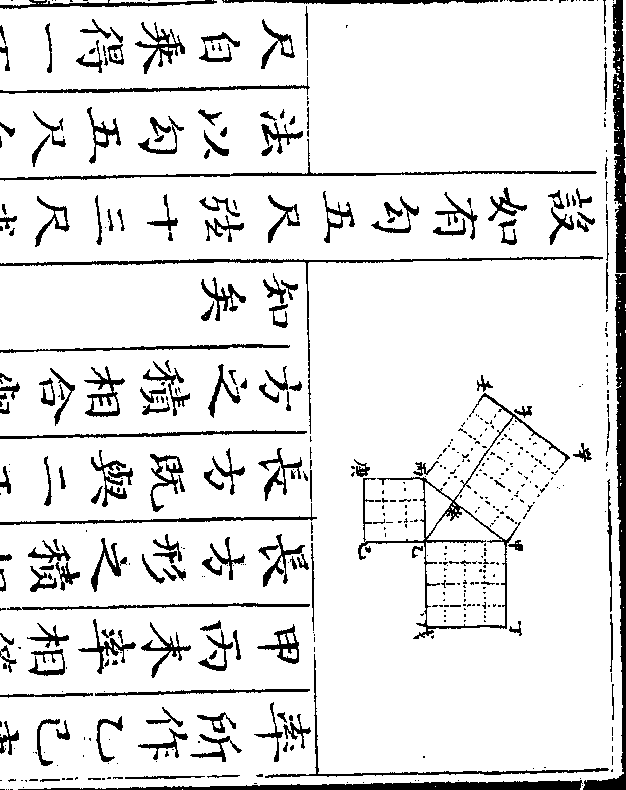
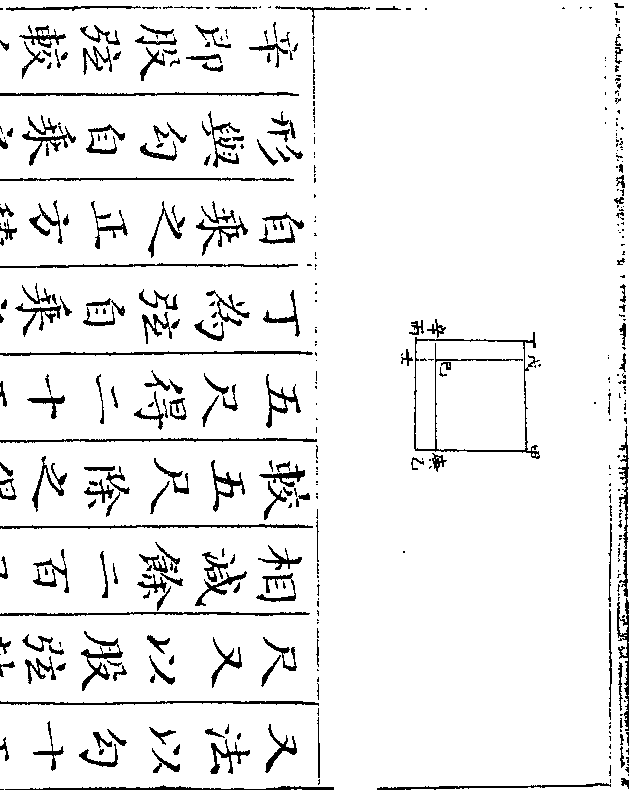
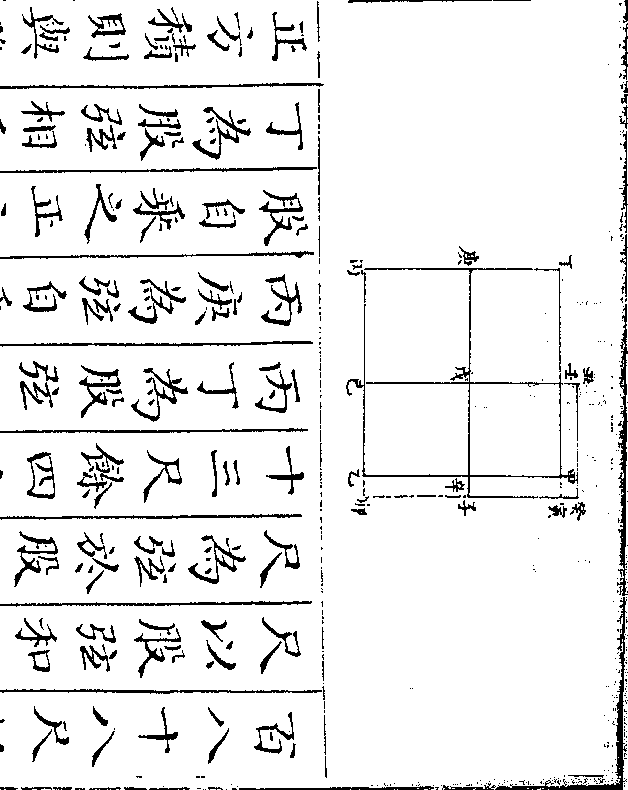
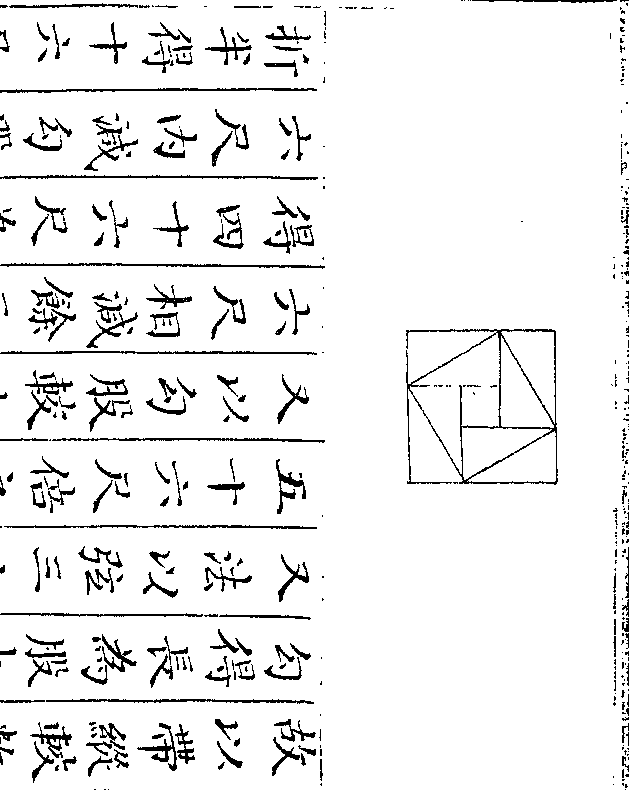
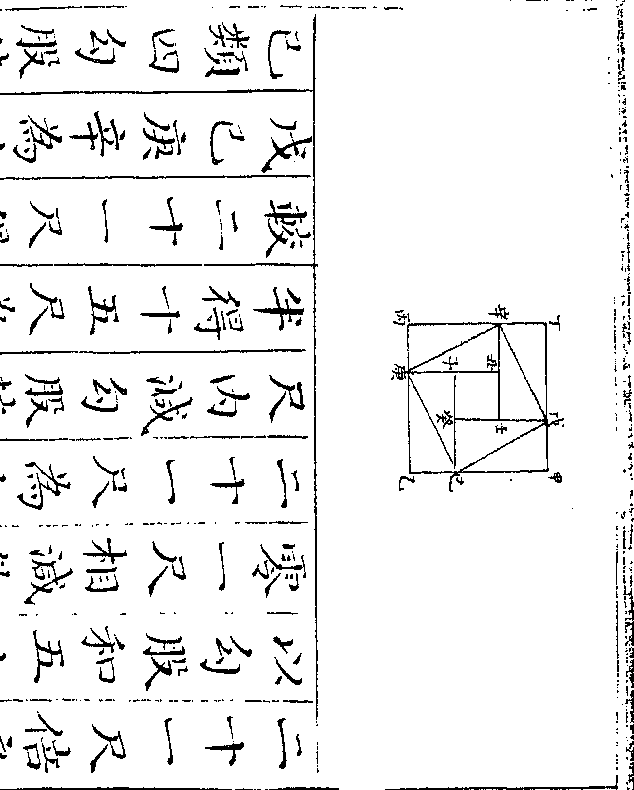
设如有玉在石中但知正方每边四寸共重一百六
十两八钱问玉有几何
法以方边四寸自乘再乘得六十四寸
御制数理精蕴 下编卷七 第 11b 页 WYG0799-0501b.png WYG0799-0501c.png

 为正方体积乃以六十四寸用玉寸方
为正方体积乃以六十四寸用玉寸方御制数理精蕴 下编卷七 第 12a 页 WYG0799-0502a.png
 定率二两六钱乘之得一百六十六两
定率二两六钱乘之得一百六十六两四钱与共重一百六十两八钱相较则
共重少五两六钱又以六十四寸用石
寸方定率二两五钱乘之得一百六十
两与共重一百六十两八钱相较则共
重多八钱乃以多少两数相并得六两
四钱为一率玉六十四寸为二率多八
钱为三率得四率八寸即玉数于共六
御制数理精蕴 下编卷七 第 12b 页 WYG0799-0502b.png WYG0799-0502c.png

 十四寸内减之馀五十六寸即石数如
十四寸内减之馀五十六寸即石数如以少五两六钱为三率得四率五十六
寸亦即石数也既得玉八寸则以玉寸
方定率二两六钱乘之得二十两八钱
即玉之重数于共重一百六十两八钱
内减之馀一百四十两即石之重数如
以石五十六寸用石寸方定率二两五
钱乘之得一百四十两亦即石之重数
也此法盖以六十四寸俱为玉计之则
御制数理精蕴 下编卷七 第 12b 页 WYG0799-0502b.png WYG0799-0502c.png

 应重一百六十六两四钱与共重数相
应重一百六十六两四钱与共重数相御制数理精蕴 下编卷七 第 13a 页 WYG0799-0503a.png
 较则共重数少五两六钱若以六十四
较则共重数少五两六钱若以六十四寸俱为石计之则应重一百六十两与
共重数相较则共重数多八钱是石六
十四寸比玉六十四寸少六两四钱即
玉六十四寸比石六十四寸多六两四
钱也是知多六两四钱而玉为六十四
寸今多八钱则玉必为八寸也又少六
两四钱而石为六十四寸今少五两六
御制数理精蕴 下编卷七 第 13b 页 WYG0799-0503b.png WYG0799-0503c.png

 钱则石必为五十六寸也
钱则石必为五十六寸也又法以玉寸方定率二两六钱与石寸
方定率二两五钱相减馀一钱为一率
一寸为二率以共积六十四寸用石寸
方定率二两五钱乘之得一百六十两
与共重一百六十两八钱相减馀八钱
为三率得四率八寸即玉数于共六十
四寸内减之馀五十六寸即石数如以
共积六十四寸用玉寸方定率二两六
御制数理精蕴 下编卷七 第 13b 页 WYG0799-0503b.png WYG0799-0503c.png

 钱乘之得一百六十六两四钱与共重
钱乘之得一百六十六两四钱与共重御制数理精蕴 下编卷七 第 14a 页 WYG0799-0504a.png
 一百六十两八钱相减馀五两六钱为
一百六十两八钱相减馀五两六钱为三率得四率五十六寸亦即石数也此
法盖以玉一寸比石一寸其重差一钱
是知多一钱而玉为一寸今多八钱则
玉必为八寸也又少一钱而石为一寸
今少五两六钱则石必为五十六寸也
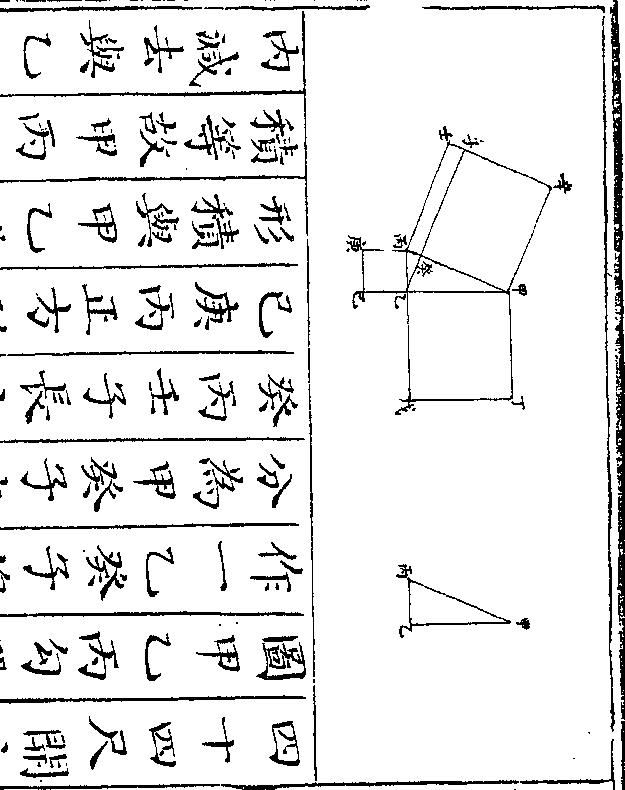
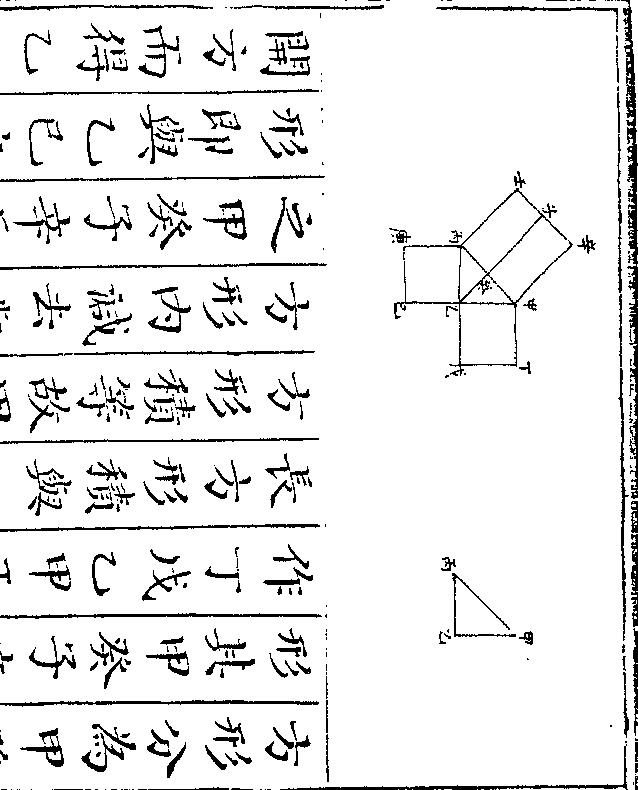
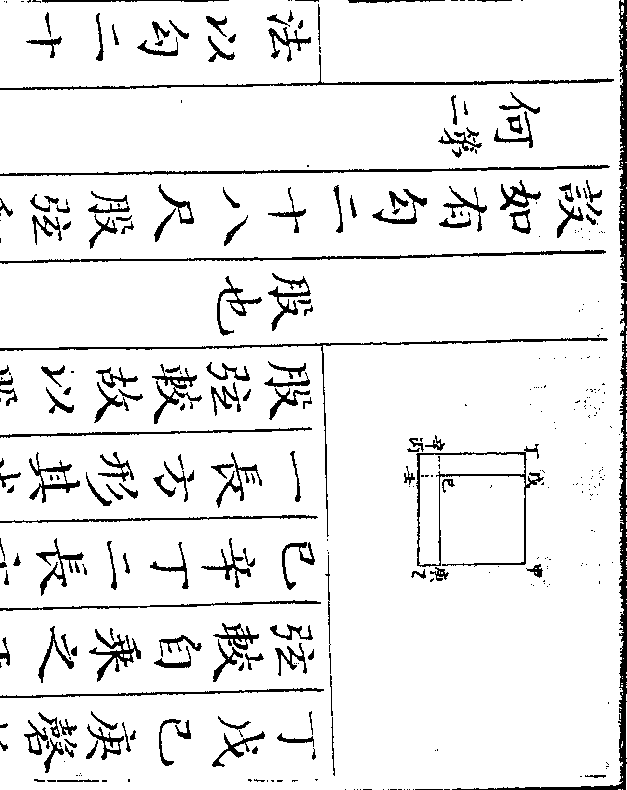
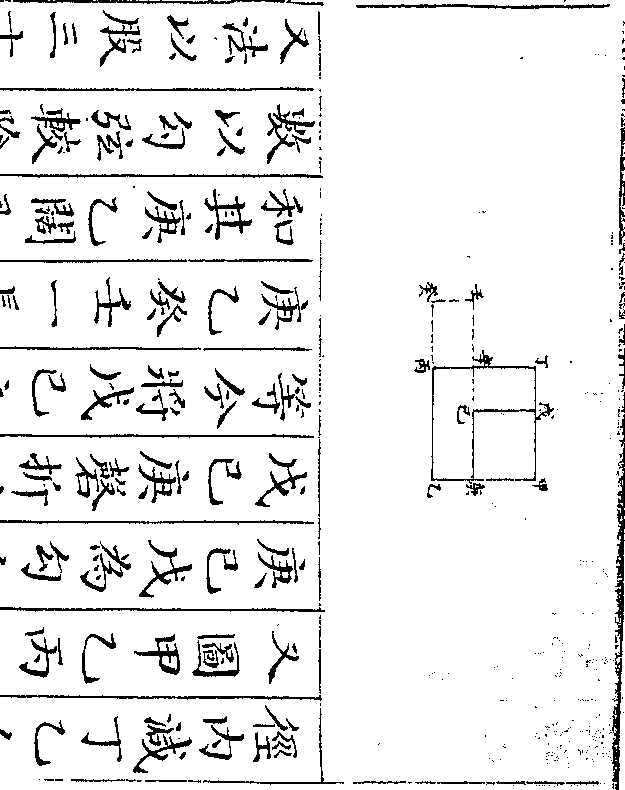
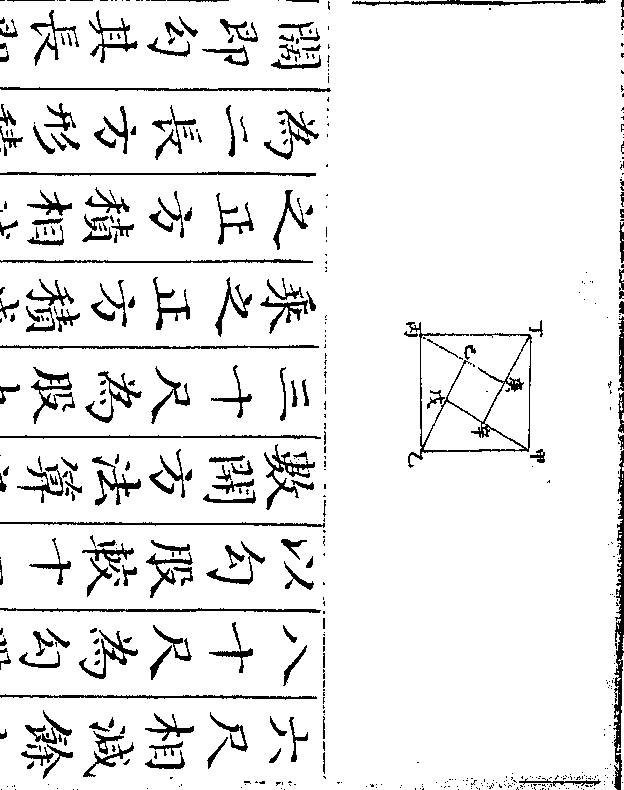
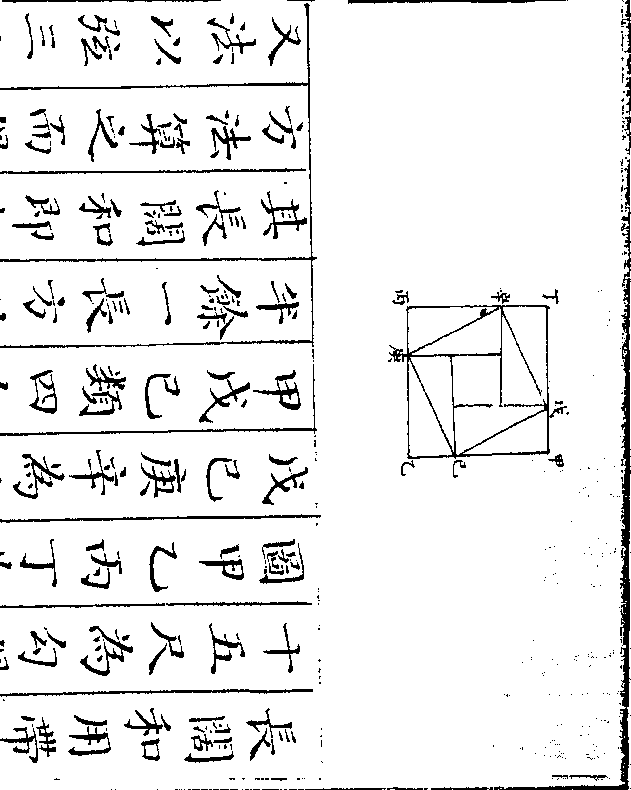
设如有金银共重三百二十一两镕于一处作成一
正方体每边三寸问金银各重几何
御制数理精蕴 下编卷七 第 14b 页 WYG0799-0504b.png WYG0799-0504c.png

 法以方边三寸自乘再乘得二十七寸
法以方边三寸自乘再乘得二十七寸为正方体积乃以二十七寸俱作金算
用金寸方定率十六两八钱乘之得四
百五十三两六钱与共重三百二十一
两相较则共重少一百三十二两六钱
又以二十七寸俱作银算用银寸方定
率九两乘之得二百四十三两与共重
三百二十一两相较则共重多七十八
两乃以多少两数相并得二百一十两
御制数理精蕴 下编卷七 第 14b 页 WYG0799-0504b.png WYG0799-0504c.png

 六钱为一率金二十七寸重四百五十
六钱为一率金二十七寸重四百五十御制数理精蕴 下编卷七 第 15a 页 WYG0799-0505a.png
 三两六钱为二率多七十八两为三率
三两六钱为二率多七十八两为三率得四率一百六十八两即金数于共重
三百二十一两内减之馀一百五十三
两即银数如以银二十七寸重二百四
十三两为二率少一百三十二两六钱
为三率得四率一百五十三两亦即银
数也此法盖因金二十七寸比银二十
七寸多二百一十两六钱即银二十七
御制数理精蕴 下编卷七 第 15b 页 WYG0799-0505b.png WYG0799-0505c.png

 寸比金二十七寸少二百一十两六钱
寸比金二十七寸少二百一十两六钱也是知金比银多二百一十两六钱而
金为四百五十三两六钱今多七十八
两则金必为一百六十八两也又银比
金少二百一十两六钱而银为二百四
十三两今少一百三十二两六钱则银
必为一百五十三两也
又法以银寸方定率九两与金寸方定
率十六两八钱相减馀七两八钱为一
御制数理精蕴 下编卷七 第 15b 页 WYG0799-0505b.png WYG0799-0505c.png

 率金一寸重十六两八钱为二率以共
率金一寸重十六两八钱为二率以共御制数理精蕴 下编卷七 第 16a 页 WYG0799-0506a.png
 积二十七寸用银寸方定率九两乘之
积二十七寸用银寸方定率九两乘之得二百四十三两与共重三百二十一
两相减馀七十八两为三率得四率一
百六十八两即金数于共重三百二十
一两内减之馀一百五十三两即银数
如以银一寸重九两为二率以共积二
十七寸用金寸方定率十六两八钱乘
之得四百五十三两六钱与共重三百
御制数理精蕴 下编卷七 第 16b 页 WYG0799-0506b.png WYG0799-0506c.png

 二十一两相减馀一百三十二两六钱
二十一两相减馀一百三十二两六钱为三率得四率一百五十三两亦即银
数也此法盖以金一寸比银一寸其重
相差七两八钱是知多七两八钱而金
为十六两八钱今多七十八两则金必
为一百六十八两也又少七两八钱而
银为九两今少一百三十二两六钱则
银必为一百五十三两也
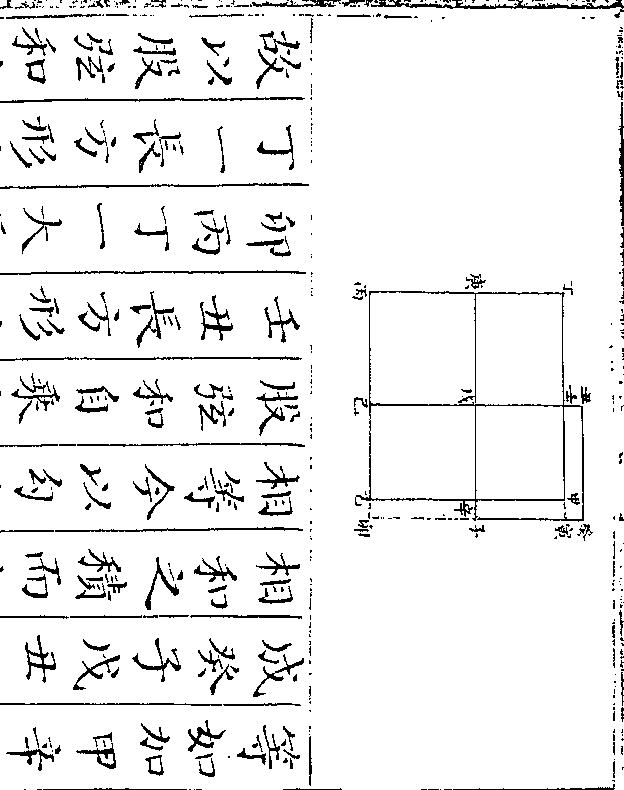
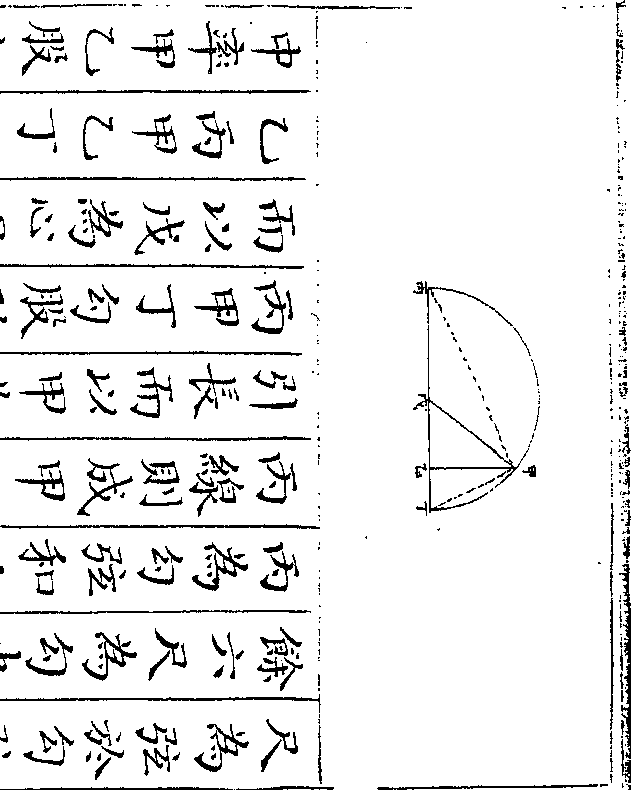
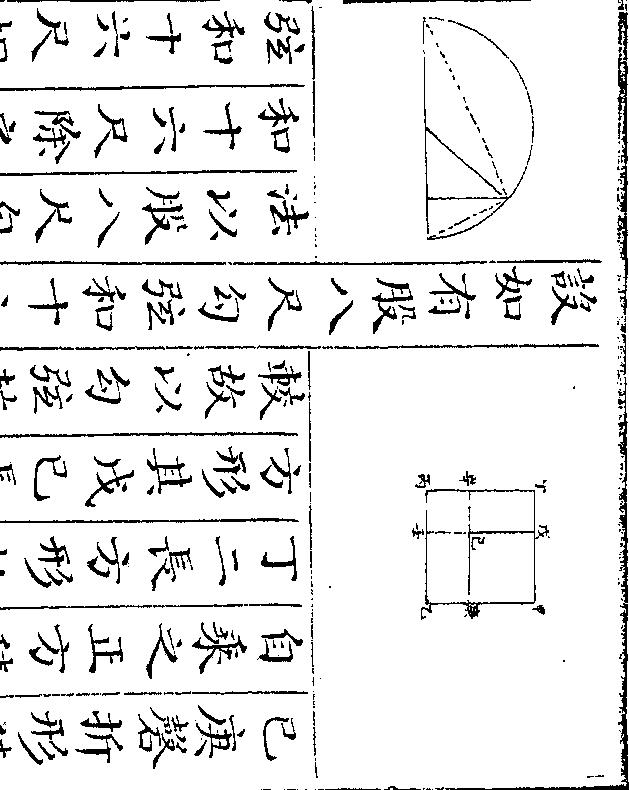
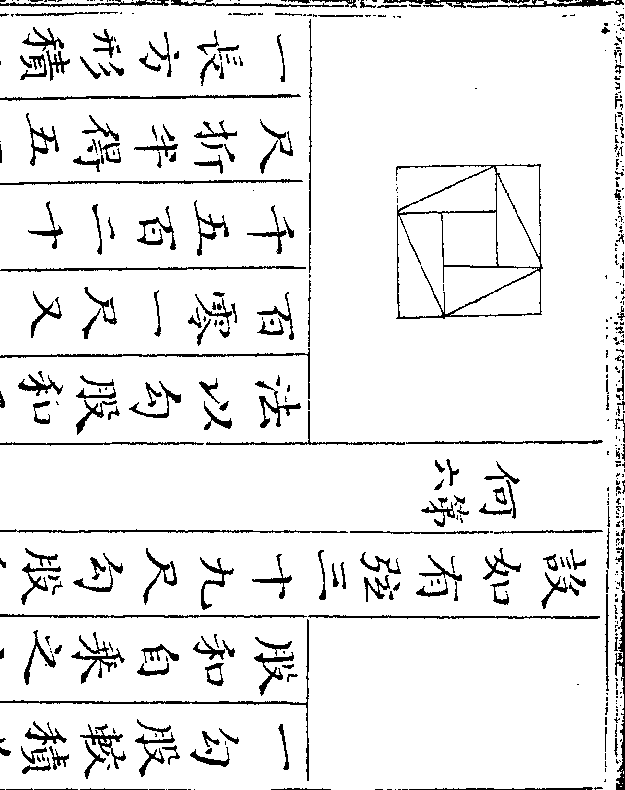
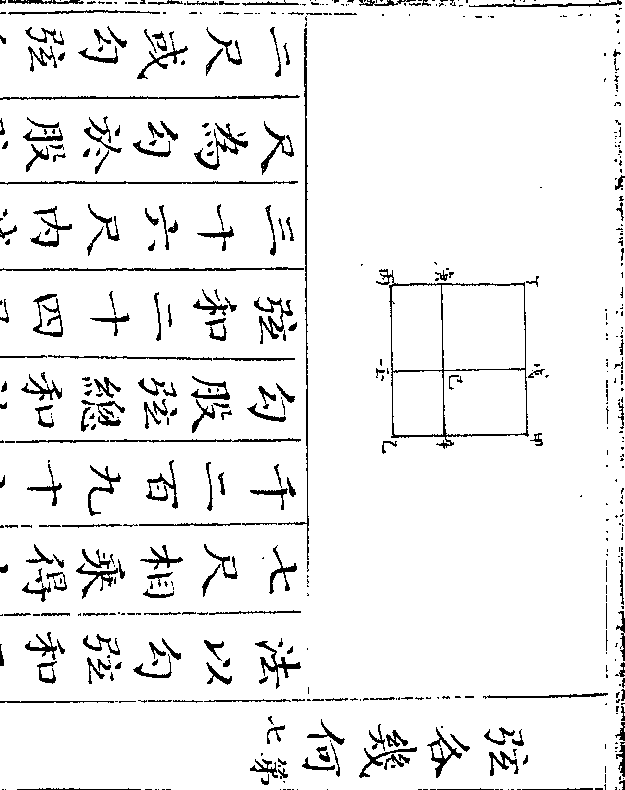
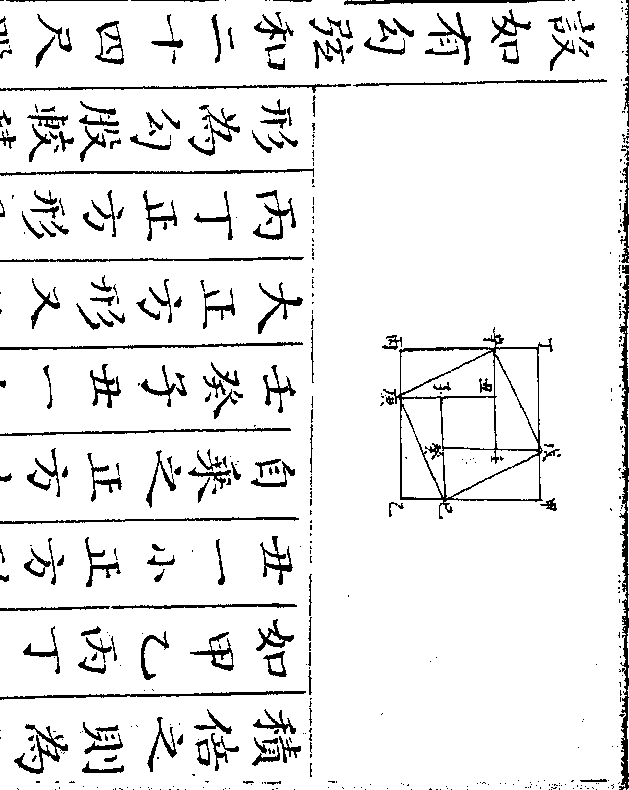
设如有金器一件内有银相参合共重一百七十两
御制数理精蕴 下编卷七 第 16b 页 WYG0799-0506b.png WYG0799-0506c.png

 四钱问金银各重若干
四钱问金银各重若干御制数理精蕴 下编卷七 第 17a 页 WYG0799-0507a.png
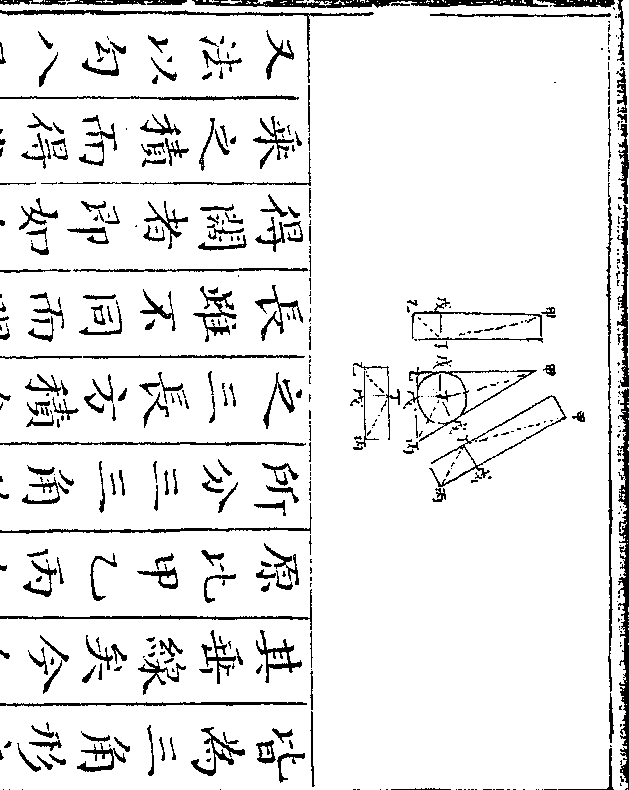
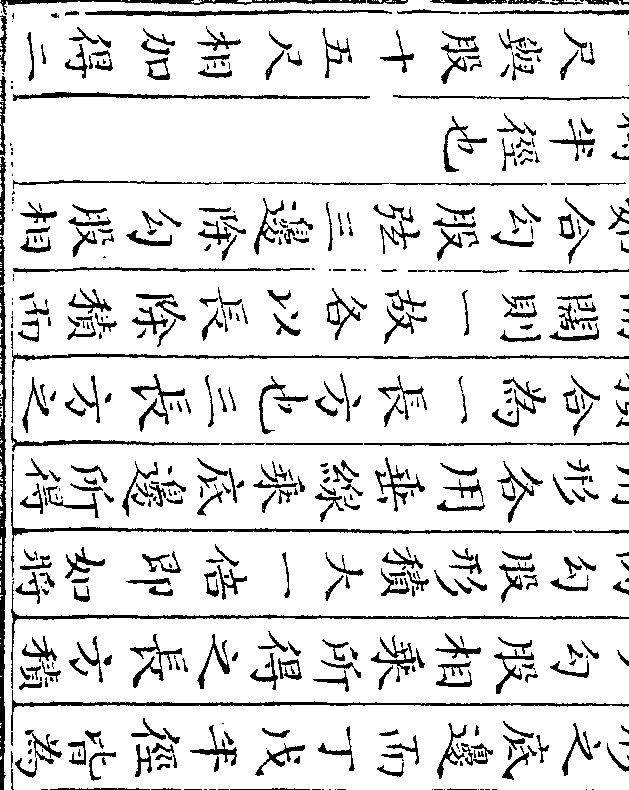
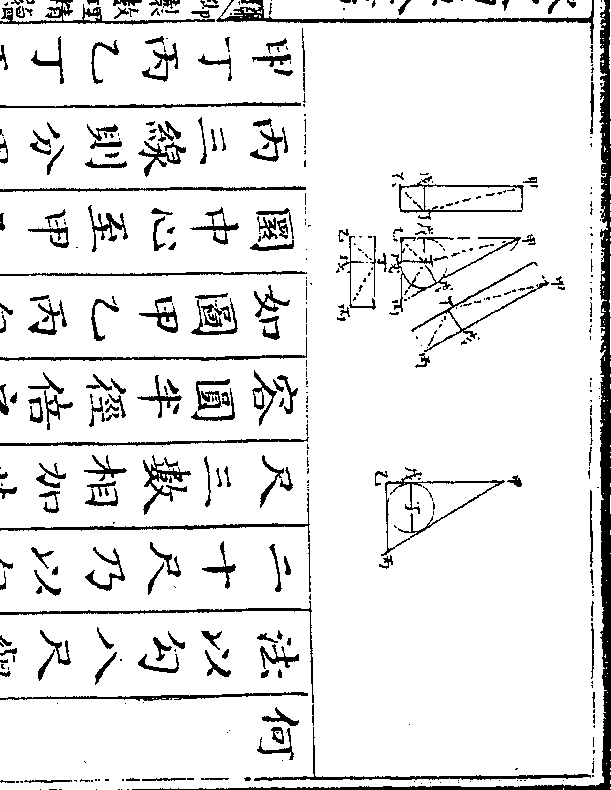
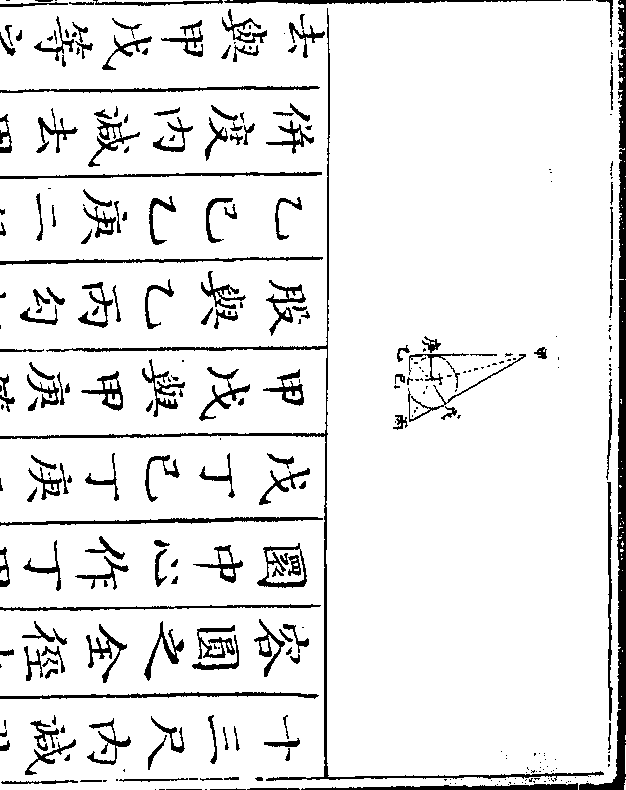
 法用一桶盛水令满将金器入内看溢
法用一桶盛水令满将金器入内看溢出之水得正方寸数几何假如得十二
寸即为金银共积以金寸方定率十六
两八钱乘之得二百零一两六钱与共
重一百七十两四钱相较则共重少三
十一两二钱又以银寸方定率九两乘
之得一百零八两与共重一百七十两
四钱相较则共重多六十二两四钱乃
御制数理精蕴 下编卷七 第 17b 页 WYG0799-0507b.png WYG0799-0507c.png

 以多少两数相并得九十三两六钱为
以多少两数相并得九十三两六钱为一率金十二寸重二百零一两六钱为
二率多六十二两四钱为三率得四率
一百三十四两四钱即金数于共重一
百七十两四钱内减之馀三十六两即
银数如以银十二寸重一百零八两为
二率少三十一两二钱为三率得四率
三十六两亦即银数也
又法以金寸方定率十六两八钱与银
御制数理精蕴 下编卷七 第 17b 页 WYG0799-0507b.png WYG0799-0507c.png

 寸方定率九两相减馀七两八钱为一
寸方定率九两相减馀七两八钱为一御制数理精蕴 下编卷七 第 18a 页 WYG0799-0508a.png
 率金一寸重十六两八钱为二率以共
率金一寸重十六两八钱为二率以共积十二寸用银寸方定率九两乘之得
一百零八两与共重一百七十两四钱
相减馀六十二两四钱为三率得四率
一百三十四两四钱即金数于共重一
百七十两四钱内减之馀三十六两即
银数如以银一寸重九两为二率以共
积十二寸用金寸方定率十六两八钱
御制数理精蕴 下编卷七 第 18b 页 WYG0799-0508b.png WYG0799-0508c.png
 乘之得二百零一两六钱与共重一百
乘之得二百零一两六钱与共重一百七十两四钱相减馀三十一两二钱为
三率得四率三十六两亦即银数也
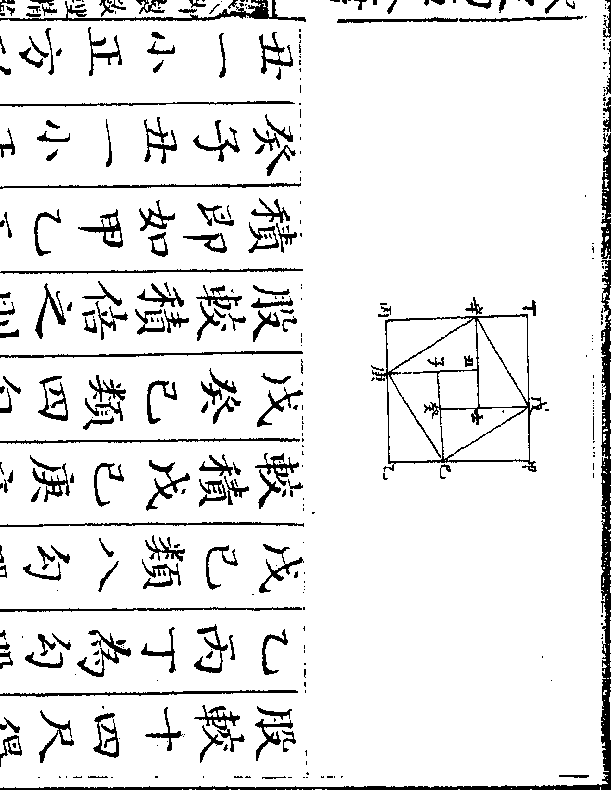
设如有金铸一器重三百两俱系九六成色今用九
九成色及九一成色二䓁金替换问各得几何
法以九六成色与三百两相乘得二百
八十八两为原金数乃以九九成色与
三百两相乘得二百九十七两与原金
二百八十八两相较则原金少九两又
御制数理精蕴 下编卷七 第 18b 页 WYG0799-0508b.png WYG0799-0508c.png

 以九一成色与三百两相乘得二百七
以九一成色与三百两相乘得二百七御制数理精蕴 下编卷七 第 19a 页 WYG0799-0509a.png
 十三两与原金二百八十八两相较则
十三两与原金二百八十八两相较则原金多十五两爰以多少两数相并得
二十四两为一率三百两为二率原金
比九一成色多十五两为三率得四率
一百八十七两五钱即九九成色金数
于共重三百两内减之馀一百一十二
两五钱即九一成色金数如以原金比
九九成色少九两为三率得四率一百
御制数理精蕴 下编卷七 第 19b 页 WYG0799-0509b.png WYG0799-0509c.png

 一十二两五钱亦即九一成色金数也
一十二两五钱亦即九一成色金数也盖九六成色金三百两为十成金二百
八十八两而九九成色金三百两为十
成金二百九十七两九一成色金三百
两为十成金二百七十三两是知九九
比九一多二十四两而九九成色金为
三百两今九六比九一多十五两则九
九成色金必为一百八十七两五钱也
又九一比九九少二十四两而九一成
御制数理精蕴 下编卷七 第 19b 页 WYG0799-0509b.png WYG0799-0509c.png

 色金为三百两今九六比九九少九两
色金为三百两今九六比九九少九两御制数理精蕴 下编卷七 第 20a 页 WYG0799-0510a.png
 则九一成色金必为一百一十二两五
则九一成色金必为一百一十二两五钱也
又法以九九与九一相减馀八分为一
率金三百两为二率以九一与九六相
减馀五分为三率得四率一百八十七
两五钱即九九成色金数于共重三百
两内减之馀一百一十二两五钱即九
一成色金数如以九九与九六相减馀
御制数理精蕴 下编卷七 第 20b 页 WYG0799-0510b.png WYG0799-0510c.png

 三分为三率得四率一百一十二两五
三分为三率得四率一百一十二两五钱亦即九一成色金数也盖九九比九
一多八分而九九成色金为三百两今
九六比九一多五分则九九成色金必
为一百八十七两五钱也又九一比九
九少八分而九一成色金为三百两今
九六比九九少三分则九一成色金必
为一百一十二两五钱也
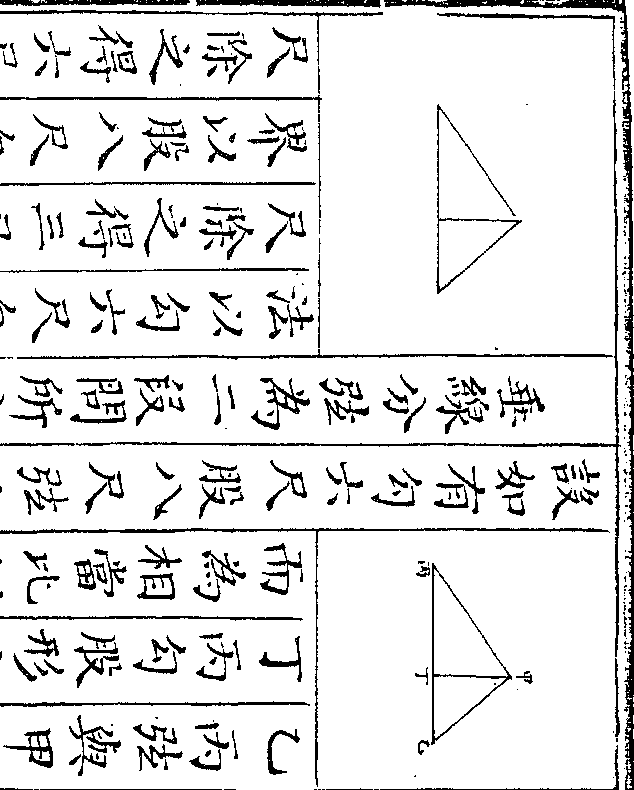
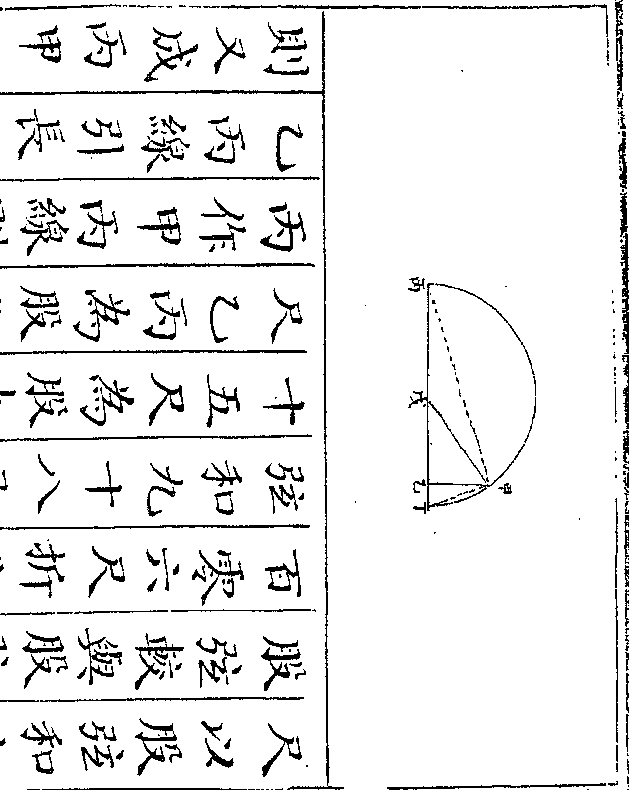
设如甲乙二人有金成色不䓁甲金一两可准银一
御制数理精蕴 下编卷七 第 20b 页 WYG0799-0510b.png WYG0799-0510c.png

 十二两乙金一两可准银八两今欲镕为一处令
十二两乙金一两可准银八两今欲镕为一处令御制数理精蕴 下编卷七 第 21a 页 WYG0799-0511a.png
 金一两准银九两问甲乙二人于一两金中各出
金一两准银九两问甲乙二人于一两金中各出金几何
法以准银九两为中数与甲金准银十
二两相较少三两与乙金准银八两相
较多一两乃以多少两数并之得四两
为一率金一两为二率比甲少三两为
三率得四率七钱五分即乙所出金数
如以比乙多一两为三率得四率二钱
御制数理精蕴 下编卷七 第 21b 页 WYG0799-0511b.png WYG0799-0511c.png

 五分即甲所出金数也此法因银十二
五分即甲所出金数也此法因银十二两与八两皆金一两所准之数虽相乘
其数不动故直以十二与八相减作一
率(以十二与九八与九之两较相并/得四即十二与八相减之馀数也)盖
乙比甲银少四两而乙金为一两今比
甲银少三两则乙金必为七钱五分也
又甲比乙银多四两而甲金为一两今
比乙银多一两则甲金必为二钱五分
也
御制数理精蕴 下编卷七 第 21b 页 WYG0799-0511b.png WYG0799-0511c.png

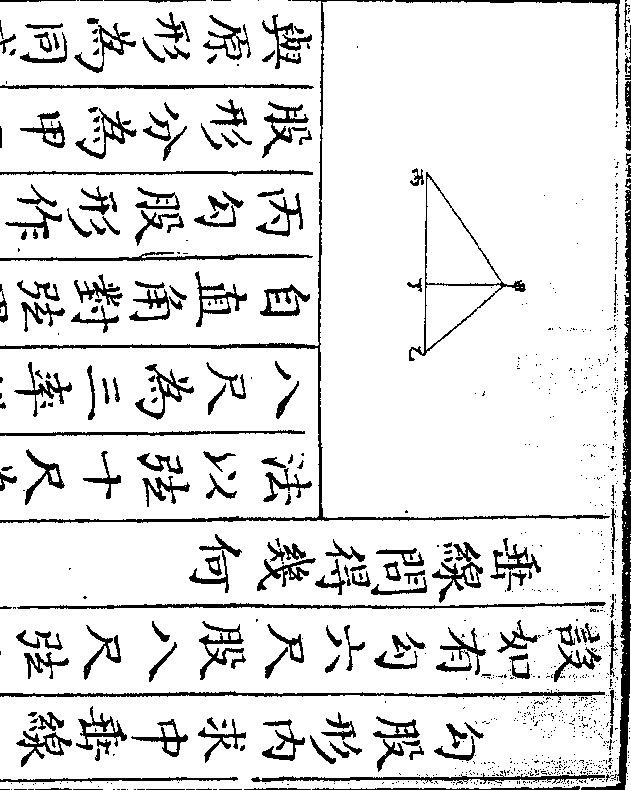
 设如有钱四千九百九十五文买栗枣共五千枚只
设如有钱四千九百九十五文买栗枣共五千枚只御制数理精蕴 下编卷七 第 22a 页 WYG0799-0512a.png
 云栗九枚钱一十一文枣七枚钱四文问二色与
云栗九枚钱一十一文枣七枚钱四文问二色与价各得若干
法先用互乘以齐其分以栗九与枣七
相乘得六十三为乘出之总物分即以
六十三乘总钱四千九百九十五文得
三十一万四千六百八十五文为乘出
之总钱数又以枣七乘栗价十一文得
七十七文为乘出之栗价以栗九乘枣
御制数理精蕴 下编卷七 第 22b 页 WYG0799-0512b.png WYG0799-0512c.png

 价四文得三十六文为乘出之枣价然
价四文得三十六文为乘出之枣价然后以栗枣共五千枚用栗价七十七文
乘之得三十八万五千文与乘出之总
钱三十一万四千六百八十五文相较
则总钱少七万零三百一十五文又以
栗枣共五千枚用枣价三十六文乘之
得一十八万文与乘出之总钱三十一
万四千六百八十五文相较则总钱多
一十三万四千六百八十五文乃以栗
御制数理精蕴 下编卷七 第 22b 页 WYG0799-0512b.png WYG0799-0512c.png

 价七十七文与枣价三十六文相减馀
价七十七文与枣价三十六文相减馀御制数理精蕴 下编卷七 第 23a 页 WYG0799-0513a.png
 四十一文为一率一枚为二率多一十
四十一文为一率一枚为二率多一十三万四千六百八十五文为三率得四
率三千二百八十五枚即栗数于共五
千枚内减之馀一千七百一十五枚即
枣数如以少七万零三百一十五文为
三率得四率一千七百一十五枚亦即
枣数也既得栗数则以九枚为一率十
一文为二率三千二百八十五枚为三
御制数理精蕴 下编卷七 第 23b 页 WYG0799-0513b.png WYG0799-0513c.png

 率得四率四千零一十五文即栗之共
率得四率四千零一十五文即栗之共价既得枣数则以七枚为一率四文为
二率一千七百一十五枚为三率得四
率九百八十文即枣之共价也如欲先
得各价则以四十一文为一率栗价七
十七文为二率多一十三万四千六百
八十五文为三率得四率二十五万二
千九百四十五文以六十三除之得四
千零一十五文即栗之共价于共钱四
御制数理精蕴 下编卷七 第 23b 页 WYG0799-0513b.png WYG0799-0513c.png

 千九百九十五文内减之馀九百八十
千九百九十五文内减之馀九百八十御制数理精蕴 下编卷七 第 24a 页 WYG0799-0514a.png
 文即枣之共价如以四十一文为一率
文即枣之共价如以四十一文为一率枣价三十六文为二率少七万零三百
一十五文为三率得四率六万一千七
百四十文以六十三除之得九百八十
文亦即枣之共价也此法九章名为贵
贱相和盖因栗九枚枣七枚其数不同
故用互乘以齐其分得栗六十三枚价
七十七文枣六十三枚价三十六文今
御制数理精蕴 下编卷七 第 24b 页 WYG0799-0514b.png WYG0799-0514c.png

 以六十三枚当一枚则为栗一枚价七
以六十三枚当一枚则为栗一枚价七十七文枣一枚价三十六文是其价各
加六十三倍故将总钱亦加六十三倍
即为栗枣共五千枚共价三十一万四
千六百八十五文而栗一枚比枣一枚
其价相差四十一文是知栗价比枣价
多四十一文而栗为一枚今共价比枣
价多一十三万四千六百八十五文则
栗必为三千二百八十五枚也又枣价
御制数理精蕴 下编卷七 第 24b 页 WYG0799-0514b.png WYG0799-0514c.png

 比栗价少四十一文而枣为一枚今共
比栗价少四十一文而枣为一枚今共御制数理精蕴 下编卷七 第 25a 页 WYG0799-0515a.png
 价比栗价少七万零三百一十五文则
价比栗价少七万零三百一十五文则枣必为一千七百一十五枚也其先求
各价者盖因栗价比枣价多四十一文
而栗价为七十七文今共价比枣价多
一十三万四千六百八十五文则栗价
少为二十五万二千九百四十五文因
各价皆为加六十三倍故以六十三除
之得四千零一十五文为栗之共价也
御制数理精蕴 下编卷七 第 25b 页 WYG0799-0515b.png WYG0799-0515c.png

 又枣价比栗价少四十一文而枣价为
又枣价比栗价少四十一文而枣价为三十六文今共价比栗价少七万零三
百一十五文则枣价必为六万一千七
百四十文亦以六十三除之得九百八
十文为枣之共价也
又法以枣七枚栗九枚共五千枚列于
上枣价四文栗价十一文共价四千九
百九十五文列于下乃以下枣价四文
遍乘上枣七枚栗九枚共五千枚得枣
御制数理精蕴 下编卷七 第 25b 页 WYG0799-0515b.png WYG0799-0515c.png

 二十八枚栗三十六枚共二万枚又以
二十八枚栗三十六枚共二万枚又以御制数理精蕴 下编卷七 第 26a 页 WYG0799-0516a.png
 上枣七枚遍乘下枣价四文栗价十一
上枣七枚遍乘下枣价四文栗价十一文共价四千九百九十五文得枣价二
十八文栗价七十七文共价三万四千
九百六十五文两下相较则枣数与枣
价同为二十八彼此减尽枣价比栗数
多四十一共价比共数多一万四千九
百六十五爰以多四十一为一率栗九
枚为二率多一万四千九百六十五为
御制数理精蕴 下编卷七 第 26b 页 WYG0799-0516b.png WYG0799-0516c.png

 三率得四率三千二百八十五枚即栗
三率得四率三千二百八十五枚即栗数于五千枚内减之馀一千七百一十
五枚即枣数如以栗价十一文为二率
得四率四千零一十五文即栗之共价
于四千九百九十五文内减之馀九百
八十文即枣之共价也若欲先得枣数
则以栗九枚价十一文移于前枣七枚
价四文移于后乃以下栗价十一文遍
乘上栗九枚枣七枚共五千枚得栗九
御制数理精蕴 下编卷七 第 26b 页 WYG0799-0516b.png WYG0799-0516c.png

 十九枚枣七十七枚共五万五千枚又
十九枚枣七十七枚共五万五千枚又御制数理精蕴 下编卷七 第 27a 页 WYG0799-0517a.png
 以上栗九枚遍乘下栗价十一文枣价
以上栗九枚遍乘下栗价十一文枣价四文共价四千九百九十五文得栗价
九十九文枣价三十六文共价四万四
千九百五十五文两下相较则栗数与
栗价同为九十九彼此减尽枣价比枣
数少四十一共价比共数少一万零四
十五爰以少四十一为一率枣七枚为
二率少一万零四十五为三率得四率
御制数理精蕴 下编卷七 第 27b 页 WYG0799-0517b.png WYG0799-0517c.png

 一千七百一十五枚即枣数如以枣价
一千七百一十五枚即枣数如以枣价四文为二率得四率九百八十文即枣
之共价也此法与方程互乘齐分之理
同其先求栗数而以枣数列于前者盖
将枣数栗数共数皆加四倍枣价栗价
共价皆加七倍则枣数与枣价相同是
为每枣一枚价一文夫枣数与枣价既
相同而减尽无馀则枣栗共数内之共
枣数与枣栗共价内之共枣价亦必相
御制数理精蕴 下编卷七 第 27b 页 WYG0799-0517b.png WYG0799-0517c.png

 同而减尽无馀所馀者即为共栗价多
同而减尽无馀所馀者即为共栗价多御制数理精蕴 下编卷七 第 28a 页 WYG0799-0518a.png
 于共栗数之较是比每栗一枚价一文
于共栗数之较是比每栗一枚价一文所多之数是知栗价比栗数多四十一
文而栗为九枚栗价为十一文今共栗
价比共栗数多一万四千九百六十五
文则栗必为三千二百八十五枚栗价
必为四千零一十五文也其先求枣数
而以栗数列于前者盖将栗数枣数共
数皆加十一倍栗价枣价共价皆加九
御制数理精蕴 下编卷七 第 28b 页 WYG0799-0518b.png WYG0799-0518c.png

 倍则栗数与栗价相同是为每栗一枚
倍则栗数与栗价相同是为每栗一枚价一文夫栗数与栗价既相同而减尽
无馀则栗枣共数内之共栗数与栗枣
共价内之共栗价亦必相同而减尽无
馀所馀者即为共枣价少于共枣数之
较是比每枣一枚价一文所少之数是
知枣价比枣数少四十一文而枣为七
枚枣价为四文今共枣价比共枣数少
一万零四十五文则枣必为一千七百
御制数理精蕴 下编卷七 第 28b 页 WYG0799-0518b.png WYG0799-0518c.png

 一十五枚枣价必为九百八十文也
一十五枚枣价必为九百八十文也御制数理精蕴 下编卷七 第 29a 页 WYG0799-0519a.png
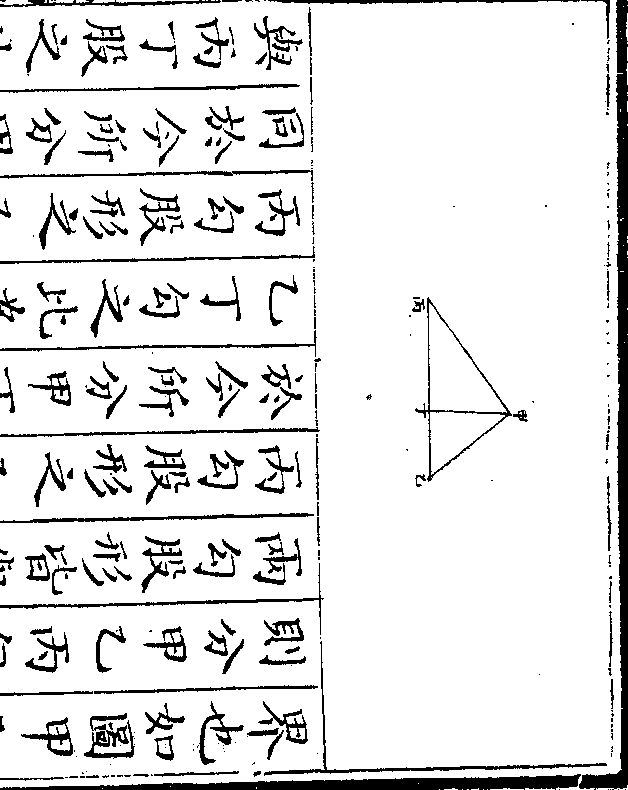
 设如有僧一百人给馒首一百个大僧一人给三个
设如有僧一百人给馒首一百个大僧一人给三个小僧三人给一个问大小僧数及各得馒首若干
法先用互乘以齐其分以大僧一人与
小僧三人相乘得三人为乘出之总僧
数即以三人乘馒首一百个得三百个
为乘出之共馒首数又以小僧三人乘
大僧馒首三个得九个为乘出之大僧
馒首数以大僧一人乘小僧馒首一个
御制数理精蕴 下编卷七 第 29b 页 WYG0799-0519b.png WYG0799-0519c.png

 仍得一个为乘出之小僧馒首数然后
仍得一个为乘出之小僧馒首数然后以共僧一百人与大僧馒首九个相乘
得九百个与乘出之共馒首三百个相
较则共馒首少六百个又以共僧一百
人与小僧馒首一个相乘得一百个与
乘出之共馒首三百个相较则共馒首
多二百个乃以大僧馒首九个与小僧
馒首一个相减馀八个为一率一人为
二率多二百个为三率得四率二十五
御制数理精蕴 下编卷七 第 29b 页 WYG0799-0519b.png WYG0799-0519c.png

 人即大僧数于共僧一百人内减之馀
人即大僧数于共僧一百人内减之馀御制数理精蕴 下编卷七 第 30a 页 WYG0799-0520a.png
 七十五人即小僧数如以少六百个为
七十五人即小僧数如以少六百个为三率得四率七十五人亦即小僧数也
既得僧数则以一人为一率三个为二
率大僧二十五人为三率得四率七十
五个即大僧馒首数又以三人为一率
一个为二率小僧七十五人为三率得
四率二十五个即小僧馒首数也如欲
先得馒首数则仍以八个为一率大僧
御制数理精蕴 下编卷七 第 30b 页 WYG0799-0520b.png WYG0799-0520c.png

 馒首九个为二率今多二百个为三率
馒首九个为二率今多二百个为三率得四率二百二十五个三归之得七十
五个即大僧馒首数于共馒首一百个
内减之馀二十五个即小僧馒首数如
以八个为一率小僧馒首一个为二率
今少六百个为三率得四率七十五个
三归之得二十五个亦即小僧馒首数
也此法用互乘得大僧三人馒首九个
小僧三人馒首一个今以三人当一人
御制数理精蕴 下编卷七 第 30b 页 WYG0799-0520b.png WYG0799-0520c.png

 则为大僧一人馒首九个小僧一人馒
则为大僧一人馒首九个小僧一人馒御制数理精蕴 下编卷七 第 31a 页 WYG0799-0521a.png
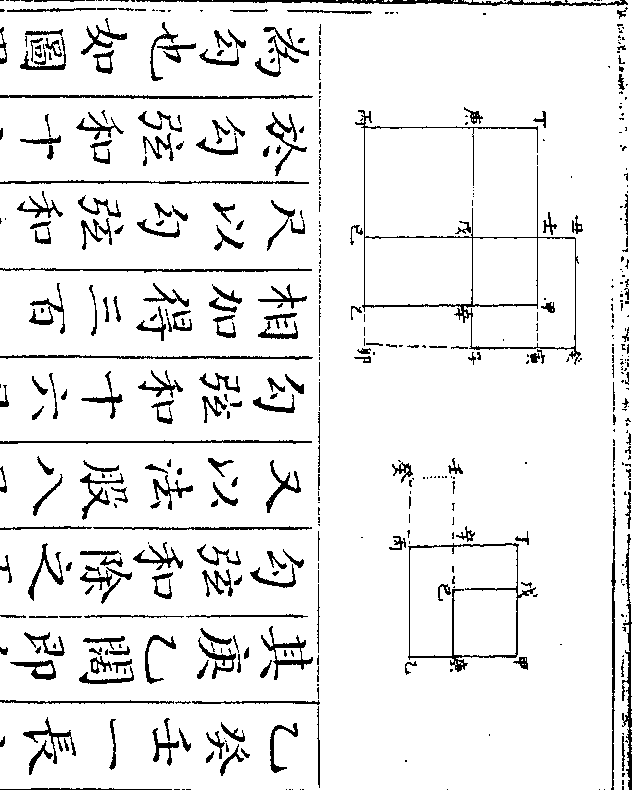 首一个是馒首为加三倍故将共馒首
首一个是馒首为加三倍故将共馒首亦加三倍即为共僧一百人共馒首三
百个而大僧一人比小僧一人馒首差
八个是知多八个而大僧为一人今多
二百个则大僧必为二十五人也又少
八个而小僧为一人今少六百个则小
僧必为七十五人也其先求馒首者因
多八个而大僧馒首为九个今多二百
御制数理精蕴 下编卷七 第 31b 页 WYG0799-0521b.png WYG0799-0521c.png

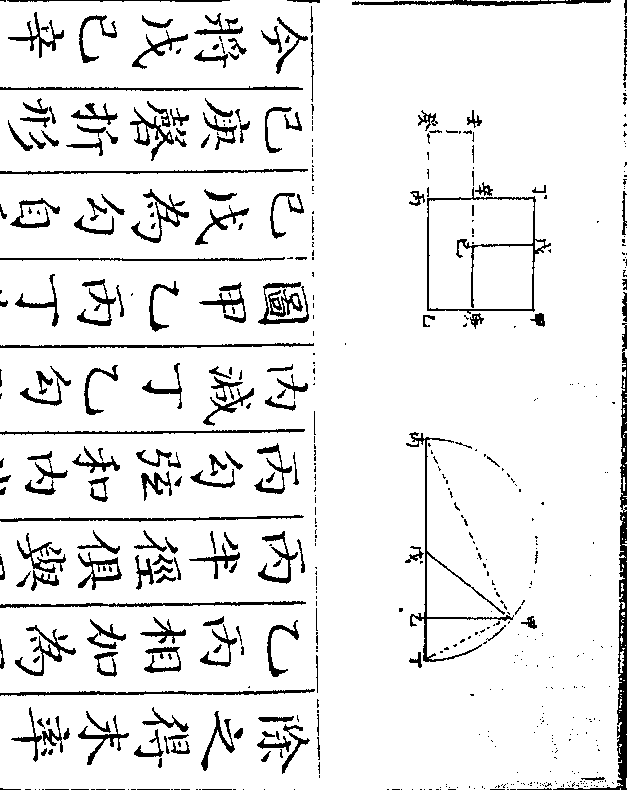 个则大僧馒首必为二百二十五个因
个则大僧馒首必为二百二十五个因馒首为加三倍故以三归之得七十五
个为大僧馒首数又少八个而小僧馒
首为一个今少六百个则小僧馒首必
为七十五个亦以三归之得二十五个
为小僧馒首数也
又法以小僧三人大僧一人共僧一百
人列于上小僧馒首一个大僧馒首三
个共馒首一百个列于下乃以下小僧
御制数理精蕴 下编卷七 第 31b 页 WYG0799-0521b.png WYG0799-0521c.png

 馒首一个遍乘上小僧三人大僧一人
馒首一个遍乘上小僧三人大僧一人御制数理精蕴 下编卷七 第 32a 页 WYG0799-0522a.png
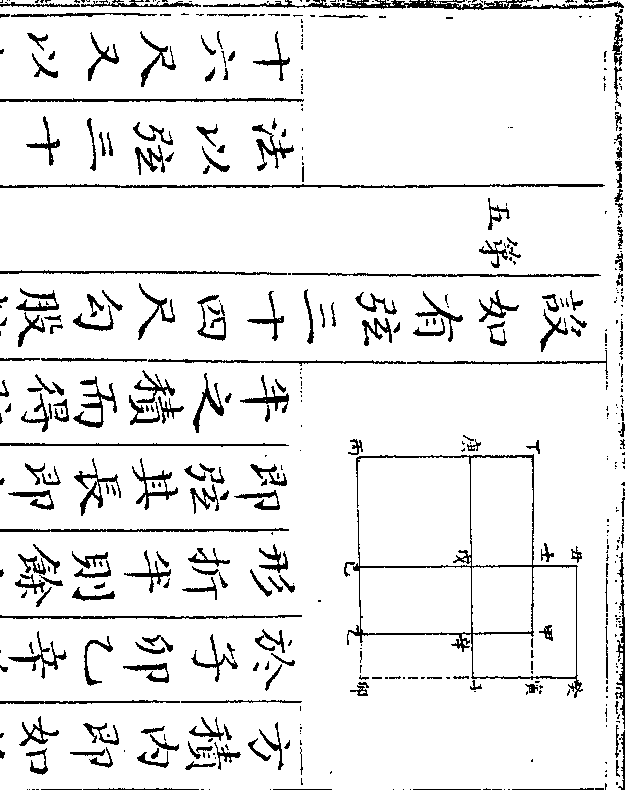 共僧一百人仍得原数又以上小僧三
共僧一百人仍得原数又以上小僧三人遍乘下小僧馒首一个大僧馒首三
个共馒首一百个得小僧馒首三个大
僧馒首九个共馒首三百个两下相较
则小僧人数与馒首数同为三彼此减
尽大僧馒首数比人数多八共馒首数
比共人数多二百爰以多八为一率大
僧一人为二率多二百为三率得四率
御制数理精蕴 下编卷七 第 32b 页 WYG0799-0522b.png WYG0799-0522c.png

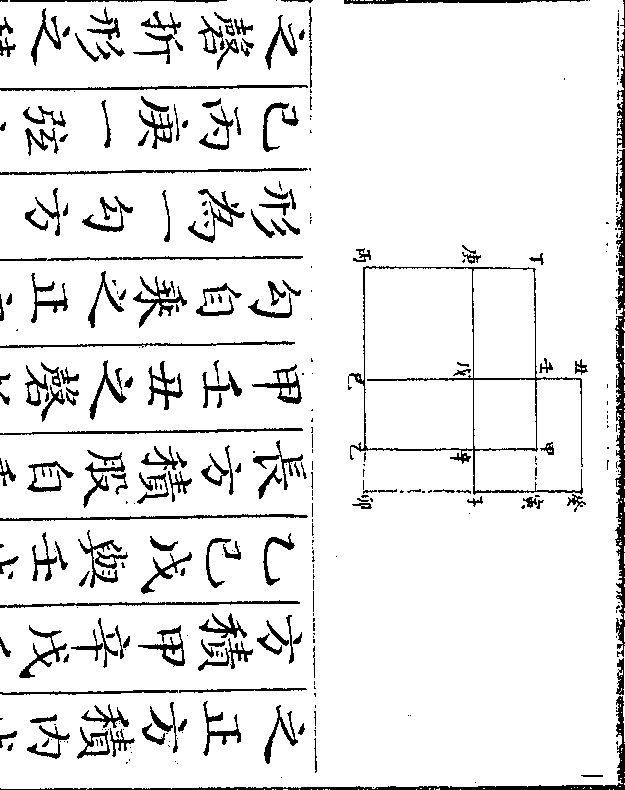 二十五人即大僧数于共一百人内减
二十五人即大僧数于共一百人内减之馀七十五人即小僧数如以大僧馒
首三个为二率得四率七十五个即大
僧馒首数于共馒首一百个内减之馀
二十五个即小僧馒首数也若欲先得
小僧数则以大僧一人馒首三个移于
前小僧三人馒首一个移于后乃以下
大僧馒首三个遍乘上大僧一人小僧
三人共僧一百人得大僧三人小僧九
御制数理精蕴 下编卷七 第 32b 页 WYG0799-0522b.png WYG0799-0522c.png

 人共僧三百人又以上大僧一人遍乘
人共僧三百人又以上大僧一人遍乘御制数理精蕴 下编卷七 第 33a 页 WYG0799-0523a.png
 下大僧馒首三个小僧馒首一个共馒
下大僧馒首三个小僧馒首一个共馒首一百个仍得原数两下相较则大僧
与大僧馒首同为三彼此减尽小僧馒
首数比人数少八共僧馒首数比共人
数少二百爰以少八为一率小僧三人
为二率少二百为三率得四率七十五
即小僧人数如以小僧馒首一个为二
率得四率二十五个即小僧馒首数也
御制数理精蕴 下编卷七 第 33b 页 WYG0799-0523b.png WYG0799-0523c.png

 此法先求大僧数而以小僧列于前者
此法先求大僧数而以小僧列于前者盖将小僧馒首大僧馒首共僧馒首数
皆加三倍则小僧人数与馒首数相同
是为每小僧一人馒首一个夫小僧数
与馒首数既相同而减尽无馀则共僧
数内之共小僧数与共馒首数内之共
小僧馒首数亦必相同而减尽无馀所
馀者即为大僧共馒首数多于共人数
之较是比每大僧一人馒首一个所多
御制数理精蕴 下编卷七 第 33b 页 WYG0799-0523b.png WYG0799-0523c.png

 之数是知馒首比人数多八个而大僧
之数是知馒首比人数多八个而大僧御制数理精蕴 下编卷七 第 34a 页 WYG0799-0524a.png
 为一人大僧馒首为三个今馒首比人
为一人大僧馒首为三个今馒首比人数多二百个则大僧必为二十五人大
僧馒首必为七十五个也其先求小僧
数而以大僧列于前者盖将大僧小僧
共僧数皆加三倍则大僧数与馒首数
相同是为每大僧一人馒首一个夫大
僧数与馒首数既相同而减尽无馀则
共僧数内之共大僧数与共馒首数内
御制数理精蕴 下编卷七 第 34b 页 WYG0799-0524b.png WYG0799-0524c.png

 之共大僧馒首数亦必相同而减尽无
之共大僧馒首数亦必相同而减尽无馀所馀者即为小僧馒首数少于小僧
数之较是比每小僧一人馒首一个所
少之数是知少八个而小僧为三人小
僧馒首为一个今少二百个则小僧必
为七十五人小僧馒首必为二十五个
也
设如有豆三十三石共换黄米京米一十九石止云
每黄米三石值豆一石每京米一石值豆三石问
御制数理精蕴 下编卷七 第 34b 页 WYG0799-0524b.png WYG0799-0524c.png

 二色米各得几何
二色米各得几何御制数理精蕴 下编卷七 第 35a 页 WYG0799-0525a.png
 法先用互乘以齐其分以黄米三石与
法先用互乘以齐其分以黄米三石与京米一石相乘得三石为乘出之共米
数即以三石乘共豆三十三石得九十
九石为乘出之共豆数以京米一石乘
豆一石仍得一石为乘出黄米所值之
豆数以黄米三石乘豆三石得九石为
乘出京米所值之豆数然后以共米一
十九石用黄米值豆一石乘之仍得一
御制数理精蕴 下编卷七 第 35b 页 WYG0799-0525b.png WYG0799-0525c.png

 十九石与乘出之共豆九十九石相较
十九石与乘出之共豆九十九石相较则共豆多八十石又以共米一十九石
用京米值豆九石乘之得一百七十一
石与乘出之共豆九十九石相较则共
豆多七十二石乃以黄米值豆一石与
京米值豆九石相减馀八石为一率一
石为二率少七十二石为三率得四率
九石即黄米数于共米十九石内减之
馀十石即京米数如以多八十石为三
御制数理精蕴 下编卷七 第 35b 页 WYG0799-0525b.png WYG0799-0525c.png

 率得四率十石亦即京米数也此法用
率得四率十石亦即京米数也此法用御制数理精蕴 下编卷七 第 36a 页 WYG0799-0526a.png
 互乘得黄米三石值豆一石京米三石
互乘得黄米三石值豆一石京米三石值豆九石今以米三石当一石则为黄
米一石值豆一石京米一石值豆九石
是豆为加三倍故将共豆亦加三倍即
为共米一十九石共豆九十九石而黄
米一石比京米一石所值豆差八石是
知豆少八石而黄米为一石今少七十
二石则黄米必为九石也又豆多八石
御制数理精蕴 下编卷七 第 36b 页 WYG0799-0526b.png WYG0799-0526c.png

 而京米为一石今多八十石则京米必
而京米为一石今多八十石则京米必为十石也
又法以黄米三石京米一石共米一十
九石列于上黄米值豆一石京米值豆
三石共豆三十三石列于下乃以下黄
米值豆一石遍乘上黄米三石京米一
石共米一十九石仍得原数又以上黄
米三石遍乘下黄米值豆一石京米值
豆三石共豆三十三石得黄米值豆三
御制数理精蕴 下编卷七 第 36b 页 WYG0799-0526b.png WYG0799-0526c.png

 石京米值豆九石共豆九十九石两下
石京米值豆九石共豆九十九石两下御制数理精蕴 下编卷七 第 37a 页 WYG0799-0527a.png
 相较则黄米与所值豆同为三石彼此
相较则黄米与所值豆同为三石彼此减尽京米所值豆比京米多八石共豆
比共米多八十石爰以多八石为一率
京米一石为二率多八十石为三率得
四率十石即京米数于共米一十九石
内减之馀九石即黄米数也如先求黄
米数则以京米一石值豆三石移于前
黄米三石值豆一石移于后乃以京米
御制数理精蕴 下编卷七 第 37b 页 WYG0799-0527b.png WYG0799-0527c.png

 值豆三石遍乘上京米一石黄米三石
值豆三石遍乘上京米一石黄米三石共米一十九石得京米三石黄米九石
共米五十七石又以上京米一石遍乘
下京米值豆三石黄米值豆一石共豆
三十三石仍得原数两下相较则京米
与所值豆俱为三石彼此减尽黄米所
值豆比黄米少八石共豆比共米少二
十四石爰以少八石为一率黄米三石
为二率少二十四石为三率得四率九
御制数理精蕴 下编卷七 第 37b 页 WYG0799-0527b.png WYG0799-0527c.png

 石即黄米数也此法先求京米数而以
石即黄米数也此法先求京米数而以御制数理精蕴 下编卷七 第 38a 页 WYG0799-0528a.png
 黄米列于前者盖将京米所值豆数黄
黄米列于前者盖将京米所值豆数黄米所值豆数共米所值豆数皆加三倍
则黄米数与所值豆数相同是为每黄
米一石值豆一石夫黄米数与所值豆
数既相同而减尽无馀则共米数内之
共黄米数与共豆数内之共黄米所值
豆数亦必相同而减尽无馀所馀者即
为共京米所值豆数多于共京米之较
御制数理精蕴 下编卷七 第 38b 页 WYG0799-0528b.png WYG0799-0528c.png

 是比每京米一石值豆一石所多之数
是比每京米一石值豆一石所多之数是知豆比米多八石而京米为一石今
豆比米多八十石则京米必为十石也
其先求黄米数而以京米列于前者盖
将京米黄米共米皆加三倍则京米数
与所值豆数相同是为每京米一石值
豆一石夫京米数与所值豆数既相同
而减尽无馀则共米数内之共京米数
与共豆数内之共京米所值豆数亦必
御制数理精蕴 下编卷七 第 38b 页 WYG0799-0528b.png WYG0799-0528c.png

 相同而减尽无馀所馀者即为黄米所
相同而减尽无馀所馀者即为黄米所御制数理精蕴 下编卷七 第 39a 页 WYG0799-0529a.png
 值豆数比黄米所少之较是比每黄米
值豆数比黄米所少之较是比每黄米一石值豆一石所少之数是知豆比米
少八石而黄米为三石今豆比米少二
十四石则黄米必为九石也
设如有船桅共五十七桨共二百零四但知大船每
只三桅六桨小船每只一桅八桨问大小船数各
若干
法先用互乘以齐其分以大船三桅与
御制数理精蕴 下编卷七 第 39b 页 WYG0799-0529b.png WYG0799-0529c.png

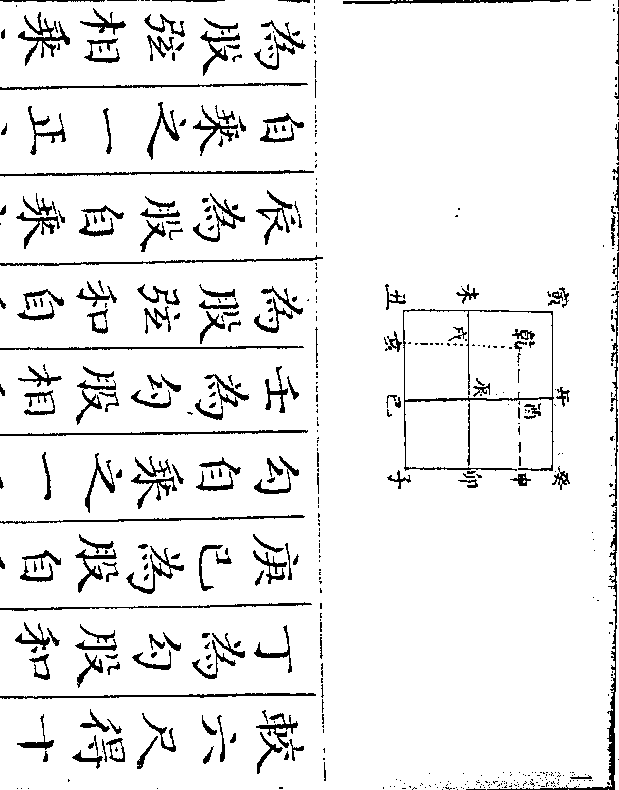 小船一桅相乘得三桅为乘出之共桅
小船一桅相乘得三桅为乘出之共桅数即以三桅乘共桨二百零四得六百
一十二为乘出之共桨数以小船一桅
乘大船六桨仍得六桨为乘出大船之
桨数以大船三桅乘小船八桨得二十
四桨为乘出小船之桨数然后以共桅
五十七用大船六桨乘之得三百四十
二与乘出之共桨六百一十二相较则
共桨多二百七十又以共桅五十七用
御制数理精蕴 下编卷七 第 39b 页 WYG0799-0529b.png WYG0799-0529c.png

 小船二十四桨乘之得一千三百六十
小船二十四桨乘之得一千三百六十御制数理精蕴 下编卷七 第 40a 页 WYG0799-0530a.png
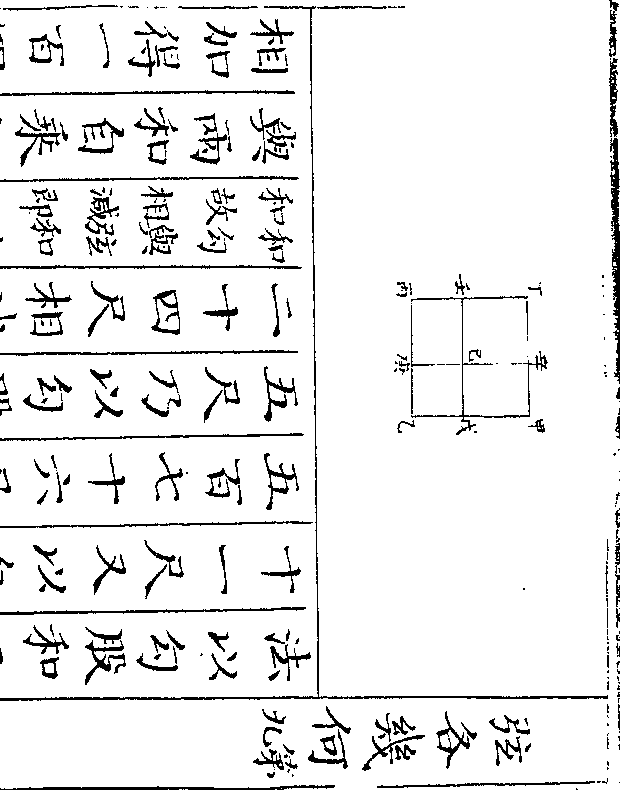 八与乘出之共桨六百一十二相较则
八与乘出之共桨六百一十二相较则共桨少七百五十六乃以大船六桨与
小船二十四桨相减馀十八桨为一率
一桅为二率少七百五十六桨为三率
得四率四十二即大船桅数三归之得
十四即大船数也于共桅五十七内减
大船桅数馀十五即小船桅数亦即小
船数如以得二百七十桨为三率得四
御制数理精蕴 下编卷七 第 40b 页 WYG0799-0530b.png WYG0799-0530c.png

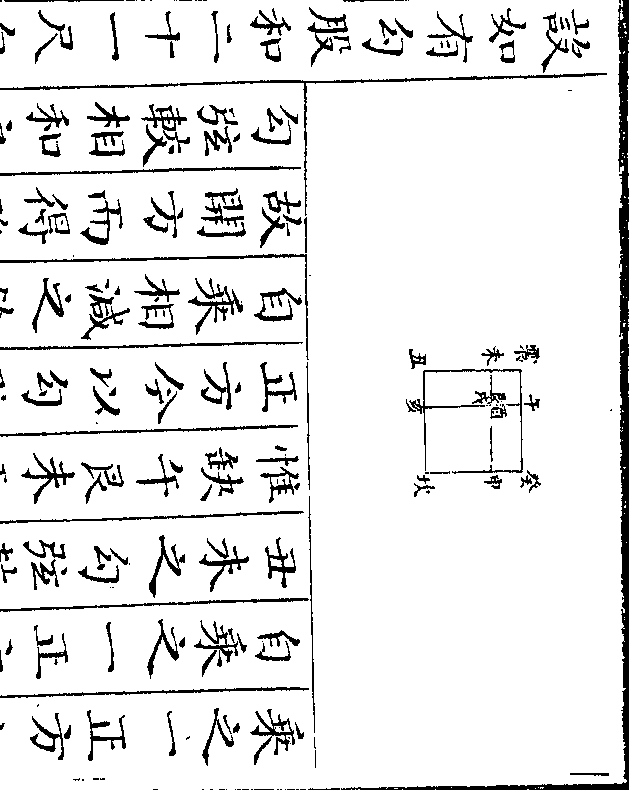 率十五亦即小船桅数也此法用互乘
率十五亦即小船桅数也此法用互乘得大船三桅六桨小船三桅二十四桨
今以三桅当一桅则为大船一桅六桨
小船一桅二十四桨是桨为加三倍故
将共桨亦加三倍即为共五十七桅共
六百一十二桨而大船一桅比小船一
桅差十八桨是知少十八桨而大船为
一桅今少七百五十六桨则大船必为
四十二桅也多十八桨而小船为一桅
御制数理精蕴 下编卷七 第 40b 页 WYG0799-0530b.png WYG0799-0530c.png

 今多二百七十桨则小船必为十五桅
今多二百七十桨则小船必为十五桅御制数理精蕴 下编卷七 第 41a 页 WYG0799-0531a.png
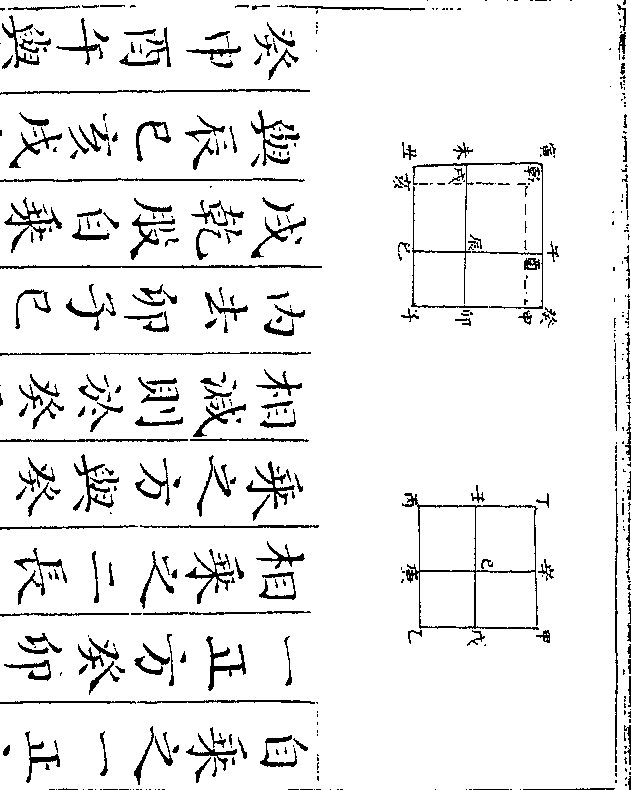 也
也又法以小船一桅大船三桅共五十七
桅列于上小船八桨大船六桨共二百
零四桨列于下乃以下小船八桨遍乘
上小船一桅大船三桅共五十七桅得
小船八桅大船二十四桅共四百五十
六桅又以上小船一桅遍乘下小船八
桨大船六桨共二百零四桨仍得原数
御制数理精蕴 下编卷七 第 41b 页 WYG0799-0531b.png WYG0799-0531c.png
 两下相较则小船桅与桨同为八彼此
两下相较则小船桅与桨同为八彼此减尽大船桅比桨多十八共桅比共桨
多二百五十二爰以多十八为一率大
船三桅为二率多二百五十二为三率
得四率四十二桅即大船桅数三归之
得十四即大船数于五十七桅内减去
大船四十二桅馀十五桅即小船桅数
亦即小船数也如欲先得小船数则以
大船三桅六桨移于前小船一桅八桨
御制数理精蕴 下编卷七 第 41b 页 WYG0799-0531b.png WYG0799-0531c.png

 移于后乃以下大船六桨遍乘上大船
移于后乃以下大船六桨遍乘上大船御制数理精蕴 下编卷七 第 42a 页 WYG0799-0532a.png
 三桅小船一桅共五十七桅得大船十
三桅小船一桅共五十七桅得大船十八桅小船六桅共三百四十二桅又以
上大船三桅遍乘下大船六桨小船八
桨共二百零四桨得大船十八桨小船
二十四桨共六百一十二桨两下相较
则大船桅与桨同为十八彼此减尽小
船桅比桨少十八共桅比共桨少二百
七十爰以少十八为一率小船一桅为
御制数理精蕴 下编卷七 第 42b 页 WYG0799-0532b.png WYG0799-0532c.png
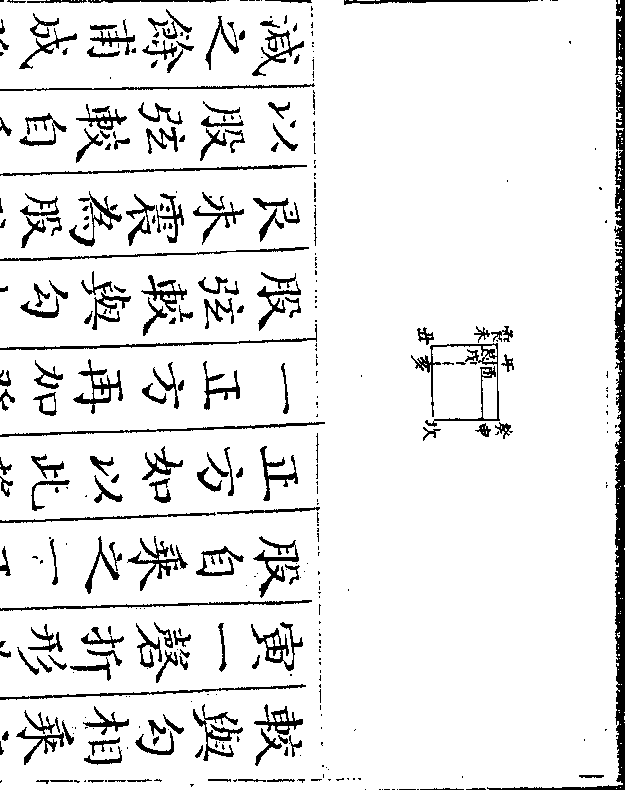 二率少二百七十为三率得四率十五
二率少二百七十为三率得四率十五桅即小船桅数亦即小船数也此法先
求大船桅数而以小船列于前者盖将
小船桅数大船桅数共船桅数皆加八
倍则小船桅数与桨数相同是为每小
船一桅一桨夫小船桅数与桨数既相
同而减尽无馀则共桅数内之小船共
桅数与共桨数内之小船共桨数亦必
相同而减尽无馀所馀者即为大船共
御制数理精蕴 下编卷七 第 42b 页 WYG0799-0532b.png WYG0799-0532c.png

 桅数多于大船共桨数之较是比每大
桅数多于大船共桨数之较是比每大御制数理精蕴 下编卷七 第 43a 页 WYG0799-0533a.png
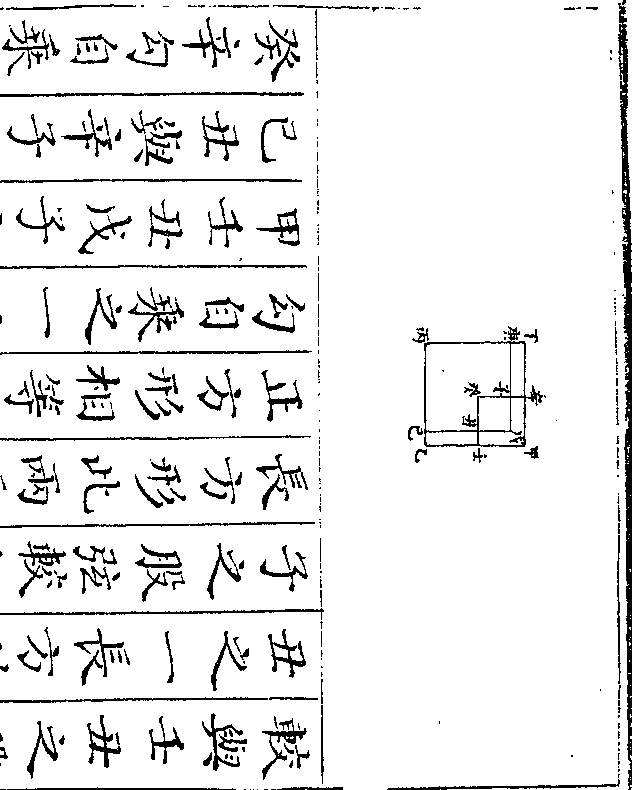 船一桅一桨所多之数是知多十八桅
船一桅一桨所多之数是知多十八桅而大船为三桅今多二百五十二桅则
大船必为四十二桅也其先求小船桅
数而以大船桅数列于前者盖将大船
桅数小船桅数共船桅数皆加六倍桨
数皆加三倍则大船桅数与桨数相同
是为大船一桅一桨夫大船桅数与桨
数既相同而减尽无馀则共桅数内之
御制数理精蕴 下编卷七 第 43b 页 WYG0799-0533b.png WYG0799-0533c.png

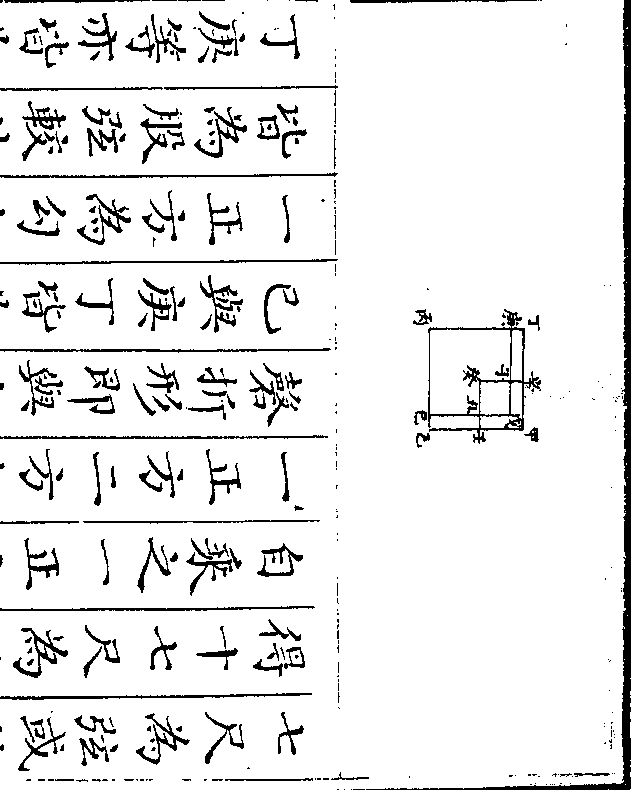 大船共桅数与共桨数内之大船共桨
大船共桅数与共桨数内之大船共桨数亦必相同而减尽无馀所馀者即为
小船共桅数少于小船共桨数之较是
比每小船一桅一桨所少之数是知少
十八桅而小船为一桅今少二百七十
桅则小船必为十五桅也
设如有银八十七两按饭银马银二项分给众人但
知三人共给二两饭银七人共给五两马银问人
数及二项银数各若干
御制数理精蕴 下编卷七 第 43b 页 WYG0799-0533b.png WYG0799-0533c.png

 法以三人与七人相乘得二十一人又
法以三人与七人相乘得二十一人又御制数理精蕴 下编卷七 第 44a 页 WYG0799-0534a.png
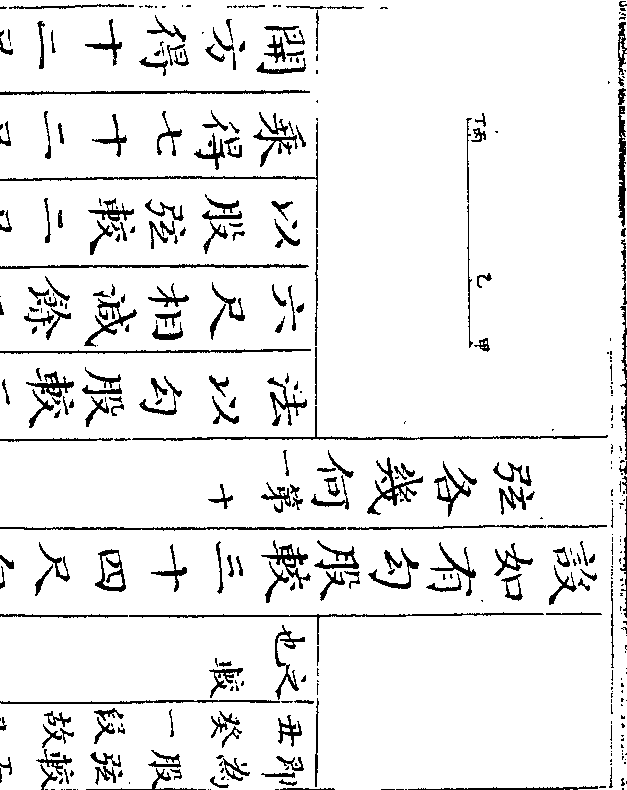 以三人乘马银五两得一十五两七人
以三人乘马银五两得一十五两七人乘饭银二两得一十四两爰以十四两
与十五两相并得二十九两为一率二
十一人为二率共银八十七两为三率
得四率六十三人即共人数也既得其
人数则以三人为一率饭银二两为二
率共六十三人为三率得四率四十二
两为饭银数于共银八十七两内减之
御制数理精蕴 下编卷七 第 44b 页 WYG0799-0534b.png WYG0799-0534c.png

 馀四十五两即马银数如以七人为一
馀四十五两即马银数如以七人为一率马银五两为二率共六十三人为三
率得四率四十五两亦即马银数也盖
三人给饭银二两则二十一人必给饭
银十四两七人给马银五两则二十一
人必给马银十五两夫二十一人既给
饭银十四两马银十五两是二十一人
共给银二十九两矣是知有二十九两
为二十一人今有八十七两则必为六
御制数理精蕴 下编卷七 第 44b 页 WYG0799-0534b.png WYG0799-0534c.png

 十三人也又三人共给饭银二两则六
十三人也又三人共给饭银二两则六御制数理精蕴 下编卷七 第 45a 页 WYG0799-0535a.png
 十三人必共给饭银四十二两七人共
十三人必共给饭银四十二两七人共给马银五两则六十三人必共给马银
四十五两也
设如赏人饭肉共用碗一百但知二人共饭一碗三
人共肉一碗问共人数及二项各用碗若干
法以二人与三人相乘得六人又以二
人乘肉一碗得二碗三人乘饭一碗得
三碗爰以三碗二碗相并得五碗为一
御制数理精蕴 下编卷七 第 45b 页 WYG0799-0535b.png WYG0799-0535c.png

 率六人为二率共碗一百为三率得四
率六人为二率共碗一百为三率得四率一百二十人即共人数也既得共人
数则以二人为一率饭碗一为二率共
一百二十人为三率得四率六十为饭
碗数于共碗一百内减之馀四十即肉
碗数如以三人为一率得四率四十亦
即肉碗数也此法因二人共饭三人共
肉其数不同故用互乘以齐其分盖二
人共饭一碗则六人必共饭三碗三人
御制数理精蕴 下编卷七 第 45b 页 WYG0799-0535b.png WYG0799-0535c.png

 共肉一碗则六人必共肉二碗夫六人
共肉一碗则六人必共肉二碗夫六人御制数理精蕴 下编卷七 第 46a 页 WYG0799-0536a.png
 既共饭三碗共肉二碗是六人共用五
既共饭三碗共肉二碗是六人共用五碗矣是知有五碗为六人今有一百碗
则必为一百二十人也又二人共饭一
碗则一百二十人必共饭六十碗三人
共肉一碗则一百二十人必共肉四十
碗也
设如有兵三千四百七十四名每三人给衫绢七十
尺每四人给裤绢五十尺问总绢若干
御制数理精蕴 下编卷七 第 46b 页 WYG0799-0536b.png WYG0799-0536c.png

 法以三人与四人相乘得十二人又以
法以三人与四人相乘得十二人又以三人乘裤绢五十尺得一百五十尺四
人乘衫绢七十尺得二百八十尺爰以
十二人为一率二百八十尺与一百五
十尺相并得四百三十尺为二率兵三
千四百七十四名为三率得四率一十
二万四千四百八十五尺为共绢数也
此法与前同但前法以共银数求共人
数故以银数为一率人数为二率此法
御制数理精蕴 下编卷七 第 46b 页 WYG0799-0536b.png WYG0799-0536c.png

 以共人数求共绢数故以人数为一率
以共人数求共绢数故以人数为一率御制数理精蕴 下编卷七 第 47a 页 WYG0799-0537a.png
 绢数为二率其比例之理一也
绢数为二率其比例之理一也设如赏人茶饭酒共用碗一千三百三十八但知三
人共茶二碗五人共酒三碗七人共饭六碗问共
人数及三项各用碗若干
法先以三人茶二碗五人酒三碗互乘
以三人与五人相乘得一十五人又以
三人乘酒三碗得九碗五人乘茶二碗
得十碗是为十五人共用茶酒十九碗
御制数理精蕴 下编卷七 第 47b 页 WYG0799-0537b.png WYG0799-0537c.png

 复与七人饭六碗互乘以十五人与七
复与七人饭六碗互乘以十五人与七人相乘得一百零五人又以十五人乘
饭六碗得九十碗七人乘茶酒共十九
碗得一百三十三碗爰以一百三十三
碗与九十碗相并得二百二十三碗为
一率一百零五人为二率共碗一千三
百三十八为三率得四率六百三十人
即共人数也既得共人数乃以三人为
一率茶碗二为二率共六百三十人为
御制数理精蕴 下编卷七 第 47b 页 WYG0799-0537b.png WYG0799-0537c.png

 三率得四率四百二十为茶碗数又以
三率得四率四百二十为茶碗数又以御制数理精蕴 下编卷七 第 48a 页 WYG0799-0538a.png
 五人为一率酒碗三为二率共六百三
五人为一率酒碗三为二率共六百三十人为三率得四率三百七十八为酒
碗数又以七人为一率饭碗六为二率
共六百三十人为三率得四率五百四
十为饭碗数也此法因用碗三项故用
两次互乘以齐其分得一百零五人应
用三项碗共二百二十三是知有二百
二十三碗为一百零五人今有一千三
御制数理精蕴 下编卷七 第 48b 页 WYG0799-0538b.png WYG0799-0538c.png

 百三十八碗则必为六百三十人也既
百三十八碗则必为六百三十人也既得共人数则以各项分数比例求之即
得各项碗之共数矣
设如有灯大小二䓁大灯居小灯三分之二但知大
灯三盏用油四两小灯四盏用油三两共用油十
八斤零七两问大小灯数各若干
法以大灯三盏与小灯四盏相乘得十
二盏又以小灯四盏乘大灯用油四两
得大灯用油十六两以大灯三盏乘小
御制数理精蕴 下编卷七 第 48b 页 WYG0799-0538b.png WYG0799-0538c.png

 灯用油三两得小灯用油九两又将大
灯用油三两得小灯用油九两又将大御制数理精蕴 下编卷七 第 49a 页 WYG0799-0539a.png
 灯用油十六两二因之(大灯二分/故用二因)得三
灯用油十六两二因之(大灯二分/故用二因)得三十二两将小灯用油九两三因之(小灯/三分)
(故用/三因)得二十七两二数相并得五十九
两为一率十二盏为二率共油十八斤
七两通为二百九十五两为三率得四
率六十盏为灯一分之数二因之得一
百二十盏即大灯数三因之得一百八
十盏即小灯数也此法因有𢃄分而互
御制数理精蕴 下编卷七 第 49b 页 WYG0799-0539b.png WYG0799-0539c.png

 乘所得之十二盏为一分之衰数又因
乘所得之十二盏为一分之衰数又因共油数为大灯二分小灯三分之共数
故亦二因十六两三因九两并之为五
分之衰数是知油五分之衰数五十九
两与灯一分之衰数十二盏之比即同
于五分共油二百九十五两与一分灯
数六十盏之比也既得一分为六十盏
故二因之得大灯数三因之得小灯数
也
御制数理精蕴 下编卷七 第 49b 页 WYG0799-0539b.png WYG0799-0539c.png

 设如有银二十五两三钱买铜铁二色其重相䓁铁
设如有银二十五两三钱买铜铁二色其重相䓁铁御制数理精蕴 下编卷七 第 50a 页 WYG0799-0540a.png
 三斤价四钱铜二斤价五钱问斤数及各价几何
三斤价四钱铜二斤价五钱问斤数及各价几何法以铁三斤与铜二斤相乘得六斤又
以铜二斤乘铁价四钱得八钱以铁三
斤乘铜价五钱得一两五钱乃以八钱
与一两五钱相并得二两三钱为一率
六斤为二率总银二十五两三钱为三
率得四率六十六斤为铜铁相䓁之斤
数又以铁三斤为一率价四钱为二率
御制数理精蕴 下编卷七 第 50b 页 WYG0799-0540b.png WYG0799-0540c.png

 今铁六十六斤为三率得四率八两八
今铁六十六斤为三率得四率八两八钱即铁价于共银二十五两三钱内减
之馀十六两五钱即铜价如以铜二斤
为一率价五钱为二率今铜六十六斤
为三率得四率十六两五钱亦即铜价
也盖铁三斤价四钱则六斤价八钱铜
二斤价五钱则六斤价一两五钱是铜
铁各六斤而共价为二两三钱故以二
两三钱与各六斤之比即同于共价二
御制数理精蕴 下编卷七 第 50b 页 WYG0799-0540b.png WYG0799-0540c.png

 十五两三钱与各六十六斤之比也既
十五两三钱与各六十六斤之比也既御制数理精蕴 下编卷七 第 51a 页 WYG0799-0541a.png
 得各斤数则以各价比例求之即得各
得各斤数则以各价比例求之即得各价数矣
设如有米九百石令甲乙二处各因米价贵贱纳之
其所纳之银适相等甲处米价每石五钱乙处米
价每石七钱问各米数及共价数几何
法以乙七钱乘甲一石得七石以甲五
钱乘乙一石得五石乃以七石与五石
相并得十二石为一率以甲七石为二
御制数理精蕴 下编卷七 第 51b 页 WYG0799-0541b.png WYG0799-0541c.png

 率总米九百石为三率得四率五百二
率总米九百石为三率得四率五百二十五石即甲处纳米之数于九百石内
减之馀三百七十五石即乙处纳米之
数如以乙五石为二率得四率三百七
十五石亦即乙处纳米之数以甲五百
二十五石与每石价五钱相乘得二百
六十二两五钱以乙三百七十五石与
每石价七钱相乘亦得二百六十二两
五钱是其所纳之银数适相䓁也盖甲
御制数理精蕴 下编卷七 第 51b 页 WYG0799-0541b.png WYG0799-0541c.png

 处每石价五钱则七石之价为三两五
处每石价五钱则七石之价为三两五御制数理精蕴 下编卷七 第 52a 页 WYG0799-0542a.png
 钱乙处每石价七钱则五石之价亦为
钱乙处每石价七钱则五石之价亦为三两五钱其价相䓁是十二石之中甲
应七石乙应五石故以十二石与甲七
石之比即同于总米九百石与甲五百
二十五石之比又十二石与乙五石之
比即同于总米九百石与乙三百七十
五石之比也
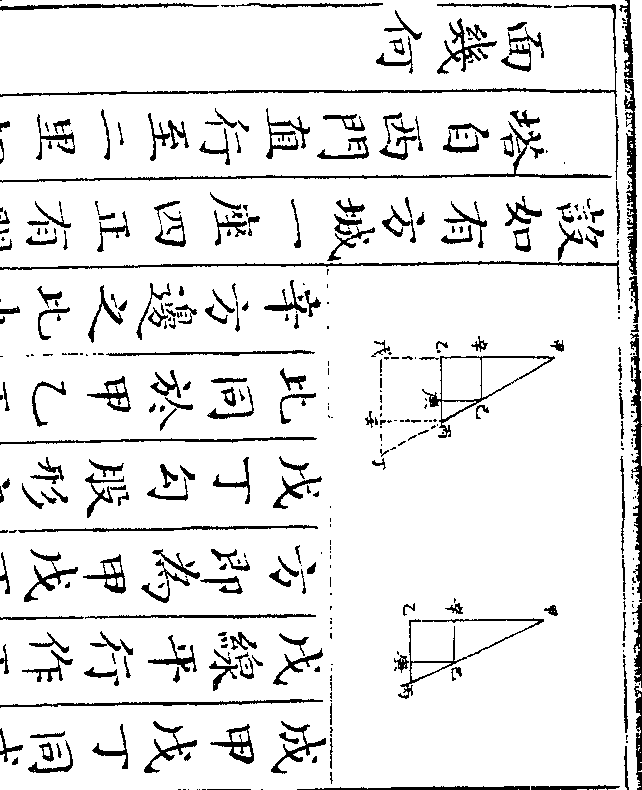
设如空车一日行三十里重车一日行二十里今载
御制数理精蕴 下编卷七 第 52b 页 WYG0799-0542b.png WYG0799-0542c.png

 米至仓往返足一日问距仓路远几何
米至仓往返足一日问距仓路远几何法以空车行三十里与重车行二十里
相乘得六百里又以重车行二十里乘
空车一日得二十日以空车行三十里
乘重车一日得三十日乃以二十日与
三十日相并得五十日为一率六百里
为二率一日为三率得四率一十二里
即距仓之里数也盖空车一日行三十
里则二十日行六百里重车一日行二
御制数理精蕴 下编卷七 第 52b 页 WYG0799-0542b.png WYG0799-0542c.png

 十里则三十日亦行六百里一往一返
十里则三十日亦行六百里一往一返御制数理精蕴 下编卷七 第 53a 页 WYG0799-0543a.png
 共五十日是知五十日往返六百里则
共五十日是知五十日往返六百里则今一日必往返十二里也
设如重车一日行五十里轻车一日行七十五里今
载米至仓五日往返三次问距仓里数几何
法以重车行五十里与轻车行七十五
里相乘得三千七百五十里又以轻车
行七十五里乘重车一日得七十五日
以重车行五十里乘轻车一日得五十
御制数理精蕴 下编卷七 第 53b 页 WYG0799-0543b.png WYG0799-0543c.png

 日乃以七十五日与五十日相并得一
日乃以七十五日与五十日相并得一百二十五日为一率三千七百五十里
为二率五日为三率得四率一百五十
里即五日往返之里数以三次除之得
五十里即距仓之里数也此法与前法
同前法一日往返一次故所得即距仓
之里数此法五日往返三次故所得为
往返三次之里数是以用三次除之而
得距仓之里数也
御制数理精蕴 下编卷七 第 53b 页 WYG0799-0543b.png WYG0799-0543c.png

 御制数理精蕴下编卷七
御制数理精蕴下编卷七