钦定四库全书
御制数理精蕴下编卷六
　　线部四
　　　和数比例
　　　较数比例

　　和数比例
比例之中有合率而复有和数者将几比例之率合
为一比例故谓之合率至于有总数又有分数以分
数合而与总数相比则谓之和数其在九章总名差
分而其实总不越比例之理故今质名之曰和数比
例其立法有以实数与实数比者如合众人数与总
物数之比即若每人数与每物数之比是也有以所
立衰数与实数比者如合众衰数与总物数之比即

若每人衰数与每物数之比是也又或以加倍数成
率者其得数亦为加倍之数或以两数相乘而成率
者其得数亦为两数相乘之数要之皆以比例而得
故于各条详加解说以明其故焉
设如南北二商合本贸易南出本银一百五十两北
　出本银二百五十两共得利银一千两按各人所
　出本银之分分之问二人各得利银几何
　　　　　法以南出本银一百五十两与北出本
　　　　　银二百五十两相并得四百两为一率

　　　　　利银一千两为二率南出本银一百五

　　　　　十两为三率推得四率三百七十五两
　　　　　即南所分利银数于共利一千两内减
　　　　　三百七十五两馀六百二十五两即北
　　　　　所分利银数也如以二人本银共四百
　　　　　两为一率二人共利一千两为二率北
　　　　　出本银二百五十两为三率推得四率
　　　　　六百二十五两即北所分利银数也此
　　　　　法盖以二人共本比共利即如每人各

　　　　　本比各利而为相当比例四率也
　　　　　又捷法以二人共出本银四百两归除
　　　　　二人共得利银一千两得每一两之利
　　　　　为二两五钱乃与各人本银数相乘即
　　　　　得各人所分利银数此又以每一两之
　　　　　利与各人所出本银之利相比而得也
设如赵周冯三人合夥生理赵出本银一千两周出
　本银八百两冯出本银六百两共得利银一千二
　百两按各人所出本银之分分之问三人各得利

　银几何

　　　　　法以三人各出本银相并得二千四百
　　　　　两为一率三人共得利银一千二百两
　　　　　为二率三人所出本银数各为三率推
　　　　　得各四率赵五百两周四百两冯三百
　　　　　两即为各人所得利银数也若用捷法
　　　　　则以三人所并本银二千四百两归除
　　　　　共得利银一千二百两得每一两之利
　　　　　为五钱按各人本银数乘之即各人所

　　　　　得利银数也
设如甲乙丙三商共出本银一千五百二十两得利
　银一百九十两甲分一百二十两乙分四十两丙
　分三十两问各人原本银若干
　　　　　法以共利银一百九十两为一率共本
　　　　　银一千五百二十两为二率每分利银
　　　　　各为三率推得各四率甲本银为九百
　　　　　六十两乙本银为三百二十两丙本银
　　　　　为二百四十两如用捷法则以共利银

　　　　　一百九十两归除共本银一千五百二

　　　　　十两得每一两利银之本银为八两乃
　　　　　以八两乘各人利银分数即得各人本
　　　　　银之数矣
设如甲丙戊三人合本贸易共得利银三千二百二
　十两甲本银三千六百两丙本银五百一十两戊
　本银不知其数但知该分利银四百八十两问其
　本银若干
　　　　　法以三人共得利银三千二百二十两

　　　　　内减戊之利银四百八十两馀二千七
　　　　　百四十两为一率甲丙二人本银相并
　　　　　得四千一百一十两为二率戊利银四
　　　　　百八十两为三率推得四率七百二十
　　　　　两即戊之本银数也此法于总利中减
　　　　　去戊利银所馀者即甲丙二人之利银
　　　　　故以甲丙二人之共利银与甲丙二人
　　　　　之共本银相比即若戊一人之利银与
　　　　　戊一人之本银相比也

设如甲乙丙三商共出本银一千五百二十两今得

　本利共银一千七百一十两甲分本利共银一千
　零八十两乙分本利共银三百六十两丙分本利
　共银二百七十两问三人所分本利各若干
　　　　　法以三人所得本利共银一千七百一
　　　　　十两为一率共出本银一千五百二十
　　　　　两为二率各人所分本利共银各为三
　　　　　率推得各四率甲本银九百六十两乙
　　　　　本银三百二十两丙本银二百四十两

　　　　　即为各人本银数以各人本银减各人
　　　　　共银甲得利银一百二十两乙得利银
　　　　　四十两丙得利银三十两即各人利银
　　　　　数也
设如有三人合本贸易第一人出本银五百两系七
　成第二人出本银一千两系八成第三人出本银
　一千五百两系九成共得利银二千两皆系十成
　问每人应得利银若干
　　　　　法以各人所出本银数与各银成色相

　　　　　乘第一人得三百五十两第二人得八

　　　　　百两第三人得一千三百五十两三数
　　　　　相加共得二千五百两为一率共得利
　　　　　银二千两为二率每人所得相乘之数
　　　　　(第一人三百五十两第二人八/百两第三人一千三百五十两)各为三
　　　　　率推得各四率第一人得二百八十两
　　　　　第二人得六百四十两第三人得一千
　　　　　零八十两即各人应得之利银数也此
　　　　　法以各银成色乘各人银数者是将各

　　　　　银成色俱变作十成银也如第一人七
　　　　　成银五百两变作十成银止得三百五
　　　　　十两第二人八成银一千两变作十成
　　　　　银止得八百两第三人九成银一千五
　　　　　百两变作十成银止得一千三百五十
　　　　　两并之得十成银二千五百两故以总
　　　　　十成银二千五百两与共利银二千两
　　　　　之比即若每人十成本银与每人应得
　　　　　利银之比也

设如甲丙戊三商合本贸易其所出本银多寡不同

　时日亦不同甲出本银六百两系八个月丙出本
　银四百五十两系六个月戊出本银五百两系十
　个月共得利银一千两问各人应分利银几何
　　　　　法以各人本银与各人月分相乘甲得
　　　　　四千八百两丙得二千七百两戊得五
　　　　　千两三数相并得一万二千五百两为
　　　　　一率共利银一千两为二率各人本银
　　　　　乘各人月分之数为三率推得各四率

　　　　　甲得三百八十四两丙得二百一十六
　　　　　两戊得四百两即为各人应得之利银
　　　　　数也此法先以各人本银乘各人月分
　　　　　者盖以各人所出本银按月分以加倍
　　　　　也三人本银各有月分则行利亦按月
　　　　　加倍也
设如乙丙丁三人合夥生理乙出本银二百两系八
　个月出本之两月后又添本银四十两丙出本银
　三百二十两系六个月出本之一月后又添本银

　八十两丁出本银一百六十两系十个月共得利

　银三百六十两问每人各该利银几何
　　　　　法以乙本银二百两与八个月相乘得
　　　　　一千六百两又以后添四十两与六个
　　　　　月相乘(因出本之两月后/又添银故用六月)得二百四十
　　　　　两此两数相加得一千八百四十两为
　　　　　乙之衰数以丙本银三百二十两与六
　　　　　个月相乘得一千九百二十两又以后
　　　　　添八十两与五个月相乘(因出本之一/月后又添银)

　　　　　(故用/五月)得四百两此两数相加得二千三
　　　　　百二十两为丙之衰数以丁本银一百
　　　　　六十两与十个月相乘得一千六百两
　　　　　即丁之衰数乃以三人衰数相加得五
　　　　　千七百六十两为一率三百六十两为
　　　　　二率各人衰数各为三率推得各四率
　　　　　乙得一百一十五两丙得一百四十五
　　　　　两丁得一百两即各人应得之利银数
　　　　　也此法因出银前后各不同故以各人

　　　　　出银节次乘各人月分而得各人衰数

　　　　　既得各人衰数则相加而与总利银为
　　　　　比即如各人衰数与各人利银相比也
设如甲乙丙三商合本贸易共得利银一千两甲本
　银三百两系十个月乙本银六百两丙本银四百
　两俱不知月分其利银则甲分五百两乙分三百
　两丙分二百两问乙丙二人出本银月分各几何
　　　　　法以甲之利银五百两为一率甲之本
　　　　　银三百两与十个月相乘得三千两为

　　　　　二率乙之利银三百两为三率推得四
　　　　　率一千八百两为乙之本银六百两与
　　　　　月分相乘之数以乙之本银六百两除
　　　　　之得三个月即乙出银之月分如以丙
　　　　　之利银二百两为三率则得四率一千
　　　　　二百两为丙之本银四百两与月分相
　　　　　乘之数以丙之本银四百两除之得三
　　　　　个月即丙出本银之月分也
设如乙丙丁三人合本贸易共得利银三百八十两

　丙得利银为乙三分之一丁得利银为乙四分之

　一乙之本银为八十两收利十二个月丙丁二人
　本银不知数但知丙收利银系八个月丁收利银
　系四个月问乙丙丁利银各若干丙与丁本银各
　若干
　　　　　法以十二分为乙之衰数(两分母相/乘之数)取
　　　　　其三分之一得四分为丙之衰数又取
　　　　　其四分之一得三分为丁之衰数将三
　　　　　衰数相并得一十九分为一率共利三

　　　　　百八十两为二率以各人衰数各为三
　　　　　率推得各四率乙之利银得二百四十
　　　　　两丙之利银得八十两丁之利银得六
　　　　　十两三宗利银相并共三百八十两以
　　　　　合前数又用乙利银二百四十两为一
　　　　　率乙本银八十两与十二个月相乘得
　　　　　九百六十两为二率丙利银八十两为
　　　　　三率推得四率三百二十两为丙本银
　　　　　八个月之共分以八个月除之得四十

　　　　　两即丙之本银数复以乙利银二百四

　　　　　十两为一率乙本银九百六十两为二
　　　　　率丁利银六十两为三率推得四率二
　　　　　百四十两为丁本银四个月之共分以
　　　　　四个月除之得六十两即丁之本银数
　　　　　也
设如甲丙戊三家每日派一人当差论各家田数定
　日之多少甲田八十亩丙田六十亩戊田五十二
　亩问各人一年内连闰月应该当差之日几何

　　　　　法以甲丙戊三家田数(甲八十丙六/十戊五十二)相
　　　　　并得一百九十二亩为一率一年连闰
　　　　　月作三百八十四日为二率各家田数
　　　　　各为三率推得各四率甲当差一百六
　　　　　十日丙当差一百二十日戊当差一百
　　　　　零四日并之得三百八十四日合一年
　　　　　连闰月之数也
设如二人居住相隔一千四百里同日起身一人日
　行八十里一人日行六十里问途中几日相会

　　　　　法以八十里与六十里相并得一百四

　　　　　十里为一率一日为二率一千四百里
　　　　　为三率推得四率十日即相会之日也
　　　　　此法以八十里六十里相并为一率者
　　　　　每一日之内两人共行一百四十里也
　　　　　一百四十里行一日则一千四百里行
　　　　　十日矣盖日行八十里者十日行八百
　　　　　里日行六十里者十日行六百里并之
　　　　　以合原数也

设如有银四百八十六两籴米麦豆三色其石数相
　等米每石价银一两二钱麦每石价银九钱豆每
　石价银六钱问石数若干
　　　　　法以米价一两二钱麦价九钱豆价六
　　　　　钱相并共得二两七钱为一率一石为
　　　　　二率总银四百八十六两为三率推得
　　　　　四率一百八十石即各色之石数也此
　　　　　法盖因三色之石数既相等故三色每
　　　　　石之共价与每一石之比即同于三分

　　　　　之共价四百八十六两与每一分之一

　　　　　百八十石之比也
设如有银一千二百两买绫绢二色绢一分绫二分
　绫每疋价银三两六钱绢每疋价银二两四钱问
　绫绢与价银各几何
　　　　　法以绫价三两六钱二因之(绫二分故/用二因)
　　　　　得七两二钱与绢价二两四钱相加共
　　　　　得九两六钱为一率绢一疋为二率总
　　　　　银一千二百两为三率推得四率一百

　　　　　二十五疋为绢数倍之得二百五十疋
　　　　　为绫数以绢每疋价银二两四钱与绢
　　　　　一百二十五疋相乘得三百两为共绢
　　　　　价以绫每疋价银三两六钱与绫二百
　　　　　五十疋相乘得九百两为共绫价也此
　　　　　法盖因绢为一分绫为二分故将绫价
　　　　　二因之与绢价相加即绫二疋绢一疋
　　　　　之共价以绫二疋绢一疋之共价与绢
　　　　　一疋之比即同于绫二分绢一分之共

　　　　　价一千二百两与绢一分一百二十五

　　　　　疋之比也
设如有银三百三十六两买罗八十疋绢一百二十
　疋罗每疋价比绢每疋价加一倍问罗价绢价各
　几何
　　　　　法以罗八十疋倍之得一百六十疋与
　　　　　绢一百二十疋相加得二百八十疋为
　　　　　一率绢一疋为二率总银三百三十六
　　　　　两为三率推得四率一两二钱即绢每

　　　　　一疋之价倍之得二两四钱即罗每一
　　　　　疋之价也此法盖因罗价比绢价加一
　　　　　倍故将罗疋数倍之与绢疋数相加为
　　　　　罗二倍绢一倍之共数而以罗二倍绢
　　　　　一倍之共数与绢一疋之比即同于罗
　　　　　二倍绢一倍之共价三百三十六两与
　　　　　绢一疋之价一两二钱之比也
设如有银七百八十五两令甲乙丙丁四人分之乙
　得甲银十分之七丙得乙银十四分之三丁得丙

　银十二分之九问各分银几何

　　　　　法以一千六百八十分(三分母连/乘之数)为甲
　　　　　衰数取甲十分之七得一千一百七十
　　　　　六分为乙衰数取乙十四分之三得二
　　　　　百五十二分为丙衰数取丙十二分之
　　　　　九得一百八十九分为丁衰数乃以四
　　　　　人衰数相并得三千二百九十七分为
　　　　　一率总银七百八十五两为二率以甲
　　　　　衰一千六百八十分为三率得四率四

　　　　　百两即甲所分之银数以乙衰一千一
　　　　　百七十六分为三率得四率二百八十
　　　　　两即乙所分之银数以丙衰二百五十
　　　　　二分为三率得四率六十两即丙所分
　　　　　之银数以丁衰一百八十九分为三率
　　　　　得四率四十五两即丁所分之银数四
　　　　　人所得银数并之得七百八十五两以
　　　　　合原数也此法因各分母不同恐难度
　　　　　尽故以分母连乘为甲衰数次各按分

　　　　　取其衰数乃并各衰数为共衰数以共

　　　　　衰数与总银数之比即同于各人衰数
　　　　　与各银数之比也
设如东西中三村共纳粮一千零三十六石东村一
　百二十户每户该纳七分西村八十户每户该纳
　五分中村六十户每户该纳四分问各村纳粮若
　干每户纳粮若干
　　　　　法以七分与东村一百二十户相乘得
　　　　　八百四十分为东村衰数以五分与西

　　　　　村八十户相乘得四百分为西村衰数
　　　　　以四分与中村六十户相乘得二百四
　　　　　十分为中村衰数乃以三村衰数相并
　　　　　得一千四百八十分为一率共纳粮一
　　　　　千零三十六石为二率各村衰数各为
　　　　　三率推得各四率东村共该纳粮五百
　　　　　八十八石西村共该纳粮二百八十石
　　　　　中村共该纳粮一百六十八石再以各
　　　　　村户数归除各村所纳粮数则东村每

　　　　　户该纳粮四石九斗西村每户该纳粮

　　　　　三石五斗中村每户该纳粮二石八斗
　　　　　如以三村共衰分数归除共纳粮数得
　　　　　每一分所纳粮数而以各村分数乘之
　　　　　即得各村共纳粮数以各户分数乘之
　　　　　即得各村每户所纳之粮数也
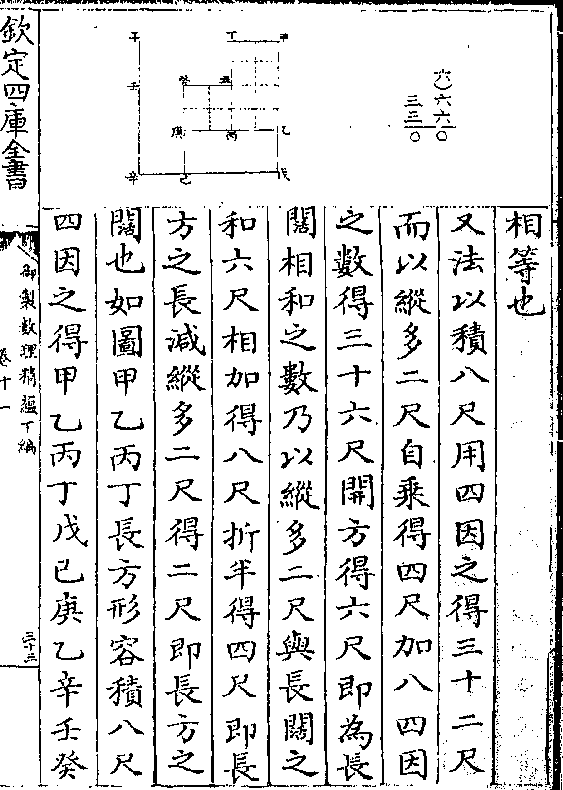
设如乙丙丁三人共纳地租银十一两五钱乙田长
　一百二十丈宽四十丈丙田长二百丈宽六十丈
　丁田长八十丈宽二十丈问每人该租银若干

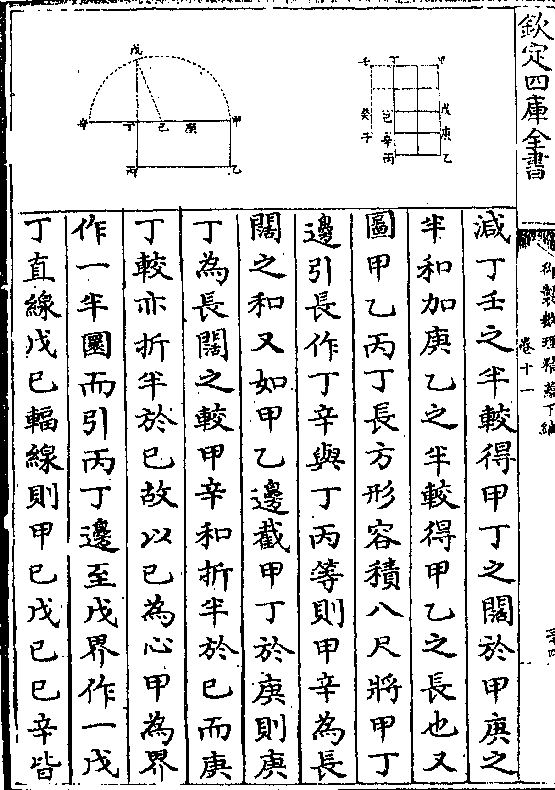
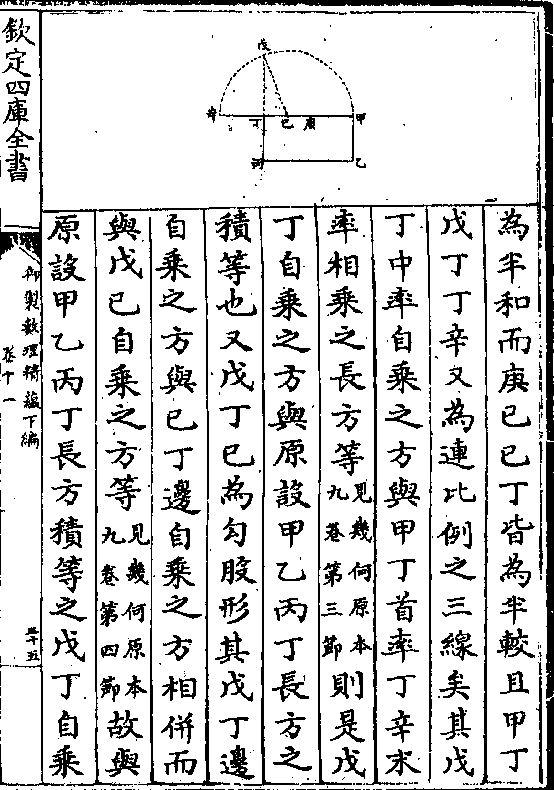　　　　　法以乙田长一百二十丈与宽四十丈
　　　　　相乘得四千八百丈丙田长二百丈与
　　　　　宽六十丈相乘得一万二千丈丁田长
　　　　　八十丈与宽二十丈相乘得一千六百
　　　　　丈三数相并共得一万八千四百丈为
　　　　　一率共地租银十一两五钱为二率各
　　　　　田长宽相乘之数各为三率推得各四
　　　　　率乙该银三两丙该银七两五钱丁该
　　　　　银一两并之为十一两五钱以合原数

　　　　　也

设如孙郑褚三家买货共载一船远近船价不同孙
　家货物九十五担每担船价六分郑家货物八十
　五担每担船价四分褚家货物五十六担每担船
　价二分五釐因中途拨浅共贴银二两五钱二分
　欲照船价分派问各该若干
　　　　　法以孙货九十五担与每担六分相乘
　　　　　得五两七钱以郑货八十五担与每担
　　　　　四分相乘得三两四钱以褚货五十六

　　　　　担与每担二分五釐相乘得一两四钱
　　　　　乃以三家船价相并共得一十两五钱
　　　　　为一率共贴银二两五钱二分为二率
　　　　　一两为三率推得四率二钱四分即为
　　　　　每一两应贴之数复以各家船价银乘
　　　　　之所得一两三钱六分八釐即孙应出
　　　　　之数所得八钱一分六釐即郑应出之
　　　　　数所得三钱三分六釐即褚应出之数
　　　　　也

设如甲丙戊三县共纳米四千石论县之大小米之

　贵贱运之远近分之甲县有三千三百六十户每
　米一石价银八钱运至六十里丙县有一千二百
　户每米一石价银一两运至三十里戊县有二千
　四百户每米一石价银六钱运至八十里问每县
　该米若干
　　　　　法以甲县米价八钱与六十里相乘得
　　　　　四百八十用此数归除甲县三千三百
　　　　　六十户得七为甲县之衰数又以丙县

　　　　　米价一两与三十里相乘得三百用此
　　　　　数归除丙县一千二百户得四为丙县
　　　　　之衰数以戊县米价六钱与八十里相
　　　　　乘得四百八十用此数归除戊县二千
　　　　　四百户得五为戊县之衰数乃以此三
　　　　　衰数相并得一十六为一率总米四千
　　　　　石为二率各县衰数各为三率推得各
　　　　　四率甲县为一千七百五十石丙县为
　　　　　一千石戊县为一千二百五十石三数

　　　　　相并共四千石以合原数也

设如甲乙丙丁戊五处共输粟二千石以田地之多
　寡道里之远近粟价之贵贱均输之甲田一万三
　千零六十亩粟每石价银二两自输本处乙田一
　万二千三百一十二亩粟每石价银一两至输所
　二百里丙田七千一百八十二亩粟每石价银一
　两二钱至输所一百五十里丁田一万三千三百
　三十八亩粟每石价银一两七钱至输所二百五
　十里戊田五千一百三十亩粟每石价银一两三

　钱至输所一百五十里每石每里车价四釐问各
　处所输若干
　　　　　法以甲粟每石价二两归除甲田一万
　　　　　三千零六十亩得六百五十三为甲衰
　　　　　数次以乙输所二百里与每石车价四
　　　　　釐相乘得八钱并入乙粟每石价一两
　　　　　共一两八钱归除乙田一万二千三百
　　　　　一十二亩得六百八十四为乙衰数次
　　　　　以丙输所一百五十里与每石车价四

　　　　　釐相乘得六钱并入丙粟每石价一两

　　　　　二钱共一两八钱归除丙田七千一百
　　　　　八十二亩得三百九十九为丙衰数次
　　　　　又以丁输所二百五十里与每石车价
　　　　　四釐相乘得一两并入丁粟每石价一
　　　　　两七钱共二两七钱归除丁田一万三
　　　　　千三百三十八亩得四百九十四为丁
　　　　　衰数次又以戊输所一百五十里与每
　　　　　石车价四釐相乘得六钱并入戊粟每

　　　　　石价一两三钱共一两九钱归除戊田
　　　　　五千一百三十亩得二百七十为戊衰
　　　　　数乃合五衰数共二千五百为一率共
　　　　　粟二千石为二率五处各衰数各为三
　　　　　率推得各四率甲为五百二十二石四
　　　　　斗乙为五百四十七石二斗丙为三百
　　　　　一十九石二斗丁为三百九十五石二
　　　　　斗戊为二百一十六石五数相并共二
　　　　　千石以合原数也此法盖因地亩以定

　　　　　粟数故粟可以均然粟之价既有贵贱

　　　　　而道里又有远近故取粟价以除地亩
　　　　　正所以均其贵贱而取车价并入粟价
　　　　　以除地亩又所以均其远近也
设如买米八十四石每米一石价一两四钱七分运
　价一钱三分今欲抽米作运价与之问正米与运
　价米各几何
　　　　　法以每石米价一两四钱七分与每石
　　　　　运价一钱三分相加得一两六钱为一

　　　　　率总米八十四石为二率每石米价一
　　　　　两四钱七分为三率推得四率七十七
　　　　　石一斗七升五合即正米数如先求运
　　　　　价米数则仍以一两六钱为一率总米
　　　　　八十四石为二率每石运价一钱三分
　　　　　为三率推得四率六石八斗二升五合
　　　　　即运价米数也既得正米数与运价相
　　　　　乘得十两零三分二釐七豪五丝为共
　　　　　运价而以运费米数与米价相乘亦得

　　　　　十两零三分二釐七豪五丝其数适相

　　　　　当也此法盖因八十四石为正米与运
　　　　　价米之总数今抽米作运费故以米价
　　　　　与运价相并亦为米价与运价之总数
　　　　　以总价与总米之比即同于米价与正
　　　　　米之比又以总价与总米之比即同于
　　　　　运价与运米之比也此法即和数差分
　　　　　之变体旧算书名为就物抽分因其以
　　　　　总米内抽运价故为抽分然要以米价

　　　　　运价之和与总米为比例故附于和数
　　　　　比例之后
设如有丝四十三斤十二两每织绢一疋用丝一斤
　与织工丝四两问织绢丝与织工丝各几何
　　　　　法以织绢丝一斤通为十六两与织工
　　　　　丝四两相加得二十两为一率总丝四
　　　　　十三斤十二两通为七百两为二率织
　　　　　工丝四两为三率得四率一百四十两
　　　　　收为八斤十二两即织工丝与总丝相

　　　　　减馀三十五斤即织绢丝也此亦就物

　　　　　抽分法也以每疋织绢丝及织工丝之
　　　　　共数与总丝之比即同于每疋织工丝
　　　　　与总织工丝之比也

　　较数比例
比例之中有和数而复有较数者以数相合而为比
例故谓之和数若夫因数之相较而成比例则谓之
较数在九章谓之匿价差分其立法盖以每一物与
较数之比即若共物与共较之比或以共物之较与
每一物价之较为比即若共物与每一物价之比也
又或有以实数相比者或有以各物分数相比者虽
未有一定之规然而总不越以彼此相差之较数为

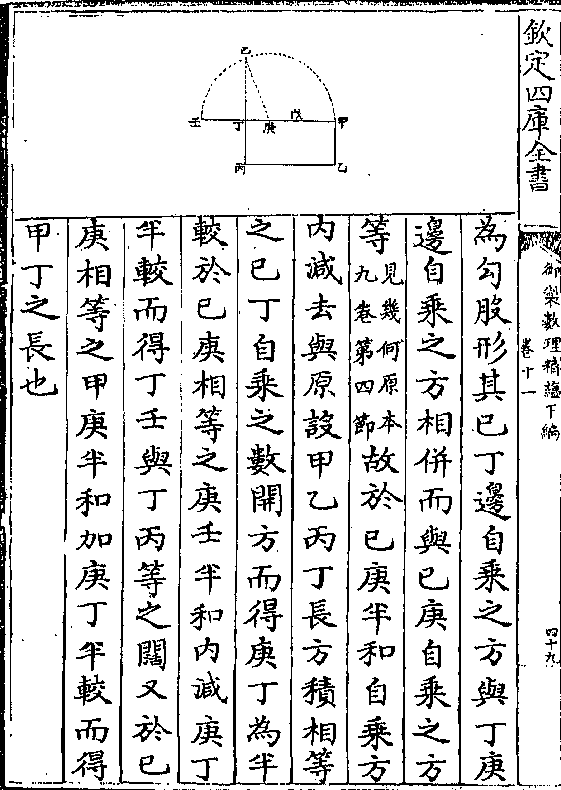
比例故今质名之曰较数比例焉
设如有钱买绫罗二色绫七尺罗九尺两价相等但
　知绫每尺比罗每尺价多三十六文问二色每尺
　价钱几何
　　　　　　法以绫一尺为一率绫比罗每尺价多
　　　　　　三十六文为二率绫七尺为三率推得
　　　　　　四率二百五十二文即绫七尺共多之
　　　　　　数又以绫七尺与罗九尺相减馀罗二
　　　　　　尺为一率绫七尺共多二百五十二文

　　　　　　为二率罗一尺为三率推得四率一百

　　　　　　二十六文即罗一尺之价加多三十六
　　　　　　文得一百六十二文即绫一尺之价以
　　　　　　一百二十六文乘罗九尺得一千一百
　　　　　　三十四文以一百六十二文乘绫七尺
　　　　　　亦得一千一百三十四文两价相等也
　　　　　　此法盖因绫一尺多三十六文则绫七
　　　　　　尺共多二百五十二文也夫绫价多二
　　　　　　百五十二文罗多二尺而其价相等则

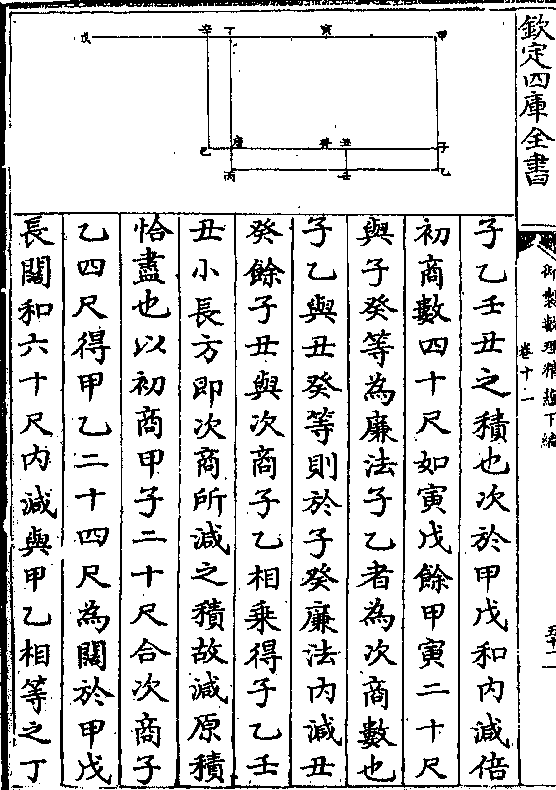
　　　　　　二百五十二文即罗二尺之价罗二尺
　　　　　　价二百五十二文则罗一尺价一百二
　　　　　　十六文也既得罗价则绫价亦可推矣
　　　　　　又法以绫七尺与罗九尺相减馀二尺
　　　　　　为一率绫比罗每尺价多三十六文为
　　　　　　二率绫七尺为三率推得四率一百二
　　　　　　十六文即罗每一尺之价加多三十六
　　　　　　文得一百六十二文即绫每一尺之价
　　　　　　如以罗九尺为三率推得四率一百六

　　　　　　十二文即绫每一尺之价减多三十六

　　　　　　文馀一百二十六文即罗每一尺之价
　　　　　　也此法共绫与共罗之较为二尺绫每
　　　　　　尺与罗每尺之较为三十六文凡共物
　　　　　　之较与共价之较相比即同于共物与
　　　　　　共价之比而共物之较与每一物价之
　　　　　　较相比亦必同于共物与每一物价之
　　　　　　比故以绫共少二尺与罗每尺价少三
　　　　　　十六文之比即同于绫共七尺与罗每

　　　　　　尺价一百二十六文之比也又以罗共
　　　　　　多二尺与绫每尺多三十六文之比亦
　　　　　　即同于罗共九尺与绫每尺价一百六
　　　　　　十二文之比也
设如有银买驼马二色马十匹驼六匹两价相等但
　知驼每匹比马每匹价多八两问二色每匹价银
　若干
　　　　　　法以驼一匹为一率驼比马每匹价多
　　　　　　八两为二率驼六匹为三率推得四率

　　　　　　四十八两即驼六匹共多之数又以马

　　　　　　十匹与驼六匹相减馀马四匹为一率
　　　　　　驼六匹共多四十八两为二率马一匹
　　　　　　为三率推得四率十二两即马一匹之
　　　　　　价加多八两得二十两即驼一匹之价
　　　　　　以二十两乘驼六匹得一百二十两以
　　　　　　十二两乘马十匹亦得一百二十两两
　　　　　　价相等也此法盖因驼一匹多八两则
　　　　　　驼六匹共多四十八两也夫驼价多四

　　　　　　十八两马多四匹而其价相等则四十
　　　　　　八两即马四匹之价马四匹价四十八
　　　　　　两则马一匹价十二两也
　　　　　　又法以驼六匹与马十匹相减馀四匹
　　　　　　为一率驼比马每匹价多八两为二率
　　　　　　驼六匹为三率推得四率十二两即马
　　　　　　每匹之价加多八两得二十两即驼每
　　　　　　匹之价如以马十匹为三率推得四率
　　　　　　二十两即驼每匹之价减多八两馀十

　　　　　　二两即马每匹之价也盖驼共少四匹

　　　　　　与马每匹价少八两之比即同于驼共
　　　　　　六匹与马每匹价十二两之比又马共
　　　　　　多四匹与驼每匹价多八两之比即同
　　　　　　于马共十匹与驼每匹价二十两之比
　　　　　　也
设如有稻一十八石稷二十二石两价相等如交换
　五石则两边俱差银一两六钱问每石价与共价
　各若干

　　　　　　法以交换五石为一率相差一两六钱
　　　　　　为二率稻一十八石为三率推得四率
　　　　　　五两七钱六分即稻一十八石共多之
　　　　　　数又以稻一十八石与稷二十二石相
　　　　　　减馀稷四石为一率稻一十八石共多
　　　　　　五两七钱六分为二率稷一石为三率
　　　　　　推得四率一两四钱四分即稷一石之
　　　　　　价以稷二十二石乘之得三十一两六
　　　　　　钱八分即稷之共价亦即稻之共价以

　　　　　　稻十八石除之得一两七钱六分即稻

　　　　　　一石之价也如交换五石则一为稻十
　　　　　　三石稷五石稻十三石价二十二两八
　　　　　　钱八分稷五石价七两二钱相加得三
　　　　　　十两零八分比共价三十一两六钱八
　　　　　　分少一两六钱一为稷十七石稻五石
　　　　　　稷十七石价二十四两四钱八分稻五
　　　　　　石价八两八钱相加得三十三两二钱
　　　　　　八分比共价三十一两六钱八分则多

　　　　　　一两六钱是两边俱差一两六钱也此
　　　　　　法盖因稻五石多一两六钱则稻十八
　　　　　　石共多五两七钱六分也夫稻多五两
　　　　　　七钱六分稷多四石而其价相等则五
　　　　　　两七钱六分即稷四石之共价稷四石
　　　　　　价五两七钱六分则稷一石价必一两
　　　　　　四钱四分而稷二十二石价必三十一
　　　　　　两六钱八分与稻十八石之价相等故
　　　　　　以十八除之得稻每一石之价也

设如有金球八银球十二两重相等今移换三则银