声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
卷十 第 1a 页 WYG0790-0417a.png
 钦定四库全书
钦定四库全书御制历象考成上编卷十
五星历理二(专论土星/)
土星平行度
用土星三次冲日求本轮均轮半径及最高
求初均数
求次均数
卷十 第 2a 页 WYG0790-0417c.png
 土星平行度
土星平行度测土星平行之法用前后两测取其距恒星之度分
等(恒星有岁差每年五十/一秒测时须加入计之)距太阳之远近左右亦等
乃计其前后相距中积若干日时及星行满次轮若
干周即可得其每日平行之率盖两测距恒星之度
既等则其行满一周天而复于故处而距太阳之远
近左右又等则两测之迟疾加减俱等而次轮之行
亦满全周而复其故处也新法历书载古测定五十
卷十 第 2b 页 WYG0790-0417d.png WYG0790-0418a.png

 九平年又十六日十分日之三或二万一千五百五
九平年又十六日十分日之三或二万一千五百五十一日又十分日之三土星行次轮五十七周(即会/日五)
(十七次冲日/亦五十七次)置中积二万一千五百五十一日又十
分日之三为实星行次轮周数五十七为法除之得
周率三百七十八日八刻一十三分五十三秒三十
八微四十一纤一十六忽四十八芒(即三百七十八/日零百分日之)
(九分二九八二□时历作/三百七十八日○九一六)乃以每周三百六十度为
实周率三百七十八日八刻一十三分五十三秒三
十八微四十一纤一十六忽四十八芒为法除之得
卷十 第 2b 页 WYG0790-0417d.png WYG0790-0418a.png

 五十七分零七秒四十三微四十一纤四十四忽三
五十七分零七秒四十三微四十一纤四十四忽三卷十 第 3a 页 WYG0790-0418c.png
 十三芒为每日土星距太阳之行(即土星在次轮周/每日之行一名岁)
十三芒为每日土星距太阳之行(即土星在次轮周/每日之行一名岁)行与每日太阳平行五十九分零八秒一十九微四
十九纤五十一忽三十九芒相减馀二分零三十六
微零八纤零七忽零六芒为每日土星平行经度(即/本)
(轮心每/日之行)既得每日之平行用乘法可得每年每月之
平行用除法可得每时每分之平行以立表
卷十 第 4a 页 WYG0790-0419a.png
 用土星三次冲日求本轮均轮半径及最高
用土星三次冲日求本轮均轮半径及最高土星之初均数生于本轮半径而求本轮半径须用
三次冲日与月离用三月食同盖星冲日之时星在
次轮最近点无次均数故测诸星本轮半径者必俟
此时也新法历书载西人多录某于汉顺帝时用土
星三次冲日推得两心差为本天半径十万分之一
万一千七百七十二用其四分之三为本轮半径四
分之一为均轮半径最高在大火宫二十三度(永建/二年)
卷十 第 4b 页 WYG0790-0419b.png WYG0790-0419c.png

 (丁/卯)后因其数与天行不合又改两心差为本天半径
(丁/卯)后因其数与天行不合又改两心差为本天半径十万分之一万一千二百七十七至明正德间西人
歌白泥复用三测推得两心差为本天半径十万分
之一万二千最高在析木宫二十七度三十五分(正/德)
(九年/甲戌)相距一千三百八十七年而两次所测最高相
差三十四度三十五分乃以三十四度三十五分为
实一千三百八十七年为法除之得每年最高行一
分二十九秒四十六微万历间西人第谷又测得两
心差为本天半径十万分之一万一千六百二十八
卷十 第 4b 页 WYG0790-0419b.png WYG0790-0419c.png

 后又定两心差为本天半径千万分之一百一十六
后又定两心差为本天半径千万分之一百一十六卷十 第 5a 页 WYG0790-0420a.png
 万二千本轮半径为本天半径千万分之八十六万
万二千本轮半径为本天半径千万分之八十六万五千五百八十七(此四分之三小/比三分之二大)均轮半径为本天
半径千万分之二十九万六千四百一十三(比四分/之一大)
(比三分/之一小)最高在析木宫二十六度二十分二十七秒
(万历十八/年庚寅)每年最高行一分二十秒一十二微用其
数推算均数与天行密合今仍用其数而述其测法
如左
假如第一次冲日日躔娵
卷十 第 5b 页 WYG0790-0420b.png WYG0790-0420c.png
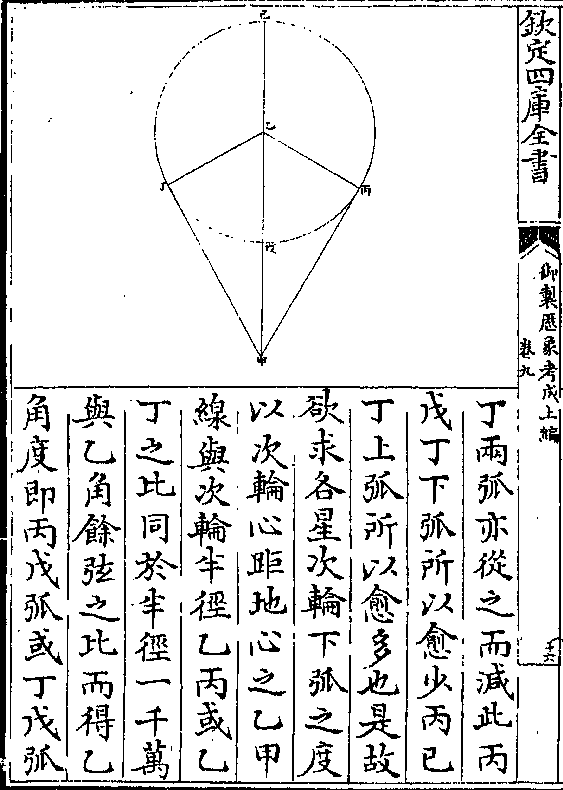
 訾宫一度零三分二十七
訾宫一度零三分二十七秒土星在鹑尾宫一度零
三分二十七秒如甲第二
次冲日日躔娵訾宫二十
一度四十七分三十九秒
土星在鹑尾宫二十一度
四十七分三十九秒如乙
第三次冲日日躔降娄宫
一十六度五十一分二十
卷十 第 5b 页 WYG0790-0420b.png WYG0790-0420c.png

 八秒土星在寿星宫一十
八秒土星在寿星宫一十卷十 第 6a 页 WYG0790-0421a.png
 六度五十一分二十八秒
六度五十一分二十八秒如丙
第一次冲日距第二次冲
日一万一千三百四十三
日五时三十六分其实行
相距二十度四十四分一
十二秒(即鹑尾宫甲点距/乙点之度亦即甲)
(丁乙角于第二次实行度/内减去第一次实行度即)
卷十 第 6b 页 WYG0790-0421b.png WYG0790-0421c.png

 (得/)其平行相距一十九度
(得/)其平行相距一十九度五十九分五十四秒(以每/日平)
(行度与距日相乘/减去全周即得)第二次
冲日距第三次冲日七百
五十五日二十时三十一
分其实行相距二十五度
零三分四十九秒(即鹑尾/宫乙点)
(距寿星宫丙点之度亦即/乙丁丙角于第三次实行)
(度内减去第二/次实行度即得)其平行相
卷十 第 6b 页 WYG0790-0421b.png WYG0790-0421c.png

 距二十五度一十九分一
距二十五度一十九分一卷十 第 7a 页 WYG0790-0422a.png
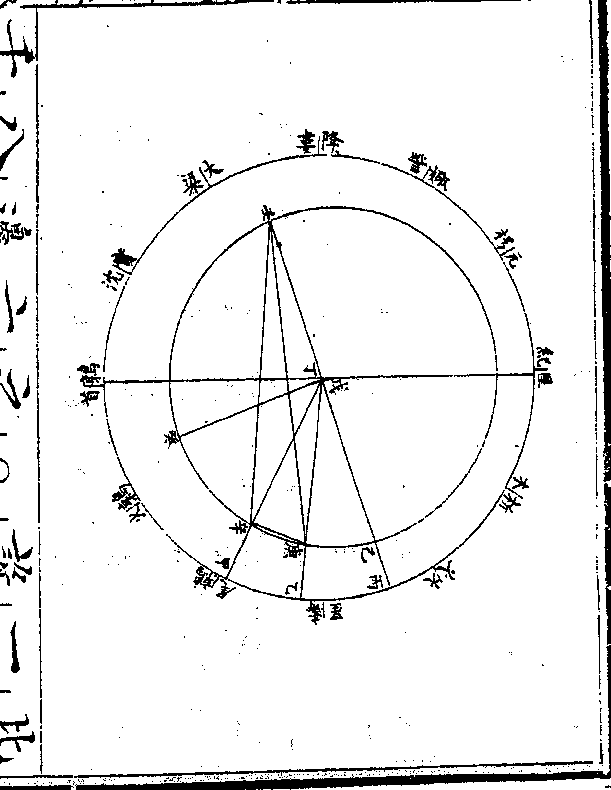
 十六秒乃用不同心圈立
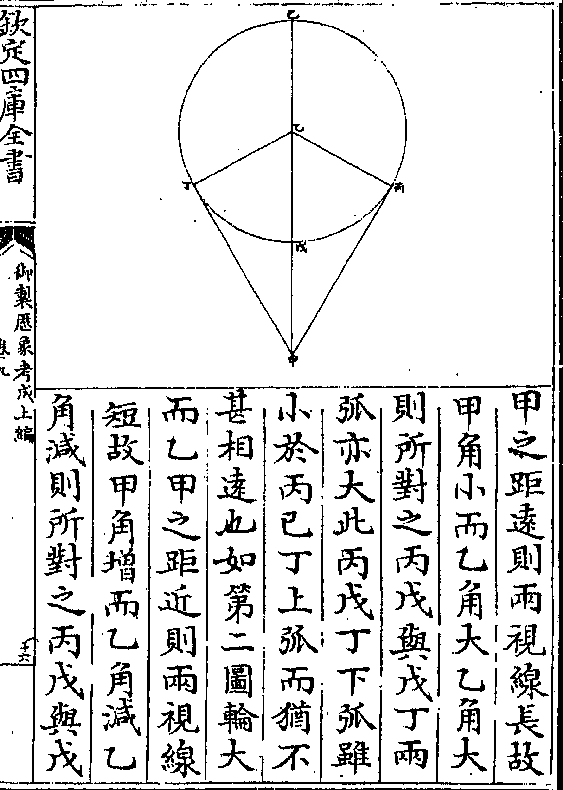
十六秒乃用不同心圈立法算之任取戊点为心作
己庚辛壬不同心圈则辛
庚弧即第一次距第二次
之平行度一十九度五十
九分五十四秒庚巳弧即
第二次距第三次之平行
度二十五度一十九分一
卷十 第 7b 页 WYG0790-0422b.png WYG0790-0422c.png

 十六秒爰从戊点过地心
十六秒爰从戊点过地心丁至圜周二界作一线为
最高线戊丁即两心差又
引丙丁线至壬自壬至甲
丁乙丁二线所割庚辛二
点作壬庚壬辛二线自庚
至辛又作庚辛线即成壬
丁辛壬丁庚壬庚辛三三
角形以求本天半径与两
卷十 第 7b 页 WYG0790-0422b.png WYG0790-0422c.png

 心差之比例先用壬丁辛
心差之比例先用壬丁辛卷十 第 8a 页 WYG0790-0423a.png
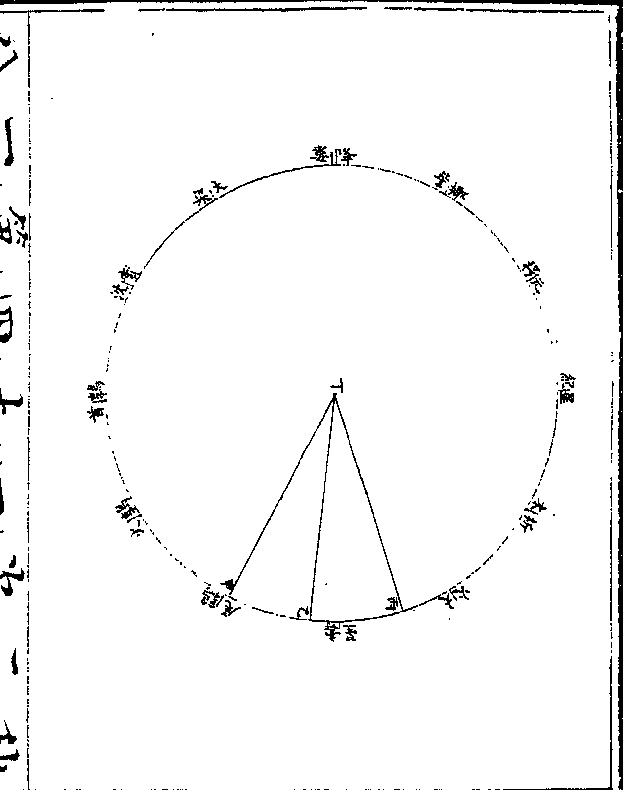 三角形求壬辛边此形有
三角形求壬辛边此形有壬角二十二度三十九分
三十五秒(壬为界角当辛/巳弧以辛庚庚)
(巳两弧相加/折半即得)有丁角一百
三十四度一十一分五十
九秒(即甲丁丙/角之馀)设丁壬边
为一○○○○○○○求
得壬辛边一八二四二六
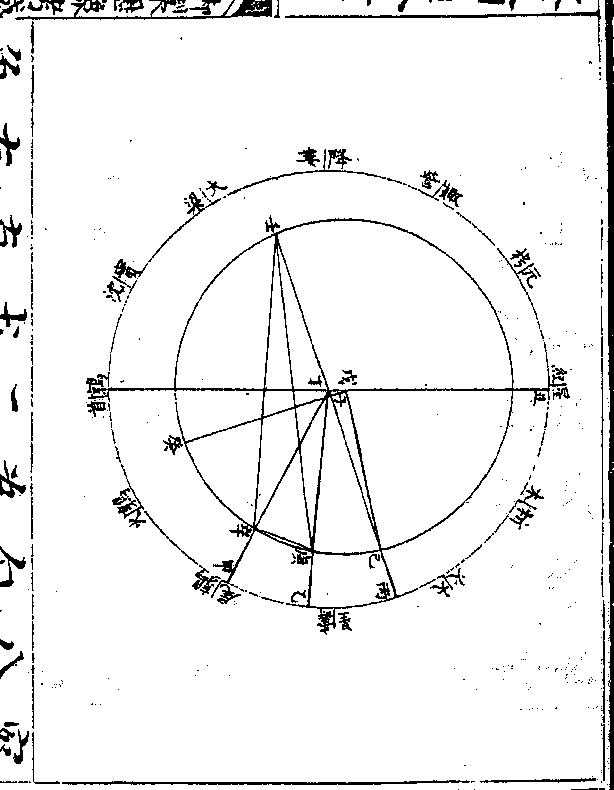
卷十 第 8b 页 WYG0790-0423b.png WYG0790-0423c.png

 三九次用壬丁庚三角形
三九次用壬丁庚三角形求壬庚边此形有壬角一
十二度三十九分三十八
秒(以庚巳弧/折半即得)有丁角一百
五十四度五十六分一十
一秒(即乙丁丙/角之馀)设丁壬边
为一○○○○○○○求
得壬庚边一九七二二九
五四末用壬庚辛三角形
卷十 第 8b 页 WYG0790-0423b.png WYG0790-0423c.png

 求庚角此形有壬辛边一
求庚角此形有壬辛边一卷十 第 9a 页 WYG0790-0424a.png
 八二四二六三九有壬庚
八二四二六三九有壬庚边一九七二二九五四有
壬角九度五十九分五十
七秒(以辛壬丁角与庚/壬丁角相减即得)求
得庚角六十度五十八分
四十秒倍之得一百二十
一度五十七分二十秒为
辛壬弧与辛巳弧四十五
卷十 第 9b 页 WYG0790-0424b.png WYG0790-0424c.png

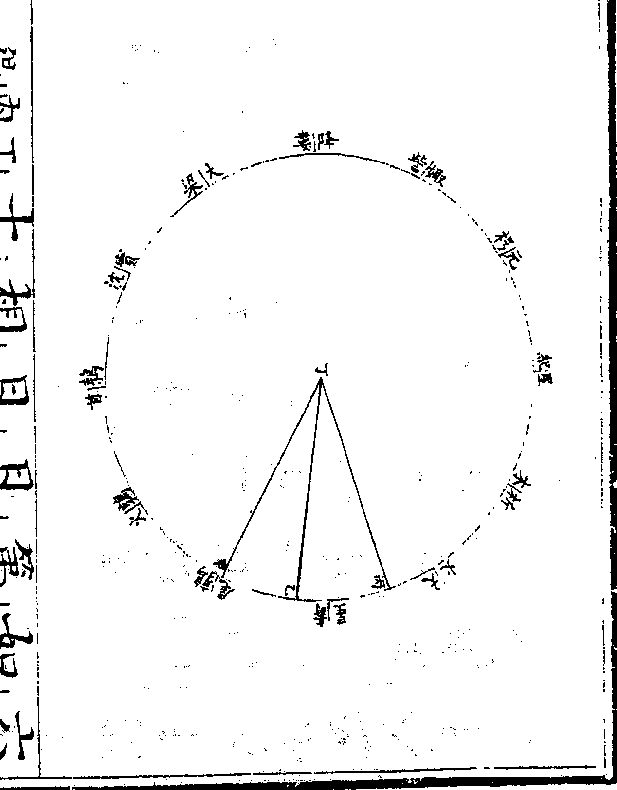 度一十九分一十秒相加
度一十九分一十秒相加得一百六十七度一十六
分三十秒为己辛壬弧于
是以本天半径命为一○
○○○○○○各用八线
表求其通弦则辛壬弧之
通弦为一七四八八六三
二己壬弧之通弦为一九
八七六八一三乃用比例
卷十 第 9b 页 WYG0790-0424b.png WYG0790-0424c.png

 法变先设之丁壬边为同
法变先设之丁壬边为同卷十 第 10a 页 WYG0790-0425a.png
 比例数以先得之辛壬边
比例数以先得之辛壬边一八二四二六三九与先
设之丁壬一○○○○○
○○之比即同于今所察
之辛壬通弦一七四八八
六三二与今所求之丁壬
边之比而得丁壬边九五
八六六七九又平分己辛
卷十 第 10b 页 WYG0790-0425b.png WYG0790-0425c.png

 壬弧于癸作戊癸线平分
壬弧于癸作戊癸线平分己壬通弦于子得子壬九
九三八四○七内减去丁
壬九五八六六七九馀子
丁三五一七二八又以己
癸弧八十三度三十八分
一十五秒与九十度相减
馀六度二十一分四十五
秒为戊巳子角(戊巳子为/直角三角)
卷十 第 10b 页 WYG0790-0425b.png WYG0790-0425c.png

 (形戊角当己癸弧故己角/为己癸弧减象限之馀)
(形戊角当己癸弧故己角/为己癸弧减象限之馀)卷十 第 11a 页 WYG0790-0426a.png
 察其正弦得一一○八一
察其正弦得一一○八一八五为戊子乃用戊子丁
勾股形以戊子为股子丁
为勾求得戊丁弦一一六
二六六三为两心差也
求最高之法亦用戊子丁
直角三角形求丁角此形
有三边有子直角求得丁
卷十 第 11b 页 WYG0790-0426b.png
 角七十二度二十三分二
角七十二度二十三分二十八秒即第三次冲日土
星距最高丑点之度也
卷十 第 12a 页 WYG0790-0426c.png
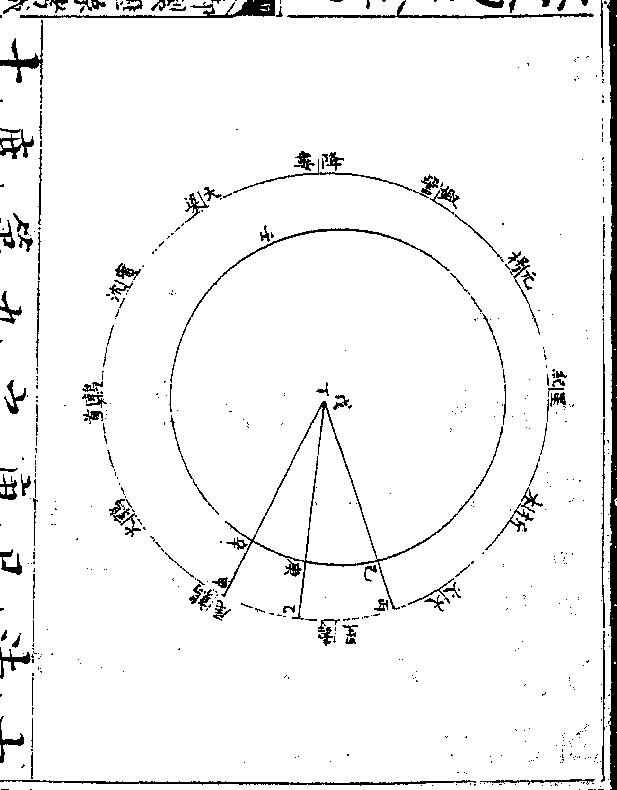
 求初均数
求初均数土星之初均数授时历名为盈缩差其盈差最大者
八度二五五二三八二一缩差最大者六度二七九
○四七一四以周天三百六十度每度六十分约之
盈差得八度零八分一十一秒四十一微缩差得六
度一十一分一十九秒三十八微冲合以外各段同
用新法历书最大之初均数为六度三十八分一十
九秒零六微(即六度零十分度之/六分三八六三三)惟星正当冲合之
卷十 第 12b 页 WYG0790-0426d.png WYG0790-0427a.png

 时止用此均数加减若在冲合前后仍有次均数之
时止用此均数加减若在冲合前后仍有次均数之加减故此名初均数以别之
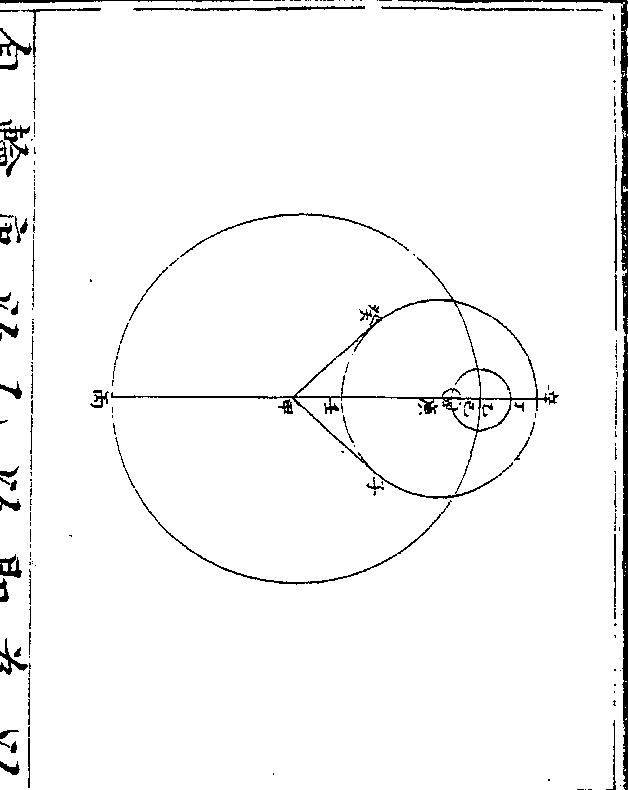
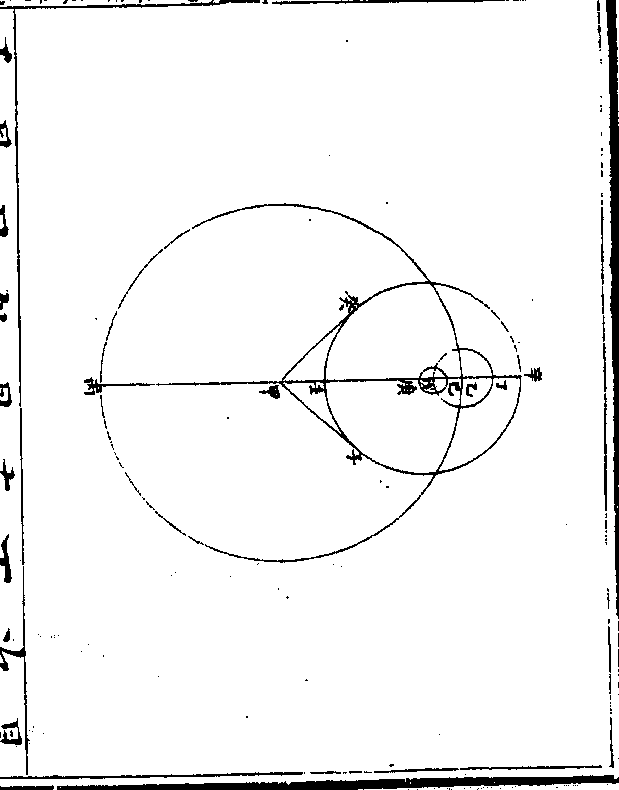
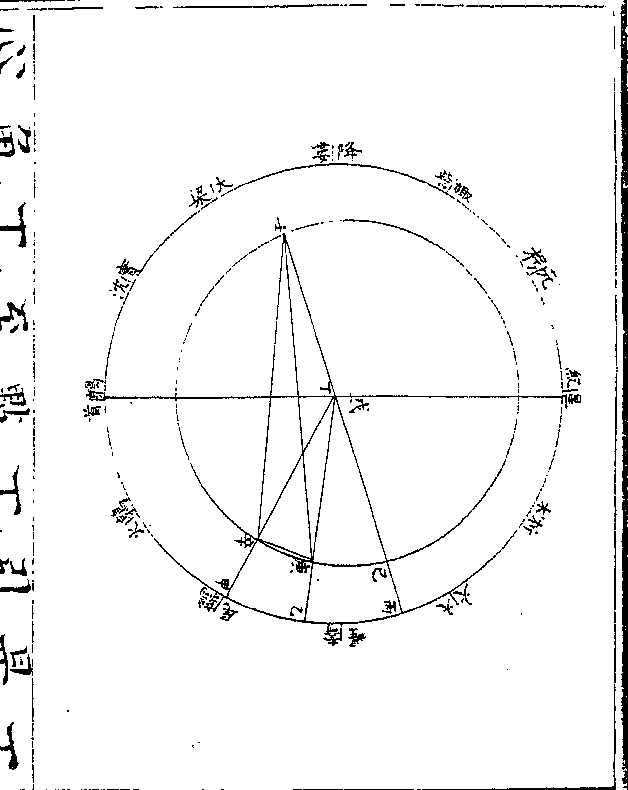
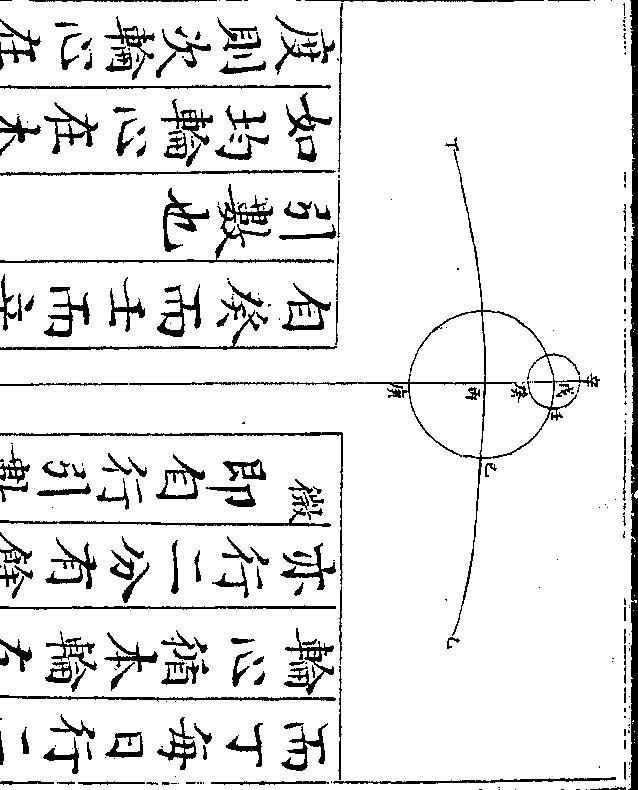
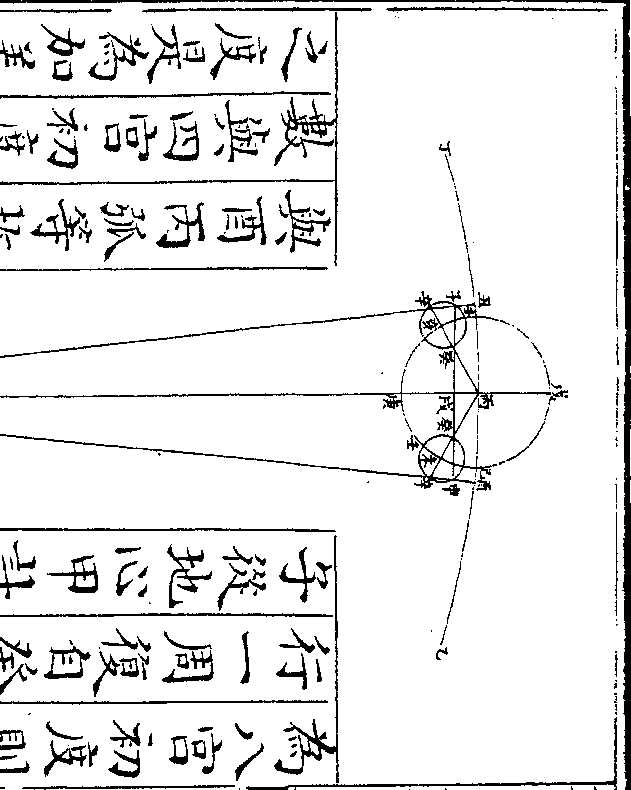
如图甲为地心即本天心乙丙丁为本
天之一弧丙甲半径为一千万戊己庚
为本轮戊丙半径为八十六万五千五
百八十七戊为最高庚为最卑辛壬癸
为均轮辛戊半径为二十九万六千四
百一十三辛为最远(去本轮/心远也)癸为最近
卷十 第 12b 页 WYG0790-0426d.png WYG0790-0427a.png

 (去本轮/心近也)本轮心循本天右旋自乙而丙
(去本轮/心近也)本轮心循本天右旋自乙而丙卷十 第 13a 页 WYG0790-0427c.png
 而丁每日行二分有馀即土星经度均
而丁每日行二分有馀即土星经度均轮心循本轮左旋自戊而已而庚每日
亦行二分有馀(微不及经度之行每年/少一分二十秒一十二)
(微/)即自行引数次轮心则循均轮右旋
自癸而壬而辛每日行四分有馀为倍
引数也
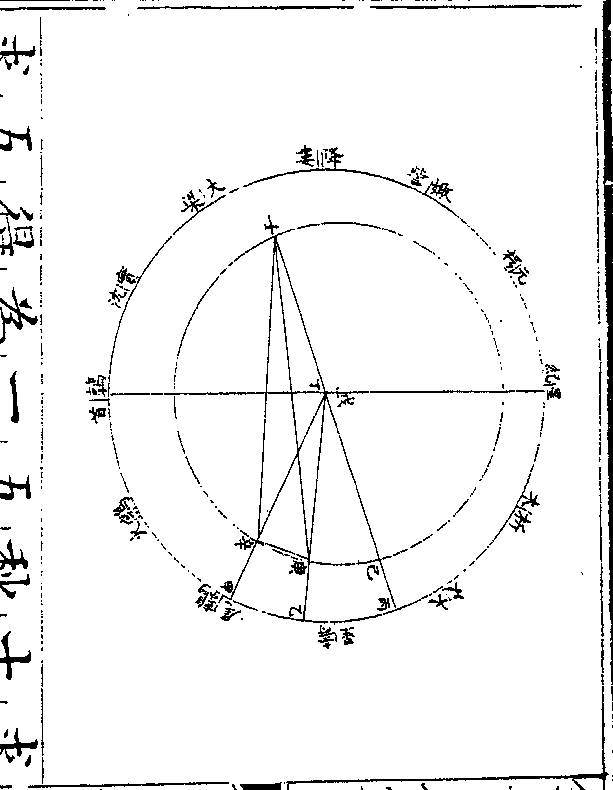
如均轮心在本轮之最高戊为初宫初
卷十 第 13b 页 WYG0790-0427d.png WYG0790-0428a.png

 度则次轮心在均轮之最近癸或均轮
度则次轮心在均轮之最近癸或均轮心从本轮最高戊向已行半周至最卑
庚为六宫初度则次轮心亦从均轮最
近癸历壬辛行一周复至癸从地心甲
计之俱成一直线无平行实行之差故
自行初宫初度及六宫初度俱无均数
也
如均轮心从本轮最高戊行三十度至
卷十 第 13b 页 WYG0790-0427d.png WYG0790-0428a.png

 子为一宫初度则次轮心从均轮最近
子为一宫初度则次轮心从均轮最近卷十 第 14a 页 WYG0790-0428c.png
 癸行六十度至丑(丑癸弧为戊/子弧之倍度)从地心
癸行六十度至丑(丑癸弧为戊/子弧之倍度)从地心甲计之当本天之寅寅丙弧为实行不
及平行之度乃用丙癸卯直角三角形
求癸卯卯丙二边此形有卯直角有丙
角三十度则癸角必六十度有癸丙边
五十六万九千一百七十四(本轮半径/内减去均)
(轮半径/之数)求得癸卯边二十八万四千五
卷十 第 14b 页 WYG0790-0428d.png WYG0790-0429a.png

 百八十七卯丙边四十九万二千九百
百八十七卯丙边四十九万二千九百一十九以卯丙与丙甲本天半径一千
万相加得一千零四十九万二千九百
一十九为卯甲边以癸卯边与丑癸通
弦二十九万六千四百一十三相加(即/均)
(轮丑癸弧六十度之通弦故与均轮半/径等若非六十度则用比例法以半径)
(一千万为一率均轮丑癸弧折半察正/弦为二率均轮子癸半径为三率得四)
(率倍之即丑/癸通弦也)得五十八万一千为丑卯
卷十 第 14b 页 WYG0790-0428d.png WYG0790-0429a.png

 边于是用甲丑卯直角三角形求得甲
边于是用甲丑卯直角三角形求得甲卷十 第 15a 页 WYG0790-0429c.png
 角三度一十分零九秒即寅丙弧为自
角三度一十分零九秒即寅丙弧为自行一宫初度之初均数是为减差以减
于平行而得实行也(凡求得初均角即/求得丑甲边为次)
(轮心距地心之数存/之为后求次均之用)若均轮心从最高
戊向己历庚行三百三十度至辰为十
一宫初度则次轮心从均轮最近癸行
卷十 第 15b 页 WYG0790-0429d.png WYG0790-0430a.png

 一周复自最近癸历壬辛行三百度至
一周复自最近癸历壬辛行三百度至已从地心甲计之当本天之午午丙弧
与寅丙弧等故自行十一宫初度之初
均数与一宫初度等但为实行过于平
行之度是为加差以加于平行而得实
行也用此法求得最高后三宫之减差
(初宫初度至/二宫末度)即得最高前三宫之加差
卷十 第 15b 页 WYG0790-0429d.png WYG0790-0430a.png

 (九宫初度至/十一宫末度)
(九宫初度至/十一宫末度)卷十 第 16a 页 WYG0790-0430c.png
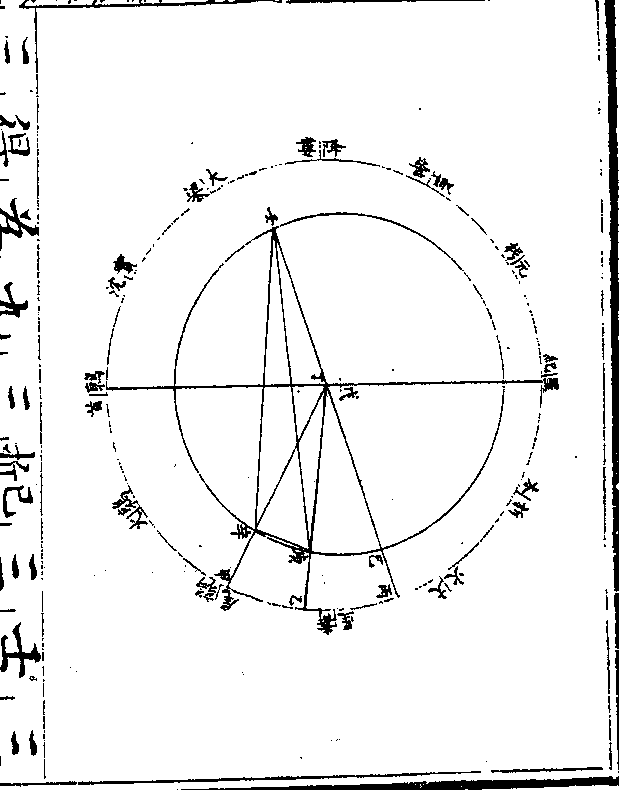
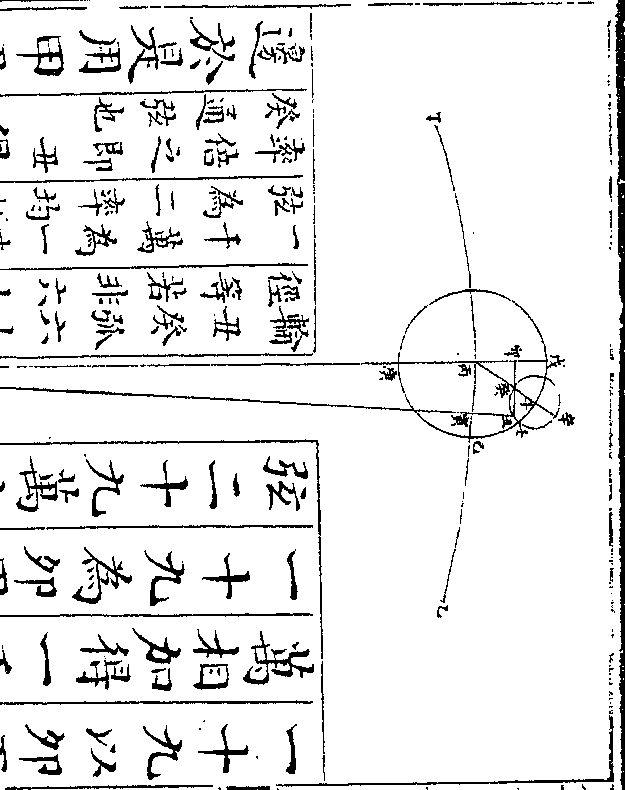
 如均轮心从本轮最高戊行一百二十
如均轮心从本轮最高戊行一百二十度至未为四宫初度则次轮心从均轮
最近癸历壬辛行二百四十度至申从
地心甲计之当本天之酉酉丙弧为实
行不及平行之度乃用丙癸戌直角三
角形求癸戌丙戌二边此形有戌直角
卷十 第 16b 页 WYG0790-0430d.png WYG0790-0431a.png

 有丙角六十度则癸角必三十度癸丙
有丙角六十度则癸角必三十度癸丙边为五十六万九千一百七十四求得
癸戌边四十九万二千九百一十九丙
戌边二十八万四千五百八十七以丙
戌边与丙甲本天半径一千万相减馀
九百七十一万五千四百一十三为戌
甲边以癸戌边与申癸通弦五十一万
卷十 第 16b 页 WYG0790-0430d.png WYG0790-0431a.png

 三千四百零二相加(即均轮申癸弧一/百二十度之通弦)
三千四百零二相加(即均轮申癸弧一/百二十度之通弦)卷十 第 17a 页 WYG0790-0431c.png
 得一百万零六千三百二十一为申戌
得一百万零六千三百二十一为申戌边于是用甲申戌直角三角形求得甲
角五度五十四分四十九秒即酉丙弧
为自行四宫初度之初均数是为减差
以减于平行而得实行也若均轮心从
卷十 第 17b 页 WYG0790-0431d.png
 最高戊向已历庚行二百四十度至亥
最高戊向已历庚行二百四十度至亥为八宫初度则次轮心从均轮最近癸
行一周复自癸历壬行一百二十度至
子从地心甲计之当本天之丑丑丙弧
与酉丙弧等故自行八宫初度之初均
数与四宫初度等但为实行过于平行
之度是为加差以加于平行而得实行
卷十 第 18a 页 WYG0790-0432a.png
 也用此法求得最卑前三宫之减差(三/宫)
也用此法求得最卑前三宫之减差(三/宫)(初度至五/宫末度)即得最卑后三宫之加差(六/宫)
(初度至八/宫末度)
卷十 第 19a 页 WYG0790-0432c.png
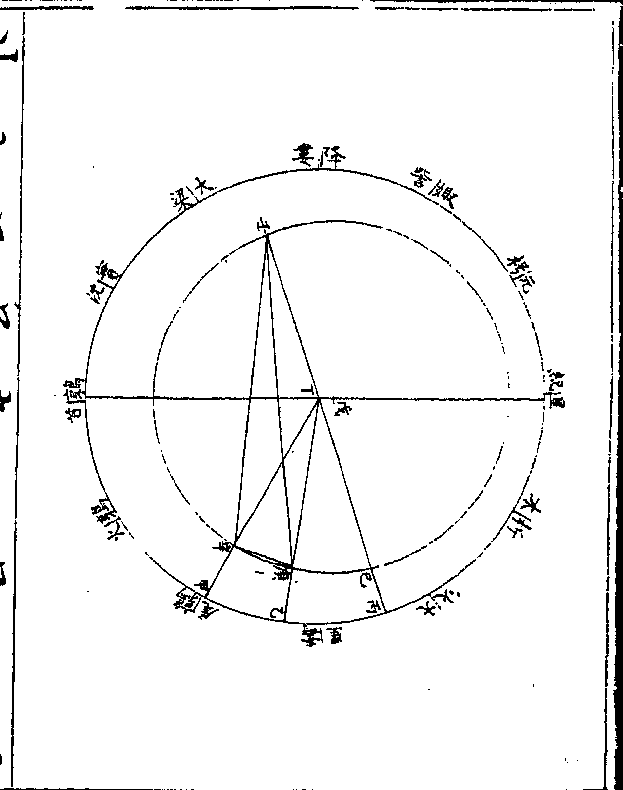
 求次均数
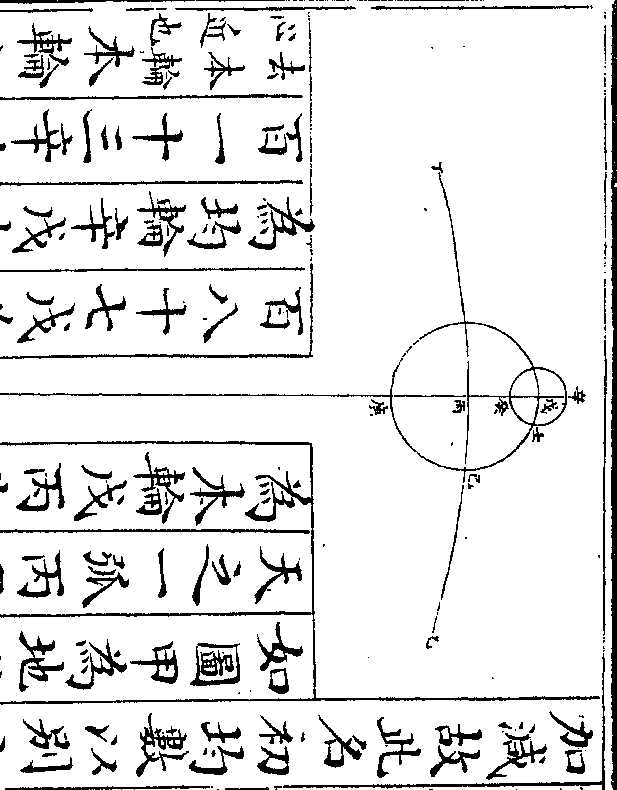
求次均数土星与太阳冲合之后即有次均其数生于次轮盖
星冲太阳之时在次轮之最近合伏之时在次轮之
最远与次轮心及地心参直故求初均数即以次轮
心立算而无次均自冲合而外星行次轮周之左右
其次轮周星体所在即次均数也新法历书载西人
多录某测得次轮半径为本天半径十万分之一万
零八百三十三其后西人第谷又改为本天半径千
卷十 第 19b 页 WYG0790-0432d.png WYG0790-0433a.png

 万分之一百零四万二千六百今从之
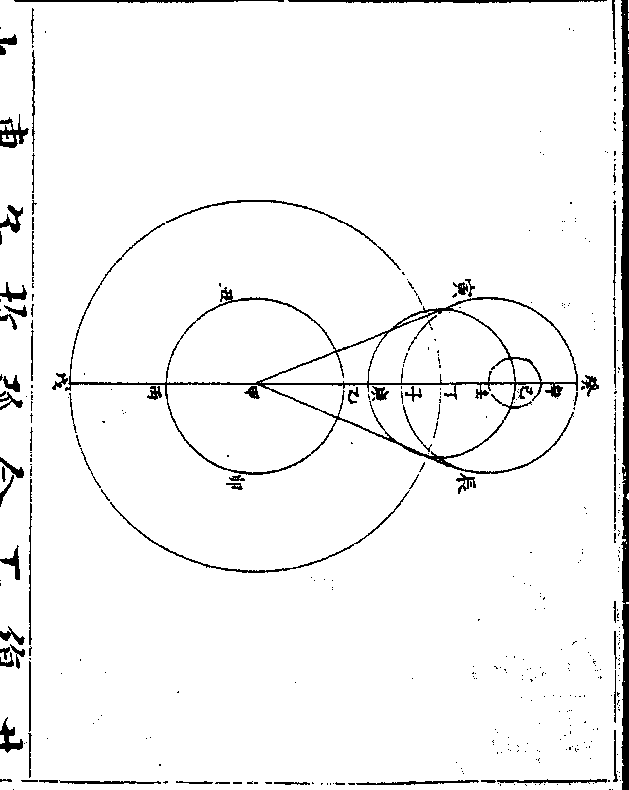
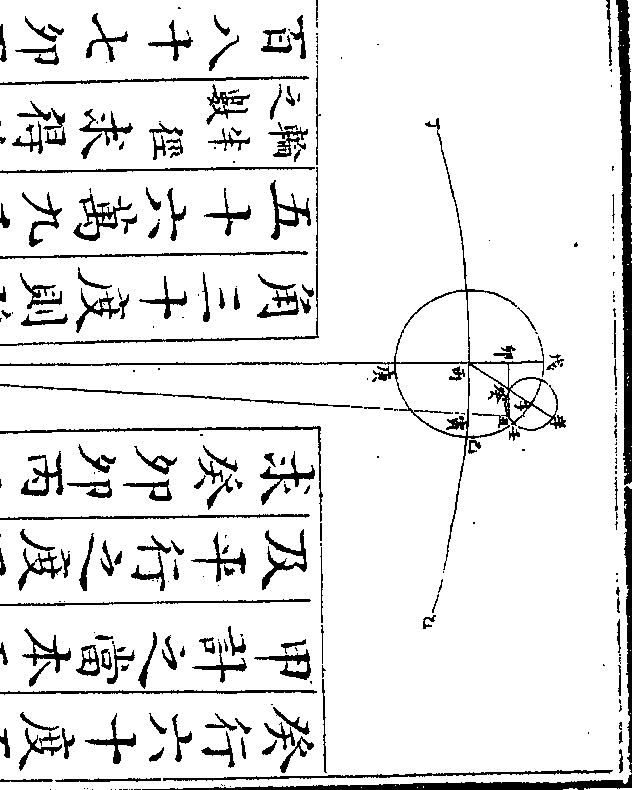
万分之一百零四万二千六百今从之如图甲为地心即本天心乙丙丁为本
天之一弧丙甲为本天半径一千万戊
丙巳为本轮全径戊丙半径为八十六
万五千五百八十七戊为最高己为最
卑庚戊辛为均轮全径庚戊半径为二
十九万六千四百一十三庚为最远辛
为最近(此远近以距/本轮心言)壬辛癸为次轮全
卷十 第 19b 页 WYG0790-0432d.png WYG0790-0433a.png

 径壬辛半径为一百零四万二千六百
径壬辛半径为一百零四万二千六百卷十 第 20a 页 WYG0790-0433c.png
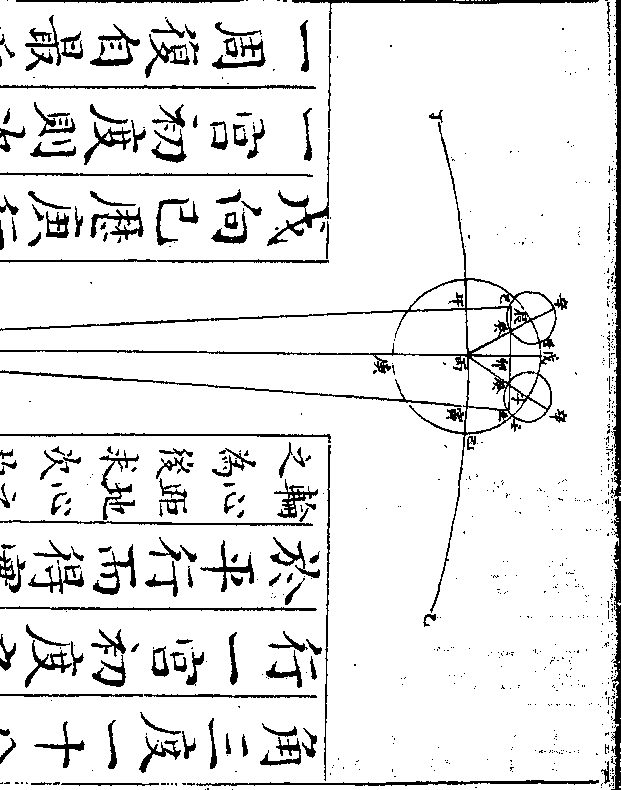 壬为最远癸为最近(此远近以/距地心言)本轮心
壬为最远癸为最近(此远近以/距地心言)本轮心从本天冬至度右旋(本天上与黄道/冬至相对之度)为
经度均轮心从本轮最高戊左旋为引
数(即自/行度)次轮心从均轮最近辛右旋为
倍引数星从次轮最远壬右旋行距日
之度(即本轮心距/太阳之度)如均轮心在本轮最
高戊为自行初宫初度次轮心在均轮
卷十 第 20b 页 WYG0790-0433d.png WYG0790-0434a.png

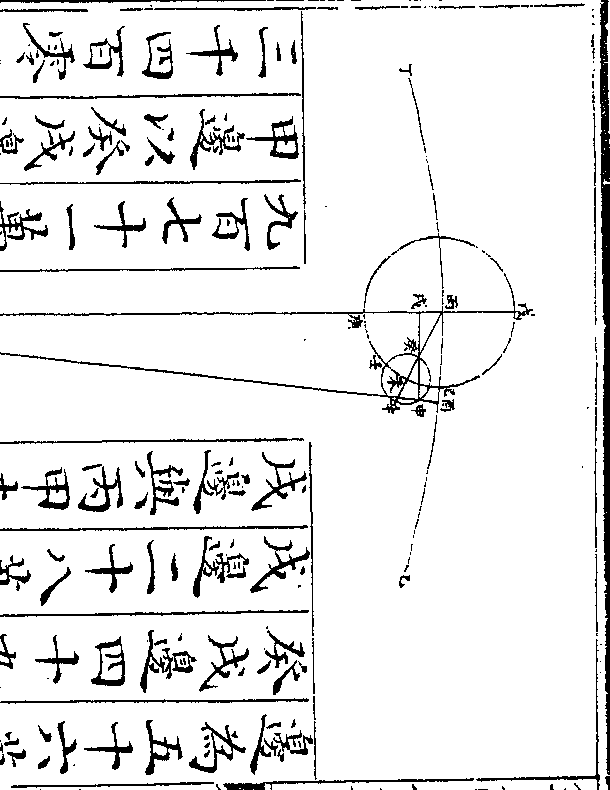 最近辛合伏之时星在次轮之最远壬
最近辛合伏之时星在次轮之最远壬冲太阳之时星在次轮之最近癸从地
心甲计之与轮心同在一直线故无均
数之加减若冲合以后则星在次轮周
之左右(冲太阳之后在次轮之右/合伏之后在次轮之左)而次
均生矣
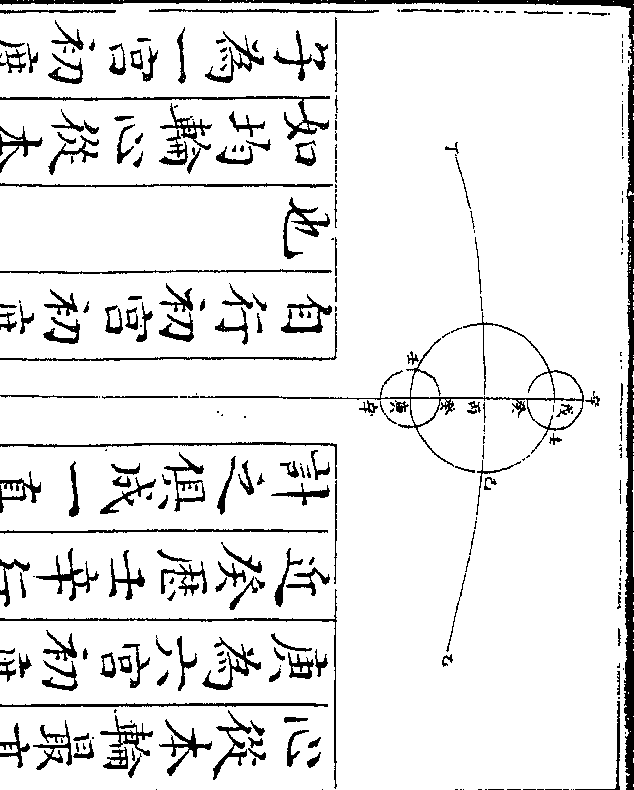
如均轮心从最高戊行三十度至子为
自行一宫初度次轮心则从均轮最近
卷十 第 20b 页 WYG0790-0433d.png WYG0790-0434a.png

 辛行六十度至丑若星在次轮之最远
辛行六十度至丑若星在次轮之最远卷十 第 21a 页 WYG0790-0434c.png
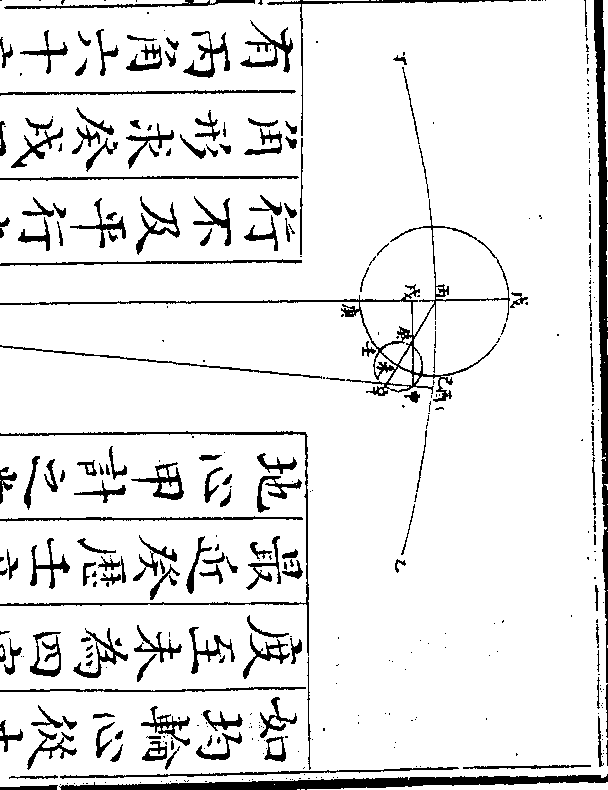 壬或在次轮之最近癸则与次轮心丑
壬或在次轮之最近癸则与次轮心丑同在一直线从地心甲计之当本天之
寅其丙甲寅角三度一十分零九秒(即/寅)
(丙/弧)为初均数而无次均数若星从次轮
最远壬历癸行三百度至卯从地心甲
计之当本天之辰其寅甲辰角即次均
卷十 第 21b 页 WYG0790-0434d.png WYG0790-0435a.png

 数乃用丑甲卯三角形求甲角(即辰/寅弧)此
数乃用丑甲卯三角形求甲角(即辰/寅弧)此形有丑角一百二十度(于壬癸卯弧三/百度内减去壬)
(癸半周馀癸卯/弧即丑角度)有卯丑半径一百零四
万二千六百有丑甲边一千零五十万
八千九百九十一(求丑甲边法见/前求初均数篇)求得
甲角四度五十四分一十八秒即辰寅
弧为次均数与初均数寅丙弧三度一
卷十 第 21b 页 WYG0790-0434d.png WYG0790-0435a.png

 十分零九秒相加得辰丙弧八度零四
十分零九秒相加得辰丙弧八度零四卷十 第 22a 页 WYG0790-0435c.png
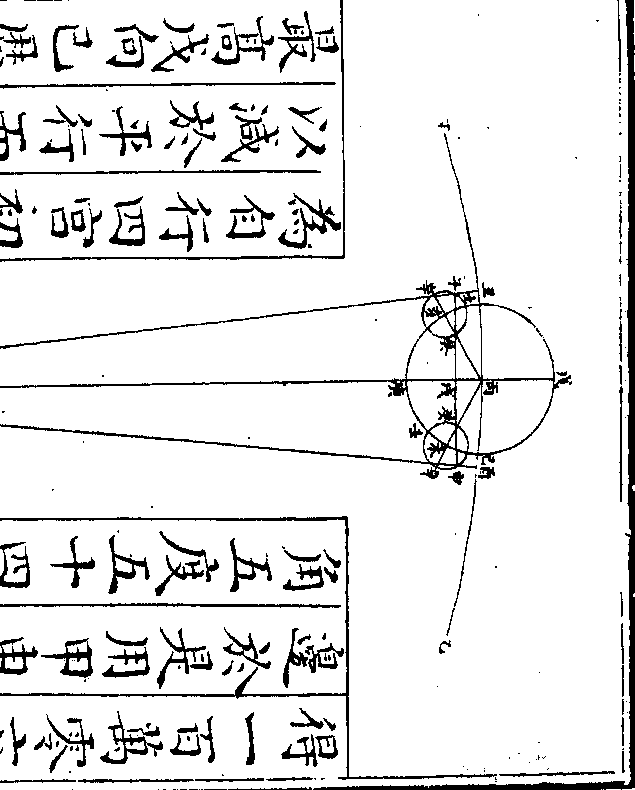 分二十七秒为实行不及平行之度是
分二十七秒为实行不及平行之度是为减差以减于平行而得实行也若均
轮心从最高戊历己行三百三十度至
己为自行十一宫初度次轮心则从均
轮最近辛行一周复行三百度至午星
卷十 第 22b 页 WYG0790-0435d.png
 从次轮最远壬行六十度至未则初均
从次轮最远壬行六十度至未则初均数丙甲申角与丙甲寅角等次均数申
甲酉角与寅甲辰角等两角相加之丙
甲酉角亦与丙甲辰角等但为实行过
于平行之度是为加差以加于平行而
得实行也(若测得平行实行之差及星/距太阳之度以推次轮半径)
(亦用丑甲卯/三角形求之)
卷十 第 23a 页 WYG0790-0436a.png
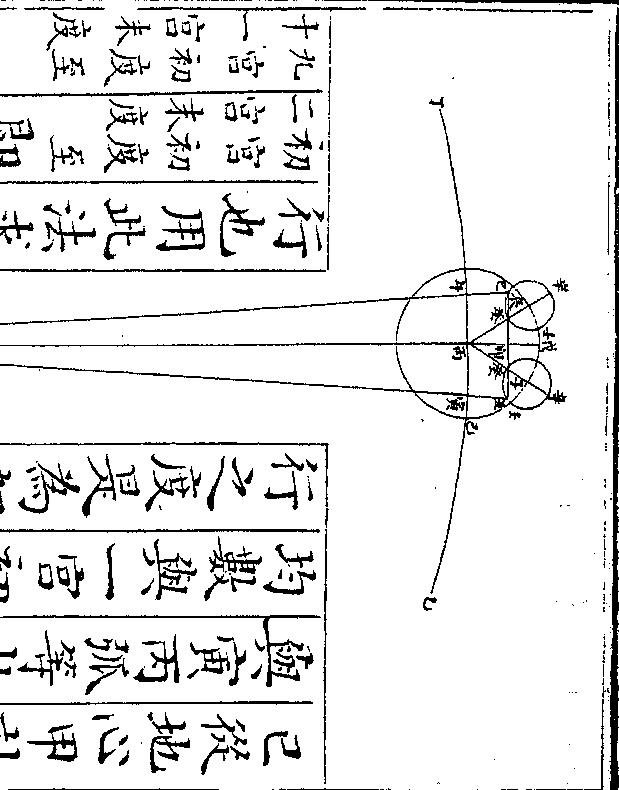
 如均轮心从最高戊行一百二十度至
如均轮心从最高戊行一百二十度至子为自行四宫初度次轮心则从均轮
最近辛历庚行二百四十度至丑若星
在次轮之最远壬或在次轮之最近癸
则与次轮心丑同在一直线从地心甲
计之当本天之寅其丙甲寅角五度五
卷十 第 23b 页 WYG0790-0436b.png WYG0790-0436c.png

 十四分四十九秒(即寅/丙弧)为初均数而无
十四分四十九秒(即寅/丙弧)为初均数而无次均数若星从次轮最远壬行四十五
度至卯从地心甲计之当本天之辰其
寅甲辰角即次均数乃用丑甲卯三角
形求甲角(即寅/辰弧)此形有丑角一百三十
五度(于半周内减去壬卯弧四十/五度馀卯癸弧即丑角度)有卯
丑半径一百零四万二千六百有丑甲
卷十 第 23b 页 WYG0790-0436b.png WYG0790-0436c.png

 边九百七十六万七千三百九十二求
边九百七十六万七千三百九十二求卷十 第 24a 页 WYG0790-0437a.png
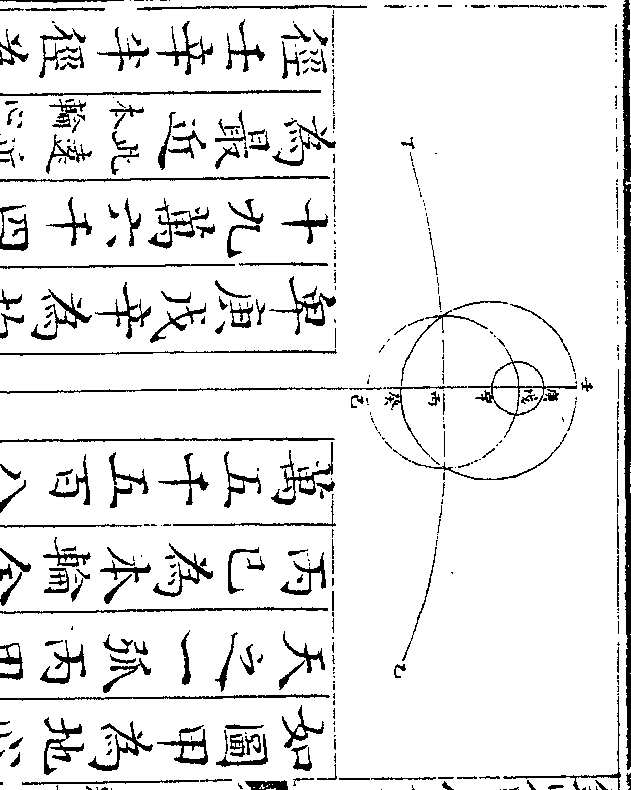 得甲角四度零五十二秒即寅辰弧为
得甲角四度零五十二秒即寅辰弧为次均数与初均数寅丙弧五度五十四
分四十九秒相减(因初均寅点在平行/丙点之后而次均辰)
(点在寅点之/前故相减)馀辰丙弧一度五十三分
五十七秒为实行不及平行之度是为
减差以减于平行而得实行也若均轮
卷十 第 24b 页 WYG0790-0437b.png WYG0790-0437c.png
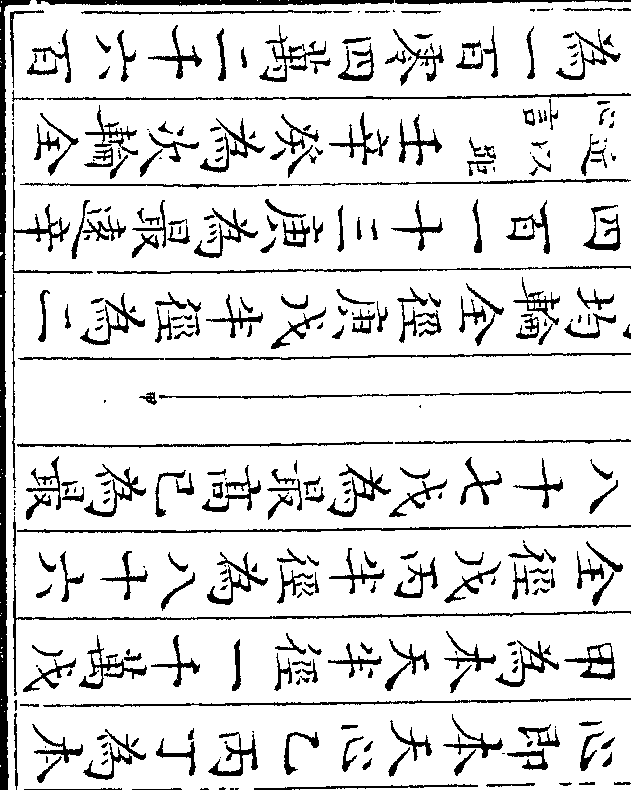
 心从最高戊历己行二百四十度至己
心从最高戊历己行二百四十度至己为自行八宫初度次轮心则从均轮最
近辛行一周复行一百二十度至午星
从次轮最远壬历癸行三百一十五度
至未则初均数丙甲申角与丙甲寅角
等次均数申甲酉角与寅甲辰角等两
卷十 第 24b 页 WYG0790-0437b.png WYG0790-0437c.png

 角相减所馀之丙甲酉角亦与丙甲辰
角相减所馀之丙甲酉角亦与丙甲辰卷十 第 25a 页 WYG0790-0438a.png
 角等但为实行过于平行之度是为加
角等但为实行过于平行之度是为加差以加于平行而得实行也
卷十 第 25b 页 WYG0790-0438b.png WYG0790-0438c.png

卷十 第 25b 页 WYG0790-0438b.png WYG0790-0438c.png

 御制历象考成上编卷十
御制历象考成上编卷十