钦定四库全书
　数学钥卷四凡例
　　　　　　　　　　　　　柘城杜知耕撰
凡例
　　一则
形为体之界在上之界曰面在下之界曰底底与面有
　长广而无厚薄故底面之积曰平积
　　二则

体之纵者曰长衡者曰广立者曰高
　　三则
底面长广及高皆等者曰立方如第一图底面皆方而
　　　　　　　　　　　　　　　　　高不与长
　　　　　　　　　　　　　　　　　广等者曰
　　　　　　　　　　　　　　　　　方体如第
　　　　　　　　　　　　　　　　　二图长广
　　　　　　　　　　　　　　　　　及高皆不
　　　　　　　　　　　　　　　　　等而角方
　　　　　　　　　　　　　　　　　者曰直体

　亦曰直方体如第三图底或方或直而傍为勾股形
　曰堑堵如第四图底或方或直而傍为三角形曰刍
　荛如第五图底或方或圆或多边而上锐至尽者曰
　锥体如第六图凡底面相等者即取底之形为体之
　名设底六边即为六边体如第七图浑然无界无棱
　者曰浑体浑圆如第八图浑撱圆如第九图面长杀
　于底长而无广者曰锐脊如第十图面之长广各杀
　于底者曰锐面如第十一图上下皆有长无广者曰

　鳖臑如第十二图
　　四则
锥及锐面等体自傍科量之度非正高五边七边等底
　中长折半之点非正心
　　五则
线之度尺容十寸寸容十分形之度尺容百寸寸容百
　分体之度尺容千寸寸容千分
　　六则
相似两形之比例为线与线再加之比例再加者谓两

　线各自乘以为比例也相似两体之比例为线与线

　三加之比例三加者谓两线各自乘再乘以为比例
　也两形有一度等者同两线之比例两体有一度等
　者同两形之比例两体有两度等者亦同两线之比
　例
　　七则
堆止一层曰平堆二层以上曰高堆
　
　

　
　
　
　
　
　
　
　
　

　数学钥卷四凡例

钦定四库全书
　数学钥卷四目录
　　　　　　　　　　　　　柘城杜知耕撰
　少广
　　一则立方求积
　　二则直体求积
　　三则堑堵求积
　　四则刍荛求积

　　五则三角体求积
　　六则六边体求积(八边十二边附/)
　　(增/)七则五边体求积(九边附/)
　　八则圆体求积
　　(增/)九则撱圆体求积
　　(增/)十则弧矢体求积
　　十一则锥体求积
　　十二则诸杂线体求积
　　(西/法)十三则浑圆求积(二法/)

　　(增/)十四则浑撱圆求积

　　十五则锐脊体求积
　　(增/)十六则鳖臑求积
　　(增/)十七则等广锐面体求积
　　十八则锐面方体求积
　　十九则锐面直体求积(二法/)　(后法增/)
　　二十则锐面圆体求积
　　(增/)二十一则锐面撱图体求积
　　(西/法)二十二则诸锐面体求积

　　二十三则求锥体之正高
　　二十四则立方以积求边一法(即开立方法/)
　　二十五则立方以积求边二法
　　(增/)二十六则方体以积求边一法(即带纵开立方/法)
　　(增/)二十七则方体以积求边二法
　　二十八则直体以积求边一法
　　(增/)二十九则直体以积求边二法
　　三十则浑圆以积求径
　　(增/)三十一则浑撱圆以积求径

　　三十二则三乘还原(即开三乘方法/附)　(五乘七乘/)

　　三十三则委粟求积
　　三十四则倚壁委粟求积
　　三十五则倚外角委粟求积
　　三十六则倚内角委粟求积
　　三十七则方平堆以周求积
　　三十八则方平堆以积求周
　　三十九则三角平堆以阔求积
　　四十则三角平堆以积求阔

　　四十一则梯形平堆以阔求积
　　四十二则六边平堆以边求积
　　四十三则六边平堆以积求边(求周附/)
　　四十四则堑堵高堆求积
　　四十五则方底高堆求积
　　四十六则三角高堆求积
　　四十七则直底高堆求积
　　四十八则直底锐面堆求积
　　四十九则三角锐面堆求积

　数学钥卷四目录

钦定四库全书
　数学钥卷四
　　　　　　　　　　　　　柘城杜知耕撰
　少广
　　一则
立方求积
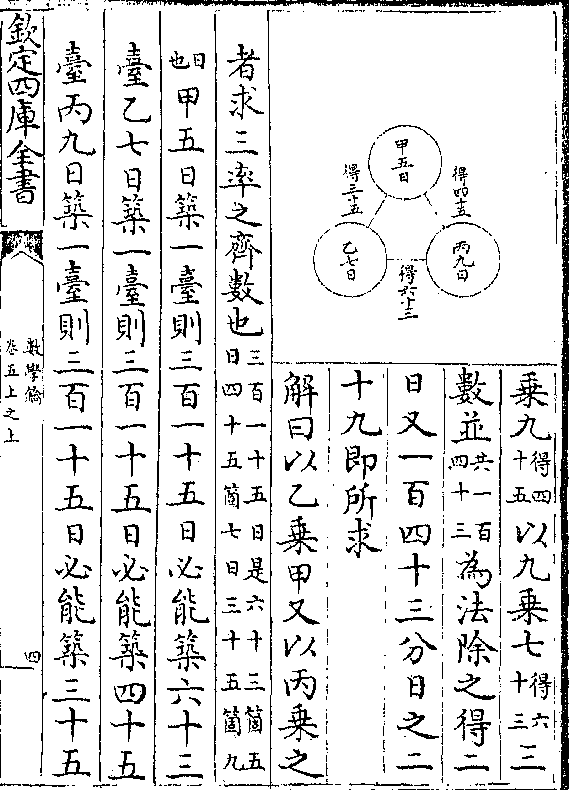
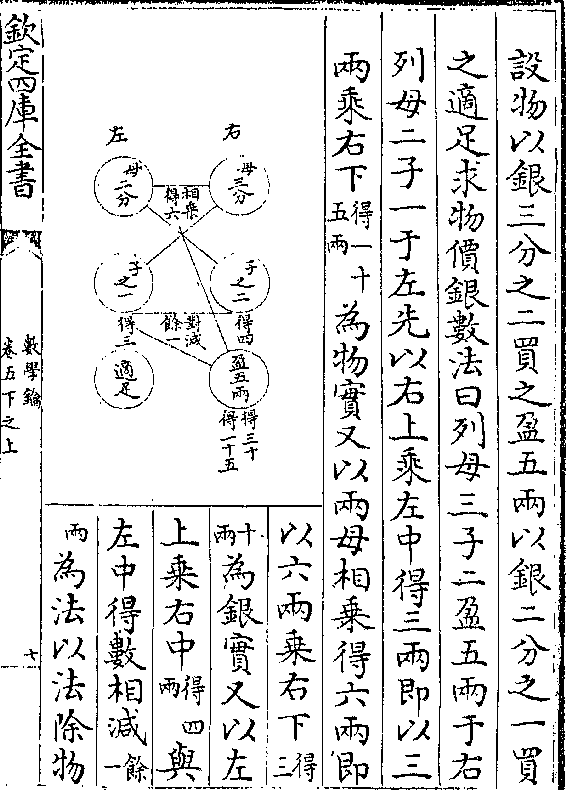
　设立方方三尺求积法曰置三尺自乘(得九/尺)再以三
　尺乘之得二十七尺即所求

　解曰算体之法先求底积(即方圆等形求/积详一二卷)以高为底
　　　　　　　积倍数如图长广各三尺相乘得九尺
　　　　　　　为底积若高二尺则二倍底积之数得
　　　　　　　一十八尺高三尺则三倍底积之数得
　　　　　　　二十七尺
　　二则
直体求积
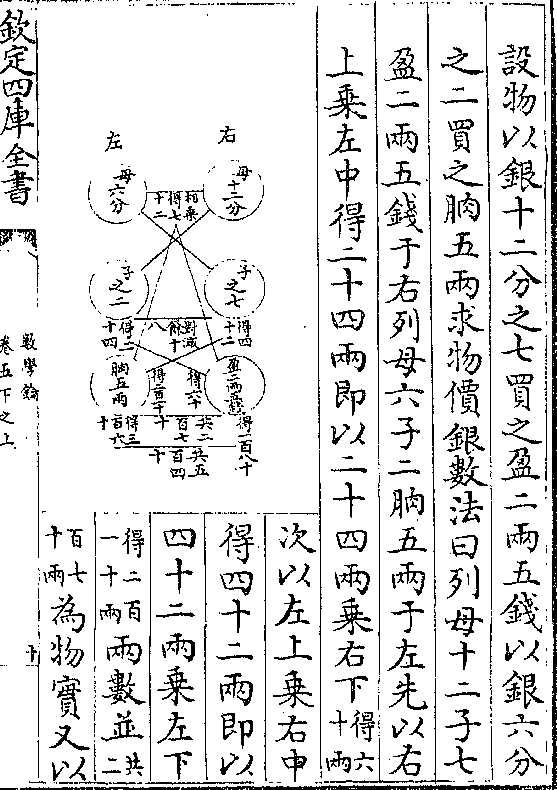
　　　　　　　　设直体长七尺广五尺高一十二尺
　　　　　　　　求积法曰以广乘长(得三十/五尺)以高乘

　　　　　　　　之得四百二十尺即所求

　解同前
　　三则
堑堵求积
　设堑堵长一十二尺广五尺高七尺求积法曰以广
　　　　　　　　　　　　　　　乘长(得六/十尺)以高
　　　　　　　　　　　　　　　乘之(得四百/二十尺)折
　　　　　　　　　　　　　　　半得二百一十
　　　　　　　　　　　　　　　尺即所求

　解曰甲乙丙丁直体与堑堵高广长各等依甲乙线
　丙乙棱分之必成二堑堵夫一直体既能当二堑堵
　则一堑堵必当半直体也故折半得积
　　四则
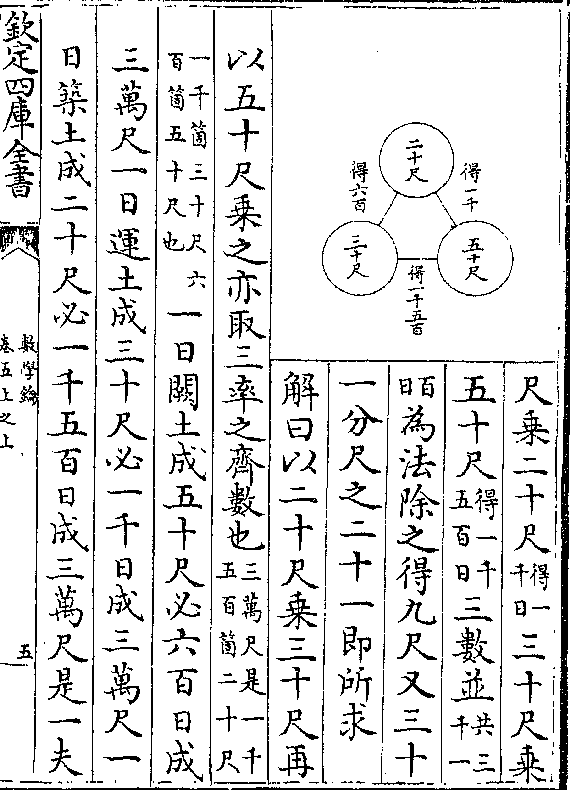
刍荛求积
　设刍荛长一十二尺广五尺高七尺求积法同堑堵
　　　　　　　　　　　　　　　解曰甲乙丙戊
　　　　　　　　　　　　　　　刍荛依丙丁线
　　　　　　　　　　　　　　　丙戊脊分之必

　　　　　　　　　　　　　　　成二堑堵各为

　相当直方之半两直方并必成一直方夫直方之两
　分既倍于刍荛之两分直方之全体不倍于刍荛之
　全体乎故亦折半得积同堑堵也
　　五则
三角体求积
　　　　　　　　　　　　　　设三角体广六尺
　　　　　　　　　　　　　　中长五尺高一十
　　　　　　　　　　　　　　二尺求积法曰置

　　　　　　　　　　　　　　长广相乘(得三/十尺)以
　高乘之(得三百/六十尺)折半得一百八十尺即所求
　解曰即刍荛但彼横此纵耳○勾股体同
　　六则
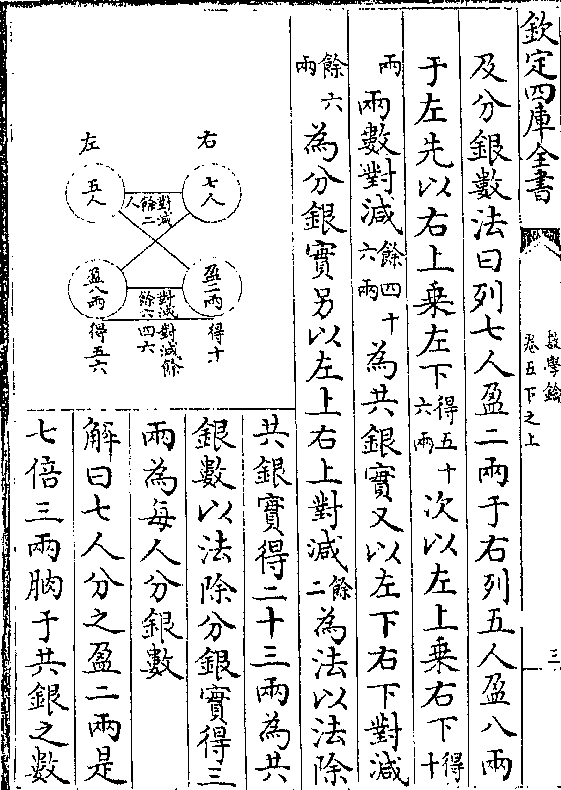
六边体求积(八边及十/二边附)
　设六边体每边广二十尺中长三十四尺六寸四分
　　　　　　　　　　　　　　　有奇高四十尺
　　　　　　　　　　　　　　　求积法曰置广
　　　　　　　　　　　　　　　三因之(得六/十尺)以

　　　　　　　　　　　　　　　长折半(得一十/七尺三)

　(寸二分/零二毫)乘之(得一千零三十九/尺二寸一分二釐)为底积再以高乘之
　得四万一千五百六十八尺四寸八分即所求
　解曰六边底依各角分之成三角形六三角求积法
　以广乘长折半(一卷/五则)不折则得两三角积故三因边
　广以底长之半乘之(底之半长即/三角之中长)即得六三角积(即/全)
　(底/积)犹平圆半径乘半周之义也(二卷/三则)若无底长之度
　则取边广为弦(全底分为六三角形每形之三边俱/等以甲乙为弦即以丙乙为弦也)
　半广为勾(丁/乙)各自乘相减平方开之得股(丙/丁)即底长

　之半(六卷/二则)○设八边底每边广二十尺求底长即以
　二十尺折半为勾(丁/乙)另置二十尺以七六五三六除
　之得二六一三一四强为弦(丙/乙)各自乘相减平方开
　之得股(丙/丁)即底长之半设十二边底每边广二十尺
　求底长即以二十尺折半为勾(丁/乙)另置二十尺以五
　一七六四除之得三八六三六八强为弦(丙/乙)各自乘
　　　　　　　　　　　　　　　相减平方开之
　　　　　　　　　　　　　　　得股(丙/丁)即底长
　　　　　　　　　　　　　　　之半按七六五

　　　　　　　　　　　　　　　三六乃四十五

　度弧之通弦四十五度为三百六十度八之一故以
　之除八边底之一边即得外切圆形之半径五一七
　六四乃三十度弧之通弦三十度为三百六十度十
　二之一故以之除十二边底之一边即得外切圆形
　之半径外切圆形之半径即三角形之腰线(丙/乙)也(见/大)
　(测及八/线表)
　　七则
五边体求积

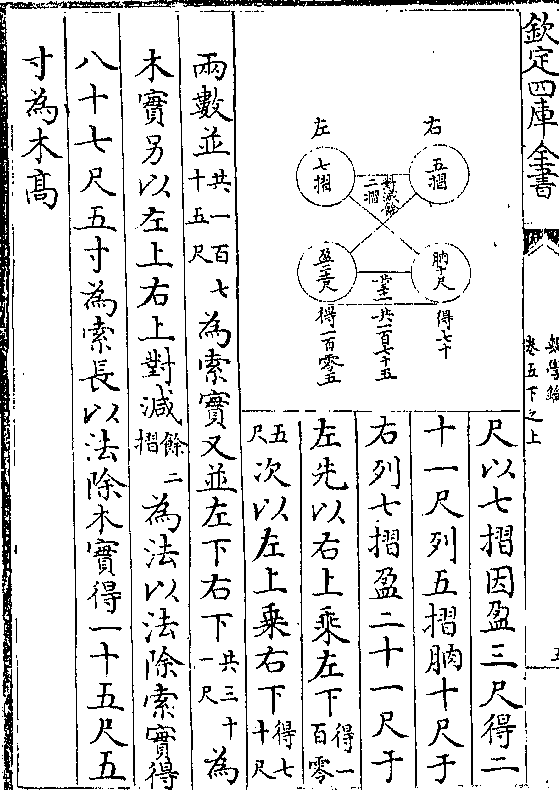
　设五边体每边广二十尺中长三十尺零七寸七分
　　　　　　　　　　　　　　　六釐六毫强高
　　　　　　　　　　　　　　　四十尺求积法
　　　　　　　　　　　　　　　曰置边广以边
　　　　　　　　　　　　　　　数五因之(得一/百尺)
　折半(得五/十尺)为实另置边广折半(得十/尺)自乘(得一/百尺)以中
　长除之(得三尺二寸四/分九釐一毫强)与中长相减(馀二十七尺五/寸二分七釐四)
　(毫/强)折半(得一十三尺七寸/六分三釐七毫强)为法乘实(得六百八十八/尺一寸八分八)
　(釐/)为底积再以高乘之得二万七千五百二十七尺

　五寸二分即所求

　　　　　　　　　解曰五边底依各角分之成三
　　　　　　　　　角形五欲求底积必先得三角
　　　　　　　　　积欲求三角积必先得三角之
　　　　　　　　　中长(丙/丁)然上则六边边为偶数
　角与角相对边与边相对其全底之长即相对两三
　角之中长令五边边为奇数边与角相对其底长(己/丁)
　小半为此三角之中线(丙/丁)大半为彼三角之腰线(己/丙)
　折半则得庚丁不能得丙丁也若欲得丙丁必先求

　己丙(于己丁底长减去/己丙馀即丁丙)欲得己丙必先求外切圆形
　之己戊径(己戊折半/即己丙)欲得己戊必先求外切圆径大
　于底长之丁戊(底长加丁/戊即己戊)欲求丁戊则用弧矢以弦
　及馀径求矢法(二卷二/十二则)今边广甲戊乙弧矢形之甲
　乙弦也边广折半自乘丁乙半弦上方形也底长己
　丁馀径也以除半弦上方形所得者丁戊矢也以矢
　减底长所馀者倍三角中长之辛丁也故半之为三
　角之中长又五因边广折半者取五三角底之半也
　若无底长之度则取边广折半为勾(丁/乙)另置边广以

　一一七五五八除之得一七零一二八八为弦(丙/乙)各

　自乘相减平方开之得股(丙/丁)即三角形之中长(六卷/二则)
　　　　　　　　　一　一七五五八乃七十二度弧
　　　　　　　　　之通弦七十二度为三百六十
　　　　　　　　　度五之一故以之除五边之一
　　　　　　　　　即得外切圆形之半径(丙/乙)为三
　角形之腰线也○设九边底每边广二十尺求三角
　分形之中长则以二十尺折半为勾(丁/乙)另置二十尺
　以六八四零四除之得二九二三八为弦(丙/乙)自乘相

　减平方开之得股(丙/丁)即三角形之中长六八四零四
　乃四十度弧之通弦四十度为三百六十度九之一
　故以之除九边之一即得三角形之腰线也
　　八则
圆体求积
　设圆体径三十尺高四十尺求积法曰置径自乘(得/九)
　　　　　　　　　　　　　　(百/尺)再以高乘之
　　　　　　　　　　　　　　(得三万/六千尺)用圆法
　　　　　　　　　　　　　　十一乘十四除

　　　　　　　　　　　　　　(二卷/四则)得二万八

　千二百八十五尺七寸有奇即所求
　解曰以径自乘再以高乘之方体积也方体与圆体
　等高则两体即若两底之比例故用平圆法求圆体
　之积也
　　九则
撱圆体求积
　设撱圆体大径三十六尺小径一十六尺高四十尺
　求积法曰置两径相乘(得五百七/十六尺)再以高乘之(得二/万三)

　(千零四/十尺)用圆法十一乘十四除得一万八千一百零
　　　　　　　　　　　　　　　二尺八寸有奇
　　　　　　　　　　　　　　　即所求
　　　　　　　　　　　　　　　解同前则及二
　　　　　　　　　　　　　　　卷十六则
　　十则
弧矢体求积
　设弧矢体矢阔八尺六寸六分零二毫弦长三十尺
　背三十六尺二寸九分零三毫六丝高四十尺求积

　法曰置半弦自乘(得二百二/十五步)以矢除之(得二十五尺/九寸八分零)

　　　　　　　　　　　　　　　(九壹/强)为馀径馀
　　　　　　　　　　　　　　　径加矢折半(得/一)
　　　　　　　　　　　　　　　(十七尺三寸二/分零五毫五丝)
　　　　　　　　　　　　　　　为法乘背(得六/百二)
　(十八尺五寸/六分九釐)另以馀径减矢折半(得八尺六寸六/分零四毫弱)为
　法乘弦(得二百五十九尺/八寸一分二釐)两数相减(馀三百六十八/尺七寸五分七)
　(釐/)折半(得一百八十四尺/三寸七分八釐)为底积再以高乘之得七
　千三百七十五尺一寸四分即所求(二卷十/七则)

　　十一则
锥体求积
　设方锥方二十尺高四十尺求积法曰置二十尺自
　　　　　　　　　　　　　　乘(得四/百尺)为底积
　　　　　　　　　　　　　　再以高乘之(得/一)
　　　　　　　　　　　　　　(万六/千尺)以锥法三
　　　　　　　　　　　　　　归之得五千三
　百三十三尺三寸三分有奇即所求
　解曰方边自乘再以高乘之方体也方锥居方体三

　之一故三归得积也何以知方锥居体三之一也试

　　　　　　　　　　　　　　　作立方如甲乙
　　　　　　　　　　　　　　　自心至各棱分
　　　　　　　　　　　　　　　之必成锥体六
　　　　　　　　　　　　　　　俱以方面为底
　　　　　　　　　　　　　　　方边之半为高
　　　　　　　　　　　　　　　更作一方体与
　　　　　　　　　　　　　　　锥体同底等高
　　　　　　　　　　　　　　　如丙丁丙丁方

　　　　　　　　　　　　　　　体既与锥体同
　底必亦与甲乙立方同底既与锥体等高必以甲乙
　方边之半为高两方体既同底则两体之比例若高
　与高丙丁体必为甲乙立方二之一矣锥体既为甲
　乙立方六之一不为等高同底丙丁方体三之一乎
　再作直体广二尺长四尺高八尺如癸辛亦自心至
　各棱分之亦成锥体六底等戊庚辛己高等辛子之
　半如丑者二底等癸壬庚戊高等庚辛之半如寅者
　二底等庚壬子辛高等辛己之半如卯者二六锥体

　形势虽殊而俱等何也丑与寅同长丑之高倍于寅

　而寅之广倍于丑折寅之广准丑之高则丑寅二体
　等矣又丑与卯同广丑之长倍于卯而卯之高倍于
　丑折丑之长准卯之高则丑卯二体亦等矣夫寅等
　于丑丑等于卯是六锥俱等矣今癸辛一直体能分
　为相等之六锥体则一锥体不为癸辛直体六之一
　乎锥体既为同底倍高直体六之一必为同底等高
　三之一无疑矣○从此推之不论方圆多边弧矢凡
　属锥体者皆为同底等高体三之一

　　十二则
诸杂线体求积
　凡体先求底积底属直线依一卷九则例属曲线及
　杂线依二卷四十则例裁之得底积再以高乘之即
　得体积
　　十三则
浑圆求积
　设浑圆径十尺求积法曰置径自乘(得一/百尺)四因之(得/四)
　(百/尺)十一乘十四除(得三百一十四尺/二寸八分六釐弱)为面积再以半

　径乘之(得一千五百七十/一尺四寸三分弱)以三归之得五百二十三

　　　　　　　　　尺八寸一分即所求
　　　　　　　　　解曰置径自乘再以十一乘十
　　　　　　　　　十四除者浑圆中丙子乙丑平
　　　　　　　　　圆积也以四因之者浑圆面积
　当平圆积四也何也浑圆面任割一分(如甲丁/己戊)欲求
　面分之容则取自甲顶至戊界之度(甲戊/线)为半径作
　平圆(如辛癸平圆辛/壬与甲戊等)其容即等若自乙丙平割浑圆
　之半取自甲顶至乙界之度为半径作平圆其容必

　与浑圆半面等今丙子乙丑平圆半径为乙庚乙庚
　　　　　　　　　　　　　与甲庚等乙庚甲庚
　　　　　　　　　　　　　两线偕甲乙线则成
　　　　　　　　　　　　　一勾股形甲乙为弦
　　　　　　　　　　　　　乙庚甲庚一为勾一
　为股也以弦为半径之平圆必倍大于或勾或股为
　半径之平圆浑圆半面既等于以甲乙弦为半径之
　平圆不倍大于以乙庚勾为半径之丙子乙丑平圆
　乎半面既倍大于丙子乙丑平圆全面不四倍大于

　丙子乙丑平圆乎法以半径乘之以三归之又何也

　平圆求积同于以圆周为底以半径为高之三角形
　(二卷/四则)故浑圆求积同于以全面为底以半径为高之
　　　　　　　　　　锥体以高乘底以三归之者
　　　　　　　　　　锥体求积之法也(本卷十/一则)○
　　　　　　　　　　又尝借西洋割圆八线表考
　　　　　　　　　　之如前径十尺之浑圆自顶
　中剖之再以乙丙线平分之依八线表例分乙丁甲
　曲线为九十度设任割球分为甲丁己戊其甲丁曲

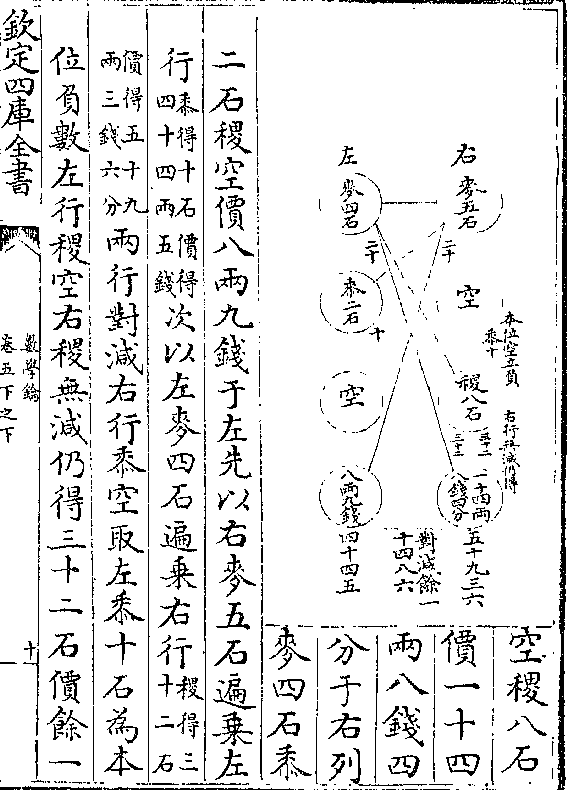　线三十度自丁戊向甲截作三十段梯形于八线表
　中求三十度通弦得五尺二十九度通弦得四尺八
　寸四分八釐一毫用梯形求积法(一卷/七则)并两数折半
　得四尺九寸二分四釐零五丝再求二十八度通弦
　得四尺六寸九分四釐七毫与二十九度通弦并而
　折半得四尺七寸七分一釐四毫依次折尽三十度
　共得通弦数七十六尺七寸五分九釐七毫五丝用
　圆径求周法(二卷/一则)求得二百四十一尺二寸四分五
　釐弱(为球分面上三十段/梯形两阔折半之数)为实复求甲丁曲线三十

　分之一得八分七釐三毫有奇(取浑圆全周以三/十六归之即得)为

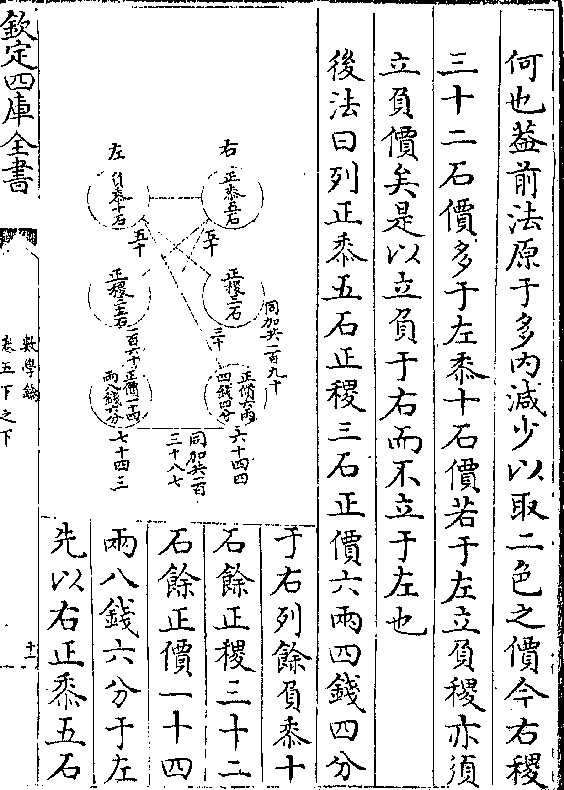　梯长乘实得割球面积二十一尺零五分有奇剐求
　甲戊直线得二尺五寸八分八釐二毫(即表中十/五度通弦)倍
　之得五尺一寸七分六釐四毫为径求圆积亦得二
　十一尺零五分有奇与前数合
　又法置径自乘再以径乘之(得一/千尺)以十一乘二十一
　除得数同
　解曰圆体与方体等高则两体之比例若两底之比
　例是方体与圆体若十四与十一也又圆体与浑圆

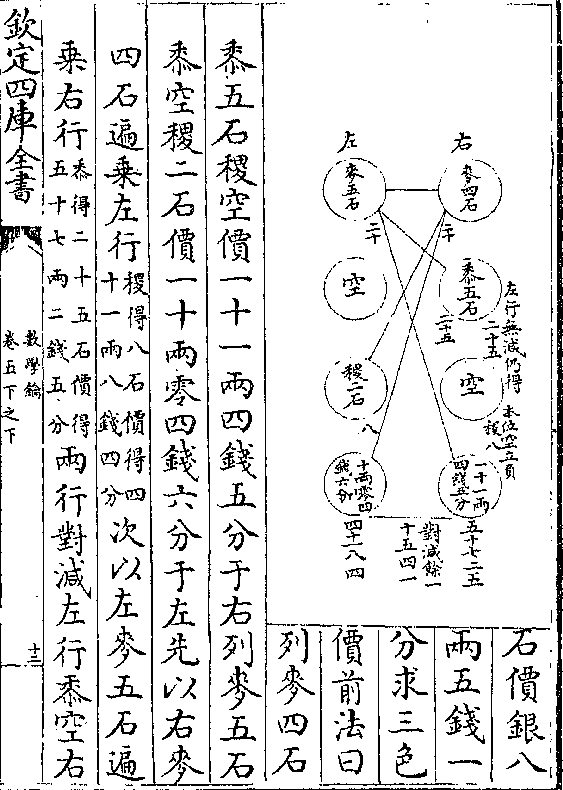　等高令圆体之底同浑圆中心之平圆则圆体之容
　　　　　　　　　必等于以平圆为底以浑圆半
　　　　　　　　　径为高(浑圆半径即固/体高度之半也)之锥体
　　　　　　　　　六(本卷十/一则)浑圆之面既四倍于
　　　　　　　　　中心平圆而浑圆求积之法又
　同锥体则浑圆之容必等于以平圆为底半径为高
　之锥体四夫以相等之锥体圆体得六而浑圆得四
　是圆体与浑圆若六之与四六之与四即三之与二
　也又以三因十四得四十二以二因十一得二十二

　各以二约之为二十一与十一则二十一与十一即

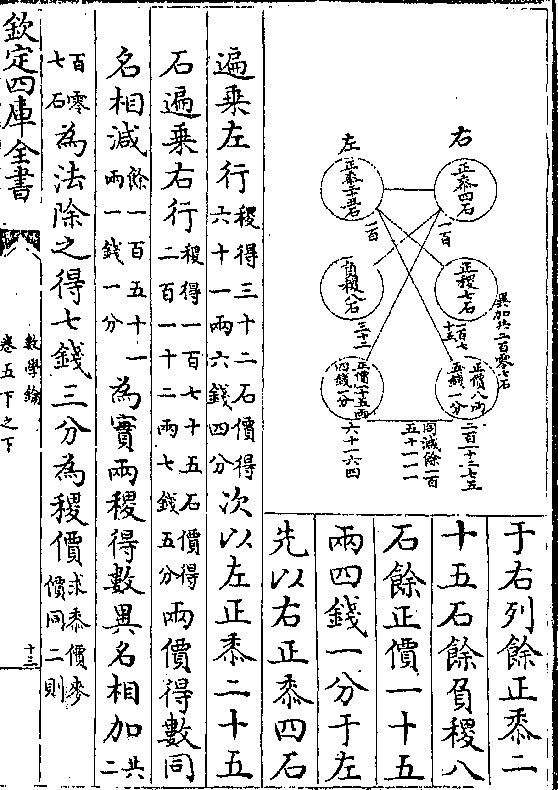　等高立方浑圆之比例也法置径自乘再乘立方也
　十一乘二十一除取立方二十一之十一为浑圆也
　　十四则
浑撱圆求积
　设浑撱圆大径四十尺小径二十尺求积法曰置小
　　　　　　　　　　　　　　　径自乘(得四/百尺)再
　　　　　　　　　　　　　　　以大径乘之(得/一)
　　　　　　　　　　　　　　　(万六/千尺)以十一乘

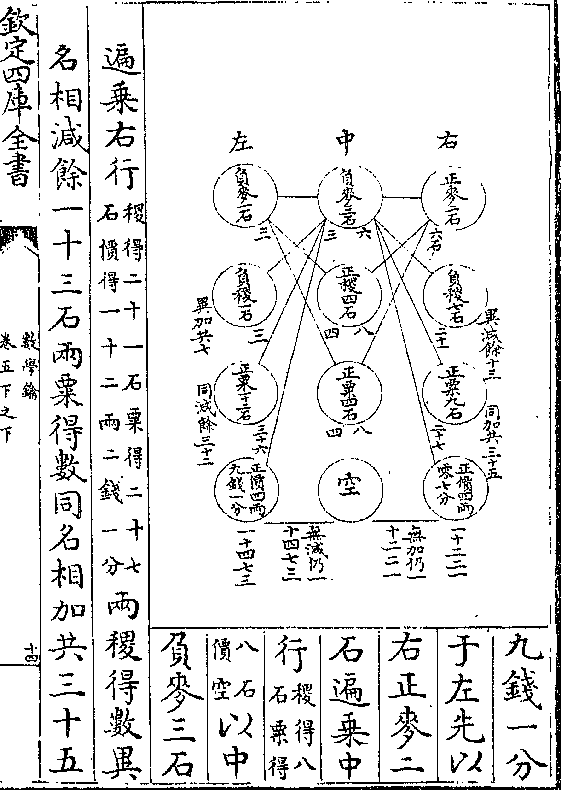　　　　　　　　　　　　　　　二十一除得八
　千三百八十尺零九寸五分即所求
　解曰小径自乘再以大径乘之甲乙方体也方体浑
　撱圆比例亦犹立方与浑圆故十一乘二十一除得
　浑撱圆之积
　　十五则
锐脊体求积
　设锐脊体脊长十尺底长十四尺广五尺高十二尺
　求积法曰倍底长加脊长(得三十/八尺)以广乘之(得一百/九十尺)

　再以高乘之(得二千二/百八十尺)以六归之得三百八十尺即

　　　　　　　　　　　　所求
　　　　　　　　　　　　解曰依甲丙乙丁两线
　　　　　　　　　　　　分之成刍荛一斜锥二
　　　　　　　　　　　　(斜锥与正/锥同论)刍荛以高乘
　底积之半得积(本卷/四则)锥以高乘底积三之一得积(本/卷)
　(十一/则)夫刍荛之底长即锐脊之脊长也若三倍脊长
　以六归之即得刍荛底长之半又两斜锥之底长即
　锐脊之脊长与底长之较也(即戊庚己辛/两线并之度)若二倍较

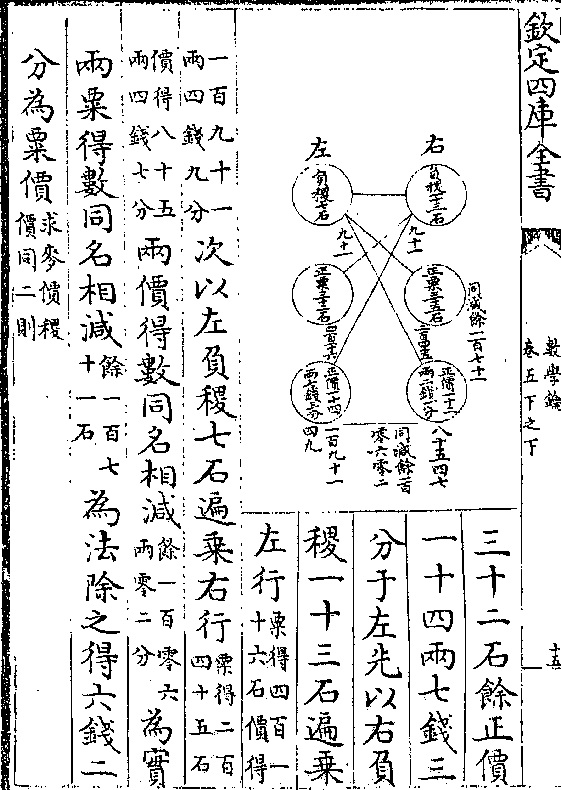
　线以六归之即得斜锥底长三之一今倍底长加脊
　长非即三倍脊长二倍较线乎以六归之以广乘之
　再以高乘之得三分体之积即全体之积法先乘后
　归亦异乘同除之意也
　　十六则
鳖臑求积
　　　　　　　　　　　　　　　设鳖臑上长二
　　　　　　　　　　　　　　　尺下长四尺高
　　　　　　　　　　　　　　　九尺求积法曰

　　　　　　　　　　　　　　　置两长相乘(得/八)

　(尺/)再以高乘之(得七十/二尺)以六归之得一十二尺即所
　求
　解曰剐作一刍荛如下图刍荛原为等高同底方体
　二之一(本卷/四则)依甲丙乙丙两线各从底棱分之成一
　锥体二鳖臑锥体原为等高同底方体三之一(本卷/十一)
　(则/)必为刍荛三之二于刍荛内减去锥体所馀三之
　一则两鳖臑也两鳖臑并既为刍荛三之一必为与
　刍荛等高同底方体六之一矣与刍荛等高同底即

　为鳖臑等高倍底者也两鳖臑既为等高倍底方体
　六之一则一鳖臑亦必为等高同底方体六之一故
　用六归也
　　十七则
等广锐面体求积
　设等广锐面体面长四尺底长一十二尺底面俱广
　　　　　　　　　　　　　　　五尺高一十二
　　　　　　　　　　　　　　　尺求积法曰并
　　　　　　　　　　　　　　　两长折半(得八/尺)

　　　　　　　　　　　　　　　以广乘之(得四/十尺)

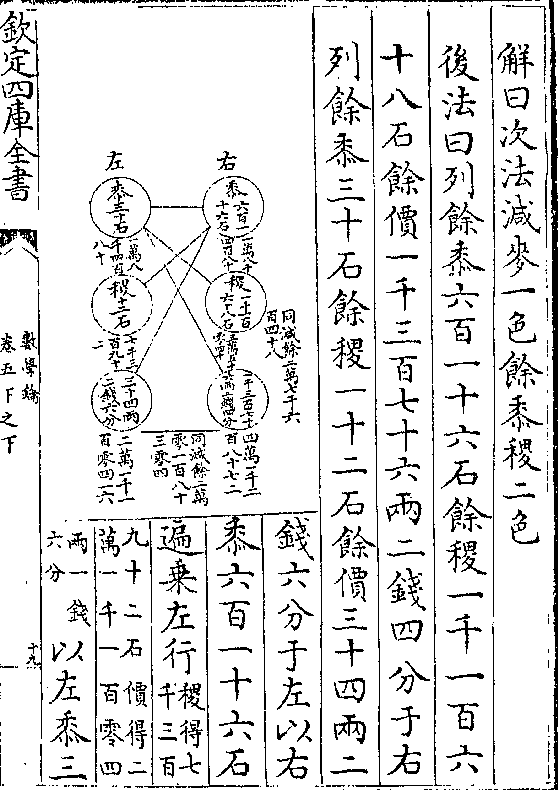　再以高乘之得四百八十尺即所求
　解曰依甲丙乙丁两线分之成一直体二堑堵全面即
　一直体底全底即一直体二堑堵底底面并而折半则
　成一直体一堑堵底矣夫直体以高乘本底得积(本卷/二则)
　堑堵以高乘半底得积(本卷/三则)今一堑堵之全底即两堑
　堵之半底也故以高乘㡳面相并折半之数得全积
　　十八则
锐面方体求积

　设锐面方体面方六尺底方八尺高一十二尺求积
　　　　　　　　　　　　　　　法曰置上方自
　　　　　　　　　　　　　　　乘(得三十/六尺)下方
　　　　　　　　　　　　　　　自乘(得六十/四尺)上
　　　　　　　　　　　　　　　下两方相乘(得/四)
　(十八/尺)三数并(共一百四/十八尺)以高乘之(得一千七百/七十六尺)以三
　归之得五百九十二尺即所求
　解曰各依面棱分之成方体一堑堵方锥各四凡九
　体而有三等三等求积之法则各殊方体以高乘底

　得积(本卷/二则)堑堵以高乘底二之一得积(本卷/三则)方锥以

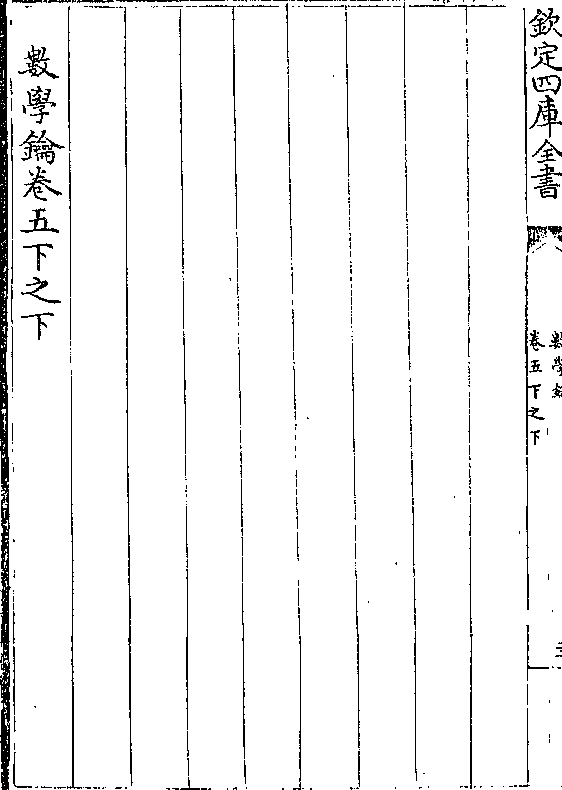　高乘底三之一得积(本卷十/一则)若从方体则与堑堵不
　合从堑堵又与方锥不合不得不用三归以就方锥
　然用三归必三倍方体之底半倍堑堵之底而后可
　今下方自乘即甲乙方形得方体之底一堑堵方锥
　之底各四上方自乘即丙丁方形得方体之底一上
　下相乘即戊己直形得方体之底一堑堵之底二合
　三形共方体底三堑堵底六方锥底四夫方体底三
　三归之仍得一堑堵底六三归之得二二堑堵底即