期注算法
　此算略载于启蒙传疑。而亦多散出于先辈遗集中。然学者犹患其难解。故间因无事。推究得如此。而至如章蔀之数岁差之法。亦皆学此算者所当讲究。故因并附著。
日日行一度。而一度九百四十分。
　此是日行一日不及天之数。而进数难于推算。故以是为日一日行天之度。月行作度亦同此。○启蒙传疑所载尹赵两算。自是别算。而非原算正法。故并略之。
月日行十二度十九分度之七。
　　按启蒙小注玉斋胡氏算率。以九百四十分。而十九归除。得四十九分四釐七毫三忽六丝八秒。(按此八秒之外。又有实馀归未尽之八秒。启蒙传疑以为弃而不用者。数无穷尽故也。然若终始弃而不用则于会朔要终之数。终有奇零不满之算。故今法则虽依传疑算法。姑置不用。而直待会朔时。乃取而作法。)而七乘之则三百四十六分三釐一毫五忽七丝六秒。此是零度排算之正法。故启蒙传疑亦因其说而置算。然会朔后通融

作算之法则未之及。故更为之法如左。
月与日会十九分度之七。一朔通分。得一万□二百二十七分法。(知得零度通分则馀可迎刃而解。故以是为先。)
　法以一朔日数二十九。乘上所得三百四十六分以下数。则得一万□□四十三分一釐五毫七忽□四秒。次以零度四百九十九。又十九归之则得二十六分二釐六毫三忽一丝五秒。实馀一丝五秒。又依上例姑置不用。以度之七乘所得二十六分以下数。则得一百八十三分八釐四毫二忽□五秒。通计全度零度所归乘之算则得一万□二百二十六分九釐九毫九忽□九秒。而九丝一秒不足。故于是乎乃取全度归除初姑置之算八秒。(即传疑中。弃置不用之八秒。)以二十九乘之。得二忽三丝二秒。添入零度姑置之算一丝五秒。共得二忽四丝七秒。就此十九归而七乘之则恰得九丝一秒。乃纳于全算中则归上满分。(如欲从简则不必算至丝秒。虽止于分数。而依此作法亦得。)
　　　　　右先归后乘法(积日)
　又法先以二十九。乘九百四十分。得二万七千二百六十分为实。以七乘之。得一十九万□八百二

十□分。而十九归之则得一万□□四十三分一釐五毫七忽八丝九秒。实馀亦九秒。姑置不用。次以七乘四百九十九。得三千四百九十三分。而十九归之则得一百八十三分八釐四毫二忽一丝。(若下算连置归之则秒位为空。故此则止于丝。)实馀一丝亦姑置不用。通计两次归乘之算。则合得一万□二百二十六分九釐九毫九忽九丝九秒。皆成九数而一算恒欠。故于是乃取两次未归姑置之算合得一丝九秒。而十九归之则得一秒。乃纳于全算中。则九秒数满归上而恰无零欠。
　　　　　
右先乘后归法(通朔)
　又法置上全日七乘所得一十九万以下数。以十九归之。得一万□□四十三分。而不满法者(以法对实而法多实少者。是为不满。)三分则不破分作釐而留置之。次置零度七乘所得三千四百以下数。以十九归之。得一百八十三分。而不满法者十六分则亦不破分作釐而留置之。所留两算合为十九分。乃以法十九归之则恰得一分。于是乎通计两次各归之全算。而以此一分足之则恰得。(此以上三法。全度零度各归之法。然实馀未归之算则必合算归除而后得。○下天算若以全度零度各置算。而依此用法则亦同。)
　

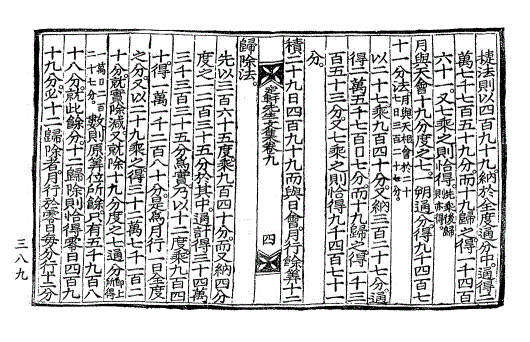捷法则以四百九十九。纳于全度通分中。通得二万七千七百五十九分。而十九归之。得一千四百六十一。又七乘之则恰得。(先乘后归则亦得。)
月与天会十九分度之七。一朔通分。得九千四百七十一分法。(月与天相会于二十七日三百二十七分。)
　以二十七。乘九百四十分。又纳三百二十七分。通得二万五千七百□七分。而十九归之。得一千三百五十三分。又七乘之则恰得九千四百七十一分。
积二十九日四百九十九而与日会。月行馀算十二归除法。
　先以三百六十五度。乘九百四十分。而又纳四分度之一二百三十五分于其中。通计得三十四万三千三百三十五分为实。乃以十二度。乘九百四十。得一万一千二百八十分。是为月行一日全度之分。又以二十九乘之。得三十二万七千一百二十分。就实除减。又就除十九分度之七通分(即上所得一万□二百二十七分)数。则原算位所馀。只有五千九百八十八分。就此馀分。十二归除则恰得零日四百九十九分。必十二归除者。月行于零日每分行十二分

故也。若以五千九百八十八分。还作月度。则以九百四十为法除之。得六度零三百四十八分。度下馀分即日法六时馀二十九分之数也。如欲得其数。以三百四十八分。又十二归除则恰得二十九。○月行一朔之数。即日行一岁之数也。故其数节节相合。月算除减之馀分。与一岁日行之馀分。同得五千九百八十八分。月算馀分作度之馀分。又与一岁作日之馀分。同得三百四十八分。又月法十九分度之七。通朔所得之数。又与一岁气盈朔虚所合之数。同得一万□二百二十七分。(闰数十日八百二十七分。而破日作分则一万□二百二十七分。)
积二十七日三百二十七分而月与天会。月行馀算十二归除法。(月与天会。虽无用之数。而布算者亦不可不知故并附。)
　依日法置周天揔分(三亿四万三千三百三十五分)为实。乃以九百四十分乘十三度。得一万二千二百二十分。又以二十七乘之。得三亿二万九千九百四十分。就实除减。又就减十九分度之七通分。(即上所得九千四百七十一分。)则只馀三千九百二十四分。就此十二归除则恰得零日三百二十七分。
三百六十五度四分度之一。通融作算。十二归除法。
　　

按历家置算。其初则固尝取法于天。而但算法既立之后。则以法运天而不以法随天。今之置算者。例多计朔以合法。余尝疑之。久而后乃得历家置算之本意。今置全度揔分三亿四万三千三百三十五分为实。以日分二万七千七百五十九分为法除之。则得十二个二万七千七百五十九分。而馀分恰得一万□二百二十七分。盖月不及日十二度十九分度之七。虽是一日之行度。而其数已先具于三百六十五度四分一之中者。已自如此。于是乎乃知上所得一朔日分及十九分度之七通分。皆是不可易之数。而一个二万七千七百五十九分者。一朔日行之本数也。十二个二万七千七百五十九分者。即一朔月行全度之本数。而馀分一万□二百二十七分。即一朔月行十九分度七之本数也。要之日行才到二万七千七百五十九分。则月行已踏尽了三亿四万三千三百三十五分而其数恰尽时。日月合朔则是朔因法而得。非法因朔而得者也。近世算家徒知计朔以合法。而不知因法以求朔。故其说终涉模糊。苟知通

全度商除则不烦通朔而朔自随之。故别为算法如左。
　先置周天揔分三亿四万三千三百三十五分为实。就减零度通分一万□二百二十七分。以其馀三亿三万三千一百□八分。十二归除则恰得二万七千七百五十九分。除者为月。得者为日。乃以日法九百四十分除之则得二十九日而馀分恰有四百九十九。
　　此算之要。不过十二乘除而已。置日法而十二乘则为月。置月法而十二除则为日。此外更无馀法。盖诸家算法。皆以日月为各度。而若元算正法则日月两度。皆以九百四十分为度。
(附)十九分作度。月与日会四乘算法。
　　此算虽非排算法意。然自永乐以来。依律历志闰法十九例。已有十九分作度之法。则亦当知所推算。故附著于此。
　法以十九分乘三百六十五度。而又纳四分度之一四分七釐五毫于其中。通得六千九百三十九分七釐五毫为实。乃以一日月行通分二百三十五分。乘二十九日。得六千八百一十五分。就实除

减则只馀一百二十四分七釐五毫。乃以四为法乘之则恰得四百九十九。(四乘无古法。而以意推之如此。)
七十六分作度。改定商量算法。
　　此则本章小注陈氏算率也。启蒙传疑不收载其说。故其算隐而不章。仅有一二算家传其略。今所誊传商量法是已。盖历家置算。固是截法。而陈氏此算则于截法之中。又加截焉。至简且约。更无馀法。此必历家由来旧诀。而非其所自刱者也。但陈氏只用其数而不及其所以得数之原。虽未知论说之如何。而顾今所传商量算诀则得其数而昧其原。既不知其同实异除之妙。又不知其算馀零分恰当得十九分度之七。故于零度月法。不少概及。而其所以为说者。颇近牵强。此所以更阅贤知而至今晦蚀者也。要之古今文字象数。才隔一手则久而埋没如此。可慨也已。玆因陈说更加推究如此云。(尝见屏谷集与人书。以七十六分法。为偶自臆揣云。岂未及细考小注陈氏说而云尔耶。小注有两陈氏。而此陈氏即陈氏普也。其论月与天会之数。实用七十六算。说见下。)
月行一度七十六分。通十二度作分则九百十二分。而十九分度之七则二十八分。
　

今置日分九百四十分。以七十六分为法除之。则得十二个七十六分。其馀分又有二十八分。而二十八分之于七十六分。恰为十九分之七。故以此为十九分度之七。
四分度之一。
　以九百四十分作一度。则二百三十五分。为四分度之一。以十九分作一度。则四分七釐五毫。为四分度之一。(以十九分而四分之。则各得四分七釐五毫。故以此为四分度之一。)以七十六分作一度。则十九分。为四分度之一。(以七十六分而四分之则各得一十九分。故以此为四分度之一。)
十九分度之七。
　以九百四十分作一度则三百四十六分三釐一毫五忽七丝八秒。为十九分度之七。以十九分作一度则单七分。为十九分度之七。(以十九分而十九归除则各得一分。而七其一则为七分。)以七十六分作一度则二十八分。为十九分度之七。(以七十六分。十九归除则各得四分。而七其四则为二十八分。)
　　按十九分度之七。有此三般样。而有得失繁简之不同。以单十九单七作度者。书传卷首晦朔图所用之算。而后来算家亦多沿袭。然布算之法。有法有实。十九分度之七。乃法也非实也。则

以单十九作度者。是以法为实者也。失之矣。以九百四十分。十九归除者。胡氏之算。此是由来排算之正法。然其数繁密。卒难凑泊。而又必通朔计分而后无零欠。则差欠简易。惟以七十六分作度而以馀分二十八分。当十九分度之七。则既无以法为实之碍。又无通分作算之烦。而恰无零欠。又推而准诸一朔。则吻然符合于四百九十九之数。而移易他不得。其法最简且捷。然七十六分全度之法。则自有旧说。而二十八零度之法则历考算家诸诀。未见有及之者。故区区臆见。恒患无考据处。及见屏谷集杂著则果有依俙说及处。始知愚见或不至甚谬。而但二十八分之为十九分度之七。则不待乘除而后得。而屏翁必欲乘除而得之。此为可疑耳。盖当初算家之别立捷法如此者。乃所以舍繁就约。而又就便于零度计分之法。今以七十六分而计除二十八分。则是即十九分度之七。又岂待别加乘除而后得耶。不论全度与零度。皆因其日分见成之数而互相准折。则无所事于乘除而自然数具。是所谓除日无岁。数车则无车

者也。秪为十九分度七之法。若用原法旧算则数极繁密。故为此捷法以通之。一日所行同得九百四十分。而揔之则为日母度。分之则为月子度。子母相包。异呼同应。亦异矣哉。要之此算立法之妙。全在于子母同分。亦在于子母各度。而以子求母。以母求子。则推算之能事毕矣。如欲见一朔日分相会之数。以子度(七十六分)乘三百六十五度。更添十九(四分度之一)而以母度(九百四十分)除之。二十九日四百九十九之数见矣。如欲见一朔月行周天之数。以母度乘二十九日。又添四百九十九。而以子度除之。则三百六十五度零十九之数见矣。知得如此则虽不用二十八分零度之法。而天与日月相会之数。皆可得而推。然若直以母度九百四十分就除则十九分度七之潜伏于九百四十分之中者。人无得而知。必须以九百四十分之九百十二分。作月七十六分之十二度。又以馀分二十八分。作月七十六分度之十九分度之七。然后其数方为微密。而但此算非算家之强生意智而为此也。实自日月两零度分母分子互乘算法中来。而此

非明于之分算例者。有未易领会者。故开释如左。
　四分度之一。即日与天会之零度。而四分为日分母。度之一为日分子。十九分度之七。即月与日会之零度。而十九为月分母。度之七为月分子。乃以两分母相乘(呼四九三十六)得七十六分。是为月行一度。又以两分子互乘两母。而日分子单一。乘月分母十九(一九九)则得一十九分。是为日行四分度之一。又以月分子单七。乘日分母四分(四七二十八)则得二十八分。是为月行十九分度之七。以此推之则七十六分推步之法。本出于日月零度互乘之算。而约得如此者。即之分算法所谓约繁以就简者也。
日与月会法。
　先以七十六分。乘三百六十五度而又纳四分度之一十九分于其中。通得二万七千七百五十九分。是为周天之度。置此为实。乃以七十六分乘十二度。而又纳十九分度之七二十八分于其中。通得九百四十分。为法除之则二十九除之后。有零分四百九十九。是为二十九日四百九十九。日与月会之数。

月与天会法。
　以月法积数二万七千七百五十九分为实。以一千□一十六分为法除之。则二十七除之后。有零分三百二十七。是为二十七日四时强。月与天会之数。(天法一千□一十六分。见书传小注即陈氏说。)
　　按陈氏普以一千一十六分。为一日月不及天之数者。只是于九百四十分中添入一个七十六分。以当天进日一度之数。
二十八分乘九百四十分。以七十六归除法。
　以二十八分。乘九百四十分。得二万六千三百二十分。以七十六为法除之。则恰得十九分度之七三百四十六分三釐一毫五忽零。与原算法归乘之算合。○又以二十八分。乘四百九十九分。得一万三千九百七十二分。以七十六除之则得一百八十三分八釐四毫零。与原算法亦合。○又以二十八分。乘二万七千七百五十九分。得七亿七万七千二百五十二分。而以七十六除之则亦恰得原算法一朔十九分度之七通分一万□二百二十七分。
　　按七十六分算法。只是九百四十分法之约取

者也。要之日月之算。同分异度。而日分月分。初无多寡。但日法则以一日所行团作一度。月法则以一日全分而分如其度。其为九百四十分则同。而所以计除者不同耳。若夫天则兼统日月而无所偏主。故与日会则度日之度而以九百四十分为一度。与月会则度月之度而以七十六分为一度。算家所谓日月俱不及天一度者。此之谓也。非谓月行赶天之数。真与日同也。以算法言之则日与月。俱以九百四十分。为一日行天之分。而日以日度计则不及天者一度。月以月度计则不及天者亦一度故也。月以日为体。而同体而异用。日与月同行。而同行而异情。期三百算法。尽于此矣。盖以一日全分而言之则同一九百四十九。而日月各得其数。以一朔积数而言之。则同一二万七千七百五十九分。而日月各合其数。日外无月。月外无日。而以日呼则日应。以月呼则月应。不费纤毫气力。而同异分合。皆从一个涂辙中来。且其十九分度之七。潜具于九百四十分统体之中。而以四揲之则全度得十九零度得七。而纵横颠倒。皆有

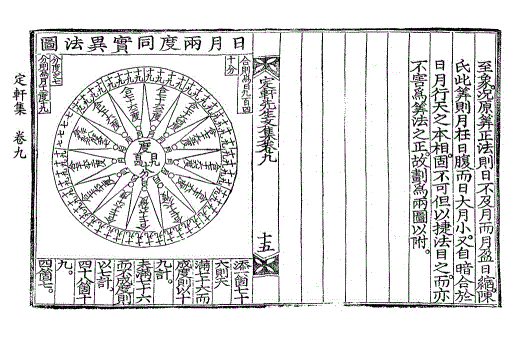至象。况原算正法则日不及月而月盈日缩。陈氏此算则月在日腹而日大月小。又自暗合于日月行天之本相。固不可但以捷法目之。而亦不害为算法之正。故划为两图以附。
日月两度同实异法图
삽화 새창열기
添一个七十六则天
满七十六而成度则以十九计。
未满七十六而不成度则以七计。
四十八个十九。
四个七。

二十八分改定晦朔图
삽화 새창열기
书传卷首原图。以与天会之数为式。既非朱子本意。而又以单十九作法。其于二十九日四百九十九之数。亦非当下符合之法。故改定如此。
按三岁一闰。六岁再闰。九岁三闰。至四闰则缩一年而十一岁置闰。又十四岁五闰。十七岁六闰。至七闰则又缩一年而十九岁置闰。其数皆本于此。
　　
算法
　先置三百六十五度四分度之一十九分于算位。除二十九日所得度数分数则只馀六度四十三分。以七十六破度作分。则为四百九十九。
　　附答崇伯书
　曾所示历算。近因无事。更加寻绎。则以月之十二个七十六。准了日分则恰得九百十二分而馀分二十八分。则果是七十六分之十九分度之七也。此是自然相合之数。然但于日月合朔之际。日大月小。大小相合。不其艰晦矣乎。愚意则日度亦以

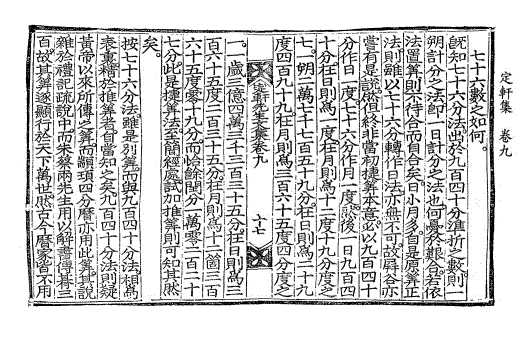七十六数之如何。
既知七十六分法。出于九百四十分准折之数。则一朔计分之法。即一日计分之法也。何忧于艰合。若依法置算则不待合而自合矣。日小月多。自是原算正法。则虽以七十六分转作日法。亦无不可。故屏谷亦尝有是说。然但终非当初捷算本意。必以九百四十分作日一度。七十六分作月一度。然后一日九百四十分。在日则为一度。在月则为十二度十九分度之七。一朔二万七千七百五十九分。在日则为二十九度四百九十九。在月则为三百六十五度四分度之一。一岁三亿四万三千三百三十五分。在日则为三百六十五度二百三十五分。在月则为十二个三百六十五度零十九分。而恰馀闰分一万零二百二十七分。此是捷算法。至简经处。试加推算则可知其然矣。
按七十六分法。虽是别算。而与九百四十分法。相为表里。精于推算者。自当知之矣。九百四十分法则疑黄帝以来所传之算。而颛顼四分历亦用此算。其说杂于礼记疏说中。而朱蔡两先生用以解书传期三百。故其算遂显行于天下万世。然古今历家皆不用

此算。而随时立算。代各异法。如汉之黄钟历。唐之大衍历及近世百分历皆是也。然类皆非自然之数。故其立法造算。虽皆依仿此算。而多有零欠。窃尝妄意如欲造历。当追复九百四十作分之法。而章蔀之数皆依此行算。然后历法方无差忒。而此可与知者道。难与不知者道也。
　陈氏普曰月行迟。常以二十七日千一十六分日之三百二十七而与天会。二十九日四百九十九而与日会。一月一周天者。以其与日会言也。其实二十七日有奇而周天。又二日有奇。始与日会。文公于十月交。以为二十九日有奇而周天。又逐及于日而与日会者。盖未详。(书传小注)
陈氏所论固得之矣。然但以诗注二十九日周天逐及日之说。谓未详者。恐或未然。月与日会既在二十九日六时强。则与天会之合在二十七日四时强。朱子夫岂不知而为此说哉。取看性理大全所载正蒙小注则已在良遂总知中矣。尝思之。朱子所谓周天之天。乃指太虚之天而言。非指运行之天而言也。盖太虚之天。即历家所谓宗动之天。而宗动之天。常静而主动。运行之天。乃所谓经星之天。而经星之天。常

动而不息。天与日月运行一昼夜。恰到得太虚本度始发之处者。惟日为然。而天与月则或过或不及。此朱子所以不以与天会为周天。而必以与日会谓之周天者也。陈氏错认朱子之意。而反疑其未详。恐自未免未详。
　　气朔分齐说
　玉斋胡氏曰闰馀全日总计二百单六日零六百七十三分。将此数于十九年内。分作七个闰月。计三七二百一十日内。少三日二百六十七分。七闰月之中合除此三日二百六十七分。均作三个月小尽。正恰好。故气朔分齐。(启蒙小注)○金农岩曰若如胡氏说则冬至入于前章晦日。合置三个大月四个小月。
　黄氏瑞节曰所谓气朔分齐者。十九年合气盈朔虚。得二百单六日。不尽六百七十三分。七闰月亦二百单六日。不尽六百七十三分。气之分与朔之分。至十九年而皆齐。此所谓气朔分齐为一章也。(正蒙小注)
　退溪曰分者限也。滚到十九岁则至朔同日。故曰分齐。
　

霁山曰若以二百单六日及六百七十三。分作七个二十九日四百九十九除之则恰尽。于是气盈朔虚之数。无有馀不足之分。故曰分齐。
按气朔分齐。先儒多为之说。而其说不同有如此。胡氏所谓三个小月则已有农翁辨驳之论。而且一章气朔之恰齐。自是本然之数。初不关于大小月之置。而谓均置三个小尽月然后分齐者亦不可知。若黄氏说则尤涉牵强。盖闰朔之所以分排如此者。本出于闰分。则岂可分闰分与月朔。对立为两而谓之分齐乎。其末泛言气朔之分者。似了不了。亦涉模糊。唯退陶分限之说最为近之。而但揆以上下文势则亦有未尽协者。上文九百四十分之分字。皆是分数之分。则不应于此独以分限言之。盖气朔分齐云者。气朔两分。互相齐等而更无馀欠之谓也。按太初历法则气与朔各有大馀小馀。而两算并行。互相参差。至十九年一章然后。两算大小馀之分。恰相齐等。假令气法大馀三十九则朔法大馀亦三十九。气法小馀七百单五则朔法小馀亦七百单五。是所谓气朔分齐者也。盖气朔分齐四字。直接上文气盈朔虚而成文。故读者往往只以盈虚两分求其齐。而多强为之

说者。然其实则不曰气盈朔虚分齐。而必曰气朔分齐者。非省文也。此气朔字实总指气朔全分而言。非但指盈虚之分而言者也。若以这个朔字谓只指朔虚之分而言。则上文本朔馀分三百四十八分。更无归宿。岂可乎哉。必以本闰两朔馀分。通融作算。而又推而至于全分然后。其数可见。若知得大小馀推算之法。则于分齐之数。思亦过半。○又按以十九乘一年闰分一万□二百二十七分。则一章通分一十九万四千三百一十三分。乃以日法除之则得二百六日零六百七十三分。以月法分之则恰得七个二十九日四百九十九。盖只言闰分则其数固自如此。然分齐云者。本非但指闰分而言。故太初历法以闰分七个四百九十九。必参合于本朔馀分三百四十八之数。以为归上添日之算。是岂但以闰分作法者耶。且一章分齐之算。则其数已具于得算之初。不在于除尽之后。而霁山说如此。亦未免可疑。岂偶未及照管得太初历法而然欤。就考史记历书。则可知其涯略。而其排算之法。有注疏诸说。然其义奥晦。未易领会。故略加疏释以附。
朔法大馀五十四。○小馀三百四十八。
　

一年朔分三百五十四日三百四十八分。而未满三百六十日。故以五十四日为大馀。以三百四十八分为小馀。其法大馀则初置五十四算。每年加五十四算。满六十则除之而留其馀算。每至闰后次年则只加二十三算。(法当置当年本算五十四。又置闰朔二十九。除减六十。而从捷法故直加二十三。)而除留如上法。若才足六十则曰无大馀。○小馀则置三百四十八算。每年加三百四十八。满九百四十则归上而于大馀添一算。留其馀。若值闰后次年则添加八百四十七分。(本算中入闰馀分四百九十九。)满归存馀如上法。若才足九百四十则曰无小馀而一算归上。
气法大馀五。○小馀二百三十五。(古法则小馀八者。盖以一度作三十二分。而八为四分之一。故以八为小馀。然如欲见分齐之形。则不如直用二百三十五分之为得。故改算率如此。)
　周天三百六十五度四分度之一二百三十五。而过了三百六十之数。故五度为大馀。二百三十五为小馀。其法不论有闰无闰。大馀则置五算。每岁加五。满六十则除之。留其馀算。若才足六十则曰无大馀。○小馀则先置本数二百三十五。每岁加本数。若满九百四十。则曰无小馀而一算归上。
　　

按逐年排算之法。亦略载于史记本文。而篇不完备。且览者未易了悟。故通计一章都数。置算如左。(四馀起数则从四算并无馀分之岁。十一月夜半甲子始。)
　气法大馀五乘十九则得九十五日。而以六十除之则只馀三十五日。而下小馀成日之四算归附。故一章大馀三十九。○小馀二百三十五乘十九则得四千四百六十五分。以日法九百四十分除之则得四日而归上。添其大馀四算。故一章小馀馀算七百单五。
　朔法大馀五十四乘十九则得一千□二十六。而除每闰次年三十一则七闰所除合为二百一十七算。而元算只馀八百□九。以六十除之则馀二十九。而下小馀成日之十算归附。故一章朔法大馀亦三十九。○小馀三百四十八乘十九则得六千六百一十二分。闰分则一章七闰。故不以十九乘而以七乘四百九十九。得三千四百九十三分。而通计则为一万□一百□五。以日法除之则得十日而归上。添其大馀十算。故朔法一章。小馀馀算亦七百单五。
　　一章合算虽如右。而若不载史记本文则无以

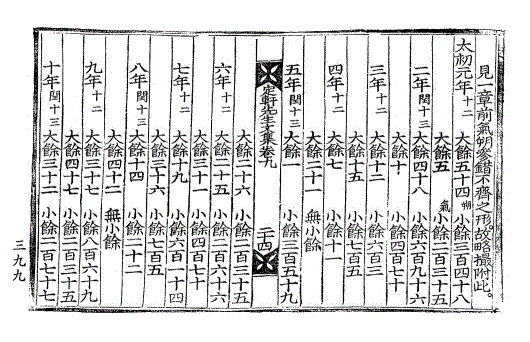见一章前气朔参错不齐之形。故略撮附此。
太初元年(十二)大馀五十四(朔)小馀三百四十八
大馀五(气)小馀二百三十五
二年(闰十三)大馀四十八小馀六百九十六
大馀十小馀四百七十
三年(十二)大馀十二小馀六百三
大馀十五小馀七百五
四年(十二)大馀七小馀十一
大馀二十一无小馀
五年(闰十三)大馀一小馀三百五十九
大馀二十六小馀二百三十五
六年(十二)大馀二十五小馀二百六十六
大馀三十一小馀四百七十
七年(十二)大馀十九小馀六百一十四
大馀三十六小馀七百五
八年(闰十三)大馀十四小馀二十二
大馀四十二无小馀
九年(十二)大馀三十七小馀八百六十九
大馀四十七小馀二百三十五
十年(闰十三)大馀三十二小馀二百七十七

大馀五十二小馀四百七十
十一年(十二)大馀五十六小馀一百八十四
大馀五十七小馀七百单五
十二年(十二)大馀五十小馀五百三十二
大馀三无小馀
十三年(闰十三)大馀四十四小馀八百八十
大馀八小馀二百三十五
十四年(十二)大馀八小馀七百八十七
大馀十三小馀四百七十
十五年(十二)大馀三小馀一百九十五
大馀十八小馀七百单五
十六年(闰十三)大馀五十七小馀五百四十三
大馀二十四无小馀
十七年(十二)大馀二十一小馀四百五十
大馀二十九小馀二百三十五
十八年(闰十三)大馀十五小馀七百九十八
大馀三十四小馀四百七十
十九年(十二)大馀三十九小馀七百单五
大馀三十九小馀七百单五
　　　　　
(欲知每岁冬至何日何时则亦用此法推之。)

此两大馀三十九。两小馀七百五之过一章后。恰相分齐者。虽除馀之算如此。而其实则一章之内。气朔全分总与之相齐。非但末算三十九与七百五互相齐等而已。今以十九乘周天三百六十五度二百三十五而得数作日。则恰得六千九百三十九日七百单五。是为气法一章总数。朔法则以十九乘三百五十四日三百四十八分而得数计其全日。又以积分作日则合得六千七百三十三日而未满日之分馀三十二。乃入闰分积日二百单六日零六百七十三分。而通计则亦得六千九百三十九日七百单五。而气朔全分。恰与之相齐。然则其曰分齐者。固不但指盈虚两分。而亦非但指大小馀分而言者也。○按一章分齐三十九与七百五。乃气朔积分所得。则乃实也非法也。而但此算一立。递相增减。则不待章内本算之积。而已知这章分齐合得几算。然则此两算者乃次章以下分齐之法母也。若就前章分齐上通加三十九与七百五而减算归算如例。则不劳积算而次章以下分齐之数。皆可预推。假如第二章则三十九上添三十九而减六十加一算。七百五上添七百五而减日分归大馀。故次章分齐则其大馀十九。小

馀四百七十。第三章则十九上添三十九。又四百七十上添七百五。而减归如例。故三章分齐则大馀五十九小馀二百三十五。第四章则五十九上添三十九。又二百三十五上添七百五。而又依例减归。故四章分齐则大馀复得三十九而小馀遂无馀分。盖其所以无馀分者。以其四个七百五。凑成三个九百四十分。而日分适足故也。盖置一章总数六千九百三十九日零七百五。而四乘之则恰得日二万七千七百五十九。而恰与一朔日分合。然则一章者固气朔分齐之数。而四章者于分齐之中。尤见其恰好者也。夫四章大馀之所以复得三十九者。置四章通日而以六十除之则可知矣。要之太初历算。必用六十除法者。盖将以配六十甲子。而欲知其日之所属干支也。如欲知甲子朔夜半冬至。则不必逐章布算。只以首四章之三十九。加于每四章之三十九。而(四章之内。次三章不变初章之零数者。小馀之分成日而归上故也。)仍以六十除之。则每过四章。必减一算。九减为八(自第五章至第八章。其分齐之数。三十九及十九等算。九减为八。)八减为七。(自第九章至十二章。又八减为七。)愈转愈减。随减随增。以至于四章之数廿变。则恰满六十而无馀分。是为章末无大馀之岁。而无大馀则小馀自随之矣。盖

气朔小馀之俱无馀分。则才过四章七十六年。必一次得之。而气朔大馀之并无馀分。则必过八十章一千五百二十年然后始得之。是为中元甲申甲子朔夜半冬至。而又进一倍则为下元甲辰。又进一倍则复得上元甲子。若置算如例而年与日皆以六十除之。则其数自如此。是所谓苟求其故则千岁之日至。可坐而致者也。意班氏所称运算转历者。其法似当如此。而但落下闳算率则以八十一章为回元之数。此则取合于黄钟之数而然耳。实非历法自然之数。故蔡西山讥其不能无差。而以为穿凿傅会。则章统之数。当依此行算然后。合于天地本然之数。按太乙统宗。亦以四千五百六十年为元统蔀章之数。
　　辨金农岩论历法
按胡氏一章四大闰之说。农岩非之是也。然胡氏说亦有可思者。盖以首一章而言之。则胡氏果误而农岩说得矣。以次章而言之则胡说未为全非。而农岩说亦有未尽其曲折者矣。若以历法小馀而言之则两家说皆非历法本意。盖闰之馀分入于小馀。而古今历家皆以小馀积分。均排于本闰两朔。未尝以闰日馀分。必为分排于闰朔之内。则又何大小多寡之

必较乎。岂农岩只泛言其数合如此。而不以历法论耶。又尝见农岩尝论静观斋历法置冬至之误。而谓次一章冬至。合入于朔章日申时云。盖只计闰馀零分六百七十三分故也。揆以太初历法则恐农岩此说亦失契勘。首一章之馀分。入于次一章之朔日者。不但闰馀之六百七十三分。而又有本朔馀分三十二分。故两算相合而七百单五。为一章分齐之数。则次章冬至合入于酉时。不合入于申时。太史公所谓正西冬至者。即酉时冬至之谓也。盖古历冬至时分不出于子午卯酉。而气法小馀二百三十五分则为卯时冬至。四百七十分则为午时冬至。七百单五分则为酉时冬至。无馀分则为子时冬至。大抵气分则出于日法四分之一。故不论章外章内。皆出于四正。而若朔分则合本闰两朔馀分而无定数。故一章之内。其数错出。而不与气分相合。必过十九岁一章然后乃与气分相齐。而气朔两分同出于四正。是即所谓分齐者也。岂农翁见近世时宪历法冬至时分多出于寅申巳亥。而为之说如此耶。古今历法有异。不可以此例彼。如欲见气朔之分章蔀之数。截然齐正处。则必须按古历而论之然后。方不差谬。故因论分齐

之算而附著如此。
　　附答崇伯书
　一章通年十九。通朔为二百三十五。合四章而通计之则得九百四十朔二万七千七百五十九日。若以九百四十朔。分置四百九十九个大月。四百四十一个小月。则其通分恰尽无零欠。次一章复为子时冬至。又只以四章二十八闰论之。则其日八百二十七日弱。而一百二十八分不足。若置十五个大闰。十三个小闰。则其数恰尽。而其不足一百二十八分。则本朔之零分入于此。盖始一章置三个大闰。次三章置四个大闰。合之于本朔大小月。而为四百九十九大月。四百四十一之小月。以是观之则七十六分九百四十分之法。于期数无往而不然。夫一章十九岁。即七十六月法四分之一也。二百三十五。即九百四十日法四分之一也。四章通年与七十六合。通朔与九百四十合。通日与一朔通分合。通闰与月法十九分之七合。通闰之日数与闰分十度零之数合。四百九十九大月与一朔二十九日零分合。四百四十一小月与三十日零分合。以此参错进退。节节相合。而必以七

十六年为限。则七十六分之法。可知其自然之妙。然每置大月者多小月者少。则胡氏三小四大之说。非可破之论。
以七十六年为小限。而见得如此。可见推算之微密。而又谓胡氏说不合全斥者。亦不为无理。然以古今历法考之。则犹有不尽然者。盖历法置月。本朔则大月多而小月少。闰朔则小月多而大月少。又胡氏此说本为第一章设。而不是次章说。则其说终涉可疑。○又按高明谓四章本朔馀分与闰馀欠数。适得相符云者得之矣。然但其措辞太简。使览者未易解。而又添作闰日之说与历家说不合。盖以二十九日四百九十九分。合两月而分置大小朔。则馀五十八分。通计一年则三百四十八分。而以十九乘之则为六千六百一十二分。就以日法除之则恰得七日零三十二分。盖一章之内。本朔大尽之月。多于小尽之月者职此之故。而通计四章则恰得二十八日零一百二十八分。其日则与每章置闰之月数同。而其零则与四章闰分之欠数相足。亦异矣哉。盖以一章之数言之。本朔馀分三十二。闰朔馀分六百七十三。故两分相合则为七百单五。是为一章小馀之终数。至四

章则四个七百五。凑成三日而无馀分。此太初历法所以四章之末。必为子时冬至者。而若其闰月大小之置则太初历法闰大月本小。而虽近世历法一章之内。罕见有四大闰。恐高明所云得其数而失其法。○又按一章闰法三大四小之说。亦是死法。古今历家。皆不拘此例。要之一朔日月相会之期。恰是二十九日四百九十九。则其通分即二万七千七百五十九分也。以此为一朔本数。就闰馀通分十九万四千三百一十三分上七归则恰得七个二万七千七百五十九分而无馀欠。是为七闰之数。然其七个四百九十九则当有所归属。故就考太初历法则于置闰后次年添入四百九十九于本朔馀分三百四十八分之中。以为归上作日之法。而未尝全归于闰朔。古今历家。虽为法不一。而大槩遵用其法。则闰月大小朔之多寡。似不必争执。○又按闰之馀分。不能独行。故必附于本朔馀分。此朔法小馀之算率也。如欲以闰分必作闰月。则四章之内。小闰月十四。大闰月亦十四。而馀分八百十二分。不满一日。若用小馀本算。则其满分成日之日。多归于本朔。而于一大一小月之外。又得五十八大月。而凑成四百九十九大月。则

岂必置四大闰而后。致其多乎。要之晓得太初历法而后。方知其肯綮。留俟面剖。
　　岁差新法
差法之不定久矣。虞喜之五十年立算。何承天之百年倍算。皆有太过不及之失。而刘焯之七十五算则几矣而犹为未密。其后许鲁斋，玉恂，郭守敬，刘诚意所立差法。皆久则必差。终不合天象。蔡九峰以为三代以前则历法简易。只随时占候而不立差法。然古历虽简而实密。且岁差乃历法之不可遗者。则岂以上古圣神之智。而不为之立法乎。特失其传耳。皇明历法乃百分历。故一岁岁差以一分五十秒立算。今之差法。又出于泰西人云。而知历者以为亦不尽合云。窃尝以九百四十分。依法作度而以意推之。则月与日一会之顷。天与日已差了一分。故一岁差法合以十二分立算。而遇闰则添一算。如是则过了四章七十六年九百四十朔。(四章之间。置二十八闰。故合本朔通为九百四十朔。)与日恰差一度。疑此乃岁差之恒数也。按玑衡宝录则其文出于皇明洪武七年甲寅。而以为岁差之度。比尧时已过五十度。而尧时冬至则日在虚一度。洪武冬至则日在箕四度云。即此年数而差数睹矣。就考

历代通考则洪武甲寅。距唐尧甲辰三千七百三十一年。而以四章七十六年经之。则恰为五十个七十六年弱。宜其所差之度。恰过五十度。而今年甲寅去洪武甲寅又四百八十一年。则其岁差之数。又可得以推矣。但星有阔狭。度有太秒。而少差则失之。是为难耳。要之岁差之法。不出于日与月相会之间。而朔分二万七千七百五十九之数。即其分限节度也。一朔差一分而计其日分则二万七千七百五十九分也。七十六年差一度。而计其日数则亦二万七千七百五十九日也。过一千四百六十一章则复还本度。而计其年数则亦二万七千七百五十九年也。如欲见其年数则以七十六乘三百六十五度又四分了七十六年而得十九。以配四分度之一二百三十五分则得之矣。(一岁差十二分则十九岁并七闰。恰差二百三十五。)先儒或以为天体至健。动而不息。故差无定数。然凡丽于天体而运行不息者。皆未尝无定数。故日月之食灾也。而精于推步者。先期指的而毫发不差。五星行度之当迟而速当速而迟者忒也。而朱子以为皆有常数。则况岁差而无定算乎。蔡西山所谓天本无差者。盖谓其有定数也。区区管测。虽未敢自信。而参以日行躔度。

既如是符合。又考之于历代年数。应验又如是。故姑记之。以俟知者。(康节差法。伊川以为永不差。而算法不传。然大略则求之于日月交感之际。今此拙算。亦不为无所本矣。)
　　附律历志八十一分法
　律历志八十一分法。蔡西山虽以为穿凿傅会。然其大法则皆依仿本算。而所差者特秒忽之间耳。族君崇伯穷经之暇。兼邃律历之学。不以余蒙算而喜相往复。反覆究诘之际。略有所窥测。欲明历算则此亦在所当究。故兼附于此。
　　答崇伯
　
混元起于甲子年甲子月甲子朔夜半甲子。而历八十章一千五百二十年而次一章之始。甲申年甲子月甲子朔夜半甲子为冬至。历八十章一千五百二十年而次一章之始。甲辰年甲子月甲子朔夜半为冬至。又历八十章一千五百二十年而年月日时皆为甲子。凡二百四十章四千五百六十年而后。与混元复会。以汉律历志三统一元之法考之。则为不同矣。夫律历志以八十一章为一统。以四千六百十七年为一元。而经之以六十甲与四章七十六年朔日子时冬至之法。则冬至之

年月日时皆不合。未知何故。太初之历。是壶遂落下闳辈之所推算者。则必无差谬之理。或拙算之不得其法耶。以其小注如淳说甲子日冬至。以八十年为纪云者推之。而皆合此。既合焉则一统当以八十章为纪。而统元之数如此不可晓。指诲如何。
律历志统元之数。则只是以会数乘朔会之数而又九之。故其数如此。然若以太初起元之数而言之。则自当依盛算所推而后合。故如淳说如此。而本志元封七年复得摄提格之下。继之以太岁在子。已得太初之云。则其意可知。岂高明偶未及勘照而有此云耶。当时所造虽曰太初历。而闳平辈所治。本非太初历。乃是律历。则律历自律历。太初自太初。若以此求彼则恐不合。
　一元月数与一元年数不合。本志九会复元下注孟康说。亦欠详备。
既得元月之后。不知除闰之法。则无以见其恰为四千六百一十七岁。其法以会数四十七。乘朔会之数一百三十五。则为六千三百四十五。而又九乘之。得五万七千一百□五。是为一元之月数。然必须除了

十九岁七闰法月数一千七百□单一然后。方得其年数。除闰则只馀五万五千四百□四。而十二归除恰得四千六百一十七岁。孟康只依文说本数而不及除闰之法。
　太岁在子。已得太初。则高见的是。而终有疑晦处。前历上元太初四千六百一十七年。至于元封七年。复得阏逢摄提格之仲冬十一月甲子朔冬至云云。夫自上元太初至元封七年四千六百一十七年。则元封一年是甲寅岁。而七年乃庚申也。十一月冬至。乃庚申之冬至也。又以为甲子朔朝则欠了四分日之三。而以历法纪之。当为癸亥朔朝也。此等处推究不得。
取考诸史纪年则元封七年实丁丑也。非甲寅非庚申。而班志说如此。无怪其推算不得。要之太岁在子已得太初。则已得太初后五十七年。即太初回元后加三章之数也。以太史公太初历算计之。则四分欠三。果如来谕所疑。此当时太史令张寿王之所抵死争执者。而但寿王所谓日分阙三则固得矣。然若其所谓去七百单五则亦有不可知者。若全然除去每章七百单五。则又何止日分阙三而已乎。寿王之论。

亦涉模糊。而其所以致疑者。则不为无理。班氏乃以妄言诋之何也。虽诋其妄。而于志中特存其语者。无乃有微意存欤。
更思之。历法一章置算之例。大馀置三十九。小馀置七百单五。而本志算法大馀虽同而小馀则置六十一。此所以甲子朔朝夜半冬至。不在于二百四十章。而退置于二百四十三章者也。依此置算则自无四分阙三之碍矣。盖本志算法。以黄钟八十一分为日法。故一章小馀。改七百单五为六十一。然以九百四十分之七百单五较准。则二釐五毫加多何者。七百单五。即九百四十分之四分三。而六十一亦八十一分之四分三强。然法当置六十分七釐五毫。而今乃直置全算一。此其所以互相参差也。是以一章小馀用七百单五则四章之后。恰得三日而无馀分。若用六十一则四章之后。虽同得三日。而更馀一算。本志谓四章朔馀一者。即其数也。以其四章之末。辄馀一算。故七百单五算法则恰过八十章。而大馀小馀俱无馀分。若六十一算法则八十章之末。小馀之数尚有馀分二十算。故虽得甲子朔日。而不得为夜半子时。必更得一章小馀六十一算然后。凑成八十一分

而恰无馀分。故以是为起统之首。盖必如是而后日法统法皆合于黄钟之数。而其法亦自巧密。寿王未尝推原其立法之意。而轻肆诋排。此其所以终归于妄言之科。而不见白于当世者也。然其立论之意则要不可少。就考太史公历书则其法与寿王言合。班氏历志则一从闳平之算。而刘歆父子又宗之。虽未知其得失如何。而其同异之所以然则有如此者。
　一章小馀之数不同。故三统之数不同者。果如尊谕。而但一章小馀之必置六十一分。未晓其算法。乞赐开示。
以黄钟八十一分。乘三百六十五度。又入四分度之一二十分二釐五毫。则通得二万九千五百八十五分二釐五毫为实。乃以一朔日分二千三百九十二分(以二十九乘八十一。又纳四十三则即一朔日分。)而十二乘之。得月法通分二万八千七百单四分。就实除之则只馀八百八十一分二釐五毫。此一岁闰分。而亦月法十九分度之七也。如欲求一章小馀终数则以十九。乘闰分八百八十一分二釐五毫。得一万六千七百四十三分七釐五毫。而以日法八十一除之则得二百单六日。而闰分只馀五十七分七釐五毫。又添入本朔馀分

三算。(一年本朔馀分三十分。而以十九乘之得数。以八十一除之则恰馀三算。)则合为六十分七釐五毫。以此推之则六十一分中二釐五毫。恐闳平辈傅会之算。而盖必置六十分七釐五毫然后方合于七百单五四分得三之数。而四章之无馀分二百四十章之得天元甲子。皆与九百四十分法毫发不差。而闳平乃以六十一分置算。其算准于历象。必不能无差。故蔡西山讥其穿凿傅会者此也。
更思之。闳平等之置六十一分者。亦有由焉。盖不以浑天全度四分度之一末算二釐五毫取准。而但求之于月法十九分度之七故也。今置一朔日分二千三百九十二分为实。以度之七乘之而十九归之则得八百八十一分二釐六毫。而归未尽之算尚馀六毫。以是而较浑天全度则一毫零加多。闳平等兼取加多之数而作算。故章末之数恰为六十一分。今以其法作算则置八百以下数。(即上一朔十九分度之七通分。而一岁闰分亦同。故一章所乘之算直用此算。)以一章十九乘之。得一万六千七百四十三分九釐四毫。乃以上归未尽之六毫。乘一章十九而十九归之。则还得六毫。乃入于全算中则全算四毫数满归上而成分。又添入本朔馀分三算于其中。遂以日分八十一除之。则得二百单六日而恰

馀六十一。○捷法则置一朔通分。(二千三百九十二分。)以一章十九乘之。得数然后。以七乘之。又以十九除之。则得一万六千七百四十四分。乃以日分八十一除之则只馀五十八分。而添入本朔馀分三算则恰得六十一分。○又法先置本朔馀分三十算。以一章十九乘之。得五百七十分。又置四十三分。以闰七乘之。得三百□一分。而合计得八百七十一分。乃以日法八十一除之则恰馀六十一。○盖以其法置算则有如此者。然但揆以上一朔日分归除之数则月行之于天度四分之一。终有溢数。而一章小馀之恰满六十一者。以其溢数之积也。夫日月相会之期。必以天度四分之一为准。而八十一之四分一。即二十分二釐五毫。则岂可于本度二釐五毫之外。添入月算溢数而为之法乎。其误也明矣。
　按本志一朔日分置二十九日八十一分日之四十三。此则元算法二十九日四百九十九之算。而其所以必置四十三者。亦未晓然。
先置日分八十一。以十二乘之。得一日月分九百七十二分。又以二十九乘之。得一朔日分二万八千一百八十八。就浑天全度(即上二万九千以下数)中除之。又就除

十九分度之七八百八十一分二釐五毫。则只馀五百一十六分。就此十二归除则恰得四十三。
　一章末算六十一分则果似差误。而蔡西山直举本算八十一分。而谓之穿凿傅会何也。
今以八十一分七乘而十九归之。次以一朔二十九乘之得数。又以四十三分七乘而十九归之得数后。合二算而计之则八百八十一分二釐六毫零。而一毫零亦加多。上通朔所得之溢数。实本于此。此西山所以直斥本算为穿凿傅会者也。且以八十一作分则本朔零日四十三分。不得不如此。而章末六十一分。因此而误。西山之直斥八十一。不亦宜乎。
按律与历。各自为数。而不可滚合者也。闳平等必欲傅合而缘饰之。此所以不能无差者也。若愚陋生于汉元封之间。而得与于十七家课历之列。则必与寿王同受妄言之罪。而高明亦入于株连之科可呵。尝疑太史公亦于是时。同请改历。而其所编历书则一遵太初旧算。又考历书则于四章之末。阙大小馀分齐之数。岂所见与闳平不合。而不欲互形其得失。故微其文而为此欤。抑或传写之际。有阙误而然耶。(用太初历法则当以甲子起元。而太史公亦以甲寅起元。不可晓。)

又按寿王谓闳平历法失历纪之数则固得之矣。而但其所以为说者。失其肯綮而不足以服其心。盖其法六十一算。即七百单五之对算。而寿王以为全去七百单五。又四分阙三。以其法求之则未尝阙三。而寿王只泛言其阙三。将何以服其心乎。如欲服其心而开其惑。则必须以其法而攻其法然后。方可以厌服。盖一章分齐之数。所以合气与朔而一之者也。今以其法求之。则气与朔不相合。若以此反诘。则彼必无辞可对。而四分阙三之误。皆将次第破绽矣。
　　答崇伯书
所示历算勘订。间不无合商处。而大槩则得之矣。落下闳八十一章法。尝疑其傅会强合。而犹未得其真脏。间因无事。以其法推之则果如此。试加推算。考见其得失如何。要之寿王当日苦口争论。决非妄言者。而自有律历志以来。枉受此名而莫之洗。天下古今之是非难定有如此者。俯仰千古。良足一慨。此去算释设为吾两人问答者。盖因前后问答而为之者也。然把贤做问头和尚。得无嵬岸耶。尝见退陶先生于龟翁。有田算之问。又考亭之论句股法也。先设问于西山。如是作过。或不至太僭否。太玄不济事之示。想

必有为而发。然玄法则虽立踦赞而犹有赢不足之算。故免不得此讥。而若向者共商之差法则恰无馀欠。若与此而并按则冤矣。奉呵。
　本志历法。全以日为纪。分作三统。而不以岁与月为纪。亦未可知也。
以六十一分。置章末之算。则二百四十三章之间。章末之恰无馀分者。只有三日。故以此纪三统。盖用太初旧算则恰过八十章而岁与日一齐无馀分。故以岁纪统。而人统在地统之前。本志算率则年月恰无馀算处。日分则尚有馀算。故更进一章。以日分尽处为纪。而地统在人统之前则虽欲合岁月为纪而不可得。
按本志求冬至法。以人统岁数乘除而作大小馀别法以求之者。虽未始不合。而似涉烦拿。愚见则不必别立大小馀算。只依太初历大小馀本算求之则似甚简易。
　假令当年气大馀五数。则五数尽处即己巳。是为己巳日冬至。又欲知冬至在几日。则以朔法大馀参互。而是年朔大馀五十四。则五十四数尽处即朔日戊午。而从戊午数至己巳则得十二数。是为

十二日冬至。他仿此。如欲就见行历书。豫知明年冬至。则大小馀数已具于当年冬至及朔日干支中。依法推之则得。假令是年至日干支值甲寅。则知是年气大馀为五十一。朔日干支值丙午。则知是年朔大馀为四十三。就此更加气朔两大馀原数通计。则得明年两大馀算而依前作法。
左传绛老年数说
　襄公三十年戊午二月癸未。绛县人就食于杞。使之年则曰臣生之年正月甲子朔。四百有四十五甲子矣。其季于今三之一也。师旷曰七十三年矣。史赵曰亥有二首六身。下二如身。是其日数也。士文伯曰二万六千六百有六旬也。○附注朱氏曰自乙巳至戊午。首末七十四年。而曰七十三年者。盖计其全数。尚未满七十三年也。
尝见霁山集。有语及此算处。而未甚精密。如欲见其实数。自有捷法。盖七十三年。即四章七十六年内。除三年之数也。其法先置四章通日二万七千七百五十九日为实。就除三个三百五十四日。又除三年一闰二十九。则已得士文伯所谓二万六千六百六旬。而零位入算亦有当除之数。盖三年朔馀又有三个

三百四十八。闰馀又有一个四百九十九故也。乃取末位取二算。破日作分。置一千八百八十分。就除二馀则恰馀三百三十七分。而全算位所馀二万六千六百六旬六日三百三十七分。是则尽七十三年之日数也。乃以六十除之则恰得四百四十五甲子。而其季甲子则只得二十六日零。盖其就役之日乃癸未。而癸未处甲子三分之一。故其言如此。非谓七十三年日数止于此而已。注家所谓计其全数则尚未满七十三年者此也。此虽小数。而春秋诸贤。皆领略于立谈之顷。才闻绛老之说。则师旷便知其年数。才闻师旷几年之说。则史赵，士文伯便知其日数。后人则书在纸面者如是其明白。而握算布数。尚未了晢。古今人不相及有如此者。儿辈之读左氏传者。多来问此算。故告之以此。如欲见四章除三年之数端的不差。以七十三乘三百五十四。得二万五千八百四十二日。而又七十三年合置二十七闰。故以二十七乘小尽月二十九日。得七百八十三日。又以七十三乘每岁朔馀三百四十八。得二万五千四百单四分。又以二十七乘每闰馀分(闰月又既皆作小尽月则每闰馀分四百九十九。不可不计。)四百九十九。得一万三千四百七十三分。合三

万八千八百七十七分。乃以日法九百四十除之则得四十一日零三百三十七分。而通融计数则亦二万六千六百六旬六日零三百三十七分。而与上除馀之数。毫发不差。若以七十三乘周天三百六十五度二百三十五分。通计得数(全度得二万六千六百四十五日。又乘二百三十五分。得一万七千一百五十五分。以日法作日则得十八日二百三十五分。)则恰得二万六千六百六旬三日零二百三十五分。盖六日与三日不同者。未满一章之前。气与朔不同故也。然又如欲以气法就朔除之则复置四章通日二万七千七百五十九日。就除三个三百五十四日。又直除三年闰馀三十二日六百单一。(历家除闰之例则如上所除。而此则依期注直除三年闰馀之数。)又除三个朔馀三百四十八。则亦与周天度所乘之日分不少差爽。注家以士文伯所言谓尚未满七十三年日数者则是矣。而若曰实七十四年云尔则殊欠曲折。盖师旷所言则以夏正计。故四百四十五甲子。在七十三年之内。左氏所载则以周正计。故其季三之一癸未在戊午二月。然以夏正计则是月乃丁巳腊月。非戊午二月也。若反其语曰以春秋周正计则自乙巳至戊午虽七十四年。而实七十三年则似稳。(若以夏正腊月为周正二月。则是生之岁正月亦当把做周正三月看。)

一法。置日数(二万六千六百六十)以日法(九百四十)通之。得二千五百□六万□四百为实。以一朔通分二万七千七百五十九分为法除之。得九百零二月。不尽二万一千七百八十二分。合不尽之数通计则为九百零三月。(此本闰合数。)就此七乘。而(一章闰数)二百三十五归之。(一章月数。)得二十七闰。而就减于本闰合数中。则只馀本月八百七十六。乃以十二计之则为七十三年。又就不尽之数(二万一千七百八十二)以九百四十作日则为二十四日弱。如此则其就食之日癸未。在戊午二月二十四日矣。(所生之日在朔日。故自朔日而计之。)