声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
湛轩书外集卷四 第 x 页
湛轩书外集卷四(南阳洪大容德保 著 五代孙 荣善 编 后学 洪命憙 校)
筹解需用
筹解需用序
孔子尝为委吏矣。曰会计当而已矣。当会计者。舍算数奚以哉。史氏言孔门诸子之盛。以身通六艺称之。古人之务实用也如此。孔氏之所以教者。其可知已。算法祖于九章。历代演之。其术亦多矣。病其各自为书。详略不一。往往逞奇索隐。殆有近于迷藏之戏者。斋居无事。谨采其宜于今而适于用者。间附己意。录为一册。其斛斗段匹之率。并以时法通之。庶得其实用而当于会计也。且习是法者。其潜心摄虑。足以养性。探赜钩深。足以益智。此其功岂异于琴瑟简编哉。呜呼。天有万化而不外乎阴阳。易有万变而不外乎刚柔。算有万术而不外乎乘除。阴阳正位而不乱。刚柔迭用而成章。正位法乎天。迭用则乎易者。其乘除之术乎。若由是而引而伸之。观小道而悟大德者。存乎其人。
筹解需用
筹解需用序
孔子尝为委吏矣。曰会计当而已矣。当会计者。舍算数奚以哉。史氏言孔门诸子之盛。以身通六艺称之。古人之务实用也如此。孔氏之所以教者。其可知已。算法祖于九章。历代演之。其术亦多矣。病其各自为书。详略不一。往往逞奇索隐。殆有近于迷藏之戏者。斋居无事。谨采其宜于今而适于用者。间附己意。录为一册。其斛斗段匹之率。并以时法通之。庶得其实用而当于会计也。且习是法者。其潜心摄虑。足以养性。探赜钩深。足以益智。此其功岂异于琴瑟简编哉。呜呼。天有万化而不外乎阴阳。易有万变而不外乎刚柔。算有万术而不外乎乘除。阴阳正位而不乱。刚柔迭用而成章。正位法乎天。迭用则乎易者。其乘除之术乎。若由是而引而伸之。观小道而悟大德者。存乎其人。
湛轩书外集卷四 第 177H 页
 筹解需用总例
筹解需用总例九九数(呼小数在上。大数在下。)
九九八十一。 八九七十二。 七九六十三。 六九五十四。 五九四十五。 四九三十六。 三九二十七。 二九十八。 一九九。
八八六十四。 七八五十六。 六八四十八。 五八四十。 四八三十二。 三八二十四。 二八十六。 一八八。
七七四十九。 六七四十二。 五七三十五。 四七二十八。 三七二十一。 二七十四。 一七七。
六六三十六。 五六三十。 四六二十四。 三六十八。 二六十二。 一六六。
五五二十五。 四五二十。 三五十五。 二五十。 一五五。
四四十六。 三四十二。 二四八。 一四四。
三三九。 二三六。 一三三。
二二四。 一二二。
一一一。
九归歌(呼大数在上。小数在下。)
一归不须归。 逢一进一十。
二一添作五。 逢二进一十。
三一三十一。 三二六十二。 逢三进一十。
四一二十二。 四二添作五。 四三七十二。 逢四进一十。
湛轩书外集卷四 第 177L 页
 五一倍作二。 五二倍作四。 五三倍作六。 五四倍作八。 逢五进一十。
五一倍作二。 五二倍作四。 五三倍作六。 五四倍作八。 逢五进一十。六一下加四。 六二三十二。 六三添作五。 六四六十四。 六五八十二。 逢六进一十。
七一下加三。 七二下加六。 七三四十二。 七四五十五。 七五七十一。 七六八十四。 逢七进一十。
八一下加二。 八二下加四。 八三下加六。 八四添作五。 八五六十二。 八六七十四。 八七八十六。 逢八进一十。
九一下加一。 九二下加二。 九三下加三。 九四下加四。 九五下加五。 九六下加六。 九七下加七。 九八下加八。 逢九进一十。
斥(一作斤)下留数(斤下。两十六除之。为留数。有两下者。通除之。)
一退六二五。(退者。斤下空一位也。) 二留一二五。 三留一八七五。 四留二五。 五留三一二五。 六留三七五。 七留四三七五。 八留单五。 九留五六二五。 十留六二五。 十一留六八七五。 十二留七五。 十三留八一二五。 十四留八七五。 十五留九三七五。
石下留数( 石下斗十五除之。留数有四。其馀并畸零。有斗下者。通除之。)
三留单二。 六留单四。 九留单六。 十二留单八。
匹下留数( 匹下。尺四十除之为留数。有尺下者。通除之。)
一退二五。 二退单五。 三退七五。 四留单一。 五留一二五。 六留一五。 七留一七五。 八留单二。 九留二二五。 十留二五。(下仿此。)
石斗率
量止于勺。十勺为合。十合为升。十升为斗。十五斗为石。(私法。二十斗为石。)
斤两率
湛轩书外集卷四 第 178H 页
 衡止于忽。十忽为丝。十丝为毫。十毫为釐。十釐为分。十分为钱。十钱为两。一十六两为斤。一百斤为秤。
衡止于忽。十忽为丝。十丝为毫。十毫为釐。十釐为分。十分为钱。十钱为两。一十六两为斤。一百斤为秤。匹尺率
度止于忽。十忽为丝。十丝为毫。十毫为釐。十釐为分。十分为寸。十寸为尺。四十尺为匹。(或三十五尺为匹。)五十匹为同。
田结率
税止于把。十把为束。十束为负。一百负为结。八结为夫。(或四结为夫。)
乘除诀
筹有衍数有约数。衍者。衍少为多。乘法是也。约者。约多为少。除法是也。如斤作两石作斗。衍少为多也。两作斤斗作石。约多为少也。(乘亦有约尺乘寸。两乘钱数降一位。除亦有衍寸除尺。钱除两数降一位。)
法实诀
元数为实。每数为法。如有钱三两。每两贸米二斗。以求米数则钱三两为实。米二斗为法以乘之。如有米六斗。每二斗作钱一两。以求钱数则米六斗为实。二斗为法以除之。乘则法实可互用。除则法实有定不可易。
定位诀
定位者。定得数头位之某数也。位数未定。则千或为万。百或为十而诸位俱乱矣。故定位。是筹法之门户。为术多歧。其要以每数为主。如问有银一千两零。每两得粟几十斗。则以十斗呼起于实之两位。逆数至实头(十两呼百斗。百两呼千斗。馀仿此。)为万斗。则以万斗定位。(乘数有十。则越位而为十万斗。)
上少下多。次一位。谓除法之实少法多者。布法。次一位以照实之第二位也。定位逆数。亦下一位以照法头。
法头当实尾数至实头位。法尾当实头数至法头位。俱得。
十一,百二,千三,万四,十万五。(馀仿此。)亦定位诀也。乘则逆数。除则顺数。单数当位。如银三千作两。每斤十六两。自实位逆上一位。(两为十六。则当用十一法。)以十两定位。(实位为单数。则上一位为十。)如银四十八两作斤。每十六两为斤。自实位顺下一
湛轩书外集卷四 第 178L 页
 位。(十六两为斤。则当用十一法。)以单斤定位。(实头为十数。则下一位为单数。)
位。(十六两为斤。则当用十一法。)以单斤定位。(实头为十数。则下一位为单数。)撞归诀
见一无除作九一。无除起一下还一。(凡归除实头法头同数而上少下多。归除不行者。以一见一。则以实一作九。又加一于下。若除数不足则起九之一。加于下位。适足为度。见二则作九二。起一下还二。馀仿此。)
方圆乘除率( 筹数有精有粗。精数析微细分。无内治。历审律之属是也。粗数从简。少差无碍。量田商功之属是也。精数从简则术疏而谬大。粗数析微。则策繁而功寡。此筹术之通变。随数而异用也。如经一周三方五斜七之类。具有畸零。实非定法。故方圆弧角之率从简而术疏。宜于粗而不宜于精。筹学所当知也。)
径求周三因。(圆法之周三径一。古率也。微率密率。比古差精而犹不免盈朒。盖粗数。不如古率之简。精数。莫如西法之密。学者详之。)
周求径三归。
径求积自乘。三因四归。(即方内圆。积四分之三。亦根于古圆率。)
周求积自乘。十二除。(十二圆积。与周自乘同数。)
周径求积。相乘四归。(周径相乘。为四圆积。)
半周求积。自乘三归。(半周自乘。为三圆积。)
半径求积。自乘三因。(半径自乘。为方积四分之一。)
半周半径。求积相乘。(半周径相乘。为全周径相乘四分之一。)
方内圆积。四归三因。(四分之三。)
圆内方积三归二因。(三分之二。)
三角内圆积。七归四因。(七分之四。)
圆内三角积。十六除七因。(十六分之七。)
六角内圆积。七归六因。(七分之六。)
圆内六角积。七归六因。(七分之六。)
弧矢求积。弦乘矢。四归三因。(弧矢为直积四分之三。又并弦矢自乘六归之。又并弦矢折半。乘矢俱得。)
立圆径求积。再自乘。又九因十六除。(再自乘。为立方体。是立方内容立圆。以平面率。各自乘为体率。)
方求斜。七因五归。(方五斜七。下同。)
斜求方五因七归。
三角面长求中长。七因六归。(中长为面长。七分之六。下同。)
湛轩书外集卷四 第 179H 页
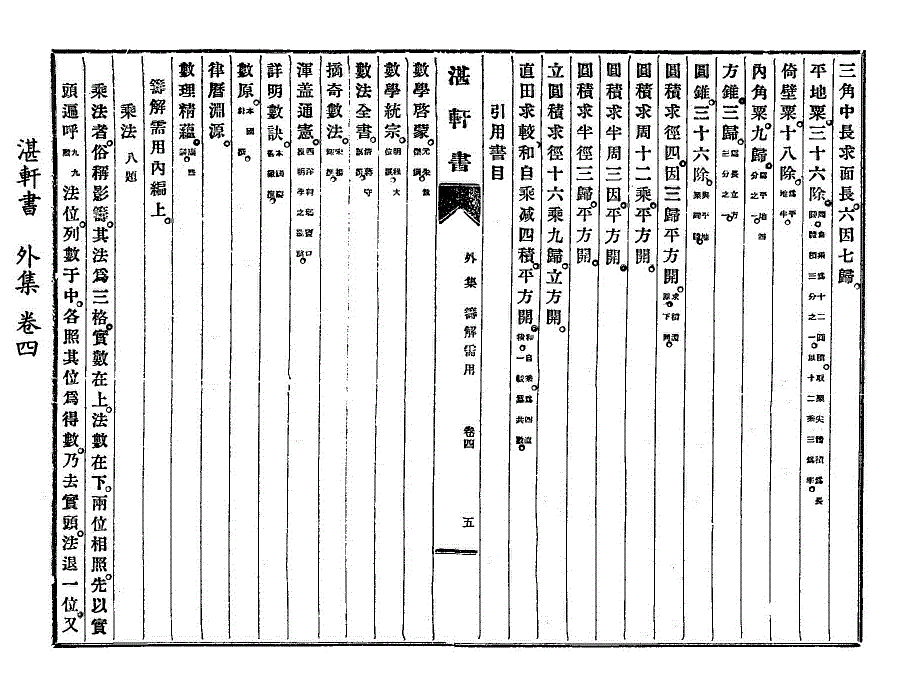 三角中长求面长。六因七归。
三角中长求面长。六因七归。平地粟。三十六除。(周自乘为十二圆积。取粟尖体积为长圆。体积三分之一。以十二乘三为率。)
倚壁粟。十八除。(为平地半。)
内角粟。九归。(为平地四分之一。)
方锥。三归。(为长立方三分之一。)
圆锥。三十六除。(与平地粟同体。)
圆积求径四。因三归平方开。(求积还原。下同。)
圆积求周十二乘。平方开。
圆积求半周三因。平方开。
圆积求半径三归。平方开。
立圆积求径十六乘九归。立方开。
直田求较。和自乘减四积。平方开。(和自乘。为四直积。一较羃共数。)
引用书目
数学启蒙。(元朱世杰撰。)
数学统宗。(明程大位撰。)
数法全书。(清蒋守诚撰。)
摘奇数法。(宋扬辉撰。)
浑盖通宪。(西洋利玛窦口授明李之藻演。)
详明数诀。(本国庆善徵撰。)
数原。(本国朴▣撰。)
律历渊源。
数理精蕴。(康熙制。)
筹解需用内编[上]
乘法(八题)
乘法者。俗称影筹。其法为三格。实数在上。法数在下。两位相照。先以实头遍呼(九九数)法位。列数于中。各照其位为得数。乃去实头。法退一位。又
湛轩书外集卷四 第 179L 页
 照位遍乘。加于得数。以下仿此。(法实之格。或实头与法尾相照。或实尾与法头。相照俱得。)
照位遍乘。加于得数。以下仿此。(法实之格。或实头与法尾相照。或实尾与法头。相照俱得。)钱三十五两。每两贸米二斗五升。问米几何。
答曰。八十七斗五升。
术曰。列钱三五于上格为实。列米二五于下格为法。(每数为两。故以法头起于实两。逆数至头为十斗。)以法之诸位。乘实之头位。(二三六○三五十五。)中格得数。为七十五斗。乃去经乘。(三。)法退一位。与实馀位相照。又以法之诸位。乘实之次位。(二五十○五五二十五。)得数为一十二斗五升。(十数上升零数当位。)各照位加之。合为八十七斗五升。
米五十四石三斗。每斗价钱三钱四分七釐。问钱几何。
答曰。二百八十二两一钱一分一釐。
术曰。五十四石通斗(以问每斗价钱。通斗以石。率十五加之。法在下。)内子。(三斗。)为八百一十三斗为实。以钱三四七为法。(起钱于单斗。逆数至头为十两。则以十两定位。○单斗起钱百斗为十两。)乘实。(三八二十四。○四八三十二。○七八五十六。)得二百七十七两六钱。(定位为十两而头位相乘。为二十四十数。上升而为百。)乃去经乘。法退一位。照位相乘。(一三三○一四四○一七七。)得三两四钱七分。(定位为十两。头位之次。当为单两。)又去乘经。法退一位乘。(三三九○三四十二○三七二十一。)得一两四分一釐。各照位加之为得数。
田六夫七结八十九负。每结纳白木一疋五尺六寸七分。问白木几何。
答曰。六十三疋三十二尺四寸九分六釐三毫。
术曰。夫通结内子。以五五八九为实。疋通尺内子。以四五六七为法。(疋下当以四十除而留之数烦就通尺以就简亦可。○起十尺于结。百尺为位。越位为千。)乘得二千五百五十二尺零。以四十归之(九归法在下)为疋。
布七疋三十三尺。每疋易粟一石七斗三升九合七勺。问粟几何。
答曰。十一石十斗二升五合六勺五二五。
术曰。布疋下。以四十归之。(疋法四十尺。凡布筹。以十为率。今疋尺之法。四十尺乘为疋。故以四十除之。以就十率之法。凡石下斗斤下两。并除而留之。其义同。)得八二五。乃以七八二五为实。粟石下。十五除之。畸零不尽。故通斗内子。以二二三九七为法。乘之得一百七十五斗零。
湛轩书外集卷四 第 180H 页
 以十五除之为石。(以求还原斗。下存其数。)
以十五除之为石。(以求还原斗。下存其数。)束伍七十五营四司三哨二旗一队。每军一人给火药六斤六两七钱四分。问火药几何。(束伍法。一队铳手十人。三队为旗。三旗为哨。五哨为司。五司为营。)
答曰。一百九万七千三百二十七斤六两六钱。
术曰。七十五营。通司(五)内子为三百七十九。又通哨(五)为一千八百九十八。又通旗(三)为五千六百九十六。又通队(三)为一万七千八十九。又以每队十人通之。得一十七万八百九十为实。火药斤下。十六除之。得四二一二五。乃以六斤四二一二五为法。乘之得一百九万七千三百二十七斤。斤下。四一二五十六加之。(斤下得数。乃十率之数。故以十六加之。以就斤下两法。乃为斤下两真数。凡石下疋下仿此。)得六两六钱。
牛黄八斤三两五钱。每斤易人蔘七斤十三两六分。问人蔘几何。
答曰。六十四斤三两八钱三分六釐八毫七丝五忽。
术曰。斤下。并十六除之。以八斤二一八七五为实。以七斤八一六二五为法。乘得六十四斤。二三九八空四六八七五。斤下加之。
绵花二十四秤六十八斤一两。每秤易绵布八疋二十五尺七寸八分九釐。问布几何。
答曰。二百十三疋十四尺二寸八分八釐六毫三丝八忽一二五。
术曰。以绵花二四六八空六二五(一两为空六二五)为实。以绵布八六四四七二五(疋下留)为法。乘得二百十三疋。三五七二一五九五三一二五。疋下。四十(布疋尺率)因之。
银一万三百四十斤六两八钱四分。每斤贸铅九十五斤一十两四钱八分一釐。问铅几何。
答曰。九十八万九千一百一十四斤三两八钱二分六毫二丝七忽半。
术曰。以银一空三四空四二七五为实。以铅九五六五五空六二五为法。乘得九八九一一四。二三八七八九二一八七五。斤下加之。
因法(八题)
湛轩书外集卷四 第 180L 页
 因法者。法之单位者。去中下二格。就实呼乘。因其位而变之。十数升上。零数当位。从头而下。此单乘之捷法也。
因法者。法之单位者。去中下二格。就实呼乘。因其位而变之。十数升上。零数当位。从头而下。此单乘之捷法也。正租四十六石。每石和法二十斗法。问为斗几何。
答曰。九百二十斗。
术曰。列四六为实。(起十斗于单石。至头为百。以百斗为位。)以二为法。(不列格。)从头而乘之。(二四八○二六十二。)变四为八。变六为十二。十升于上。并八为九。
岁一十二月。每月三十日。问为日几何。
答曰。三百六十日。
周天三百六十五度四分度之一。通分内子。问为数几何。
答曰。一千四百六十一。
布二十三同。每同五十疋。问为疋几何。
答曰。一千一百五十疋。
易六十四卦。每卦六爻。问为爻几何。
答曰。三百八十四爻。
周天三百六十度。每七十年。恒星行一度。问恒星一周天。为年几何。
答曰。二万五千二百年。
日十二时。每刻八刻。问为刻几何。
答曰。九十六刻。
周田四十六井。每井九百亩。问为亩几何。
答曰。四万一千四百亩。
加法(八题)
加法者。法头为一数者。去头一。以馀数为法。就实呼乘。加于本位。十数当位。(满十者。姑留本位。以待毕加。)零数下加。从尾而上。此头一乘之捷法。但三位以上。易错不可用也。
岁三百五十四日。每日一十二时。问为时几何。
答曰。四千二百四十八时。
湛轩书外集卷四 第 181H 页
 术曰。列三五四为实。(起十时于单日。至头为千。以千时为位。)以时一十二。去头一。馀二为法。从尾而乘之。(二四八○二五十○二三六。)八加于四之下。十加于五之当位。六加于三之下。
术曰。列三五四为实。(起十时于单日。至头为千。以千时为位。)以时一十二。去头一。馀二为法。从尾而乘之。(二四八○二五十○二三六。)八加于四之下。十加于五之当位。六加于三之下。麻布三十三疋。每疋价钱一两三钱。问钱几何。
答曰。二十九两九钱。
天银三百四十五两。每两换锭银一两四钱。问锭银几何。
答曰。四百八十三两。
米二十七石。每石一十五斗。问为斗几何。
答曰。四百五斗。
南草四十八斤。每斤一十六两。问为两几何。
答曰。七百六十八两。
良马行三十五日。每日行一百七十里。问合行里几何。
答曰。五千九百五十里。
银二十三两。每两换钱一两八钱。问钱几何。
答曰。四十一两四钱。
月行十三度十九分度之七。通分内子。问为数几何。
答曰。二百五十四。
商除法(八题)
商除者。商量而除之。其法为三格。中置实数。下数法数。量法实。任置商数于上。法商相乘。以除实数。不足则减商。有馀则添商。取其适足。有不满法者。(实之馀数。不满法数。)法退一位。以商除之。此乘法之还原也。
军布钱八十七两五钱。每人二两五钱。问人几何。
答曰。三十五人。
术曰。列钱八七五于中为实。列二五于下为法。(起人于单两。至头为十。以十人为位。)任置四十于上为商数。法商相呼(二四八○四五二十)实数。不足为十二两五钱。乃减商为二。法商相呼。(二二四○二五十。)合除五十而实数多于法数。为实数。有馀。
湛轩书外集卷四 第 181L 页
 乃更添商为三。法商相呼。(二三六○三五十五。)合除七十五。不满法者。为一十二两五钱。法退一位。又任置六于初商三十之下。法商相呼。(二六十二○五六三十。)实数不足为二两五钱。乃减商为五。(二五十○五五二十五。)合除十二两五钱。实数恰尽。
乃更添商为三。法商相呼。(二三六○三五十五。)合除七十五。不满法者。为一十二两五钱。法退一位。又任置六于初商三十之下。法商相呼。(二六十二○五六三十。)实数不足为二两五钱。乃减商为五。(二五十○五五二十五。)合除十二两五钱。实数恰尽。车行八十里。轮周一十六尺。问轮转几何。(一千八百尺为里。)
答曰。九千转。
术曰。八十里通尺。得一十四万四千尺。以一四四空空空为实。轮周一六为法。但法位下实一位。以一当实之第二位。(定位法。上少下多。次一位。凡法数多于实数者。仿此。○起单转于单尺空。位至法头相当之第二位为千。以千转为位。)乃置商数九于实数第二位之上。与法数头位三位相当。法商相呼。(一九九○六九五十四。)除实恰尽。
钱一百五两三钱。欲贸米每斗价四钱五分。问米几何。
答曰。二百三十四斗。
术曰。钱一空五三为实。四五为法。四空相当(亦次一位。○起单斗于钱。至法头相当第二位为百。以百斗为位。)置商。以法商相呼。(二四八○二五十。)除实九十两。馀一十五两三钱。为不满法。法退一位。更置商三。法商相呼。(三四十二○三五十五。)除实一十三两五钱。馀一两八钱。为不满法。法又退更置商四。法商相呼。(四四十六○四五二十。)除实恰尽。
粟七百七十四斗三升。每五斗三升四合作钱一两。问钱几何。
答曰一百四十五两。
术曰。粟七七四三为实。五三四为法。得商一四五。除实恰尽。
绵布三十六疋二十尺五寸。每六十三尺五寸易绵䌷一疋。问绵䌷几何。
答曰。二十三疋。
术曰。绵布通尺内子。以一四六空五为实。六三五为法。得商二三。
结役钱四百二十两七钱五分。每田一夫纳钱七十六两五钱。问田几何。
答曰。五夫四结。
术曰。钱四二空七五为实。七六五为法。得尚五五为五夫。半夫下。以八
湛轩书外集卷四 第 182H 页
 (八结为夫)因之。
(八结为夫)因之。麻布二十七疋二十九尺五寸五分。每二疋五尺三寸五分。易金箔一钱。问金箔几何。
答曰。一两三钱。
术曰。麻布通尺内子。以一一空九五五为实。以八五三五为法。除之。
银二十斤一十。两每九两九钱。易朱砂一两。问朱砂几何。
答曰。一斤一两三分两之一。
术曰。以三三空(银通两)为实。以九九为法。得商二斤一两。两下畸零。以之分命之。得九十九分两之三十三(法数为分母实。馀为分子。法有二位。故分母头位为十实。馀头位与法位相当。故亦为十。)约之。(约分法。在下。)
归除法(八题)
归除者。归其头位而除其下位也。其法为二格。实数在上。法数在下。先以法头呼实头。九归以归之为得数。以法之次位以下。与得数九九相呼照位。除实。法退一位。以次归除之。恰尽而止。盖商除之捷法也。
大洋海路九万里。舶行每日量得二百五十里。问到大洋为日几何。
答曰。三百六十日。
术曰。九空空空空为实。二五为法。(法头为百。下实二位。以百日为位。○定数诀。十一百二千三万四法之二百当实之九万。顺万而下。一为千二为百也。)以二归九。(逢六进三十。○即逢二进一十。凡三次也。)进得三百于原九之上位。实馀为三万。乃以法之次位与得三相呼(三五十五)以除实。馀一万五千为不满法。法退一位。以二归之。(二一添作五。)为五当位五千。又过于法数。则又以二归五。(即实之五千。○逢二进一十。)以二为一十而进于上。与原添作之五。合得六实。馀为三千。乃以法五与得六相呼。(五六三十。)除实恰尽。
白木八百五尺。作大同木。问为疋几何。(三十五尺为疋。)
答曰。二十三疋。
术曰。八空五为实。三五为法。(八下空位为十。以十疋为位。)以三归八。(逢六进二十。○即逢三进一十。凡二次也。)进得二十于原八之上位。实馀为二百五尺。乃以法五呼。得二(二五
湛轩书外集卷四 第 182L 页
 十)以除实。馀一百五为不满法。法退一位。以三归一。(三一三十一。)以一为三。(为得数。)加一于下空位。实馀为一十五。乃以法五呼得三。(三五十五)除实恰尽。
十)以除实。馀一百五为不满法。法退一位。以三归一。(三一三十一。)以一为三。(为得数。)加一于下空位。实馀为一十五。乃以法五呼得三。(三五十五)除实恰尽。钱一千一十七两。令四十五人分之。问人得钱几何。
答曰。二十二两六钱。
术曰。钱一空一七为实。四五为法。次一位(上少下多)归除之。得二二六。
绵布五十五同三十一疋。每一同雇价一疋半。问原布几何。
答曰。五十四同。
术曰。绵布通疋内子以二七八一为实。以五一五(即一同五十疋并雇价一疋半也)为法。归除之。
粟米三十二斗五升。每粟一斗舂。精米六升五合。问原粟几何。
答曰。五十斗。
术曰。粟三二五为实。六五为法。归除之。
银四十两八钱八分。欲贸贡缎。每尺价七钱三分。问贡缎几何。
答曰。五十六尺。
术曰。银四空八八为实。七三为法。归除之。
粜米二千三百三十四石四斗。每户八斗二升。问民户几何。
答曰。四千二百七十户。
术曰。米通斗内子以三五空一四为实。八二为法。归除之。
钱二百三十一两二钱六分。共贸甘草九十三斤。问斤价几何。
答曰。二两四钱八分三分分之二。
术曰。钱二三一二六为实。九三为法。归除之。不满分者为之分(九十三分分之六十二)约之。
(附)作九下还法
凡归除法。实头位同数而上少下多。虽次一位而归除不行者。变实头作九。又加头数于实之次位(头数一则作九加一。头数二则作九加二。以至头数九则因九加九。所谓见一无除作九一也。)而除之。除实不足。则起九之一。作头数而下还于次位。(头数一则下还亦一。
湛轩书外集卷四 第 183H 页
 头数二则下还亦二。以下仿此。所谓撞归法也。)犹不足则至再至三。适足而至。
头数二则下还亦二。以下仿此。所谓撞归法也。)犹不足则至再至三。适足而至。钱二两一钱。令二十二人分之。问人得钱几何。
答曰。九分一十一分分之六。
术曰。二一为实。二二为法。归除之。(逢二进一十。)法次一位。二又进十。则越二位。归除不行。乃就实变二作九。加二于下。并一为三而除之。(二九十八。)实馀一钱二分之分命之。
布三千四百五十六尺。每三十五尺为疋。问为疋几何。
答曰。九十八疋二十六尺。
术曰。三四五六为实。三五为法。归除之。(见三无除作九三○五九四十五。)变三作九。加三于下。并四为七。除四而为三。下五除五而为空。得数为九。实馀为三空六。法次一位。又归除之。(见三无除作九三○起一下还三○五八四十。)变三作九。加三于下。起九之一作三而加于下。并三为六。得数为八除四十。实馀二六。
米九十一斗。令九十二户分之。问户得米几何。
答曰。九升八合九勺二十三分勺之三。
术曰。九一为实。九二为法。归除之。(见九无除作九九○二九十八。)因九为九。加九于下。并一为十除十八。得数为九。实馀为八二。法次一位。又归除之。(九八下加八○二八十六。)得数为八。实馀为八四。法次一位。(九八下加八○逢九进一十○二九十八。)得数为九。实馀为一合二勺之分命之。
九归法(八题)
九归者。九归以归之也。法之单位者。只列实一格。以法数九归以归之。当其位而变之。此单除之捷法而因法之还原也。
米一百二十斗。令二十户分之。问户得米几何。
答曰。六斗。
术曰。米一二为实。以二为法。就实位而归之。(二一添作五○逢二进一十。)变一作五。进二作一。并五而为六。
路程一千一百一十里。每三十里为息。问为息几何。
湛轩书外集卷四 第 183L 页
 答曰。三十七息。
答曰。三十七息。术曰。一一一为实。以三归之。(三一三十一○三二六十二○逢三进一十。)变一为三。加一于下为二。变二为六。加二于下为三。进三作一。并六而为七。得三七。
布一万三百二十尺。每四十尺为疋。问为疋几何。
答曰。二百五十八疋。
术曰。一空三二为实。以四归之。(四一二十二○四二添作五○四三七十二○逢四进一十。)变一为二。加二于下。变二作五。变三为七。加二于下。为四作一。并七而为八。
人蔘一十二斤五两五钱二分。每五斤。易牛黄一斤。问得牛黄几斤。
答曰。二斤七两五钱四釐。
术曰。一二三四五(斤下留)为实。以五归之。(五一倍作二○五二倍作四○五三倍作六○五四倍作八○逢五进一十。)斤下加之。
军一十万一千一十六人。欲作六花阵。问每阵得军几何。
答曰。一万六千八百三十六人。
术曰。一空一空一六为实。以六归之。(六一下加四○六四六十四○六五八十二○六二三十二○六三添作五○逢六进一十。)
粟一千三百斗二升一勺。每七斗易麻布一疋。问布几何。
答曰。一百八十五疋二十九尺七寸二分。
术曰。一三空空二空一为实。以七归之。(七一下加三○七六八十四○七四五十五○七五七十一○七三四十二○七二下加六○逢七进一十。)疋下四十因之。
田一千三结一负五束二把。每八结纳米一石。问米几何。
答曰。一百二十五石五斗六升五合三勺半。
术曰。一空空三空一五二为实。以八归之。(八一下加二○八二下加四○八四添作五○八三下加六○八六七十四○八五六十二○八七八十六○逢八进一十。)石下十五加之。
钱一千一百一十一两一分一釐一毫二丝。令九人分之。问人得钱几何。
答曰。一百二十三两四钱四分五釐六毫八丝。
术曰。以钱为实。以九归之。(九一下加一○九二下加二○九三下加三○九四下加四○九四下加四○九五下加
湛轩书外集卷四 第 184H 页
 五○九六下加六○九七下加七○逢九进一十。)
五○九六下加六○九七下加七○逢九进一十。)定身除法(六题)
定身除者。一曰求一除。先定身而后除之也。法之有两位而头位为一数者。亦列实一格。取其头位。商定身数。去法头一耴。其馀与身相呼。(九九数。)照位除实。此商除之捷法。加法之还原也。三位以上亦可用。但为二格。法数在下。以头一呼实而商身。(凡六题。逢一进一十。用归除亦可。撞归法。见一无除作九一。亦归除之用。)
米四百八十斗。每一十五斗作一石。问为石几何。
答曰。三十二石。
术曰。四八为实。以五为法。就实商定。定身三而除之。(三五十五。)实馀三十斗。定身二而除之。(二五十。)恰尽。
银七百六十八两。每一十六两作一斤。问为斤几何。
答曰。四十八斤。
术曰。七六八为实。以六为法定身。四而除之。(四六二十四。)实馀十。(十者满十而留在本位也。)二八(十二同位)定身。八而除之。(六八四十八。)恰尽。
米七百五十一石六斗。每一石船价三斗。问元米几何。
答曰。六百二十六石二斗五升。
术曰。米通斗内子以一一二七一为实。以八为法。(米一石并船价为一十八斗去头一以八为法。)以实头一作十退。加于次位为十一。(以一一数少定除不得也。)定身六而除之。(六八四十八。)身得六。实馀四七一。又定身二而除之。(二八十六。)身得六百二十。实馀十一一。(十一同位。)定身六而除之。(六八四十八。)合得六百二十六石。馀三斗畸零。先以十五加之为四五。定二而除之。(二八十六。)为馀九。定身五而除之。(五八四十。)恰尽。(石下当先除之得数。以石率十五加之。为真数。此以畸零先加后除。下仿此。)一法。七五一四(石下留)为实。以二(米一石并船价为一石三斗。石下留去头一。)为法定身而除之。亦得六百二十六石。馀二斗畸零。先以十五加之为三而除之。亦得。
钱二百三十二两。每一十二两五钱。贸人蔘一钱。问人蔘几何。
答曰。一两八钱五分六釐。
湛轩书外集卷四 第 184L 页
 术曰。二三二为实于上。一二五为法于下。以法头一呼。实定身(一一一)除之。(一二二○一五五。)身得一。实馀十七。又定身(一八八)而除之。(二八十六○五八四十。)身得八。实馀七。又定身(一五五)而除之。(二五十○五五二十五。)身得五。实馀七五。又定身(一六六)而除之。(二六十二○五六三十。)恰尽。
术曰。二三二为实于上。一二五为法于下。以法头一呼。实定身(一一一)除之。(一二二○一五五。)身得一。实馀十七。又定身(一八八)而除之。(二八十六○五八四十。)身得八。实馀七。又定身(一五五)而除之。(二五十○五五二十五。)身得五。实馀七五。又定身(一六六)而除之。(二六十二○五六三十。)恰尽。官仓籴米四百五十五石一十一斗四升。每石耗一斗二升。问元籴米几何。
答曰。四百二十二石。
术曰。四五五七六(石下留)为实一。空八(一石并耗石下留)为法。定身而除之。
一法。六八三六四(通斗内子)为实。一六二(一石通斗并耗)为法。除之亦得。
当归二十五斤一十三两。每一斤一十五两易甘草一斤。问甘草几何。
答曰。一十三斤三十一分斤之一十。
术曰。二五八一二五(斤下留)为实。一九三七五(斤下留)为法。除之得一十三斤。实馀六二五之分命之。
四率法(六题)
四率法者。西学之比例也。其用浩博。令耴贸易小数。以资恒用。所谓异乘同除是也。二率与三率。相乘为实。一率为法。除之得四率。
原钱二两五钱。贸米七斗五升。令钱七十五两。问米几何。
答曰。二百二十五斗。
术曰原钱二两五钱为一率。原米七斗五升为二率。令钱七十五两为三率。二率三率相乘(钱米相乘为异乘)为实。一率为法除之。(以钱除钱为同除。)得四率。(三率乘二率。则斗起于两。至十而位十。过上则位百。一率除实则起两于斗。至百而位百。○斗两相代。二两为单。当位而位百。亦可。)
原米七斗五升价钱二两五钱。今米二百二十五斗。问价钱几何。
答曰。七十五两。
术曰。原米为一率。原钱为二率。今米为三率。
原钱七十五两。贸米二百二十五斗。今钱二两五钱。问米几何。
答曰。七斗五升。
湛轩书外集卷四 第 185H 页
 术曰。原钱为一率。原米为二率。今钱为三率。
术曰。原钱为一率。原米为二率。今钱为三率。原米二百二十五斗价钱七十五两。今米七斗五升。问价钱几何。
答曰。二两五钱。
术曰。原米为一率。原钱为二率。今米为三率。
原夫工七十五人。八日垦田一百五十亩。今夫工一百五十人。一十六日。问垦田几何。
答曰。六百亩。
术曰。原夫工乘八日。得六百人为一率。原田一百五十亩为二率。今夫工乘一十六日。得二千四百人为三率。
原白木一百二十疋运九十里。雇钱七钱五分。今白木二千四百疋运一千八百里。问雇钱几何。
答曰。三百两。
术曰。原木乘原运为一率。原雇钱为二率。今木乘今运为三率。
一率一十万。欲作相连比例率。使一率并四率之数。与二率三倍之数适等。问二率三率四率各为数几何。(益实归除法。)
答曰。二率三万四千七百二十九。
三率一万二千零六十一。
四率四千一百八十七。
术曰。求二率则一率自乘。再乘(一千万亿)为甲实。一率自乘。又三因(三百亿)为甲法。以除甲实为甲得。(三万。)自乘再乘。(二十七万亿。)益于甲实。为甲益实。(一千零二十七万亿。)甲得乘甲法为甲乘。(九百万亿。)反减甲益实。馀(一百二十七万亿)为乙实。甲法除乙实为乙得。(四千。)并甲得(三万四千)自乘再乘。(三十九万三千零四十亿。)益于甲实。为乙益实。(一千零三十九万三千零四十亿。)乙得乘甲法为乙乘。并甲乘反减乙益实。馀(一十九万三千零四十亿)为丙实。甲法除丙实为丙得。(七百○原得六百零以零数太多进为七百。)并甲乙两得。(三万四千七百。)自乘再乘。(四十一万七千八百一十九亿二千三百万。)益于甲实。为丙益实。(一千零四十一万七千八百一十九亿七千三百万。)丙得乘甲法为丙乘。并甲乙两乘。反减丙益实。
湛轩书外集卷四 第 185L 页
 馀(七千八百一十九亿二千三百万)为丁实。甲法除丁实为丁得。(二十。)并甲乙丙三得。(三万四千七百二十。)自乘再乘。(四十一万八千五百四十二亿一千零四万八千。)益于甲实。为丁益实。(一千零四十一万八千五百四十二亿一千零四万八千。)丁得乘甲法为丁乘。并甲乙丙三乘。反减丁益实。馀(二千五百四十二亿一千零四万八千)为戊实。甲法除戊实为戊得。(九○原得八零数太多进为九。)并甲乙丙丁四得。(三万四千七百二十九。)自乘再乘。(四十一万八千八百六十七亿六千六百四十万零二千四百八十九。)益于甲实。为戊益实。(一千零四十一万八千八百六十七亿六千六百四十万零二千四百八十九。)戊得乘甲法为戊乘。并甲乙丙丁四乘。反减戊益实。(馀一百六十七亿六千六百四十万零二千四百八十九不尽。)共除得三万四千七百二十九。求三率则二率自乘。一率除之。
馀(七千八百一十九亿二千三百万)为丁实。甲法除丁实为丁得。(二十。)并甲乙丙三得。(三万四千七百二十。)自乘再乘。(四十一万八千五百四十二亿一千零四万八千。)益于甲实。为丁益实。(一千零四十一万八千五百四十二亿一千零四万八千。)丁得乘甲法为丁乘。并甲乙丙三乘。反减丁益实。馀(二千五百四十二亿一千零四万八千)为戊实。甲法除戊实为戊得。(九○原得八零数太多进为九。)并甲乙丙丁四得。(三万四千七百二十九。)自乘再乘。(四十一万八千八百六十七亿六千六百四十万零二千四百八十九。)益于甲实。为戊益实。(一千零四十一万八千八百六十七亿六千六百四十万零二千四百八十九。)戊得乘甲法为戊乘。并甲乙丙丁四乘。反减戊益实。(馀一百六十七亿六千六百四十万零二千四百八十九不尽。)共除得三万四千七百二十九。求三率则二率自乘。一率除之。求四率则二率三倍之内。减一率。(又三率自乘。二率除之。)
一率一十万。欲作相连比例率。使一率并四率之数。与两二率并三率之数适等。问二率三率四率各为数几何。(益实兼减实归除法。)
答曰。二率四万四千五百零四。
三率一万九千八百零六。
四率八千八百一十四。
术曰。求二率则一率自乘。再乘(一千万亿)为甲实。一率自乘。又二因(二百亿)为甲法。以除甲实为甲得。(四万○原得五万为尽数因减实大于益实退为四万。)自乘再乘。(六十四万亿。)益于甲实。为甲益实。(一千零六十四万亿。)复以甲得自乘。(一十六亿。)以一率再乘。(一百六十四万亿。)反减甲益实。馀(九百零四万亿)为甲正实。甲得乘甲实为甲乘。(八百万亿。)反减甲正实。馀(一百零四万亿)为乙实。甲法除乙实为乙得。(四千○原得五千退为四千。)并甲得(四万四千)自乘再乘。(八十五万一千八百四十亿。)益于甲实。为乙益实。(一千零八十五万一千八百四十亿。)复以甲乙两得(四万四千)自乘。(一十九亿三千六百万。)以一率再乘。(一百九十三万六千亿。)反减乙益实。馀(八百九十一万五千八百四十亿)为乙正实。乙得乘甲法为乙乘。(八十万亿。)并甲乘反减乙正实。馀(一千一万五千八百四十亿)为丙实。甲法除丙实为丙得。(五百。)并甲乙两得。(四万四千五百。)自乘再乘。(八十八万一千二百一十一亿二千五百万。)益于甲实。为丙益实。(一千零八十八万一千二百一十一亿二千五百万。)复以甲乙丙三得(四万四千五百)自乘。(一十九亿八千零二十五
湛轩书外集卷四 第 186H 页
 万。)以一率再乘。(一百九十八万零二百五十亿。)反减丙益实。馀(八百九十万零九百六十一亿二千二百万)为丙正实。丙得乘甲法为丙乘。(一十万亿。)并甲乙两乘。反减丙正实。馀(九百六十一亿二千五百万)为丁实。甲法除之。上少下多。乃以丁为空。次一位除之为戊得。(四。)并甲乙丙丁四得。(四万四千五百零四。)自乘再乘。(八十八万一千四百四十八亿九千零一十三万六千零六十四。)益于甲实。为戊益实。(一千零八十八万一千四百四十八亿九千零一十三万六千零六十四。)复以甲乙丙丁四得自乘。(一十九亿八千零六十万零六千零一十六。)以一率再乘。(一百九十八万零六百零六亿零一百六十万。)反减戊益实。馀(八百九十万零八百四十二亿八千八百五十三万六千零六十四)为戊正实。戊得乘甲法为戊乘。(八百亿。)并甲乙丙丁四乘。反减戊正实。(馀四十二亿八千八百五十三万六千零六十四不尽。)共除得四万四千五百零四。
万。)以一率再乘。(一百九十八万零二百五十亿。)反减丙益实。馀(八百九十万零九百六十一亿二千二百万)为丙正实。丙得乘甲法为丙乘。(一十万亿。)并甲乙两乘。反减丙正实。馀(九百六十一亿二千五百万)为丁实。甲法除之。上少下多。乃以丁为空。次一位除之为戊得。(四。)并甲乙丙丁四得。(四万四千五百零四。)自乘再乘。(八十八万一千四百四十八亿九千零一十三万六千零六十四。)益于甲实。为戊益实。(一千零八十八万一千四百四十八亿九千零一十三万六千零六十四。)复以甲乙丙丁四得自乘。(一十九亿八千零六十万零六千零一十六。)以一率再乘。(一百九十八万零六百零六亿零一百六十万。)反减戊益实。馀(八百九十万零八百四十二亿八千八百五十三万六千零六十四)为戊正实。戊得乘甲法为戊乘。(八百亿。)并甲乙丙丁四乘。反减戊正实。(馀四十二亿八千八百五十三万六千零六十四不尽。)共除得四万四千五百零四。求三率。则二率自乘。一率除之。
求四率。则二率倍之。并三率内减一率。(又三率乘。二率除之。)
连比例首率一十万。欲分为中末两率。问各为数几何。(理分中末线。)
答曰。中率六万一千八百零三。
末率三万八千一百九十七。
术曰。求中率则首率自乘为长方积。仍以首率为长广。较以带纵较数直方开之。
求末率。则中率反减首率。
又首率为股。首率折半为胊。推得弦内减勾馀为中率。反减首率。为末率。
之分法(二十六题)
除法之有畸零者之分以通之。法数为分母。实馀为分子。通分以还原。合分以稽数。约分而就简。古人云。不患乘除而患通分。盖筹学之奥妙也。
钱四两。令三人分之。问人得钱几何。
答曰。一两三钱三分三分分之一。
术曰。四为实。以三归之。得一三。三馀一畸零。至于无穷。故以法为分母。
湛轩书外集卷四 第 186L 页
 实馀为分子而命之。
实馀为分子而命之。甲出钱二分两之一。乙出钱五分两之二。问合钱几何。
答曰。一十分两之九。
术曰。两分母相乘。(二五十。)得一十。为合分母。两分子互乘两母。(一五五○二二四。)并得九。为合分子。
甲出米三分斗之二。乙出米五分斗之四。问合米几何。
答曰。一斗十五分斗之七。
术曰。两分无相乘。(三五十五。)为合分母。两分子互乘两母。(二五十○三四十二。)并得二十二。为合分子。子多于母。以母除子为斗。馀分为子。
甲出银二分斤之一。乙出银四分斤之三。丙出银九分斤之八。问合银几何。
答曰。二斤三十六分斤之五。
术曰。三分母转乘。先以甲母乘乙母(二四八)得八。再以乘丙母(八九七十二)得七十二。为合分母。三分子互转乘两母。甲子转乘。(一四四○四九三十六。)得三十六。乙子转乘。(二三六○六九五十四。)得五十四。丙子转乘。(二八十六○一四四○四六二十四。)得六十四。三子并得一百五十四。为合分子。子多于母。以母除子为斤。馀分为子约之。
麻布四十五疋。每疋价钱三分两之二。问合钱几何。
答曰。三十两。
术曰。布疋乘分子(无通分故只▣分子)为实。分母为法。除之。
粟三十二斗七分斗之五。每斗价钱三分。问钱几何。
答曰。九钱八分七分分之一。
术曰。粟通分内子。乘斗价为实。分母除之。不满法者命之。
南草一十斤三分斤之一。每斤价钱一钱九分钱之七。问合价钱几何。
答曰。一两八钱三分二十七分分之一十九。
术曰。南草通分内子斤价。通分内子相乘为实。两分母相乘为法。除之。
湛轩书外集卷四 第 187H 页
 原钱二两三分两之一。贸米一十四斗。今钱七两。问米几何。(以下四率。)
原钱二两三分两之一。贸米一十四斗。今钱七两。问米几何。(以下四率。)答曰。四十二斗。
术曰。原钱通内为一率。原米为二率。今钱乘原钱分母为三率。
原米一十四斗价钱二两三分两之一。今米四十二斗。问价钱几何。
答曰。七两。
术曰。原米乘原钱分母为一率。原钱通内为二率。今米为三率。
原钱七两贸米四十二斗。今钱二两三分两之一。问米几何。
答曰。一十四斗。
术曰。原钱乘今钱分母为一率。原米为二率。今钱通内为三率。
原米四十二斗价钱七两。今米一十四斗。问价钱几何。
答曰。二两三分两之一。
术曰。原米为一率。原钱为二率。今米为三率。
原开河三日三分日之一。开积四十五尺五分尺之一。今五十日。问积几何。
答曰。六百七十八尺。
术曰。原日通内乘原积分母为一率。原积通内为二率。今日乘原日分母为三率。
原开河积四十五尺五分尺之一。用日三日三分日之一。今开积六百七十八尺。问用日几何。
答曰。五十日。
术曰。原开积通内乘原日分母为一率。原日通内为二率。今开积乘原开积分母为三率。
原开河五十日积六百七十八尺。今三日三分日之一。问开积几何。
答曰。四十五尺五分尺之一。
术曰。原日乘今日分母为一率。原开积为二率。今日通内为三率。
原开河积六百七十八尺。用日五十日。今开积四十五尺五分尺之一。问
湛轩书外集卷四 第 187L 页
 用日几何。
用日几何。答曰。三日三分日之一。
术曰。原开积乘今开积分母为一率。原日为二率。今开积通内为三率。
原车行三十五里三分里之二。雇价二两七分两之六。今车行九十六里九分里之八。问雇价钱几何。
答曰。七两二千二百四十七分两之一千七百一十一。
术曰。原车行通内乘原雇钱分母。转乘今车行分母为一率。原雇钱通内为二率。今车行通内乘原车行分母为三率。
原车行九十六里九分里之八。雇钱七两二千二百四十七分两之一千七百一十一。今车行三十五里三分里之二。问雇钱几何。
答曰。二两七分两之六。
术曰。原车行通内乘今车行分母。转乘原雇钱分母为一率。原雇钱通内为二率。今车行通内乘原车行分母为三率。
原雇钱二两七分两之六。车行三十五里三分里之二。今雇钱七两二千二百四十七分两之一千七百一十一。问车行几何。
答曰。九十六里九分里之八。
术曰。原雇钱通内乘今雇钱分母。转乘原车行分母为一率。原车行通内为二率。今雇钱通内乘原雇钱分母为三率。
原雇钱七两二千二百四十七分两之一千七百一十一。车行九十六里九分里之八。今雇钱二两七分两之六。问车行几何。
答曰。三十五里三分里之二。
术曰。原雇钱通内乘今雇钱分母。转乘原车行分母为一率。原车行通内为二率。今雇钱通内乘原雇钱分母为三率。
正方面积一十尺。问每方尺几何。(以下开方之分。)
答曰。三尺七分尺之一强。
术曰。置为实平方开之馀实一尺。不尽倍商。(商为方倍之为两方。)添八廉一。(为两方之
湛轩书外集卷四 第 188H 页
 隅角。)共七为分母。实馀一为分子。(廉乘商。加方添廉为分母。亦得。○开方之分。可见大较。终有盈朒。实非精率。还原则原尺自乘。添入馀尺乃准。)
隅角。)共七为分母。实馀一为分子。(廉乘商。加方添廉为分母。亦得。○开方之分。可见大较。终有盈朒。实非精率。还原则原尺自乘。添入馀尺乃准。)正方面积四万五千六百七十八尺。问每方尺几何。
答曰。二百一十三尺四百二十七分尺之三百九。
术曰。置积为实平方开之馀实三百九尺。倍商添廉为分母。实馀为分子。
正立方积二十八尺。问每方尺几何。
答曰。三尺三十七分尺之一。
术曰。置积为实立方开之馀实一尺。商自乘。(商为一方线自乘。为一方面。)三因之。(为三方面。)得二十七。又三因之商。(商为一方三因之为三方。)得九。并之添廉一。(为三方之隅角。)共三十七为分母。实馀一为分子。(廉乘商加隅。隅乘商加方。三因商并方添廉为分母。亦得。)
正立方积一万五千七百三十六尺。问每方尺几何。
答曰。二十五尺一千九百五十一分尺之一百一十一。
术曰。置积为实立方开之馀实一百一十一尺。商自乘。又三因之。得一千八百七十五。又三因商。得七十五。并之添廉为分母。实馀为分子。
句股面句八十二尺股二百五十七尺。问弦尺几何。
答曰。二百六十九尺五百三十九分尺之四百一十二。
术曰。句股各自乘。并之得七万二千七百七十三平方开。馀实四百一十二。倍商添廉为母。实馀为分子。
(附)约分法(二题)
子母相减得等数(等数得一者无约分)为法。除原母为约母。除原子为约子。
有三十六分之一十二。问约之为几何。
答曰。三分之一。
术曰。以原分子减原分母。得一十二。为子母等数。再以原分母为实。等数为法。除之为约分母。原分子为实。等数为法。除之为约分子。
有七十二分六十四。问约之为几何。
湛轩书外集卷四 第 188L 页
 答曰。九分之八。
答曰。九分之八。术曰。以子减母母馀八。再以母减子得八为法。除原母为约母。除原子为约子。
量田法(五题)
量田多形。本国惟用五种。凡不等之形。作各形。故有二作三作之名。其求积之法。各有其率。
方田一亩九十六尺。问积几何。
答曰。九千二百一十六尺。
术曰。自乘。
直田长四十九尺广二十四尺。问积几何。
答曰。一千一百七十六尺。
术曰。长广相乘。
句股田。句三十六尺。股六十二尺。问积几何。
答曰。一千一百一十六尺。
术曰。句股相乘折半。
圭田长九十三尺。广三十四尺。问积几何。
答曰。一千五百八十一尺。
术曰。长广相乘折半。
梯田东广四十六尺。西广八十六尺。长一百二十五尺。问积几何。
答曰。八千二百五十尺。
术曰。并二广折半乘长。
先乘后折半亦得。
(附)解负法(一题)
国典。以六等分田。旧法。六等各有量尺。长短有差。积一百尺为税一负。中古均其尺别为法。以十五差之。其率二等八五。三等单七。四等五五。五等单四。六等二五。置原积。各以等率乘之为实税。六把以上升为束。
湛轩书外集卷四 第 189H 页
 五把以下乘之。假如田积一万尺。一等为一结。二等为八十五负。三等为七十负。四等为五十五负。五等为四十负。六等为二十五负。
五把以下乘之。假如田积一万尺。一等为一结。二等为八十五负。三等为七十负。四等为五十五负。五等为四十负。六等为二十五负。方田一面一百二十八尺。问都积及六等各税几何。
答曰。都积一万六千三百八十四尺。
一等。一结六十三负八束。
二等。一结三十九负三束。
三等。一结一十四负七束。
四等。九十负一束。
五等。六十五负五束。
六等。四十一负。
术曰。方面田自乘。得都积一等。依本税。二等以下。各以率乘之。
衰分法(五题)
衰分者。分等差配之法。各等乘差数而并之曰抛差。反减原数。以馀为实。以各等共户为法。除得末户该分。各以率乘之。
粜米九百四十七斗六升。民户分三等差配之。大户多中户三斗八升。中户多小户三斗五升。大户四十二。中户三十六。小户二十五。问每等及每户该分各几何。
答曰。大户五百一十六斗六升。每户一十二斗三升。
中户三百六斗。每户八斗五升。
小户一百二十五斗。每户五斗。
术曰。置大户并两多(七斗三升)乘之。得三百六斗六升。置中户以多(三斗五升)乘之。得一百二十六斗。并之得四百三十二斗六升。为抛差反减原米。馀五百一十五斗为实。以共户(一百三)除之。得五斗为小户该分。各以率添之。各以户乘之。
还粟九千六百三十石一十四斗。民户分四等。各差四斗。大户三千七百二。中户二千九百四十七。小户二千四百九十三。残户一千九百四十。问
湛轩书外集卷四 第 189L 页
 每等及每户该分各几何。
每等及每户该分各几何。答曰。大户一石三斗。共四千四百四十二石六斗。
中户十四斗。共二千七百五十石八斗。
小户一十斗。共一千六百六十二石。
残户六斗。共七百七十六石。
术曰。大户三因之。中户二因之。小户一因之。并得一万九千四百九十三。以差四斗乘之。得七万七千九百七十二为抛差。还粟通内。内减抛差。馀六万六千四百九十二为实。以四等共户(一万一千八十二)除之。得六斗为残户该分。各加差数。各乘其户。
赈谷五千二百八十三石九斗。饥户分六等。各差一斗五升赈之。甲等六百六十六户。乙等五百五十五户。丙等四百四十四户。丁等三百三十三户。戊等二百二十二户。己等一百一十一户。四朔分赈。原谷恰尽。问每等及每户每朔该分各几何。
答曰。甲等一十一斗。共四百八十八石六斗。
乙等九斗五升。共三百五十一石七斗五升。
丙等八斗。共二百三十六石一十二斗。
丁等六斗五升。共一百四十四石四斗五升。
戊等五斗。共七十四石。
己等三斗五升。共二十五石一十三斗五升。
术曰。甲等五因之。(分六等而将求己等该分。故五因之。若分五等则当四因之。馀仿此。)乙等四因之。丙等三因之。丁等二因之。戊等一因之。并五数共得七千七百七十。以差一斗五升乘之。得一万一千六百五十五为抛差。原谷通内四归之。得一万九千八百一十三斗五升。(此每朔六等共谷之数。)内减抛差。馀八千一百五十八斗五升为实。以六户共户(二千三百三十一)为法。除之得三斗五升为己等。每户每朔该分。各加差数。各乘其户。各以四因之。
北京至广东边徼。设一百站。第一站。置驿马二百匹。第二站以下。挨次各
湛轩书外集卷四 第 190H 页
 减一匹。问合马匹几何。
减一匹。问合马匹几何。答曰。一万五千五十匹。
术曰。一百站。减第一站以一匹。因之以减第一站马匹馀一百。一匹为第一站百马匹。并入第一站数。以乘一百站。得数折半。
粜米四百八十斗。分大中小残独五等人。户欲大中二户合分。与小残独三户合分等数。问各该分几何。
答曰。大户一百二十八斗。
中户一百一十二斗。
小户九十六斗。
残户八十斗。
独户六十四斗。
术曰。置总米为实。另以虚衰数一二三四五。分配五等。户大五中四小三残二独一。乃并大五中四得九。又并小三残二独一得六。以减九馀三。却于前五衰内。各增三。大得八。中得七。小得六。残得五。独得四。并得三十为法。除实得一十六斗。为各户衰数。以乘各户虚衰增数。得各户该分。
盈朒法(五题)
盈朒者。即所谓盈不足也。隐其数。作盈朒而索之。各有其率。
有人买物。每人出钱五两。盈六两。每人出钱三两。朒四两。问人钱各几何。(盈不足。)
答曰。人五。
钱一十九两。
术曰。盈朒互乘。以出五乘朒四。出三乘盈六。并得三十八两为钱实。并盈朒共十两为人实。两出相减。馀二两为法。除人实得人数。除钱实得钱数。
有人买物。人出钱三两五钱。盈六两。人出钱三两三钱。盈二两八钱。问人
湛轩书外集卷四 第 190L 页
 钱各几何。(两盈。)
钱各几何。(两盈。)答曰。人一十六。
钱五十两。
术曰。互乘相减。馀十两为钱实。两盈相减为人实。两出馀为法。除人实得人数。除钱实得钱数。
有人买物。人出钱五两。朒四两。人出钱五两四钱。朒二两。问人钱各几何。(两不足。)
答曰。人五。
钱二十九两。
术曰。同两盈。
有人买物。人出钱二两五钱。盈六两。人出钱三两三钱。适足。问人钱各几何。(盈适足。)
答曰。人三十。
钱六十九两。
术曰。盈六两为人实。两出相减。馀二钱为法。除之得人数。各以每人二两三钱。乘之得钱数。
有人买物。人出钱七两。不足一十四两。人出钱九两。适足。问人钱各几何。(不足适足。)
答曰。人七。
钱六十三两。
术曰。同盈适足。
面积法(五题)
面积者。平面之积。量田之类也。长一尺广一尺谓之积一尺。如口字是也。长二尺广二尺谓之积四尺。如田字是也。长三尺广三尺谓之积九尺。如井字是也。长二尺广一尺谓之积二尺。如日字是也。长三尺广一尺谓之积三尺。如目字是也。长三尺广二尺谓之积六尺。如用字是也。
湛轩书外集卷四 第 191H 页
 正方面一方一十九尺。问积几何。
正方面一方一十九尺。问积几何。答曰。三百六十一尺。
术曰。自乘加方田法。
长方面长三十五尺。广一十八尺。问积几何。
答曰。六百三十尺。
术曰。长广相乘。如直田法。
圆面周八十四尺。径二十八尺。问积几何。
答曰。五百八十八尺。
术曰。周径各折半相乘。又周自乘十二除之。又径自乘。更以七五乘之。又周径相乘四归之。又径自乘。三因之四归之并得。
弧矢面。弦长五十六步。矢阔一十八步。问积几何。
答曰。七百五十六步。
术曰。弦矢相乘。四归之三因之。
三角面。每方一十四尺。问积几何。
答曰。八十四尺。
术曰。置尺六因之七归之得中。长一十二尺。更以面尺折半以乘之。
体积法( 十八题)
体积者。物之有长有广兼有高厚之形也。长一尺广一尺高一尺谓之积一尺。正方形如斗是也。长方形如升是也。正圆形如球是也。长圆形如竹筒是也。
正方体。每面二十五尺。问积几何。
答曰。一万五千六百二十五尺。
术曰。再自乘。(先以廿五乘廿五得六百廿五尺。再以廿五乘六百廿五尺。乃合问。)
长方体。长二十八尺。广一十五尺。高一十八尺。问积几何。
答曰。七千五百六十尺。
术曰。长广相乘又乘高。(先以一十五乘二十八。得四百二十尺。再以一十八乘四百二十尺。乃合问。○乘用加法可。)
湛轩书外集卷四 第 191L 页
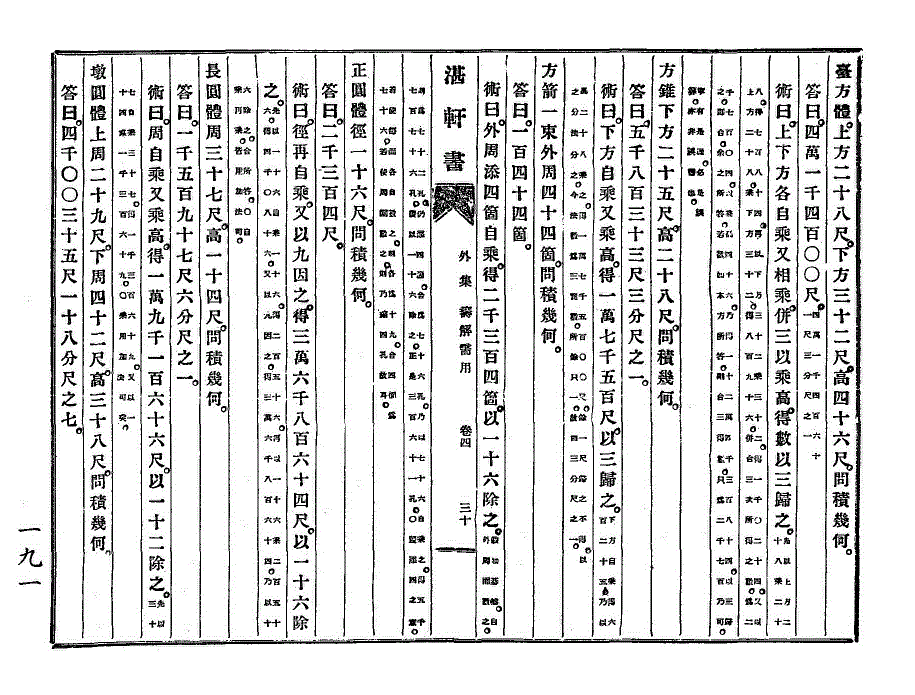 台方体。上方二十八尺。下方三十二尺。高四十六尺。问积几何。
台方体。上方二十八尺。下方三十二尺。高四十六尺。问积几何。答曰。四万一千四百〇〇尺。(四万一千四百六十一尺三分尺之一。)
术曰。上下方各自乘又相乘。并三以乘高。得数以三归之。(先以上方二十八乘二十八。得七百八十四。再以下方三十二乘三十二。得一千〇二十四。又以上方二十八。乘下方三十二。得八百九十六。并合三次所得之数。为二千七百〇四。以乘高四十六。乃得一十二万四千三百八十四。以三归之。即合。余之所答。若欲如本方所答。则合三得数。只为二千七百乃可。宁有是理。必是误算。亦非误书也。)
方锥下方二十五尺。高二十八尺。问积几何。
答曰。五千八百三十三尺三分尺之一。
术曰。下方自乘又乘高。得一万七千五百尺。以三归之。(下方自乘得六百二十五。乃以高二十八乘之。得一万七千五百〇〇尺。馀一尺归之不得。以之分法分之。今法数为三实数。所馀只一。故曰三分尺之一。)
方箭一束外周四十四个。问积几何。
答曰。一百四十四个。
术曰。外周添四个自乘。得二千三百四个。以一十六除之。(假如棋盘。自外周而数之。则为七十二孔。仍添四个。合为七十六孔。乃以七十六自乘之。得五千七百七十六孔。复以一十六除之。正是三百六十一孔。○盖添四之意。若使每面各自数之。则各为十九。合四面为七十六。若使周围数之。则乃缩四孔故耳。)
正圆体径一十六尺。问积几何。
答曰。二千三百四尺。
术曰。径再自乘。又以九因之。得三万六千八百六十四尺。以一十六除之。(先以一十六自乘一十六。得二百五十六。再以一十六乘二百五十六。得四千〇八十六。又以九因之。得三万六千八百六十四。乃以十六除之。合所答。○自乘再乘。皆用加法可。)
长圆体周三十七尺。高一十四尺。问积几何。
答曰。一千五百九十七尺六分尺之一。
术曰。周自乘又乘高。得一万九千一百六十六尺。以一十二除之。(先以三十七自乘三十七。得一千三百六十九。又以一十四乘一千三百六十九。○乘用加法可矣。)
墩圆体上周二十九尺。下周四十二尺。高三十八尺。问积几何。
答曰。四千〇〇三十五尺一十八分尺之七。
湛轩书外集卷四 第 192H 页
 术曰。上下周各自乘又相乘。并三以乘高。得一十四万五千二百七十四尺。以三十六除之。(上周自乘。得八百四十一。下周得一千七百六十四。上下相乘。一千二百一十八。并三合为三千八百二十三。)
术曰。上下周各自乘又相乘。并三以乘高。得一十四万五千二百七十四尺。以三十六除之。(上周自乘。得八百四十一。下周得一千七百六十四。上下相乘。一千二百一十八。并三合为三千八百二十三。)圆锥下周五十四尺。高三十七尺。问积几何。
答曰。二千九百九十七尺。
术曰。下周自乘又乘高。得一十万七千八百九十二尺。以三十六除之。(下周得二千九百一十六。○除法。用撞归法。见三无除作九三是也。)
圆箭一束外周五十四个。问积几何。
答曰。二百七十一个。
术曰。外周添六个。仍乘外周。得三千二百四十。以一十二除之。加心箭一个。(外周添六为六十。以六十乘乘五十四。得三千二百四十。除得二百七十个。更加一个。始合答。○乘用因法乃可。定位不可不审。)
积粟长一十五石。广九石。高一十七石。问积几何。(以下杂体积。)
答曰。二千二百九十五石。
术曰。长广相乘又乘高。(置一十五石。以九因之。得一百三十五石。以一十七乘之。合答。○亦用加法甚便。)
平地聚粟。下周二十五尺五寸。高八尺。问积几何。
答曰。一百四十四尺五寸。
术曰。下周自乘又乘高。得五千二百二尺。以三十六除之。(二十五五乘。二十五五得。六百五十〇二寸五分。以八因之。得五千二百〇二尺〇〇。除之合答。)
倚壁聚粟。下周一十二尺七寸五分。高八尺。问积几何。
答曰。七十二尺二寸五分。
术曰。周自乘又乘高。得一千三百尺五寸。以一十八除之。(以下周一十二尺七寸五分。乘一十二尺七寸五分。得一百六十二尺五寸六分二里五毫。以高八尺因之。得一千三百〇〇尺五寸。○除用撞归法。即见一无除作九一。又九一下还一者也。次用归除。合所答。○十八除之者。盖用三十六之折半也。)
内角聚粟。下周六尺三寸七分五釐。高八尺。问积几何。
答曰。三十六尺一寸二分五釐。
术曰。周自乘又乘高。得三百二十五尺一寸二分五釐。以九除之。(以下周自
湛轩书外集卷四 第 192L 页
 乘得四十〇尺六寸五分〇六毫二丝五忽。乃乘高得三百二十五尺一寸二分五里。除之合所答。○除用归除法。)
乘得四十〇尺六寸五分〇六毫二丝五忽。乃乘高得三百二十五尺一寸二分五里。除之合所答。○除用归除法。)筑城。上广一十八尺。下广三十六尺。高四十六尺。长一万一千五百二十尺。问积几何。
答曰。一千四百三十万七千八百四十尺。
术曰。并上下广折半。(梯田求积之意。)以乘高又乘长。(并上下广合五十四尺内折半。则为二十七尺。以廿七尺乘高四十六尺。得千二百四十二尺。以乘长。即合答。)
筑垣。上广三尺。下广四尺。高九尺。长三千八百五十尺。问积几何。
答曰。一十二万一千二百七十五尺。
术曰。并两广折半。以乘高又乘长。(并两广合七尺内折半。为三尺五寸。以三尺五寸乘高。得三十一尺五寸。以乘长合答。)
开河。广二十六尺。下广一十八尺。深一十五尺。长五千四百尺。问积几何。
答曰。一百七十八万二千尺。
并两广折半。以乘深又乘长。(并两广合四十四折半二十二。以二十二乘深。得三百三十。以乘长合答。)
筑堤。上广六尺四寸。下广一十二尺四寸。高九尺二寸。长三千八百尺。问积几何。
答曰。三十二万八千六百二十四尺。
术曰。同筑垣。(并两广合一十八尺八寸折半为九尺四寸。以九尺四寸乘高九尺二寸。得八百六十四尺八寸。乃乘长合所答。○盖此定位。或为初学之疑难。其乘高时则法实尾数皆零。故法首数起于实之寸。故得数首位。当为百尺。乘长时则法首数起于实之尺。故得数首位当为三十万也。此等处。不可不先审定位。)
开方法(十四题)
开方多术。平方立方。为其要领。面积求方。为开平方。体积求方。为开立方。平方者。自乘之还原。立方者。再乘之还原。平方为四格。商为上格。实为次格。又次格为方。最下格为廉。廉起于实。单数下进退。常超一位。先定商于上。以廉乘商为方。商方相乘除实。乃以廉乘商加于方。一退廉再退续。商如前。立方为五格。方下廉上。别有隅格廉进退超二位。以廉乘商为隅。隅商相乘为方商方相乘除实。乃以廉乘商加于隅。隅商相
湛轩书外集卷四 第 193H 页
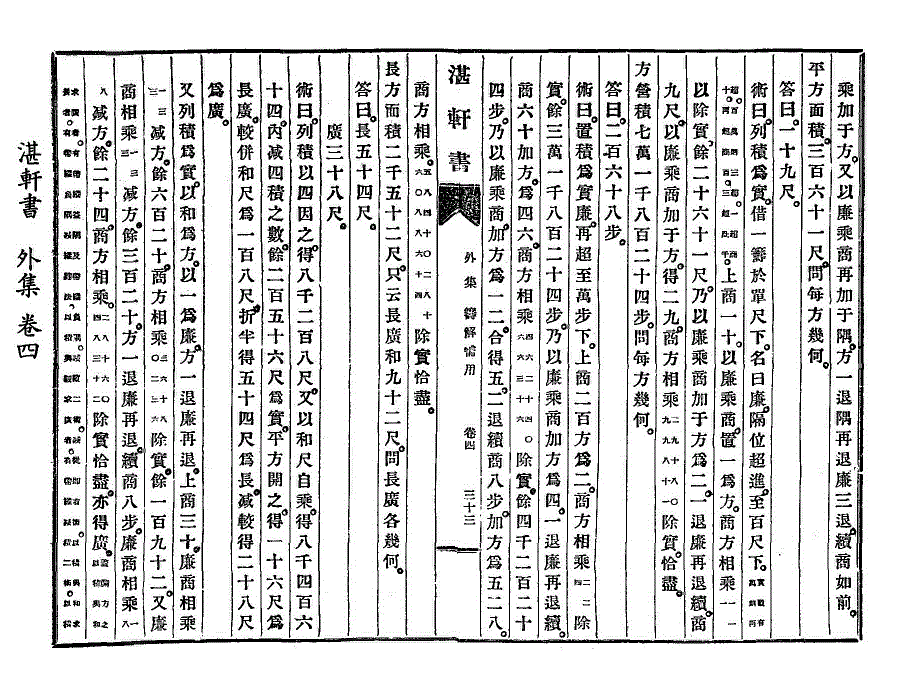 乘加于方。又以廉乘商再加于隅。方一退隅再退廉三退。续商如前。
乘加于方。又以廉乘商再加于隅。方一退隅再退廉三退。续商如前。平方面积。三百六十一尺。问每方几何。
答曰。一十九尺。
术曰。列积为实。借一筹于单尺下。名曰廉。隔位超进。至百尺下。(实数有万则再超。百万则三超。一超商十。再超商百。三超商千。)上商一十。以廉乘商。置一为方。商方相乘(一一一)以除实。馀二十六十一尺。乃以廉乘商加于方为二。一退廉再退续。商九尺。以廉乘商加于方。得二九。商方相乘(二九十八○九九八十一)除实。恰尽。
方营积七万一千八百二十四步。问每方几何。
答曰。二百六十八步。
术曰。置积为实廉。再超至万步下。上商二百方为二。商方相乘(二二四)除实。馀三万一千八百二十四步。乃以廉乘商加方为四。一退廉再退续。商六十加方。为四六。商方相乘(四六二十四○六六三十六)除实。馀四千二百二十四步。乃以廉乘商。加方为一二。合得五。二退续商八步。加方为五二八。商方相乘(五八四十○二八十六○八八六十四)除实恰尽。
长方面积二千五十二尺。只云长广和九十二尺。问长广各几何。
答曰。长五十四尺。
广三十八尺。
术曰。列积以四因之。得八千二百八尺。又以和尺自乘。得八千四百六十四。内减四积之数。馀二百五十六尺为实。平方开之。得一十六尺为长广。较并和尺为一百八尺。折半得五十四尺为长。减较得二十八尺为广。
又列积为实。以和为方。以一为廉。方一退廉再退。上商三十。廉商相乘(一三三)减方。馀六百二十。商方相乘(三六十八○二三六)除实。馀一百九十二。又廉商相乘(一三三)减方。馀三百二十。方一退廉再退。续商八步。廉商相乘(一八八)减方。馀二十四。商方相乘(二八十六○四八三十二)除实恰尽。亦得广。(盖开方之以积与和求广者。有带纵益隅及带纵负隅。减纵二术。减从即有术。以积与和求长者。有带纵负隅减纵翻法。以积与较求广者。有带纵减积二术。以积
湛轩书外集卷四 第 193L 页
 与较求长者。有负纵益积及带减纵二术。此外随变错综。备见诸书。并不具载。)
与较求长者。有负纵益积及带减纵二术。此外随变错综。备见诸书。并不具载。)直营积七万一千八百二十四步。只云长广和六百七十步。问长广各几何。
答曰。长五百三十六步。
广一百三十四步。
术曰。列积四因之。得二十八万七千二百九十六。和步自乘。得四十四万八千九百。内减四积之数。馀一十六万一千六百四为实。平方开之。得四百二为长广。较并和步折半为长。减较为广。
又以减从法求广。则列积为实。以和为方。以一为廉。方再进廉四进。上商一百。廉商相乘(一一一)减方。馀五万七千。商方相乘(一五五○一七七)除实。馀一万四千八百二十四。又廉商相乘(一一一)减方。馀四万七千。方一退廉再退。续商三十。廉商相乘(一三三)减方。馀四千四百。商方相乘(三四十二○三四十二)除实。馀一千六百二十四。又廉商相乘(一三三)减方。馀四千一百。方一退廉再退。续商四步。廉商相乘(一四四)减方。馀四百空六。商方相乘(四四十六○四六二十四)除实恰尽。亦得广。
今有直田积一千四百五十六步。只云长广较三十步。问长广各几何。
答曰。长五十六步。
广二十六步。
术曰。列积为实。以较为方。一为廉。方一进廉再退。上商二十。廉商相乘(一二二)加方。得五百。商方相乘(二五十)除实。馀四百五十六。又廉商相乘(一二二)加方。得七百。方一退廉再退。续商六步。廉商相乘(一六六)加方。得七十六。商方相乘(六七四十二○六六三十六)除实恰尽。得广加较得长。
正圆面积五百八十八尺。问周径各几何。
答曰。周八十四尺。
径二十八尺。
术曰。先求周则列积十二乘之。得七千五十六为实。平方开之。得周三
湛轩书外集卷四 第 194H 页
 归之为径。
归之为径。先求径则四因之三归之。得七百八十四为实。平方开之。得径三因为周。
圆营积七万一千八百二十四步。问周径各几何。
答曰。周九百二十八步三分。(馀一十二步二分五釐一十二分釐之一十一。)
径三百九步四分。(馀二十七步七分三釐。)
术曰。求周则置积十二乘之。得八十六万一千八百八十八为实。平方开之。得周馀一百四十七步一分一釐。十二除之。(还原。)为馀实数。
求径则置积四因之三归之。得九万五千七百六十五步三分步之一。通分内子。(还四因原数。)得二十八万七千二百九十六为实。平方开之。但以分母三为廉。如初商三百。以廉乘商。以九为方。商方相乘以二七除实也。得径尺馀一百一十步九分二釐。三因之四归之。(本以四因三归而得数。故三因四归以还原。)又以分母三归之。(本以通分得数。故归之以还原。)为馀实数。
三角面积八十四尺。只云每面中长和二十六尺。问每面中长各几何。
答曰。每面一十四尺。
中长一十二尺。
术曰。置积倍之。(为长方面积。)又四因之。得六百七十二。和自乘得六百七十六。内减积数馀四尺为实。平方开之。得二尺为面。中较加和。折半得每面尺。减较得中长尺。
三角营积一万四千一百一十二步。只云每面中长和三百四十尺。问每面中长各几何。
答曰。每面一百九十六步。
中长一百四十四步。
术曰。置积倍之。又四因之。得一十一万二千八百九十六。自和乘得一十一万五千六百。内减积数。馀二千七百四为实。平方开之。得五十二步为面。中较加和。折半得面步。减较得中步。
湛轩书外集卷四 第 194L 页
 弧矢面积二百四十尺。只云弦矢和四十八尺。问弦矢各几何。
弧矢面积二百四十尺。只云弦矢和四十八尺。问弦矢各几何。答曰。弦四十尺。
矢八尺。
术曰。置积三归之四因之。(弧矢面为长方面四分之三。)又四因之。得一千二百八十。和自乘。得二千三百四。内减积数。馀一千二十四为实。平方开之。得三十二尺为弦矢。较加和折半。得弦减较得矢。
偃月营积七千八百六十四万三千二百步。只云弦矢和二万九千六百九十六步。问弦矢各几何。
答曰。弦二万五千六百步。
矢四千九十六步。
术曰。置积三归之四因之。又四因之。得四亿一千九百四十三万四百。和自乘。得八亿八千一百八十五万二千四百一十六。内减积数。馀四亿六千二百四十二万二千一十六为实。平方开之。得二万一千五百四步为弦矢。较加和折半。得弦减较得矢。
正立方积一万五千六百二十五尺。问每方几何。
答曰。二十五尺。
术曰。置积为实。借廉一于单尺下。隔二位超进至千尺下。(实数有百万。则再超。一超商十。再超商百。)上商二十。以廉乘商。另置二于廉上为隅。隅商相乘。置四于隅上为方。商方相乘(二四八)以除实。馀七千六百二十五尺。乃以廉乘商加于隅。隅商相乘(二四八)加于方。又以廉乘商。再加于隅。方得一二隅得六。方一退隅再退廉三退。续商五尺加隅为六五。隅商相乘(五六三十○五五二十五)加于方。合为一五二五。商方相乘(一五五○五五二十五○二五十五五二十五)馀实。恰尽。
正方台积九万七千三百三十六步。问每方各几何。
答曰。四十六步。
术曰。置积为实。廉再超至千尺。下上商四十。隅为四。方为一六。商方相乘(一四四○四六二十四)除实。馀三万三千三百三十六步。乃以廉乘商加于隅。
湛轩书外集卷四 第 195H 页
 隅商相乘(四八三十二)加于方。又以廉乘商。再加于隅方。得四八。隅得一二。方一退隅再退廉三退。续商六。加隅为一二六。隅商相乘(一六六○二六十二○六六三十六)加方。为五五六。商方相乘(五六三十○五六三十○五六三十○六六三十六)除实。恰尽。
隅商相乘(四八三十二)加于方。又以廉乘商。再加于隅方。得四八。隅得一二。方一退隅再退廉三退。续商六。加隅为一二六。隅商相乘(一六六○二六十二○六六三十六)加方。为五五六。商方相乘(五六三十○五六三十○五六三十○六六三十六)除实。恰尽。立圆积六万二千二百八尺。问径几何。
答曰。四十八尺。
术曰。置积以一十六乘之。得九十九万五千三百二十八。以九除之。得一十一万五百九十二为实。立方开之。
西洋圆舶积三万六千步。问径几何。
答曰。四十步。
术曰。置积以一十六乘之。以九除之。得六万四千步为实。立方开之。
军营开方法
今有军总一万七千九百五十六人。每人纵横占地四步。问积几何。
答曰。七万一千八百二十四步。
术曰。置军数以四步因之。合问。
今有营积七万一千八百二十四步。欲为方营。问方面步几何。
答曰。二百六十八步。
术曰。置积为实。以一为廉。平方开之。(倍方之法一退者不再倍)合问。
今有营积如上。欲为圆营。问周径各几何。
答曰。径三百零九步四分。(馀二十七步七分三釐。)
周九百二十八步三分。(馀一十二步二分五釐十二分釐之十一。)
术曰。求径者。以圆田术置积数。四因之三归之。得九万五千七百六十五步三分步之一。通分内子。得二十八万七千二百九十六为实。以三为廉。平方开之。合问。馀一百一十步零九分二釐。三因之归之。得八十三步一分九釐。(开方之实。以四因三归而得数。故三因四归。所以还原而求其本也。)以分母三归之。得二十七步七分三釐。(本以通分得数。故亦还原以求本。)为馀实数。
求周者。置积数身外加二。(圆田求周十二乘之。)得八十六万一千八百八十八为
湛轩书外集卷四 第 195L 页
 实。以一为廉。平方开之。合问。馀一百四十七步一分一釐身外减二。(还原求本)为馀实数。
实。以一为廉。平方开之。合问。馀一百四十七步一分一釐身外减二。(还原求本)为馀实数。三廉开方。术曰。列通分数为实。借分母三为廉法。再超至万步下。上商三百。以廉乘商。(三三九。)上置九万为方法。乃命上商除实。(三九二十七。)二十七万馀一万七千二百九十六倍方法。得一十八万。方法再退。(为一千八百。法当一退。以上小下多。故次一位。)商数亦随方而退。(只退其位不降其数。)廉法四退。(方再退故廉亦再超。)至六步下。乃上商九步。(商必从廉间一为百位。此当为零步。)以廉乘商。(三九二十七。)上增二十七步于方法。合得一千八百二十七。乃命上商除实。(一九九○八九七十二○二九十八○七九六十三。)一万六千四百四十三。馀八百五十三。倍增方为五十四。合得一千八百五十四。方商一退。廉法再退。乃上商四分以廉乘商。(三四十二。)上增十二于方法。合得一百八十五步五分二釐。乃命上商除实。(一四四○四八三十二○四五二十○四五二十○二四八。)七百五十二步零八釐。馀一百一十步零九分二釐。(三因径以求周。三归周以求径。亦得。各求之而分数之或差。馀分之不齐也。)
(以径还原自乘。而三因之四归之。得数。以馀数添之。得原积。以周还原自乘。而身外减二得数。以馀数添之得原积。)
今有营积如上。欲为偃月营。问弦矢各几何。
答曰。弦四百三十八步七分。(馀二十六步七分九釐。)
矢二百一十九步三分五釐。
术曰。置积八因之三归之。得一十九万一千五百三十步零三分步之二。通分内子。得五十七万四千五百九十二为实。以分母三为廉。平方开之。合问。馀二百一十四步三分一釐。八归之三因之。又以分母三归之。求矢者折半弦步。
今有营积如上。欲为三角营。问径几何。
答曰。三百七十九步。(馀三步半。)
术曰。置积倍之为实。平方开之。合问。馀七步半之。
杂法(二十一题)
高竿影长三十五尺二寸。傍立短竿长十尺。影长六尺四寸。问高竿长几
湛轩书外集卷四 第 196H 页
 何。
何。答曰。五十五尺。
术曰。高竿影乘长竿长为实。短竿影为法除之。
金毬一只。因无大秤。以小秤称之不足。加锤称得六十七斤。原锤重一斤十两。加锤重一斤四两八钱。问实斤几何。
答曰。一百二十斤九两六钱。
术曰。并两锤重通两。为四十六两八钱。以乘称得数。即六十七斤。此则不通两得三千一百三十五斤六。此为斤下留之六数也。为实。以原锤通两二十六为法除之。(置三千一百三十五斤六。以二十六除之。初用归除得一百二十斤。实馀一十五斤六。则用撞归法。见一无除作九一。六九五十四除之。法退一位。逢二进一十。乃得九两六钱。)
原秤称物。八斤二两。因失去原锤。今欲买锤配之。不知轻重。另将别锤重二斤五两称之。原物只得六斤。问原锤重几何。
答曰。一斤一十一两三钱二分三釐一十三分釐之一。
术曰。只得重通两为九十六两。与别锤重通两为三十七两相乘。得三千五百五十二两为实。以原称重通两一百三十两为法除之。(得二十七两三钱二分三里除之不尽者。实馀一里。以之分法命之。当为一百三十分里之一。而约之取简。故曰一十三分里之一。○二十七两内。以十六两作一斤。馀十一两零。始合答。)
轻秤称重物法。(假如今之药秤。只称得二十两。而有物重过三四十两者。则用此法。○锤轻不能称重物。故以他铁。或钱加于锤上。至于称得重物。为几两然后依术除之。)
大锤知本重法。(今有秤。失其锤。忘其轻重。而曾以其锤称此物。则为八斤二两。今借他锤称此物。则为六斤。当依术乘除。可知本锤重之几何。)
钱一文。日增一倍。至三十日。问为数几何。
答曰。一十亿七千三百七十四万一千八百二十四文。(作钱为一千〇七十三万七千四百一十八两二钱四分。)
术曰。置一文八因之凡十次。(八是三日倍数。○置一文。以八因之。凡十次 因单八○二次六十四。○三次五百一十二○四次四千九十六○五次三万二千七百六十八○六次二十六万二千一百四十四○七次二百九万七千一百五十二○八次
湛轩书外集卷四 第 196L 页
 一千六百七十七万七千二百一十六○九次一亿三千四百二十一万七千七百二十八○十次即合所答此其一法也。)
一千六百七十七万七千二百一十六○九次一亿三千四百二十一万七千七百二十八○十次即合所答此其一法也。)又以三十二。(乃五日倍数。)乘之。凡三次得数。自乘。(三十二三次乘。乃十五日。○置一文以三十二乘之。三次后自乘○三十一。○再次一千二十四○三次三万二千七百六十六。是为得数。以三万二千七百六十六。乘三万二千七百六十六。即合答。此又捷法。)
又以六十四乘之凡五次。(六十四是六日倍数。)并得。(三法俱可。○置一文。以六十四乘之初乘六十四。○再次四千九十六○三次二十六万二千一百四十四。○四次一千六百七十七万七千二百一十六。○五次即合所答。)
三人聚银殖利。甲银八两三钱。乙银六两五钱。丙银四两八钱。今本利并为三十九两二钱。问各该分几何。
答曰。甲银一十六两六钱。
乙银一十三两。
丙银九两六钱。
术曰。以本利并银乘甲银。得三百二十五两三钱六分为实。并三本银。得一十九两六钱。为法除之。得甲分。乙丙仿此。(即异乘同除术。)
米窖方五十二尺。高三十尺。问米斛几何。
答曰。六千七百六十斛。
术曰。方自乘又以高乘之。得八万一千一百二十尺为实。以斛法一十二尺为法除之。(斛法。以长三尺广二尺高二尺积十二尺为率。)
纹银五十两。欲镕作八成。问得银几何。
答曰。六十二两五钱。
术曰。纹银为实。以八成为法除之。
银一十二两五钱。足色金五十两。同鍊作金。问分数几何。
答曰。八成。
术曰。足色金为实。并金银为法除之。
甲银九成二两。乙银七成二两。一垆合镕。问共银成数及甲乙该分几何。
答曰。共银八成四两。
甲该分一两二钱五分。
湛轩书外集卷四 第 197H 页
 乙该分一两七钱五分。
乙该分一两七钱五分。术曰。甲银二两折纹银一两八钱。乙银二两折纹银一两四钱。并得纹银三两二钱。以原银共四两除之。得八成。即以八为法。除甲乙各折。纹银得各。
北京至杭州。四千二百七十五里。马从北京往南。日行一百二十里。船从杭州往北。日行七十里。问船马几日相会。各行里几何。
答曰。二十二日半。
马行二千七百里。
船行一千五百七十五里。
术曰。原里为实。并船马日行里数为法除之。得日数。各以各行里数乘之。得各行都数。
驽马发行七日后。良马赶去六日。行一千一百七十里追及之。问良马驽马每日各行里几何。
答曰。良马日行一百九十五里。
驽马日行九十里。
术曰。以六日除原里。得良马行。并先后日。得一十三。除原里。得驽马行。
径一百尺。问周古率徽率密率新率各几何。
答曰。古率三百尺。
徽率三百一十四尺。
密率三百一十四尺二寸八分五釐七分釐之五。
新率三百一十四尺一寸五分九釐。
术曰。置径三因之。得古率。
置径一百五十七乘之。五十归之。得徽率。
置径二十二乘之。七归之。得密率。
置径三十一万四千一百五十九乘之。一十万归之。得新率。(径一十万尺。周三十一万四千一百五十九尺。为西法新率。)
湛轩书外集卷四 第 197L 页
 方一百尺。问斜弦古率新率各几何。
方一百尺。问斜弦古率新率各几何。答曰。古率一百四十尺。
新率一百四十一尺四寸二分。
术曰。置方七乘之。五归之。得古率。(方五斜七率。)
置方以七尺空七一乘之。五归之。得新率。(依句股率。方五各自乘。并之开方七空七一零。)
正三角每面一百尺。问中长古率新率各几何。
答曰。古率八十五尺七分尺之五。
新率八十六尺六寸二釐七分釐之三。
术曰。置面六因之。七归之。得古率。(面七中方为古率。)
置面以六空六二一七乘之。七归之。得新率。(依句股率。面七为弦。半面三尺五寸为句弦。羃减句羃。馀开方。得六尺空六二一七。)
方田每方六十尺。内有圆田径亦六十尺。问四隅方角剩积各几何。
答曰。二百二十五尺。
术曰。方六十尺再折半。得十五尺。自乘。又方积减圆积。馀九百尺。为方田四角剩积。四归之亦得。
西瓜一枚。正圆中球。任割一面。面径五寸。心厚五分。问西瓜本径几何。(句及股弦较求弦。)
答曰。一尺三寸。
术曰。面径折半为句。自乘为实。心厚为高弦。较为除之。得一尺二寸五。为股加较。
圆球径二尺六寸。任割一面。心厚八寸。问面径几何。
答曰。二尺四寸。
术曰。本径减心厚。以乘心厚为实。开方倍之。
塔前八十五尺。有小方池。人立池上。望塔顶。恰射池心。人目至池为三尺五寸。自足心至池心一尺八寸。问塔高几何。
答曰。一百六十五尺二寸九分寸之七。
湛轩书外集卷四 第 198H 页
 术曰。人目至池三尺五寸为股定。心至池心一尺八寸为小句。池心至塔底八十五尺为大句。小股乘大句。得二百九十七尺五寸为实。小句为法除之。(用镜或水盂亦可。)
术曰。人目至池三尺五寸为股定。心至池心一尺八寸为小句。池心至塔底八十五尺为大句。小股乘大句。得二百九十七尺五寸为实。小句为法除之。(用镜或水盂亦可。)立表长四尺。表上覆矩尺。稍俯上端。从矩角望野中人家。墙下有与尺端三除弦直。更从矩角。回望下端。与表后一寸五分地三除弦直。问人家远几何。
答曰。一百六尺三分尺之二。
术曰。表高四尺自乘。得一十六尺为实。地距表一寸五分为法除之。
临河立表。上加短竿。射彼岸三际弦直。问河阔几何。
术曰。固结表竿。勿令游移。旋表竿回射手。除锲其处而量之。即得河阔。