钦定四库全书
　

九章算术卷一　　　　　晋　刘　徽　注
　　　　　　　　　　　　唐　李淳风　注释
方田以御田畴界域
今有田广十五步从十六步问为田几何答曰一亩
又有田广十二步从十四步问为田几何答曰一百六
十八步
方田术曰广从步数相乘得积步

　此积为田幂凡广从相乘谓之幂
　淳风等按经云广从相乘得积步注云广从相乘谓
　之幂观斯注意积幂义同以理推之固不当尔何则
　幂是四方单布之名积乃众数聚居之称循名责实
　二者全殊虽欲同之窃恐不可今以据言幂者据广
　从之一方其言积者举众步之都数经云相乘得积
　步即是都数之明文注云谓之为幂全乖积步之本
　意此注前云积为田幂于理得通复云谓之为幂繁

　而不当今者注释存善去非略为科简遗诸后学
以亩法二百四十步除之即亩数百亩为一顷
　淳风等按此为篇端故特举顷亩二法馀数不复言
　者从此可知一亩之田广十五步从而疏之令为十
　五行则每行广一步而从十六步又横而截之令为
　十六行则每行广一步而从十五步此即从疏横截
　之步各自为方凡有二百四十步一亩之地步数正
　同以此言之则广从相乘得积步验以二百四十步

　者亩法也百亩者顷法也故以除之即得
今有田广一里从一里为田几何答曰三顷七十五亩
又有田广二里从三里问为田几何答曰二十二顷五
十亩
里田术曰广从里数相乘得积里以三百七十五乘之
即亩数
　按此术广从里数相乘得积里方里之中有三顷七
　十五亩故以乘之即得亩数也

今有十八分之十二问约之得几何答曰三分之二
又有九十一分之四十九问约之得几何答曰十三分
之七
约分
　按约分者物之数量不可悉全必以分言之分之为
　数繁则难用设有四分之二者繁而言之亦可为八
　分之四约而言之则二分之一也虽则异词至于为　数亦同归尔法实相推动有参差故为术者先治诸

　分
术曰可半者半之不可半者副置分母子之数以少减
多更相减损求其等也以等数约之
　等数约之即除也其所以相减者皆等数之重叠故
　以等数约之
今有三分之一五分之二问合之得几何答曰十五分
之十一
又有三分之二七分之四九分之五问合之得几何答

曰得一六十三分之五十又有二分之一三分之二四分之三五分之四问合之
得几何答曰得二六十分之四十三
合分
　淳风等按合分知数非一端分无定准诸分子杂互
　群母参差粗细既殊理难从一故齐其众分同其群
　母令可相并故曰合分
术曰母互乘子并以为实母相乘为法

　母互乘子约而言之者其分粗繁而言之者其分细
　虽则粗细有殊然其实一也众非错杂非细不会乘
　而散之所以通之通之则可并也凡母互乘子谓之
　齐群母相乘谓之同同者相与通同共一母也齐者
　子与母齐势不可失本数也方以类聚物以群分数
　同类者无远数异类者无近远而通体知虽异位而
　相从也近而殊形知虽同列而相违也然则齐同之
　术要矣错综度数动之斯谐其犹佩觿解结无往而

　不理焉乘以散之约以聚之齐同以通之此其算之
　纲纪乎其一术者可令母除为率率乘子为齐
实如法而一不满法者以法命之
　今欲求其实故齐其子又同其母令如母而一其馀
　以等数约之即得知所谓同法为母实馀为子皆从
　此例
其母同者直相从之
今有九分之八减其五分之一问馀几何答曰四十五

分之三十一
又有四分之三减其三分之一问馀几何答曰十二分
之五
减分
　淳风等按诸分子母数各不同欲知馀几减馀为实
　故曰减分
术曰母互乘子以少减多馀为实母相乘为法实如法
而一

　母互乘子者知以齐其子也以少减多者知齐故可
　相减也母相乘为法者同其母也母同子齐故如母
　而一即得
今有八分之五二十五分之十六问孰多多几何答曰
二十五分之十六多多二百分之三
又有九分之八七分之六问孰多多几何答曰九分之
八多多六十三分之二
又有二十一分之八五十分之十七问孰多多几何答

曰二十一分之八多多一千五十分之四十三
课分
　淳风等按分各异名理不齐一较其相近之数故曰课分
　也
术曰母互乘子以少减多馀为实母相乘为法实如法
而一即相多也
　淳风等按此术母互乘子以少分减多分与减分义
　同惟相多之数意与减分有异减分知其馀数有几

　课分知其馀数相多也
今有三分之一三分之二四分之三问减多益少各几
何而平答曰减四分之三者二三分之二者一并以益
三分之一而各平于十二分之七
又有二分之一三分之一四分之三问减多益少各几
何而平答曰减三分之二者一四分之三者四并以益
二分之一而各平于三十六分之二十三
平分

　淳风等按平分知诸分参差欲令齐等减彼之多增
　此之少故曰平分也
术曰母互乘子
　齐其子也
副并为平实
　淳风等按母互乘子副并为平实知定此平实主限
　众子所当损益知限为平(案此注有舛误据首问第/二数母三第三数母四互)
　(乘第一数子一得十二第一数母三第三数母四互/乘第二数子二得二十四第一第二数母各三互乘)

　(第三数子三得二十七并之共六十三为平实母三/三相乘又与四乘得三十六为法列数凡三即以三)
　(乘二十得三十六乘二十四得七十二乘二十七得/八十一为列实亦以三乘法三十六得一百八平实)
　(六十三减列实三十六少二十七减七十二馀九减/八十一馀十八约之九为一则十八为二而二十七)
　(为三平实六十三为七法一百八为十二命为十二/分之七设以十二作三数三分之一则四也三分之)
　(二则八也四分之三则九也定平实七立限八减一/九减二皆七所减之一二益于四亦七损多益少适)
　(如其限宜云定此平实立限如限为/平立讹作主如讹作知遂不可通)
母相乘为法
　母相乘为法知亦齐其子又同其母

以列数乘未并者各自为列实亦以列数乘法
　此当副并列数为平实若然则重有分故反以列数
　乘周齐
　淳风等按问云所平之分多少不定或三或二列位
　无常平三知置位三重平二知置位二重凡此之例
　一准平分不可豫定多少故直云列数而已
以平实减列实馀约之为所减并所减以益于少以法
命平实各得其平

今有七人分八钱三分钱之七问人得几何答曰人得
一钱二十一分钱之四
又有三人三分人之一分六钱三分钱之一四分钱之
三问人得几何答曰人得二钱八分钱之一
经分
　淳风等按经分者自合分已下皆与诸分相齐此乃
　直求一人之分以人数分所分故曰经分也
术曰以人数为法钱数为实实如法而一有分者通之

　母互乘子知齐其子母相乘者同其母以母通之者
　分母乘全内子散全则为积分积分则与子相通故
　可令相通凡数相与者谓之率率知自相与通有分
　则可散分重叠则约也等除法实相与率也故散分
　者必令两分母相乘为法也
重有分者同而通之
　又以法分母乘实实分母乘法此谓法实俱有分故
　令分母各乘全分内子又令分母互乘上下

今有田广七分步之四从五分步之三问为田几何答
曰三十五分步之十二
又有田广九分步之七从十一分步之九问为田几何
答曰十一分步之七
又有田广五分步之四从九分步之五问为田几何答
曰九分步之四
乘分
　淳风等按乘分者分母相乘为法子相乘为实故曰

　乘分
术曰母相乘为法子相乘为实实如法而一
　凡实不满法者而有母子之名若有分以乘其实而
　长之则亦满法乃为全耳又以子所乘乘故母当报
　除报除者实如法而一也今子相乘则母各当报除
　因令分母相乘而连除也此田有广从难以广谕设
　有问者曰马二十匹直金十二斤今卖马二十匹三
　十五人分之人得几何答曰三十五分斤之十二其

　为之也当如经分术以十二斤金为实三十五人为
　法设更言马五匹直金三斤今卖马四匹七人分之
　人得几何答曰人得三十五分斤之十二其为之也
　当齐其金人之数皆合初问入于经分矣然则分子
　相乘为实者犹齐其金也母相乘为法者犹齐其人
　也同其母为二十马无事于同但欲求齐而已又马
　五匹直金三斤完全之率分而言之则为一匹直金
　五分斤之三七人卖四匹马一人卖七分马之四分

　子与人交互相生所从言之异而计术则三术同归
　也
今有田广三步三分步之一从五步五分步之二问为
田几何答曰十八步
又有田广七步四分步之三从十五步九分步之五问
为田几何答曰一百二十步九分步之五
又有田广十八步七分步之五从二十三步十一分步
之六问为田几何答曰一亩二百步十一分步之七

大广田
　淳风等按大广田知初术直有全步而无馀分次术
　空有馀分而无全步此术先见全步复有馀分可以
　广兼三术故曰大广
术曰分母各乘其全分子从之
　分母各乘其全分子从子者通全步内分子如此则
　母子皆为实矣
相乘为实分母相乘为法

　犹乘分也
实如法而一
　今为术广从俱有分当各自通其分命母入者须还
　出之故令分母相乘为法而连除之
今有圭田广十二步正从二十一步问为田几何答曰
一百二十六步
又有圭田广五步二分步之一从八步三分步之二问
为田几何答曰二十三步六分步之五

术曰半广以乘正从
　半广知以盈补虚为直田也亦可半正从以乘广按
　半广乘从以取中平之数故广从相乘为积步亩法
　除之即得也今有斜田一头广三十步一头广四十二步正从六十
四步问为田几何答曰九亩一百四十四步
又有斜田正广六十五步一畔从一百步一畔从七十
步步问为田几何答曰二十三亩七十步

术曰并两斜而半之以乘正从若广又可半正从若广
以乘并亩法而一
　并而半之者以盈补虚也今有箕田舌广二十步踵阔五步正从三十步问为田
几何答曰一亩一百三十五步
又有箕田舌广一百一十七步踵广五十步正从一百
三十五步问为田几何答曰四十六亩二百三十二步
半

术曰并踵舌而半之以乘正从亩法而一
　中分箕田则为两斜田故其术相似又可并踵舌半
　正从以乘之
今有圆田周三十步径十步
　淳风等按术意以周三径一为率周三十步合径十
　步今依密率合径九步十一分步之六
问为田几何答曰七十五步
　此于徽术当为田七十步一百五十七分步之一百

　三
　淳风等按依密率为田七十一步二十二分步之一
　十三
今有圆田周一百八十一步径六十步三分步之一
　淳风等按周三径一周一百八十一步径六十步三
　分步之一依密率径五十七步二十二分步之一十
　三
问为田几何答曰十一亩九十步十二分步之一

　此于徽术当为田十亩二百八步三百一十四分步
　之一百一十三　淳风等按依密率当为田十亩二百五步八十八分
　步之八十七
术曰半周半径相乘得积步
　按半周为从半径为广故广从相乘为积步也假令
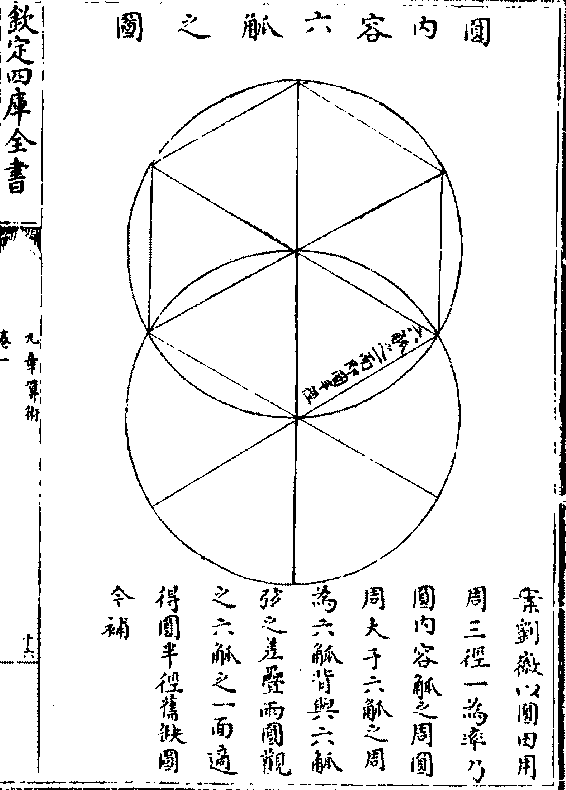
　圆径二尺圆中容六觚之一面(案六觚原本讹作六/弧考六角形其平面)
　(亦有六八角形其平面亦有八古人谓之六觚八觚/若截圆形为六古人谓之觚背具弧即圆周不得云)

　(圆中容六弧之一面后或言弧或言觚义各不/同原本觚皆讹作弧遂蒙混不可通今并改正)与圆
　径之半其数均等合径率一而外周率三也(案刘徽/以周三)
　(径一乃六觚之率圆内容六觚其觚面适为六弧之/弦圆周大于六觚之周为六弧背与六弧弦之差其)
　(说非图莫显今/补图附于后)

　
　
　
　
　
　
　
　

　又按为圆以六觚之一面乘一弧半径(案一弧二/字衍当删)二
　因而六之(案此句有讹舛当改云/三之上衍二因而三字)得十二觚之幂若
　又割之次以十二觚之一面乘一弧之半面(案一弧/之三字)
　(亦衍/当删)四因而六之(案此句亦有讹舛当云/六之上衍四因而三字)则得二十
　四觚之幂割之弥细所失弥少割之又割以至于不
　可割则与圆周合体而无所失矣觚面之外又有馀
　径以面乘径则幂出觚矣若夫觚之细者与圆合体
　则表无馀径表无馀径则幂不外出矣以一面乘半

　径觚而裁之每辄自倍故以半周乘半径而为圆幂
　此一周径谓至然之数非周三径之一率也周三者
　从其六觚之环耳以推圆规多少之较(案较原本讹/作觉今改正)
　乃弓之与弦也然世传此法莫肯精覈学者踵古习
　其谬失不有明据辩之斯难凡物类形象不圆则方
　方圆之率诚著于近则虽远可知也由此言之其用
　博矣谨按圆验更造密率恐空设法数昧而难譬故
　置诸检括谨详其记注焉

　割六觚以为十二觚术曰置圆径二尺半之为一尺
　即圆里觚之面也(案觚之而原本讹作弦之面后觚/之半面讹作弧之半面今改正)
　令半径一尺为弦(案原本讹作/为弧今改正)半面五寸为句为之
　求股以句幂二十五寸减弦幂馀七十五寸开方除
　之下至秒忽又一退法求其微数微数无各知以为
　分子以下为分母约作五分忽之二故得股八寸六
　分六釐二秒五忽五分忽之二(案二秒原本讹/作二丝今改正)以减
　半径馀一寸三分三釐九毫七秒四忽五分忽之三

　谓之小句(案此下原本衍小句知/半面五寸之句九字)觚之半面又谓之
　小股为之求弦其幂二千六百七十九亿四千九百
　一十九万三千四百四十五忽馀分弃之(案此句原/本讹作全)
　(分并之考弦幂五忽之下尚有一六馀分无所谓全/分也当是传写舛误遂不可通后数条皆云馀分弃)
　(之令据/以改正)开方除之即十二觚之一面也
　割十二觚以为二十四觚术曰亦令半径为弦半面
　为句为之求股置上下弦幂四而一得六百六十九
　亿八千七百二十九万八千三百六十一忽馀分弃

　之即句幂也以减弦幂其馀开方除之得股六寸六
　分五釐九毫二秒五忽五分忽之四以减半径馀三
　分四釐七秒四忽五分忽之一谓之小句觚之半面
　又谓之小股为之求小弦其幂六百八十一亿四千
　八百三十四万九千四百六十六忽馀分弃之开方
　除之即二十四觚之一面也
　割二十四觚以为四十八觚术曰亦令半径为弦半
　面为句为之求股置上下弦幂四而一得一百七十

　亿三千七百八万七千三百六十六忽馀分弃之即
　句幂也以减弦幂其馀开方除之得股九寸九分一
　釐四毫四秒四忽五分忽之四以减半径馀八釐五
　毫五秒五忽五分忽之一谓之小句觚之半面又谓
　之小股为之求小弦其幂七百七十一亿一千二十
　七万八千八百一十三忽馀分弃之开方除之得小
　弦一寸三分八毫六忽馀分弃之即四十八觚之一
　面以半径一尺乘之又以二十四乘之得幂三万一

　千三百九十三亿四千四百万忽以百亿除之得幂
　三百一十三寸六百二十五分寸之五百八十四即
　九十六觚之幂也
　割四十八觚以为六十六觚术曰亦令半径为弦半
　面为句为之求股置次上弦幂四而一得四十二亿
　七千七百五十六万九千七百三忽馀分弃之即句
　幂也以减弦幂其馀开方除之得股九寸九分七釐
　八毫五秒八忽十分忽之九以减半径馀二釐一毫

　四秒一忽十分忽之一谓之小句觚之半面又谓之
　小股为之求小弦其幂四十二亿八千二百一十五
　万四千一十二忽馀分弃之开方除之得小弦六分
　五釐四毫三秒八忽馀分弃之即九十六觚之一面
　以半径一尺乘之又以四十八乘之得幂三万一千
　四百一十亿二千四百万忽以百亿除之得幂三百
　一十四寸六百二十五分寸之六十四即一百九十
　二觚之幂也以九十六觚之幂减之馀六百二十五

　分寸之一百五谓之差幂倍之为分寸之二百一十
　(为分寸者蒙上省文谓六百/二十五分寸之二百一十也)即九十六觚之外弧田
　所谓以弦乘矢之凡幂也(案弧田下原本衍/九千六字今删)加此幂
　于九十六觚之幂得三百一十四寸六百二十五分
　寸之一百六十九则出圆之表矣故还就一百九十
　二觚之全幂三百一十四寸以为圆幂之定率而弃
　其馀分以半径一尺除圆幂倍之得六尺二寸分分
　即周数令径自乘为方幂四百寸与圆幂相折圆幂

　得一百五十七为率方幂得二百为率方幂二百其
　中容圆幂一百五十七也圆率犹为微少按弧田图
　令方中容圆圆中容方内方合外之半半然则圆幂
　一百五十七其中容方幂一百也(案一百原本讹/作二百今改正)又
　令径二尺与周六尺二寸八分相约周得一百五十
　七径得五十则其相与之率也周率犹为微少也晋
　武库中汉时王莽作铜斛其铭曰律嘉量斛内方尺
　而圆其外庣旁九釐五毫幂一百六十二寸深一尺

　积一千六百二十寸容十斗以此术求之得幂一百
　六十一尺有奇其数相近矣此术微少而斛差幂六
　百二十五分寸之一百五以十二觚之幂为率消息
　当取此分寸之三十六(案取此分寸亦蒙上省文谓/六百二十五分寸之三十六)
　(也/)以增于一百九十二觚之幂以为圆幂三百一十
　四寸二十五分寸之四置径自乘之方幂四百寸令
　与圆幂通相约圆幂三千九百二十七方幂得五千
　是为率方幂五千中容圆幂三千九百二十七圆幂

　三千九百二十七中容方幂二千五百也以半径一
　尺除圆幂三百一十四寸二十五分寸之四倍之得
　六尺二寸八分二十五分寸之八即周数也全径二
　尺与周数通相约径得一千二百五十周得三千九
　百二十七即其相与之率若此者盖尽其纤微矣举
　而用之上法仍约耳当求一千五百三十六觚之一
　面得三千七十二觚之幂而裁其微分数亦宜然重
　其验耳

　淳风等按旧术求圆皆以周三径一为率若用之求
　圆周之数则周少径多用之求其六觚之田乃与此
　率合会耳何则假令六觚之田觚间各一尺为面自
　然从角至角其径二尺可知(案二尺原本讹/作一尺今改正)此则周
　六径二与周三径一已合恐此犹为难晓今更引物
　为喻设令刻物作圭形者六枚枚别三面皆长一尺
　攒此六物悉使锐头向里则成六觚之周角径亦皆
　一尺更从觚角外畔围绕为规则六觚之径尽达规

　矣当面径短不至外规若以径言之则为规六尺径
　三尺面径皆一尺(案此三句有舛误当云若以言觚/言之则为周六尺径二尺面皆一)
　(尺言觚二字讹作径周讹作规二讹/作三面字下又衍径字遂不可通)面径股不至外
　畔定无二尺可知故周三径一之率于圆周乃是径
　多周少径一周三理非精密盖术从简要举大纲略
　而言之刘徽特以为疏遂改张其率但周径相乘数
　难契合徽虽出斯一法终不能究其纤毫也祖冲之
　以其不精就中更推其数今者修撰攈摭诸家考其

　是非冲之为密故显之于徽术之下冀学者知所裁
　焉(案冲之密率较徽率为密其约率较徽率为/疏淳风等所称密率皆约率以之讥徽似误)
又术曰周径相乘四而一
　此周与上觚同耳周径相乘各当一半而今周径两
　全(案原本两讹/作田今改正)故两母相乘为四以报除之于徽术
　以五十乘周一百五十七而一即径也以一百五十
　七乘径五十而一即周也新术径率犹当微少据周
　以求径则失之长据径以求周则失之短诸据见径

　以求幂者皆失之于微少据周以求幂者皆失之于
　微多
　淳风等按依密率以七乘周二十二而一即径以二
　十二乘径七而一即周依术求之即得

又术曰径自相乘三之四而一
　按圆径自乘为外方三之四而一者是为圆居外方
　四分之三也若令六觚之一面乘半径其幂即外方
　四分之一也因而三之即亦居外方四分之三也是

　为圆里十二觚之幂耳取以为圆失之于微少于徽
　新术当径自乘又以一百五十七乘之二百而一
　淳风等按密率令径自乘以十一乘之十四而一即
　圆幂也
又术曰周自乘十二而一
　六觚之周其于圆径三与一也故六觚之周自相乘
　为幂若圆径自乘者九方九方凡为十二觚者十有
　二故曰十二而一即十二觚之幂也今此令周自乘

　非但为圆径自乘者九方而已然则十二而一所得
　又非十二觚之幂也若欲以为圆幂失之于多矣以
　六觚之周十二而一可也于徽新术直令圆周自乘
　又以二十五乘之三百一十四而一得圆幂其率三
　百一十四者周自乘之幂也置周数六尺二寸八分
　令自乘得幂三十九万四千三百八十四分又置圆
　幂三万一千四百分皆以一千二百五十六约之得
　此率

　淳风等按方面自乘即得其积圆周求其幂假率乃
　通(案假原本讹/作股今改正)但此术所求用三一为率圆田正法
　半周及半径以相乘今乃用全周自乘故须以十二
　为母何者据全周而求半周则须以二为法就全周
　而求半径复假六以除之是二六相乘除周自乘之
　数依密率以七乘之八十八而一
今有田下周三十步径十六步问为田几何答曰一
百二十步

今有田下周九十九步径五十一步问为田几何答
曰五亩二十六步四分步之一
术曰以径乘周四而一
　此术不验故推方锥以见其形假令方锥下方六尺
　高四尺四尺为股下方之半三尺为句正面邪为弦
　弦五尺也令句弦相乘(案句弦原本讹/作句股今改正)四因之得六
　十尺即方锥四面见者之幂若令其中容圆锥圆锥
　见幂与方锥见幂其率犹方幂之与圆幂也(案圆幂/原本讹)

　(作圆锥/今改正)按方锥下六尺则方周二十四尺以五尺乘
　而半之则亦方锥之见幂故求圆锥之数折径以乘
　下周之半即圆锥之幂也今田上径圆穹而与圆
　锥同术则幂失之于少矣然其术难用故略举大较
　施之大广田也求圆锥之幂犹求圆田之幂也今用
　两全相乘故以四为法除之(案原本脱/四字今补)亦如圆田矣
　开立圆术说圆方诸率甚备可以验此
今有弧田弦三十步矢十五步问为田几何答曰一亩

九十七步半
又有弧田弦七十八步二分步之一矢十三步九分步
之七问为田几何答曰二亩一百五十五步八十一分
步之五十六
术曰以弦乘矢矢又自乘并之二而一
　方中之圆圆里十二觚之幂合外方之幂四分之三
　也方中合外方之半则朱实合外方四分之一也弧
　田半圆之幂也故依半圆之体而为之术以弦乘矢

　而半之(案弦原本讹/作弧今改正)则为黄幂矢自乘而半之则为
　二青幂青黄相连(案注文此书旧有图而缺又上圆/田注内亦引弧田图详考其说非)
　(图不显今/补图于后)为弧体法当用规今觚面不至外畔(案原/本讹)
　(作令弧而不至/外畔今改正)失之于少矣圆旧术以周三径一为
　率俱得十二觚之幂(案原本讹作十二/弧之弧今改正)亦失之子少
　也与此相似指验半圆之幂耳若不满半圆者益复
　疏阔宜句股锯圆材之术以弧弦为锯道长以矢为
　句深而求其径(案此谓弧矢形求圆径其术以弧/弦折半自乘矢除之加矢为圆径)既

　知圆径则弧可割分也割之者半弧田之弦以为股
　其矢为句为之求弦即小弧之弦也以半小弧之弦
　为句半圆径为弦为之求股以减半径其馀即小弦
　之矢也割之又割使至极细但举弦矢相乘之数则
　必近密率矣然于算数差繁必欲有寻究也若但度
　田取其大旧术为约耳

今有环田中周九十二步外周一百二十二步径五步
　此欲令与周三径一之率相应故言径五步也据中
　外周以徽术言之当径四步一百五十七分步之一
　百二十二也
　淳风等按依密率合径四步二十二分步之十七
问为田几何答曰二亩五十五步
　于徽术当为田二亩三十一步一百五十七分步之
　二十三

　淳风等按依密率为田二亩三十步二十二分步之
　十五
术曰并中外周而半之以径乘之为积步
　此田截而中之周则为长(案此处有脱误当云截/齐中外之周周则为长)并
　而半之知亦以盈补虚也此可令中外周各自为圆
　田以中圆减外圆馀则环实也
又有环田中周六十二步四分步之三外周一百一十
三步二分步之一径十二步三分步之二

　此田环而不通匝故径十二步三分步之二若据上
　周求径者此径失之于多过周三径一之率盖为疏
　矣于徽术当径八步六百二十八分步之五十一
　淳风等按依周三径一考之合径八步二十四分步
　之一十一依密率合径八步一百七十六分步之一
　十三
问为田几何答曰四亩一百五十六亩四分步之一
　于徽术当为田二亩二百三十二步五千二十四分

　步之七百八十七也依周三径一为田三亩二十五
　步六十四分步之三十五
　淳风等按密率为田二亩二百三十一步一千四百
　八分步之七百一十七也
术曰置中外周步数分母子各居其下(案原本脱母/字今据注补)母
互乘子通全步内分子(案此句上下皆有脱文当云分/母相乘通全步内分子并而半)
(之/)以中周减外周馀半之(案此别记术之小异亦有脱/文当云又可以中周减外周)
(馀半之以/益中周)径亦通分内子以乘周为实分母相乘为法除

之为积步馀积步之分(案此句下有脱文当云/馀积步之分等数约之)以亩法
除之即亩数也
　按此术并中外周步数于上以分母子置于下母互
　乘子者为中外周俱有馀分故以互乘齐其子母相
　乘同其母子齐母同故通全步内分子半之(上二字/ 有脱)
　(文当云并/而半之)知以盈补虚得中平之周周则为从径则
　为广故广从相乘而得其积既合分母还须分母出
　之故令周径分母相乘而连除之即得积步不尽以

　等数除之而命分以亩法除积步得亩数也
　
　
　
　
　
　
　九章算术卷一