声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
卷八 第 1a 页 WYG0795-0937c.png
 钦定四库全书
钦定四库全书大统历志卷八
宣城梅文鼎撰
月食通轨
录各有食之望下等数
经望全分 盈缩历全分 盈缩差全分
迟疾历全分 迟疾限数 迟疾差全分
加减差全分 定望全分(某甲子将本日日出分推/在卯时何刻望在何刻已)
卷八 第 1b 页 WYG0795-0937d.png
 (下者退一日也○按说见定朔望条卯时者举例言其/实即以日出分如发敛条求之便得某时刻又按其定)
(下者退一日也○按说见定朔望条卯时者举例言其/实即以日出分如发敛条求之便得某时刻又按其定)(望退一日法只据其小馀在日出/分已下者断之并不必求时刻也)
交汎全分 定入迟疾历 定入迟疾限(此限/与前)
(同者便不必书出损益分并行度○按其/实此处损益分不言何用似总不必书出)
定限行度 晨分(月出之时刻也先/于复圆者有带食)
日出分 日入分 昏分(月出之时刻/也复于初亏)
(有带食○按载晨昏分者所以定更点也其带食分只/用日出入分不用晨昏盖晨刻日未出月则犹见昏前)
(日已入月则已/见也○注误)
卷八 第 2a 页 WYG0795-0938a.png
 天正赤道度 天正黄道度 交定度(以上诸法皆/与日食同)
天正赤道度 天正黄道度 交定度(以上诸法皆/与日食同)推卯酉前后分法
视定望小馀如在二千五百分已下者就为卯前分也
如在已上者去减半日周五千分馀为卯后分也又如
在七千五百分已下者内减去五千分就为酉前分也
如在已上者去减一万分馀为酉后分也(已上已下皆/指定望小馀)
(而/言)
按凡卯酉前后分皆据子午言之卯前分是距子正
卷八 第 2b 页 WYG0795-0938b.png
 后之分也故即以小馀在卯前者定之卯后分是距
后之分也故即以小馀在卯前者定之卯后分是距午正前之分也故以小馀减半日周其馀则是自午
正逆数以前距数也酉前分是距午正后之分也故
以半日周减小馀其减不尽者则是自午正顺数以
后距数也酉后分是距子正前之分也故以小馀减
日周其馀则是自子正逆数以前距数也
推时差分法
置日周一万内减去卯前卯后分或酉前后分(满千分/者命为)
卷八 第 3a 页 WYG0795-0938c.png
 (十分满百分/者命为单分)得为时差分也
(十分满百分/者命为单分)得为时差分也推食甚定分法
置所推时差分加入定望小馀共得为食甚定分也
按气刻时三差皆起于唐长庆中宣明历于日食用
之月食则皆不用后之诸历或有用月食时差者其
数大约与日食相仿皆于近卯酉则差稍多近子午
则差渐少其以之定食甚分则皆子前减子后加以
加减其定望小馀而得也所异者朔食时差多望食
卷八 第 3b 页 WYG0795-0938d.png
 时差少耳今依通轨所载推之则近卯酉者差反少
时差少耳今依通轨所载推之则近卯酉者差反少近子午者差反多又不问子前子后皆以加定望小
馀而无减法种种皆与历经相反则何如不用之为
得乎且日食何以有时差以月之掩日去日尚远也
日光尚在但不见耳据所不见而言之故以时而差
若月食则不然闇虚者日气所冲食则与月相著譬
如呵气著镜光体尽亏一如晦朔安得有左右视之
差乎此唐宋诸历所以多不用也即曰用之所差不
卷八 第 4a 页 WYG0795-0939a.png
 过九十馀分然亦不至反其所用如此也窃依元史
过九十馀分然亦不至反其所用如此也窃依元史所载月食时差法定之如左
依历经求月食甚定分法
置卯酉前后分(有千法实皆定三/有百法实皆定二)自相乘(言十加/定一子)退二
位去二子如四百七十八而一(去二子不满法又去一/子以所定二子为百分)
(一子为/十分)为时差子前以减子后以加皆加减定望分为
食甚定分依发敛求之即食甚辰刻
按卯酉前后分即前所推卯前卯后分或酉前酉后
卷八 第 4b 页 WYG0795-0939b.png
 分自相乘者如求南北差法即以所得卯酉前后分
分自相乘者如求南北差法即以所得卯酉前后分为法与实也凡卯酉前后分皆自子午起算以自相
乘则近卯酉差多近子午差少矣退二位法同日食
时差以得数后有百万退作万有十万退作千而后
归除之也如四百七十八而一者是以四百七十八
归除之如四百七十八分为一分也子前减子后加
者凡望时之月在日所冲故日在子前月乃在午前
其日食午前减故月食亦子前减也日在子后月乃
卷八 第 5a 页 WYG0795-0939c.png
 在午后日食午后加故月食亦子后加也其差多者
在午后日食午后加故月食亦子后加也其差多者不过一百三十分有奇而止故以四百七十八为法
归除之也
推食甚入盈缩历及食甚入盈缩差并食甚入盈缩
历行定度三法俱与日食同只换望日
推月食入阴阳历法
视所推交定度如在交中度一百八十一度八九六七
已下者便为入阳历也如在已上者内减去交中度馀
卷八 第 5b 页 WYG0795-0939d.png
 为入阴历也
为入阴历也按交中度数原生于阴阳历月入阳历则在黄道南
行一百八十一度有奇毕复入黄道北而行阴历一
百八十一度有奇毕则又复入阳历矣行阳历阴历
各一次谓之交终半之为交中今交定度在一百八
十一度已下是月尚在黄道南就为入阳历度数也
其在已上者是月已在黄道北故于交定度内减去
一百八十一度八九六七馀者命为入阴历度数也
卷八 第 6a 页 WYG0795-0940a.png
 阳历数自交初起算阴历数自交中起算也
阳历数自交初起算阴历数自交中起算也推交前交后度法
视所推月食入阴阳历如在后准一十五度五十分已
下者便为交后度也如在前准一百六十六度三九六
八已上者置交中度内减去阴阳历为交前度也
按凡言交者皆月出入黄道十字相交之际也凡阴
历在后准已下者是距阳历交阴历后未远尚在十
五度内故为阴历交后度也凡阴历在前准已上者
卷八 第 6b 页 WYG0795-0940b.png
 是逆距阴历交阳历前已近只在十五度内故为阴
是逆距阴历交阳历前已近只在十五度内故为阴历交前度也阳历同十五度五十分者月食限一十
三度○五分或有十五度五十分而入食限者盖以
盈缩差加减之则亦十三度有奇故以十五度五十
分为食准也其前准度虽多逆计其所距后交之数
亦同也
推月食分秒法
置月食限一十三度○五分内减去交前或交后度(十/度)
卷八 第 7a 页 WYG0795-0940c.png
 (定三单度定二○按定子法疑有误若如所云则月食/必无十分者安得有既内外之分乎愚意当是十度定)
(定三单度定二○按定子法疑有误若如所云则月食/必无十分者安得有既内外之分乎愚意当是十度定)(五单度/定四也)以定法八十七分(去/一)为法除之(不满法去一子/所定有三子为)
(十分二子/为单分)得为月食分秒也不及减者必不食也十分
已下者用三限辰刻法十分已下者用五限辰刻法
按月食限度多于日食者闇虚大而月小也故不问
阴阳历只距交前后一十三度○五分内即能相掩
而有食也凡定望正当交度其食十五分渐离其处
食分渐杀假如距交前后一度七十四分则于食十
卷八 第 7b 页 WYG0795-0940d.png
 五分内减二分只食八分又如距交前后九度五十
五分内减二分只食八分又如距交前后九度五十七分则于食十五分内减一十一分只食四分也故
置食限一十二度○五分以距交前后度减之即如
于食十五分内减去若干分秒也其减不尽者则正
是今所合食之分秒故以定法除之而得盖月食定
法即十五分其食限之一也如食限不及减为不食
者是距交前后度多于月食限是已在十三度○五
分之外闇虚虽大至此亦不能相掩断为不食也
卷八 第 8a 页 WYG0795-0941a.png
 推月食定用分法
推月食定用分法置月食分三十分减去所推月食分秒馀(十分定三/单分定二)为
实却以月食分秒(十分定三单分定二○按十分宜定/一今加定三子者以分下有十有秒)
(也故亦以定六子为百/分法实共知定四子也)为法乘之(言十定一定有六子/为百分五子为十分)
得为开方积立天元一于单微之下依平方法开之得
为开方数(有十/定一)复以四千九百二十分(定五○按以六/分乘八百二十)
(分得四千九百二十食/分又按元史数同日)为法乘开方数(有十/定一)得数又以
其前推得定限行度(去四子空/度去三子)为法除之(不满法去一/子定有二子)
卷八 第 8b 页 WYG0795-0941b.png
 (为百分一/子为十分)得为所推定用分也
(为百分一/子为十分)得为所推定用分也定用分者亦月食自初亏复距食甚之时刻也然日
食只十分而月食则有十五分者闇虚大也闇虚之
大几何曰大一倍何以知之以算月食用三十分知
之也依日食条论两圆相切法闇虚半径十分月半
径五分两边相切则两半径联为一直线共十五分
为两心之距以此距线用闇虚心为心运作大圆正
得全径三十分也此大圆边距闇虚边四周各五分
卷八 第 9a 页 WYG0795-0941c.png
 为两圆相切时月心所到之界其两之距十五分即
为两圆相切时月心所到之界其两之距十五分即大圆半径常用为弦而以食甚时两心之距为勾食
甚时月心侵入大圆边之数为勾弦较其数与月食
分秒同以此与大圆全径相减馀即勾弦和和较相
乘为股实开方积也其开方数为股即自亏复至食
甚月心所行之白道也
四千九百二十乘者何也依日食条论又是十分八
百二十而用其六也盖所得月体又小于日一分也
卷八 第 9b 页 WYG0795-0941d.png
 然历经所用与日食同此不同者盖改率也或亦改
然历经所用与日食同此不同者盖改率也或亦改三应数时所定而作史时未入如盈缩立成等耳
推三限辰刻等法
置所推食甚定分内减去定用分馀为初亏分也不及
减者加日周减之复置食甚定分内加入定用分共得
为复圆分也满日周去之时刻依合朔推之
按三限辰刻同日食理不复赘
卷八 第 10a 页 WYG0795-0942a.png
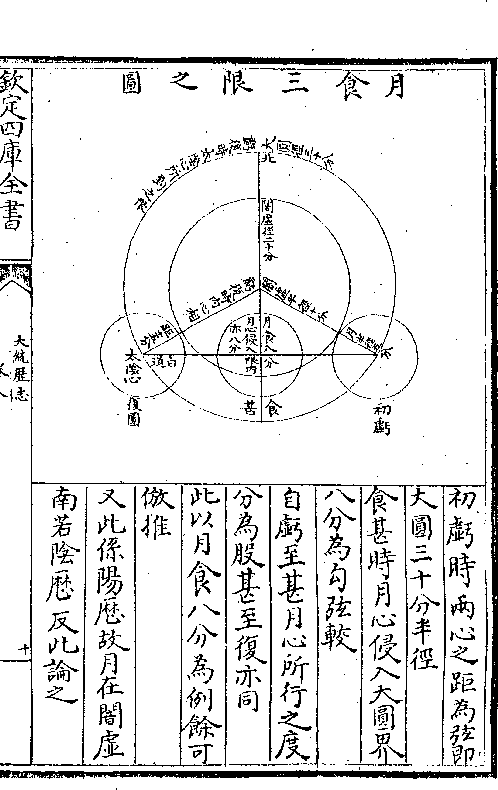 初亏时两心之距为弦即
初亏时两心之距为弦即大圆三十分半径
食甚时月心侵入大圆界
八分为勾弦较
自亏至甚月心所行之度
分为股甚至复亦同
此以月食八分为例馀可
仿推
又此系阳历故月在闇虚
南若阴历反此论之
卷八 第 10b 页 WYG0795-0942b.png
 推既内分法
推既内分法置月食限一十五分(按历经作月食既/一十分今从之)内减去所推月
食分秒自单以下全分馀(十分定二单分定三○句误/按此处无十分当是有分定)
(二十秒/定一也)为实却以月食分秒自单分以下分秒(单分定/二十秒)
(定/一)为法乘之(言十定一所定有五子/为十分四子为单分)得为开方积立天
元一于单微之下依平方法开之得为开方数就置开
方数(十分定五单分定四○按十分定五句误此处开/方数必无十分当作十秒定三有分定四也分加)
(定四子者以/有秒微也)复以四千九百二十分(定/五)为法乘之(言十/定一)
卷八 第 11a 页 WYG0795-0943a.png
 得数又以所推定限行度(去四子空/度去三子)为法除之(不满法/去一子)
得数又以所推定限行度(去四子空/度去三子)为法除之(不满法/去一子)(所定有六子为百/分五子为十分)得为所推既内分也
按历经原是以既内分与一十分相减相乘此则改
为一十五分今以大圆掩小圆率求得既内小平圆
径一十分与历经合故断从历经也
月食十分则既矣此时月体十分全入闇虚而月之
边正切闇虚之心两心之距正得五分以此五分为
半径自闇虚心作小平圆其全径十分其边各距闇
卷八 第 11b 页 WYG0795-0943b.png
 虚心五分为食既时月心所到之界过此界则为既
虚心五分为食既时月心所到之界过此界则为既内矣假如月食十二分食既时月心正掩小圆之边
食甚时月体则入闇虚内二分而月心亦侵入小平
圆二分故即用此二分为勾弦较以与小平圆全径
相减馀为勾弦和和较相乘得积开方得股即月心
从食既至食甚在闇虚内所行小平圆之白道也于是
亦如前法变为度分而计其行率则知月入闇虚以后行至食
甚所历时刻之数而命为既内之分也此既内分食甚至复圆同论
卷八 第 12a 页 WYG0795-0944a.png
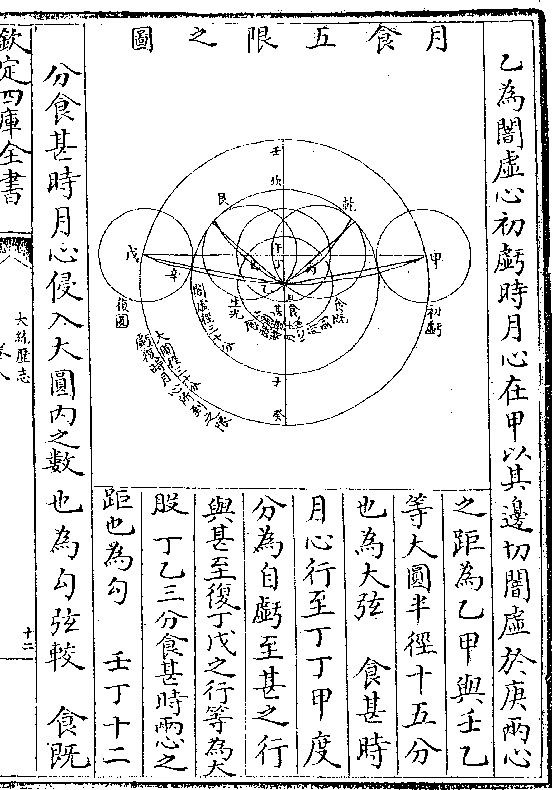 乙为闇虚心初亏时月心在甲以其边切闇虚于庚两心
乙为闇虚心初亏时月心在甲以其边切闇虚于庚两心之距为乙甲与壬乙
等大圆半径十五分
也为大弦 食甚时
月心行至丁丁甲度
分为自亏至甚之行
与甚至复丁戊之行等为大
股丁乙三分食甚时两心之
距也为勾 壬丁十二
分食甚时月心侵入大圆内之数也为勾弦较 食既
卷八 第 12b 页 WYG0795-0944b.png
 时月心在丙丙心之距乙丙与生光之时己乙之距
时月心在丙丙心之距乙丙与生光之时己乙之距等小平圆半径五分也为小弦 丙丁为月心自既
至甚之行与自甚至生光己下之行等为小股 丁
巳三分仍为勾 午丁二分为食甚时月心侵入小
平圆之数为勾弦较 丙至丁所历时刻与己丁时
刻等是为既内分 甲至丙所历时刻与已至戊等
是为既外分 此以阴历月食十二分为式馀皆仿
论
卷八 第 13a 页 WYG0795-0945a.png
 开方数
开方数壬丁十二丁癸十八相乘二一六平方开之得丁甲
十四(六/九)午丁二分丁艮八分相乘十六平方开之得
丁丙四分
推既外分法
置所推定用分内减去既内分馀为既外分也
按既外分者是月食初亏至食既生光至复圆所占
时刻也原所推定用是自亏初复末中距食甚之数
卷八 第 13b 页 WYG0795-0945b.png
 则是既内既外总数也故于其中减去既内所占时
则是既内既外总数也故于其中减去既内所占时刻其馀便是既外时刻也
推五限辰刻等法
置食甚定分内减去定用分为初亏分初亏分加既外
分为食既分食既分加既内分为食甚分食甚分加既
内分为生光分生光分加既外分为复圆分也不及减
者加日周减之满日周去之推时刻同前
按月食所以有五限辰刻异于日食者日食只十分
卷八 第 14a 页 WYG0795-0945c.png
 故其食而既也即其食甚也才食而既其光即生则
故其食而既也即其食甚也才食而既其光即生则其生光之分亦即其食甚也若月食则十五分自食
既以至生光历时且久为刻皆殊中折二数以知食
甚总计亏复故有五限也以定用减小馀者所算定
用原是食甚距初亏之数也故以减食甚得初亏以
既外加初亏及生光者所算既外原是初亏距食既
生光距复圆数也故以加初亏得食既以加生光得
复圆至于所算既内原是食既至生光折半之数即
卷八 第 14b 页 WYG0795-0945d.png
 是食既生光中距食甚之数也故以加食既得食甚
是食既生光中距食甚之数也故以加食既得食甚以加食甚得生光不及减加日周者是食甚在子正
后初亏等在子正前也加满日周去之者是食甚等
在子正前复圆等在子正后也凡言时刻同前者皆
用发敛也
推月食入更点法
视望下盈缩历与太阳立成同日之日晨分就加一倍
得数用五千分而一(句误一按当作/五而 下同)得为更法分也(定/数)
卷八 第 15a 页 WYG0795-0946a.png
 (满法得十分不/满法得百分也)将更法又用五千分而一得为点法分
(满法得十分不/满法得百分也)将更法又用五千分而一得为点法分也(定数满法得百分不满法得十分也○句误甚按当/作满法者百已上不满法者二百已上也大约更法)
(有千者则/不满法)
按更点倍晨分者凡日入后二刻半而昏日未出前
二刻半而晨晨则辨色未昏则不禁行晨昏启闭以
此为节是益昼五刻损夜五刻圣人扶抑之道无所
往而不存也其晨分皆自本日子正距异之数夜之
有晨分犹日之有半昼分也逆推子正前距昏之数
卷八 第 15b 页 WYG0795-0946b.png
 正与相等故倍其晨分即为全夜之刻也于是以五
正与相等故倍其晨分即为全夜之刻也于是以五除之即其夜每更所占时刻之数也假如晨分二千
五百倍之五千五除之则知每一更分占有一十分
也满法者是在五千分已上故知得数为千分不满
法者是在五千分已下故知得数为百分于是又置
更法以五除之即其夜每点所占刻数也假如更法
分一千五除之则知每点中占有二百分也其点法
得数无论满法不满法总是百分不必定数盖千已
卷八 第 16a 页 WYG0795-0946c.png
 上数则不满法岂有转少作十分之理十分句误又
上数则不满法岂有转少作十分之理十分句误又除法只是单五每夜五更每更五点五千分误当作
五而一或以五除之也
推初亏等更点法
视初亏分如在晨分已下者就加入晨分共为初亏更
分也如在昏分已上者内减去昏分馀为初亏更分也
却以元推更法分为法除之命起一更算外得为初亏
更数也将减馀不及满更法数却以元推点法分为法
卷八 第 16b 页 WYG0795-0946d.png
 除之命起一点算外得为初亏点数也次四限更点仿
除之命起一点算外得为初亏点数也次四限更点仿此而推各得更点也(若在日入已上昏分已下者命为/昏刻若在日出以下晨分以上者)
(命为晨刻/皆无更点)
按初亏等分如在晨分已下者是在子后也加入晨
分是逆从子前昏刻算起也其在昏分已上是在昏
后也故减去昏分即是减去昼刻截从初昏算起也
究之二者则总是从初更初点起算其加后减后则
知此所得数距初更初点已若干数于是以本日更
卷八 第 17a 页 WYG0795-0947a.png
 法为法除之其满过更法有几数便知已过几更故
法为法除之其满过更法有几数便知已过几更故算外命为更数也其不满更法而馀者则正是初入
此更已来未满之数故又以点法除之其满过点法
有几数便知在此更中已过几点故算外命为点数
便知所推初亏等尚在第几更第几点中未满也其
有总不满更法数者则只是初更其有以点法除总
不满法者则只是初点也
推月食起复方位法
卷八 第 17b 页 WYG0795-0947b.png
 视月食入阴阳历如是阳历者初起东北食甚正北复
视月食入阴阳历如是阳历者初起东北食甚正北复圆于西北也如是阴历者初起东南食甚正南复圆于
西南也若食在八分已上者无论阴阳历皆初起正东
复圆于正南也
按月食起复方位主月体言之即人所见月之上下
左右也以卯位言之则东为下西为上北为左南为
右也以酉位言之则东为上西为下南为左北为右
也月食入阴阳历亦主月道言之如是阳历食是月
卷八 第 18a 页 WYG0795-0947c.png
 在日道南闇虚掩之者在其北故食起东北甚于正
在日道南闇虚掩之者在其北故食起东北甚于正北复于西北也如是阴历食是月在日道北闇虚掩
之者在其南故食起东南甚于正南复于西南也其
食在八分已上者是月食闇虚正相掩而过故食起
正东复于正西也凡闇虚在日所冲太阳每日行一
度闇虚随之而移月之行天既视闇虚为速故其食
也皆闇虚光在东月自西来道有必经无所于避遂
入其中而为所掩既受谪矣则始能行而出于闇虚
卷八 第 18b 页 WYG0795-0947d.png
 之东却视闇虚又在月西故月食亏初皆在东复末
之东却视闇虚又在月西故月食亏初皆在东复末皆在西也又按历经此亦据午地言之
推月有𢃄食分法同日食推
月有𢃄食例
昏(月未出已复光若干/月已出见复光若干) 晨(月未入见复光若干/月已入未复光若干)
昏(月未出已食若干/月已出见食若干) 晨(月未入见食若干月/已食不见食若干)
按月带食法同日食而只互易其晨昏书法者何也
盖月食于望望者日月相望故日出则月入月出则
卷八 第 19a 页 WYG0795-0948a.png
 日入故易日之昏为月之晨易日之晨为月之昏也
日入故易日之昏为月之晨易日之晨为月之昏也其所以同者何也假如日入分在复圆分已下是复
圆在日入月出后于日为见食甚不见复末者于月
则见为复末不见食甚也若日出分在复圆分已下
是复圆在日出月入后于日为见复末不见食甚者
于月则为见食甚不见复末也之二者总是以食甚
分减其日出入分其所推带食分则总是日月出入
前距食甚之数其以减食分而馀者亦总是日月出
卷八 第 19b 页 WYG0795-0948b.png
 入后未复光之数故总谓之已复光未复光而以所
入后未复光之数故总谓之已复光未复光而以所推带食分录于前也又如日入分在初亏分已上是
初亏在日入月出前于日为见亏初不见食甚者于
月则为见食甚不见亏初也若日出分在初亏分已
上是食甚在日出月入后于日为见食甚不见亏初
者于月则为见亏初不见食甚也之二者总是以日
出入分减其食甚分其所推带食分则总是日月出
入后距食甚之数其以减食分而馀者亦总是日月
卷八 第 20a 页 WYG0795-0948c.png
 出入前已食之数故总谓之见食不见食而以所推
出入前已食之数故总谓之见食不见食而以所推带食分录于后也馀详日食○又按历经月食既者
以既内分减带食差馀进一位如既外分而一以减
既分即月带食出入所见之分不及减者为带食既
出入盖凡所推带食差是食甚所距日出入数今以
既内分减之而馀者即是日出入后距食既前或日
出入前距生光后其间所有时刻也进一位者即是
以既分乘之也又以既外分除之则知其食既生光
卷八 第 20b 页 WYG0795-0948d.png
 距日出入时于既外全数中分得几许时刻即知其
距日出入时于既外全数中分得几许时刻即知其于食既全数内分得几许食分也故以减月食既十
分即为月带食出入之分也不及减者是带食差少
于既内分其日出入分已在既内分内故为带食既
出入也
推食甚月离黄道宿次度法
置元推食甚入盈缩历行定度全分如是盈历者加半
周天一百八十二度六二八七五及天正黄道箕宿度
卷八 第 21a 页 WYG0795-0949a.png
 共得为黄道定积度也如是缩历者正加天正黄道箕
共得为黄道定积度也如是缩历者正加天正黄道箕宿度内减去七十五秒馀为黄道定积度也无论盈缩
历皆以其黄道各宿次积度钤挨及减之馀为食甚月
离黄道某宿次度分也
按月食黄道之积度者逆计月离度前距天正日躔
宿度之数也元推食甚入盈缩历行定度则是所求
日躔距天正宿度数乃月食所冲也如日在北正月
食于南正故盈历加半周天便是食甚月离宿度又
卷八 第 21b 页 WYG0795-0949b.png
 加天正箕宿度便知食甚月离距天正黄道箕宿初
加天正箕宿度便知食甚月离距天正黄道箕宿初度若干也其缩历行定度则是日躔距夏至宿度数
故即用其数为月离盖月食日冲日躔夏至宿后第
几度月食亦即在冬至宿后第几度故不必加半周
天也内减去七十五秒者盈历缩历相距半岁周不
及半周天七十五秒其今岁缩历以后距来岁盈历
亦止半岁周若论其后距本岁盈历则反多一分五
十秒即多于半周天七十五秒也减此益彼即各相
卷八 第 22a 页 WYG0795-0949c.png
 距半周天平分天度而相望其冲也其止加天正箕
距半周天平分天度而相望其冲也其止加天正箕宿度意同盈历其不问盈缩皆减黄道积度钤是算
外命宿度同日食不赘
依授时历经黄赤道法(勿庵/补定)
求四正后赤道积度
置天正冬至所在宿赤道全度以天正赤道减之馀为
距后度以赤道宿度累加之即得其宿距冬至后赤道
积度加满象限去之为四正宿距后度亦以赤道宿度
卷八 第 22b 页 WYG0795-0949d.png
 累加之满象限去之即各得其宿距春分夏至秋分后
累加之满象限去之即各得其宿距春分夏至秋分后赤道积度
按四正者四时正气即二至二分也凡天正赤道度
是前距其宿初度之数故以减其宿全度即各得后
距其宿末度之数也于是以后宿赤道累而加之即
知各至后各宿距冬至度所积之度也满象限去之
者加满象限是其宿当四正所在故减去象限即知
四正所在后距其宿末度之数也于是又以赤道各
卷八 第 23a 页 WYG0795-0950a.png
 宿度累而加之即各得四正后每象宿所距四正度
宿度累而加之即各得四正后每象宿所距四正度之数也
求赤道变黄道
置各宿距四正后赤道积度用黄赤道立成视在至后
者以第三格赤道积度相挨者减之馀(有十定三/有分定二)为实
以上第二格黄道率乘之(不用乘只/加定四子)以下第四格黄道
率为法除之(有度去四有十去三不满法再去/一视定有四子为度三子为十分)加入第
一格黄道积度即为其宿距至后黄道积度其夏至后
卷八 第 23b 页 WYG0795-0950b.png
 再加半周天即各得其宿距天正黄道积度也若在分
再加半周天即各得其宿距天正黄道积度也若在分后者以第一格赤道积度相同者减之只用小馀(有十/定三)
(有分/定二)为实以下第四格黄道率为法(有度定四/空度定三)乘之(言/十)
(定/一)得数以上第二格赤道率除之(不用除只去四子视/定有四子为度三子)
(为十/分)加入第三格黄道积度即得其宿距分后积度其
春分后再加一象限其秋分后再加三象限即各得其
宿距天正黄道积度也于是各置其宿距天正黄道积
度以其前宿黄道积度减之即各得其宿黄道本度也
卷八 第 24a 页 WYG0795-0950c.png
 秒就近约为分
秒就近约为分按至后不用乘者其立成黄道率只是一度乘过数
不动故只加定四子也分后不用除者其立成赤道
率亦是一度除过数亦不动故只虚去四子也夏至
后加半周天春分后加一象限秋分后加三象限者
此所求黄道积度皆距四正起算故各以四正距天
正黄道数加之即其宿前距天正之数也盖至后黄
道虽减于赤道分后黄道虽加于赤道其实至四立
卷八 第 24b 页 WYG0795-0950d.png
 之后则加之极而反减减之极而反加总计一象皆
之后则加之极而反减减之极而反加总计一象皆得九十一度有奇此天道所以如环平陂往复间不
容发也减前宿积度为其宿本度者积度既是距天
正数原包有前宿在内故减之即得本度也(秒就近/约为分)
(者凡秒五十已上收为分已下弃/之就整数也其七十五秒寄虚度)
求天正冬至黄道度
置周天度三百六十五度二五七五内减去天正前一
宿距天正黄道积度馀命为天正冬至宿黄道度分也
卷八 第 25a 页 WYG0795-0951a.png
 若径求者置象限以其年天正赤道度减之馀为天正
若径求者置象限以其年天正赤道度减之馀为天正前宿距秋分后赤道积度依赤道变黄道法求出其宿
距分后黄道积度以减象限馀即命为天正黄道度
按周天度是自天正后积至天正前黄道总数故减
去前宿距天正黄道积度即得天正距所在宿初度
之数也径求法除象限者即是自天正前距秋分后
赤道总数也内减去天正赤道度其馀即是前宿距
秋分后赤道积度也赤道变黄道法即是以立成第
卷八 第 25b 页 WYG0795-0951b.png
 一格积度减馀以第四格度率乘以第一格度率除
一格积度减馀以第四格度率乘以第一格度率除加入第三格积度而命为前宿距秋分后黄道积度
也又以减象限者此所为象限即是自天正前距秋
分后黄道总数故减去前宿距秋分黄道积度其馀
即是天正冬至距其宿初度黄道之数也
求黄道宿积度定钤
置天正冬至宿黄道度及分如入其宿距至后黄道积
度及分共得为天正冬至宿黄道定积度以各宿黄道
卷八 第 26a 页 WYG0795-0951c.png
 度累加之即各得其宿黄道定积度
度累加之即各得其宿黄道定积度按分至每岁有差黄道即因而易即不能每岁步之
当于六十六年岁差一度时更定度钤始为无弊也
凡冬至所在宿皆有前后距其黄道皆减于赤道今
所推其宿至后积度是自冬至日躔后距其宿末度
黄道数其天正黄道宿度则是自冬至日躔前距其
宿初度黄道数也合二数则是自其宿初度距其宿
末度总数故即命为天正宿定积度也于是以各宿
卷八 第 26b 页 WYG0795-0951d.png
 黄道度累加之即各得其宿所距天正宿初度之数
黄道度累加之即各得其宿所距天正宿初度之数而命为定积度也
求日月食甚宿次黄道度及分秒法同通轨
又术置所推食甚盈缩历缩历加半周天为黄道定积
度月食盈缩历俱加半周天满周天分去之为黄道定
积度皆径以距天正黄道积度相挨者减之即各得日
月食甚黄道宿度及分秒
按此法不用定积度钤故亦不加天正黄道度然必
卷八 第 27a 页 WYG0795-0952a.png
 每年步定黄道积度方可用之也
每年步定黄道积度方可用之也赤道宿度
角十二(一/十) 亢九(二/十) 氐十六(三/十)
房五(六/十) 心六(五/十) 尾十九(一/十)
箕十(四/十)
右东方七宿七十九度二十分
斗二十五(二/十) 牛七(二/十) 女十一(三/五)
虚八(九十/五太) 危十五(四/十) 室十七(一/十)
卷八 第 27b 页 WYG0795-0952b.png
 壁八(六/十)
壁八(六/十)右北方七宿九十三度八十分太
奎十六(六/十) 娄十一(八/十) 胃十五(六/十)
昴十一(三/十) 毕十七(四/十) 觜初(五/)
参十一(一/十)
右西方七宿八十三度八十五分
井三十三(三/十) 鬼二(二/十) 柳十三(三/十)
星六(三/十) 张十七(二十/五) 翼十八(七十/五)
卷八 第 28a 页 WYG0795-0952c.png
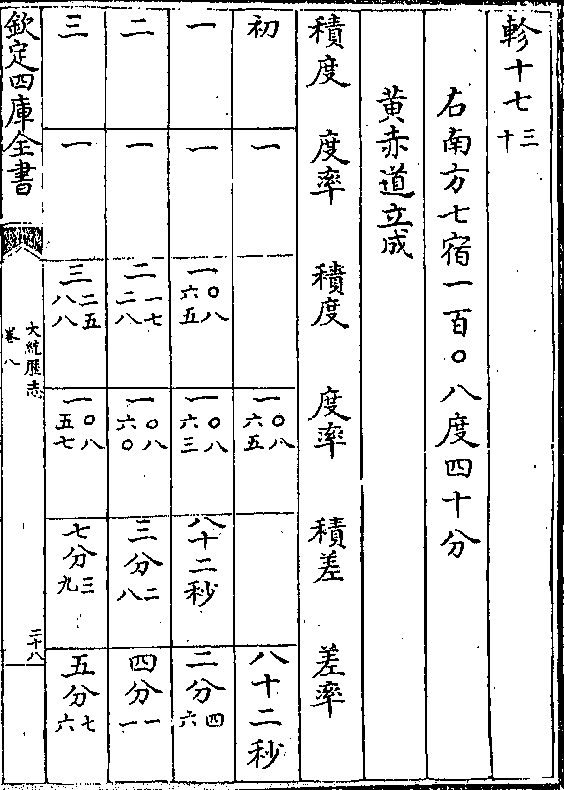 轸十七(三/十)
轸十七(三/十)右南方七宿一百○八度四十分
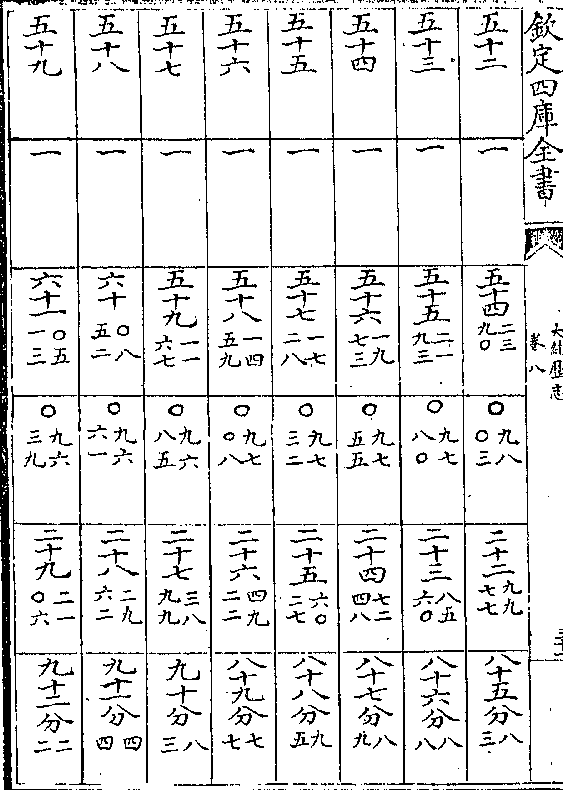
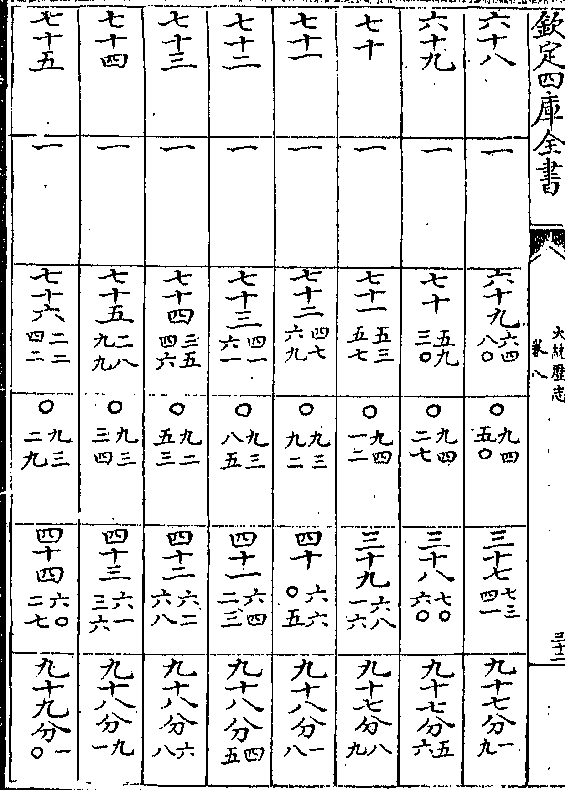
黄赤道立成
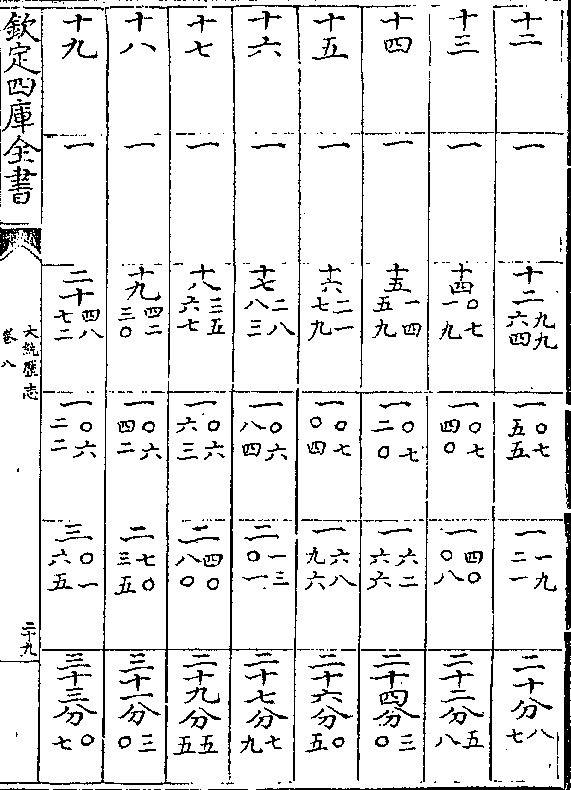
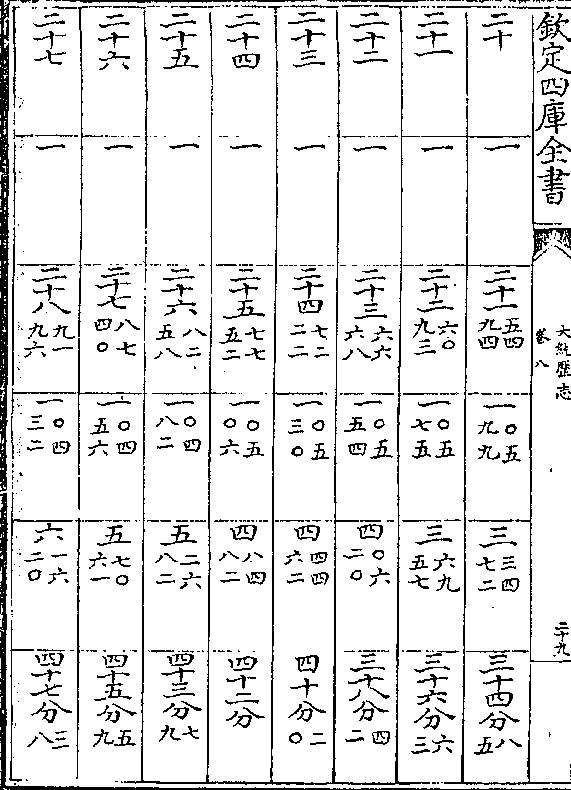
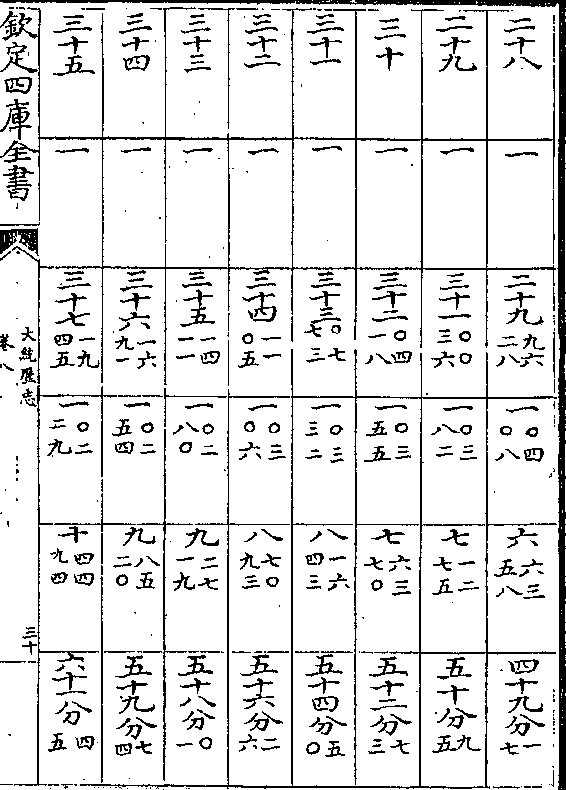
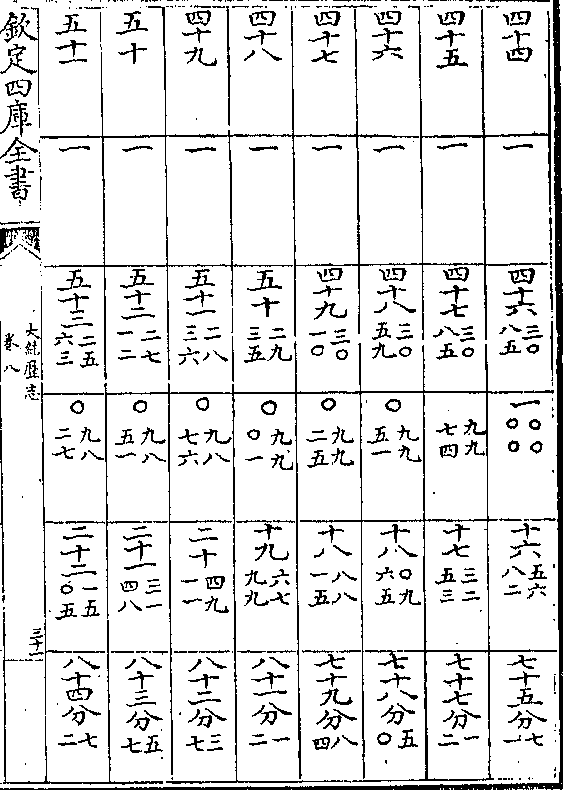
积度 度率 积度 度率 积差 差率
卷八 第 28b 页 WYG0795-0952d.png

卷八 第 29a 页 WYG0795-0953a.png
卷八 第 29b 页 WYG0795-0953b.png
卷八 第 30a 页 WYG0795-0953c.png
卷八 第 30b 页 WYG0795-0953d.png

卷八 第 31a 页 WYG0795-0954a.png
卷八 第 31b 页 WYG0795-0954b.png
卷八 第 32a 页 WYG0795-0954c.png

卷八 第 32b 页 WYG0795-0954d.png
卷八 第 33a 页 WYG0795-0955a.png

卷八 第 33b 页 WYG0795-0955b.png

卷八 第 34a 页 WYG0795-0955c.png
卷八 第 34b 页 WYG0795-0955d.png

卷八 第 35a 页 WYG0795-0956a.png
 附郭守敬传
附郭守敬传初刘秉忠以大明历自辽金承用二百馀年浸以后天
议欲脩正而卒十三年江左既平世祖思用其言遂以
守敬与王恂率南北日官分掌测验推步于下而命张
文谦与枢密张易为之主领裁奏于上左承许衡参预
其事守敬首言历之本在于测验而测验之器莫先仪
表今司天浑仪宋皇祐中汴京所造不与此处天度相
符比量南北二极约差四度表石年深亦复欹侧守敬
卷八 第 35b 页 WYG0795-0956b.png
 乃尽考其失而移置之既又别图高爽地以木为重棚
乃尽考其失而移置之既又别图高爽地以木为重棚创作简仪高表用相比覆又以为天枢附极而动昔人
尝展管望之未得其的作候极仪极辰既位天体斯正
作浑天象象虽形似莫适所用作玲珑仪以表之矩方
测天之正圜莫若以圜求圜作仰象古有经纬结而不
动守敬易之作立运仪日有中道月有九行守敬一之
作證理仪表高景虚罔象非真作景符月虽有明察景
则难作窥几历法之验在于交会作日月食仪天有赤
卷八 第 36a 页 WYG0795-0956c.png
 道轮以当之两极低昂标以指之作星晷定时仪又作
道轮以当之两极低昂标以指之作星晷定时仪又作正方案九表悬正仪座正仪为四方行测者所用又作
仰规覆矩图异方浑盖图日出入永短图与上诸仪互
相参考十六年改局为太史院以恂为太史令守敬为
同知太史院事给印章立官府及奏进仪表式守敬当
帝前指陈理数至于日晏帝不为倦守敬因奏唐一行
开元间令南宫说天下测景书中见者凡十三处今疆
宇比唐犹大若不远方测验日月交食分数时刻不同
卷八 第 36b 页 WYG0795-0956d.png
 昼夜长短不同日月星辰去天高下不同即日测验人少可先南北立
昼夜长短不同日月星辰去天高下不同即日测验人少可先南北立表取直测景帝可其奏遂设监候官一十四员分道而
出东至高丽西极滇池南踰珠崖北尽铁勒四海测验
凡二十七所十七年新历告成守敬与诸臣同上奏曰
臣等窃闻帝王之事莫重于历自黄帝迎日推策帝尧
以闰月定四时成岁舜在璇玑玉衡以齐七政爰及三
代历无定法周秦之间闰馀乖次西汉造三统历百二
十年而后是非始定东汉造四分历七十年而仪式方
卷八 第 37a 页 WYG0795-0957a.png
 备又百二十一年刘洪造乾象历始悟月行有迟疾及魏黄
备又百二十一年刘洪造乾象历始悟月行有迟疾及魏黄初间始以日食课其疏密魏杨伟作景初历始立交食起
亏术又百八十年姜岌造三纪甲子元历始悟以月食推验
日宿度所在又五十七年何承天造元嘉历始悟以朔望及
弦皆定大小馀及以晷景验气又六十五年祖冲之造大明
历始悟太阳有岁差之数极星去不动处一度馀又五
十二年张子信始悟日月交道有表里五星有迟疾留逆
又三十三年张胄玄造大业历始立五星入气加减法及月
卷八 第 37b 页 WYG0795-0957b.png
 应食不食术刘焯造皇极历始悟日行有盈缩及立推黄道
应食不食术刘焯造皇极历始悟日行有盈缩及立推黄道月道又三十五年傅仁均造戊寅元历颇采旧议始用定
朔又四十六年李淳风造麟德历以古历章蔀元首分度
不齐始为总法用进朔以避晦晨月见又六十三年一行
造大衍历始以朔有四大三小定九服交食轨漏之异及
创立岁星差合术又九十四年徐昂造宣明历始悟日食有
气刻时三差人七十二年边冈造崇玄历始立相减相乘法
以求黄道月道又六十三年王朴造钦天历始变五星法迟
卷八 第 38a 页 WYG0795-0957c.png
 留逆行舒亟有渐又九十八年周琮造明天历始悟日
留逆行舒亟有渐又九十八年周琮造明天历始悟日法积年自然之数又三十六年姚舜辅造纪元历始悟
食甚泛馀差数以上计千一百八十二年历经七十改
其创法者十有三家自是又百七十四年圣朝专命臣
等改修新历臣等用创造简仪高表凭其测实数所考
正者凡七事一日冬至自丙子年立冬后依每日测到
晷景逐日取对冬至前后日差同者为准得丁丑年冬
至在戊戌日夜半后八刻半又定丁丑夏至在庚子日
卷八 第 38b 页 WYG0795-0957d.png
 夜半后七十刻又定戊寅冬至在癸卯日夜半后三十
夜半后七十刻又定戊寅冬至在癸卯日夜半后三十三刻巳卯冬至在戊申日夜半后五十七刻庚辰冬至
在癸丑日夜半后八十一刻各减大明历十八刻远近
相符前后应准二曰岁馀自大明历以来凡测景验气
得冬至时刻真数者有六用以相距各得其时合用岁
馀考验四年相符不差仍自宋大明壬寅年距至今日
八百一十年每岁合得三百六十五日二十四刻二十
五分其二十五分为今历岁馀合用之数三曰日躔用
卷八 第 39a 页 WYG0795-0958a.png
 至元丁丑四月癸酉望月食既推求日躔得冬至日躔
至元丁丑四月癸酉望月食既推求日躔得冬至日躔赤道箕宿十度黄道箕九度有奇仍凭每日测到太阳
躔度或凭星测月或凭月测日或径凭星度测日立术
推算起自丁丑正月至巳卯十二月凡三年共得一百
三十四事皆躔于箕与月食相符四曰月离自丁丑以
来至今凭每日测到逐时太阴行度推算变从黄道求
入转极迟疾并平行处前后凡若干转计五十一事内
除去不真的外有三十事得大明历入转后天又因考
卷八 第 39b 页 WYG0795-0958b.png
 验交食加大明历三十刻与天道合五曰入交自丁丑
验交食加大明历三十刻与天道合五曰入交自丁丑五月以来凭每日测到月道去极度数比拟黄道去极
度得月道交于黄道出入度仍依日食法度推求皆有
食分得入交时刻与大明历所差不多六曰二十八宿
距度自汉太初历以来距度不同互有损益大明历则
于度下馀分附以太半少皆私意牵就未尝实测其数
今新仪皆细刻周天度分每度为三十六分以距线代
管窥宿度馀分并依实测不以私意牵就七曰日出入
卷八 第 40a 页 WYG0795-0958c.png
 昼夜刻大明历日出入昼夜刻皆据汴京为准其刻数与大都不同今更
昼夜刻大明历日出入昼夜刻皆据汴京为准其刻数与大都不同今更以本方北极出地高下黄道出入内外度立术推求每日日
出入昼夜刻得夏至极长日出寅正二刻日入戌初二
刻昼六十二刻夜三十八刻冬至极短日出辰初二刻
日入申正二刻昼三十八刻夜六十二刻永为定式所
创法凡五事一曰太阳盈缩用四正定气立为升降限
依立招差求得每日行分初末极差积度比古为密二
曰月行迟疾古历皆用二十八限今以万分日之八百
卷八 第 40b 页 WYG0795-0958d.png
 二十分为一限凡析为三百三十六限依垛叠招差求
二十分为一限凡析为三百三十六限依垛叠招差求得转分进退其迟疾度数逐时不同盖前所未有三曰
黄赤道差旧法以一百一度相减相乘今依算术勾股
弧矢方圆斜直所容求到度数积差差数与天道实吻
合四曰黄赤道内外度据累年实测内外极度二十三
度九十分以圆容方直矢截勾股为法求每日去极与
所测相符五曰白道交周旧法黄道变推白道以斜求
斜今用立浑比量得月与赤道正交距春秋二正黄赤
卷八 第 41a 页 WYG0795-0959a.png
 道正交一十四度六十六分拟以为法推逐月每交二
道正交一十四度六十六分拟以为法推逐月每交二十八宿度分于理为尽十九年恂卒时历虽颁然其推
步之法与夫立成之数尚皆未有定稿守敬于是比次
篇类整齐分秒裁为推步七卷立成二卷历议拟稿三
卷转神选择二卷上中下三历注式十二卷二十三年
继为太史令遂上表奏进又有时候笺注二卷修改源
流一卷其测验书有像象法式二卷二至晷景考二十
卷五星细行考五十卷古今交食考一卷新测二十八
卷八 第 41b 页 WYG0795-0959b.png
 舍杂坐诸星入宿去极一卷新测无名诸星一卷月离
舍杂坐诸星入宿去极一卷新测无名诸星一卷月离考一卷并藏之官
大统历志卷八