声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
卷一 第 1a 页 WYG0795-0820c.png
 钦定四库全书
钦定四库全书大统历志卷一
宣城梅文鼎撰
大统历法一
法源
史载历法必载其所以历法之原如太初诸历起数钟
律一行大衍求端河洛是也古今历法惟授时历独以
测验算术为宗以为与天既合则律吕之损益易象之
卷一 第 1b 页 WYG0795-0820d.png
 奇偶悉在其中不必一一牵附矣考郭守敬传有修改
奇偶悉在其中不必一一牵附矣考郭守敬传有修改源流一卷仪像法式二卷历议拟稿三卷二至晷景考
二十卷五星细行考五十卷古今交食考一卷新测二
十八舍杂坐诸星入宿去极一卷新测无名星一卷并
藏之官又齐履谦传之授时历有经串经以著定法串
以纪成数履谦又作经串演撰八法一卷以求其法之
所以然数之所从出作元史者漫无采摭而仅存履谦
之历议录历经之初稿及仪象大略而已其三应改率
卷一 第 2a 页 WYG0795-0821a.png
 及立成之数与夫黄赤道割圆弧矢之法日月五星平
及立成之数与夫黄赤道割圆弧矢之法日月五星平立定三差之原尽削不载使作者精意湮没识者憾焉
今据大统历及通轨及历草诸书稍为铨次著于篇而
仍以法原为首其目七曰勾股测望曰弧矢割圆曰黄
赤道差曰黄赤道内外度曰白道交周曰日月五星平
立定三差曰里差刻漏
勾股测望
北京立四丈表冬至日测得正午景长七丈九尺八寸
卷一 第 2b 页 WYG0795-0821b.png
 五分 以简仪测到冬至日南至地平二十六度四十
五分 以简仪测到冬至日南至地平二十六度四十六分五十秒为半弧背 求得矢度五度九十一分半
置周天半径截矢馀五十四度九十六分为股乃本
地去戴日下之度 以弦股别勾术求得勾二十六度
一十七分六十六秒为日下至地度即冬至日出地半
弧弦 北京立四丈表夏至日测得正午景长一丈一
尺七十一分(按元史作一丈/二尺三寸六分) 以简仪测到夏至日南
至地平七十四度二十六分半为半弧背 求得矢度
卷一 第 3a 页 WYG0795-0821c.png
 四十三度七十四分少 置周天半径截矢馀一十七
四十三度七十四分少 置周天半径截矢馀一十七度一十三分二十五秒为勾乃本地去戴日下之度以
勾弦别股术求得股五十八度四十五分半为日下至
地度即夏至日出地半弧弦 以二至日度相并得一
百度七十三分折半得五十度三十六分半为北京赤
道出地度转减周天四之一馀四十度九十四分九十
三秒七十五微为北京北极出地度
弧矢割圆
卷一 第 3b 页 WYG0795-0821d.png
 周天径一百二十一度七十五分少
周天径一百二十一度七十五分少半径六十○度八十七分半(又为黄赤/道大弦)
二至黄赤道内外半弧背二十四度(所测/就整)
二至黄赤道弧矢四度八十四分八十二秒
黄赤道大勾二十三度八十分七十秒
黄赤道大股五十六度○二分六十八秒
割圆求矢术 置半弧背度自之为半弧背羃周天径
自之为径羃又为上廉 二羃相乘得数为正实 径
卷一 第 4a 页 WYG0795-0822a.png
 羃乘径得数为益从方 半弧背倍之乘径得数为下
羃乘径得数为益从方 半弧背倍之乘径得数为下廉置初商为上法以乘上廉得数以减益从方馀为从
方 置初商自之以减下廉馀以初商乘之得数为从
廉 从方从廉相并为下法 下法乘上法以减正寔
而定初商有不尽者次第商除则次商又为上法 置
初商倍之得数与次商相并以乘上廉得数以减益从
方馀为从方 并初商次商而自之又以初商自之并
二数以减下廉馀以初商倍数并次商乘之得数为从
卷一 第 4b 页 WYG0795-0822b.png
 廉从方从廉相并为下法 下法乘上法以减馀寔而
廉从方从廉相并为下法 下法乘上法以减馀寔而定次商有不尽者如法商之
皆以商得数为矢度之数(黄赤道/同用)
如以半弧背一度求矢度 术曰置半弧背一度自之
得一度为半弧背羃 置周天径一百二十一度太自
之得一万四千八百二十三度○六分二十五秒为径羃
(又为/上廉)
二羃相乘得一万四千八百二十三度○六分二五为
卷一 第 5a 页 WYG0795-0822c.png
 正寔 径羃又乘径得一百八十○万四千七百○七
正寔 径羃又乘径得一百八十○万四千七百○七度八十五分九十三秒七五为益从方 半弧背一度
倍之得二度以乘径得二百四十三度五十分为下廉
初商八十秒(为上/法) 置初商八十秒乘上廉一万四千
八百二十三度○六二五得一百一十八度五八四五
以减益从方一百八十○万四千七百○七度八五九
三七五馀一百八十○万四千五百八十九度二七四
八七五为从方 又置初商八十秒自之得六十四微
卷一 第 5b 页 WYG0795-0822d.png
 以减下廉馀二百四十三度四九九九九三六仍以八
以减下廉馀二百四十三度四九九九九三六仍以八十秒乘之得一度九四七九九九四八八为从廉 以
从廉从方并之共得一百八十○万四千五百九十一
度二三二八七四四八八为下法 下法乘上法得一
万四千四百三十六度七十二分九七八二九九五九
○四以减正寔馀寔三百八十六度三十三分二七一
七○○四○九六
次啇二秒(为上/法) 置初啇八十秒倍之得一分六十秒
卷一 第 6a 页 WYG0795-0823a.png
 加次啇二秒得一分六十二秒乘上廉一万四千八百
加次啇二秒得一分六十二秒乘上廉一万四千八百二十三度○六二五得一分六十二秒乘上廉一万四
千八百二十三度○六二五得二百四十○度一二三
六一二五以减益从方馀一百八十○万四千四百六
十七度七二五七六二五为从方 又置初次啇八十
二秒自之得六十七微加初啇八十秒自之数得一秒
三十一微以减下廉馀二百四十三度四九九八六九
以前所得一分六十二秒乘之得三度九十四分四六
卷一 第 6b 页 WYG0795-0823b.png
 九七八七七八为从廉 以从廉从方并得一百八十
九七八七七八为从廉 以从廉从方并得一百八十○万四千四百七十一度六十七分○四六○三七七
八为下法 下法乘上法得二百六十○度八九四三
三四○九二○七五五六以减馀寔仍馀二十五度四
三八三八二九一二○二○四四(不足一秒弃/不用后同)
凡求得矢度八十二秒
如以半弧背二度求矢度用上法得矢三分二十八秒
如以半弧背二十四度求矢度用上法得矢四度八十
卷一 第 7a 页 WYG0795-0823c.png
 四分八十二秒
四分八十二秒如以半弧背四十四度求矢度用上法得矢一十六度
五十六分八十二秒
馀度各如上法求到矢度以为黄赤相求及其内外度
之根(数详/后)
黄赤道差
求黄道各度下赤道积度术 置周天半径度分内减
去黄道矢度馀为黄赤道小弦 置黄赤道小弦以黄
卷一 第 7b 页 WYG0795-0823d.png
 赤道大股乘之(大股见/割圆)为寔黄赤道大弦(半/径)为法寔如
赤道大股乘之(大股见/割圆)为寔黄赤道大弦(半/径)为法寔如法而一为黄赤道小股 置黄道矢自乘为寔以周天
全径为法寔如法而一为黄道半背弦差 以差去减
黄道积度(即黄道/半弧背)馀为黄道半弧弦 置黄道半弧弦
自之为股羃黄赤道小股自之为勾羃二羃并之以开
平方法除之为赤道小弦 置黄道半弧弦以周天半
径(亦为赤/道大弦)乘之为寔以赤道小弦为法而一为赤道半
弧弦 置黄赤道小股(亦为赤道/横小勾)以赤道大弦(即周天/半径)
卷一 第 8a 页 WYG0795-0824a.png
 乘之为寔以赤道小弦为法而一为赤道横大勾以减
乘之为寔以赤道小弦为法而一为赤道横大勾以减半径馀为赤道横弧矢 横弧矢自之为寔以周天全
径为法而一为赤道半背弦差 以差加赤道半弧弦
为赤道积度 如黄道半弧背一度求赤道积度 术
曰置周天半径六十○度八十六分五十秒(即黄赤/道大弦)内
减黄道矢八十二秒馀六十○度八六六八为黄赤道
小弦 置黄赤道小弦以黄赤道大股五十六度○二
六八乘之得三千四百一十○度一七二○三○二四
卷一 第 8b 页 WYG0795-0824b.png
 为寔以黄赤道大弦六十○度八七五为法寔如法而
为寔以黄赤道大弦六十○度八七五为法寔如法而一得五十六度○一分九十二秒为黄赤道小股(又为/赤道)
(小/勾) 置矢度八十二秒自之得六十七微以周天径一
百二十二度七五为法除之得五十五纤为黄道半背
弦差 置黄道弦背一度内减黄道半弧背差馀为半
弧弦因差在微以下不减即用一度为半弧弦 置黄
道半弧弦一度自之得一度为股羃 黄赤道小股五
十六度○一九二自之得三千一百三十八度一五○
卷一 第 9a 页 WYG0795-0824c.png
 七六八六四为勾羃二羃并得三千一百三十九度空
七六八六四为勾羃二羃并得三千一百三十九度空七六八六四为弦寔平方开之得五十六度○二八一
为赤道小弦 置黄道半弧弦一度以周天半径(即赤/道大)
(弦/)乘之得六十○度八七五为寔以赤道小弦五十六
度○二八一为法除之得一度○八分六十五秒为赤
道半弧弦 置黄赤道小股五十六度○一九二(又为/赤道)
(小/勾)以赤道大弦半径六十○度八七五乘之得三千四
百一十○度一六八八为寔以赤道小弦为法除之得
卷一 第 9b 页 WYG0795-0824d.png
 六十○度八十六分五十三秒为赤道横大勾 置半
六十○度八十六分五十三秒为赤道横大勾 置半径六十○度八十七分五十秒内减赤道大勾六十○
度八十六分五十三秒馀九十七秒为赤道横弧矢
置赤道横弧矢九十七秒自之得九十四微○九以周
天径为法除之得七十七纤为赤道背弦差 置赤道
半弧弦一度○八分六十五秒加赤道背弦差为赤道积
度今差在微以下不加即用半弧弦为积度 凡求得
赤道积度一度○八分六十五秒如黄道二度下赤道
卷一 第 10a 页 WYG0795-0825a.png
 积度二度一十七分二十八秒
积度二度一十七分二十八秒如求黄道二十四度下赤道积度用上法得赤道积度
二十五度七十七分五十二秒
如求黄道四十四度下赤道积度用上法得赤道积度
四十六度三十○分八十五秒
馀度各如上法求到各黄道度下赤道积度乃至后之
率其分后以赤道度求黄道及此求之得数并同
卷一 第 10b 页 WYG0795-0825c.png
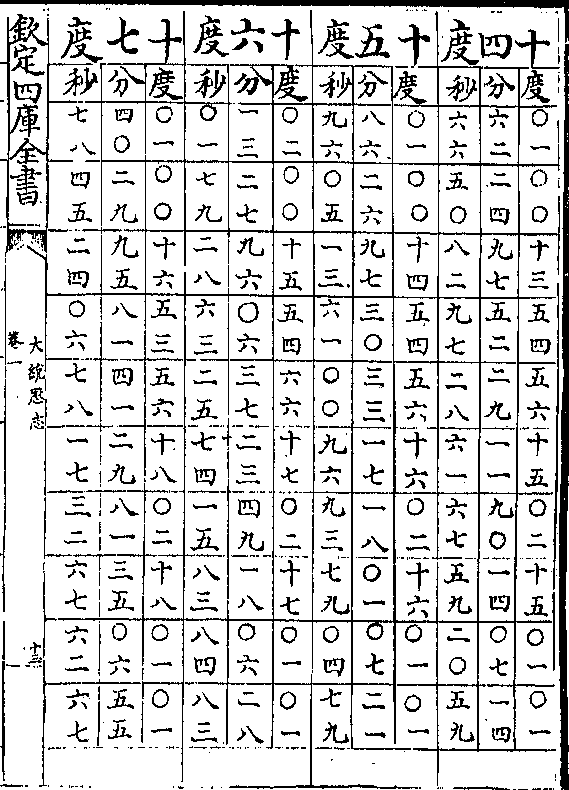
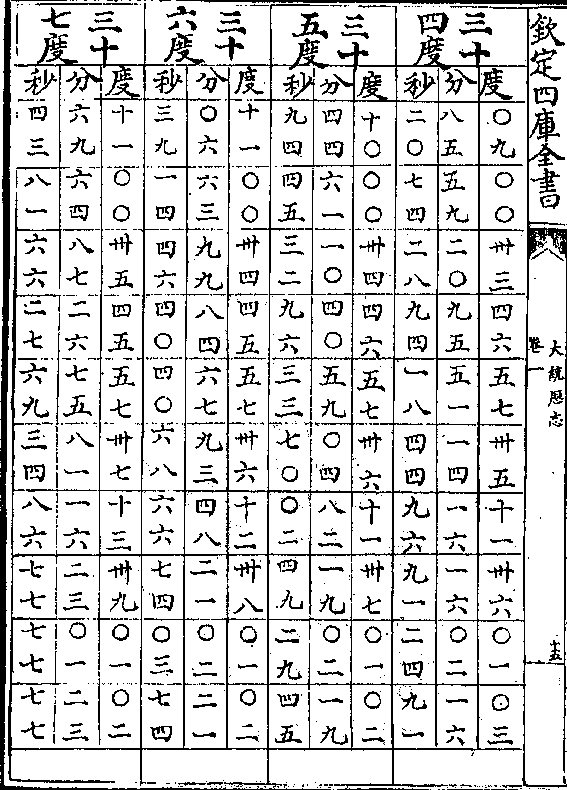
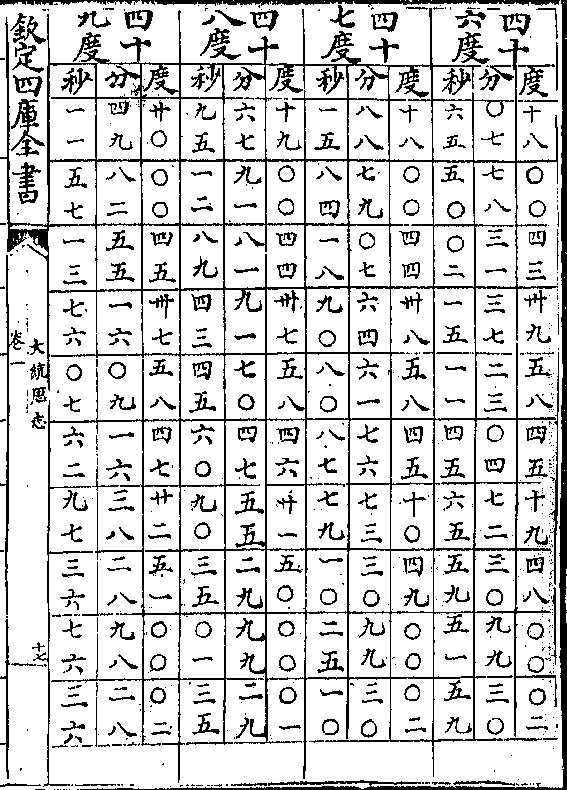
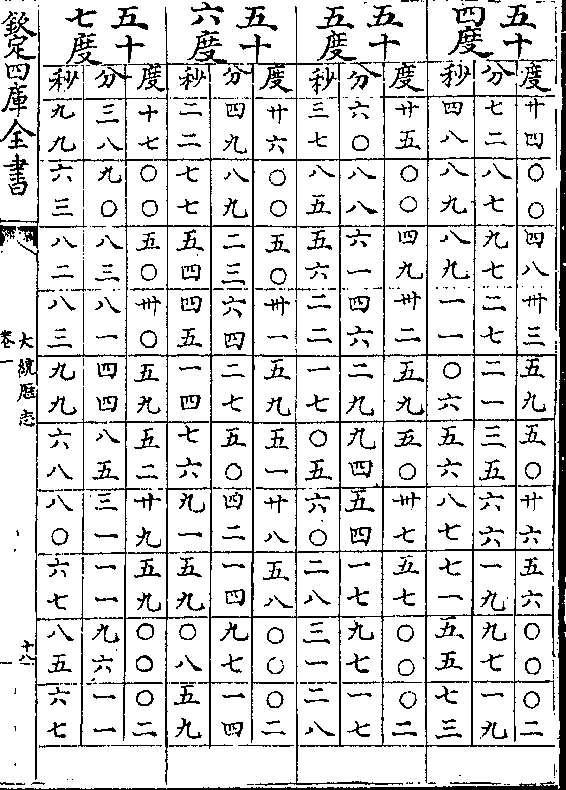
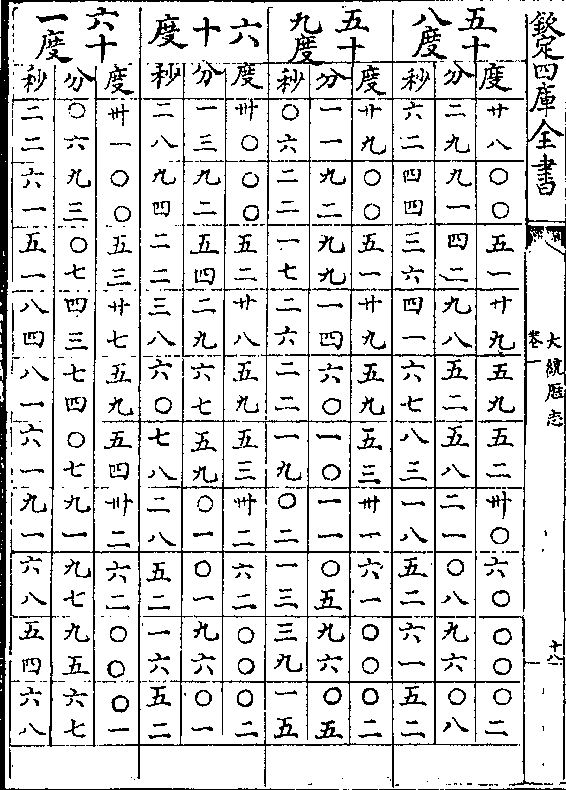
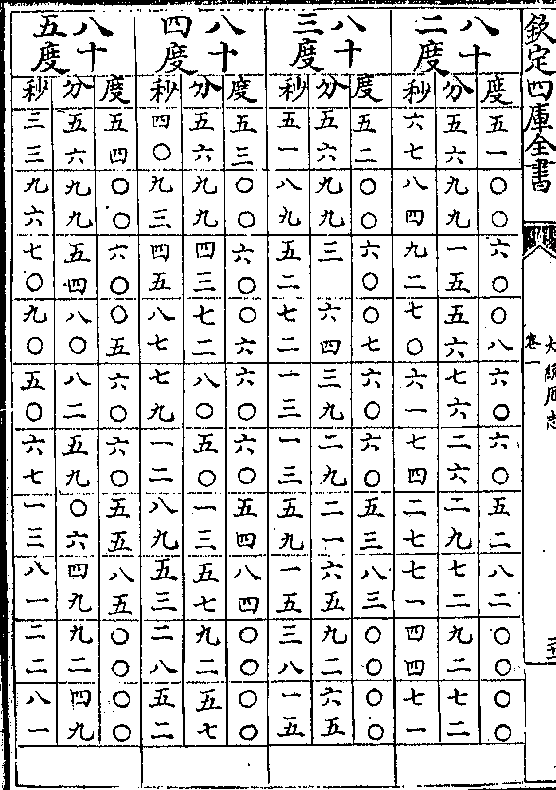
 黄赤道相求弧矢诸率立成
黄赤道相求弧矢诸率立成卷一 第 11a 页 WYG0795-0825d.png

卷一 第 11b 页 WYG0795-0826a.png

卷一 第 12a 页 WYG0795-0826b.png

卷一 第 12b 页 WYG0795-0826c.png
卷一 第 13a 页 WYG0795-0826d.png

卷一 第 13b 页 WYG0795-0827a.png

卷一 第 14a 页 WYG0795-0827b.png

卷一 第 14b 页 WYG0795-0827c.png

卷一 第 15a 页 WYG0795-0827d.png
卷一 第 15b 页 WYG0795-0828a.png

卷一 第 16a 页 WYG0795-0828b.png

卷一 第 16b 页 WYG0795-0828c.png
卷一 第 17a 页 WYG0795-0828d.png

卷一 第 17b 页 WYG0795-0829a.png
卷一 第 18a 页 WYG0795-0829b.png
卷一 第 18b 页 WYG0795-0829c.png

卷一 第 19a 页 WYG0795-0829d.png

卷一 第 19b 页 WYG0795-0830a.png

卷一 第 20a 页 WYG0795-0830b.png

卷一 第 20b 页 WYG0795-0830c.png

卷一 第 21a 页 WYG0795-0830d.png
卷一 第 21b 页 WYG0795-0831a.png

卷一 第 22a 页 WYG0795-0831b.png

按郭守敬创法五端内一曰黄赤道差此其根率也
旧法以一百一度相减相乘授时立术以勾股弧矢
卷一 第 22b 页 WYG0795-0832a.png

方圆斜直所容求其差数合于浑象之理视古为密
顾至元历经所载甚略又误以黄道矢度为积差黄
道矢差为差率今正之
卷一 第 23a 页 WYG0795-0832b.png

卷一 第 23b 页 WYG0795-0833a.png

卷一 第 24a 页 WYG0795-0833b.png
卷一 第 24b 页 WYG0795-0834a.png
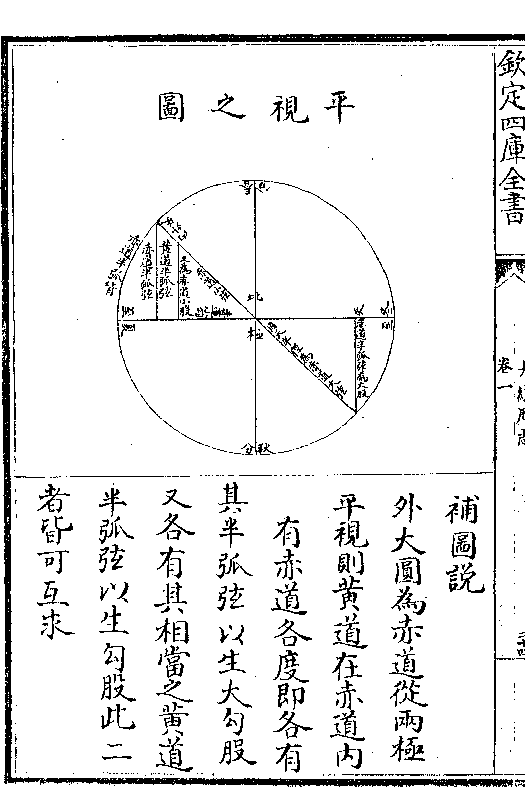
 按旧史无图然表亦图之属也今勾股割圆弧矢黄
按旧史无图然表亦图之属也今勾股割圆弧矢黄赤道推变诸法寔为历家测算之本非图不明因存
其要者数端
卷一 第 25a 页 WYG0795-0834b.png

大统历志卷一