声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
卷二 第 1a 页 WYG0786-0482c.png
 钦定四库全书
钦定四库全书圣寿万年历卷二
明 朱载堉 撰
步月离第五
月平行十三度三十六分八十七秒半
离周三百三十六限十六分六十秒
离中百六十八限八分三十秒
离象八十四限四分十五秒
卷二 第 1b 页 WYG0786-0482d.png
 转周二十七日五十五刻四十六分
转周二十七日五十五刻四十六分转中十三日七十七刻七十三分
转象六日八十八刻八十六分半
转差一日九十七刻六十分
转应七日五十刻三十四分
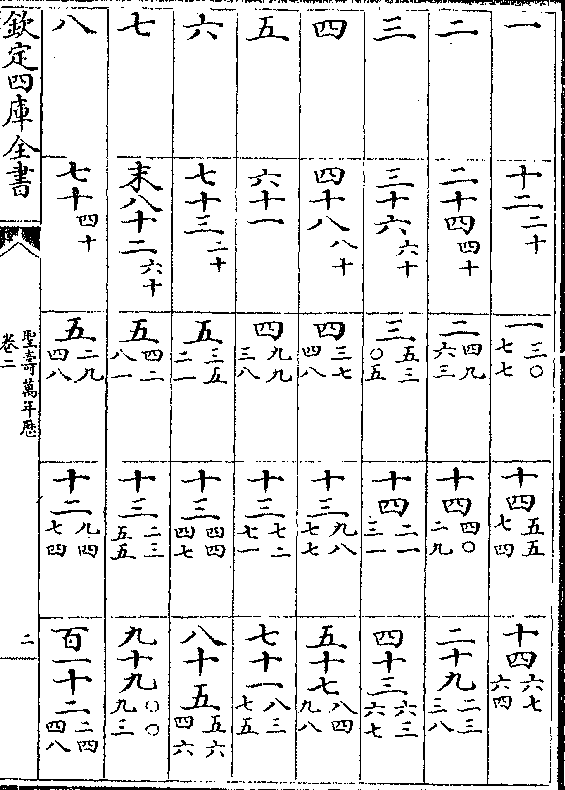
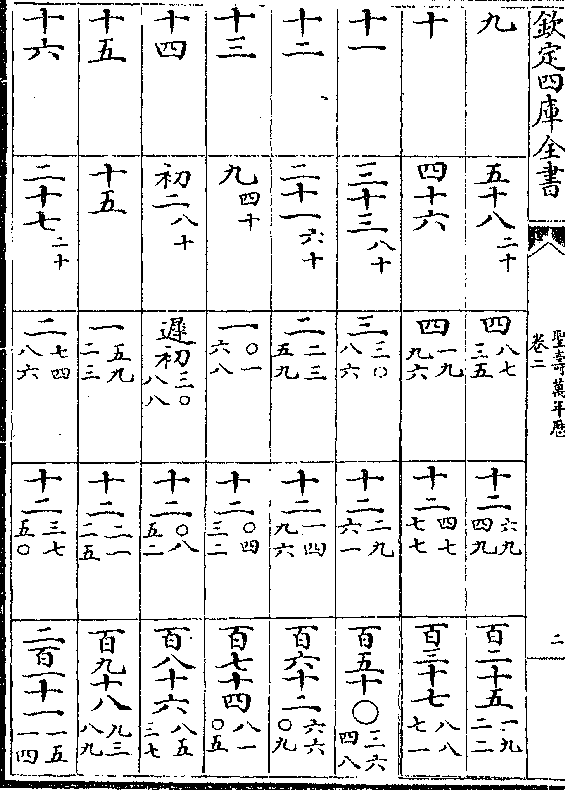
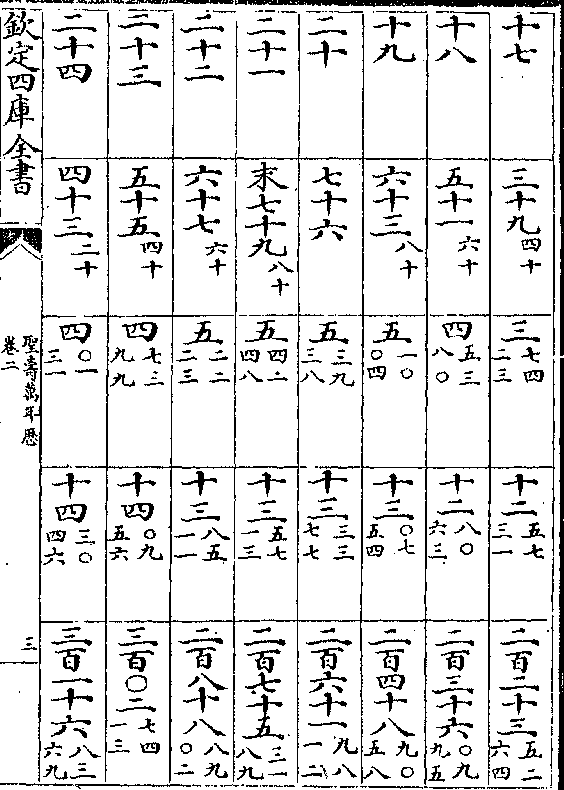
疾迟度率及积度
入转日 初末限 疾迟度 转度率 转积度
初 初 疾初 十四(六七六四) 初
卷二 第 2a 页 WYG0786-0483a.png
卷二 第 2b 页 WYG0786-0483b.png
卷二 第 3a 页 WYG0786-0483c.png
卷二 第 3b 页 WYG0786-0483d.png

求经朔弦望入转
置岁定积减去转应满转周去之不尽即所求入转大
小馀各加其月朔积及弦望策满转周去之为所求经
朔弦望入转大小馀若径求次朔入转以转差加之
求疾迟初末限
卷二 第 4a 页 WYG0786-0484a.png
 置入转大小馀以十二限二十分乘之在离中已下为
置入转大小馀以十二限二十分乘之在离中已下为疾已上减去离中为迟在离象已下为初已上反减离
中为末又法视入转大小馀在转中已下为疾已上减
去转中为迟在转象已下为初已上反减转中为末以
十二限二十分乘之为疾迟初末限
求疾迟差
置立差三秒二十五忽以所求限大馀乘之加平差二
分八十一秒又以限乘之用减定差千一百一十一分
卷二 第 4b 页 WYG0786-0484b.png
 馀再以限乘之满万为度不满退除为分秒如是求次
馀再以限乘之满万为度不满退除为分秒如是求次限积度相减馀为疾迟分以乘所得初末限下小馀万
约为分加入其限积度为疾迟差
求疾迟限下行度
置平行度及分秒以转象乘之八十四除之所得为一
限平行度不满退除为分秒以其限疾迟分疾初迟末
益迟初疾末损损益一限平行度为所入疾迟限下行
度
卷二 第 5a 页 WYG0786-0484c.png
 求加减差
求加减差置所求盈缩疾迟差各以八百二十乘之如所入疾迟
限下行度而一为分不满退除为秒盈迟名为加差缩
疾名为减差
求定朔弦望
置经朔弦望大小馀各以其加减差加减之满或不足
进退大馀即定朔弦望视前后定朔两千同者前月大
尽不同者前月小尽无中气者为闰月若定弦望小馀
卷二 第 5b 页 WYG0786-0484d.png
 在日出分已下者退一日
在日出分已下者退一日求定朔弦望加时及每日夜半晨昏入转
置经朔弦望入转大小馀以定朔弦望加减差加减之
为定朔弦望加时入转以定朔弦望小馀减之为定朔
弦望晨前夜半入转累加一日为每日晨前夜半入转
各以其日晨分加之为晨入转昏分加之为昏入转满
转周去之
求定朔弦望加时黄道日度
卷二 第 6a 页 WYG0786-0485a.png
 置经朔弦望入盈缩大小馀以加减差加减之为定朔
置经朔弦望入盈缩大小馀以加减差加减之为定朔弦望入历在盈便为积日在缩加岁中为积日命日为
度以盈缩差盈加缩减之为加时日行定积度以岁首
冬至加时黄道日度加而命之各得定朔弦望加时黄
道日度及分秒
求定朔弦望加时黄道月度
凡定朔加时日月同度以日行定积度即月行定积度
弦望则各置其加时日行定积度以象策上弦一加望
卷二 第 6b 页 WYG0786-0485b.png
 再加下弦三加之为加时月行定积度如前加而命之
再加下弦三加之为加时月行定积度如前加而命之满躔周及黄道宿度去之不尽各得定朔弦望加时黄
道月度及分秒
求定朔弦望夜半晨昏黄道月度
置所求入转日转度率与次日转度率相减馀以所求
入转小馀乘之万约为分前多后少减前少后多加加
减转度率为转定度以乘定朔弦望小馀万约为分用
减加时定积度馀为晨前夜半定积度以转定度乘其
卷二 第 7a 页 WYG0786-0485c.png
 日晨昏分万约为分各加夜半定积度为晨昏定积度
日晨昏分万约为分各加夜半定积度为晨昏定积度加命如前各得夜半晨昏黄道月度及分秒
求每日夜半晨昏黄道月度
累计相距日数转度率为转积度与定朔弦望夜半相
距度相减馀如相距日数而一为日差距度多为加距
度少为减加减每日转度率为行定度以累加定朔弦
望夜半定积度为每日夜半定积度累加定朔弦望晨
昏定积度为每日晨昏定积度加命如前即每日夜半
卷二 第 7b 页 WYG0786-0485d.png
 晨昏黄道月度及分秒(注历自朔至望皆用昏度既望已后则用晨度)
晨昏黄道月度及分秒(注历自朔至望皆用昏度既望已后则用晨度)求每日夜半晨昏赤道月度
视所求夜半晨昏黄道月行定积度在象策已下为至
后满象策去之为分后犹多再去之为至后复多仍去
之为分后以其黄道积度减之馀以赤道率乘之如黄
道率而一所得以加赤道积度及所去象策各为赤道
定积度以岁首冬至加时赤道日度加而命之满赤道
宿度去之即每日夜半晨昏赤道月度及分秒
卷二 第 8a 页 WYG0786-0486a.png
 步交道第六
步交道第六正交三百六十三度七十九分三十四秒
中交百八十一度八十九分六十七秒
距交十四度六十六分六十六秒
交周二十七日二十一刻二十二分二十四秒
交中十三日六十刻六十一分十二秒
交差二日三十一刻八十三分六十九秒
交应二十日四十七刻三十四分
卷二 第 8b 页 WYG0786-0486b.png
 求经朔弦望入交
求经朔弦望入交置岁定积减去交应满交周去之不尽即所求入交大
小馀各加其月朔积及弦望策满交周去之为所求经
朔弦望入交大小馀若径求次朔入交以交差加之
求定朔弦望加时及每日夜半入交
置经朔弦望入交大小馀以定朔弦望加减差加减之
为定朔弦望加时入交以定朔弦望小馀减之为定朔
弦望晨前夜半入交累加一日为每日晨前夜半入交
卷二 第 9a 页 WYG0786-0486c.png
 满交周去之
满交周去之求朔后平交入转及加减差
置经朔入交与交周相减馀为朔后平交大小馀以加
经朔入转为朔后平交入转在转中已下为疾已上去
之为迟依月离篇求疾迟之加减差命为正交日加减
差
求正交日辰
置朔后平交与经朔相并以正交日加减差迟加疾减
卷二 第 9b 页 WYG0786-0486d.png
 之为正交大小馀满旬周去之命甲子算外即正交日
之为正交大小馀满旬周去之命甲子算外即正交日辰及加时小馀
求正交加时黄道月度
置朔后平交大小馀以月平行度及分秒乘之为距后
度以所求月朔积命日为度并之为岁前冬至距正交
定积度以冬至加时黄道日度加而命之满躔周及黄
道宿度去之不尽为正交加时黄道月度及分秒
求正交在二至后初末限
卷二 第 10a 页 WYG0786-0487a.png
 置冬至距正交定积度及分秒在躔中已下为冬至后
置冬至距正交定积度及分秒在躔中已下为冬至后已上去之为夏至后在象策已下为初限已上反减躔
中馀为末限
求汎差距差定限度
置初末限度以距交乘之如象策而一为汎差反减距
交馀为距差以二十四乘汎差如距交而一所得交在
冬至后减夏至后加皆加减九十八度为定限度及分
秒
卷二 第 10b 页 WYG0786-0487b.png
 求月离赤道正交宿度
求月离赤道正交宿度冬至后初限加末限减视春正夏至后初限减末限加
视秋正以距差加减春秋二正赤道宿度为月离赤道
正交宿度及分秒
求正交后赤道宿积度入初末限
各置春秋二正赤道所当宿全度及分以月离赤道正
交宿度及分秒减之馀为正交后积度以赤道宿度累
加之满象策去之为半交后再去之为中交后又去之
卷二 第 11a 页 WYG0786-0487c.png
 为半交后视各交积度在半象已下为初限已上反减
为半交后视各交积度在半象已下为初限已上反减象策馀为末限
求每交月离白道积度及宿次
置定限度与初末限相减相乘退位为分为定差正交
中交后为加半交后为减以差加减正交后赤道积度
为月离白道定积度以前宿白道定积度减之各得月
离白道宿次及分
求定朔弦望加时月离白道宿度
卷二 第 11b 页 WYG0786-0487d.png
 各以月离赤道正交宿度距所求定朔弦望加时月离
各以月离赤道正交宿度距所求定朔弦望加时月离赤道宿度为正交后积度满象策去之为半交后再去
之为中交后又去之为半交后视交后积度在半象已
下为初限已上用减象策为末限以初末限与定限度
相减相乘退位为分分满百为度为定差正交中交后
为加半交后为减以差加减月离赤道正交后积度为
定积度以正交宿度加之以其所当月离白道宿度去
之各得定朔弦望加时月离白道宿度及分秒
卷二 第 12a 页 WYG0786-0488a.png
 求每日月临午位黄道宿度
求每日月临午位黄道宿度置月离赤道定积度及中星所临宿积度上弦前后视
昏度望前后视夜半度下弦前后视晨度月在中星已
下为前已上为后以月星积度相减(不及则加躔周而后减之)馀以
其日转定度乘之如躔周而一所得前减后加其日夜
半晨昏月离黄道定积度以岁首冬至加时黄道日度
加而命之满黄道宿度去之即月临午位黄道宿度及
分秒
卷二 第 12b 页 WYG0786-0488b.png
 求每日月临午位赤道宿度
求每日月临午位赤道宿度置月临午位黄道积度及分秒依前篇求赤道积度以
岁首冬至加时赤道日度加而命之满赤道宿度去之
即月临午位赤道宿度及分秒
求每日月临午位时刻更点
置月临午位赤道积度及分秒以其日晨前夜半中星
积度及分秒减之(不及则加躔周而后减之)馀以百乘之如躔周而
一为刻不满退除为分秒下弦已后上弦已前月中在
卷二 第 13a 页 WYG0786-0488c.png
 昼依时刻法求之上弦已后下弦已前月中在夜依更
昼依时刻法求之上弦已后下弦已前月中在夜依更点法求之
求每日月离赤道交后初末限
置月离赤道正交后积度以赤道宿度及分累加之至
所求月临午位赤道宿度及分秒在躔中已下为正交
后已上去之为中交后在象策已下为初限已上反减
躔中馀为末限
求月离半交白道出入赤道内外度
卷二 第 13b 页 WYG0786-0488d.png
 置各交汎差度及分秒以二十五乘之六十一除之所
置各交汎差度及分秒以二十五乘之六十一除之所得视月离黄道正交在冬至后宿度为减夏至后宿度
为加皆加减二十三度九十分为月离赤道后半交白
道出入赤道内外度折半以辰策除之为定差
求月离出入赤道内外白道去极度
置每日月离赤道交后初末限度及分秒用减象策馀
为白道积用其积度减之馀以其差率乘之百约之以
加其下积差为每日积差(月离白道积差差率旧附日躔篇黄赤道率下)倍辰
卷二 第 14a 页 WYG0786-0489a.png
 策以积差减之馀以定差乘之为每日月离出入赤道
策以积差减之馀以定差乘之为每日月离出入赤道内外度内减外加象策为每日月离白道六极度及分
秒
求随处月去地度及表景汎数定数
置所求日月临午位白道去极度及分并其处北极出
地度及分用减躔中馀即其处月去地度为弧半背(术与
日同见晷漏篇)
步交食第七
卷二 第 14b 页 WYG0786-0489b.png
 日食交外限六度定法六十一
日食交外限六度定法六十一日食交内限八度定法八十一
月食限十三度五分定法八十七
求交食凡例
凡日食必在朔月食必在望馀日虽交不食视朔望汎
交大小馀近交周上下与交周相减馀为距正交分近
交中上下与交中相减馀为距中交分倍之不满交差
为入食限定朔加时在夜定望加时在昼若无带食则
卷二 第 15a 页 WYG0786-0489c.png
 不必推出入带食则须推之
不必推出入带食则须推之凡定望加时在日出后而月食初亏于日出前者则退
一日只以昨夜言望注历时宜预推当退望而不退是
为错误
求日食时差及距午分
视定朔小馀在五十刻已下用减五十刻馀为中前分
已上减去五十刻馀为中后分以中前后分与五十刻
相减相乘如九十六而一为刻不满退除为分秒中前
卷二 第 15b 页 WYG0786-0489d.png
 名减中后名加命为时差以并中前或中后分为距午
名减中后名加命为时差以并中前或中后分为距午分
求食甚入盈缩定度
日食置定朔加时黄道日行定积度以时差加减之为
食甚入盈缩定度月食不用时差直以定望加时黄道
日行定积度便为食甚入盈缩定度满躔中去之
求日食南北差
视食甚入盈缩定度在象策已下为初限已上用减躔
卷二 第 16a 页 WYG0786-0490a.png
 中馀为末限以初末限自相乘千八百七十除之为度
中馀为末限以初末限自相乘千八百七十除之为度不满退除为分秒用减四度四十六分馀为南北汎差
距午分乘之半昼分除之所得用减汎差(不及减反减之)为南
北定差在缩初盈末正交加中交减在盈初缩末正交
减中交加(系反减者应加却减之应减却加之)
求日食东西差
置食甚入盈缩定度与躔中相减相乘千八百七十除
之为度不满退除为分秒为东西汎差距午分乘之二
卷二 第 16b 页 WYG0786-0490b.png
 十五刻除之为东西定差(若在汎差已上则倍汎差相减馀为定差)在缩中
十五刻除之为东西定差(若在汎差已上则倍汎差相减馀为定差)在缩中前盈中后正交加中交减在盈中前缩中后正交减中
交加(虽系倍减者加减只如常)
求交限度
日食置正交中交度及分秒以六度十五分为损益差
正交损之中交益之以南北东西定差加减之为交限
度月食则不须损益加减直以正交中交度及分秒为
交限度
卷二 第 17a 页 WYG0786-0490c.png
 求交定度
求交定度置朔望汎交大小馀以月平行度乘之以盈缩差盈加
缩减之为交定度若在十五度半已下并入正交度及
分秒为交定度
求食差
视交定度在正交限已下中交限已上为交内在正交
限已上中交限已下为交外各与限度相减馀为食差
求所食分秒
卷二 第 17b 页 WYG0786-0490d.png
 各置食限以其食差减之馀如定法而一为所食分秒
各置食限以其食差减之馀如定法而一为所食分秒不及减者不食食分少者日光赫盛或不见食
求定限行度
置定朔望加时入转大小馀依月离求所入疾迟限下
行度减去八百二十分馀为定限行度
求定用分
日食置二十分月食置二十分与所食分秒相减相乘
平方开之所得日以七因月以六因各进二位皆以八
卷二 第 18a 页 WYG0786-0491a.png
 百二十乘之如定限行度而一为定用分
百二十乘之如定限行度而一为定用分求三限时刻
日食置定朔小馀以时差加减之为食甚分月食不用
时差但以定望全分为食甚分各以定用分减食甚为
初亏加食甚为复圆依时刻法求之即三限时刻
求五限时刻
月食十分已上者减去十分馀为既内复与十分相减
相乘如定用分求之为既内分以减食甚分为食既以
卷二 第 18b 页 WYG0786-0491b.png
 加食甚分为生光馀同前法共所求三限为五限
加食甚分为生光馀同前法共所求三限为五限求月食更点
置其日晨分倍之五约为更法又五约为点法乃置五
限诸分昏分已上减昏分晨外已下加晨分以更法加
入如法而一为更数不满以点法加入如法而一为点
数
求带食带复
视其日日出入分在初亏分已上食甚分已下为带食
卷二 第 19a 页 WYG0786-0491c.png
 在食甚分已上复圆分已下为带复各与日出入分相
在食甚分已上复圆分已下为带复各与日出入分相减馀名前后差在日出入分已下为前已上为后各以
所食分秒乘之如定用分而一为日出入前后食复分
日食日出已后日入已前为见日出已前日入已后为
不见月食日出已前日入已后为见日出已后日入已
前为不见此与旧法不同(详见古今交食考)
旧历无论出入前后日月一例求之是属错误
求起复方所
卷二 第 19b 页 WYG0786-0491d.png
 日食起于西复于东食分少者交外偏南交内偏北月
日食起于西复于东食分少者交外偏南交内偏北月食起于东复于西食分少者交外偏北交内偏南皆指
北极所在为北日月所在为南不必据午地论旧历日
月食八分已上即言正东正西今惟月食十分已上者
始言之
求食甚宿度
置食甚入盈缩定度(日食在盈无所加在缩加躔中月食在盈加躔中在缩无所加)为
黄道定积置冬至距后赤道积度在定积已下者满象
卷二 第 20a 页 WYG0786-0492a.png
 策去之馀依黄道术求之用减定积满象策去之即食
策去之馀依黄道术求之用减定积满象策去之即食甚躔离黄道宿度及分秒
步五纬第八
合应
土星二百六十二日三千二十六分
木星三百一十日千八百三十七分
火星三百四十三日五千一百七十六分
金星二百三日八千三百四十七分
卷二 第 20b 页 WYG0786-0492b.png
 水星九十一日七千六百二十八分
水星九十一日七千六百二十八分周率
土星三百七十八日九百一十六分
木星三百九十八日八千八百分
火星七百七十九日九千二百九十分
金星五百八十三日九千二十六分
水星百一十五日八千七百六十分
历应
卷二 第 21a 页 WYG0786-0492c.png
 土星八千六百四日五千三百三十八分
土星八千六百四日五千三百三十八分木星四千一十八日六千七十三分
火星三百一十四日四十九分
金星六十日千九百七十五分
水星二百五十三日七千四百九十七分
度率
土星二十九日四千二百五十五分
木星十一日八千五百八十二分
卷二 第 21b 页 WYG0786-0492d.png
 火星一日八千八百七分半
火星一日八千八百七分半金星一日
水星一日
伏见
土星十八度
木星十三度
火星十九度
金星十度半
卷二 第 22a 页 WYG0786-0493a.png
 水星夕伏晨见十九度晨伏夕见十六度半
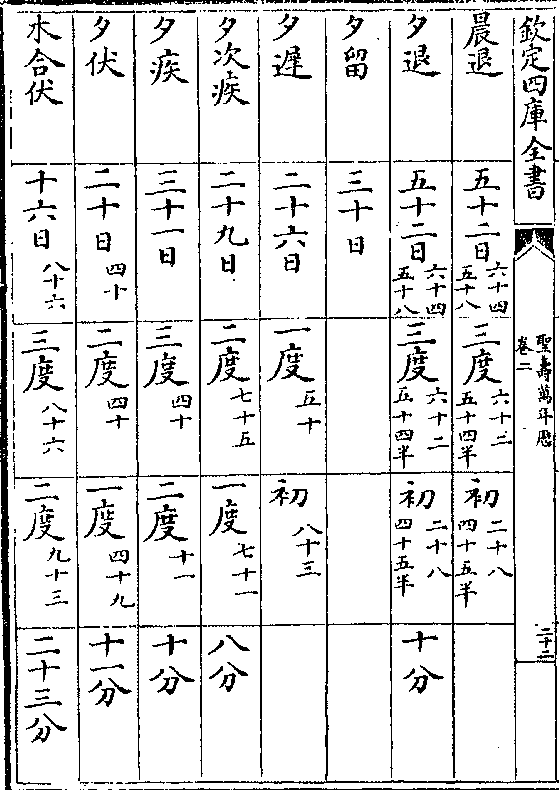
水星夕伏晨见十九度晨伏夕见十六度半诸段积日积度
卷二 第 22b 页 WYG0786-0493b.png
卷二 第 23a 页 WYG0786-0493c.png

卷二 第 23b 页 WYG0786-0493d.png

卷二 第 24a 页 WYG0786-0494a.png
卷二 第 24b 页 WYG0786-0494b.png

卷二 第 25a 页 WYG0786-0494c.png

卷二 第 25b 页 WYG0786-0494d.png

卷二 第 26a 页 WYG0786-0495a.png

卷二 第 26b 页 WYG0786-0495b.png

求五星平合日
置岁定积各加其星合应满其周率去之不尽反减周
率馀即所求岁首冬至后平合日及分杪
卷二 第 27a 页 WYG0786-0495c.png
 求诸段积日积度
求诸段积日积度副置平合日及分秒累加段日即诸段积日命日为度
累加平度退则减之即诸段积度及分秒
求诸段入历
置岁定积各以其星历应并所求平合日及分秒加之
如其度率而一为度不满退除为分秒满日躔历率去
之不尽为所求平合入历度累加限度各得其段入历
度及分秒
卷二 第 27b 页 WYG0786-0495d.png
 求盈缩初末度
求盈缩初末度置各段入历度及分秒若在躔中已下为盈已上减去
躔中为缩其土木金水四星诸段在象策已下为初限
已上用减躔中馀为末限其火星诸段盈者在二因辰
策已下缩者在四因辰策已下为初限已上用减躔中
馀为末限
求盈缩差
土星盈者立差二秒八十三忽加平差四分十秒二十
卷二 第 28a 页 WYG0786-0496a.png
 二忽减定差千五百一十四分六十一秒缩者立差三
二忽减定差千五百一十四分六十一秒缩者立差三秒三十一忽加平差一分五十一秒二十六忽减定差
千一百一分七十五秒
木星盈缩立差二秒三十六忽加平差二分五十九秒
十二忽减定差千八十九分七十秒
金星盈缩立差一秒四十一忽加平差三忽减定差三
百五十一分五十五秒
水星盈缩立差一秒四十一忽加平差二十一秒六十
卷二 第 28b 页 WYG0786-0496b.png
 五忽减定差三百八十七分七十秒
五忽减定差三百八十七分七十秒火星盈初缩末立差十一秒三十五忽减平差八十三
分十一秒八十九忽减定差八千八百四十七分八十
四秒缩初盈末立差八秒五十一忽减平差三分二秒
三十五忽减定差二千九百九十七分六十三秒(新改缩初
盈末立差一秒二十四忽减平差二十分三十秒减定差四千三百九十二分)
各置立差以所求初末限度及分秒乘之加减平差再
乘之用减定差又乘之满万为度不满退除为分秒为
卷二 第 29a 页 WYG0786-0496c.png
 盈缩差
盈缩差又法置所求初末限下小馀以其限盈缩分乘之万约
为分加入其限积度亦为盈缩差
求诸段定积日及日辰
各置其段积日以其盈缩差盈加缩减之即其段定积
日及分秒以岁首黄钟正律大小馀加之满旬周去之
其大馀命甲子算外即得日辰及加时小馀
求诸段所在日月
卷二 第 29b 页 WYG0786-0496d.png
 各置其段定积日及分秒加闰馀减朔策馀如朔策而
各置其段定积日及分秒加闰馀减朔策馀如朔策而一为月数不尽为入经朔已来日数其月数命正月若
在朔策已下不及减者为入年前十一月已上去之为
入十二月俱以日辰所在为定凡闰馀在十六日以上
则其年有闰依束汎闰术定之
求诸段加时定积度
各置其段积度以其盈缩差盈加缩减之(金星再之水星三之)即
诸段加时定积度以岁首冬至加时黄道日度加而命
卷二 第 30a 页 WYG0786-0497a.png
 之即其星其段加时所在宿度及分秒
之即其星其段加时所在宿度及分秒求诸段初日晨前夜半所在宿度
各以其段初行率乘其段加时小馀百约为分顺减退
加其日加时定积度即其段初日晨前夜半定积度加
命如前即得所在宿度及分秒
求诸段日率度率及平行分
各以其段日辰与后段日辰相距数为日率以其段夜
半积度与后段夜半积度相减馀为度率各置度率及
卷二 第 30b 页 WYG0786-0497b.png
 分秒以其日率除之即其段平行分
分秒以其日率除之即其段平行分求诸段增减差及日差
以本段前后平行分相减为其段汎差倍而退位为增
减差前多后少者加为初减为末前少后多者减为初
加为末以加减其段平行分为初末日行分
又倍增减差为总差以日率减一除之为日差
求前后伏迟退段增减差
前伏者置后段初日行分加其日差之半为末日行分
卷二 第 31a 页 WYG0786-0497c.png
 后伏者置前段末日行分加其日差之半为初日行分
后伏者置前段末日行分加其日差之半为初日行分以减伏段平行分馀为增减差
前迟者置前段末日行分倍其日差减之为初日行分
后迟者置后段初日行分倍其日差减之为末日行分
以前后近留之迟段平行分减之馀为增减差
土木火三星退行者六因平行分退一位为增减差
金星前后退伏者三因平行分半而退位为增减差
前退者置后段初日行分以其日差减之为末日行分
卷二 第 31b 页 WYG0786-0497d.png
 后退者置前段末日行分以其日差减之为初日行分
后退者置前段末日行分以其日差减之为初日行分以本段平行分减之馀为增减差
水星退行者半平行分为增减差
皆以增减差加减平行分为初末日行分前多后少者
加为初减为末前少后多者减为初加为末
又倍增减差为总差以日率减一除之为日差
求每日晨前夜半星行宿度
各置其段初日行分以日差累损益之后少则损之后
卷二 第 32a 页 WYG0786-0498a.png
 多则益之为每日行度及分秒乃置其段初日晨前夜
多则益之为每日行度及分秒乃置其段初日晨前夜半定积度顺加退减满宿度去之即每日晨前夜半星
行宿度及分秒
求平合见伏入太阳盈缩历
置其星其段定积日及分秒在岁中已下为盈已上去
之为缩多则再去之复为盈各在初限已下为初限已
上反减岁中馀为末限即其星平合见伏入历日及分
秒
卷二 第 32b 页 WYG0786-0498b.png
 求平合见伏星与太阳行差
求平合见伏星与太阳行差各以其星其段初日星行分与其段初日太阳行分相
减馀为行差若金水二星退行在退合者以其段初日
星行分并其段初日太阳行分为行差其水星夕伏晨
见者直以其段初日太阳行分为行差
求定合定见定伏汎积日
土木火三星各以平合晨见夕伏定积日便为定合伏
见汎积日及分秒
卷二 第 33a 页 WYG0786-0498c.png
 金星置其段盈缩差水星倍置之各以其段行差除之
金星置其段盈缩差水星倍置之各以其段行差除之为日不满退除为分秒在平合夕见晨伏者盈减缩加
在退合夕伏晨见者盈加缩减各加减定积日为定合
伏见汎积日及分秒
求定合定积日定积度
土木火三星各以平合行差除其段初日太阳盈缩积
为距合差日不满退除为分秒以太阳盈缩积减之为
距合差度副置其星定合汎积以距合差日差度盈减
卷二 第 33b 页 WYG0786-0498d.png
 缩加之为其星定合定积日定积度及分秒此与下条
缩加之为其星定合定积日定积度及分秒此与下条言盈缩者皆指太阳非谓木星
金水二星顺合退合者各以平合退合行差除其日太
阳盈缩积为距合差日不满退除为分秒顺加退减太
阳盈缩积为距合差度顺合者以距合差日差度盈加
缩减其星定合汎积为其星定合定积日定积度及分
秒退合者以距合差日盈减缩加以距合差度盈加缩
减加减其星退定合汎积为其星退定合定积日定积
卷二 第 34a 页 WYG0786-0499a.png
 度及分秒加命如前各得所求日辰及宿度分秒
度及分秒加命如前各得所求日辰及宿度分秒径求合伏定日者土木火三星以夜半黄道日度减其
星夜半黄道度馀在其日太阳行分已下者金水二星
以其星夜半黄道度减夜半黄道日度馀在其日本星
行分已下者各为其日合伏系合退伏者视其日夜半
黄道日度未行到本星度及视次日太阳行过本星度
而本星退行过太阳宿度者为其日合退伏
求定见定伏定积日
卷二 第 34b 页 WYG0786-0499b.png
 土木火三星各置定见定伏汎积日及分秒以岁中折
土木火三星各置定见定伏汎积日及分秒以岁中折半晨加夕减之在岁中巳下自相乘已上倍岁中反减
之馀亦自相乘七十五而一为分不满退除为秒以其
星见伏度乘之十五除之所得满行差而一为日不满
退除为分秒见加伏减汎积为其星定见定伏定积日
及分秒加命如前即得定见定伏日辰
金水二星各以伏见日行差除其段初日太阳盈缩积
为日不满退除为分秒夕见晨伏盈加缩减晨见夕伏
卷二 第 35a 页 WYG0786-0499c.png
 盈减缩加加减其星定见定伏汎积日及分秒为常积
盈减缩加加减其星定见定伏汎积日及分秒为常积若在岁中巳下为冬至后已上去之为夏至后在岁中
折半已下自相乘已上反减岁中馀亦自相乘冬至后
晨夏至后夕十八而一为分冬至后夕夏至后晨七十
五而一为分以其星见伏度乘之十五除之所得满行
差而一为日不满退除为分秒晨见夕伏冬至后加夏
至后减夕见晨伏冬至后减夏至后加皆加减常积为
其星定见定伏定积日及分秒加命如前即得定见定
卷二 第 35b 页 WYG0786-0499d.png
 伏日辰
伏日辰圣寿万年历卷二