钦定四库全书
　历算全书卷五十六
　　　　　　　　　　　　　宣城梅文鼎撰
　方圆幂积一卷
　　方圆幂积说
历书周径率至二十位然其入算仍用古率(十一与十/四之比例)
(本祖冲之径七周/二十二之密率)岂非以乘除之际难用多位欤今以
表列之取数殊易乃为之约法则径与周之比例即方

圆二幂之比例(径一则方周四圆周三一四一五九二/六五而径上方幂与员幂亦若四与三)
(一四一五九二六五尾/数八位并以表为用)亦即为立方立圆之比例(同径/之立)
(方与圆柱若四与二一四有奇则同径/之立方与立员若六与三一四有奇)殊为简易直截
癸未岁匡山隐者毛心易乾乾偕其婿中州谢野臣惠
访山居共论周径之理因反覆推论方员相容相变诸
率庚寅在吴门又得锡山友人杨昆生定三方员订注
图说益觉精明甚矣学问贵相长也
　　方圆相容

新法历书曰割圆亦属古法盖人用圭表等测天天圆
而圭表直与圆为异类讵能合欤此所以有割圆之法
也新法名为八线表云
又云径一围三绝非相准之率然径七围二十二则盈
径五十围百五十七则朒或详绎之则径一万围三万
一四五九虽亦小有奇零不尽然用之颇为相近
今算得平方与同径之平圆其比例若四○○与三一
四五九平方内容平员平员内复容平方则内方与外

方内员与外员之幂皆加倍之比例
　　　　　　　假如戊己庚辛平方内容甲乙丙丁
　　　　　　　员员内又容甲乙丙丁小平方小方
　　　　　　　内又容壬丑癸子小平员如此递互
　　　　　　　相容则其幂积皆如二与一也
假外大平方(戊己/庚辛)之积一百则内小平方之积(甲丁/乙丙)必
五十平员亦然
若求其径则成方斜之比例大径如斜小径如方

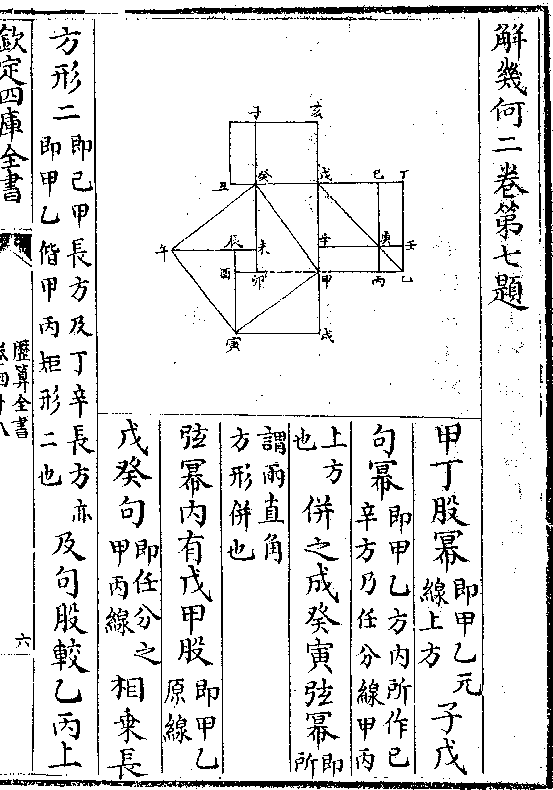假如内小平方积一百以甲丁或丙乙为径(甲丙或丁/乙并同)
开方求一百之根得径一十其外大平方积二百以甲
乙或丁丙为径(或用戊庚或己辛或己/戊或辛庚为径并同)开方求二百之
根得径一十四一四有奇
甲乙为甲丁方之斜故斜径自乘之幂与其方幂若二
与一而其径与斜径若一十与一十四(一四奇/)也折半
则为五与七(○七奇/)故曰方五则斜七有奇也
三边形内容平员平员内又容三边则其幂之比例为

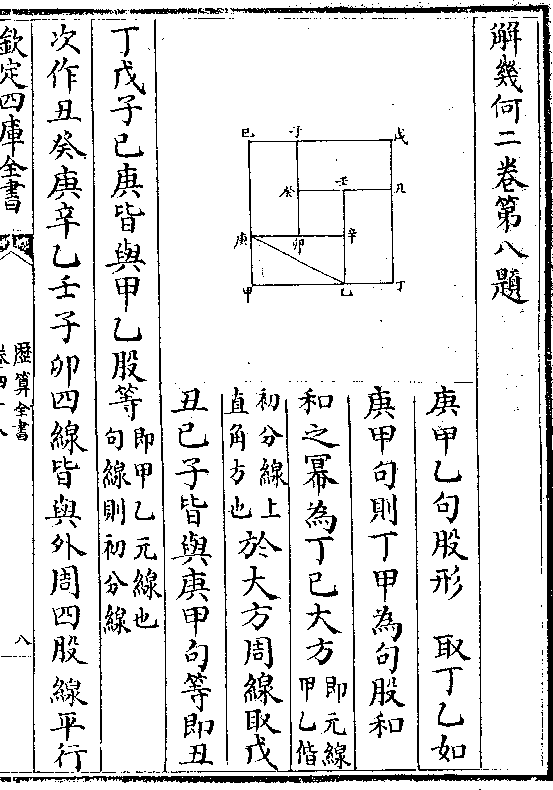
　　　　　　　四与一甲乙丙三边形内容丁戊己
　　　　　　　平员平员内又容丁戊己小三边则
　　　　　　　内小三边形为外大三边形四之一
　　　　　　　内外两平员之幂其比例亦为四与一
若有多层皆以此比例递加
浑员内容立方立方内又容浑员如此递互相容则外
员径上幂与内员径上幂为三倍之比例外立方与内
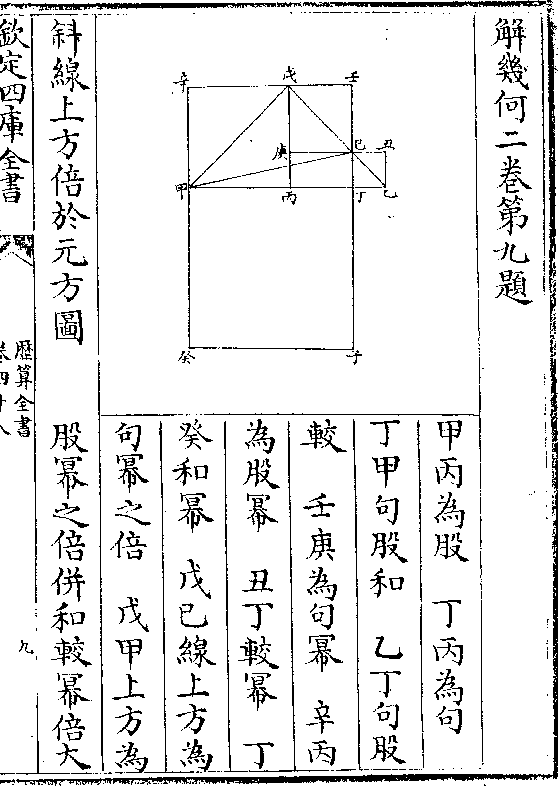
立方之径幂亦然丙庚丁浑员内容丙甲丁乙立方丙

戊及戊甲皆立方边(丙辛及甲辛并同丙/乙及甲丁等亦同)丙戊甲辛为
立方面(馀六面/并同)丙甲(为方面/斜线)丙丁(为立方体/内对角线)即浑员径(乙/甲)
(同其辛壬及己戊皆/亦对角若作线亦同)丙乙及甲丁等又皆为立楞(戊壬及/辛己同)
　　　　　　　　解曰立方面上斜径之幂为方幂之倍(句股/法也)
　　　　　　　　(斜为弦方为句又为股并句股实/成弦实故倍方幂即成斜径之幂)又以斜径
　　　　　　　　为股立方之立楞为句求得立方体内两对
　　　　　　　　角之斜径为弦此弦实内有股实(即面上斜/径之幂为)
　　　　　　　　(方幂/者二)有句实(即立楞之幂立楞原即方/边故其幂即立方面幂)共得方

幂三而此丙对角斜径即浑员之径内小员径又在立方体内
即以方径为径其径之幂即立方面也故曰三倍比例也
立方内又容立员则内员径即立方之径
若求其径则外径大于内径若一十七有奇与一十
内径之幂百开方得一十为径则外径之幂三百开方得一
十七(又三十五/之一十一)为径若有几层互容皆以此比例递加即得
若求其体积则为五倍有奇之比例(若有多层亦以/此比例递加)
假如内容立方积一千则外大立方积五千一百九十四有奇

解曰立积一千则其径幂一百而外大立积之径幂三
百又以径一十七(又三十五/之一十一)乘之得五千一百九十四
(又七/之二)　此言大方积又在图上浑员之外
积之比例
立方同径之立员其比例为六○○与三一四
立方同径之员柱其比例为四○○与三一四
员柱与同径之立员其比例为三与二
　　方圆周径相求

同积较径　为方变员员变方之用
凡方圆同积则员径大方径小其比例若一一二八三
七九与一○○○○○○
解曰员径一一二八三七九则方径一○○○○○○也
法曰有员径求其同积之方径当以一○○○○○○乘
以一一二八三七九除
有方径求其同积之员径当以一一二八三七九乘以
一○○○○○○除

凡方员同积则员径上平方与方径上平方其比例若
四○○○○○○○○与三一四一五九二六五
解曰员径自乘四○○○○○○○○则方径自乘三
一四一五九二六五
法曰有员径求其同积之方径当以三一四一五九二
六五乘之四○○○○○○○○除之得数平方开之
得方径
有方径求其同积之员径当以四○○○○○○○○

乘三一四一五九二六五除得数平方开之得员径
凡方员同积则员径与方径若一○○○○○○与○
八八六二二六
解曰员径一○○○○○○则方径八八六二二六也
法曰有员径求同积之方径以八八六二二六乘员径
一○○○○○○除之即得方径
有方径求同积之员径以一○○○○○○乘方径八
八六二二六除之即得员径

约法
以一一二八二七九乘方径去末六位得同积之员径
以○八八六二二六乘员径去末六位得同积之方径
同积较周
凡方员同积则员周小方周大其比例若一○○○○
○○与一一二八三七九亦若八八六二二六与一○
○○○○○
解曰员周一○○○○○○则方周一一二八三七九

也
方周一○○○○○○则员周八八六二二六也
约法
以一一二八三七九乘员周去末六位得同积之方周
以○八八六二二六乘方周去末六位得同积之员周
凡方员同积则其径与径周与周为互相视之比例
解曰方周与员周之比例若员径与方径也
论曰凡同积之周方大而员小同积之径则又方小而

员大所以能互相为比例
约法
以方周乘方径为实员周除之得员径若以员径除实
亦得员周
以员周乘员径为实方周除之得方径若以方径除实
亦得方周　皆用异乘同除例如左
一　员周一○○○○○○　　一　方周一○○○○○○
二　方周一一二八三七九　　二　员周○八八六二二六

三　方径○二八二○九四(七五/)　三　员径○二八二○九四(七五/)
四　员径○三一八三○九(八八/)　四　方径○二五○○○○
　　积七九五七七(四四八○○○/○○○)　　积六二五○○○○○○○○
一　员径一○○○○○○　　　一　方径一○○○○○○
二　方径○八八六二二六　　　二　员径一一二八三七九
三　方周三五四四九○四　　　三　员周三五四四九○四
四　员周三一四一五九二　　　四　方周四○○○○○○
　　积七八五三九(八一六○○○/○○○)　　积一○○○○○○○○○○○○

第四率并与一率乘得四倍积四除之得本积
论曰以上皆方员周径互相求乃同积之比例方员交
变用之即比例规变面线之理
同径较积较周　即方内容员员外切方
凡方员同径则方积大员积小周亦如之其比例若四
○○○○○○○○与三一四一五九二六五
方径一○○○○周四○○○○　积一○○○○○○○○
员径一○○○○周三一四一五奇积○七八五三九八一六

方径二○○○○周四○○○○　积四○○○○○○○○
员径二○○○○周六二八三一奇积三一四一五九二六五
凡径倍者周亦倍而其积为倍数之自乘亦谓之再加
比例授时历谓之平差
径二倍周亦二倍而其积则四倍径三倍周亦三倍而
其积九倍乃至径十倍周亦十倍而积百倍径百倍周
亦百倍而积万倍皆所加倍数之自乘数亦若平方谓
之再加也

同周较积较径
凡方员同周则员积大方积小径亦如之其比例若四
○○○○○○○○与三一四一五九二六五
方周一○○○○○○径○二五○○○○积六二五○○○○○○○○
员周一○○○○○○径○三一八三○九八八积七九五七七四七○○○○
方周四○○○○○○径一○○○○○○积一○○○○○○○○○○○○
员周四○○○○○○径一二七三二三九五四积一二七三二三九五四○○○○
论曰周四则径与积同数但其位皆升皆视周数之位

今用百万为周则积升六位成万亿矣故虽同而实不
同不惟不同而且悬绝定位之法所以当明也
问位既大升而数不变何耶曰周径相乘得积之四倍
于是四除其积即得所求平积此平幂之公法也兹方
员之周既为四则以乘其径而复四除之即还本数矣
惟周数之四或十或百或千万亿无定而除法之四定
为单数故无改数而有进位也
又论曰周四倍之径与周一之径为四倍其积则十六

倍所谓再加之比例
浑圆内容立方径一万寸求圆径　法以方斜一万四
千一百四十二寸为股自乘得二亿为股实以方径一
万寸为句自乘得一亿为勾实并勾股实为三亿为弦
实开方得弦一万七千三百二十○半寸命为浑圆之
径
又以浑圆径求围得五万四千四百十四寸弱　周径
相乘得九亿四千二百四十七万六九九四寸为浑幂

以四除浑幂得二亿三千五百六十一万九千二百四
十八寸奇为大平圆幂即立方一万寸外切浑圆之腰
围平幂也
圆柱积四万○千八百十○亿四三一八四九八四寸
　以浑圆径乘平圆幂得之
倍圆柱积以三除之得浑圆积二万七千二百○六九
五四五六六五六寸
约法　立方径一千尺其积一十尺　外切之浑圆径

一十七尺三二○五　浑圆积二千七百二十○尺六
九五四　约为二千七百二十一尺弱
试再用径上立方求浑圆积法(即立方内求/所容浑圆)以浑圆径
自乘再乘得浑圆径上立方以圆率(三一/四奇)乘之得数六
除之得浑积并同
立方与员柱若四○○与三一四奇(同径之/员柱也)
立方为六方角所成员柱为六员角所成其所容角体
并六而方与员异故其比例如同径之周　此条为积

之比例
员周上自乘之方与浑员面幂若三一四奇与一○○
浑员面幂与员径上平方形亦若三一四奇与一○○
皆员周与径之比例
浑员面幂与员径上平员若四与一
员柱面幂与员径上平员若六与一(六员角之底皆/外向合成此数)
平员并为一而员柱幂为其六倍浑员幂为其四倍浑
员为员柱三之二即此可徵积之比例如其面也以上

四条并面幂之比例浑员体与员角体若四与一
浑员面既为平员之四倍从面至心皆成角体故体之
比例亦四倍
立方面与径上平方若六与一(六面/故也)
立方体与浑员体若六○○与三一四奇
浑员面与径上平方既若三一四奇与一○○而立方
面与径上平方若六与一平方同为一○○而立方面
为其六倍浑员面为其三倍一四奇故立方之面与浑

员之面亦若六○○与三一四奇也而体之比例同面
故亦为六○○与三一四奇
立员得员柱三之二
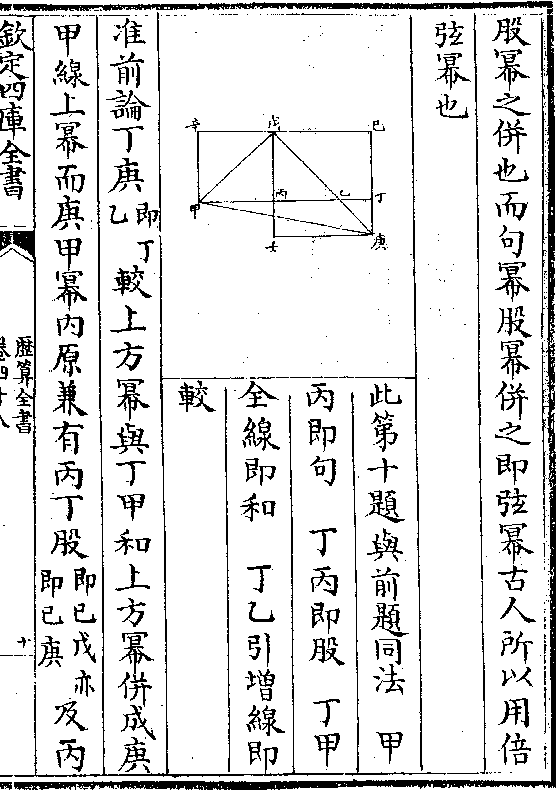
　　　　　　　　论曰凡员柱之面及底皆立员径
　　　　　　　　上平员也旁周似员筒亦如截竹
　　　　　　　　周围并以员径为高即员径乘员
　　　　　　　　周幂也为径上平员之四倍与浑
员面幂同积(半径乘半周得平员则全/径乘全周必平员之四倍)合面与底共得

平员之六倍而浑员面幂原系平员之四倍是员柱幂
六而浑员幂四也而体积之比例准此可知亦必为三
之二矣(三之二即六/之四之半)
问体积之比例何以得如面幂曰试于员柱心作员角
　　　　　　　　体至面至底成员角体二皆以半
　　　　　　　　径为高平员为底其馀则外如截
　　　　　　　　竹而内则上下并成虚员角于是
　　　　　　　　纵剖其一边而令员筒伸直以其

　　　　　　　　幂为底以半径为高成长方锥(底/阔)
　　　　　　　　(如全径直如员周高/如半径锥只一点)此体即同四
　　　　　　　　员角(或纵剖为四方锥亦同皆以/周四分之一为底阔以全径)
　　　　　　　　(为底长以半径为高其体并同员/角何也以周四之一乘全径与半)
　　　　　　　　(径乘半周同故方底同员底/而其高又同则方角同员角)合面
　　　　　　　　底二员用共六员角矣而浑员体
　　　　　　　　原同四员角(浑员面为底半径为/高作员锥即同四员)
　　　　　　　　(角/)是员柱浑员二体之比例亦三

与二也
员角体得员柱三之一　凡角体并同
准前论员柱有六员角试从中腰平截为两则有三员
角而员筒体原当四员角今截其半仍为二员角或面
或底原系一员角合之成三员角以为一扁员柱然则
员角非员柱三之一乎
若立方形各从方楞切至心则成六方角(皆以方面为/底半径为高)
从半径平切之为扁立方则四周之四方角皆得一半

成两方角而或底或面原有一方角亦是三方角合成
一扁立方而方角体亦三之一矣
浑员体分为四则所分角体各所乘之浑幂皆与员径
上平员幂等
甲戊丙丁浑员体　从丑乙辰乙癸乙子乙卯乙寅乙等各半
径各自其浑幂透至乙心而以半径旋行而割切之则成上
下两员角体一甲卯辰丑乙(以甲丑卯辰割浑员之面为/底乙为其锐此割员曲径自)
(丑而甲而辰居/员周三之一)一丙癸寅子乙(以子丙寅癸浑员之割面为/底乙为其锐此割员曲径亦)

　　　　　　　　(三之一如三百六/十之一百二十)此上下两角体
　　　　　　　　相等皆居全浑体四之一中腰成
　　　　　　　　鼓形而上下两面并挖空各成虚
　　　　　　　　员角(其外则周遭皆凸面如丑戊/子及辰丁癸之割员状此割)
　　　　　　　　(员曲径自辰而丁而癸居员周/六之一为三百六十之六十)
此鼓形体倍大于上下两角体居浑员全体之半若从
戊乙丁腰横截之为二则一如仰盂一如覆碗而其体
亦浑员四之一也

如此四分浑体而其割员之面幂即各与员径上之平
员幂等故曰浑员面幂与径上平员若四与一也
问何以知中腰鼓体能倍大于上下两角体曰试于子
丙乙癸角体从子寅癸横切之则成子未癸午小员面
　　　　　　　　为所切乙子寅癸小员角体之底
　　　　　　　　乃子寅小半径乘子未癸小半周
　　　　　　　　所成也然则以子寅小半径乘子
　　　　　　　　未癸小半周又以乙寅半半径为

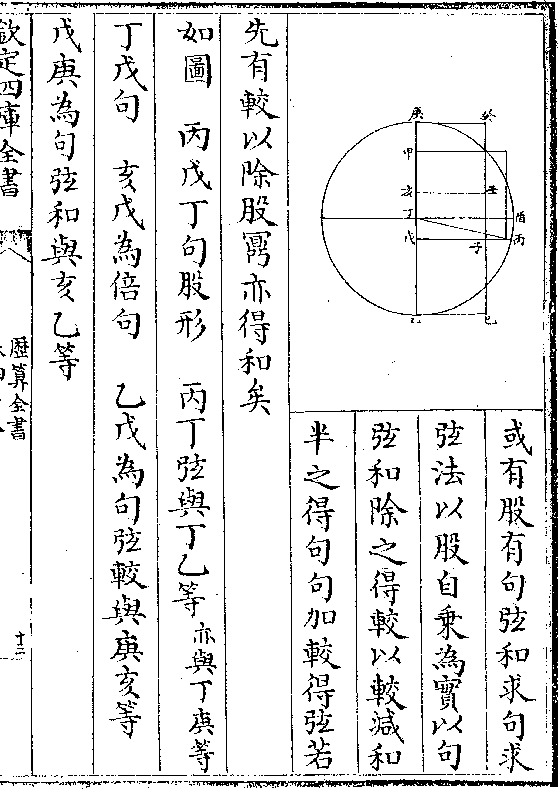高乘之而取其三之一即小角体矣
　　　　　　　　试又于中腰鼓体从丑子及卯寅
　　　　　　　　及辰癸诸立线周遭直切之脱去
　　　　　　　　其外鼓凸形即成员柱体之外周
　　　　　　　　截竹形又从酉乙申横切之为两
　　　　　　　　(一仰盂/一覆碗)则此覆碗体举一式为例
　　　　　　　　可直切断而伸之亦可成方角体
　　　　　　　　此体以乙寅半半径乘子未癸午

　　　　　　　　小员全周为底(其形/长方)又以小半径
　　　　　　　　子寅(子寅即/乙申)为高而乘之取三之
　　　　　　　　一为长方角体此长方角体必倍
　　　　　　　　大于小员角体何也两法并以小
　　　　　　　　半径及半半径两次连乘取三之
　　　　　　　　一成角体而所乘者一为小员全
　　　　　　　　周一为小员半周故倍大无疑
　　　　　　　　也

　　　　　　　　又丙癸寅子亦可成角体与乙子
　　　　　　　　寅癸等覆碗体既倍大则兼此两
　　　　　　　　角体矣
准此而论仰盂体必能兼甲丑卯辰及乙辰卯丑两角
体亦无疑也
　　　　　　　　又角体内既切去一小角体又挖
　　　　　　　　去一相同之小角体则所馀者为
　　　　　　　　丙癸寅子员底仰盂体

　　　　　　　　鼓体内既挖去如截竹之体则所
　　　　　　　　馀者为内平(如丑子/及辰癸)外凸(如子戊/丑及辰)
　　　　　　　　(丁/癸)之空圈体而此体必倍大于员
　　　　　　　　底仰盂体何以知之盖两体并以
　　　　　　　　半径为平面(丑子与癸/丙并同)并以员周
　　　　　　　　六之一为凸面而腰鼓之平面以
半径循员周行员底仰盂之平面则以半径自心旋转
周行者两头全用旋转者在心之一头不动而只用一

头则只得其半矣故决其为倍大也
准此而甲丑卯辰亦为挖空之员覆碗体而只得鼓体
之半矣由是言之则上下角体各得中腰鼓体之半而
鼓体倍大于角形浑体平分为四夫复何疑
曰浑体四分如此真无纤芥之疑体既均分为四则其
浑体外幂亦匀分为四亦无可复疑但何以知此所分
四分之一必与径上平员相等耶曰此易明也凡割浑
员一分而求其幂法皆从其所切平面员心作立线至凸

面心而以其高为股员面心至边之半径为勾勾股求
其斜弦用为半径以作平员即与所割圆体之凸面等幂
假如前图所论上下两角体从丑卯辰横线切之则以甲卯
为股卯丑为句求得甲丑弦与半径同以作平员与丑卯辰
甲凸面等然则此角体之凸面岂不与径上平员等幂乎
　　　　　　　　　甲亢半径与甲丑同以作丑
　　　　　　　　　亢平员与甲丑卯辰凸面等
　　　　　　　　　幂

试又作甲戊线为半径之斜线(甲乙与戊乙皆半/径为句为股故也)以为
半径而作平员必倍大于半径所作之平员而浑员半
幂与之等则浑员半幂不又为平员之倍乎
　　　　　　　　(如图甲丑为半径作乙庚房平员/与丙戊甲平员等亦与甲辰卯丑)
　　　　　　　　(割员凸面等为/浑幂四之一也)
　　　　　　　　(甲戊为半径作戊心亥平员与甲/丁乙戊半浑幂等而倍大于乙庚)
　　　　　　　　(房亦倍大于丙戊甲平员/则平员居浑幂四之一)
如是宛转相求无不吻合则平员为浑员幂四之一信矣

取浑幂四之一法
当以半径为通弦以一端抵圆径之端为心旋而规之
则所割浑幂为四之一而其浑幂与圆径上平员幂等
　　　　　　　　甲辰(即丁/乙)之自幂一百辰卯之自
　　　　　　　　乘幂(七十/五)如四与三则辰丑通弦
　　　　　　　　为径以作平员亦丁戊全径上平
　　　　　　　　员四分之三也大小两平员各为
　　　　　　　　底以半径为高而作员角体其比

例亦四与三也
今浑员径上平员(即下戊径/上平员)所作之员角体既为浑积
四之一则辰丑通弦径所作之员角体即浑体十六之
三矣(即甲丑卯辰角体及/乙丑卯辰角体之合)若以丑辰通弦上平员为底
半半径为高而作角体即浑体三十二之三
分浑体为四又法
甲乙丙浑员体　从员周分为三(一丑甲辰一辰癸丙/一丙子丑各得周三)
(之/一)又从辰从丙从丑依各半径(辰乙丙乙/丑乙皆是)至乙心旋而

　　　　　　　　切之则成三角体者三各得浑体
　　　　　　　　四之一(一辰甲丑乙一丑子丙/乙一丙癸辰乙说见前)则
　　　　　　　　其所馀亦浑体四之一也(此馀形/有三平)
　　　　　　　　(员面以辰丑丑丙辰丙为员径而/并挖空至乙心如员锥之幂有两)
(凸面以辰丑丑丙辰丙之员周为界/以乙为顶皆弧三角形三角并锐)两凸面各得浑员幂八之一
按辰丑即一百二十度通弦也准前论以此通弦为圆
径作平员为底半半径为高而成员角体此员角体积
即为浑员体积三十二分之三(即先所论员/角体八之三)

若依此切浑员体成半平半凸之体其积为浑积三十
二之五(即员角体/八之五)
环堵形面幂　锥形面幂
有正方正员面欲于周作立围之堵墙而幂积与之倍
法于方面取半径为高即得
　　　　　　　　　甲乙丙平方于其周作立起之
　　　　　　　　　方围形如环堵取平方乙丙半
　　　　　　　　　径为高则方围面幂倍大于平方

论曰从平方心乙对角分平方为四成四三角形并以
方根为底半径为高于是以此四三角形立起令乙锐
上指则皆以乙丙半径为高而各面皆半幂故求平方
以半径乘周得幂也然则依方周作方墙而以半径为
高岂不倍大于平方幂乎
准此论之凡六等边八等边以至六十四等边虽至多
边之面而从其各周作墙各以其半径为高则其幂皆倍
于各平幂矣然则平员者多边之极也若于其周作立

圈如环而以其半径为高则环形幂积亦必倍大于平员
有方锥员锥于其周作围墙而幂积与之倍
法于锥形之各斜面取其至锐之中线(如乙/丙)以为环墙
之高即得
　　　　　　　　　方墙如环堵底用方周高如乙
　　　　　　　　　丙即斜面自锐至底之斜立中
　　　　　　　　　线
解曰此以锥体之斜面较幂也

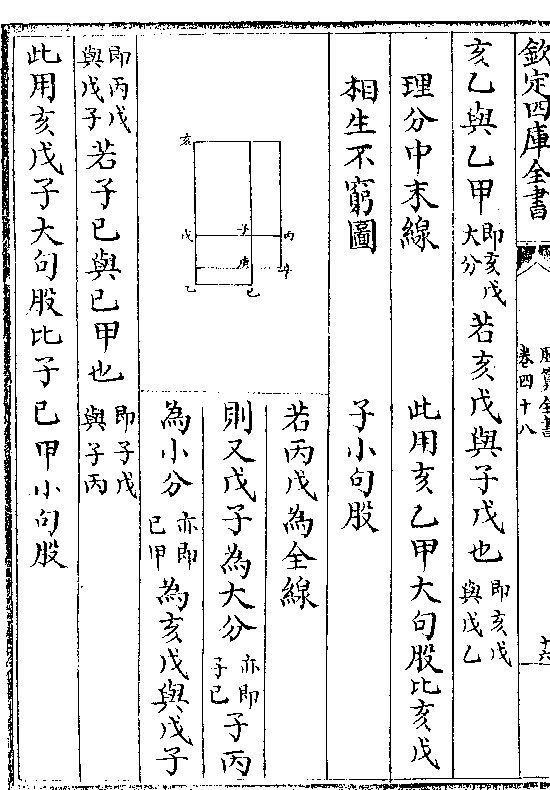论曰凡方锥皆有棱两棱交于锐各成三角面而斜立
从此斜立之三角面自锐至根阔处平分之得中线(乙/丙)
于是自棱剖之成四三角面而植之则中线直指天顶
而各面皆圭形为半幂故凡锥体亦可以中线乘半周
得幂也然则于底周作方墙而以中线为高四面补成
全幂岂不倍大乎
准此论之凡五棱六棱以上至多棱多面之锥体尽然
矣而员锥者多棱多面之极也则以其斜立线为高而

自其根作员环则其员环之幂亦必倍大于员锥之幂
前条所论切浑员之算得此益明盖员仰盂员覆碗及
挖空之鼓形其体皆一凸面一平面相合而成其凸面
弧径皆割浑员圈六之一其平面之阔皆半径然而不
同者其内面挖空之平幂一为锥形(仰盂覆碗之/内空如笠)一为
环形也(鼓体之内/空如截竹)准前论挖空之环幂必倍大于锥形
之幂则其所负之割浑员体亦必环形所负倍大于锥
形而挖空之鼓体必能兼员覆碗员仰盂之二体

　　撱圆算法(订历书之误/)
偶查撱圆求体法见其截小分之法有误今以数考之
假如撱圆形长径为一千四百尺短径七百尺大分截
长径一千○五十尺
　　　　　　　　甲己三百五十戊乙七百相并得
　　　　　　　　一千○五十　以此乘
　　　　　　　　己乙一千○五十尺　以此除
　　　　　　　　两数相同

右依历书先求得庚壬甲圆角形为第三率再用截大
分轴己乙为法为第一率以截小分轴甲己并戊乙半
长径为第二率求得小分之容与圆角形等夫小分之
容形外为弧线圆角之容形外为直线小分必大于圆
角而今等是不合也况自此而截小分渐小则乙己大
分轴反大于甲己小轴及戊乙并之数而求小分之容
反将更小于圆角矣有是理哉(小分渐小如辛癸甲则/其甲己小于己戊而己)
(乙者己戊与戊乙并也则其/数亦大于甲己与戊乙并矣)

　　　　　　　　又如截大分长七百二十分己乙
　　　　　　　　为其轴甲己为其小分轴六百八
　　　　　　　　十分
依历书法甲己小分轴(六百/八十)为一率甲乙长径(一千/四百)并
戊乙短径(七/百)共(二十/一百)为二率求到庚壬乙圆角体为三
率则所得四率为大分之容者比圆角容大三倍有奇
亦恐无是理也何也圆角在圆柱形为三分之一而撱
形必小于柱形不宜有三倍之比例也(虽壬庚略小于/丙丁在中腰相)

(近可以/不论)今试求之(用第/一图)依勿庵改法
假如截己乙大分轴一千○五十尺求庚己壬平圆面
法先求庚己　依勿庵补法以己戊(三百五/十尺)自乘(一十/二万)
(二千五/百尺)与甲戊(七百/尺)自乘(四十九/万尺)相减馀(三十六万七/千五百尺)
开方得己庚相当之原数　再以丙戊(三百五/十尺)乘之甲
戊(七百/尺)除之为己庚实数倍之为庚壬线
再以壬庚线上方变为平员今用简法(因长径甲乙与/短径丙丁原是)
(折半之比/例故也)竟以减馀(三十六万七/千五百尺)命为庚壬线上方以

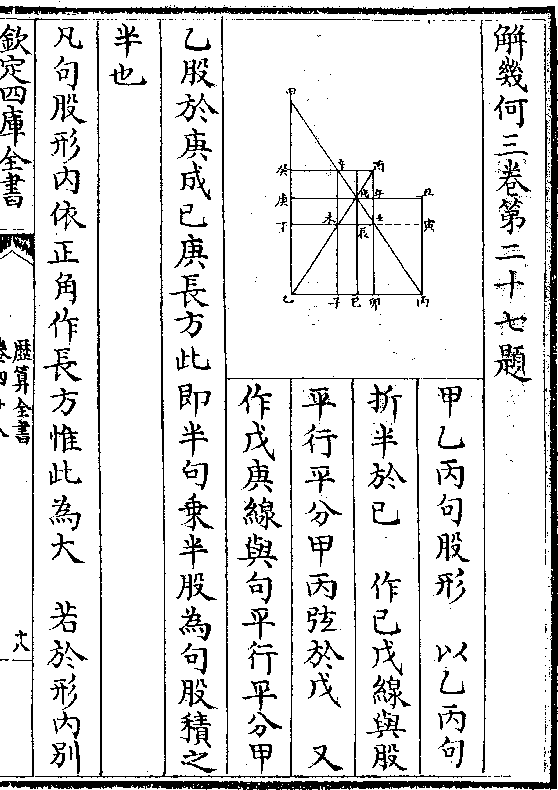十一乘之得(四百○四万/二千五百尺)又以十四除之得(二十八万/八千七百)
(五十/尺)为庚壬线上所截撱体之平圆面
法以平圆面各乘其(大分/小分)之轴(一千○五十尺/三百五十尺)皆成圆
柱形乃三除之为(大/小)分内所容之(大/小)圆角形
再以长径(一千四/百尺)乘大圆角为实小轴(三百五/十尺)除之为
所截撱形之大分
以长径(一千四/百尺)乘小圆角为实大轴(一千○/五十尺)除之为所
截撱形之小分

今用简法　置平圆面三除之得(九万六千二/百五十尺)以小分
轴(三百/五十)乘之得庚甲壬小圆角形(三千三百六十八/万七千五百尺)
置小圆角四因三除之得(四千四百九十一万六千/六百六十六又三之二)为
所截小圆分
又置圆面三除之积(九六二/五○)以大分轴(一千○/五十尺)乘之得
庚子乙大圆角形(一亿○一百○六/万二千五百尺)
置圆角形(一○一○六/二五○○)用四因之得(四亿○四百/二十五万尺)为所
截大圆分

小圆分大圆分两形并之(共四亿四千九百一/十六万六六六六)为撱形
全积
另求撱形全积
置短径(七/百)自乘得(四十/九万)以长径(一千/四百)乘之得(六亿八千/六百万)
以十一因之二十一除之得(三亿五千九百三/十三万三三三)为真撱
圆全积
以真撱圆积与两截形并相较其差为九十分之一而
弱

若用历书法　求得截小分(二千三百六十八/万七千五百尺)与小圆
角同
截大分(六亿○六百三/十七万五千)为大圆角之六倍
相并得(六亿四千○○六/万二千五百尺)为撱圆全积　与撱圆真积
相较其差更甚
如是辗转推求则知撱体大截分不可算今别立法
凡撱体皆先如法求其全积再如法求其小分截积以
小分截积减全积馀为大分截积此法无弊可存

　
　
　
　
　
　
　
　

　
　
　
　
　
　
　
　历算全书卷五十六