钦定四库全书
　历算全书卷五十三
　　　　　　　　　　　　　宣城梅文鼎撰
　三角法举要卷四
　或问(三角大意略具首卷中而入算取用仍有疑端/喜同学之好问事事必求其所以然故不惮为)
　　　(之详复以/畅厥旨)
　　一三角形用正弦为比例之理
　　一和较相求之理

　　一用切线分外角之理
　　一三较连乘之理
　　　附三较求角

问各角正弦与各边皆不平行何以能相为比例曰凡
　三角形一边必对一角其角大者正弦大而所对之
　边亦大角小者正弦小而所对之边亦小故边与边
　之比例如正弦与正弦也
　　　　　　　　两正弦为两边比例图
　　　　　　　　乙丙丁三角形丁乙边大对丙角
　　　　　　　　丁丙边小对乙角术为以丁乙边
　　　　　　　　比丁丙边若丙角之正弦与乙角

之正弦
解曰试以丁丙为半径作丁甲线为丙角正弦又截戊
乙如丁丙半径作戊己线为乙角正弦丁甲正弦大于
戊己故丁乙边亦大于丁丙
问丁甲何以独为丙角正弦也曰此以丁丙为半径故
　也若以丁乙为半径则丁甲即为乙角之正弦
　如图用丁乙为半径作丁甲线为乙角正弦又引丙
　丁至戊令戊丙如丁乙半径作戊己线为丙角正弦

　　　　　　　　即见乙角之正弦丁甲小于戊己
　　　　　　　　故丁丙边亦小于丁乙
　　　　　　　　解曰正弦者半径所生也故必两
　　　　　　　　半径齐同始可以较其大小前图
　截戊乙如丁丙此图引丁丙如丁乙所以同之也
三正弦递相为三边比例图
　乙丁丙钝角形丁钝角对乙丙大边丙次大角对乙
　丁次大边乙小角对丁丙小边其各边比例皆各角

　正弦之比例
　　　　　　　　试以乙丁为半径作丁甲线为乙
　　　　　　　　小角之正弦又引丙丁边至戊使
　　　　　　　　戊丙如乙丁作戊己线为丙角之
　　　　　　　　正弦又展戊丙线至庚使庚丙如乙
　丙作庚辛线为丁钝角之正弦(如此则三边皆若/弦三正弦皆若股)
　其比例为以乙丙大边(同庚/丙)比乙丁次边(同戊/丙)若丁
　钝角之正弦庚辛与丙角之正弦戊己

　又以乙丁次大边(同戊/丙)比丁丙小边若丙角之正弦
　戊己与乙角之正弦丁甲
　又以丁丙小边比乙丙大边(同庚/丙)若乙小角之正弦
　丁甲与丁钝角之正弦庚辛
问庚辛何以为丁角正弦曰凡钝角以外角之正弦为
　正弦试作乙癸线为丁角正弦(乙丁癸角外角也故/其正弦即为丁钝角)
　(正/弦)必与庚辛等何也庚丙辛句股形与乙丙癸形等
　(庚丙弦既同乙丙又同用丙角辛/与癸又同为方角故其形必等)则庚辛必等乙癸

　而乙癸既丁角正弦矣等乙癸之庚辛又安得不为
　丁角正弦乎(凡取正弦必齐其半径此以丁甲为乙/角正弦是用乙丁为半径也而取丙角)
　(正弦戊己必引戊丙如乙丁其丁角正弦庚也/辛又即外角之正弦乙癸是三半径皆乙丁)
　　　　　　　　试取壬丙如丁丙作庚壬线即同
　　　　　　　　乙丁半径则壬角同丁角壬外角
　　　　　　　　即丁外角而庚辛正弦之半径仍
　　　　　　　　为乙丁(庚壬同/乙丁故)
　　　　　　　　此以庚壬当乙丁易乙丁丙形为

　庚壬丙则庚辛正弦亦归本位与前图互明
试以各角正弦同居一象限较其弧度
　如图甲乙丙形丙角最大其正弦乙丁亦最大所对
　甲乙边亦最大甲角次大其正弦丑壬亦次大所对
　　　　　　　　乙丙边亦次大乙角最小其正弦
　　　　　　　　丙卯亦小所对丙甲边亦最小(丙/乙)
　　　　　　　　(二角正弦并乙丙为半径甲角取/正弦截丑甲如乙丙亦以乙丙为)
　　　　　　　　(半/径)乃别作一象弧(如戊/己)仍用乙丙

　　　　　　　　为半径(取戊庚/如乙丙)而以先所得各角
　　　　　　　　之馀弦取度于丁作乙丁为丙角
　　　　　　　　之正弦于壬作丑壬为甲角之正
　　　　　　　　弦于卯作丙卯为乙角之正弦即
　如元度而各角之差数睹矣(戊庚半径既同乙丙则/丁庚即丁丙而为丙角)
　(馀弦又壬庚即甲壬为甲角馀/弦卯庚即卯乙为乙角馀弦)
　解曰角无大小以弧而知其大小今乙丁正弦其弧
　乙己是丙角最大也丑壬正弦其弧丑己是甲角次

　大也丙卯正弦其弧丙己是乙角最小也而对边之
　大小亦如之故皆以正弦为比例也
或疑钝角之度益大其正弦反渐小而其所对之边则
　渐大何以能相为比例乎曰此易知也凡钝角正弦
　即外角之正弦而外角度原兼有馀两角之度故钝
　角之正弦必大于馀两角而得为大边之比例也
　如乙丙甲钝角形丙钝角最大其正弦乙丁亦最大
　而所对乙甲边亦最大乙角次大其正弦丙卯亦次

　大而所对甲丙边亦次大甲角最小其正弦丑壬亦
　小而所对乙丙边亦最小(截甲丑如乙丙从丑/作丑壬即甲角正弦)
　　　　　　　　乃从乙作乙庚弧(以丙为心乙/丙为半径)为
　　　　　　　　丙外角之度又作辛丙半径与甲
　　　　　　　　乙平行分乙庚弧度为两则辛庚
　　　　　　　　即甲角之弧度其馀辛乙亦即乙
　　　　　　　　角之弧度从辛作辛未正弦与丑
　　　　　　　　壬等又自庚截癸庚度如辛乙则

　癸庚亦乙角之弧作癸子正弦与丙卯等此显丙外
　角之度兼有乙甲两角之度其正弦必大于两角正
　弦也虽丙钝角加大而外角加小则乙甲两角必又
　小于外角又何疑于钝角正弦必为大边比例乎
试更以各角切员观之则各角之对边皆为其对弧之
　通弦
　如图三角形以各角切员则乙丙边为丙戊乙弧之
　通弦而对甲角甲丙边为丙己甲弧之通弦而对乙

　　　　　　　　角甲乙边为乙庚甲弧之通弦而
　　　　　　　　对丙角则是各角之对边即各角
　　　　　　　　对弧之通弦也夫通弦者正弦之
　　　　　　　　倍数则三边比例即三正弦之比
　　　　　　　　例矣
又试以各边平分之则皆成各角之正弦
　于前图内更以各边所当之弧皆平分之(丙戊乙弧/平分于戊)
　(点丙己甲弧平分于己点/乙庚甲弧平分于庚点)自员心(丁/)各作半径至其

　　　　　　　　　　点即分各边为两平分(以丁/壬戊)
　　　　　　　　　　(半径分乙丙边于壬以丁辛/己半径分甲丙边于辛以丁)
　　　　　　　　　　(癸庚半径分甲乙边于癸/则所分之边皆为两平分)则
　　　　　　　　　　弧之平分者即原设各角之
　　　　　　　　　　度而边之平分者即皆各角
　　　　　　　　　　之正弦(丙丁戊角以丙戊为/弧丙壬为正弦而丙)
　　　　　　　　　　(丁戊角原为丙丁乙角之半/必与甲角同大故丙戊半弧)
　　　　　　　　　　(即甲角之本度丙壬半边即/甲角之正弦乙丁戊角亦然)

　(准此论之则甲丁己角原为甲丁丙角之半必与/乙角同大故甲己半弧即乙角之本度甲辛半边)
　(即乙角之正弦己丁丙角亦然又乙丁庚角原为/乙丁甲角之半必与丙角同大故乙庚半弧即丙)
　(角之本度乙癸半边即丙/角之正弦庚丁甲角亦然)夫分其边之半即皆成
　正弦则边与边之比例亦必如正弦与正弦矣(全/与)
　(全若半/与半也)
问三角之本度皆用半弧何也曰量角度必以角为员
　心真度乃见今三角皆切员边则所作通弦之弧皆
　倍度也故半之乃为角之本度

　如图以甲角为心甲丁为半径作员则其弧丑丁子
　乃甲角之本度也而平分之丙戊及戊乙两弧并与
　丑丁子弧等(试作戊丙及乙戊两弦必相等又/并与丑子弦等凡弦等者弧亦等)故乙
　　　　　　　　　　　戊丙弧必为甲角之倍度
　　　　　　　　　　　(馀角/类推)
　
　
　

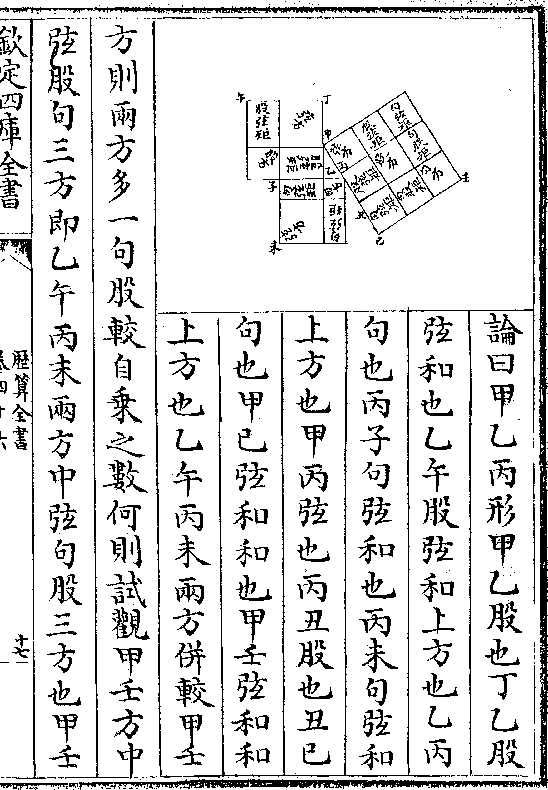
问三边求角何以用和较相乘也曰欲明和较之用当
先知和较之根凡大小两方以其边相并谓之和相减
谓之较和较相乘者两方相减之馀积也
　　　　　　　　如图甲癸小方丁癸大方于大方
　　　　　　　　内依小方边作己庚横线又取己
　　　　　　　　辛如小方边作辛壬线成己壬小
　　　　　　　　方与甲癸等大方内减己壬小方
　　　　　　　　则所馀者为乙庚及庚壬两长方

形夫乙己及丁庚及庚辛并两边之较也甲己庚则和
也若移庚壬长方为乙甲长方即成丁甲大长方而为
较乘和之积故凡两方相减之馀积为实以和除之得
较以较除之亦得和矣
依此论之若有两方形相减又别有两方相减而其馀
积等则为公积故以此两方之和较相乘为实而以彼
两方之和为法除之得彼两方之较或以彼两方之较
为法除之亦必得和

　　　　　　　　　　(如图有方二十九之幂八百/四十一与方二十七之幂七)
　　　　　　　　　　(百二十九相减成较二乘和/五十六之积)
　　　　　　　　　　(又有方十六之幂二百五十/六与方十二之幂一百四十)
　　　　　　　　　　(四相减成较四乘和二十八/之积)
　　　　　　　　　　(两积同为一百一十二故以/先有之较二和五十六相乘)
(为实以今有之和二十八为法/除之即得较四为今所求数)
是故三角形以两弦之和乘较为实以两分底之和为
法除之得较者为两和较相乘同积也两和较相乘同

积者各两方相减同积也
何以明之曰凡三角形以中长线分为两句股则两形
同以中长线为股而各以分底线为句是股同而句不
同也句不同者弦不同也弦大者句亦大弦小者句亦
小故两弦上方相减必与两句上方相减之馀积等而
两和较相乘亦等
如图甲乙丙三角形以甲丁中长线分为两句股形则
丙乙为两句之和(未寅及子/卯并同)丙戊为两句之较(未子及/寅卯并)

　　　　　　　　　　(同/)未卯长方为两句之较乘
　　　　　　　　　　和也又丙己为两弦之和(辰/壬)
　　　　　　　　　　(同/)酉丙为两弦之较(辰癸及/辛庚壬)
　　　　　　　　　　(午并/同)癸壬长方为两弦之较
　　　　　　　　　　乘和也此两长方必等积
问两弦上方大于两句上方何以知其等积曰依句股
法弦上方幂必兼有句股上方幂是故甲丙弦幂内(即/癸)
(甲大/方)必兼有甲丁股丙丁句两幂乙甲弦幂内(即辛己/小方)

亦兼有甲丁股乙丁句两幂则是甲丁股幂者两弦幂
所同也其不同者句幂耳(股幂既同则弦幂相减时股/幂俱对减而尽使非句幂不)
(同巳无/馀积)然则两弦幂相减之馀积(于癸甲大方内减己/辛相同之申甲小方)
(所馀者癸辛申丙/两长方成磬折形)岂不即为两句幂相减之馀积乎(于/丁)
(子方内减丁寅相同之戊丑小方所形/所馀者丑子及戊未两长方成磬折)由是言之两和较
相乘之等积信矣(于弦幂相减之癸辛申丙磬折形内/移申丙补庚壬即成和较相乘之癸)
(壬长方又于句幂相减之丑子未戊磬折形内移戊未/补丑卯即成和较相乘之未卯长方两磬折形既等积)
(则两长方/亦等积)

问和较之列四率与诸例不同何也曰此互视法也同
文算指谓之变测古九章谓之同乘异除乃三率之别
调也何则凡异乘同除皆以原有两率之比例为今两
率之比例其首率为法必在原有两率之中互视之术
则反以原有之两率为二为三以自相乘为实其首率
为法者反系今有之率与异乘同除之序相反故曰别
调也
然则又何以仍列四率曰以相乘同实也三率之术二

三相乘与一四相乘同实故可以三率求一率(二三相/乘以一)
(除之得四以四除之即仍得一若一四相乘/以二除之亦可得三以三除之亦仍得二)互视之术
以原有之两率自相乘与今有之两率自相乘同实故
亦以三率求一率(原两率自相乘以今有之率除之得/今有之馀一率若今两率自相乘以)
(原有之率除之亦即/得原有之馀一率)但三率之术以比例成其同实互
视之术则以同实而成其比例既成比例即有四率故
可以列而求之也
如图长方形对角斜剖成两句股则相等而其中所成

　　　　　　　　　　小句股亦相等(甲壬戊与甲/己戊等则甲)
　　　　　　　　　　(乙丙与甲辛丙等丙丁戊与/丙庚戊等并长方均剖故也)
　　　　　　　　　　即所成长方之积亦必相等
　　　　　　　　　　(于甲壬戊句股形内减去相/等之甲乙丙及丙丁戊两小)
(句股存乙丙丁壬长方又于甲己戊句股形内减去相/等之甲辛丙及丙庚戊两小句股存辛己庚丙长方所)
(减之数等则所存之数亦等故两长/方虽长阔不同而知其必为等积)今以甲乙为首率
乙丙为次率丙丁为三率丁戊为四率则乙丁长方(即/乙)
(丙丁/壬形)为二三相乘之积(此形以乙丙二率为阔丙丁三/率为长是二率三率相乘也)

辛庚长方(即辛己/庚丙形)为一四相乘之积(此形以辛丙为长/丙庚为阔而辛丙)
(原同甲乙乃一率也丙庚原同丁戊/乃四率也是一率四率相乘也)既两长方相等则
二三相乘与一四相乘等实矣此列率之理也
　一　　甲乙
　二　　丙乙
　三　　丙丁
　四　　戊丁
在异乘同除本术则甲乙及丙乙为原有之数丙丁为

今有之数戊丁为今求之数其术为以原有之甲乙股
比原有之丙乙句若今有之丙丁股与戊丁句也故于
原有中取丙乙句与今有之丙丁股以异名相乘为实
又于原有中取同名之甲乙股为法除之即得今所求
之丁戊句是先知四率之比例而以乘除之故成两长
方(二率乘三率成乙丁长方以/首率除之必变为辛庚长方)故曰以比例成其同实
也
互视之术则乙丙与丙丁为原有之数甲乙为今有之

数丁戊为今求之数术为以乙丙较乘丙丁和之积若
丙庚较(即丁/戊)乘丙辛和(即甲/乙)之积故以原有之乙丙较
丙丁和自相乘为实以今有之甲乙和(即辛/丙)为法除之
即得今所求之丁戊较(即丙/庚)是先知两长方同积而以
四率取之故曰以同实成其比例也
然则又何以谓之互视曰三率之用以原有两件自相
比之例为今有两件自相比之例是视此之差等为彼
之差等如相慕效故大句比大股若小句比小股(大句/小于)

(大股几倍小句亦小于小股几倍又大句/大于小句几倍大股亦大于小股几倍)互视之用以
原有一件与今一件相比之例为今又一件与原又一
件相比之例是此视彼之所来以往彼亦视此之所往
以来如互相酬报故弦之较比句之较反若句之和比
弦之和(弦之和大于句故句之较反大于弦若和之数/弦大于句几倍则较之数句大于弦亦几倍)
是以别之为互视也
如图以甲乙为一率丙乙为二率丙丁为三率丁戊为
四率作甲戊弦成两句股次引甲乙及丁戊会于壬成

　　　　　　　　　　乙丁长方为二三相乘之积
　　　　　　　　　　亦引乙丙至庚引丁丙至辛
　　　　　　　　　　作甲辛及戊庚线并引长之
　　　　　　　　　　会于己成辛庚长方为一四
　　　　　　　　　　相乘之积是先有比例而成
　　　　　　　　　　同实之长方
　　　　　　　　　　如图乙丙乘丙丁为乙丁长
　　　　　　　　　　方辛丙乘丙庚为辛庚长方

　　　　　　　　　　两长方以角相连于丙次引
　　　　　　　　　　己辛及乙壬会于甲引己庚
　　　　　　　　　　及壬丁会于戊乃作甲戊线
　　　　　　　　　　则辛丙与丙丁若乙丙与丙
　　　　　　　　　　庚是先知同实而成其比例
　　　　　　　　　　也

问三角形两又术用外角切线何也曰此分角法也一
角在两边之中则角无所对之边边无所对之角不可
以正弦为比例今欲求未知之两角故借外角分之也
然则何以用半较角曰较角者本形中未知两角之较
也此两角之度合之即为外角之度必求其较角然后
可分而较角不可求故求其半知半较知全较矣此用
半较角之理也
如图甲丙乙形先有丙角则甲丙丁为外角外角内作

　　　　　　　　　　　丙辛线与乙甲平行则辛
　　　　　　　　　　　丙丁角与乙角等辛丙甲
　　　　　　　　　　　角与甲角等
　其辛丙庚角为两角之较而辛丙己角其半较也己
　丙丁及己丙甲皆半外角也以半较角与半外角相
　减成乙角(于丁丙己内减辛丙己/其馀丁丙辛即乙角度)若相加亦成甲角
　(于己丙甲加辛丙己/成辛丙甲即甲角度)
半较角用切线何也曰此比例法也角与所对之边并

以正弦为比例今既无正弦可论而有其所对之边故
即以边为比例(角之正弦可以例边则/边之大小亦可以例角)是故乙丁者两
边之总也乙癸者两边之较也而戊己者半外角之切
线也壬己者半较角之切线也以乙丁比乙癸若戊己
与壬己故以切线为比例也
然则何以不径用正弦曰凡一角分为两角则正弦因
度离立不同在一线不可以求其比例其在一线者惟
切线耳而边之比例与切线相应切线比例又原与正

弦相应故用切线实用正弦也
　　　　　　　　　　　如图甲丙丁外角其弧甲
　　　　　　　　　　　己丁于辛作辛丙线分其
　　　　　　　　　　　角为两则小角之弧丁辛
　　　　　　　　　　　其正弦卯丁大角之弧辛
　　　　　　　　　　　甲其正弦甲丑(小角正弦/当乙角之)
　　　　　　　　　　　(对边甲丙大角正弦/当甲角之对边乙丙)
今欲移正弦之比例于一线先作甲丁通弦割分角线

于子则子甲与子丁若甲丑与卯丁(甲丑子与丁卯子/两句股形有子交)
(角等丑卯皆正角即两形相似而比例等然则子甲者/大形之弦子丁者小形之弦而甲丑者大形之股卯丁)
(者小形之股也弦与弦若股与股/故子甲比子丁若丑甲与卯丁)而甲丁即两正弦之
总(甲丁为子甲子丁之总/亦即为甲丑卯丁之总)辰子即两正弦之较(以子丁/减子甲)
(其较辰子是辰子为子甲子丁/之较亦即为甲丑卯丁之较)平分甲丁半之于酉则
酉丁为半总酉子为半较其比例同也(全与全若半与/半故甲丁与辰)
(子为两正弦之总与较则半之而为酉/丁与酉子亦必若两正弦之总与较)
于是作午戊切员线(引平分线丙酉至己分甲己丁弧/于己自己作午戊线与己丙为十)

(字垂线即此/线为切员线)与甲丁平行引诸线至其上(引丙甲至午/引丙丁至戊)
(引丙辰割庚点至未/引丙卯割辛点至壬)则午戊切线上比例与甲丁通弦
等而正弦之比例在切线矣(先以甲丁与辰子当两正/弦之总与较今午戊与未)
(壬亦可当两正弦之总与较则先以酉丁与酉子为半/总半较者今亦以己戊与己壬为半总半较矣)
故曰用切线实用正弦也(切线与正弦所以能同比/例者以有通弦作之合也)
问三较连乘之理曰亦句股术也以句股为比例而以
三率之理转换之则用法最精之处也故三较连乘即
得容员半径上方乘半总之积

　　　　　　　　　　假如甲乙丙三角形甲丙边
　　　　　　　　　　一百五十甲乙边一百二十
　　　　　　　　　　二乙丙边一百一十二术以
　　　　　　　　　　半总一百九十二较各边得
　　　　　　　　　　甲丙之较四十二甲乙之较
　　　　　　　　　　七十乙丙之较八十三较连
　　　　　　　　　　乘得数二十三万五千二百
　　　　　　　　　　即容员半径自乘又乘半总

之积也
　置三较连乘数以半总除之得数(一千二百/二十五)平方开
　之得容员半径(三十/五)倍之得容员径(七/十)
　置三较连乘数以半总乘之得数(四千五百一十/五万八千四百)平
　方开之得三角形积(六千七/百二十)
　若如常法求得中长线(一百/二十)以乘乙丙底而半之所
　得积数亦同
　然则何以见其为句股比例曰试从形心如法作线

　分为六句股形(形心即/容员心)又引甲丙边至卯使卯丙如
　乙戊引甲乙边至辰使乙辰如己丙则甲卯甲辰并
　半总(六小句股形之句各于其两/相同者而取其一即成半总)而丙卯为甲丙边
　　　　　　　　　　之较(即乙戊/或乙辛)乙辰为甲乙边
　　　　　　　　　　之较(即己丙/或辛丙)甲己为乙丙边
　　　　　　　　　　之较(己丙同辛丙又丙卯同/乙辛则卯己同乙丙而)
　　　　　　　　　　(甲己为其较若用辰戊以/当乙丙则甲戊为较亦同)又
　　　　　　　　　　从卯作卯壬十字垂线至壬

　(此线与丁己/员半径平行)引甲丁分角线出形外遇于壬成甲卯
　壬大句股形与甲己丁小句股之比例等(从辰作辰/壬线成甲)
　(辰壬大句股与甲戊丁/小句股为比例亦同)术为以丁己比壬卯若甲己
　与甲卯也次以丁己自乘方为一率以丁己乘壬卯
　之长方为次率则其比例仍若甲己三率与甲卯四
　率也(乘之者并丁己故所乘之/丁己与壬卯比例不变也)
　以数明之甲己八十甲卯一百九十二为二倍四分
　比例丁己三十五壬卯八十四亦二倍四分比例丁

　己自乘一千二百二十五丁己乘壬卯二千九百四
　十亦二倍四分比例故曰比例等
　又移辛点至癸截丙癸如丙卯则乙癸亦如乙辰引
　丙卯至午使卯午同乙辰(亦同/乙癸)引乙辰至未使辰未
　同丙卯(亦同/丙癸)则午丙及未乙并同乙丙又作丙壬乙
　壬午壬未壬四线成午丙壬及乙未壬及乙丙壬各
　三角形皆相等(丙卯壬句股形与未辰壬等则丙壬/必等未壬又午卯壬句股形与乙辰)
　(壬等则午壬等乙壬而午丙壬及乙未壬两三角形/必等矣其乙丙壬三角形既以乙丙与两三角形同)

　　　　　　　　　　(底又同用丙壬乙壬/两弦亦不得不等)于是自
　　　　　　　　　　癸作癸壬垂线(卯壬辰壬并/垂线故癸壬)
　　　　　　　　　　(亦必/垂线)成丙癸壬句股形与丙
　　　　　　　　　　卯壬形等即成癸丙卯壬四
　　　　　　　　　　边形与丁己丙辛小四边形
　　　　　　　　　　为相似形(卯与癸俱方角而方/小形之己与辛亦)
　(角则大形之丙角与壬角合之亦两方角也而小形之/丙角原为大形丙角之外角合之亦两方角也则小形)
　(之丙角与大形之壬角等而小形之丁角亦与大形/之丙角等是大小两形之四角俱等而为相似形)

　则丁己丙句股形与丙卯壬形亦相似而比例等(大/小)
　(两四边形各均剖其半以成句股则其/相似之比例不变全与全若半与半也)术为以丁己
　比己丙若丙卯与卯壬也
　一　丁己
　二　己丙
　三　丙卯　即甲丙之较戊乙
　四　卯壬
　凡三率法中二三相乘一四相乘其积皆等则己丙

　乘丙卯之积即丁己乘卯壬之积可通用也先定以
　丁己自乘比丁己乘卯壬若甲己与甲卯今以三率
　之理通之为以丁己自乘比己丙乘丙卯亦若甲己
　与甲卯
　一　丁己自乘方　　　即容员半径自乘
　二　己丙乘丙卯长方　即甲乙之较乘甲丙之数
　三　甲己　　　　　　即乙丙之较
　四　甲卯　　　　　　即半总

　复以三率之理转换用之则三较连乘之积(以己丙/较乘戊)
　(乙较为二率又以甲己较为三率/乘之是二三相乘即三较连乘)即容员半径自乘
　方乘半总之积也(以丁己半径自乘为首率以甲卯/半总为四率乘之是一四相乘也)
　(凡一四相乘必与/二三相乘之积等)
　以数明之丁己(三十/五)卯壬(八十/四)相乘得二千九百四
　十己丙(七/十)丙卯(四十/二)相乘亦二千九百四十故可通
　用
　己丙乘丙卯(二千九/百四十)又以甲己(八/十)乘之得二十三万

　五千二百丁己自乘(一千二百/二十五)又以甲卯(一百九/十二)乘
　之亦二十三万五千二百故可通用
问三较之术可以求角乎曰可其所求角皆先得半角
即锐钝通为一术矣
术曰以三边各减半总得较各以所求角对边之较乘
半总为法以馀两较各与半径全数相乘又自相乘为
实法除实得数平方开之为半角切线捡表得度倍之
为所求角

　　　　　　　　　　假如甲乙丙三角形甲丙边
　　　　　　　　　　七十五甲乙边五十六乙丙
　　　　　　　　　　边六十一与半总九十六各
　　　　　　　　　　相减得甲丙之较二十一甲
　　　　　　　　　　乙之较四十乙丙之较三十
　　　　　　　　　　五
　　　　　　　　　　今求乙角术以乙角所对边
　　　　　　　　　　甲丙之较(二/一)乘半总(九/六)得数

　　　　　　　　　　(二○/一六)为法以馀两较(甲乙较/四○乙)
　　　　　　　　　　(丙较/三五)各乘半径全数又自相
　　　　　　　　　　乘得数(一四○○○○○/○○○○○○○)为
　　　　　　　　　　实法除实得数(六九四四四/四四四四四)
　　　　　　　　　　平方开之得数(八三三/三三)为半
　　　　　　　　　　角切线捡表(三十九度四十/八分一十九秒)
　　　　　　　　　　倍之得乙角(七十九度三十/六分三十八秒)
　次求丙角术以丙角所对边甲乙之较(四/○)乘半总得

　数(三八/四○)为法馀两较(甲丙二一/乙丙三五)各乘半径全数又自
　相乘得数(七三五○○○○/○○○○○○)为实法除实得数(一九/一四)
　(○六二/五○○)平方开之得半角切线(四三七/五○)捡表(二十三/度三十)
　(七分五十/二秒半)倍之得丙角(四十七度一十/五分四十五秒)
　次求甲角术以甲角所对边乙丙之较(三/五)乘半总得
　数(三三/六○)为法馀两较(甲丙二一/甲乙四○)各乘半径全数又自
　相乘得数(八四○○○○○/○○○○○○)为实法除实得数(二五/○○)
　(○○○/○○○)平方开之得半角切线(五○○/○○)捡表(二十六/度三十)

　(三分五/十三秒)倍之得甲角(五十三度○七/分四十六秒)
问前条用三较连乘今只用一较为除法何也曰前条
求总积故三较连乘今有专求之角故以对边之较为
法也然则用对边何也曰对边之较在所求角之两旁
为所分小句股形之句今求半角切线故以此小句为
法也
如求乙半角则所用者角旁小句股(心戊乙或/心丁乙)其句(乙/戊)
(或乙/丁)并二十一即对边甲丙之较也术为以乙戊比心

戊若半径与乙角(小形之角/即半角也)之切线
　　　　　　　　　其与半总相乘何也曰将以半
　　　　　　　　　总除之又以小形句(即对边/之较)除
　　　　　　　　　之今以两除法(一半总一对边/之较即小形句)
　　　　　　　　　相乘然后除之变两次除为一
次除也(古谓之异/除同除)
用两次除亦有说乎曰前条三较连乘必以半总除之
而得容员半径之方幂今欲以方幂为用故亦以半总

除也然则又何以对边之较除曰非但以较除也乃以
较之幂除也何以言之曰原法三较连乘为实今只以
两较乘是省一乘也既省一对边之较乘又以对边之
较除之是以较除两次也即如以较自乘之幂除之矣
馀两较相乘先又各乘半径何也曰此三率之精理也
凡线与线相乘除所得者线也幂与幂相乘除所得者
幂也先既定乙戊句为首率心戊股(即容员/半径)为次率半
径为三率乙角切线为四率而今无心戊之数惟三较

连乘中有心戊(即容员/半径)自乘之幂(即三较连乘半/总除之之数)故变
四率并为幂以乙戊句幂为首率(即对边之/较除两次)心戊股幂
为次率(即半总除/连乘数)半径之幂为三率(即半径/自乘)得半角切
线之幂为四率(即分形/之乙角)
　　　　　　　　　一　乙戊　　今用乙戊自乘
　　　　　　　　　二　心戊　　　　心戊自乘
　　　　　　　　　三　半径　　　　半径自乘
　　　　　　　　　四　乙角切线　　切线自乘

故得数开方即成切线
又术
以三较连乘半总除之开方为中垂线(即容员/半径)以半径
全数乘之为实各以所求角对边之较除之即得半角
切线
　一　乙戊(乙角对/边之较)　丙戊(丙角对/边之较)　甲己(甲角对/边之较)
　二　心戊中垂线　心戊中垂线　心己中垂线(亦即/心戊)
　三　半径全数　　半径全数　　半径全数

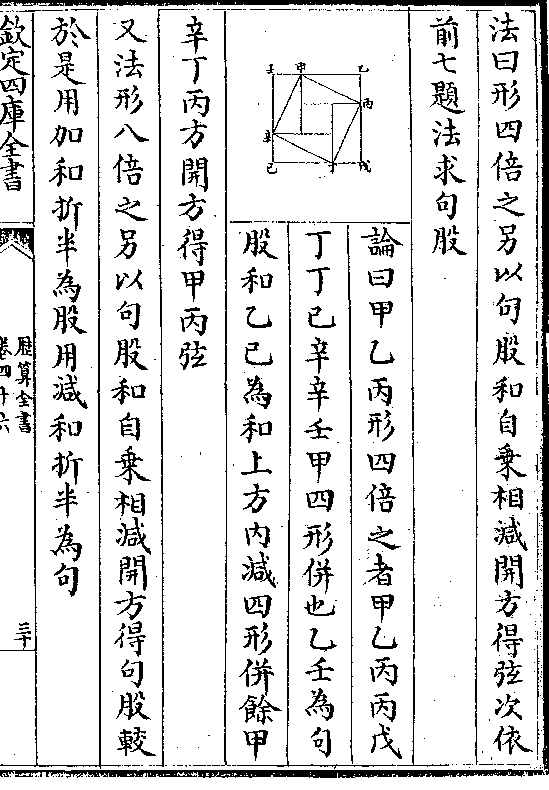　四　乙半角切线　丙半角切缘　甲半角切线
此即用前图可解乃本法也
论曰常法三边求角倘遇钝角必于得角之后又加审
焉以钝角与外角同一八线也今所得者既为半角则
无此疑实为求角之捷法

补遗
问以边求角(句股第/二术)因和较乘除而知正角乃定其为
句股形何也曰古法句弦较乘句弦和开方得股今大
边(壬/丁)与小边(癸/丁)以和较相乘为实癸壬边为法除之而
仍得癸壬是适合开方之积也则大边小边之和较即
句弦之和较而癸为正角成句股形矣(凡句股形弦为/大边而对正角)
(今丁壬边最大即弦也/故所对之癸角为正角)
试再以丁壬与壬癸之和较求之

　　　　　　　　如法用丁壬壬癸相加得和(一百/九十)
　　　　　　　　(六/丈)相减得较(一十/六丈)较乘和(三千一/百三十)
　　　　　　　　(六/丈)为实丁癸(五十/六丈)为法除之亦仍
　　　　　　　　得五十六丈何则股弦较乘和亦
开方得句故也
然则句股弦和较之法又安从生曰生于割圜
试以丁壬弦为半径作戊丁丙己圜　全径二百一十
二　半径一百○六　乙丁正弦九十(即癸/壬股)　乙壬馀

　　　　　　　　　弦五十六(即癸/丁句)　丙乙正矢五
　　　　　　　　　十(即句/弦较)　乙庚大矢一百六十
　　　　　　　　　二(即句/弦和)　正矢乘大矢得数八
　　　　　　　　　千一百开方得正弦(即句弦和/乘较开方)
　　　　　　　　　(得/股)
然则此八千一百者既为正矢大矢相乘之积又为正
弦自乘之积故以正弦自乘为实而正矢除之可以得
大矢大矢除之亦得正矢(即乙丁股自乘为实而以句/弦较丙乙除之得乙庚为句)

(弦和若以句弦和/除之亦得句弦较)
更之则正矢乘大矢为实以正弦除之仍得正弦矣(即/句)
(弦较丙乙乘句弦和乙庚为实以/乙丁股为法除之而仍复得股)
论曰句股形在平圜内其半径恒为弦若正弦馀弦则
为句为股可以互用故其理亦可互明(以丁壬及丁癸/二边取和较求)
(壬癸边为句弦求股以丁壬及壬癸二边/取和较求丁癸边为股弦求句一而已矣)
问数则合矣其理云何曰仍句股术也
如上图于圜径两端(如丙/如庚)各作通弦线至正弦(丁/乙)之锐

　　　　　　　　　(如庚乙/丙乙)成丙乙庚大句股形又
　　　　　　　　　因中有正弦成大小两句股形
　　　　　　　　　(乙丁庚为大形/乙丙丁为小形)而相似(以乙丁/线分正)
　　　　　　　　　(角为两则小形乙角为大形乙/角之馀而与庚角等即大形乙)
　　　　　　　　　(角亦与小形丙角/等故两形相似)则乙丁正弦
既为小形之股又为大形之句其比例为丙丁(小形/句)与
乙丁(小形/股)若乙丁(大形/句)与丁庚(大形/股)也故正矢(丁/丙)乘大
矢(丁/庚)与正弦(乙/丁)自乘等积(丙庚全径为正弦所分其一/丁丙正矢为小形之句而乙)

(丁正弦为其股其一丁庚大矢为/大形之股而乙丁正弦为其句)
一　丁丙正矢　小形句　　凡二率三率相乘与一
二　乙丁正弦　小形股　　四相乘等积故乙丁自
三　乙丁正弦　大形句　　乘即与丁丙丁庚相乘
四　丁庚大矢　大形股　　等积也
论曰凡割圜算法专恃句股古法西法所同也故论句
股者必以割圜而论割圜者仍以句股如根株华实之
相须乃本法非旁證也

或疑切线分外角以正弦为比例恐不可施于钝角作
此明之
　
　
　
　
甲丙乙钝角形先有丙角及丙甲丙乙二边求馀角
一率丁乙(边/总)二率癸乙(边/较)三率己戊(半外角/切线)四率壬己

(半较角/切线)
论曰试作壬丙线与乙甲平行分外角为两则壬丙丁
即乙角其正弦卯丁又甲丙壬即甲角其正弦甲丑以
两句股(丑子甲/卯子丁)相似之故能令两正弦(丑甲/卯丁)之比例移
于通弦以成和较(丑甲与卯丁既若子甲与子丁则丁/甲即两正弦之和辰子即两正弦之)
(较/)而半外角半较角之算以生(半外角为和半较角为/较并与两正弦之和较)
(同比例即与两边/之和较同比例)并如锐角
又论曰此所分大角为钝角故甲丑正弦作于形外然

虽在形外而引分角线至丑适与之会即能成丑子甲
句股形与卯子丁相似而生比例
　
　
　
　
(丙乙甲形先有丙角求馀角与法为边总丁乙与边/较乙癸若半外角切线戊己 半较角切线未己)
(此亦因所分为钝角故卯丁正弦在形外馀又大边/为半径故乙癸较亦在形外而丁乙为和 并同前)

　
　
　
　
　
　
(丙甲乙形先有丙角求馀角半法为边总丁乙与边较/乙癸若半外角切线己戊与 较角切线己壬 此因)
(先得钝角故所分之内反无钝角而正弦所/作之小句股并在外角之内同锐角法矣)

　
　
　
　
　
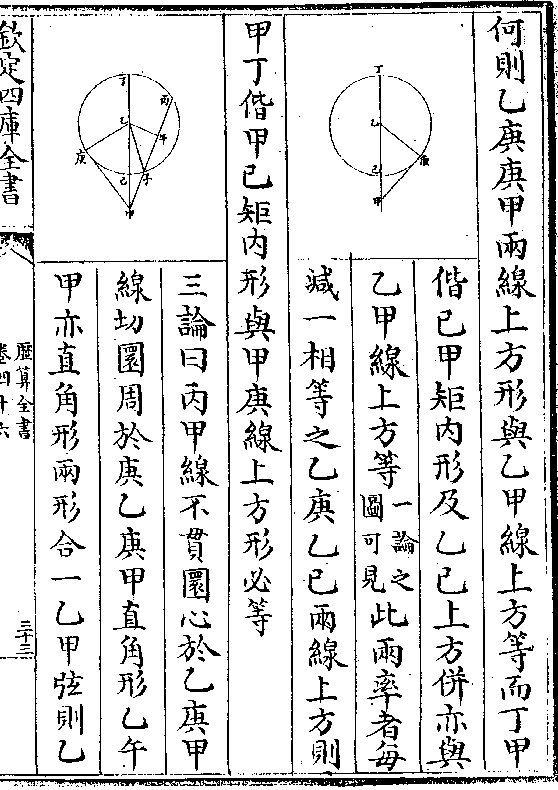
(丙甲乙形先得丙角及丙甲句乙丙弦如法作丙壬线/与乙甲股平行分外角为两则句弦和丁乙与句弦较)
(癸乙若半外角切线己戊与半较角切线己壬所此以/丙甲为半径作外角弧而即用丙甲为正弦知 得为)
(正/角)

　
　
　
　
　
(甲乙丙形先得丙角求馀角辛如法作丙庚线与乙甲/句平行次截辛丁如庚甲作 丙线分外角为两则小)
(角之正弦卯丁大角之正弦即丙甲而成两句股相似/为切线比例 法为句弦和丁乙与句弦较乙癸若半)
(外角切线己戊与半较角切线己壬辛此以丙甲为半/径作外角弧而即用丙甲为正弦知 丙甲为正角而)

(丁辛同庚甲即辛丙甲同丁丙庚又即同丙乙/甲而乙为正角矣以乙正角减外角馀为甲角)
论曰右并以先不知其为句股形故求之而得正角凡
正角之弧九十度别无正弦而即以半径全数为正弦
得此明之
　
　
　
　

(甲乙丙形先有正角求馀角己法为句股和丁乙与句/股较癸乙若半外角切线戊 与半较角切线己壬)
论曰此因先得者为正角故其外角亦九十度而半外
角四十五度之切线即同半径全数馀并同前
又论曰句股形求角本易不须外角而外角之用得此益明

(以大边为半径作外角弧分角线丙未与次大边平行/ 边总乙丁与边较乙癸若半外角切线戊己与半较)
(角切线/壬己)
　
　
　
　
(以次大边为半径作外角弧分角线丙未与小边乙甲/平行大边总丁癸与边较乙癸若半外角切线己戊与)
(半较角切/线己壬)

问平三角形以一边为半径得三正弦比例不识大边
亦可以为半径乎(小边次边为半径/已具前条故云)曰可
　　　　　　　　如乙丙丁钝角形引乙丁至辰如
　　　　　　　　乙丙大边而用为半径以丁为心
　　　　　　　　作丑辰亥半弧从辰作辰午为丁
　　　　　　　　钝角正弦又作丁斗半径与乙丙
　　　　　　　　平行则斗牛为丙角正弦又截女
　　　　　　　　丑弧如辰斗作女丁半径则女亢

为乙角正弦合而观之丁角正弦(辰/午)最大故对边乙丙
亦大丙角正弦(斗/牛)居次故对边乙丁亦居次乙角正弦
(女/亢)最小故对边丁丙亦小
又问若此则三边任用其一皆可为半径而取正弦是
已然此乃同径异角之比例也若以三边为弦三正弦
为股则同角异边之比例也两比例之根不同何以相
通曰相通之理自具图中乃正理非旁證也试于前图
用乙丁次边为弦其股乙癸与斗牛平行而等则丙角

　　　　　　　　正弦也又截酉丁如丁丙小边为
　　　　　　　　弦其股酉壬与女亢平行而等则
　　　　　　　　乙角正弦也又辰丁大边为弦(即/乙)
　　　　　　　　(丙/)其股辰午原为丁大角正弦也
　　　　　　　　于是三边并为弦三对角之正弦
　　　　　　　　并为股成同角相似之句股形而
　　　　　　　　比例皆等可以相求矣
一大边(乙丙即/辰丁)　　　　一丁角正弦(辰/午)

二丁角正弦(辰/午)　　　　二大边乙丙
三次边乙丁　小边(丁丙即/酉丁)三丙角正弦(乙/癸)乙角正弦(酉/壬)
四丙角正弦(乙/癸)乙角正弦(酉/壬)四次边乙丁　小边丁丙
此如先得大边(乙丙即/辰丁)与所对大角(丁/)故用辰午丁大
句股形为法求馀二句股也(乙癸丁/酉壬丁)皆同用丁角而形
相似故法可相求其实三正弦皆大边为半径所得故
其理相通未有理不相通而法可相求者故曰皆正理
非旁證也

又试于乙丙丁形(或钝角或/锐角同理)以丁丙小边为半径作房
箕壁象弧(以乙/为心)如上法取三正弦(以尾壁弧为丁角度/其正弦尾虚又箕壁)
(弧为丙角度其正弦箕危又戍/壁弧为乙角度其正弦戍申)成同径异角之比例又
如法用三边为弦三正弦为股(乙戍即丁丙小边配乙/角正弦戍申原如弦与)
　　　　　　　　　　(股又本形乙丁次边为弦则/丁甲为股与箕危平行而等)
　　　　　　　　　　(丙角正弦也又引乙丁至子/成子乙即乙丙大边以为弦)
　　　　　　　　　　(则子寅为股与尾虚平/行而等丁角正弦也)则并
　　　　　　　　　　为相似之句股形而比例等

一小边丁丙(即戍/乙)
二(乙角/正弦)戍申
三大边乙丙(即乙/子)　次边丁乙
四(丁角/正弦)子寅(即尾/虚)　(丙角/正弦)丁甲(即箕/危)
此如先得小边(丁/丙)与所对小角(乙/)故以戍申乙小句股
形为法求两大句股也(丁甲乙/子寅乙)皆同用乙角而形相似
又试以乙丁次边为半径作象限如前(以丙/为心)取三正弦
(张娄为丁角弧度张井其正弦氐娄为丙角弧/度氐参其正弦室娄为乙角弧度室奎其正弦)成同径

　　　　　　　异角之比例又仍用三边为弦三正
　　　　　　　弦为股(引丁丙至翌与大边乙丙等/成翌丙弦其股翌胃与张井)
　　　　　　　(平行而等丁角正弦也又乙丁次边/成氐丙弦其股氐参原为丙角正弦)
　　　　　　　(又丁丙小边为弦其股丁柳与/室奎平行而等乙角正弦也)即复
成相似之句股形而比例等
一次边乙丁(即氐/丙)
二(丙角/正弦)氐参
三大边乙丙(即翌/丙)　小边丁丙

四(丁角/正弦)张井(即翌/胃)　(乙角/正弦)丁柳(即室/奎)
此如先得次边(乙/丁)及所对丙角故以氐参丙句股为法
求大小二句股也(求翌胃丙为以小求大/求丁柳丙为以大求小)皆同用丙角
而比例等
问员内三角形以对弧为角倍度设有钝角小边何以
取之(或问内原设锐角两/边并大于半径故云)曰法当引小边截大边作角
之通弦(如图乙甲丙钝角形在平员内以各角切员而/乙甲边小于半径则引乙甲出员周之外乃以)
(甲角为心平员心丁为界作子丁丑弧截引长边于子/截大边于丑则丑甲子甲并半径与丁甲等而丑子为)

　　　　　　　　　(通/弦)又平分对边作两通弦(从员/心作)
　　　　　　　　　(丁乙丁丙两半径截乙戊丙员/周为甲角对边所乘之弧而半)
　　　　　　　　　(之于戊作乙戊丙/戊二线成两通弦)则此两通弦
　　　　　　　　　自相等又并与丑子通弦等夫
　　　　　　　　　子丁丑弧甲角之本度也丙戊
弧乙戊弧皆对弧之半度也而今乃相等(通弦等者/弧度亦等)是
甲角之度适得对弧乙戊丙之半而乙戊丙对弧为甲
角之倍度矣

　
　
　
　
　
　
　
　

　
　
　
　
　
　
　
　历算全书卷五十三