钦定四库全书
　历算全书卷四十九
　　　　　　　　　　　　　宣城梅文鼎撰
　句股阐微卷四
　几何增解
　　方斜较求原方(几何约论线第十四/条有用法今解其理)
甲乙丙丁正方形　甲乙其对角线　戊乙为方斜之
较　于戊乙上作庚癸乙戊小方则丙庚与庚戊等

　　　　　　　　　　　　论曰法于方之一角甲
　　　　　　　　　　　　作员而以丙甲方径为
　　　　　　　　　　　　员之半径则乙丙为切
　　　　　　　　　　　　员线乙辛为自员外割
　　　　　　　　　　　　员之全线乙戊较为割
　　　　　　　　　　　　员在外之馀线而两线
　　　　　　　　　　　　皆出一点则乙戊乘乙
辛之矩形与乙丙切线方形等

夫乙丙即原设方也今以同乙戊之癸乙为横乙辛为
直作乙已长方(即乙戊乘/乙辛之矩)又移切甲己长方为子甲长
方又移卯补午移辰补酉移丑补寅则复成乙丙甲丁
方形矣而丑卯午酉等斜剖半方形皆以乙戊较为半
方形之边是庚戊及丙庚皆与乙戊等而亦自相等又
何疑焉
用法　有方斜之较乙戊求原方形之一边法以乙戊
较作小方形取其斜乙庚再引长之截丙庚如乙戊得

乙丙如所求
从此图生一测员之法　假有员城八面开门正西门
如戊门外有塔如乙其距如乙戊西南门如丙距塔若
干步如乙丙问城径
法以乙丙之距自乘得数为实以乙戊之距为法法除
实得乙辛于乙辛内减去乙戊即员城之径　捷法但
倍乙丙即得城径
有员城正西之门如戊西南之门如丙人立于庚可两

见之而庚丙与庚戊皆等问城径
法以庚戊自乘成戊癸小方以方斜之法求其斜距为
乙庚以乙庚加庚丙为乙丙即城半径
　按此即几何约之用法也
又以句股法解之
又论曰试于庚丙上作丙子较线上方引庚戊至丁则
丁庚又为丙子方之斜而丁戊与乙丙等从丁戊作丁
壬甲戊为元方如所求

　　　　　　　　　　又论曰此即句弦和较相乘
　　　　　　　　　　开方得股也　乙甲丁甲皆
　　　　　　　　　　如弦　戊甲甲辛(甲丙/甲壬)皆如
　　　　　　　　　　句　乙戊如句弦较(丁丙/同)
　　　　　　　　　　乙辛如句弦和　和较相乘
　　　　　　　　　　成癸辛长方　开方得丁戊
股(乙丙/同)

　　切线角与员周角交互相应(几何三卷三十/二三十三增题)
乙丙丁三角形在员内有甲乙切员线则所作丙乙甲
　　　　　　　　　角与丙丁乙角同大又丁乙戊
　　　　　　　　　角与丁丙乙角同大所谓交互
　　　　　　　　　相应也
　　　　　　　　　论曰丁角以乙丙弧分论度而
丙乙甲角亦以乙丙弧分之度为度故丙乙甲角即丁
角也丙角以丁乙弧分为度而丁乙戊角亦以丁乙弧

分为度故丁乙戊角即丙角也　凡用员周度为角度
皆以两度为一度详后第三增题
若丁为钝角则丙乙甲亦钝角两钝角同以丙辛乙弧
为度故也其丙锐角与丁乙戊锐角则同以丁乙弧为
　　　　　　　　　度
　　　　　　　　　又增题　员内三角形一角移
　　　　　　　　　动则馀二角变而本角度分不
　　　　　　　　　变交互相应之角度亦不变

　　　　　　　　　如上图(三图/)丁角移至辛则丙
　　　　　　　　　角加大而相应之辛乙戊角亦
　　　　　　　　　从之而大以辛丁乙弧大于丁
　　　　　　　　　乙弧也辛乙戊大则辛乙丙小
矣其较皆为丁辛弧　若丁角虽移至辛而其度不变
相应之丙乙甲角亦不变以所用之丙乙弧不变也
又丙角移至壬则丁角加大相应之壬乙甲亦从之而
大以壬丙乙弧大于丙乙弧也壬乙甲大则壬乙丁小

矣其较皆为丙壬弧　若丙角虽移至壬其度不变相
应之丁乙戊亦不变以所用之丁乙弧不变也
　
　　　　　　　　　此图同论但丁角移则丙角变
　　　　　　　　　小丙角移亦然

　　又增题　切员线作角与员周弧度相应图
有子甲戊员有乾艮线相切于子从子点出线与切线
作角必割员周之度其大小皆相应但皆以员周两度
当角之一度
如用子午正线则所作两旁子角皆正角(百八十度分/两正角各皆)
(九十/度)而亦剖员为半周(两半员并/百八十度)是两度当一度
又如用子辛线作辛子艮钝角(四十/五度)而本线割员周于
辛为九十度象限亦两度当一度

又如用子辛线作辛子乾钝角形(百三十/五度)而线割辛午
乾员分(为二百/七十度)三象限亦两度当一度
又如于员内任作辛子乙角形乙辛子角所乘之子甲
乙弧六十度乾子乙角同用子甲乙弧亦六十度然其
实度是坎寅弧实只三十度亦两当一也
又子乙辛角乘子癸壬辛弧(一象/限)艮子辛角亦割子癸
壬辛弧(一象/限)然其实度为震酉弧只四十五度亦两当
一也所以者何曰试作辛乙线移角于辛则所乘弧(子/甲)

　　　　　　　　　　　(乙/)六十度皆实度也今也
　　　　　　　　　　　角在心是员周也非员心
　　　　　　　　　　　也凡员周之角小于员心
　　　　　　　　　　　一倍故也
　　　　　　　　　　　论曰员周至员心正得员
　　　　　　　　　　　径之半故所作角为折半
　　　　　　　　　　　比例试作乙丙线成辛乙
　　　　　　　　　　　丙句股形又从心作心周

线与辛乙平行则所作周心丙角与乙辛丙等而此心
周线平剖乙丙句亦平分乙周丙于周而正得其半矣
系句股形平分弦线作点从此作线与股平行即平分
句线为两
又论曰查角度之法皆以切点为心作半员即见真度
此不论半员大小或作于员内或作于员外并同　作
于员外其度开明易于简查
又论曰试于所切圈心作横径线与切线平行如辛丙

线引长之出员外而以查角度之线割员周而过之则
皆成大小句股形而所过横线上点皆即八线中之切
线为句股形之股角度斜线为横线所截处即八线中
割线常为弦而切点至员心之半径常为句
如子辛角度线割横线于辛成辛心子句股形其所当
角度为酉中四十五度则辛心即四十五度之切线辛
子即四十五度之割线馀并同　其子心即半径也
又论曰角度半员有大小而子心半径常为句者以所

作横线在员心欲用员度相较也若于半员之端(如中/如外)
作横线与切线平行其所作切线割线亦同比例而即
以各半员之半径为句矣
不但此也即任于子心外直线上任作一横线其所作
句股并同但皆以十字交处距子点之度命为半径此
八线割员之法所由以立也

　　量无法四边形捷法
　　　　　　　　　　甲乙丙丁形求其容　先作
　　　　　　　　　　乙丁对角线分为两三角形
　　　　　　　　　　　次自丙作丙戊横线与乙
　　　　　　　　　　丁线相交于丑为十字正角
而取戊点与甲齐平则戊丑即甲庚也次以丙戊点折
半于己　次作壬癸线与乙丁平行而等　又作壬辛
癸子二线皆与己丙平行而等　得辛癸长方即原形

之容

　　取平行线简法
　　　　　　　　　　　法曰乙丙线欲于甲点作
　　　　　　　　　　　线与之平行法于线外任
　　　　　　　　　　　取巳点为心甲点为界作
　　　　　　　　　　　辛甲丁庚圈分次以庚为
心取甲辛之度为界截员分得丁点末自丁作戊丁甲
线此线必与乙丙平行矣
论曰凡圈内两直线相距之度等则其线必平行如(丁/甲)

与(庚/辛)两线俱在一圈之内而所距之(甲/辛)圈分与(庚/丁)圈分
等是相距之度等而其线平行也因读数度衍得此法
似较他处为捷
　　补测量全义斜坡用切线法(系勿庵补/)
斜三角形有一角两边求馀边
　　　　　　　　　　　法用切线分外角求得馀
　　　　　　　　　　　角即以得边可不用垂线
　　　　　　　　　　　如甲乙己斜角形　有乙

甲及己甲二边　有甲角求乙己边
法以己甲线引长之成乙甲丙角为原有甲角之外角
(以元有甲角/减半周得)次分外角之度而半之为半外角而求其
切线为三率并乙甲己甲二边为首率又以二边相较
为次率次率乘三率为实首率为法除之得半较角之
切线以查表得半较角之度以减半外角得己角末用
正弦法得己乙边　法为己角正弦与乙甲若甲角正
弦与乙己

　三率法
一　两线之和　　　己丙
二　两线之较　　　己丁
三　半外角之切线　戊癸
四　半较角之切线　壬戊
用外角者乙己两角之和度而较角者乙己两角之较
度(以用切线/故半之也)
论曰又如后图己甲引至丙而乙甲亦引至辛则乙甲

丙及丁甲寅两角皆原有甲角之外角再作甲戊线平
分外角则丁甲戊及寅甲戊皆半外角　又作甲壬线
　　　　　　　　　　　　　　与乙已平行则壬
　　　　　　　　　　　　　　甲癸角即同己角
　　　　　　　　　　　　　　壬甲辛角即同乙
　　　　　　　　　　　　　　角再于甲戊半径
　　　　　　　　　　　　　　之端作癸戊辛十
　　　　　　　　　　　　　　字线切员于戊则

戊癸及戊辛皆半外角之切线也再以壬甲癸角减壬
甲辛角其较为壬甲子角则壬甲戊即半较角而壬戊
其切线也
其比例为己丙(二边/和)与己丁(二边/较)若癸辛(外角全切线/即乙己丁角)
(和度之/全切)与壬子(较角度之/全切线)则亦若癸戊(半外角/切线)与壬戊
(即半较角/之切线)何也全与全若半与半也

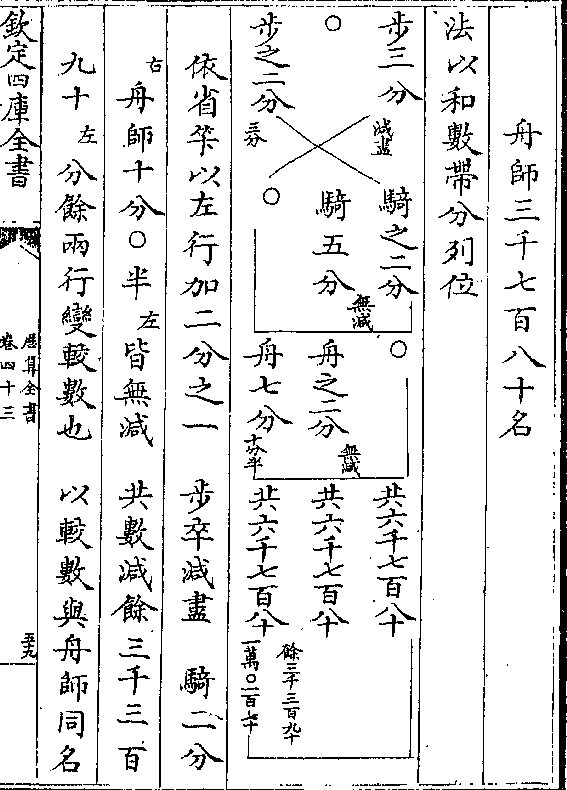
理分中末线
　　　　　　　　　　甲乙线求作理分中末线
　　　　　　　　　　法以甲乙全线折半于庚乃
　　　　　　　　　　作垂线于甲端为丙甲如半
　　　　　　　　　　线甲庚之度为句全线为
股次作丙乙线为弦
次以丙为心乙为界作乙丁圈界　次引丙甲句至丁
则丙丁即丙乙也　末以甲为心丁为界作丁戊己圈

分则甲己为理分中末之大分己乙为小分其比例为
甲乙与甲己若甲己与己乙也
递加法　借右图以乙为心甲为界运规截丁已圈分
于戊自戊作线向甲成甲戊线与甲丁等乃自戊作戊
乙线与乙甲等成甲乙戊三角形
此形甲戊两角悉倍于乙角乃平分戊角作戊辛线此
线与甲戊并大亦与乙辛同大成辛戊甲相似三角形
则甲乙与乙辛(即戊/辛)若乙辛与辛甲也又平分辛角作

　　　　　　　　　　　　辛壬线与壬戊与辛甲
　　　　　　　　　　　　皆同大则成甲辛壬三
　　　　　　　　　　　　角形与辛戊甲相似则
　　　　　　　　　　　　乙辛(即戊辛亦/即戊甲)与辛甲
　　　　　　　　　　　　(即辛壬/戊壬)若辛甲与壬甲
也如此递半则其角比例并同
一(乙甲/)　　　二(乙戊即戊/辛戊甲)　三(辛甲即辛/壬戊壬)　四(辛癸即壬/癸壬甲)
五(癸甲即癸/子壬子)　六(癸丑即丑/子子甲)　七(丑甲即丑/寅寅子)　八(丑卯即卯/寅寅甲)

九(卯甲/)　若能知其数则以大分递乘全数除之得细数
　　　　　　　先得甲乙为大分而求乙己全分及
　　　　　　　乙庚小分　用此图亦为半圆内求
　　　　　　　容方法则以乙巳全分加乙庚小分
　　　　　　　折半于戊得戊己为半径若先得戊
己则以戊己(即戊/丁)为弦作丁甲戊句股使戊甲句半于
丁甲股则丁甲即为戊己理分中末之大分
解曰甲庚(即乙/己)全数与丁甲(大分/)若丁甲(大分即/甲乙)与甲

己小分(即乙/庚)也
　　以量分
甲乙线十数求作理分中末线
　　　　　　　　　　先依甲乙线作甲乙丁丙正
　　　　　　　　　　方形(四面皆/十数)　次任用一面
　　　　　　　　　　平分之如甲丙平分于壬(甲/壬)
　　　　　　　　　　(及壬丙/皆五数)甲乙之半数也(甲丙/与甲)
(乙等其/分亦等)　次自壬向乙角作乙壬斜线其数一十一(一/八)

(○三/三九)　次自壬量甲壬或丙壬之度(即甲乙/之一半)移置于乙
壬线上截壬癸如甲壬则其馀癸乙即理分中末之大
分其数六(一八○/三三九)末以癸乙之度移置于甲乙线上如
乙戊则乙戊为大分戊甲为小分其数三(八一九/六六○)
　　简法
　　　　　　　作句股形　令甲壬句如甲乙股之
　　　　　　　半乃以壬为心甲为界作虚线圆分
　　　　　　　截乙壬弦于癸

末以乙为心癸为界作圆分截甲乙线于戊
则乙戊为大分甲戊为小分
　　又简法
以甲乙全线为半径作半圆形则乙庚乙辛皆与甲乙等
　　　　　　　　次平分乙辛于己
　　　　　　　　次以己为心庚为界运规割甲乙
　　　　　　　　线于戊(戊己之度/即同己庚)
　　　　　　　　则乙戊为大分　甲戊为小分

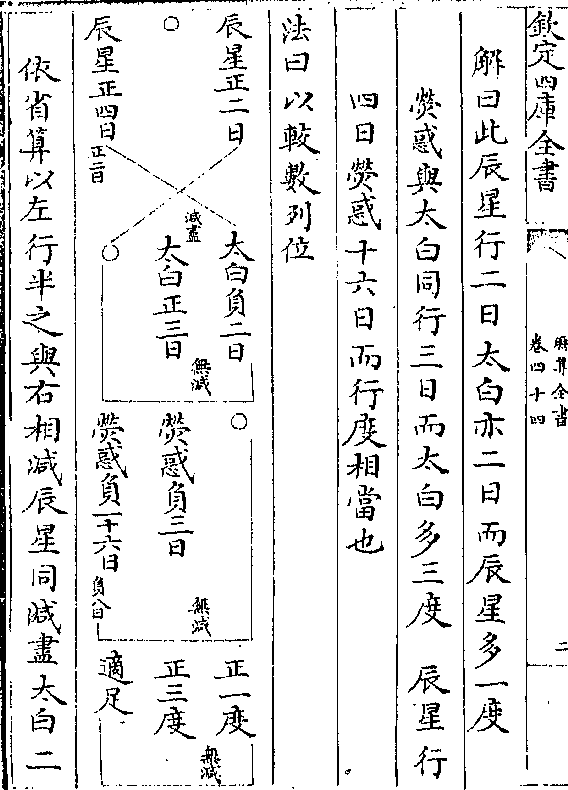
　　又简法
　　　　　　　　作子寅丑卯十字线相交于乙
　　　　　　　　次以乙为心甲为界运规截十字
　　　　　　　　线于甲于庚于辛则乙庚乙辛皆
　　　　　　　　与设线甲乙等乃折半(乙辛/)于己
以己为心庚为界运规截甲乙于戊　则乙戊大分甲
戊小分皆得矣　此法可于平面圆器上求之
　　附长方变正方法

甲乙丙丁长方形欲变正方以长方形之横边(乙/丙)直边
(丙/丁)二线取其中比例即所求
　　　　　　　　　　取中比例法以丙丁乙丙(即/戊)
　　　　　　　　　　(丙/)联为一直线(丁/戊)而折半于
　　　　　　　　　　己以己为心丁若戊为界作
　　　　　　　　　　半圆次引乙丙横线至圆界
　　　　　　　　　　截圆界于庚成丙庚线即乙
　　　　　　　　　　丙及丙丁二线之中比例线

次于丙庚线上作小方形其容与甲乙丙丁长方形等
如右图丙庚线上方形为丙壬乃子壬癸句股形内之
容方也而甲丙长方形则子壬癸句股外之馀方也馀
方与容方等积
　　简法
　　　　　　　　　先引丁丙边至午引乙丙边至
　　　　　　　　　未次以丙角为心乙为界作小
　　　　　　　　　员界虚线截引长线于戊

次以丁戊线折半于己次引乙丙至未次以己为心戊
为界运规作小圆界截引长线于庚　则丙庚即所变
方形之一边　末依丙庚线作方形与甲乙丙丁长方
形等积　其法以丙为心庚为界运规截丙辛与丙庚
等
　　理分中末线用法
一用以分平圆为十平分
　法为半径与三十六度之分圆若全分与理分中末

　之大分也
一用以分平圆为五平分
　历书言以全分为股理分中末之大分为句求其弦
　即半径全数为股三十六度之分圆为句求得七十
　二度之分圆为弦
一用以量十二等面体
　法为立方边与所容十二等面边若理分中末之全
　分与其小分也又十二等面体之边与内容立方边

　若理分中末之大分与其全分也又立方内容十二
　等面体其内又容小立方则外立方与内立方若理
　分中末之全与其大分也
一用以量二十等面体
　法为立方边与所容二十等面边若理分中末之全
　与其大分也
一用以量圆灯
　法为圆灯边与其自心至角线若理分中末之大分

　与其全分也此自心至角之线即为外切立方立圆
　及十二等面二十等面之半径又为内切八等面之
　半径圆灯为有法之形即此可见
　　用理分中末线说
言西学者以几何为第一义而传只六卷其有所秘耶
抑为义理渊深翻译不易而姑有所待耶测量全义言
有法之体五其面其积皆等其大小相容相抱与球相
似几何十一十二十三十四卷诸题极论此理又几何

六卷言理分中末线为用甚广量体所必需几何十三
卷诸题全赖之古人目为神分线又言理分中末线求
法见本卷三十题而与二卷十一题同理至二卷十一
题则但云无数可解详见九卷其义皆引而未发故虽
有此线莫适所用疑之者十馀年辛未岁养病山阿游
心算学于量体诸法稍得窥其奥爰证历书之误数端
于十二等面二十等面得理分中末之用及诸体相容
之确数故以立方为主其内容十二等面边得理分线

之末二十等面边得理分线之中反覆推求了无凝滞
始信几何诸法可以理解而彼之秘为神授及吾之屏
为异学皆非得其平也其理与法详几何补编

遥量平面法
　　　　　　　　　　　　　　　　甲乙庚辛为
　　　　　　　　　　　　　　　　所欲量之平
　　　　　　　　　　　　　　　　面而不能到
　　　　　　　　　　　　　　　　　如仰视殿
　　　　　　　　　　　　　　　　上承尘而人
在殿外又如峭壁悬崖之上有碑若碣凡平面之物人
从地面斜视灼然可见而不能到

或平面在下如田池之类人从台上俯视可见或临深
崖瞰谷底其理不异但倒用其图即是
欲量甲乙庚辛平面而不能到可到者丙丁则先知丙
丁之距及丙丁所作各角即可以知之
先求甲乙线　法于丙于丁各安平圆仪各以指尺向
甲向乙又自相向各作角成甲丙丁甲丁乙乙丁丙
凡三角形者三依第一法用甲丙丁形此形有丙丁线
(两测/之距)有丙角有丁角自有甲角可求甲丁线法为甲角

之正弦与丙丁若丙角之正弦与甲丁也
次仍依第一法用乙丁丙形此形亦有丙丁线(两测/之距)有
丙角有丁角自有乙角可求乙丁线
法为乙角之正弦与丙丁若丙角之正弦与乙丁也(此/丙)
(角与前形之/丙角不同)
次仍依第一法用甲丁乙形此形有甲丁乙丁两线及
两线间所作之丁角(与前形丁/角不同)可求甲乙线为所测之
一边　法自甲角作甲戊垂线至戊分乙丁线为两而

甲丁乙三角形分为两句股形　其一甲戊丁句股形
有丁角　有甲丁线为弦可求甲戊句戊丁股
法为全数与甲丁弦若丁角之正弦与甲戊句　又全
数与甲丁弦亦若丁角之馀弦与戊丁股也
其一甲戊乙句股形有甲戊句　有乙戊股(戊丁减乙/丁得之)
可求甲乙弦
法以甲戊句乙戊股各自乘而并之开方得甲乙即所
测平面之一边

第二求庚辛线　法亦于丙于丁各安平员仪(即先所/安之元)
(处/)各以指尺向庚向辛又自相向各作角成庚丙丁
庚丁辛　辛丙丁　凡三角形亦三
依第一法用庚丙丁形　此形有丙丁线(两测/之距)有丙角
　有丁角自有庚角可求庚丁线
法为庚角之正弦与丙丁若丙角之正弦与庚丁也(此/丙)
(角与前两/丙角不同)
依上法用辛丙丁形　此形有丙角(此丙角又/与上不同)有丁角

自有辛角　可求辛丁线(丁角与/前不同)
法为辛角之正弦与丙丁若丙角之正弦与辛丁也
仍依上法用庚丁辛形此形有庚丁辛丁两线及两线
间所作丁角(此丁角/又不同)可求庚辛线为所测之又一边
法自庚角作庚己垂线至己分辛丁线为两而庚丁辛
三角形分为两句股形
其一庚己丁句股形有丁角有庚丁线为弦可求庚己
句己丁股

法为全数与庚丁弦若丁角之正弦与庚己句亦若丁
角之馀弦与己丁股也
其一庚己辛句股形有庚己句有辛己股(己丁减辛/丁得之)可
求庚辛弦
法以庚己句辛己股各自乘而并之开方得庚辛为所
测平面之又一边(即甲乙/之对边)
第三求甲庚线
法于丁点侧安平仪以指尺向甲向庚作甲丁庚角成

甲丁庚形此形有甲丁庚丁两线及两线所作之丁角
(此丁角在甲丁/庚丁两线间)可求甲庚线为所测形之侧边
法自庚角作甲丁之垂线至壬分甲丁线为两而甲丁
庚三角形分为两句股形
其一庚壬丁句股形　有庚丁线为弦有丁角可求庚
壬句壬丁股(法同前用丁角/之正弦馀弦)
其一庚壬甲句股形　有庚壬句甲壬股(丁壬减甲/丁得甲壬)依
句股法可求甲庚弦线为所测平面之侧边

第四求乙辛线
法亦于丁点侧安平仪指尺向乙向辛作乙丁辛角成
乙丁辛形　此形有乙丁辛丁两线及两线所作之丁
角此(丁角在辛丁/乙丁两线间)可求乙辛线为所测形之又一侧边
法自辛角作乙丁之垂线至癸分乙丁线为两而乙丁
辛三角形分为两句股形
其一辛癸丁句股形有辛丁线为弦有丁角可求辛癸
句癸丁股(法亦同前用丁/角之正弦馀弦)

其一辛癸乙句股形有辛癸句乙癸股(癸丁减乙/丁得乙癸)依句
股法可求乙辛弦线为所测平面之又一侧边
如此则所测形之四边皆具乃用后法求其幂
第五求乙庚线
法仍于丁点斜立平仪以指尺向乙向庚作乙丁庚角
成乙丁庚形此形有庚丁乙丁两线及两线所作之丁
角(此丁角又在乙/丁庚丁两线间)可求乙庚线为所测形内之对角斜
线

乙庚丁角形内自庚角作乙丁之垂线至卯分乙丁线
为两而乙庚丁三角形亦分为两句股形
其一庚卯丁句股形　有庚丁线为弦有丁角可求庚
卯句卯丁股(依上法用丁角/之正弦馀弦)
其一庚卯乙句股形　有庚卯句有卯乙股(卯丁减乙/丁得卯乙)
依句股法可求乙庚弦线为所测平面形内对角之斜
线
既有乙庚线则所测甲乙辛庚平面形分为两三角形

可以求其幂积
其一乙甲庚形有乙庚底　有甲庚甲乙两腰　法以
两腰相减为较相并为和和乘较为实乙庚底为法除
之得乙午以减乙庚得午庚半之得子庚乃用句股法
以甲庚子庚各自乘相减为实开方得甲子垂线垂线
半之以乘乙庚底得乙甲庚形平积
其乙辛庚形有乙庚底　有乙辛辛庚两腰如上法以
乙辛辛庚相减为较又相并为和和乘较为实乙庚底

为法除之得乙辰为底较以减乙庚得辰庚半之得丑
庚乃用句股法以丑庚庚辛各自乘相减为实开方得
丑辛垂线垂线半之以乘乙庚底得乙辛庚形平积
末以两三角形积并之为所测甲乙辛庚平面四不等
形之总积
　右法可以不用丈量而遥知亩步即有种种异态以
　三角御之足矣新法历书言测量详矣然未著斯法
　意者其在几何后数卷中为未译之书欤

　庚午蜡月既望晤远西安先生谈及算数云量田可
　以不用履亩初闻之甚不以为然归而思之得此法
　然未知其所用者即此与否而此法固己足用矣
　若用有纵衡细分之测器指尺一量即得无烦布算
　矣

测量用影差义疏
凡方形内从角剖成两句股形必相似而等(正方或长/方并同)
　
　
　
方形内作对角斜线分为两句股又于斜线上任取一
点作直线纵横相交如十字而悉与方边平行分方形
为大小四句股形此四句股形各两两相似而等(大形/丙与)

(丁等小形/庚与辛等)
　　　　　　　　则其四句股旁之两馀方形虽不
　　　　　　　　相似而其容必等
　　　　　　　　解曰于原斜线所分相等句股内
各减去相等之大小两句股则其馀亦等(丙戊庚形内/减去大形丙)
(小形庚馀戊又于丁己辛形内减去大形丁小形辛馀/己原形既等所减又等则其馀必等故戊己两长方虽)
(不相似而其/容必等也)
　　句股测远

　　　　　　　　　　　　有甲乙之距人在戊立
　　　　　　　　　　　　表又立表于丁使戊丁
　　　　　　　　　　　　乙为一直线再于丙立
表使丙丁与乙戊如十字之半而与甲乙平行则丁戊
小股与丙丁小句若丙庚大股与甲庚大句也
法以丙丁小句为二率乙丁大股为三率(即丙庚/)相乘
为实戊丁小股为一率为法法除实得大句甲庚再以
庚乙加之得甲乙

假如丙丁两表相距(三步/)人在戊窥丁到乙远(戊丁十/)
(二步丁乙十八步/)欲求甲乙之距
法以丙丁(三步/)乘乙丁(十八步/)得(五十四步/)为实戊丁
(十二步/)为法除之得(四十五步/)为甲庚加丙丁(三步即/)
(乙庚/)共四十八步为甲乙
解曰此以乙丙长方形变为丙癸也依前论乙丙实形
丙癸虚形不相似而容积等故也
　　重测法

　
　
　
有巽乙甲井方池欲遥望测其甲乙之一面方并乙丁
之距
法立表于丁望测方池之东北角乙至东南角巽使丁
乙巽为一直线　再于丁横过立一表于丙使丙丁为
乙丁之横立正线(丙丁横六步四分/)次从丁退而北行

至(戊/)量得(十二步/)　从戊斜望池西北隅(甲/)不能当(丙/)
表而出其间如(戌/)又于戌立表(戌丁/)之距(四步/)　再退
而北行至(己/)从(己/)窥(甲/)正过(丙/)表己丙甲为一直线量
得己丁之距(三十六步/)
法以(丙丁六步四分/)为一率(丁己三十六步/)为二率(戊/)
(丁四步/)为三率　二三相乘得(一百四十四步/)为实一
率(六步四分/)为法除之得(二十二步半/)为辛己于辛己
内减丁戊(十二步/)馀(十步半/)为壬己是为景差

次以(戌丁四步/)减(丙丁六步四分/)馀(丙戌二步四分/)以
戊丁(十二步/)乘之得(二十八步八分/)为句实　景差(十/)
(步半/)为法除句实得二步(八分弱/)为甲申大句之距加
丙丁(六步四分即申乙/)得共(九步二分弱/)为甲乙即方
池一面之阔
次以辛己(二十二步/半)减丁己(三十六步/)馀(十三步半/)辛
丁为二率丁戊(十二步/)为三率相乘得(一百六十二步/)
为股实　景差(十步半/)为法除之得(十五步八分半弱/)

为乙丁大股之距
解曰此以四表重测改为三表乃巧算也　若测高则
重测本为前后二表者亦改用一表故当先知本法然
后明其所以然下文详之
　　试先明四表本法
有甲乙之阔先立(丁/)表从戊测之戊(人目/)丁(表/)乙(远物/)
(之末端/)三者参相直　次于(丁/)表横过与(甲乙/)平行作
戊丁乙直线之横直线此线上取戊立表人目从(戊/)过

(戌/)表窥甲远物之西端亦参相直但于戊丁乙线为斜
弦成句股形　量得戌丁两表横距(四步/)丁戊(人目距/)
(东表/)直距(十二步/)
次于丁戊直线退而北行至己　又于西表戌作戌乾
癸直线与丁戊平行此平行线内取癸立西后表人目
从(己/)过(癸/)至甲参相直成己甲癸斜弦　亦从(癸/)横行
至(丁己/)线寻(辛/)立东后表此后两表(癸辛/)之距为前表
(戌丁/)等(四步/)　又量得(辛己/)为东后表距人目之数(辛/丁)

(二十二步半/)次以丁戊(十二/)减辛己(二十二半/)得(十步/)
(半/)为壬己景差　末以己辛(二十二半/)减(己丁三十六/)
馀(十三步半/)为前后表间之距　以表横距(四步/)乘之
得(五十四步/)为表间积(即丁癸长方/)　置表间积为实
以景差(十步半/)为法除之得(五步一半弱/)加表横距(四/)
(步/)　　得共(九步二分弱/)为所测远物甲乙之阔
解曰前表测得成(戊乙甲/)句股形内有戌乙馀方与形
外戌坤馀方等积　后表测得(己乙甲/)句股形内有癸

乙馀方与形外酉癸馀方等积　于(癸乙/)内减(戌乙/)于
(酉癸/)内减(寅癸即丑戌/)则所馀之(癸丁/)及(酉辰/)两馀方
亦必等积也故以(丁癸/)变(辰酉/)而得(辰寅/)亦即(甲庚/)也
　　次明改用三表之理
用三表者于(丙丁/)两表间增一(戌/)表其实则于(戌丁/)两
表外增一(丙/)表也前增一表而无后表则无从而得景
差故以三率法求而得之其实(癸辛/)即后表也其理与
四表同

然不用(癸子/)形而用(戌子/)形何也曰准前论(辰酉/)形与
(丁癸/)形等积而(午癸/)形与(丁癸/)形亦等积(两馀方在己/丙丁句股形)
(内外/故等)则(酉辰/)与(午癸/)亦等积矣各减同用之(卯未/)则所
馀之(酉卯/)与(卯癸/)二形亦自相等积而(卯癸/)原与(戌子/)
等故用(戌子/)变为(卯酉/)而得(卯寅/)即得(甲申/)矣是故(戌/)
(子/)可名句实也
其以(辛丁/)乘(戊丁/)为股实何也曰此三率法也(丁乙/)外
加(丁辛/)前后两测之表距故(辛壬即戊丁/)外亦加(壬己/)

两测之景差法为壬己与辛丁若戊丁与丁乙也
准此测高可用一表而成两测(即借前测远之/图而以横为直)
假如有(甲乙/)高立(丙丁/)表人目在(戊/)测之则表之端不
相值而参相直于表之若干度如(戊/)退若干步至(己/)测
之正对表端(丙/)其法并同
　因看数度衍中破勾测远条疑其图不真因作此以
　證明其说
　　测量图说

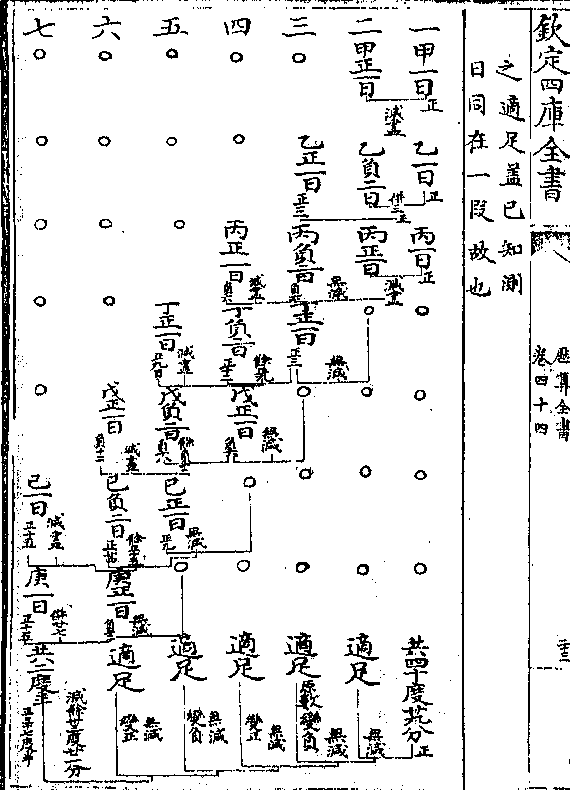
　　　　　　　　　　　　　　一测股六十四尺
　　　　　　　　　　　　　　八寸(壬丁/)　二测
　　　　　　　　　　　　　　句四十三尺二寸
　　　　　　　　　　　　　　(丙丁/)　三大股三
　　　　　　　　　　　　　　千六百八十五尺
　　　　　　　　　　　　　　二寸(乙丁即/丙午)四大
　　　　　　　　　　　　　　句二千四百五十
　　　　　　　　　　　　　　六尺八寸(甲/午)加(午/乙)

得二千五百尺为甲乙之高
解曰癸丁长方形即古人所谓表间积也以景差壬辛
(即丑/子)除之变为寅子形是寅子与癸丁同积也　而申
癸形原与癸丁同积则寅子与申癸亦同积也　于内
各减同用之申子而寅未与未癸亦同积矣夫未癸即
氐己也是戊丁(即亥己/)乘丙己之积也故可命为句实
而以景差壬辛(即申未/)除之得甲午句也(甲午即戌酉/)
其取股实何也曰三率法也表在丁其景丁戊　后表

在庚则其景庚壬后表之远于前表者为庚丁故后景
之大于前景者为辛壬则其比例为辛壬与庚丁若丁
戊(即庚辛/)与丁乙也
试引癸庚至箕截庚箕如庚壬又截尾箕如壬辛于尾
于箕各作与庚乙平行线而于乙作垂弧为乙牛联之
作长方形又作丁心线截之作箕乙线斜分之则其理
著矣

三角形求外切圆法
设如锐角形有甲丙边七十五尺甲乙边六十一尺
　　　　　　　　　　乙丙边五十六尺　问外切
　　　　　　　　　　圆径若干　答曰外切圆半
　　　　　　　　　　径三十八尺一寸二分五氂
　　　　　　　　　　法先求得甲丁中长线六十
　　　　　　　　　　尺为一率甲乙边六十一尺
为三率甲丙边折半得戊甲三十七尺五寸为三率二

率与三率相乘一率除之得四率(三八一二五/)为甲乙
圆半径
解曰此甲丁乙三角形与甲己戊三角形同式故其线
为相比例率也若甲为钝角其理亦同
以甲丙折半为三率故四率亦为半径若以甲丙全线
为三率则四率必得甲辛为全径矣盖甲辛丙形与甲
乙丁形同式也何以见甲乙丁形与甲辛丙形同式盖
两形之乙角辛角同当甲庚丙弧分则二角必相等而

丁丙又同为直角则两甲角亦必等而为同式无疑矣
又界角比心角所当之弧大一倍今己心角所当甲庚
弧适当乙界角所对甲庚丙之一半则两角为等可知
而戊为直角与丁角等则两甲角必等故甲己戊与甲
乙丁亦为同式形也
三角举要有量法未著算例因作此补之
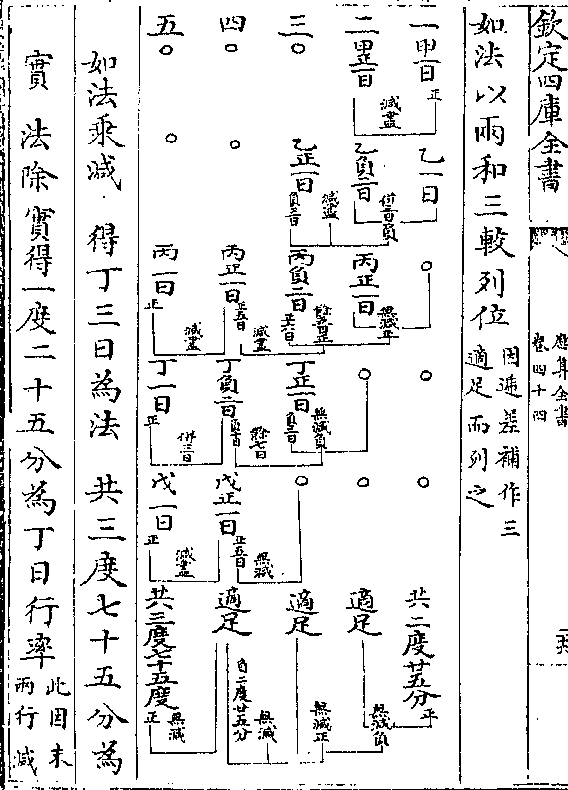
又如甲乙丙钝角形　求外切员径(甲/辛)　半径(甲/己)
法先求得中长线(乙/丁)得(乙丁/丙)句股形

　　　　　　　　　　　次作(乙/辛)线成(甲乙/辛)大句股
　　　　　　　　　　　形
　　　　　　　　　　　又甲乙半之于戊从员心
　　　　　　　　　　　(己/)作直线过戊至庚又成
　　　　　　　　　　　(甲戊/己)句股形
　　　　　　　　　　　一率　乙丁股(形内/垂线)
　
　　　　　　　　　　　三率　甲戊股(即甲乙/之半)

四率　甲辛弦(即外切/员径)　　四率　甲己弦(即切员/半径)
解曰三句股形皆相似故可以三率比例求之
问何以知其为相似形也曰原设形之丙角与甲乙辛
形之辛角所当者同为甲庚乙员分则两角等而乙丁
丙形之丁角与甲乙辛大形之乙角又皆正角则馀角
亦等而为相似形
又甲己为甲辛之半甲戊为甲乙之半戊正角与大形
乙正角等又同用甲角则己戊亦乙辛之半而为相似

形
一系凡三角形求得形内垂线为法　垂线左右两原
边相乘　为实　法除实得外切员径　锐钝同法
假如甲乙丙钝角形求得中垂线乙丁六分为法　左
右两斜边(甲乙十八分/乙丙十分)相乘(一百八/十分)为实　法除实得
外切员径甲辛三十分　即可借用前图(分寸畸零/稍为整顿)

　
　
　
　
　
　
　
　

　
　
　
　
　
　
　
　历算全书卷四十九