声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
历算全书 卷四十五 第 1a 页 WYG0795-0067a.png
 钦定四库全书
钦定四库全书历算全书卷四十五
宣城梅文鼎撰
方程论卷六
方程御杂法
算术之有方程犹量法之有句股必深知诸算术而后
能言方程犹之必深知诸量法而后能治句股故以
是终
历算全书 卷四十五 第 1b 页 WYG0795-0067b.png
 诸方田少广凡属量法者往往有可以句股立算而诸
诸方田少广凡属量法者往往有可以句股立算而诸法不能治句股方程之于粟布差分也亦然故杂法
不能御方程而方程能御杂法
例如后
假如有粮一万九千石𣲖与甲乙丙三县各以其人户
多少米价贵贱僦值远近舟车险易而均输之 甲
县户三万米价每石一两四钱远输二百里用车载
二十石行一里僦值一钱三分 乙县户二万米价
历算全书 卷四十五 第 2a 页 WYG0795-0067c.png
 一两二钱远输五百里用舟载二十五石行一里僦
一两二钱远输五百里用舟载二十五石行一里僦值三分 丙县户一万米价一两二钱远输二百里
道险可用负担每负六斗行五十里顾值一钱八分
法曰各以其县米价并僦值之数命其户以方程较数
列之 以甲县车载二十石除其僦值一钱三分得
六釐五毫(每载一石行/一里数也)以乘二百里得一两三钱并
米价一两四钱共二两七钱 以乙县舟运二十五
石除其僦值三分得一釐二毫以乘五百里得六钱
历算全书 卷四十五 第 2b 页 WYG0795-0067d.png
 并米价一两二钱共一两八钱
并米价一两二钱共一两八钱以丙县负担六斗除其顾值一钱八分以乘一石得
三钱又以五十里除之二百里乘之得一两二钱并
米价共二两四钱
原法以各县米价并僦值之数以除其户为衰列而
并之并衰为法各衰乘总米为实法除实得各县米
今用方程则不须尔竟以二两七钱命甲县之衰为
二十七户以一两八钱命乙县之衰为一十八户以
历算全书 卷四十五 第 3a 页 WYG0795-0068a.png
 二两四钱命丙县之衰为二十四户以三县衰命为
二两四钱命丙县之衰为二十四户以三县衰命为适足而列之
如三色有空法乘 馀丙县异并一百一十四户为
法 正三十四石二斗为实 法除实得丙县每户
历算全书 卷四十五 第 3b 页 WYG0795-0068b.png
 粮三斗 以丙一户三斗减共一石九斗馀一石六
粮三斗 以丙一户三斗减共一石九斗馀一石六斗乙县四户除之得每户粮四斗
以乙二户八斗甲县三户除之得每户二斗又三
分斗之二各以每户率乘其县之户总得各县转
计开
甲县三万户 共粮八千石 共僦车值一万○四百两
每户粮二斗六升六合又三之二 每三户粮八斗
每户僦值三钱四分又三之二 每三户僦值一两○四分
历算全书 卷四十五 第 4a 页 WYG0795-0068c.png
 总计米价与其僦值每户共银七钱二分
总计米价与其僦值每户共银七钱二分乙县二万户 共粮八十石 其僦船值四千八百两
每户粮四斗 僦值二钱四分
总计米价僦值每户亦七钱二分
丙县一万户 共粮三千石 共顾担夫银三千六百两
每户粮三斗 僦值三钱六分
总计米价僦值每户亦七钱二分
以米言之
历算全书 卷四十五 第 4b 页 WYG0795-0068d.png

论曰此因米价不等加以僦值不同故以法均之粮虽
不均而每户所出之银数则均若但均其米乃不均
矣是故均之以不均斯谓能均
问官米二百六十五石令三等人户出之甲上等二十
户每户多中等七斗乙中等五十户每户多下等五
历算全书 卷四十五 第 5a 页 WYG0795-0069a.png
 斗丙下等一百一十户其则例各若干
斗丙下等一百一十户其则例各若干法以和较列位(依省算以和数/十之一列之)
如法乘减 得丙户十八为法 二十一石六斗为
实 法除实得一石二斗为下等每户则例 加正五
历算全书 卷四十五 第 5b 页 WYG0795-0069b.png
 斗为中等则 又加七斗为上等则
斗为中等则 又加七斗为上等则计开
甲上等每户二石四斗 二十户共四十八石
乙中等每户一石七斗 五十户共八十五石
丙下等每户一石二斗 一百一十户共一百三十二石
合计之共二百六十五石
问有米六百七十四石以四等里甲输纳乙为甲十之
八丙为乙十之七丁为丙十之六其甲乙各八十户
历算全书 卷四十五 第 6a 页 WYG0795-0069c.png
 丙丁各七十户问各若干
丙丁各七十户问各若干解曰十之八即非二八差分十之七十之六即非三
七四六差分故与带分条所设不同合而观之可也
法以和较列位
历算全书 卷四十五 第 6b 页 WYG0795-0069d.png
 如法乘减而重列其馀与三行对
如法乘减而重列其馀与三行对又以馀数与四行平列
数益多用省算法四除减馀然后列之
如法乘减馀丁六百七十四为法 五万六千六百
历算全书 卷四十五 第 7a 页 WYG0795-0070a.png
 一十六石无减为实 法除实得八十四石为丁共
一十六石无减为实 法除实得八十四石为丁共数 十因丁数六除之为丙共数 十因丙数七除
之为乙共数 十因乙数八除之为甲共数
计开
甲共数二百五十石以八十户除之得每户三石一斗
二升五合 乙共数二百石为甲十之八以八十户
除之得每户二石五斗 丙共数一百四十石为乙
十之七以七十户除之得每户二石 丁共数八十
历算全书 卷四十五 第 7b 页 WYG0795-0070b.png
 四石为丙十之六以七十户除之得每户一石二斗
四石为丙十之六以七十户除之得每户一石二斗总计之共六百七十四石
论曰此所问是总数相差非每户相差也故原列者总
户而得亦总户之米若云问每户之差则当以每户
列之而所得者亦每户米也如后例
假如共米六百七十四石以四色人户出之甲八十户
乙亦八十户乙每户如甲十之八丙丁各七十户丙
每户如乙十之七丁每户如丙十之六
历算全书 卷四十五 第 8a 页 WYG0795-0070c.png
 问各户则例
问各户则例法以户细数列位
依省算以首行退位十而一与次行对减而重列之
又半其减馀然后列之与三行对
历算全书 卷四十五 第 8b 页 WYG0795-0070d.png

又列减馀以对末行
如法乘减异并一千二百九十二为法 一千四百
一十五石四斗无减为实 法除实得一石○九升
又三百二十三之一百七十八为丁每户则例(法实/皆四)
历算全书 卷四十五 第 9a 页 WYG0795-0071a.png
 (约/之)
(约/之)十因丁则六除之得一石八斗二升又三百二十三
之一百八十九为丙每户则例
十因丙则七除之得二石六斗○又三百二十三之
二百七十为乙每户则例
十因乙则八除之得三石二斗六升又三百二十三
之十四半为甲每户则例
计开
历算全书 卷四十五 第 9b 页 WYG0795-0071b.png
 甲每户三石二斗六升又三百二十三之十四半
甲每户三石二斗六升又三百二十三之十四半八十户共二百六十石○八斗三升又三百二十三
之一百九十一
乙每户二石六斗○又三百二十三之二百七十 为
甲每户十之八
八十户共二百○八石六斗六升又三百二十三之
二百八十二
丙每户一石八斗二升又三百二十三之一百八十九
历算全书 卷四十五 第 10a 页 WYG0795-0071c.png
 为乙每户十之七
为乙每户十之七七十户共一百二十七石八斗 ○ 又三百二十三
之三百一十
丁每户一石○九升又三百二十三之一百七十八
为丙每户十之六
七十户共七十六石六斗八升又三百二十三之一
百八十六
合计共六百七十四石(凡六百七十三石九斗七升又/九百六十九分以三百二十三)
历算全书 卷四十五 第 10b 页 WYG0795-0071d.png
 (收之为升/得此数)
(收之为升/得此数)问有均分两银庚以其五之二与甲则甲之数多于庚
一百六十八两若以甲二十一之九与庚则庚之数
多于甲一百八十两原数几何
法以所用益彼之分与此所存之馀分相减而列之
(庚与甲五之二/庚自存五之三)相减馀五之一(是为以庚五之一较/甲全分而甲多一百)
(六十八/两也)
(甲与庚廿一之九二/甲自存廿一之十)相减馀二十一之三(是为以甲二十一之/三较庚全分而庚多)
历算全书 卷四十五 第 11a 页 WYG0795-0072a.png
 (一百八/十两也)
(一百八/十两也)庚虽自存五之三而甲股内有庚所与之二故以相
减而馀之一分与甲相较
甲虽自存二十一之一十二而庚股内有甲所与之
九故以相减而馀之三分与庚相较
甲一百○二分为法除实一千○二十两得十两为
历算全书 卷四十五 第 11b 页 WYG0795-0072b.png
 甲之一分 二十一分共二百一十两 减负一百
甲之一分 二十一分共二百一十两 减负一百六十八两馀四十二两为庚之一分 五分亦共二百
一十两
计开
(庚/甲)各原银二百一十两(庚五之二计八十四两其五之/三仍一百二十六两 甲二十)
(一之九计九十两其二十/一之十二仍一百二十两)
庚以八十四与甲(甲共有二百九十四/庚仍馀一百二十六)相较甲多一百
六十八
历算全书 卷四十五 第 12a 页 WYG0795-0072c.png
 甲以九十与庚(庚共有三百二十/甲仍馀一百)相较庚多一百八十
甲以九十与庚(庚共有三百二十/甲仍馀一百)相较庚多一百八十此设问之意也
以(庚之一分四十二/甲全分二百一十)相较甲亦多一百六十八
以(甲之三分计三十/庚全分二百一十)相较庚亦多一百八十
此列位之理也
论曰右例以此之分益彼而转与此之馀分相较与带
分条所设不同 带分条此之分较彼全分其全分
即是原数 今则一损一增以相较非原数也故曰
历算全书 卷四十五 第 12b 页 WYG0795-0072d.png
 不同
不同及其相减而列为较数也则亦是此之分较彼原数
矣是之谓尾同而首异
相减列位亦有变为和数者如后所设
问有两银庚以其五之三与甲则甲之数多于庚二百
五十二两若以甲廿一之十三与庚则庚之数多于
甲二百六十两
法亦以所与彼之分与其馀分相减列之
历算全书 卷四十五 第 13a 页 WYG0795-0073a.png
 庚(与甲五之三/自存五之二)相减馀五之一(此为所用之分多于/存分是变和数也)
庚(与甲五之三/自存五之二)相减馀五之一(此为所用之分多于/存分是变和数也)(庚五之一偕甲全分/共二百五十二两也)
甲(与庚二十一之十三/自存二十一之八)相减馀二十一之五(此亦用/分多存)
(分少是变和数也百甲二十一之/五偕庚全分共二 六十两也)
甲所以多如许者不惟其全数之故其所得于庚之
分又多于庚之馀分者一也故甲所多之数乃是
甲全数偕庚之一分所共也
庚所以多如许者亦不惟其全数之故其所得甲之
历算全书 卷四十五 第 13b 页 WYG0795-0073b.png
 分又多于甲之存分者五也故庚所多数亦是庚
分又多于甲之存分者五也故庚所多数亦是庚全数偕甲之五分所共也
甲一百分为法除实一千而得十两为一分 以甲
五分计五十两减共二百六十两馀二百一十两为
庚原银 五除之得四十二两为一分 以减共二
百五十二两亦得二百一十两为甲原银
历算全书 卷四十五 第 14a 页 WYG0795-0073c.png
 庚五之三计一百二十六两以加甲银共三百三十六
庚五之三计一百二十六两以加甲银共三百三十六两 内减去庚自存五之二计八十四两 仍多二
百五十二两 即是甲全数偕庚一分之数也
甲二十一之十三计一百三十两以加庚银共三百四
十两 内减去甲自存二十一之八计八十两 仍
多二百六十两即是庚全数偕甲五分之数也
论曰右例以此之分偕彼全分而为和数亦与带分和
数同然以相减而得之亦是尾同首异 带分条和
历算全书 卷四十五 第 14b 页 WYG0795-0073d.png
 数较数据问而分 今则设问只是较数相减列
数较数据问而分 今则设问只是较数相减列位乃有和较之分
依例推之亦有变为一和一较者皆以所用之分与
所存分相减而得之 列位时巳变不待其重列减
馀也故又与寻常较变和者异
总论曰此二条者皆一损一益例也
问金九锭银十一锭其重适等若交易其一则银多十
三两其原重若干
历算全书 卷四十五 第 15a 页 WYG0795-0074a.png
 法以相差十三两半之得六两五钱为一锭之较
法以相差十三两半之得六两五钱为一锭之较解曰交易一锭而差是一多一少故半之为一锭之
较 银得较而增重故与金同名
银二锭除实得银每锭重二十九两二钱半 加正
六两五钱得金每锭三十五两七钱半
计开
历算全书 卷四十五 第 15b 页 WYG0795-0074b.png
 金每锭三十五两七钱五分 金九锭(得三百二十一/两七钱五分)
金每锭三十五两七钱五分 金九锭(得三百二十一/两七钱五分)银每锭二十九两二钱五分 银十一锭(亦得三百二十/一两七钱五分)
金八锭二百八十六两加银一锭共三百一十五两二
钱半
银十锭二百九十二两半加金一锭共三百二十八两
二钱半
共多一十三两 若交易二锭而差二十六两则以
二锭倍作四锭除之亦得六两五钱为一锭之较
历算全书 卷四十五 第 16a 页 WYG0795-0074c.png
 馀可类推(或半相差二十六两为一十三两命/为金二锭银二锭之较尤为平稳)
馀可类推(或半相差二十六两为一十三两命/为金二锭银二锭之较尤为平稳)论曰此条旧列差分同文算指改立借衰互徵之法皆
不知宜入方程也
凡以两家之数相交易而差若干皆半其所差而列
之为所交易之较何也一增一减而差若干则原所
差者其半也
问甲有朱砂银七锭壬有矿银九锭相较甲原多十五
两今以甲二锭易壬三锭则甲多二十七两
历算全书 卷四十五 第 16b 页 WYG0795-0074d.png
 法以原多十五两今多二十七两相减馀十二两半之
法以原多十五两今多二十七两相减馀十二两半之得六两为甲二锭壬三锭之较(甲得较而增重/故与壬同名)
壬三锭除七十二两得壬每锭二十四两 以九锭
乘得二百一十六两加正一十五两共二百三十一
两甲七锭除之得每锭三十三两
计开
历算全书 卷四十五 第 17a 页 WYG0795-0075a.png

甲以二锭与壬馀五锭一百六十五两加易得壬三锭
七十二两共二百三十七两
壬以三锭与甲馀六锭一百四十四两加易得甲二锭
六十六两共二百一十两
相较甲多二十七两
此问意也
历算全书 卷四十五 第 17b 页 WYG0795-0075b.png

问甲银七锭壬九锭相较壬原少十五两今以一锭相
交易壬多三两
法以原少十五两今多三两并得十八两而半之得九
两为一锭之较(壬得之而变轻为/重故与甲同名)
历算全书 卷四十五 第 18a 页 WYG0795-0075c.png
 壬二锭除四十八两得每锭二十四两 加九两得
壬二锭除四十八两得每锭二十四两 加九两得甲每锭三十三两
计开
甲六锭一百九十八两加壬一锭二十四两共二百二十二两
壬八锭一百九十二两加甲一锭三十三两共二百二十五两
相较壬多三两 此交易一定之数 馀同前问
论曰此三问皆同法第一问盈偕适足故即用原数第
二问两盈故相减第三问盈偕不足故相并然皆半
历算全书 卷四十五 第 18b 页 WYG0795-0075d.png
 之为较故三法一法也
之为较故三法一法也又按于七锭中取一即七之一同带分之理故又作
问明之
问有金不知总任意分为二而较之则庚多八两须令
辛以金还庚如庚存数三之二庚亦以金还辛如辛
存数四之三则其数适均
法以庚自存三分今添二分共五 以辛自存四分今
添三分共七通为两家适足数之分
历算全书 卷四十五 第 19a 页 WYG0795-0076a.png
 又以多八两半之四两命为庚所添二分辛所添三
又以多八两半之四两命为庚所添二分辛所添三分之较(辛失之而减重/故与辛同名)
解曰合而观之庚以五之二辛以七之三相交易则
庚多八两若还其原数庚仍为五分辛仍为七分
则适足也
辛一分得二十两 七分共一百四十两 五除之
历算全书 卷四十五 第 19b 页 WYG0795-0076b.png
 得庚之一分二十八两
得庚之一分二十八两计开
其相易(庚二分五十六两/辛三分六十两)较之辛多四两即相易几
锭之理
历算全书 卷四十五 第 20a 页 WYG0795-0076c.png
 总论曰此皆两相交易也又与庚甲损一益一者不同
总论曰此皆两相交易也又与庚甲损一益一者不同凡损一益一者损庚之几分与甲则甲有增数而转
以甲之既增者与庚之馀数相较也 损庚益甲以
相较是明有增损
今两相交易则损庚之分与辛亦损辛之分与庚然
后以既损且增之庚与亦增之辛相较也
两相交易则末尝明有增损但以相易之数不同而
增损隐寓于其中 以上四条皆同此论
历算全书 卷四十五 第 20b 页 WYG0795-0076d.png
 问两数不知总但云取甲之九加乙则乙与甲等若取
问两数不知总但云取甲之九加乙则乙与甲等若取乙之九加甲则甲倍于乙其原数各若干
答曰甲六十三 乙四十五
解曰云取甲之九加乙是损甲之九而益乙以九
也取乙之九加甲是损乙之九而益甲以九也与
刋误条所举甲乙二仓法不同彼是取甲仓几何
以益乙而共得几何不言与甲仓较取乙仓几何以益甲
而共得几何亦不言与乙仓较是所益者有增数而所取者
历算全书 卷四十五 第 21a 页 WYG0795-0077a.png
 无损数如云以此之全数偕彼之几分而共得几何乃和数也
无损数如云以此之全数偕彼之几分而共得几何乃和数也今所列者乃较数也益此损彼则相较几何故不同也
然又与带分条较数不同彼是取彼几分与此全数
较今所列者是取彼几数加此而转与彼之馀数较
当细辨之
又此是以数相增损而得其相较之分
前数条则是以分相损增而得其相较之数
二者大异不但与带分条别也
历算全书 卷四十五 第 21b 页 WYG0795-0077b.png
 法以所加之九数命甲乙所相当之数乘之为较数列
法以所加之九数命甲乙所相当之数乘之为较数列位
甲倍乙是甲二乙一合之则三以乘九得二十七为
较甲得此而当倍乙故与乙同名
甲乙等是各一也合之则二以乘九得十八为较乙
得此而与甲等故与甲同名
历算全书 卷四十五 第 22a 页 WYG0795-0077c.png
 馀乙一为法
馀乙一为法并四十五为实
法一即以四十五命为乙数
异加十八得六十三为甲数
试更列之
同减馀甲一为法 异并六十三为实 法一即以
历算全书 卷四十五 第 22b 页 WYG0795-0077d.png
 六十三为甲原数 异加正二十七共九十乙二除
六十三为甲原数 异加正二十七共九十乙二除之得四十五为乙原数
论曰此难题设问也算法统宗收入均输另有求法算
海说详推论借银相当加半倍者不可通用因别立
术然复未确不如用方程之为无弊
又论曰甲与乙九而相等是甲多于乙者二九也 乙
与甲九而甲倍于乙是倍乙多于甲者三九也何也
甲得乙九数而后当倍乙则倍乙中各除九数共二
历算全书 卷四十五 第 23a 页 WYG0795-0078a.png
 九而甲又添九数岂非三九乎
九而甲又添九数岂非三九乎问甲乙银不知数但云甲借乙六钱五分则比乙一有
半乙借甲六钱五分则乙与甲等各原银若干
法以甲一乙一有半并之共二半以乘六钱五分得一
两六钱二分半为乙一有半多于甲之较
以甲乙相等各一并之共二以乘六钱五分得一两
三钱为甲多于乙之较
乃列之
历算全书 卷四十五 第 23b 页 WYG0795-0078b.png

同减馀半乙为法异并二两九钱二分半为实 法
除实得五两八钱五分为乙银 异加正一两三钱
共七两一钱五分为甲银
计开
甲原银七两一钱五分
乙原银五两八钱五分
历算全书 卷四十五 第 24a 页 WYG0795-0078c.png
 相差一两三钱 若损甲之六钱五分以加乙则各
相差一两三钱 若损甲之六钱五分以加乙则各得六两五钱是相等也
若损乙六钱五分馀五两二钱 益甲六钱五分得
七两八钱是甲之数如乙一有半也
若以乙原银加半得八两七钱七分半以与甲原甲原银
相较则多一两六钱二分半
论曰甲以六钱五分借与乙而相等是甲原多乙两个
六钱五分也乙以六钱五分借与甲而甲如乙一有
历算全书 卷四十五 第 24b 页 WYG0795-0078d.png
 半是一个半乙原多于甲两个半六钱五分也何也
半是一个半乙原多于甲两个半六钱五分也何也甲取乙六钱五分而后能当乙有半则此一个半乙
共减去一个半六钱五分甲又加一个六钱五分岂
非共差两个半六钱五分乎
又论曰此即算海说详所设之问以驳统宗者彼自立
术以为当矣不知其宜用方程也
试更设问以明之
今有二数不知总但云丙与丁二数则相等若丁与丙
历算全书 卷四十五 第 25a 页 WYG0795-0079a.png
 二数则丙如三丁问原数各若于
二数则丙如三丁问原数各若于依前术列位(合丙丁各一共二以乘二得四为丙多/于丁之较 合丙一丁三共四以乘二)
(得八为三丁多/于一丙之较)
同减馀丙二为法 异并二十为实 法除实得一
十为丙数 同减负四馀六为丁数
计开
历算全书 卷四十五 第 25b 页 WYG0795-0079b.png
 丙原数十 原多于丁者四
丙原数十 原多于丁者四丁原数六 三之则十八多于丙者八
若损丙之二以益丁则各得八故相等
若损丁之二以益丙则丙得十二丁得四故丙如三丁
论曰丙以二与丁而等是丙多于丁者两个二也 丁
以二与丙而丙如三丁是三丁之数共多于丙者四
个二也何也丙增一个二其三个丁各少一个二共
四个二也
历算全书 卷四十五 第 26a 页 WYG0795-0079c.png
 又论曰因算海说详立术未确故复设此以相考用方
又论曰因算海说详立术未确故复设此以相考用方程能合彼问而彼所立术殊不能通之此问
问戊己银不知数但戊以五十两与己则己如戊之倍
己以五十两与戊如三己
依前术列位(并戊二己一共三以乘五十得一百五/十为二戊多于一己之较 并戊一己)
(三共四以乘五十得二百/为三己多于一戊之较)
历算全书 卷四十五 第 26b 页 WYG0795-0079d.png
 同减馀己五为法 异并五百五十两为实 法除
同减馀己五为法 异并五百五十两为实 法除实得一百一十两为己银 异加正一百五十两共
二百六十两戊二除之得一百三十两为戊银
计开
戊原银一百三十两 倍之二百六十两多于己一百
五十两
己原银一百一十两 三之得三百三十两多于戊二
百两
历算全书 卷四十五 第 27a 页 WYG0795-0080a.png
 此列位之理
此列位之理戊加五十两得一百八十两己损五十两得六十两则
戊如三己 己加五十两得一百六十两戊损五十两
得八十两则己如戊之倍
此则问意
问香炉二座不知重有一盖重百两以加甲炉则甲多
于乙两倍以加乙炉则乙多于甲一倍其炉各重若
干
历算全书 卷四十五 第 27b 页 WYG0795-0080b.png
 解曰多乙两倍是三倍也甲得盖如三乙也 多甲
解曰多乙两倍是三倍也甲得盖如三乙也 多甲一倍是两倍也乙得盖如两甲也
法以盖重为较而列之 甲得盖如三乙是三乙之重
于甲者如盖也故与乙同名 乙得盖如倍甲是两
甲之重于乙者如盖也故与甲同名
炉同减馀乙炉五为法 较异并三百两为实
历算全书 卷四十五 第 28a 页 WYG0795-0080c.png
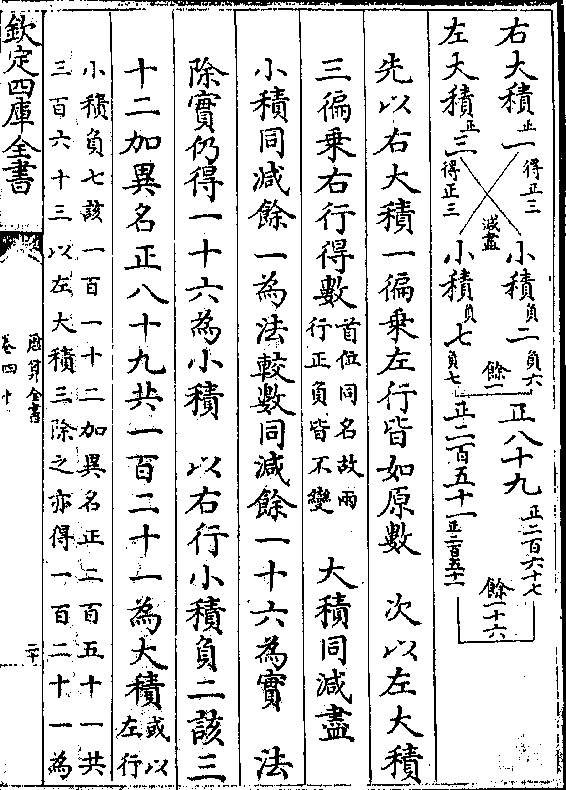 法除实得六十两为乙炉重
法除实得六十两为乙炉重异加一百两共一百六十两甲二除之得八十两为
甲炉重
计开
甲炉八十两 加盖共一百八十两则如乙炉重者三
乙炉六十两 加盖共一百六十两则如甲炉重者倍
论曰此与前所设戊己银数以五十两损戊益己而己
倍于戊以五十两损己益戊而戊如二己异何也以
历算全书 卷四十五 第 28b 页 WYG0795-0080d.png
 五十两损彼益此虽亦相差一百两然非真有一百
五十两损彼益此虽亦相差一百两然非真有一百两之益乃因彼之所损而合成其数耳此之加盖则
实增一百两矣而于彼又无所损因炉盖乃两家公
物非若戊己之银必取诸彼以与此也故其法不同
若改问各铸炉而均铸盖则必于炉重各加半盖乃
合原金得数与戊己银同矣
问调兵征倭内有南北西三处兵马南兵已知四万其
北兵为南兵与西兵二之一西兵为南兵与北兵三
历算全书 卷四十五 第 29a 页 WYG0795-0081a.png
 之一各若干
之一各若干法以南兵为西北之较而列之
西兵得南兵而数倍于北是倍北数而多于西兵者
数如南兵也
北兵得南兵而数如三西兵是三其西兵而多于北
者亦如南兵也
历算全书 卷四十五 第 29b 页 WYG0795-0081b.png
 馀北兵五为法 并十六万为实 法除实得三万
馀北兵五为法 并十六万为实 法除实得三万二千为北兵数异加正四万共七万二千西兵三除
之得二万四千为西兵数
计开
南兵四万
西兵二万四千 偕南兵则六万四千其二之一则如北兵也
北兵三万二千 偕南兵则七万二千其二之一则如西兵也
论曰此与香炉借盖为较同 其所用较乃是南兵而
历算全书 卷四十五 第 30a 页 WYG0795-0081c.png
 非取于西北兵故得之有增而不得无损与借物于
非取于西北兵故得之有增而不得无损与借物于彼而转与其所借之馀物相较者不同
问二人携银不知数但减乙六两与甲则甲倍于乙减
甲三两与乙则相等其原数若干
解曰此所损益又是不同之数然其理则一故亦依前
术乘其较数而列之(合甲一乙二共三以乘六两得十/八两为倍乙多于一甲之较合甲)
(乙各一共二以乘三两得/六两为甲多于乙之较)
列位
历算全书 卷四十五 第 30b 页 WYG0795-0081d.png

同减馀乙一为法 异并二十四两为实 法一即
以实为乙数 异加六两为甲数
计开
乙二十四两 倍之得四十八两多于甲一十八两
甲三十两 原多于乙六两
若损乙六两得十八两加甲六两得三十六两是甲如
历算全书 卷四十五 第 31a 页 WYG0795-0082a.png
 乙之倍
乙之倍若损甲三两加乙三两各得二十七两则相等
问二商各携母银但云取乙十二两与甲则乙有甲六
之一取甲十五两与乙则甲有乙十之一
依前术列位(并六与一共七以乘十二两得八十四/两为六乙多于一甲之较 并十与一)
(共十一以乘十五两得一百六/十五两为十甲多于一乙之较)
历算全书 卷四十五 第 31b 页 WYG0795-0082b.png
 同减馀甲五十九为法 异并一千○七十四两为
同减馀甲五十九为法 异并一千○七十四两为实 法除实得一十八两又五十九之一十二为甲
数 异加正八十四两共一百○二两(又五十九/之一十二)乙
六除之得一十七两(又五十/九之二)为乙数
计开
甲银一十八两(又五十九/之一十二)十之则一百八十二两(又五/十九)
(之/二)多于乙者一百六十五两
乙银一十七两(又五十/九之二)六之则一百○二两(又五十九/之一十二)
历算全书 卷四十五 第 32a 页 WYG0795-0082c.png
 多于甲者八十四两
多于甲者八十四两若损乙一十二两与甲则甲有三十两(又五十九/之一十二)乙仅
有五两(又五十/九之二)而乙于甲为六之一
若损甲一十五两与乙则乙有三十二两(又五十/九之二)甲仅
三两(又五十九/之一十二)而甲于乙为十之一(以五十九通二/两得一百一十)
(八加子二从之共一百二十是三十两又/五十九之一百二十岂非十倍于甲乎)
论曰乙得甲六之一是六乙当一甲也然必损乙之十
二两与甲而后成此数是于一甲中添十二两而于
历算全书 卷四十五 第 32b 页 WYG0795-0082d.png
 六乙中各减十二两也一添一减共七个十二两是
六乙中各减十二两也一添一减共七个十二两是为八十四两也
甲得乙十之一是十甲当一乙也然必损甲之十五两
与乙而后成此数是于一乙中添十五两而其十甲
中皆各减十五两也一添一减共十一个十五两是
为一百六十五两也
损乙之十二两与甲而乙为甲六之一若其原数则以
六乙当一甲而乙多八十四两矣
历算全书 卷四十五 第 33a 页 WYG0795-0083a.png
 损甲之十五两与乙而甲为乙十之一若其原数则以
损甲之十五两与乙而甲为乙十之一若其原数则以十甲当一乙而甲多一百六十五两矣
问有两数不知总但损甲六数与己则甲如己四之三
而多二数若以己之二十损与甲则己如甲四之三
而少五数其原数各几何
法以四甲三己共七乘六得四十二又以四甲乘多二
数得八而益之共五十为四甲多于三己之数(损甲/六益)
(己故较与甲同名其二数/甲所多也故以之益数)
历算全书 卷四十五 第 33b 页 WYG0795-0083b.png
 以四己三甲共七乘二十得一百四十又以四己乘
以四己三甲共七乘二十得一百四十又以四己乘少五数得二十以相减馀一百二十为四己多于三
甲之较(损己二十益甲故较与己同名/其五数巳所少也故以之减较)
己同减馀七为法 异并六百三十为实 法除实
得九十为己原数四因己数同减一百二十馀二百
四十甲三除之得八十为甲原数
历算全书 卷四十五 第 34a 页 WYG0795-0083c.png
 计开
计开甲八十
己九十
以列位之理言之
甲四共三百二十 己三共二百七十 是甲多五十
甲三共二百四十 己四共三百六十 是己多一百
二十
以问之意言之
历算全书 卷四十五 第 34b 页 WYG0795-0083d.png
 甲损六数馀七十四 己加六数共九十六 以九十
甲损六数馀七十四 己加六数共九十六 以九十六四分之而取其三得七十二 是为甲如己四之
三而多二数
己损二十馀七十 甲加二十共一百 以一百四分
之而取其三得七十五 是为己如甲四之三而少
五数
论曰以甲当己四之三是四甲当三己也然必以六数
减甲增己而成则是四甲中各减六而三己中各增
历算全书 卷四十五 第 35a 页 WYG0795-0084a.png
 六共四十二也以甲当己四之三而多二数则以四
六共四十二也以甲当己四之三而多二数则以四甲当三己而共多八数也 合而观之此四十二者
四甲多于三己之数也此八数者亦四甲多于三己
之数也故皆与甲同名而列其较为五十也
以己当甲四之三是四己可当三甲也然必以二十减
己增甲而成则是四己中各减二十而三甲中各增
二十共一百四十也 以己当甲四之三而少五数
则以四己当三甲而共少二十也 合而观之此一
历算全书 卷四十五 第 35b 页 WYG0795-0084b.png
 百四十者四己多于三甲之数也与己同名也而其
百四十者四己多于三甲之数也与己同名也而其二十者则四己少于三甲之数也与己异名也故以
相减而馀者列为己同名之较也
损甲六数与己而甲如己四之三仍多二数若其原数
则以四甲当三己而共多五十矣
损己二十与甲而己如甲四之三却少五数若其原数
则以四己当三甲而共多一百二十矣
问有三数损甲一百益乙则甲如乙六之二若损乙五
历算全书 卷四十五 第 36a 页 WYG0795-0084c.png
 十益丙则乙如丙十五之九若损丙三十益甲则甲
十益丙则乙如丙十五之九若损丙三十益甲则甲如丙二之一而少五数各若干
法以甲六乙二共八以乘一百共八百为六甲当二乙
之较(损甲益乙故/与甲同名)
以乙十五丙九共二十四乘五十得一千二百为十
五乙当九丙之较(损乙益丙故/与乙同名)
以丙一甲二共三乘三十得九十又以甲二乘少五
数共十而加之共一百为一丙当二甲之较(损丙益/甲故与)
历算全书 卷四十五 第 36b 页 WYG0795-0084d.png
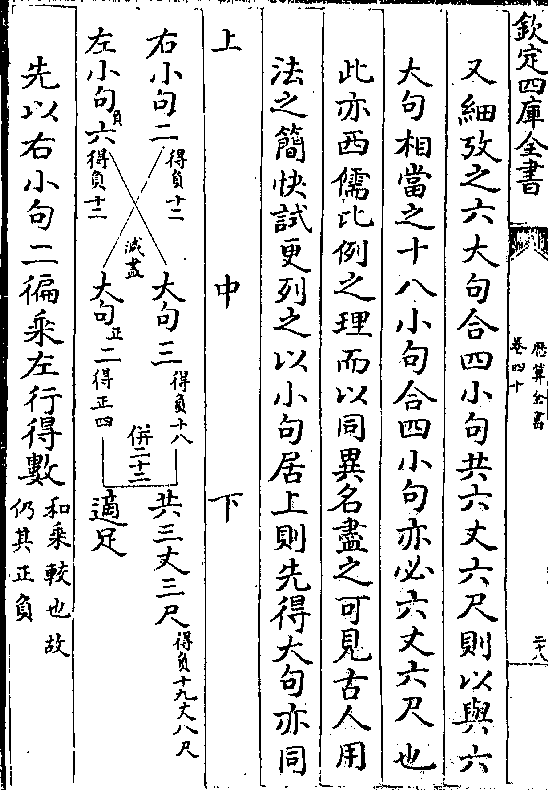 (丙同名其甲所少五数即/丙所多也故亦与丙同名)
(丙同名其甲所少五数即/丙所多也故亦与丙同名)如法递减馀丙五十四为法 异并三万七千八百
为实 法除实得七百为丙数 丙数同减一百馀
六百甲二除之得三百为甲数 六因甲数一千八
历算全书 卷四十五 第 37a 页 WYG0795-0085a.png
 百同减八百馀一千乙二除之得五百为乙数 十
百同减八百馀一千乙二除之得五百为乙数 十五乘乙数得七千五百同减一千二百馀六千三百
丙九除之仍得七百为丙数(反覆相求列/位之理著矣)
计开
甲三百
乙五百
丙七百
甲损一百馀二百乙增一百得六百是甲为乙六之二
历算全书 卷四十五 第 37b 页 WYG0795-0085b.png
 乙损五十馀四百五十丙增五十得七百五十是乙为
乙损五十馀四百五十丙增五十得七百五十是乙为丙十五之九
丙损三十馀六百七十其二之一则三百三十五甲增
十得三百三十是甲为丙二之一而少五数
问二人共数一百原所得之数不均今以甲三之一与
乙五之一相易则适均其原所得若干
法以三分通甲数损一与乙而存其二分 又以五分
通乙数损一与甲而存其四分
历算全书 卷四十五 第 38a 页 WYG0795-0085c.png
 乃以和数列之
乃以和数列之乙七为法 馀五十为实 法除实得七又七之一
为乙之一分 以乙分母五乘之得三十五又七之
五(为乙/数)以减一百得六十四又七之二为甲数
计开
甲六十四(又七/之二)其三之一为二十一(又七/之三)其三之二为
历算全书 卷四十五 第 38b 页 WYG0795-0085d.png
 四十二(又七/之六)
四十二(又七/之六)乙三十五(又七/之五)其五之四为二十八(又七/之四)其五之一为
七(又七/之一)以甲三之一加乙五之四五十也 以乙五
之一加甲三之二亦五十也
论曰此以分相增损而为和数亦与刋误条甲乙二仓
异彼是以其全数偕彼几分此则以所存之馀数偕
彼几分也既云相易则实有增损非如甲乙仓虚借
增率而无损也
历算全书 卷四十五 第 39a 页 WYG0795-0086a.png
 问二人物数不均若于甲取三之一于乙取四之一以
问二人物数不均若于甲取三之一于乙取四之一以和合而平分之以凑原存数则各五十而适均其原
数各若干
法以三分通甲数而倍之为六分损其一与乙馀五分
以四分通乙数而倍之为八分损其一与甲馀七分
以和数列位
解曰以四之一与三之一和合而平分之是各取其
数之半也 于三之一取其半是六之一以与乙
历算全书 卷四十五 第 39b 页 WYG0795-0086b.png
 而甲馀其五也于四之一取其半是八之一以与
而甲馀其五也于四之一取其半是八之一以与甲而乙馀其七也
偏乘对减以得法实 法除实得五又十七分之十
五为乙八之一 以乙分母八乘之得四十七又十
七分之一为乙原数 以两五十共一百减乙原数
馀五十二又十七分之一十六为甲原数
历算全书 卷四十五 第 40a 页 WYG0795-0086c.png
 计开
计开甲原数五十二(又十七分/之十六)三除之得十七(又十七分/之十一)为
甲三之一 以三之一转减甲馀三十五(又十七/分之五)为
甲所存三之二
乙原数四十七(又十七/分之一)四除之得十一(又十七分/之十三)为乙
四之一以四之一转减乙馀三十五(又十七/分之五)为乙所
存四之三
以甲三之一乙四之一和合之共二十九(又十七/分之七)半之
历算全书 卷四十五 第 40b 页 WYG0795-0086d.png
 得十四(又十七分/之十二)为和合平分之数以加甲乙存数
得十四(又十七分/之十二)为和合平分之数以加甲乙存数各得五十
论曰甲去三之一乙去四之一所存之数已均矣故以
平分之数加之而适均
又法
以甲分母三通甲为三分以乙分母四通乙为四分
又总计各得五十六共一百为和数
以甲取三之一馀三之二乙取四之一馀四之三命
历算全书 卷四十五 第 41a 页 WYG0795-0087a.png
 为适足(甲取三之一乙取四之一以和合平分/而等则其所存者亦等也故命之适足)
为适足(甲取三之一乙取四之一以和合平分/而等则其所存者亦等也故命之适足)乃以和较杂列位
如法乘甲同减尽 乙异并一十七分为法 正二
百无减就为实 法除实得一十一又十七之十三
为乙之一分以分母四乘之得四十七又十七分
之一为乙原数 以乙原数减共数一百馀五十二
历算全书 卷四十五 第 41b 页 WYG0795-0087b.png
 又十七分之十六
又十七分之十六按此所得与前无异而较捷故并存之
问甲乙丙三人共博甲赢乙金二之一乙赢丙金三之
一丙又赢甲金四之一事毕各剩金七百其原携金
若干
法以各分母通其原数又各减其赢去之一而列之
(以七百/为和数)
和数列位
历算全书 卷四十五 第 42a 页 WYG0795-0087c.png

如法减并 丙七分为法 二千一百为实 法除
实得三百为丙之一分 以丙分母三乘之得九百
为丙原金 以丙之一分减乙剩七百馀四百为乙
所馀二之一 二因之得八百为乙原金 以乙二
历算全书 卷四十五 第 42b 页 WYG0795-0087d.png
 之一减甲剩金七百馀三百为甲自剩四之三 三
之一减甲剩金七百馀三百为甲自剩四之三 三除之得一百为甲三之一 四乘之得四百为甲原
金
计开
甲原金四百 加赢乙四百(二之/一也)共八百 除丙又赢
去甲一百(四之/一也)仍馀七百
乙原金八百 加赢丙三百(三之/一也)共一千一百 甲赢
去四百(乙二之/一也)仍馀七百
历算全书 卷四十五 第 43a 页 WYG0795-0088a.png
 丙原金九百 赢甲一百(四之/一也)共一千 乙赢去三百
丙原金九百 赢甲一百(四之/一也)共一千 乙赢去三百(丙三之/一也)亦仍馀七百
论曰此与刋误条骡马递借一匹同但马一骡二驴三
即是原物偕所借之一而为和数今乙一丙二甲三
却是各所存之馀分偕所赢之一分而为和数也得
数大异者马骡即是全数今则用分故丙之全数转
多于乙若以一分计则乙之分自多于丙如马力之
于骡矣
历算全书 卷四十五 第 43b 页 WYG0795-0088b.png
 又论曰此三条皆是两相交易而又是和数与前数条
又论曰此三条皆是两相交易而又是和数与前数条金银交易几锭不同
难题歌曰一条竿子一条索索比竿子长一托双折索
子去量竿却比竿子短一托
解曰一托者五尺也
法以零整杂列位 因双折是二之一故以二通索
历算全书 卷四十五 第 44a 页 WYG0795-0088c.png
 法一即以实一丈命为绳之一分 分母二因之得
法一即以实一丈命为绳之一分 分母二因之得绳长二丈 减负五尺馀得竿长一丈五尺
假如有绳长不知数但云比竿长六尺若三折其绳则
短于竿八尺
法二除实三丈得竿长一丈五尺 加正六尺得绳
长二丈一尺
历算全书 卷四十五 第 44b 页 WYG0795-0088d.png
 论曰原法别有求法然不如方程稳捷故作此问以明
论曰原法别有求法然不如方程稳捷故作此问以明之若用难题法不能通矣故方程能御杂法而杂法
不能御方程 此条统宗原入均输今改正
问井不知深先将绳折作三条入井汲永绳长四尺复
将绳折作四条入井亦长一尺其井深绳长各若干
法以两母(三/四)相乘得十二分为绳母数 以母(三/四)互乘
其子(之一/之一)得(四/三)是为以绳十二分之四汲水而长四
尺以绳十二分之三汲水而长一尺也
历算全书 卷四十五 第 45a 页 WYG0795-0089a.png

馀一分为法 即以实三尺命为绳十二分之一
以十二分乘一分得三十六尺为绳长 以绳之三
分计九尺同减负一尺得八尺为井深
计开
井深八尺
绳长三十六尺
历算全书 卷四十五 第 45b 页 WYG0795-0089b.png
 三折之得一十二尺 比井多四尺
三折之得一十二尺 比井多四尺四折之得九尺 比井多一尺
论曰此条原属盈朒今以方程御之尤简易故曰方程
能御杂法也
试更之则先得井深
法一省除即以八尺命为井深 加正四尺共十二
历算全书 卷四十五 第 46a 页 WYG0795-0089c.png
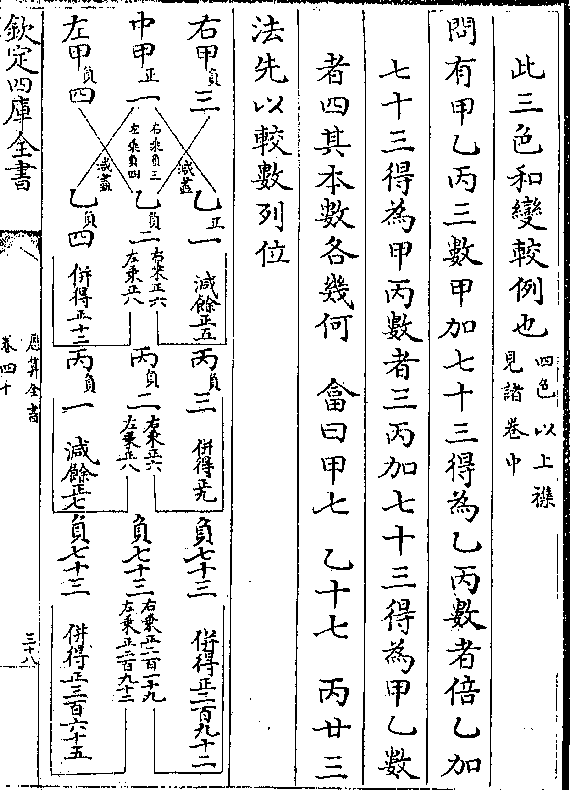 尺绳之四分除之得三尺为一分 一十二分母乘
尺绳之四分除之得三尺为一分 一十二分母乘之得绳长三十六尺
论曰此馀八尺者即物实也前以馀三尺为绳长实者
即人实即此可悟盈朒章作法之原要之是二色方
程法耳(人实物实不同而除法/则同故皆可以互求)
今有绢一疋欲作帐幅先摺成六幅比旧帐长六寸改
折作七幅却又短四寸其绢并旧帐幅各长若干(折/作)
(六幅以较长即六之/一七幅即七之一)
历算全书 卷四十五 第 46b 页 WYG0795-0089d.png
 法如前以(六/七)幅相乘得四十二分为总母 以(六/七)互乘
法如前以(六/七)幅相乘得四十二分为总母 以(六/七)互乘其(之一/之一)得(之七分/之六分)为所用之分而列之(以绢四十二/之七则长于)
(帐六寸短以绢四十二/之六则 于帐四寸)为较数
法一 实一尺即为绢之一分 以分母四十二乘
之得绢长四丈二尺 以绢之七分计七尺减负六
寸馀六尺四寸为旧帐之长
历算全书 卷四十五 第 47a 页 WYG0795-0090a.png
 计开
计开旧帐幅六尺四寸
绢长四丈二尺
均作六幅得七尺 比帐长六寸
均作七幅得六尺 比帐短四寸
论曰此与井不知深皆是以一物之细分与一整物较
皆零整杂用之法也
又以上三条盈朒章旧有求法然皆因所较之井深与
历算全书 卷四十五 第 47b 页 WYG0795-0090b.png
 旧帐幅皆为一数而不变故可用盈朒之法若亦有
旧帐幅皆为一数而不变故可用盈朒之法若亦有分数不同则非盈朒所能御此方程之用能包盈朒
诸法而诸法不能御方程
今有台不知高从上以绳缒而度之及台三之二而馀
六尺双折其绳度之及台之半而不足三尺问台之
高及绳之长若何
法以台(三/二)之(二/一)用母相乘为母之法通台为六分 又
用母互乘子为子之法变台三之二为六之四台之
历算全书 卷四十五 第 48a 页 WYG0795-0090c.png
 半为六之三 又以双折通绳为二 皆以化整为
半为六之三 又以双折通绳为二 皆以化整为零而列之
馀绳二分为法 并三十尺为实 因二为分母与
法同省除与乘径以实三十尺为绳长 减负六尺
馀二十四尺以台之四分除之母六乘之得三十六
尺为台高
历算全书 卷四十五 第 48b 页 WYG0795-0090d.png
 计开
计开台高三十六尺
绳长三十尺
台三之二高二十四尺 以绳度之馀六尺
台之半高一十八尺 以半绳一十五尺比之短三尺
今有井不知深以乙绳汲之馀绳二尺以庚绳汲之亦
馀绳四尺双折庚绳三折乙绳以相续而汲之适足
问井深及二绳各长若何
历算全书 卷四十五 第 49a 页 WYG0795-0091a.png
 法以乙绳通为三 庚绳通为二
法以乙绳通为三 庚绳通为二以三色列之 井整数乙庚用分
以隔行之同名仍为较数列之 馀较皆与庚同名
历算全书 卷四十五 第 49b 页 WYG0795-0091b.png
 馀庚一分为法 即以实一丈命为庚二之一 倍
馀庚一分为法 即以实一丈命为庚二之一 倍之得庚绳二丈 减负二尺得乙绳一丈八尺(用减/馀之)
(右行盖乙正/三即全数也)
又减负二尺得井深一丈六尺(用原列之右行亦以/乙负三即全数故)
计开
井深一丈六尺
乙绳一丈八尺 比井多二尺
庚绳二丈 比井多四尺
历算全书 卷四十五 第 50a 页 WYG0795-0091c.png
 三折乙绳六尺加双折庚绳一丈共一丈六尺即同
三折乙绳六尺加双折庚绳一丈共一丈六尺即同井深
论曰此二条与前井深绢帐同理然即非盈朒所能御
又按田之横直亦可以绳折比量水面亦然
今有直田欲截一段之积只云截长六步不足积七步
截长八步又多积九步问所截之积及原阔
法以较数列之(其原阔即截长/每一步之积)
上 中 下
历算全书 卷四十五 第 50b 页 WYG0795-0091d.png

长二步除积十六步得原阔八步 以截长六步乘
阔得四十八步加不足七步得截积五十五步
论曰此盈朒中方田也然无关于方田之实用故入盈
朒然不知宜入方程也
试更作问
今有方田欲截横头之积改为直田但云截阔五步则
历算全书 卷四十五 第 51a 页 WYG0795-0092a.png
 不足十二步截阔九步则如所截之积一有半问所
不足十二步截阔九步则如所截之积一有半问所截直田积并原田之方
如法列位
阔一步半为法 积十八步为实 法除实得原方
一十二步 以阔五步乘方得六十步加不足十二
步得截直田七十二步
历算全书 卷四十五 第 51b 页 WYG0795-0092b.png
 计开
计开原方田方十二步 积一百四十四步
截直田七十二步 宜截阔六步
若此条则盈朒不能御
今有米换布七疋多四斗换九疋适足问原米若干及
布价
法列位
上 中 下
历算全书 卷四十五 第 52a 页 WYG0795-0092c.png

布二疋为法 四斗为实 法除实得布价每疋二
斗 以九疋适足乘布价得原米一石八斗
论曰此盈朒中粟布法也
试更设问
今有榖换绢十疋馀三石以榖之半换绢六疋不足五
斗问原榖若干及绢价
历算全书 卷四十五 第 52b 页 WYG0795-0092d.png
 法列位
法列位法一免除 得绢每疋价二石 以十疋乘价加馀
三石得原谷二十三石
若此条则非盈朒所能御
论曰直田截积及米换布盈朒本法也愚所设方田截
积及谷换绢非盈朒本法也乃带分盈朒之变例也
历算全书 卷四十五 第 53a 页 WYG0795-0093a.png
 (如旧法芝麻粜/银是其例也)虽盈胸亦有求法颇多转折非其质
(如旧法芝麻粜/银是其例也)虽盈胸亦有求法颇多转折非其质矣不如用方程之省约
今有芝麻不知总但云取麻八分之三粜银十两不足
二石取麻三分之一粜银八两适足问原麻总数及
每银一两之麻
法先以麻(八/三) (之三/之一)用母相乘得二十四为母母互乘
子得(之九/之八)为所用之分而列之 依省算左加九之
一而径减
历算全书 卷四十五 第 53b 页 WYG0795-0093b.png

法一两省除即以麻二石命为银每两之麻 以银
八两麻八分适足省乘除径以二石为麻之一分以
二十四分乘得原麻四十八石
计开
原麻四十八石 银每两麻二石
其八之三计一十八石 银十两该二十石 故不足
历算全书 卷四十五 第 54a 页 WYG0795-0093c.png
 二石
二石其三之一计一十六石 银八两恰该一十六石 故
适足
若问麻每石之银则以二石为法转除一两得每石
价五钱
按此条宜入方程旧列带分盈胸之末
问者若云有银买麻以麻八之三与之则馀二石以麻
三之一与之适足问原麻及银所买
历算全书 卷四十五 第 54b 页 WYG0795-0093d.png

依法求得二石为麻之一分 以总母廿四分乘之
得原麻四十八石 以九分乘二石减负二石得银
所买麻十六石
论曰此所设问则盈朒带分本法也然不能知每价以
历算全书 卷四十五 第 55a 页 WYG0795-0094a.png
 方程法求之亦同 观此益见前条之宜入方程也
方程法求之亦同 观此益见前条之宜入方程也今有黄连木香不知数但云取连三之一换木香七之
二则连多二斤取连四之三换木香五之四则连少
一斤若于五之四内减去木香三斤则连多一斤
法先以通分齐其分
乃列位
历算全书 卷四十五 第 55b 页 WYG0795-0094b.png

如法乘减 馀木香二十二分为法 异并黄连二
十二斤为实 法除实得每木香一分(即三十五/分之一)换
黄连一斤 以木香十分换黄连十斤异加正二斤
共十二斤以黄连正四分除之得黄连每三斤为一
分 以分母十二乘之得总黄连三十六斤
另并黄连多一斤少一斤共二斤为法除减木香三
历算全书 卷四十五 第 56a 页 WYG0795-0094c.png
 斤得每黄连一斤换木香一斤半(原少连一斤减木/香三斤而转多连)
斤得每黄连一斤换木香一斤半(原少连一斤减木/香三斤而转多连)(一斤故/知其数)
此连所换之木香一斤半即其三十五分之一分也
以三十五分乘之得木香五十二斤半
计开
黄连三十六斤
木香五十二斤半
每黄连一斤换木香一斤半
历算全书 卷四十五 第 56b 页 WYG0795-0094d.png
 三分三十六斤而取其一得一十二斤为黄连三之一
三分三十六斤而取其一得一十二斤为黄连三之一七分五十二斤半而取其二得十五斤为木香七之二
该换连十斤今连有十二斤是连多二斤也
四分三十六斤而取其三得二十七斤为黄连四之三
五分五十二斤半而取其四得四十二斤为木香五之
四该换连二十八斤今连只二十七斤是连少一斤
也
若于木香五之四减三斤馀三十九斤该换连二十六
历算全书 卷四十五 第 57a 页 WYG0795-0095a.png
 斤今连有二十七斤是连多一斤也
斤今连有二十七斤是连多一斤也论曰凡较数方程有若干物共几色又有其所较之价
银若钱之类今所用较数即用其物之斤两而无银
若钱微有不同乃古者贸迁有无交易之术也专用
银若钱以权物价后世事耳
问绫每尺多罗价三十六文今买绫六尺罗八尺其共
价绫比罗少三十六文
答曰绫每尺一百六十二文 罗每尺一百二十六文
历算全书 卷四十五 第 57b 页 WYG0795-0095b.png

罗二尺除二百五十六尺得罗价每尺一百二十六
文 加多三十六文得绫价每尺一百六十二文
问银二千九百二十八两买绫一百五十疋罗三百疋
绢四百五十疋只云绫每疋比罗多四钱七分罗每
疋多绢一两三钱五分 答曰绫每疋四两三钱二
分 罗每疋三两八钱五分 绢每疋二两半
历算全书 卷四十五 第 58a 页 WYG0795-0095c.png

绢九百疋为法除实二千二百五十两得绢价二两五
钱 加多一两三钱半得罗价三两八钱半 又加
多四钱七分得绫价四两三钱二分
今有兄弟三人不知年小弟谓长兄曰我年比汝四之
历算全书 卷四十五 第 58b 页 WYG0795-0095d.png
 三次兄比汝六之五比我多八岁
三次兄比汝六之五比我多八岁法以带分别之 皆变零从整
季弟二 除一百四十四岁得年七十二岁 加八
岁得仲兄年八十 六因仲年五除之得伯年九十
历算全书 卷四十五 第 59a 页 WYG0795-0096a.png
 六岁
六岁计开
伯九十六岁 仲八十岁(为伯年/六之五) 季七十二岁(为伯年/四之三)
今有四人分钱但云乙得甲六之五丙得甲四之三丁
得甲二十四之十七其丁与丙差四文
甲正五 乙负六 空 空 适足(此行不用乙/无对故也)
历算全书 卷四十五 第 59b 页 WYG0795-0096b.png

丁四除二百七十二得丁钱六十八文
加四文得丙钱七十二文
四乘丙钱三除之得甲钱九十六文
五乘甲钱六除之得乙钱八十文
计开
甲九十六文
历算全书 卷四十五 第 60a 页 WYG0795-0096c.png
 乙八十文
乙八十文丙七十二文
丁六十八文
甲六之一得一十六以五因得八十文为六之五乙数也
甲四之一得二十四以三因得七十二为四之三丙数也
甲二十四之一得四以一十七因得六十八为二十
四之一十七丁数也
论曰此虽四色实三色也故径以三色取之
历算全书 卷四十五 第 60b 页 WYG0795-0096d.png
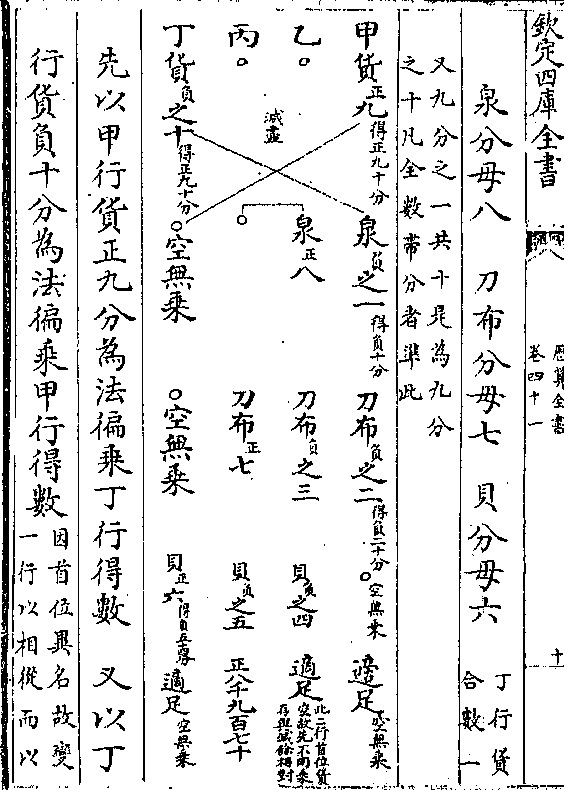 今有七人递差分钱但知首二人共七十七文次二人
今有七人递差分钱但知首二人共七十七文次二人共六十五文不知各数亦不知馀人数
法以递差故知倍乙当甲丙倍丙当乙丁而列之
重列减馀与三行 减馀变较
历算全书 卷四十五 第 61a 页 WYG0795-0097a.png

重列减馀与四行
丁八为法除实二百四十八文得三十一文为丁数
倍丁数与六十五文相减得递差三文 以差递
加得甲乙丙数以差递减得戊己庚数 皆加减丁
历算全书 卷四十五 第 61b 页 WYG0795-0097b.png
 数得之
数得之计开 甲四十文 乙三十七文 丙三十四文 丁三十一文
戊二十八文 己二十五文 庚二十二文
今有银二百四十两以四人递差分之只云甲多丁一
十八两
如前法以倍乙当甲丙倍丙当乙丁 又依省算移甲
于丁位
和较列位
历算全书 卷四十五 第 62a 页 WYG0795-0097c.png

重列两减馀
又重列减馀与末行
历算全书 卷四十五 第 62b 页 WYG0795-0097d.png

甲四除二百七十六两得甲数六十九两 甲数内
减十八两得丁数五十一两 以甲数减二百四十两
馀一百七十一两丙三除之得丙数五十七两 并
丙数甲数一百廿六两半之得乙数六十三两
计开
甲六十九两 乙六十三两 丙五十七两 丁五十
历算全书 卷四十五 第 63a 页 WYG0795-0098a.png
 一两 递差六两
一两 递差六两今有米二百四十石五人递差分之其甲乙二人与戊
丁丙三人共数等
如前法列位 依省算倒甲位自下而上
历算全书 卷四十五 第 63b 页 WYG0795-0098b.png

重列减馀与三行
又重列减馀与四行
又重列减馀与末行
历算全书 卷四十五 第 64a 页 WYG0795-0098c.png

甲十五除九百六十得甲数六十四石 倍甲数减
一百廿石馀得递差八石 以差递减各数得乙丙
丁戊数
计开
历算全书 卷四十五 第 64b 页 WYG0795-0098d.png
 细分之递差八石
细分之递差八石论曰凡差分章竹筒七节盛米之类皆可以此法求之
兹不烦列
历算全书卷四十五