声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
历算全书 卷四十 第 1a 页 WYG0794-0874a.png
 钦定四库全书
钦定四库全书历算全书卷四十
宣城梅文鼎撰
方程论卷一
正名
名不正则言不顺诸本方程皆以二色三色四色等分
款立法而不分和较宜其端绪纷纠而说之滋谬也故
先正其名
历算全书 卷四十 第 1b 页 WYG0794-0874b.png
 正名有四一和数二较数三和较杂四和较交变和
正名有四一和数二较数三和较杂四和较交变和者无正负如只云某物如干某物如干共价如干以
问每物各价者是也较者有正负如云以某物如干
与某物如干相较多价如干或少价如干或相当适
足者是也杂者半有正负半无正负如一行云某物
某物各如干共价如干而其一行则又云以某物如
干较某物如干差价如干或价相当适足者是也变
者或先无正负而变为有正负或先有正负变而无
历算全书 卷四十 第 2a 页 WYG0794-0875a.png
 正负三色以往重列减馀兼用两行者是也
正负三色以往重列减馀兼用两行者是也总论曰万算皆生于和较和较可以御万算分合之义
也万物之未形一而已矣一且未有况万乎及其有
也有一则有二有二则有三自此以至于无穷而数
生焉矣和者诸数之合也较者诸数之分也分则有
差故谓之较较与和相求而法立焉矣故一与一和
则二也一与二和则三也一与二之较一也一与三
之较二也万算虽多准此矣故和较者万算之纲也
历算全书 卷四十 第 2b 页 WYG0794-0875b.png
 算之用至于句股方程至矣尽矣窥高致远探赜穷
算之用至于句股方程至矣尽矣窥高致远探赜穷幽无所不备然其用不出于和较且以方程言之凡
方程列位皆以下位为之端如所列下一位为上中
两位之总价则和也若下一位为上中两位相差之
价则较也较故分正负和故不分正负虽不立正负
然必以两和互乘对减以得其差然后其数可得而
知矣故三色以往先无正负者有时而正负立焉故
方程之法以和求较而已矣较者易知和者难知和
历算全书 卷四十 第 3a 页 WYG0794-0875c.png
 之中有较较之中又有较此万数之所由生万法之
之中有较较之中又有较此万数之所由生万法之所由起
和数方程例
方程用互乘对减与差分章贵贱相和法同但贵贱相
和有总物总价又有每物每价不过以带分之故难
用匿价分身而变为换影之术耳方程则有总物总
价而无每数又有三色四色以至多色头绪纷然自
非递减何取之此古人别立一章之意也
历算全书 卷四十 第 3b 页 WYG0794-0875d.png
 用法曰二色者任以一色列于上以一色列于中以总
用法曰二色者任以一色列于上以一色列于中以总价列于下于是以列上者为乘法左右互乘又互遍
乘中下得数左右对减其上一色必两相若而减尽
其中一色对减必有相差之数下价对减亦必有相
差之数数相差则减不能尽于是取其馀数以为用
一为法一为实以法除实而得中一色每价乃以中
价乘原列中物得中物总价以中物总价减原列两
色之总价得上物总价以原列上物除之得上一色
历算全书 卷四十 第 4a 页 WYG0794-0876a.png
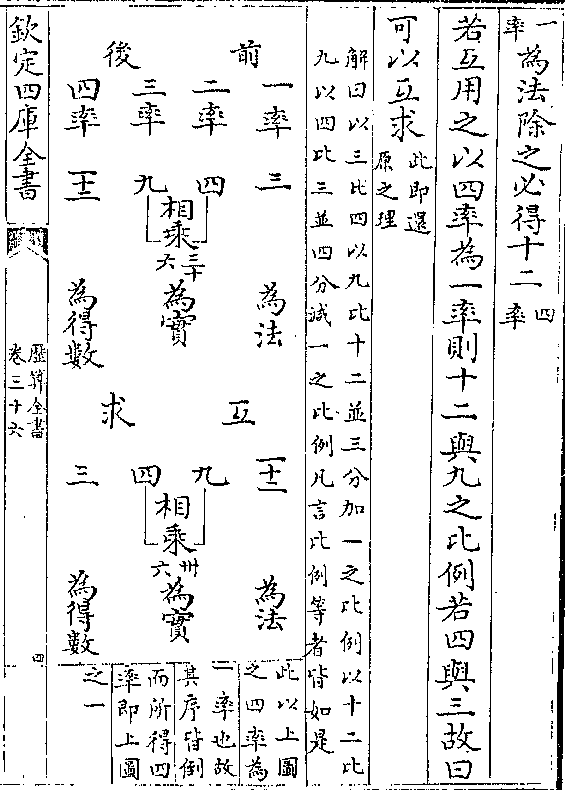 每价(若更以中一色列于上依法求之亦先得上/一色价矣故上中之位可以互更也详见后)
每价(若更以中一色列于上依法求之亦先得上/一色价矣故上中之位可以互更也详见后)假如有山田三亩场地六亩共折输粮实田五亩七分
又有山田五亩场地三亩共折实田五亩五分问田
地每亩折实科则各如干
答曰每山田一亩折实田九分每地一亩折实田三
分亩之一
法各列位
上 中 下
历算全书 卷四十 第 4b 页 WYG0794-0876b.png

先以右上田三亩为法遍乘左行得数
次以左上田五亩为法遍乘右行得数 上位各得
田十五亩对减尽 中位左得地九亩去减右行三
十亩馀地二十一亩为法下位左折田得十六亩五
分去减右行二十三亩五分馀折田七亩为实 以
法除实不满法约为三之一为地每亩折实田之数
历算全书 卷四十 第 5a 页 WYG0794-0876c.png
 (地一亩折田三分三釐三毫/不尽即地三亩折田一亩也) 就以右行折实田共
(地一亩折田三分三釐三毫/不尽即地三亩折田一亩也) 就以右行折实田共四亩七分内除原地六亩折实田二亩馀二亩七分
以右上田三亩除之得九分为田每亩折实之数(或/以)
(左行折田内减左原地三亩该折实田一亩馀四亩/五分以左上田五亩除之亦得九分为田每亩折实)
(之/数)
论曰以右上田三亩遍乘左行得数是各三之也为五
亩田者三亩三亩地者三则为田地共折实五亩五
分者亦三也
历算全书 卷四十 第 5b 页 WYG0794-0876d.png
 以左上田五亩遍乘右行得数是各五之也为三亩
以左上田五亩遍乘右行得数是各五之也为三亩田者五为六亩地者五则为田地折实共四亩七分
者亦五也
于以对减而上位田各十五亩减而尽则其数同也
惟中位地馀二十一亩在右行则是右行之地多于
左行之地二十一亩也
而下位折实数亦馀七亩在右行则是右行折实之
数亦多于左行折实之数七亩也
历算全书 卷四十 第 6a 页 WYG0794-0877a.png
 合而观之此所馀折实七亩者正是馀地二十一亩
合而观之此所馀折实七亩者正是馀地二十一亩之所折也
此以田地问折数故以地二十一亩为法折七亩为
实也若以折数问原田地则以折七亩为法地二十
一亩为实法除实得每折一亩原地三亩于是以右
地六亩折二亩减折四亩七分馀二亩七分为法除
右田三亩得每折一亩原田一亩又九分亩之一即
一分一釐一毫一一不尽也
历算全书 卷四十 第 6b 页 WYG0794-0877b.png
 若更置以地列于上则先得田折数如后图
若更置以地列于上则先得田折数如后图上 中 下
先以左上地三亩遍乘右行得数
次以右上地六亩遍乘左行得数 上位各得地十
八亩对减尽 中位左得田三十亩内减去右得九
亩馀二十一亩为法 下位折田左得三十三亩内
历算全书 卷四十 第 7a 页 WYG0794-0877c.png
 减去右得十四亩一分馀十八亩九分为实 以法
减去右得十四亩一分馀十八亩九分为实 以法除实得九分为田每亩折实数
就以右田三亩折二亩七分减右折实共四亩七分
馀二亩以右上地六亩除之不满法命为三分亩之
一为地每亩折实数(或于左行折实五亩五分内减/去左田五亩该折四亩五分馀)
(一亩以左地三亩除之亦/得地折实每亩三之一)
论曰以右上地六亩遍乘左行是各六之也为三亩地
者六为五亩田者六为地三亩田五亩之折实田共
历算全书 卷四十 第 7b 页 WYG0794-0877d.png
 五亩五分者亦六也以左上地三亩遍乘右行是各
五亩五分者亦六也以左上地三亩遍乘右行是各三之也为地六亩者三为田三亩者三为地六亩田
三亩之折实共四亩七分者亦三也以之对减而地
在上位者各十八亩既对减而尽则其各十八亩之
折实在折实共数中者亦必对减而尽也田在中位
者既对减去九亩而仅馀左行之二十一亩则其各
九亩之折实在共数中者亦必对减而尽也由是以
观则其所馀之左下折田十八亩九分正是左中馀
历算全书 卷四十 第 8a 页 WYG0794-0878a.png
 田二十一亩之所折也故以馀田二十一亩为法而
田二十一亩之所折也故以馀田二十一亩为法而以馀折田十八亩九分为实即田之折数可知知田
数知地亩矣
若以折问田亩则一十八亩九分折为法二十一亩
田为实实如法而一得每折一亩原田一亩又九分
之一于是以分母九通右行田三亩得二十七分而
以一亩又九分之一共一十分为法除之得二亩七
分以减共折四亩七分馀折二亩以除右地六亩得
历算全书 卷四十 第 8b 页 WYG0794-0878b.png
 每折一亩原地三亩(以上二色例也三色四色以至/多色凡和数者皆同但须重例)
每折一亩原地三亩(以上二色例也三色四色以至/多色凡和数者皆同但须重例)(减馀以求之今不悉/具于后诸条中详之)
较数方程例
凡较数方程分正负之价与盈朒略同但盈朒章有盈
朒又有出率方程则但有总物与盈朒而无每出之
率又兼数色所以不同又盈朒者是有每率而不知
总所言盈朒适足是总计所出以与原立总价相较
之数也方程正负则是两总物自相较之数若不立
历算全书 卷四十 第 9a 页 WYG0794-0878c.png
 正负则下价之与上物不知其孰为同异矣此正负
正负则下价之与上物不知其孰为同异矣此正负之法异于盈朒也(负与正对所以分别同异盖对数/之所馀即正数之所欠故谓之负)
(与负责之负略相似老子言万物负阴而抱阳盖正/即正面负即反面也开方法有负隅言隅之空隙也)
(郭太史历经三差法有负减言反减也本于平差内/减去立差今立差反多于平差故于立差内反减平)
(差是为负减兼此数端/而正负之义可见矣)
法曰任以一色为正则以相当之一色为负(此据二色/者言之三)
(色以上或以一色与多色相当或以/多色与多色相当其法皆同二色)正物之价多为
正价负物之价多为负价正与负为异名异名相并
历算全书 卷四十 第 9b 页 WYG0794-0878d.png
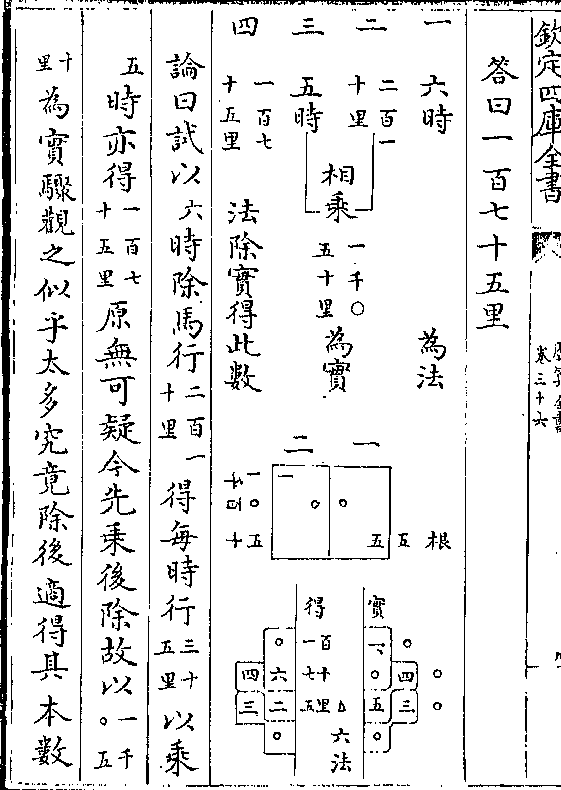 正与正负与负为同名同名相减
正与正负与负为同名同名相减首位同名者仍其正负不变(首位同数同名即/可减去此正法也)
首位异名变其一一以相从(首位亦同数但不同名/故变而同之则亦同数)
(同名而可减尽矣首位既变则其行内皆从而变此/通法也盖必如是则同减异加始归画一而于和较)
(交变之用/尤便也)
其法皆于互乘时以得数变之盖减并只用得数也
只变一行其相对之行不必再变二色三色以至多
色并同何也三色以上行数虽多而乘并之用皆以
历算全书 卷四十 第 10a 页 WYG0794-0879a.png
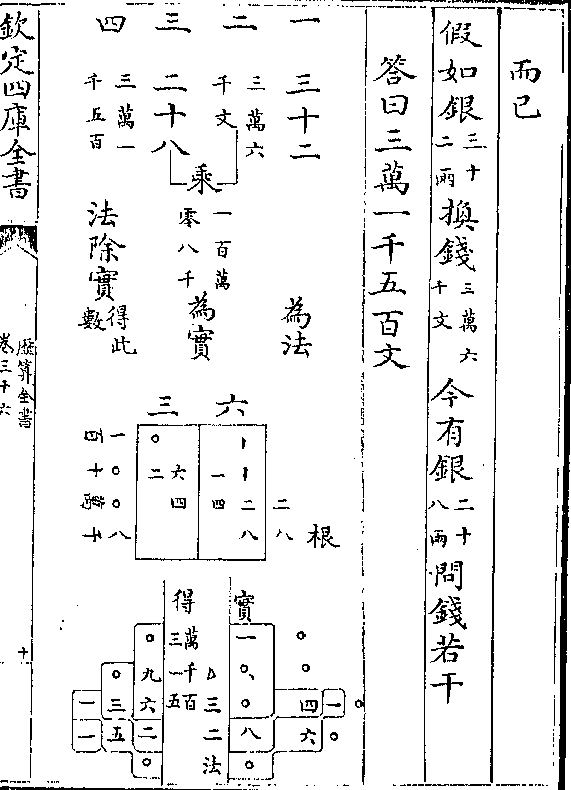 各相对之一行论同异即同二色之理
各相对之一行论同异即同二色之理论曰和数方程有减无并皆同名故也较数方程有减
有并或同名或异名也减并者方程之纲要正负淆
则同异之名混而并减皆失矣今诸本所言正负同
异誃离舛错虽加减得数皆偶合耳西人论句股三
角八线割圜几何原本可谓详矣矣至方程增立诸
率亦复草草未穷其故也
用法曰以一色列于上以相当之一色列于中任以一
历算全书 卷四十 第 10b 页 WYG0794-0879b.png
 色为主而分正负(此亦以二色为例三色以上皆以/两相当者主其一以分正负皆与)
色为主而分正负(此亦以二色为例三色以上皆以/两相当者主其一以分正负皆与)(二色/法同)
以两色相较之价列于下以正物为主而分同异或
正物所多之价命之为正或正物所少之价命之为
负(正物之所少即/负物之所多)或正物负物之价两相若命之适
足则空位列之亦以列上位者为乘法左右互乘遍
乘中下以首位为主而变正负得数对减其上一色
必数相若且又同名而减尽中一色与下价或同名
历算全书 卷四十 第 11a 页 WYG0794-0879c.png
 或异名异名者并之同名者对减取其减并之数以
或异名异名者并之同名者对减取其减并之数以为用一为法一为实以法除实得中一色每价以原
列中物乘之得中物总价以与原列下价同名相减
异名相并得数以原列上物除之得上一色每价(其/上)
(中亦可/互求)
假如以研七枚换笔三矢研多价四百八十文若以笔
九矢换研三枚笔多价一百八十文问笔研价各如
干
历算全书 卷四十 第 11b 页 WYG0794-0879d.png
 答曰笔每矢价五十文 研每枚价九十文
答曰笔每矢价五十文 研每枚价九十文法各列位
上 中 下
先以左行研负三遍乘右行得数(首位异名须变一/行以相从故研正)
(变为负笔负变为正价正/变为负皆于得数变之)
次以右行研正七遍乘左行得数(右行既变则左行/不必再变故研负)
历算全书 卷四十 第 12a 页 WYG0794-0880a.png
 (笔正价正/皆仍旧)
(笔正价正/皆仍旧)于是以上研各负二十一同名相减尽 次以中笔
两正同名相减馀五十四为法 再以下价左正右
负异名相并得二千七百为实 以法除实得五十
文为笔价 以左行笔正九乘笔价得四百五十内
减同名价一百八十馀二百七十以左研负三除之
得九十为研价或以右笔负三共价一百五十加异
名价正四百八十共六百三十以右研七除之亦得
历算全书 卷四十 第 12b 页 WYG0794-0880b.png
 研价九十
研价九十论曰左行原是九笔多于三研一百八十文乘后得数
则是六十三笔多于二十一研共一千二百六十文
也右行原是七研多于三笔四百八十文乘后得数
则是九笔少于二十一研一千四百四十文也于是
以两行得数较之上位研负二十一两行尽同研之
数同则其价亦同惟中位笔数左行多五十四枝则
是左行笔多价一千二百六十文者以多此五十四
历算全书 卷四十 第 13a 页 WYG0794-0880c.png
 笔而右行笔少价一千四百四十文者以少此五十
笔而右行笔少价一千四百四十文者以少此五十四笔也夫右行笔价原少于二十一研者一千四百
四十文以左行多五十四笔而反多于二十一研者
一千二百六十文是此五十四笔既补却右行之所
少而仍多此数也故并右行之所多共此二千七百
以为五十四笔之价知笔价知研价矣
若先求研价者以研列中为除法以笔列上为乘法
如后图
历算全书 卷四十 第 13b 页 WYG0794-0880d.png
 问者或云笔三矢换研七枚少价四百八十文又有研
问者或云笔三矢换研七枚少价四百八十文又有研三枚以换笔九矢少价一百八十文则其下价为两
负(四百八十是笔少于研之价/一百八十是研少于笔之价)
先以左行笔负九遍乘右行得数(首位异名宜变一/行故其正负皆更)
(之/)
次以右行笔正三遍乘左得数(右变则左不变/故正负皆仍之)
历算全书 卷四十 第 14a 页 WYG0794-0881a.png
 于是以得数较其同异而为之减并 笔各负二十
于是以得数较其同异而为之减并 笔各负二十七同名减尽研正同名相减馀五十四为法 价正
负异名并得四千八百六十为实 实如法而一得
九十为研价 以研价乘左正研三得二百七十异
加价负一百八十共四百五十以左负笔九除之得
五十为笔价或以右研七价六百三十与价四百八
十同减馀一百五十以笔三除之亦得笔价五十
论曰左行原是研三少于笔九者一百八十文乘后得
历算全书 卷四十 第 14b 页 WYG0794-0881b.png
 数则是九研少于二十七笔者五百四十文也 右
数则是九研少于二十七笔者五百四十文也 右行原是三笔少于七研者四百八十文乘后得数则
是六十三研多于二十七笔者四千三百二十文也
夫两行笔皆二十七则其价同也而右行研价多于
笔四千三百二十文左行研价反少于笔五百四十
文是两行研价相差者共四千八百六十文也推求
其说则只是两行中相差五十四研之故也故减去
相同之笔用此相差之研以除此相差之研价而每
历算全书 卷四十 第 15a 页 WYG0794-0881c.png
 研之价可知矣
研之价可知矣若如难题所列以研为正笔为负问者当云以七研
换三笔研多价四百八十以三研换九笔研少价一
百八十文则价右正左负(难题系/书名)
左右研正遍乘得数(首位本同名故/其正负皆不变)研减尽笔馀五
十四为法价异并二千七百为实法除实得笔价以
历算全书 卷四十 第 15b 页 WYG0794-0881d.png
 次得研价如前若以笔为正研为负则其价右负左
次得研价如前若以笔为正研为负则其价右负左正
依法先得研价如第一图
以前四图或以笔为正或以笔为负或以研为正或
以研为负或以价为两正或以价为两负或以价为
一正一负其所呼正负之名无一同者要其为同异
历算全书 卷四十 第 16a 页 WYG0794-0882a.png
 加减之用则一也
加减之用则一也试以一行中同异言之其左行之价必与笔同名何
也左行之价乃笔多于研之数也故与笔同名而与
研异名也 其右行之价必与研同名何也右行之
价乃研多于笔之数也故与研同名而与笔异名也
试以两行中同异言之其上位皆减尽其中位皆相
减为法其下价皆相并为实其减也皆以同名其研
也皆以异名 此下价异并例也
历算全书 卷四十 第 16b 页 WYG0794-0882b.png
 假如有大小馀句不知数但云倍小馀句以当三大馀
假如有大小馀句不知数但云倍小馀句以当三大馀句则不及一丈五尺三寸若倍大馀句则如七小馀
句
答曰大馀句六尺三寸 小馀句一尺八寸
法以正负列位
先以左小馀句负七遍乘右得数(首位异名宜变以/相从故小句变负)
历算全书 卷四十 第 17a 页 WYG0794-0882c.png
 (大句下负/数皆变正)
(大句下负/数皆变正)次以右小馀句正二遍乘左得数(右行既变则此行/不变下适足无乘)
(亦无/正负) 乘讫乃较之 小馀句各十四同减尽 大
馀句同减馀一十七为法 下正数十丈零七尺一
分无对不减就为实 以法除实得六尺三寸为大
馀句 乃置左行二大句该一丈二尺六寸以左行
相当适足之七小句除之得一尺八寸为小馀句(或/用)
(右行三大句该一丈八尺九寸以同名负一丈五尺/三寸减之馀三尺六寸以右行二小句除之亦得一)
历算全书 卷四十 第 17b 页 WYG0794-0882d.png
 (尺八/寸)合问
(尺八/寸)合问论曰以左小句遍乘右是各七之也为小句二大句三
者七其相较之数亦七也 以右小句遍乘左是各
二之也为小句七大句二者二其相当适足者亦二
也但以首位必同名然后可减故以右小句正变而
为负以从左名也小句变为负则所与相较之大句
不得不变而正矣 于是小句同减尽大句同名减
去四馀右行正十七下较数无减仍馀十丈○七尺
历算全书 卷四十 第 18a 页 WYG0794-0883a.png
 一寸然则此所馀者正是减馀大句之数矣何也小
一寸然则此所馀者正是减馀大句之数矣何也小句十四左右皆同若只如左行四大句则与小句相
当适足矣而今右行独馀此较数者非以右多十七
大句之故乎
试以大句列于上则先得小句如后图
如法左乘右更其正负 右乘左仍其正负 大句
历算全书 卷四十 第 18b 页 WYG0794-0883b.png
 同减尽 小句同减馀正一十七在左行为法 下
同减尽 小句同减馀正一十七在左行为法 下较数负三丈○六寸在右行无对不减就用为实以
法除实得一尺八寸为小句 就以左行小句七该
一丈二尺六寸以左相当适足之大句二除之得六
尺三寸为大句(或于右行正一丈五尺三寸加异名/小句负二该三尺六寸共一丈八尺)
(九寸以右大句三除/之亦得六尺三寸)
论曰左行原是小句七以当大句二适足今以右大句
乘而各三之则是小句二十一以当大句六而亦适
历算全书 卷四十 第 19a 页 WYG0794-0883c.png
 足也 右行原是大句三以当小句二而大句多一
足也 右行原是大句三以当小句二而大句多一丈五尺三寸今以左大句乘而各二之则是大句六
以当小句四而多三丈○六寸也 以两行之得数
较之大句既减尽惟左行之小句馀一十七则是左
行得数所以相当适足者以多此十七小句之故而
右行小句得数小于大句三丈○六寸者以少此十
七小句之故也然则此三丈○六寸者正是十七小
句之数也(依此论可见左行之所多即右行之所/少故左行名正者用于右行即为负而)
历算全书 卷四十 第 19b 页 WYG0794-0883d.png
 (隔行之异名/即为同名)
(隔行之异名/即为同名)此下较无减例也
假如有大小方积不知数但云一大方积以当二小方
积多数八十九若以三大方积当七小方积仍多二
百五十一
答曰大方积一百二十一 小方积一十六
法以正负列位
上 中 下
历算全书 卷四十 第 20a 页 WYG0794-0884a.png

先以右大积一遍乘左行皆如原数 次以左大积
三遍乘右行得数(首位同名故两/行正负皆不变) 大积同减尽
小积同减馀一为法较数同减馀一十六为实 法
除实仍得一十六为小积 以右行小积负二该三
十二加异名正八十九共一百二十一为大积(或以/左行)
(小积负七该一百一十二加异名正二百五十一共/三百六十三以左大积三除之亦得一百二十一为)
历算全书 卷四十 第 20b 页 WYG0794-0884b.png
 (大/积)
(大/积)论曰左行原是大积三多于七小积者二百五十一乘
后得数亦同 右行原是大积一多于二小积者八
十九乘后得数则是大积三多于六小积者二百六
十七也 于是以两行对勘其大积既减尽惟小积
左行馀负一其下较数则右行馀正十六夫此十六
数者与大积同名是右行大积之数也右行少一小
积而大积之盈数多十六左行多一小积而大积之
历算全书 卷四十 第 21a 页 WYG0794-0884c.png
 盈数少十六然则此十六数者正是此一小积之数
盈数少十六然则此十六数者正是此一小积之数矣若以小方积为正则其下较数为两负(皆小积所/少之数也)
(故皆/为负)
上 中 下
依法遍乘对减馀大积一为法 馀负一百二十一
为实 法除实不动就以一百二十一为大积 右
历算全书 卷四十 第 21b 页 WYG0794-0884d.png
 大积一该一百二十一同名减负八十九馀三十二
大积一该一百二十一同名减负八十九馀三十二以小积二除之得一十六为小积
此是右行多一大方积故多一同名之数一百二十
一同在一行易知不须重论
以上二图正负所呼迥异然所同者两行之较数皆
与大方积同名何也皆大方积多于小方积之数故
与大方积同名而与小方积异名也
此下较同减例也
历算全书 卷四十 第 22a 页 WYG0794-0885a.png
 总论曰凡较数方程原列较数是本行中正与负之较
总论曰凡较数方程原列较数是本行中正与负之较也其乘后得数同减异加而得者则是两行中正与
正之较或负与负之较也故本行中以异名相较而
两行对减或加是以两行之同名相较
假如原列较数与正物同名是正多于负之较也若列
较与负同名是负多于正之较也故曰本行中异名
相较也
假如乘后得数而两行之较数皆与正物同名则两较
历算全书 卷四十 第 22b 页 WYG0794-0885b.png
 亦自同名乃以之对减而馀在一行则知此一行正
亦自同名乃以之对减而馀在一行则知此一行正物必多于对行之正物而其所多之数即如此所馀
之较数矣
假如两行较数皆与负物同名则两较亦自同名以之
对减而馀在一行则知此一行负物必多于对行之
负物而其所多之数正是此所馀之较数矣此同名
相减之理也
假如右行较数与正同名而左行较数却与负同名则
历算全书 卷四十 第 23a 页 WYG0794-0885c.png
 一是正多于负之数而一是负多于正之数也夫正
一是正多于负之数而一是负多于正之数也夫正与负原相待负多于正之数即正少于负之数也于
是用异名相加法以左行负多于正之数变为正少
于负之数以相并则知右行之正数必多于左行之
正物而其所多几何正是此两较之并数矣此异名
相加之理也
合同减异并而观之总是两行中同名相较也
又论曰较数方程以两相较而为用虽有三色四色乃
历算全书 卷四十 第 23b 页 WYG0794-0885d.png
 至多色其相较也必两此正负所由立也立正负以
至多色其相较也必两此正负所由立也立正负以别同异犹彼我也夫彼我者岂有一定之称哉以此
为正则以彼为负若以彼为正则此反为负矣正负
之相呼犹彼我之相视也故曰无定虽然无定者正负
有定者同异其无定者在未立正负之先其有定者
在既立正负之后既以一为主则同乎此者皆同名
异乎此者皆异名矣是故无定而实有定也
今试以所列方程最下位观之其言正负者必上物
历算全书 卷四十 第 24a 页 WYG0794-0886a.png
 之较数也不言正负者必上物之和数也较数有盈
之较数也不言正负者必上物之和数也较数有盈有朒有适足和则否
假如下价盈则为正正与正同名试于正物价之中减
去下同名正价之盈则所馀之价必与负物之价相
当矣 正与负异名试又取上负物之价以加下异
名正价则又必与正物之价相当矣
假如下价朒则为负(正物之朒负/物之盈也)负与负同名试于负
物价之中减去下同名负价则所馀之价必与正物
历算全书 卷四十 第 24b 页 WYG0794-0886b.png
 之价相当矣 负与正异名试又取上正物之何以
之价相当矣 负与正异名试又取上正物之何以加下异名负价又必与负物之价相当矣
假如下价适足空位无盈朒则其上正负物价必自相
当
又论曰正负之术分别同异全在有交变之法以通其
穷要其为用惟在使两行之首位同名而已何也方
程以互乘递减立法每乘一次即减去一色然惟和
数则一乘之后即可对减若较数则有同数而不同
历算全书 卷四十 第 25a 页 WYG0794-0886c.png
 名之时若不减首位即不成方程若径以异名而减
名之时若不减首位即不成方程若径以异名而减势必以同名而并法不画一而于后条和较交变之
时益混淆而难用故以法变之使首位之同数者无
不同名而仍为同名利减焉首位既以同名减则凡
减者皆同名凡并者皆异名而其法画一矣故首位
既变则行内之正负皆变何也从首位也行内之正
负既皆从首位而变由是而原与首位同名者皆与
隔行之首位同名也原与首位异名者即与隔行之
历算全书 卷四十 第 25b 页 WYG0794-0886d.png
 首位异名也如此则隔行之同减异并亦清矣正负
首位异名也如此则隔行之同减异并亦清矣正负犹阴阳也牝牡也各行中各有正负犹两仪之生四
象也乘而交变犹刚柔相推而生变化也隔行之正
本行以为负隔行之负本行以为正真阴真阳互居
其宅也同名相减者阴阳之偏不得其配也异名相
并者阴阳得类雌雄相食也是皆有自然之理焉可
以思古人立法之原矣
(以上亦以二色者举例三色以上乃至多色正负/之用尤显详具诸卷中兹不赘列然其理著矣)
历算全书 卷四十 第 26a 页 WYG0794-0887a.png
 和较相杂方程例
和较相杂方程例方程之用以御隐杂妙在杂与变知其杂则杂而不用
矣知其变则变而不失其常矣诸书所论胥未及此
故求之甚详去之愈远也
用法曰凡方程和较杂者和较从和法列之不立正负
较数从较法列之明立正负 其偏乘得数后在
较数行中者仍其正负之名在和较行中者皆变从
乘法之名(和数原无正负则无可变但乘后得数取/其与较数之首位同名而已首位既同名)
历算全书 卷四十 第 26b 页 WYG0794-0887b.png
 (下不得不/同名矣)
(下不得不/同名矣)凡两较者下价或有减有并而中物只同减若一和
一较者下价亦有减有并而中物皆异并此以两色
言之三色以上随数通变皆以同异名御之
假如有大小句不知数但云三其大句倍其小句共三
丈三尺若倍大句则如六小句问若干
答曰大句九尺 小句三尺
法以一和一变列位(适足者以相较而/得名即同较义)
历算全书 卷四十 第 27a 页 WYG0794-0887c.png

右行和数也不立正负 左行较数也明立正负
右乘左而三之和乘较也故其正负皆如故
左乘右而二之较乘和也故得数皆为正从乘法之
名也 如法遍乘讫以两行对勘 大句同名相减
尽 小句异名相并得二十二为法 正数六丈六
尺无减就为实 法除实得三尺为小句 以左行
历算全书 卷四十 第 27b 页 WYG0794-0887d.png
 小句六共一丈八尺为实以大句二为法除之得九
小句六共一丈八尺为实以大句二为法除之得九尺为大句(或于右行共三丈三尺内同减小句二共/六尺馀二丈七尺以大句三除之亦得九)
(尺/)
论曰右行大句三小句二共三丈三尺乘后得数则是
六大句四小句共六丈六尺也 左行大句二小句
六其数相当乘后得数则是六大句十八小句亦相
当适足也 于以对减而两大句同减尽则其数同
也而右行正数犹有六丈六尺左则无有其故何也
历算全书 卷四十 第 28a 页 WYG0794-0888a.png
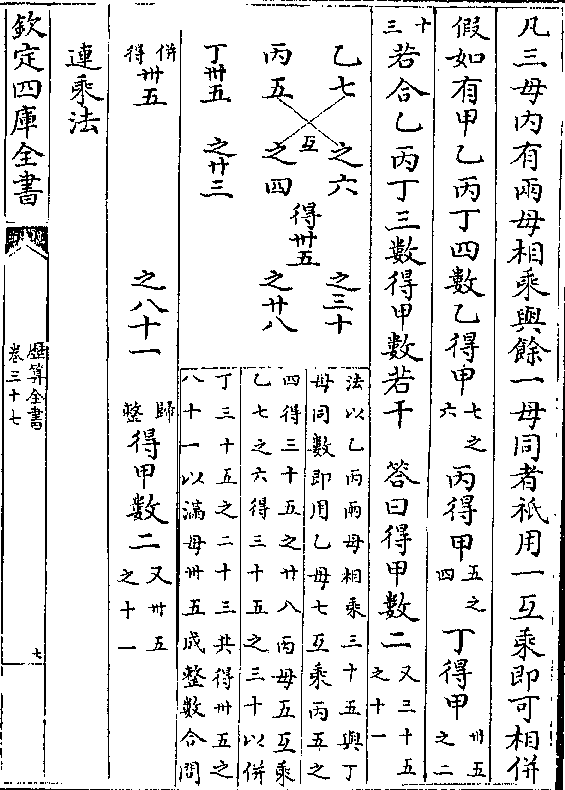 右行正数中有小句四而左则无且不惟无之而
右行正数中有小句四而左则无且不惟无之而已其相对之负数反有十八小句焉是左行正数
又自除却十八小句之数也右行正数多四小句
左行正数又自除却十八小句则是右行正数之
多于左行正数者二十二小句也故并此二十二
小句为右行所多之正物其六丈六尺则右行之
正数也以正物除正数而小句可知知小句知大
句矣
历算全书 卷四十 第 28b 页 WYG0794-0888b.png
 又细考之六大句合四小句共六丈六尺则以与六
又细考之六大句合四小句共六丈六尺则以与六大句相当之十八小句合四小句亦必六丈六尺也
此亦西儒比例之理而以同异名尽之可见古人用
法之简快试更列之以小句居上则先得大句亦同
上 中 下
先以右小句二遍乘左行得数(和乘较也故/仍其正负)
历算全书 卷四十 第 29a 页 WYG0794-0888c.png
 次以左小句六遍乘右行得数(较乘和也故皆命/为负与乘法同名)两
次以左小句六遍乘右行得数(较乘和也故皆命/为负与乘法同名)两小句同减尽 两大句异并二十二为法 负数十
九丈八尺无减就为实法除实得大句九尺 以右
行大句三该二丈七尺减共三丈三尺馀六尺以小
二句除之得小句三尺
论曰小句互乘之后则其数同也小句数同则负数亦
同而右行之负数独有十九丈八尺左则无有者以
右之负数中有大句十八而左则无不惟无也其所
历算全书 卷四十 第 29b 页 WYG0794-0888d.png
 对之正数中反有大句四是左行负数中又原少四
对之正数中反有大句四是左行负数中又原少四大句也右负数多十八大句左负数少四大句是右
之负数多于左之负数者共二十二大句也然则右
之负数独有此十九丈八尺者正是此二十二大句
之数也
此和数与适足偕也
假如有江湖两色船载物不知数但云江船五以较湖
船一则江多二千八百石江船三湖船五则共载二
历算全书 卷四十 第 30a 页 WYG0794-0889a.png
 千八百石问船力若干 答曰江船六百石 湖船
千八百石问船力若干 答曰江船六百石 湖船二百石
法以一和一较列位
如法左右遍乘得数
江船同减尽 湖船异并二十八为法 载物同减
馀五千六百石为实 法除实得二百石为湖船数
历算全书 卷四十 第 30b 页 WYG0794-0889b.png
 以湖船数加右行异名正二千八百共三千石以
以湖船数加右行异名正二千八百共三千石以右江船五除之得江船数六百石(或以湖船五共一/千石同减左行二)
(千八百石馀一千八百石以/左江船三除之亦得六百石)
论曰遍乘后江船数同则其载数亦同今以两正数相
减而左多五千六百者以左正数中有湖船二十五
而右则无不惟无也其所对之负数中反有湖船三
是右行正数中又自少三湖船也左多二十五右少
三是左正数多于右数者共二十八湖船也然则左
历算全书 卷四十 第 31a 页 WYG0794-0889c.png
 之正数独多五千六百者正此二十八湖船之数也
之正数独多五千六百者正此二十八湖船之数也此和数偕一正也负亦同
和变交变方程例
凡方程三色以上以减馀重列则有和变较较变和者不可不
察也 若非和较之杂则二色方程之中物有减无并矣若
非和较之变则三色四色方程和数者有减无并矣夫
和数较数非自我命之名也其下价之为和为较不可诬也
用法曰和变较者但和数减馀有分在两行者兼而用
历算全书 卷四十 第 31b 页 WYG0794-0889d.png
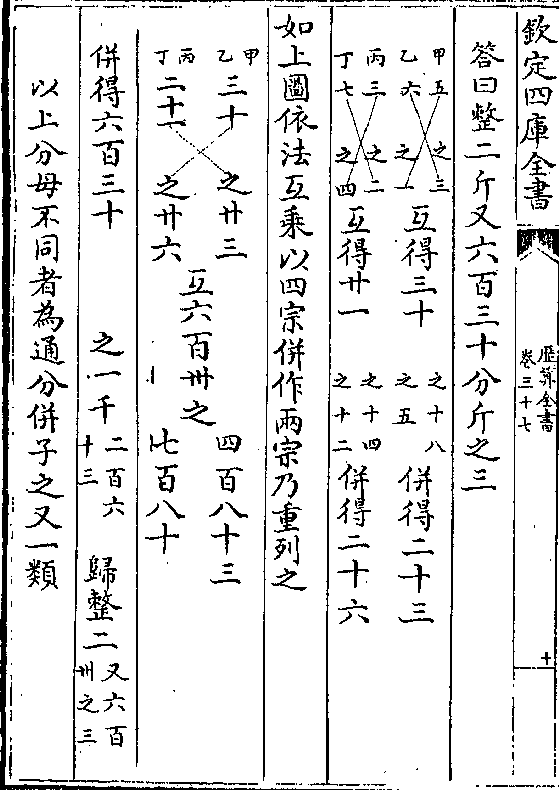 之即变较数也 和既变较即以较数法列之其法
之即变较数也 和既变较即以较数法列之其法以一行之馀数命为正以一行之馀数命为负 其
下馀价以与中位馀物同在一行者即为同名从其
正负而命之 若下价减尽无馀者命为适足
若减馀只在一行者无变也只用和数法
较变和者但视较数减馀或有一行内皆正或皆负
者即变和数也即如和数法列之不立正负(其较数/异并者)
(以一行为主而以隔行之/之异名从本行为同名)
历算全书 卷四十 第 32a 页 WYG0794-0890a.png
 若减馀行内有正负者无变也只用较数法
若减馀行内有正负者无变也只用较数法若有两异并而一位左正右负一位右正左负亦仍
为较数不变虽减馀分在两行而一行馀正物一行
馀负物亦和数也何也隔行之异名乃同名也
若减馀同名而分馀于两行即仍为较数不变何也
隔行之同名乃异名也
若两异并皆左正右负或皆左负右正亦和数也
和较重列有俱变为较者有只变一行为较而馀行
历算全书 卷四十 第 32b 页 WYG0794-0890b.png
 如故者较数重列有俱变为和者有只变一行为和
如故者较数重列有俱变为和者有只变一行为和而其馀如故者皆如上法以和较杂列之
若四色以上有和变较较复变和者有较变和和复
变较者皆以前法御之
假如以衡校弓弩之力但云大神臂弓二弩九小弓二
共重七百一十斤又有神臂弓三弩二小弓八共五
百二十五斤又有神臂弓五弩三小弓二共五百一
十五斤问各力
历算全书 卷四十 第 33a 页 WYG0794-0890c.png
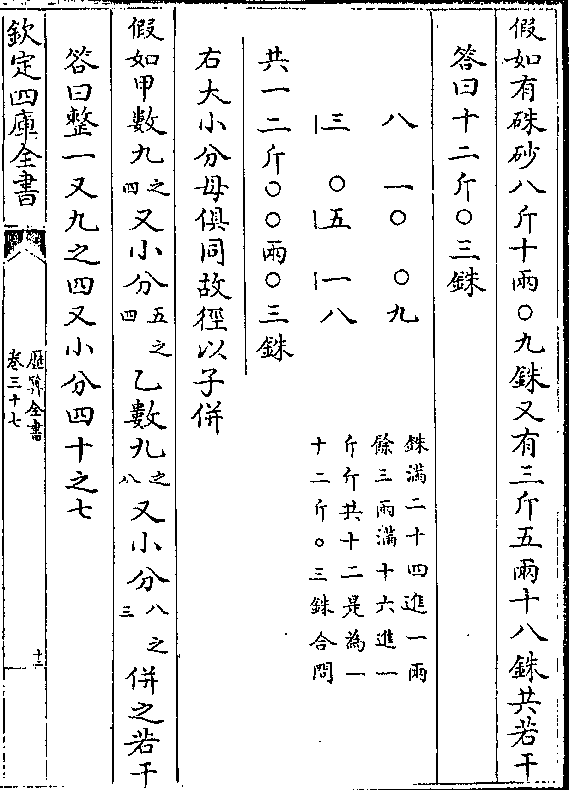 答曰大神臂弓力五十五斤 弩力六十斤 小弓
答曰大神臂弓力五十五斤 弩力六十斤 小弓力三十斤
法先以和较列位(凡三色者可任以一行为主与馀二/行数相乘而减并之故前后之行可)
(互更也详/见第三卷)
先以中行神臂弓二为法遍乘左右得数(此以中行/为主与左)
历算全书 卷四十 第 33b 页 WYG0794-0890d.png
 (右互乘取其行间/易为减并之用也)
(右互乘取其行间/易为减并之用也)次以右行神臂三遍乘中行得数与中行对减 神
臂弓中右各六对减尽 中弩二十七内减去右弩
四馀二十三(中行/馀也) 中小弓六去减右小弓十六馀
十(右行/馀也) 中力二千一百三十内减去右一千○五
十馀一千○八十斤(中行/馀也)
以上减馀分在两行已变较数矣即用较数之法分
正负列之而以弩与力命为同名(弩与力同在/中行故也)
历算全书 卷四十 第 34a 页 WYG0794-0891a.png
 次以左行神臂五遍乘中行得数而以中左两行对
次以左行神臂五遍乘中行得数而以中左两行对减 神臂弓各十减而尽 中弩得四十五内减去
左行弩六馀三十九
中行小弓得十内减去左小弓四馀六 中力得三
千五百五十内减去左一千○三十馀二千五百二
十斤
以上减馀俱在中行仍为和数也不分正负
论曰此和数方程变为一和一较也何也中右得数两
历算全书 卷四十 第 34b 页 WYG0794-0891b.png
 大弓减尽则其力相若也弩数相减而馀在中行是
大弓减尽则其力相若也弩数相减而馀在中行是中行之弩力多于右行也小弓相减而馀在右行是
右行小弓之力多于中行也弩力中多于右小弓力
右多于中而今共力相减惟中多一千○八十斤则
是此一千○八十斤者非馀弩馀弓之共数而馀弩
所多于馀弓之较数也虽欲不分正负不可得也
如中左对减而馀弩馀小弓俱在中行则中行之馀
力二千五百二十斤者仍为馀弩馀小弓共数无正
历算全书 卷四十 第 35a 页 WYG0794-0891c.png
 负之可分也故以此两减馀者依和较杂法重列而
负之可分也故以此两减馀者依和较杂法重列而求之
如前对减既于共力中清出首一色大神臂弓不与
弩小弓杂矣然所馀之力尚为弩小弓共数与其较
数而未能分别此二色之每数也故必重测
依和较杂法以左右馀弩互遍乘得数(左乘右和乘/较也故仍其)
历算全书 卷四十 第 35b 页 WYG0794-0891d.png
 (正负右乘左较乘和也故/变从乘法之名皆曰正)
(正负右乘左较乘和也故/变从乘法之名皆曰正)弩同减尽 小弓异并五百二十八为法 力同减
馀一万五千八百四十为实 法除实得三十斤为
小弓力 以小弓力乘右行馀小弓十得三百斤异
如力正一千○八十斤共一千三百八十斤以馀弩
二十三除之得六十斤为弩力(或于左行共力二千/五百二十斤内同减)
(小弓六该一百八十斤馀二千三百四十斤以馀弩/三千九除之得六十斤亦同即此可见两减馀之为)
(一和/一较)乃于原列任取右行八小弓力二百四十斤二
历算全书 卷四十 第 36a 页 WYG0794-0892a.png
 弩力一百二十斤以减共力五百二十五斤馀一百
弩力一百二十斤以减共力五百二十五斤馀一百六十五斤以大神臂弓三除之得五十五斤为大神
臂弓力
论曰两弩正数同而其力不同者小弓之故也左行和
数也是弩偕小弓之力也右行较数也是弩力中减
去小弓之力而馀者也合而观之则是左行之弩力
有小弓一百三十八以为之益而右行之弩力反减
去小弓三百九十然则左行正数之多于右行者凡
历算全书 卷四十 第 36b 页 WYG0794-0892b.png
 共差小弓五百二十八而左行正数所以多于右行
共差小弓五百二十八而左行正数所以多于右行一万五千八百四十斤者正是此小弓五百二十八
之力也
凡此减馀之数亦可互求若更置之以小弓列上则
先得弩力如后图
上 中 下
历算全书 卷四十 第 37a 页 WYG0794-0892c.png
 依法右左遍乘得数(左乘右和乘较也故仍其正负/右乘左较乘和也故变从乘法)
依法右左遍乘得数(左乘右和乘较也故仍其正负/右乘左较乘和也故变从乘法)(之名皆名/之曰负)
小弓同减尽 弩异并得五百二十八为法 力异
并得三万一千六百八十为实 法除实得六十斤
为弩力 以弩力乘右行弩二十三得一千三百八
十斤同减正一千○八十斤馀三百斤以小弓十除
之得小弓力
论曰两小弓同名负其数既同而左行负数之力有若
历算全书 卷四十 第 37b 页 WYG0794-0892d.png
 干右则无之而且反小于正数之力若干者何也以
干右则无之而且反小于正数之力若干者何也以左行负数中有弩三百九十右则无之而其所对之
正数反有弩一百三十八以为之除算则是左负数
之多于右者共五百二十八弩也右负数少此五百
二十八弩而正数力遂多六千四百八十斤左负数
多此五百二十八弩则不但补却右行之所少而又
自有力二万五千二百斤然则左行共多于右三万
一千六百八十斤者正是此五百二十八弩之力也
历算全书 卷四十 第 38a 页 WYG0794-0893a.png
 此三色和变较例也(四色以上杂/见诸卷中)
此三色和变较例也(四色以上杂/见诸卷中)问有甲乙丙三数甲加七十三得为乙丙数者倍乙加
七十三得为甲丙数者三丙加七十三得为甲乙数
者四其本数各几何 答曰甲七 乙十七 丙廿三
法先以较数列位
历算全书 卷四十 第 38b 页 WYG0794-0893b.png
 先以中行甲正一遍乘右左得数皆如故(只变中行/故两行之)
先以中行甲正一遍乘右左得数皆如故(只变中行/故两行之)(正负俱不变又是一数/为乘法故数亦不变)
次以右行甲负三遍乘中行次以左行甲负四遍乘
中行各得数(左右既省不变故变中行以从/之首位变负下三位俱变正)
次以中右得数相减并 甲同减尽 中乙得正六
同减左得正一馀正五 中丙得正六异并右得负
三共得正九中较数得正二百一十九异并右负七
十三共得正二百九十二
历算全书 卷四十 第 39a 页 WYG0794-0893c.png
 次以中左得数相减并 甲同减尽 中乙得正八
次以中左得数相减并 甲同减尽 中乙得正八异并左得负四共得正十二 中丙得正八同减左
得正一馀七正 中较数得正二百九十二异并左
负七十三共得正三百六十五以上减并之数皆同
名又皆在一行知已变为和数重列之不分正负(依/此)
(显虽同名而或乙正在中丙正在左即不/得变和数也何也左行之正中行之负也)
论曰此较数变为和数也以中右之得数言之中行六
个乙六个丙共多于三个甲者二百一十九右行一
历算全书 卷四十 第 39b 页 WYG0794-0893d.png
 个乙少于三个甲三个丙者七十三于是两相对较
个乙少于三个甲三个丙者七十三于是两相对较则两行之甲皆三个其数本同而中行之乙丙多于
甲二百一十九者因中行之乙多于右行之乙者五
个又有同名之丙六个以益之而中行之甲又非若
右行之甲与三个丙同名是又少三个丙也夫甲股
内少则乙丙股内多合而观之则是中行之乙丙股
内共多五个乙九个丙而右行之乙股内共少此五
个乙九个丙也夫中行之乙丙股内多五个乙九个
历算全书 卷四十 第 40a 页 WYG0794-0894a.png
 丙便多于三个甲者二百一十九右行之乙股内少
丙便多于三个甲者二百一十九右行之乙股内少五个乙九个丙则不惟不多而反少于三个甲者七
十三然则并此多二百一十九少七十三共二百九
十二者正是此五个乙九个丙之共数而非其较数
也故不分正负
又以中左之得数言之中行正数是八个乙八个丙负
数是四个甲而正数多者二百九十二左行正数是
一个丙负数是四个甲四个乙而正数少者七十三
历算全书 卷四十 第 40b 页 WYG0794-0894b.png
 于是两相对勘则两行负数之甲皆四个其数本同
于是两相对勘则两行负数之甲皆四个其数本同惟中行之正数内比左正数多七个丙又加八个乙
而中行之负数又比左负数少四个乙合而观之是
中行之正数比左行共多十二个乙与七个丙而左
行之正数比中行共少十二个乙七个丙也然则中
行正数之多于负数二百九十二者以多此十二个
乙七个丙而左行正数之反少于负数七十三者以
少此十二个乙七个丙也则是并此多二百九十二
历算全书 卷四十 第 41a 页 WYG0794-0894c.png
 少七十三之数共三百六十五者正是此十二个乙
少七十三之数共三百六十五者正是此十二个乙七个丙之共数而非其较数也故亦不分正负
如法以乙数左右互遍乘得数相减(无正负故/有减无并)
乙减尽 丙减馀七十三为法 下位馀一千六百
七十九为实 法除实得二十三为丙数以丙数
乘左行 丙七得一百六十一以减共三百六十
历算全书 卷四十 第 41b 页 WYG0794-0894d.png
 五馀二百○四以左乙十二除之得一十七为乙数
五馀二百○四以左乙十二除之得一十七为乙数又以乙数异加原列右行负七十三共九十内减原
右行丙三该六十九馀二十一以原右行甲三除之
得七为甲数
论曰此同文算指所立叠借互徵设问之一也原法繁
重今改用方程简易如此
此所设问三色方程耳以西术求之已不胜其难况
四色以往乃至多色乎此亦足见方程之不可废而
历算全书 卷四十 第 42a 页 WYG0794-0895a.png
 古人别立一章之诚有实用也
古人别立一章之诚有实用也此三色较变和例也 四色以往至于多色则其变
益多要不出于和较例具后诸卷中兹不详列
历算全书 卷四十 第 42b 页 WYG0794-0895b.png

历算全书卷四十