声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
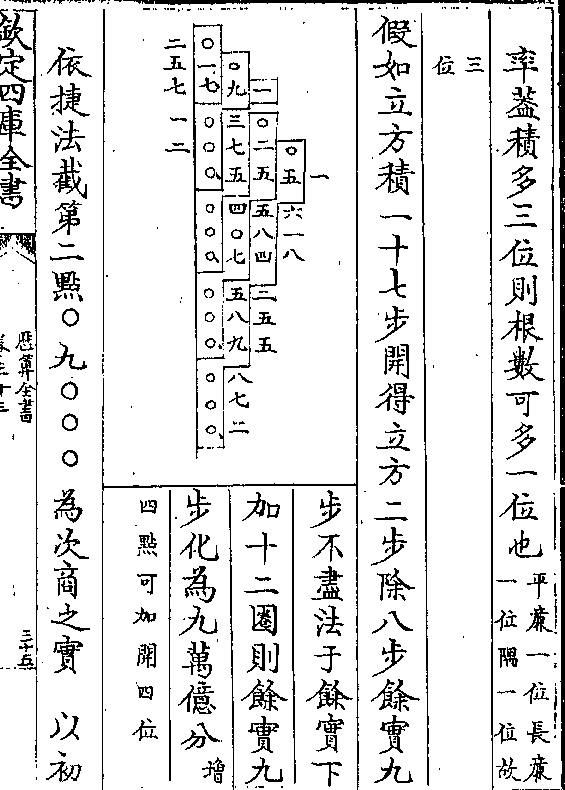
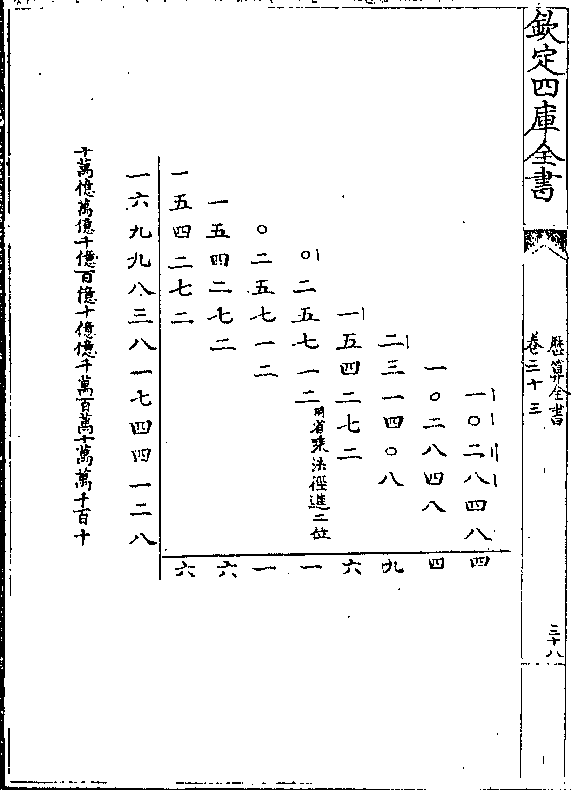
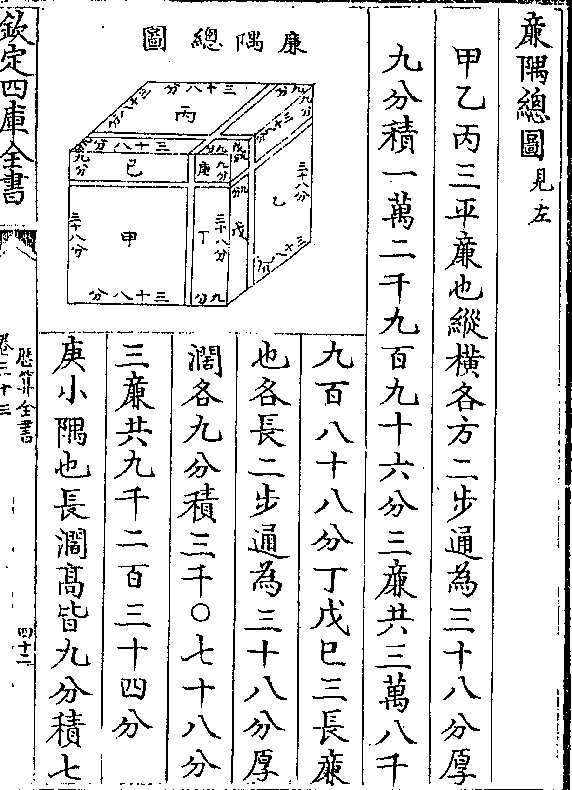
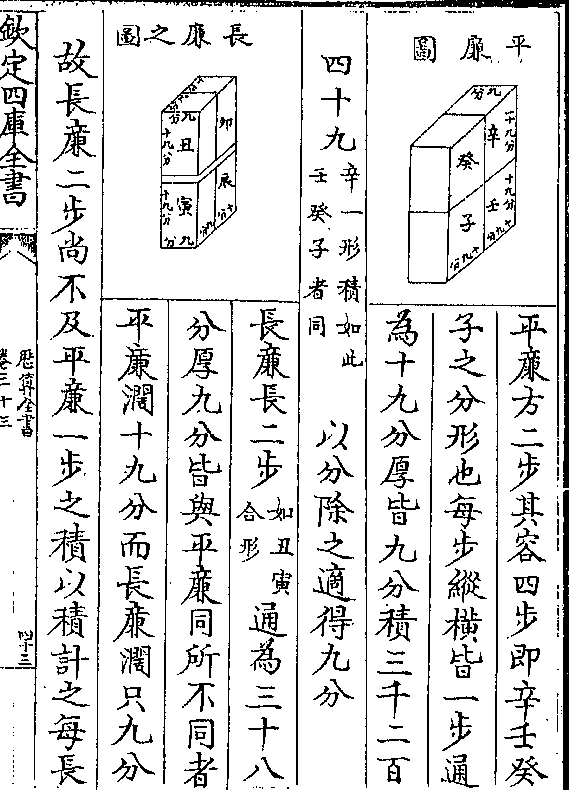
历算全书 卷三十九 第 1a 页 WYG0794-0826a.png
 比例尺式(即度数尺也原名比例规以两尺可/开可合有似作圆之器故亦可云规)
比例尺式(即度数尺也原名比例规以两尺可/开可合有似作圆之器故亦可云规)用薄铜板或厚纸或坚木(黄杨/木等)作两长股如图任长一
尺上下广如长八之一两股等长等广股首上角为枢
历算全书 卷三十九 第 1b 页 WYG0794-0826b.png
 以枢心为心从心出各直线以尺大小定线数今折中
以枢心为心从心出各直线以尺大小定线数今折中作五线两股两面共十线可用十种比例之法线行相
距之地取足书字而止尺首半规馀地以固枢也用时
张翕游移
历算全书 卷三十九 第 2a 页 WYG0794-0826c.png
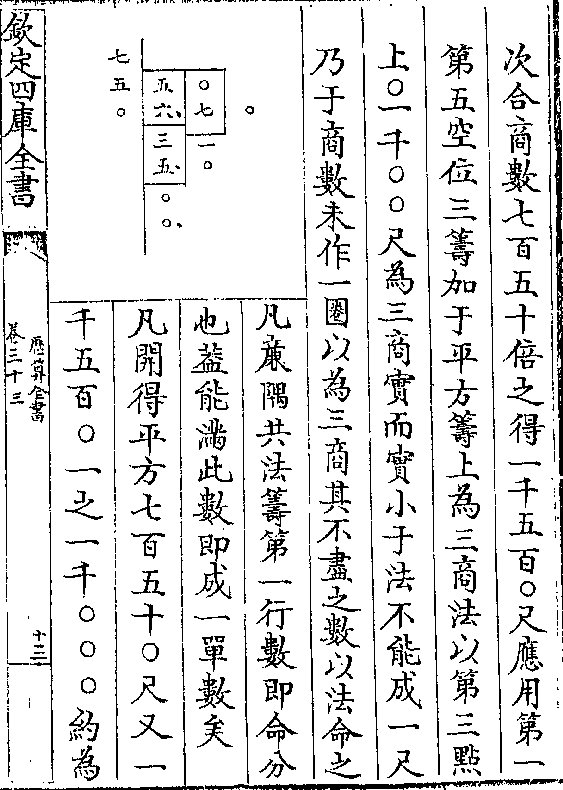 比例尺又式
比例尺又式前式两股相叠此式两股相并股上两用之际以为心
规馀地以安枢其一规面与尺面平而空其中其一剡
历算全书 卷三十九 第 2b 页 WYG0794-0826d.png
 规而入于彼尺之空令密无罅也枢欲其无偏也两尺
规而入于彼尺之空令密无罅也枢欲其无偏也两尺并欲其无罅也枢心为心与两尺之合线欲其中绳也
张尽令两首相就成一直线可作长尺或以两尺横直
相得成一方角可作矩尺
历算全书 卷三十九 第 3a 页 WYG0794-0827a.png
 规式(此本为画圆之器尺算赖之/以取底数盖相须为用者也)
规式(此本为画圆之器尺算赖之/以取底数盖相须为用者也)用铜或铁亦如尺作两股但尺式扁方此可圆也首为
历算全书 卷三十九 第 3b 页 WYG0794-0827b.png
 枢可张可翕末锐以便于尺上取数也当其半腰缀一
枢可张可翕末锐以便于尺上取数也当其半腰缀一铜条横贯之势曲而长如割圆象限之弧与枢相应得
数后用螺钉固之
凡算例假如有言取某数为底线者并以规之两锐于
平分线上量而得之其用底线为得数者并以规取两
尺上弦线相等之距于平分线上量而命之故规之两
锐可当横尺数度衍以横尺比量反不如用规之便利
而得数且真也
历算全书 卷三十九 第 4a 页 WYG0794-0827c.png
 第一平分线
第一平分线此线为诸线之根取数贵多尺大可作一千然过密
又恐其不清也故以二百为率
分法 如设一直线欲作百分先平分之为二又平分
历算全书 卷三十九 第 4b 页 WYG0794-0827d.png
 之为四又于每一分内各五分之则已成二十
之为四又于每一分内各五分之则已成二十分矣于是用更分法取元分四改为五分(如甲/乙丙)
(有丙戊丁三点是元分之四也今/复匀作五分加己庚辛壬四点)则元分与次
分之较(如壬丙/及巳戊)皆元分五之一亦即设线百分
之一分准此为度而周布之即百分以成
解曰元分为设线百分为二十分之一即每一分内
函五分也今壬丙己戊既皆五分之一则甲壬己乙
皆五分之四亦即百分之四也又丙辛庚戊皆三而
历算全书 卷三十九 第 5a 页 WYG0794-0828a.png
 辛丁丁庚皆二也任用一度参差作点互相考订即
辛丁丁庚皆二也任用一度参差作点互相考订即成百分匀度矣(每数至十至百/皆作字记之) 或取元分六复五
分之亦同何则元分一内函五分则元分四共函二
十分故可以五分之若元分六即共函三十分故亦
可五分之其理一也
用法一 凡设一直线任欲作几分假如四分即以规
量设线为度而数两尺之各一百以为弦乃张尺以
就度令设线度为两弦之底置尺(置尺者置不复动/故亦可云定尺下)
历算全书 卷三十九 第 5b 页 WYG0794-0828b.png
 (仿/此)数两尺之各二十五以为弦敛规取二十五两点
(仿/此)数两尺之各二十五以为弦敛规取二十五两点间之底以为度即所求分数(即四分中一分也以此/为度而分其线即成四)
(分/) 若求极微分如一百之一如上以一百为弦设
线为底置尺次以九十九为弦取底比设线其较为
百之一 若欲设线内取零数如七之三即以七十
为弦设线为底置尺次以三十为弦敛规取底即设
线七之三
谨按尺算上两等边三角形分之即两句股也两
历算全书 卷三十九 第 6a 页 WYG0794-0828c.png
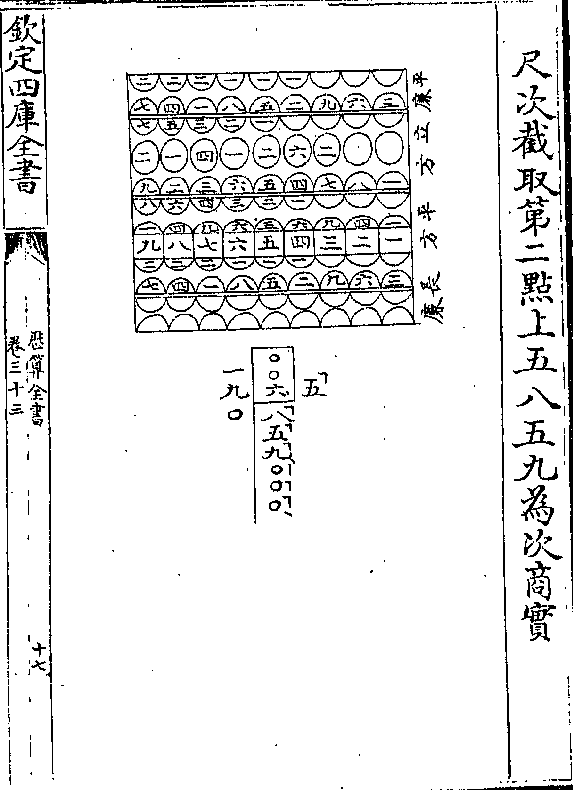 句联为一线而在下直谓之底宜也若两尺上数
句联为一线而在下直谓之底宜也若两尺上数原系斜弦改而称腰于义无取今直正其名曰弦
用法二 凡有线求几倍之以十为弦设线为底置尺
如求七倍以七十为弦取底即元线之七倍若求十
四倍则倍得线或先取十倍更取四倍并之
用法三 有两直线欲定其比例以大线为尺末之数
(尺百即百/千即千)置尺敛规取小线度于尺上进退就其两
弦等数如大线为一百小线为三十七即两线之比
历算全书 卷三十九 第 6b 页 WYG0794-0828d.png
 例若一百与三十七可约者约之(约法以两大数约/为两小数其比例)
例若一百与三十七可约者约之(约法以两大数约/为两小数其比例)(不异如一百与三/十约为十与三)
用法四 有两数求相乘假如以七乘十三先以十点
为弦取十三点为底置尺次检七十之等弦取其底
得九十一为所求乘数(若以十为弦七为底置尺而/检一百三十点之底得数亦)
(同/)
(论曰乘法与倍法相通故以七乘十三是以十三之/数七倍之是七个十三也以十三乘七是以七数十)
(三倍之是十三个/七也故得数并同)
历算全书 卷三十九 第 7a 页 WYG0794-0829a.png
 用法五 有两数求相除假如有数九十一七人分之
用法五 有两数求相除假如有数九十一七人分之即以本线七十为弦取九十一为底置尺次检十点
之弦取底必得十三为所求
又法以九十一为弦用规取七十为底置尺敛规取
一十为底进退求其等弦亦得十三如所求
(论曰算家最重法实今当以七人为法所分九十一/数为实乃前法以法数七为弦实数九十一为底又)
(法反之而所得并同何也曰异乘同除以先有之两/率为比例算今有之两率虽曰三率实四率也徵之)
(于尺则大弦与大底小弦与小底两两相比明明四/率较若列眉故先有之两率当弦则今所求者在底)
历算全书 卷三十九 第 7b 页 WYG0794-0829b.png
 (是以弦之比例例底也若先有之率当底则今所求/者在弦是以底之例例弦也但四率中原缺一率比)
(是以弦之比例例底也若先有之率当底则今所求/者在弦是以底之例例弦也但四率中原缺一率比)(而得之固不必先审/法实殊为简易矣)
(然则乘除一法乎曰凡四率中所缺之一率求而得/之谓之得数乘则先缺者必大数也故得亦大数除)
(则先缺者必小数也故得亦小数所不同者此耳是/故乘除皆有四率得尺算而其理愈明亦诸家所未)
(发/也)
假如有银九十六两四人分之法以人数取四十分
为底置银数九十六两为弦定尺敛规取一十分为
底进退求其等弦得二十四两为每人得数
历算全书 卷三十九 第 8a 页 WYG0794-0829c.png
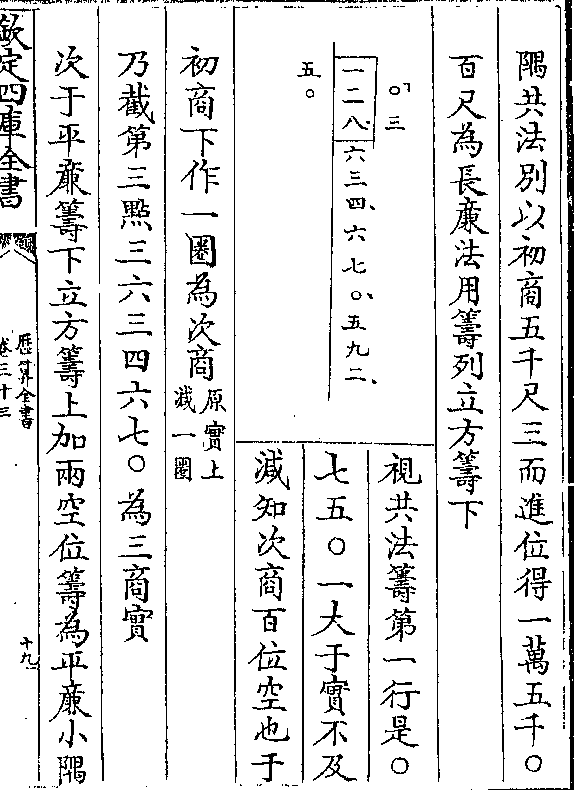 又法取银数九十六两为底置一百分为弦定尺敛
又法取银数九十六两为底置一百分为弦定尺敛规于二十五分等弦取其底亦得二十四两为每人
数
又如有数一百二十三欲折取三分之一法以规取
三十分为底置一百二十三等数为两弦定尺敛规
取一十数为底进退求其等数为弦必得四十一命
为三分之一如所求
用法六 凡所求数大尺所不能具则退位取之
历算全书 卷三十九 第 8b 页 WYG0794-0829d.png
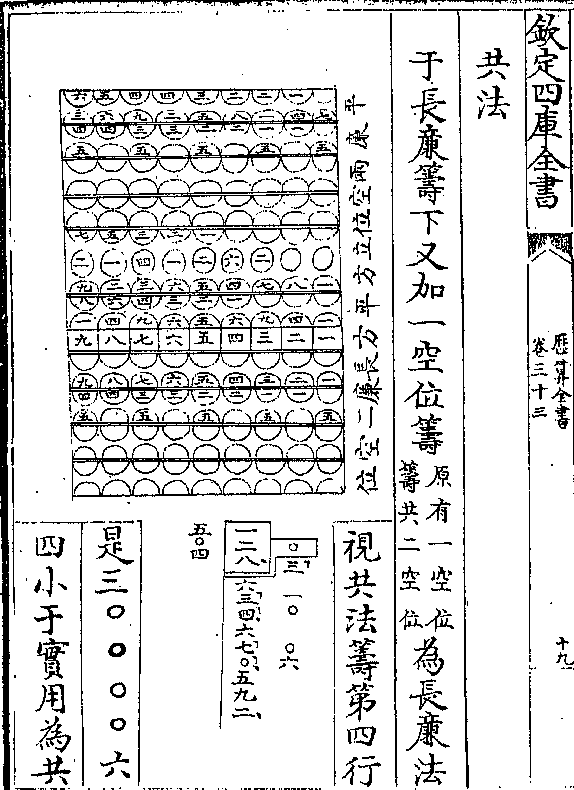 假如有数一百二十欲加五倍即退一位取一十二
假如有数一百二十欲加五倍即退一位取一十二为底以尺之一十点为两弦定尺取两弦五十点之
底(即五/倍)得六十进一位命所得为六百(以一十二当/一百二十是)
(一而当十故进位命之也凡/用尺算须得此通融之法)
又法以规取一十数为底于尺之一十二点为两弦
(一十二以当一百二十是一当/十也或二十四亦可为一当五)定尺展规取五十数
(以当/五倍)为底进退求其等数之弦必得六十进位成六
百
历算全书 卷三十九 第 9a 页 WYG0794-0830a.png
 假如有银十三两每两换钱一千二百文法退二位
假如有银十三两每两换钱一千二百文法退二位以规取十二分(当一千二百以尺/上一数当一百)为底置一十点(即/每)
(两之/位)为弦定尺然后寻一百三十点(即十三/两之位)为弦展
规取其底得一百五十六分进二位命之得共钱一
十五千六百
又如有银四两每两换钱九百六十文法作两次乘
先乘六十取六数为底置一十点为弦定尺展规取
四十点之底得二十四次乘九百取九数为底置一
历算全书 卷三十九 第 9b 页 WYG0794-0830b.png
 十点为弦定尺展规取四十点之底得三十六进一
十点为弦定尺展规取四十点之底得三十六进一位并之得三八四末增一○为进位得三千八百四
十文
(三二四/ 六) 因每两是九百六十故末位增○
(三八四○/千百十文)
假如有数一百二十欲折取三分之一法以规取六
十(折半/法也)为底置九十分为弦定尺然后寻两弦之三
十分点(即三/之一)取其底于本线比之必二十命所得为
历算全书 卷三十九 第 10a 页 WYG0794-0830c.png
 四十(加倍法也先折/半故得数加倍)凡所用数在一十点以内近心
四十(加倍法也先折/半故得数加倍)凡所用数在一十点以内近心难用则进位取之如前条所设宜用六数九数为底
其点近心取数难清即进位作六十取数用之是进
一位也但先进一位者得数后即退一位命其数此
可于前假如中详之(用尺时有退位得数后进位命/其数用尺时有进位得数后退)
(位命其数其理相/通故不另立假如)或先进二位者得数亦退二位或
先加倍者得数折半并同一法
用法七 凡四率法有中两率同数者谓
历算全书 卷三十九 第 10b 页 WYG0794-0830d.png
 之连比例假如有大数(三十/六)小
之连比例假如有大数(三十/六)小数(二十/四)再求一小数与此两数
为连比例法以大数为弦(如辛/甲)
小数为底(如辛/巳)定尺再以辛巳
底为弦(如甲/丁)而取其底(如丁/戊)其
数必(十/六)则三十六与念四之比
例若念四与十六也(其比例为/三分损一)若先有小数(十/六)大数
(二十/四)而求连比例之大数则以小数为底(如丁/戊)大数
历算全书 卷三十九 第 11a 页 WYG0794-0831a.png
 为弦(如丁/甲)定尺再以丁甲弦为底(如辛/巳)取其弦(如辛/甲)
为弦(如丁/甲)定尺再以丁甲弦为底(如辛/巳)取其弦(如辛/甲)其数必三十六则十六与念四若念四与三十六也
(其比例为/三分增一)他皆仿此(原书有断比例法今按断比例/即古法之异乘同除西法谓之)
(三率前各条中用尺取数皆/异乘同除之法故不更立例)
用法八 凡句股形有句有股有弦共
历算全书 卷三十九 第 11b 页 WYG0794-0831b.png
 三件先有两件而求其不知
三件先有两件而求其不知之一件法以尺作正角取之
假如有句(八/尺)股(十五/尺)欲知其
弦法以规量取八十点为底
一端指尺上之六十四点一
端指又一尺之四十八点以
定尺则尺成正角乃于尺上
取八十点为句又于一尺上
历算全书 卷三十九 第 12a 页 WYG0794-0831c.png
 取一百五十点为股张规以就所识句股之两点必
取一百五十点为股张规以就所识句股之两点必一百七十退一位得弦十七尺如所求(取句股数时/原进一位故)
(所得弦数退一/位命之说见前)
若先有弦(十七/尺)股(十五/尺)求其句则以规取一百七十点
为句股之弦乃以规端指一百五十点以馀一端又于
一尺上寻所指之点必八十也如上退位得句八尺
或先有弦(十七/尺)句(八/尺)求其股亦以规取(一百/七十)而一端指
(八/十)寻又一端之所指必得(一百/五十)命(一十/五尺)为股如所求
历算全书 卷三十九 第 12b 页 WYG0794-0831d.png
 凡杂三角形内无正角不可以句股
凡杂三角形内无正角不可以句股算法先作角假如先有一角及角
旁之两边求馀一边法于平分线
(任用一笾/如甲乙)取数为底分圆线(六/十)度为
两弦定尺以规取所设角之底(为平分线上任用/甲乙边等度之底)定
尺则尺间角如所设(如乙/角)乃于两尺上依所设取角
旁两边之数于两尺各作识(如甲乙/丙乙)遂用规取斜距
之底(如甲/丙)即得馀一边如所求
历算全书 卷三十九 第 13a 页 WYG0794-0832a.png
 又法 假如乙甲丙三角
又法 假如乙甲丙三角形有甲角(五十三度/○七分)甲乙
边(五十/六尺)甲丙边(七十/五尺)而求
乙丙边法以规取一百分
为分圆线上六十度之底敛规取五十三度强之底
移于平分线上作百分之底定尺乃于尺上取五十
六点(如甲/乙)又一尺上取七十五点(如甲/丙)乃以规取两
点斜距之底于尺上较之即得六十一尺(如乙/丙)命为
历算全书 卷三十九 第 13b 页 WYG0794-0832b.png
 所求边(分圆线/见后)
所求边(分圆线/见后)用法十 有小图欲改作大几倍之图用前倍法假如
有小图阔一尺二寸今欲展作五倍即取十二为十
点之底定尺展规取五十点之底必得六十命为六
尺如所求
用法十一 平圆形周径相求法于平分线上作两识
以一百八十八半弱上为周六十为径各书其号假
如有径(七十/一)求周法以规取七十一加于径点为底
历算全书 卷三十九 第 14a 页 WYG0794-0832c.png
 定尺展规取周点之底即得周二百二十三如所求
定尺展规取周点之底即得周二百二十三如所求(以周求径/反此用之)
用法十二 求理分中末线法于线上定三点于九十
六定全分五十九又三之一
为大分三十六又三之二为
小分假如有一直线(一百四/十四)
欲分中末线即以设线加于
全分点为底取其大小分点之底即得(八十/九强)为大分(五/十)
历算全书 卷三十九 第 14b 页 WYG0794-0832d.png
 (五/弱)为小分
(五/弱)为小分(按平线上既作周径之号若又作此则太繁不如另/作一线其上可寄五金线也 又按原书全分七十)
(二大分四十二又三之一小分二/十七又三之二大有讹错今改定)
以上十二用法姑举其概其实平分线之用不止于
是善用者自知之耳
历算全书 卷三十九 第 15a 页 WYG0794-0833a.png
 第二平方线(旧名分面线凡平方形有积有边积谓之也/幂亦谓之面边线亦谓之根即开平方法)
第二平方线(旧名分面线凡平方形有积有边积谓之也/幂亦谓之面边线亦谓之根即开平方法)原为一百不平分今按若尺小欲其清则但为五十
分亦可假如有积六千四百则以平分线之二十自
乘得四百于积为十六倍之一若置二十分于一点
为底求十六点之底则得方根八十或置于二点为
历算全书 卷三十九 第 15b 页 WYG0794-0833b.png
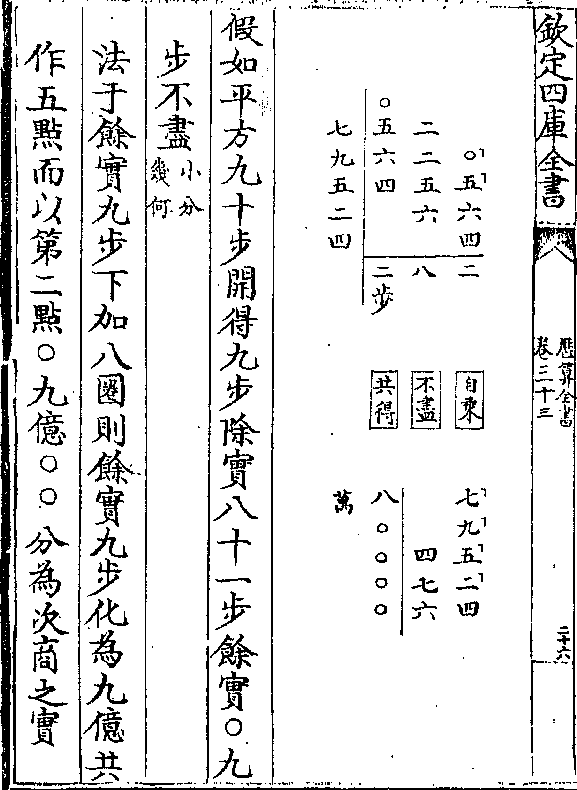 底则求三十二点之底或置于三点为底则求四十
底则求三十二点之底或置于三点为底则求四十八点之底皆同
分法有二 以算一以量
以算分
算法者自枢心(甲/)任定一度命为十分(如甲/乙)即平方
历算全书 卷三十九 第 16a 页 WYG0794-0833c.png
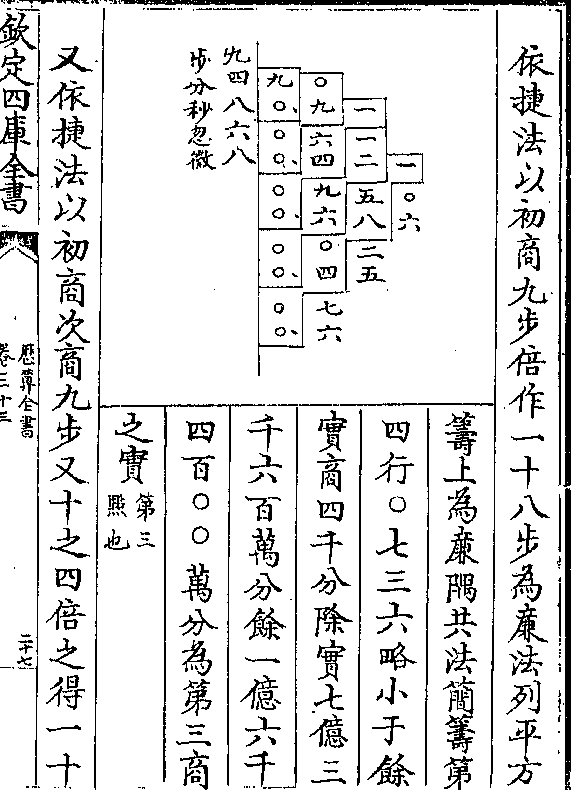 积一百分之根今求加倍平方二百分之根为十四又
积一百分之根今求加倍平方二百分之根为十四又念九之四即于甲乙线上加四分强(如/丙)命甲丙为倍积
之根求三倍则开平方三百分之根得十七又三十五
之十一即又于甲乙线上加十分半弱(如/丁)即甲丁为三
倍积之根求四倍则平方四百之根二十即以甲乙倍
之得甲戊为四倍积之根五六七以上并同(按用方根/表甚简易)
以量分
以任取之甲乙度作正方形(如丙/乙甲)乃于乙甲横边引长之
历算全书 卷三十九 第 16b 页 WYG0794-0833d.png
 以当积数丙乙直边引长之作垂线以当根数如求倍
以当积数丙乙直边引长之作垂线以当根数如求倍积之根即于横
线上截丁乙为
甲乙之倍次平
分甲丁于戊戊为心甲为界作半圈截垂线于巳即己
乙为二百分之边求三倍则乙丁三倍于甲乙四倍以上并同
又捷法 如前作句股形法定两尺间成正方角如甲
乃任于尺上取甲乙命为一点而又于一尺取甲丙度
历算全书 卷三十九 第 17a 页 WYG0794-0834a.png
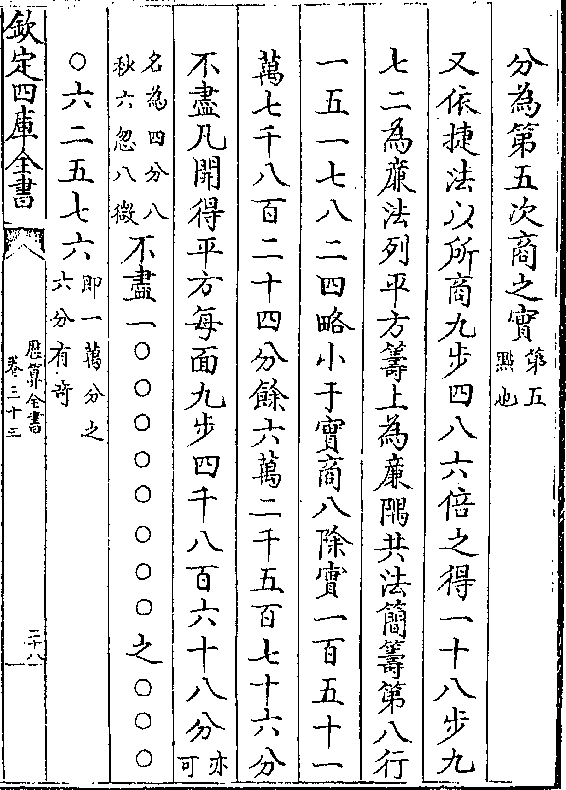 与甲乙相等即皆为一百之根次取乙丙底加于甲乙
与甲乙相等即皆为一百之根次取乙丙底加于甲乙尺上为二百之根甲丁又自丁至丙作
斜弦以加于甲乙尺上为三百之根甲
戊又自戊至丙作弦以加于甲乙尺上
为四百之根甲已如此递加即得各方
之根其加法俱从尺心起(如求得丙乙即以丙加甲/乙加丁成甲丁他皆仿此)
试法 甲乙为一正方形之边倍其度即四倍方积之边
否即不合三倍得九倍方积之边四倍得十六五倍得
历算全书 卷三十九 第 17b 页 WYG0794-0834b.png
 二十五又取三倍之边倍之即十二倍之边(四其/三也)再加
二十五又取三倍之边倍之即十二倍之边(四其/三也)再加一倍得二十七倍之边(九其/三也)再加倍得四十八倍之边
(十六其/三也)再加倍得七十五倍之边(二十五/其三也)若以五倍之边
倍之得二十倍之边(四其/五也)再加倍得四十五倍之边
(九其/五也)再加倍得八十倍之边(十六其五也如凡言倍其度/者线上度也 正方四百分)
(之边二十分甲乙正方一百分之边十分其大为一倍也/言几倍方积者积数也如边二十者积四百即尺上所书)
用法一 有平方积求其边(即开/平方)法先其设数与某数能
相为比例得几倍如法求之假如有平方积一千二百
历算全书 卷三十九 第 18a 页 WYG0794-0834c.png
 二十五尺欲求其根以约分法求得
二十五尺欲求其根以约分法求得二十五为设数四十九之一即以规
于平分线取五点为平方线上一点
之底定尺展规于四十九点取其底
即得一边三十五尺为平方根(积二十五方根五加四/十九倍为积一千二百)
(二十五方/根三十五) 或用四十九为设数(一千二百/二十五尺)二十五之
一即以规取七点为平方一点之底而取平方二十五
点之底亦得方根三十五如所求(积四十九方根七加/二十五倍为积一千)
历算全书 卷三十九 第 18b 页 WYG0794-0834d.png
 (二百二十五则其方根三十五又法若无比例可求/者但以十分为一点之底定尺有假如在用法七)
(二百二十五则其方根三十五又法若无比例可求/者但以十分为一点之底定尺有假如在用法七)用法二 凡同类之平面形可并为一大形(或方或圆/或三角多)
(边等形但形相/似即为同类)假如有平面正方四形求作一大正
方形与之等积其第一形之幂积为二第二形之积
为三第三形之积四有半第四形之积六又四之三
法先并其积得(十六叉/四之一)乃任取第一小形之边为
底二点为弦定尺(若用第二形之边为底/定尺即用三点为弦)而于十六点
又四之一取其底为大形边其面积与四形总数等
历算全书 卷三十九 第 19a 页 WYG0794-0835a.png
 若但有同类之形而不知面积亦
若但有同类之形而不知面积亦不知边数则先求其积之比例如
甲乙丙丁方形四法以小形甲之
边为底平方线第一点为弦定尺
次以乙形边为底进退求等数得
第二点外又五分之一即命其积
为二又五之一(此与小形一之/比例不拘丈尺)次
丙形边为底求得(二又四/之三)丁形边
历算全书 卷三十九 第 19b 页 WYG0794-0835b.png
 得(四又六/之五)并诸数及甲形一得(十/又)
得(四又六/之五)并诸数及甲形一得(十/又)(六十分之/四十七)约为(五之/四弱)向元定尺上
寻十点外十一点内之距取其五
之四为等数之两弦(即十/一弱)用其底
为大方形边其面积与四形并数
等
(此加形法也圆面及三角等面凡/相似之形并可相并其法同上)
历算全书 卷三十九 第 20a 页 WYG0794-0835c.png
 用法三 平面形求作一同类之他形大于设形几倍
用法三 平面形求作一同类之他形大于设形几倍(以设形之边为/一点之底定尺) 假如有正方形面
积四百其边二十今求别作一方形
其容积大九倍法以设形边(二/十)为平
方线一点之底定尺而取平方九点等数之底得(六/十)
如所求(边六十其方积三千六百/以比设形积为大九倍)
用法四 平面形求别作一同类之形为设形几分之
几(以设形之边为命分/定尺而于得分取数) 假如有平方形积三千六
历算全书 卷三十九 第 20b 页 WYG0794-0835d.png
 百其边六十今求作小形为设形九之
百其边六十今求作小形为设形九之四法以设形边(六/十)为平方第九点之底
定尺而取第四点之底得(四/十)如所求(边/四)
(十其积一千六百以比设形积为/九之四也九为命分四为得分)
此减积法也圆面三角等俱同一法
用法五 有两数求中比例(即三率连比/例之第二率)
假如有二与八两数求其中比例法先以大数为平
方线八点之底而取二点之底得四如所求
历算全书 卷三十九 第 21a 页 WYG0794-0836a.png
 二与四如四与八皆加倍之比例故四为
二与四如四与八皆加倍之比例故四为二与八之中率
用法六 有长方形求作正方形 假如长方形横二
尺直八尺如上图求得中比例之数为四尺以作正
方形之边则其面积与直形等
直八尺横二尺 其积一十六尺
方形各边并四尺其积亦十六尺
用法七 有设积求其方根而不能与他数为比例则
历算全书 卷三十九 第 21b 页 WYG0794-0836b.png
 以一十数为比例
以一十数为比例假如平积二百五十五用十数比之为二十五倍半
即取十数为平方线一点之底而取二十五点半之
底得十六弱为方根(十六自乘积二百五十六今只/欠一小数故命之为十六弱)
历算全书 卷三十九 第 22a 页 WYG0794-0836c.png
 第三更面线
第三更面线历算全书 卷三十九 第 22b 页 WYG0794-0836d.png

(凡平面形方必中矩圆必中规其馀各形并/等边等角故皆为有法之形而可以相求)
分法
历算全书 卷三十九 第 23a 页 WYG0794-0837a.png
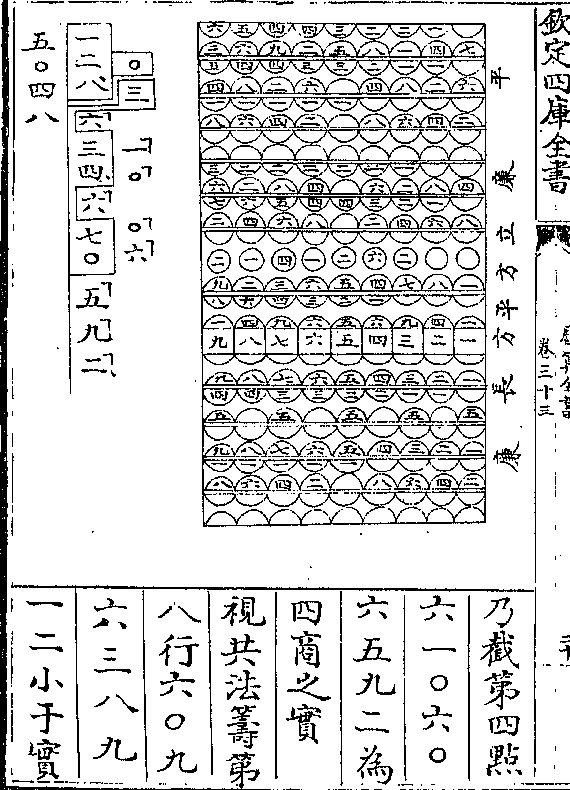
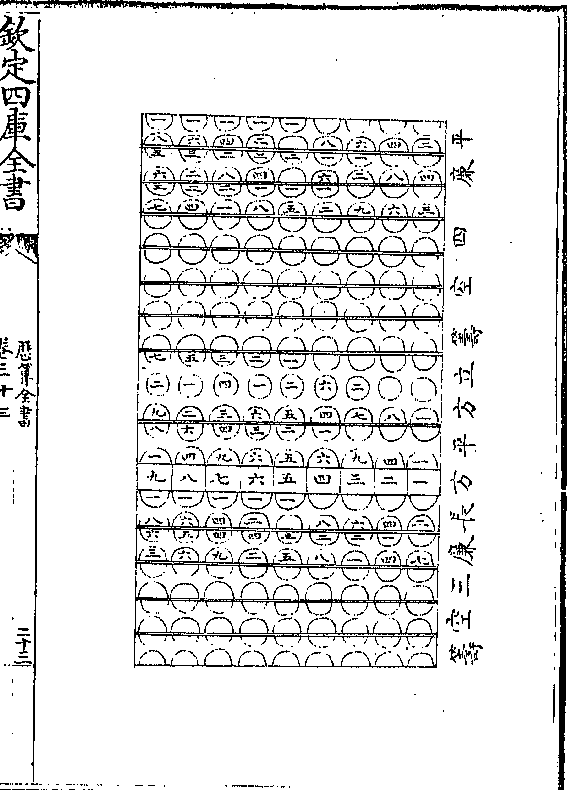
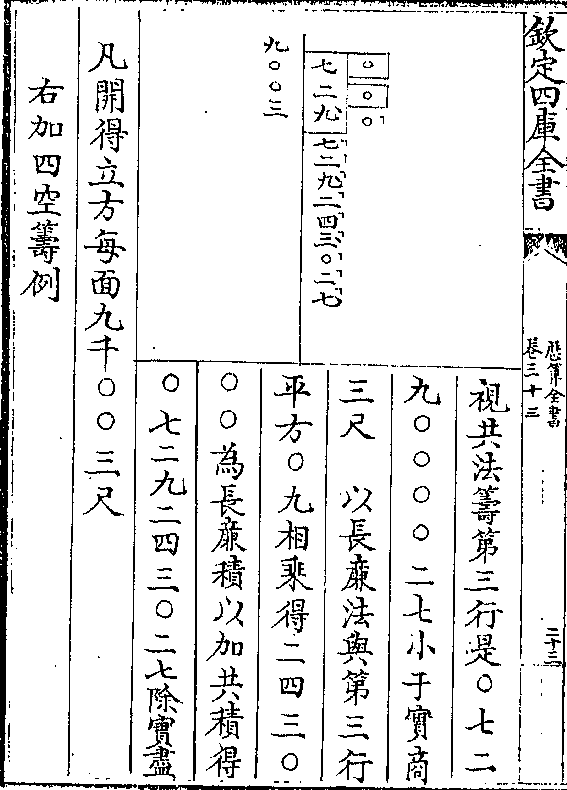
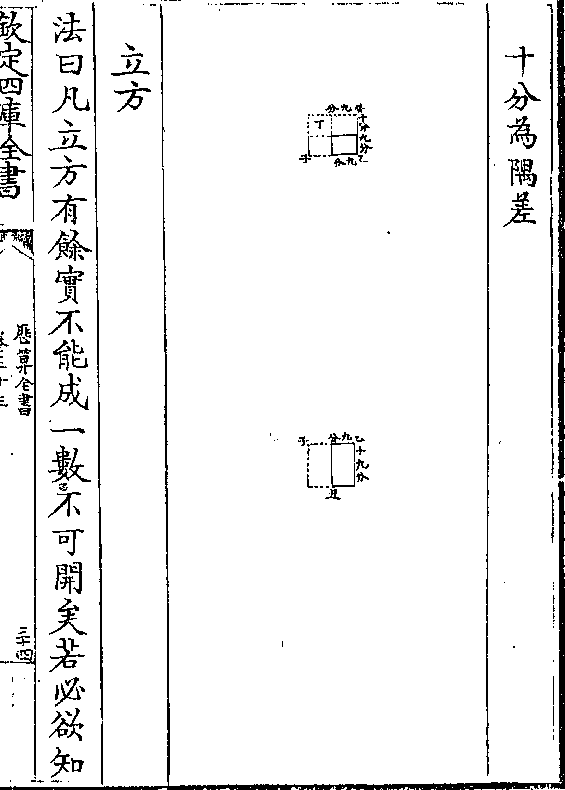 置公积四三二九六四以开方得正方形之根六五
置公积四三二九六四以开方得正方形之根六五八三边形之根一千五边形之根五○二六边形之
根四○八七边形之根三四五八边形之根二九九
九边形之根二六○十边形之根二三七十一边形
之根二一四十二边形之根一九七圜径七四二以本
线为千平分而取各类之数从心至末取各数加本类之号
用法一 有平面积求各类之根(凡三角及多边各平/面形其边既等故并)
(以形之一边为根/圆形则以径为根)法先以设数于平方线上求其正
历算全书 卷三十九 第 23b 页 WYG0794-0837b.png
 方根以此为度于更面线之正方号为底定尺次于
方根以此为度于更面线之正方号为底定尺次于各形之号取底即得所求各形边
假如有平面三等边形积二千七百七十一寸欲求
其边法以设积于平方线上如法开其平方根(依前/卷用)
(法七以设数为十数之二百七十七倍强各降一位/命为一数之二十七倍又十之七强乃以一数为平)
(方一点之底定尺而于其二十七点十之七强/取底数得五寸二六进一位作五尺二寸半强)以所
得方根为更面线正方号之底定尺而取三等边号
之底得八尺为三等边形根如所求
历算全书 卷三十九 第 24a 页 WYG0794-0837c.png
 用法二 有平面形不同类欲相并为一大形法先以
用法二 有平面形不同类欲相并为一大形法先以各形边为更面线上各本号之底定尺而取其正方
号之底作线为所变正方形之边次以所变方边于
分面线上求其积数而并之为总积
假如有甲(三/角)乙(五/边)丙三形欲相并先以甲边为三角
号之底定尺而取其正方号之底作线于甲形内(如/此)
(则甲形已变/为正方下同)书其数曰十次以乙边为五边号之底
如前取其平方底向平方线求之得二十一半(其法/以甲)
历算全书 卷三十九 第 24b 页 WYG0794-0837d.png
 (边为平方十点之底定尺而以乙/所变方边进退求等度之弦命之)即
(边为平方十点之底定尺而以乙/所变方边进退求等度之弦命之)即于乙形作方底线书之次以丙圆径
为平圆号之底如前求得十六弱并
三数得四十七半弱为总积(此因三/形之边)
(无数姑以小形命十数定尺而所/得各方积并小形十数之比例)
若三形内先知一形之面积即用其
所变方边定尺则所得皆真数如上
三形但知丙形之积十六(或十六尺/或十六寸)
历算全书 卷三十九 第 25a 页 WYG0794-0838a.png
 (等/)如法以丙形边变方边于平方线十六点为底定
(等/)如法以丙形边变方边于平方线十六点为底定尺馀如上法求之亦必得甲为十数乙为二十一半
总积四十七半但前条所得是比例之数比例虽同
而尺有大小故以此所得为真数也
末以总数于原定尺上寻平方线四十七点半处取
其底度为平方边则此大平方形与三形面积等
若欲以总积为五边形则以所得大平方边为更面
线正方号之底定尺而于五边形之号取其底即所
历算全书 卷三十九 第 25b 页 WYG0794-0838b.png
 求五边形之一边(若欲作三角或/圆形并同一法)
求五边形之一边(若欲作三角或/圆形并同一法)用法三 有平面形欲变为他形如上法以本形边为
本号之底定尺而取所求他形号之底
假如有三角形欲改平圆则以所设三角形之边加
于本尺三角形之号为底定尺而取平圆号之底求
其数命为平圆径所作平圆必与所设三角形同积
用法四 有两平面形不同类欲定其相较之比例如
前法各以所设形变为平方
历算全书 卷三十九 第 26a 页 WYG0794-0838c.png
 假如有六边形有圆形相较即如法各变为平方求
假如有六边形有圆形相较即如法各变为平方求其数平圆数二十六边数三十六即平员为六边形
三十六之二十以二十减三十六得十六为两形之
较
历算全书 卷三十九 第 27a 页 WYG0794-0839a.png
 第四立方线(旧名分体线无凡平方形如棋局其四边/横直相等而 高与厚之数立方则如方)
第四立方线(旧名分体线无凡平方形如棋局其四边/横直相等而 高与厚之数立方则如方)(匮有横有直又有高而皆相等平方之积曰平积亦/曰面积亦曰幂积如棋局中之细分方罫立方之积)
(曰体积亦曰立积并/如骰子之积累成方)
(旧图误以尺枢心甲书于一点上今改正甲乙一亦/即一十则其内细数亦不平分旧图作十平分亦误)
历算全书 卷三十九 第 27b 页 WYG0794-0839b.png
 (今删/去)
(今删/去)分法有二一以算一以量
以算分 从尺心甲任定一点为乙则甲乙之度当
十分边之积为一千(十分自乘之再乘之即成一千/假如立方一尺其积必千寸)纪
其号曰一次加一倍为立积二千开立方求其根得
十二又三之一即于甲乙上加二又三之一为甲丙
纪其号曰二再加一倍立积三千开立方得数纪三
以上并同
历算全书 卷三十九 第 28a 页 WYG0794-0839c.png
 捷法 取甲乙边四分之一加甲乙成甲丙即倍体
捷法 取甲乙边四分之一加甲乙成甲丙即倍体边又取甲丙七分之一加甲丙成甲丁即三倍体边
又取甲丁十之一加甲丁成甲戊即四倍体边再加
如图
(右加法与开立方数所差不远然尾数不清难为/定率姑存其意)
又捷法用立方表
历算全书 卷三十九 第 28b 页 WYG0794-0839d.png
 以量分 如后图作四率连比例而求其第二盖元
以量分 如后图作四率连比例而求其第二盖元体之边与倍体之边为三加之比例也(假如边为一/倍之则二若)
(求平方面则复倍之为四是再加之比例也今求立/方体必再倍之为八故曰三加 三加者即四率)
(连比/例也)
几何法曰第二线上之体与第一线上之体若四率
连比例之第四与第一(第一为元边线第二为加倍/之边线第三以边线自乘为)
(加倍线上之面第四以边线再自乘为加倍线上之/体今开立方是以体积求边线即是以第四率求第)
(二率/也)
历算全书 卷三十九 第 29a 页 WYG0794-0840a.png
 假如有立方体积又有加倍之积
假如有立方体积又有加倍之积法以两积变为线(元积如辛庚/倍积如辛巳)作
壬巳辛庚长方形次于壬巳壬庚
两各引长之以形心(戊/)为心作圈
分截引长线于子于午作子午直
线切辛角(如不切辛角必渐试/之令正相切乃止)即辛庚(一/率)午庚(二/率)子
巳(三/率)己辛(四/率)为四率连比例末用第二率午庚为倍
积之一边其体倍大于元积
历算全书 卷三十九 第 29b 页 WYG0794-0840b.png
 若辛巳为辛庚之三倍四倍则午庚边上体积亦大
若辛巳为辛庚之三倍四倍则午庚边上体积亦大于元积三倍四倍(以上/仿此)
解四率连比例之理
试于辛点作卯辛为子午之垂线次
用子壬度从午作卯午直线截卯辛
线于卯又从卯作直线至子又从辛
点引辛庚边至辰引辛巳边至丑成
各句股形皆相似而比例等
历算全书 卷三十九 第 30a 页 WYG0794-0840c.png
 (卯辛午句股形从辛正角作垂线至/丑分为两句股形则形相似而比例)
(卯辛午句股形从辛正角作垂线至/丑分为两句股形则形相似而比例)(等为午丑辛形以午丑为句丑辛为/股辛丑卯形以丑辛为句丑卯为股)
(则午丑与丑辛若丑辛与丑卯为连/比例也 卯辛子句股形从辛正角)
(作垂线至辰分两句股形亦形相似/而比例等 卯辰辛形卯辰为句辰)
(辛为股辛辰子形辰辛为句辰子为/股则卯辰与辰辛若辰辛与辰子)
(亦连比例也而辰辛即丑卯故合之/成四率连比例)
一率 辛庚 即午丑
二率 午庚 即丑辛 亦即辰卯
历算全书 卷三十九 第 30b 页 WYG0794-0840d.png
 三率 子巳 即辛辰 亦即丑卯
三率 子巳 即辛辰 亦即丑卯四率 己辛 即辰子
试法 元体边倍之即八倍体积之边若三之即二十
七倍之边四之即六十四倍体积之边五之即一百
二十五倍体积之边
又取二倍边倍之得十六(八其/二也)再倍之得一二八倍
体积之边(六十四/其二也)
三加比例表(平方立方同理即连比例/)
历算全书 卷三十九 第 31a 页 WYG0794-0841a.png
 第一率 第二率 第三率 第四率
第一率 第二率 第三率 第四率按第一率为元数第二率为线即根数也第三率为
面平方幂积也第四率为体立方积也开平方开立
历算全书 卷三十九 第 31b 页 WYG0794-0841b.png
 方并以积求根故所用者皆二率也(比例规解乃云/本线上量体任)
方并以积求根故所用者皆二率也(比例规解乃云/本线上量体任)(用其边其根其面其对角线其/轴皆可其说殊不可晓今删去)
用法一 有立积求其根(即开立方/)
假如有立方积四万法先求其与一千之比例则四
万与一千若四十与一即取十数为分体线上一点
之底定尺而取四十点之底得三十四强即立方之
根(说见/平方)
用法二 有两数求其双中率(谓有连比例之第一与/第四而求其第二第三)
历算全书 卷三十九 第 32a 页 WYG0794-0841c.png
 法以小数为一率用作本线一点之底而取大数之
法以小数为一率用作本线一点之底而取大数之底为二率既有二率可求三率
假如有两数为三与二十四欲求其双中率法约两
数之比例为一与八即以小数三为本线一点之底
定尺而于八点取底得六为第二率末以二率四率
依法求中率得十二为三率
一率三 二率六 三率十二 四率二十四
用法三 设一体求作同类之体大于设体为几倍(此/乘)
历算全书 卷三十九 第 32b 页 WYG0794-0841d.png
 (体之/法)
(体之/法)假如设立方体八千其边二十求作加八倍之体为
六万四千问边若干法以设体根二十为本线一点
之底定尺而取八点之底得四十即大体边如所求
用法四 有同类之体欲并为一法累计其积而并之
为总积求其根即得
假如有三立方体甲容一十乙容十三
又四之三丙容十七又四之一并得四
历算全书 卷三十九 第 33a 页 WYG0794-0842a.png
 十一即以甲容一十为本线一点之底
十一即以甲容一十为本线一点之底定尺而取四十一点之底为总体边如
所求 若设体无积数则以小体命为
一十而求其比例然后并之
用法五 有两同类之体求其比例与其较(此分体/之法)
假如甲丙两立方体欲求其较而不知容积之数法
以甲小体边为一点之底定尺而以丙边为底进退
历算全书 卷三十九 第 33b 页 WYG0794-0842b.png
 求其等数如所得为九即其比例为九与一以一减
求其等数如所得为九即其比例为九与一以一减九其较八即于八点取底为较形之边
用法六 有立方体欲别作一体为其几分之几
假如有立方体欲另作一体为其八之五则以设体
边为本线八点之底定尺而于五点取底为边作立
方体即其容为设体八之五
历算全书 卷三十九 第 34a 页 WYG0794-0842c.png
 第五更体线(旧名变体线/)
第五更体线(旧名变体线/)体之有法者曰立方曰立圆曰四等面曰八等面曰
十二等面曰二十等面凡六种外此皆不能为有法
之体
历算全书 卷三十九 第 34b 页 WYG0794-0842d.png
 六等面体各面皆正方即立方也有
六等面体各面皆正方即立方也有十二棱八角测量全义曰设边一百
求其容为一○○○○○○
浑圆体亦曰球体即立圆也几何补
编曰同径之立方积与立圆积若六
○○○○○○与三一四一五九二
历算全书 卷三十九 第 35a 页 WYG0794-0843a.png
 设径一百求其容为五二三五九八
设径一百求其容为五二三五九八此三角平面形相合而成有六棱四
角测量全义曰设边一百求其容为
一一七四七二半
历算全书 卷三十九 第 35b 页 WYG0794-0843b.png
 此体各面亦皆三等边形有十二棱
此体各面亦皆三等边形有十二棱六角测量全义曰设边一百求其容
为四七一四二五有奇
历算全书 卷三十九 第 36a 页 WYG0794-0843c.png
 此体各面皆五等边有三十棱二十
此体各面皆五等边有三十棱二十角测量全义曰设边一百求其容为
七六八六三八九
历算全书 卷三十九 第 36b 页 WYG0794-0843d.png
 此体各面亦皆三等边有三十棱十
此体各面亦皆三等边有三十棱十二角按几何补编二十等面体设边
一百其积二百一十八万一八二八
测量全义作边一百容五二三八○
九相差四倍故今不用
分法
置公积百万依算法开各类之根则立方六等面体
历算全书 卷三十九 第 37a 页 WYG0794-0844a.png
 之根为一百四等面体之根为二○四八等面体之
之根为一百四等面体之根为二○四八等面体之根为一二八半十二等面体之根为五○半强二十
等面体之根为七七圆球之径为一二四(原本十二/等面根五)
(○二十等面根七六圆径一/二六今并依几何补编改定) 因诸体中独四等面
体之根最大故本线用二○四平分之从心数各类
之根至本数加字
用法一 有各类之立体以积求根(即开各类有/法体之方)
法皆以设积于立方线求其根乃移置更体线求本
历算全书 卷三十九 第 37b 页 WYG0794-0844b.png
 号之根即得
号之根即得假如有十二等面体其积八千问边若干法以一千
之根十为立方一点之底定尺而取八点之底得二
十为所变立方之根次以二十为本线上立方号之
底而取十二等面号之底得一十○强即十二等面
之一边(他仿/此)
用法二 有各类之立体以根求积 法先以所设根
变为正方根乃于立方线求其积
历算全书 卷三十九 第 38a 页 WYG0794-0844c.png
 假如有二十等面体其边三十一弱问积法以根三
假如有二十等面体其边三十一弱问积法以根三十一弱为本线二十等面号之底定尺而取立方号
之底得四十弱为所变立方之边次于立方线以一
十为一点之底而以四十进退求等数得(十/六)点命其
积(一万/六千)如所求(边一十其积一千则/边四十积一万六千)
用法三 有不同类之体欲相并为一(此以体相加之/法并变为正方)
(体积即/可相并)
假如有三立体甲浑圆体(径一百/二十四)乙二十等面体(边/七)
历算全书 卷三十九 第 38b 页 WYG0794-0844d.png
 (十/七)丙十二等面体(边五十/○半)欲相并用前条法各以积
(十/七)丙十二等面体(边五十/○半)欲相并用前条法各以积变为立方积则三体之积皆一百万并之得三百万
如所求
用法四 有不同类之两体求其比例与其较(此以体/相减之)
(法/)法各变为立方体即可相较以得其比例并同更
面线法
历算全书 卷三十九 第 39a 页 WYG0794-0845a.png
 第六分圆线(即各弧度之通弦也旧名分弦线亦曰分圈/)
第六分圆线(即各弧度之通弦也旧名分弦线亦曰分圈/)分法有二一以量一以算
历算全书 卷三十九 第 39b 页 WYG0794-0845b.png
 以量分 法作半方形如甲乙丙令甲丙斜弦与本线
以量分 法作半方形如甲乙丙令甲丙斜弦与本线等长以乙方角为心甲为界作象限
弧如甲丁丙乃匀分之为九十度各
识之次从甲点作直线至各度移入
尺上识其号 若尺小可作六十度
即本线之长为六十度号 若尺大可作一百八十
度即本线之半为六十度号
以算分 法用正弦表倍之为倍度之通弦 假如求
历算全书 卷三十九 第 40a 页 WYG0794-0845c.png
 六十度通弦即以三十度之正弦(五○○/○○)倍之得(一/○)
六十度通弦即以三十度之正弦(五○○/○○)倍之得(一/○)(○○/○○)即六十度之通弦他皆若是
试法十八为半周十之一(即全圈二/十之一也)三十六为半周五
之一(即全圈/十之一)四十五为半周四之一(即全圈/八之)七十二
为半周五之二(即全圈/五之一)九十为半周之半(即全圈四/之一谓之)
(象/限)百二十度为半周三之二(即全圈/三之一)
用法一 有圆径求若干度之弧以半径当六十度取
之
历算全书 卷三十九 第 40b 页 WYG0794-0845d.png
 假如有甲乙丙全圈有甲丙径求五十
假如有甲乙丙全圈有甲丙径求五十度之弧即以甲丙径半之于丁以甲丁
半径为本线六十度之底定尺而取五十
度之底如甲乙直线以切圆分即得甲戊乙弧为五
十度如所求
用法二 若以弧问径则反之
如先有弧分如甲戊乙为五十度而问全径法从弧
两端联之作直线如(甲/乙)用为本线五十度之底定尺
历算全书 卷三十九 第 41a 页 WYG0794-0846a.png
 而取六十度之底为半径(甲/丁)倍之得全径(甲/丙)
而取六十度之底为半径(甲/丁)倍之得全径(甲/丙)用法三 直线三角形求量角度
法以角为心任用规截角旁两线作通弦如法得角
度
假如甲丙乙三角形不知角法任用甲丁度以甲为
心作虚圈截甲丙线于丁截甲乙线于
戊次作丁戊直线次即用甲丁原度以
乙为心如法截甲乙于辛截丙乙于庚
历算全书 卷三十九 第 41b 页 WYG0794-0846b.png
 作辛庚直线末以甲丁为六十度之底定尺乃用丁戊
作辛庚直线末以甲丁为六十度之底定尺乃用丁戊为底进退求其等度之号得甲角之度用辛庚为底
亦得乙角之度合两角减半周得丙角度
如甲角六十五乙角四十则丙角必七十五
用法四 平面等边形求其径
假如有五等边平面形欲求径作图(即对角辏/心直线)法以
设边为分圆线七十二度之底而取其六十度之底
为半径以作平圆末以原设边为度分其周为五平
历算全书 卷三十九 第 42a 页 WYG0794-0846c.png
 分即成五等面如所求(他等边/形并同)
分即成五等面如所求(他等边/形并同)五等边形有一边如丙乙如法求
得乙甲半径以甲为心乙为界作
平圆而以丙乙边度分其圆得丁
戊己等点作线联之即成五等边形而所作圆即外
切之圆
历算全书 卷三十九 第 43a 页 WYG0794-0847a.png
 第七正弦线(旧名节气线以其造平仪时有分节气之/用也然正弦在三角法中为用甚多不止)
第七正弦线(旧名节气线以其造平仪时有分节气之/用也然正弦在三角法中为用甚多不止)(一事不如直言/正弦以免挂漏)
正弦线不平分亦近枢心大而渐小与分圆同
分法 全尺为一百平分尺大可作一千于正弦表取
历算全书 卷三十九 第 43b 页 WYG0794-0847b.png
 数从枢心至各度分之每十度加号
数从枢心至各度分之每十度加号简法 第一平分线可当此线其线两傍一书平分号
一书正弦号
又法 分圆线可当此线以分圆线两度当正弦一度
纪其号
假如分圆六十度齘即纪正弦三十但分圆之号直
书则正弦横书以别之
历算全书 卷三十九 第 44a 页 WYG0794-0847c.png
 解曰凡正弦皆倍度分圆之半故其比例等然则分
解曰凡正弦皆倍度分圆之半故其比例等然则分圆之一度即正弦之半度而半度亦可取用为尤便
也
如图甲乙为通弦甲丙乙丙皆正弦
用法一 有设弧求其正弦法以九十度当半径
假如有七十五度之弧求正弦即以本圈半径为正
历算全书 卷三十九 第 44b 页 WYG0794-0847d.png
 弦线九十度之底定尺而取七十五之底为正弦如
弦线九十度之底定尺而取七十五之底为正弦如所求
用法二 有弧度之正弦数求径数则以前条反用之
假如有七十五度之正弦数即用为本线七十五度
之底定尺而取其九十度之底得半径数
用法三 句股形有角度有弦求句求股法以弦当半
径正弦当句与股
假如句股形之弦二丈有对句之角
历算全书 卷三十九 第 45a 页 WYG0794-0848a.png
 三十度即取平分线之二十当弦数
三十度即取平分线之二十当弦数为正弦线九十度之底而取三十度
之底得一十即其句一丈
又于其角之馀弦(即六十/度正弦)取底得(一十七又/三之二弱)即其股
为(一丈七尺/三寸二分)
若以句求弦则反之如句一丈其句与弦所作之角
为六十度其馀角三十度即取一十数为三十度之
底定尺而取九十度之底得二十命其弦二丈
历算全书 卷三十九 第 45b 页 WYG0794-0848b.png
 用法四 三角形以边求角 假如三角形有乙甲边
用法四 三角形以边求角 假如三角形有乙甲边甲丙边及丙角度而求乙角法以乙甲
边数为丙角正弦之底定尺而以甲丙
边为底进退求其等度取正弦线上号为乙角度如
所求
用法五 三角形以角求边
假如三角形有戊角度己角度及庚己边而求庚戊
边法以庚己边为戊角正弦之底定尺而取己角正
历算全书 卷三十九 第 46a 页 WYG0794-0848c.png
 弦之底得数即为庚戊边如所求 馀
弦之底得数即为庚戊边如所求 馀详三角法举要
用法六 作平仪求太阳二至日离赤道纬度
如图以十字分大圆直者为两
极横者为赤道横直交于圆心
即地心也赤道即春秋分日行
之道也地心至两极半径为正
弦线九十度之底定尺取二十
历算全书 卷三十九 第 46b 页 WYG0794-0848d.png
 三度半之底于地心上下各作点于直线于此点作
三度半之底于地心上下各作点于直线于此点作横线与赤道平行为二至日道近北极者夏至近南
极者冬至也
又求作各节气日道
法先求黄道线
法于夏至之一端作斜线过地心至冬至之又一端即成
黄道日行其上一岁一周天者也以黄道半径为九十度
之底定尺每十五度正弦取底移至黄道半径上(并从地/心起度)
历算全书 卷三十九 第 47a 页 WYG0794-0849a.png

于地心上下各识之即各节气日躔黄道上度也(或/三)
(十度取底则/所得皆中气)
历算全书 卷三十九 第 47b 页 WYG0794-0849b.png
 乃自黄道上各点作直线并与赤道平行即各节气
乃自黄道上各点作直线并与赤道平行即各节气日行之道此与分至日道皆东升西没一日一周者
也其各线两端
抵大圆处即各
节气赤道纬度
也春分以后在
赤道北秋分以
后在赤道南
历算全书 卷三十九 第 48a 页 WYG0794-0849c.png
 试法于二至日道两端作横线联之(如甲/乙)次以此横
试法于二至日道两端作横线联之(如甲/乙)次以此横线之半为度(如丙/乙)过赤道处(如/丙)为心作半圈于大圆
之上(如乙戊/甲半圆)亦如法作半圈于下两半圈各匀分十
二分作识(若但求中气/可分六分)上下相向作直线联之即必
与先所作日行道合为一线 又以甲丙为正弦九
十度之底定尺而于其各正弦取底亦即与原定日
道纬度线合(如丙辛三十度之正弦也与赤道旁第/一纬线合丙丁六十度之正弦也与第)
(二纬线合左右/上下考之并同)
历算全书 卷三十九 第 48b 页 WYG0794-0849d.png
 用法七 定时刻(仍用平仪/)
用法七 定时刻(仍用平仪/)法以平仪上赤道半径为正弦线九十度之底定尺
而于各时刻距卯酉之度取其正弦于赤道作识(过/两)
(极轴线处即卯正酉正也距此而上三十度午前为/辰正午后为申正距此而下三十度子前为戌正子)
(后为寅正距此而上六十度午前为巳正午后为未/正距此而下六十度子前为亥正子后为丑正至圆)
(周处上为午/正下为子正)即春秋分之时刻也欲作各时初正及
刻准此求之并以正弦为用(每时分初正各加距十/五度初正又各分四刻)
(每刻加距三度又四分/之三并取正弦如前法)又以二至日道之半径为正
历算全书 卷三十九 第 49a 页 WYG0794-0850a.png
 弦九十度之底定尺如
弦九十度之底定尺如法取各正弦作识即二
至之时刻也 末以分
至线上时刻作弧线联
之即得各节气之时刻
准此论之平仪作时刻亦用正弦比例规解以正
弦名节气线切线名时刻线区而别之非是
历算全书 卷三十九 第 50a 页 WYG0794-0850c.png
 第八切线(旧名时刻线今按平仪时刻原用正弦惟以/日景取高度定时刻斯用切线耳又如浑盖)
第八切线(旧名时刻线今按平仪时刻原用正弦惟以/日景取高度定时刻斯用切线耳又如浑盖)(通宪等法亦皆切线其用/甚多故不如直名切线)
切线不平分先小渐大至九十度竟平行无界故只
用八十度或只作六十度亦可
历算全书 卷三十九 第 50b 页 WYG0794-0850d.png
 分法 简切线本表八十度之切线五六七即于尺上
分法 简切线本表八十度之切线五六七即于尺上作五六七平分次简各度数分之逢十加识
用法一 三角形求角
假如乙甲丁三角形求乙角任截角
旁线于丙得乙丙十寸自丙作垂线
戊丙量得七寸次用十数为切线四十五度之底定
尺而以戊丙七数为底进退求等度得三十五度为
乙角
历算全书 卷三十九 第 51a 页 WYG0794-0851a.png
 用法二 求太阳地平上高度(用直表/)
用法二 求太阳地平上高度(用直表/)法曰凡地平上直立之物皆可当表以表高数为切
线四十五度之底定尺而取表影数为底进退求等
度得日高度之馀切线
假如表高一丈影长一丈五尺法以丈尺变为数用
一十数当表高为切线四十五度之底定尺次以一
十五数当影长为底进退求等度得五十六度十九
分为日高之馀度以减九十度得日高三十三度四
历算全书 卷三十九 第 51b 页 WYG0794-0851b.png
 十一分
十一分癸丙地平上日高度与壬辛
等其馀度癸丁为日距天顶
与戊辛等甲戊为表长其影
戊已乃日距天顶之切线在
日高癸丙为馀切线也
用法三 求太阳高度用横表
植横木于墙以候日影即得倒影为正切线之度
历算全书 卷三十九 第 52a 页 WYG0794-0851c.png
 假如横表长一尺倒影在墙壁者长一尺五寸法用
假如横表长一尺倒影在墙壁者长一尺五寸法用十数当横表为四十五度之底定尺次以十五数当
影长进退求等度得五十六度十九分即命为日
高之度
凡亭台之内日影可到者量其檐际之深可当
横表
卯寅墙 子甲为横表
太阳光从丁过表端甲射丑成子丑倒影丁丙为
历算全书 卷三十九 第 52b 页 WYG0794-0851d.png

日在地平上高度与午子度等故以子丑倒影为日
高度之正切线也
按直表之影低度则影长高度则渐短日度益高则
历算全书 卷三十九 第 53a 页 WYG0794-0852a.png
 影极短故以馀切线当直影(前图/是也)横表之影低度则
影极短故以馀切线当直影(前图/是也)横表之影低度则影短高度则渐长日度益高则影极长故以正切线
当倒影(后图/是也)比例规解乃俱倒说今正之
用法四 求北极出地度分 假如江宁府立夏后九
日午正立表一丈测得影长为
二尺四寸法以一百数当表高
为切线四十五度之底定尺而
以二十四数为底进退求等数
历算全书 卷三十九 第 53b 页 WYG0794-0852b.png
 得一十三度半如法以减九十度得七十六度半为
得一十三度半如法以减九十度得七十六度半为日出地平上高度简黄赤距度表是日太阳北纬一
十九度以减日高度得赤道高五十七度半转减九
十度得北极高三十二度半捷法以直表所得一十
三度半加太阳北纬十九度即得三十二度半为北
极高度
解曰直表所得太阳距天顶度也加北纬即赤道距
天顶度亦即北极出地度
历算全书 卷三十九 第 54a 页 WYG0794-0852c.png
 又如顺天府立春后四日如法
又如顺天府立春后四日如法用横表三尺得倒影二尺一寸
依切线法求得日高三十五度
简表得本日太阳南纬一十五
度以加日高度得赤道高五十
度以减九十度得北极高四十度
历算全书 卷三十九 第 55a 页 WYG0794-0853a.png
 第九割线(旧名表心线今按割线非表心又割线之/用甚多非只作日晷一事故直名割线为)
第九割线(旧名表心线今按割线非表心又割线之/用甚多非只作日晷一事故直名割线为)(是/)
割线不平分先小后大并与切线略同故亦只作八
十度或只作六十度亦可
历算全书 卷三十九 第 55b 页 WYG0794-0853b.png
 分法 用割线本表八十度之割线五七五平分之其
分法 用割线本表八十度之割线五七五平分之其初点与切线四十五度等次依表作度加识
用法一 三角形以割线求角
假如有甲乙丙三角形求甲角法任
于甲角旁之一边截戊甲十寸作垂
线如戊丁截又一边于丁得丁甲十
九寸次以十数为割线初点之底定尺而以十九数
为底进退求等数得五十八度一十七分为甲角之
历算全书 卷三十九 第 56a 页 WYG0794-0853c.png
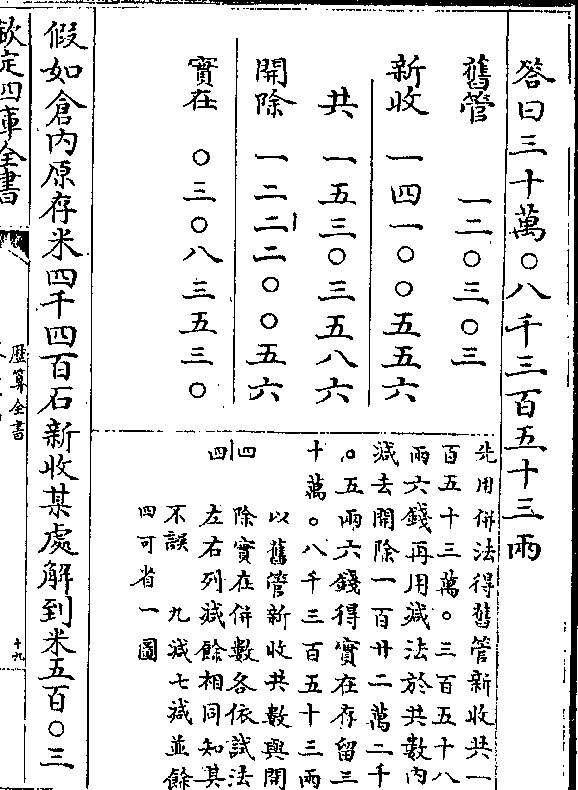 度
度用法二 作平面日晷(兼用割切二线/)
法曰先作子午直线卯酉横线十字相交于甲以甲
为正午时从甲左右尽横线尽处为度于切线八十
二度半为底定尺次于本线七度半取底向卯酉横
线上识之自甲点起为第一时如甲丙甲乙次每加
七度半取底如前作识为各时分(如七度半加之成/十五度即第二时)
(又递加如二十二度半三十度三十七度半四十五/度五十二度半六十度六十七度半七十五度至八)
历算全书 卷三十九 第 56b 页 WYG0794-0853d.png
 (八十二度半合/线末元定之点)若递加三
(八十二度半合/线末元定之点)若递加三度四十五分而取底作识
即每时四刻全矣(按每七/度半加)
(点乃二刻也今每三度/四十五分则一刻加点)
订定法曰横线上定时刻
讫次取甲交点左右各十
二刻之度(即元定四十五/度之切线亦即)
(半径/全数)为割线上北极高度之底定尺而取割线初点
历算全书 卷三十九 第 57a 页 WYG0794-0854a.png
 之底为表长(如壬/庚) 次以表长当半径为切线四十
之底为表长(如壬/庚) 次以表长当半径为切线四十五之底定尺而检北极高度之正切取底自甲点向
南截之如甲壬以壬为表位
又于北极高度之馀切线取底
自表位壬向南截之如壬辛以
辛为晷心 末自晷心辛向横
线上原定时刻作斜直线引长
之得时刻 时刻在子午线西
历算全书 卷三十九 第 57b 页 WYG0794-0854b.png
 者乙为午初丁为巳正癸为巳初又加之即辰正又加
者乙为午初丁为巳正癸为巳初又加之即辰正又加之即辰初在子午线东者丙为未初戊为未正巳为申
初又加之即申正又加之即酉初并递加四刻
谨按卯酉线即赤道线也二分之日日
躔赤道日影终日行其上庚甲割线正
对赤道正午时日影从庚射甲成庚甲影弦若已末
午初则庚点之影不射甲而射乙而庚甲影弦如半
径乙甲如切线矣以庚甲为切线上半径而递取各
历算全书 卷三十九 第 58a 页 WYG0794-0854c.png
 七度半之切线以定左右各时刻之点并日影从庚
七度半之切线以定左右各时刻之点并日影从庚所射也然此时庚甲之度无所取故即用赤道线四
十五度之切线代之用切线实用庚甲也(庚甲既为/切线之半)
(径则必与四十五/度之切线同长)
以四十五度当半径而取切线以定时刻此天下所
同也然赤道高度随各方北极之高而变庚甲割线
何以能常指赤道则必于表之长短及表位之远近
别之故以庚甲当北极高度之割线而取其初点为
历算全书 卷三十九 第 58b 页 WYG0794-0854d.png
 表长初点者半径也本宜以半径求割线今先有割
表长初点者半径也本宜以半径求割线今先有割线故转以割线求半径也既以庚壬表长为半径庚
甲为割线则自有壬甲切线而表位亦定矣表位既
定则庚甲影弦能指赤道矣何以言之表端壬庚甲
角既为极高度则庚角必赤道高度而庚甲能指赤
道也故北极度高则庚角大甲角小而庚壬表短壬
甲之距远北极度低则赤道高甲角大而庚壬表长
壬甲之距近比例规解乃以表位定于甲点失其理
历算全书 卷三十九 第 59a 页 WYG0794-0855a.png
 矣遂复误以割线为表长馀割线为晷心而强以割
矣遂复误以割线为表长馀割线为晷心而强以割线名为表心线名实尽乖贻误来学此皆习其业者
原未深谙强为作解而即有毫釐千里之差立法者
之精意亡矣故特为阐明之
庚壬表上指天顶下指地心为半径
壬表位壬甲为正切线辛晷心辛壬
为馀切线甲角即赤道高度壬庚甲
角即北极高度与辛角等
历算全书 卷三十九 第 59b 页 WYG0794-0855b.png
 用法三 先有表求作日晷(借用前图可解/)
用法三 先有表求作日晷(借用前图可解/)法先作子午直线任于线中定一点为表位如壬
乃以表长数壬庚为切线四十五度之底定尺而
取本方北极出地度之底得壬甲正切度于表位
北作点(如/甲)次于甲点作卯酉横线与子午线十字
相交即赤道线春秋分日影所到也又取极高馀
度之底得壬辛馀切线于表位南作点(如/辛)即晷心
也若自表端庚作直线至晷心辛即为两极轴线
历算全书 卷三十九 第 60a 页 WYG0794-0855c.png
 辛指南极庚指北极也次以表长(庚/壬)与壬甲正切相
辛指南极庚指北极也次以表长(庚/壬)与壬甲正切相连作正方角则庚壬如句壬甲如股而取其弦线庚
甲即极出地正割线也次以庚甲为切线四十五度
之底定尺而各取七度半之底累加之于甲点左右
作识于卯酉横线上末自晷心辛作线向所识点
即得午前后时刻并如前法
用法四 有立面向正南作日晷并同平面法但以
北极高度之馀切线定表位以正切线定晷心则
历算全书 卷三十九 第 60b 页 WYG0794-0855d.png
 自晷心作线至表端能上指北极为两极轴线又立
自晷心作线至表端能上指北极为两极轴线又立晷书时刻并逆旋与平面反然以立晷正立于北与
平晷相连成垂线则其时刻一一相符
用法五 用横表作向东向西日晷
假如立面向正东法于近南作直线上指天顶下
指地心近上作横线与地平相应两线相交于甲
以甲为心于两线间作象限弧自下起数至本方
北极出地度止自此向甲心作斜直线以分弧度
历算全书 卷三十九 第 61a 页 WYG0794-0856a.png
 此线即为赤道次以甲为表
此线即为赤道次以甲为表位用横表乙甲之长取数为
切线四十五度之底定尺递
取十五度切线从心向赤道
线累加之作识定时即春秋
分日影所到也(若分二刻则/递取七度半)
(细分每刻则递取/三度四十五分)次于甲心作横斜线如丁戊为赤
道之垂线其馀时刻点各作线与丁戊平行(亦并与/赤道十)
历算全书 卷三十九 第 61b 页 WYG0794-0856b.png
 (字相/交)次于元定尺上(即以表长为四/十五度所定)取二十三度半
(字相/交)次于元定尺上(即以表长为四/十五度所定)取二十三度半之切线为度于甲左右截之为界(如丁甲/如戊甲)即二至
卯正时日影所到也(二分日卯正则乙甲表正对日/光无影分前后则有纬度而影)
(亦渐生日日不同然不离丁戊线至二至而极冬至/影在北如丁夏至影在南如戊以此为界向西酉正)
(时亦/然)仍用元尺取(每十五度之/黄赤距纬)切线作于丁戊线内
从甲点左右作识得各节气卯正日影(或取三十度/切线则所得)
(每月中气/酉正亦然)
次以乙甲表长为割线初点之底定尺而取十五度
历算全书 卷三十九 第 62a 页 WYG0794-0856c.png
 之割线为二分日在辰初刻之影弦如乙辛即天元
之割线为二分日在辰初刻之影弦如乙辛即天元赤道上日离午线十五度其光过乙至辛所成也就
以乙辛割线为切
线四十五度之底
而取二十三度半
之底自辛点左右
截横线并如辛壬
为冬夏至辰初刻日影所到之界(辛壬在南为夏至/其在北为冬至亦)
历算全书 卷三十九 第 62b 页 WYG0794-0856d.png
 (然/)又递取(每三十度之/黄赤距纬)切线从辛至壬作点为各中
(然/)又递取(每三十度之/黄赤距纬)切线从辛至壬作点为各中气界(此向南日影界乃赤道北半周节气/其辛点向北作界为南半周亦然)自此而辰
正而巳初而巳正以至午初并同乃于节气界作线
联之即成正东日晷其面正西立晷作法并同但其
时刻逆书自下而上最下为未初次未正次申初次
申正次酉初而至酉正则横表正对日光而无影矣
此亦二分日酉正也其馀节气亦有短影而不出本
线与卯正同
历算全书 卷三十九 第 63a 页 WYG0794-0857a.png
 新增时刻线(以切线分时刻本亦非误但切线无半度/取度难清今另作一线得数既易时刻尤)
新增时刻线(以切线分时刻本亦非误但切线无半度/取度难清今另作一线得数既易时刻尤)(真/)
分法 依尺长短作直线(如后图/乙丙)于线端作横垂线(如/乙)
(甲为乙/丙垂线)又作直线略短与设线平行交横线如十字
(如甲巳线交/横线于甲)以甲为心作象限弧六平分之为时限
历算全书 卷三十九 第 63b 页 WYG0794-0857b.png
 各一分内四平之为刻限次于甲心出直线过各时
各一分内四平之为刻限次于甲心出直线过各时限至直线成六时过各刻限者成刻乃作识纪之(并/如)
(后/图)
尺短移直线近甲心取之(移进线并与原直线平行/以遇第六时第二刻为度)
(如已戊虚线遇丁戊线于/戊即戊为第六时之二刻)
历算全书 卷三十九 第 64a 页 WYG0794-0857c.png
 用法 凡作日晷并以所设半径置第三时为底定尺
用法 凡作日晷并以所设半径置第三时为底定尺而取各时刻之底移于赤道线上午前午后并起午
正左右为第一时依次加识即各得午正前后时刻
(并如/前法)
历算全书 卷三十九 第 65a 页 WYG0794-0858a.png
 第十五金线(即轻重之学/)
第十五金线(即轻重之学/)物有轻重以此权之独言五金者以其有定质也
五金之性情有与七政相类者因以为识
金(太/阳)水银(水/星)铅(土/星)银(太/阴)铜(太/白)铁(火/星)锡(木/星)
历算全书 卷三十九 第 65b 页 WYG0794-0858b.png
 分法 用各分率及立方线
分法 用各分率及立方线比例率 (先取诸色金造成立方体其大小/一般无二乃权其轻重以为比例)
黄金一
水银一又七十五分之三十八(仪象志作九十/五分之三十八)
铅一又二十三分之一十五
银一又三十一分之二十六
铜二又九分之一
铁二又八分之三
历算全书 卷三十九 第 66a 页 WYG0794-0858c.png
 锡二又三十七分之二十一(比例规解原作三十七分/之一则锡率反小于铜铁)
锡二又三十七分之二十一(比例规解原作三十七分/之一则锡率反小于铜铁)(而轻重之序乖/今依仪象志)
金体最重故以为准自尺心向外任定一度为金之
根率自此依各率增之并以金度为立方线上十分
之底定尺次依各率为底进退求等数取以为各色
五金之根率自心向金率点外作识
解曰此同重异积之率也于立方线上求得方根作
识于尺则同重异根之率也金体重则其积最少(谓/立)
历算全书 卷三十九 第 66b 页 WYG0794-0858d.png
 (方体/积)各色之金(谓银/铅等)体并轻于金故必体积多而后
(方体/积)各色之金(谓银/铅等)体并轻于金故必体积多而后能与之同重然立积虽有多少非开方不得其根之
大小故必于立方线求之也
又解曰先以同大之立方权之得各率者同根异重
之率也而即列之为同重异根之率何也盖以根求
重则金最重而他色轻以重求根则金最小而他色
大其事相反然其比例则皆等假如金与铜之比例
为一与二强若体同大则金倍重于铜矣若其重同
历算全书 卷三十九 第 67a 页 WYG0794-0859a.png
 者则铜之体必倍大于金其理一也
者则铜之体必倍大于金其理一也又法 用立方根比例率
黄金一六六弱
水银一九一弱
铅二○二
银二○四
铜二一三
铁二二二
历算全书 卷三十九 第 67b 页 WYG0794-0859b.png
 锡二二八
锡二二八用法一 有某色金之立方体求作他色金之立方体
与之同重(或立圆及各种/等面体并同)
假如有金球之径又有其重今作银球与之等重求
径若干法以金球径数置本线太阳号为底定尺而
取太阴号之底数作银球之径即其重与金球等
用法二 若同类之体其根同大求其重
假如有金银两印章体俱正方而其大等既知银重
历算全书 卷三十九 第 68a 页 WYG0794-0859c.png
 而求金重法以银图章之根数置太阴号为底定尺
而求金重法以银图章之根数置太阴号为底定尺而取太阳号底数次于分体线上以银章重数为两
弦太阳号底定尺而转以太阴底数(即银章/根数)进退求
等弦得数即金章之重
历算全书 卷三十九 第 69a 页 WYG0794-0860a.png
 轻重比例三线法(附/)
轻重比例三线法(附/)重学为西法一种其起重运重诸法以人巧补天工实
宇宙有用之学五金轻重又重学中一种盖他物难为
定率可定者独五金耳然比例规解虽载其术而数多
牴牾未可全据愚参以灵台仪象志其义始确因广
之为三线曰重比例曰重之容比例曰重之根比例既
列之矩算复为之表若论以发其凡康熙壬戌长夏勿
庵梅文鼎谨述
历算全书 卷三十九 第 69b 页 WYG0794-0860b.png
 重比例(异色之物/) (体积同轻重异/)
重比例(异色之物/) (体积同轻重异/)历算全书 卷三十九 第 70a 页 WYG0794-0860c.png
 解曰重比例者同积也积同而求其重则重者数多轻
解曰重比例者同积也积同而求其重则重者数多轻者数少若反其率则为容积比例矣
用法 假如有金一件不知重法以水盛器中令满权
其重乃入金其中则水溢溢定出金乃复权之则水
之重必减于原数矣乃以所减之重变为线于比例
尺置于水点为底乃于金点取大底即金重也 又
如有玉刻辟邪今欲作铜者与之同大问用铜几何
法如前以玉器入水取水减重之数置水点为底取
历算全书 卷三十九 第 70b 页 WYG0794-0860d.png
 铜点大底即得所求(若作诸器用蜡为模亦同或以/蜡轻难入水者竟以蜡重于蜡)
铜点大底即得所求(若作诸器用蜡为模亦同或以/蜡轻难入水者竟以蜡重于蜡)(点为底而取铜/点大底更妙也)
重之容比例(轻重同则容积异亦谓异色之物/)
历算全书 卷三十九 第 71a 页 WYG0794-0861a.png
 解曰容比例者同重也同重而求其积则重者积数少
解曰容比例者同重也同重而求其积则重者积数少轻者积数多反其率亦即为轻重之比例矣
又解曰容积比例以立方求其根则为根比例矣故轻
重当为三线也
用法 假如有水若干重盛器中满十分有澒与水同
重盛此器中问几何满法以水满十分之数作水点
之底而取澒点小底则知澒在器中得几分
用法二 有同重之两色物欲知其立方根法以容比
历算全书 卷三十九 第 71b 页 WYG0794-0861b.png
 例求其同重之积再于分体线求其根
例求其同重之积再于分体线求其根用法三 有金或铜锡等不知重法如前入水求得水
溢所减之重变为线乃以水重置金点为底(若铜锡/亦置铜)
(锡/点)于水点取大底(此借容比例求/重故反用其率)若用蜡模铸铜器
亦以蜡重置铜点为底(而于蜡点取大底/即得合用铜斤)
解曰有二法三法则只须容比例一线足矣盖反用之
可以求重既得容可以求根(用三线者取其便用一/线者取其简可任意为)
(之/也)
历算全书 卷三十九 第 72a 页 WYG0794-0861c.png
 又容比例(附/)
又容比例(附/)历算全书 卷三十九 第 72b 页 WYG0794-0861d.png
 又客比例
又客比例历算全书 卷三十九 第 73a 页 WYG0794-0862a.png
 解曰容比例有三率也其实一率而已第一率以水
解曰容比例有三率也其实一率而已第一率以水为主取其便用也第二率以金为主取其便携也
第三率平列乃立方之积数也其作线于尺则皆
一率而已矣
此外仍有通分之法亦愚所演然其理皆具原表中故
仍载表而附之故后
轻重原表
历算全书 卷三十九 第 74a 页 WYG0794-0862c.png
 右表灵台仪象志所引重学一则也其法同重者以
右表灵台仪象志所引重学一则也其法同重者以直推见容积同积者以横推见重重比例容比例皆
在其中矣既得容可以求根则根之比例亦在其中
矣比例规解五金线盖原于此原书金与蜡之比例
讹廿一为拱九今改定
通分法(亦容比例之率/)
分母
澒九五
历算全书 卷三十九 第 74b 页 WYG0794-0862d.png
 铅拱三乘得二一八五
铅拱三乘得二一八五银卅一又乘得六七七三五
铜○九又乘得六○九六一五
铁○八又乘得四八七六九二○
锡卅七又乘得一八○四四六○四○为金率
以澒分母九十五除金率得一八九九四三二以乘分
子卅八得七二一七八四一六加金率得二五二六
二四四五六为澒率
历算全书 卷三十九 第 75a 页 WYG0794-0863a.png
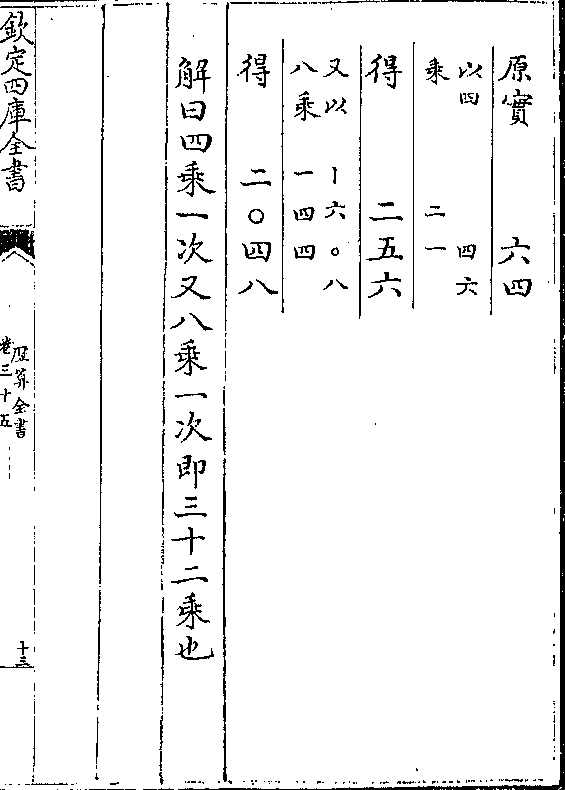 以铅母廿三除金率得七八四五四八○以乘子十五
以铅母廿三除金率得七八四五四八○以乘子十五得一一七六八二二○○加金率得二九八一二八
二四○为铅率
以银母卅一除金率得五八二○八四○以乘子拱六得一五
一三四一八四○加金率得三三一七八七八八○为银率
以铜母九除金率得二○○四九五六○以乘子一得如
原数加金率二得三八○九四一六四○为铜率
以铁母八除金率得二二五五五七五五以乘子三得六
历算全书 卷三十九 第 75b 页 WYG0794-0863b.png
 七六六七二六五加金率二得四二八五五九三四五为铁
七六六七二六五加金率二得四二八五五九三四五为铁率
以锡母卅七除金率得四八七六九二○以乘子拱一得
一○二四一五三二○加金率二得四六三三○七四
○○为锡率
历算全书 卷三十九 第 76a 页 WYG0794-0863c.png

按自古历算诸家于尾数不能尽者多不入算故曰
半已上收为秒巳下弃之其有不欲弃者则以大半
少强弱收之
假如一百分则成一整数(九十为一弱/一十为一强)百二十五为
历算全书 卷三十九 第 76b 页 WYG0794-0863d.png
 少即四分之一也(若二十为少弱/三十为少强)五十为半(四十为/半弱六)
少即四分之一也(若二十为少弱/三十为少强)五十为半(四十为/半弱六)(十为/半强)七十五为太即四分之三也(七十为太弱/八十为太强)
重之根比例(异色同重之立方/)
历算全书 卷三十九 第 77a 页 WYG0794-0864a.png

历算全书 卷三十九 第 78a 页 WYG0794-0864c.png
 附求重心法
附求重心法乙甲癸子形求重心先作乙甲线分为(乙子甲/乙癸甲)两三角
形次用三角形求心术求(乙子/甲乙)
(癸/甲)之形心在(丙/丁)作丙丁线联之
又作子癸线分为(癸乙子/癸甲子)两
三角形求(癸乙子/癸甲子)形之心在(庚/辛)
作庚辛线联之 此二线相交
于壬则壬为本形心即重心也 试作乙巳正角线至
历算全书 卷三十九 第 78b 页 WYG0794-0864d.png
 子癸线上又作甲戊线至子癸线上此两线之比例即
子癸线上又作甲戊线至子癸线上此两线之比例即两形大小之比例也(法为癸乙子形与癸甲子形/之比例若乙巳与甲戊也)
以此比例于庚辛两心距线上求得壬点为全形之重
心(法为乙巳线与甲/戊若辛壬与庚壬)
如图子巳与癸戊之比例
若丁壬与丙壬也馀并同
前图
历算全书 卷三十九 第 79a 页 WYG0794-0865a.png
 一率 子巳与癸戊二线并
一率 子巳与癸戊二线并二率 子巳
三率 丁丙
四率 丁壬
历算全书 卷三十九 第 79b 页 WYG0794-0865b.png

历算全书卷三十九