钦定四库全书
　历算全书卷三十八
　　　　　　　　　　　　　宣城梅文鼎撰
　笔算卷五
　　开平方法
测量句股全恃开方开方有平有立而平之用博以其
有实无法故别为一术以佐乘除之所穷
平方者面羃也其形正方故亦为自乘之积开平方者以

自乘之积求正方之边故西法谓之测面其边谓之方根
法先列实　依除法作两直线以所用方积列于右直
线之右自上而下至单位止无单作○
次作点定位　自单位作一点起每隔一位点之有一
点则商一位(如有二点则商数有十/有三点则商数有百)
次定初商　皆自原实最上一点截定为初商之实(如/点)
(在首位即以一位为初商实点/在次位即合两位为初商实)以自乘数约而商之皆
以点处为本位点上一位为进位(本位者单数也如一/商一四商二九商三)

(其自乘皆本位不论百与万以上皆作单数用进位者十数也/如一六商四二五商五以至八一商九其自乘皆有进位不论)
(千与万以上上/皆作十数用)
又法　以初商实入表皆视初商实有与表同数或稍大于表
数者用之以命初商(如一商一四商二此与表数相同也如二/三亦商一五六七八皆商二此比表数稍)
(大也若至九则商三又为相同之数矣十至十五皆商三/皆比表数稍大至十六商四又为相同之数他皆仿此)
　　初商表(凡初商三以下减积在本位四/以上减积合两位此表明之)
　
　

用表捷法(但视初商实不满表上自乘积者退一格即商数/如不满○四即商一不满○九即商二他仿此)
既得商数即书于左直线之右皆对初点之进位书之(凡商得/一二三)
(四书于点/之上一位)五以上又进一位(凡商得五六七八九/书于点之上两位)
次减实　以初商数自乘书于左直线之左皆以本位对初点
(如初商一二三自乘一四九皆本位即对初点书之如初/商四五六七八九其自乘皆有进位则以下一字对初点)
就以此命为减数以对减右直线所列方积如减积不尽则有次商
次商之法　倍初商得数为次商廉法对原实位书于右直线
之左(视实冇二点则初商是十有三点初商是百四点初商是/千各取倍数对原列方积千百十零之位书之倍而言十)

(者亦进/位对之)截原实第二点为次商之实(次商减积/至此点止)以廉法约实为
次商数(并依除/法约之)挨书于初商之下即用次商数为隅法亦书于
廉法之下为次商廉隅共法(省曰次/商法)以与次商数相乘书其数
于左直线之左(皆以法首位所乘之进位对次商数书之若言/如之数亦以○位对之法有几位遍乘而挨书)
(之点至次点止上又法先以法尾位隅法乘次商数以本位对/次 书之进位 一字书之依乘法例自下而上法有几位皆)
(遍乘而迭进书之/至次商数止亦同)命为次商减积数以对减右直线馀积而定
次商(皆减积至/次点止)如减数大于馀积则改次商(亦改/隅法)如上乘减及
减而止次商减积不尽则有三商

三商之法　合初商次商数倍之为廉法(简法只以隅法加倍/增入次商法内即三)
(商廉/法)截原实第三点为三商之实(三商减积至/三点而止)馀并同次商如
减积不尽则有四商
四商以上并同三商法
审○位之法　若次商廉法大于第二点以上馀积或数适相同是商
得○位也(凡商得一数者其减积必与廉法同而多一数以为/隅故仅同者无隅积也即不能商一数而成○位)
则书○于初商之下以当次商亦增○于廉法之下为三商廉
法三商以上有○并同(若应商几位而于初商或次商即已减积/至尽是末几位皆商得○也俱补作○)

命分之法　若已商得单数而仍有馀积当以法命之(以商得/方根倍)
(之加隅一为分母不尽之/数为分子命为几分之几)虽未商得单数而馀积甚少不能成
单一数亦以法命之(前审○位云廉法大于馀积者但取第二/点以上相较不论千百十零其所谓不能)
(商一数者或是一千或是一百不拘定是/单一也故商○之后仍有所商与此不同)
还原法以商得方根自之有不尽者以不尽之数加入之即得原实
又简法作直线于左方以应减之积依并法并之必合原实有
不尽数亦加入之并同除法还原
　　初商本位式(凡初商一二三者减积言如在本位然初商/一二三四者书商数于点之上一位 以书)

　　(商数之位言之亦本位也两/本位法此一式中皆可明之)
假如有方田积二百五十六步问每面方若干
　答曰每面方十六步
　
　　　　　　　　列实(作两直线列方积于右直线之右/)
　　　　　　　　作点定位(自单位起每隔一位作一点共/两点宜商两次 初商是十)

　初商(点在实首位即以实首位○二为初商实以自/乘数约之得一为初商初商是一宜对点上一)
　(位书于左直线之右有两点初商是一十自乘一百/为减数书左线之左遥对右行初点○二百书之就)
　(以对减初商实于二百内减一百仍馀/馀一百改书之初商减积未尽有次商)
　次商(倍初商一十作二十对原列方积十步位书于/右线之左为廉法 以第二点馀实一五六为)
　(次商实用廉法约实可商七步因无隅积只约六步/为次商以书于初商之下即用六步为隅法以书于)
　(廉法之下合廉隅共二十六步为次商法以乘次商/六步得廉积一百二十步隅积三十六步皆对次商)
　(位书起每挨一位书之至次点止共得次/商减数一百五十六以对减馀实恰尽)共开得平
　方根一十六步合问

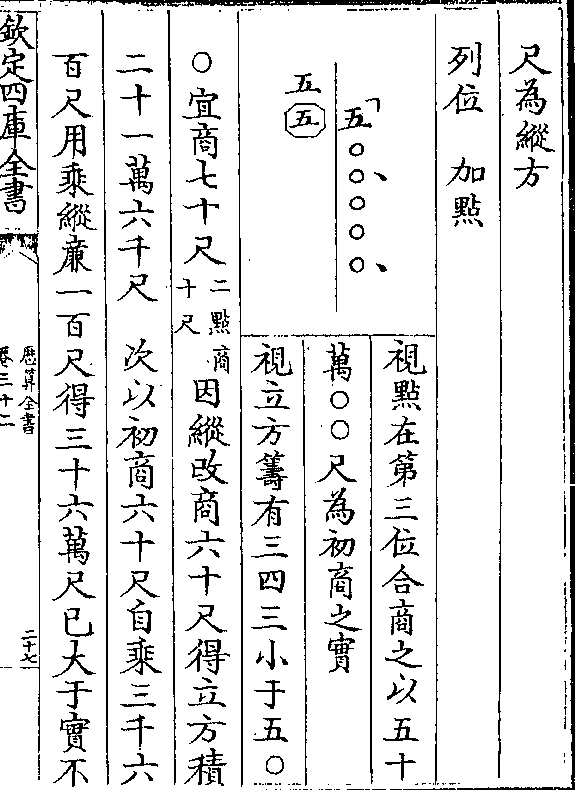
　　　　　　　　甲乙丙丁四形合为正方形(四面皆一/十六步)
　　　　　　　　甲分形正方(四而皆十步积一百步即/初商积)
　　　　　　　　丙丁二分形皆长方(广六步长十步积/六十步两形共积)
　　　　　　　　(一百二十步/即次商廉积)
　　　　　　　　乙小分形亦正方(面皆六步积三十六/步即次商隅积)
　　　　　　　　自乘还原法置方一十六步为实即以
　　　　　　　　十六步为法乘之得二百五十六步合
　　　　　　　　原数

　　初商进位式(凡初商四五六七八九减积言十在进位凡/初商五六七八九书商数于点之上两位)
　　(书商数以点上一位为本位则此其/进位也两进位法此一式中皆有之)
假如方积三十五万八千八百零一尺问方若干
　答曰方五百九十九步
　
　　　　　　　　　　列位(同/前)
　　　　　　　　　　作点定位(有三点宜商三/次初商是百)
　

　初商(点在实次位即合两位三五为初商实入表表中有小/于三五者是二五其方根五即以五为初商数对实初)
　(点上两位书左直线之右又即以表中自乘数二五遥对实/三五书于左直线之左就以对减初商实馀一○改书之以)
　(待次/商)
　次商(倍初商五百作一千○百对实千百位书于右直线之/左为廉法 以第二点上馀实一○八八为次商实用)
　(廉法约之得九为次商续书于初商之下即以次商九为隅/法书廉法之下合廉隅共一○九为次商法以乘次商九得)
　(廉积九隅积八一对次商位书起至次点止共得减数九/万八千一百以减次商实馀一○七改书之以待三商)
　三商(以次商隅法九十倍作一百八十于次商法一千之下/抹去○九改书一八共一一入为廉法 以第三点上)
　(馀积一○七○一为三商实用廉法约之得九为三商续书/于次商下即以三商九为隅法书于廉法之下合廉隅共一)

　(一八九为三商法以乘三商九步得廉积一万○六百二十/隅积八十一对三商位书起至第三点止共得减数一万○)
　(七百○一以对/减三商实恰尽)凡开得方根五百九十九尺
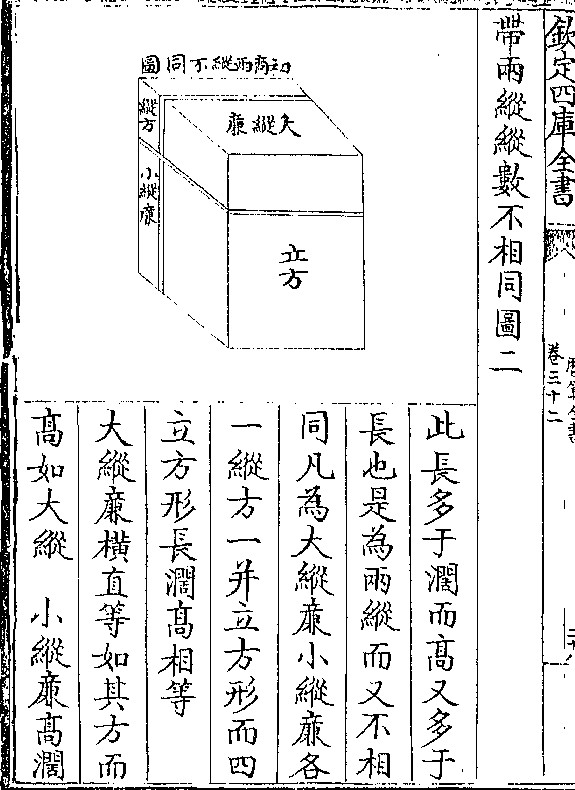
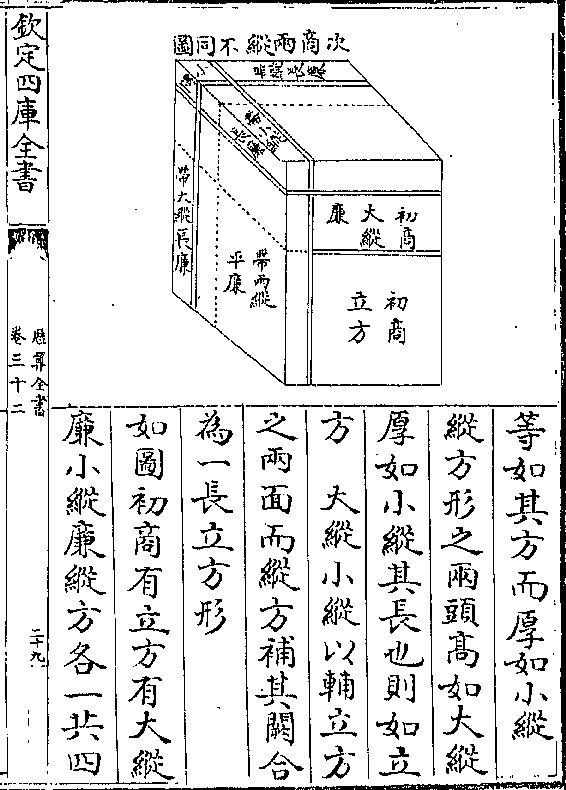
　　　　　　　　　　　初商甲(方五百尺积/二十五万尺)
　　　　　　　　　　　次商(丁/戊)二廉(各长五百尺阔九/十尺共积九万尺)
　　　　　　　　　　　隅乙(方九十尺积/八千一百尺)
　　　　　　　　　　　三商(已/庚)二廉(各长五百九十尺阔/九尺共积一万○六)
　　　　　　　　　　　(百二/十尺)隅丙(方九尺积/八十一尺)
　　　　　　　　　　　七形合成正方共积(三十五万八千/八百○一○)

　　商○位式
假如方积八十二万六千二百八十一尺问方若干
　答曰九百○九尺
　
　　　　　　　　　　列位
　　　　　　　　　　作点定位(并同/前条)

　初商(点在次位合两位八二为初商实表入表得八一小于/八二其方根九即为初商在五以上对初点上两位书)
　(之亦以表数八一对实八二书于左线之/左以减初商实馀○一改书之以待次商)
　次商(倍初商九百作一千八百对原实位书之为廉法以第/三点上馀实○一六二为次商实以廉法约之法大实)
　(小不能商一数是商得○位也纪○于初/商之下即于实首位销去一○馀俟三商)
　三商(因次商是○增○于廉法之下共一八○为廉法以第/三点上馀实一六二八一为三商实用廉法约实得九)
　(尺为三商书于次商○之下即以九为隅法书于廉法之下/共廉隅法一八○九以乘三商九得廉积一万六千二百隅)
　(积八十一减/三商实恰尽)凡开得方根九百○九尺
计开

　初商方九百尺　积八十一万尺
　续商廉(各阔九尺/长九百尺)共积(一万六千/二百尺)　隅方九尺积(八十/一尺)
　通共八十二万六千二百八十一尺
假如方积二十五亿○七百○○万四千九百尺问方若干
　答曰五万○七十尺
　　　　　　　　　　　　　　列位(原积尾位是百/补作两○列之)
　　　　　　　　　　　　　　作点定位(有五点当商五/次 初商是万)

　初商(以实首两位二五为初商实入表得五为初商/书于点上两位次以自乘数对实列之相减尽)
　次商(倍初商五万尺得一十○万为廉法对原实位书之以/第二点上馀实○○○七为次商实实有三○无可商)
　(是次商○也书○于初商五之下/亦于实首销去一○以待三商)
　三商(因次商○增○于廉法下得一○○为廉法○以第三/点上馀实○○七○○为三商实实仍有两 位是三)
　(商亦○也又书○于次商○之下/于实首复销去一○以待四商)
　四商(因三商亦○又增○于廉法之下得一○○○为廉法/ 以第四点上○七○○四九为四商实用廉法约之)
　(得七十尺书于三商○之下即以七为隅法增于廉法下共/廉隅法一○○○七以乘四商七得廉积七百万隅积四千)
　(九百以对减/四商实恰尽)

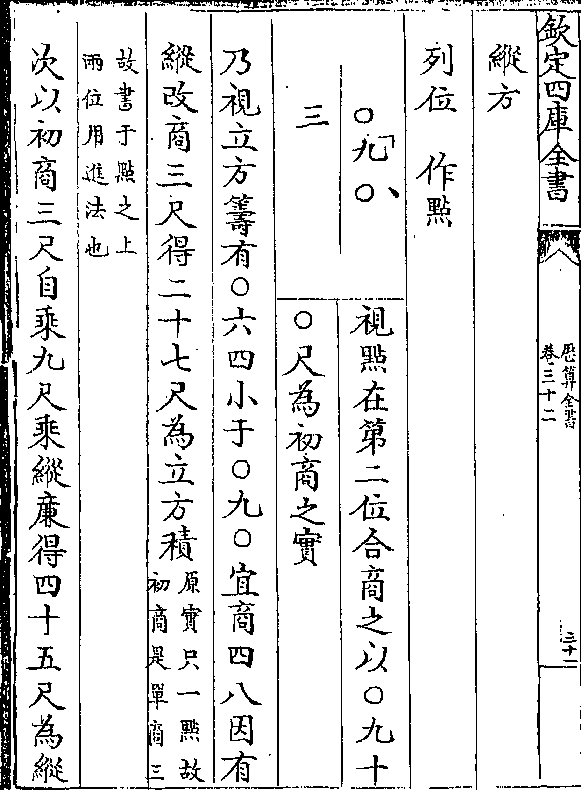　五商(五点宜有五商而四商已减/实尽无可商作○于四商)
　凡开得方根五万○○七十○尺
　　命分式
假如方积五百七十六万四千八百尺问方根若干
　答曰二千四百尺(又四千八百○一/分尺之四千八百)
　　　　　　　　　　　　列位(实尽于百位如前/法补作两圈列之)
　　　　　　　　　　　　作点定位(有四点宜商四/次初商是千)

　初商(以实首○五为初商实入表得二为初商以/自乘数○四减实○五改书馀一以待次商)
　次商(倍初商二千得四千为廉法约以第二点上馀/实一七六为次商实用廉法 之得四为次商)
　(即以为隅法书廉法下共廉隅法四四以乘次商四/得廉积一百六十万隅积一十六万共减积一百七)
　(十六万次/商实减尽)
　三商(倍次商隅法四作八增入次商法共四八为三/商廉法以第三点上馀实○○四八为三商实)
　(有两○无可商作○于三商/位消去实首一○以待四商)
　四商(三商○亦增○于廉法下共四八○为廉法与/以第四点上馀实○四八○○为四商实仅)
　(廉法相同是无隅积也不能商一数作○于四商位/其不尽之数以法命之法以廉法四千八百○加隅)

　(一共四千八百○一为命分之母以不尽之数四千/八百为分子命为四千八百○一分尺之四千八百)
　(即一尺/弱也)
　共开得平方二千四百尺又四千八百○一之四千
　八百
此虽未开至单尺之位而馀实甚少不能成一单尺故
即以法命之若馀实是四千八百○一尺则商得平方
二千四百○一尺矣今止四千八百尺是少一尺故不
能成一单尺也

　
　
　
　
　
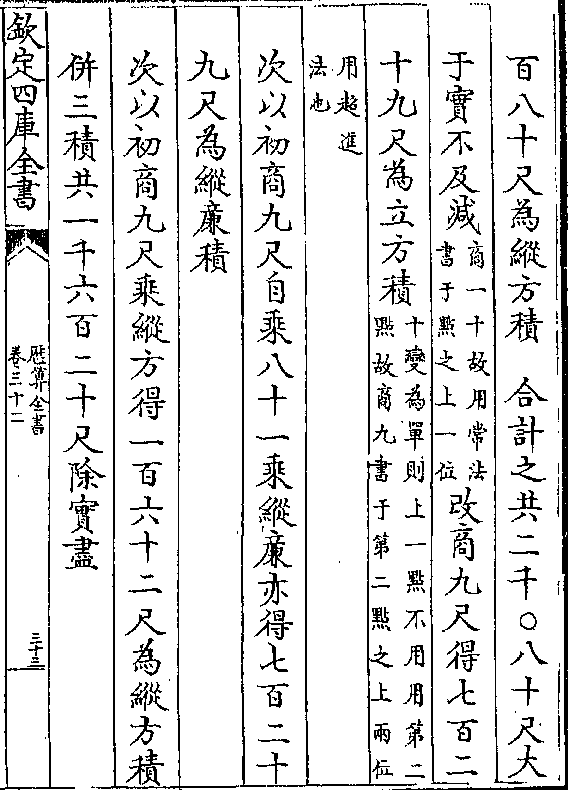
　　开方分秒(凡开方欲知分秒法于馀实下每增两○位则/多开一位为分秒之数 平方之积尺有百寸)
　　(寸有百分皆以百/为母故增两○)
假如有平方积二十四尺平方开之得方四尺不尽八尺问分

秒若干　答曰方四尺零八寸九分八釐九毫有奇
　　　　　　　　　　　　如常列位作点点在次位即以
　　　　　　　　　　　　二四两位合商得方四尺减其
　　　　　　　　　　　　自乘一十六尺馀八尺用命分
　　　　　　　　　　　　法以商四尺倍作八尺又加隅
　　　　　　　　　　　　一得九为命分母不尽为分子
　　　　　　　　　　　　命为方四尺又九分尺之八

今欲知其寸(九分尺之八者是以尺作九分而今有其八/言每方四尺之外仍𢃄此畸零是其中有寸)
　法于馀实下加两○化八尺为八百寸(每尺纵横十/寸故其积百)
　(寸/)用为次商实以初商四尺倍之得八尺亦化八十
　寸(商数是每边之/数故尺只十寸)对馀实十寸位书之(即第一/○位)为廉
　法用廉法约实可商九寸因恐无隅积只商八寸书
　于初商四尺之下亦即以次商八寸为隅法书于廉
　法八十寸之下共廉隅八十八寸以乘次商八寸得
　廉积六百四十寸隅积六十四寸共廉隅积七百○

　四寸自次商位书起至第二○位止以对减馀实仍
　馀九十六寸命为奇数
凡商得每方四尺八寸有奇
再求其分
　法于实下又加两○以馀九十六寸化九千六百分(解/见)
　(上/)为三商实　商数四尺八寸亦化四百八十分倍
　之为九百六十分移对馀实百分十分之位书之为
　廉法以廉法约实商得九分为三商书次商之下亦

　即以三商九分为隅法书于廉法九百六十分之下
　共廉隅九百六十九分以乘三商九分得廉积八千
　六百四十分隅积八十一分共积八千七百二十一
　分自三商位书起至第四○位止以对减馀实仍馀
　八百七十九分命为奇数
凡商得每方四尺八寸九分有奇
再求其釐
　法于馀实下又加两○以馀八百七十九分化八万

　七千九百釐为四商实　次倍商数四尺八寸九分
　作九尺七寸八分化为九千七百八十釐移对馀实
　依千百十之位书之为廉法　用廉法约实得八釐
　为四商书于三商之下即以四商八为隅法增于廉
　法末共廉隅法九千七百八十八釐以乘四商八釐
　得廉积七万八千二百四十釐隅积六十四釐自四
　商位书起至第六○位止以减馀实仍馀九千五百
　九十六釐

凡商得每方四尺八寸九分八釐有奇
再求其毫
　如法于馀实下又加两○化馀实为九十五万九千六
　百毫为五商实　次倍商数四八九八作九尺七寸
　九分六釐化为九万七千九百六十毫为廉法移对
　馀实万千百十之位书之用廉法约实得九毫为五
　商书四商下亦即以五商九为隅法增入廉法下共
　廉隅九万七千九百六十九毫以乘五商九毫得廉

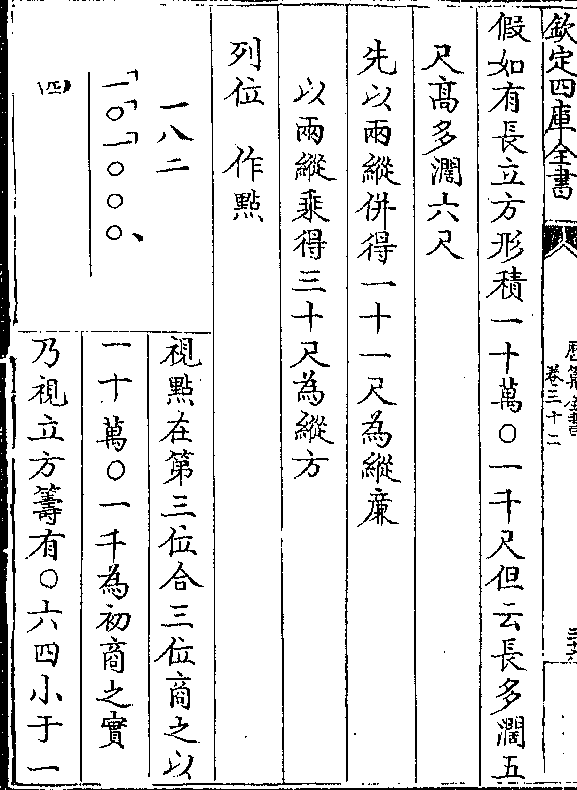　积八十八万一千六百四十毫隅积八十一毫对五
　商位书起至第八○位止以减馀实仍馀七万七千
　八百七十九毫
凡商得方四尺八寸九分八釐九毫又九万七千九百
七十九之七万七千八百七十九即奇数也
　右单数下已开四位(尺为单位析为寸/分釐毫凡四位)其不尽者
　是不满一毫之数于单数为十万分之一(如欲再/求忽微)
　(亦如/上法)

　
　
　
　
　
　
　
　

　　开方𢃄纵(𢃄纵者长方形也以方为阔加纵数为长其法/与开方无异但须以商得数乘纵数为纵积并)
　　(入方积以减原积不及减者改商之其次商亦倍初/商加纵为廉法但倍方而不倍纵 三商以上并同)
假如有长田积六百二十四步阔不及长二步问长阔各若干
　答曰长二十六步阔二十四步

　列位(以实列右线之右步以纵二步/列右线之左对实 位列之)
　如常作点定位
　初商(以○六为初商实商得二十步自乘应减方积/四百步又以商数乘纵二步得纵积四十步如)
　(法列之以减原实仍/馀一百八十四步)
　次商(倍初商二十步作四十步加纵二步共四十二/步为廉法以约馀实得商四步即以为隅法合)
　(廉隅纵共四十六用乘次商四得廉积一百六十步/隅积十六步纵积八步共减积一百八十四步恰尽)
　　命为阔二十四步　　加纵二步为长二十六步
　合问

以图明之
　　　　　　　　　　甲为初商方形(长阔各二十/步积四十步)
　　　　　　　　　　已初商纵形(阔二步四长亦二/十步积 十步)
　　　　　　　　　　戊丙并次商廉(长各二十步十阔/四步 积八 步)
　　　　　　　　　　乙次商隅(方四步步积/一十六)
　　　　　　　　　　丁次商纵廉(长四步八阔二/步 积 步)
　　　　　　　　　　(以上五者合之为一长方形步/共长二十六步 阔二十四)
　　　　　　　　　　(积六百二十/四步合原数)

若纵数有比例可求者先以比例分其积平方开之得
阔因以知长
假如有直田积四百五十步但云长多阔一倍问长阔
若干
　答曰阔十五步　长三十步
　法平分其积得二百二十五步平方开之得阔十五
　步
　置阔十五步倍之得长三十步合问

假如有长田积二百五十二步但云长比阔多四分之
三问长若干
　答曰　阔一十二步长二十一步
　法以多三分加分母四共七为法以分母四乘积为
　实法除实得一百四十四步开方得阔一十二步
　置阔一十二步七因四除之得二十一步为长(长比/阔多)
　(九步于十二步/为四分之三)

　　开立方法
平方者方田之属也但取面羃之积立方者方仓之属
也必求其内容之积故平方曰面立方曰体有面而后
有体有线而后有面故皆以线为根
假如长二尺者线数也线有长短而无广狭若以此线
横展之长亦二尺阔亦二尺则其积四尺为面面者平
方形也面有阔狭而无厚薄又以此面层累而厚之长
阔皆二尺高亦二尺则其积八尺为体体者立方形也

立方有虚有实如筑方台则实凿方池作方窖则虚然
其立方之积数一也
法先立位(同平/方)　作点(自单位起每隔二位点之/以最上一点为初商实)　定
位(视有若干点则商几位如有二点则商/数有十有五点则商数有百并同平方)
初商法　以自乘再乘数约而商之(如一商一八商二/二七商三之类)
书商数于左线之右(凡商得一数者书于点上一位商/得二三四五者书于点上两位商)
(得六七八九者/书于点上三位)即以自乘再乘数书于左线之左以对
减初商实(初商减积/至初点止)

次商法　以初商自乘而三之为平廉法(亦曰/方法)　以初商三之
为长廉法(亦曰/廉法)皆对原实千百位书之　截第二点上馀实为
次商实(次商减积/至次点止)以平廉法约实得次商(列初/商下)即以次商为隅
法列长廉次(亦按千百/位列之)乃以次商乘平廉法为平廉积又以次
商自乘以乘长廉及隅法为长廉小隅积俱挨书之以减馀积
不及减者改商
三商法　以馀实另列之　合初商次商自乘而三之为平廉
法　合初商次商三之为长廉法　截第三点上馀实为三商

实(三商减积/至此点止)　亦即以三商为隅法(馀并/同前)
四商以上并同三商
命分法　合平廉长廉法再加隅一为命分母不尽之数为命
分子(并同/平方)
还原法　置商数自乘得数再以商数乘之即合原实(有不尽者以不/尽之数加入之)
　　初商表(用法与平/方表同)

　
　
　
　
　
　
　
　

假如立方积五千八百三十二尺问方若干
　答曰方一十八尺
　
　
　　　　　　　　　列实
　　　　　　　　　作点定位(有两点初/商是十)

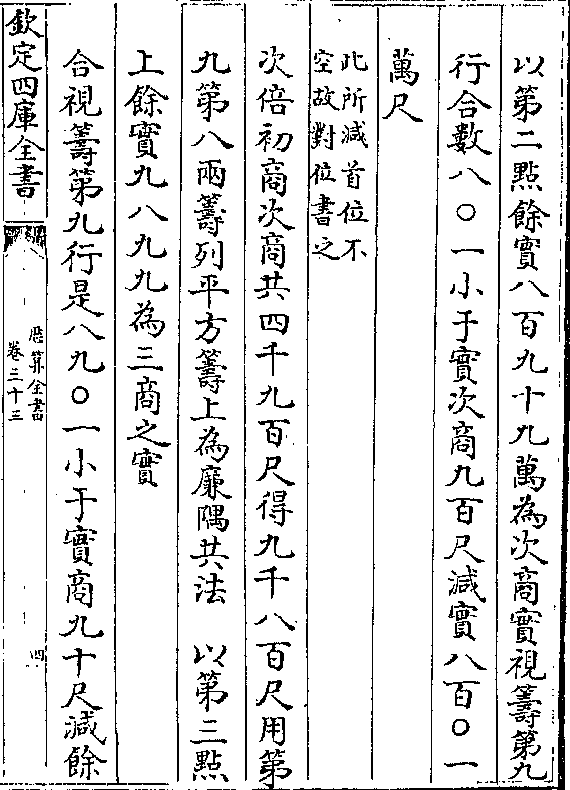　初商(以五千为初商实约商一十自乘再/乘得一千为应减积减原实馀四千)
　次商(以初商自乘而三之得三百为平廉法二又以初商三/之得三十为长廉法 以平廉法约第 点上馀实得)
　(八尺为次商即以为隅法并如法列之乃以次商乘平廉法/得二千四百为平廉积又以次商自乘得六十四以乘长廉)
　(及隅法得长廉一千九百二十隅积五百/一十二共减积四千八百三十二恰尽)
　
　
　
　

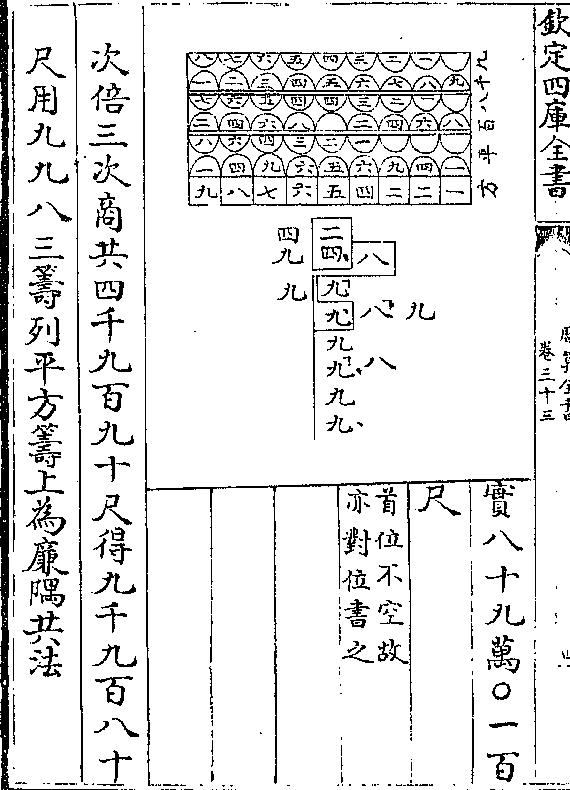以图明之
　　　　　　　　　　　甲为初商方形(长阔皆十尺/积一千尺)
　　　　　　　　　　　乙为次商平廉凡三以辅于
　　　　　　　　　　　方之三面(长阔皆十尺厚八/尺积八百尺共积)
　　　　　　　　　　　(二千四/百尺)
　　　　　　　　　　　丙为次商长廉亦三以辅三
　　　　　　　　　　　平廉之隙(长十尺阔与厚皆/八尺积六百四十)
　　　　　　　　　　　(尺共积一千/九百二十尺)

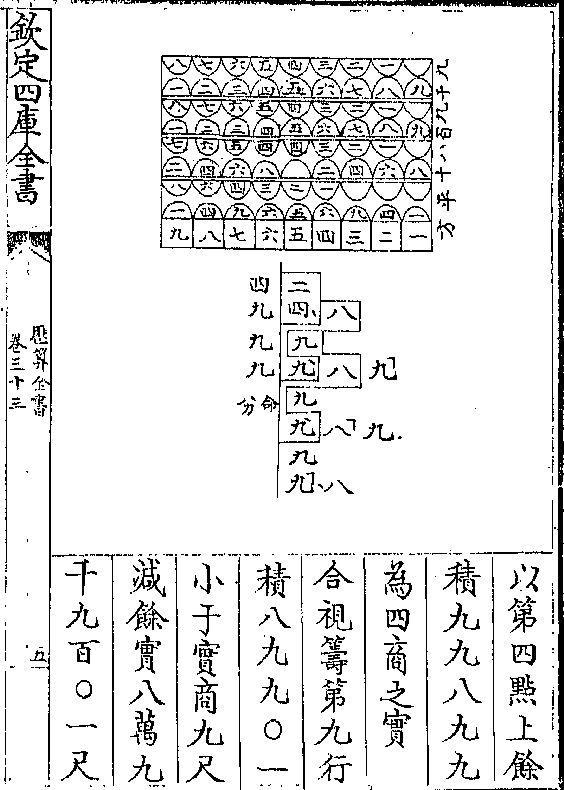　丁为次商隅如小立方以补三长廉之隙(长阔高皆八尺积/五百一十二尺)
假如立方积二千二百五十九亿七千七百八十一万一千五
百七十尺问方根若干答曰方六千零九十尺(又一亿一千/一百二十八)
　(万二千五百七十一之一亿一千/一百二十八万二千五百七十)
　　　　　　　　　　　　　　　列实(实尾无单/位补作○)
　　　　　　　　　　　　　　　作点定位(有四/点初)
　　　　　　　　　　　　　　　(商是/)
　　　　　　　　　　　　　　　千

　初商(合实三位约之商六千对初点上三位列之以六千自/乘再乘得减积二千一百六十亿其馀积改书以待次)
　(商/)
　次商(日乘初商而三之得一亿○八百万为平廉法位/以初商三之得一万八千为长廉法各对原实)
　(列之次以第二点上馀实为次商实实首有两○无可/商是 商○也作○于初商之下即于实首消去两○)
　(馀俟/三商)
　三商(次商○即以次商法为三商法尺以第三点上馀实为/三商实以平廉法约之商九十 即以为隅法对实十)
　(位列之乃以九十乘平廉法得平廉积九十七亿二千万又/以九十自乘得八千一百以乘长廉及隅法得长廉积一亿)
　(四千五百八十万隅积七十二万九千共/减积九十八亿六千六百五十二万九千)

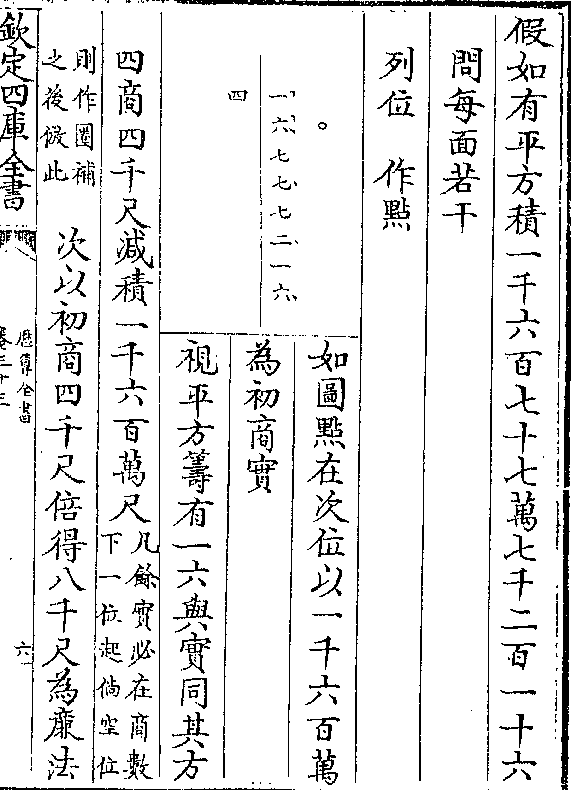　四商(以第四点上馀实另列之二合三次商数六○九自乘/而三之得一亿一千一百 十六万四千三百为平廉)
　　　　　　　　　　　　　　　　(法得又以六○九三/之 一万八千二百)
　　　　　　　　　　　　　　　　(七十为长廉法廉以/法约实仅与两 法)
　　　　　　　　　　　　　　　　(之数相同无隅积不/能成一单数以法命)
　　　　　　　　　　　　　　　　(之合平廉长廉数加/隅一为命分母馀实)
　　　　　　　　　　　　　　　　(为命/分子)
　命为立方六千○九十尺又(一亿一千一百二十八万二千/五百七十一尺之一亿一千一)
　(百二十八万二/千五百七十)

　自乘　　　　　　再乘
　
　
　
　
　
　
　历算全书卷三十八