钦定四库全书
　历算全书卷三十
　　　　　　　　　　　　宣城梅文鼎撰
　　筹算一
　作筹之度
凡筹以牙为之或纸或竹片皆可长短任意以方正为
　度
凡筹背面皆平分九行每行以曲线界之为两半圆状

凡筹背面皆相对第一筹之阴即为第九便检寻也二
　与八三与七四与六五与空位皆仿此共五类类各
　五筹当珠盘二十五位或更加之亦可　外有开方
　大筹为平方立方之用详见别卷
　筹式列左

　作筹之理
凡筹每行以曲线界之成两位其下为本位上为进位
　假如本位一两则进位为十两
凡列两筹则行内成三位下之进位与上之本位两半
　圆合成一位故也　列三筹则成四位　列四筹则
　成五位　五筹以上皆仿此
凡筹有明数有暗数明数者筹面所有之数是也暗数
　者行数也假如第一行即为一数第二行即为二数

凡筹与行数相因而成积数假如第二筹之第四行即
　为八数第九筹之第八行即为七二数
　筹算之资
凡用筹算当先知并减二法今各具一则
　并法
并者合也合众散数为一总数也又谓之垛积　其法
　先列散数自上而下对位列之千对千百对百十对
　十单对单以类相附

　列讫并为一总数　其法从最下小数起自下而上
　如画卦之法　数满十者进位作暗马而本位书其
　零
　　　　　　　　　　　　　恐混原数故以此
　　　　　　　　　　　　　别之便覆核也
假如有米三千四百八十石又五千○六十八石又二
万六千九百石合之共几何
　

　　　　　　　　　　如图散数三宗依法并之为
　　　　　　　　　　一总数得三万五千四百四
　　　　　　　　　　十八石
　
　减积法
减者去也于总数内减去几何则知其仍馀几何也减
　与并正相反减而剩者谓之减馀
　其法以应减去之数列左以原有之总数列右而对

　减之
　千对减千百对减百十对减十单对减单
　减而尽者抹去之　减而不尽者改而书之
　本位无数可减合上位减之假如欲减八十而原数
　只有七十但其上位有一百则合而减之于一百七
　十内减八十仍馀九十
假如有银三十二万五千三百一十两支放过二十九
　万五千三百○五两仍馀几何

　　　　　　　　　　依法减之仍馀三万○○○
　　　　　　　　　　五两
　
　　　十万千百十两
　如图先于三十万内减二十万馀一十万改三为一
　　次减九万而万位无九合上位共一十二万减之
　馀三万抹去一二改书三
　次减五千　次减三百　皆减尽皆抹去之书作○

　　次减五两而两位无五于一十两内减之抹去一
　○改书○五　减讫馀二○○○三
凡算有乘有除乘者用并法除者用减法
　筹算之用
凡算先别乘除乘除皆有法实实者现有之物也法者
　今所用以乘之除之之规则也
凡筹算皆以实列位而以筹为法法有几位则用几筹
　如法有十系两位则用两筹法有百系三位则用三

　筹
凡法实不可误用唯乘法或可通融若除法必须细认
　俱详后

　乘法
勿庵氏曰凡理之可言者皆其有数者也数始于一相
　缘以至于无穷故曰一与一为二二与一为三自此
　以往巧历不能尽乘之义也故首乘法
解曰乘者增加之义其数渐升如乘高而进也亦曰因
　言相因而多也珠算有因法有乘法在筹算总一乘
　法殊为简易
法曰凡两数相乘任以一为实一为法

　假如以人数给粮或以人为实粮为法或以粮为实
　人为法皆可
　凡算先列实(列书之于纸或粉板亦可依千/百十零之位列之自左而右)
　　次以法数用筹乘之
　　法有几位则用几筹
　　(假如法为六十四则用第六第四两筹法为/三百八十四则用第三第八第四共三筹)
　凡乘皆从实末位最小数起
　　视原实某数即于筹其行取数列之

　　(假如实是二则/取第二行数)
　凡列乘数皆自下而上如画卦
　凡实有几位挨次乘之但次乘之数必高于前所列
　　之数一位
　　(假如先乘者是单次乘/者必是十故进位列之)
　乘讫乃以并法并之合问

　
　
　
　
　
　
　
　

又法
　凡法尾空位者省不乘但于并数之后补作圈于其
　下以存其位尤为简捷
　　　　　　　　　　　　　如上图乘讫并得三○
　　　　　　　　　　　　　○○因法尾有空又补
　　　　　　　　　　　　　作一圈是为三○○○
　　　　　　　　　　　　　○则知所得三万
　　　　　　　　　　　　　定位法见前

　又若田为一亩二分则所得为三合何也亩下有分
　故得数之三○○其尾○又是勺下之分也此定位
　之精理须细审之

一四二四四四五七五共九位因实尾空位(无零年/故也)用
省乘法加一○于末位下共十位而以尾○命为分得
一十四万二千四百四十四日五十七刻五十○分合
问
　
　
　
　

　除法
勿庵氏曰天地之道盈虚消息而已无有盈而不虚无
　有消而不息乘者息也盈也除者消也虚也二者相
　反而不能相无其数每相当不失毫釐如相报也邵
　子曰算法虽多乘除尽之矣故除法次之
解曰除者分物之法也原作几何今作几分分之则成
　各得之数而除去原数也有归除有商除珠算任用
　筹算则独用商除为便以意商量用之故曰商除

法曰凡除以所分之物为实今欲作几分分之为法法
　与实须审定倘一倒置则毫釐千里矣(假如有粮若/干分给若干)
　(人则当以粮为实以人之数为法除之盖粮数是所/分之物人数是用以分之之法也若倒用以粮分人)
　(则所误/多矣)　凡法有几位则用几筹　乃列实(自上而/下直书)
　(之/)　视筹之第几行中积数有与原实相同者或略
　少于实者用其数以减原实而得初商　有不尽者
　如法再商或三商以上皆如之实尽而止　馀实不
　满法以法命之

　凡商数皆以筹之行数为其数(假如所减是等第一/行即商一数第二行)
　(即商/二数)
书商数法曰凡书商数皆与减数第一位相对　若所
　减第一位是○则补作○于原实首位上而对之(此/定)
　(位之/根)
定位法曰除毕以商得数与原实对位求之皆于法首
　位之上一位命为单数(程大位曰归于法前得零/古法实如法而一是也)
　此有二法　有法少实多者从原实内寻法首位认

　定逆转上一位命为单数(如米则为单石钱/则为单文之类)既得单
　数则上而十百千万下而分秒忽微皆定矣此为正
　法
　有法反多实反少者乃变法也法从原实首位逆溯
　而上至法首位止又上一位命为单数(此是虚位借/之以求实数)
　既得单数乃顺下求之命所得为分秒之数
　
　

初商除尽式　　　　法此欲分为七十二分也故以七二为
假如太阳每　　　　　法用两筹
岁行天三百　　　　实三六○　　如图先列三百六十度
六十度分为　　　　　百十　　　为实次简两筹行内有
七十二候每　　　　　　　　　　三六○与实相同用减
候几何度　　　　　　　　　　　原实恰尽　次查所简
(答/曰)每候五度　　　　　　　　　　系筹之第五行商作五
　又查所减第一位是三将商数五对三字书之

定位法曰此法少于实也宜于原实内寻十度位即法
　首位也法首再上一位为单度定所得为五度
　假令实是三千六百则所得为五十度如后图
　　　　　　　　　定位法曰此亦法少于实也法亦于
　　　　　　　　　原实内寻法首十位再上一位为单
　　　　　　　　　位单位空补作圈再上一位是十度
　　　　　　　　　定所得为五十度用筹同而得数迥
　　　　　　　　　异定位之法所以当明也

再商式　　　　　　法此欲分为一十二分也故以一二
假如皇极经世　　　　为法用两筹
一元共一十二　　　实　　　　　　如图列实(一元/总数)简
万九千六百年　　　○一二九六○○筹第一行是○一
分为一十二会　　　　十万千百十年二商作一数(第一/行故)
各几何　　　　　　　　　　　　　(商/一)减实一十二万
答曰每会一万　　　　　　　　　　馀九千六百不尽
○八百年　　　　　　　　　　　　再用筹如法除之

　又因所减数是○一二故于原实首补作圈而以商
　得一对此○位书之(即所减筹上/第一位也)此定位之根不可
　错须细审之
　　　　　　　　　　简两筹第八行是○九六与馀实
　　　　　　　　　　相合再商八(第八行/故也)减馀实九千
　　　　　　　　　　六百恰尽
　　　　　　　　　　此所减数亦是○九六故以商得
　　　　　　　　　　八进位书之以暗对其○

　如此审定商数位置已知不错而初商次商隔一位
　不相接是得数有空位也乃于其间补作圈为一○
　八
　假如隔两位则作两圈三位以上仿此求之若非于
　商数审其位置鲜不误矣此算中一大关键也非此
　则不能定位
定位诀曰此亦法少于实也从原实内寻法首十位再
　上一位是单年单位空补作圈又上一位是十十亦

　空亦补作圈又上一位是百知所得为八百年也知
　百知千万矣定为一万○八百年
　
　
　
　
　
　

假如黄钟之　　　　　　法此欲分得二千一百八十
实一十七万　　　　　　　七乃为一分故以二一八
七千一百四十　　　　　　七为法用四筹
七其分法二
千一百八十
七问若干分
答曰八十一
分

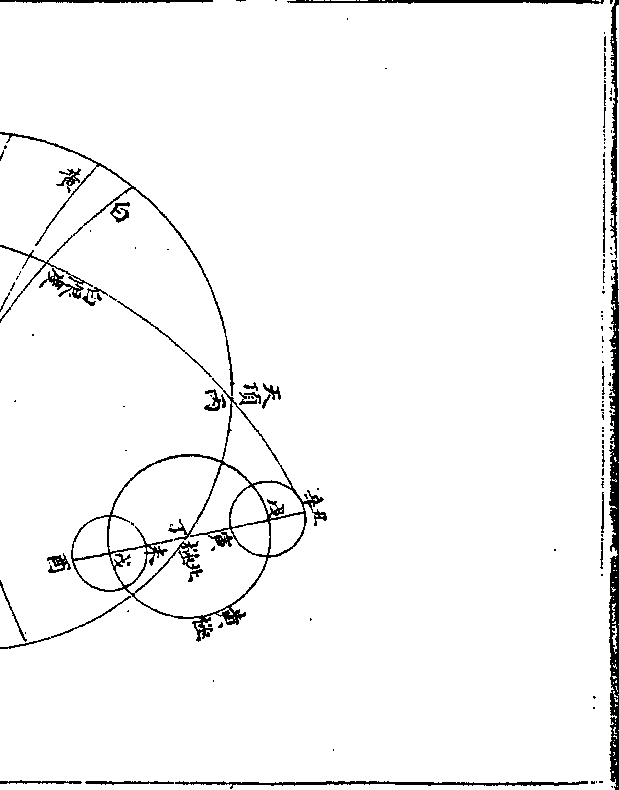　二千一百八十七再商之
　
　　　　　　　　　简筹第一行是○二一八七正合
　　　　　　　　　馀实再商一除实恰尽
　　　　　　　　　次商一进位书暗对所减○位
　　　　　　　　　定位诀从原实寻法首位千逆转
　　　　　　　　　上一位得单分则馀位皆定
　

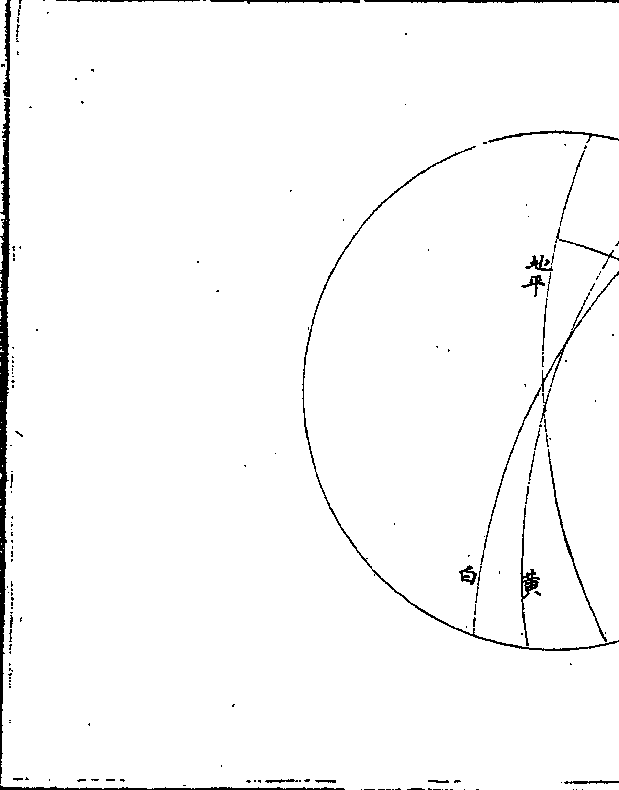按筹算原书于定位颇略又其为法原实横而商数纵
各居其方不相依附定位颇难故虽历书间有讹位今
特详之而两两直书于定位尤易亦足见余之非好为
异也

　
　
　
　
　
　
　
　

四商法
假如有小珠三十四　　　　　此欲分为九分有奇也(以/钱)
万三千一百五十四　　　　　(为主则六分五釐是其/奇零九分之分去声)故
粒换得大珠重九钱　　　　　以(九六/五)为法用筹三根
六分五釐每大珠一　　　　　如后图列实先简筹第(三/)
钱换小珠几何粒　　　　　　行(二八/九五)略少于实商(三/)减
答曰每钱换三万五　　　　　实(二十八万/九千五百)馀实(五万三/千六百)
千五百六十粒　　　　　　　(五十/四)以候续商

　　　　　　　　　次简筹第(五/)行是(四八/二五)为略少于馀
　　　　　　　　　　实商(五/)减馀实(四万八千/二百五十)仍馀(五/千)
　　　　　　　　　　(四百/○四)以待第三商
原实　　　　　　　又简筹第(五/)行是(四八/二五)为略少于馀
　　　　　　　　　　实又商(五/)减馀实(四千八百/二十五)仍馀
商数　　　　　　　　(五百七/十九)知尚有第四商也
　　　　　　　　　又简筹第(六/)行是(五七/九○)与馀实恰合
四次商数俱对首位　　商作(六/)除馀实(五百七/十九)恰尽

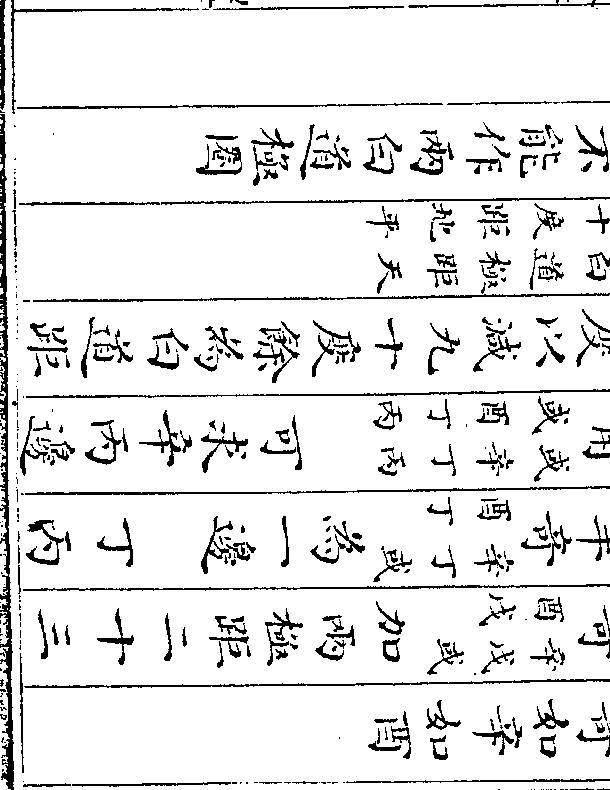定位诀从原实中寻法首(单/)位逆转上一位得(单/)粒定
所得为(三万五千五/百六十○粒)命为大珠每钱所换小珠之数
　五园问曰法是钱数实是粒数不类也何定位亦如
　是准乎勿庵曰此定位之法所以的确不易也且钱
　与粒不类子疑之固矣抑知单与单之为一类乎盖所问
　是每钱若干故钱数为单位若问每分若干则法首
　钱数为十位得为(三千五百/五十六)矣故定位须详问意乃
　要诀也

法有○筹式　　　　　法此欲分作(九百○/七分)也故以(九○/七)
假如布二万　　　　　　为法用三筹
一千七百六　　　　　　　　　　　如图简筹第(二/)行
十八丈给与　　　　　　　　　　　(一八/一四)商作(二/)减实
九百○七人　　　　　　　　　　　(一万八千/一百四十)馀(三千/六百)
各几何　　　　　　　　　　　　　(二十/八丈)次简第(四/)行
答曰(每人二/十四丈)　　　　　　　　　　　(三六/二八)商(四/)除实尽
　以上例皆法少于实故法首在原实中乃本法也

　
　
　
　
　
　
　
　

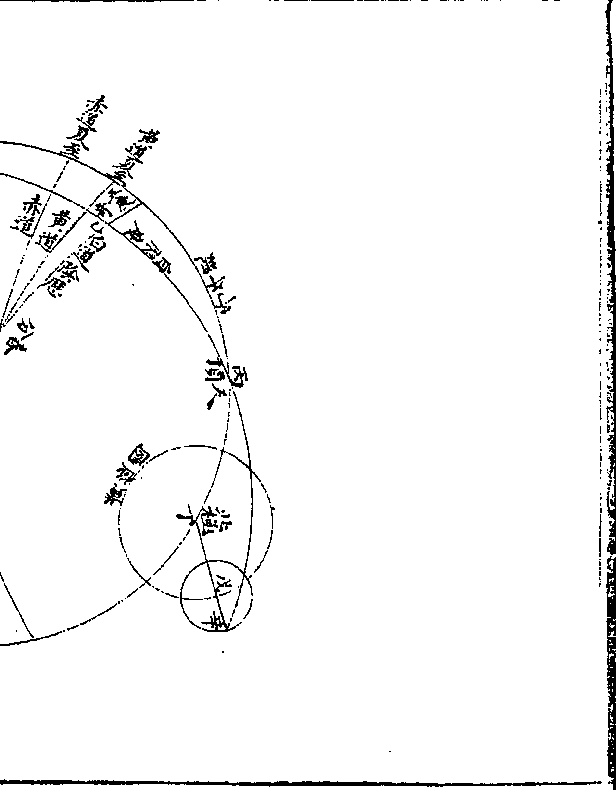
　以上两例皆法多于实者其法首位或在原实中必
　原实首位也或不在原实中则在其原实上几位也
　要之皆不能满法其所得必为分秒乃通变之法也
论曰除者分也吾欲作几分分之则为法所分之物为
　实所分之物能如所欲分之数则为满法满法则成
　一整数假如(三十/六)人分布而布有(三十/六)丈则各人分
　得一丈古云实如法而一正谓此也程大位算法统
　宗曰归于法前得零其意亦同此立法之本意也

　乃有所分之物原少于所欲分之数是不满法也既
　不满法则不能成一整数而所分者皆分秒之数假
　如(三十/六)人分布(二十/七)丈则每人不能分一丈只各得
　(七尺/五寸)是于(一/丈)内得其(七分/五秒)也然必先知整数然后可
　以知分秒故必于原实上虚拟一满法之位若曰能
　如此则分得整数矣而今不能则所分得者皆分秒
　也于是视所拟整数虚位距商数若干位而命之若
　相差一位则得为十之一(如两有钱/尺有寸)隔位则为百之

　一(如两有分/丈有寸)此乃通变之法要其为法上得零则一
　而已矣
又论曰此原实即不满法也若馀实不满法除之终不
　能尽则以命分之法御之详后
　命分法
法曰凡除法商数至单已极而有馀实不尽者不能成
　一整数也则以法命之此有二法
一法即以除法为命分不尽之数为得分则云几十几

　分之几
解曰命分者以一整数拟作若干分而命之如满此数
　则成一整数而今数少故命之也得分者今所仅有
　之数在命分数内得若干也(命分者古谓之分母/得分者古谓之分子)
假如古历以九百四十分为日法每年三百六十五日
　又九百四十分日之二百三十五约为四之一(约法/见后)
一法除之至尽古历家所谓退除为分秒是也单下有
　一位命为十分之几有两位命为百分之几十几三

　位则命分千四位则命分万皆以除得数为得分
假如授时历法每岁三百六十五日二千四百二十五
　分是以万分为日即命分也
　式如后
假如五尺为步每方一步积二十五尺今有积二百四
　十尺得若干步
　答曰九步又五分步之三

　　　　　　　　　　如图列实简筹第九行是二二
　　　　　　　　　　五商作九(第九/行故)减实二百二十
　　　　　　　　　　五尺馀一十五不尽以法命之
　　　　　　　　　　命为九步又二十五分步之一
　　　　　　　　　　十五约为五之三(约分法/见后)
　
　　　　　　　　　　若用第二命分法再列馀实加
　　　　　　　　　　○位商之以得其分秒如后

　　　　　　　　　　馀实下加一圈则一十五尺通
　　　　　　　　　　为一百五十分可再商矣
　　　　　　　　　　简等第六行是一五○商六分
　　　　　　　　　　除馀实恰尽
　　　　　　　　　　命分九步六分(即十分/步之六)
　　　　　　　　　　(命分第二法与法多于实/除法同故皆曰除分秒也)
若馀实为一十六尺则又不尽一尺法当于不尽一
○之下再加一圈为一○○使此一尺化为一百分而

再除之得四釐共九步六分四釐(即百分步/之六十四)
　约分法
约分者约其繁以从简也
法曰母数子数平列相减而得其纽数即以纽数为法
　转除两原数而得其可约之分
凡约分相减不拘左右但以少减多如左少右多则以
　左减右左多右少则以右减左若减之后或多者变
　而少则转减之必减至左右相同无可减而止即纽

　数也(若一减之即得纽/数则不必转减)
解曰纽数者互相减之馀数相等者也以此除两数则
　皆可分乃两数之枢纽
　若相减至尽而无纽数者则不可约
假如母数二十五子数一十五约之若干
　答曰五之三
　一○　先以(十/五)　　复以(一/十)　○五
　二五　减(二十/五)一○转减(十/五)　一○

　一五　馀(一十/○)一五　馀(○/五)　　○五
　复以(○/五)转减(一/十)馀(○五左右皆/五即为纽数)以纽数(○/五)为法转除
　母(二十/五)得(五/)除子数(一十/五)得(三/)故曰五之三盖母数
　是五个五子数是三个五也
　　此转减例
又如母数九百四十子数二百三十五约之若干
　答曰四之一
　先以(二百三/十五)减(九百/四十)馀(七百/○五)又减之馀(四百七/十○)又减

　之馀(二百三/十五)
　　　　　　左右皆(二百三/十五)即纽数也
　　　　　　以纽数(二百三/十五)转除母数(九百/四十)得(四/)除
　　　　　　子数(二百三/十五)得一故曰四之一
　　　　　　母数是四个(二百三/十五)
　　　　　　子数是一个(二百三/十五)
　此不转减例
　历算全书卷三十