声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
历算全书 卷二十九 第 1a 页 WYG0794-0652c.png
 钦定四库全书
钦定四库全书历算全书卷二十九
宣城梅文鼎撰
古算衍略
古算器考
或有问于梅子曰古者算学亦有器乎曰有曰何器曰
古用筹筹何似曰汉书言之矣用竹径一分长六寸二
百七十一而成六觚为一握度长短者不失毫釐量多
历算全书 卷二十九 第 1b 页 WYG0794-0652d.png
 少者不失圭撮权轻重者不失黍累又世说言王衍持
少者不失圭撮权轻重者不失黍累又世说言王衍持牙筹会计此用筹之明證也曰若是则筹可用竹亦可
用牙矣然则即今之筹笇非欤曰非也今西历用筹亦
起徐李诸公盖从历家之立成而成即立成表之活者
耳故一筹即备九数若古之用筹用以纪数而无字画
故一筹只当一数乘除之时以筹纵横列于几案一望
了然观古算字作算盖象形也然则起于何时曰是不
可考然大易揲蓍亦以一蓍当一数则其来远矣蓍策
历算全书 卷二十九 第 2a 页 WYG0794-0653a.png
 所以决疑非常用之物故特隆重其制而加长长则不
所以决疑非常用之物故特隆重其制而加长长则不可以横故皆纵列惟分二象两之后挂一策以别之使
无凌杂馀皆纵列也又其数只四十九故四揲以稽其
实数其用专专则诚也布算之法有十百千万之等以
乘除而升降又日用必需之物故其制短使几案可列
其言六寸成觚者有度量之用古尺既小于今尺才四
寸奇盖亦取其便于手握耳(浦江吴氏中馈录有算条/巴子切肉长三寸各如算)
(子样亦可以/想其长短)然则其用之若何曰五以下皆纵列六以
历算全书 卷二十九 第 2b 页 WYG0794-0653b.png
 上则横置一筹以当五而纵列其馀(式详/后)然则十百千
上则横置一筹以当五而纵列其馀(式详/后)然则十百千万何以列之曰其式皆自左而右略如珠笇之位亦如
西域欧逻写算之位皆顺手势不得不同也曰亦有徵
欤曰有之蔡九峰洪范皇极数所纪算位一至五皆纵
列六至九皆横一于上以当五又自一之一至九之九
皆并列两位自左而右此用于宋者也又授时历草所
载乘除法实之式皆纵横排列自左而右以万千百十
零为序此用于元者也左传史赵言亥有二首六身下
历算全书 卷二十九 第 3a 页 WYG0794-0653c.png
 二如身为绛县老人日数士文伯知其为二万六千六
二如身为绛县老人日数士文伯知其为二万六千六百六旬而孟康杜预颜师古释之皆以为亥字二画在
上其下三六为身如笇之六盖横一当五又竖一于横
一之下则为六矣与皇极同也又言下亥二画竖置身
傍盖即竖两笇为二万又并三六为六千六百六旬而
四位平列与历草同此又用于三代及汉晋者也
曰历草又有一至五横纪之处何欤曰此亦非起于历
草也何以知之唐人论书法横直多者有俯仰向背之
历算全书 卷二十九 第 3b 页 WYG0794-0653d.png
 法若直如笇子便不是书其言笇子即所列筹也然兼
法若直如笇子便不是书其言笇子即所列筹也然兼横直画言之则唐人用筹为算亦有横直可知乾凿度
云卧算为年立算为日盖位数多者恐其相混故三十
三二十二之类笇位皆一纵一横以别之纵即立算横
即卧算也乾凿度不知作于何人然其在汉魏以前无
可疑者则横直相错之法古有之矣五以下既可易纵
为横则六以上横一当五者亦可易之而纵又何疑于
历草哉曰然则今用珠盘起于何时曰古书散亡苦无
历算全书 卷二十九 第 4a 页 WYG0794-0654a.png
 明据然以愚度之亦起明初耳何以知之曰归除歌括
明据然以愚度之亦起明初耳何以知之曰归除歌括最为简妙此珠盘所恃以行也然九章比类所载句长
而涩盖即是时所创后人踵事增华乃更简快是书为
钱塘吴信民作其年月可考而知则珠盘之来则自不
远
按钦天监历科所傅通轨凡乘除皆有定子之法惟
珠算则可用然则珠算即起其时又尝见他书元统
造大统历访求得郭伯玉善算以佐成之即郭太史
历算全书 卷二十九 第 4b 页 WYG0794-0654b.png
 之裔也然则珠盘之法盖即伯玉等所制亦未可定
之裔也然则珠盘之法盖即伯玉等所制亦未可定曰南雷答牧斋流变三叠之问既云长水分别算位本
位是竖进一位即是横本位是横进一位即是竖又引
凿度卧算立算以證之矣然其所图算位俱作圆点殊
无横直之形何耶曰南雷固言今之算器数分于珠是
指珠算也又云长水之算只用今器其所谓横竖者分
别算位南雷之意盖谓长水姑借横竖之语以分算位
而实用珠算非实有横竖也然以(鼎/)观之疏既以一横
历算全书 卷二十九 第 5a 页 WYG0794-0654c.png
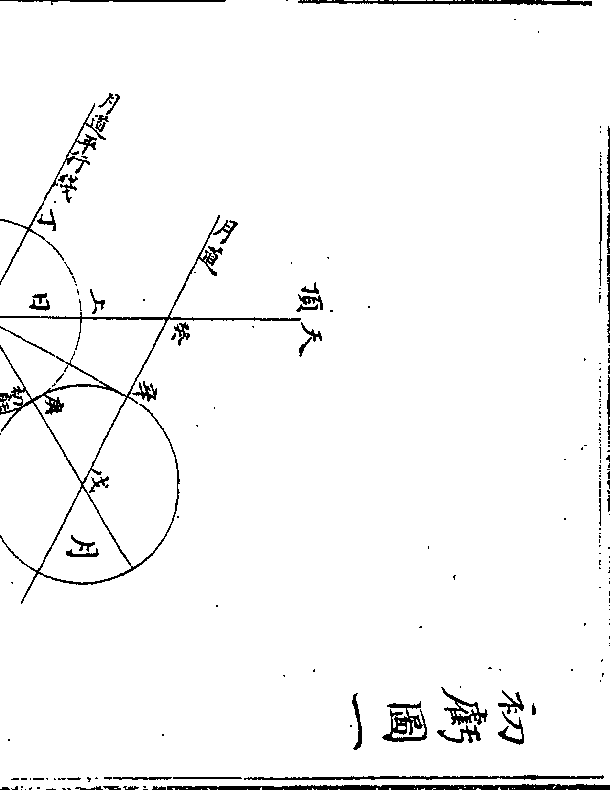 二竖当十二复以一竖二横当百二十终以一横二竖当
二竖当十二复以一竖二横当百二十终以一横二竖当千二百而皆曰进动算位明是用筹非用珠也故当十
进百之时则当取去第一叠零位之二竖而加十位之
一横为二横又添一竖于百位则成百二十矣故曰进
动算位为第二叠也百进千则又取去十位之二横而
增一竖于百位为二竖又别增一横于千位成千二百故亦曰
进动算位为第三叠也说本明晰与今珠算何涉乎若
如南雷所图则横竖字为赘文矣是故布筹可纵可横
历算全书 卷二十九 第 5b 页 WYG0794-0654d.png
 此亦一證
此亦一證又按朱子语类云潜虚之数用五只似如今算位一
般其直一画则五也下横一画则为六横二画则为
七此又一證也(蔡九峰皇极数以横画当五故下竖/一画为六竖二画为七与此相反然)
(理则相通历草则兼/用之盖皆本之古法)
历算全书 卷二十九 第 6a 页 WYG0794-0655a.png
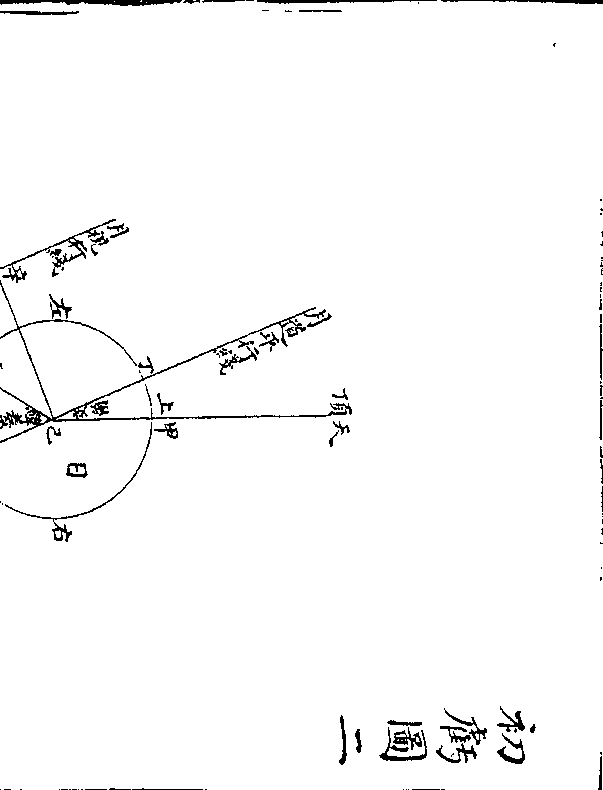 古布算式
古布算式皇极数图(见性理大全/)
历算全书 卷二十九 第 6b 页 WYG0794-0655b.png
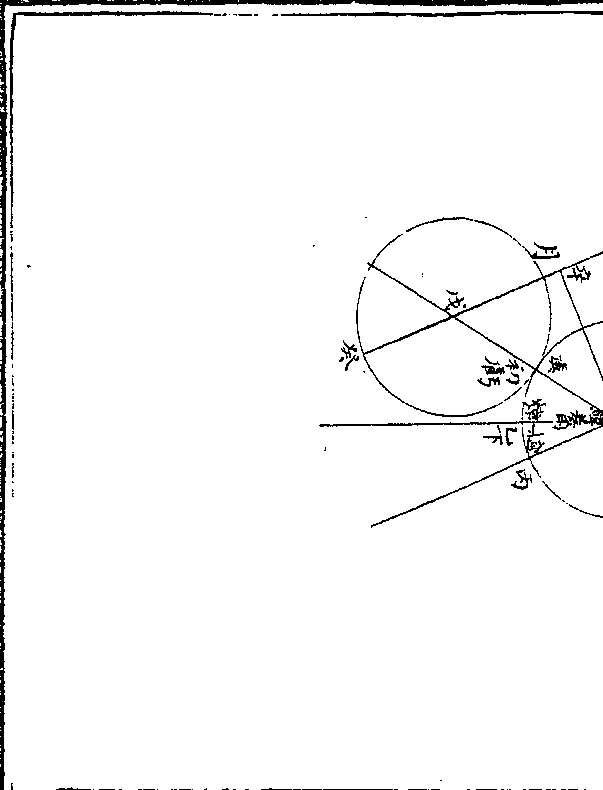 历草算式
历草算式立差 定平差 定平积
右式皆因数有雷同故纵横列之以为别亦自然之理也
历算全书 卷二十九 第 7a 页 WYG0794-0655c.png
 乘除法实式(亦见历草/)
乘除法实式(亦见历草/)历算全书 卷二十九 第 8a 页 WYG0794-0656a.png
 亥字二首六身考
亥字二首六身考左传襄公三十年三月癸未绛县老人曰臣生之岁正
月甲子朔四百有四十五甲子矣其季于今三之一也
师旷曰鲁叔仲惠伯会郤成子于承匡之岁也(注鲁文/公十一)
(年乙/巳岁)七十三年矣(注自乙巳岁至今年戊午首末七十/四年而曰七十三者盖计其全数而)
(言未满七/十三年也)史赵曰亥有二首六身(注言亥字上二画为/首六画为身如算之)
(六者三也春秋/时有此字体□)下二如身是其日数也(注如往也言除/下亥上二画往)
(置身旁也□便是此老人从初生年起至今癸未日之/日数也盖以亥之二画为二万之数以三六之算为六)
历算全书 卷二十九 第 8b 页 WYG0794-0656b.png
 (千六百六/旬之数也)士文伯曰然则二万六千六百有六旬也
(千六百六/旬之数也)士文伯曰然则二万六千六百有六旬也按古法每年三百六十五日又四分之一七十三年
该二万六千六百六十三日又四分之一故注以正
月甲子为夏正建寅之月而三月癸未杜氏长历及
孔疏皆以为当作二月为夏之十二月也其癸未日
长历以为是二十三日然则春秋所纪者自用周正
而晋人所言者自是夏正故鲁史纪戊午二月者晋
人所言则仍为丁巳之十二月所以士文伯云七十
历算全书 卷二十九 第 9a 页 WYG0794-0656c.png
 三年也
三年也历算全书 卷二十九 第 10a 页 WYG0794-0657a.png
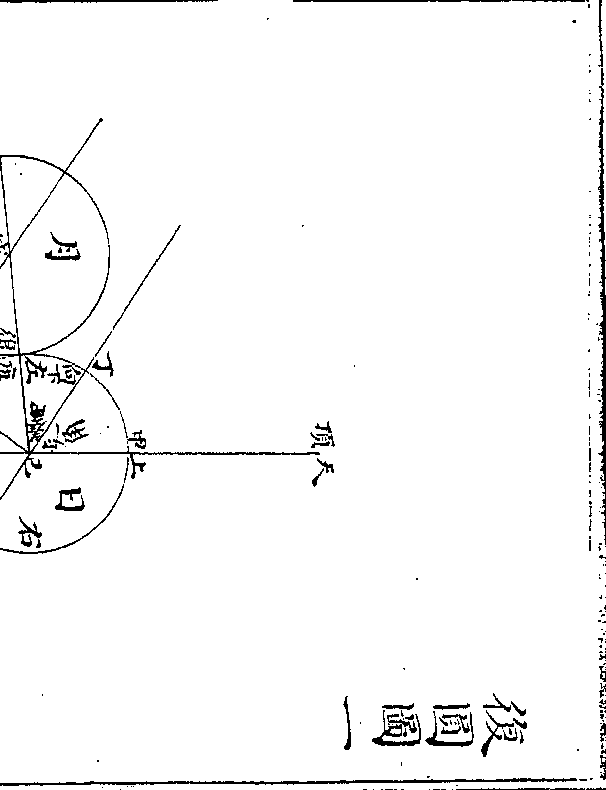
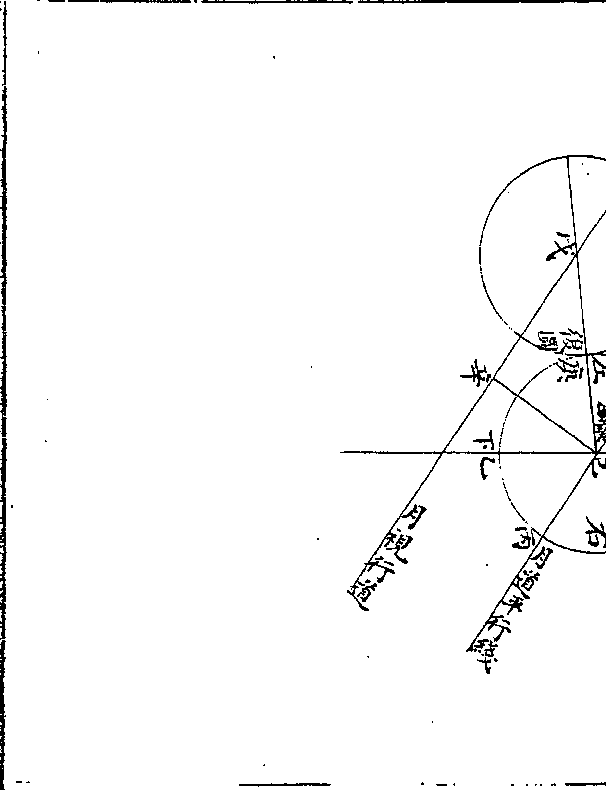
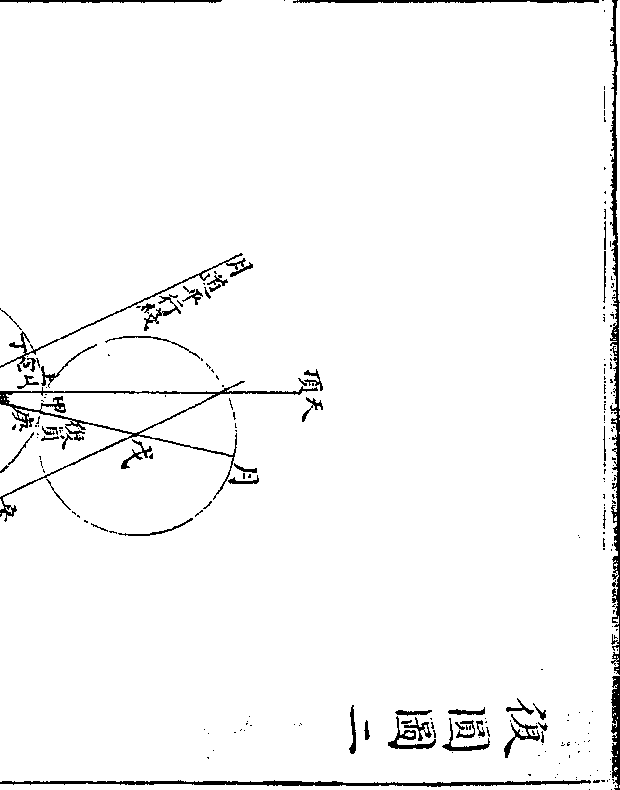
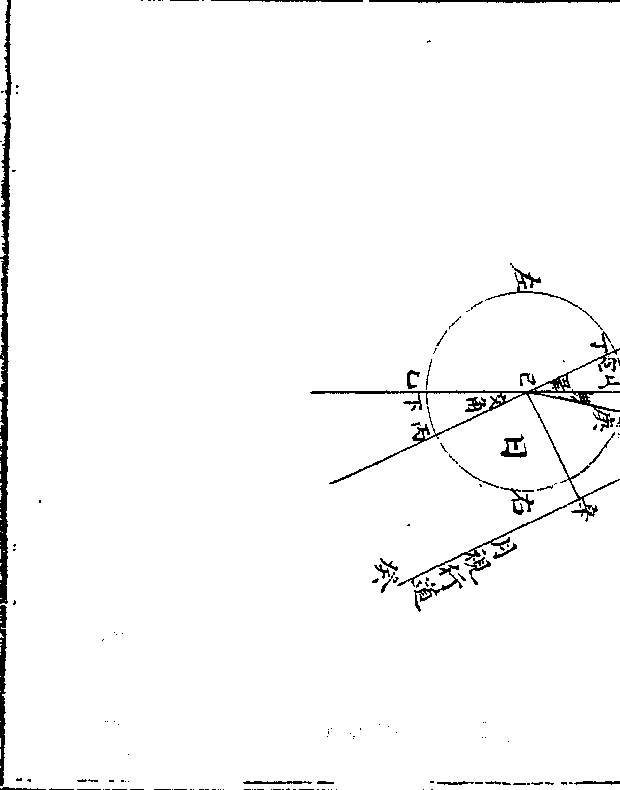
 筹有色以分正负
筹有色以分正负沈存中括笔谈曰天有黄赤二道月有九道此皆强名
非实有也亦由天之有三百六十五度天何尝有度以
日行三百六十五日而一期强谓之度以步日月五星
行次而巳日之所由谓之黄道南北极之中间度最均
处谓之赤道月行黄道南谓之朱道北谓之黑道东谓
之青道西谓之白道黄道内外各四并黄道而九日月
之行有迟有速难以一术御故因其合散分为数段每
历算全书 卷二十九 第 10b 页 WYG0794-0657b.png
 段以一色名之欲以别算位而已如算法用赤筹黑筹
段以一色名之欲以别算位而已如算法用赤筹黑筹以别正负之数历家不知其意遂以为实有九道甚可
嗤也
按此又宋算用筹之明證
历算全书 卷二十九 第 11a 页 WYG0794-0657c.png
 方田通法序
方田通法序学必有原不得其原不可以为学九数之学具列周官
而孔子言游艺在志道据德依仁后唐十经博士期业
成以五年可形下视哉客岁之冬从竹冠先生饮令弟
乐翁所得观先生捷田歌括离奇出没杯酒间未深领
其趣属他故羁治城且匝月既无携书可破岑寂乃稍
忆所疑演而通之因浩然叹数学之有源虽至近若方
田而易简中精深尔尔也算具不具仗三寸不聿为之
历算全书 卷二十九 第 11b 页 WYG0794-0657d.png
 今年春里中有事履亩或见问桐陵法遂出斯编相质
今年春里中有事履亩或见问桐陵法遂出斯编相质命曰方田通法云
阏逢执徐日躔在奎勿庵梅文鼎识
历算全书 卷二十九 第 12a 页 WYG0794-0658a.png
 方田通法
方田通法太极生生之数
数始于天一终于地十十亦一也天地之地始终乎一
故曰太一太一者太极也自极而仪而象而卦皆加一
倍三加而止万事托始焉是故制器者尚其象玑衡八
尺周于八方寻常则之以度百物盖取诸此
两地之数
一生二二者两地也两一则二两二则四两四则八两
历算全书 卷二十九 第 12b 页 WYG0794-0658b.png
 八则十有六四象相交成十六事卦有内外也庾以命
八则十有六四象相交成十六事卦有内外也庾以命斗秉以命斛斤两则之以权百物盖取诸此
参天之数
一生二二生三三者参天也参一而三参二而六参四
而十有二参八而二十有四作历者以纪中节八节二
十四气八卦二十四爻也是故玉衡之尺八而玑围二
十有四斤之两十有六而铢二十有四二十有四者权
度之所生数之纲也从而十之以为地纪而亩法生焉
历算全书 卷二十九 第 13a 页 WYG0794-0658c.png
 亩法
亩法二百四十步 古法步百为亩亩百为夫今二百四十
步为亩相傅起于唐太宗
步法
五 合参两则五犹合四行为土土之生数也倍五则
十土之成数也乘者从生故平方五尺为步而用以乘
除者从成故积步二百四十为亩而用以除
方田原法
历算全书 卷二十九 第 13b 页 WYG0794-0658d.png
 以所丈田横步与其纵步相乘得数为实以一亩二百
以所丈田横步与其纵步相乘得数为实以一亩二百四十步为法除之满法为亩不满退除为分釐 田之
为字衡缩相交矩其外格其内象平方也田不能皆方
或圆或直或梯或斜或如牛角或为矢弧不皆方故为
之法以方之大约不离横纵者近是九章之术首列方
田君子絜矩之道欤
截归法
或八归三归各一次或四归六归各一次或五因一十
历算全书 卷二十九 第 14a 页 WYG0794-0659a.png
 二归 邵子曰三八二十四也四六亦二十四也倍十
二归 邵子曰三八二十四也四六亦二十四也倍十二亦二十四也丈量家用截法可以观已
减法
或折半减二或减六减五各一次 即定身除也
飞归法
进一除二四 进二除四八 进三除七二 进四除
九六 五除一二 一四四作六 一六八作七 一
九二作八 二一六作九 见一加三隔位四 见二
历算全书 卷二十九 第 14b 页 WYG0794-0659b.png
 加六隔位八 不尽者留法喝之
加六隔位八 不尽者留法喝之又
三六作一五 六作二五 八四作三五 一○八作
四五 一三二作五五 一五六作六五 一八作七
五 二○四作八五 二二八作九五
留法
一留退四一六六 二留退八三三三 三留一二五
四留一六六六六 五留二○八三三 六留二五
历算全书 卷二十九 第 15a 页 WYG0794-0659c.png
 七留二九一六六 八留三三三三三 九留三七
七留二九一六六 八留三三三三三 九留三七五 其法是除用之似乘以其为除后得数也故谓之
留 若用以喝稍者言退者本位不则进一位或稍子
位多者喝完总移进之更妙
凡加留减者如加减法只记原实于各挨身加减之若
原用因法者则又下一位挨加减之皆记原实以留法
喝之言退者各又退一位
以上截留飞减四法皆于乘土之后用以求亩惟留法
历算全书 卷二十九 第 15b 页 WYG0794-0659d.png
 则有不尽故长于喝稍
则有不尽故长于喝稍后有用两求斤留法附录之 一退六二五 二一二
五 三一八七五 四二五 五三一二五 六三七
五 七四三七五 八五 九五六二五 十六二五
十一六八七五 十二七五 十三八一二五 十
四八七五 十五九三七五
新增径求亩步法
其法不用乘土以所得横纵之步先得者为实后得者
历算全书 卷二十九 第 16a 页 WYG0794-0660a.png
 为法径求之可以抵掌而办原法二十有二竹冠道士
为法径求之可以抵掌而办原法二十有二竹冠道士衍为百二十有三勿庵氏引而伸之且三百八十有四
也倚数之妙乃至斯乎而岂有外于参两乎又岂有加
于所谓一者乎法列如后
减二 即十二除凡法之可以两者皆减二是为亩法
之半或折半六归之
八除 或二十五于下位加之凡法之可以参者皆八
除是为亩法三分之一
历算全书 卷二十九 第 16b 页 WYG0794-0660b.png
 四十八除 即折半飞归也凡法之可以五者皆四十
四十八除 即折半飞归也凡法之可以五者皆四十八除是两其亩法也
四除 或二十五乘之凡法之可以六者皆四除是为
亩法六分之一
六除 凡法之可以四者皆六除是为亩法四分之一
三除 凡法之可以八者皆三除是为亩法八分之一
下加 凡法之上位得一者皆下加
上加 凡法之下位得一者皆上加凡加毕再用留法
历算全书 卷二十九 第 17a 页 WYG0794-0660c.png
 或飞归之
或飞归之折半 凡法之十二者皆折半为亩法六分之五
减六 凡法之可以十五者皆减六即两求斤留法也
为亩法三分之二又为六分之四
减五 凡法之可以十六者皆减五即十五除也为亩
法八分之五
加留减留 凡法之可借上者皆加留可借下者则减
留所以通其穷也
历算全书 卷二十九 第 17b 页 WYG0794-0660d.png
 随数喝亩 凡二十四则随数喝之
随数喝亩 凡二十四则随数喝之倍法 凡四十八五除之即二因也
减八 即亩法八分之六也凡法之可以八分用六者
十八除之又为四分之三
九除 即亩法八分之三凡法之可以八分用三者九
除之
二十一除 即亩法八分之七凡法之可以八分用七
者二十一除
历算全书 卷二十九 第 18a 页 WYG0794-0661a.png
 因法代除 如四十八则二因之如七十二则三因九
因法代除 如四十八则二因之如七十二则三因九十六则四因又如十二五因一四四六因一六八七
因一九二八因二一六九因又如六用二五因八四
用三五因一○八用四五因一三二用五五因一五
六用六五因一八用七五因二○四用八五因二二
八用九五因
加法代除 如三加二五即一二五乘所以代八除也
三六加五即十五乘也又如四二径加七五五四二
历算全书 卷二十九 第 18b 页 WYG0794-0661b.png
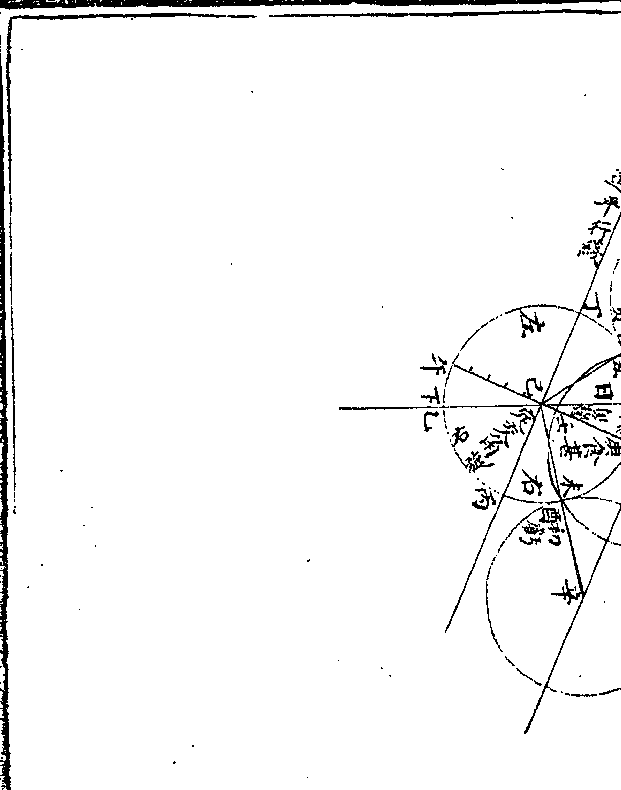 次加五皆不用除
次加五皆不用除历算全书 卷二十九 第 19a 页 WYG0794-0661c.png

历算全书 卷二十九 第 20a 页 WYG0794-0662a.png

历算全书 卷二十九 第 21a 页 WYG0794-0662c.png

历算全书 卷二十九 第 22a 页 WYG0794-0663a.png

历算全书 卷二十九 第 23a 页 WYG0794-0663c.png
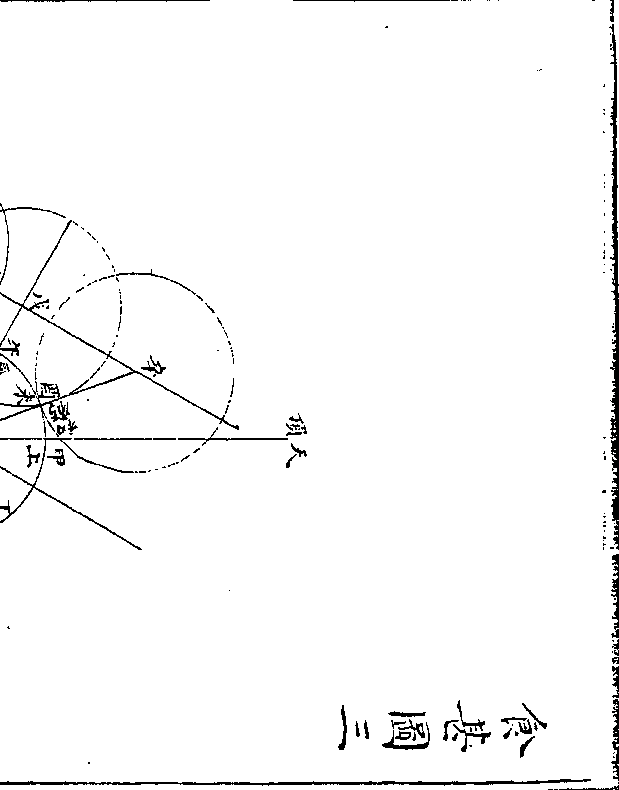
历算全书 卷二十九 第 24a 页 WYG0794-0664a.png
 原法歌诀(出桐陵/)
原法歌诀(出桐陵/)量田捷法少人知 不乘一数便留之 二弓折半六
而一 三步之中用八归 四步由来六归是 五步
还宜六八归 六数四归无走作 八上三归无改移
十二将来折一半 十六三而加倍齐 二十四中
随数喝 廿五中分六八归 三十二上尤甚准 四
因还要用三归 四十八上加一倍 八卦宫中谁得
知 三归八因尤甚准 胜如神见不差池 七二倍
历算全书 卷二十九 第 24b 页 WYG0794-0664b.png
 之加遍五 九十六上四因之 十五之中逢二八
之加遍五 九十六上四因之 十五之中逢二八七五之中四八归 三七半时当八八 九弓加五四
归奇 十八折之加五定 三六之中加五施 此是
明师真口诀 千金不度世人知
附归除捷法
多上空加一(多上者实多于法也空者实首隔一位也/凡实多于法则于实前隔一位上一子若)
(法实两数/等亦同)
依前除莫疑(依前者即以前/法数除之也)
历算全书 卷二十九 第 25a 页 WYG0794-0664c.png
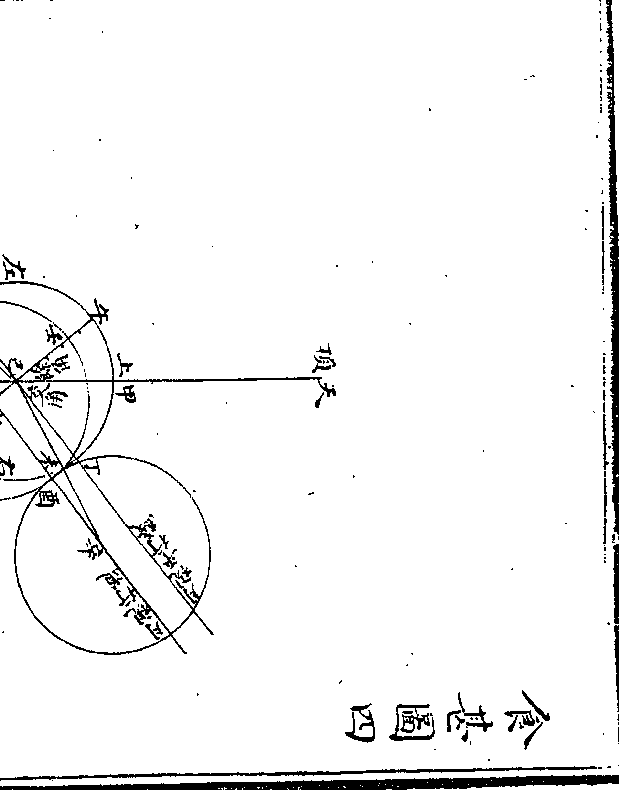 少前数上五(少前者实少于法也即于实/之前位上五子 不隔位)
少前数上五(少前者实少于法也即于实/之前位上五子 不隔位)折半数除之(折半除者用法数之半而除/之也 用五乘代折半甚捷)
无除随上一(无除者上五之后不及除半数也/既不及除随于实前位上一子)
化下照前除(化下者退下一位也照前除者/即依法数降一位而除之也)
历算全书 卷二十九 第 26a 页 WYG0794-0665a.png
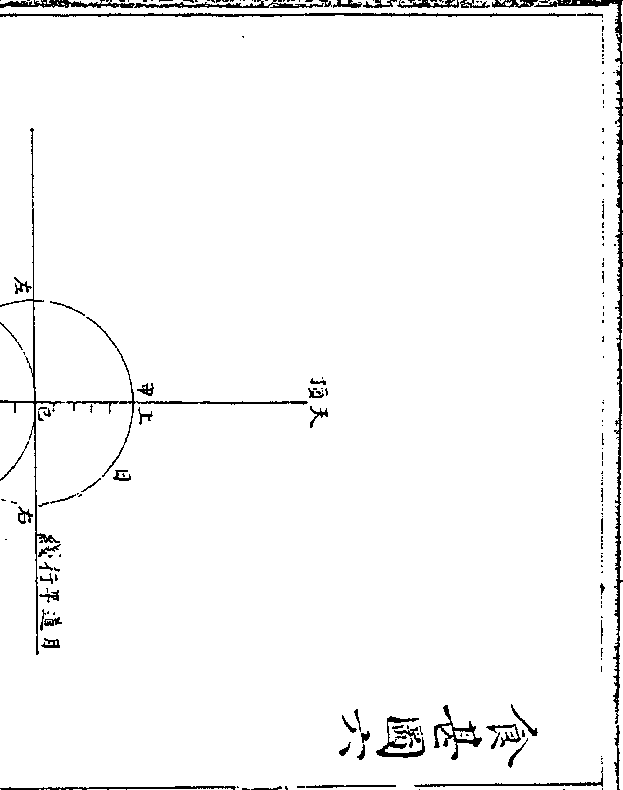
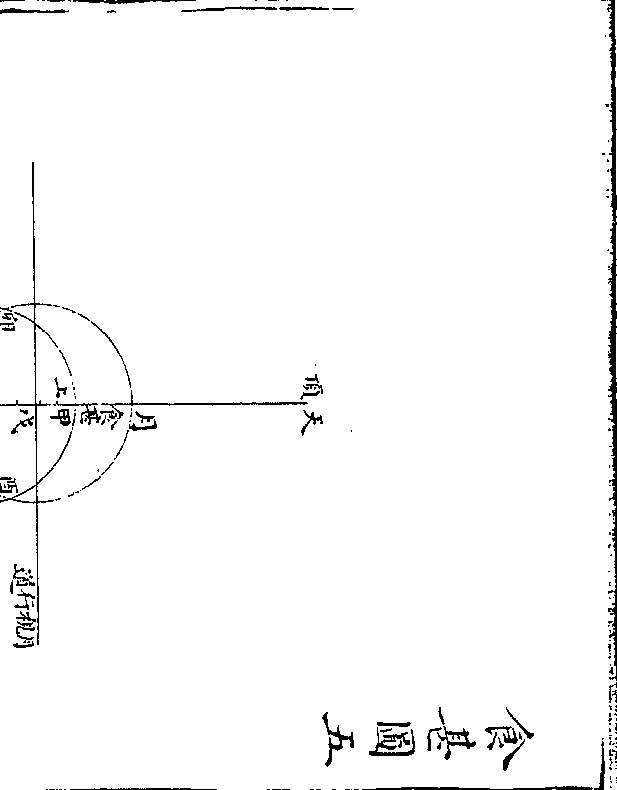 区田图刋误
区田图刋误按区田古法并以方一尺五寸为区通计每亩可二千
七百区空一行种于所种行内隔一区种一区除隔空
外可种六百七十五区(此亦约略之说后又云每区一/斗每亩可收六十六石而诗亦)
(云限将一亩作田规计区/六百六十二并大同小异)是四分而种其一也今农书
之图黑白相间是二分种一与说相背且如所图既不
便于营治亦不便于浇灌反不如姜田之用阔沟通人
行之为便矣谨依古说改作之如左
历算全书 卷二十九 第 26b 页 WYG0794-0665b.png
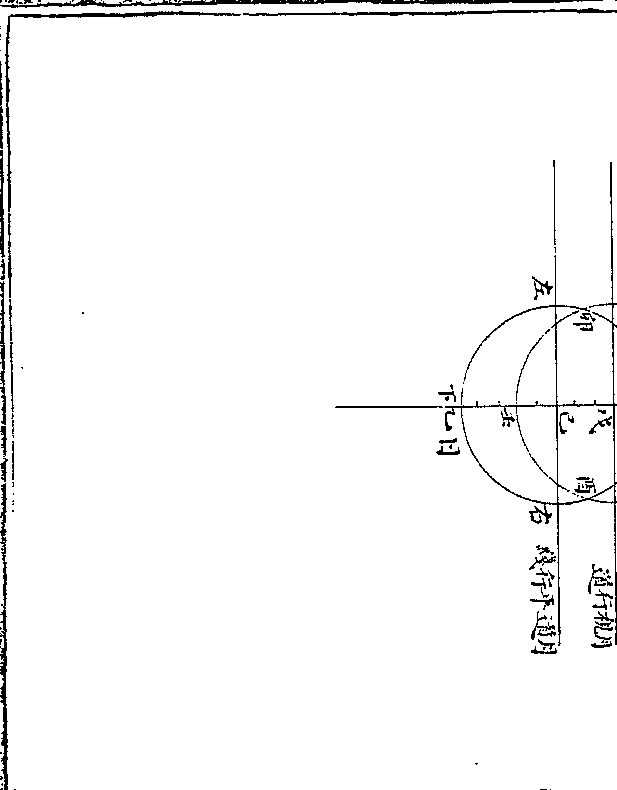 又按四分种一亦是约略之数若细求之则四边近田
又按四分种一亦是约略之数若细求之则四边近田塍处可只空半区要以随方就圆使其易行亦不在拘拘
于尺寸之间也孟子曰此其大略也若夫润泽之则在
君与子吾于区田亦云
如甲乙为田内每画方一尺五寸为区(如甲/子)直行每隔
一行种一行(如甲戊/丙巳)因得横行亦然(如庚甲/辛癸)其播种之
区四面合之各成小平方如丙辛方中间子丑为种地
卯寅方中间午未方为种地皆居小平方之中央又蝉
历算全书 卷二十九 第 27a 页 WYG0794-0665c.png
 联而下通计每田一亩为种区者约四之一图中白者
联而下通计每田一亩为种区者约四之一图中白者是空地黑者是种区
历算全书 卷二十九 第 28a 页 WYG0794-0666a.png
 区田说
区田说向读嵇叔夜养生论谓区种之法亩可得粟数十钟已
读王氏农书详著其法而农政全书载汜胜之书及务
本书谓汤有七年之旱伊尹作为区田教民粪种负水
浇田诸山陵倾坂及田邱城上皆可为之王祯田古人
每区收榖一斗每亩可收六十六石今人学种可减半
计贾思协曰兖州刺史刘仁之昔在洛阳于宅田七十
步之地域为区田收粟三十六石然则一亩之收过百
历算全书 卷二十九 第 28b 页 WYG0794-0666b.png
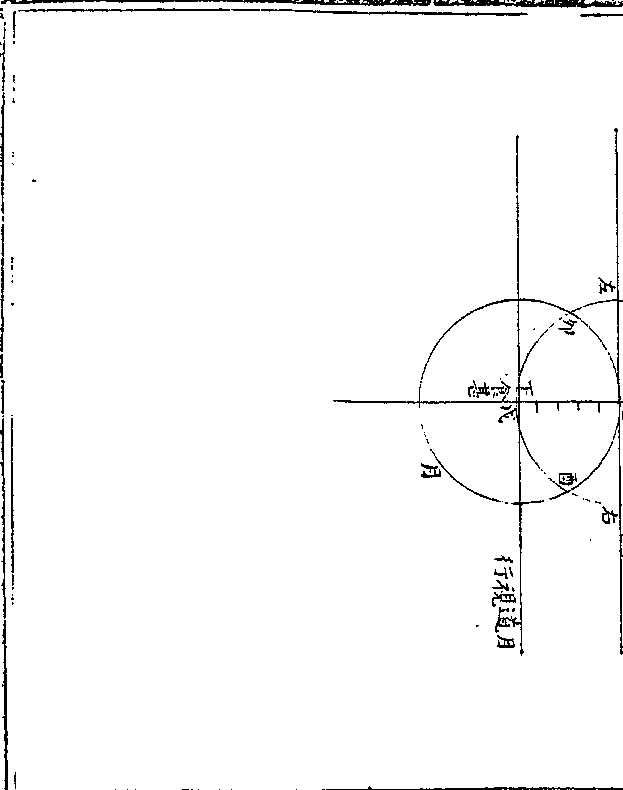 石矣古说彰彰如是而或者疑之(徐玄扈先生以为/古今斗斛之异)余
石矣古说彰彰如是而或者疑之(徐玄扈先生以为/古今斗斛之异)余以为不必疑也盖徵之于姜芋矣吾乡土瘠每亩收稻
麦不过数石而芋则每亩二十馀石多者三十馀石姜
之下者二十馀石其上者至四十馀石然而种姜一亩
有稻田六亩以上之工岂非粪多力勤之效乎考姜田
营治之法其耕甚深在一尺以上通水沟虽止数寸而
畦土斜杀而上种姜棱背相距空间与棱背略相等是
亦空一行种一行也即区种之遗法也姜田惟空直行
历算全书 卷二十九 第 29a 页 WYG0794-0666c.png
 而区田复空横行是其功又倍于姜田也多收之数又
而区田复空横行是其功又倍于姜田也多收之数又何疑焉(又考遂宁王灼晦叔糖霜谱蔗田亦云区种而/其深耕摩劳开渠阔尺深尺五及今年为蔗田)
(明年改种五榖以休/地诸法并同姜田) 又按区田每区方一尺五寸(贾/氏)
(说又有方深各六寸及/方九寸深六寸诸法)盖欲于城上斜坡立区故为此
制若平田亦可变通
历算全书 卷二十九 第 30a 页 WYG0794-0667a.png
 畸零法解(乘法/)
畸零法解(乘法/)假如其处地亩被水所淹今涸出五分之四于中又有
高地居七分之四问若干
答曰高地为三十五之十六
法用母乘母子乘子 两母(五/七)相乘
三十五为母 两子(四/四)相乘十六为
子 乘得三十五之十六
解曰分总地为五分而涸出居其四四又将此涸出之
历算全书 卷二十九 第 30b 页 WYG0794-0667b.png
 四分分为七分而高地居其四若以总地分三十五分
四分分为七分而高地居其四若以总地分三十五分则高地居其十六矣
本法置实子五之四以法子七之四乘之得十六为实
法母七为法除之得五之二又小分七之二为高地
然七除不尽当用通分法以小分母七通原分母五为
三十五得数二通为十四加入之二共十六是三十五
之十六也
今不用七除其子而以七乘其母得数亦同(母既七倍/而子不动)
历算全书 卷二十九 第 31a 页 WYG0794-0667c.png
 (是七之一也故/乘母即同除子)
(是七之一也故/乘母即同除子)以数明之 设原数三千五百亩内涸出五之四是二千
八百亩也以此二千八百亩分为七分而高地居其四
是一千六百亩也则高地于原数为三十五之十六矣
又假如有米一宗内分七之四于预备仓收贮又于预
备仓内取五之四先给赈荒问若干
答曰三十五之一十六 法见前
解曰分总米为七分而预备仓得其四又分预备仓米
历算全书 卷二十九 第 31b 页 WYG0794-0667d.png
 为五分而先给赈济者得其四若以总米分为三十五
为五分而先给赈济者得其四若以总米分为三十五分则先给赈济者得其十六
本法置实七之四以法子之四乘之得一十六为实
法母五为法除之得三又五之一如法用通分以小分
五通大分七为三十五又通得数三为十五加子一为
十六即三十五之十六也
今不用五除子而用五乘母即得三十五之十六省通
分矣(母乘得五倍则/子为五之一)
历算全书 卷二十九 第 32a 页 WYG0794-0668a.png
 以数明之 设原米四千二百石分为七分而取其四
以数明之 设原米四千二百石分为七分而取其四为预备仓是二千四百石也预备仓米又分五分而
取其四以给赈是一千九百二十石也若分原米为
三十五分每分一百二十石则给赈米得十六分(四/千)
(二百是三十五个一百二十石一千九/百二十是十六个一百二十石故也)
又法
法用倒位互除以代乘法 以法子四
除实母七得一七五为母 以法母五
历算全书 卷二十九 第 32b 页 WYG0794-0668b.png
 除实子四得○八○为子 乘得一七五之八○
除实子四得○八○为子 乘得一七五之八○各进位而倍之即三十五之十十六
本法四乘五除今不以四乘其子而反以四除其母即
得数同也(母既改为四之一而子不动即子为四倍故/除母可代乘子也然除法多有不尽不如母)
(乘母子乘/子为便)
还原
历算全书 卷二十九 第 33a 页 WYG0794-0668c.png
 畸零除法
畸零除法假如营兵奉裁五之一留五之四其所支月饷为某仓
米七之四问未裁时月饷几何
答曰该支仓米七之五
法用倒位互乘以当除法 以法子之
四乘实母七得二十八为母 以法母
五乘实子之四得二十为子 除得二
十八之二十 约为七之五
历算全书 卷二十九 第 33b 页 WYG0794-0668d.png
 解曰兵奉裁留五之四其原额未裁则五之五也故其
解曰兵奉裁留五之四其原额未裁则五之五也故其原支仓米亦必七之五乃四而增一之比例
本法置实七之四 以法母五乘之得七之二十为实
以法子之四为法除之得七之五
今不用四除其子而以四乘其母得数亦同(母既四倍/于原母而)
(原子不动如四之一/故乘母可代除子)
又法
法以法母五除实母七得一四为母
历算全书 卷二十九 第 34a 页 WYG0794-0669a.png
 又以法子之四除实子之四得一○为
又以法子之四除实子之四得一○为子 除得一四之一○ 约之亦得七
之五
此不用五乘其子而以五除其母得数亦同(母既五除/则为原母)
(五之一而原子不动如五/倍矣故除母可当乘子)
论曰以上三法所得并同然倒位乘尤妙盖以乘代除
则无畸零不尽之数故也
以数明之 设营兵三千其五之四则二千四百也仓
历算全书 卷二十九 第 34b 页 WYG0794-0669b.png
 米二千五百二十石其七之四则一千四百四十石
米二千五百二十石其七之四则一千四百四十石也七之五则一千八百石也兵二千四百而给米一
千四百四十石则兵三千当给一千八百石
还原
用倒位互除 以代乘法 法子四除
实母二十八得七为母 法母五除实
子二十得四为子 乘得七之四复合
原数
历算全书 卷二十九 第 35a 页 WYG0794-0669c.png
 问仓米七之四可给营兵五之四若仓米全发给兵几
问仓米七之四可给营兵五之四若仓米全发给兵几何
答曰给兵五之七
如法倒位 以法子之四乘实母五得
二十为母 以法母七乘实子之四得
二十八为子 除得二十○之二十八 约为五之
七 子大于母收为一又五之二是可给原额兵而
仍多五分之二也
历算全书 卷二十九 第 35b 页 WYG0794-0669d.png
 解曰原给仓米七之四而今全给七分是四分而增其
解曰原给仓米七之四而今全给七分是四分而增其三也故兵亦四分增三(于五之四增五之/三即为五之七)
本法置实之四以法母七乘之得五之二十八为实法
子四为法除之得五之七(今以四乘母代四/除子与前条同)
以前数明之仓米二千五百二十石分为七分则每分
三百六十石营兵三千分为五分则每分六百以仓
米四分给兵四分是每米三百六十石给兵六百名
也今仓米全给为三百六十石者七则兵为六百者
历算全书 卷二十九 第 36a 页 WYG0794-0670a.png
 亦七是四千二百名也除三千名满原额净多一千
亦七是四千二百名也除三千名满原额净多一千二百名之饷为五分之二(以七除五不尽/故不用又法)
历算全书 卷二十九 第 36b 页 WYG0794-0670b.png
历算全书卷二十九