声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
历算全书 卷七序 第 1a 页 WYG0794-0109a.png
 序
序历家所凭全恃测验昔者蔡邕上书愿匍匐浑仪之下
按度考数著于篇章以成一代盛典古人之用心盖可
想见然则儒者端居斗室足不履观台目不睹浑象安
所得测验之事而亲之而安从学之曰所恃者有测验
之法之理在则句股是也遭秦之厄天官书器散亡汉
落下闳鲜于妄人等追寻坠绪历代相承考订加详至
于今日厥理大著则句股之用于浑圆是也今夫测量
历算全书 卷七序 第 1b 页 WYG0794-0109b.png
 之法方易而圆难古用径一围三聊举成数非有所不
之法方易而圆难古用径一围三聊举成数非有所不知也自刘徽祖冲之各为圆率逮元赵友钦定为径一
则围三一四一五九二与今西术略同皆割圆以得之
非句股奚藉焉(西法割圆比例以直角三边形为/主即句股也但异其名不异其实)然用
句股测平圆犹易用句股测浑圆更难历家所测皆浑
圆也非平圆也古有黄赤道相准之率大约于浑器比
量仅得梗槩未能彰诸笇术近代诸家以相减相乘推
变其差损益有序稍为近之而未亲也惟元郭太史守
历算全书 卷七序 第 2a 页 WYG0794-0110a.png
 敬始以弧矢命笇有平视侧视诸图推步立成诸数黄
敬始以弧矢命笇有平视侧视诸图推步立成诸数黄赤相求斯有定率视古为密由今观之皆句股也但其
立法必先求矢又用三乘方取数不易故但能列其一
象限中度率不复能求其细分之数历书之法则先求
角既因弧以知角复因角以知弧而句股之形能预定
其比例又佐之八线互用以通其穷其法以三弧度相
交辄成三角则此三弧度者各有其相应之弦弧与弧
相割即弦与弦相遇而句股生焉苟熟其法则正反斜
历算全书 卷七序 第 2b 页 WYG0794-0110b.png
 侧八线犁然各相得而成句股(八线比例以半径全数/为弦正弦馀弦为句为)
侧八线犁然各相得而成句股(八线比例以半径全数/为弦正弦馀弦为句为)(股又以割线为弦切线与半径全数为/其句股表中所列句股形凡五千四百)于是乎黄可变
赤赤可变黄可以经度知纬可以纬度知经罗络钩连
旁通曲畅分秒忽微胪陈笇位求诸中心可无纤芥之
疑告诸同学亦如指掌之晰即不必匍匐浑仪之下可
以不窥牖而见天道赖有此具也全部历书皆弧三角
之理即皆句股之理顾未尝正言其为句股使人望洋
无际(彼云直角三边形此云句股乃西国/方言译书时不知此理遂生分别)又译书者识
历算全书 卷七序 第 3a 页 WYG0794-0110c.png
 有偏全笔有工拙语有浅深详略所载图说不无渗漏
有偏全笔有工拙语有浅深详略所载图说不无渗漏之端影似之谈与臆参之见学者病之兹稍为摘其肯
綮从而疏剔订补以直截发明其所以然窃为一言以
蔽之曰析浑圆寻句股而已盖于是而知古圣人立法
之精虽弧三角之巧岂能出句股范围然句股之用亦
必至是而庶无馀蕴尔历法之深微奥衍不啻五花八
门其章句之诘曲离奇不啻羊肠絙度而由是以启其
扃钥庶将掉臂游行若揭日月而骋康庄矣文虽不多
历算全书 卷七序 第 3b 页 WYG0794-0110d.png
 实为此道中开辟涂径盖积数十年之探索而后能会
实为此道中开辟涂径盖积数十年之探索而后能会通简易故亟欲与同志者共之余老矣禹服九州之大
历代圣人教泽所渐被必有好学深思其人所冀大为
阐发俾古人之意晦而复昭一线之传引而弗替则生
平之志愿毕矣岂必身擅其名然后为得哉余拭目俟
之康熙二十三年上元甲子长至之吉勿庵梅文鼎书
于柏枧山中
历算全书 卷七序 第 4a 页 WYG0794-0111a.png
 钦定四库全书
钦定四库全书历算全书卷七
宣城梅文鼎撰
弧三角举要卷一
弧三角体势
弧三角与平异理故先体势知体势然后可以用算而
算莫先于正弧犹平三角之有句股形也故以为弧度
之宗正弧形之之角取法于黄赤交角则有定度而馀
历算全书 卷七序 第 4b 页 WYG0794-0111b.png
 角取法于过极圈交黄道之角则随度而移互用之其
角取法于过极圈交黄道之角则随度而移互用之其理益显故有求馀角法弧三角以一角对一边而比例
等与平三角同而其理回别故有弧角比例法斜弧无
相对之弧角则比例之法穷故有垂弧法三角求边则
垂弧之法又穷故有次形法垂弧与次形合用则有捷
法弧与角各有八线而可以互视故有相当法(馀详环/中秦尺)
(及堑堵/测量)
弧度与天相应
历算全书 卷七序 第 5a 页 WYG0794-0111c.png
 弧三角之法以测浑员浑员之大者莫如天员之至者
弧三角之法以测浑员浑员之大者莫如天员之至者亦莫如天故弧三角之度皆天度也
以平测员其难百倍以员测员其简百倍而得数且真
是故测天者必以弧度而论弧度者必以天为法
测弧度必以大圈
浑球上弧度有极大之圈乃腰围之一线也如赤道带
天之纮原止一线如黄道如子午规如地平规尽然
又如测得两星相距之远近亦为大圈之分(若以此两/星之距弧)
历算全书 卷七序 第 5b 页 WYG0794-0111d.png
 (引而长之必匝于浑员之体而成/大圈不论从衡斜侧皆同一法)
(引而长之必匝于浑员之体而成/大圈不论从衡斜侧皆同一法)球上大圈必相等
所以必用大圈者以其相等也 浑球上从衡斜侧皆
可为大圈而其大必相等者以俱在腰围之一线也如
黄道赤道及子午规地平规俱系大圈必皆相等不相
等即非大圈故惟大圈可相为比例(任测两星之距不/必当黄赤道而能)
(与二道相比例者/以其皆大圈也)
球上两大圈无平行者
历算全书 卷七序 第 6a 页 WYG0794-0112a.png
 大圈在浑球既为腰围之一线则必无两圈平行之法
大圈在浑球既为腰围之一线则必无两圈平行之法若平行即非大圈(如黄赤道并止一线而无广即无地/可容平行线也子午规地平规亦然)
球上圈能与大圈平行者皆小圈谓之距等圈
离大圈左右作平行圈皆曰距等圈谓其四围与大圈
相距皆等(如于黄道内外作纬圈其与黄道相距或近/则四面皆近或远则四面亦皆远无毫忽之)
(不同平行故也赤道/纬圈地平高度并同)而其自相距亦等故曰距等也(如/黄)
(道内外或近或远处处可作距等圈而皆与/黄道平行即其圈亦自相平行故并为等距)距等圈皆
小于大圈(如黄道内外纬圈但离数分其围即小于黄/道其距益远其圈益小小之极至一点而止)
历算全书 卷七序 第 6b 页 WYG0794-0112b.png
 (诸纬圈/并然)不能与大圈为比例(大圈惟一距等圈无数无/一同者无法可为比例)
(诸纬圈/并然)不能与大圈为比例(大圈惟一距等圈无数无/一同者无法可为比例)故为比例者必大圈也
历算全书 卷七序 第 7a 页 WYG0794-0112c.png
历算全书 卷七序 第 8a 页 WYG0794-0113a.png
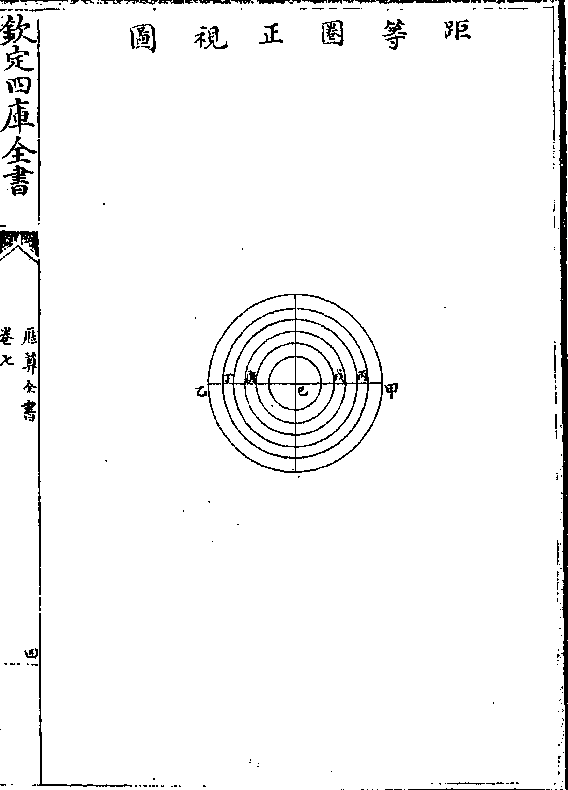
 如图甲乙为大圈大圈只一丙丁及戊庚等皆小圈小
如图甲乙为大圈大圈只一丙丁及戊庚等皆小圈小圈无数渐近圆顶己即其圈愈小而成一点大小悬殊
故不可以相为比例
大圈之比例以度不拘丈尺
凡圈皆可分三百六十度(每圈平分之成半周四平分/之成象限象限又各平分之)
(为九十度成/三百六十度)而球大者其大圈大球小者其大圈小皆
以本球之围径自为比例不拘丈尺(尽本球之围分为/全周之度其球上)
(之度即皆以此为准但在本球上为最/大故谓之大圈非以丈尺言其大小)古人以八尺浑
历算全书 卷七序 第 8b 页 WYG0794-0113b.png
 仪准周天盖以此也又如古浑仪原有三重其在内之
仪准周天盖以此也又如古浑仪原有三重其在内之环周必小于外而其度皆能相应者在内环周虽小而
在内之浑员以此为大圈即在内之各度并以此为准
故也
大圈之度为公度
凡球上距等圈亦可平公三百六十度而其圈皆小于
本球之大圈又大小不伦则其所分之细度亦皆小于
大圈而大小不伦矣惟本球腰围大圈上所分之度得
历算全书 卷七序 第 9a 页 WYG0794-0113c.png
 为公度故凡言度者必大圈也
为公度故凡言度者必大圈也历算全书 卷七序 第 10a 页 WYG0794-0114a.png
 如图甲乙为大圈一象限丙丁及戊庚各为距等小圈
如图甲乙为大圈一象限丙丁及戊庚各为距等小圈一象限象限虽同而大小迥异又如甲辛为大圈三十
度丙壬及戊癸亦各为小圈之三十度其为三十度虽
同而大小亦异再细考之至一度或至一分亦大小异
也故惟大圈之度为公度
大圈即本球外周其度即外周之度而横直皆相等
平员有径有周浑员亦有径有周立浑员于前则外周
可见即腰围之大圈也旋而视之皆可为外周故大圈
历算全书 卷七序 第 10b 页 WYG0794-0114b.png
 之横直皆等(皆以外周度/为其度故等)
之横直皆等(皆以外周度/为其度故等)历算全书 卷七序 第 11a 页 WYG0794-0114c.png

历算全书 卷七序 第 11b 页 WYG0794-0114d.png
 如图子午规为浑仪外周其度三百六十乃横度也地
如图子午规为浑仪外周其度三百六十乃横度也地平为腰围度亦三百六十乃横度也横度直度皆得为
外周故其度相等若依北极论之则赤道又为腰围而
亦即外周也推是言之浑球上大圈从衡斜侧皆相等
何则旋而视之皆得为腰围即皆得为外周故也
大圈上相遇有相割无相切大圈相割各成两半分
球上从衡斜侧既皆成大圈则能相割矣而皆为浑员
之外周则必无相切之理(若相切者必在外周/之内为距等小圈)
历算全书 卷七序 第 12a 页 WYG0794-0115a.png

历算全书 卷七序 第 12b 页 WYG0794-0115b.png
 如图甲丙乙为大圈半周能割大圈于甲于乙而不能
如图甲丙乙为大圈半周能割大圈于甲于乙而不能相切丙丁成小圈则能切大圈于丙于丁
历算全书 卷七序 第 13a 页 WYG0794-0115c.png

历算全书 卷七序 第 13b 页 WYG0794-0115d.png
 如图甲庚辛乙为大圈半周割外圈于甲于乙则甲己
如图甲庚辛乙为大圈半周割外圈于甲于乙则甲己乙乙子甲亦各成半周若壬癸距等圈割大圈于庚于
辛而庚辛非半周
球上两大圈相割必有二处此二处必相距一百八十
度而各成两平分如黄赤二道相交于春分必复相交
于秋分即二分之距必皆半周一百八十度而黄道成
两半分赤道亦两平分也若距等圈与大圈相割必不
能成两平方
历算全书 卷七序 第 14a 页 WYG0794-0116a.png
 两大圈相遇则成角
两大圈相遇则成角球上大圈既不平行则其相遇必相交相割而成角弧
三角之法所由以立也角有正有斜斜角又有锐钝共
三种而角两旁皆弧线与直线角异
历算全书 卷七序 第 15a 页 WYG0794-0116c.png
 如图己午戊子为子午规辛午乙子为地平规两大圈
如图己午戊子为子午规辛午乙子为地平规两大圈正相交于南地平之午北地平之子则皆正角而四角
皆等并九十度角也(正角一名直角一名/十字角一名正方角)
历算全书 卷七序 第 16a 页 WYG0794-0117a.png
 如图午辛子为地平规丁辛癸为赤道规两大圈斜相
如图午辛子为地平规丁辛癸为赤道规两大圈斜相交于辛则丁辛子钝角大于九十度丁辛午锐角小于
九十度两角相并一百八十度减锐角其外角必钝若
减钝角亦得锐角也故有内角即知外角 又两锐角
相对两钝角相对其度分必等故有此角即知对角
凡此数端并与平三角同然而实有不同者以角两旁
之为弧线也
弧线之作角必两
历算全书 卷七序 第 16b 页 WYG0794-0117b.png
 直线剖平员作角形如分饼角旁两线皆半径至周而
直线剖平员作角形如分饼角旁两线皆半径至周而止弧线剖浑幂作角形如剖瓜角旁两弧线皆半周必
复相交作角而等(如黄赤道交于/二分其角相等)
角有大小量之以对角之弧其角旁两弧必皆九十度
弧线角既如瓜瓣则其相距必两端狭而中阔其最阔
处必离角九十度此处离两角各均即球上腰围大圈
也故其度即为角度(如黄赤道之二分交角二十三度/半即二至时距度此时黄赤道离)
(二分各九十度乃/腰围最阔处也)
历算全书 卷七序 第 17a 页 WYG0794-0117c.png
 大圈有极
大圈有极大圈能分浑员之面幂为两则各有最中之处而相对
是为两极两极距大圈四面各九十度
历算全书 卷七序 第 18a 页 WYG0794-0118a.png
 如图甲辛乙为赤道大圈己为北极己为南极甲己丁
如图甲辛乙为赤道大圈己为北极己为南极甲己丁己等弧线距北极各九十度距南极亦然 若己为天
顶甲辛乙为地平大圈亦同如甲正北辛正东乙正南
丁东北丙东南所在不同而甲乙等高弧距天顶各九
十度皆等
大圈上作十字弧线引长之必过两极两极出弧线
至大圈必皆十字正交
如赤道上经圈皆与赤道正交为十字角则其圈必上
历算全书 卷七序 第 18b 页 WYG0794-0118b.png
 过北极下过南极也然则从两极出弧线过赤道必十
过北极下过南极也然则从两极出弧线过赤道必十字正交矣
大圈之极为众角所辏
如赤道上逐度经圈皆过两极则极心一点为众角之
宗(经圈之弧在赤道上成十字者本皆平/行渐远渐狭至两极则成角形之锐尖)角无论大小
皆辏于极而合成一点离此一点外即成锐钝之形而
皆与赤道度相应所谓量角以对弧度而角两旁皆九
十度以此
历算全书 卷七序 第 19a 页 WYG0794-0118c.png
历算全书 卷七序 第 19b 页 WYG0794-0118d.png
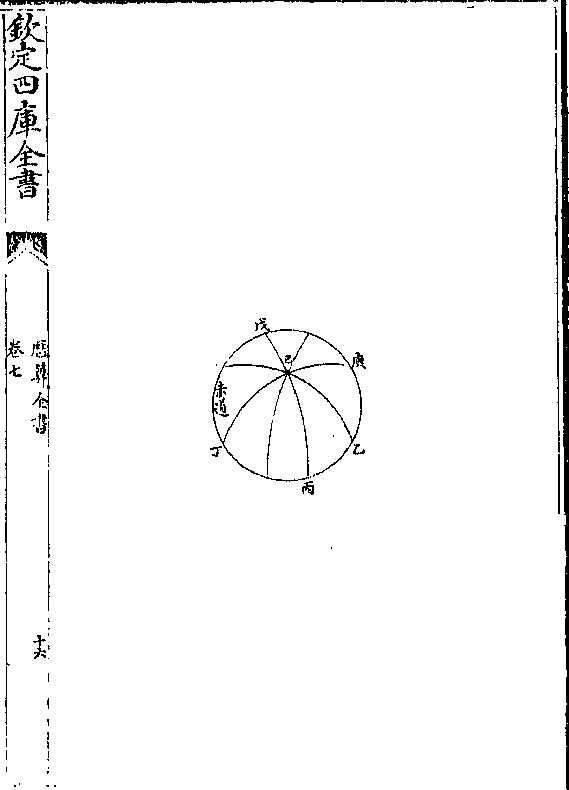
 如图己为北极即众角之顶锐其所当赤道之度如乙
如图己为北极即众角之顶锐其所当赤道之度如乙丙等则己角为锐角如丙庚等则己角为钝角 若己
为天顶外圈为地平亦然
角度与角旁两弧之度并用本球之大圈度故量角
度者以角为极
有弧线角不知其度亦不知角旁弧之度法当先求本
球之九十度(其法以角旁二弧各引长之使复作角乃中/分其弧即成本弧之九十度而角旁弧之度)
(可/知)以角为心九十度为界作大圈(与角旁两弧并本球/大圈而其分度等)
历算全书 卷七序 第 20a 页 WYG0794-0119a.png
 乃视角所当之弧(即角旁两九/十度弧所界)于大圈上得若干度分
乃视角所当之弧(即角旁两九/十度弧所界)于大圈上得若干度分即角度也故曰以角为极
三大圈相遇则成三角三边
此所谓弧三角形也如黄道赤道既相交于二分又有
赤道经圈截两道而过之则成乙丙甲弧三角形
历算全书 卷七序 第 21a 页 WYG0794-0119c.png
 知图己为北极戊辛为赤道丁庚为黄道二道相交于
知图己为北极戊辛为赤道丁庚为黄道二道相交于春分成乙角又己壬为过极经圈自北极己出弧线截
黄道于丙得丙乙边为黄道之一弧亦截赤道于甲成
甲乙边为赤道之一弧而过极经圈为二道所截成丙
甲边为经圈之一弧是为三边即又成丙角甲角合乙
角为三角
弧三角不同于平三角之理
弧三角形有三角三边共六件以先有之三件求馀三
历算全书 卷七序 第 21b 页 WYG0794-0119d.png
 件与平三角同所不同者平三角形之三角并之皆一
件与平三角同所不同者平三角形之三角并之皆一百八十度弧三角不然其三角最小者比一百八十度
必盈(三边在一度以下可借平三角立算因/其差甚微然其角度视半周必有微盈)但不得满
五百四十度(角之极大者合之以/比三半周必不能及)
平三角之边小仅咫尺大则千百万里弧三角边必在
半周以下(不得满一/百八十度)合三边不得满三百六十度(如满/全周)
(即成全员而/不得成三角)
平三角有两角即知馀角弧三角非算不知
历算全书 卷七序 第 22a 页 WYG0794-0120a.png
 平三角有一正角馀二角必锐弧三角则否(有三正角/两正角者)
平三角有一正角馀二角必锐弧三角则否(有三正角/两正角者)(其馀角有钝有锐或两锐/两钝或一锐一钝不等)
平三角有一钝角馀二角必锐弧三角则否(其馀角或/锐或正或)
(钝甚有三/钝角者)
平三角以不同边而同角为相似形同边又同角为相
等形弧三角则但有相等之形而无相似之形以同角
者必同边也
平三角但可以三边求角不可以三角求边弧三角则
历算全书 卷七序 第 22b 页 WYG0794-0120b.png
 可以三角求边(弧三角之边皆员度也初无丈尺可言故/三角可以求边若干三角边各有丈尺则)
可以三角求边(弧三角之边皆员度也初无丈尺可言故/三角可以求边若干三角边各有丈尺则)(必有先得之边以为之例所以不同相前条言有相等/之形无相似之形亦谓其所得之度 等非谓其丈尺)
(等/也)
弧三角用八线之理
平三角用八线惟用于角弧三角用八线并用于边平
三角以角之八线与边相比弧三角是以角之八线与
边之八线相比平三角有正角即为句股若正弧三角
形实非句股而以其八线辏成句股
历算全书 卷七序 第 23a 页 WYG0794-0120c.png
 平三角以角求边是用弧线求直线也(有角即/有弧)以边求
平三角以角求边是用弧线求直线也(有角即/有弧)以边求角是用直线求弧线也然角以八线为用仍是以直线
求直线也句股法也弧三角以边求角以角求边并是
以弧线求弧线也而角与边并用八线仍是以直线求
直线也亦句股法也(盖惟直线/可成句股)所不同者平三角所成
句股形即在平面而弧三角所成句股不在弧面而在
其内外
弧三角之点线面体
历算全书 卷七序 第 23b 页 WYG0794-0120d.png
 测量家有点线面体弧三角备有之其所测之角即点
测量家有点线面体弧三角备有之其所测之角即点也但其点俱在弧面(如于浑球任指一星为所测之点/即角度从兹起如太阳太阴角度)
(并从其中心/一点论之)
弧三角之边即线也但其线皆弧线(如浑球上任指两/星即有距线或于)
(一星出两弧线与他星相距即/成角而角旁两线皆弧线也)
弧三角之形即面也但其面皆浑球上面幂之分形
弧三角之所丽即浑体也剖浑员至心即成锥体而并
以弧三角之形为底(详堑堵/测量)
历算全书 卷七序 第 24a 页 WYG0794-0121a.png
 浑员内点线面体与弧三角相应
浑员内点线面体与弧三角相应前条点线面体俱在球面可以目视器测但皆弧线难
相比例(比例必用句股句/股必直线故也)赖有相应之点线面惟在浑
体内历员可指虽不可以目视而可以算得弧三角之
法所以的确不易也 如浑球中剖则成平员即面也
于是以球面之各点(即弧三角/之各角)依视法移于平员面即
浑员内相应之点也又以弧与角之八线移至平面成
句股以相比例是浑员内相应之线也 又如弧三角
历算全书 卷七序 第 24b 页 WYG0794-0121b.png
 之三边各引长之成大圈各依大圈以剖浑员即各成
之三边各引长之成大圈各依大圈以剖浑员即各成平员面是亦浑员内相应之面也二平员面相割成瓜
瓣之体三平员面相割成三楞锥体若又依八线横割
之即成堑堵诸体是浑员体内相应之分体也此皆与
弧面相离在浑员之内非剖浑员即不可见而可以算
得即不啻目视而器测矣
大圈与浑员同心
球上大圈之心即浑员之心(若依各大圈剖浑员成平/员面其平员心即浑员之)
历算全书 卷七序 第 25a 页 WYG0794-0121c.png
 (心/)若距等小圈则但以浑员之轴为心而不能以浑员
(心/)若距等小圈则但以浑员之轴为心而不能以浑员心为心同心者亦同径(大圈以浑员径为径若距/等圈则但以通弦为径)浑体
内诸线能与弧三角相应者以此(浑员体内诸线皆宗/其径弧三角既以大)
(圈相割而成必宗大圈/之径径同故内外相应)弧三角之边不用小圈亦以此
也(距等圈既与大圈异径则其度不齐不能成/边而所作之角必非真角无从考其度分也)
弧三角视法
弧三角非图不明然图弧线于平面必用视法变浑为
平
历算全书 卷七序 第 26a 页 WYG0794-0122a.png
 平置浑仪从北极下视则惟赤道为外周不变而黄道
平置浑仪从北极下视则惟赤道为外周不变而黄道斜立即成撱形 其分至各经圈本穹然半员今以正
视皆成员径是变弧线为直线也
历算全书 卷七序 第 27a 页 WYG0794-0122c.png
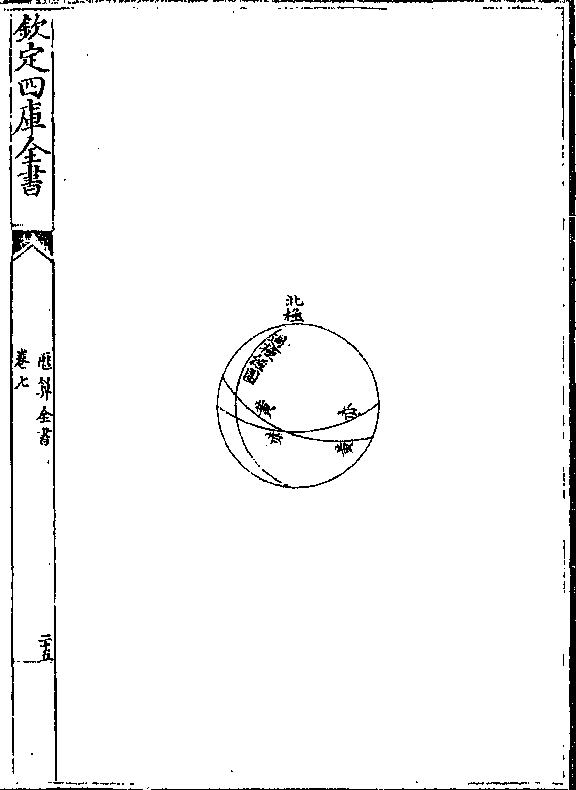
 立置浑仪使北极居上而从二分平视之则惟极至交
立置浑仪使北极居上而从二分平视之则惟极至交圈为外周不变其赤道黄道俱变直线为员径而成辏
心之角(即大距度/平面角)是变弧线角为直线角也(又距等圈/亦变横线)
(而成各度正弦/与员径平行)其赤道上逐度经圈之过黄赤道者虽
变撱形而其正弦不变且历算可见如在平面而与平
面上之大距度正弦同角成大小句股比例是弧面各
线皆可移于平面也故视法不但作图之用即步算之
法已在其中
历算全书 卷七序 第 27b 页 WYG0794-0122d.png
 以上谓之正视(以黄赤道为式若于六合仪取/天顶地平诸线亦同他可类推)
以上谓之正视(以黄赤道为式若于六合仪取/天顶地平诸线亦同他可类推)历算全书 卷七序 第 28a 页 WYG0794-0123a.png
历算全书 卷七序 第 29a 页 WYG0794-0123c.png
 以上谓之旁视(浑员上有垛叠诸线从旁侧视之/庶几可见虽不能按度肖形而大)
以上谓之旁视(浑员上有垛叠诸线从旁侧视之/庶几可见虽不能按度肖形而大)(意不失以显弧三/角之理为用亦多)
角之矢
如图甲丙乙丁半浑员以甲戊乙弧界之则其弧面分
两角为一锐一钝以视法移此弧度于相应之平面亦
一锐一钝即分员径为大小二矢而戊丙正矢为戊甲
丙锐角之度(戊乙丙/亦同)戊丁大矢为戊甲丁钝角之度(戊/乙)
(丁亦/同)故得矢即得角
历算全书 卷七序 第 30a 页 WYG0794-0124a.png
 角之八线
角之八线如前图丙戊弧为甲锐角之度与丙庚等则丙戊之在
平面者变为直线即为甲锐角之矢而戊巳为角之馀
弦戊庚为角之正弦丙辛为角之切线己辛为角之割
线皆与平面丙庚弧之八线等
丁巳戊过弧为甲钝角之度与丁乙庚过弧等则丁戊
在平面者变为钝角之大矢而戊巳馀弦戊庚正弦丙
辛切线己辛割线并与锐角同(平面钝角之八线与外/角同用弧三角亦然)
历算全书 卷七序 第 30b 页 WYG0794-0124b.png
 正弧斜弧之角与边分为各类
正弧斜弧之角与边分为各类凡三角内有一正角谓之正弧三角形三角内并无正
角谓之斜弧三角形
正弧三角形之角有三正角者有二正角一锐角者有
二正角一钝角者(以上种种/不须用算)又有一正角两锐角者(内/分)
(二种一种两锐角同度/一种两锐角不同度)有一正角两钝角者(内分二种/一种两钝)
(角同度一种两/钝角不同度)有一正角一锐角一钝角者(内分二种/一种锐钝)
(角角合之成半周一种合/锐钝两角不能成半周)计正弧之角九种而用算者
历算全书 卷七序 第 31a 页 WYG0794-0124c.png
 六也
六也正弧三角形之边有三边并足者(足谓足/九十度)有二边足一
边小者(在象限以/下为小)有二边足一边大者(过象限以上为/大○以上三种)
(可不/用算)有三边并小者(内分二种一种二边/等一种二边不等)有二边大而
一小者(内分三种一种二大边等一种二大边/不等一种小边为一大边减半周之馀)计正弧
之边八种而用算者五也
二边俱小则馀边必不能大故无二小一大之形
二边俱大则馀边亦不能大故无三边并大之形
历算全书 卷七序 第 31b 页 WYG0794-0124d.png
 一边若足则馀边亦有一足故无一边足之形
一边若足则馀边亦有一足故无一边足之形历算全书 卷七序 第 32a 页 WYG0794-0125a.png
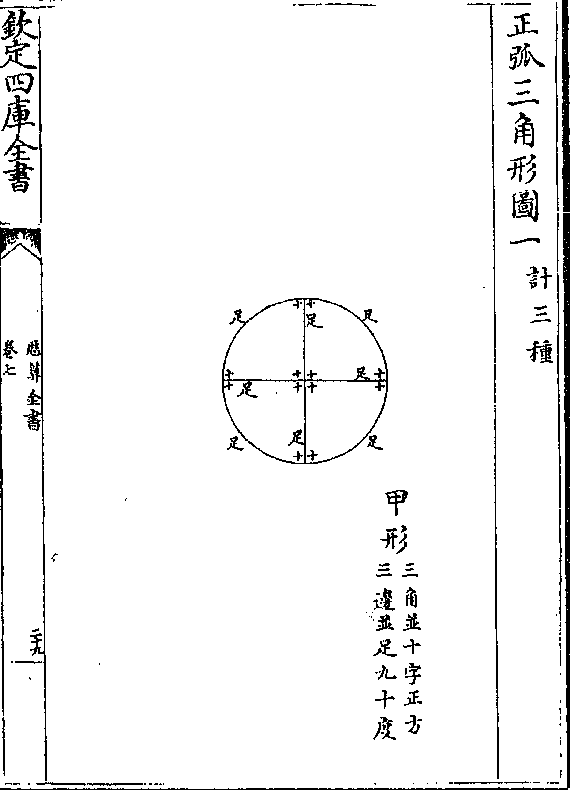 正弧三角形图一(计三种/)
正弧三角形图一(计三种/)历算全书 卷七序 第 33a 页 WYG0794-0125c.png

历算全书 卷七序 第 33b 页 WYG0794-0125d.png
 正弧三角形图二(讣三种/)
正弧三角形图二(讣三种/)历算全书 卷七序 第 34a 页 WYG0794-0126a.png

以上正弧形三种有同度之边与角谓之二等边形
内有己形虽无同等之边角而有共为半周之边角
历算全书 卷七序 第 34b 页 WYG0794-0126b.png
 度虽不同而所用之正弦则同即同度也
度虽不同而所用之正弦则同即同度也凡边等者角亦等后仿此
历算全书 卷七序 第 35a 页 WYG0794-0126c.png
 正弧三角形图三(计三种/)
正弧三角形图三(计三种/)历算全书 卷七序 第 35b 页 WYG0794-0126d.png

以上正弧形三种边角与丁戊巳三种无异但无同
度之边凡正弧三角形共九种
历算全书 卷七序 第 36a 页 WYG0794-0127a.png
 斜弧三角形之角有三角并锐者(内分三种一种有二/角相等一种三角不)
斜弧三角形之角有三角并锐者(内分三种一种有二/角相等一种三角不)(相等一种/三角俱等)有二角锐而一钝者(内分四种一种二锐角/相等一种二锐角不相)
(等一种钝角为一锐角减半周之馀一种/二锐角相等而又并为钝角减半周之馀)有二角钝而
一锐者(内分四种一种二钝角相等一种二钝角不相/等一种锐角为一钝角减半周之馀一种二钝)
(角相等而又并为/锐角减半周之馀)有三角并钝者(内分三种一种有二/角相等一种三角不)
(相等一种/三角相等)计斜弧之角十有四种
斜弧三角形之边有一边足二边小者(内分二种一种/二小边相等一)
(种二小/边不等)有一边足二边大者(内分二种一种二大边/等一种二大边不等)有
历算全书 卷七序 第 36b 页 WYG0794-0127b.png
 一边足一边小一边大者(内分二种一种大小二边合/之成半周一种合二边不能)
一边足一边小一边大者(内分二种一种大小二边合/之成半周一种合二边不能)(成半/周)有三边并小者(内分三种一种三边不等一/种二边等一种三边俱等)有二
边大而一小者(内分四种一种二大边等一种二大边/不等一种小边为一大边减半周之馀)
(一种二大边等而又并/为小边减半周之馀)有二边小而一大者(内分四种/一种二小)
(边等一种二小边不等一种大边为一小边减半周/之馀一种二小边等而又并为大边减半周之馀)有
三边并大者(内分三种一种三边不等一/种二边等一种三边俱等)计斜弧之边
二十种
历算全书 卷七序 第 37a 页 WYG0794-0127c.png
 斜弧三角形图一(计四种/)
斜弧三角形图一(计四种/)历算全书 卷七序 第 37b 页 WYG0794-0127d.png

以上斜弧形四种并三角三边同度谓之三等边形内有二
等边者其一边为等边减半周之馀与三等边同法(以同用/正弦故)
历算全书 卷七序 第 38a 页 WYG0794-0128a.png
 斜弧三角形图二(计十二种/)
斜弧三角形图二(计十二种/)历算全书 卷七序 第 39a 页 WYG0794-0128c.png

历算全书 卷七序 第 39b 页 WYG0794-0128d.png

以上斜弧三角形十二种并二等边形内有四种以大小二边
度成半周与二等边同法(小边为大边减半周/之馀则同用一正弦)
历算全书 卷七序 第 40a 页 WYG0794-0129a.png
 斜弧三角形图三(计十种锐历书只九/种遗一 二钝形)
斜弧三角形图三(计十种锐历书只九/种遗一 二钝形)历算全书 卷七序 第 41a 页 WYG0794-0129c.png

历算全书 卷七序 第 41b 页 WYG0794-0129d.png

以上斜弧三角形十种并三边不等(用算只/四种)
凡斜弧三角形共二十六种
通共弧三角形三十五种(内除正弧三种不须/用算实三十二种)
历算全书 卷七序 第 42a 页 WYG0794-0130a.png

历算全书 卷七序 第 42b 页 WYG0794-0130b.png
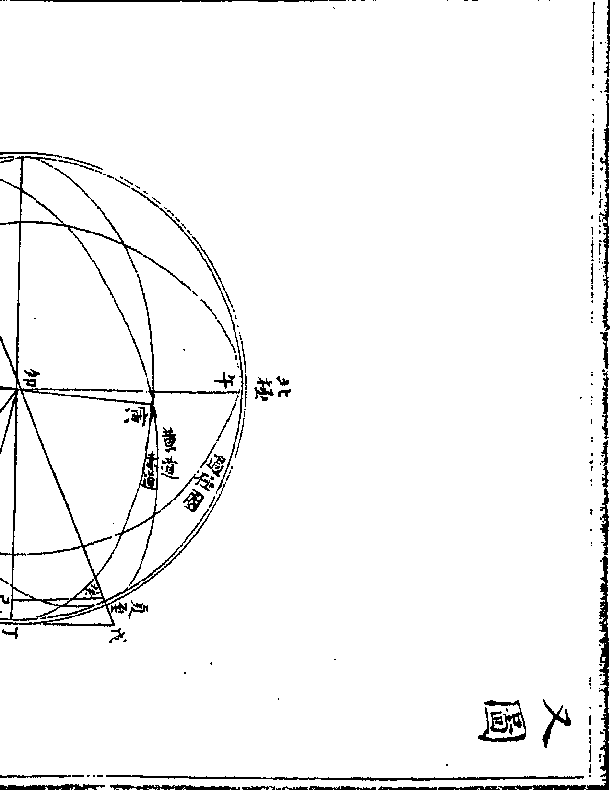
 乙丁寅为赤道乙丙癸为黄道乙与寅为春秋分癸为
乙丁寅为赤道乙丙癸为黄道乙与寅为春秋分癸为夏至午癸丁辰为极至交圈午与辰为南北极午丙甲
为过极经圈
丙乙为黄道距二分之度甲乙为赤道距二分之度(卯/同)
(升/度)丙甲为黄赤距纬成丙乙甲三角弧形甲为正角乙
春秋分角与浑员心卯角相应
癸丁弧为黄赤大距(即乙角之弧亦/为卯角之弧)癸巳为乙角正弦
卯巳其馀弦戊丁为乙角切线戊卯其割线卯癸及卯
历算全书 卷七序 第 43a 页 WYG0794-0130c.png
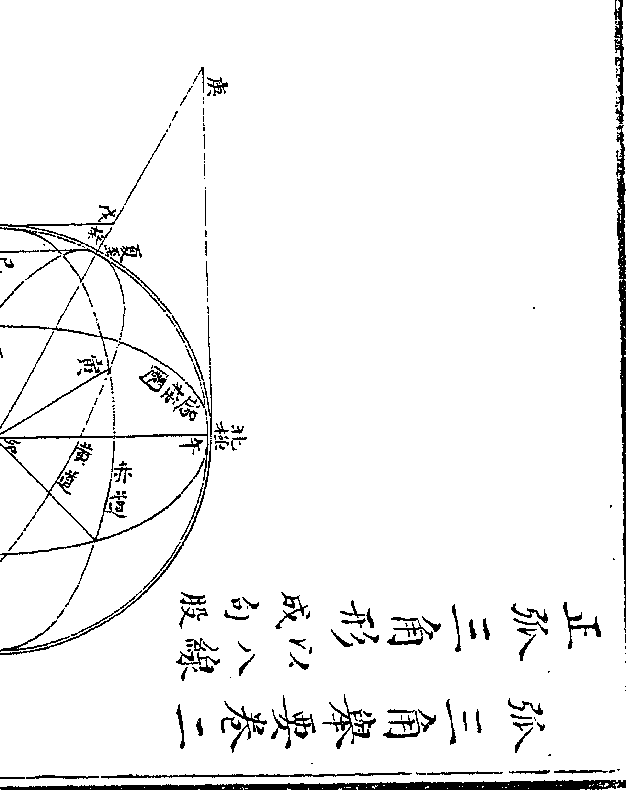 丁皆半径成癸巳卯及戊丁卯两句股形
丁皆半径成癸巳卯及戊丁卯两句股形又午卯半径庚午为乙角馀切庚卯为乙角馀割成午
卯庚倒句股形
丙辛为丙甲距度正弦丙壬为丙乙黄道正弦作辛壬
线与丁卯平行成丙辛壬句股形
子甲为丙甲距度切线甲丑为甲乙赤道正弦作子丑
线与丙壬平行成子甲丑句股形
酉乙为丙乙黄道切线未乙为甲乙赤道切线作酉未
历算全书 卷七序 第 43b 页 WYG0794-0130d.png
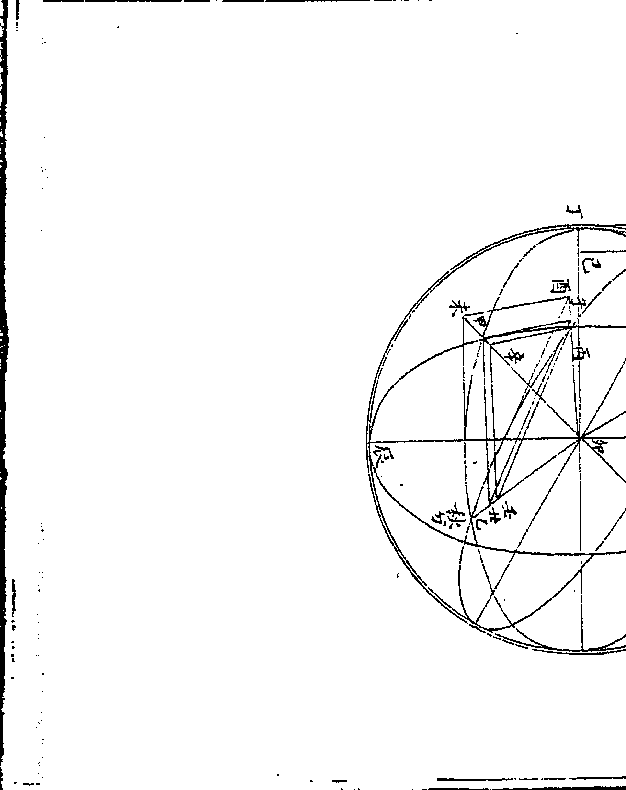 线与子甲平行成酉未乙句股形
线与子甲平行成酉未乙句股形前二句股形在癸丁大距弧内外(癸巳卯用正馀弦/在弧内戊丁卯用)
(割切线/出弧外)后三句股形在丙乙甲三角内外(丙辛壬在/丙角用两)
(正弦在浑员内子甲丑在甲角兼用正弦切线/半在内半在外酉未乙用两切线在浑员外)
论曰此五句股形皆相似故其比例等何也赤道平安
从乙视之则丁乙象限与丁卯半径视之成一线而辛
壬联线甲丑正弦未乙切线皆在此线之上矣以其线
皆平安皆在赤道平面与赤道半径平行故也(是为/句线)
历算全书 卷七序 第 44a 页 WYG0794-0131a.png
 赤道平安则黄道之斜倚亦平其癸乙象限与癸卯半
赤道平安则黄道之斜倚亦平其癸乙象限与癸卯半径从乙视之亦成一线而丙壬正弦子丑联线酉乙切
线皆在此线之上矣以其线皆斜倚皆在黄道平面与
黄道半径平行故也(是为/弦线)
黄赤道相交成乙角而赤道既平安则从乙窥卯卯乙
半径竟成一点而乙丑壬卯角合成一角矣
诸句股形既同角而其句线皆同赤道之平安其弦线
皆同黄道之斜倚则其股线皆与赤道半径为十字正
历算全书 卷七序 第 44b 页 WYG0794-0131b.png
 角而平行矣是故形相似而比例皆等也(其卯午庚倒/句股形为相)
角而平行矣是故形相似而比例皆等也(其卯午庚倒/句股形为相)(当之用与诸句股形/亦相似而比例等)
又论曰丙辛壬形两正弦(丙辛/丙壬)俱在浑体之内其理易
明子甲丑形甲丑正弦在浑体内子甲切线在浑体之
外已足诧矣酉未乙形两切线(酉乙/未乙)俱在浑体之外虽
习其术者未免自疑历书置而不言盖以此耶今为补
说详明欲令学者了然心目庶以用之不疑
用法
历算全书 卷七序 第 45a 页 WYG0794-0131c.png
 假如有丙乙黄道距春分之度求其距纬丙甲法为半
假如有丙乙黄道距春分之度求其距纬丙甲法为半径癸卯与乙角之正弦癸巳若丙乙黄道之正弦丙壬
与丙甲距纬之正弦丙辛也
一 半径全数 癸卯 弦
二 乙角正弦 癸巳 股
三 黄道正弦 丙壬 弦
四 距纬正弦 丙辛 股
若先有丙甲距度而求丙乙黄道距二分之度则反用
历算全书 卷七序 第 45b 页 WYG0794-0131d.png
 之为乙角之正弦癸巳与半径癸卯(若欲用半径为一/率以省除则为半)
之为乙角之正弦癸巳与半径癸卯(若欲用半径为一/率以省除则为半)(径午卯与乙角之馀/割庚卯其比例亦同)若丙甲距纬之正弦丙辛与丙乙
黄道之正弦丙壬也
一 乙角正弦 癸巳 半径全数 午卯 股
二 半径全数 癸卯 乙角馀割 庚卯 弦
三 距纬正弦 丙辛 股
四 黄道正弦 丙壬 弦
右丙辛壬形用法
历算全书 卷七序 第 46a 页 WYG0794-0132a.png
 假如有甲乙赤道同升度求距纬丙甲法为半径卯丁
假如有甲乙赤道同升度求距纬丙甲法为半径卯丁与乙角之切线丁戊若甲乙赤道之正弦甲丑与丙甲
距纬之切线子甲也
一 半径全数 卯丁 句
二 乙角正切 丁戊 股
三 赤道正弦 甲丑 句
四 距纬正切 子甲 股
若先有丙甲距纬而求甲乙赤道则反用之为乙角之
历算全书 卷七序 第 46b 页 WYG0794-0132b.png
 切线戊丁与半径丁卯(或用半径为一率则为半径/卯午与乙角之馀切午庚)若
切线戊丁与半径丁卯(或用半径为一率则为半径/卯午与乙角之馀切午庚)若丙甲距纬之切线子甲与甲乙赤道之正弦甲丑也
一 乙角正切 戊丁 半径全数 卯午 股
二 半径全数 丁卯 乙角馀切 午庚 句
三 距纬正切 子甲 股
四 赤道正弦 甲丑 句
右子甲丑形用法
论曰以上四法历书所有但于图增一卯午庚句股形
历算全书 卷七序 第 47a 页 WYG0794-0132c.png
 则互视之理更明
则互视之理更明假如有丙乙黄道距二分之度径求甲乙赤道同升度
法为半径卯癸与乙角之馀弦卯巳若丙乙黄道之切
线酉乙与甲乙赤道之切线未乙也
一 半径全数 卯癸 弦
二 乙角馀弦 卯巳 句
三 黄道正切 酉乙 弦
四 赤道正切 未乙 句
历算全书 卷七序 第 47b 页 WYG0794-0132d.png
 若先有甲乙赤道而求其所当黄道丙乙法为半径丁
若先有甲乙赤道而求其所当黄道丙乙法为半径丁卯与乙角之割线戊卯若甲乙赤道之切线未乙与丙
乙黄道之切线酉乙也
一 半径全数 丁卯 句
二 乙角正割 戊卯 弦
三 赤道正切 未乙 句
四 黄道正切 酉乙 弦
论曰以上两条酉未乙形用法予所补也有此二法黄
历算全书 卷七序 第 48a 页 WYG0794-0133a.png
 赤道可以自相求而正角弧形之用始备矣外此仍有
赤道可以自相求而正角弧形之用始备矣外此仍有三弧割线馀弦之用具如别纸
十馀年前曾作弧三角所成句股书一册稿存儿辈
行笈中觅之不可得也庚辰年乃复作此至辛己夏
复得旧稿为之惘然然其理固先后一揆而说有详
略可以互明不妨并存以徵予学之进退因思古人
毕生平之力而成一事良自不易世有子云或不以
覆瓿置之乎康熙辛己七夕前两日勿庵梅文鼎识
历算全书 卷七序 第 48b 页 WYG0794-0133b.png
 是日也为立秋之辰好雨生凉炎歊顿失稍简残帙
是日也为立秋之辰好雨生凉炎歊顿失稍简残帙殊散人怀
历算全书 卷七序 第 49a 页 WYG0794-0133c.png

历算全书 卷七序 第 49b 页 WYG0794-0133d.png
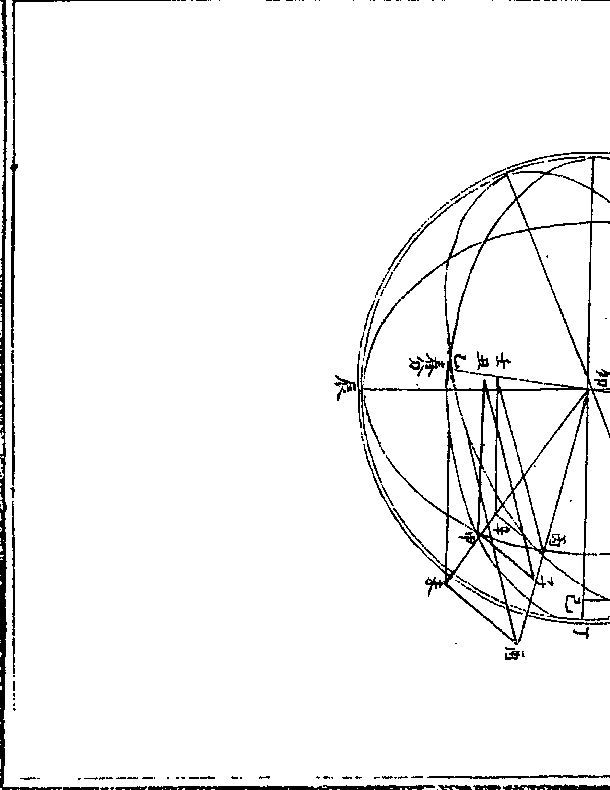
 甲乙丙正弧三角形即测量全义第七卷原图稍为酌
甲乙丙正弧三角形即测量全义第七卷原图稍为酌定又增一酉未乙形
历算全书 卷七序 第 50a 页 WYG0794-0134a.png

历算全书 卷七序 第 50b 页 WYG0794-0134b.png
 测员之用甚博非止黄赤也然黄道赤道南北极二分
测员之用甚博非止黄赤也然黄道赤道南北极二分二至诸名皆人所习闻故仍借用其号以便识别
案图中句股形凡五皆形相似
其一癸巳卯形
以癸卯半径为弦(即黄道/半径)癸巳正弦为股(即黄赤大/距弧之正)
(弦/)巳卯馀弦为句(即黄赤大距/弧之馀弦)
其二戊丁卯形
以戊卯割线为弦(即黄赤大距/弧之正割线)戊丁切线为股(即黄赤/大距弧)
历算全书 卷七序 第 51a 页 WYG0794-0134c.png
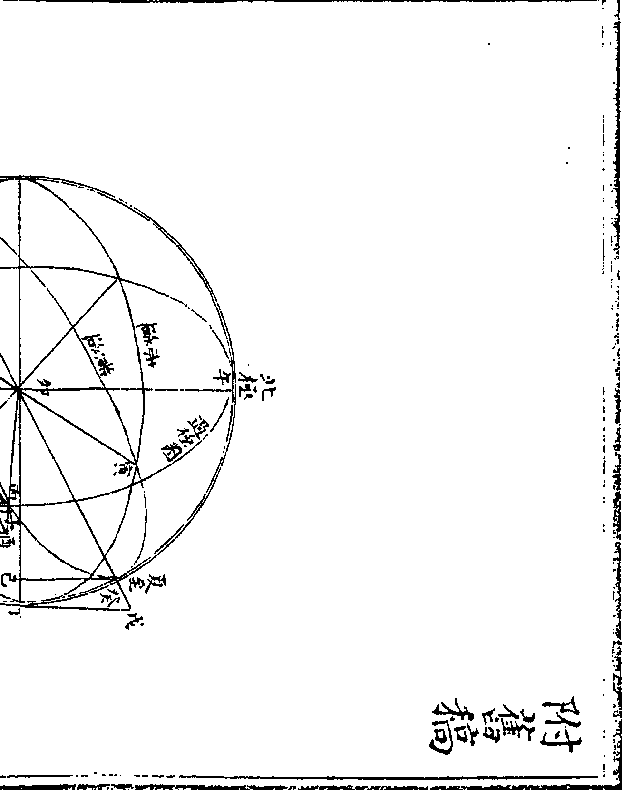 (之正/切线)丁卯半径为句(即赤道/半径)
(之正/切线)丁卯半径为句(即赤道/半径)以上二句股形生于黄赤道之大距度乃总法也两
句股形一在浑体之内一出其外同用卯角(即黄道/心亦即)
(春分/角)
其三丙辛壬形
以丙壬正弦为弦(即黄经乙丙弧之正弦以丙卯黄/道半径为其全数而卯壬其馀弦)丙
辛正弦为股(即黄赤距纬丙甲弧之正弦亦以丙卯/黄道半径为其全数而辛卯其馀弦)辛
壬横线为句
历算全书 卷七序 第 51b 页 WYG0794-0134d.png
 法于赤道平面上作横线联两馀弦成卯壬辛平句
法于赤道平面上作横线联两馀弦成卯壬辛平句股形此形以距纬馀弦(卯/辛)为弦黄经馀弦(卯/壬)为股而
辛壬其句也此辛壬线既为两馀弦平句股形之句
亦即能为两正弦立句股形之句矣历书以辛壬为
丙辛之馀弦误也然则当命为何线曰此非八线中
所有乃立三角体之楞线也
其四子甲丑形
以子丑斜线为弦(此亦立三角体之楞/线也非八线中之线)子甲切线为股
历算全书 卷七序 第 52a 页 WYG0794-0135a.png
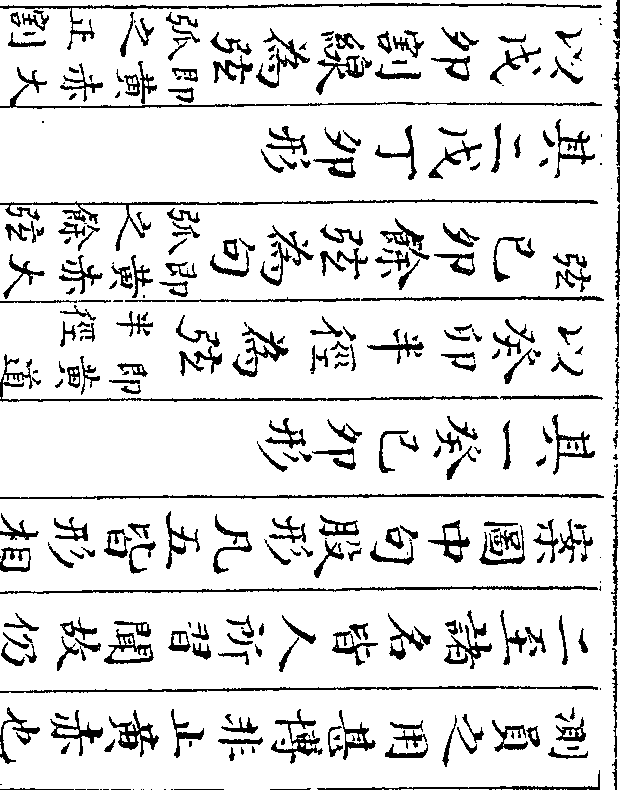 (即黄赤距纬弧之正切线以赤道半/径甲卯为其全数而子卯其割线也)甲丑正弦为句(即/赤)
(即黄赤距纬弧之正切线以赤道半/径甲卯为其全数而子卯其割线也)甲丑正弦为句(即/赤)(经乙甲弧之正弦亦以赤道半径/甲卯为其全数而丑卯其馀弦也)
其五酉未乙形
以酉乙切线为弦(即黄经丙乙弧之正切线以黄赤半/径卯乙为其全数而酉卯其割线也)
酉未立线为股(此亦立三角之楞/线非八线中之线)未乙切线为句(即赤/经乙)
(甲弧之正切线亦以黄赤半径卯/乙为其全数而未卯其割线也)
以上三句股形生于设弧之度第三形在浑体之内
第四形半在浑体之内而出其外第五形全在浑体
历算全书 卷七序 第 52b 页 WYG0794-0135b.png
 之外
之外问既在体外其状何如曰设浑圆在立方之内而以
两极居立方底盖之心以乙春分居立方立面之心
则黄赤两经之切线酉乙未乙皆在方体之立面而
未乙必为句酉乙必为弦于是作立线联之即成
酉未乙句股形矣此一形历书遗之予所补也(详/堑)
(堵测/量)
论曰此五句股形皆同角故其比例等然与弧三角真
历算全书 卷七序 第 53a 页 WYG0794-0135c.png
 同者乙角也
同者乙角也第一(癸巳/卯形)第二(戊丁/卯形)两形皆乙角原有之八线即春秋
分角也其度则两至之大距也
或先有角以求边则以此两形中线例他形中线得
线则得边矣
或先有边以求角则以他形中线例此两形中线得
线则亦得角矣(盖卯角即乙角也○若欲求丙/角则以丙角当乙角如法求之)
第三形(丙辛/壬形)以黄经之正弦(丙/壬)黄赤距度之正弦(丙/辛)为
历算全书 卷七序 第 53b 页 WYG0794-0135d.png
 弦与股是以黄经与距纬相求
弦与股是以黄经与距纬相求或先有乙角有黄经以求距纬(用乙角实用/壬角下同)
或先有乙角有距纬以求黄经
或先有黄经距纬可求乙角亦可求丙角
第四形(子甲/丑形)以黄赤距纬之切线(子/甲)赤经之正弦(甲/丑)为
股与句是以距纬与赤经相求
或先有乙角有赤经以求距纬(用乙角实用/丑角下同)
或先有乙角有距纬以求赤经
历算全书 卷七序 第 54a 页 WYG0794-0136a.png
 或先有赤经距纬可求乙角亦可丙角
或先有赤经距纬可求乙角亦可丙角第五形(酉未/乙形)以赤经之正切(未/乙)黄经之正切(酉/乙)为句与
弦是黄赤经度相求
或先有乙角有黄经以求赤道同升度
或先有乙角有赤道同升以求黄经
或先有黄赤二经度可求乙角亦可求丙角
又论曰诸句股形所用之卯壬丑乙四角实皆乙角何
也侧望则弧度皆变正弦而体心卯作直线至乙为卯
历算全书 卷七序 第 54b 页 WYG0794-0136b.png
 壬丑乙线即半径也今以侧望之故此半径直线化为
壬丑乙线即半径也今以侧望之故此半径直线化为一点则乙角即卯角亦即壬角亦即丑角矣
历算全书 卷七序 第 55a 页 WYG0794-0136c.png

历算全书 卷七序 第 55b 页 WYG0794-0136d.png
 癸丁为乙角之度(即黄赤大距/二至纬度)癸乙为黄道半径丁乙
癸丁为乙角之度(即黄赤大距/二至纬度)癸乙为黄道半径丁乙为赤道半径戊丁为乙角切线癸巳为乙角正弦戊乙
为乙角割线已乙为乙角馀弦癸巳乙戊丁乙皆句股
形其乙角即卯角
丙甲为设弧距度其正弦丙辛其切线子甲
丙乙为所设黄道度其正弦丙壬(因侧望弧度/正弦成一线)偕距度
正弦丙辛成句股形其乙角即壬角
甲乙为所设赤道同升度其正弦甲丑(因侧望弧度/正弦成一线)偕
历算全书 卷七序 第 56a 页 WYG0794-0137a.png
 距度切线子甲成句股形其乙角即丑角
距度切线子甲成句股形其乙角即丑角酉乙为所设黄经切线未乙为赤道同升度切线此两
线成一酉未乙句股形在体外真用乙角
正弧三角形求馀角法
凡弧三角有三边三角先得三件可知馀件与平三角
同理前论正弧形以黄赤道为例而但详乙角者因春
分角有一定之度人所易知故先详之或疑求乙角之
法不可施于丙角兹复为之条析如左(仍以黄道上过/极经圈之交角)
历算全书 卷七序 第 56b 页 WYG0794-0137b.png
 (为/例)
(为/例)历算全书 卷七序 第 57a 页 WYG0794-0137c.png
 假如有乙丙黄道度有乙甲赤道同升度而求丙交角
假如有乙丙黄道度有乙甲赤道同升度而求丙交角则为乙丙之正弦与乙甲之正弦若半径与丙角之正
弦也
历算全书 卷七序 第 57b 页 WYG0794-0137d.png
 假如有丙甲距度及乙甲同升度而求丙交角则为丙
假如有丙甲距度及乙甲同升度而求丙交角则为丙甲之正弦与乙甲之切线若半径与丙角之切线
历算全书 卷七序 第 58a 页 WYG0794-0138a.png
 假如有丙甲距度及乙丙黄道度而求丙交角则为乙
假如有丙甲距度及乙丙黄道度而求丙交角则为乙丙之切线与丙甲之切线若半径与丙角之馀弦
历算全书 卷七序 第 58b 页 WYG0794-0138b.png
 又如有丙交角有乙丙交道度而求乙甲同升度则为
又如有丙交角有乙丙交道度而求乙甲同升度则为半径与丙角之正弦若乙丙之正弦与乙甲之正弦
历算全书 卷七序 第 59a 页 WYG0794-0138c.png
 或先有乙甲同升度而求乙丙黄道度则以前率更之
或先有乙甲同升度而求乙丙黄道度则以前率更之为丙角之正弦与半径若乙甲之正弦与乙丙之正弦
历算全书 卷七序 第 59b 页 WYG0794-0138d.png
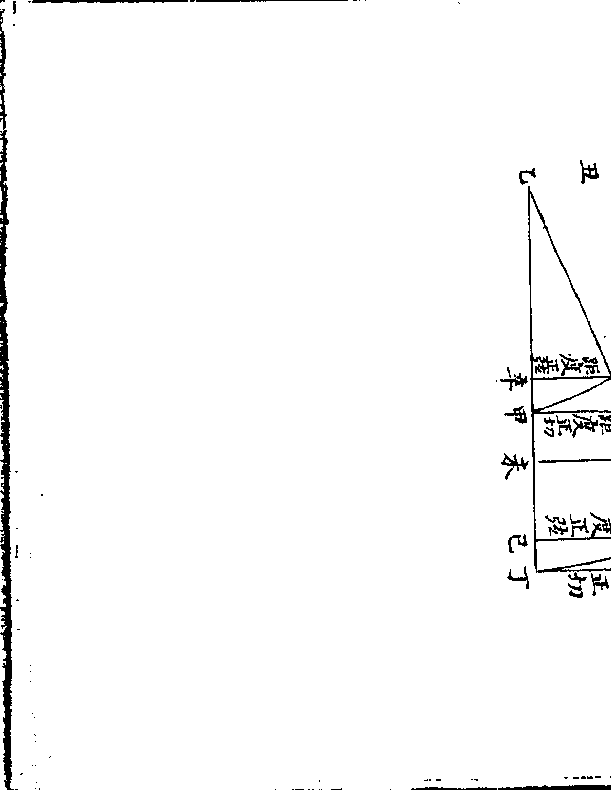 又如有丙交角有乙甲同升度而求丙甲距度则为丙
又如有丙交角有乙甲同升度而求丙甲距度则为丙角之切线与半径若乙甲之切线与丙甲之正弦
历算全书 卷七序 第 60a 页 WYG0794-0139a.png
 或先有丙甲距度而求乙甲同升度则以前率更之为
或先有丙甲距度而求乙甲同升度则以前率更之为半径与丙角切线若丙甲正弦与乙甲切线
历算全书 卷七序 第 60b 页 WYG0794-0139b.png
 又如有丙交角有乙丙黄道度求丙甲距度则为半径与
又如有丙交角有乙丙黄道度求丙甲距度则为半径与丙角馀弦若乙丙切线与丙甲切线
历算全书 卷七序 第 61a 页 WYG0794-0139c.png
 或先有丙甲距度而求乙丙黄道则以前率更之为丙
或先有丙甲距度而求乙丙黄道则以前率更之为丙角馀弦与半径若丙甲切线与乙丙切线
历算全书 卷七序 第 61b 页 WYG0794-0139d.png
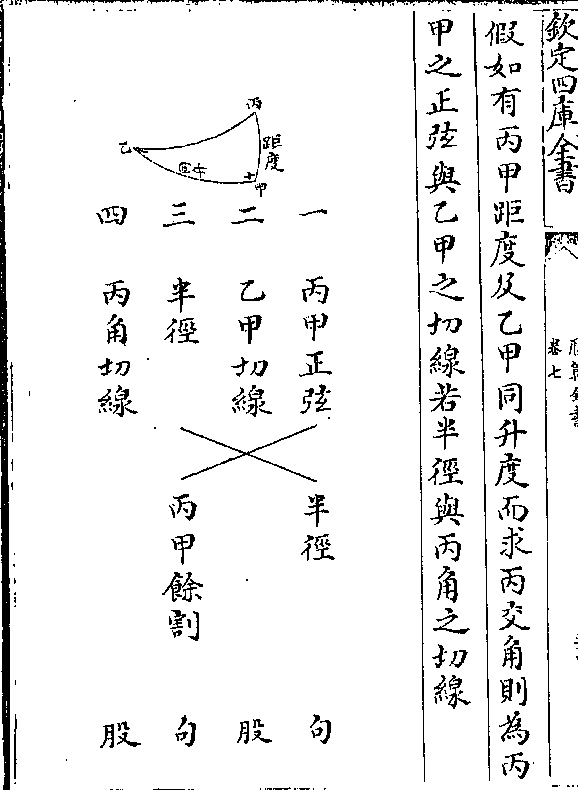 论曰求丙角之法一一皆同乙角更之而用丙角求馀边
论曰求丙角之法一一皆同乙角更之而用丙角求馀边亦如其用乙角也所异者乙角定为春分角则其度不变
丙角为过极经圈交黄道之角随度而移(交角近大距则/甚大类十字角)
(近春分只六十六度半弱中间交角/度度不同他形亦然皆逐度变丙角)有时大于乙角有时
小于乙角(乙角不及半象限则丙角大乙/角过半象限则丙角有时小)故必求而得之
又论曰丙交角既随度移而甲角常为正角何也凡球
上大圈相交成十字者必过其极今过极经圈乃赤道
之经线惟二至时则此圈能过黄赤两极其馀则但过
历算全书 卷七序 第 62a 页 WYG0794-0140a.png
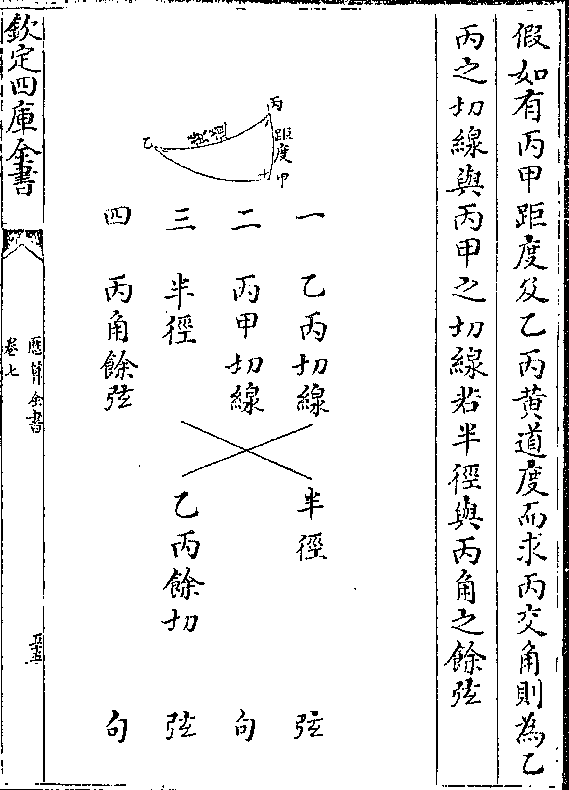 赤道极而不能过黄道极故其交黄道也常为斜角(即/丙)
赤道极而不能过黄道极故其交黄道也常为斜角(即/丙)(角/)交赤道则常为正角(即甲/角)
又论曰丙角与乙角共此三边(一乙丙黄道一乙甲/赤道一丙甲距度)其
所用比例者亦共此三边之八线(三边各有正弦/亦各有切线)而所
成句股形遂分两种可互观也
乙角所成诸句股皆以戊丁卯为例
内角所成诸句股皆以亥辰卯为例
并如后图
历算全书 卷七序 第 63a 页 WYG0794-0140c.png

历算全书 卷七序 第 63b 页 WYG0794-0140d.png
 如图丙角第一层句股兑乙心形即乙角之壬丙辛也
如图丙角第一层句股兑乙心形即乙角之壬丙辛也在乙角两正弦交于丙在丙角两正弦交于乙皆弦与
股之比例而同弦不同股(乙角丙角并以乙丙黄道正/弦为弦而乙角所用之股为)
(丙甲正弦丙角所用则乙甲/正弦皆正弦也而弦同股别)
丙角第二层句股女甲亢形即乙角之子甲丑也乙角
丙角并以一正弦一切线交于甲为句与股之比例而
所用相反(乙角于乙甲用正弦于丙甲用切线丙角则/于乙甲用切线于丙甲用正弦皆乙甲丙甲)
(两弧之正弦切/线而所用迥别)
历算全书 卷七序 第 64a 页 WYG0794-0141a.png
 丙角第三层句股艮丙氐形即乙角之酉乙未也在乙
丙角第三层句股艮丙氐形即乙角之酉乙未也在乙角以两切线联于乙在丙角以两切线交于丙皆弦与
句之比例而同弦不同句(乙丙两角并以乙丙切线为/弦而乙角以乙甲切线为句)
(丙角以丙甲切线为句/皆切线也而弦同句别)
历算全书 卷七序 第 65a 页 WYG0794-0141c.png
 球面弧三角形弧角同比例解
球面弧三角形弧角同比例解第一题
正弧三角形以一角对一边则各角正弦与对边之正
弦皆为同理之比例
历算全书 卷七序 第 65b 页 WYG0794-0141d.png
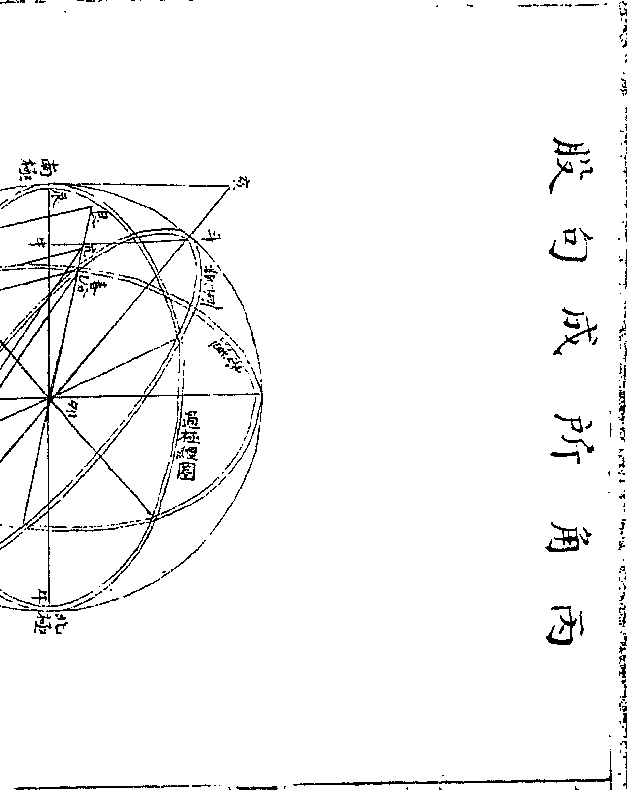
 如图乙甲丙弧三角形(甲为/正角) 法为半径与乙角之正
如图乙甲丙弧三角形(甲为/正角) 法为半径与乙角之正弦若乙丙之正弦与丙甲之正弦更之则乙角之正角
与对边丙甲之正弦若半径与乙丙之正弦也又丙角
之正弦与其对边乙甲之正弦亦若半径与乙丙之正
弦也合之则乙角之正弦与其对边丙甲之正弦亦若
丙角之正弦与其对边乙甲之正弦
论曰乙丙两角与其对边之正弦既并以半径与乙丙
为比例则其比例亦自相等而两角与两对边其正弦
历算全书 卷七序 第 66a 页 WYG0794-0142a.png
 皆为同比例
皆为同比例又论曰甲为正角其度九十而乙丙者甲正角所对之
边也半径者即九十度之正弦也以半径比乙丙之正
弦即是以甲角之正弦比对边之正弦故以三角对三
边皆为同比例
第二题
凡四率比例二宗内有二率三率之数相同则两理之
首末二率为互视之同比例(即斜弧比例之所/以然故先论之)
历算全书 卷七序 第 66b 页 WYG0794-0142b.png
 假如有甲乙丙丁四率甲(四/)与乙(八/)若丙(六/)与丁(十/二)皆
假如有甲乙丙丁四率甲(四/)与乙(八/)若丙(六/)与丁(十/二)皆加倍之比例也
又有戊乙丙辛四率戊(二/)与乙(八/)若丙(六/)与辛(二十/四)皆
四倍之比例也
此两比例原不同理特以两理之第二第三同为乙
(八/)丙(六/)故两理之第一第四能互用为同理之比
例(先理之第一甲四与次理之第四辛二十四若/次理之第一戊二与先理之四丁十二皆六倍)
(之比/例也)
历算全书 卷七序 第 67a 页 WYG0794-0142c.png

历算全书 卷七序 第 67b 页 WYG0794-0142d.png
 论曰凡二率三率相乘为实首率为法得四率今两理
论曰凡二率三率相乘为实首率为法得四率今两理所用之实皆乙(八/)丙(六/)相乘(四十/八)之实惟甲(四/)为法则
得十二若戊(二/)为法则得二十四矣法大者得数小法
小者得数大而所用之实本同故互用之即为同理之
比例也
试以先理之四率更为首率其理亦同(丁与辛若戊与/甲皆加倍比例)
若反之令两四率并为首率亦同(甲与戊若辛与/丁皆折半比例)并如
后图
历算全书 卷七序 第 68a 页 WYG0794-0143a.png

历算全书 卷七序 第 68b 页 WYG0794-0143b.png
 第三题
第三题斜弧三角形以各角对各边其正弦皆为同比例
历算全书 卷七序 第 69a 页 WYG0794-0143c.png
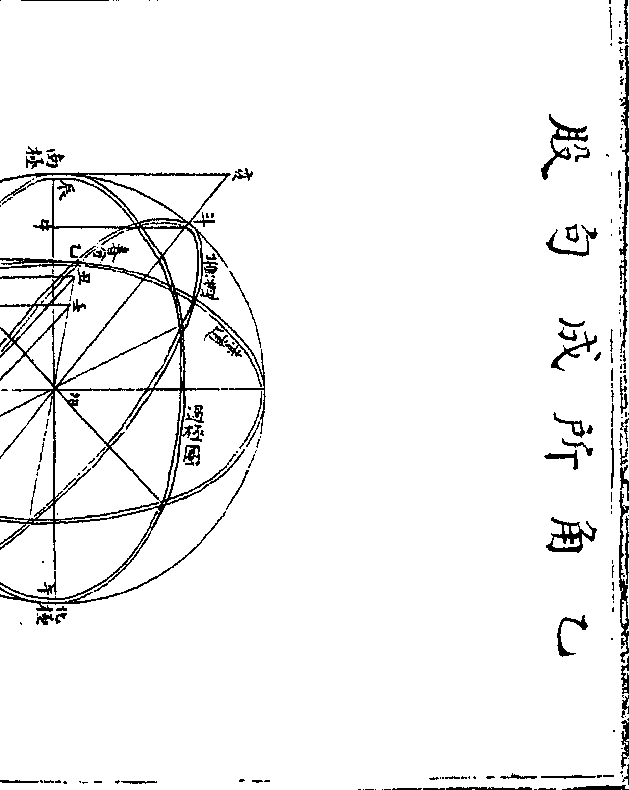 乙丙丁斜弧三角形任从乙角作乙甲垂弧至对边分
乙丙丁斜弧三角形任从乙角作乙甲垂弧至对边分元形为两正角形甲为正角
依前正角形论各对边之正弦与所对角之正弦比例
皆等
乙甲丁形丁角正弦与乙角正弦若半径(即甲角/正弦)与丁
乙正弦是一理也
乙甲丙形丙角正弦与乙甲正弦若半径与乙丙正弦
是又一理也
历算全书 卷七序 第 69b 页 WYG0794-0143d.png
 两理之第二同为乙甲第三同为半径则两理之首末
两理之第二同为乙甲第三同为半径则两理之首末二率为互视之同比例故丁角之正弦与乙丙之正弦
若丙角之正弦与丁乙之正弦也
又如法从丁角作丁戊垂弧至对边分两形而戊为正
角则乙角正弦与丁丙正弦亦若丙角正弦与乙丁正
弦 又从丙作垂弧分两形而壬为正角则乙角与丁
丙亦若丁角与乙丙
一 丁角正弦 丙角正弦
历算全书 卷七序 第 70a 页 WYG0794-0144a.png

历算全书 卷七序 第 70b 页 WYG0794-0144b.png
 乙丙丁斜弧三角形丁为钝角 法从乙角作乙甲垂
乙丙丁斜弧三角形丁为钝角 法从乙角作乙甲垂弧于形外亦引丙丁弧会于甲成乙甲丁虚形亦凑成
乙甲丙虚实合形甲为正角
历算全书 卷七序 第 71a 页 WYG0794-0144c.png
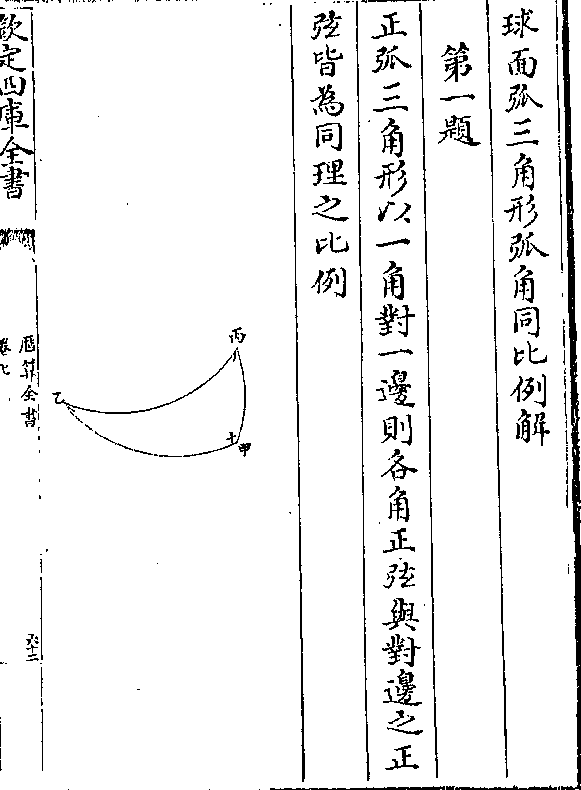 乙甲丁形丁角之正弦与乙甲边若半径与乙丁边正
乙甲丁形丁角之正弦与乙甲边若半径与乙丁边正弦一理也 乙甲丙形丙角之正弦与乙甲边若半径
与乙丙正弦又一理也 准前论两理之第二第三既
同则丁角正弦与乙丙正弦若丙角正弦与乙丁正弦
也
论曰丁角在虚形是本形之外角也何以用为内角曰
凡钝角之正弦与外角之正弦同数故用外角如本形
角也
历算全书 卷七序 第 71b 页 WYG0794-0144d.png
 若用乙角与丁丙边则作丙庚弧于形外取庚正角其
若用乙角与丁丙边则作丙庚弧于形外取庚正角其理同上或作丁戊垂弧于形内取戊正角分两形则如
前法并同
历算全书 卷七序 第 72a 页 WYG0794-0145a.png
 用法
用法凡弧三角形(不论正/角斜角)但有一角及其对角之一弧则其
馀有一角者可以知对角之弧而有一弧者亦可以知
对弧之角皆以其正弦用三率比例求之
历算全书 卷七序 第 72b 页 WYG0794-0145b.png
 假如乙丁丙三角形先有丁角及相对之乙丙弧则其
假如乙丁丙三角形先有丁角及相对之乙丙弧则其馀但有丙角可以知乙丁弧有乙角可以知丁丙弧此
为角求弧也若有乙丁弧亦可求丙角有丁丙弧亦可
求乙角此为弧求角也
一 丁角正弦 一 乙丙正弦
二 乙丙正弦 二 丁角正弦
三 丙角正弦 乙角正弦 三 乙丁正弦 丁丙正弦
四 乙丁正弦 丁丙正弦 四 丙角正弦 乙角正弦
历算全书 卷七序 第 73a 页 WYG0794-0145c.png

历算全书 卷七序 第 73b 页 WYG0794-0145d.png

历算全书卷七