钦定四库全书
　历算全书卷三
　　　　　　　　　　　　　宣城梅文鼎撰
　　历学疑问三
　　　论盈缩高卑
问日有高卑加减始于西法欤曰古历有之且详言之
矣但不言卑高而谓之盈缩耳曰日何以有盈缩曰此
古人积候而得之者也秦火以还典章废阙汉晋诸家

皆以太阳日行一度故一岁一周天自北齐张子信积
候合𩞾加时始觉日行有入气之差而立为损益之率
又有赵道严者复准晷景长短定日行进退更造盈缩
以求亏食至隋刘焯立躔度与四序升降为法加详厥
后皆相祖述以为步日躔之准盖太阳行天三百六十
五日惟只两日能合平行(一在春分前三日一在秋分/后三日一年之内能合平行)
(者惟此/二日)此外日行皆有盈缩而夏至缩之极每日不及
平行二十分之一冬至盈之极又过于平行二十分之

一两者相较为十分之一以此为盈缩之宗而过此皆
以渐而进退焉此盈缩之法所由立也曰日躔既每日
有盈缩则岁周何以有常度曰日行每日不齐而积盈
积缩之度前后自相除补故岁周得有常度也(细考之/古今岁)
(周亦有微差此只论/其大较则实有常度)今以授时之法论之冬至日行甚
速每日行一度有奇历八十八日九十一刻当春分前
三日而行天一象限(古法周天四之一为九/十一度三十分奇下同)谓之盈初
历此后则每日不及一度其盈日损历九十三日七十

一刻当夏至之日复行天一象限谓之盈末历夫盈末
之行每日不及一度而得为盈历者以其前此之积盈
未经除尽总度尚过于平行故仍谓之盈若其每日细
行固悉同缩初此盈末缩初可为一法也试以积数计
之盈初日数少而行度多其较为二度四十分盈末日
数多而行度少其较亦二度四十分以盈末之所少消
盈初之所多则以半岁周之日(共一百八十二/日六十二刻奇)行半周
天之度(一百八十二度/六十二分奇)而无馀度矣夏至日行甚迟每

日不及一度历九十三日七十一刻当秋分后三日而
行天一象限谓之缩初历此后则每日行一度有奇其
缩日损历八十八日九十一刻复当冬至之日而行天
一象限谓之缩末历夫缩末之行每日一度有奇而亦
得为缩历者以其前此之积缩未能补完总度尚后于
平行故仍谓之缩若其每日细行则悉同盈初此缩末
盈初可为一法也试以积数计之缩初日数多而行度
少其较为二度四十分缩末日数少而行度多其较亦

二度四十分以缩末之所多补缩初之所少则亦以半
岁周之日行半周天之度而无欠度矣夫盈历缩历既
皆以前后自相除补而无馀欠则分之而以半岁周行
半周天者合之即以一岁周行一周天安得以盈缩之
故疑岁周之无常度哉
　　　再论盈缩高卑
问日有盈缩是矣然何以又谓之高卑曰此则回回泰
西之说也其说曰太阳在天终古平行原无盈缩人视

之有盈缩耳夫既终古平行视之何以得有盈缩哉盖
太阳自居本天而人所测其行度者则为黄道黄道之
度外应太虚之定位(即天元黄道与/静天相应者也)其度匀剖而以地
为心太阳本天度亦匀剖而其天不以地为心于是有
两心之差而高卑判矣是故夏至前后之行度未尝迟
也以其在本天之高半故去黄道近而离地远远则见
其度小(谓太阳本/天之度)而人自地上视之迟于平行矣(缩初/盈末)
(半周是太阳本天高处故在本天行一/度者在黄道不能占一度而过黄道迟)是则行度之所

以有缩也冬至前后之行度未尝速也以其在本天之
低半故去黄道远而离地近近则见其度大(亦谓本天/之匀度)
而人自地上视之速于平行矣(盈初缩末半周是太阳/本天低处故在本天行)
(一度者在黄道占一/度有馀而过黄道速)是则行度之所以有盈也且夫行
度有盈缩而且日日不同则不可以筹策御而今以圜
法解之不同心之理通之在高度不得不迟在卑度不
得不速高极而降迟者不得不渐以速卑极而升速者
不得不渐以迟迟速之损益循圜周行与算数相会是

则盈缩之徵于实测者皆一一能得其所以然之故此
高卑之说深足为治历明时之助者矣
太阳之平行者在本天太阳之不平行者在黄道平行
之在本天者终古自如不平行之在黄道者晷刻易率
惟其终古平行知其有本天惟其有本天斯有高卑以
生盈缩不平行之率以平行而生者也惟其盈缩多变
知其有高卑惟其盈缩生于高卑验其在本天平行平
行之理又以不平行而信者也夫不平行之与平行道

相反矣而求诸圜率适以相成是盖七曜之所同然而
在太阳尤为明白而易见者也(月五星多诸小轮加减/故本天不同心之理惟)
(太阳/最明)
　　　论最高行
问以高卑疏盈缩确矣然又有最高之行何耶曰最高
非他即盈缩起算之端也盈缩之算既生于本天之高
卑则其极缩处即为最高如古法缩历之起夏至也极
盈处即为最卑如古法盈历之起冬至也(亦谓之最高冲/或省曰高冲)

然古法起二至者以二至即为盈缩之端也西法则
极盈极缩不必定于二至之度而在其前后又各年不同
故最高有行率也其说曰上古最高在夏至前今行过
夏至后每年东移四十五秒(今又定为一年行/一分一秒十微)何以徵
之曰凡最高为极缩之限则自最高以后九十度及相
近最高以前九十度其距最高度等则其所缩等何也
以视度之小于平度者并同也(古法以盈末缩初通/为一限亦是此意)高
衡为极盈之限则自高冲以后九十度及相近高冲以

前九十度其距高冲度等则其所盈亦等何也以视度
之大于平度者并同也(古法以缩末盈初通/为一限亦是此意)今据实测
则自定气春分至夏至一象限(即古盈/末限)之日数与自夏
至后至定气秋分一象限(即古缩/初限)之日数皆多寡不同
又自定气秋分至冬至一象限(即古缩/末限)之日数与自冬
至后至定气春分一象限(即古盈/初限)之日数亦多寡不同
由是观之则极盈极缩不在二至明矣曰若是则古之
实测皆非欤曰是何言也言盈缩者始于张子信而后

之历家又谓其损益之未得其正由今以观则子信时
有其时盈缩之限后之历家又各有其时盈缩之限测
验者各据其时之盈缩为主则追论前术觉其未尽矣
此岂非最高之有动移乎又古之盈缩皆以二十四气
为限至郭太史始加密算立为每日每度之盈缩加分
与其积度由今考之则郭太史时最高卑与二至最相
近(自历元戊辰逆溯至元辛巳三百四十八年而最高/卑过二至六度以今率每年最高行一分一秒十微)
(计之其时最高约与夏至同度以西又旧率每年高行/四十五秒计之其时最高已行过夏至一度三十馀分)

(其距度亦不/为甚远也)故盈缩起二至初无谬误测算虽密秪能
明其盈缩细分若最高距至之差无缘可得非考验之
不精也
　　　论高行周天
问最高有行能周于天乎抑只在二至前后数十度中
东行而复西转乎曰以理徵之亦可有周天之行也曰
然则何以不徵诸实测曰无可据也历法西传曰古西
士去今一千八百年以三角形测日轨记最高在申宫

五度三十五分今以年计之当在汉文帝七年戊辰(自/汉)
(文帝戊辰顺数至历元/戊辰积一千八百算外)此时西历尚在权舆越三百馀
年至多禄某而诸法渐备然则所谓古西士之测算或
非精率然而西史之所据止此矣又况自此而逆溯于
前将益荒远而高行之周天以二万馀年为率亦何从
而得其起算之端乎是故以实测而知其最高之有移
动者只在此千数百年之内其度之东移者亦只在二
至前后一宫之间若其周天则但以理断而已曰以理

断其周天亦有说欤曰最高之法非特太阳有之而月
五星皆然其加减平行之度者亦中西两家所同也故
中历太阳五星皆有盈缩太阴则有迟疾在西法则皆
曰高卑视差而已然则月孛者太阴最高之度也而月
孛既有周天之度矣太阳之最高何独不然故曰以理
徵之最高得有周天之行也
　　　论小轮
问以最高疏盈缩其义已足何以又立小轮曰小轮即

高卑也但言高卑则当为不同心之天以居日月小轮
之法则日月本天皆与地同心特其本天之周又有小
轮为日月所居是故本天为大轮负小轮之心向东而
移日月在小轮之周(即边/也)向西而行大轮移一度日月
在小轮上亦行一度大轮满一周小轮亦满一周而盈
缩之度与高卑之距皆不谋而合回回历以七政平行
为中心行度益谓此也

凡日月在小轮上半顺动天西行故其右移之度迟
于平行为减在小轮下半逆动天而东故其右旋之度
速于平行为加(五星/同理)若在上下交接之时小轮之度直
下不见其行谓之留际留际者不东行不西行无减无
加与平行等此小轮上逐度之加减以上下而分者也
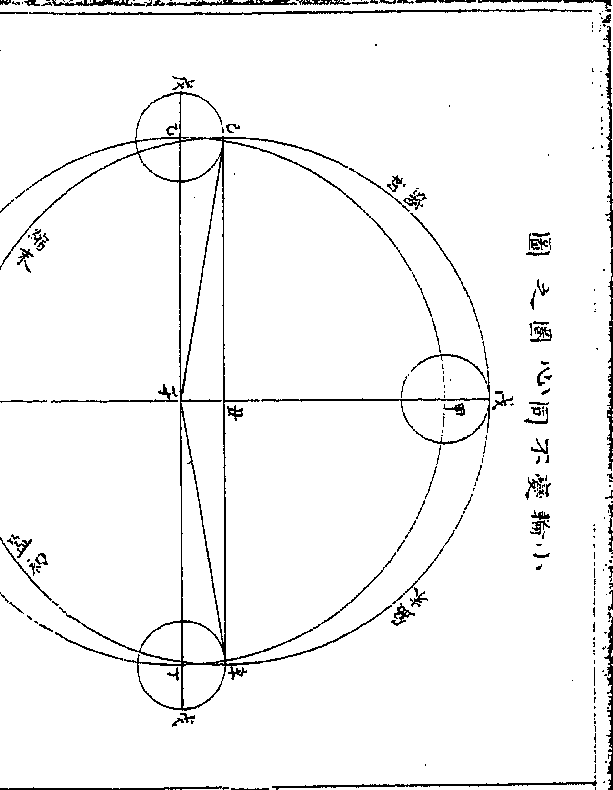
(用第一图自辛留际过戊最高至已为上半皆西行自/已留过际庚最卑至辛为下半皆东行巳辛两留际循)
(小轮之旁/不见其动)
若以入表则分四限小轮上半折半取中为最高小轮

下半折半取中则为最卑最卑最高之点皆对小轮心
与地心而成直线七政居此即与平行同度故为起算
之端假如七政起最高在小轮上西行能减东移之度
半象限后西行渐缓所减渐少至一象限而及留际不
复更西即无所复减然积减之多反在留际何也七政
至此其视度距小轮心之西为大也在古法则为缩初
(用第一图自戊至巳一象限其/减度最大为己甲小轮半径)既过留际而下转而东
行本为加度因前有积减仅足相补其视行仍在平行

之西至一象限而及最卑积减之数始能补足而复于
平行是为缩末(用第一图自巳留际/至庚最卑一象限)
又如七政至最卑在小轮下东行能加东移之度半象
限后东行渐缓所加渐少至一限象而又及留际不复
更东亦无所复加然积加之多亦在留际何也七政至
此其视度距小轮心之东为大也在古法则为盈初(第/一)
(图自庚最卑至辛留际一象限/加度最大为甲辛小轮半径)过留际而上复转西行
即为减度然因前有积加仅足相消其视行仍在平行

之东至一象限而复及最高积加之度始能消尽而复
于平行是为盈末(第一图自辛留际/至戊最高一象限)此则表中入算加
减从小轮之左右而分者也
　　　再论小轮及不同心轮
小轮之用有二其一为迟速之行在古历则为日五星
之盈缩月之迟疾西法则总谓之加减即前所疏者是
也其一为高卑之距即回回历影径诸差是也凡七政
之居小轮最高其去人远故其体为之见小焉其在最

卑去人则近故其体为之加大焉验之于日月交食尤
为著明(别条/详之)是故所谓平行者小轮之心而所谓迟速
者小轮之边与其心前后之差(即东/西)所谓高卑者小轮
之边与其心上下之距也知有小轮而进退加减之行
度远近大小之视差靡所不贯矣
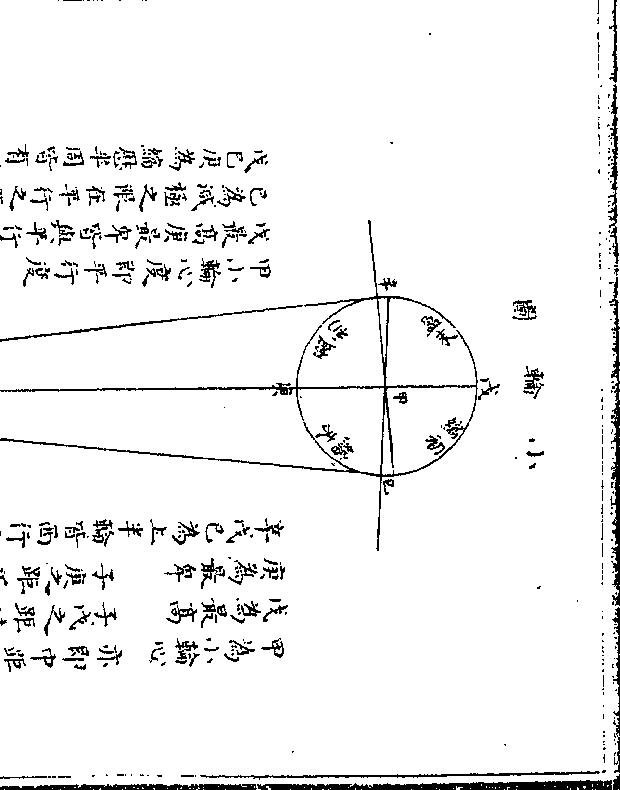
然则何以又有不同心之算曰不同心之法生于小轮
者也试以第二图明之甲乙丙丁圈七政之本天即小
轮心所行之道也以子为心即地心也假如小轮心在

甲则七政在戊为小轮最高小轮心自甲东移一象限
至乙七政之在小轮亦从戊西行一象限至巳为留际
小轮心东移满半周至丙七政在小轮亦行半周至庚
为最卑由是小轮心东移满二百七十度至丁七政亦
行小轮二百七十度至留际辛小轮心东移满一周复
至甲七政行小轮上亦行满一周复至最高戊若以小
轮上七政所行之戊巳庚辛诸点联之即成大圈此圈
不以地心为心而别有其心故曰不同心圈也如图地

心在子不同心圈之心在丑丑子两心之差与小轮之
半径等故可以小轮立算者亦可以不同心立算而行
度之加减与视径之大小亦皆得数相符也
　　　论小轮不同心轮孰为本法
问二者之算悉符果孰为本法曰晶宇寥廓天载无垠
吾不能飞形御气翱步乎日月之表小轮之在天不知
其有焉否耶然而以求朓朒之行则既有其度矣以量
高卑之距则又有其差矣虽谓之有焉可也至不同心

之算则小轮实巳该之何也健行之体外实中虚自地
以上至于月天大气所涵空洞无物故各重之天虽有
高卑而高卑两际只在本天(七政各重之天相去甚远/其间甚厚故可以容小轮)
(而其最高最卑皆/不越本重之内)非别有一不同之心绕地而转也(不/同)
(心之天既同动天西运/则其心亦将绕地而旋)况七政两心之差各一其率若
使其不同之心皆绕地环行亦甚涣而无统矣愚故曰
不同心之算生于小轮而小轮实已该之观回回历但
言小轮可知其为本法而地谷于西术最后出其所立

诸图悉仍用小轮为说亦足以徵矣
　　　论小轮不同心轮各有所用
问小轮与不同心轮既异名而同理择用其一不亦可
乎曰论相因之理则不同心之算从小轮而生论测算
之用则小轮之径亦从不同心而得故推朒朓之度于
小轮特亲(小轮心即平行度也从最高过轮心作线至/地心为平行指线剖小轮为二则小轮右半)
(在平行线西为朒左半在/平行线东为朓观图易了)而求最高之行以不同心立
算最切然则其理互通其用相辅并存其说亦足以见

圜行之无方而且可为参稽之藉矣
最高在天不可以目视不可以器测惟据朓朒之度以
不同心之法测之而得其两心之差是即为小轮之半
径于以作图立算而朓朒之故益复犁然是故不同心
者即测小轮之法也
　　　论小轮心之行及小轮上七政之行皆非自动
问小轮心逆动天而右旋日月五星之在小轮也又逆
本天而顺动天以左旋何若是其交错欤意者七政各

有能动之性而其动也又恒以逆为顺欤今夫鱼溯川
而游顺鳞鬐也鸟逆风而翔便羽毛也夫七政之行亦
将若是而已矣曰子以小轮心自为一物而不与本天
相连乎曰非也小轮心常在本天之周殆相连耳曰七
政居小轮之周岂不若小轮心之在本天乎曰然曰然
则小轮心在本天七政在小轮体皆相连其非若鱼之
川泳鸟之云飞也审矣然则何为而有动移曰小轮心
非能自动也小轮之动本天之动也七政亦非自动也

七政之动小轮之动也其故何也盖小轮之心既与本
天相连必有定处因本天为动天所转与之偕西而不
及其速以生退度故小轮心亦有退度焉历家纪此退
度以为平行(回回历所谓/中心行度)故曰小轮之动本天之动也
然则小轮心者小轮之枢也枢连于本天不动故轮能
动而七政者又相连于小轮之周者也小轮动则七政
动矣故曰七政之动小轮之动也七政虽动不离小轮
轮心虽移不离本天又恒为周动而有定法岂若游鳞

征鸟之于波澜风霄而莫限所届哉
　　　再论小轮上七政之行
问本天移故小轮心移小轮动故七政动是则然矣然
何以七政在小轮上西行不与轮心同势岂非七政自
有行法欤曰七政之居小轮也有一定之向本天挈小
轮心东移而七政在小轮上常向最高殆其精气有以
摄之也故轮心东移一度小轮上七政亦西迁一度以
向最高譬之罗金小轮者其盘也小轮心者置针之处

也七政所居则针所指之午位也试为大圆周分三百
六十度(以法/周天)别为大圈加其上使与大圆同心而可运
(以法同/心轮)乃置罗金于大圈之正午而依针以定盘则针
之午即盘之午(此如小轮在最高而七政/居其顶与最高同处也)于是运大圈
东转使罗金离午而东(此如本天挈小/轮而东移也)则盘针之指午
者必且西移而向丁向未(因正午所定之盘不复更置/则此时之丁之未实为针之)
(午此如小轮从本天东移而七政/西迁居小轮之旁以向最高之方)盘东移一度针亦西
移一度盘东移一宫针亦西移一宫盘东行半周至大

圆子位则针在盘上亦西移半周而反指盘之子(此时/盘之)
(子实针之午此如小轮心行至最高冲而七政居/小轮之底在小轮为最卑而所向者最高之方也)盘东
移三百六十度而复至午针亦西移一周而复其故矣
是何也针自向午不以盘之东移而改其度自盘上观
之见为西移耳七政之常向最高何以异是(七政在小/轮上常向)
(最高之方观/第二图可见)
　　　论小轮非一
问小轮有几曰小轮以算视行视行非一故小轮亦非

一也凡算视行有二法或用不同心轮则惟月五星有
小轮而日则否何也以盈缩高卑即于不同心之轮可
得其度故不以小轮加减而小轮之用已藏其中也或
用同心轮负小轮则日有一小轮月五星有两小轮其
一是高卑小轮为日五星之盈缩月之迟疾即不同心
之算七政所同也其一是合望小轮在月为倍离(即晦/朔弦)
(望/)在五星为岁轮(即迟留/逆伏)皆以距日之远近而生故太
阳独无也若用小均轮则太阳有二小轮其一为平高

卑二为定高卑而月五星则有三小轮其一二为平高
卑定高卑与太阳同其三为太阴倍离五星岁轮与太
阳异也凡此皆以齐视行之不齐有不得不然者然小
轮之用不同而名亦易相乱(如月离以高卑轮为自行/轮又称本轮又曰古称小)
(轮其定高卑轮五星称小均轮月离称均轮或称又次/轮至于距日而生之轮月离称次轮五星或称次轮或)
(称年岁轮然亦/曰古称小轮)今约以三者别之一曰本轮七政之平
高卑是也一曰均轮七政平高卑之轮上又有小轮以
加减之为定高卑此两小轮相须为用二而一者也一

曰次轮月五星距日有远近而生异行故曰次轮而五
星次轮则直称之岁轮也
　　　论七政两种视行(七政从天月/五星又从日)
问小轮有三又或为二何也曰小轮旧只用二(一本轮/一次轮)
新法用三(一本轮一均/轮一次轮)然而均轮者所以消息乎本轮
为本轮微细之用故曰二而一者也是则轮虽有三实
则两事而已何谓两曰七政皆从天以生本轮而月五
星又从乎日以生次轮天西行故七政之本轮皆从天

而西转其行皆向最高也(日月五星之在本轮俱向本/天最高其本轮心离最高一)
(度本轮周亦行/一度似为所摄)日天东移故月五星之合望次轮皆从
日而东运其行皆向日也(月五星离日若干次轮度/亦行若干是为日所摄)惟
本轮从天于是有最高卑之加减而其行度必始于最
高(本轮行始于本天最高而均轮即始于本轮之最高/卑故本轮均轮至最高卑皆无加减为起算之端)
惟次轮从日于是有离日之加减而其行度必始于会
日(月次轮行始于朔望星次轮始于合伏故/月至朔望五星合日冲日皆无次轮加减)是故七政
皆以半周天之宿度行缩历半周天之宿度行盈历历

宿度三百六十而本轮一周起最高终最高也(因最高/有行分)
(故视周天稍赢然大致/不变月之迟疾亦然)次轮则月以历黄道一周而又
过之凡三百八十九度奇而行二周起朔望终朔望也
五星岁轮(即次/轮)则土以行黄道十二度奇木以三十三
度奇火以四百○八度奇金以五百七十五度奇水以
一百十四度奇而皆一周起合伏终合伏也治历者用
三小轮以求七政之视行惟此二者故曰两事也(金水/二星)
(会日后皆行黄道宿一周/又复过之然后再与日会)

　　　论天行迟速之原
问天有重数则在外者周径大而其度亦大故土木之
行迟在内者周径小而其度亦小故金水月之行速七
政之行势略同特其度有大小而分迟速耳以是为右
旋之徵不亦可乎曰此必七政另为一物以行于本天
之上故可以度之大小为迟速也今七政既与天同体
而非另为一物则七政之东升西没即其本天之东升
西没也且使各天之行各自为政则其性岂无缓急而

自外至内舒亟之次如是其有等乎盖惟七政之天虽
有重数而总为一天制动之权全在动天故近动天者
不得不速近地而远动天者不得不迟固自然之理势
也曰若是则周径大小可勿论矣曰在外者为动天所
掣而西行速故其东移之差数迟又以其周径大而分
度阔则其差又迟是故恒星六七十年而始差一度近
动天也然以周径之大小准之此所差之一度以视月
天将以周计矣在内者远于动天而西行迟故其东移

之差速又以其周径小而分度狭则其差又速是故月
天一日东移十三四度者近地而远动天也然以周径
计之此所差之十三四度以视日天尚不能成一度矣
然则周径之大小但可兼论以考其差而非所以迟速
之原也左旋之说可以无疑
　　　论中分较分
问中分较分何也曰较分者是五星在最卑(本/轮)时逐度
(岁轮/周)次均之增数也凡算次均皆设岁轮心在本轮最

高而逐度(岁轮/周)定其均数(或视差在轮心东为加西/为减以生迟留逆㐲诸行)列
之于表命曰次均再设心在最卑亦逐度定其均数所
得必大于最高法以先所得最高时逐度之均数(即次/均)
减之其馀为较分若曰此岁轮上逐度视差在最卑时
应多此数也所以者何视差之理远则见小近则见大
岁轮之在最卑去地为近比在最高必大故也
然则又何以有中分曰较分者次均之较而中分者又
较分之较也使岁轮心常在最高与最卑则只用次均

与较分亦已足矣无如自最高至最卑中间一百八十
度岁轮皆得递居则次均之较各异(岁轮心行于本轮/离最高而下以渐)
(近地则星在岁轮周逐度所生之次均必皆渐大于在/最高时而心离最高时时不等即次均之所增亦必不)
(等而较/分悉变)势不能一一为表故以中分括之其法以本轮
之度分为主若岁轮各度在本轮最卑时较分若干今
在本轮他度则较分只应若干也故以最卑之较分命
其比例为六十分(即中分/之全分)而其馀自离最卑一度起各
有所减减至最高而无中分则亦无较分只用次均本

数矣是故较分于次均恒为加而以中分求较分则于
较分恒为减(表所列较分皆轮心在最卑之数各以中/分乘之六十除之变为轮心未至最卑之)
(较分视在最/卑皆为小数)其比例为岁轮心在某度之较分与在最
卑之较分若中分与六十分也故曰中分者较分之较
也
　　　再论中分
问中分之率既皆以较分为六十分之比例则皆以本
轮度距最卑之远近而得中分之多寡乃五星之中分

各有异率何欤曰中分之率生于距地之远近而五星
各有其本天半径之比例则其平行之距地远近悬殊
而两心差亦各不同则又有本轮半径与其本天半径
之比例矣至于岁轮之大小复参错而不齐如土木本
天大而岁轮小金星本天小而岁轮大而火星在水星
之上则火星本天大而岁轮反大水星本天小而岁轮
反小积此数端而较分之进退纾亟攸分此五星之中
分所以各一其率也要其以最卑为较分之大差当中

分之六十一而已矣
　　　论回回历五星自行度
问诸家多以五星自行度为距日度然乎曰自行度生
于距日远近然非距日之度何也星在黄道有顺有逆
有疾有迟其距太阳无一平行而自行度终古平行故
但可谓之距合伏之行而非距日之度也此在中土旧
法则为段目其法合计前后两合伏日数以为周率周
率析之为疾行迟行退行及留而不行诸段之目疾与

迟皆有顺行度数退则有逆行度数其度皆黄道上实
度也回历不然其法则以前合伏至后合伏成一小轮
小轮之心行于黄道而星体所行非黄道也乃行于小
轮之周耳近合伏前后行轮上半顺轮心东行而见其
疾冲日前后行轮下半则逆轮心西行而见其迟留且
退其实星在轮周环转自平行也故以轮周匀分三百
六十度为实前合伏至后合伏日率为法除之得轮周
每日星行之平度是之谓自行度也若以距太阳言则

顺轮心而见疾距日之度必少逆轮心而迟退距日之
度必多安所得平行之率哉故曰自行者星距合伏之
行而非距日之行也
　　　论回回历五星自行度二
曰自行度既非距日度又谓其生于距日何也曰星既
在轮周行矣而轮之心实行于黄道与太阳同为右旋
而有迟速当合伏时星与轮心与太阳皆同一度(星在/轮之)
(顶作直线过轮心至太阳直射地/心皆在黄道上同度如月之合朔)然不过晷刻之间而

巳自是以后太阳离轮心而东轮心亦随太阳而东太
阳速轮心迟轮心所到必在太阳之后以迟减速而得
轮心每日不及太阳之恒率是则为距日行也(即平行/距日)
然而轮心随太阳东行星在轮周亦向太阳而东行太
阳离轮心相距一度(黄道/上度)星在轮周从合伏处(轮/顶)东行
亦离一度(小轮/上度)太阳离轮心一象限(如月/上弦)星在轮周亦
离合伏一象限乃至太阳离轮心半周与轮心冲星在
轮周亦离合伏半周居轮之底复与轮心同度而冲太

阳(自轮顶合伏度作线过轮心至星之体又过地心/以至太阳黄道上躔度皆成一直线如月之望)再
积其度太阳离轮心之冲度而东轮心亦自太阳之冲
度而东然过此以往太阳反在轮心之后假如轮心不
及太阳积至三象限则太阳在轮心后只一象限(因其/环行)
(故太阳之行速在前者半周以后太阳反在/轮心之后若追轮心未及者然○如月下弦)星在轮周
亦然(自轮底行一象限则离轮顶合伏为/三象限而将复及合伏尚差一象限)逮太阳离轮
心之度满一全周而轮心与太阳复为同度则星在轮
周亦复至合伏之度而自行一周矣(星轮心太阳三者/皆复同为一直线)

(以直射地心如/月第二合朔)凡此星行轮周之度无一不与轮心距
日之度相应(主日而言则为太阳离轮心之度主星而/言则为轮心不及太阳之距度其义一也)
故曰自行之度生于距日然是轮心距日非星距日也
　　　论回回历五星自行度三
问轮心距日与星距日何以不同乎曰轮心距日平行
星距日不平行惟其不平行是与自行度之平行者判
然为二故断其非距日度也惟其平行是与自行度相
应故又知其生于距日也

然则自行度不得为星距日度独不得为轮心距日度
乎曰轮心距日虽与自行相应能生其度然其度不同
轮心是随日东行倒算其不及于日之度星在轮周环
行是顺数其行过合伏之度不同一也又轮心距日是
黄道度七政所同星离合伏自行是小轮周度小于黄
道度又各星异率(小轮小于黄道而小轮周亦匀分三/百六十度其度必小于黄道度而各)
(星之小轮周径各/异度亦从之而异)不同二也若但以自行之初与日同
度自行半周每与日冲而径以距日与自行混而为一

岂不毫釐千里哉
　　　论新图五星皆以日为心
问五星天皆以日为心然乎曰西人旧说以七政天各
重相裹厥后测得金星有弦望之形故新图皆以日为
心但上三星轮大而能包地金水轮小不能包地故有
经天不经天之殊然以实数考之惟金水抱日为轮确
然可信若木火土亦以日为心者乃其次轮上星行距
日之迹非真形也

凡上三星合伏后必在太阳之西而晨见于是自岁轮
最远处东行而渐向下及距日之西渐远至一象限内
外星在岁轮行至下半为迟留之界再下而退行冲日
则居岁轮之底此合伏至冲日在日西半周也冲日以
后转在日东而夕见又自轮底行而向上过迟留之界
而复与日合矣此冲日至合伏在日东半周也
故岁轮上星行高下本是在岁轮上下而自太阳之相
距观之即成大圆而为围日之形以日为心矣其理与

本轮行度成不同心天者同也
但如此则上三星之圆周左旋与金水异
夫七政本轮皆行天一周而高卑之数以毕虽有最高
之行所差无几故可以本轮言者亦可以不同心天言
也若岁轮则不然如土星岁轮一周其轮心行天不过
十二度奇木星则三十三度奇上下旋转止在此经度
内不得另有天周之行知为距日之虚迹也
又如金星岁轮一周其轮心平行五百七十馀度则大

于天周二百馀度水星岁轮一周轮心平行一百一十
五度奇则居天度三之一皆不可以天周言
惟火星岁轮之周其平行四百馀度与天周差四十度
数略相近故历指竟云以太阳为心而要之总是借虚
率以求真度非实义也
　
　
　历算全书卷三