钦定四库全书
　律吕阐微卷二
　　　　　　　　　　　婺源　江永　撰
律率

从来言律者皆云黄钟九寸既得九寸用三分损一益
一以生十一律其法似巧妙一若天地生成有此法与
数者洎生至仲吕不能复得黄钟说者曰律吕之数往
而不返夫律吕效法天地者也天地之气今岁节气既
终来岁节气即续无丝毫之间断独律吕往而不返天

地岂留其有憾乎有谓仲吕极不生者淮南子刘安之
说也有谓仲吕后犹生六十律强立之名自执始至南
事者京房之说也有谓仲吕所生为变律且有变律子
声者杜佑之说也三家之说皆非是独朱载堉因㮚氏
为量有内方尺而圆其外之文悟出天地以方圆相函
而自然之数出其中皆以句股乘除开方之法求之由
倍律而正律由正律而半律皆有真率真数疏密以渐

而差每一律与三分损益所得者微强而不甚相远其
相生也可隔八可相连可左旋而顺亦可右旋而逆仲
吕与黄钟如母子之相随应钟与黄钟黄钟与大吕如
兄弟之相比夫妇之相偶皆一气相联无丝毫之间断
因律管长短推出管体厚薄与空围大小外周内周外
径内径平幂积实皆方圆相函自然之真数此数千年
未泄之秘载堉始发之虽起伶伦州鸠师旷之徒见之
亦当叹其妙绝今载其说更推本于图书发明理数之
所以然使此理昭晰无疑千万世言律学者更无可凿

智翻案之理惟其算周径幂积所用之密率犹有未真
确者俟律体篇详之
载堉之推律亦因其舅祖何氏辨刘歆班固九寸外加
一寸为尺之谬又以十分之法解史记生钟分始知律
原从十起先有体而后有用遂因方内圆外之文悟方
圆相函之理倍律二尺正律一尺半律五寸皆以十为
率也倘一矢口即曰黄钟九寸虽有微妙理数隐于方

圆相函之中亦无由生其悟矣
律数精微载堉深通算学故能启悟乘除开方不惮烦
劳推至二十馀位皆从艰苦得之宋儒言格物穷理此
一项工夫欠缺者多矣

推十二倍律正律之真率

朱载堉曰律家三分损其二三分益其一历家四分度
之一四分日之一与夫方则直五斜七圆则周三径一
等率皆举大略而言之耳非精义也新法算律与方圆
皆用句股术其法本诸周礼㮚氏为量内方尺而圆其

外夫内方尺而圆其外则圆径与方斜同知方之斜即
知圆之径矣度本起于黄钟之长则黄钟之长即度法
一尺命平方一尺为黄钟之率(按㮚氏之方尺自是周家之尺耳非即黄钟之)
(尺也因一尺之数同故命之以为黄钟之率)东西十寸为句自乘得百寸为
句幂(按幂方眼也音觅俗或作幂音莫)南北十寸为股自乘得百寸为
股幂相并共得二百寸为弦幂(按句股求弦术句股各自乘并之为弦幂开方)
(得斜弦)乃置弦幂为实开平方法除之(按开平方法初商为大平方次商以)

(后迭加两廉一隅以除实)得弦一尺四寸一分四釐二毫一丝三忽
五微六纤二三七三○九五○四八八○一六八九为
方之斜即圆之径亦即蕤宾倍律之率(按圆内方尺其幂百寸圆外方)
(二尺其幂四百寸方斜圆径之幂二百得内方之倍外方之半蕤宾为午律犹一岁夏至在前后冬至之间所)
(以应蕤宾者其幂得黄钟倍律之半故也既得蕤宾遂可求南吕得南吕遂可求应钟以应钟为法遂可求诸)
(律其机阕要妙在先得蕤宾自然之理数千古其谁知之)以句十寸乘之(按内方十寸当为根)
(数也)得平方积一百四十一寸四十二分一十三釐五十
六毫二十三丝七十三忽○九五○四八八○一六八
九为实开平方法除之得一尺一寸八分九釐二毫○

七忽一微一纤五○○二七二一○六六七一七五即
南吕倍律之率仍以句十寸乘之(一尺进为百寸)又以股十寸
乘之(百寸进为千寸)得立方积一千一百八十九寸二百○七
分一百一十五釐○○二毫七百二十一丝○六十六
忽七一七五为实开立方法除之(按开立方法初商自乘再乘为大立方次)
(商以后与前商乘为平廉又乘为长廉迭加三平廉三长廉一隅以除实)得一尺○五分九
釐四毫六丝三忽○九纤四三五九二九五二六四五

六一八二五(立方之方根也)即应钟倍律之率(按南吕至应钟隔无射一律以)
(立方积求立方根得之理数甚奇)盖十二律黄钟为始应钟为终终而
复始循环无端此自然真理犹贞后元生坤尽复来也
是故各律皆以黄钟正数十寸乘之为实皆以应钟倍
数十寸○五分九釐四毫六丝三忽○九纤四三五九
二九五二六四五六一八二五为法除之即得其次律
也安有往而不返之理哉旧法往而不返者盖由三分
损益算术不精之所致也是故新法不用三分损益别
造密率其详如左

　按载堉谓旧法往而不返由三分损益算术不精之
　所致愚谓古人亦非算术不精也九九八十一之数
　始于三管子有起五音凡首先主一而三之四开以
　合九九之说伶州鸠有纪之以三平之以六成于十
　二之说老子有道生一一生二二生三三生万物之
　说汉人有太极元气函三为一之说始动于子参之
　于丑以至参之于亥为应钟得十七万七千一百四

　十七之数一若以此为万物终始自然之数矣下生
　者倍其实三其法上生者四其实三其法黄钟九寸
　林钟六寸太蔟八寸三律得寸之全无零分汉人遂
　有黄钟为天统林钟为地统太蔟为人统之说矣其
　推说愈近理则其信三分损益也愈固恶知此外仍
　有算律之法哉又以旧法较今法林钟得黄钟三分
　之二以倍律言之当为一三三三三不尽而新率为
　一三三四八有奇太蔟得黄钟九分之八倍律当为
　一七七七七不尽而新率为一七八一七有奇其数

　与三分损益所得者切近而稍赢安得不以三分损
　益为自然之数哉至仲吕不能反生黄钟则无如之
　何矣独淮南子所载诸律之数何承天刘焯算之似
　欲破三分损益之说载之晋书宋书然而奇零小数
　半分以下弃之半分已上收之终无确数其黄钟生
　林钟之法置黄钟八十一分为实以五百乘之得四
　万○五百分以七百四十九为法除之得五十四分

　为林钟除实未尽则弃之矣七百四十九者与仲吕
　正律之长相近以此为法似矣然九之下仍有小数
　新法黄钟生林钟置黄钟之率十亿为实五亿乘之
　七亿四千九百一十五万三千五百三十八除之得
　林钟则以七四九为法除实求林钟者尚未确是以
　仲吕终不能反生黄钟皆由方圆相函勾股乘除开
　方一窍未启故载堉云新法盖二千馀年所未有自
　我朝始诚然也
又曰造率始于黄钟必先求蕤宾者犹冬夏二至也次

求夹钟及南吕者犹春秋二分也太极生两仪两仪生
四象此之谓也始于黄钟者履端于始也中于蕤宾者
举正于中也终于应钟者归馀于终也律与历一道也
黄钟为宫蕤宾为中应钟为和此三律者律吕之纲纪
也
　按载堉言次求夹钟及南吕本书未言求夹钟之法
　今补之

法曰求得蕤宾倍律之率以句十寸折牛为五寸乘之
得平方积七十寸○七十一分○六釐七十八毫一十
一丝八十六忽五四七五二四四○○八四四五为实
开平方法除之得八寸四分○八毫九丝六忽四一五
二五三七一四五四三○三一一二五即夹钟正律之
率倍之一六八一七九二八三○五○七四二九○八
六○六二二五一为夹钟倍律之率又或以南吕之平
方积倍之二八二八四二七二二四七四六一九○　○
九七六○三三七八开平方法除之即夹钟倍律之率

(原阙)
积算旁通图(有奇零者无时尽列算多位见开方之妙)
二(本是二尺进作二百寸为实以上文所载应钟倍律之数十寸五分有奇为法除之馀律放此)
　右乃黄钟倍律积算(置黄钟倍律积算进一位为实以应钟倍律积算为法除之得)

　(大吕)
一八八七七四八六二五三六三三八六九九三二八
三六二六
　右乃大吕倍律积算(置大吕倍律积算进一位为实以应钟倍律积算为法除之得)
　(太蔟)
一七八一七九七四三六二八○六七八六○九四八
○四五二
　右乃太蔟倍律积算(置太蔟倍律积算进一位为实以应钟倍律积算为法除之得)
　(夹钟)

一六八一七九二八三○五○七四二九○八六○六
二二五一
　右乃夹钟倍律积算(置夹钟倍律积算进一位为实以应钟倍律积算为法除之得)
　(姑洗)
一五八七四○一○五一九六八一九九四七四七五
一七六　　　　○
　右乃姑洗倍律积算(置姑洗倍律积算进一位为实以应钟倍律积算为法除之得)

　(仲吕)
一四九八三○七○七六八七六六八一四九八七九
九二八一
　右乃仲吕倍律积算(置仲吕倍律积算进一位为实以应钟倍律积算为法除之得)
　(蕤宾)
一四一四二一三五六二三七三○九五○四八八○
一六八九
　右乃蕤宾倍律积算(置蕤宾倍律积算进一位为实以应钟倍律积算为法除之得)
　(林钟)

一三三四八三九八五四一七○○三四三六四八三
○八三二
　右乃林钟倍律积算(置林钟倍律积算进一位为实以应钟倍律积算为法除之得)
　(夷则)
一二五九九二一○四九八九四八七三一六四七六
七二一
　右乃夷则倍律积算(置夷则倍律积算进一位为实以应钟倍律积算为法除之得)

　(南吕)
一一八九二○七一一五○二七二一○六六七一七
五
　右乃南吕倍律积算(置南吕倍律积算进一位为实以应钟倍律积算为法除之得)
　(无射)
一一二二四六二○四八三○九三七二九八一四三
三五三三
　右乃无射倍律积算(置无射倍律积算进一位为实以应钟倍律积算为法除之得)
　(应钟)

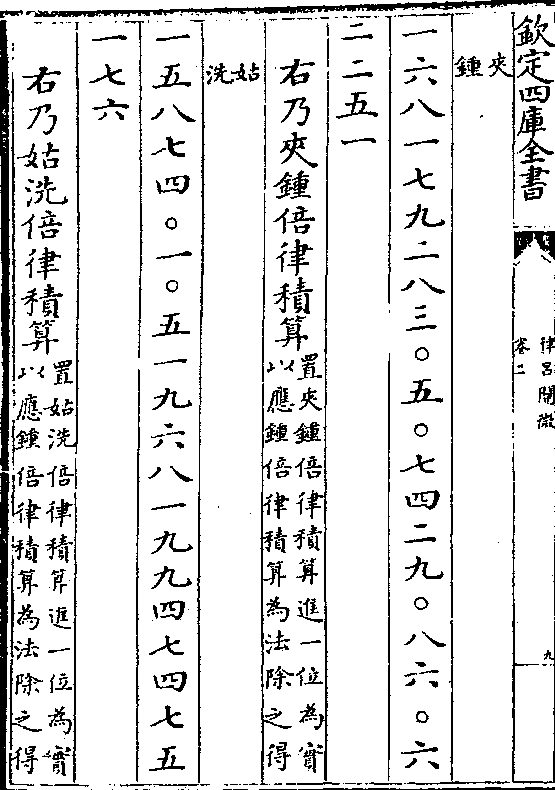一○五九四六三○九四三五九二九五二六四五六
一八二五
　右乃应钟倍律积算(置应钟倍律积算进一位为实以应钟倍律积算为法除之得)
　(黄钟)
新造密率二种(倍律命寸为兆正律命寸为亿欲初学者知命法之变通云尔)
黄钟之率二十兆(本是二十寸命作二十兆)
大吕之率十八兆八千七百七十四万八千六百二十

五亿三千六百三十三万八千六百九十九
太蔟之率十七兆八千一百七十九万七千四百三十
六亿二千八百○六万七千八百六十
夹钟之率十六兆八千一百七十九万二千八百三十
亿○五千○七十四万二千九百○八
姑洗之率十五兆八千七百四十万○一千○五十一
亿九千六百八十一万九千九百四十七
仲吕之率十四兆九千八百三十万○七千○七十六
亿八千七百七十六万八千一百四十九

蕤宾之率十四兆一千四百二十一万三千五百六十
二亿三千七百三十万○九千五百○四
林钟之率十三兆三千四百八十三万九千八百五十
四亿一千七百万○○三千四百三十六
夷则之率十二兆五千九百九十二万一千○四十九
亿八千九百四十八万七千三百一十六
南吕之率十一兆八千九百二十万○七千一百一十

五亿○○二十七万二千一百○六
无射之率十一兆二千二百四十六万二千○四十八
亿三千○九十三万七千二百九十八
应钟之率十兆○五千九百四十六万三千○九十四
亿三千五百九十二万九千五百二十六
黄钟之率十亿(本是十寸命作十亿)
大吕之率九亿四千三百八十七万四千三百一十二
太蔟之率八亿九千○八十九万八千七百一十八
夹钟之率八亿四千○八十九万六千四百一十五

姑洗之率七亿九千三百七十万○○五百二十五
仲吕之率七亿四千九百一十五万三千五百三十八
蕤宾之率七亿○七百一十万○六千七百八十一
林钟之率六亿六千七百四十一万九千九百二十七
夷则之率六亿二千九百九十六万○五百二十四
南吕之率五亿九千四百六十万○三千五百五十七
无射之率五亿六千一百二十三万一千○二十四

应钟之率五亿二千九百七十三万一千五百四十七
补半律之率(本书未推今推之)
黄钟之率五亿(本是五寸命作五亿)
大吕之率四亿七千一百九十三万七千一百五十六
太蔟之率四亿四千五百四十四万九千三百五十九
夹钟之率四亿二千○四十四万八千二百○七
姑洗之率三亿九千六百八十五万○二百六十二
仲吕之率三亿七千四百五十七万六千七百六十九
蕤宾之率三亿五千三百五十五万三千三百九十

林钟之率三亿三千三百七十万○九千九百六十三
夷则之率三亿一千四百九十八万○二百六十二
南吕之率二亿九千七百三十万○一千七百七十八
无射之率二亿八千○六十一万五千五百一十二
应钟之率二亿六千四百八十六万五千七百七十三
　按诸律之率固皆以应钟之率为法求得之而各律
　自乘有平幂其倍半有自然相应者开列于后(此律自乘)

　(之积非空围之面幂)
黄钟倍律之幂折半为蕤宾倍律之幂　蕤宾倍律之
幂折半为黄钟正律之幂　黄钟正律之幂折半为蕤
宾正律之幂　蕤宾正律之幂折半为黄钟半律之幂
　黄钟半律之幂折半为蕤宾半律之幂

右子午对冲之例也

大吕倍律之幂折半为林钟倍律之幂　林钟倍律之
幂折半为大吕正律之幂　大吕正律之幂折半为林
钟正律之幂　林钟正律之幂折半为大吕半律之幂

　大吕半律之幂折半为林钟半律之幂

右丑未对冲之例也

太蔟倍律之幂折半为夷则倍律之幂　夷则倍律之
幂折半为太蔟正律之幂　太蔟正律之幂折半为夷
则正律之幂　夷则正律之幂折半为太蔟半律之幂
　太蔟半律之幂折半为夷则半律之幂

右寅申对冲之例也

夹钟倍律之幂折半为南吕倍律之幂　南吕倍律之
幂折半为夹钟正律之幂　夹钟正律之幂折半为南
吕正律之幂　南吕正律之幂折半为夹钟半律之幂
　夹钟半律之幂折半为南吕半律之幂

右卯酉对冲之例也

姑洗倍律之幂折半为无射倍律之幂　无射倍律之
幂折半为姑洗正律之幂　姑洗正律之幂折半为无
射正律之幂　无射正律之幂折半为姑洗半律之幂
　姑洗半律之幂折半为无射半律之幂

右辰戌对冲之例也

仲吕倍律之幂折半为应钟倍律之幂　应钟倍律之
幂折半为仲吕正律之幂　仲吕正律之幂折半为应
钟正律之幂　应钟正律之幂折半为仲吕半律之幂
　仲吕半律之幂折半为应钟半律之幂

右已亥对衡之例也

　已上六例载堉书所未言今推得之此方圆相函内

　内倍半自然相应之道也律之空围面幂积实其例
　亦如此方与方圆与圆其理同也
方圆相函列律图
　自有律书以来未有此图天地之秘密泄于此图观
　　　　　　　　　　　　　　　　　　　　　

　按载堉之说非图不显作此图以明之方函圆圆又
　函方皆自然之理即有一定之数列线为律外十二
　线为倍律中十二线为正律其半律亦有十二在内
　线愈密不能图只图其一律之疏密自有差次无忽
　密忽疏之病律之长短皆两斜线界定非由三分损益
　观此则新旧二法真伪判然矣

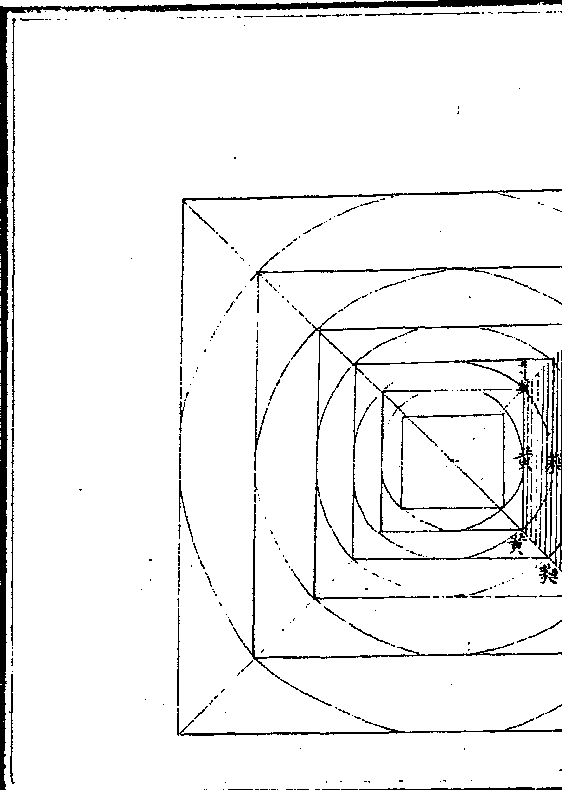
方圆相函外内周径幂积图
　考工记㮚氏为量内方尺而圆其外此图外圆之第二层
　方之第三层也今各增其内外之方圆迭相函容径与径
　幂与幂各以倍半相应此律吕长短所由生外内周径面
　幂实积所由出此天地自然之理数不假人力安排者也
　　　　　　　　　　　　　　　　　　　　　　　

李文贞公光地曰律之以损益相生何也曰凡象数皆
起于阴阳象者阴阳相变者也数者奇偶相生者也故
方之内圆必得外圆之半其外圆必得内圆之倍圆之
内方亦必得外方之半其外方亦必得内方之倍律之
上生为下生之倍下生为上生之半其理一也盖方圆
函盖奇偶乘负阴阳变化天地生生之道也苟其象之所
生同数之所起同则上下无不应也外内无不合也倍
半无不和也故司马迁律书谓之同数今西人算学谓
之比例易曰同声相应同气相求此之谓也夫金石之

铿訇与丝竹之繁细物性迥然殊矣而各以其性为声
律则无不相应者岂非同类比例之谓乎
　按文贞公深明象数之学以方圆倍半之理推原声
　律相生倍半相应直抉造化之微此朱载堉所以因
　㮚氏之文能别推出密率新法者也然文贞公设问
　犹言损益相生不云律生于方圆相容之形岂未见
　载堉之书暗与之相符与今作此图明之方六层圆

　五层方圆有方圆之倍半平幂有平幂之倍半律之
　长短围径之大小幂积之多寡其理皆具此图之中
　要其所以然者河图已以象数示人矣俟象数篇详
　之
律数相较图

正律数　　　一较　　　　再较　　　三较

黄钟十
大吕九四三八七四三一二　(五六一二五六八八)　三一五
○○九四

太簇八九○八九八七一八　(五二九七五五九四)　二九七
三二九一　(一七六八三)
夹钟八四○八九六四一五　(五○○○二三○三)　二八○
六四一二　(一六六八七)
姑洗七九三七○○五二五　(四七一九五八九○)　二六四
八九○三　(一五七五一)
仲吕七四九一五三五五八　(四四五四六九八七)　二五○

○二三○　(一四八六七)
蕤宾七○七一○六七八一　(四二○四六七五七)　二三五
九九○三(一四○三二)
林钟六六七四一九九二七　(三九六八六八五四)　二二二
七四五一　(一三二四五)
夷则六二九九六○五二四　(三七四五九四○三)　二一○
二四二六　(一二五○二)
南吕五九四六○三五五七　(三五三五六九六七)　一九八
四四三四　(一一七八九)

无射五六一二三一○二四　(三三三七二五三三)　一八七
三○五六　(一一一三七)
应钟五二九七三一五四七　(三一四九九四七七)　一七六
七九三○　(一○五一二)
半黄钟五　(二九七三一五四七)
　凡数前后相较必以渐而差如八线表度分匀而诸
　线各有差率是为真数律之渐而短也亦然其以应

　钟之率为法而除实也则同以其前后相差之数一
　较再较三较皆以渐可见新法为真数旧法三分损
　益得之者忽多忽失不以其渐矣(自黄钟至仲吕律分多吕分少自蕤)
　(宾至应钟律分少吕分多)

诸律相生

朱载堉曰新法不拘隔八相生而相生有四法或左旋
或右旋皆循环无端也以證三分损益往而不返之误
其一黄钟生林钟林钟生太蔟太蔟生南吕南吕生
姑洗姑洗生应钟应钟生蕤宾蕤宾生大吕大吕生夷

则夷则生夹钟夹钟生无射无射生仲吕仲吕生黄钟
长生短五亿乘之短生长十亿乘之皆以七亿四千九
百一十五万三千五百三十八除之
　按此隔八左旋相生也七亿四千九百一十五万三
　千五百三十八者仲吕之率也仲吕复生黄钟者也
　用其率以除实自然循环矣旧法三分损一益一亦
　是以五以十乘本律而以七十五为法除之七十五

　者七亿五千万也实少法强是以不能复生黄钟又
　如晋宋书算淮南子之法以七百四十九为除法七
　百四十九者七亿四千九百万也法又稍弱是以亦
　不能循环此新法之所以妙也仲吕之率亦不必以
　应钟迭求而后得也应钟之率自乘而倍之平方开
　之即仲吕之率矣
　用横黍百分律者黄钟长十寸如法乘除所得亿约
　为寸
　用斜黍九十分律者黄钟长九寸长生短者本律之

　率折半为实九亿乘之短生长者本律之率为实九
　亿乘之如法除之所得亿约为寸
　用纵黍八十一分律者黄钟长八寸一分长生短者
　八十一亿乘本律之率折半退位为实短生长者不
　折半但退位为实如法除之所得亿约为寸
其二黄钟生仲吕仲吕生无射无射生夹钟夹钟生夷
则夷则生大吕大吕生蕤宾蕤宾生应钟应钟生姑洗

姑洗生南吕南吕生太蔟太蔟生林钟林钟生黄钟长
生短五亿乘之短生长十亿乘之皆以六亿六千七百
四十一万九千九百二十七除之
　按此隔八右旋相生也六亿六千七百四十一万九
　千九百二十七者林钟之率也末位林钟生黄钟故
　用林钟之率
其三黄钟生大吕大吕生太蔟太蔟生夹钟夹钟生姑
洗姑洗生仲吕仲吕生蕤宾蕤宾生林钟林钟生夷则
夷则生南吕南吕生无射无射生应钟应钟生黄钟半

律此系长生短皆以五亿乘之皆以五亿二千九百七
十三万一千五百四十七除之
　按此相连左旋相生也五亿二千九百七十三万一
　千五百四十七者应钟之率也末位应钟生黄钟半
　律故用应钟之率
其四黄钟半律生应钟应钟生无射无射生南吕南吕
生夷则夷则生林钟林钟生蕤宾蕤宾生仲吕仲吕生

姑洗姑洗生夹钟夹钟生太蔟太蔟生大吕大吕生黄
钟此系短生长皆以十亿乘之皆以九亿四千三百八
十七万四千二百一十二除之
　按此相连右旋相生也九亿四千三百八十七万四
　千三百一十二者大吕之率也末位大吕生黄钟故
　用其率
　已上四法反覆循环相生可见十二律有一气连贯
　之妙四法以第一法为要此五声宫徵商羽角之相
　通旋宫之法所由出也诸律比例相生其理已具洛

　书第六卷详之
　又按隔八相生诸家之说不同有以阳律下生阴吕
　上生大吕夹钟仲吕用倍数者前汉志之法也蔡氏
　从之有以黄钟至仲吕为阳皆下生蕤宾至应钟为
　阴皆上生者淮南子郑康成之法也朱子从之吕不
　韦之法则黄钟大吕太簇夹钟姑洗仲吕蕤宾七律
　皆用半而上生林钟夷则南吕无射应钟五律皆用

　全而下生其说与诸家大异盖诸家谓黄钟下生林
　钟者用全律吕氏谓黄钟上生林钟者用半律吕氏
　之说即管子宫主生徵百有八之理也论声律之体
　固如诸家之说声律之用当主管吕之说祇论长短
　不论阴阳载堉亦尝称引管子之言矣亦谓长律用
　半短律用全矣载堉又引朱子语有大阴阳小阴阳
　之说谓此论精妙非蔡氏所及究之上下相生别有
　妙理徒以阴阳言者尚未尽其妙也今不录
　律吕阐微卷二