钦定古今图书集成历象汇编历法典

　第一百十八卷目录

历法典第一百十八卷

算法部汇考十

《算法统宗六》少广章第四上

此章如田截纵之多益广之少。故曰少广如方田，还原之意以方法除积幂，而求方，以圆法除方实而求圆，所注开平方、平圆，头绪繁穴，初学者难。今注释简明列于后。
开平方法认商歌

一百一十定无疑，一千三十有零馀。九千九九不离十，一万才为一百推。得商方除倍作廉，次商名隅并廉除，馀数续商隅又倍，只依此法取空虚。
解曰：平方者，乃方面自乘之积也。开者以求方面之数也，一百一十定无疑者，谓如积一百步可约方面十步，已无疑矣，一千三十有零，馀者谓积一千步可约方。面三十步有零也。九千九九不离十者，谓如积九千步约方面九十步，自乘九九八十一也，一万才为一百步，自乘得一万步也。此言约初商之诀，再具商积于后。

开平方初商定首位诀，是自乘之数也。
商一步积一步　　　商一十步积一百步
商二步积四步　　　商二十步积四百步
商三步积九步　　　商三十步积九百步
商四步积一十六步　商四十步积一千六百步商五步积二十五步　商五十步积二千五百步商六步积三十六步　商六十步积三千六百步商七步积四十九步　商七十步积四千九百步商八步积六十四步　商八十步积六千四百步商九步积八十一步　商九十步积八千一百步法曰：置积为实，别置一算名曰下，法于实数之下〈自末位至首常超一位〉，约实一下定一数，千百下定十数，万下定百数，百万下定千数，实上商置第一位，得若干下位。亦置上商若干，名曰方，法与上商相呼，除实若干馀实若干，乃以二乘方法〈即倍法也〉。得若干为廉法。续商置第二位于上商之次，得若干下法，亦置续商若干为隅法〈隅法者，乃曲尺样二廉之角。为隅则小方也〉。于倍方之次共若干皆与续商相呼，除实尽得平方一面数，如不尽仍前再商之或数不足以法命之，何谓之命，若馀实若干不尽，却以所商得平方数若干倍之，再添一个共得若干，便商得面方多一数也。因此数不足而为之，命平圆不尽数亦仿此，但立方立圆于此不同。
若要还原，如算方田法，以面方数自乘，即见积也。若还原遇面方下，原有不尽数者，以面方数自乘并入不尽数，便可见积也。
开方求率作法本源图开方求率作法本源图

右图，吴氏九章内，虽有自开平方至五乘方，却不云如何作用。注释未见详明。今依图式自上一，得二为平方率又并〈三三〉得三，三为立方率，又并〈四六四〉得四六四为三乘方率，向下求出三十馀乘方皆取自然生率之妙，今略具五乘方图式可为求廉率之梯阶也。
又考其平方形如方田，以平方面自乘，得平方积数是一乘方。
其立方形，如骰子样以平方。面自乘得平方。积再以高，方面乘之，得立方积，数是二乘方。
其三乘方以平方面自乘得平方积数，再以高方面乘得立方积数，又以方面乘得，三乘方积数故曰三乘方，然其形不知如何模样，只是取数而已，或至十乘方三十馀乘方，皆是先贤取生率之妙，以明开方正律亦不可废。
开平方〈有实而无法商约而除之也〉

今有平方积，三百二十四步，问每方面若干。
答曰：得每方面一十八步。
方廉隅法之图方廉隅法之图

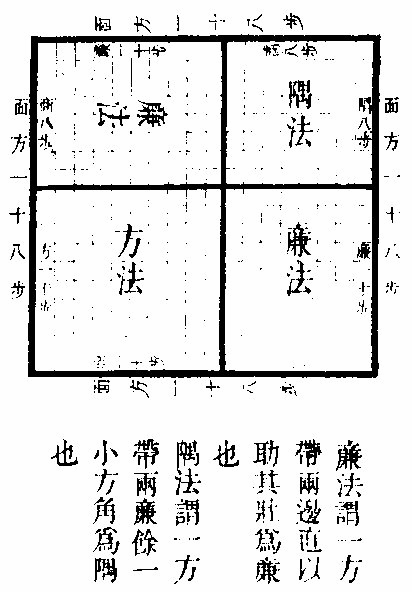
法曰：置积三百二十四步为实，约初商一十步，于实左另置下法一十步，于实右名曰方，法与上商相呼一，一除实一百步馀实二百二十四步，就以方法一十步倍之，得二十名曰廉，法又约，次商八步于左，初商一十之次共得一十八步，亦置八步于实右，廉法二十步之次名曰隅，法共得二十八步，与左位次商八步相呼，二八除实一百六十步，又将左八对右八相呼，八八除实六十四步恰尽。若还原自乘是也。
右法以明方廉隅之名也。

假如今有阔算盘，共子三百六十一个，问每面子若干。
答曰：每面一十九个。
法曰：置棋子为实，约初商一十步于实左，另置下法一十步于实右，左右相呼，一一除实。一百个馀实二百六十一个，就以下法一十倍之，得二十，次商九个于左，初商一十之次亦置九个于右，倍方二十之次共得二十九，皆与左次商九相呼，二九除实，一百八十个，又左九对右九相呼，除实八十一个恰尽。今列开平方法，定分左中右式〈凡看字亦照算盘，自左至右〉。
图缺
今有方田，积三千一百三十六步。问平一面若干。答曰：五十六步。
法曰：置田积为实，约实定初商五十步于左，另置下法五十步于右，左右相呼，五五除实二千五百步馀积六百三十六步，就以下法五十步倍之，得一百步。次商六步于左，初商五十之下亦置六步于右，倍方一百隔位之下共得一百零六步，皆与次商六步相呼。一六除实六百步，又左六对右六相呼，六六除实三十六步恰尽。
今有方田，积二十万零七千九百三十六步。问平方一面若干。
答曰：四百五十六步。
法曰：置方积为实，约初商四百于左位，亦置四百于右位，为方法与上商相呼，四四除实一十六万馀实四万七千九百三十六步，就以方法四百倍作八百为廉法，次商五十于左初，商四百之下亦置五十于右廉法。八百之下为隅，法共八百五十皆与次商五十呼除，先以左五对右八呼五八除实四万，又左五对右五呼五五除实二千五百馀实五千四百三十六步，却以下法次商五十倍之。并廉共得九百，又为廉法又商六步于左，初次商四百五十之下，亦置六步于廉法，九百隔位之下共九百零六，皆与左再商六步呼，除先左六对右九呼六九除实五千四百。又左六对右六呼六六除实三十六步恰尽合问。今有方砖一千四百六十一块，欲为平方。问一面方若干。
答曰：一面方三十八块又七十七块之十七。
法曰：置砖积为实，初商三十块于左，另置下法三十于右，为方法，左右相呼，三三除实九百馀实五百六十一块。就以方法三十倍，作六十为廉，法次商八于左初商三十之下，亦置八于右，廉法六十之下为隅，法共六十八，皆与上商八相呼，六八除实四百八十，又呼八八除实六十四，馀实一十七不尽。却将所商三十八倍之，再添一块共得一方数七十七，命一十七何谓之命。以原总数内除去一十七，另加上七十七便商得面方三十九块，因此不及，而为之命，馀仿此。
今有方田，积七万一千八百二十四步。问平方一面若干。
答曰：每一面方二百六十八步。
法曰：置方田积为实，以开平方法除之，初商二百于左，位亦置二百于右，位为方法以左二对右二相呼，二二除实四万讫，馀实三万一千八百二十四步；就以方法二百倍，作四百为廉，法次商六十，于左。初商二百之下。亦置六十于廉法四百之下，为隅。法共四百六十，皆与次商六十呼，除先以左六对右四呼四六，除积二万四千又左六对右六呼六，六除积三千六百馀实四千二百二十四步，却以右位次商六十倍加六十于四百之下，共五百二十。皆为廉法，又商八于左初次商二百六十之，下亦置八于右廉，法五百二十之下皆与上商八步呼。除先以左八对右五呼除，五八除积四千又呼，二八除一百六十，又呼八八除实六十四步恰尽。
一方四廉两隅演段图一方四廉两隅演段图

演段解曰：其初商二百自乘得积四万，是大方积也。次商六十内有阔六十，长二百两段故倍，初商二百作四百为廉，法与左次商六十乘得二万四千是两个阔六十长，二百之积。其次商六十自乘得三千六百是中方积，又商八步内有阔八步长二百六十两段，故倍初。次商二百六十为五百二十，却以八步乘得积四千一百六十是两个阔八步长二百六十步小廉积也。其又商八步，自乘得积六十四步，是小方隅积也。凡平圆先用开平方法，后用十二除为圆。
归除开平方

今有平方积，五万四千七百五十六步。问平方一面若干。
答曰：二百三十四步。
归除开平方法曰：置积五万四千七百五十六步，为实，于盘中见实，约商二百于实左，另置二百于右下。左右相呼，二二除实四万步，馀实一万四千七百五十六步，以右下二百步倍之得四百步为法，归除之呼四一，二十二逢四进一十得商三十步，就置三十步于右四百之下，相呼三三除实，九百步馀实一千八百五十六步，就以右下三十步倍之，得六十步共四百六十步为法，归除之，呼四一二十二逢八进二十得商四步，亦置四步于右六之下，相呼四六除实二百四十步，又呼四四除实一十六步恰尽。以左上所商得二百三十四步，为平方一面之数也。
今有平方积四百九十步，欲为平方。问：每面若干。答曰：每面二十二步又四十五分步之六。
归除开平方法曰：置积四百九十为实，于盘中见实四百，商二十步于实左，另置二十步于右下，左右相呼，二二除实，四百步馀实九十步，就以右位二十步倍之得四十步为法，归除之呼逢八进二步。就以二步于右四十之下相呼，二二除实四步，馀实六步不尽，以直方命之法曰：以所商二十二步倍之，又添一步共得四十五步为分母命之曰四十五分步之六也。
解曰：若以积四百九十步，加入四十五步，减去分子六步，仍得五百二十九步，便商二十三步。所谓不及故为之命也。
归除平方带纵歌

平方带纵法最奇，四因积步不须疑。纵多自乘加因积，又用开方法除之。再以纵多并开积，折半方为长数施，若问阔步知多少，将长减却纵多基。
今有直田积一千七百五十步，长比阔多一十五步。问：长阔各该若干。
答曰：长五十步。阔三十五步。
法曰：置积一千七百五十步，以四因之，得七千步，另以纵多一十五步自乘得二百二十五步相并，共得七千二百二十五步为实，以开平方法除之，约商八十于左，亦置八十于右，左右相呼。八八除实六千四百步馀实八百二十五步，就以下法八十倍之，得一百六十步为法，归除之呼，逢五进五于初商八十之次，共得八十五步。下法亦置五于一百六十之下，共一百六十五步，左五对右六相呼，五六除实三百步又左，五对右五呼五五除实二十五步，恰尽。得左商八十五步如长阔相和之，步加入纵多一十五步。共得一百步折半得五十步，于内减去纵多一十五步，馀三十五步即是阔也。
带纵开平方法歌〈兼商除〉

平方带纵法为奇，下位先安纵步基。上商得数加纵内，纵方下法并为题。上下相呼除实毕，倍方不倍纵开馀。馀数续商方再倍，何愁此术不能知。
法曰：如有田积若干只，云阔不及长若干。问阔者几何，则置田积若干为实，以不及若干为纵，列于下法以带纵开平方法，除之实上初商，得若干下法，亦置初商若干于纵内，共得若干皆与上商相呼，除实若干馀实若干另以下法初商若干倍之〈倍方不倍纵〉。次商若干于左位初商之次下，法亦置次商若干于倍方之。次共若干皆与次商相呼，除实尽，得阔数，加不及数为长。若要还原以所商得阔若干，为实，另以所得商数〈加上纵多共若干，或减不及馀若干〉。若干乘之见积。今有田积一千七百五十步，只云长比阔多一十五步。问：长阔各若干。
答曰：长五十步。阔三十五步。
法曰：置积为实以多一十五步为纵列于下位。以带纵开平方法除之，初商三十于左位，另于下法亦置三十。加于纵上共得四十五步，与上商相呼左三对右四呼三四除实一千二百，又左三对右五呼三五除实，一百五十另以下法，初商三十倍作六十加纵多十五，共得七十五次商五于左，位另于下法亦置五于倍方之下共八十，皆与次商五相呼，左五对右八呼五八。除实四百步，恰尽得阔三十五步，加多一十五步为长合问。
又法名减积开平方，置田积为实，于中另置不及十五步于右位，为减积。上商三十于左位，另以下法亦置三十于右为方，法以乘减积一十五步，得四百五十步，以减中实馀实一千三百步，却以初商三十与上商三十，相呼三三减积九百，馀实四百就以方法、三十倍作六十为廉法，次商五步于左三十之次下位亦置五步以乘减积一十五步得七十五步，以减中积仍馀实，三百二十五步，却以下位廉法六十并。入次商五步共六十五步，皆与上商五步呼五六除实，三百五五除二十五步，得广三十五步合问。若问纵照前布列。上商五十步以乘不及十五步，得七百五十步并加前积共二千五百步，却呼五五除实二千五百步，尽得纵合问。
今有圭田，积一百二十六步，阔不及长九步。问：长阔各若干。
答曰：长二十一步，阔一十二步。
法曰：倍田积得二百五十二步，为实以不及九步，为纵方于右上商十步，下法亦置十步于纵，九步上共一十九步，与上商十步除实一百九十步，馀六十二步，另以下法初商一十倍之，作二十次商二步于左下法，亦置二步加于纵方，九上共三十一步，皆与上商二相呼除实尽，得阔一十二步，加不及九步，得长合问。
今有句股，田积四百八十六步，只云句少弦一十八步。问：各若干。
答曰：句阔二十七步，股长三十六步，弦斜四十五步。
法曰：倍积得九百七十二步为实，以弦差一十八步折半得九步为纵，方开平方法除之得句二十七步，加差一十八步为弦，斜四十五步，另以句自乘弦自乘二数相减，馀一千二百九十六步，为实以开平方法除之，得股长三十六步合问。
今有句股田积四百八十六步，只云股少弦九步。问：各若干。
答曰：股三十六步，句二十七步，弦四十五步。
法曰：三因积得一千四百五十八步，为实。以弦差九步折半得四步五分为纵，方开平方法除之，得股长三十六步，加九步为弦四十五步。另以股自乘弦自乘二数相减馀七百二十九步为实。以开平方法除之得句阔二十七步合问。
长阔相和歌〈与减纵开平方法同〉

长阔相和不识情，四因积步莫差争。和步自乘减去积，馀用开方差步名。却将和步加差步，折半当为长数成。要知阔步如何见，长步减差阔便明。
今有直田积一千九百二十步，长阔相和九十二步。问：长阔各若干。
答曰：长六十步，阔三十二步。
法曰：置田积以四因之，得七千六百八十步，另以和步九十二步自乘得八千四百六十四步，减去因积馀七百八十四步为实，以开平方法除之得，长阔相差二十八步，加入和步九十二步共一百二十步，折半得长六十步，内减差步二十八步馀得阔三十二步合问。
又法名减纵开平方，置田积一千九百二十步为实，以相和九十二步于右为减纵，上商三十以减九十二步馀纵六十二步，与上商三十相呼，三六除实一千八百又呼，二三除六十馀实六十步，又以上商三十再减馀纵六十二，仍馀纵三十二，次商二又减纵二馀纵三十与，次商二相呼，二三除实六十合问。若先问长者，仍前布列先商长，六十减纵亦得。今有句股田积九百六十步，长阔相和九十二步。问：长阔各若干。
答曰：长六十步，阔三十二步。法曰：置田积以八因之〈或倍田积以四因同〉，得七千六百八十步，另以和步自乘得八千四百六十四步相减，馀七百八十四步，以平方开之，得长阔相差二十八步加入。和步共一百二十步，折半得长六十步，内减差步二十八馀得阔三十二。步合问。若以减纵开平方法算置积倍之得一千九百二十步，为实。以相和九十二步为减纵，如前商之即得。
长阔相差歌〈与带纵开平方法同〉

长阔相差要识情，积数将来以四乘。差步自乘加入积，开方得数以和名，和步加差须折半，此为长数更无零以长减差便为阔，学者留心仔细寻。
今有直田积一千九百二十步，长阔相差二十八步。问：长阔各若干。
答曰：长六十步，阔三十二步。
法曰：置田积以四因之，得七千六百八十步，另以相差二十八步自乘得七百八十四步，加入积数共八千四百六十四步为实，以开平方法除之，得长阔相和九十二步，加入差步二十八共一百二十步，折半得长六十步，内减相差二十八步，馀得阔三十二步合问。
又法名带纵开平方，置田积一千九百二十步为实，以相差二十八步为带纵，列于右上，商三十于左，右位亦置三十加于纵，上共得五十八步，皆与上商三十相呼，三五除实一千五百又呼，三八除实二百四十馀实一百八十，另以下法初商三十倍之，得六十加差二十八共得八十八步。次商二于左三十之次下法亦置一于倍方之次，共九十步，皆与次商二相呼，二九除实一百八十，恰尽。得阔三十二步，加差二十八步得长六十步合问。如句股出积长阔相差。问答倍积用法同前。
平圆法歌

平圆之法若求周，十二乘积数可求。求径四因三而一，开平方法以除收。
法曰：问外周者置积若干：以圆法十二乘得若干为实，以开平方法除之得周，若要还原如圆田以外周自，乘又以十二除之，见积若周下，原有不尽数者以周自乘并入，不尽，以十二除见积。问径者置积若干，以四因三归，得若干为实以开平方法除之，得径算圆居方四分之三。故用四因三归之，若要还原如圆，田以径自乘并入不尽，数以三因四归之见积。若问周问径遇有馀，积不尽之数，依开平方法下命之。
今有圆田积二千三百五十二步。问：平圆周若干。答曰：周一百六十八步。
法曰：置圆田积步以十二乘之得二万八千二百二十四步为实，以开平方法除之，初商一百于左，位于下法亦置一百为方，法呼一，一除积一万馀积一万八千二百二十四，就以方法一百倍之，得二百为廉，法续次商六十于左，初商一百之下右。位亦置六十于廉，法二百之下为隅，法共二百六十，皆与上商六十呼除先呼二六，除积一万二千又呼，六六除积三千六百馀积二千六百二十四，另以右位次商六十倍作一百二十并入廉，法二百共三百二十，又为廉法再商八步，于左位初次商一百六十之。下于右位亦置八步，又为隅法于廉，法之下共三百二十八，皆与上商八呼，除先呼三八除积二千四百，又呼二八除积一百六十又，呼八八除积六百四十恰尽。今有圆田积二千三百五十二步。问：平圆径若干。答曰：径五十六步。
法曰：置积步先以四因，后用三归得三千一百三十六步为实，以开平方法除之，初商五十于左位，亦置五十于右位，为方法左右相呼，五五除积二千五百馀积六百三十六步，却以右位五十倍作一百为廉，法次商六于左，初商五十之次，亦置六于右廉法一百隔一位，下为隅法。共一百零六皆与上商六相呼，一六除积六百，又左六对右六呼，六六除积三十六步恰尽。
今有圆积五万四千个，欲为平圆。问：径若干。
答曰：径二百六十八个又五百三十七个之一百七十六。
法曰：置积数先以四因，后用三归之得七万二千为实，以开平方法除之，初商二百于左位于下法右位亦置二百为方，法呼二二除积四万，馀积三万二千。就以右位二百倍之，得四百为廉法，次商六十于左。亦置六十于右，廉法四百之次为隅法相呼四六除积二万四千又呼六六除积三千六百馀积四千四百，却以右位六十倍之，并入廉法共五百二十皆为廉法。又商八于左二百六十之次右位，亦置八于廉法之次，共五百二十八，皆与上商八呼，除先呼五八除积四千，又呼二八除积一百六十，又呼八八除积六十四，馀积一百七十六不尽。却将所商数倍之再加一个，得五百三十七，命之一百七十六，若于总内减去一百七十六加上五百三十七，便商得径二百六十九也。
开平方通分法

今有积一千五百九十步六十四分步之一。问：平方一面若干。
答曰：三十九步又八分步之七〈即八分七釐五毫〉。法曰：置积一千五百九十步，以分母六十四分乘之，加入分子一共得一十万零一千七百六十一分，以开平方法除之，得方面三百一十九分为实，另以分母六十四以开平方法除之，得八分为法，除之得方面三十九步不尽七，命之曰八分步之七。
今有方田一段，面方四步一十八分步之一十七。问：斜弦步、方积步各若干。
答曰：斜弦七步，方积二十四步五分。
法曰：置四步以分母一十八乘之，加入分子一十七共得八十九步，自乘得七千九百二十一步，另以分母分子相减，馀一，以乘分子十七，如故并前共得七千九百三十八步为实另以分母十八自乘得三百二十四为法，除之得二十四步五分为方积，倍之得四十九步以开平方法除之，得斜弦七步。但方面下有零分数，求积者仿此。
右商法开方归除开方二者听从人便。
方圆三棱总歌

方圆三棱求周数，各减总一分明布。十六乘方带纵八，十二乘圆加纵六。十八三棱添纵九，俱用带纵开方术。倍方不倍纵开除，何愁外周不知数。
还原束法歌

四方之束添八乘，十六归除数颇明。圆束外周加六凑，乘来十二法除清。三角加九乘周数，十八归除不差争。各要临时添一数〈即中心也〉，束积推详数可成。今有方箭八十一根。问：外周若干。
方箭图

答曰：外周三十二根。
法曰：〈此是八个周中包一〉置方箭八十一根减去中心一根馀八十根。以十六乘之，得一千二百八十根为实，

于中位以八为纵列，于右位用带纵开平方法除之。初商三十于左位下法，亦置三十于右纵八之。上共三十八左右对呼。三三除实九百，又左三对右八呼。三八除二百四十，就以下法初商三十倍作六十〈不倍纵〉，次商二于左，初商三十之次下。法亦置二于倍方之次，共得七十，左二对右七呼二七，除实一百四十恰尽。得周三十二根。合问。
今有方箭一束，外周三十二根。问：总积若干。
答曰：八十一根。
法曰：置外周三十二根于左，亦置三十二根于右，加内周八共四十相乘得一千二百八十为实，以方束法十六除之，得八十。加上中心一，共得八十一根。合问。
凡方物乃是八个，周中包一自内之外每层加八。自外之内每层减八，故以八归，外周即知层数，如外周三十二是四八即是四层。馀仿此。

今有圆箭一百二十七根。问：外周若干。
答曰：外周三十六根。
圆箭图

法曰：〈此是六个周中包一〉置圆箭一百二十七根减去中心一，馀一百二十六根。以十二乘之，得一千五百一十二根为实，于中以纵六列于右。

用带纵开平方法除之，初商三十，于左下法亦置三十于右纵六之。上共三十六，左右相呼。三三除实九百，又呼三六除实一百八十，就以右位，初商三十倍作六十〈不倍纵〉。次商六于初商三十之，次下法亦置六于倍方之次，共七十二，左六对右，七呼。六七除实四十二，又左六对右二呼，二六除实一十二恰尽。合问。今有圆箭一束，外周三十六根。问：总积若干。
答曰：一百二十七根。
法曰：置外周三十六于左，亦置三十六于右，加内周六，共四十二。相乘得一千五百一十二为实，以圆束法十二除之，得一百二十六。加中心一。合问。
凡圆物乃是六个周中，包一。自内之外每层加六。自外之内每层减六。故以六归，外周即知层数。如外周三十六是六六即是六层。馀仿此。

今有三棱物九十一个。问：外周若干。
三棱图

答曰：外周三十六个。
法曰：〈此是九个周中包一〉置三棱物九十一个减去中心一个馀九十个，以十八乘，得一千六百二十个，为实。

以九为纵，列于右。用带纵开平方法除之，初商三十于左下。法亦置三十于右纵九之，上共三十九，左右相呼，三三除实九百，又呼三九除实二百七十除实四百五十，另以下法初商三十倍作六十〈不倍纵〉。共六十九次商。六个于左初商三十之次下，法亦置六于倍，方之次共七十五，以左六对右七，呼六七除实四百二十，又左六对右五呼五六，除实三十恰尽。合问。今有三棱物，外周三十六个。问：总积若干。
答曰：九十一个。
法曰：置外周三十六于左，亦置三十六于右，加内周九共四十五，相乘得一千六百二十为实，以束法十八除之，得九十，加中心一。合问。
凡三棱物乃是九个周中包一，自内之外每层加九，自外之内每层减九，以九归外周即知层数，如外周三十六是四九即四层。馀仿此。

假如方箭积六十四根。问：外周若干。
答曰：外周二十八根。
法曰：此是双层者，只以方箭积为实，以开平方法除之得一面方八根，却减去一根得七根，以四因得外周二十八根。若前方箭积八十一根，乃是单层者，若只以方箭为实，以开平方法除之得一面方九根。却减去一根得八根，以四因亦得外周三十二根。
面方八数为双乃八八六十四也，九数为单乃九九八十一也。此法捷径无差，双层单层皆可用。
演段根源开方图解

夫算之术入则诸问，出则直田。盖直田能致诸用而有此说，故立演段，盖欲演算之片段也。知片段则能穷根源，既知根源而心无朦昧矣。今摘数问详注图解以明后学，其馀自可引而伸之，不待尽述。
直田长阔相乘，与万象同意。

今有直田积八百六十四步，只云阔不及长一十二
带纵平方图

步。问：长阔各若干。答曰：长三十六步，阔二十四步。
法曰：置积为实以不及十二，列于右为带纵开平方法除之，初商二十于左下法亦置二十加于纵上，共三十二皆与上商二十相呼。除实六百四十馀实二

百二十四，却以下法初商二十倍之，共五十二次商。四于初商二十之次下法亦置四于倍方之，次共五十六。皆与左次商四相呼除实恰尽，得阔二十四步加差一十二步，得长三十六步。合问。
今有直田积八百六十四步，只云长阔相差一十二步。问：长阔相和共若干。
答曰：长阔相和六十步。
法曰：置田积以四因得三千四百五十六步，另以差一十二步自乘得一百四十四步，并四因积共三千
长阔相差求和图

六百步，乃是相和之积，用开平方法除之，得长阔相和六十步合问。若问长数加差折半即得。
演段解曰：四因积者，乃是四长四阔积居边共三千四百五十六步，却以相差一十二步自乘得一百四十四步，补中得相和积二

千六百步，以开平方法除之，得长阔相和六十步也。今有直田积八百六十四步，只云长阔相和六十步。问：长阔相差若干。
答曰：长阔相差一十二步。
法曰：置田积以四因得三千四百五十六步，另以相和六十步，自乘得三千六百步，却减去四，因积三千四百五十六步馀一百四十四步，乃相差自乘，积用开平方法除之，得长阔相差一十二步。合问。
长阔相和求差图同前。
解曰：其相和六十步，自乘积三千六百步，内有四因积四个共三千四百五十六步，居边有一个相差，自乘积一百四十四步，用开平方法除之，得长阔相差十二步。

今有直田积八百六十四步，只云长阔相和六十步。问：长阔各若干。
答曰：长三十六步，阔二十四步。
法曰：置积为实，以相和六十步于右，为减纵开平方法除之，上商二十于左，就将右纵减去上商二十馀
减纵开方图

四十，与上商二十相呼，除实八馀实六十四步，又以上商二十再减馀纵二十，仍馀纵二十次商，四步亦减馀纵二十，仍净馀纵十六与次商四相呼，除实尽得阔二十四步，以减相和六十步，馀得长三十六步。合问。
减纵翻

解曰：若不益积便用减纵，或有不可益积者须用减纵之术，先问阔者用此。若先问长则用减纵翻积法。法曰：置积为实，以相和为减纵开平方法除之，上商三十以减纵六十馀纵三十，与上商三十相呼，合除

积九百而积实不及，乃命翻法除原积八百六十四馀负积三十六为实，再置上商三十以减馀纵三十讫。次商六步下法亦置六为隅，法与上商六呼，除负积恰尽。得长三十六步。合问。
今有方田一段，圆田一段，共积二百五十二步。只云方面圆径适等。问：方圆径各若干。
答曰：方面圆径各一十二步。
法曰：置共积为实，以四因得一千零八步，并方四圆三共七为法除之，得一百四十四步。以开平方法除
方圆求径图

之得方面一十二步，圆径亦同。
术曰：四因方圆共积得四个方积，四个圆积，其四个圆积，恰折三个方积。故用七除得一个方积，以开平方法除之得方圆径。旧法四因共积得一千零八步为实，以开平方法除

之并方四圆三共七为隅，于下法初商一十，以隅七乘得七十为方，法与上商一十相呼，除实七百馀实三百零八步，另倍方法得一百四十为廉，法次商二步以隅。七乘得十四，并入廉法一百四十共一百五十四。与次商二步相呼除实恰尽。合问。
减积带纵开平方

今有大小方田二段，相并共积四百步，只云大方田面比。小方田面多四步。问：大小方面，并积各若干。答曰：大方面一十六步，计积二百五十六步。小方面一十二步计积一百四十四步。
法曰：置共积于中，另置大方田面，多小方田面四步自乘得一十六步，以减共积四百步，馀积三百八十四步，折半得一百九十二步为实。又另置大方面多小方面四步为纵方，以带纵开平方法除之，初商一十于左下法亦置一十于纵方之上，共一十四步，皆与上商一十相呼，除实一百四十步馀实五十二步。却以下法初商一十倍作二十并入纵四步共二十四步。次商二步于左初商一十之次下，法亦置二步
方积带纵开平方图

于纵方之次，共二十六步。皆与次商二步相呼，除实恰尽，得小方面一十二步。加四步得大方面一十六。步各以方面自乘得各积。合问。
解曰：共积是一段大方积，一段小方积。其大方积内有一段小方积，一
段大多小方自乘积如隅，又大多小的两段长阔积如廉，每廉长即小方面数，阔即大多小数。先用大多小方步数自乘得数以减共积者，是减云。大方田一段小隅积馀积折半是一段小方积。一段长阔廉积〈就如一段直田〉。用带纵开平方法除之，求出一段小方面数，加多步为大方数也。

今有大中小方田三段相并，共积八百步。只云大方田面比中方田面多四步，中方田面比小方田面多四步。问：大半小方面并积各若干。
大小三方总一图

答曰：大方面二十步，计积四百步。中方面一十六步，计积二百五十六步。小方面一十二步，计积一百四十四步。
法曰：置共积于上，另置大方面多小方面八步，自乘得六十四步。又以中方面多小方面四步自乘得一

十六步。并二数共八十步，以减共积八百步，馀积七百二十步。以三归之得二百四十步，为实。初商一十自乘得一百步，以减实积馀实一百四十步，次商二并初商共十二，自乘得一百四十四，内除初商自乘一百馀四十四，以减馀实又馀实九十六，却以三因得二百八十八，另并大方多中四小八共十二，倍之得二十四与初商十步，相呼一二，除二一四除四又与次商二相呼，二二除四，二四除八，得小方面十二。步加多四步得中方，面十六步又加多四步。得大方面二十步，各以方面自乘，得各积。合问。
若四段则用四归，五段则用五归。

假如大小圆田二段共积，只云大圆径多小圆径者，法置共积以四因，三归得数仍如前方田算，或只云大圆周多小圆周者，法置共积以十二乘，得数仍如大小方田算。
假如大小立方二所共积，只云大立方面多小立方面者。法置共积另置大立方面多小立方面数，自乘再乘以减共积馀积折半为实，初商自乘再乘得数。除实讫，次商若干并入初商，共若干。自乘再乘得数内减去初商，自乘再乘数馀若干除实讫，仍馀实若干倍之，却以大多小数并入初商。次商数共若干以初次商若干乘得数，又以大多小数乘得若干，却以三因之。得若干除实恰尽，得小立方面数加多数得大立方面数，各以方面自乘再乘得各积立方。三所共积用三归，若四所共积用四归。馀仿此。
开立方法歌〈自乘为平方再乘为立方〉

自乘再乘除实积，三因初商方另列。次商遍乘名为廉，方法乘廉除次积。次商自再乘名隅，依数除积方了毕。初次三因又为方，三商遍乘仿此的。
认商歌

一千商十定无疑，三万才为三十馀。九十九万不离十，百万方为一百推。
解曰：谓如积一千步约商一十步，又如积三万就约商三十步，又如积九十九万步就约商九十步。如积一百万步可约商一百步，乃自乘再乘之积而求原数也。此谓有实无法，故曰约之。

商一步　　积一步起至七步止，皆商一步。
商二步　　积八步起至二十六步止。
商三步　　积二十七步起至六十三步止。
商四步　　积六十四步起至一百二十四步止。商五步　　积一百二十五步起至二百一十五步止。商六步　　积二百一十六步起至三百四十二步止。商七步　　积三百四十三步起至五百一十一步止。商八步　　积五百一十二步起至七百二十八步止。商九步　　积七百二十九步起至九百九十九步止。商一十步　积一千步起至七千步止。
商二十步　积八千步起至二万六千步止。
商三十步　积二万七千步起至六万步止。
商四十步　积六万四千步起至一十二万步止。商五十步　积一十二万五千步起至二十一万止。商六十步　积二十一万六千步起至三十四万止。商七十步　积三十四万三千步起至五十一万止。商八十步　积五十一万二千步起至七十二万止。商九十步　积七十二万九千步起至九十九万止。商一百步　积一百万步起至七百万步止。
已上皆言初商首位之积，以所商自乘再乘之数。次商用法不同。

法曰：置积为实，别置一算，名曰下法。于实数之下〈自末位至首常超二位〉。约实自千至九十馀万俱定十，及百万后俱定百。实上商置第一位得若干下法，亦置初商若干自乘再乘得若干除实讫，馀实若干却以三乘下法初。商若干，得若干为方。法列位次商置第一位于初商之次，得若干下法。亦置次商若干于初商之次，共得若干就以次商若干遍乘，得若干为廉，法再以方，法乘廉，得若干除实讫，馀实若干却以次商若干自乘再乘得若干为隅。法除实尽得立方面数。若有不尽数仍前再商之，或有不尽数以法命之，何谓之命。若馀实若干不尽，却以所商得立方数若干自乘。得若干又以三因之，得若干，另以所商得立方数若干，用三因之。得若干再添一个，共得若干便商得多一立方数也。因此不及而为之命也〈立圆法遇有不尽者，亦仿此〉。若要还原，以立方面自乘再乘，见积。若还原遇立方原有不尽数者，以立方面自乘再乘，并入不尽数，见积。
今有物三千三百七十五尺。问：立方面若干。
答曰：立方面一十五尺。
法曰：置物三千三百七十五尺为实，约初商得一十于左下，法亦置一十于右，自乘得一百，再乘得一千。除实讫馀实二千三百七十五尺，却以三乘下法一十得三十为方，法列位次商五尺于左，初商之次下法亦置次商五于初商一十之次，共一十五就以五遍乘之，得七十五为廉。法再以方，法三十乘廉法七十五得二千二百五十，除实讫馀实一百二十五，恰以次商五自乘再乘得一百二十五为隅，法除实恰尽。
图缺缺图缺
今有积一百九十五万三千一百二十五尺。问：立方面若干。
答曰：立方面一百二十五尺。
法曰：置积尺数为实，约初商一百自乘再乘得一百万，除实讫馀实九十五万三千一百二十五尺，恰以三乘下法一百得三百为方，法列位次商二十于初商一百之次下位，亦置二十于初商一百之次，共一百二十。就以二十乘之，得二千四百为廉，法再以方法三百乘廉法得七十二万。除实讫馀实二十三万三千一百二十五尺，恰以次商二十自乘再乘得八千为隅法，除实讫馀实二十二万五千一百二十五。另以三乘下法一百二十得三百六十，又为方法列位再商五于左初次商一百二十之下，共一百二十五，就以五乘之得六百二十五，又为廉法。再以方法三百六十乘廉法六百二十五得二十二万五千。除实讫，再以再商五自乘再乘得一百二十五又为隅法，除实恰尽。合问。
今有积四千一百五十尺。问：立方面若干。
答曰：立方面一十六尺，又八百一十七之五十四。法曰：置积为实，初商一十自乘再乘得一千尺，除实讫馀实三千一百五十，却以三乘下法一十得三十为方法，列位次商六尺于上，初商一十之次共一十六，就以六乘之得九十六为廉法，再以方法三十乘廉法九十六，得二千八百八十，除实讫馀实二百七十恰以次商六自乘再乘得二百一十六为隅法，除实讫馀实五十四尺不尽，以法命之，却以所商立方一十六尺自乘得二百五十六，又以三因，得七百六十八。另以十六以三因之，得四十八。再添一个并入共得一立方数，积八百一十七之五十四也。何谓之，命以原总数除去五十四加上八百一十七，便商得面方一十七，因此不及而为之命。
假如今有银一万两。问：立方每面若干。
答曰：八寸九分三釐〈有畸难尽〉。
法曰：置银一万两为实，以银率每寸一十四两为法，除之得七百一十四寸二分八釐，又为实以开立方法除之，初商八寸于左，亦置八寸于右为下法。自乘得六十四寸，再乘得五百一十二寸，除实讫馀实二百零二寸二分八釐。却以三乘下法八寸得二十四寸为方法，次商九分于初商八寸之次，亦置九分于右初商，八寸之次，共八寸九分，就以九分遍乘得八寸零一为廉法，再以方法二十四寸乘廉法得一百九十二寸二分四釐，除实讫馀实十寸○○四毫。恰以次商九分自乘再乘得七寸二分九釐除实讫，馀实不尽一寸七分五釐。