钦定古今图书集成.历象汇编.历法典.算法部
钦定古今图书集成历象汇编历法典
第一百二十七卷目录
算法部汇考十九
几何要法
几何要法
历法典第一百二十七卷
算法部汇考十九
《几何要法》〈明郑洪猷著〉
序目:世之执牛耳盟者,幽言,理至度数之学,则以为迂,而无当于道,而刍狗置之。夫度数而斤斤术艺也者,则刍狗置也。可度数之中,大而授时定历,正律审音,算量分秒不爽。水泉灌溉有资,与夫力小任重,营建机巧毕具,而兵家制胜,列营阵,揣形势,策攻守,所须乎此者,尤亟用之。如斯其广且切也。此而可刍狗视之,将羲画虞璿,亦枯而不灵之器,而禹奏平成,可舍句股勿用,而姬公测验,必《周髀》是问。何为也。始信理脱数而藏,《易》借以覆短。数传理而见,则有物有事,假作不得,假说亦不得也。善哉。《几何原本》之帙译,自西国裁自徐太史先生之手,其中比分栉解,义数详明,可以佐隶首商高之不逮,可以补十经九执之遗亡,而梓甘翟襄不擅长焉者。神而明之,引类而伸之。先王制器,前用之法备见矣。特初学,望洋而叹,不无惊其繁。余因晤西先生,得受几何要法,其意约而达,简而易从。如攻坚木,先其易者,后其节目,久也。相说以解先河而后海,昔有言之矣。不操缦而能安弦,有是学乎,爰是订而副诸梓,人僭数语弁其端;有笑而诧,猷以俗吏,而迂谭度数之理也,猷乌知。
论线〈计界说十六 章数十七 要法三十〉总论
几何家者,脱物体而空穷度数,数其截者,度其完者。度有三:曰线,曰面,曰体。线以度长短;面以度广狭;体以度厚薄。线自点始,点引为线,线展为面,面运为体。点者无长,线者无广,面者无厚。点为线之界,线为面之界,面为体之界,体不可为界。点、线、面、体,几何之论起焉。
界说章第一〈凡十六则〉
界者,一物之始终。解篇中,所用名目,作界说。
第一界
几何者,度与数之府也。
第二界
点者无分,无长短广狭厚薄,故无分,如左图甲点。〈甲〉真圆真平相遇处,止一点,毕世积点,不能结线也。
凡图十干,为识干,尽用十二支等字。
第三界
图

线止有长,无广厚,如一平面光照之,有光无光之间,不容一物,是线也。如上甲乙图,毕世积线,不能结面。
第四界
面者,有长有广无厚,一体所见为面。凡体之影,极似
图
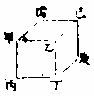
于面,无厚之极也。如上甲乙丙丁图,毕世积面,不能结体。
第五界
体有长有广有厚,如上甲乙丙丁戊己庚图。
第六界
分者,几何之几何也。小能度大,而尽之无赢不足者,以小为大之分,若小不能尽。度大当称几分几何之几,如
上甲乙四,与丙丁八,戊己十二等数皆能尽分者,则甲乙四为丙丁八戊己十二之分;若庚辛四与壬癸六一即赢二,即不足,不能尽度者,不得正名为分,则称之为三分六之二。〈他数仿此〉
第七界
点者,非几何,故不能为线及诸几何之分。
第八界
线非广狭之几何,故不能为面之分。
第九界
面非厚薄之几何,故不能为体之分。
第十界
图

线有曲直:线之一点能遮两界,是直线,如上图甲乙;不遮,则不直,如下图丙丁。
第十一界
图

面之中间,线能遮两界,不碍不空,是平面,如上图甲乙丙丁;不遮,则不平,如下图戊己庚。
图

第十二界
直线垂于横线之上,为横线之垂线。如上图丁乙为甲丙之垂线
图
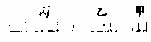
第十三界
两直线于同面,行至无穷,不相离,亦不相远,终不得相遇者,为平行线。如上甲乙丙丁两线
第十四界
两几何以几何相比之理为比例,两几何者,或两数,或两线,或两面,或两体,各以同类大小相比,谓之比例。若线与面,或数与线,此异类不为比例;若同类相比,而不以几何,亦不为比例也,如白线与黑线,或有穷之线与无穷之线,虽则同类,实无比例。有穷之线毕世倍之,不能及无穷之线故也。
凡比例有三种:有数之比例;有量法之比例;有乐律之比例。本卷论量法之比例。
第十五界
比例相续不断,为连比例。其中率与前后两率递相。
图

为比例而中率,既为前率之后,又为后率之前,如上图甲二与乙四比,乙四又与丙八比是也。
图

第十六界
中率一取不再用,为断比例。如上图甲四自与乙八比,丙六自与丁十二比是也。
备器章第二
几何在历家,则多用图画。图必先备器,器有三:曰尺,曰规,曰矩。尺以画线而贵直;规以画圜而贵调;矩以画方而贵准。器准矣,不识用法,则茫无措手。今以用法著于篇。
审尺章第三
画图,首画线,线贵直,线界于尺,故先求尺直。
如甲乙为尺,面丙丁为尺,侧一棱先以丙丁画一戊
图

己线,丙合戊,丁合己,次转丙丁棱画一己戊线,丙合己,丁合戊,不出不入,则尺直矣。不直再当琢削。
画线章第四
尺既直矣,线可无曲,然画时又有法,须以铁或铜铸笔上,长其柄,令可把手,下截阔出,复渐窄而下,其正
图

面削极平,背令稍圆,去末寸许,作一小窝,窝下渐细,至末,用时以墨汁入小窝,
以平面紧倚尺作线,则墨汁自就下,或恐墨污其地,将尺削去丙丁,侧一棱,则墨线莹细如丝,即作于规末亦得。
审平面章第五
平面者,诸方皆作直线。
图

法曰:如甲乙丙丁为面,欲审其平,即用直尺施于甲,角绕面运转,不碍不空,全合直尺,是平面也。
引线章第六
图

有一短直线,求平引长之。
法曰:如有甲乙线,欲平引长之,先以甲为心,以乙为界,画小半圜;以乙为
心,任取一度于小半圜,上下各作规,界线为丙为丁;次以丙丁为心,任取一度,向前作短界线相交,为戊末,引甲乙线至戊,则得所求。若欲更引长,仍依此法。
平分直线章第七〈法有二〉
有有界之线,求两平分之。
第一法
图

如有甲乙线,求两平分。先以甲为心,任用一度,但须长于甲乙线之半,愈长愈准,向上向下各作一短界线,次
用元度;以乙为心,亦如之,两界线交处,即丙丁末,用尺作丙丁直线,即甲乙有界之线,两平分于戊矣。
第二法
若所分之线下面无地可作短界线,即于甲乙线上,
图

先画两短界线于丙,次或开或收,规度仍前,从甲从乙;向上又作两短界线于丁,规度愈相远,画线愈准,末以丙丁二交,用尺如前,画线则得所求。
作垂线章第八〈法有四〉
有一直线,任于一点上求作垂线。
第一法
甲乙直线任指一点于丙,求丙上作垂线。先于丙点,左右任用一度,愈远愈准,各截一界,为丁为戊。次以
图

丁为心,任用一度,但须长于丙丁线。向丙上方作短界线,次用元度,以戊为心,亦如之,两界线交处为己,从己至丙,以尺画线,则得所求。
第二法
图

于丙左右,如上法,截取丁与戊,即任用一度,以丁为心,于丙上下方各作短界线;次用元度,以戊为心,亦如之,则上交为己,下交为庚,末作己庚直线,视直线交于丙点,即得所求。若丙
点在甲乙端上,则当暗引长甲乙线后,如前作亦得。
第三法
若直线甲端上求立垂线,又甲点外无地可暗引线,则先以甲乙原线上方任取一点为丙,以丙为心,甲
图
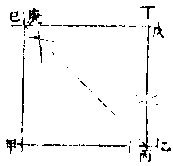
为界,作大半圜,圜界与甲乙线相遇为丁,次自丁至丙依前法作直线,引长之至戊,为戊丁线。戊丁与圜界相遇,为己末,自己至甲作直线即所求。
第四法
图
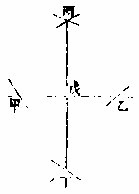
若甲乙线所欲立垂线之点,乃在线末甲界上,甲外无馀线可截,则于甲乙线上任取一点为丙,如前一二法,于丙上立丁丙垂线,次以甲丙丁角
两平分之,〈分法在后三卷第四章〉为己丙线;次以甲丙为度,于丁丙垂线上截戊丙线,又用元度,以戊为心,向己作短界线,为庚末。自庚至甲作直线得所求。
立垂线章第九〈法有四〉
有无界直线,线外有一点,求自彼点作垂线至直线上。
第一法
如有甲乙无界直线,直线外有丙点,求自丙点作垂线至甲乙线。先以丙为心,向直线两处各作小半圜,
图
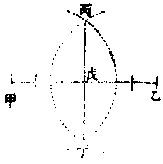
或两短界线为甲为乙,次仍用一度,以甲为心,向丙点相望处作短界线;又以乙为心,亦如之,两线相交处,为丁末。自丙至丁作直线截甲乙线于戊,则丙戊为垂线。
图
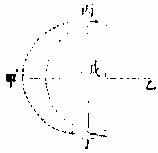
第二法
于甲乙线上近甲或乙任取一点为心,以丙为界,作一圜界于丙点,及相望处各稍引长之,次于甲乙线上视
图
前心,或相望,如前图,或进或退,如后图。任移一点为心,以丙为界,作一圜界与前圜交处,得丁末。自丙至丁作直线,得丙戊垂线。
图
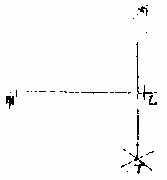
第三法
若丙点垂于甲乙线之界,不能于丙点左石画圜,如前二图。又或不能暗引长甲乙线,则当以甲为心,于丙点及相望处,各作短界线于丙于丁;又
进以乙为心,以丙为界,仍相望作两短界线末,从丙丁二交处作直线,则得所求。
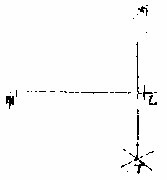
第四法
若甲乙线在面之边,且下无地可措规,如前四图,则
当用前章第三法,或以丙为心,任指甲乙线上两点,为丁为戊。次任取一度,以丁为心,向丙上作短界线;次用元度,以戊为心,仍向丙上作短界线交于己末。自己至丙作直线引长之。
至庚,得所求。又有便法,在后平行线中。
作平行线章第十〈法有三〉
一点求作直线与原设直线平行。
第一法
于甲点,求作直线与乙丙线平行。先任作甲丁线与乙丙斜交,次以丁为心,任作戊己圜界;次用元度,以甲为心,作庚辛圜界,稍长于戊己。次取戊己圜线为度,于庚辛圜界截取庚辛
末。自甲至辛作直线即所求。
第二法
先以甲点为心于乙丙线,近乙处任指一点作短界线为丁;次任用一度,以丁为心,向丙截取一分,作短
界线为戊。又用丁戊元度,以甲为心,对甲平行作短界线为己,次用甲丁元度,以戊为心,对甲平行作短界线于己末。自甲至己作直线即所求。
注曰:凡有不等度,须一度用一规,
始元度不爽,如一规而数易,其度则元,度永不复矣。此丁先生秘法。 以上二法,以甲点定远近,若无甲点任指所欲远近为界,可当甲点。
第三法
此法比前法更简易,即西本几何亦未载,乃敝师伯先生所授,如有甲乙线,任远近,求作平行线。近甲取心,向上以所求远近为度,作小半圜,次用元度,近乙取心,向上复作小半圜,末
以尺依半圜为界,作直线即所求。
注曰:以上平行数法,可推用作沿边直线之垂线。如有甲乙线,求乙线界上作一垂线。先以乙
为心,向甲任取一点为丙,又用元度,以丙为心;向甲指一点为丁,又以乙为心,任取一度,向上方作一短界线,愈远愈准;又以丁为心,用元度,仍向上方作一短界线与前界线相交于戊,次自戊至丙作垂线,末以前作平行线法,随用一法,以丙乙为度,作平行线正垂在乙点上,即得所求。
求分一直线,任为若干平分章第十一〈法有四〉
凡造历象数,欲分直线为不等分,不谙其法,大费手力,抑且不准,宜熟后法以便用。
第一法
如甲乙线,求五平分。先从甲任作甲丙线,为丙甲乙角;次从甲向丙任作五平度,为甲丁、丁戊、戊己、己庚、庚辛,次作辛乙直线,末用平行线法,作丁壬、戊癸、己子、庚丑四线,皆与辛乙平行,即壬癸、子丑与甲乙为五平分。
第二法
如甲乙线,求五平分。即从乙任作乙丙线,为丙乙甲角;次于乙丙任取一点为丁,作丁戊线与甲乙平行;次从丁向戊任作五平分,为丁己、己庚、庚辛、辛壬、壬癸,而丁癸线令小于甲乙,次从甲过癸作甲子线遇乙丙于子;
末从子作子壬、子辛、子庚子己,四线各引长之,而分甲乙于丑、于寅、于卯、于辰,为五平分。
第三法
如甲乙线,求五平分。即从甲、从乙作甲丁、乙丙两平行线;次从乙任作戊己、庚辛、四平分;次用元度,从甲作壬癸、子丑四平分;末作戊丑、己子、庚癸、辛壬四线相联,即分甲乙于己、于辰、于卯、于寅,为五平分。
第四法
图图
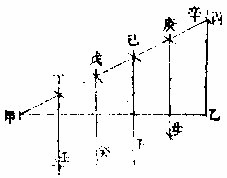
右图之法,极简极神,可分百千不等之线,与百千不等之分。先作一器,如丙丁、戊己为平行线。任平分为若干格,器愈大,格愈密,其用愈广。格每分作平行线相联。今欲分甲乙为五平分,即规取甲乙之度,以一规髀任抵戊丙线上,一规髀抵第五庚辛线上,如不在庚辛者,即渐移之至线界而止,既至壬,即戊壬之分,为甲乙之分。
图图

又如右图:有甲乙线,求十七平分。先以规取甲乙之度,以一规髀抵戊丙线一处,以一规髀抵此器庚辛,第十七格为壬;次从戊至壬画一直线;次取所过两格相距之度,以此为准,分甲乙直线,则得十七分矣。或图小而所分者大,欲广其用,则递倍之。如图:一尺欲分一丈,为十九分。须取一丈十分之一,为一尺用。前法为十九分,后以尺递十倍之,则一丈已分为一百九十分矣。每十分作识,如所求。馀以此推之。
一直线求截所取之分章第十二〈法有二〉
第一法
如有甲乙直线,求截取三分之一。先从甲任作一甲丙线,为丙甲乙角;次从甲向丙,任作所命三分之平度,如甲丁、丁戊、戊己,为三分也;次作乙己直线;末作丁庚线,与己乙为平行线,即甲庚为甲乙三分之一也。
第二法
如甲乙直线,求截取七分之三。先以
前章之法,分甲乙线为七分后,取其三于庚,则得所求也。如欲截取十分之七、十四分之九等不均之数,亦如之。
有一直线,求截各分如所设之分。章第十三〈一法〉
法曰:甲乙线,求截各分如所设,甲丙任分之丁戊者,谓甲乙所分,各分之比例,若甲丁、丁戊、戊丙也。先以甲乙、甲丙两线相联于甲,任作丙甲乙角;
次作丙乙线相联;末从丁、从戊,作丁己、戊庚两线,皆与丙乙平行,即分甲乙线于己、于庚,若甲丙分于丁戊焉。
有直线,求两分之,而两分之比例若所设两线之比例章第十四〈一法〉
法曰:如甲乙线,求两分之,而两分之比例若所设丙与丁。先从甲,仍作甲戊线为戊甲乙角;次截取甲己与丙等,己庚与丁等;次作庚乙线联之;末
作己辛线与庚乙平行,即分甲乙于辛,而甲辛与辛乙之比例若丙与丁。
有两直线,求别作一线,相与为连比例章第十五〈法有二〉
第一法
图

有甲乙甲丙两线,求别作一线相与为连比例者,任合两甲乙、甲丙为甲角,而甲乙与甲丙之比例,若甲丙与所求他线也。先于甲乙引长之,为乙
丁与甲丙等;次作乙丙线相联;次从丁作丁戊线与丙乙平行;末于甲丙引长之,遇于戊,即丙戊为所求线。〈若以甲丙为前率仿此〉
第二法
图

以甲乙、乙丙两线联作甲乙丙直角,次以甲丙线联之,而甲乙引长之,末从丙作丙丁为甲丙之垂线,遇引长线于丁,即乙丁为所求线。
三直线,求别作一线,相与为断比例。章第十六
法曰:甲乙、乙丙、甲丁三直线,求别作一线,相与为断比例者,谓甲丁与他线之比例,若甲乙与乙丙也。先以甲乙、乙丙作直线,为甲丙;次以甲丁线合甲丙,任作甲角;次作丁乙线相联;次从丙作丙戊线与丁乙平行;末自甲丁引长之;遇丙戊于戊,即丁戊为所求线。
两直线,求别作一线,为连比例之中率章第十七
法曰:甲乙、乙丙两直线,求别作一线为中率者,谓甲
乙与他线之比例,若他线与乙丙也。先以两线作一直线为甲丙;次以甲丙两平分于戊;次以戊为心,甲丙为界,作甲丁丙半圜;末从乙至圜界作
乙丁垂线,即乙丁为甲乙、乙丙之中率。〈以上原本卷之一〉
论圜〈计界说十二 章数二十九 要法三十二〉总说
圜成于线,线有二种:为曲,为直。直线或单或众,前卷已详之。众线或三而成三角形;或四而成方形;或多而成诸不等形。曲线或半或全。半线有不等之用;全线或成圜形,或成卵形、等角形及方形。卵形详见后卷。今先论圜形。
界说章第一〈凡十二则〉
第一界
圆形于平地居一界之间为圜。
第二界
外圆线为圜之界。
第三界
圜之中处为圜心。
第四界
图

自圜之界,作一直线过中心至他界,为圜径。如上图甲丁、乙戊为圜界,丙为心,甲乙为径。
第五界
凡直线切圜界,过之而不与界交者,为切线。如上图
甲乙丙线是也。若先切圜界,而引之入圜内,则谓之交线。如丁戊是也。
第六界
图

凡两圜相切而不相交者,为切圜;相切而相入者,为交圜。如上图。
第七界
图
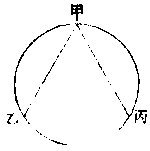
凡直线形居他直线形内,而此形之各角切他形之各边,为形内切形。如上图丁戊己为甲乙丙形内切形。
第八界
凡直线形居他直线形外,而此形之各边切他形之各角,为形外切形。如前图甲乙丙为丁戊己形外切形。其馀各形,仿此二例。
第九界
图

直线形之各角切圜之界,为圜内之切形。如上图甲乙丙形之三角,各切圜界于甲、于乙、于丙三者是也。圜之
界切直线形之各角为形外切圜。同上图。
第十界
图

直线形之各边切圜之界为圜外切形。如上甲乙丙形之三边切圜于丁、于己、于戊,是也。
第十一界
一圜之界切直线形之各边,为形内切圜。如前图。
第十二界
图

一直线之两界各抵圜界,为合圜线。如上图之甲乙线。
造规章第二〈法有四〉
圜形以至圆为准,至圆必出于规,规必欲极准极顺,其用甚活,乃堪造历。凡造规之法有四,详列于后。
第一法
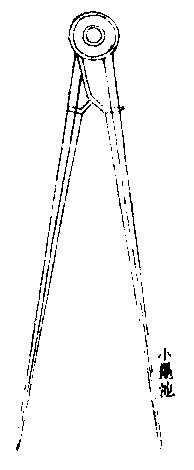
先以铜或铁范成二股,上阔下窄,至末而锐,近头小半截作凹凸状,令可相合;次以钉钉其圆头,贵宽紧得宜,任意可开收,规下半截为规髀,一规髀作墨池,如首卷第三章法以适用。凡欲造历象,必须备规。其造式见后。
规图
第二法
凡规有三用:一画虚线。则须铅条,当先以铜叶为管,虚其中,横开小路,上套小铜圜,可上下松紧以出入。铅条末略奓出,以留小圜。如下甲图。一画墨线。则当作墨路,如前章法。如下乙图。一画铜板线。须以纯钢为末,如下丙图,右三髀俱,另作不相连本规,其本规如前法造,但截去一髀,临截处长半寸许,作一小箱状,虚其中,亦令方可受规髀柄,如下图丁处,箱而作旋螺,用时任入一规髀,以铜消息,如旋螺者贯定之。如下戊图,则任意可画线,而一规可具三用矣:此为第二法。如下图。
图
第三法
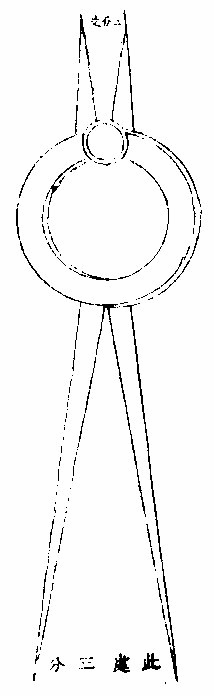
造历恒用规,依比例法分线、分圜,或以大形移变小形,或以小度移变大度,其分法稍难。今作一四髀规,或铜、或铁,略如剪形,上下作四规髀,上短下长,令上准,下度或半、或三之一、或十之一及种种不等,则作线圜时,或欲以大变小:先以下髀取度,次以上髀移度;或欲以小变大:先以上髀取度,次以下髀移度,则得所求。其或半或三之一或十之一,俱从髀之长短而分,下愈长,则度愈大;上愈短,则度愈促。
图

第四法
前三种规长不踰尺,止堪小用。如欲造玑衡大器,则当更变其式。如下图:其规以铜范为极,方条上下如一。任作几尺于条左,末作锥,垂下二三寸,以纯钢为之,更造一锥与前锥等。上方寸许,仍凿方孔,令透,可受方条,任远近可推移。方孔旁更凿圆孔,仍前法作旋螺,贯定方条,使两锥坚定,不爽分毫,可画大圜。如下图。
图

有圜求两平分之章第三〈一法〉
图
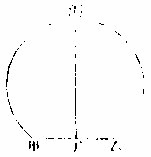
如有甲乙丙圜,求两平分:用尺任以圜一处为界,正过心画一直线,则圜体两平分矣。
有圜之分求两平分之章第四〈一法〉
图
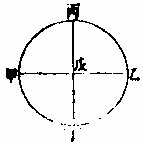
如有甲乙丙圜分,求两平分之:先于圜分两界作甲乙线,次两平分之于丁,从丁作丙丁为甲乙之垂线,
一卷第八章
即丙丁分甲乙圜分为两平分。若有圜不露其心,又求两平分之,亦如此法。
有圜求四平分之章第五〈一法〉
图

凡立天象,多用四分圜为周天四象限,故造法不可不准。如有甲乙丙圜,求四平分:先以前法,作甲乙线,过戊心两平分之次;依作垂线法于戊心
上,自丙至丁作垂线,得所求。
有圜求六平分之章第六〈一法〉
图
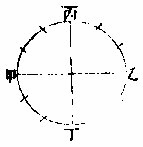
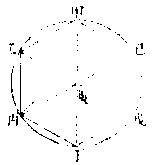
凡历家分周天度,多用六数,或十二,或二十四。今详其法:如有一圜,求作六分,不用他法,惟以画圜之元规,周圜界六步,则自然分为甲乙丙丁戊己六平分矣。
有圜求十二平分之章第七〈一法〉
图

先以本卷五章法四,平分于甲乙丙丁;次以画圜元规,从甲、从乙,上下各指一点,又从丙、从丁,左右各指一点,
则得所求。若欲二十四分,每分为两,则得所求矣。
有圜求三百六十平分之章第八〈一法〉
凡历家所用细分周天度,以三百六十为率。今详其法:
如有甲乙丙圜,先依前法四,平分之为四象限;次以规元度,依前法十二平分,为十二宫,就以所分十二宫各三分之,各包十度;次每十两平分之,各包五次;每宫又五平分之,各包六。今用六度之规,至终不改,从子宫初一度步起完一周,又次从初五度、初十度、
图图
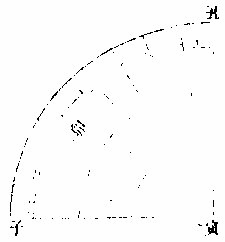
十五度、二十度、二十五度各步完一周,则平分三百六十分矣。
有圜之分任截几度章第九〈一法〉
图
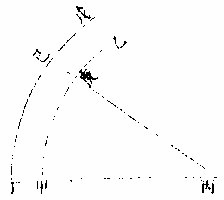
如有甲乙圜之一分,欲取三十五度,如用常法,必须先求圜分之心,依后十一章之法,成圜后均分为三百六十,乃取三百六十之三十五分,其法颇繁。今有
图

简妙之法:先备一铜板,分一子丑寅象限为九十分,合极准。设有甲乙圜之界,自甲起,欲取三十五度之分,先从甲至圜心作甲丙半径线,如与子丑寅象限
半径相合,则移彼度子卯至甲乙线上,至庚,即得所求矣。如大小不合,则以规取子丑寅半径,以丙为心,或甲乙内,或甲乙外,作一圜分;若丁戊圜在外,则当引长甲丙线至丁,取子丑寅限三十五度,以丁为始,移于丁戊圜上,至己从丙心过己,作一直线截甲乙于庚,则甲庚为甲乙圜上三百六十分之三十五也。若所范铜板,欲其用广,当从寅心重重作圜与子丑平行,又自子丑外圜逐度引直线至寅心后,所欲取圜分之度。若其半径与子寅不等,或同于他子丑内圜之半径,则可径移其度于所分圜上,不尔仍用前法。
有圜求寻其心章第十〈一法〉
图
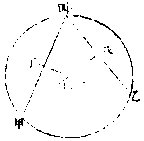
如有甲乙丙丁圜,欲求其心。先于圜之两界任作一戊己直线,次以平分线法,作丙丁垂线,两平分之于庚,则庚为圜心。
有圜之分求成圜章第十一〈一法〉
图

如有甲乙丙圜分,求成圜。先于圜分任取三点于甲、于乙、于丙,从甲至丙、丙至乙,各作一直线,各两平分于丁、于戊,次于丁戊上各作垂线,相交处
为己;末以己为心,以圜为界,旋转,即得所求。
任设三点不在一直线,求作一过三点之圜章第十二〈法有二〉
第一法
如有甲乙丙三点,求作一圜贯之。先以甲为心,任取
图

一度,向乙上下各作小圜分;又以乙为心,向甲仍用元度上下各作小圜分,相交处为丁、为戊;次又以甲为心,向丙上下作小圜分如前;次以丙为
心,亦如之,相交处为己、为庚;次从丁至戊、从己至庚,各作直线,相交处为辛;末以辛为心,任取一点为界,旋规成圜,即得所求。
第二法
图

先以三点作三直线,相联成甲乙丙三角形;次平分两线于丁、于戊;次于丁戊上各作垂线,令相遇于己;末以己为心,甲为界,作圜,即得所求。
有圜,求作合圜线与所设线等此。设线不大于圜之径线章第十三〈一法〉
图
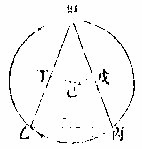
如有甲乙丙圜,求作合线与所设丁线等。其丁线不大于圜之径线,径为圜内之最大线,更大不可合。先作甲乙圜径为乙丙,若乙丙与丁等者,即
是合线。若丁小于径者,即于乙丙上截取乙戊与丁等,次以乙为心,戊为界,作甲戊圜,交甲乙丙圜于甲;末作甲乙合线,即与丁等何者,甲乙与乙戊等,则与丁等。
三角形求作形外切圜章第十四〈一法〉
图

甲乙丙角形,求作形外切圜:先平分两边于丁、于戊;次于丁戊上各作垂线,为己丁、己戊,而相遇于己;末以己为心,甲为界,作圜,必切甲乙丙,而为三角形之形外切圜。
三角形求作形内切圜章第十五〈一法〉
甲乙丙角形,求作形内切圜:先以甲乙丙角、甲丙乙角各两平分之,作乙丁、丙丁两直线相遇于丁;次自
图

丁至角形之三边,各作垂线,为丁己、丁庚、丁戊;末以丁为心,戊为界,作圜,即过庚己,为戊庚己圜,而切角形之甲乙、乙丙、丙甲三边于戊、于己、于庚,此为形内切圜。
有圜求作圜内三角切形与所设三角形等角章第十六
甲乙丙圜求作圜内三角切形其三角与所设丁戊己形之三角各等先作庚辛线切圜于甲次作庚甲
图
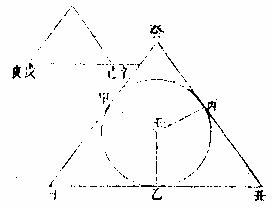
乙角与设形之己角等次作辛甲丙角与设形之戊角等末作乙丙线即圜内三角切形与所设丁戊己形等角
有圜求作圜外三角切形与所设三角形等角章第十七
甲乙丙圜,求作圜外三角切形,其三角与所设丁戊己形之三角各等。先于戊己边各引长之,为庚辛;次于圜界,抵心作甲壬线;次作甲壬乙角,与丁戊庚等;
图
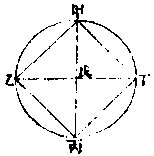
次作乙壬丙角,与丁己辛等;末于甲乙丙上作癸子、子丑、丑癸三垂线,此三线各切圜于甲、于乙、于丙,而相遇于子、于丑、于癸,
若作甲丙线,即癸甲丙、癸丙甲两角小于两直角,而子癸、丑癸两线必相遇馀仿此,
此癸子丑三角与所设丁戊己三角各等。
有圜求作内切圜直角方形章第十八
图
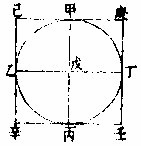
有甲乙丙丁圜,求作内切圜直角方形:先作甲丙、乙丁两径线,以直角相交于戊;次作甲乙、乙丙、丙丁、丁甲等四线,即甲乙丙丁为内切圜直角方形也。
有圜求作外切圜直角方形章第十九〈法有二〉第一法
甲乙丙丁圜,其心戊,求外切圜直角方形:先作甲丙、
图

乙丁两径线,以直角相交于戊;次于甲乙、丙丁作庚己、己辛、辛壬、壬庚四线,为两径;末界之垂线,而相遇于己、于辛、于壬、于庚,即己庚壬辛为外形。
第二法
以戊甲为度,依平行线法,作己庚、辛壬上下两线,与乙丁平行;次用元度,作己辛、庚壬左右两线,与甲丙平行,即得所求。同前图。
有直角方形求作形内切圜章第二十
图

甲乙丙丁直角方形,求作形内切圜:先以四边各两平分于戊、于己、于庚、于辛,而作辛己、戊庚两线相交于壬;末以壬为心,戊为界,作圜,必过戊己
庚辛,而切甲丁、丁丙、丙乙、乙甲四边,是为形内切圜。
有直角方形求作形外切圜章第二十一
图

甲乙丙丁直角方形,求作外切圜:先作对角两线,为甲丙、乙丁,而交于戊;末以戊为心,甲为界,作圜,必过乙丙
丁甲而为形外切圜。
有圜求作圜内五边切形其形等边等角章第二十二
图

如有甲乙丙丁戊圜,求作五边内切圜形等边等角:先作己庚辛两边等角形,而庚辛两角各倍大于己角;次于圜内作甲丙丁角形,与己庚辛角形各等角;次以甲丙丁、甲丁丙两角,各两平分,作丙戊、丁乙两线;末作甲
乙、乙丙、丙丁、丁戊、戊甲五线,相联,即甲乙丙丁戊为五边内切圜形,而五边五角俱自相等。
有一圜求作内切圜五边及十边形章第二十三
如有甲乙丙圜,心为丁,先作甲丙过心线;次作乙丁
图
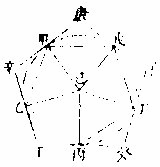
垂线;次平分丁丙线于戊,作乙戊线;次取戊乙度,移于径线,为戊己;次作乙己直线,盖乙己为甲乙丙圜五分之一,以此为度,可作内切圜五边形。
丁己度可作内切圜十边形。
有圜求作圜外五边切形其形等边等角章第二十四
甲乙丙丁戊圜,求作五边外切圜形等边等角:先依
图
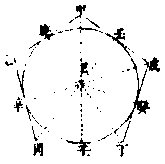
前章法,作圜内甲乙丙丁戊五边等边等角切形;次乃从己心,作己甲、己乙、己丙、己丁、己戊五线;次从此五线作庚辛、辛壬、壬癸、癸子、子庚五垂线,相遇于庚、于辛、于壬、于癸、于子,五垂
线既切圜,即成外切圜五边形,而等边等角。
五边等边等角形求作形内切圜章第二十五
甲乙丙丁戊五边等边等角形,求作内切圜:先分乙甲戊、甲乙丙两角,各两平分其线,为己甲、己乙,而相
图

遇于己;目己作己丙、己丁、己戊三线;次从己向各边作己庚、己辛、己壬、己癸、己子五垂线;末作圜,以己为心,庚为界,必过辛壬癸子庚而为甲乙丙丁戊五边形之内切圜。
五边等边等角形求作形外切圜章第二十六
甲乙丙丁戊五边等边等角形,求作外切圜:先分乙
图
甲戊、甲乙丙两角,各两平分其线,为己甲、己乙,而相遇于己;次从己作己丙、己丁、己戊三线,与己甲、己乙俱等;末以己为心,甲为界,作圜,必过乙丙丁戊甲,即得所求。
求作圜内六边切形其形等边等角章第二十七
图

如有甲乙丙丁戊己圜,其心庚,求作六边内切圜形等边等角:先作甲丁径线;次以丁为心,庚为界,作圜,两圜相交于丙、于戊;次从庚心,作丙庚、戊庚两线,各引长之,为丙己、戊乙;末作
甲乙、乙丙、丙丁、丁戊、戊己、己甲六线相联,即得所求。
求作圜内十五边切形其形等边等角章第二十八
如有甲乙丙圜,求作十五边内切圜形,等边等角:先
图

作甲乙丙内切圜平边三角形,即各边当圜十五分之五;次从甲作甲戊己庚辛内切圜五边形,等角各边,当圜十五分之三,而戊乙得十五分之二;次以戊乙圜分取乙己度,两平行
于壬,则壬乙得十五分之一;次作壬乙线,依壬乙共作十五合圜线,即得所求。
以此为例,推用递分可作无量数形。
圜内有同心圜,求作一多边形切大圜,不至小圜其多边为偶数而等章第二十九
如有甲乙丙丁戊两圜,同以己为心,求于甲乙丙大圜内作多边切形,不至丁戊小圜,其多边为偶数而等:先从己心,作甲丙径线,截丁戊圜于戊也;次从戊
作庚辛,为甲戊之垂线,即庚辛线切丁戊圜于戊也;次以甲丙两平分于乙,乙丙两平分于壬,以壬丙两平分于癸,则丙癸圜分必小于丙庚,而作丙癸合圜线,即丙癸为所求切圜形
之一边也,次以癸丙为度,递分一圜各作合圜线,得所求形。〈以上原本卷之二〉
论线〈计界说十 章数十四 要法十四〉界说章第一〈凡十则〉
第一界
图

角者,两线纵横相遇,所作线有曲直。两直相遇为直线角;两曲相遇为曲线角。一直一曲相遇为杂线角。曲杂两线角更有别论,今先明直线角。
第二界
图
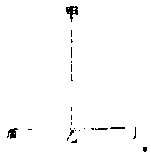
凡直线正垂于横直线之上,必成两直角相等。如上图甲乙为垂线,丙丁为横线,而乙之左右两角相等,为两直角。若反以甲乙为横线,则丙丁为甲乙垂线也。
如今用矩尺,一纵一横互相为直线,互相为垂线。
第三界
垂线斜交于横直线之上,必成两不等角。两不等角
图

一大于直角,一小于直角。大为钝角,小为锐角。如上图戊己庚为钝角,戊己辛为锐角。故直角惟一,而锐钝两角其大小不等,乃至无数。
第四界
凡二直线不能为有界之形,故直线之形有界者,至少有三角。有三直线为边,名曰三边形,亦曰三角形。如上图三边形止有三种
第五界
图

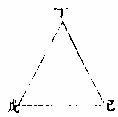
三边线相等为等边三角形,亦为平边三角形。如上甲乙丙图
第六界
两边线相等为一不等三角形。如上丁戊己图。
第七界
图

三边线俱不等为不等边三角形。如上庚辛壬图。
第八界
图
三边形有一直角为三边直角形;有一钝角为三边钝角形;有三锐角为三边各锐角形。如上三图。
第九界
凡三边形恒以在下者为底,在上边为腰,如上图甲乙、甲丙为腰,乙丙为底。
第十界
图

凡言角者,俱用三字为识,其第二字即所指角也。如甲乙丙角,其乙字指角。
三髀规章第二
规以二髀为常法,或倍之于两端为四髀,前卷已详之矣。兹有三髀规,新式造法两髀如常,如前二卷中所设是也。旁一髀即附于二髀之枢,稍引长之,出头,其头端上有眼,衔旁一髀,令其圆活,可上下左右。如下图用法见后。
图

于有界直线上求立等边三角形章第三
如甲乙直线上,求立等边三角形:先以甲为心,乙为
图

界,或上,或下,作短界线;次以乙为心,甲为界,作短界线,两线交处为丙;末自甲至丙、丙至乙,各作直线,即所求。
于有界直线卜求立一不等三角形章第四
图

如甲乙直线,以甲为心,任取一度,或长或短,于甲乙线上,用前法作一短界线;次以乙为心,用前度亦如之,两
短界线交处为丙,从丙至甲至乙各作直线,即所求。
于有界直线上求立三不等角形章第五
如甲乙直线,以甲为心,或长或短,用一度,如前作短
图
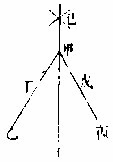
界线;次以乙为心,甲度长,今用短度,甲度短,今用长度,于甲乙不等作短界线,交处为丙,从丙至甲至乙作两直线,即所求。
有直线角求两平分之章第六
如乙甲丙角,求两平分之:先于甲乙线任截一分,为
图
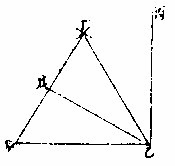
甲丁;次于甲丙线截甲戊与甲丁等;次或用元度,或任取一度,以丁为心,向乙丙间作一短界线;次以戊为心,亦如之,两线交处为己,从甲至己作直线,即所求。若向乙丙无地可作短
图
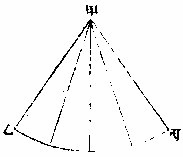
界线,则宜仍以丁以戊为心,向甲上作短界线为己,从己至甲作直线,即所求如上图。
有直角求三平分之章第七
图
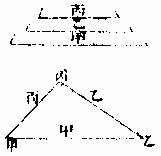
如甲乙丙直角,求三平分之先:任于一边,立平边角形,为甲乙丁;次分对直角一边,为两平分丁戊,从此边对角作垂线至乙,即所求。
有角任分为若干分章第八
图
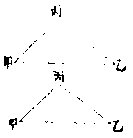
如乙甲丙角,欲分为四、为八、为十六等分,则先分两分;又各两分之,得四;又各两分之,得八;又各两分之,得十六。愈分则愈倍,任欲分为几分。如三
五七九之类,则先以甲为心,向乙作一圜分,次以规分圜分,任作几何分,末从所分度至甲作直线,即所求。如上图。
有三直线求作三角形其三边如所设三直线等章第九
图

如甲乙丙三线,每两线并大于一线,任以一线为底,以底之甲为心,第二、第三线为度,向上作短界线,两界线交处为丙;次向下作丙甲、丙乙两腰,
即所求。
设一三角形求别作一形与之等章第十
图
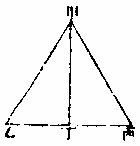
以所设三角形之三边,当甲乙丙三线。以前法作之,即所求。或又用前所备三髀规,以规形所设三角形,度移于别处,即所求。
一直线任于一点上求作一角如所设角等章第十一
如甲乙线上有丙点,求作一角,如所设丁戊己角等:
图
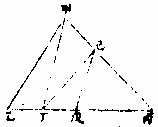
先于戊丁线任取一点为庚,于戊己线任取一点为辛,自庚至辛作直线;次以前法于甲乙线上作丙壬癸角,形与戊庚辛角等,即所求。
有三角形求两平分之章第十二
图

如有甲乙丙三角形,求两平分之:任于一边,两平分之于丁,向角作直线,即所求。
凡角形,任于一边任作一点,求从点分两形为两平分章第十三
有甲乙丙角形,从丁点求两平分之:先自丁至相对甲角,作甲丁直线;次平分乙丙线于戊,作戊己线与甲丁平行;末作己丁直线,即分本形为两平分。
有三边直角形以两边求第三边长短之数章第十四
如甲乙丙三角形,甲边直角先得甲乙、甲丙两边长
图

短之数。如甲乙六、甲丙八,求乙丙边长短之数。其甲乙、甲丙上,所作两直角方形,并既与乙丙上所作直角方形等,〈原本卷四十七〉则甲乙之幂,〈自乘之数曰幂〉得三十六;甲丙之幂,得六十四,并之得百。而乙丙之幂亦百,百开方得十,即乙丙数十也。又设先得甲乙、乙丙,如甲乙六、乙丙十,而求甲丙
之数,其甲乙、甲丙上两直角方形并既与乙丙上直
角方形等,则甲乙之幂得三十六,乙丙之幂得百,百减三十六,得甲丙之幂六十四,六十四开方,得八,即甲丙八也。求甲乙仿此。〈以上原本卷之三〉
论方形〈计界说八 章数十三 要法十四〉界说章第一〈凡八则〉
第一界
图

方形者,四直线,两纵两横,相遇所成。亦谓之四边形。如上甲图。
第二界
图

四边形之四线等,而四直角者,为直角方形。如上甲图。
第三界
图
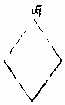
四边两两相等,而俱直角者,为长直方形。如上乙图。
第四界
图

四边等,但非直角者,为斜方形。如上丙图。
第五界
图

四边两两相等,但非直角者,为长斜方形。如上丁图。
第六界
图

已上方形四种,谓之有法四边形。四种之外他方形,皆谓之无法四边形。如上戊图等。本卷多以直方形为论,为其多有用也。
第七界
图

凡形,每两边有平行线,为平行线方形。如上己图。
第八界
图

凡作平行线方形,若于两对角作一直线,其直线为对角线也。又于两边纵横间各作一平行线,其两平行线与对角线必交罗相遇,即此形分为四平行线方形,其两形有对角线者,为角线方形;其两形无对角线者,为
馀方形。如甲乙丙丁方形,于丙乙两角作一线,为对角线;又依乙丁平行作戊己横线,依甲乙平行作庚辛纵线,其对角线与戊己、庚辛两线交罗相遇于壬,即作大小四平行线方形矣,则庚壬己丙及戊壬辛乙谓之角线方形。而甲庚壬戊及壬己丁辛谓之馀方形。
审矩章第二
凡作方形,必欲用矩,故先论审矩法,后论弃矩求方之法。矩以两尺纵横而成,然必成直角方准。若稍出入,必为锐钝两角,而不能成矩。今欲审直角,先审两尺之棱,如首卷第一法。后于他坚体上,作半圜,中画
图

径线;次以矩角,倚半圜之界,视二尺棱,正切径线与圜相交之处,则矩准而可用矣。若有出入,则当更改,或于坚体上作一直线,更作一垂线,四边作直角,以一矩准四直角,不爽则至准矣。
一直线上求立直角方形章第三
图

如甲乙线上,求立直角方形:先于甲乙两界各立垂线,为丁甲,为丙乙,皆与甲乙线;等次作丁丙线相联,即得所求。
有直线形求作直角方形与之等章第四
甲直线无法四边形,求作直角方形与之等:先作乙丁形与甲等〈本卷第五第六章〉而直角;次任用一边引长之,如丁丙引之至己,而丙己与乙丙等;次以丁己两平分于庚,其庚点,或在丙点,或在丙点之外。若在丙,即
图
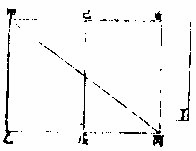
乙丁是直角方形与甲等矣。若庚在丙外,即以庚为心,丁己为界,作丁辛己半圜;末从乙丙线引长之,遇圜界于辛,即丙辛上直角方形与甲等。如上图丙辛壬癸。
有三角形,求作平行方形与之等,而方形角又与所设角等章第五
设甲乙丙角形丁角,求作平行方形与甲乙丙角形等,而有丁角先分一边为两平分,如乙丙边平分于
图

戊;次作丙戊己角与丁角等;次自甲作直线与乙丙平行,而与戊己线遇于己;末自丙作直线与戊己平行,为丙庚,而与甲己线遇于庚,则得己戊丙庚平行方形与甲乙丙角形等而有丁角。
有多边直线形,求作一平行方形与之等,而方形角又与所设角等章第六
设甲乙丙五边形丁角,求作平行方形与五边形等,
图

而有丁角先分五边形为甲乙丙三三角形;次依前章法作戊己庚辛平行方形与甲等,而有丁角;次于戊辛己庚两平行线引长之,作庚辛壬癸平行方形与乙等,而有丁角;末复引
前线作壬癸子丑平行方形与丙等,而有丁角;即此三形并为一平行方形,与甲乙丙并形等而有丁角。自五边以上可至无穷,俱仿此法。
有多直角方形,求并作一直角方形与之等章第七
如五直角方形,以甲乙丙丁戊为边,任等不等,求作
图

一直角方形与五形等:先作己庚辛直角,而己庚线与甲等,庚辛线与乙等;次作己辛线,旋作己辛壬直角,而辛壬与丙等;次作己壬线,旋作己壬癸直角,而壬癸与丁等;次作己癸线,旋作己癸子直角,而癸子与戊等;末作己子线,而己子线上所作直角方
形即所求。
有平行方形,求作三角形与之等,而三角形一角如所设角等章第八
如有甲乙丙丁平行方形戊角:先作丁乙己角与戊
图

等,遇甲丙线于己;次以乙丁线引长之,为庚,取丁庚度与乙丁等;末作己庚直线,乙丙庚三角形与甲乙丙丁平行方形等,而有戊角,即所求。
一直线上,求作平行方形与所设三角形等,而方形角又与所设角等章第九
设甲线乙角形丙角,求于甲线上,作平行方形与乙
图

角形等,而有丙角:先依本卷第五章法,作丁戊己庚平行方形与乙角形等,而戊己庚角与丙角等;次于庚己线引长之,作己辛线;次作辛壬线与戊己平行;次于丁戊引长之,与辛壬线遇于壬;次自壬至己作对角线引
出之,又自丁庚引长之,与对角线遇于癸;次自癸作直线与庚辛平行,又于壬辛引长之,与癸线遇于子;末于戊己引长之至癸子线得丑,即己丑子辛平行方形如所求。如欲即于甲线立形,则先依本章法,作己辛子丑方形;次于甲线一界,作寅角如辛己丑角等;次取寅卯如己丑等;末成平行方形,即得所求。
设不等两直角方形,如一以甲为边,一以乙为边,求别作两直角方形自相等,而并之又与元设两形并等章第十
先作丙戊线与甲等,次作戊丙丁直角形,而丙丁线
图

与乙线等;次作戊丁线相联;末于丙丁戊角、丙戊丁角各作一角,皆半于直角;己戊、己丁两腰相遇于己,而相等,即己戊、己丁两线上,所作两直角方形自相等,而并之,又与丙戊、丙丁上所
作两直角方形亦相等。
两直线形不等,求相等之较几何章第十一
图

甲与乙两直线形,甲大于乙,以乙减甲,求较几何:先任作丁丙、己戊平行方形与甲等;次于丙丁线上依丁角,作丁丙辛庚平行方形与乙等,即得辛庚戊己为相减之较矣。
有圜,求作一直角方形与之等章第十二
方圆圆方之法,自古名贤究析而未准。吾师丁先生,几何六卷之末,设此神法。其法之用甚广。今撮其要,以推作方圆圆方之法:先设甲乙丙丁直角方形,次
图

以乙为心,以甲为界,作甲丁限象,任分为若干度,今姑分为九十度。又分甲乙丙丁两线,如前数为九十,次自乙心至象限,逐度皆作虚线;次从甲乙、丙丁两线对望,作平行线,其与限象线交处俱作点;次从甲作曲线贯诸点,贯诸点之线,则甲戊线为方圆圆方之根线,而乙甲为边,
图

乙丁为底,次自甲至戊作一直线;若乙戊直线与所设欲方之圜半径等,则甲乙线为所设圜限象之界线;若圜半径长,则于乙丁线上截乙己与半径等,引长甲乙线,作己庚与戊甲线平行,庚至乙即长径圜象限之界线;若圜半径短,则于乙丁线上截乙辛与半径等,作辛壬线与
戊甲平行,则壬至乙即短径圜限象之界线。今有子
丑圜,或大或小,其半径与乙辛等,先作一寅卯直线立一辰己垂线;次从己起取己午、午未各与乙壬等;次取己申与乙辛等;次两平分申未于酉,以酉为心,以申或未为界作半圜,切垂线于辰;末取己辰作直角方形之一边,则此方形与所设圜等。以此可推,不特一方与一圜,即方之一边线与圜一限象等,方之半边线与圜半限象等。
有直角方形,求作一圜与之等章第十三
图缺如有甲线为方之边,先取一圜,依前法,求其作方之线,如前度得申己;次作辰申直线;次截戊己如所设甲线等;次自戊作戊卯线与辰申平行;末以己卯为半径之度,作一圜即得所求。
推用一法
依两章方圆圆方之法,可推任有直线形可作一圜与之等。又任设一圜,可作直线形与之等,须先依前章法,求多边直线形,作一方形与之等;次依本章法,作一圜形与直角方形等;则得一圜与所设直线形等。若又有圜,求作一三角形,先依本章法,作一方与所设圜等;次依前法,作三角形如所设方形等,则所作三角形如原设圜等。〈以上原本卷之四〉