钦定四库全书

　　同文算指通编卷五

　　明　李之藻　撰

　　杂和较乘法第八

　　诸物互和未易缕析必取互乘之数较馀为用以少除
多得一数以推其他而纤悉见矣若条缕多者别立正
负为算别同异以分加减总归于去烦就简故率除首
列同乘减尽一数而其馀则名类相同者减之相异者加

之其最繁者亦视首列所主为用如首以同名减则其
下同减而异并首以异名减则其下异减而同并大要
与盈朒相近而又济盈朒之穷(旧名方程用前叠借互徵亦同头绪多者用此为便)
问鼎三彝二共重一百五十五两又鼎四彝五共重二
百六十五两鼎彝各重若干将二项左右对列各作三
段递互遍乘之又相对较之视其馀数以少除多而互
得其重如以彝乘则反得鼎重以鼎乘则反得彝重且
如以右鼎遍乘左行(鼎四得一十二彝五得一十五重二百六十五得七百九十五)以

左鼎遍乘右行(鼎三得一十二彝二得八重一百五十五得六百二十)各得数相
减两鼎数相等减尽不用两彝数减馀七又两重减馀
一百七十五以少除多七为法一百七十五为实除得
彝重二十五两以右中彝二乘之得五十两以减右总
馀一百零五两亦以右鼎三除得每鼎重三十五两

　　鼎三(以乘左行得一十二)彝二(得八)重一百五十五两(得六百二十)
鼎四(以乘右行得一十二)彝五(得一十五)重二百六十五两(得七百九十五)

　　右法若以彝遍乘其以七为法亦同所得减馀之实

凡二百四十五以法除之先得每鼎三十五两以右
鼎三乘之得共鼎一百五两以减右行重数馀一百
两为二彝重数若以左彝四乘之得共鼎一百四十
两以减左行重数馀一百二十五两为五彝重数

　　问纱三匹绢四疋共价四两八钱又纱七疋绢二疋共
价六两八钱纱绢各价若干亦将二项左右列之各三
段遍乘如以右纱遍乘左行(纱七得二十一绢二得六价六两八钱得二十两四
钱)左纱遍乘右行(纱三同上绢四得二十八价四两八钱得三十三两六钱)各得数

对减其两纱减尽不用两绢减馀二十二为法两总减
馀一十三两二钱为实以法除实得绢每疋价六钱就
以右绢四乘得共价二两四钱以减右总价尚馀二两
四钱为右纱三疋之价得每疋价八钱

　　纱三(与左乘得二十一)绢四(得二十八)共四两八钱(得三十三两六钱)
纱七(与右乘得二十一)绢二(得六)共六两八钱(得二十两四钱)

　　右式若以绢遍乘其法同前但减馀之实一百七十
六以法除之亦得八钱为疋纱之价以右纱三乘得

二两四钱以减右总价馀二两四钱为四绢之价若
以左纱七乘得五两六钱就减左总价馀一两二钱
为二绢之价

　　问笔三管换砚七个贴砚价四百八十文别以砚三个
换笔九管贴笔价一百八十文笔砚各价几文依前左
右三行列之而以砚为正笔为负互乘得数却于正负
同名者对减异名者对加求之

　　砚正七(正二十一)笔负三(负九)价正四百八十文(正一千四百四十)

砚正三(正二十一)笔负九(负六十三)价负一百八十文(负一千二百六十)

　　右砚正七乘左(砚正二十一笔负六十三价负一千二百六十)左砚正三亦乘
右(砚正同上笔负得九价正一千四百四十)得数两砚正同名减尽两笔负
同名减馀五十四为法两价正负异名加并得二千七
百为实以法除实得五十文为一笔之价取右行笔负
之三乘之得一百五十加入价正四百八十共六百三
十即右砚七个总价以七除得九十文为一砚之价若
取一笔之价以左行笔负之九乘之得四百五十则当

就内减总一百八十馀二百七十即左行三砚之价

　　若移置笔负为法遍乘者得异并之实四千八百六
十文以法除之(五十四)得九十文为砚价

　　问七钏九钗共重九两四钱钏重钗轻于中互换其一
轻重适等不知各重若干此依互换者列位一系六钏
一钗一系一钏八钗而中分其总重之数

　　钏六　　钗一　　　　四两七钱

　　钏一　　钗八(四千八)　四两七钱(二十八两二钱)

　　先以右钏六遍乘左行(钗八得四十八价四两七钱得二十八两二钱)次以左
钏一遍乘右行(钏一价四两七钱)对减馀四十七者为法馀二
十三两五钱者为实以法除实得五钱为一钗数以减
右行总重(四两七钱)馀四两二钱即六钏共数六除之得每
钏重七钱

　　若移用右行钏一左行钗八为法遍乘者得减馀之
实三十二两九钱以法除之(四十七)先得七钱为一钏
之重

　　问钱一万文以卖二马一牛则不足半马之价以卖一
马二牛则馀半牛之价其牛马价各若干此当以不足
半马者损为一马零二分马之一及一牛以馀半牛者
益之为一马及二牛零二分牛之一依法列之而以整
带零之法乘除之

　　马一匹二之一　牛一头　　　　　价一万文

　　马一匹(一匹二之一)　牛二头二之一(三头四之三)价一万文(一万五千)

　　先以右马遍乘左行(马一匹二之一牛三头四之三价一万五千)次以左马遍

乘右行(马如上牛二价一万文)其两马减尽两牛减馀二头又四
之三为法两价减馀五千文为实以法除实得一千八
百一十八文又十一之二为牛价以减右行总价(一万文)
馀八千一百八十一文又十一之九以马一匹又二之
一除之得五千四百五十四文又十一之六为马价
问甲乙二窖积粟不知各几何但云取乙三之一与甲
及取甲二之一与乙则各满二千石其原窖几何此零
法照前列位互乘甲得六千乙得四千减馀二千为实

而以两母相并得五为法除之得四百以乙母之三乘
之得一千二百石为乙窖原粟馀八百石以甲母二乘
得一千六百石为甲粟其必各以母乘者盖前所除得
只是子数必归母见整故也

　　甲二之一　　　　二千石(六千)

　　乙三之一　　　　二千石(四千)

　　问治地不知亩数每工种麦三畦种菽四畦共三百零
一工其菽麦数并工数各若干此为双头单脚互乘取

三四左右列之并得七为法其下列工数

　　麦三畦

　　菽四畦

　　若求菽数者右三乘总工(九百三)以法除得一百二十九
为菽畦以四乘得工五百一十六即以右三除得麦畦
数若求麦数者左四乘总工(一千二百四)以法除得一百七
十二为麦畦以三乘得工数如前亦以左四除得菽畦
问犒夫不知数但云二人共饭三人共酒四人共肉总

用饭酒肉六十五分计夫若干列三位维乘(二乘三得六又三乘
四得一十二又四乘二得八)并得二十六为法另用乘并之法(二乘三得
六以乘四得二十四)得数以乘总分(六十五)　二人

　　得一千五百六十为实　三人　六十五分

　　以法除得六十为夫数　　四人

　　问银二百六十四两买牛羊共一百牵每牛三头价二
十两每羊四羫价一两五钱内牛羊并价各若干以牛
羊各价依子母左右列之互乘得数(牛乘羊四两五钱羊乘牛八十两)

减馀七十五两七钱为法另列总牵总价于下如求牛
数者先以羊四乘总价(一千五十六)以羊价乘总牵(一百五十)减
馀(九百零六)为实以法除得一两二钱为牛衰以右位牛三
乘得三十六头以二十乘得共价二百四十两就总
内减牛数馀为羊数

　　牛三　　二十两

　　羊四　　一两五钱

　　若先求羊数者以牛三乘总价(七百九十二)以牛价乘总牵

(二千)减馀(一千二百零八)为实亦以法除之得一十六为羊衰以
左位羊四乘得六十四羫以一十五乘得二十四两就总
内减羊亦得牛数

　　问用匠五千名包砖板堤共四千九百九十五方定
限每日匠九名包板堤十一方匠七名包砖堤四方
砖板堤匠各若干以母子左右对列互乘得数(九乘四得三十
六七乘十一得七十七)减馀四十一为法另列总匠总堤于
下

　　九名　十一方

　　七名　四方

　　若求板堤数者左七乘总方(三万四千九百六十五)四乘总匠(二万)
减馀(一万四千九百六十五)为实以法除之得三百六十五为板
衰以乘右九得板匠三千二百八十五名以乘十一得
板堤四千一十五方于总内除板堤馀皆砖数或求砖
堤数者右九乘总方(四万四千九百五十五)十一乘总匠(五万五千)减
馀(一万零四十五)为实以法除之得二百四十五为砖衰以乘

左七得砖匠一千七百一十五方以乘四得砖堤九百
八十方于总内除砖堤馀即板数

　　问七人醵金不知总数亦不知各数第云甲乙共二十
三两七钱戊己庚共二十六两一钱亦不知丙丁共数
此七人各若干法先求隔母且以甲乙二列左戊己庚
三列右取右衰三增一为四(与后章求隔母法同)仍以右衰(三)乘
之得数(十二)减半(六)又减去右衰(三)馀三为右中率取左
衰(二)乘总位(七人)得数(十四)内减右衰(三)馀十一为左中率

而各以共金数列其下

　　右三　三　　　二十六两一钱

　　左三　一十一　二十三两七钱

　　乃以左二遍乘右(中三得六下二十六两一钱得五十二两二钱)以右三遍乘
左(中十一得三十三下二十三两七钱得七十一两一钱)各得数相减中馀二十
七为法下馀一十八两九钱为实以法除实得七钱为
隔母之数别取甲乙共数(二十三两七钱)并入隔母七(得二十四两七
钱)减半得一十二两二钱为甲金数内减差数七得十

一两五钱为乙金数其馀以七递减各得(丙十两八钱丁十两一钱
戊九两四钱己八两七钱庚八两)

　　问竹筒一茎九节下大上细下三节共盛粟三升九合
上四节共盛粟三升中二节不知数要见每节盛粟若
干亦先求隔母数为逐节相较之率取上三列左下四
列右以右四加一为五与右四相乘得数(二十)减半(一十)又
减右四得六为右中率别以左三乘总位(九)得数(二十七)
内减右中率六得二十一为左中率各以所共盛之数

从之

　　右四　　六　　　三升

　　左三　　二十一　三升九合

　　乃以左三遍乘右(中六得一十八下三得九分)以右四遍乘左(中二十一
得八十四下三升九合得一十五分六釐)得数相减中馀六十六为法下馀
六十六为隔母率别以左三共粟为实(三升九合)以法(六十六)
乘之(得二百五十七分四釐)以三除之(因系三节故也)得八十五分八釐
是第八节数加母率(六分六釐)得九十二分四釐是第九节

数若减母数(六分六釐)得七十九分二釐是第七节数其馀
递减母率(第六节得七十二分六釐第五节得六十六分第四节得五十九分四釐第三节得五十
二分八釐第二节得四十六分二釐第一节得三十九分六釐)而仍以法除之(第一节六合第
二节七合第三节八合第四节九合第五节一升第六节一升一合第七节一升二合第八节一升三合第九
节一升四合)其以中馀(六十六)为法下馀为实以法除实者得
一合为隔母率以三除左总(三升九合)得一升三合为第八
节数以一合加减之亦得第七节第九节数以次推之
同前

　　问四雀六燕七鹪共集于衡重八钱九分又三雀五燕
九鹪共重八钱一分又五雀七燕八鹪共重一两六分
三禽各重若干法置左右中三行三色及总重作四段
列之先以右行五雀遍乘中行(雀一十五燕二十五鹪四十五共重四两零五)

　　再置前图减馀而以右燕四遍乘左行左燕二亦乘右行

　　馀四燕　馀廿一鹪(四十二)共馀八钱七分(一两七钱四分)

　　馀二燕　馀三鹪(十二)　　共馀二钱一分(八钱四分)

　　乘讫对减鹪馀三十为法共重馀九钱为实以法除实
得三分为一鹪之衡就以乘左馀鹪三得九分以减左

重馀一钱二分为二燕之衡即知每燕重六分也(既得一鹪
之衡以乘右馀鹪二十一及减右重亦得每燕六分)乃于前左行原价八钱九分
之内减去原鹪七(二钱一分)原燕六(三钱六分)各重数其馀三钱
二分以雀四除之得雀重八分(或于前右行中行原数内减乘皆同)

　　问牛一头马一匹驴三匹皆载物七百斤上坡皆不能
上牛借马一匹马借驴一匹驴借牛一匹方上其三等力
各若干列左中右三行以三畜及总物为四段

　　正牛一　借马一　　○　　　　七百斤

　　○　　　正马二(二)　借驴一(一)　七百斤

　　借牛一　○负一(二)　正驴三(六)　七百斤(一千四百斤)

　　先右行正牛一遍乘左行得数又以左行借牛一遍乘
右行得数(乘借马一一如一乘物仍七百斤)对减尽因左行中○无减
乃仿右马乘出之数为立负马一以俟另乘次以中行
正马二遍乘左行中下得数(负一得二原驴得六下物一千四百斤)复以
左行负一为法遍乘中行中下得数(正马得二借驴得一下物仍七百斤)
以对减正负马同名减尽正借驴异名相并得七为法

下物同名相减馀七百斤为实以法除实得驴力一百
斤取中行物实(七百)内减一驴之力馀六百即二马之力
以二除得每马三百斤又于右行物实(七百)亦减一马之
力馀四百即一牛力右法或更置其位先求一马之力

　　借驴一　正马二(左六)○　　　七百(二千一百左减馀一千四百)

　　○　　　借马一(六)正牛一(六)七百(四千二百左减馀三千五百)

　　正驴三　○负六(六)借牛一(一)七百(七百)

　　先以右行借驴一遍乘左行中下得数亦即以左行正

驴三遍乘右行中下得数(正马得六下物二千一百)因左马空○乃
如右马乘得之数亦置负六相减三畜俱减尽下物馀
一千四百次以中行借马一遍乘左行中下得数而以
左行负六遍乘中行中下(借马六正牛六下物四千二百)牛数正借异
名以相并得数七为法下物中左同名相减得三千五
百又以右下馀物减之得二千一百为实以法除实得
三百斤为一马之力然后取右行物实减二马力馀一
百见一驴之力又取左行物实减三驴之力馀四百见

一牛之力

　　问朱二斤黄三斤价钱二千四十文又黄五斤碌六斤
价六百四十文朱三斤碌七斤价二千九百八十文三色
各价若干依式左右中列之

　　朱二　黄三(九)　○　　　价二千四十文(六千一百二十)

　　○　　黄五(四十五)碌六　　价六百四十文

　　朱三　○负九(四十五)碌七(一十四)价二千九百八十文(五十九百六十)

　　先以右行朱二遍乘左行得数(碌得一十四价得五千九百六十)次以

左行朱三遍乘右行得数(黄得九价得六千一百二十文)于左行○位
照右立负九而与右行相对三色俱减尽其价馀一百
六十文又以中行黄五另列右遍乘左行(碌七十价得八百)以
左行负九另列左遍乘右行(碌得五十四价得五千七百六十)

　　黄五(四十五)碌六(五十四)　　价六百四十(五千七百六十)

　　○负九(四十五)碌馀一十四(七十)价馀一百六十(八百)

　　以相减黄与○同数减尽碌系正负异名并得一百二
十四为法两价同名相减馀四千九百六十为实以法

除实得四十文为碌一斤之价乃于前图中行原价内
减碌六斤价(二百四十)馀四百文悉黄价以黄五除之得每
斤价八十文又于右行原价减黄三斤价(二百四十)馀一千
八百文悉朱价以二除之得每斤九百文

　　问雁二雉三换谷五斗七升雁五兔四换谷一石雉二
兔二换谷五斗三升每色每个价谷若干先以右行雁
二遍乘左行得数(雁一十兔八谷二石)亦以左行雁五遍乘右行
(雁一十雉十五谷二石八斗五升)以相减雁尽系○照立负十五兔无

减仍八谷馀八斗五升

　　雁二　雉三(左一十五)○　　　谷五斗七升(左二石八斗五升)

　　○　　雉三(左四十五)兔二(左三十)谷五斗三升(左七石九斗五升)

　　雁五○负十五(中四十五)兔四(右八中二十四)谷一石(右二减馀八斗五升中乘二石五斗五升)
另以中行雉三遍乘左行中下(雉负四十五兔二十四谷二石五斗五升)左
行雉负遍乘中行中下(雉四十五兔三十谷七石九斗五升)以相对雉减
尽兔系正负异并得五十四为法价榖同名相减馀
五石四斗为实以法除实得一斗为一兔价就于中行

谷内减二兔价馀三斗三升悉雉价以中雉三除之得
每雉一斗一升即于右行谷内减三雉价馀二斗四升
悉雁价以右雁二除之得每雁一斗二升

　　问卖二牛五羊买十三豕馀价银五两卖一牛一豕买
三羊适足卖六羊八豕买五牛不足三两各价若干此
以卖为正买为负馀为正不足为负而正为主则同减
异并负为主则同并异减如前求之列左右中三
行以右行牛二遍乘中行得数(牛正二羊负六豕正二)其中

行牛一亦遍乘右行(牛二同正减尽羊正五与中行负六异名并得负十一豕
负十三与中行豕正二系异名并得正十五价正五中空无减)又右行牛二遍乘
左行(牛十羊十二豕十六价六)其左行牛五亦遍乘右行(牛十正负
异名减尽羊正二十五与左正十二同名并得正三十七豕负六十五异减豕正馀得负四十九价正二
十五异减左负馀负一十九)依法或减或并讫

　　牛正二(中二　左一十)羊正五(中五　　左二十五)豕负十三(中十三　左六十五)正五两(中五　　左二十五)

　　牛正一(右二)羊负三(右六)豕正一(右二)　○足

　　牛负五(右一十)羊正六(右十二)豕正八(右一十六)负三两(右六)

　　乃别列减并之数仍分正负互乘之如后图羊负十一
为法以乘左行中下(羊正得四百零七豕负得五百三十九价负得二十两九钱)亦
以羊正三十七而乘右行中下(羊负同数异名减尽豕正得五百五十五与左
豕负异名减馀一十六价正一十八两五钱与左异减馀二两四钱)以减馀豕正一十六
为法价正二百四十为实以法除实得豕价一两五钱
就以右行豕正十五乘(二十二两五钱)加正价(五两)共二十七两
五钱俱羊价以十一除之得每羊二两五钱复以前图
右行豕负十三乘豕价得数(一两五钱)加入正价(五两)共二十

四两五钱为牛羊总价内减右行五羊之价(一十二两五钱)馀
一十二两悉牛价以牛二除之得每牛六两

　　羊负一十一　豕正一十五(五百五十五)价正五(一十八两五钱)

　　羊正三十七(四百七)豕负四十九(五百三十九)价负一十九(二十两九钱)

　　问买柰二梨四共钱四十文梨二桃七亦共钱四十文
桃四榴七共钱三十文梨八柰一共钱二十四文各价
几文列甲乙丙丁四行每行五段先以甲丁柰为法彼
此互乘以甲柰二遍乘丁(梨空桃空榴一十六钱四十八文)丁柰一遍

乘甲(桃榴俱空钱仍四十文对减馀八文)因丁梨空当照甲立负四次当
以乙丁柰互乘乙无柰取梨二遍与丁乘(梨负得八桃空榴三十二
钱一十六文)丁亦以负梨四遍乘乙(梨八减尽桃二十八榴空钱一百六十文并得
一百七十六文)因丁桃空亦照乙立负二十八次以丙桃遍乘
丁(桃一百一十二榴一百二十八钱七百零四文)丁亦以桃负二十八遍乘丙
(桃一百一十二减尽榴一百九十六减馀六十八钱八百四十文减馀一百三十六)相减讫取此
馀榴六十八为法馀钱一百三十六文为实其甲乙与
丁互乘之数但求应立负数以为乘母而减并之数皆

置不用者也以法除实得二文为榴价乃就丙价三十
文内减七榴之价(十四)馀钱一十六文俱桃价以四除得
每桃四文又于乙价四十文内减七桃之价(二十八文)馀钱
一十二文俱梨价以二除得每梨六文又于甲价四十
文内减四梨之价馀一十六文俱柰价以二除得每柰
八文

　　甲柰二　梨四　○　　　○　　　四十文

　　乙○　　梨二桃七(二十八)　○　　　四十文

　　丙○　　○　　桃四　　榴七(一百九十六)三十文(八百四十文)
丁柰一　○负四(八)○负二十八　榴八(一十六　　一百二十八)二十四文(四十八文)

　　问井不知深用甲绳二不及泉借乙绳一补之
及泉用乙绳三则借丙一用丙绳四则借丁一
用丁绳五则借戊一用戊绳六条则借甲一乃
俱及泉其井深若干五等绳各长若干列五行
以五绳之数为母借绳一为子先取甲二乘乙
三得六以乘丙得二十四以乘丁得一百二十

以乘戊得七百二十并入子一共七百二十一
为井深积列位

　　一　甲二　乙一　○　　○　　　　　七百二十一

　　二　○　　乙三　丙一　○　　○　　七百二十一

　　三　○　　○　　丙四　丁一　○　　七百二十一

　　四　○　　○　　○　　丁五　戊一　七百二十一

　　五甲一　　○(负一)　○(负一)○(负一)戊六　七百二十一

　　乃取五行为主而以一二三四俱与相乘先以一行甲

二为法遍乘五行(甲一得二戊六得十二积七百二十一得一千四百四十二)五行
甲一亦乘一行对减(甲二得二减尽乙一得一因五行乙空立负一积七百二十一得本
数以减五行仍馀七百二十一)次以二行乙三为法乘五行(乙负一得负三戊正
十二得三十六积七百二十一得二千一百六十三)五行乙负一亦乘二行(乙三得三
对减尽丙一得一因五行丙空立负一积七百二十一得本数并入五行积二十一百六十三共二千八百八
十四)再以三行丙四为法乘五行(戊正三十六得一百四十四积二千八百八十
四得一万一千五百三十六)五行丙负一亦乘三行(丙四得四减尽丁一得一因
五行丁空立负一积得本数与五行积一万一千五百三十六对减馀一万八百一十五)又以四行

丁五为法乘五行(丁负一得五戊正一百四十四得七百二十积一万八百一十五得五万
四千七十五)五行丁负一亦乘四行(丁五得五减尽戊一得一并入五行戊正七百二十
共七百二十一积得本数并入五行积五万四千七十五得五万四千七百九十六)乃以最后所
得求之以积五万四千七百九十六为实戊七百二十
一为法除之得戊绳七尺六寸以减四行总积(七百二十一)
馀六百四十五以丁五除之得一百二十九为丁绳一
丈二尺九寸以减三行积(七百二十一后同)馀五百九十二以
丙四除之得丙绳一丈四尺八寸亦减二行积馀五百

七十三以乙三除得乙绳一丈九尺一寸以减一行积
馀五百三十以甲二除得甲绳二丈六尺五寸

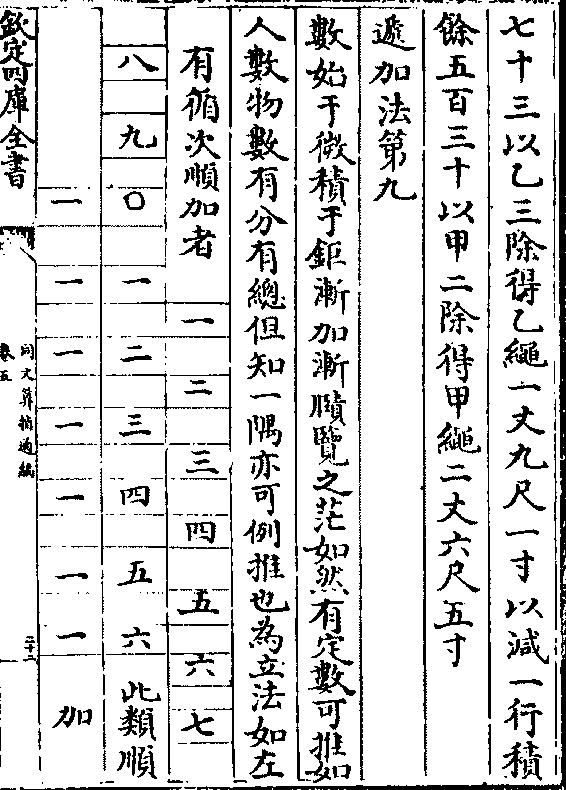
　　递加法第九

　　数始于微积于钜渐加渐赜览之茫如然有定数可推如
人数物数有分有总但知一隅亦可例推也为立法如左

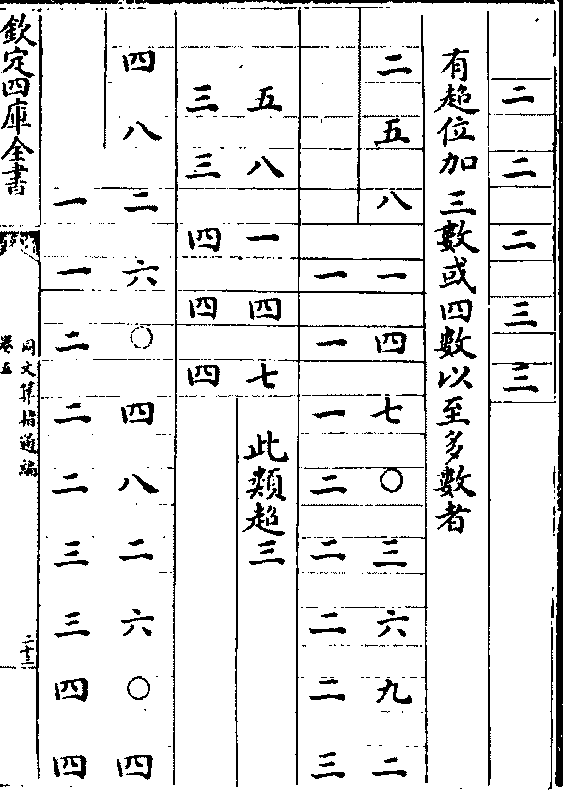
　　右超位加各审其母如超一超二超三四之类各以所超
为母其间少者易知多者难定大率以退位减之馀数即
母

　　凡超位数截取三位较之其前后二位数必倍于中位数

　　若截四位较之则前后二位与中二位数等

　　以上皆取位置匀列超母相同者论之虽所超多位如超
五超六至千万位但同超母者截取前后远数相并较其
进内挨身两位相并其数皆等

　　右凡加数以求总积之实不论累加超加及超二超三
等但系递加者只除首位单一不用外取次位与末位
数并为实其中间亦不拘几位但察自前至后布位之
数为法乘之所得之数皆倍各位实积之数以减半得
总数如右式以前四后三十七并之共四十一数系一
十二位以一十二乘四十一得四百九十二减半为二
百四十六即其十二位之全数若以前四后十六并之

共二十数系五位乘得一百减半得五十即五位全数
也(如欲连首位算则再加一云)

　　此超八

　　递加者

　　右式假如方箭一束外周六十四枝问中积数几何者
凡方物必以八包一每层超八递加今置中心一枝不
算(即首位之一)以内层之八并外周六十四共七十二以八
位乘之得数(五百七十六)减半得八位之总数加中心之一

为二百八十九枝凡平方面有中心之一者仿此

　　此超六递加者



　　右式假如圆箭一束外周三十六枝问中积者凡圆物
必以六包一每层以六递加今置中心一枝不算外以
内层之六并外周三十六共四十二以六位乘之得数
(二百五十二)减半得六位之总数再加中心之一为一百二
十七枝凡平圆面仿此

　　此超九

　　递加者

　　右式假如有三棱物一束外周七十二枝问积者凡三
棱物必以外九包中一每层超九递加置中心一枝不
算外以内层之九并外周七十二共八十一以八位乘
之得数(六百四十八)减半得八位之总数再加中一为三百
二十五枝凡三棱面者仿此

　　若顺数而加自一而二而三而四以递相加者另是一

法但取最后二大数相乘得数亦以减半即得最后第
二位以至首位之数惟馀最后第一位在外又并入得
全数




　　右式假如有物倚墙一面尖堆最下一行阔十五枚问
总积若干取最下二行(一十五一十四)相乘得数(二百一十)减半(一百

○五)又加入下行十五得一百二十枚合总

　　一法取下行加一为法以乘下行得数减半亦同

　　若首位不系一数而自二数或三或四为首者并首尾
二位为实而以首位数减尾位数其馀数加一为法乘
之减半合总

　　假如有物倚墙一面平堆下阔十四枚上阔四枚问总
积者并首尾二位得一十八为实就尾位减首位得一
十外加一共一十一乘之盖原系十一位也以乘得数

(一百九十八)减半得九十九枚合总

　　又假如众人醵钱首位出八文末位出六十文问总数
总人者以首位减末位馀五十二外加一系五十三位
乃并首尾二位钱数以乘五十三得三千六百四文合
总

　　若自一而三而九俱以阳数超加者但看位数以自乘得全
数

　　此皆阳位但据位数自乘如系一十位自乘得一百之
类其阳数超加已知首尾两位之数而未知中间若干
位者但取尾位之数外加一以减半得位数如右式尾
位十九加一得二十减半则十位也但系阳数虽至百
千万位皆同此法

　　若自二而四而六俱以阴数超加者取最后一位之数
减半即得位数再以减半数外加一而与位数相乘即
得自首至尾全数

　　四　取二十四减半见位数又减半加一为十三

　　二　以乘位数十二得一百五十六见全数

　　又若自二数起递加至一百数止但取一百减半知是
共五十位再加一为五十一以乘位数五十得二千五
百五十即五十位之全数

　　若多中起数超位递加但知位数及首位数及所超母

数而未知最后一位数者但审布位若干于内减一以
乘超母(如超一则一为母超八则八为母之类)得数加入首位数即得尾
位之数既得首尾二位乃照前首尾相并而以位乘减
半得全数


　　此超八递加者计十位减一为九与八相乘得七十
二再加首位三得七十五为末位数又以七十五加

三得七十八以乘十位得七百八十减半三百九十合
全数

　　假如有牛四十区但云第一区是三十头馀区递加二
十头今问第四十区几头依前法就四十减一为三十
九与超母二十相乘得七百八十再加首区三十知是
八百一十乃最后一区之数也再问各区总数几何照
法以首区三十加末区共八百四十以乘区数四十得
三万三千六百减半得一万六千八百头为各总数

　　若但知末区数及母数位数而不知首区数者照前以
区数减一与母数相乘得数而以末区数减之即得首
区之数(如前乘得七百八十而末区系八百一十相差三十即知首区系三十头)




　　假如发兵破一贼巢有二十人先登以登城先后叙赏
其第二十人赏银一百两第十九人赏一百三十两其

馀递加三十两问第一人该银几何此以二十为位减
一为十九以乘超母三十得五百七十再加尾位一百
得六百七十两为第一人所赏之数也若问此二十人
共银几何照法并首尾二数得七百七十与位数二十
相乘减半得七千七百两见全数

　　若但举总数及超数及首尾共数而不知系几位亦不知首
尾二位数各若干者以总数为实以首尾数减半为法除
之得位数又以位数减一乘超母得数即用此数为主若

　　以并首尾共数减其半即尾数若

　　以较首尾共数减其半即首数

　　右式假如贷钱起息每日增钱六文共积子母钱三百
二十文不言每日细数但云并初末日共钱一百六十
文问初末日各几文其起息计几日者以日为位立总
钱三百二十为实并初末减半得八十除之得四日依
法减一为三乘增母之六得一十八以并初末数得一
百七十八减半是末数若以较初末数馀一百四十二

减半是初数

　　若但举中积及位数及首尾之较若干以求首尾各几
何者倍中积为实以位为法除之得数以较减之半其
馀得首数乃以较加之得尾数



　　右假如织布自冬至始历十三日共织一千三百五十

二寸因晷渐长其功日加六寸末日视首日多织七十
二寸问首日末日各织几许者倍中积得二千七百四
寸为实以积日十三为法除之得二百零八以较减之
得数又减半合首数六十八以较并入亦减半合末数
一百四十

　　若但知位数总数及超母数而未知每位得若干数者
取位数列之去尾数馀并之(如系九位则但用一二三四五六七八共三十六数
除九不用)以乘超母得数减总乃以位数归其馀得首位数

乃以超母递加得各位细数


　　假如兄弟九人递差三岁共二百○七岁欲知每人几
何者照右法置母数(三)乃取位数内除去尾数九只以
八位细数并之得三十六以乘母得数(一百零八)以减总数
馀九十九以九除之得最幼一人岁数(一十一)乃以三递
加之得诸人岁数

　　共八位以一十

　　七为超母总数

　　九百九十六

　　假如钞九百九十六锭分给八人递差一十七锭各若
干取位数除去尾八并自一至七之数共二十八以乘
超母一十七得数(四百七十六)以减总馀五百二十以八除
得最少一人数(六十五)仍以一十七递加得诸人数

　　若超位递加但知系几位及各位总数而未知超母几

位亦未知各位细数与首尾二位数第云前几位共若
干后几位共若干以求各位细数者依母子互乘法求
之以所知前几位后几位为母以前共若干后共若干
为子互乘得数相较为实又并其母减半以较总位馀
若干而以两母相乘之数乘之得数为法以法除实得
超母加入所知之数如系二位者加入折半得多者数
如系三位者加入三归得中数乃依超母递加递减得
全数

　　假如八人差等分钱但知甲乙共七十七文己庚辛共
六十六文问每人几文者以二人乘六十六(得一百三十二)以
三人乘七十七(得二百三十一)以相较馀九十九为实并分母
(二三)得五减半得二零二之一以减总位(八)馀五零二之
一仍以分母所乘之六乘之得三十三为法以法除实
得三为超母之数并入甲乙减半得四十为甲衰若求

己庚辛则三归之得中间之庚衰乃以超母递加递减
得全数○外如系戊己庚辛四位者三归之得己庚共
数又加减超母之半得己庚数

　　倍加法第十

　　数有挨次递加者以一数为递母而累加之其母不易
焉另有以倍而加者

　　右法皆取乘法如第一式倍一加者以二一见二以二
二见四以二四见八以二八见十六也第三式倍一加
者以二三见六以二六见十二也第二式倍三加者以
三三见九以三九见二十七以三个二十七见八十一
也此由少进多之法假如欲寻其母则取挨身小数减
其大数知之以二减尽者倍一也以三减尽者倍二也

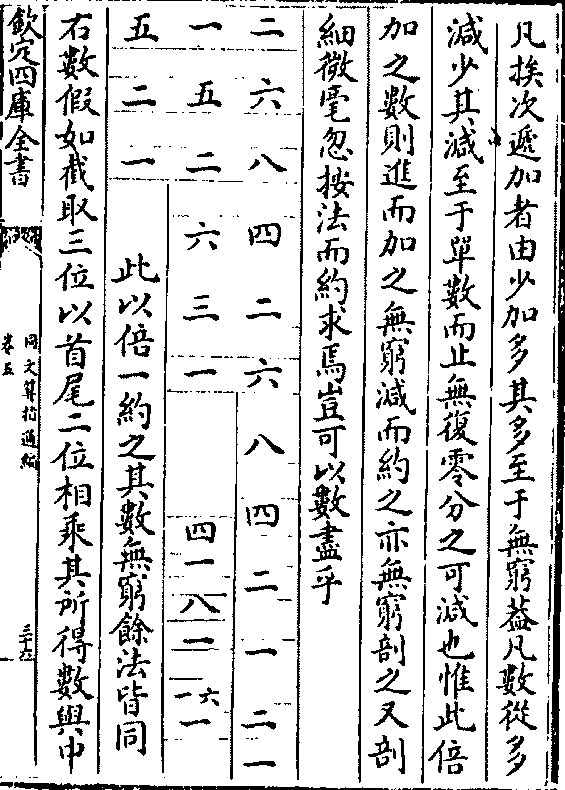凡挨次递加者由少加多其多至于无穷盖凡数从多
减少其减至于单数而止无复零分之可减也惟此倍
加之数则进而加之无穷减而约之亦无穷剖之又剖
细微毫忽按法而约求焉岂可以数尽乎



　　此以倍一约之其数无穷馀法皆同

　　右数假如截取三位以首尾二位相乘其所得数与中

一位数之自乘者等(假如八四二共三位以二八相乘得十六以中间之四自乘亦十六)
若截取四位而以首尾二位相乘其所得数与中二数
相乘者亦等(假如十六○八○四○二○共四位以十六乘二得卅二以中间之八与四乘亦得卅二)
虽至许多位但以首尾二位相乘其所得数与挨身次
二位俱相等步步乘入皆无不同至于最中若有单位
以之自乘亦复如是

　　此外乘与进

　　内乘皆同中

　　单自乘亦同

　　凡倍加之数不论几位欲知总数但取首尾二位为主
以首最小数减尾最大数而以其所剩大数依后法求之
如系加一倍者(即二因)先取尾大数倍之内减首数得全
数如一二四八(六二四一三六)此七位者取尾六十四倍得一
百二十八数减首位一得一百二十七即此七位之细
数(加一倍者自一起手用此法其加二加三者虽亦自一起手但各另有倍母则另如后法以倍母为首位
不以一为首位云)如系加二倍者(即三因法)取尾后最多数内先减

首位之数而以馀数二归(缘三因者系加二倍故以二为倍母而用二)取其
所得之数并入尾位大数即得中间几位细数凡四因
五因以至六七等类皆同此法而四因三归五因四归
(各减因数之一者依所倍之数为母也)馀皆同

　　此系四因者三

　　倍于本数以相

　　加也用尾位数

　　内减首位数实

　　剩四万九千一

　　百四十九以倍母之三除之得一万六千三百八十
三加入四万九千一百五十二共得六万五千五百
三十五是八位全数

　　又有加一倍又二之一递进者即四六衰分法也

　　此一因半

　　右四六衰分倍加系一因有半者若欲求其各位总数
亦取尾位数(四十五又十六之九)内减首位数(除四得四十一又十六之九)如
前法亦减除法一数(十一因半减其一也如前三因者用二及四因用三之类)而用
半以除之(以半为倍母以除之者是一化为二)得八十三零八之一以并
尾数总共得一百二十八零十六分之十一也为七位
细数

　　凡二因半三因半等类仿此其除法俱只减其一数

　　凡倍加数不论共有几位但就中抽取一位自乘但看

自首挨来是几位假如第五位其前有四位矣今以五
位自乘其所得之数即与此后第四位之数相同(即九位)
不特此也又如取第五位与第七位相乘其五位前凡
有四位则其第七位后亦管四位其五位七位乘得之
数即与第十一位之数相同如后式

　　假如后式十六系第五位前有四位后亦管到四位今
以十六自乘得二百五十六恰与后四位之数相同

　　又假如三十二系第六位前有五位

　　今以三十二自乘得一千二十四即合后第五位之数一
又假如八系第四位与七位之六十四相乘以八前凡
有三位则六十四之后亦管到三位今以八乘六十四
得五百十二数亦与第十位之数相合其相离亦三位故也
又法不必算其前后之位但看所自乘数为第几位以
本位数加一倍内减一即得同数之位假如第六位倍

六得十二内减一为十一位则第六位自乘所得之数
正合第十一之数与前法理同而更为捷径

　　又法不必减一但先排倍数于右次排位数于左相对
而于位前加一(即以○见所减之一)其馀以次察之

　　凡所得位数但系自乘者只一位以位数倍之但系互
乘者有两位以两位数积之

　　右式假如以四自乘得十六矣其四之本位是二位倍
二得四则十六之数即第四位之数也此一位自乘之法
又假如八乘三十二得二百五十六数其八之本位系
三位三十二之本位系五位三与五并共得八即系第
八位数　　以上乃首位起一者

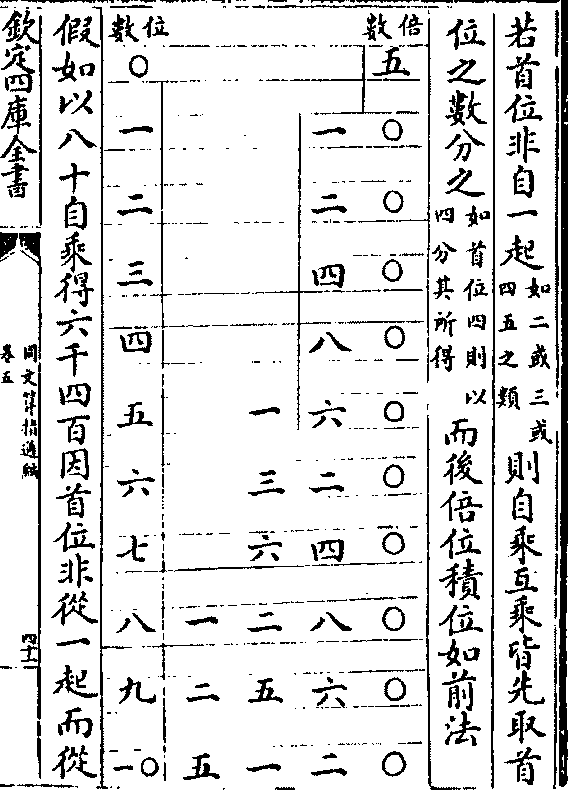　　若首位非自一起(如二或三或四五之类)则自乘互乘皆先取首
位之数分之(如首位四则以四分其所得)而后倍位积位如前法





　　假如以八十自乘得六千四百因首位非从一起而从

五起先以首位之五而分之得一千二百八十数仍取
列位之四倍之为八则对八之数

　　又假如以四十与六百四十相乘得二万五千六百以
首位之五分之得五千一百二十次以两位相积其一
是三其一是七合对十之数

　　凡倍一加者(即二因)就中随意截取一位以其本数减一
即合此位以前各位之细数此除本身而言然必从一
数起者合此

　　假如截取一百二十八数内减一得一百二十七数即
合第六位以前之总数盖自六位之六十四以前各位
细数总得此

　　又假如右式以对八位之二百五十六数而求本位以

前各位之总依前法以次位求之次位减一得五百一
十一乃对八以前各位细总也若就以此八位为主外
加一作五百一十二以自乘得二十六万二千一百四
十四数内再减一此何数乎按实对八之位乃系第九
位此前既有九位此后亦管九位乃是第十八位以前
各位细数也盖以倍位所对之本数自乘则得对位加
倍之本数此用倍位法看之如不以本数乘而以积出
本位以前诸位之全数乘则又推得本位以后相对若

千位之全数此则不用倍位而用实位得之者实位者
如本位前实有九位则本位后再管十位即其相对之
位之全数也须减一数始合不减一数则进越一位矣

　　假如借银一忽每日加息一倍至第六十四日该息几
何依前法推之试如一二四八此四位共十五数加一
自乘得二百五十六内减一馀二百五十五即系八位
之数盖自首位一至第八位之一百二十八其细数乃二
百五十五数也再以此加一(二百五十六)自乘得六万五千

五百三十六内减一馀六万五千五百三十五即知其
为第十六位之数再以此数加一得六万五千五百三
十六自乘得四十二亿九千四百九十六万七千二百
九十六内减一即知其为第三十二位之数凡四十二
亿九千四百九十六万七千二百九十五数又以之加
一自乘得一千八百四十四兆六千七百四十四万零
七百三十七亿又九百五十五万一千六百一十六忽
内减一即知其为第六十四值之数凡一十八兆四千

四百六十七亿四千四百零七万三千七百九两五钱
五分一釐六毫一丝六忽也





　　同文算指通编卷五